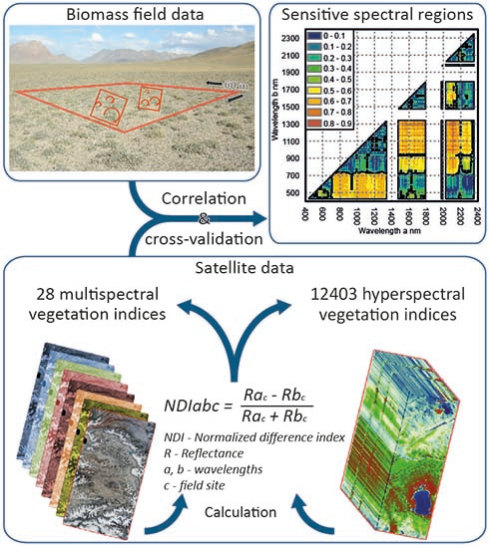
Potential of Space-Borne Hyperspectral Data for Biomass Quantification in an Arid Environment: Advantages and Limitations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Area

2.2. Data
2.2.1. Landsat OLI Data
2.2.2. Hyperion Data
2.2.3. Atmospheric Correction
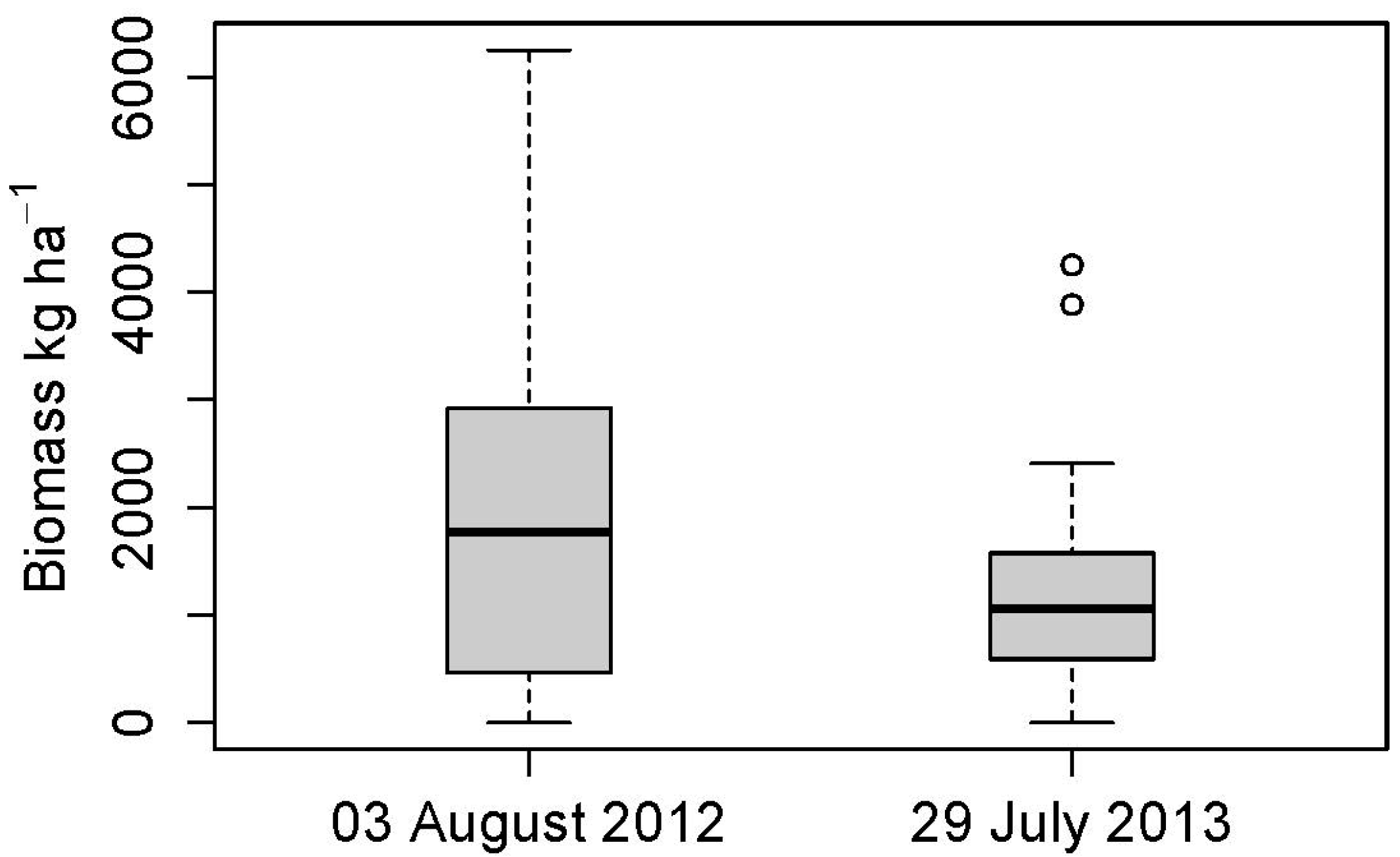
2.2.4. Field Data
2.3. Spectral Index Computation and Statistical Analysis
3. Results
3.1. Visual Comparison of Biomass-Index Correlations
3.2. Modeling Performance of Feature Sets
| Modeled Mean RMSE (kg∙ha−1) | Modeled Mean R2 | Modeled Mean Bias (kg∙ha−1) | Modeled Mean RMSErel (%) | |
|---|---|---|---|---|
| Hyperion western sites (H2012) | 1121 | 0.54 | −23 | 58 |
| Hyperion eastern sites (H2013) | 937 | 0.29 | 69 | 77 |
| Landsat OLI western sites (LS2013a) | 1528 | 0.15 | 11 | 78 |
| Landsat OLI eastern sites (LS2013b) | 973 | 0.16 | 53 | 80 |
3.3. Variable Selection Frequency of Indices
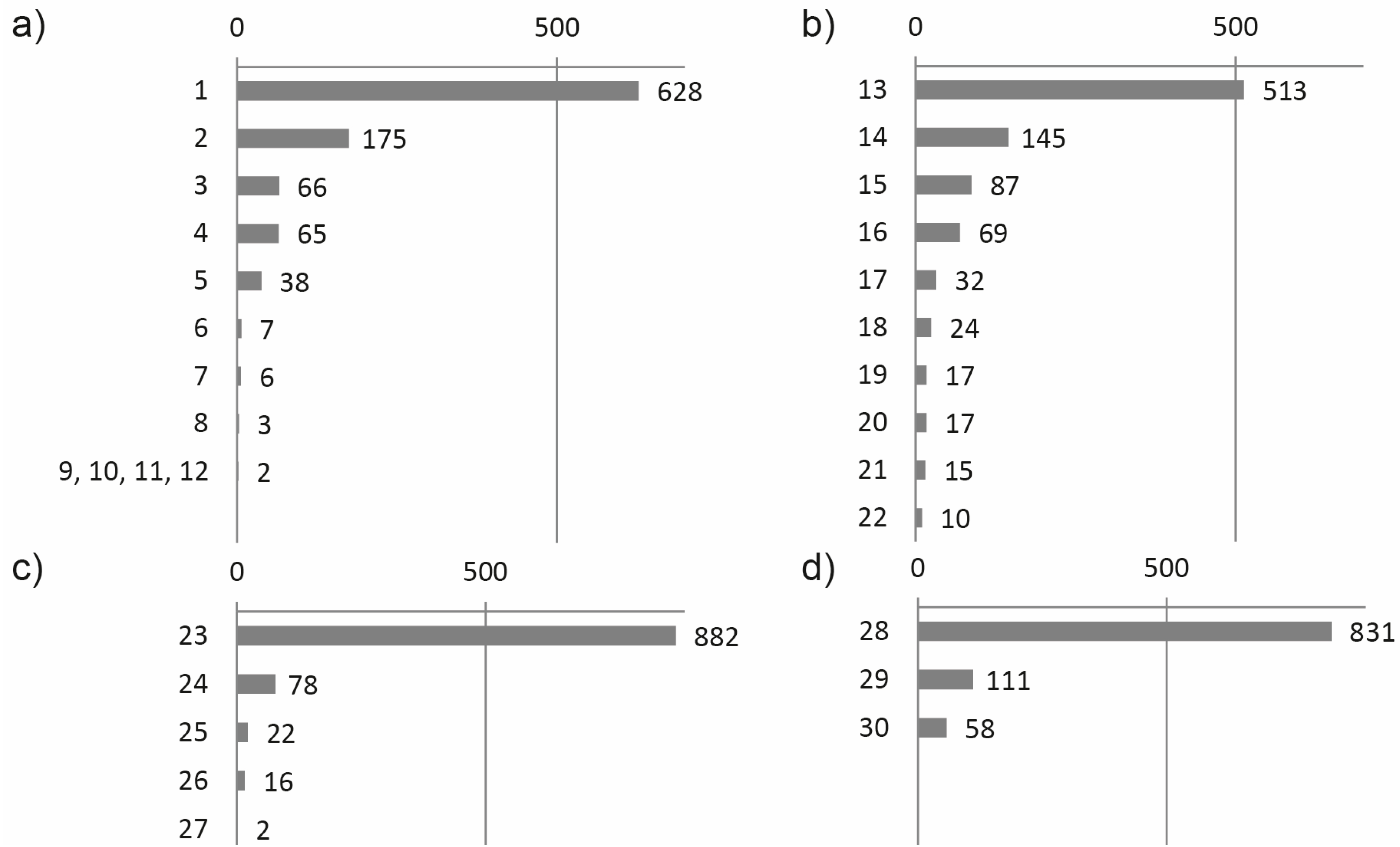
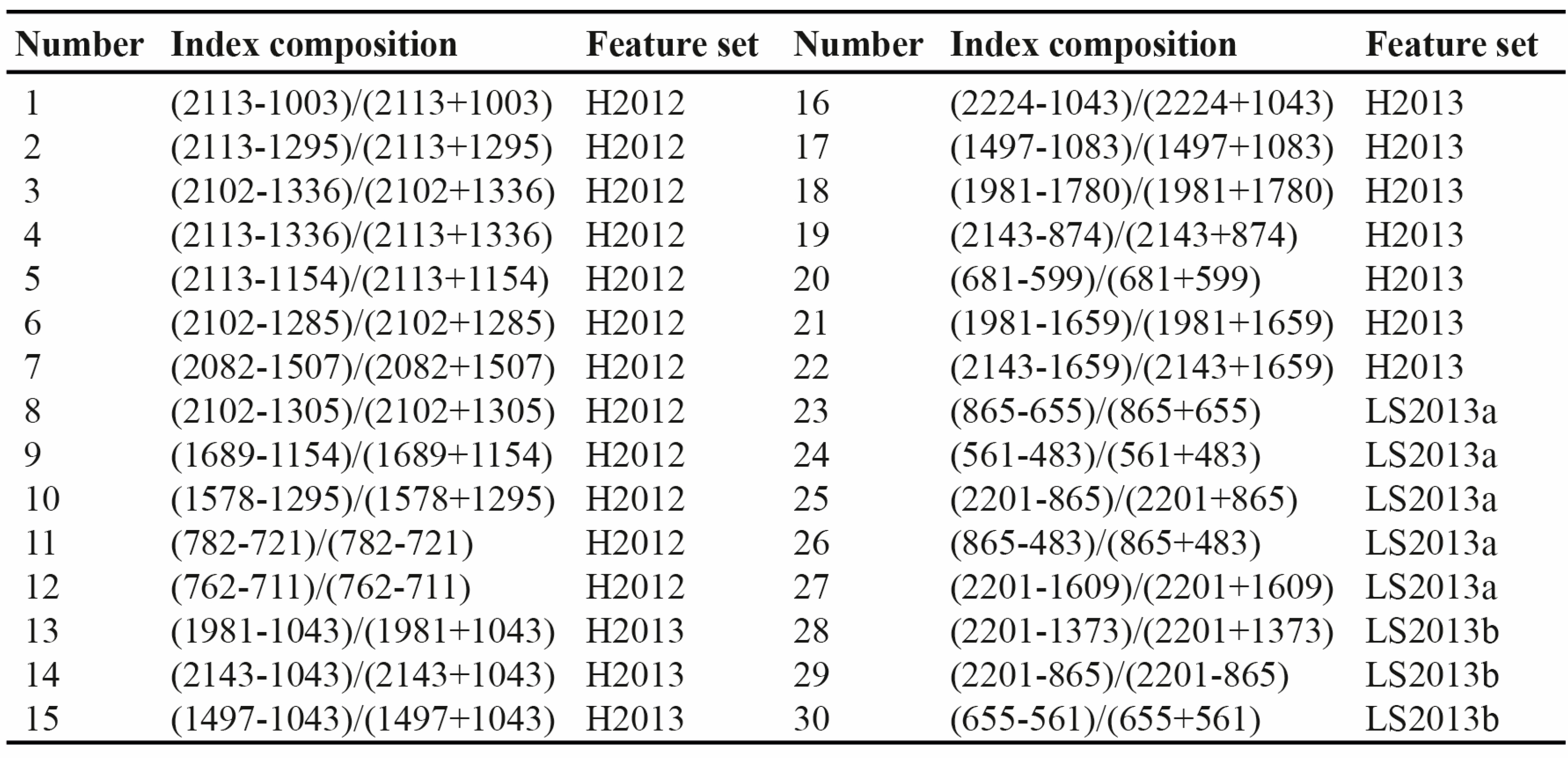
4. Discussion
4.1. Hyperspectral Indices for Dwarf Shrub Biomass Detection
4.2. Transferability of Spectral Indices Sensitive to Dwarf Shrub Biomass
4.3. Modeling Performance of Sensors
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sommer, S.; Zucca, C.; Grainger, A.; Cherlet, M.; Zougmore, R.; Sokona, Y.; Hill, J.; Della Peruta, R.; Roehrig, J.; Wang, G. Application of indicator systems for monitoring and assessment of desertification from national to global scales. Land Degrad. Dev. 2011, 22, 184–197. [Google Scholar] [CrossRef]
- Asner, G.P.; Green, R. Imaging spectroscopy measures desertification in United States and Argentina. Eos Trans. AGU 2001, 82, 601–606. [Google Scholar] [CrossRef]
- Eisfelder, C.; Kuenzer, C.; Dech, S. Derivation of biomass information for semi-arid areas using remote-sensing data. Int. J. Remote Sens. 2012, 33, 2937–2984. [Google Scholar] [CrossRef]
- Zandler, H.; Brenning, A.; Samimi, C. Quantifying dwarf shrub biomass in an arid environment: Comparing empirical methods in a high dimensional setting. Remote Sens. Environ. 2015, 158, 140–155. [Google Scholar] [CrossRef]
- Swatantran, A.; Dubayah, R.; Roberts, D.; Hofton, M.; Blair, J.B. Mapping biomass and stress in the Sierra Nevada using lidar and hyperspectral data fusion. Remote Sens. Environ. 2011, 115, 2917–2930. [Google Scholar] [CrossRef]
- Schwieder, M.; Leitão, P.; Suess, S.; Senf, C.; Hostert, P. Estimating fractional shrub cover using simulated EnMAP data: A comparison of three machine learning regression techniques. Remote Sens. 2014, 6, 3427–3445. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Enclona, E.A.; Ashton, M.S.; van der Meer, B. Accuracy assessments of hyperspectral waveband performance for vegetation analysis applications. Remote Sens. Environ. 2004, 91, 354–376. [Google Scholar] [CrossRef]
- Lewis, M.; Jooste, V.; de Gasparis, A.A. Discrimination of arid vegetation with airborne multispectral scanner hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1471–1479. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Chen, Z.; Groeneveld, D.P. Detection of trace quantities of green vegetation in 1990 AVIRIS data. Remote Sens. Environ. 1993, 44, 271–279. [Google Scholar] [CrossRef]
- Serrano, L.; Penuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in Mediterranean vegetation from AVIRIS data: Decomposing biochemical from structural signals. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Oldeland, J.; Dorigo, W.; Wesuls, D.; Jürgens, N. Mapping bush encroaching species by seasonal differences in hyperspectral imagery. Remote Sens. 2010, 2, 1416–1438. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Mariotto, I.; Gumma, M.K.; Middleton, E.M.; Landis, D.R.; Huemmrich, K.F. Selection of hyperspectral narrowbands (HNBs) and composition of hyperspectral twoband vegetation indices (HVIs) for biophysical characterization and discrimination of crop types using field reflectance and Hyperion/EO-1 data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 427–439. [Google Scholar] [CrossRef]
- Asner, G.P.; Wessman, C.A.; Bateson, C.; Privette, J.L. Impact of tissue, canopy, and landscape factors on the hyperspectral reflectance variability of arid ecosystems. Remote Sens. Environ. 2000, 74, 69–84. [Google Scholar] [CrossRef]
- Oldeland, J.; Dorigo, W.; Lieckfeld, L.; Lucieer, A.; Jürgens, N. Combining vegetation indices, constrained ordination and fuzzy classification for mapping semi-natural vegetation units from hyperspectral imagery. Remote Sens. Environ. 2010, 114, 1155–1166. [Google Scholar] [CrossRef]
- Okin, G.S.; Roberts, D.A.; Murray, B.; Okin, W.J. Practical limits on hyperspectral vegetation discrimination in arid and semiarid environments. Remote Sens. Environ. 2001, 77, 212–225. [Google Scholar] [CrossRef]
- Vanselow, K.A. The High-Mountain Pastures of the Eastern Pamirs (Tajikistan): An Evaluation of the Ecological Basis and the Pasture Potential. Ph.D. Thesis, Friedrich Alexander University, Erlangen-Nuremberg, Germany, 2011. [Google Scholar]
- Vanselow, K.; Samimi, C. Predictive mapping of dwarf shrub vegetation in an arid high mountain ecosystem using remote sensing and random forests. Remote Sens. 2014, 6, 6709–6726. [Google Scholar] [CrossRef]
- Tajik Met Service, Dushanbe, Tajikistan. Climatic data for the Pamir Region. 2013.
- Kraudzun, T.; Vanselow, K.A.; Samimi, C. Realities and myths of the Teresken Syndrome—An evaluation of the exploitation of dwarf shrub resources in the Eastern Pamirs of Tajikistan. J. Environ. Manage. 2014, 132, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Aster Global Digital Elevation Model, version V002; NASA LP DAAC/U.S. Geological Survey: Sioux Falls, SD, USA, 2009.
- Peña, M.A.; Brenning, A.; Sagredo, A. Constructing satellite-derived hyperspectral indices sensitive to canopy structure variables of a Cordilleran Cypress (Austrocedrus chilensis) forest. ISPRS J. Photogramm. Remote Sens. 2012, 74, 1–10. [Google Scholar] [CrossRef]
- Campbell, P.K.E.; Middleton, E.M.; Thome, K.J.; Kokaly, R.F.; Huemmrich, K.F.; Lagomasino, D.; Novick, K.A.; Brunsell, N.A. EO-1 Hyperion reflectance time series at calibration and validation sites: Stability and sensitivity to seasonal dynamics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 276–290. [Google Scholar] [CrossRef]
- Aqua AIRS Level 3 Daily Standard Physical Retrieval (AIRS+AMSU), version 006; NASA Goddard Earth Science Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2013.
- Justice, C.O.; Townshend, J.G. Integrating ground data with remote sensing. In Terrain Analysis and Remote Sensing; Townshend, J.G., Ed.; Allen and Unwin: London, UK, 1981; pp. 38–58. [Google Scholar]
- Fourty, T.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: Direct and inverse problems. Remote Sens. Environ. 1996, 56, 104–117. [Google Scholar] [CrossRef]
- Chen, Z.; Elvidge, C.D.; Groeneveld, D.P. Monitoring seasonal dynamics of arid land vegetation using AVIRIS data. Remote Sens. Environ. 1998, 65, 255–266. [Google Scholar] [CrossRef]
- Martin, M.E.; Aber, J.D. High spectral resolution remote sensing of forest canopy lignin, nitrogen, and ecosystem processes. Ecol. Appl. 1997, 7, 431–443. [Google Scholar] [CrossRef]
- Takahashi, T.; Yasuoka, Y.; Fujii, T. Hyperspectral remote sensing of riparian vegetation and leaf chemistry contents. In Proceedings of 23rd Asian Conference on Remote Sensing, Kathmandu, Nepal, 25–29 November 2002.
- Nagler, P.L.; Inoue, Y.; Glenn, E.; Russ, A.; Daughtry, C.S. Cellulose absorption index (CAI) to quantify mixed soil–plant litter scenes. Remote Sens. Environ. 2003, 87, 310–325. [Google Scholar] [CrossRef]
- Daughtry, C.S. Discriminating crop residues from soil by shortwave infrared reflectance. Agron. J. 2001, 93, 125–131. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 289–300. [Google Scholar]
- Asner, G.P.; Heidebrecht, K.B. Imaging spectroscopy for desertification studies: Comparing AVIRIS and EO-1 Hyperion in Argentina drylands. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1283–1296. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Enclona, E.A.; Ashton, M.S.; Legg, C.; De Dieu, M.J. Hyperion, IKONOS, ALI, and ETM+ sensors in the study of African rainforests. Remote Sens. Environ. 2004, 90, 23–43. [Google Scholar] [CrossRef]
- Serbin, G.; Hunt, E.R., Jr.; Daughtry, C.S.T.; McCarty, G.W.; Doraiswamy, P.C. An improved ASTER index for remote sensing of crop residue. Remote Sens. 2009, 1, 971–991. [Google Scholar] [CrossRef]
- Elvidge, C.D. Visible and near infrared reflectance characteristics of dry plant materials. Int. J. Remote Sens. 1990, 11, 1775–1795. [Google Scholar] [CrossRef]
- Elvidge, C.D. Examination of the spectral features of vegetation in 1987 AVIRIS data. In Proceedings of the First AVIRIS Performance Evaluation Workshop, Pasadena, CA, USA, 6–8 June 1988; Jet Propulsion Laboratory: Pasadena, CA, USA, 1988; pp. 97–101. [Google Scholar]
- Serbin, G.; Daughtry, C.S.T.; Hunt, E.R.; Reeves, J.B.; Brown, D.J. Effects of soil composition and mineralogy on remote sensing of crop residue cover. Remote Sens. Environ. 2009, 113, 224–238. [Google Scholar] [CrossRef]
- Singh, R.B.; Ray, S.S.; Bal, S.K.; Sekhon, B.S.; Gill, G.S.; Panigrahy, S. Crop residue discrimination using ground-based hyperspectral data. J. Indian Soc. Remote Sens. 2013, 41, 301–308. [Google Scholar]
- Schmidt, H.; Karnieli, A. Sensitivity of vegetation indices to substrate brightness in hyper-arid environment: The Makhtesh Ramon Crater (Israel) case study. Int. J. Remote Sens. 2001, 22, 3503–3520. [Google Scholar]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Thome, K.J.; Biggar, S.F.; Wisniewski, W. Cross comparison of EO-1 sensors and other earth resources sensors to Landsat-7 ETM+ using Railroad Valley Playa. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1180–1188. [Google Scholar] [CrossRef]
- Mariotto, I.; Thenkabail, P.S.; Huete, A.; Slonecker, E.T.; Platonov, A. Hyperspectral versus multispectral crop-productivity modeling and type discrimination for the HyspIRI mission. Remote Sens. Environ. 2013, 139, 291–305. [Google Scholar] [CrossRef]
- Sternberg, M.; Shoshany, M. Influence of slope aspect on Mediterranean woody formations: Comparison of a semiarid and an arid site in Israel. Ecol. Res. 2001, 16, 335–345. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved forest biomass estimates using ALOS AVNIR-2 texture indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zandler, H.; Brenning, A.; Samimi, C. Potential of Space-Borne Hyperspectral Data for Biomass Quantification in an Arid Environment: Advantages and Limitations. Remote Sens. 2015, 7, 4565-4580. https://doi.org/10.3390/rs70404565
Zandler H, Brenning A, Samimi C. Potential of Space-Borne Hyperspectral Data for Biomass Quantification in an Arid Environment: Advantages and Limitations. Remote Sensing. 2015; 7(4):4565-4580. https://doi.org/10.3390/rs70404565
Chicago/Turabian StyleZandler, Harald, Alexander Brenning, and Cyrus Samimi. 2015. "Potential of Space-Borne Hyperspectral Data for Biomass Quantification in an Arid Environment: Advantages and Limitations" Remote Sensing 7, no. 4: 4565-4580. https://doi.org/10.3390/rs70404565
APA StyleZandler, H., Brenning, A., & Samimi, C. (2015). Potential of Space-Borne Hyperspectral Data for Biomass Quantification in an Arid Environment: Advantages and Limitations. Remote Sensing, 7(4), 4565-4580. https://doi.org/10.3390/rs70404565