Analysis of Geometric Primitives in Quantitative Structure Models of Tree Stems
Abstract
: One way to model a tree is to use a collection of geometric primitives to represent the surface and topology of the stem and branches of a tree. The circular cylinder is often used as the geometric primitive, but it is not the only possible choice. We investigate various geometric primitives and modelling schemes, discuss their properties and give practical estimates for expected modelling errors associated with the primitives. We find that the circular cylinder is the most robust primitive in the sense of a well-bounded volumetric modelling error, even with noise and gaps in the data. Its use does not cause errors significantly larger than those with more complex primitives, while the latter are much more sensitive to data quality. However, in some cases, a hybrid approach with more complex primitives for the stem is useful.1. Introduction
The reconstruction of precise structure models of trees is important in understanding tree growth and decay, competition for resources, soil processes, photosynthesis, etc. The models can be used to compute, e.g., volumes, biomass estimates and size distributions. Terrestrial laser scanning (TLS) offers fast and accurate point clouds from which plant geometry can be reconstructed.
Many possible reconstruction methods from TLS data have been presented [1]. These methods can be divided roughly into three classes according to the way the tree structure is modelled. One class comprises the voxel methods, where volumetric models are constructed by partitioning the point cloud into voxels [2–4]. However, the ability of the voxel methods to model the tree structure is limited. The second class includes the parametric surface methods, where a single continuous surface is used to present a single branch [5,6]. In some of these methods, the cross-section of a stem or branch can be modelled as splines or other parameterizable curves [7]. The third class, and the one that we focus on, consists of shape-fitting methods, which use a geometric primitive to represent a part of a branch. A branch is modelled as a collection of these primitives [8,9]. Thies et al. [10] have presented a method that uses overlapping cylinder primitives to assess stem properties, and we have previously presented a reconstruction process based on geometric primitives [11].
Most of the published shape-fitting methods use the (rectangular) circular cylinder as their elementary building block. This choice is a compromise between simplicity and realistic reconstruction, as it is well known that the cross-section boundary of stems is never exactly a circle. For example, when the largest possible circle is fitted inside the cross-sections of eucalyptus trees, as much as 7% of the area is left outside the circle [12]. On average, the ratio between the minor and major diameters of various coniferous tree species is 0.96, indicating some elliptic features [13]. For branches, the ratio is expected to be even smaller due to gravity. Thus, it is a fair question if the use of circular cylinders is acceptable in such cases and if other shapes, that a priori appear more suitable, could be used instead with better results. Here, we study how the choice of the geometric primitive affects the model error and robustness of the reconstruction process and what are the pros and cons of using different shapes. In addition to the circular cylinder (circyl), we study the elliptical cylinder (ellcyl), the circular cone (cone) and the polygonal cylinder (polcyl) as the possible elementary blocks or geometric primitives (see Figure 1). In addition, we use polyhedral cylinder surfaces (trian), which are triangulated meshes, to reconstruct tree stems. Similar triangulated surfaces have been previously used for reconstruction with data collected with a digitizer from tree stems [14] and root systems [15] and for TLS data and root systems [16].
There is also another intuitive objection against the use of cylinders in particular, but also other geometric primitives: blocks or primitives cannot be attached to each other, such that the resulting surface is continuous and without gaps. However, we will show that, for most purposes, this is only an aesthetic problem, as all of the structural and geometric properties, such as the branching structure, branching angles, tapering, volumes, lengths, curvatures, etc., can be modelled accurately. Indeed, if all we need are the structural and geometric properties, it is actually better to leave out continuity (and the related details) altogether in the modelling process, as these would only make it more difficult, slower and less reliable.
In the building-block approach, the first step is some segmentation of the point cloud into parts to which the geometric primitives are fitted. The segmentation process described in [11] was used in this study. This method divides the TLS point cloud efficiently into small surface patches that conform to the tree surface. These sets are used to segment the point cloud into branches and each segment further into sub-segments that are then reconstructed using shape fitting. In this study, mainly the tree stems are considered when testing the different reconstruction schemes, because of better data quality and the easy assessment of the results based on visualizations. However, in Section 4.5, we will briefly demonstrate how the approaches work with branches.
Shape fitting geometric primitives with their basic properties are presented in Section 2. The main reconstruction results presented in Sections 4–5 are discussed in relation to other works in Section 6 and presented in more compact form in Section 7. Some of the fitting problems considered here require strong initial values for the iterative fitting procedures to converge correctly, and the rest require meaningful, accurate parameters for usable results. In Section 3, procedures for finding good initial values and parameters from the data are presented, and the sensitivity of the fitting problems on the initial values is studied. In Section 4, we use generated stem models and simulated laser-scanning to study the error related to the shapes, as well as the effects of data quality. The simulated shapes are not meant to represent any particular trees; rather, they were chosen to portray various geometric characteristics in a somewhat exaggerated manner to analyse the performance and inherent properties of each geometric primitive. In Section 5, real field data are used in further tests. As no volume estimates are available for the field data, we use reconstructed models as references in Section 5.1. Simulated laser scanning is carried out for the reference models, and the resulting point clouds are reconstructed for the second time, in order to show how the approaches work with more realistic stem models.
2. Shapes
Here, we consider various geometric shapes suitable as geometric primitives. The shapes are shown in Figure 1, and they are described in Sections 2.1 to 2.5. Cylinders and cones have a few common parameters: the starting point p in three dimensions, the axis direction a (unit vector) and the length h in the axis direction. The shapes are rectangular, so the top and bottom planes are perpendicular to the axis a.
2.1. Circular Cylinder
The simplest reconstruction shape is the circular cylinder (circyl), which requires only one additional parameter: the radius r. When using a circyl, the cross-section of a fraction of a branch is approximated as a disk with the radius r. For the circyl, the envelope area E = 2πrh and volume V = πr2h. The parameters of each circyl are iteratively fitted to the dataset, as described in [11]. Each cylinder fitting is done iteratively starting from initial values. For cylinder and cone fitting details and parametrization, see [17].
2.2. Elliptic Cylinder
The elliptic cylinder (ellcyl) approximates the cross-section as an ellipse. Three additional parameters are used to model the ellipse: a pair of semiaxes radii (r1, r2) and the direction α of the major semiaxis (measured as the angle from a reference direction). We use the following approximation for the envelope area:
The volume V can be computed accurately V = πr1r2h.
As a fitting problem when compared to the circyl, the additional parameters make the ellcyl more complex and time consuming. Therefore, we implement ellcyl fitting in two steps:
Estimate axis direction by fitting a circyl.
Project the points onto a plane perpendicular to the axis direction. Fit an ellipse to the two-dimensional data.
Since the steps are done in sequence, the procedure is not fully iterative.
2.3. Polygon Cylinder
The cross-section of a cylinder can be defined by any closed curve. However, it is sensible to keep the shape complexity to a minimum to achieve reasonable robustness and computational cost. Therefore, we use a polygon, which is a closed circuit of vertices v1, v2, …, vk, connected by straight lines, that in this case is assumed not to intersect itself. In a polygon cylinder (polcyl), the sequence defines the base of the cylinder and the sequence the top of the cylinder.
The perimeter p of a polygon is the sum of distances between consecutive vertices and the envelope area E = ph. The area of the polygon can be found by projecting the vertices onto a plane orthogonally and by using Gauss’ area formula for these 2D points :
To fit a polygon cylinder to a point cloud , we propose the following algorithm.
Estimate the axis direction a either by the approaches described in Section 3 or by fitting a circyl.
Project the points onto a plane perpendicular to the axis a. The projected set is denoted by P⊥a.
Compute a centre point c for the set P⊥a either by computing the mean or by least-squares circle fitting [18].
Divide the elements of the set P⊥a into k sectors around the centre point c.
For each sector i, compute the mean point . If a sector has no elements, interpolate using the next and previous non-empty sectors.
Transform the points back to the original coordinate system. The transformed sequence (vi) is the base of the reconstructed polcyl.
2.4. Cones
A circular cone (cone) is a shape that is limited by a base circle and circular cross-sections that smoothly taper to a single point, the apex. A part of a branch is usually not the shape of a complete cone with an apex, but a truncated cone where the top is cut off. The fitting problem, however, remains essentially the same as in the cylindrical case. Fitting a cone to 3D data is an extension of this, since a cone has a minimum of six parameters [17]. There are two common ways to parametrize a circular truncated cone, either by using the taper angle or a pair of radii. Here, the latter is chosen: r1 is the radius of the base, and r2 is the radius of the top. In that case, the surface area and the enclosed volume . Cone fitting is done iteratively starting from initial values.
2.5. Polyhedron/Triangulation
A polyhedron is a considerably more general and flexible shape than cylinders or cones. In principle, the whole surface model of a tree could be given as a continuous polyhedron. However, due to insufficiencies in TLS data, it can be impossible to reliably reconstruct a tree as a single polyhedron surface, so sub-polyhedra as geometric primitives are an efficient means of interpolating between the gaps and for smoothing (regularizing) the effect of noise and outliers. Modelling a part of a tree as a polyhedron captures features in both the axial and radial directions. Polyhedron models are detailed and, compared to the other shapes, require more space for storing the data and are slower to compute.
Given an axis direction a and a reference point p, a point cloud can be partitioned into cells the following way:
In the axis direction, divide the data into layers (Ri)i=1,…,M of equal height.
Further divide each layer into sectors (Cj)j=1,…,N.
A cell Pi,j = Ri ∩ Cj ⊂ P.
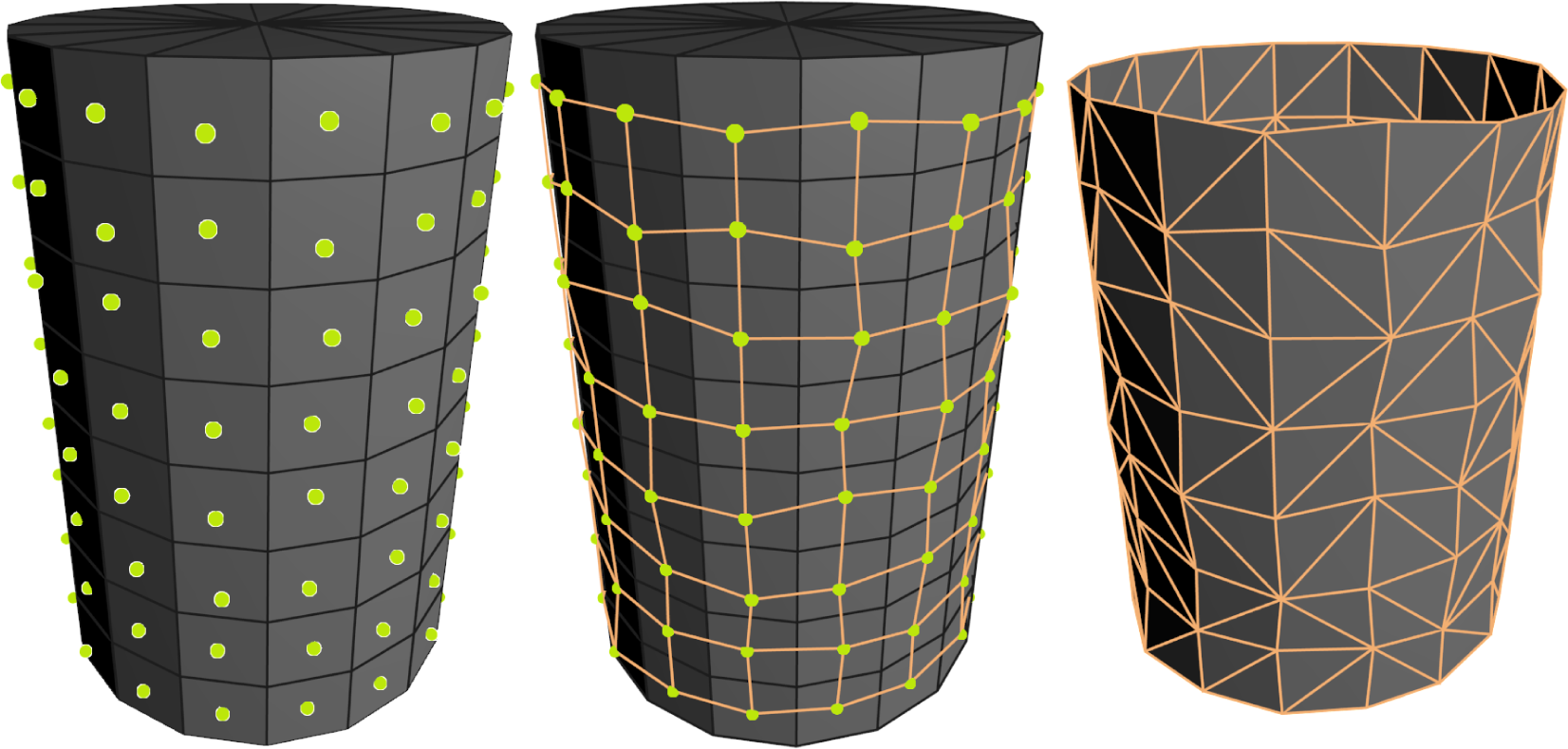
Compute the centre point vi,j of each cell (Figure 2, left).
Form triangle edges by connecting centre point pairs horizontally, vertically (Figure 2, centre) and diagonally (Figure 2, right).
If a cell is empty, its centre point is interpolated linearly using the vertices in the cells above and below. If interpolation is not possible in the axis direction, it can be done in the radial direction by using the previous and next non-empty vertices in the same layer of cells.
3. Initial Values
Next, we discuss initial estimates for shape parameters from point cloud data. These are needed in the iterative fitting problems, circyl, ellcyl and cone, as well as parameters for the partitioning in the polcyl and trian reconstructions.
Let Si, i = 1,…, n be the subsegments of a segment, computed, e.g., as described in [11]. An axis point estimate is computed as the mean of the subsegment points: . There are different ways to estimate the axis direction , but we use the axis point estimates of consecutive subsegments: . This only works when there are at least two subsegments. For the last subsegment, we use the same direction as for second to last one. We have also presented alternative ways to estimate the axis direction; see Section 2.6 in [11]. Given the line defined by the axis point and direction estimates, the radius estimate is the mean distance from the points of the subsegment to this line.
3.1. Sensitivity Analysis
To analyse the sensitivity of the shape fitting problems to their initial values, we used the curved cylinder model shown in Figure 3. TLS was simulated on the object, and reconstructions were computed from the point cloud with perturbations to the initial values. The appearance, volume and area of the resulting models were compared to the original.
For circyl and cone, all three initial values (radius, axis point, axis direction) are required, but polcyl and trian reconstructions do not need a radius estimate. ellcyl fitting was left out of the analysis, because the results are expected to be very similar to those of the circyl, due to the implementation. Furthermore, cone fitting also has the tapering parameter, but tests showed that when perturbed from 0 to 45°, the relative error in both the volume and area varied only in the magnitude of 10−3. Note that the magnitude of the error is not as important as its variation under increasing perturbation.
For the radius, perturbation was introduced by scaling the original estimate by factors from 0.1 to 2.5. The test showed that circyl and cone are both very indifferent to the radius estimate. With factors between 1.3 and 2.0, the perturbation had a minor effect on cone models, but the relative error stayed below 5% for both volume and area.
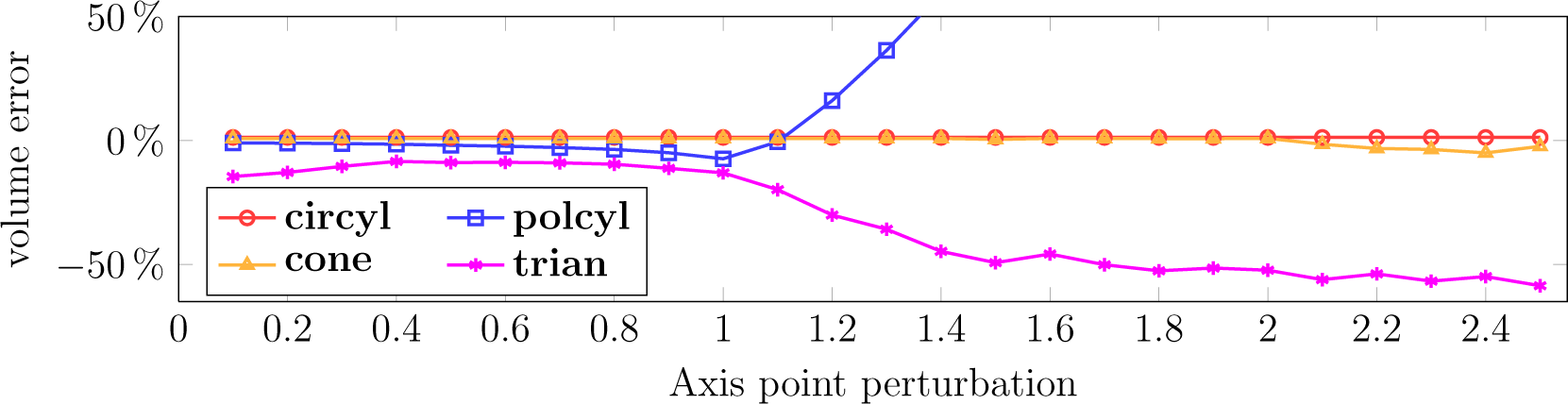
The axis point estimate was perturbed by moving it to a random direction perpendicular to the estimated axis direction. The magnitude of the move was the estimated radius scaled by a factor varied again from 0.1 to 2.5. The effect of the perturbation on the model volume is presented in Figure 4. For all of the shapes, the error remains small with scaling factor values lower than one. With larger values, as the axis point estimate moves outside the estimated cylinder hull, the error for polcyl starts to rise close to linearly for both quantities. At 2.5, the errors are 500% and 150%, for the volume and area, respectively. trian overestimates the area by ∼10% and underestimates the volume by up to 50% with factor values above 1.5.
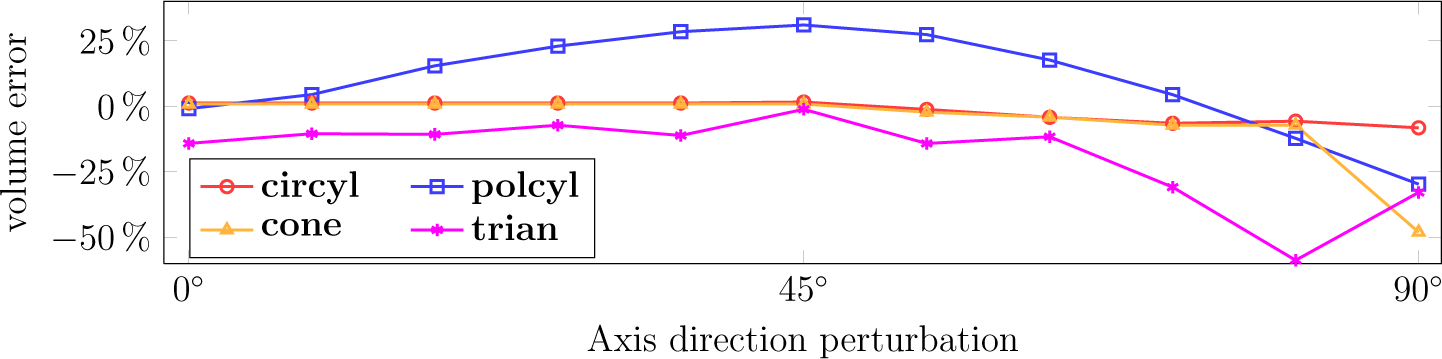
The axis direction estimate was perturbed by rotating it in a random direction by an angle varying from 0° to 90°. The results for the volume are shown in Figure 5. The iterative fitting methods, circyl and cone, remain unaffected with perturbations smaller or equal to 45°. Even at 81°, the errors in the volume are only 5% and 7%, respectively. polcyl is very sensitive to the axis direction, even at small angle perturbations. With large perturbations, the trian model error can be up to 50% underestimation.
Above, each of the initial values was studied individually. In real cases, the perturbation is never specific to a single property, but rather all of them.
4. Reconstruction from Generated Data
The reconstruction accuracy for the different shapes was studied using generated stem objects in order to better show the differences of the approaches. For this purpose, eight stem models were created using the 3D modelling software Blender. Some of the models are non-realistic, because the differences in the modelling approaches would not otherwise be visible. For a more realistic case, models derived from real oak trees were used in Section 5.1. The models were imported into Matlab, where simulated TLS measurements were made. The resulting point clouds were reconstructed using all of the shapes.
4.1. Generation Process
The models (see Figure 6) are 15-m tall and consist of 302 consecutive 32-vertex rings. The diameter of the stems remains constant for the first 2 m at 0.40 m and then tapers smoothly to 0.12 m at the top. Stems 2–4 are unrealistically elliptic on purpose, and Stems 4, 6 and 8 have random perturbations on the surface.
The simulated scans consisted of three positions around the model with an angular sampling resolution of 0.036° and a distance between the scanner and the models of ∼5 m. The scanner positions are visualized in Section 4.4. The scans were co-registered perfectly and were made with two noise levels: no noise and uniformly distributed noise between −3 mm and 3 mm.
4.2. Reconstruction Results
Because of randomness in the surface patch generation, the reconstruction was repeated 10 times for each shape to analyse the deviation σt associated with the underlying segmentation. The reconstruction accuracy of the different shapes was determined by comparing the total volume and surface area of the reconstructed model with the original one. Table 1 lists the average and maximum error for the volume and area of the noisy measurements and the volume of the noiseless measurements in relative error percentages. The standard deviations σ of different stem models and the average standard deviation σt associated with the segmentation randomness are also listed in percentage points. It is clear that the differences in the results between the noiseless and noisy measurements are very small, and thus, only the noisy data were used in further tests.
Stems 4 and 6 with the large flanges were the hardest to reconstruct accurately. Especially with the former, the combination of the flanges and highly elliptic cross-sections caused high errors in both volume and area. With the non-elliptic stems without flanges, reconstruction accuracy was much better for all of the shapes. The fitted cylinders and cones had an average length of 30 cm, whereas trian had a layer height of 10 cm.
With the circyl, all but the elliptic stems (2,3,4) were reconstructed with error between ±3.50% in the volume. In the surface area, the flanges in Stem 6 caused underestimation of over 7%, but with the other non-elliptic stems, the error was again between ±3%. The standard deviation σ seems relatively high, but it is heavily affected by the elliptic stems.
Using the ellcyl usually resulted in 2%–3% error in volume and area, either from over- or under-estimation. It did have the lowest average error, but also the highest average standard deviation σt. Overall, ellcyl seemed more unstable than the other approaches.
The polcyl approach seems to underestimate both the volume and the area by ∼2.5% on average. The largest error appears again in Stems 4 and 6, which have large flanges. The standard deviation of the average error is lower than with the iterative approaches, but slightly higher than with trian.
The large flanges were particularly hard for cone to model: too much tapering in the first cone caused errors of over 20%. On stems without flanges or elliptic cross-sections, the volume was underestimated only by ∼5% and the area by 4%. The standard deviation of the average error was the highest of all of the shapes.
The trian approach underestimates the volume of most stems by 3% to 5%, although Stem 6 causes higher error up to 10%. The surface area is reconstructed more accurately, with the average and maximum errors of −2.34% and 8.47%. The average standard deviation σt is considerably lower than with any other approach, and if Stem 6 is discarded, the maximum deviation is only 0.05 percentage points (pp). The standard deviation of the average errors σ was also the lowest of all. For taper curve comparison, see the Supplementary Material.
To illustrate how the error is distributed vertically within the models, Figure 7 shows the taper curve for Stem Model 7, and the respective error curves for each approach. Error curves are computed as the difference between the taper curves of the reconstructed model and the original one. The first meter is discarded in the figure for clearer visualization.
The taper curves obtained with different models are very similar along most of the stem. Larger differences only occur near the bulges of the original model. It seems that the cone models are affected the most by these fast variations in the original diameter, but none of the approaches can model the bulges correctly.
At the bottom half of the stem, where there are no bulges, the error level stays low and relatively stable. On the top half, i.e., starting from 8 m, the trend of the error starts to rise almost linearly and turns from under- to over-estimation. This is due to the fact that as the diameter gets smaller, the noise becomes more relevant and also the sample density drops. At 15 m, the trend of the diameter error gets close to 2 cm.
Figure 8 shows how the different approaches are able to reconstruct the cross-sections along the vertical axis of Stem 8. The circyl seems to get the size of the cross-sections right, but is unable to capture the finer details. The trian approach captures the finer detail in the cross-sections, as it has better vertical resolution, but still noticeable differences remain.
4.3. Effect of Shape Parameters
The Stem Model 7 was used to test the effect of the length of the shapes on the reconstruction accuracy. The results showed that by using too short subsegments (less than 14 cm), the orientation could not be accurately determined, which resulted in overlapping primitives and, thus, overestimation in lengths and volumes. With larger lengths (up to 42 cm), the overestimation changed to slight underestimation, but was less than 5% for circyl and ellcyl and less than 8% for polcyl, and for cone, the volume error was close to 15%.
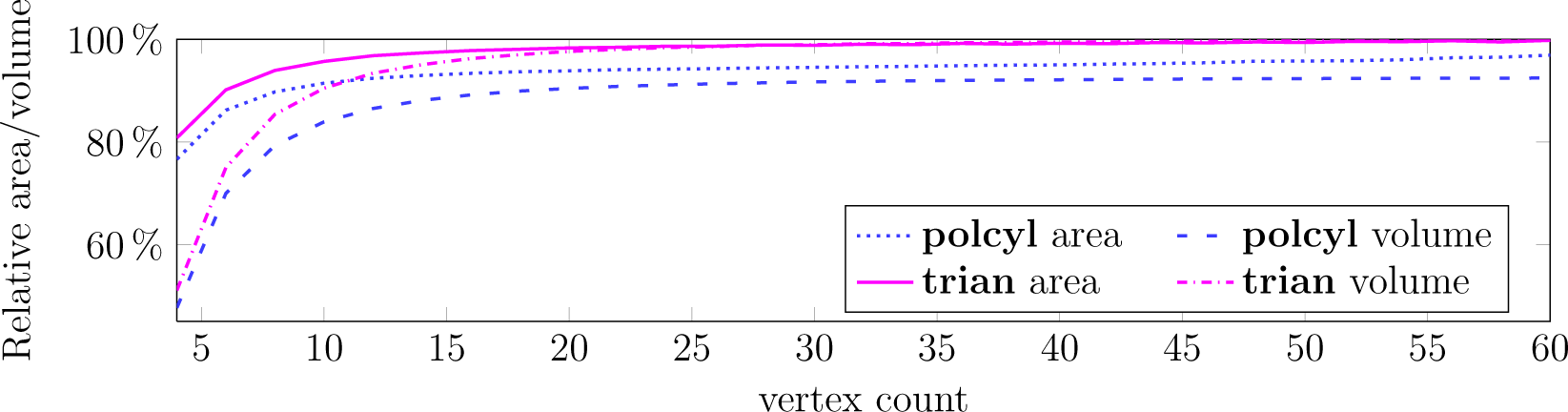
The effect of polcyl and trian vertex count was studied by reconstructing Stem 7 with the vertex count varying from four to 60. The results are visualized in Figure 9. Increasing the vertex count makes the reconstructions more accurate for both shapes. Already with 20 vertices, the reconstructed volume is underestimated by less than 10% and 3% with the polcyl and trian, respectively.
4.4. Data Quality
There are a number of factors that contribute to the quality of the scanning data and affect the reconstruction result. We tested how the different shapes handle changes in the sampling resolution, occluded parts and the number of scan positions. Because all of the approaches remain quite unaffected by a realistic amount of measurement noise, its effects were not investigated further. Similarly, registration errors and environmental factors, e.g., wind, were ignored.
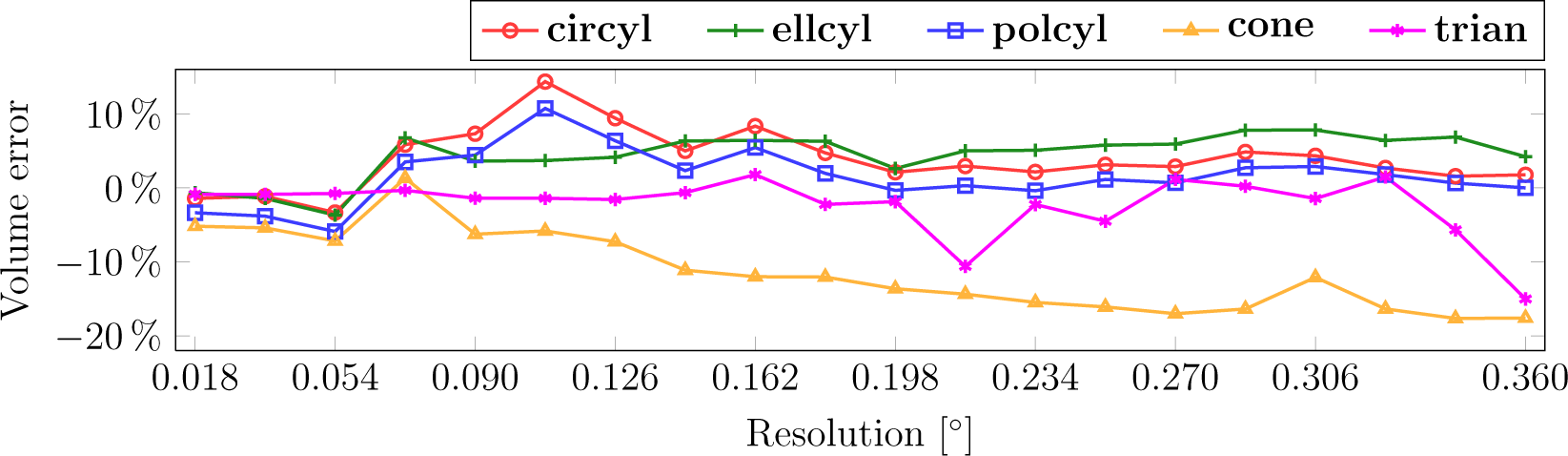
The effect of the scanning resolution is shown in Figure 10 for the Stem Model 7. The resolution varied from 0.018° to 0.360°. Changing the point density forced us to change the parameters of the underlying segmentation process manually for each resolution, making the testing very tedious and probably not definitive. All of the cylinder-based approaches behaved quite similarly: slight underestimation with the finest resolutions and up to 10% overestimation with the crudest resolutions in the volume. With the area, the errors were even smaller, e.g., with 0.036° resolution, the circyl had an error of −6.54%. The underestimation in cone models increased steadily and was close to 18% at the end.
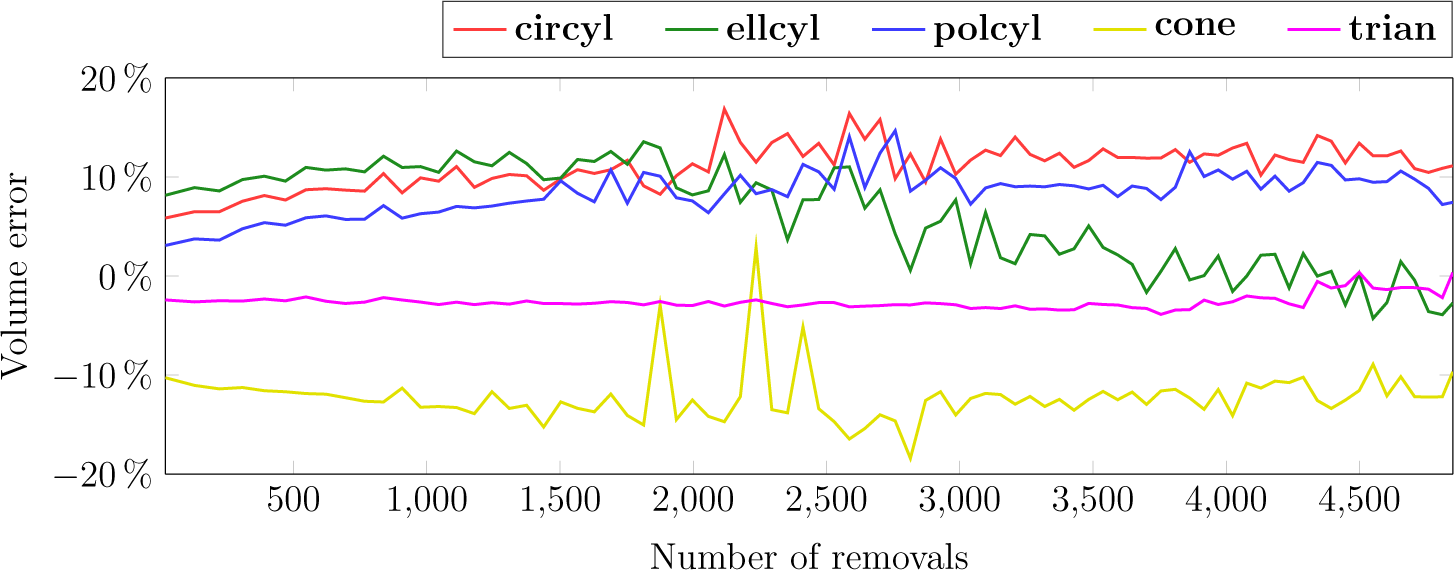
The effects of local occlusions were studied by iteratively degenerating the point cloud of Stem 7 scanned with a resolution of 0.036° by removing spherical sections. The radius of the sections varied linearly from 16 cm at the bottom to 8 cm at the top of the stem. The extractions we distributed vertically in a way that more of them were in the upper parts of the stem. The number of spherical extractions was increased from zero to 4850 with a total of 81 steps. Figure 11 shows examples of the four steps. Reconstruction was repeated 20 times for each step, and the resulting volume errors were averaged. The relative volume errors of the reconstructions as a function of the number of extractions is visualized in Figure 12.
Interestingly, trian was here the most stable approach, probably because it interpolated vertices into empty cells. The stability is weaker for the surface area: from about 3500 removals to 4850, the surface area error went from −1.3% to +6.0%. For the other shapes, the results were similar for both the area and volume. ellcyl is the most unstable of the five approaches: after about 2000 removals, the volume starts to decrease due to ellipse fittings not converging and using initial values that are visibly too small. With the other shapes, circyl, polcyl and cone, the volume error increases slightly from zero to 2000 and remains relatively stable after that at +10%, +10% and −10%, respectively.
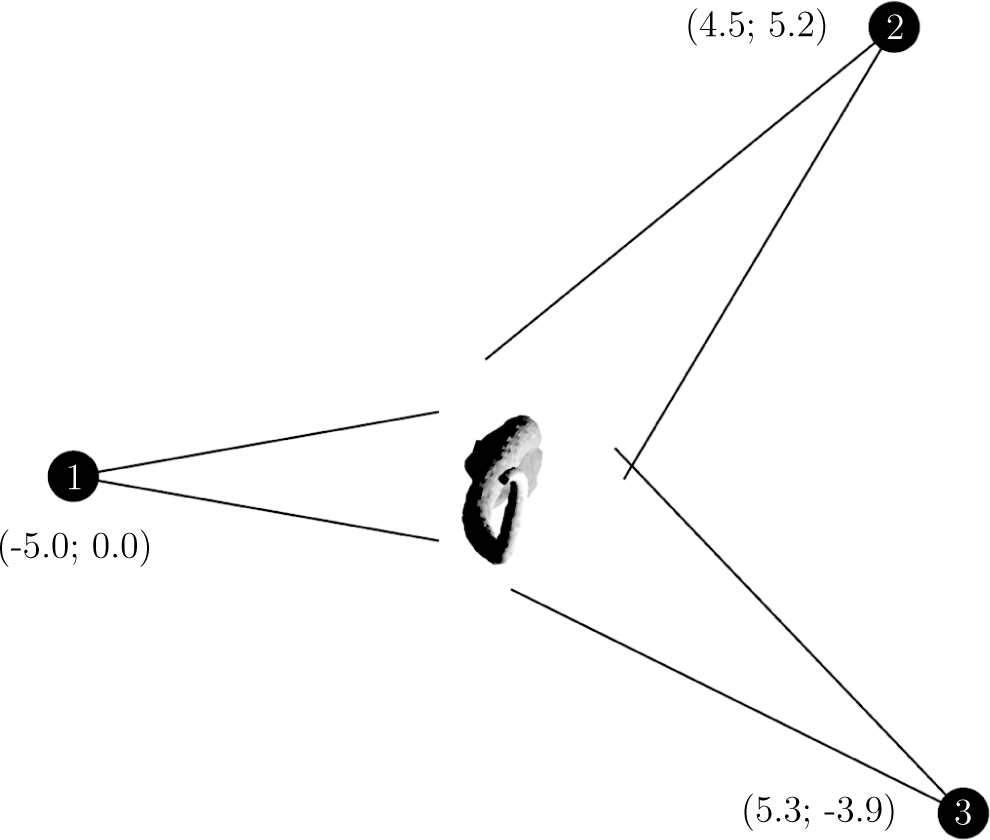
In earlier tests, the object was always scanned all-around from three positions. This is not always possible, so the effect of the number of scanning positions was studied by using all possible combinations of the three directions visualized in Figure 13. The results are listed in Table 2 for Stem Model 7.
With a single scanning direction, all of the approaches produce high errors above 10%, at least for some directions. trian produces physically impossible results (negative volume) with a single scan. With two scanning directions, the methods apart from trian produce quite accurate results. The trian approach still gives errors of several tens of percents. circyl has the smallest deviation and a mean closest to zero in these three cases. With all three directions, all of the approaches work well.
This stability test is of particular importance when considering fast scans of entire plots (from a few scanning positions) rather than detailed ones of individual trees. In such cases, the robustness of circyl (i.e., its strong regularization) may be a crucial factor.
4.5. Reconstruction of Complete Trees
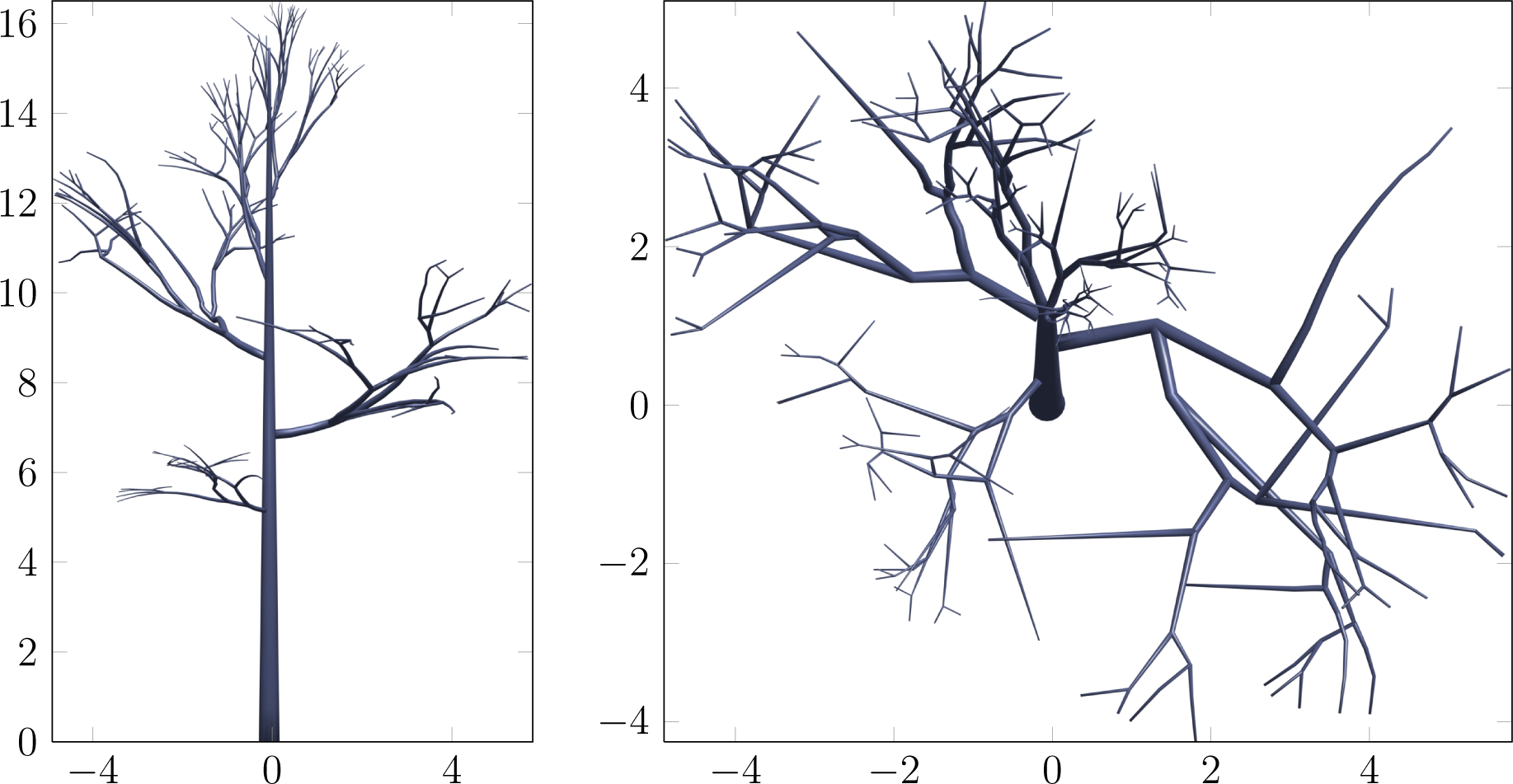
To test how the approaches reconstruct branches, we generated a tree model with 40,600 triangles visualized in Figure 14. Laser scanning was simulated from the same positions as before in Figure 13 and the same resolution 0.036° and simulated measurement noise (uniform ±3 mm). The resulting point cloud consisted of 108,000 points. The tree was reconstructed 10 times with all of the approaches and compared to the known volume and area of the model. When the fitting of either the initial cylinder or the final shape did not converge, the cylinder defined by the initial values was used. Thus, parts of the ellcyl, polcyl and cone models are circular cylinders.
The average normalized volume and standard deviations are listed in Table 3. The results show that the iterative methods have average and maximum volume underestimation errors below 4%. Their standard deviation is also close to just one pp. polcyl overestimates the volume by a few percentages, where as the trian approach produces an overestimation error of over 50% on average. The high error level is caused by the lack of point coverage on the top parts of the branches. For example models and data tables, see the Supplementary Material.
5. Reconstruction from Measured Data
To test the modelling approaches with measured data, scans were conducted in an 80-year-old oak plantation located in southeastern England (51.1533°N, 0.8512°W, 80 m asl). The plantation covers a total ground area of about 85 ha managed as a commercial forest of mixed species dominated at 75% by Quercus robur (English oak). A 30 × 30 m experimental area was selected and the understory removed before data acquisition. TLS data were recorded at nine positions (see Figure 15) over the experimental area in April 2012 (leaf-off). The TLS used was the single return HDS-6100 (Leica Geosystems Ltd., Heerbrugg, Switzerland).
In this study, we used scans from the bottom 14 m of eight oak stems, with a sampling resolution of 0.036°, and six of the eight scanning positions with the best visibility were selected for each stem. A thinned-out point cloud and reconstructed models of one of the stems, Stem 5, are shown in Figure 16.
The diameter at breast height (dbh) was manually measured using a girth tape, and it was compared to the reconstructed values. The average and maximum error percentages in the reconstructed dbh are listed in Table 4, together with the average standard deviation σt over 10 repeats within single stems, the deviation σ between the stems and the average distance from the measurements to the model surface. The dbh of the stems ranged from 27.7 cm to 41.6 cm.
The cone models have the highest average error close to 12% and the highest deviation. Because approximately the first 1.5 m is modelled as a single cone, the tapering of that cone is usually overestimated due to the bulging at the very bottom of the stems. The accuracy of the dbh measurements could be further improved for all of the cylinder and cone models, if a block were fitted to a short section over the breast height. The trian models have high errors, as well, but the underestimation is systematic. Because of the finer vertical resolution of trian models, the error in the diameter could be caused by the offset between the zero point of the model and the field ground level. The same systematic error could affect other shapes more, if they were shorter. The average distance between the measurements and the model surface was smallest with the trian and polcyl models, as expected, since they have the largest number of parameters.
In the bottom half of the stems, the ratio of the minor and major radii of the fitted elliptic cylinders for all the stems was 0.92, and the variance was small. On the upper half, the ratio started to decline, and the variance was four-times larger. The same effect was visible for the tapering angle of the fitted cones. The visualizations of the models showed that unrealistically tapering cones and elliptic cylinders were fitted to the upper parts of the stems. On average, the ellipse radii ratio was 0.87 and the cone tapering angle 0.33°. Thus, additional constrains should be introduced when using these shapes for stem parts with high noise or a low number of returns.
5.1. Second Order Reconstructions
To better estimate the volume and area error levels and distribution, the following procedure was used. The original point clouds were used to reconstruct reference trian models, with 32 vertices, for the stems respectively. Simulated TLS was then carried out with the same settings and scanner locations as in Section 4, except that no additional noise was added to the measurements. The resulting point clouds were then used to compute second order reconstructions ten times with all of the shapes, including trian with 20 vertices. The results are listed in Table 5, and they are in agreement with the results using generated stem models in Section 4. Here, the differences between the shapes are minimal, because the oak stems are simpler than the generated stem models. The average volume underestimation for all of the shapes other than cone is below 3%. For taper curve comparison, see the Supplementary Material.
6. Discussion
The results show that in terms of robustness to data quality and initial values, the use of the circular cylinder as a geometric primitive in reconstruction approaches (e.g., [8–11]) is justified. The expected error in volume and surface are low even when comprehensive data are not available. However, the circular cylinder is not able to model the fine structure of the stem cross-section. For this purpose, the trian models are better, but they require comprehensive input data. The resulting models require a lot more disk space to be stored and slower computations, when comparing to the circular cylinder, which is sufficiently compact for massive-scale automatic reconstructions [19].
Simple eccentricity characteristics, e.g., the ratio between the largest and smallest diameter, can be computed from the ellcyl models, and for the English oak stems, the ratio was 0.92 (at lowest 3 m), which seems realistic when comparing to the value of 0.96 measured for various coniferous species [13]. Similar estimates could be computed from the polcyl and trian models. None of the presented structure models include information about the inner structure, e.g., pith eccentricity [20], and for that purpose, destructive measurements are still needed.
The problem with using more complex shapes is the increased requirement for measurement coverage around the object. Lack of coverage combined with shape fitting instability can lead to very high errors. Thus, it would be beneficial to analyse, e.g., the radial coverage locally around a given axis to determine the maximum complexity of the shape that should be fitted to those measurements. By implementing such local coverage analysis, the resulting models would consist of several types of geometric primitives. Especially, the lower part of stems has, in most cases, sufficient coverage for polcyl or trian reconstruction. Thus, the resulting model would consist of the stem polyhedron and a collection of cylinders for the top part of the stem and the branches. Another possibility is to make several reconstructions with different shapes for a single part and store all of them in the same model. Which representation to use could be determined later depending on the application (cf. [21]).
The data in Section 4 were generated using a combination of 3D modelling and simulated laser-scanning. By further developing and optimizing the scanning part, it would be possible to model entire forest plots with understory and to simulate scans containing multiple trees or even to simulate continuous scans with moving scanners. Furthermore, on the tree level, this type of simulation offers an inexpensive way to study how to model tree abnormalities, such as cankers, seams or buttress roots. This way, it is possible to start with ideal data without any noise or occlusion present and to degenerate them in various ways to get data similar to real measurements.
7. Conclusions
In this study, reconstruction approaches based on four different geometric primitives and a triangulation approach were tested with both measured and simulated data. For all of the shape fitting approaches, the sub-segmentation procedure presented [11] was used, but most of the results are applicable to any reconstruction procedures using the same geometric primitives [9,10]. Using simulated data provided correct reference values of quantities, such as the volume, surface area and taper curves. These also served as a way to determine how much of the error was caused by the modelling and how much by the quality of the data. The most noticeable differences in the modelling approaches occurred in their ability to adapt to different shapes of stems and in their robustness to the quality of data. Adding a realistic amount of measurement noise did not noticeably change the reconstruction results in terms of volume or surface area. None of the tested approaches could accurately model complex cross-sections, such as flanges. On the other hand, the polyhedron method has been shown to give a good representation of complicated stump shapes that are not well represented by the other primitives [16,22].
Circular cylinder The circyl primitive is the most commonly used [9–11]. It is robust, as it is very indifferent to perturbations in all of the initial values of the fitting. Even coarse data-based estimates converge towards the correct solution; e.g, the axis direction estimate can be up to 45° off without causing any error, and after that, the error was below 10%. For the generated stems, the average volume overestimation was 1.36% with an average standard deviation of 7.33 pps. The surface area was underestimated with an average of 4.40% ± 6.76 pp. With field data, dbh was underestimated by 1.12%, on average, with a standard deviation of 1.94 pp.
Elliptic cylinder The ellcyl fitting was implemented as a combination of circyl fitting and two-dimensional ellipse fitting to fine-tune the cross-section. Thus, in the initial values, it performed as circyl. With the generated data, it had the lowest average error at 0.20% for the volume and −0.96% for the area. The deviation between repeats was the highest at 1.86 pp for the volume and 1.50 pp for the area. The high deviation means that ellcyl fitting can be unpredictable, but implementing the fitting as a single iterative process might help stabilize it. If the data are comprehensive and have good quality, the ellcyl fitting can produce good results. Furthermore, ellcyls fitted to the measured stems were elliptical rather than circular, as the ratio of the major and minor radii was 0.87 on average.
Polygon-based cylinder The polcyl reconstruction is not an iterative process, so accurate initial values are crucial. Even small perturbations to the axis direction estimate caused volume and area errors over 10%. However, in the tests with the generated and measured stems, the initial values received from the data were sufficient to produce error levels similar to the circyl, and when visualized, the models appeared accurate. On the generated stems, the average error in the volume was −2.51% ± 2.53 pp and on the area −2.58% ± 3.99 pp. As expected, the polcyl was more robust on the stem cross-section shape and reconstructed the elliptic stems more accurately than circyl and cone. With 26 vertices on the base polygon, the cylinder was able to reconstruct the dbh of the measured stems with an average diameter error of 7.38%.
Circular cone The cone handles initial value perturbations almost identically to the circyl. Using cone resulted in an average 5.00% ± 11.93 pp underestimation of the volume and 7.2% ± 8.74 pp of the area with the generated stems. It almost always resulted in the smallest volume of all of the models. Especially problematic was the bulging at the bottom of the stems, resulting in overestimation on the cone tapering. This caused high errors in the dbh values of the models. Most of the cone fitted to the measured stems tapered only a little, 0.33° on average. Thus, the difference in volume in comparison to circyl is not probably worth the increased instability, especially as the difference is expected to decrease with the primitive length. If one were to use longer cones, the stability and accuracy should be increased.
Polyhedron The trian approach is fairly sensitive to the values of the axis point and axis direction, of which the former had the larger effect on accuracy. It requires full coverage around the object: where the other primitives performed well with just two scans, it required all three positions or the volume error was close to 30%. On the other hand, it was not sensitive to local occlusions in the data. With the generated stem models, it produced a volume error of −4.62% ± 2.32 pp, and the error in the surface area was even lower. The average diameter error in dbh was −4.84%, but seemed systematic and could be caused by either the selection of breast height in the model or too small a number of vertices used.
Overall The results show that any of the models, even with cruder than normal resolution, can achieve accurate volume and area estimation. The average volume error for all models was below 5%, and using, e.g., the circular cylinder model on extremely elliptic stems, resulted in a maximum volume error below 14%. These ties well with the field-calibrated studies of [16,23], as the volume and length errors are similar in all studies. In [16], it is shown that a hybrid version of polyhedral and cylindrical modelling is accurate, even for the highly complex shapes of stump-root systems. Furthermore, [24] shows that using allometric equations to predict the volume of eucalyptus trees results in a 36.6% average error with the species-specific equation and a 29.9% error with the generic eucalyptus equation, while circular cylinder structure models produce an error of 9.7%.
Extrapolating the stem-based results to branches predicts that increased occlusions and relative noise levels and lower point density will increase the demand of robustness and the stability of the fitting scheme used. Thus, the general recipe is to use circyl for branches and, when necessary, more complex primitives for parts of the stem. However, the advantage gained by the latter is not significant, at least in terms of volume. For a fast and compact processing of a large number of trees, the circyl approach is rather sufficient. Taking into account the typical systematic errors and glitches that occur in field campaigns, a rule-of-thumb volumetric error from any surface modelling approach can be expected to be ±10%. The effect of the wind and co-registration error are expected to increase the error level, especially for the branches, but they were not considered in this study.
Acknowledgments
This study was funded by the Academy of Finland research projects Inverse Problems of Regular and Stochastic Surfaces and Centre of Excellence in Inverse Problems.
Author Contributions
Markku Åkerblom created the stem models for the generated data section, reconstructed the models for both data types, computed the results, created the figures and wrote the main text. Pasi Raumonen created the reconstruction procedure, guided the ideas of this manuscript, wrote parts of the text and gave feedback on it. Mikko Kaasalainen supervised the whole process from the idea-stage to the final manuscript, wrote parts of the text and gave vital feedback on rest of the text. Eric Casella carried-out the in situ measurements and provided the data used in Section 5, wrote the description of the measurements and gave feedback on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar]
- Gorte, B.; Pfeifer, N. Structuring laser-scanned trees using 3D mathematical morphology. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 929–933. [Google Scholar]
- Lefsky, M.; McHale, M.R. Volume estimates of trees with complex architecture from terrestrial laser scanning. J. Appl. Remote Sens. 2008, 2, 023521–023521. [Google Scholar]
- Vonderach, C.; Voegtle, T.; Adler, P. Voxel-base approach for estimating urban tree volume from terrestrial laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, B8. [Google Scholar]
- Xu, H.; Gossett, N.; Chen, B. Knowledge and heuristic-based modelling of laser-scanned trees. ACM Trans. Graph. 2007, 26, 19:1–19:13. [Google Scholar]
- Yan, D.M.; Wintz, J.; Mourrain, B.; Wang, W.; Boudon, F.; Godin, C. Efficient and robust tree model reconstruction from laser scanned data points, Proceedings of the 11th IEEE International conference on Computer-Aided Design and Computer Graphics, Huangshan, China, 19–21 August 2009; pp. 572–576.
- Pfeifer, N.; Winterhalder, D. Modelling of tree cross sections from terrestrial laser scanning data with free-form curves. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Pfeifer, N.; Gorte, B.; Winterhalder, D. Automatic reconstruction of single trees from terrestrial laser scanner data. Proceedings of the 20th ISPRS Congress, Istanbul, Turkey, 12–23 July 2004; pp. 114–119.
- Cheng, Z.L.; Zhang, X.P.; Chen, B.Q. Simple reconstruction of tree branches from a single range image. J. Comput. Sci. Technol. 2007, 22, 846–858. [Google Scholar]
- Thies, M.; Pfeifer, N.; Winterhalder, D.; Gorte, B. Three-dimensional reconstruction of stems for assessment of taper, sweep and lean based on laser scanning of standing trees. Scand. J. For. Res. 2004, 19, 571–581. [Google Scholar]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens 2013, 5, 491–520. [Google Scholar]
- Medhurst, J.; Ottenschlaeger, M.; Wood, M.; Harwood, C.; Beadle, C.; Valencia, J.C. Stem eccentricity, crown dry mass distribution, and longitudinal growth strain of plantation-grown Eucalyptus nitens after thinning. Can. J. For. Res. 2011, 41, 2209–2218. [Google Scholar]
- Tong, Q.; Zhang, S. Stem form variations in the natural stands of major commercial softwoods in eastern Canada. For. Ecol. Manag. 2008, 256, 1303–1310. [Google Scholar]
- Yoshimoto, A.; Surový, P.; Konoshima, M.; Kurth, W. Constructing tree stem form from digitized surface measurements by a programming approach within discrete mathematics. Trees 2014, 28, 1577–1588. [Google Scholar]
- Danjon, F.; Reubens, B. Assessing and analyzing 3D architecture of woody root systems, a review of methods and applications in tree and soil stability, resource acquisition and allocation. Plant Soil. 2008, 303, 1–34. [Google Scholar]
- Smith, A.L.; Astrup, R.; Raumonen, P.; Liski, J.; Krooks, A.; Kaasalainen, S.; Åkerblom, M.; Kaasalainen, M. Tree root system characterization and volume estimation by terrestrial laser scanning and quantitative structure modelling. Forests 2014, 5, 3274–3294. [Google Scholar]
- Lukács, G.; Martin, R.; Marshall, D. Faithful least-squares fitting of spheres, cylinders, cones and tori for reliable segmentation. In Computer Vision-ECCV’98; Springer Berlin Heidelberg: Berlin, Germany, 1998; pp. 671–686. [Google Scholar]
- Wolberg, J. Data Analysis Using the Method of Least Squares: Extracting the Most Information from Experiments; Springer-Verlag Berlin Heidelberg: Berlin, Germany, 2006. [Google Scholar]
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerblom, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W4, 189–196. [Google Scholar]
- Robertson, A. Centroid of wood density, bole eccentricity, and tree-ring width in relation to vector winds in wave forests. Can. J. For. Res. 1991, 21, 73–82. [Google Scholar]
- Godin, C.; Caraglio, Y. A multiscale model of plant topological structures. J. Theor. Boil. 1998, 191, 1–46. [Google Scholar]
- Liski, J.; Raumonen, P.; Kaasalainen, S.; Repo, A.; Krooks, A.; Akujärvi, A.; Kaasalainen, M. Indirect emissions of forest bioenergy: detailed modeling of stump-root systems. Glob. Change Biol. Bioenergy. 2014, 6, 777–784. [Google Scholar]
- Kaasalainen, S.; Krooks, A.; Liski, J.; Raumonen, P.; Kaartinen, H.; Kaasalainen, M.; Puttonen, E.; Anttila, K.; Mäkipää, R. Change detection of tree biomass with terrestrial laser scanning and quantitative structure modelling. Remote Sens. 2014, 6, 3906–3922. [Google Scholar]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Non-destructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2014, 6, 198–208. [Google Scholar]








| circyl | ellcyl | polcyl | cone | trian | |||
|---|---|---|---|---|---|---|---|
| Noiseless | Volume | ∆Vmax | −12.61 | −19.20 | −8.23 | −24.59 | −11.40 |
| ∆Vavg | 1.22 | 0.34 | −2.62 | −5.13 | −4.63 | ||
| σ | 7.02 | 3.59 | 2.35 | 11.58 | 2.33 | ||
| σt | 0.70 | 2.09 | 0.90 | 0.81 | 0.15 | ||
| Noisy (±3 mm) | Volume | ∆Vmax | −13.81 | −19.20 | −8.40 | −24.43 | −11.42 |
| ∆Vavg | 1.36 | 0.20 | −2.51 | −5.00 | −4.62 | ||
| σ | 7.33 | 4.72 | 2.53 | 11.93 | 2.32 | ||
| σt | 0.80 | 1.86 | 0.99 | 0.95 | 0.15 | ||
| Area | ∆Amax | −21.21 | −17.83 | −10.92 | −26.04 | −8.47 | |
| ∆Aavg | −4.40 | −0.96 | −2.58 | −7.20 | −2.34 | ||
| σ | 6.76 | 5.69 | 3.99 | 8.74 | 3.44 | ||
| σt | 0.59 | 1.50 | 0.86 | 0.65 | 0.10 | ||
| Pos. | circyl | ellcyl | polcyl | cone | trian |
|---|---|---|---|---|---|
| 1 | 2.63 | −19.80 | 14.62 | −7.38 | −104.51 |
| 2 | 19.66 | 3.68 | 20.69 | −2.02 | 31.18 |
| 3 | 3.28 | −0.44 | 12.19 | −12.46 | −121.47 |
| 1,2 | −2.26 | 0.20 | −1.37 | −8.18 | 31.66 |
| 1,3 | −1.44 | 0.38 | −5.29 | −7.32 | −26.72 |
| 2,3 | −1.78 | 6.45 | −0.73 | −8.21 | 43.05 |
| 1,2,3 | −2.62 | −1.04 | −5.58 | −7.46 | −1.43 |
| circyl | ellcyl | polcyl | cone | trian | ||
|---|---|---|---|---|---|---|
| Volume | ∆Vmax | −1.31 | −2.71 | 7.47 | −5.32 | 328.09 |
| ∆Vavg | −0.28 | −0.75 | 2.93 | −3.25 | 56.72 | |
| σt | 0.65 | 1.14 | 2.35 | 1.83 | 93.43 | |
| Area | ∆Amax | −4.89 | −5.05 | −2.15 | −8.07 | 126.76 |
| ∆Aavg | −3.52 | −2.29 | 0.13 | −5.90 | 27.90 | |
| σt | 0.90 | 1.89 | 1.07 | 1.32 | 45.16 | |
| circyl | ellcyl | polcyl | cone | trian | |
|---|---|---|---|---|---|
| ∆Dmax | −7.08 | 7.63 | −7.38 | −23.28 | −6.69 |
| ∆Davg | −1.12 | −0.41 | −1.51 | −11.57 | −4.84 |
| σ | 1.94 | 1.94 | 1.83 | 6.19 | 1.39 |
| σt | 1.10 | 1.56 | 1.04 | 2.30 | 0.01 |
| davg | 1.19 | 1.07 | 0.88 | 1.11 | 0.71 |
| circyl | ellcyl | polcyl | cone | trian | ||
|---|---|---|---|---|---|---|
| Volume | ∆Vmax | −6.69 | −6.32 | −8.96 | −9.60 | −7.76 |
| ∆Vavg | −1.33 | −0.18 | −2.30 | −5.45 | −2.72 | |
| σ | 2.87 | 3.68 | 2.99 | 2.17 | 2.28 | |
| σt | 0.37 | 2.62 | 0.98 | 1.08 | 0.49 | |
| Area | ∆Amax | −10.73 | −9.32 | −8.19 | −12.67 | −5.24 |
| ∆Aavg | −5.80 | −3.97 | −3.86 | −8.04 | −3.59 | |
| σ | 2.67 | 2.98 | 1.96 | 2.74 | 1.02 | |
| σt | 0.26 | 2.69 | 0.67 | 0.67 | 0.34 | |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markku, Å.; Raumonen, P.; Kaasalainen, M.; Casella, E. Analysis of Geometric Primitives in Quantitative Structure Models of Tree Stems. Remote Sens. 2015, 7, 4581-4603. https://doi.org/10.3390/rs70404581
Markku Å, Raumonen P, Kaasalainen M, Casella E. Analysis of Geometric Primitives in Quantitative Structure Models of Tree Stems. Remote Sensing. 2015; 7(4):4581-4603. https://doi.org/10.3390/rs70404581
Chicago/Turabian StyleMarkku, Åkerblom, Pasi Raumonen, Mikko Kaasalainen, and Eric Casella. 2015. "Analysis of Geometric Primitives in Quantitative Structure Models of Tree Stems" Remote Sensing 7, no. 4: 4581-4603. https://doi.org/10.3390/rs70404581
APA StyleMarkku, Å., Raumonen, P., Kaasalainen, M., & Casella, E. (2015). Analysis of Geometric Primitives in Quantitative Structure Models of Tree Stems. Remote Sensing, 7(4), 4581-4603. https://doi.org/10.3390/rs70404581






