Abstract
The reliable simulation of gross primary productivity (GPP) at various spatial and temporal scales is of significance to quantifying the net exchange of carbon between terrestrial ecosystems and the atmosphere. This study aimed to verify the ability of a nonlinear two-leaf model (TL-LUEn), a linear two-leaf model (TL-LUE), and a big-leaf light use efficiency model (MOD17) to simulate GPP at half-hourly, daily and 8-day scales using GPP derived from 58 eddy-covariance flux sites in Asia, Europe and North America as benchmarks. Model evaluation showed that the overall performance of TL-LUEn was slightly but not significantly better than TL-LUE at half-hourly and daily scale, while the overall performance of both TL-LUEn and TL-LUE were significantly better (p < 0.0001) than MOD17 at the two temporal scales. The improvement of TL-LUEn over TL-LUE was relatively small in comparison with the improvement of TL-LUE over MOD17. However, the differences between TL-LUEn and MOD17, and TL-LUE and MOD17 became less distinct at the 8-day scale. As for different vegetation types, TL-LUEn and TL-LUE performed better than MOD17 for all vegetation types except crops at the half-hourly scale. At the daily and 8-day scales, both TL-LUEn and TL-LUE outperformed MOD17 for forests. However, TL-LUEn had a mixed performance for the three non-forest types while TL-LUE outperformed MOD17 slightly for all these non-forest types at daily and 8-day scales. The better performance of TL-LUEn and TL-LUE for forests was mainly achieved by the correction of the underestimation/overestimation of GPP simulated by MOD17 under low/high solar radiation and sky clearness conditions. TL-LUEn is more applicable at individual sites at the half-hourly scale while TL-LUE could be regionally used at half-hourly, daily and 8-day scales. MOD17 is also an applicable option regionally at the 8-day scale.
1. Introduction
Efforts to mitigate climate change require the stabilization of atmospheric CO2 concentrations [1], which is significantly regulated by exchanges of carbon between terrestrial ecosystems and the atmosphere. Terrestrial gross primary productivity (GPP) is the largest component of the global carbon flux [2] and about 120 Pg C year−1 globally, considerably larger than the carbon annually emitted by human activities (about 9 Pg C year−1) [3]. Consequently, even a small change in GPP is likely to have a significant impact on atmospheric CO2 concentration. Thus, accurately simulating terrestrial GPP is of great significance to quantifying the global carbon cycle and predicting the future trajectories of the atmospheric CO2 concentration.
Two approaches have been widely employed to investigate the spatial and temporal variability in GPP using remotely sensed data: (i) remote sensing driven process-based models, and (ii) light use efficiency (LUE) models [4]. The former is based on the mechanistic description of the photosynthetic biochemical processes and scales the Farquhar instantaneous leaf-level biochemical model [5] to the canopy level using big-leaf, two-leaf, and multilayer scaling approaches. A number of process-based models have been successfully applied to quantify spatial-temporal variations of GPP at regional and global scales using remotely sensed vegetation parameters, such as leaf area index (LAI) and land cover types, as inputs. However, the application of these process-based models is limited by the complexity and uncertainty of their parameterization [6].
In contrast, LUE models, such as CASA [7], MOD17 [8], EC-LUE [9], and VPM [10], were developed according to the LUE argument of Monteith [11,12] that productivity is linearly related to the amount of absorbed photosynthetically active radiation (APAR). A fundamental assumption underlying LUE models is that plant canopies behave like a big single-leaf and their LUE is independent of the directional nature of solar radiation and vegetation structure [13].
Many studies have indicated that both GPP and LUE vary with both quantity and quality of incoming solar radiation. Gu et al. [14] detected a 20% increase in Harvard Forest photosynthesis after the 1991 Pinatubo eruption owing to the increase of diffuse radiation caused by volcanic aerosols. Flux site data indicated that canopy LUE was enhanced under diffuse sunlight in comparison with that under direct radiation [13,15,16]. Choudhury et al. [17] estimated an increase of 110% in crop LUE under diffuse radiation. Alton et al. [18] conducted a study for three forest sites (two broadleaf and one needleleaf) and found that the canopy LUE was enhanced by 6–33% under diffuse radiation. Alton [19] indicated that the enhancement of canopy LUE due to diffuse radiation varied with vegetation types, most significantly for tundra shrubs. Cai et al. [20] found that a single-leaf LUE model performed very well for a 56-year-old Douglas-fir stand when, instead of using total incident photosynthetically active radiation (PAR), they used the sum of incident diffuse PAR and a relatively small fixed fraction (22%) of incident direct PAR. Recently, Zhang et al. [21] reported that canopy LUE generally decreased with increasing sky clearness index, which is the ratio of solar radiation observed on the ground to radiation received at the top of the atmosphere, over 5 ChinaFLUX sites, including a temperate forest, a subtropical forest, a tropical rain forest, and two grassland sites. Therefore, the assumption that LUE is independent of the quality of radiation and GPP linearly increases with absorbed photosynthetic radiation would induce underestimation/overestimation of GPP in cloudy/clear skies [22,23].
Conceptually, a canopy is composed of clumps of sunlit and shaded leaves exposed to different levels of irradiance and showing variable LUE. Sunlit leaves receive both direct and diffuse radiation while shaded leaves mainly interact with diffuse beams. Under clear skies, solar irradiance is high and dominated by direct beams. Sunlit leaves are easily light saturated, and photosynthesis can even decrease with increasing radiation because of elevated temperature and enhanced photorespiration [13]. Consequently, the overall LUE of sunlit leaves is normally low [23]. In contrast, a large number of shaded leaves are only exposed to diffuse radiation, which is normally much lower than the radiation saturation point. Therefore, the photosynthesis of shaded leaves is typically light-limited. Under cloudy conditions, solar irradiance is dominated by diffuse sunlight, allowing shaded leaves to capture a large fraction of the solar irradiance. Even though the total incident radiation may be lower than that on clear days, the apparent improvement of the LUE for shaded leaves could lead to the enhanced LUE for the whole canopy [15,19].
More and more process models now calculate photosynthesis for sunlit and shade leaves separately [24,25,26]. However, this strategy has not been adopted by LUE models. To remedy this limitation, He et al. [23] recently developed a two-leaf LUE model on the basis of the MOD17 model. This new model considered differences in radiation absorption and in LUE of sunlit and shaded leaves. Validation at 6 ChinaFLUX sites demonstrated the improvement of the two-leaf LUE models over the MOD17 model in simulating GPP, especially at forest sites, with a R2 value increasing about 0.1 and a root mean square error (RMSE) value decreasing about 0.64 g C m−2 day−1 on average.
In the two-leaf LUE model developed by He et al. [23], GPP of sunlit and shaded leaves increases linearly with APAR. However, many studies have shown a nonlinear increase of photosynthesis of sunlit leaves with increasing APAR because of light saturation of photosynthesis, especially at short temporal scales (minutes to hours) [15,27,28,29,30,31]. Recently, Wang et al. [6] developed a two-leaf temperature and vegetation type dependent rectangular hyperbolic model, which links quantum yield (α) and maximum photosynthetic rate (Pm) with the maximum carboxylation rate at 25 °C. The model is able to simulate GPP as accurately as a process-based model.
Previously, linear LUE models have been mostly used to calculate GPP at daily, 8-day, and even longer temporal scales [7,8,9,10,32,33]. Recently, this type of models is used to calculate GPP at short temporal scales. For example, Carbon Tracker, a system to optimize terrestrial carbon flux, uses the Carnegie-Ames Stanford Approach (CASA) biogeochemical model to calculate GPP every three hours as the prior carbon flux [34]. Such application of linear LUE models might induce biases in simulated GPP since observations have indicated the nonlinear response of canopy GPP to incoming PAR at short temporal scales [15,27,28,29,30,31]. Therefore, the assessment of applicability of different types of LUE models in simulating GPP at different temporal scales is of great significance to improving the simulation of GPP using remote sensing data.
In this study, the ability of nonlinear two-leaf LUE, linear two-leaf LUE, and MOD17 to simulate GPP at half-hourly, daily, and 8-day temporal scales were verified using GPP derived from net ecosystem productivity (NEP) measured at globally distributed 58 sites as benchmarks. The main goals of this study are: (1) to compare the performance of the MOD17, linear and nonlinear two-leaf LUE models at three different temporal scales (half-hourly, daily and 8-day); (2) to analyze the possible causes for the different performances of three LUE models. For simplicity, the MOD17, linear two-leaf LUE, and nonlinear two-leaf LUE models will be referred to hereinafter as MOD17, TL-LUE, and TL-LUEn, respectively.
2. Data and Methods
2.1. Data
In this study, we used meteorological data and ecosystem fluxes measured with the eddy covariance (EC) technique at 58 sites pertaining to the FLUXNET network and the processed MODIS leaf area index (LAI) product (MOD15A2) to simulate GPP at half-hourly, daily and 8-day temporal scales. The meteorological and flux data belongs to the LaThuile FLUXNET dataset and can be freely downloaded [35]. The sites were selected on the basis of the availability of key datasets, such as LAI, meteorology, and land surface C fluxes. GPP derived from tower measured NEP was used as benchmarks for model parameter optimization and model evaluation. All flux data were processed in the manner proposed within the Fluxnet project [36,37] as described by [38,39,40,41]. The 58 sites included 21 needle-leaf-forest (NF) sites, with 1 deciduous needle-leaf-forest (DNF) sites and 20 evergreen needle-leaf-forest (ENF) sites, 11 broadleaf-forest (BF) sites, with 2 evergreen broadleaf-forest (EBF) sites and 9 deciduous broadleaf-forest (DBF) sites, 4 mixed-forest (MF) sites, 7 crop (CROP) sites, 7 grassland (GRASS) sites, and 8 shrub (SHRUB) sites, located in Asia, Europe, and North America (Figure 1). The observations covered the period from January 2001 to December 2007 with at least two years of data for each site. In total, 143 site-years of data were used, of which 85 site-years of data were selected for parameter optimization (17 BF, 11 CROP, 10 GRASS, 6 MF, 29 NF, and 12 SHRUB site-years). The remaining 58 site-years of data were used for model evaluation, with one year of data for each site. Detailed information about each site is given in Table 1.
Figure 1.
Distribution of all sites with data used for parameter optimization and validation in this study. The background is the MODIS global land cover product (MCD12C1) in 2003.

Table 1.
Name, location, vegetation type, and period of data used for each site.
| Site Name | Country | Lat. (°) | Long. (°) | Veg. Type | Opti. Years | Vali. Years | Reference |
|---|---|---|---|---|---|---|---|
| Austin Cary (ACA) | USA | 29.74 | −82.22 | NF | 2003 | 2005 | Gholz and Clark (2002) [42] |
| ARM_SGP_Main (ASM) | USA | 36.61 | −97.49 | CROP | 2003 | 2004 | Fischer et al. (2007) [43] |
| Audubon (AUD) | USA | 31.59 | −110.51 | GRASS | 2003 | 2004 | Wilson and Meyers (2007) [44] |
| BC-DFir1949 (BD49) | Canada | 49.87 | −125.33 | NF | 2003 | 2004 | Humphreys et al. (2006) [45] |
| Bartlett Experimental (BEP) | USA | 44.06 | −71.29 | BF | 2005 | 2006 | Jenkins et al. (2007) [46] |
| BC-Harvest Dfir2000 (DF00) | Canada | 49.87 | −125.29 | NF | 2003 | 2004 | Humphreys et al. (2006) [45] |
| BC-Harvest Dir1988 (DF88) | Canada | 49.53 | −124.9 | NF | 2004 | 2005 | Humphreys et al. (2006) [45] |
| Bondville (BON) | USA | 40.01 | −88.29 | CROP | 2004,2005 | 2006 | Wilson and Meyers (2007) [44] |
| Changbaishan (CBS) | China | 42.40 | 128.10 | MF | 2003 | 2004 | Zhang et al. (2006a,b) [47,48] |
| Dinghushan(DHS) | China | 23.17 | 112.53 | BF | 2003 | 2004 | Zhang et al. (2000) [49] |
| Donaldson (DON) | USA | 29.75 | −82.16 | NF | 2003 | 2004 | Gholz and Clark (2002) [42] |
| El Saler (ES) | Spain | 39.35 | −0.32 | NF | 2001,2002 | 2003 | Reichstein et al. (2006) [50] |
| Fort Peck (FPE) | USA | 48.31 | −105.1 | GRASS | 2003 | 2004 | Wilson and Meyers (2007) [44] |
| Fyodorovskoye (FY) | Russia | 56.46 | 32.92 | NF | 2001 | 2003 | Milyukova et al. (2002) [51] |
| Goodwin Creek (GCR) | USA | 34.25 | −89.87 | GRASS | 2004,2005 | 2006 | Wilson and Meyers (2007) [44] |
| Hainich (HA) | Germany | 51.08 | 10.45 | BF | 2001,2002 | 2003 | Mund et al. (2010) [52] |
| Harvard Forest (HAF) | USA | 42.54 | −72.17 | BF | 2005 | 2006 | Urbanski et al. (2007) [53] |
| Haibei (HB) | China | 37.67 | 101.33 | GRASS | 2003 | 2004 | He et al. (2013) [23] |
| Hesse (HES) | France | 48.67 | 7.07 | BF | 2001,2002 | 2003 | Granier et al. (2002) [54] |
| Howland Forest (HOF) | USA | 45.2 | −68.74 | MF | 2003 | 2004 | Hollinger et al. (1999, 2004) [55,56] |
| Hyytiala (HY) | Finland | 61.85 | 24.29 | NF | 2001 | 2002 | Kramer et al. (2002) [57] |
| Kendall (KED) | USA | 31.74 | −109.94 | GRASS | 2006 | 2007 | Scott (2010) [58] |
| Kennedy (KEN) | USA | 28.61 | −80.67 | SHRUB | 2004 | 2005 | Powell et al. (2006) [59] |
| Loobos (LOB) | Netherlands | 52.17 | 5.74 | NF | 2001,2002 | 2003 | Dolman et al. (2002) [60] |
| Mead Irrigated (MEI) | USA | 41.17 | −96.48 | CROP | 2003,2004 | 2005 | Verma et al. (2005) [61] |
| Mead Rainfed (MER) | USA | 41.18 | −96.44 | CROP | 2004 | 2005 | Verma et al. (2005) [61] |
| Metolius Intermediate (MIN) | USA | 44.45 | −121.56 | NF | 2005 | 2007 | Law et al. (2003) [62] and Thomas et al. (2009) [63] |
| Mead Irrigated Rotation (MIR) | USA | 41.16 | −96.47 | CROP | 2004 | 2005 | Verma et al. (2005) [61] |
| Mize (MIZ) | USA | 29.76 | −82.24 | SHRUB | 2003 | 2004 | Brocha et al. (2012) [64] |
| Morgan Monroe State (MMS) | USA | 39.32 | −86.41 | BF | 2003,2005 | 2006 | Schmid et al. (2000) [65] |
| Metolius New Young Pine (MNY) | USA | 44.32 | −121.6 | NF | 2004 | 2005 | Ruehr et al. (2012) [66] and Vickers et al. (2012) [67] |
| Missouri Ozark (MOZ) | USA | 38.74 | −92.2 | BF | 2005,2006 | 2007 | Gu et al. (2006) [68] |
| North Carolina Loblolly Pine (NCL) | USA | 35.8 | −76.67 | NF | 2005 | 2006 | Noormets et al. (2009) [69] |
| Neustift (NEU) | Austria | 47.12 | 11.32 | GRASS | 2002 | 2003 | Wohlfahrt et al. (2008) [70] |
| Niwot Ridge (NR) | USA | 40.03 | −105.55 | NF | 2003,2006 | 2007 | Monson et al. (2002) [71] |
| ON EpeatlandMerBleue (OEM) | Canada | 45.41 | −75.52 | SHRUB | 2001 | 2004 | Lafleur et al. (2003) [72] |
| Puechabon (PUE) | France | 43.74 | 3.6 | BF | 2001,2002 | 2003 | Allard et al. (2008) [73] |
| QC-Black Spruce (QMB) | Canada | 49.69 | −74.34 | NF | 2004 | 2005 | Bergeron et al. (2007) [74] |
| Qianyanzhou(QYZ) | China | 26.73 | 115.07 | NF | 2003 | 2004 | Yu et al. (2006) [75] |
| Renon (REN) | Italy | 46.59 | 11.43 | NF | 2002 | 2003 | Montagnani et al. (2009) [76] |
| Rosemount G19 (RG19) | USA | 44.72 | −93.09 | CROP | 2004,2005 | 2006 | Griffis et al. (2008) [77] |
| Rosemount G21 (RG21) | USA | 44.71 | −93.09 | CROP | 2004,2005 | 2006 | Bavin et al. (2009) [78] |
| Roccarespampani1 (ROC) | Italy | 42.39 | 11.92 | BF | 2002 | 2003 | Keenan et al. (2009) [79] |
| Sky Oaks New (SON) | USA | 33.38 | −116.64 | SHRUB | 2004,2005 | 2006 | Luo et al. (2007) [80] |
| Soroe (SOR) | Denmark | 55.48 | 11.65 | MF | 2001,2002 | 2003 | Pilegaard et al. (2001) [81] |
| Santa Rita Mesquite (SRM) | USA | 31.82 | −110.87 | SHRUB | 2004,2005 | 2006 | Scott (2010) [58] |
| San Rossore (SRO) | Italy | 43.73 | 10.29 | NF | 2001,2002 | 2003 | Migliavacca et al. (2011) [82] |
| Tharandt (THA) | Germany | 50.96 | 13.57 | NF | 2001,2002 | 2003 | Grünwald and Bernhofer (2007) [83] |
| Tomakomai (TMK) | Japan | 42.74 | 141.52 | NF | 2001,2002 | 2003 | Hirano et al. (2003) [84] |
| Tonzi Ranch (TRA) | USA | 38.43 | −120.97 | SHRUB | 2004,2005,2006 | 2007 | Baldocchi et al. (2004) [85] |
| UCI 1850 (U50) | Canada | 55.88 | −98.48 | NF | 2003 | 2004 | Goulden et al. (2011) [86] |
| UCI 1989 (U89) | Canada | 55.92 | −98.96 | SHRUB | 2003 | 2004 | Goulden et al. (2011) [86] |
| UCI 1998 (U98) | Canada | 56.64 | −99.95 | SHRUB | 2003 | 2004 | Goulden et al. (2011) [86] |
| UMBS (UMBS) | USA | 45.56 | −84.71 | BF | 2003,2004 | 2006 | Curtis et al. (2005) [87] |
| Vaira Ranch (VRA) | USA | 38.41 | −120.95 | GRASS | 2003,2004 | 2007 | Baldocchi et al. (2004) [85] |
| Vielsalm (VSA) | Belgium | 50.31 | 6.00 | MF | 2001,2002 | 2003 | Aubinet et al. (2001) [88] |
| Willow Creek (WCR) | USA | 45.81 | −90.08 | BF | 2003 | 2005 | Bolstad et al. (2004) [89] |
| Wetzstein (WET) | Germany | 50.45 | 11.46 | NF | 2002 | 2003 | Rebmann et al. (2009) [90] |
2.2. Methods
2.2.1. Models Used
TL-LUEn, TL-LUE, and MOD17 models were used in this study. The MOD17 algorithm is described in detail in Running et al. [8,91]. It relies on the assumption that GPP is linearly related to APAR [11,12,92]. The TL-LUE model stems from the MOD17 algorithm and discriminates the differences of upper and bottom canopy in receiving direct radiation and diffuse radiation and in their LUE. As a consequence, canopy GPP simulated by TL-LUE nonlinearly changes with incoming PAR. The TL-LUEn adopts the same methodology as the TL-LUE model to separate sunlit and shaded leaves and calculate their APAR. However, it takes the rectangular hyperbolic model to calculate GPP for sunlit and shaded leaves. The MOD17, TL-LUE, and TL-LUEn models are described in Equations (1–3), respectively, i.e.,
where εmax is the maximum LUE in MOD17; fPAR is the fraction of PAR absorbed by vegetation and calculated from LAI using the Beer’s Law (fPAR=1-e−k*LAI, where k is the light extinction coefficient and set as 0.5 as [23]); εmsu and εmsh are the maximum LUE of sunlit and shaded leaves in TL-LUE, respectively; εm is the quantum yield when incident PAR approaches zero and β is the maximum canopy photosynthetic flux density at light saturation in TL-LUEn [13]; f(VPD) and g(Tamin) denote the constrains imposed by atmospheric vapor pressure deficit (VPD) and minimum air temperature, respectively, and are used to downscale the maximum LUE values to real ones. APARmsu and APARmsh are the PAR absorbed by sunlit and shaded leaves per unit LAI; LAImsu and LAImsh are the leaf area index for sunlit and shaded leaves.
In above equations, the two attenuation scalars, f(VPD) and g(Tamin), range from 0 (total inhibition) to 1 (no inhibition) and are calculated using the same formulas for MOD17, TL-LUE, and TL-LUEn. Parameters VPDmax, VPDmin, Tamin_min, and Tamin_max used to calculate f(VPD) and g(Tamin) depend on vegetation types [91] and are listed in Table 2.
In Equations (2) and (3), APARmsu and APARmsh are calculated as:
where α is the albedo varying with vegetation types (Table 2), PARdif and PARdir are the diffuse and direct components of incoming PAR, respectively, and they are empirically calculated (see Equation (6)); PARdif,u is the diffuse PAR under the canopy and calculated following [24]; (PARdif – PARdif,u)/LAI denotes the absorbed diffuse PAR per unit leaf area within the canopy; C indicates multiple scattering of total PAR within the canopy [24]; φ is the mean leaf-sun angle and set as 60º[24]; θ is the mean solar zenith angles of half an hour, a day, and 8 days. The average solar zenith angle in each half an hour is calculated according to latitude, Julian day, and local time [93]. The average solar zenith angle in a given day is calculated according to latitude and Julian day [24]. The 8-day average solar zenith angle is the mean of the daily average solar zenith angles during the 8 days period.
Diffuse and direct PAR are empirically partitioned as [24]:
where PARdif is the estimated diffuse PAR; R is the sky clearness index (R=S/(S0cosθ)), S and S0 are the incoming solar radiation on the ground surface and solar constant (1367 Wm−2), respectively. In the conversion of incoming solar radiation into PAR, a constant of 0.5 is used [23] (PAR=0.5S).
LAImsu and LAImsh in Equations (2) and (3) are calculated as [24]:
where Ω is the clumping index, which changes with land cover types, season and solar zenith angle. It was only assigned according to vegetation types here (Table 2) since spatially and temporally variant data are not available for this parameter.

Table 2.
Model parameters used for different vegetation types.
| Vegetation Type* | DBF | ENF | EBF | MF | GRASS | CROP | savannas | OS | WS |
|---|---|---|---|---|---|---|---|---|---|
| εmax (g C/MJ)** | 1.044 | 1.008 | 1.259 | 1.116 | 0.604 | 0.604 | 0.888 | 0.774 | 0.768 |
| Tamin_max (°C) | 7.94 | 8.31 | 9.09 | 8.5 | 12.02 | 12.02 | 8.61 | 8.8 | 11.39 |
| Tamin_min (°C) | −8 | −8 | −8 | −8 | −8 | −8 | −8 | −8 | −8 |
| VPDmax (kpa) | 4.1 | 4.1 | 4.1 | 4.1 | 4.1 | 4.1 | 4.1 | 4.1 | 4.1 |
| VPDmin (kpa) | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 9.3 |
| Albedo | 0.18 | 0.15 | 0.18 | 0.17 | 0.23a | 0.23b | 0.16 | 0.16 | 0.23 |
| Clumping index (Ωc) | 0.8 | 0.6 | 0.8 | 0.7 | 0.9 | 0.9 | 0.8 | 0.8 | 0.8 |
*DBF: deciduous broadleaf forest; ENF: evergreen needleleaf forest; EBF: evergreen broadleaf forest; MF: mixed forest; GRASS: grassland; CROP: cropland; savannas: savannas; OS: open shrublands; WS: woody savannas; a Tang et al. [94]. b Grant et al. [95]. c Singarayer et al. [96]; ** Running et al. [91].
2.2.2. Parameter Optimization
The derived GPP in 85 calibration site-years was used to optimize parameters in MOD17, TL-LUEn, and TL-LUE models. The optimization was implemented using the Markov chain Monte Carlo (MCMC) method [97,98]. In the optimization, three models were driven using the same locally measured meteorological data and smoothed MODIS LAI. The MCMC simulation, as a stochastic simulation method, is based on Bayesian Theory, in which parameters are random variables instead of deterministic, but unknown constants in the classic thoughts. The fundamental formula of Bayesian Theory is:
where π(θ | x) is the posterior density of parameter (a term distribution under the condition of given sample x); π(θ) is the prior distribution of parameter (the knowledge possessed before measurement); and p(x | θ) is a likelihood function.
To determine the posterior density π(θ|x), the prior density and the likelihood function should be given in advance. We specified the prior density function as a uniform distribution over the following ranges:
The lower and upper limits of εm (unit: g C MJ−1) and (unit: µg C m−2 s−1) were set according to the values compiled from 100 published datasets by Ruimy et al. [99]. The upper limits of εmsu, εmsh and εmax (unit: g C MJ−1) were assigned on the basis of previous findings [32,100]. In the optimization, these parameters were assumed uniformly distributed in the given limits with equal probability for all possible values.
The likelihood function was specified according to the distribution of simulation errors, which were assumed following a multivariate Gaussian distribution with a zero mean. This assumption is commonly made in many studies [101,102,103]. With this assumption, the likelihood function can be written as:
where Oi and Pi are the tower-derived GPP and simulated GPP, respectively; are the standard error of tower-derived GPP.
The sampling of parameters was implemented using the Metropolis-Hastings (M-H) algorithm. To find an effective proposal distribution, we first made a test run of the algorithm with 50,000 simulations. Based on the test run, a Gaussian distribution N(0, cov0(θ)) was constructed (cov0(θ) is a diagonal matrix with its diagonal elements equal to the estimated variances of parameters θ). Then, the following proposal distribution was adopted to execute the consecutive MCMC simulations formally for 30,000 times:
where θk is the new parameters generated from its predecessor θk−1.
The running means and standard deviations of parameter samples need time to approach stable. For bettering the statistical analysis of parameters, we discarded the initial 10,000 samples in the burn-in period and only used the remaining 20,000 samples for further analysis of each parameter. The histograms of the samples for each parameter indicate these parameters were well constrained in most situations because the posterior density functions were near the normal distribution (see Figure A1 in Appendix). Uncertainties of estimated parameters were quantified with a 95% highest-probability density interval. Means of parameter θi were estimated as followings and used for model validation:
where N is the number of samples in the M-H algorithm.
2.2.3. Parameter Sensitivity Analysis
Sensitivity of simulated GPP to parameters in three LUE models was analyzed using the factorial approach [104,105,106]. This method facilitates the statistically based representation of combinations of errors in several parameter sets. For a two-level complete factorial design, each of the model parameters is assigned upper and lower values based on specified perturbations of the magnitudes of the parameters, and the model is run using all combinations of parameter values. For n different parameters, this would require 2n simulation runs. Each parameter here was perturbed by an arbitrary magnitude ±10% [105].
The main effect of a parameter, which is also referred to the parameter sensitivity, is calculated as the average difference between a run in which the parameter is at its upper level (+10%) and a run in which the parameter at its lower level (−10%), but other parameters remain unchanged. For example, there are 4 simulation runs for TL-LUEn when considering the parameters εm and β. They are both εm and β at their lower levels (simulation #1), εm at its upper level and β at its lower level (simulation #2), εm at its lower level and β at its upper level (simulation #3), and both εm and β at their upper levels (simulation #4). The main effect of εm in TL-LUEn are the average of the difference between simulation #2 and simulation #1, and the difference between simulation #4 and simulation #3. A larger value of main effect indicates higher sensitivity of simulated GPP.
2.2.4. Model Performance Assessment
The performance of TL-LUEn, TL-LUE, and MOD17 was assessed using root mean square error (RMSE) and determination coefficient (R2). The paired t test was then conducted to evaluate the significance regarding the differences in R2, RMSE between TL-LUEn and TL-LUE, TL-LUEn and MOD17, and TL-LUE and MOD17 when all vegetation types lumped together at three temporal scales for model evaluation, respectively [13].
3. Results
3.1. Optimized Model Parameters
Table 3 shows the averages of optimized εm, εmax, εmsu and εmsh for 6 different vegetation types at half-hourly, daily and 8-day temporal scales, respectively. εm was generally larger than εmsh, εmsu, and εmax. It increased sizably when the temporal scales increasing from half-hourly to 8-day, especially for CROP. CROP always had the highest εm in all the three temporal scales. At the half-hourly scale, three forest types, including BF, MF and NF, had lower εm values than CROP and SHRUB, but higher than GRASS. Through metadata analysis for more than 100 published datasets, Ruimy et al. [99] reported that CROP has the highest εm (about 5.17 g C MJ−1) at the half-hourly scale, followed by forests (about 4.37 g C MJ−1, mainly BF sites), and GRASS has the smallest one (about 2.71 g C MJ−1), similar to the identified changes of εm with vegetation types here.
Optimized εmax was in between εmsh and εmsu for all vegetation types and at all temporal scales. εmsh is larger than εmsu and εmax due to the fact that shaded leaves are only exposed to diffuse radiation, which enters a canopy from all directions and distributes more evenly than direct radiation within the canopy [107,108]. The intensity of light absorbed by shaded leaves is normally lower than light saturation point. Thus, they have higher light use efficiency than sunlit leaves. The values of εmax, εmsu and εmsh showed smaller variations than εm across three temporal scales (Table 3). As expected, CROP had the highest εmax, εmsu, and εmsh values, which are 1.78, 1.21 and 5.23 g C MJ−1 at the half-hourly scale, 1.80, 0.95 and 4.67 g C MJ−1 at the daily temporal scale, and 1.80, 0.96 and 4.26 g C MJ−1 at the 8-day scale, respectively. MF had the second largest ones, followed by BF and NF. GRASS had the lowest εmax, εmsu and εmsh values among all 6 vegetation types. The εmax, εmsu and εmsh of GRASS were lower than half of the corresponding values of CROP at the three temporal scales, respectively. In general, the average optimized εmax was close to the default values used in the MOD17 algorithm (Table 2) for all vegetation types except CROP, which had much higher optimized εmax than the default (0.604 g C MJ−1). Many studies have indicated that the underestimation of CROP GPP by the MOD17 algorithm is mainly due to the low value of εmax used [109]. It has been reported that the mean LUE of croplands can approach 2.80 g C MJ−1 [110,111,112], slightly higher than the average value of about 2.0 g C MJ−1 optimized in this study.
The parameter β in the TL-LUEn model showed complex changes with temporal scales and vegetation types. At the half-hourly scale, non-forest types had a relatively higher β value than forests, which is consistent with the findings reported by Ruimy et al. [99] and Wang et al. [6]. At the daily temporal scale, GRASS had the highest β (286.28 µg C m−2 s−1), followed by CROP, NF, MF, SHRUB and BF. At the 8-day temporal scale, the β values of BF, CROP, GRASS, MF, NF and SHRUB were 163.58, 214.64, 483.41, 267.39, 335.02, and 369.31 µg C m−2 s−1, respectively

Table 3.
Average, standard deviation, variation of coefficient (CV), and uncertainties range of optimized εm, β, εmsu, εmsh and εmax for 6 different vegetation types at half-hourly, daily and 8-day temporal scales (εm, β in TL-LUEn, εmsu, εmsh in TL-LUE, and εmax in MOD17). The uncertainty was quantified with a 95% highest-probability density interval and averaged over each biome.
| εm (g C MJ−1) | β (µg C m−2 s−1) | εmsu (g C MJ−1) | εmsh (g C MJ−1) | εmax (g C MJ−1) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | CV (%) | Uncertainty | Mean | STD | CV(%) | Uncertainty | Mean | STD | CV(%) | Uncertainty | Mean | STD | CV(%) | Uncertainty | Mean | STD | CV(%) | Uncertainty | |
| Half-hourly | ||||||||||||||||||||
| BF | 3.52 | 1.72 | 48.93 | ±1.32 | 147.84 | 112.19 | 75.88 | ±77.50 | 0.58 | 0.15 | 25.20 | ±0.10 | 2.37 | 0.68 | 28.94 | ±0.39 | 0.88 | 0.24 | 27.39 | ±0.09 |
| CROP | 4.34 | 1.07 | 24.64 | ±1.46 | 470.48 | 235.03 | 49.96 | ±177.09 | 1.21 | 0.39 | 32.06 | ±0.16 | 5.23 | 1.90 | 36.34 | ±0.91 | 1.78 | 0.62 | 35.07 | ±0.16 |
| GRASS | 2.14 | 1.35 | 63.22 | ±1.13 | 273.55 | 333.25 | 121.83 | ±143.44 | 0.48 | 0.23 | 48.42 | ±0.16 | 1.69 | 1.06 | 62.74 | ±0.70 | 0.64 | 0.37 | 58.17 | ±0.14 |
| MF | 3.59 | 0.97 | 27.14 | ±1.27 | 214.63 | 83.46 | 38.89 | ±91.48 | 0.78 | 0.18 | 22.77 | ±0.13 | 3.33 | 0.83 | 24.91 | ±0.45 | 1.26 | 0.24 | 19.20 | ±0.11 |
| NF | 2.79 | 2.19 | 78.67 | ±0.92 | 308.14 | 272.11 | 88.31 | ±161.84 | 0.66 | 0.22 | 33.20 | ±0.16 | 2.35 | 0.79 | 33.57 | ±0.56 | 0.88 | 0.29 | 33.24 | ±0.11 |
| SHRUB | 2.41 | 3.48 | 144.64 | ±0.94 | 540.16 | 481.89 | 89.21 | ±242.72 | 0.53 | 0.17 | 32.29 | ±0.20 | 1.70 | 0.63 | 37.08 | ±0.95 | 0.65 | 0.24 | 36.44 | ±0.21 |
| Daily | ||||||||||||||||||||
| BF | 4.39 | 3.10 | 70.56 | ±1.05 | 99.88 | 93.92 | 94.04 | ±16.16 | 0.47 | 0.16 | 34.76 | ±0.02 | 2.06 | 0.63 | 30.47 | ±0.06 | 0.95 | 0.29 | 30.23 | ±0.02 |
| CROP | 12.02 | 5.05 | 42.06 | ±2.85 | 189.06 | 79.53 | 42.06 | ±23.26 | 0.95 | 0.30 | 31.47 | ±0.02 | 4.67 | 1.55 | 33.27 | ±0.12 | 1.80 | 0.58 | 32.19 | ±0.03 |
| GRASS | 6.06 | 5.94 | 98.14 | ±3.46 | 286.28 | 399.60 | 139.58 | ±143.94 | 0.44 | 0.26 | 58.18 | ±0.05 | 1.56 | 0.98 | 62.91 | ±0.17 | 0.69 | 0.44 | 63.51 | ±0.04 |
| MF | 3.41 | 0.73 | 21.48 | ±0.32 | 147.65 | 53.43 | 36.19 | ±14.80 | 0.61 | 0.14 | 22.19 | ±0.02 | 2.97 | 0.65 | 21.98 | ±0.06 | 1.40 | 0.26 | 18.76 | ±0.02 |
| NF | 2.69 | 1.79 | 66.53 | ±0.59 | 152.09 | 77.61 | 51.03 | ±36.93 | 0.54 | 0.15 | 28.38 | ±0.05 | 2.21 | 0.74 | 33.31 | ±0.11 | 0.98 | 0.32 | 32.24 | ±0.02 |
| SHRUB | 5.60 | 3.86 | 68.87 | ±5.13 | 105.57 | 51.30 | 48.59 | ±25.56 | 0.44 | 0.15 | 33.76 | ±0.05 | 1.84 | 0.64 | 34.68 | ±0.26 | 0.75 | 0.21 | 28.66 | ±0.05 |
| 8-day | ||||||||||||||||||||
| BF | 4.64 | 2.78 | 59.92 | ±1.37 | 163.58 | 271.85 | 166.19 | ±84.65 | 0.53 | 0.18 | 34.42 | ±0.11 | 1.83 | 0.59 | 32.27 | ±0.19 | 0.97 | 0.30 | 31.04 | ±0.05 |
| CROP | 14.79 | 5.21 | 35.26 | ±2.28 | 214.64 | 197.90 | 92.20 | ±82.78 | 0.96 | 0.27 | 27.95 | ±0.09 | 4.26 | 1.59 | 37.44 | ±0.31 | 1.80 | 0.58 | 32.00 | ±0.09 |
| GRASS | 3.19 | 3.93 | 123.31 | ±1.20 | 483.41 | 489.70 | 101.30 | ±192.63 | 0.48 | 0.29 | 59.81 | ±0.14 | 1.33 | 0.79 | 58.88 | ±0.28 | 0.70 | 0.45 | 64.58 | ±0.10 |
| MF | 2.39 | 0.38 | 15.97 | ±0.71 | 267.39 | 172.78 | 64.62 | ±150.71 | 0.79 | 0.18 | 22.48 | ±0.23 | 2.51 | 0.63 | 24.95 | ±0.31 | 1.45 | 0.27 | 18.64 | ±0.07 |
| NF | 2.31 | 1.66 | 71.68 | ±0.79 | 335.02 | 341.62 | 101.97 | ±206.24 | 0.68 | 0.25 | 36.09 | ±0.17 | 1.81 | 0.63 | 34.79 | ±0.28 | 1.01 | 0.34 | 33.65 | ±0.07 |
| SHRUB | 2.08 | 1.61 | 77.58 | ±1.19 | 369.31 | 399.01 | 108.04 | ±242.47 | 0.47 | 0.14 | 30.39 | ±0.14 | 1.62 | 0.77 | 47.12 | ±0.33 | 0.74 | 0.22 | 29.68 | ±0.13 |
3.2. Model Performance in Calibration Site-Years
At the half-hourly scale, TL-LUEn showed slightly better performance than TL-LUE when data in all 85 calibration site-years were lumped together (Figure 2). With the increase of temporal scales from half an hour to 8 days, the difference of TL-LUEn and TL-LUE became almost indistinguishable. The improvement of both TL-LUE and TL-LUEn over MOD17 was obvious at all three temporal scales. At the half-hourly scale, the average RMSE of MOD17 were larger than that of TL-LUEn by 8.1 mg C m−2 (30min)−1, and the corresponding average R2 was lower than that of TL-LUEn by 0.050 (Figure 2a,b). At the daily scale, MOD17 output an average RMSE higher by 0.3 g C m−2 day−1 and R2 lower by 0.051 than TL-LUEn (Figure 2c,d). As to the 8-day scale, the average RMSE of MOD17 was 1.0 g C m−2 8days−1 larger than that of TL-LUEn, and the corresponding average R2 was 0.025 lower than that of TL-LUEn (Figure 2e,f).
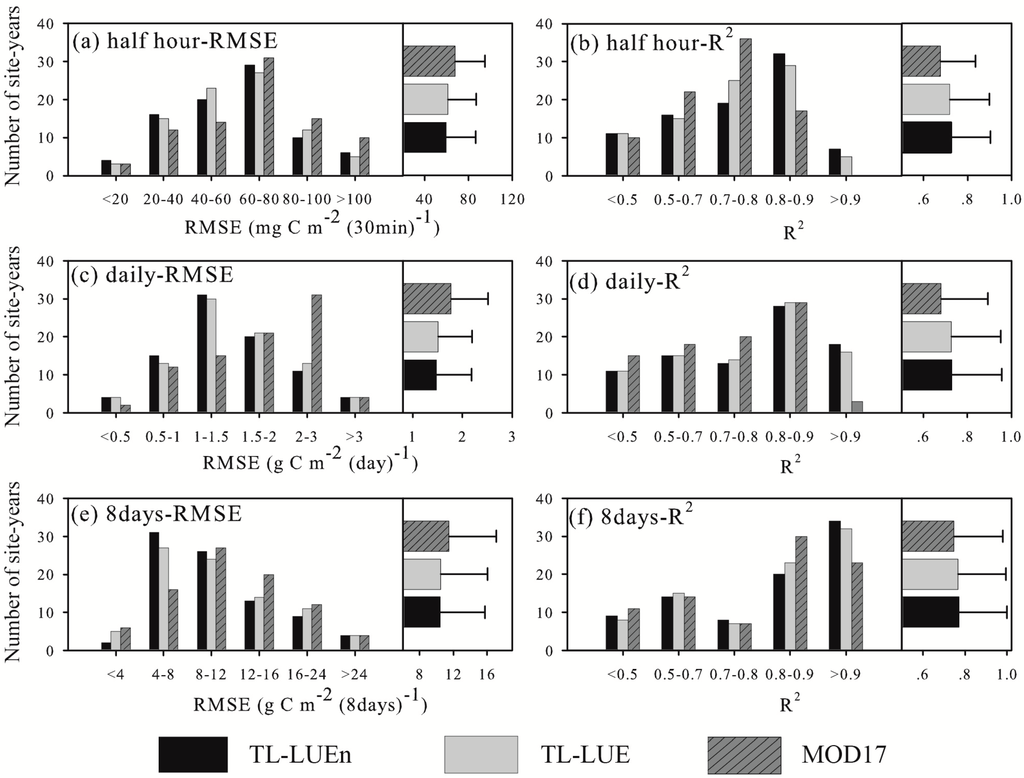
Figure 2.
The number of site-years within different root mean square error (RMSE) and R2 classes (left) and the averages of RMSE and R2 (right) of GPP simulated using the TL-LUEn, TL-LUE, and MOD17 models in 85 calibration site-years at half-hourly (a,b), daily (c,d), and 8-day (e,f) temporal scales, respectively.
At three different temporal scales, the number of site-years in the same RMSE and R2 classes was similar for TL-LUEn and TL-LUE, confirming their similar ability to simulate GPP (see Figure 2). MOD17 performed poorer than TL-LUEn and TL-LUE in most site-years, indicated by larger RMSE and smaller R2. For example, at the half-hourly temporal scale, the number of site-years with small RMSE values (below 60 mg C m−2 (30min)−1), was 29 for MOD17, 40 for TL-LUEn, and 41 for TL-LUE, respectively. The R2 of GPP simulated by MOD17 was mostly in the range of 0.5–0.8 (in 58 site-years) while the R2 of GPP simulated by the TL-LUEn and TL-LUE mostly ranged from 0.7 to 0.9 (58 site-years for TL-LUEn and 59 site-years for TL-LUE).
TL-LUEn performed better than TL-LUE for most vegetation types except CROP at the half-hourly and daily scale. However, it performed no better than TL-LUE for MF, NF and SHRUB at the 8-day scale (see Figure 3). Both TL-LUEn and TL-LUE outperformed MOD17 for most vegetation types at three temporal scales except for CROP at the half-hourly scale. The superiority of TL-LUEn and TL-LUE over MOD17 was most significant at forest sites.
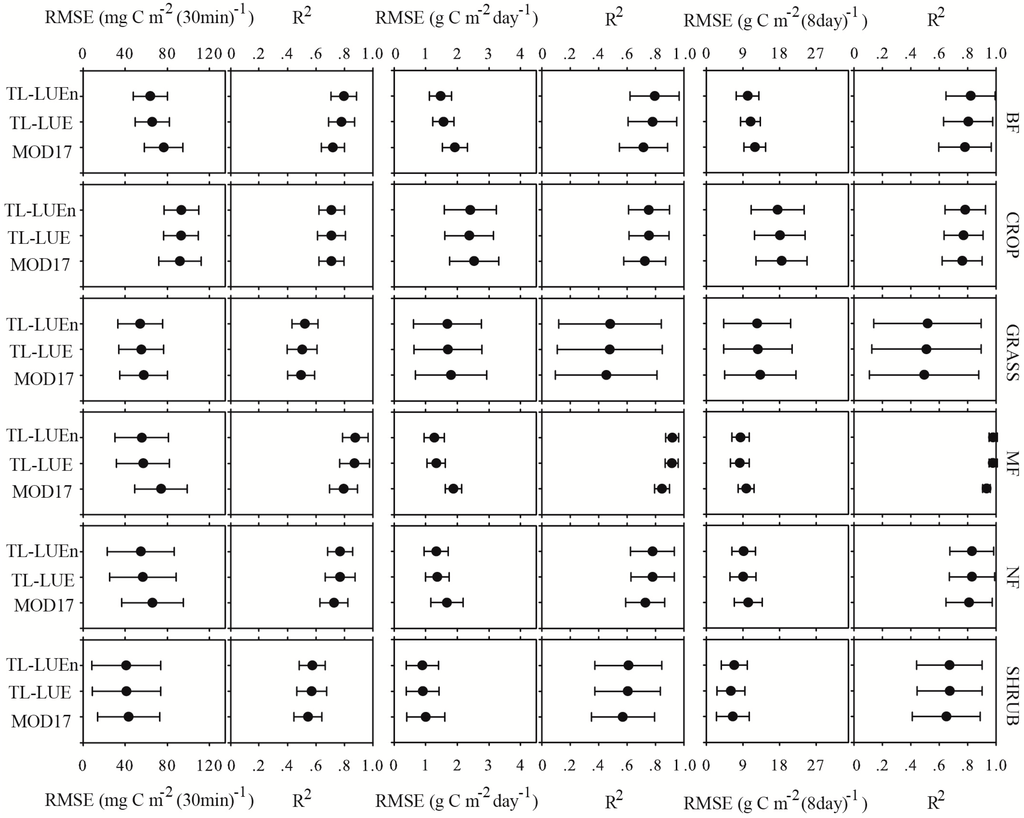
Figure 3.
Average RMSE and R2 of GPP simulated using calibrated TL-LUEn, TL-LUE and MOD17 in the calibration site-years at half-hourly (the first and second columns), daily (the third and fourth columns), and 8-day (the last two columns) scales for individual vegetation types. Note: Broadleaf forest (BF); Mixed forest (MF); Needleleaf forest (NF); Crop (CROP); Grass (GRASS); Shrub (SHRUB). Solid black circles are the means and horizontal error bars denote standard deviations.
3.3. Model Performance in Evaluation Site–years
3.3.1. Model Performance at the Half-hourly Scale
Model evaluation shows that TL-LUEn performed slightly better than TL-LUE in simulating half-hourly GPP when data in all 58 validation site-years was lumped together (Figure 4a,b). The RMSE and R2 of GPP simulated using TL-LUE against measurements averaged 64.3 mg C m−2 (30min)−1 and 0.732, respectively, while the corresponding values of TL-LUEn were 63.9 mg C m−2 (30min)−1 and 0.735, respectively. However, the differences in RMSE value between TL-LUEn and TL-LUE were not significant (p = 0.45) as well as the differences in R2 between the two models (p = 0.27) (Table 4). The performance of MOD17 was the poorest, with average RMSE and R2 values equaled to 70.1 mg C m−2 (30min)−1 and 0.690, respectively. In addition, the differences in both the two statistics (RMSE, R2) between TL-LUEn and MOD17, and TL-LUE and MOD17 were significant, with p values smaller than 0.0001 (Table 4).
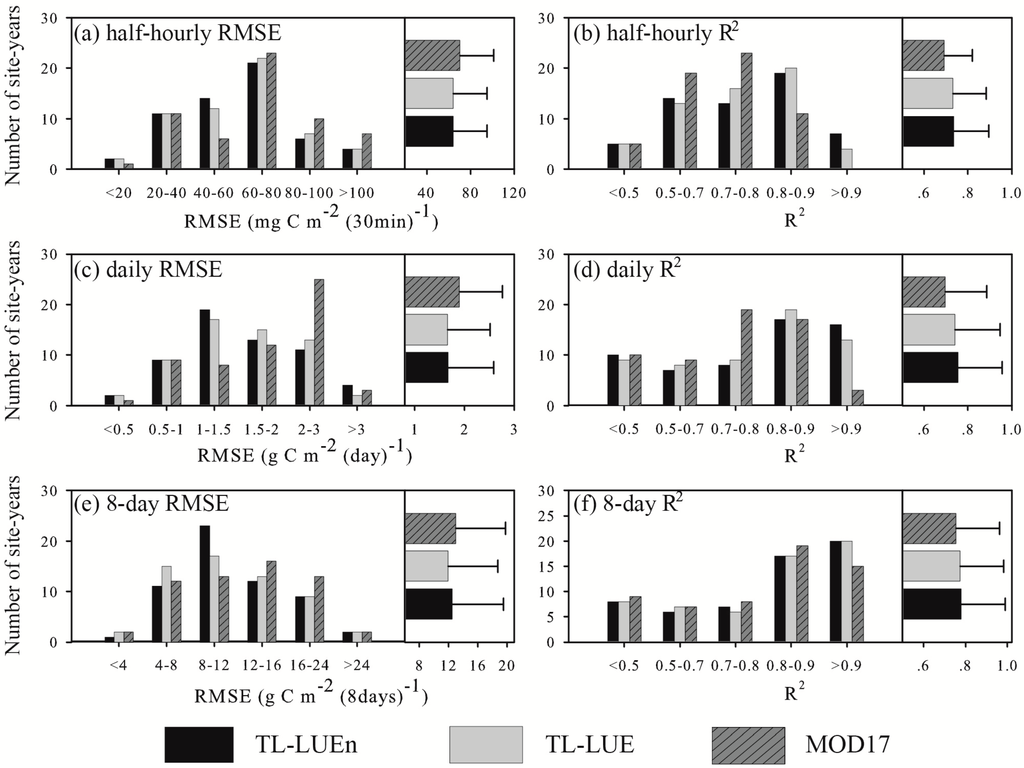
Figure 4.
The number of site-years within different RMSE and R2 classes (left) and the averages of RMSE and R2 (right) of gross primary productivity (GPP) simulated using the TL-LUEn, TL-LUE, and MOD17 models in 58 validation site-years at half-hourly (a,b), daily (c,d), and 8-day (e,f) temporal scales, respectively.
In 58 evaluation site-years, the RMSE of GPP simulated using TL-LUEn, TL-LUE, and MOD17 was larger than 80 mg C m−2 (30min)−1 at 10, 11 and 17 sites, respectively. The R2 of GPP simulated using MOD17 mostly ranged from 0.5 to 0.8 (at 42 sites) while the R2 of GPP simulated using TL-LUEn and TL-LUE was in the range from 0.7 to 0.9 at 39 and 40 sites, respectively (Figure 4a,b). TL-LUEn performed better than TL-LUE at 31 sites. The poorer performance of TL-LUEn relative to TL-LUE occurred at CROP, GRASS, SHRUB and NF sites. MOD17 only performed better than TL-LUE and TL-LUEn at 9 sites (Table A1 in the Appendix).

Table 4.
Statistics of the Paired t Tests on the differences between TL-LUEn and TL-LUE, TL-LUEn and MOD17, and TL-LUE and MOD17 in RMSE and R2 for model validation when all vegetation types lumped together at half-hourly, daily and 8-day scale.
| RMSE | R2 | |||||||
|---|---|---|---|---|---|---|---|---|
| TL-LUEn − TL-LUE | TL-LUEn − MOD17 | TL-LUE − MOD17 | TL-LUEn − TL-LUE | TL-LUEn − MOD17 | TL-LUE − MOD17 | |||
| Half-hourly | t stat | −0.75 | −4.33 | −5.09 | t stat | 1.12 | 6.10 | 7.13 |
| p | 0.45 | 0.00 | 0.00 | p | 0.27 | 0.00 | 0.00 | |
| Daily | t stat | 0.33 | −4.88 | −7.63 | t stat | 0.53 | 7.61 | 9.30 |
| p | 0.75 | 0.00 | 0.00 | p | 0.60 | 0.00 | 0.00 | |
| 8-day | t stat | 2.24 | −1.35 | −5.96 | t stat | 0.98 | 4.70 | 0.98 |
| p | 0.03 | 0.18 | 0.00 | p | 0.33 | 0.00 | 0.33 | |
Overall, TL-LUEn performed better than TL-LUE for BF, GRASS, MF and SHRUB, but poorer than TL-LUE for CROP and NF (see Figure 5). TL-LUEn and TL-LUE outperformed MOD17 for all vegetation types but CROP. The improvement of TL-LUE and TL-LUEn over MOD17 was most significant for forests (BF, MF and NF). Averaged over all forest sites, the RMSE of MOD17 was larger than those of TL-LUEn and TL-LUE by 10.1 mg C m−2 (30min)−1 and 8.8mg C m−2 (30min)−1, respectively. The corresponding average R2 of MOD17 was 0.063 and 0.060 lower than those of TL-LUEn and TL-LUE, respectively.
3.3.2. Model Performance at the Daily Scale
TL-LUEn showed better performance than TL-LUE at the daily scale when 58 validation site-year data was lumped together (Figure 4c,d). The average RMSE of GPP simulated by TL-LUEn and TL-LUE was both 1.7 g C m−2 day−1. The average R2 of GPP simulated by TL-LUEn was slightly larger than that of TL-LUE. Results of the paired t test on the differences in average RMSE value between TL-LUEn and TL-LUE were not significant (p = 0.75), as well as the differences in average R2 value between the two models (p = 0.60) (Table 4). The average RMSE value of MOD17 was 1.9 g C m−2 day−1. The average R2 value of MOD17 was smaller than the corresponding values of TL-LUEn and TL-LUE by 0.046 and by 0.045, respectively. In addition, the differences in average RMSE value and R2 value between TL-LUEn and MOD17, and TL-LUE and MOD17 were significant, with p values were all smaller than 0.0001.
In 58 validation site-years, MOD17 produced larger RMSE and lower R2 than TL-LUE and TL-LUEn at most sites. The RMSE of GPP simulated using MOD17, TL-LUE, and TL-LUEn was larger than 2.0 g C m−2 day−1 at 28, 15, and 15 sites, respectively. The values of R2 above 0.9 occurred at only 3 sites for MOD17, at 13 sites for TL-LUE, at 16 sites for TL-LUEn, respectively (Figure 4c,d). TL-LUEn showed better ability to simulate GPP than TL-LUE at 29 sites. MOD17 only outperformed TL-LUEn and TL-LUE at 12 and 8 sites, respectively, mainly CROP, SHRUB and GRASS sites (Table A2 in the Appendix).
As to MF, NF and SHRUB, TL-LUEn performed with a higher RMSE and R2 than TL-LUE. TL-LUEn only outperformed TL-LUE for BF, but performed poorer for CROP and GRASS (see Figure 5). Overall, TL-LUEn and TL-LUE outperformed MOD17 for forests and SHRUB. For three forest types, both TL-LUEn and TL-LUE outperformed MOD17. The average RMSE of both TL-LUEn and TL-LUE was 0.4 g C m−2 day−1 smaller than that of MOD17 while the average R2 of TL-LUEn and TL-LUE was 0.063 and 0.057 higher than that of MOD17, respectively. As to CROP and GRASS, both average RMSE and R2 of GPP simulated by TL-LUEn were higher than those of MOD17, while TL-LUE outperformed MOD17 with a smaller RMSE and a higher R2 (see Figure 5).
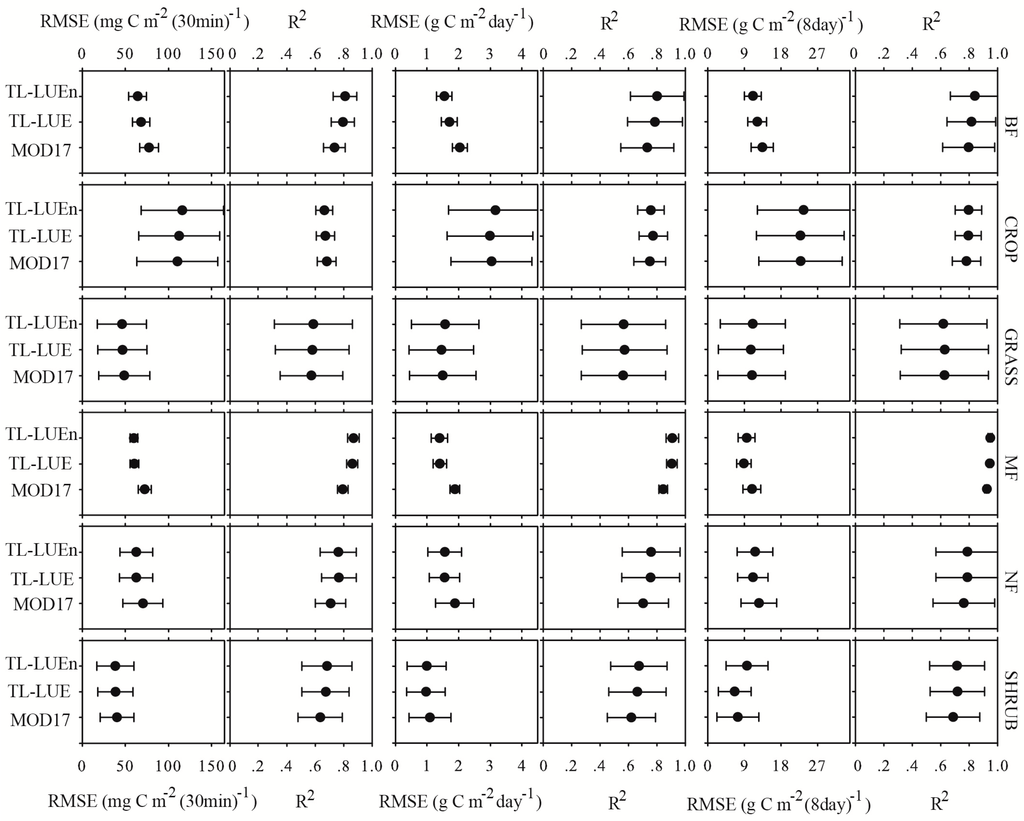
Figure 5.
Average RMSE and R2 of GPP simulated using calibrated TL-LUEn, TL-LUE and MOD17 in the validation site-years at half-hourly (the first and second columns), daily (the third and fourth columns), and 8-day (the last two columns) scales for individual vegetation types. Note: Broadleaf forest (BF); Mixed forest (MF); Needleleaf forest (NF); Crop (CROP); Grass (GRASS); Shrub (SHRUB). Solid black circles are the means and horizontal error bars denote standard deviations.
3.3.3. Model Performance at the 8-day Scale
When data in all 58 validation site-years was lumped together, TL-LUEn performed similarly with TL-LUE at the 8-day scale (Figure 4e,f). The differences between the two models were significant (p < 0.05) in average RMSE value but was not significant (p = 0.33) in average R2 value (Table 4). TL-LUEn outperformed MOD17 with significant differences (p < 0.05) in their average R2 value but not significant differences in their RMSE value (p = 0.18), while TL-LUE outperformed MOD17 with significant differences (p < 0.0001) in their average RMSE value but not significant differences in their average R2 value (p = 0.33) (Figure 4e,f, Table 4). However, the improvement of both TL-LUE and TL-LUEn over MOD17 was smaller in comparison with the improvement at half-hourly and daily temporal scales. MOD17 produced an average RMSE value of 13.0 g C m−2 (8days)−1 and an average R2 value of 0.755. The average RMSE and R2 of TL-LUE were 12.0 g C m−2 (8days)−1 and 0.775, respectively.
The RMSE of GPP simulated by TL-LUEn, TL-LUE and MOD17 were smaller than 12 g C m−2 (8days)−1 at 35, 34 and 27 sites. The three models had similar numbers of sites in each R2 class. TL-LUEn performed poorer than TL-LUE at 32 sites, while MOD17 outperformed TL-LUEn and TL-LUE at 20 and 13 sites, respectively, which were mainly non-forest and NF sites (Table A3 in the Appendix).
TL-LUEn only performed better than TL-LUE for BF. As to non-forest types (CROP, GRASS and SHRUB), TL-LUEn performed similarly with MOD17. The average RMSE and R2 of the former were larger than those of the latter by 1.0 g C m−2 (8days)−1 and 0.012, respectively. TL-LUE outperformed MOD17 in all the three non-forest types. As to forests, both TL-LUEn and TL-LUE showed a better performance than MOD17 with an average RMSE smaller than that of MOD17 by 1.5 g C m−2 (8days)−1 and 1.6 g C m−2 (8days)−1 and corresponding average R2 larger than that of MOD17 by 0.030 and 0.022, respectively.
4. Discussion
4.1. The Ability of the Three LUE Models to Simulate GPP
At the half-hourly temporal scale, TL-LUEn and TL-LUE performed better than MOD17 for three types of forests (MF, BF, and NF), GRASS and SHRUB and their differences between these vegetation types are significant. With the increase of temporal scales, the improvement of TL-LUEn and TL-LUE over MOD17 gradually became less distinct. The changes in the ability of TL-LUEn, TL-LUE, and MOD17 to simulate GPP with vegetation types and temporal scales are, at least in part, related to the different structure of various vegetation types and the different response of canopy GPP to incident PAR described by three models. It was found that scaling up in time tended to linearize the relationship between CO2 flux and PAR [99]. Observations also showed that changes in canopy GPP with incident PAR are nonlinear at the half-hourly scale and become approximately linear at the daily and 8-day scales [29]. GPP simulated by MOD17 always linearly increase with incident PAR while the increase of GPP with incident PAR is nonlinear in both TL-LUEn and TL-LUE. The non-linearity of TL-LUEn and TL-LUE can be modified through changing parameters εm, β, εmsu, and εmsh. For example, if εmsu equals εmsh in the TL-LUE model, the response of simulated canopy GPP to incident PAR would be close to linear. This is the reason why the improvement of TL-LUEn and TL-LUE over MOD17 is much smaller at the 8-day scale than at the half-hourly temporal scale.
The better performance of TL-LUEn and TL-LUE models over MOD17 changed with vegetation types, most significantly for forests, then for SHRUB, GRASS. Leuning et al. [113] pointed out that the canopy CO2 exchange rates of crops is a quasi-linear function of absorbed PAR. In contrast, forests and sparse vegetation often show a markedly nonlinear response of canopy CO2 exchange rates to absorbed PAR [99,113,114]. TL-LUEn and TL-LUE are able to capture both the nonlinear and linear responses of GPP to incident PAR while MOD17 is only able to describe the linear change of canopy GPP with incident PAR. Therefore, TL-LUEn and TL-LUE outperform MOD17 for forests, shrub and grass sites. The higher performance is the most significant for forests at the half-hourly scale.
The linear response of GPP to PAR in MOD17 led to the underestimation/overestimation of GPP under conditions of low/high incident PAR, which has been confirmed by Propastin et al. [22] and He et al. [23]. TL-LUEn and TL-LUE were, at least partially, able to correct this weakness. Figure 6, Figure 7 and Figure 8 show the RMSE of simulated GPP as a function of incident PAR at three different temporal scales. Under medium PAR conditions, TL-LUEn, TL-LUE, and MOD17 performed similarly. The improvement of TL-LUEn and TL-LUE over MOD17 mainly occurred under low or high incident PAR conditions.
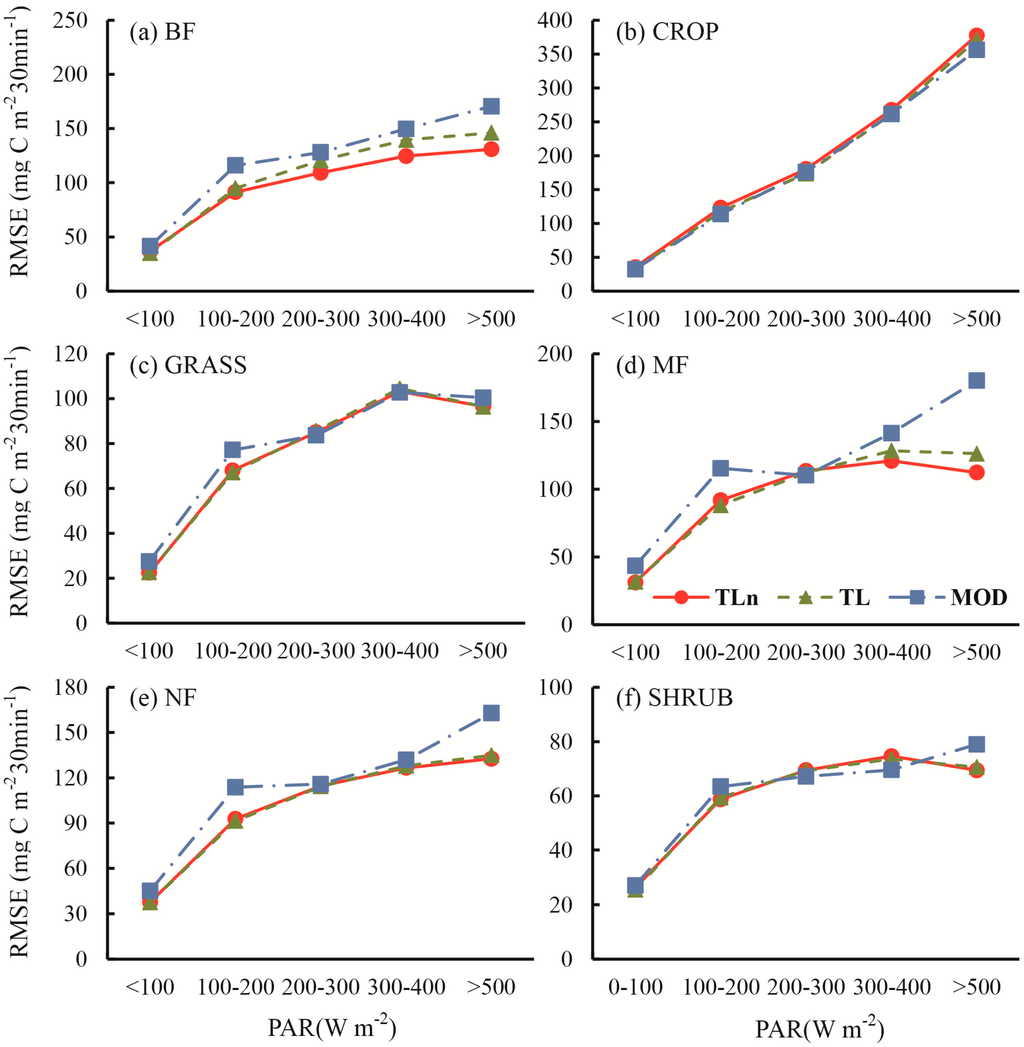
Figure 6.
The RMSE of modeled GPP against tower-derived GPP within different photosynthetically active radiation (PAR) classes for six different vegetation types: (a) BF, (b) CROP, (c) GRASS, (d) MF, (e) NF and (f) SHRUB, at the half-hourly scale.
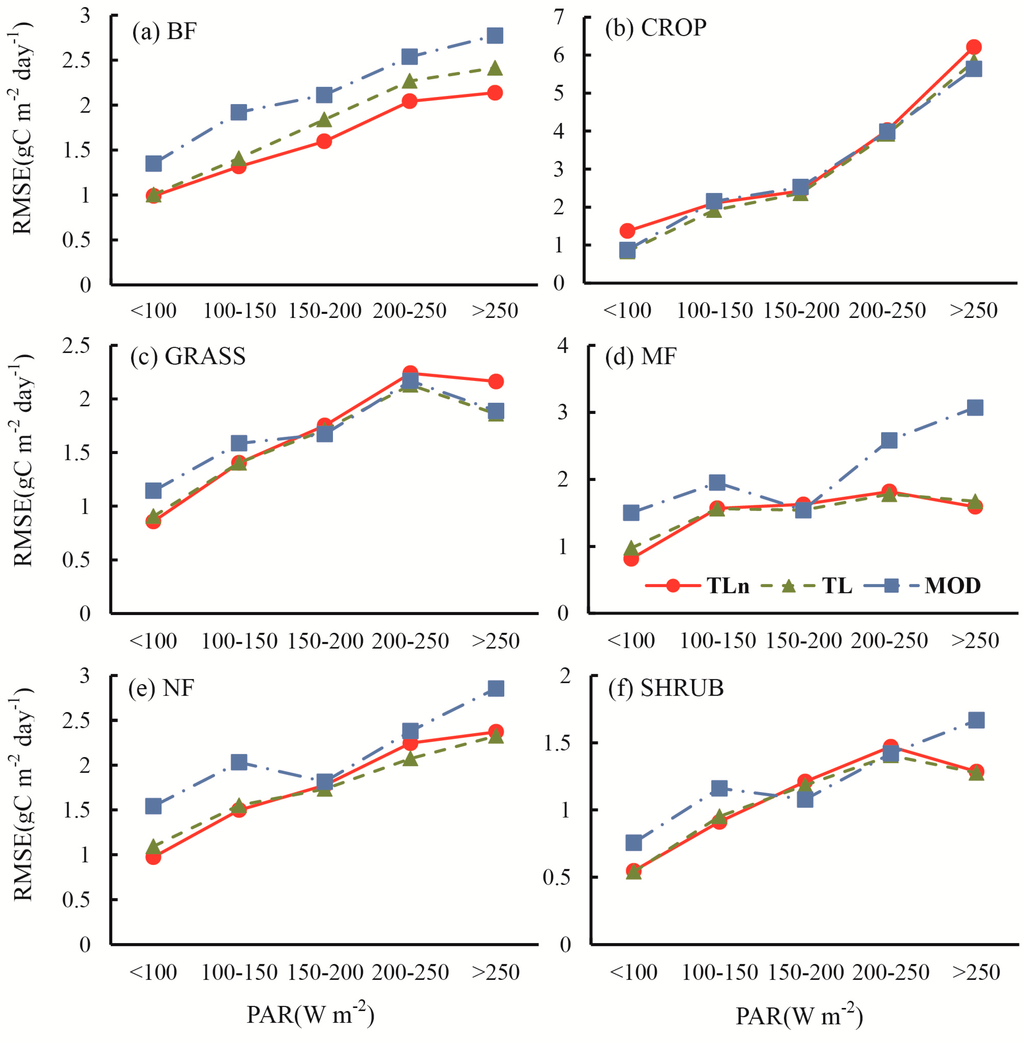
Figure 7.
The RMSE of modeled GPP against tower-derived GPP within different PAR classes for 6 different vegetation types: (a) BF, (b) CROP, (c) GRASS, (d) MF, (e) NF and (f) SHRUB, at the daily scale.
The ratio of diffuse to direct PAR changed with clearness index. Under conditions of low clearness index, canopy LUE is high [23] owing to more diffuse PAR being absorbed by shaded leaves with high LUE. MOD17 did not differentiate the different effects of diffuse and direct PAR on GPP and tended to underestimate/overestimate GPP under low/high clearness index conditions (Figure 9). In TL-LUEn and TL-LUE, incident PAR is first decomposed into diffuse and direct components according to clearness index. Under conditions of low clearness index, increased diffuse PAR will be mainly absorbed by shaded leaves, which have high LUE. Thus, GPP simulated by TL-LUEn and TL-LUE is higher than that simulated by MOD17 (Figure 9). In contrast, when clearness index is high, increased direct PAR will be mostly absorbed by sunlit leaves, which have low LUE. Consequently, GPP simulated by TL-LUEn and TL-LUE is lower than that simulated by MOD17. Therefore, the systematic biases of GPP simulated by MOD17 model under low and high clearness index can be alleviated by TL-LUE and TL-LUEn.
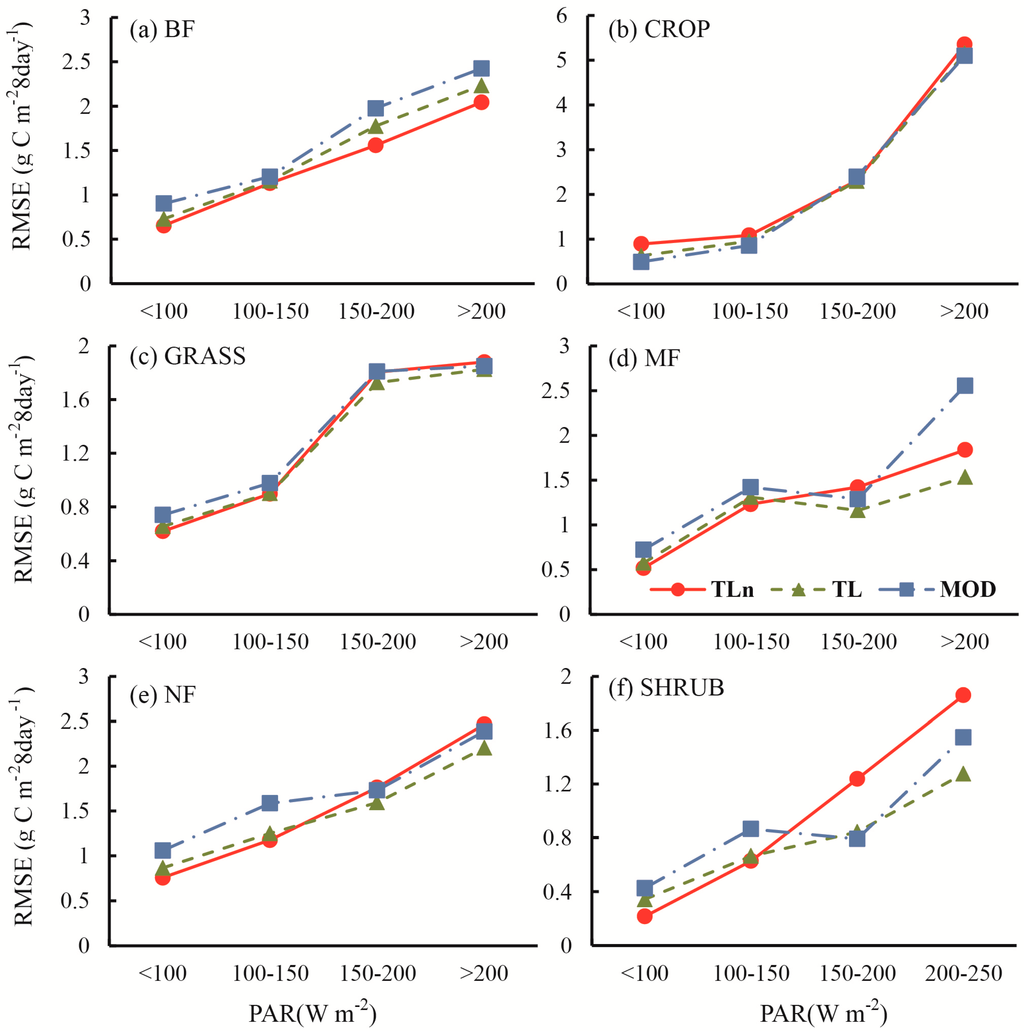
Figure 8.
The RMSE of modeled GPP against tower-derived GPP within different PAR classes for 6 different vegetation types: (a) BF, (b) CROP, (c) GRASS, (d) MF, (e) NF and (f) SHRUB, at the 8-day scale.
4.2. The Applicability of Different Models
The different performances of three LUE models at different temporal scales and for different vegetation types suggest that it should be selective when using them. Prior to regional simulations of GPP using these models, we must be careful with the applicability of the optimized parameters.
In this study, optimized parameters changed significantly among different vegetation types. The across-site variability of these parameters is also sizeable even for a specific vegetation type (Table 3). The sensitivity of simulated GPP to εm and β in TL-LUEn, to εmsu and εmsh in TL-LUE, and to εmax in MOD17 was assessed using the factorial approach described in section 2.2.3. The calculated main effect of εmax, εm, β, εmsu and εmsh are 20%, 11.50%, 8.50%, 8.09% and 11.91% at the half-hourly scale, and 20%, 10.72%, 9.28%, 6.84% and 13.16% at the daily scale, and 20%, 11.26%, 8.74%, 7.52% and 12.48% at the 8-day scale, respectively (Table 5). The sensitivity of simulated GPP to εmax in MOD17 is higher than the sensitivity of simulated GPP to individual parameters in TL-LUEn and TL-LUE. The sensitivity of simulated GPP to the simultaneous uncertainties of εm and β in TL-LUEn and to the simultaneous uncertainties of εmsu and εmsh in TL-LUE is the same as the sensitivity of simulated GPP to εmax in MOD17. In addition, parameters in TL-LUE and MOD17 showed similar variations within each vegetation type, indicated by the similar CV in Table 3. However, as the two parameters in TL-LUEn vary not only with biomes but also with temperature [6], optimized εm and β exhibited larger variations and uncertainties than εmax, εmsu, and εmsh for all vegetation types (Table 3).
Above analyses on the performance of three models at different temporal scales and their sensitivity to parameter uncertainties indicate that TL-LUEn is more applicable in individual site at the half-hourly scale. TL-LUE can be used regionally at the half-hourly, daily, and 8-day scales. MOD17 is also a good option for simulating regional GPP at the 8-day temporal scale and it is able to simulate GPP with accuracy close to TL-LUE.
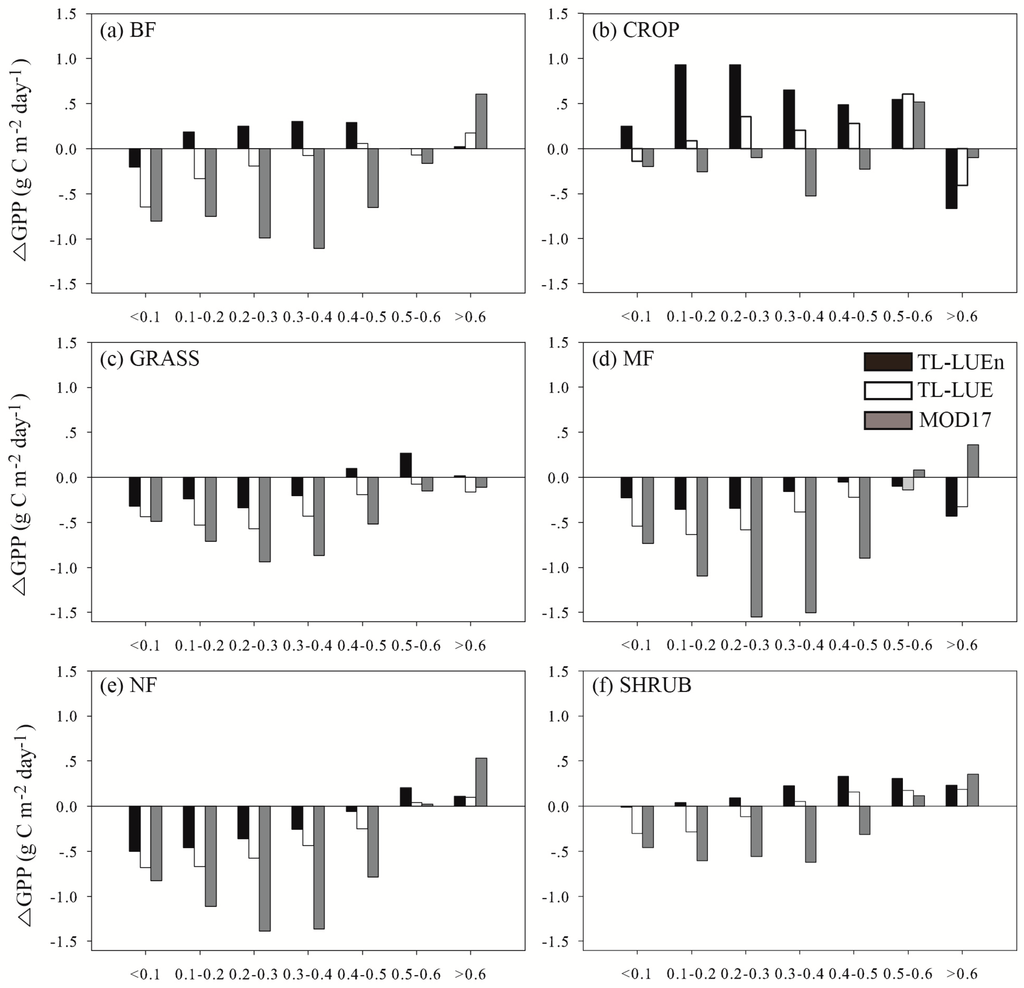
Figure 9.
The average differences of modeled daily GPPs with observations for different ranges of clearness index Q. ΔGPP means the difference between the simulated and tower-derived daily GPP for certain biome. (a–f) denoteΔGPP for 6 different vegetation types (BF, CROP, GRASS, MF, NF and SHRUB), respectively.

Table 5.
Design of the 22 complete factorial sensitivity analyses for parameters of TL-LUEn, TL-LUE with all the vegetation types lumped together at half-hourly, daily, and 8-day scales.
| Simulations | TL-LUEn | TL-LUE | MOD17 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| εm | β | ΔGPPrel(%) | εmsu | εmsh | ΔGPPrel(%) | εmax | ΔGPPrel(%) | ||
| Half-hourly | 1 | - | - | −10.00 | - | - | −10.00 | - | −10.00 |
| 2 | + | - | 0.78 | + | - | −1.91 | |||
| 3 | - | + | −2.23 | - | + | 1.91 | |||
| 4 | + | + | 10.00 | + | + | 10.00 | + | 10.00 | |
| Main effect(%) | 11.50 | 8.50 | 8.09 | 11.91 | 20.00 | ||||
| Daily | 1 | - | - | −10.00 | - | - | −10.00 | - | −10.00 |
| 2 | + | - | 0.72 | + | - | −3.16 | |||
| 3 | - | + | −0.73 | - | + | 3.16 | |||
| 4 | + | + | 10.00 | + | + | 10.00 | + | 10.00 | |
| Main effect (%) | 10.72 | 9.28 | 6.84 | 13.16 | 20.00 | ||||
| 8-day | 1 | - | - | −10.00 | - | - | −10.00 | - | −10.00 |
| 2 | + | - | 0.60 | + | - | −2.48 | |||
| 3 | - | + | −1.92 | - | + | 2.48 | |||
| 4 | + | + | 10.00 | + | + | 10.00 | + | 10.00 | |
| Main effect (%) | 11.26 | 8.74 | 7.52 | 12.48 | 20.00 | ||||
Note: Columns three-four and six-seven show contrast coefficients for εm, β in TL-LUEn, and εmsu, εmsh in TL-LUE, respectively. A plus symbol indicates that the parameter was set at 110% of the estimate while a minus symbol indicates 90% of the estimate. ΔGPPrel is the relative differences between the simulated GPP calculated by introducing a perturbation to a certain parameter and the simulated GPP calculated using optimized parameters.
4.3. Uncertainties and Remaining Issues
Both TL-LUEn and TL-LUE separate a canopy into sunlit and shaded leaves, and TL-LUEn further describe nonlinear response of their respective photosynthesis to APAR. These two models demonstrated powerful ability to simulate GPP. However, there are still some uncertainties remained. As indicated by Gebremichael and Barros [105], uncertainties in meteorological and LAI data, parameters, and model structure all might induce errors of simulated GPP. The change of linear response of GPP to VPD and PAR to nonlinear one and the inclusion of a soil moisture scalar might improve GPP simulation.
Similar to MOD17, TL-LUEn and TL-LUE only use VPD and minimum air temperature as environmental constraints on GPP. VPD represents the effect of atmospheric dryness on vegetation photosynthesis as a result of stomatal conductance. Soil moisture also plays an important role in regulating GPP via effects on leaf cell turgor pressure directly affecting photosynthesis or by stomatal conductance [10,115,116]. Because VPD and soil water availability did not co-vary, it would be most appropriate to have soil water availability as a constraint on photosynthesis in addition to VPD [117]. In MOD17, soil drought stress was approximated through the increase in the sensitivity of GPP to VPD [118]. Photosynthesis is considered to be totally shut off during periods of very high VPD, but in fact soil moisture and other environmental conditions might be still favorable to maintain photosynthetic activity at a certain level even if atmosphere is very dry [105]. Thus, the lack of soil water availability as a photosynthetic constraint in all three LUE models surely increases uncertainties in simulated GPP, especially for crops and grasses with shorter roots and high dependence on shallow soil moisture.
In this study, parameters in three LUE models are assumed invariant seasonally, which could induce some uncertainties in optimized parameters and calculated GPP. Many studies have shown that these parameters vary with both temperature and vegetation types [14,119,120]. Wang et al. [6] recently reported that with the consideration of seasonal changes of two parameters associated with temperature, the two-leaf nonlinear hyperbolic model (i.e., TL-LUEn) could simulate GPP as well as a process-based model. Chen et al. [121] indicated that the exclusion of seasonality of parameters in one-leaf and two-leaf LUE models is one of major drivers responsible for the failure of these models to capture the seasonality of GPP well. Thus, the proper representation of seasonal variations of these parameters needs further investigation.
Simulated GPP is also affected by the quality of meteorological and LAI inputs. In the calibration and validation periods, the models were driven by tower-measured meteorological data and processed MODIS LAI. The errors caused by inaccuracies of meteorological inputs are likely relative small [41]. However, the MODIS LAI contained considerable uncertainties, especially for crops [122], mainly caused by uncertainties in land cover and surface reflectance inputs and in the LAI inversion algorithm, and by the prevalence of persistent cloud cover [105]. The four variables in both TL-LUEn and TL-LUE (APARmsh, APARmsu, LAImsh and LAImsu), are all linked to LAI [23]. Our analysis showed that GPP simulated by TL-LUEn and TL-LUE is slightly more sensitive to LAI than that simulated by MOD17 (not shown here), which could be one of possible explainers for the poorer performance of TL-LUEn and TL-LUE relative to MOD17 at crop sites. Of course, this speculation is still worth of deep study.
The LUE of crops changes with species. At the BON, MIR, MER, RG19, and RG21 crop sites, the corn or soybeans were cultivated every other year. At the ASM site, the dominant species was wheat in 2003–2004 and 2006, while it was changed to corn in 2005. Corn is a C4 plant while soybeans and wheat are C3 plants. The LUE of corn is much higher than that of soybeans and wheat. The application of optimized parameters of C3/C4 plants for C4/C3 plants in the validation years might result in large uncertainties in simulated GPP. This is a possible cause for the poorer performance of models for crops in the validation period than in the calibration period. In addition, the uneven numbers of flux sites for different vegetation types could also result in uncertainties in the identified overall robustness of individual models.
5. Conclusions
In this study, the ability of three different types of LUE models (MOD17, TL-LUE and TL-LUEn) to simulate GPP at various temporal scales for different vegetation types was assessed using measurements at 58 flux sites in Asia, Europe and North America. The main conclusions that were drawn as follows:
- (1)
- Optimized model parameters vary distinctly not only among different vegetation types, but also among different sites for the same vegetation type, especially for TL-LUEn. The parameters in TL-LUEn change sizably with temporal scales while the parameters in TL-LUE and MOD17 are almost invariant with temporal scales.
- (2)
- The overall performance of TL-LUEn was slightly but not significantly better than TL-LUE at half-hourly and daily scale, while the overall performance of both TL-LUEn and TL-LUE were significantly better (p < 0.0001) than MOD17 at the two temporal scales. The improvement of TL-LUEn over TL-LUE was relatively small in comparison with the improvement of TL-LUE over MOD17. However, the differences between TL-LUEn and MOD17, and TL-LUE and MOD17 became less distinct at 8-day scale.
- (3)
- At the half-hourly temporal scale, TL-LUEn and TL-LUE outperformed MOD17 for all vegetation types but CROP. The outperformance of TL-LUEn and TL-LUE over MOD17 was more distinct for forests than for GRASS and SHRUB vegetation types. With the increase of temporal scales, the improvement of both TL-LUEn and TL-LUE over MOD17 decreased. At the daily temporal scale, both TL-LUEn and TL-LUE performed better than MOD17 for forests and SHRUB. TL-LUE also outperformed MOD17 slightly for other non-forest types (CROP and GRASS). TL-LUEn only performed better than TL-LUE for BF. At the 8-day temporal scale, TL-LUEn only outperformed MOD17 for forests while TL-LUE performed better than MOD17 for all vegetation types. TL-LUEn only slightly outperformed TL-LUE for BF.
- (4)
- The improvement of TL-LUEn and TL-LUE over the MOD17 for forests was mainly achieved by the correction of the underestimation of GPP under low incident PAR and the overestimation of GPP under high incident PAR occurring in the MOD17.
- (5)
- TL-LUEn is more applicable at individual sites at the half-hourly scale. TL-LUE could be regionally used at half-hourly, daily and 8-day scales, owing to its excellent performance and small parameter variations at different temporal scales and for most vegetation types. MOD17 is also an applicable option at 8-day scale.
Acknowledgements
This work was supported by Chinese Academy of Sciences for Strategic Priority Research Program (No. XDA05050602-1), National Basic Research Program of China (2010CB950702), National Natural Science Foundation of China (41371070), and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
This work used eddy covariance data acquired by the FLUXNET community and in particular by the following networks: AmeriFlux (U.S. Department of Energy, Biological and Environmental Research, Terrestrial Carbon Program (DE-FG02-04ER63917 and DE-FG02-04ER63911)), AfriFlux, AsiaFlux, CarboAfrica, CarboEuropeIP, CarboItaly, CarboMont, ChinaFlux, Fluxnet-Canada (supported by CFCAS, NSERC, BIOCAP, Environment Canada, and NRCan), GreenGrass, KoFlux, LBA, NECC, OzFlux, TCOS-Siberia, USCCC. We honestly thank all PIs of flux sites for providing the data for us. We appreciate the financial support to the eddy covariance data harmonization provided by CarboEuropeIP, FAO-GTOS-TCO, iLEAPS, Max Planck Institute for Biogeochemistry, National Science Foundation, University of Tuscia, Université Laval and Environment Canada and US Department of Energy and the database development and technical support from Bekeley Water Center, Lawrence Berkeley National Laboratory, Microsoft Research eScience, Oak Ridge National Laboratory, University of California - Berkeley, University of Virginia.
Author Contributions
Weimin Ju, Xiaocui Wu, Yanlian Zhou and Mingzhu He designed the research. Xiaocui Wu, Mingzhu He, and Yanlian Zhou processed data preparation, and ran the models. Xiaocui Wu and Weimin Ju mainly analyzed data and prepared the manuscript and figures. Beverly E. Law, T. Andrew Black, Hank A. Margolis, Alessandro Cescatti, Lianhong Gu, Leonardo Montagnani, Asko Noormets, Tim Griffis, Kim Pilegaard, Andrej Varlagin, Riccardo Valentini, Peter Blanken, Shaoqiang Wang, Huiming Wang, Shijie Han, Junhua Yan, Yingnian Li provided data, and reviewed and polished the manuscript. Bingbing Zhou and Yibo Liu helped to prepare the figures and polished the manuscript. All the authors contributed to the data analysis and paper writing and shared equally in the editing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Le Quéré, C.; Raupach, M.R.; Canadell, J.G.; Marland, G. Trends in the sources and sinks of carbon dioxide. Nature 2009, 2, 831–836. [Google Scholar]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; AltafArain, M.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Le Quéré, C.; Andres, R.J.; Boden, T.; Conway, T.; Houghton, R.A.; House, J.I.; Marland, G.; Peters, G.P.; van der Werf, G.R.; Ahlstrom, A.; et al. The global carbon budget 1959–2011. Earth Syst. Sci. Data 2013, 5, 165–185. [Google Scholar] [CrossRef]
- Zhang, F.M.; Chen, J.M.; Chen, J.Q.; Gough, C.M.; Martin, T.A.; Dragoni, D. Evaluating spatial and temporal patterns of modis gpp over the conterminous U.S. Against flux measurements and a process model. Remote Sens. Environ. 2012, 124, 717–729. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of c3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.M.; Chen, J.M.; Gonsamo, A.; Zhou, B.; Cao, F.F.; Yi, Q.X. A two-leaf rectangular hyperbolic model for estimating GPP across vegetation types and climate conditions. J. Geophys. Res. 2014. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem.Cy. 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-drived measure of global terrestrial primary production. BioSciense 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.G.; Zhou, G.S.; Zhou, G.Y.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Monteith, J.L.; Moss, C.J. Climate and the efficiency of crop production in britain. Philos. Trans. R. Soc. London, Ser. B. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Gu, L.H.; Baldocchi, D.; Verma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. 2002. [Google Scholar] [CrossRef]
- Gu, L.H.; Baldocchi, D.D.; Wofsy, S.C.; Munger, J.W.; Michalsky, J.J.; Urbanski, S.P.; Boden, T.A. Response of a deciduous forest to the mount pinatubo eruption: Enhanced photosynthesis. Science 2003, 299, 2035–2038. [Google Scholar] [CrossRef] [PubMed]
- Law, B.E.; Falge, E.; Baldocchi, D.D.; Bakwin, P.; Berbigier, K.; Davis, A.J.; Dolman, M.; Falk, J.D.; Fuentes, A.; Goldstein, A.; et al. Environmental controls over carbon dioxide and water vapor exchange of terrestrial vegetation. Agric. For. Meteorol. 2002, 113, 97–120. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D.; Berry, S.L.; Noble, I.R. On the direct effect of clouds and atmospheric particles on the productivity and structure of vegetation. Oecologia 2001, 129, 21–30. [Google Scholar] [CrossRef]
- Choudhury, B.J. Estimating gross photosynthesis using satellite and ancillary data: Approach and preliminary results. Remote Sens. Environ. 2001, 75, 1–21. [Google Scholar] [CrossRef]
- Alton, P.B.; North, P.R.; Los, S.O. The impact of diffuse sunlight on canopy light-use efficiency, gross photosynthetic product and net ecosystem exchange in three forest biomes. Glob. Change Biol. 2007, 2007, 776–787. [Google Scholar] [CrossRef]
- Alton, P.B. Reduced carbon sequestration in terrestrial ecosystems under overcast skies compared to clear skies. Agric. For. Meteorol. 2008, 148, 1641–1653. [Google Scholar] [CrossRef]
- Cai, T.; Black, T.A.; Jassal, R.S.; Morgenstern, K.; Nesic, Z. Incorporating diffuse photosynthetically active radiation in a single-leaf model of canopy photosynthesis for a 56-year-old douglas-fir forest. Int. J. Biometeorol. 2009, 53, 135–148. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Yu, G.R.; Zhuang, J.; Gentry, R.; Fu, Y.L.; Sun, X.M.; Zhang, L.M.; Wen, X.F.; Wang, Q.F.; Han, S.J.; et al. Effects of cloudiness change on net ecosystem exchange, light use efficiency, and water use efficiency in typical ecosystems of china. Agric. For. Meteorol. 2011, 151, 803–816. [Google Scholar] [CrossRef]
- Propastin, P.; Ibrom, A.; Knohl, A.; Erasmi, S. Effects of canopy photosynthesis saturation on the estimation of gross primary productivity from modis data in a tropical forest. Remote Sens. Environ. 2012, 121, 252–260. [Google Scholar] [CrossRef]
- He, M.Z.; Ju, W.M.; Zhou, Y.L.; Chen, J.M.; He, H.L.; Wang, S.Q.; Wang, H.M.; Guan, D.X.; Yan, J.H.; Hao, Y.B.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary production. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- DePury, D.G.G.; Farquhar, G.D. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell Environ. 1997, 20, 537–557. [Google Scholar] [CrossRef]
- Wang, Y.P.; Leuning, R. A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I: Model description and comparison with a multi-layered model. Agric. For. Meteorol. 1998, 91, 89–111. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Turner, D.P.; Urbanski, S.; Bremer, D.; Wofsy, S.C.; Meyers, T.; Gower, S.T.; Gregory, M. A cross-biome comparison of daily light use efficiency for gross primary production. Glob. Change Biol. 2003, 9, 383–395. [Google Scholar] [CrossRef]
- Gao, Y.N.; Yu, G.R.; Yan, H.M.; Zhu, X.J.; Li, S.G.; Wang, Q.F.; Zhuang, J.H.; Wang, Y.F.; Li, Y.N.; Zhao, L.M.; et al. A modis-based photosynthetic capacity model to estimate gross primary production in northern China and the tibetan plateau. Remote Sens. Environ. 2014, 148, 108–118. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Change Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Thanyapraneedkul, J.; Muramatsu, K.; Daigo, M.; Furumi, S.; Soyama, N.; Nasahara, K.N.; Muraoka, H.; Noda, H.M.; Nagai, S.; Maeda, T.; et al. A vegetation index to estimate terrestrial gross primary production capacity for the Global Change Observation Mission-Climate (GCOM-C)/Second-Generation Global Imager (SGLI) satellite sensor. Remote Sens. 2012, 4, 3689–3720. [Google Scholar] [CrossRef]
- Yuan, W.P.; Cai, W.W.; Xia, J.Z.; Chen, J.Q.; Liu, S.G.; Dong, W.J.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; Bernhofer, C.; Black, A.; Blanken, P.D.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the lathuile database. Remote Sens. Environ. 2014, 192–193, 108–120. [Google Scholar]
- Song, C.H. Optical remote sensing of terrestrial ecosystem primary productivity. Progr. Phys. Geogr. 2013, 37, 834–854. [Google Scholar] [CrossRef]
- Peters, W.; Jacobson, A.R.; Sweeney, C.; Andrews, A.E.; Conway, T.J.; Masarie, K.; Miller, J.B.; Bruhwiler, L.M.P.; Pétron, G.; Hirsch, A.I.; et al. An atmospheric perspective on north american carbon dioxide exchange: Carbontracker. Proc. Natl. Acad. Sci. USA 2007, 104, 18925–18930. [Google Scholar] [CrossRef] [PubMed]
- Fluxdata.org. Available online: http://www.fluxdata.org/default.aspx (accessed on 10 Decmber 2013).
- Baldocchi, D.D.; Falge, E.; Gu, L.H.; Olson, R.; Hollinger, D.; Running, S. W.; Anthoni, P.; Bernhofer, Ch.; Davis, K.; Evans, R.; et al. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Breathing of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Papale, D.; Valentini, A. A new assessment of european forests carbon exchange by eddy fluxes and artificial neural network spatialization. Glob. Change Biol. 2003, 9, 525–535. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Change Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of net ecosystem exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Moffat, A.M.; Papale, D.; Reichstein, M.; Hollinger, D.Y.; Richardson, A.D.; Barr, A.G.; Beckstein, C.; Braswell, B.H.; Churkina, G.; Desai, A.R.; et al. Comprehensive comparison of gap-filling techniques for eddy covariance net carbon fluxes. Agric. For. Meteorol. 2007, 147, 209–232. [Google Scholar] [CrossRef]
- Gholz, H.L.; Clark, K.L. Energy exchange across a chronose-quence of slash pine forests in florida. Agric. For. Meteorol. 2002, 112, 87–102. [Google Scholar] [CrossRef]
- Fischer, M.L.; Billesbach, D.P.; Riley, W.J.; Berry, J.A.; Torn, M.S. Spatiotemporal variations in growing season exchanges of CO2, H2O, and sensible heat in agricultural fields of the southern great plains. Earth Interact. 2007, 11, 1–21. [Google Scholar] [CrossRef]
- Wilson, T.B.; Meyers, T.P. Determining vegetation indices from solar and photosynthetically active radiation fluxes. Agric. For. Meteorol. 2007, 144, 160–179. [Google Scholar] [CrossRef]
- Humphreys, E.R.; Black, T.A.; Morgenstern, K.; Cai, T.; Drewitt, G.B.; Nesic, Z.; Trofymow, J.A. Carbon dioxide fluxes in coastal douglas-fir stands at different stages of development after clearcut harvesting. Agric. For. Meteorol. 2006, 140, 6–22. [Google Scholar] [CrossRef]
- Jenkins, J.P.; Richardson, A.D.; Braswell, B.H.; Ollinger, S.V.; Hollinger, D.Y.; Smith, M.L. Refining light-use efficiency calculations for a deciduous forest canopy using simultaneous tower-based carbon flux and radiometric measurements. Agric. For. Meteorol. 2007, 143, 64–79. [Google Scholar] [CrossRef]
- Zhang, J.H.; Han, S.J.; Yu, G.R. Seasonal variation in carbon dioxide exchange over a 200-year-old chinese broad-leaved korean pine mixed forest. Agric. For. Meteorol. 2006a, 137, 150–165. [Google Scholar] [CrossRef]
- Zhang, J.H.; Yu, G.R.; Han, S.J.; Guan, D.X.; Sun, X.M. Seasonal and annual variation of CO2 flux above a broad-leaved korean pine mixed forest. Sci. China Series D: Earth Scie. 2006b, 49, 63–73. [Google Scholar]
- Zhang, L.; Luo, Y.Q.; Yu, G.R.; Zhang, L.M. Estimated carbon residence times in three forest ecosystems of eastern China: Applications of probabilistic inversion. J. Geophys. Res. 2000. [Google Scholar] [CrossRef]
- Reichstein, M.; Ciais, P.; Papale, D.; Valentini, R.; Running, S.; Vivoy, N.; Cramer, W.; Granier, A.; Ogée, J.; Allard, V.; et al. Reduction of ecosystem productivity and respiration during the european summer 2003 climate anomaly: A joint flux tower, remote sensing and modelling analysis. Glob. Change Biol. 2006, 13, 634–651. [Google Scholar] [CrossRef]
- Milyukova, I.M.; Kolle, O.; Varlagin, A.V.; Vygodskaya, N.N.; Schulze, E.D.; Lloyd, J. Carbon balance of a southern taiga spruce stand in european russia. Tellus B 2002, 54, 429–442. [Google Scholar] [CrossRef]
- Mund, M.; Kutsch, W.; Wirth, C.; Kahl, T.; Knohl, A.; Skomarkova, M.; Schulze, E. The influence of climate and fructification on the inter-annual variability of stem growth and net primary productivity in an old-growth, mixed beech forest. Tree Physiol. 2010, 30, 689–704. [Google Scholar] [CrossRef] [PubMed]
- Urbanski, S.; Barford, C.; Kucharik, C.; Pyle, E.; Budney, J.; McKain, K.; Fitzjarrald, D.; Czikowsky, M.; Munger, J.W. Factors controlling CO2 exchange on timescale from hourly to decadal at harward forest. J. Geophys. Res. 2007. [Google Scholar] [CrossRef]
- Granier, A.; Pilegaard, K.; Jensen, N.O. Similar net ecosystem exchange of beech stands located in france and denmark. Agric. For. Meteorol. 2002, 114, 75–82. [Google Scholar] [CrossRef]
- Hollinger, D.Y.; Goltz, S.M.; Davidson, E.A.; Lee, J.T.; Tu, K.; Valentine, H.T. Seasonal patterns and environmental control of carbon dioxide and water vapour exchange in an ecotonal boreal forest. Glob. Change Biol. 1999, 5, 891–902. [Google Scholar] [CrossRef]
- Hollinger, D.Y.; Aber, J.; Dail, B.; Davidson, E.A.; Goltz, S.M.; Hughes, H.; Leclerc, M.Y.; Lee, J.T.; Richardson, A.D.; Rodrigues, C.; et al. Spatial and temporal variability in forest-atmosphere CO2 exchange. Glob. Change Biol. 2004, 10, 1689–1706. [Google Scholar] [CrossRef]
- Kramer, K.; Leinonen, I.; Bartelink, H.H.; Berbigier, P.; Borghetti, M.; Bernhofer, C.; Cienciala, E.; Dolman, A.J.; Froer, O.; Gracia, C.A.; et al. Evaluation of six process-based forest growth models using eddy-covariance measurements of CO2 and H2O fluxes at six forest sites in europe. Glob. Change Biol. 2002, 8, 213–230. [Google Scholar] [CrossRef]
- Scott, R.L. Using watershed water balance to evaluate the accuracy of eddy covariance evaporation measurements for three semiarid ecosystems. Agric. For. Meteorol. 2010, 150, 219–225. [Google Scholar] [CrossRef]
- Powell, T.; Bracho, R.; Li, J.; Dore, S.; Hinkle, C.; Drake, B. Environmental controls over net ecosystem carbon exchange of scrub oak in central florida. Agric. For. Meteorol. 2006, 141, 19–34. [Google Scholar] [CrossRef]
- Dolman, A.J.; Moors, E.J.; Elbers, J.A. The carbon uptake of amid latitude pine forest growing on sandy soil. Agric. For. Meteorol. 2002, 111, 157–170. [Google Scholar] [CrossRef]
- Verma, S.B.; Dobermann, A.; Cassman, K.G.; Walters, D.T.; Knops, J.M.; Arkebauer, T.J.; Suyker, A.E.; Burba, G.G.; Amos, B.; Yang, H.; et al. Annual carbon dioxide exchange in irrigated and rainfed maize-based agroecosystems. Agric. For. Meteorol. 2005, 131, 77–96. [Google Scholar] [CrossRef]
- Law, B.E.; Sun, O.; Campbell, J.; Van Tuyl, S.; Thornton, P. Changes in carbon storage and fluxes in a chronosequence of ponderosa pine. Glob. Change Biol. 2003, 9, 510–524. [Google Scholar] [CrossRef]
- Thomas, C.K.; Law, B.E.; Irvine, J.; Martin, J.G.; Pettijohn, J.C.; Davis, K.J. Seasonal hydrology explains interannual and seasonal variation in carbon and water exchange in a semi-arid mature ponderosa pine forest in central oregon. J Geophys. Res. 2009, 114, G04006. [Google Scholar]
- Bracho, R.G.; Starr, G.; Gholz, H.; Martin, T.A.; Cropper, J.W.P.; Loescher, H.W. Controls on carbon dynamics by ecosystem structure and climate for southeastern us slash pine plantations. Ecol. Monogr. 2012, 82, 101–128. [Google Scholar] [CrossRef]
- Schmid, H.; Grimmond, C.; Cropley, F.; Offerle, B.; Su, H. Measurements of CO2 and energy fluxes over a mixed hardwood forest in the mid-western united states. Agric. For. Meteorol. 2000, 103, 357–374. [Google Scholar] [CrossRef]
- Ruehr, N.K.; Martin, J.; Law, B.E. Effects of water availability on carbon and water exchange in a young ponderosa pine forest: Above- and belowground responses. Agric. For. Meteorol. 2012, 164, 136–148. [Google Scholar] [CrossRef]
- Vickers, D.; Thomas, C.K.; Pettijohn, C.; Martin, J.G.; Law, B.E. Five years of carbon fluxes and inherent water-use efficiency at two semi-arid pine forests with different disturbance histories. Tellus B 2012, 64, 17159. [Google Scholar] [CrossRef]
- Gu, L.H.; Meyers, T.; Pallardy, S.G.; Hanson, P.J.; Yang, B.; Heuer, M.; Hosman, K.P.; Riggs, J.S.; Sluss, D.; Wullschleger, S.D. Direct and indirect effects of atmospheric conditions and soil moisture on surface energy partitioning revealed by a prolonged drought at a temperate forest site. J. Geophys. Res. 2006. [Google Scholar] [CrossRef]
- Noormets, A.; Gavazzi, M.J.; McNulty, S.G.; Domec, J.C.; Sun, G.; King, J.; Chen, J. Response of carbon fluxes to drought in a coastal plain loblolly pine forest. Glob. Change Biol. 2009, 16, 272–287. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Hammerle, A.; Haslwanter, A.; Bahn, M.; Tappeiner, U.; Cernusca, A. Seasonal and inter-annual variability of the net ecosystem CO2 exchange of a temperate mountain grassland: Effects of weather and management. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Monson, R.K.; Turnipseed, A.A.; Sparks, J.P.; Harley, P.C.; Scott Denton, L.E.; Sparks, K.; Huxman, T.E. Carbon sequestration in a high-elevation, subalpine forest. Glob. Change Biol. 2002, 8, 459–478. [Google Scholar] [CrossRef]
- Lafleur, P.; Roulet, N.; Bubier, J.; Frolking, S.; Moore, T. Interannual variability in the peatland-atmosphere carbon dioxide exchange at an ombrotrophic bog. Glob. Biogeochem.Cy. 2003. [Google Scholar] [CrossRef]
- Allard, V.; Ourcival, J. M.; Rambal, S.; Joffre, R.; Rocheteau, A. Seasonal and annual variation of carbon exchange in an evergreen mediterranean forest in southern france. Glob. Change Biol. 2008, 14, 714–725. [Google Scholar] [CrossRef]
- Bergeron, O.; Margolis, H.; Black, T.; Coursolle, C.; Dunn, A.; Barr, A.; Wofsy, S. Comparison of carbon dioxide fluxes over three boreal black spruce forests in canada. Glob. Change Biol. 2007, 13, 89–107. [Google Scholar] [CrossRef]
- Yu, G.R.; Wen, X.F.; Sun, X.M.; Tanner, B.D.; Lee, X.H.; Chen, J.Y. Overview of ChinaFlux and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
- Montagnani, L.; Manca, G.; Canepa, E.; Georgieva, E.; Acosta, M.; Feigenwinter, C.; Janous, D.; Kerschbaumer, G.; Lindroth, A.; Minach, L.; et al. A new mass conservation approach to the study of CO2 advection in an alpine forest. J. Geophys. Res. 2009. [Google Scholar] [CrossRef]
- Griffis, T.J.; Sargent, S.D.; Baker, J.M.; Lee, X.; Tanner, B.D.; Greene, J.; Swiatek, E.; Billmark, K. Direct measurement of biosphere-atmosphere isotopic CO2 exchange using the eddy covariance technique. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Bavin, T.K.; Griffis, T.J.; Baker, J.M.; Venterea, R.T. Impacts of reduced tillage and cover cropping on the greenhouse gas budget of a maize/soybean rotation ecosystem. Agr. Ecosyst. Environ. 2009, 134, 234–242. [Google Scholar] [CrossRef]
- Keenan, T.; Garcia, R.; Friend, A. D.; Zaehle, S.; Gracia, C.; Sabate, S. Improved understanding of drought controls on seasonal variation in mediterranean forest canopy CO2 and water fluxes through combined in situ measurements and ecosystem modeling. Biogeosciences 2009, 6, 1423–1444. [Google Scholar] [CrossRef]
- Luo, H.; Oechel, W.; Hastings, S.; Zulueta, R.; Qian, Y.; Kwon, H. Mature semiarid chaparral ecosystems can be a significant sink for atmospheric carbon dioxide. Glob. Change Biol. 2007, 13, 386–396. [Google Scholar] [CrossRef]
- Pilegaard, K.; Hummelshoj, P.; Jensen, N.O.; Chen, Z. Two years of continuous co2 eddy-flux measurements over a danish beech forest. Agric. For. Meteorol. 2001, 107, 29–41. [Google Scholar] [CrossRef]
- Migliavacca, M.; Reichstein, M.; Richardson, A.D.; Colombo, R.; Sutton, M.A.; Lasslop, G.; Tomelleri, E.; Wohlfahrt, G.; Carvalhais, N.; Cescatti, A. Semiempirical modeling of abiotic and biotic factors controlling ecosystem respiration across eddy covariance sites. Glob. Change Biol. 2011, 17, 390–409. [Google Scholar] [CrossRef]
- Grünwald, T.; Bernhofer, C. A decade of carbon, water and energy flux measurements of an old spruce forest at the anchor station tharandt. Tellus B 2007, 59, 387–396. [Google Scholar] [CrossRef]
- Hirano, T.; Hirata, R.; Fujinuma, Y.; Saigusa, N.; Yamamoto, S.; Harazono, Y.; Takada, M.; Inukai, K.; Inoue, G. Co2 and water vapor exchange of a larch forest in northern japan. Tellus B 2003, 55, 244–257. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Xu, L.K.; Kiang, N. How plant functional type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak-grass savanna and an annualgrassland. Agric. For. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef]
- Goulden, M.L.; McMillan, A.M.S.; Winston, G.C.; Rocha, A.V.; Manies, K.L.; Harden, J.W.; Bond-Lamberty, B.P. Patterns of NPP, GPP, respiration, and nep during boreal forest succession. Glob. Change Biol. 2011, 17, 855–871. [Google Scholar] [CrossRef]
- Curtis, P.S.; Vogel, C.S.; Gough, C.M.; Schmid, H.P.; Su, H.B.; Bovard, B.D. Respiratory carbon losses and the carbon use efficiency of a northern hardwood forest, 1999–2003. New Phytol. 2005, 167, 437–456. [Google Scholar] [CrossRef] [PubMed]
- Aubinet, M.; Chermanne, B.; Vandenhaute, M.; Longdoz, B.; Yernaux, M.; Laitat, E. Long term carbon dioxide exchange above a mixed forest in the belgian ardennes. Agric. For. Meteorol. 2001, 108, 293–315. [Google Scholar] [CrossRef]
- Bolstad, P.V.; Davis, K.J.; Martin, J.; Cook, B.D.; Wang, W. Component and whole-system respiration fluxes in northern deciduous forests. Tree Physiol. 2004, 24, 493–504. [Google Scholar] [CrossRef] [PubMed]
- Rebmann, C.; Zeri, M.; Lasslop, G.; Mund, M.; Kolle, O.; Schulze, E.; Feigenwinter, C. Treatment and assessment of the co2-exchange at a complex forest site in thuringia, germany. Agric. For. Meteorol. 2009, 150, 684–691. [Google Scholar] [CrossRef]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the earth observing system. In Methods in Ecosystem Science; Sala, O.E., Jackson, R.B., Mooney, H.A., Howarth, R.W., Eds.; Springer-Verlag: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Monteith, J.L. The photosynthesis and transpiration of crops. Exp. Agric. 1966, 2, 1–14. [Google Scholar] [CrossRef]
- Michalsky, J.J. The astronomical almanac's algorithm for approximate solar position (1950–2050). Solar Energy 1988, 40, 227–235. [Google Scholar] [CrossRef]
- Tang, S.; Chen, J.M.; Zhu, Q.; Li, X.; Chen, M.; Sun, R.; Zhou, Y.; Deng, F.; Xie, D. LAI inversion algorithm based on directional reflectance kernels. J. Environ. Manage. 2007, 85, 638–648. [Google Scholar] [CrossRef] [PubMed]
- Grant, I.F.; Prata, A.J.; Cechet, R.P. The impact of the diurnal variation of albedo on the remote sensing of the daily mean albedo of grassland. J. Appl. Meteorol. 2000, 39, 231–244. [Google Scholar] [CrossRef]
- Singarayer, J.S.; Ridgwell, A.; Irvine, P. Assessing the benefits of crop albedo bio-geoengineering. Environ. Res. Lett. 2009, 4, 045110. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte carlo sampling methods using markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Ruimy, A.; Jarvis, P.G.; Baldocchi, D.D.; Saugier, B. Co2 fluxes over plant canopies and solar radiation: A review. Adv. Ecol. Res. 1995, 26, 1–51. [Google Scholar]
- Li, A.N.; Bian, J.H.; Lei, G.B.; Huang, C.Q. Estimating the maximal light use efficiency for different vegetation through the casa model combined with time-series remote sensing data and ground measurements. Remote Sens. 2012, 4, 3857–3876. [Google Scholar] [CrossRef]
- Braswell, B.H.; Sacks, W.J.; Linder, E.; Schimel, D.S. Estimating diurnal to annual ecosystem parameters by synthesis of a carbon flux model with eddy covariance net ecosystem exchange observations. Glob. Change Biol. 2005, 11, 335–355. [Google Scholar] [CrossRef]
- Raupach, M.R.; Rayner, P.J.; Barrett, D.J.; Defries, R.S.; Heimann, M.; Ojima, D.S.; Quegan, S.; Schmullius, C.C. Model-data synthesis in terrestrial carbon observation: Methods, data requirements and data uncertainty specifications. Glob. Change Biol. 2005, 11, 378–397. [Google Scholar] [CrossRef]
- Xu, T.; White, L.; Hui, D.F.; Luo, Y.Q. Probabilistic inversion of a terrestrial ecosystem model: Analysis of uncertainty in parameter estimation and model prediction. Glob. Biogeochem. Cy. 2006, 20, GB2007. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1978. [Google Scholar]
- Gebremichael, M.; Barros, A.P. Evaluation of modis gross primary productivity (GPP) in tropical monsoon regions. Remote Sens. Environ. 2006, 100, 150–166. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E. Model sensitivity and uncertainty analysis. In Water Resources Systems Planning and Management; UNESCO: Rome, Italy, 2005; pp. 255–290. [Google Scholar]
- Sinclair, T.R.S.T. Soybean radiation-use efficiency as influenced by nonuniform specific leaf nitrogen distribution and diffuse radiation. Crop Sci. 1993, 33, 808–812. [Google Scholar] [CrossRef]
- Hammer, G.L.; Wright, G.C. A theoretical analysis of nitrogen and radiation effects on radiation use efficiency in peanut. Austr. J. Agric. Res. 1994, 45, 575–589. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.S.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; Ahl, D.E. Evaluation of modis NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Papale, D.; Ardö, J.; Goulden, M.J.; Kiely, G.; Richardson, A.D.; Rotenberg, E.; Veenendaal, E.M.; Filella, I. Patterns and controls of the variability of radiation use efficiency and primary productivity across terrestrial ecosystems. Glob. Ecol. Biogeogr. 2011, 19, 253–267. [Google Scholar] [CrossRef]
- Xiao, J.F.; Zhuang, Q.L.; Law, B.E.; Baldocchi, D.D.; Chen, J.Q.; Richardson, A.D.; Melillo, J.M.; Davis, K.J.; Hollinger, D.Y.; Wharton, S.; et al. Assessing net ecosystem carbon exchange of u. S. Terrestrial ecosystems by integrating eddy covariance flux measurements and satellite observations. Agric. Forest Meteorol. 2011, 151, 60–69. [Google Scholar] [CrossRef]
- Chen, T.; van der Werf, G.R.; Dolman, A.J.; Groenendijk, M. Evaluation of cropland maximum light use efficiency using eddy flux measurements in North America and Europe. Geophys. Res. Lett. 2011, 38, L14707. [Google Scholar]
- Leuning, R.; Kelliher, F. M.; DePury, D.G.G.; Schulze, E.D. Leaf nitrogen, photosynthesis, conductance and transpiration: Scaling from leaves to canopy. Plant Cell Environ. 1995, 18, 1183–1200. [Google Scholar] [CrossRef]
- Hollinger, D.Y.; Kelliher, F.M.; Byers, J.N.; Hunt, J.E.; McSeveny, T.M.; Weir, P.L. Carbon dioxide exchange between an undisturbed old-growth temperate forest and the atmosphere. Ecology 1994, 75, 134–150. [Google Scholar] [CrossRef]
- Leuning, R.; Cleugh, H.A.; Zegelin, S.J.; Hughes, D. Carbon and water fluxes over a temperate eucalyptus forest and a tropical wet/dry savanna in australia: Measurements and comparison with modis remote sensing estimates. Agric. Forest Meteorol. 2005, 129, 151–173. [Google Scholar] [CrossRef]
- Hashimoto, H.; Wang, W.L.; Milesi, C.; Xiong, J.; Ganguly, S.; Zhu, Z.; Nemani, R. Structural uncertainty in model-simulated trends of global gross primary production. Remote Sens. 2013, 5, 1258–1273. [Google Scholar] [CrossRef]
- Law, B.E.; Waring, R.H. Combining remote sensing and climatic data to estimate net primary production across oregon. Ecol. Appl. 1994, 4, 717–728. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Zhao, M.S.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from modis using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1908–1925. [Google Scholar] [CrossRef]
- Ide, R.; Nakaji, T.; Oguma, H. Assessment of canopy photosynthetic capacity and estimation of GPP by using spectral vegetation indices and the light–response function in a larch forest. Agric. For. Meteorol. 2010, 150, 389–398. [Google Scholar] [CrossRef]
- Polley, H.W.; Emmerich, W.; Bradford, J.A.; Sims, P.L.; Johnson, D.A.; Saliendra, N.Z.; Svejcar, T.; Angell, R.; Frank, A.B.; Phillips, R.L.; et al. Physiological and environmental regulation of interannual variability in co2 exchange on rangelands in the western united states. Glob. Change Biol. 2010, 16, 990–1002. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; Liu, Z.; Che, M.; Chen, B. Evaluating parameter adjustment in the modis gross primary production algorithm based on eddy covariance tower measurements. Remote Sens. 2014, 6, 3321–3348. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Vannan, S.K.S.; Pan, J.Y.; Roman, M.O.; Yang, X.Y.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G.; et al. Intercomparison of modis albedo retrievals and in situ measurements across the global fluxnet network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef]
Appendix
Figure A1.
Histograms of the 20000 samples for each parameter generated by the Metropolis-Hasting Algorithm. Note: Only the best and worst cases are shown for each temporal scale owing to space limitation.

Table A1.
Assessment of half-hourly GPP simulated using TL-LUEn, TL-LUE and MOD17 for the 58 evaluation site-years.
| ID | RMSE (mg C m −2 (30min)−1) | R2 | ||||||
|---|---|---|---|---|---|---|---|---|
| TL-LUEn | TL-LUE | MOD17 | TL-LUEn | TL-LUE | MOD17 | |||
| BF | BEP | 63.381 | 66.958 | 76.423 | 0.819 | 0.783 | 0.689 | |
| DHS | 60.435 | 63.478 | 71.283 | 0.724 | 0.703 | 0.633 | ||
| HA | 59.667 | 64.036 | 71.053 | 0.910 | 0.888 | 0.807 | ||
| HAF | 71.021 | 72.580 | 85.082 | 0.862 | 0.853 | 0.801 | ||
| HES | 76.049 | 85.382 | 99.336 | 0.807 | 0.774 | 0.671 | ||
| MMS | 73.369 | 75.175 | 82.751 | 0.770 | 0.759 | 0.709 | ||
| MOZ | 68.622 | 68.328 | 73.618 | 0.770 | 0.758 | 0.711 | ||
| PUE | 49.406 | 49.861 | 54.236 | 0.806 | 0.801 | 0.770 | ||
| ROC | 79.484 | 80.577 | 84.508 | 0.636 | 0.640 | 0.635 | ||
| UMBS | 49.415 | 66.195 | 79.444 | 0.900 | 0.895 | 0.851 | ||
| WCR | 56.459 | 59.721 | 75.943 | 0.899 | 0.887 | 0.822 | ||
| Average RMSE | 64.301 | 68.390 | 77.607 | Average R2 | 0.809 | 0.795 | 0.736 | |
| CROP | ASM | 48.448 | 50.368 | 46.187 | 0.599 | 0.578 | 0.642 | |
| BON | 112.395 | 108.419 | 102.831 | 0.639 | 0.650 | 0.635 | ||
| MEI | 142.000 | 139.843 | 134.365 | 0.678 | 0.687 | 0.711 | ||
| MER | 161.440 | 158.377 | 158.585 | 0.688 | 0.700 | 0.728 | ||
| MIR | 178.555 | 175.665 | 174.733 | 0.724 | 0.736 | 0.771 | ||
| RG19 | 70.821 | 69.495 | 72.853 | 0.737 | 0.744 | 0.709 | ||
| RG21 | 99.387 | 85.314 | 83.437 | 0.582 | 0.600 | 0.579 | ||
| Average RMSE | 116.149 | 112.497 | 110.427 | Average R2 | 0.664 | 0.671 | 0.682 | |
| GRASS | AUD | 21.885 | 21.481 | 22.053 | 0.200 | 0.212 | 0.276 | |
| FPE | 34.699 | 34.544 | 35.134 | 0.541 | 0.531 | 0.496 | ||
| GCR | 55.747 | 56.305 | 58.141 | 0.831 | 0.823 | 0.815 | ||
| HB | 11.792 | 14.484 | 17.945 | 0.906 | 0.853 | 0.795 | ||
| KED | 33.405 | 33.165 | 32.512 | 0.498 | 0.502 | 0.518 | ||
| NEU | 80.230 | 81.569 | 93.599 | 0.821 | 0.821 | 0.767 | ||
| VRA | 85.744 | 84.997 | 82.802 | 0.310 | 0.315 | 0.352 | ||
| Average RMSE | 46.215 | 46.649 | 48.884 | Average R2 | 0.587 | 0.580 | 0.574 | |
| MF | CBS | 65.447 | 67.410 | 78.617 | 0.819 | 0.813 | 0.750 | |
| HOF | 55.397 | 58.873 | 70.669 | 0.881 | 0.862 | 0.776 | ||
| SOR | 62.126 | 60.641 | 78.508 | 0.915 | 0.909 | 0.832 | ||
| VSA | 56.961 | 55.160 | 62.589 | 0.861 | 0.862 | 0.819 | ||
| Average RMSE | 59.983 | 60.521 | 72.596 | Average R2 | 0.813 | 0.805 | 0.750 | |
| NF | ACA | 77.015 | 76.300 | 75.549 | 0.413 | 0.413 | 0.402 | |
| BD49 | 74.576 | 78.571 | 106.579 | 0.847 | 0.834 | 0.720 | ||
| DH00 | 56.199 | 63.847 | 63.684 | 0.605 | 0.602 | 0.561 | ||
| DH88 | 50.135 | 52.940 | 76.208 | 0.881 | 0.877 | 0.782 | ||
| DON | 87.427 | 87.770 | 84.239 | 0.682 | 0.680 | 0.685 | ||
| ES | 64.787 | 57.208 | 60.443 | 0.770 | 0.769 | 0.726 | ||
| FY | 65.602 | 61.214 | 67.128 | 0.844 | 0.855 | 0.770 | ||
| HY | 31.505 | 30.950 | 38.836 | 0.951 | 0.947 | 0.885 | ||
| LOB | 75.394 | 73.753 | 80.112 | 0.782 | 0.781 | 0.739 | ||
| MIN | 62.065 | 59.961 | 64.929 | 0.826 | 0.828 | 0.788 | ||
| MNY | 42.416 | 45.296 | 44.548 | 0.738 | 0.721 | 0.663 | ||
| NCL | 93.203 | 91.163 | 116.335 | 0.838 | 0.842 | 0.793 | ||
| NR | 38.822 | 36.581 | 43.257 | 0.792 | 0.805 | 0.739 | ||
| QMB | 26.751 | 25.044 | 29.041 | 0.633 | 0.673 | 0.597 | ||
| QYZ | 78.560 | 78.520 | 80.415 | 0.756 | 0.758 | 0.747 | ||
| REN | 77.531 | 79.238 | 79.692 | 0.663 | 0.657 | 0.617 | ||
| SRO | 81.280 | 78.843 | 77.470 | 0.725 | 0.719 | 0.682 | ||
| THA | 67.968 | 68.762 | 76.497 | 0.850 | 0.848 | 0.765 | ||
| TMK | 59.161 | 64.370 | 105.229 | 0.935 | 0.919 | 0.799 | ||
| U50 | 34.898 | 30.674 | 36.441 | 0.633 | 0.710 | 0.606 | ||
| WET | 70.679 | 72.746 | 75.443 | 0.862 | 0.862 | 0.803 | ||
| Average RMSE | 62.665 | 62.560 | 70.575 | Average R2 | 0.763 | 0.767 | 0.708 | |
| SHRUB | KEN | 59.876 | 58.965 | 62.697 | 0.811 | 0.811 | 0.789 | |
| MIZ | 73.406 | 73.674 | 73.614 | 0.840 | 0.844 | 0.831 | ||
| OEM | 16.690 | 19.447 | 23.973 | 0.818 | 0.785 | 0.713 | ||
| SON | 28.248 | 29.451 | 25.293 | 0.381 | 0.400 | 0.391 | ||
| SRM | 30.431 | 29.824 | 30.056 | 0.450 | 0.457 | 0.462 | ||
| TRA | 55.896 | 52.920 | 51.908 | 0.639 | 0.663 | 0.680 | ||
| U89 | 23.456 | 21.613 | 27.365 | 0.779 | 0.781 | 0.679 | ||
| U98 | 20.229 | 23.686 | 27.612 | 0.746 | 0.648 | 0.543 | ||
| Average RMSE | 38.529 | 38.698 | 40.315 | Average R2 | 0.683 | 0.674 | 0.636 | |

Table A2.
Assessment of daily GPP simulated using TL-LUEn, TL-LUE and MOD17 for the 58 evaluation site-years.
| ID | RMSE (g C m −2 day −1) | R2 | ||||||
|---|---|---|---|---|---|---|---|---|
| TL-LUEn | TL-LUE | MOD17 | TL-LUEn | TL-LUE | MOD17 | |||
| BF | BEP | 1.291 | 1.401 | 1.818 | 0.914 | 0.883 | 0.794 | |
| DHS | 1.328 | 1.418 | 1.695 | 0.379 | 0.362 | 0.321 | ||
| HA | 1.590 | 1.646 | 2.165 | 0.929 | 0.909 | 0.829 | ||
| HAF | 1.495 | 1.650 | 2.155 | 0.940 | 0.923 | 0.851 | ||
| HES | 1.522 | 1.905 | 2.503 | 0.914 | 0.880 | 0.781 | ||
| MMS | 1.810 | 1.792 | 1.895 | 0.849 | 0.854 | 0.829 | ||
| MOZ | 1.824 | 1.782 | 2.055 | 0.780 | 0.770 | 0.706 | ||
| PUE | 1.477 | 1.624 | 1.888 | 0.549 | 0.524 | 0.450 | ||
| ROC | 2.006 | 2.045 | 2.063 | 0.689 | 0.670 | 0.682 | ||
| UMBS | 1.318 | 2.147 | 2.330 | 0.924 | 0.944 | 0.917 | ||
| WCR | 1.343 | 1.402 | 1.848 | 0.949 | 0.941 | 0.891 | ||
| Average RMSE | 1.546 | 1.710 | 2.038 | Average R2 | 0.801 | 0.787 | 0.732 | |
| CROP | ASM | 1.095 | 1.061 | 1.165 | 0.608 | 0.630 | 0.595 | |
| BON | 3.166 | 2.821 | 2.793 | 0.727 | 0.737 | 0.696 | ||
| MEI | 3.054 | 2.911 | 3.076 | 0.852 | 0.867 | 0.845 | ||
| MER | 4.742 | 4.396 | 4.350 | 0.855 | 0.879 | 0.863 | ||
| MIR | 5.375 | 5.075 | 4.996 | 0.835 | 0.876 | 0.875 | ||
| RG19 | 2.223 | 2.202 | 2.345 | 0.741 | 0.740 | 0.710 | ||
| RG21 | 2.476 | 2.480 | 2.570 | 0.691 | 0.691 | 0.664 | ||
| Average RMSE | 3.162 | 2.992 | 3.042 | Average R2 | 0.758 | 0.774 | 0.750 | |
| GRASS | AUD | 0.609 | 0.611 | 0.618 | 0.412 | 0.435 | 0.427 | |
| FPE | 1.147 | 1.093 | 1.091 | 0.493 | 0.507 | 0.511 | ||
| GCR | 2.312 | 1.493 | 1.608 | 0.803 | 0.806 | 0.790 | ||
| HB | 0.328 | 0.349 | 0.357 | 0.912 | 0.917 | 0.913 | ||
| KED | 0.949 | 0.948 | 0.958 | 0.574 | 0.578 | 0.560 | ||
| NEU | 2.785 | 2.755 | 2.860 | 0.740 | 0.746 | 0.733 | ||
| VRA | 2.907 | 2.938 | 2.991 | 0.025 | 0.020 | 0.013 | ||
| Average RMSE | 1.577 | 1.455 | 1.498 | Average R2 | 0.566 | 0.573 | 0.564 | |
| MF | CBS | 1.550 | 1.603 | 1.868 | 0.899 | 0.893 | 0.842 | |
| HOF | 1.039 | 1.123 | 1.661 | 0.932 | 0.922 | 0.840 | ||
| SOR | 1.386 | 1.361 | 2.024 | 0.951 | 0.948 | 0.887 | ||
| VSA | 1.606 | 1.542 | 1.966 | 0.853 | 0.862 | 0.811 | ||
| Average RMSE | 1.395 | 1.407 | 1.880 | Average R2 | 0.909 | 0.906 | 0.845 | |
| NF | ACA | 1.417 | 1.406 | 1.473 | 0.338 | 0.337 | 0.319 | |
| BD49 | 1.567 | 1.714 | 2.756 | 0.922 | 0.908 | 0.755 | ||
| DH00 | 1.495 | 1.483 | 1.619 | 0.805 | 0.809 | 0.746 | ||
| DH88 | 1.357 | 1.518 | 2.270 | 0.908 | 0.912 | 0.780 | ||
| DON | 2.057 | 2.032 | 2.073 | 0.287 | 0.279 | 0.318 | ||
| ES | 1.358 | 1.416 | 1.712 | 0.440 | 0.432 | 0.397 | ||
| FY | 1.747 | 1.703 | 2.062 | 0.877 | 0.874 | 0.795 | ||
| HY | 0.851 | 0.849 | 1.111 | 0.955 | 0.955 | 0.915 | ||
| LOB | 1.849 | 1.824 | 2.175 | 0.876 | 0.878 | 0.839 | ||
| MIN | 2.284 | 2.294 | 2.407 | 0.726 | 0.726 | 0.716 | ||
| MNY | 1.191 | 1.096 | 1.155 | 0.800 | 0.796 | 0.742 | ||
| NCL | 1.826 | 1.917 | 2.612 | 0.862 | 0.858 | 0.801 | ||
| NR | 1.030 | 1.053 | 1.194 | 0.796 | 0.799 | 0.751 | ||
| QMB | 0.618 | 0.638 | 0.727 | 0.789 | 0.779 | 0.726 | ||
| QYZ | 1.217 | 1.260 | 1.530 | 0.903 | 0.909 | 0.863 | ||
| REN | 1.906 | 1.871 | 2.016 | 0.779 | 0.778 | 0.751 | ||
| SRO | 2.68 | 2.213 | 2.425 | 0.424 | 0.437 | 0.416 | ||
| THA | 1.878 | 1.864 | 2.305 | 0.847 | 0.847 | 0.752 | ||
| TMK | 1.368 | 1.422 | 2.266 | 0.965 | 0.962 | 0.884 | ||
| U50 | 0.771 | 0.817 | 0.965 | 0.819 | 0.808 | 0.738 | ||
| WET | 2.288 | 2.276 | 2.645 | 0.818 | 0.818 | 0.773 | ||
| Average RMSE | 1.560 | 1.556 | 1.881 | Average R2 | 0.759 | 0.757 | 0.704 | |
| SHRUB | KEN | 1.070 | 1.073 | 1.398 | 0.641 | 0.641 | 0.559 | |
| MIZ | 2.377 | 2.345 | 2.536 | 0.401 | 0.410 | 0.451 | ||
| OEM | 0.590 | 0.459 | 0.520 | 0.866 | 0.899 | 0.847 | ||
| SON | 0.896 | 0.746 | 0.696 | 0.383 | 0.340 | 0.348 | ||
| SRM | 0.730 | 0.730 | 0.748 | 0.661 | 0.657 | 0.628 | ||
| TRA | 1.252 | 1.211 | 1.325 | 0.730 | 0.716 | 0.658 | ||
| U89 | 0.466 | 0.559 | 0.727 | 0.909 | 0.889 | 0.810 | ||
| U98 | 0.578 | 0.662 | 0.777 | 0.804 | 0.755 | 0.665 | ||
| Average RMSE | 0.995 | 0.973 | 1.091 | Average R2 | 0.674 | 0.663 | 0.621 | |

Table A3.
Assessment of 8-day GPP simulated using TL-LUEn, TL-LUE and MOD17 for the 58 evaluation site-years.
| Vegetation
Type | ID | RMSE(g C m −2 (8days) −1) | R2 | |||||
|---|---|---|---|---|---|---|---|---|
| TL-LUEn | TL-LUE | MOD17 | TL-LUEn | TL-LUE | MOD17 | |||
| BF | BEP | 8.797 | 9.867 | 11.087 | 0.940 | 0.908 | 0.875 | |
| DHS | 8.040 | 8.081 | 9.379 | 0.489 | 0.483 | 0.454 | ||
| HA | 11.839 | 12.680 | 15.534 | 0.948 | 0.919 | 0.893 | ||
| HAF | 10.318 | 11.533 | 13.496 | 0.952 | 0.939 | 0.905 | ||
| HES | 11.323 | 13.312 | 17.844 | 0.940 | 0.913 | 0.858 | ||
| MMS | 12.139 | 13.032 | 12.506 | 0.878 | 0.862 | 0.873 | ||
| MOZ | 10.735 | 12.913 | 13.328 | 0.859 | 0.799 | 0.788 | ||
| PUE | 10.386 | 11.343 | 13.264 | 0.564 | 0.518 | 0.443 | ||
| ROC | 14.711 | 14.755 | 14.760 | 0.731 | 0.727 | 0.738 | ||
| UMBS | 14.479 | 16.448 | 16.701 | 0.966 | 0.956 | 0.960 | ||
| WCR | 9.311 | 10.438 | 9.748 | 0.961 | 0.952 | 0.956 | ||
| Average RMSE | 11.098 | 12.218 | 13.422 | Average R2 | 0.839 | 0.816 | 0.795 | |
| CROP | ASM | 9.940 | 7.639 | 8.004 | 0.646 | 0.668 | 0.658 | |
| BON | 22.047 | 21.025 | 20.760 | 0.760 | 0.753 | 0.722 | ||
| MEI | 21.868 | 22.272 | 23.100 | 0.883 | 0.878 | 0.868 | ||
| MER | 36.640 | 34.434 | 33.774 | 0.889 | 0.888 | 0.883 | ||
| MIR | 41.373 | 39.191 | 38.325 | 0.870 | 0.886 | 0.897 | ||
| RG19 | 14.858 | 15.987 | 16.825 | 0.797 | 0.776 | 0.738 | ||
| RG21 | 18.381 | 18.880 | 19.199 | 0.718 | 0.708 | 0.694 | ||
| Average RMSE | 23.587 | 22.775 | 22.855 | Average R2 | 0.795 | 0.794 | 0.780 | |
| GRASS | AUD | 4.462 | 4.377 | 4.424 | 0.505 | 0.531 | 0.520 | |
| FPE | 8.178 | 7.494 | 7.389 | 0.565 | 0.601 | 0.614 | ||
| GCR | 12.983 | 10.570 | 11.432 | 0.841 | 0.84 | 0.832 | ||
| HB | 1.467 | 1.825 | 1.632 | 0.977 | 0.963 | 0.973 | ||
| KED | 7.285 | 6.912 | 6.773 | 0.620 | 0.670 | 0.656 | ||
| NEU | 20.615 | 20.126 | 20.91 | 0.776 | 0.779 | 0.769 | ||
| VRA | 22.565 | 22.917 | 23.431 | 0.032 | 0.020 | 0.010 | ||
| Average RMSE | 11.079 | 10.603 | 10.856 | Average R2 | 0.617 | 0.629 | 0.625 | |
| MF | CBS | 9.285 | 10.630 | 11.117 | 0.944 | 0.936 | 0.918 | |
| HOF | 6.798 | 6.388 | 7.703 | 0.96 | 0.955 | 0.935 | ||
| SOR | 11.469 | 9.027 | 12.070 | 0.959 | 0.960 | 0.938 | ||
| VSA | 10.844 | 9.517 | 12.613 | 0.929 | 0.933 | 0.906 | ||
| Average RMSE | 9.599 | 8.891 | 10.876 | Average R2 | 0.948 | 0.946 | 0.924 | |
| NF | ACA | 9.207 | 9.107 | 9.201 | 0.349 | 0.382 | 0.380 | |
| BD49 | 10.080 | 10.342 | 13.791 | 0.943 | 0.952 | 0.904 | ||
| DH00 | 10.258 | 10.962 | 10.835 | 0.846 | 0.850 | 0.841 | ||
| DH88 | 9.043 | 10.307 | 14.822 | 0.943 | 0.949 | 0.880 | ||
| DON | 14.970 | 14.370 | 14.779 | 0.217 | 0.213 | 0.215 | ||
| ES | 11.749 | 10.039 | 12.075 | 0.490 | 0.467 | 0.437 | ||
| FY | 13.414 | 13.072 | 14.767 | 0.889 | 0.888 | 0.829 | ||
| HY | 5.923 | 5.976 | 6.865 | 0.971 | 0.964 | 0.951 | ||
| LOB | 15.885 | 13.218 | 14.689 | 0.943 | 0.940 | 0.926 | ||
| MIN | 17.790 | 17.128 | 17.869 | 0.832 | 0.830 | 0.829 | ||
| MNY | 7.965 | 7.875 | 8.036 | 0.870 | 0.857 | 0.808 | ||
| NCL | 10.917 | 13.249 | 17.512 | 0.872 | 0.857 | 0.808 | ||
| NR | 6.918 | 7.253 | 7.520 | 0.853 | 0.851 | 0.852 | ||
| QMB | 8.092 | 7.034 | 7.159 | 0.589 | 0.586 | 0.577 | ||
| QYZ | 8.782 | 8.131 | 9.146 | 0.951 | 0.953 | 0.939 | ||
| REN | 14.123 | 13.660 | 13.975 | 0.862 | 0.863 | 0.862 | ||
| SRO | 20.316 | 15.779 | 18.341 | 0.466 | 0.478 | 0.433 | ||
| THA | 14.245 | 13.288 | 14.906 | 0.899 | 0.896 | 0.872 | ||
| TMK | 9.117 | 9.443 | 10.819 | 0.968 | 0.972 | 0.963 | ||
| U50 | 5.158 | 4.878 | 5.818 | 0.895 | 0.887 | 0.854 | ||
| WET | 20.463 | 18.842 | 21.864 | 0.878 | 0.882 | 0.862 | ||
| Average RMSE | 11.639 | 11.141 | 12.609 | Average R2 | 0.787 | 0.787 | 0.763 | |
| SHRUB | KEN | 5.735 | 6.356 | 8.740 | 0.701 | 0.660 | 0.535 | |
| MIZ | 18.357 | 16.033 | 19.194 | 0.454 | 0.475 | 0.435 | ||
| OEM | 8.708 | 3.493 | 3.302 | 0.933 | 0.938 | 0.912 | ||
| SON | 13.356 | 5.074 | 4.735 | 0.403 | 0.407 | 0.455 | ||
| SRM | 5.992 | 5.427 | 5.358 | 0.737 | 0.734 | 0.721 | ||
| TRA | 14.741 | 8.007 | 8.603 | 0.758 | 0.797 | 0.758 | ||
| U89 | 4.485 | 4.168 | 4.582 | 0.868 | 0.909 | 0.895 | ||
| U98 | 5.674 | 4.391 | 4.793 | 0.867 | 0.813 | 0.782 | ||
| Average RMSE | 9.631 | 6.619 | 7.413 | Average R2 | 0.715 | 0.717 | 0.687 | |
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).