Estimating Roof Solar Energy Potential in the Downtown Area Using a GPU-Accelerated Solar Radiation Model and Airborne LiDAR Data
Abstract
:1. Introduction
2. Case Study Area and Data Collection
2.1. Case Study Area

2.2. Data Collection
3. Methods
3.1. GPU-Based Solar Radiation Model—SHORTWAVE-C
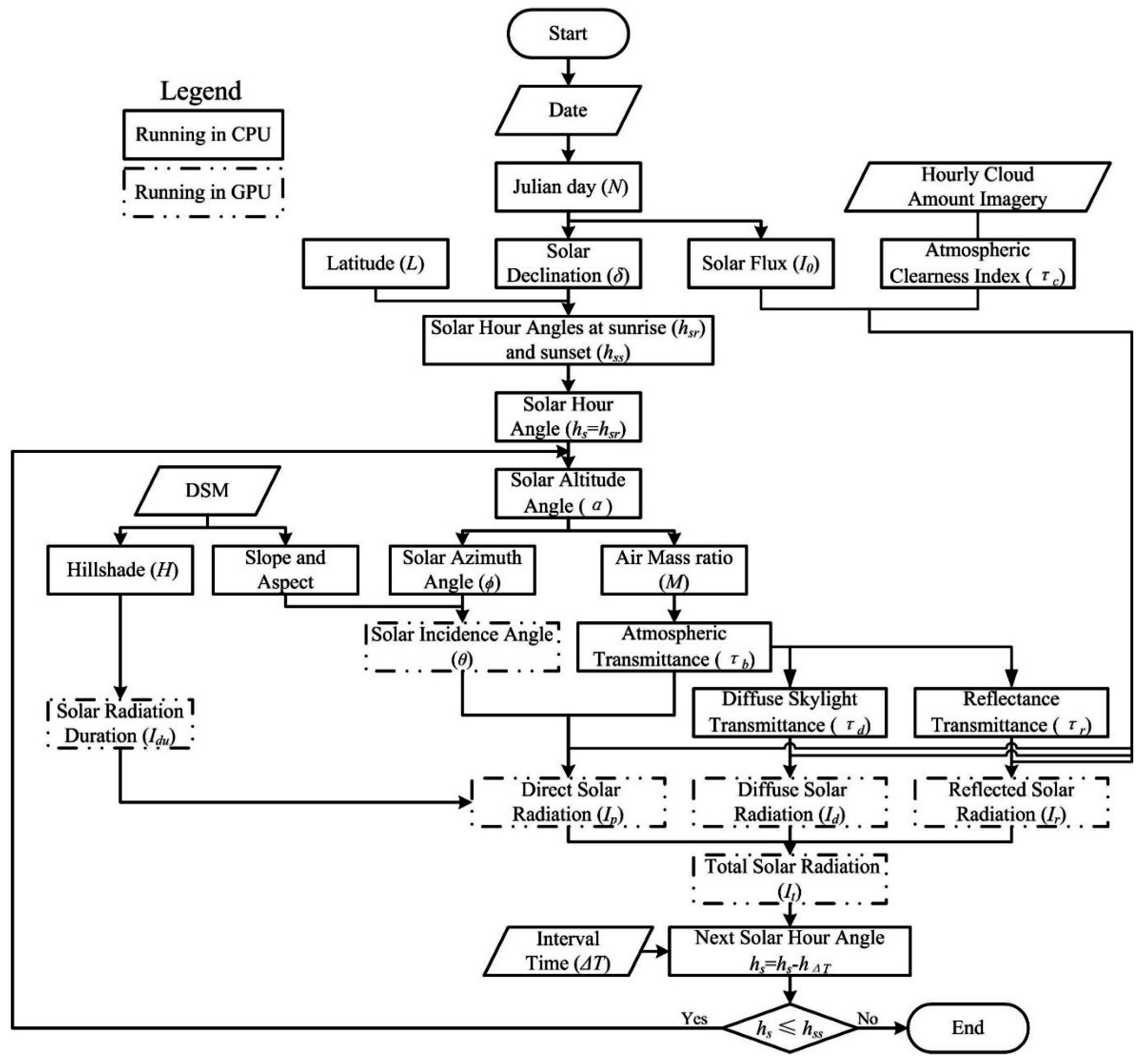
3.1.1. SHORTWAVE-C Algorithm
3.1.2. GPU Acceleration
3.2. Object-Based Method to Locate Suitable Roofs for Utilization of Solar Energy
3.2.1. Automated Extraction of Building Footprints
3.2.2. Segmentation of Roof Planes
3.2.3. Selection of Suitable Locations for Solar Panel Installation
| Attributes | Definition | |
|---|---|---|
| Geometric attributes | Roof plane centroid point () | |
| Roof plane perimeter (P) | ||
| Roof plane area (S) | ||
| Topographic attributes | Average slope (A_slope) | |
| Average aspect (A_aspect) | ||
| Solar radiation attributes | Monthly average total solar radiation (MA_TSR) | |
| Seasonal average total solar radiation (SA_TSR) | ||
| Yearly average total solar radiation (YA_TSR) | ||
| Monthly average solar illumination duration (MA_SID) | ||
| Seasonal average solar illumination duration (SA_SID) | ||
| Yearly average solar illumination duration (YA_SID) | ||
- Suitable roof plane area. In terms of practical installation of the solar panel on roof planes, the area of roof plane should not be too small. We defined 10 m2 as the threshold value for our case study. If the roof plane area is equal or larger than 10 m2, it will be considered as a potential installation location.
- Suitable roof plane slope. If the roof plane has a slope that is too steep, it is not appropriate to install solar panels. Thus, we chose roof planes whose slope is equal or lower than 45 degrees for installing solar panels.
- Suitable roof plane aspect. As Shanghai is located in the North hemisphere, roof planes facing south receive a higher solar radiation than those north-facing. In this study, the aspect should be south, southeast, southwest facing, or horizontal.
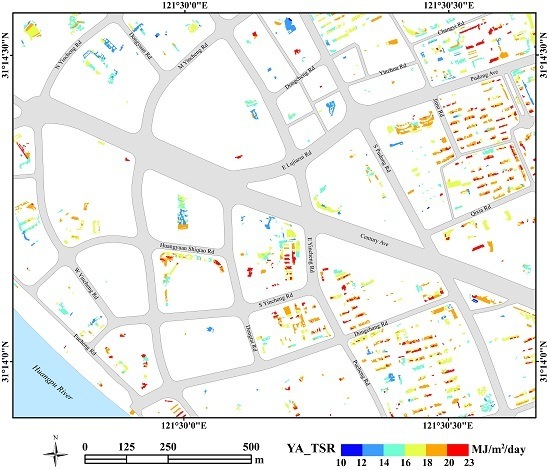
- High yearly average total solar radiation. The selected positions should receive at least some minimum yearly average solar radiation. The yearly average total solar radiation of building rooftops in Lujiazui region ranges from 2.0 to 23.8 MJ/m2/day, and the mean value is around 13.1 MJ/m2/day. Thus, we selected 10 MJ/m2/day as the threshold value for the yearly average total solar radiation.
- Long sunlight duration. To receive stable solar radiation for a long time, the desirable rooftops should have long average daily sunlight duration all year round. For building roofs in Lujiazui region, the maximum, minimum, and mean value of yearly average solar illumination duration is 11.9, 0, and 5.8 h, respectively. The sites that can receive more than 5 h sunlight are chosen as potential locations.
4. Results and Discussion
4.1. Spatio-Temporal Distribution of Solar Radiation

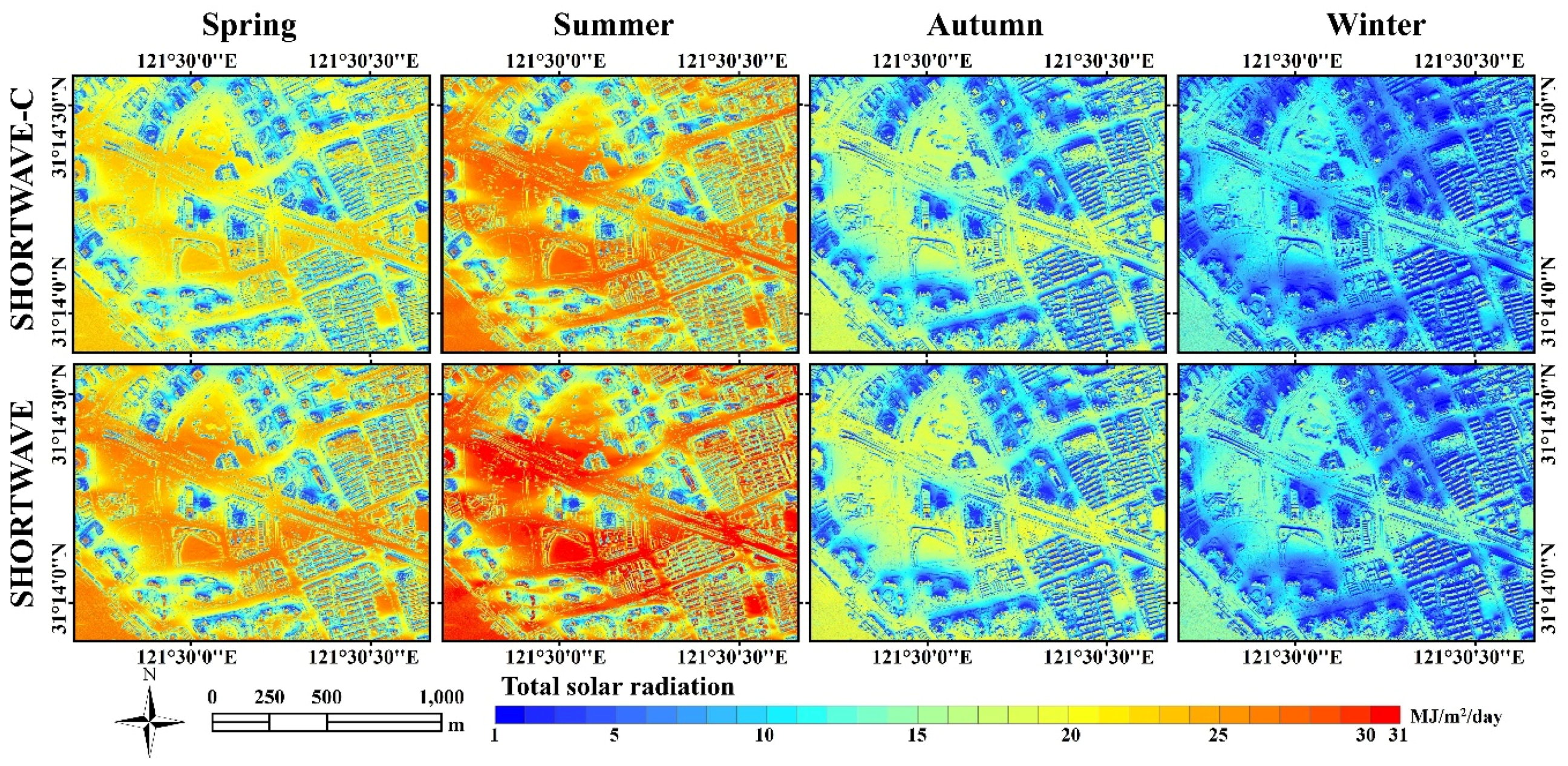
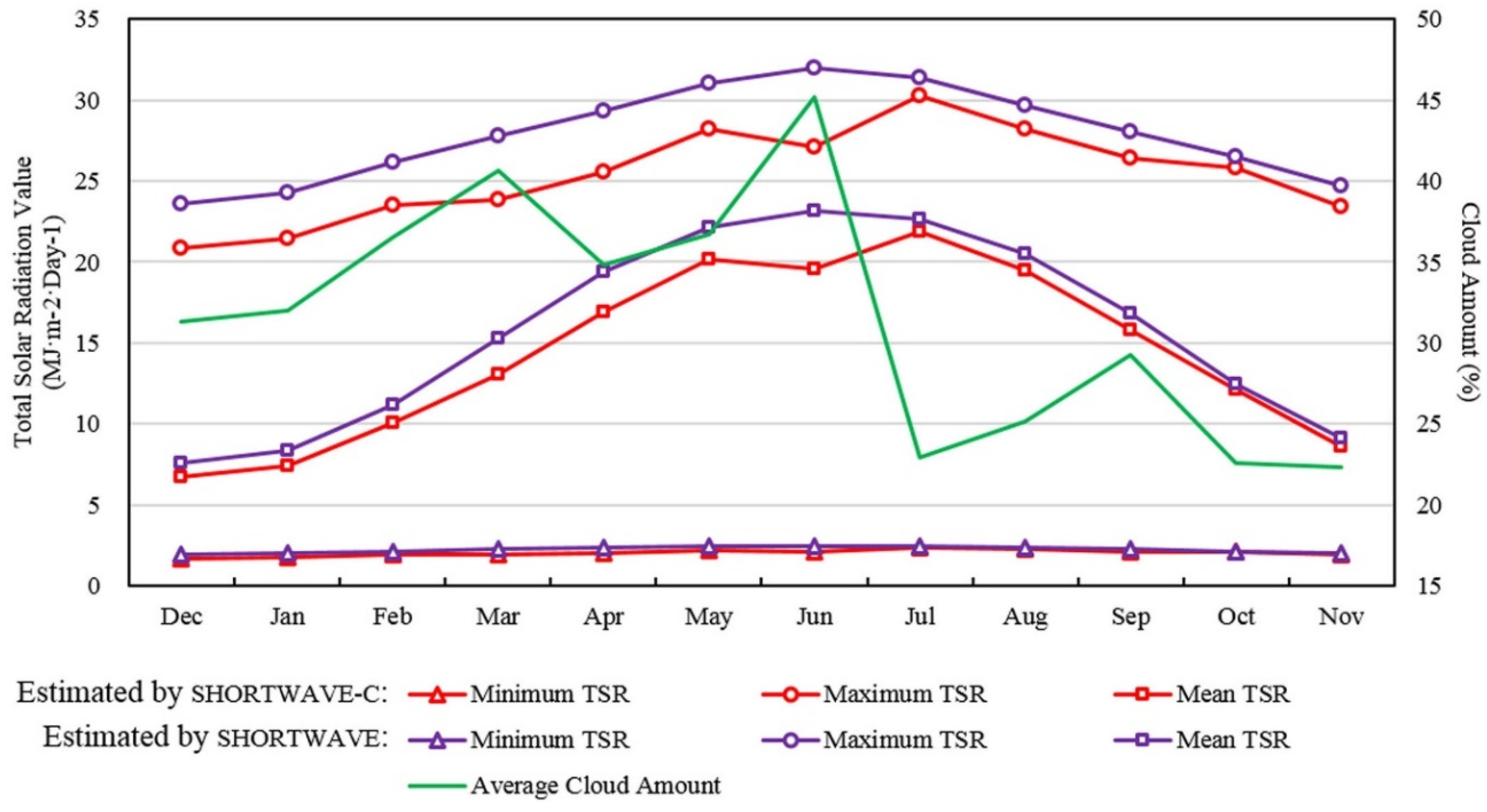
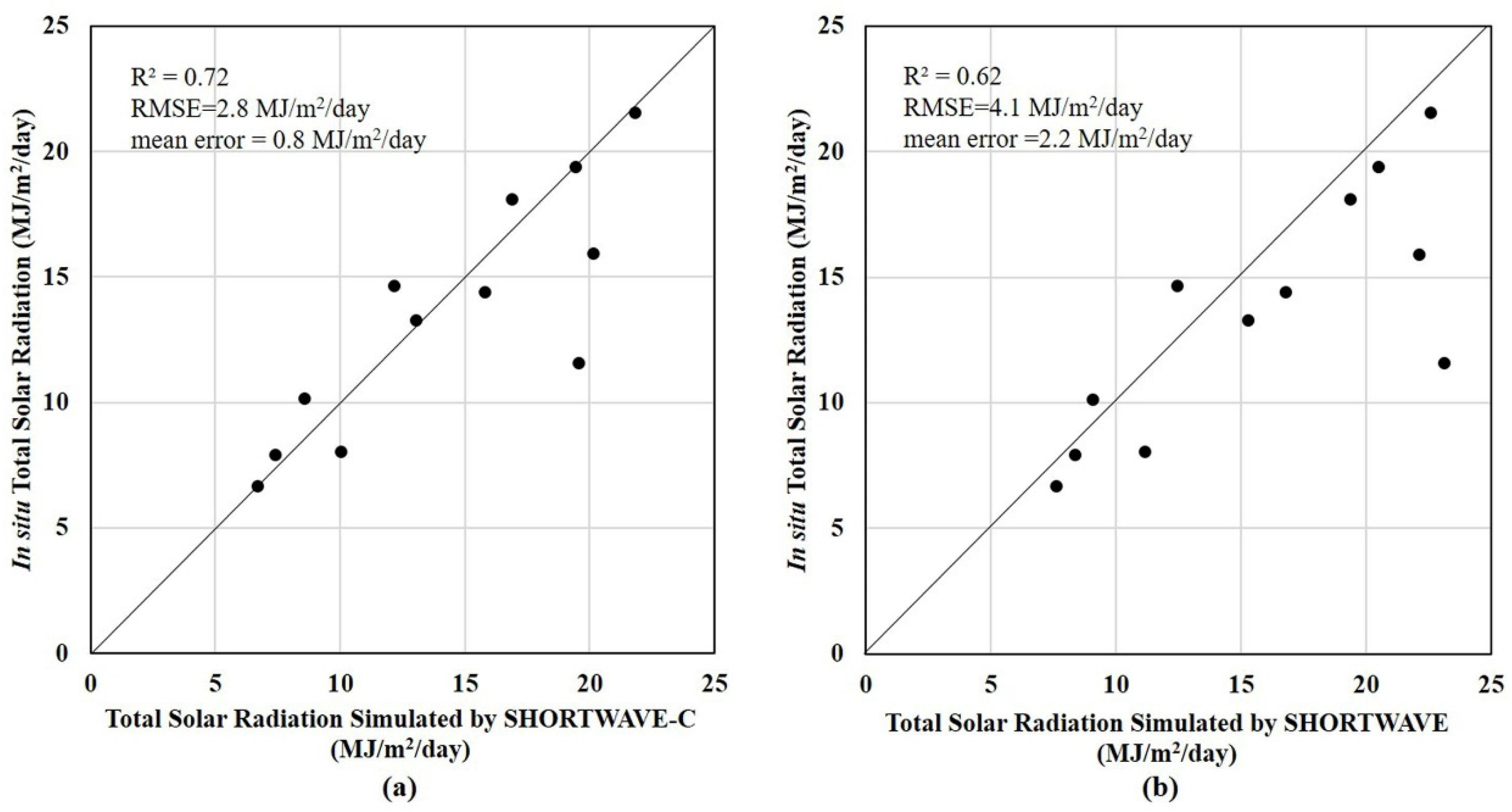

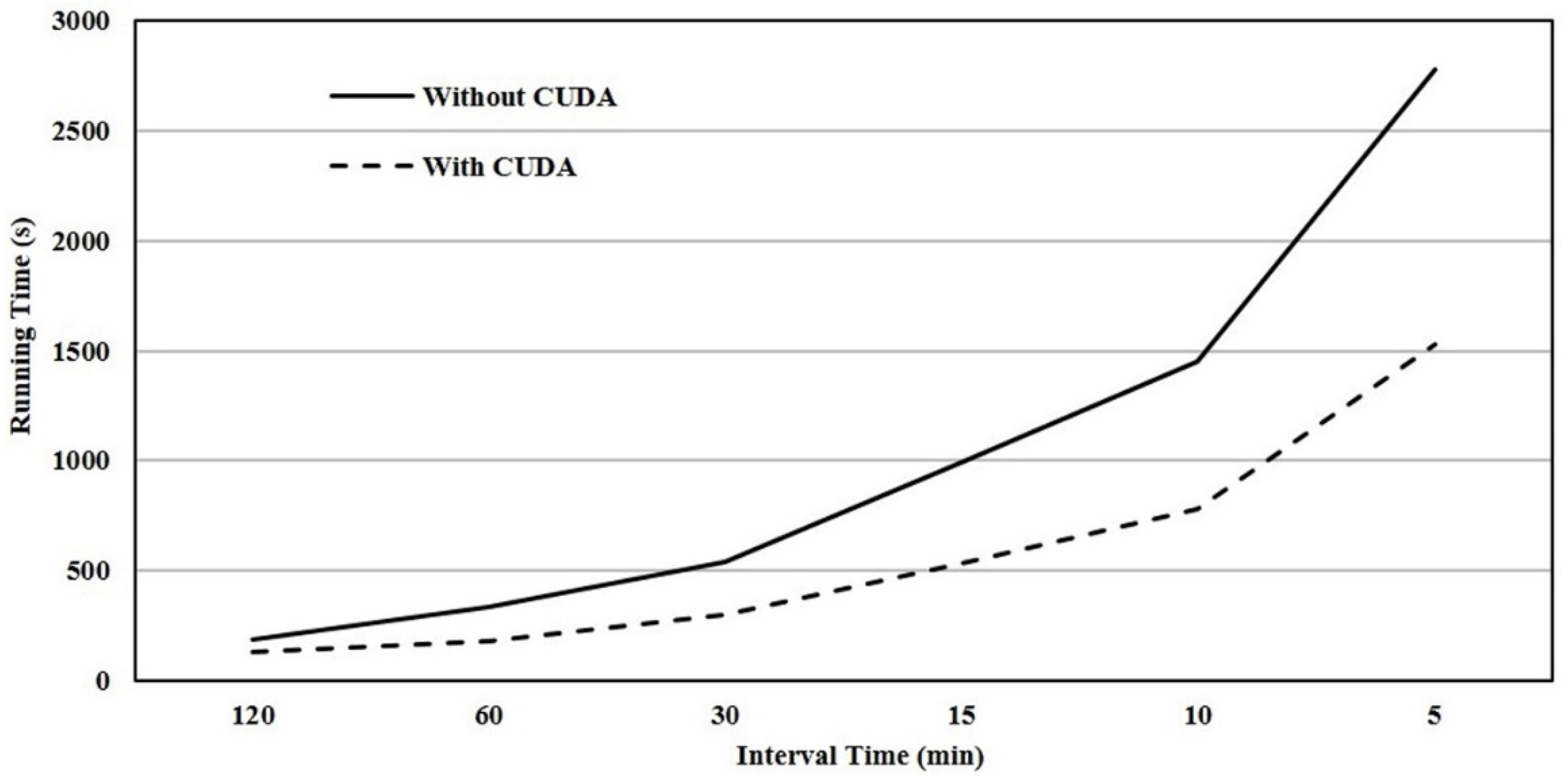
4.2. Efficiency of GPU-Accelerated Solar Radiation Model
| Interval Time (min) | Running Time (s) | Speedup Ratio (%) | |
|---|---|---|---|
| Without CUDA | With CUDA | ||
| 120 | 187.896 | 127.407 | 32.2 |
| 60 | 331.692 | 181.385 | 45.3 |
| 30 | 537.467 | 297.858 | 44.6 |
| 15 | 991.275 | 530.285 | 46.5 |
| 10 | 1447.410 | 776.731 | 46.3 |
| 5 | 2778.064 | 1529.491 | 44.9 |
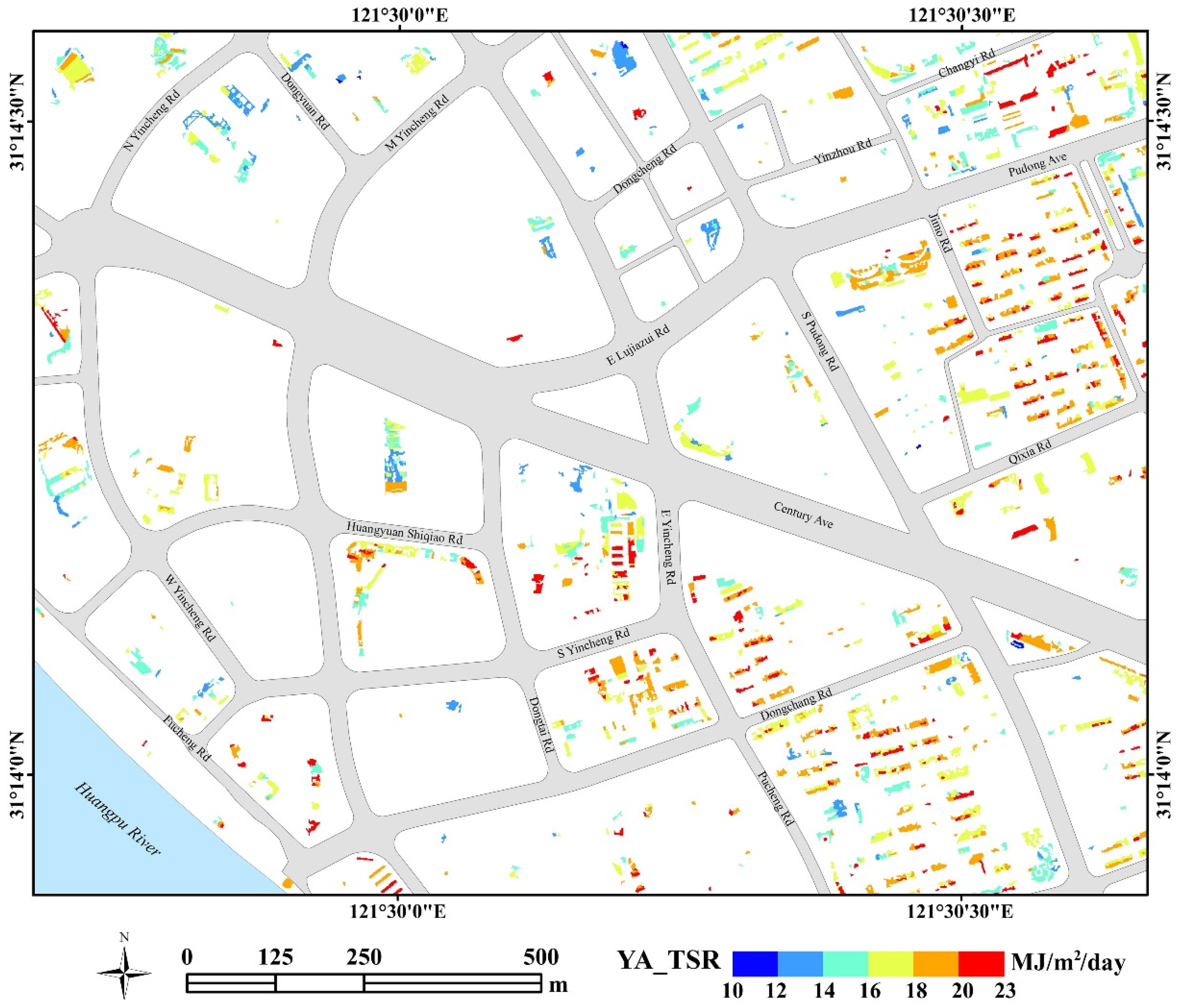
4.3. Suitable Roofs for Utilization of Solar Energy in the Lujiazui Region
| Attributes | Min | Max | Mean |
|---|---|---|---|
| S (m2) | 3 | 2407 | 53 |
| A_slope (degree) | 0.7 | 89.3 | 44.6 |
| YA_TSR (MJ/m2/day) | 2.4 | 23.0 | 13.3 |
| YA_SID (hours) | 0 | 11.5 | 5.9 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van der Hoeven, M. World Energy Outlook 2013; International Energy Agency: Tokyo, Japan, 2013. [Google Scholar]
- Ramachandra, T.V.; Shruthi, B.V. Spatial mapping of renewable energy potential. Renew. Sustain. Energy Rev. 2007, 11, 1460–1480. [Google Scholar] [CrossRef]
- Bull, S.R. Renewable energy today and tomorrow. Proc. IEEE 2001, 89, 1216–1226. [Google Scholar] [CrossRef]
- Solangi, K.H.; Islam, M.R.; Saidur, R.; Rahim, N.A.; Fayaz, H. A review on global solar energy policy. Renew. Sustain. Enery Rev. 2011, 15, 2149–2163. [Google Scholar] [CrossRef]
- British Petrol. Statistical Review of World Energy 2013; British Petrol: London, UK, 2013. [Google Scholar]
- Hassan, M.A.; Beliveau, Y. Design, construction and performance prediction of integrated solar roof collectors using finite element analysis. Constr. Build. Mater. 2007, 21, 1069–1078. [Google Scholar] [CrossRef]
- Camargo, L.R.; Zink, R.; Dorner, W.; Stoeglehner, G. Spatio-temporal modeling of roof-top photovoltaic panels for improved technical potential assessment and electricity peak load offsetting at the municipal scale. Comput. Environ. Urban Syst. 2015, 52, 58–69. [Google Scholar] [CrossRef]
- Kumar, L.; Skidmore, A.K.; Knowles, E. Modelling topographic variation in solar radiation in a GIS environment. Int. J. Geogr. Inf. Sci. 1997, 11, 475–497. [Google Scholar] [CrossRef]
- Dubayah, R.; Rich, P.M. Topographic solar radiation models for GIS. Int. J. Geogr. Inf. Syst. 1995, 9, 405–419. [Google Scholar] [CrossRef]
- Robinson, D. Urban morphology and indicators of radiation availability. Sol. Energy 2006, 80, 1643–1648. [Google Scholar] [CrossRef]
- Li, D.H.W.; Wong, S.L. Daylighting and energy implications due to shading effects from nearby buildings. Appl. Energy 2007, 84, 1199–1209. [Google Scholar] [CrossRef]
- Levinson, R.; Akbari, H.; Pomerantz, M.; Gupta, S. Solar access of residential rooftops in four California cities. Sol. Energy 2009, 83, 2120–2135. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Wang, R.Z. Experiences on solar heating and cooling in China. Renew. Sustain. Energy Rev. 2008, 12, 1110–1128. [Google Scholar] [CrossRef]
- Fu, P.; Rich, P.M. A geometric solar radiation model with applications in agriculture and forestry. Comput. Electron. Agric. 2002, 37, 25–35. [Google Scholar] [CrossRef]
- Barazzetti, L.; Brumana, R.; Oreni, D.; Previtali, M.; Roncoroni, F. True-orthophoto generation from UAV images: Implementation of a combined photogrammetric and computer vision approach. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 1, 57–63. [Google Scholar] [CrossRef]
- Szabó, S.; Enyedi, P.; Horváth, M.; Kovács, Z.; Burai, P.; Csoknyai, T.; Szabó, G. Automated registration of potential locations for solar energy production with Light Detection And Ranging (LiDAR) and small format photogrammetry. J. Clean. Prod. 2015. [Google Scholar] [CrossRef]
- Gamba, P.; Houshmand, B. Digital surface models and building extraction: A comparison of IFSAR and LIDAR data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1959–1968. [Google Scholar] [CrossRef]
- Priestnall, G.; Jaafar, J.; Duncan, A. Extracting urban features from LiDAR digital surface models. Comput. Environ. Urban Syst. 2000, 24, 65–78. [Google Scholar] [CrossRef]
- Sun, S.; Salvaggio, C. Aerial 3D building detection and modeling from airborne LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1440–1449. [Google Scholar] [CrossRef]
- Sun, S. Automatic 3D Building Detection and Modeling from Airborne LiDAR Point Clouds. Ph.D. Thesis, Institute of Technology, New York, NY, USA, 2013. [Google Scholar]
- Zhou, Q.Y.; Neumann, U. Fast and extensible building modeling from airborne LiDAR data. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geograpic Information Systems, Irvine, CA, USA, 5–7 November 2008; pp. 1–8.
- Lafarge, F.; Descombes, X.; Zerubia, J.; Pierrot-Deseilligny, M. Automatic building extraction from DEMs using an object approach and application to the 3D-city modeling. ISPRS J. Photogramm. Remote Sens. 2008, 63, 365–381. [Google Scholar] [CrossRef]
- Arefi, H. Levels of detail in 3D building reconstruction from LiDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 485–490. [Google Scholar]
- Huang, Y.; Yu, B.; Zhou, J.; Hu, C.; Tan, W.; Hu, Z.; Wu, J. Toward automatic estimation of urban green volume using airborne LiDAR data and high resolution remote sensing images. Front. Earth Sci. 2013, 7, 43–54. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Yue, W.; Shu, S.; Tan, W.; Hu, C.; Huang, Y.; Wu, J.; Liu, H. A voxel-based method for automated identification and morphological parameters estimation of individual street trees from mobile laser scanning data. Remote Sens. 2013, 5, 584–611. [Google Scholar] [CrossRef]
- Yu, B.; Liu, H.; Wu, J.; Lin, W. Investigating impacts of urban morphology on spatio-temporal variations of solar radiation with airborne LIDAR data and a solar flux model: A case study of downtown houston. Int. J. Remote Sens. 2009, 30, 4359–4385. [Google Scholar] [CrossRef]
- Santos, T.; Gomes, N.; Freire, S.; Brito, M.; Santos, L.; Tenedório, J. Applications of solar mapping in the urban environment. Appl. Geogr. 2014, 51, 48–57. [Google Scholar] [CrossRef]
- Verso, A.; Martin, A.; Amador, J.; Dominguez, J. GIS-based method to evaluate the photovoltaic potential in the urban environments: The particular case of Miraflores de la Sierra. Sol. Energy 2015, 117, 236–245. [Google Scholar] [CrossRef]
- Martín, A.M.; Domínguez, J.; Amador, J. Applying LiDAR datasets and GIS based model to evaluate solar potential over roofs: A review. AIMS Energy 2015, 11, 326–343. [Google Scholar] [CrossRef]
- Jo, J.H.; Rose, Z.; Cross, J.; Daebel, E.; Verderber, A.; Kostelnick, J.C. Application of airborne LiDAR data and geographic information systems (GIS) to develop a distributed generation system for the town of normal, IL. AIMS Energy 2015, 3, 173–183. [Google Scholar] [CrossRef]
- Kim, D.; Ramanathan, V. Solar radiation budget and radiative forcing due to aerosols and clouds. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Tooke, T.R.; Coops, N.C.; Christen, A.; Gurtuna, O.; Prevot, A. Integrated irradiance modelling in the urban environment based on remotely sensed data. Sol. Energy 2012, 86, 2923–2934. [Google Scholar] [CrossRef]
- Kasten, F. The linke turbidity factor based on improved values of the integral rayleigh optical thickness. Sol. Energy 1996, 56, 239–244. [Google Scholar] [CrossRef]
- Lee, C.A.; Gasster, S.D.; Plaza, A.; Chang, C.I.; Huang, B. Recent developments in high performance computing for remote sensing: A review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 508–527. [Google Scholar] [CrossRef]
- Zhang, J.; You, S. High-performance quadtree constructions on large-scale geospatial rasters using GPGPU parallel primitives. Int. J. Geogr. Inf. Sci. 2013, 27, 2207–2226. [Google Scholar] [CrossRef]
- Hu, X.; Li, X.; Zhang, Y. Fast filtering of LiDAR point cloud in urban areas based on scan line segmentation and GPU acceleration. IEEE Geosci. Remote Sens. Lett. 2013, 10, 308–312. [Google Scholar]
- Lukač, N.; Žalik, B. GPU-based roofs’ solar potential estimation using LiDAR data. Comput. Geosci. 2013, 52, 34–41. [Google Scholar] [CrossRef]
- Feng, Y.; Guo, R.; Cheng, Y. Research on three dimentional city model reconstruction based on LiDAR. Geomat. Spat. Inf. Technol. 2008, 31, 8–11. (In Chinese) [Google Scholar]
- Zhang, K.; Chen, S.; Whitman, D.; Shyu, M.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Hu, Z.; Wu, J.; Wu, B.; Shu, S.; Yu, B. Simulating and mapping the variations of solar radiation at the Lujiazui region of shanghai using airborne LiDAR data. In Proceedings of the 2010 International Conference on Remote Sensing, Hangzhou, China, 5–6 October 2010; pp. 305–308.
- Huang, Y.; Yu, B.; Hu, Z.; Wu, J.; Wu, B. Locating suitable roofs for utilization of solar energy in downtown area using airborne LiDAR data and object-based method: A case study of the Lujiazui region, Shanghai. In Proceedings of the 2012 Second International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Shanghai, China, 8–11 June 2012; pp. 322–326.
- Zimmermann, N.E. Calculation of Direct Solar Radiation (n-lat_ corrected). Available online: http://www.wsl.ch/staff/niklaus.zimmermann/programs/aml.html (accessed on 20 October 2007).
- Redweik, P.; Catita, C.; Brito, M. Solar energy potential on roofs and facades in an urban landscape. Sol. Energy 2013, 97, 332–341. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Tovar-Pescador, J.; Pozo-Vázquez, D.; Alsamamra, H. A comparative analysis of DEM-based models to estimate the solar radiation in mountainous terrain. Int. J. Geogr. Inf. Sci. 2009, 23, 1049–1076. [Google Scholar] [CrossRef]
- Antonic, O. Modelling daily topographic solar radiation without site-specific hourly radiation data. Ecol. Model. 1998, 113, 31–40. [Google Scholar] [CrossRef]
- Kreith, F.; Kreider, J.F. Principles of Solar Engineering; Hemisphere Publishing Corporation: Washington, DC, USA, 1978. [Google Scholar]
- Cartwright, T.J. Modeling the World in a Spreadsheet: Environmental Simulation on a Microcomputer; Johns Hopkins University Press: Baltimore, MD, USA, 1993. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]
- Gul, M.S.; Muneer, T.; Kambezidis, H.D. Models for obtaining solar radiation from other meteorological data. Sol. Energy 1998, 64, 99–108. [Google Scholar] [CrossRef]
- NVIDIA Corporation. NVIDIA Compute Unified Device Architecture Programming Guide Version 2.0; NVIDIA Corporation: Santa Clara, CA, USA, 2008. [Google Scholar]
- Kirk, D. NVIDIA CUDA software and GPU parallel computing architecture. In Proceedings of the 6th International Symposium on Memory management, Montreal, QC, Canada, 21–22 October 2007; pp. 103–104.
- Yu, B.; Liu, H.; Wu, J.; Hu, Y.; Zhang, L. Automated derivation of urban building density information using airborne LiDAR data and object-based method. Landsc. Urban Plan. 2010, 98, 210–219. [Google Scholar] [CrossRef]
- Chaves, A.; Bahill, A.T. Locating sites for photovoltaic solar panels. ArcUser 2010, 13, 24–27. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Chen, Z.; Wu, B.; Chen, L.; Mao, W.; Zhao, F.; Wu, J.; Wu, J.; Yu, B. Estimating Roof Solar Energy Potential in the Downtown Area Using a GPU-Accelerated Solar Radiation Model and Airborne LiDAR Data. Remote Sens. 2015, 7, 17212-17233. https://doi.org/10.3390/rs71215877
Huang Y, Chen Z, Wu B, Chen L, Mao W, Zhao F, Wu J, Wu J, Yu B. Estimating Roof Solar Energy Potential in the Downtown Area Using a GPU-Accelerated Solar Radiation Model and Airborne LiDAR Data. Remote Sensing. 2015; 7(12):17212-17233. https://doi.org/10.3390/rs71215877
Chicago/Turabian StyleHuang, Yan, Zuoqi Chen, Bin Wu, Liang Chen, Weiqing Mao, Feng Zhao, Jianping Wu, Junhan Wu, and Bailang Yu. 2015. "Estimating Roof Solar Energy Potential in the Downtown Area Using a GPU-Accelerated Solar Radiation Model and Airborne LiDAR Data" Remote Sensing 7, no. 12: 17212-17233. https://doi.org/10.3390/rs71215877
APA StyleHuang, Y., Chen, Z., Wu, B., Chen, L., Mao, W., Zhao, F., Wu, J., Wu, J., & Yu, B. (2015). Estimating Roof Solar Energy Potential in the Downtown Area Using a GPU-Accelerated Solar Radiation Model and Airborne LiDAR Data. Remote Sensing, 7(12), 17212-17233. https://doi.org/10.3390/rs71215877