Temporal and Spatial Assessment of Four Satellite Rainfall Estimates over French Guiana and North Brazil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
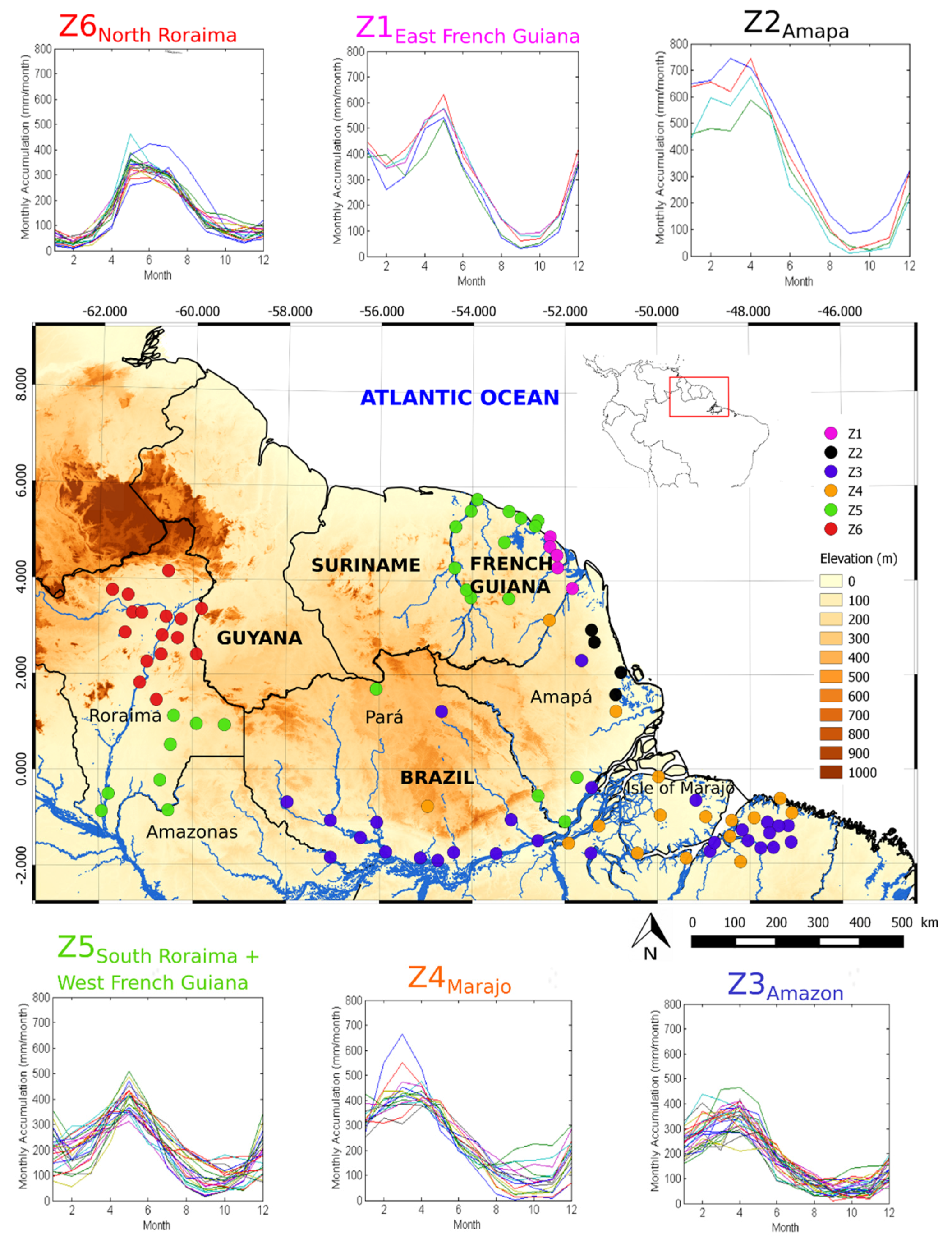
| Zones | Average Yearly Aggregate (mm/y) | SDII (mm/d) | Rainy (%) |
|---|---|---|---|
| Z2Amapá | 4101 | 19.6 | 59 |
| Z1East French Guiana | 3581 | 13.5 | 74 |
| Z4Marajó | 2855 | 15.3 | 54 |
| Z5South Roraima + West French Guiana | 2446 | 12.6 | 55 |
| Z3Amazon | 2153 | 13.5 | 46 |
| Z6North Roraima | 1809 | 15 | 34 |
2.2. Precipitation Products
2.2.1. TRMM-TMPA V7 and TRMM-TMPA RT
2.2.2. PERSIANN
2.2.3. CMORPH
2.3. Rain Gauges
2.4. Data Quality Control
2.5. Methodology
| In Situ | |||
|---|---|---|---|
| Rain | No Rain | ||
| Satellites | Rain | A | B |
| No rain | C | D | |
| Probability of Detection (POD) of rainy days | A/(A + C) |
| Probability of correct no-rain detection | D/(D + B) |
| False alarme ratio FAR | B/(A + B) |
3. Results and Discussion
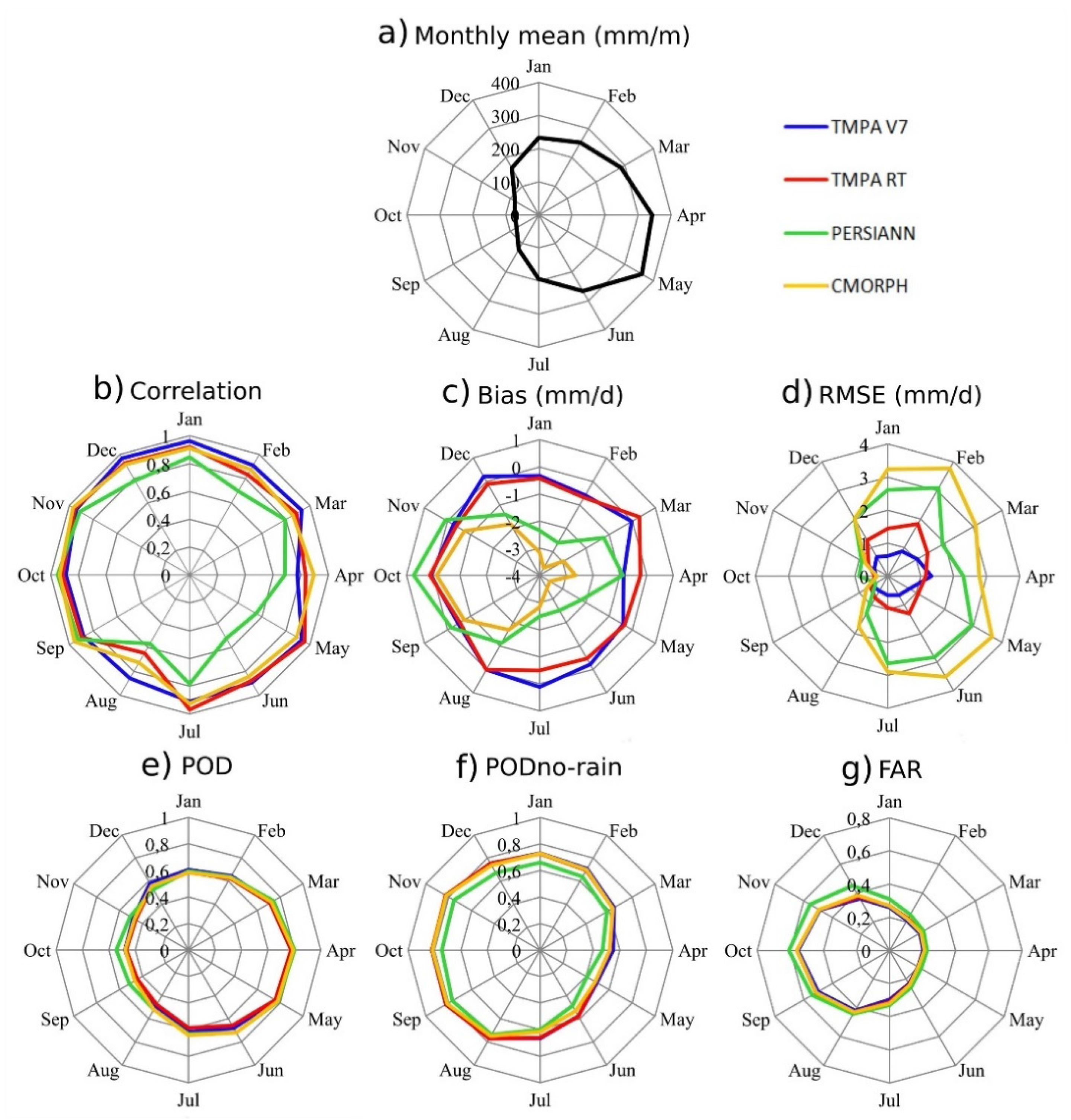
3.1. Overall Comparison of Rainfall Products
| Correlation | Bias (mm/d) | RMSE (mm/d) | POD | FAR | |
|---|---|---|---|---|---|
| TMPA V7 | 0.401 | −0.238 | 14.627 | 0.667 | 0.301 |
| TMPA RT | 0.365 | −0.295 | 14.888 | 0.649 | 0.310 |
| PERSIANN | 0.348 | −1.430 | 13.693 | 0.669 | 0.331 |
| CMORPH | 0.380 | −2.313 | 13.356 | 0.674 | 0.305 |
3.2. Comparison of Daily Averages
3.3. Comparison of Rainfall Intensity Categories

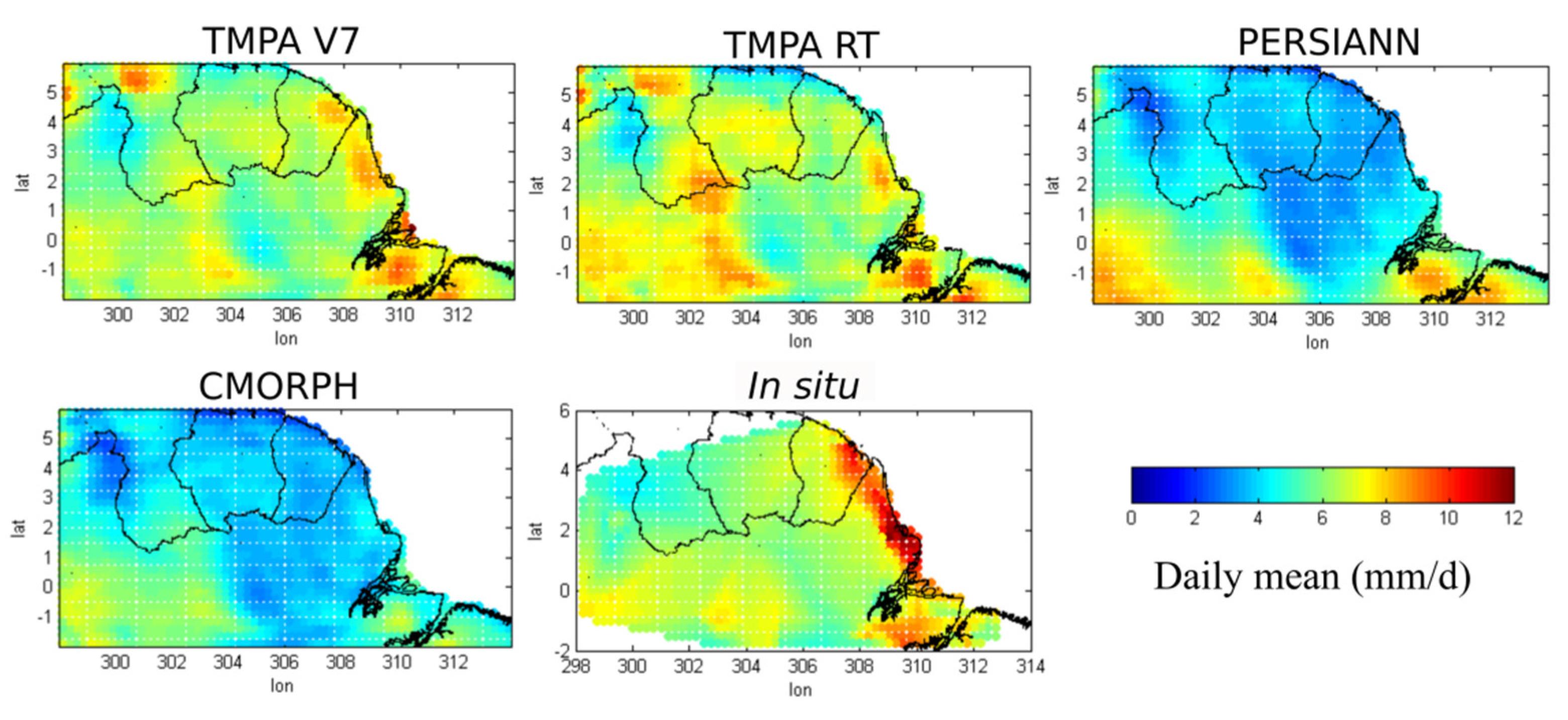
3.4. Spatial Analysis
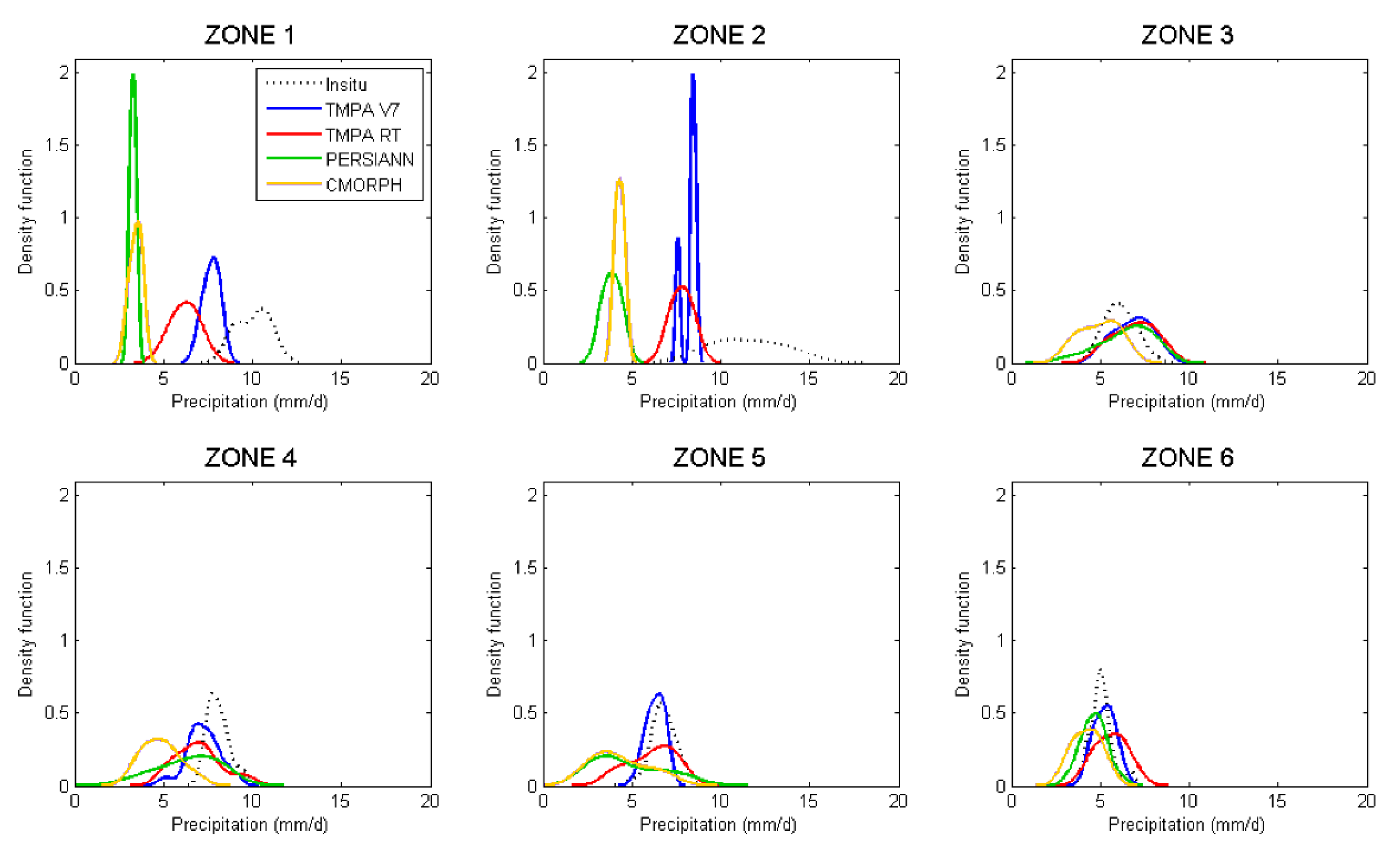
3.4.1. Comparison of Precipitation Probability Distributions
3.4.2. Error Metrics
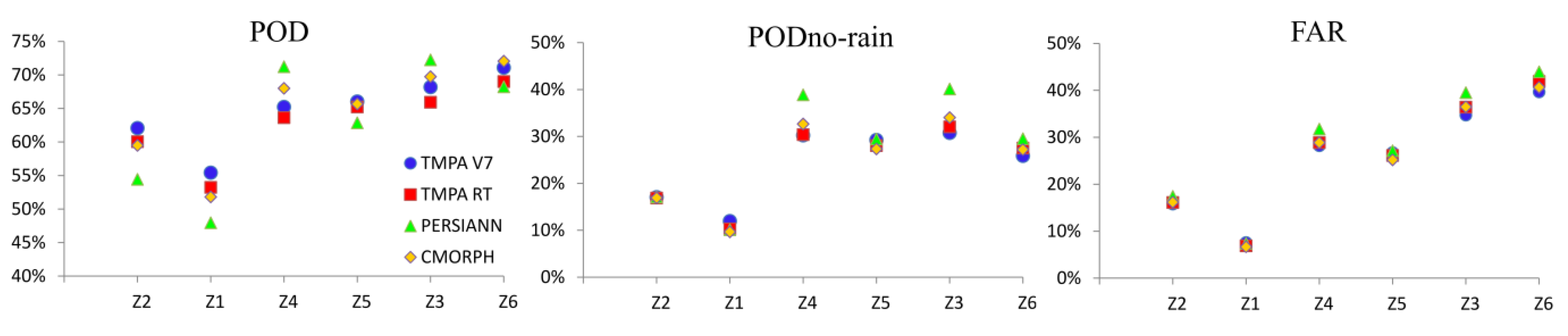

4. Conclusions
- (1)
- The probabilistic density analyses for the six different areas indicate that products exhibit a greater degree of accuracy in the least rainy areas. Convective-type rainfall (Z1East French Guiana and Z2Amapá.) is more poorly estimated by satellite products.
- (2)
- In Z4Marajó and Z5South Roraima+West French Guiana, near large bodies of water, the bias for TMPA V7 is close to zero.
- (3)
- In Z3Amazon, over the areas near a big river, PERSIANN shows the best bias with a slight overestimation, low error variance and the best score for the events’ detection.
- (4)
- In Z6North Roraima, the drier area, all products have satisfying performances with very little difference between them. PERSIANN and TMPA V7 showed the same performance.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Derin, Y.; Yilmaz, K.K. Evaluation of multiple satellite-based precipitation products over complex topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar] [CrossRef]
- Toté, C.; Patricio, D.; Boogaard, H.; van der Wijngaart, R.; Tarnavsky, E.; Funk, C. Evaluation of satellite rainfall estimates for drought and flood monitoring in Mozambique. Remote Sens. 2015, 7, 1758–1776. [Google Scholar] [CrossRef]
- Kidd, C. Satellite rainfall climatology: A review. Int. J. Climatol. 2001, 21, 1041–1066. [Google Scholar] [CrossRef]
- International Precipitation Working Group. Available online: http://www.isac.cnr.it/~ipwg/ (accessed on 2 December 2015).
- Barrett, E.C. Precipitation measurement by satellites: Towards community algorithms. Adv. Space Res. 1993, 13, 119–136. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.; Sorooshian, S.; Gupta, H.V.; Wagener, T. Intercomparison of rain gauge, radar, and satellite-based precipitation estimates with emphasis on hydrologic forecasting. J. Hydrometeorol. 2005, 6, 497–517. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; De Roo, A. Validation of satellite-based precipitation products over sparsely gauged African river basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Roca, R.; Chambon, P.; Jobard, I.; Kirstetter, P.-E.; Gosset, M.; Bergès, J.C. Comparing satellite and surface rainfall products over West Africa at meteorologically relevant scales during the AMMA campaign using error estimates. J. Appl. Meteorol. Climatol. 2010, 49, 715–731. [Google Scholar] [CrossRef]
- Qiao, L.; Hong, Y.; Chen, S.; Zou, C.B.; Gourley, J.J.; Yong, B. Performance assessment of the successive Version 6 and Version 7 TMPA products over the climate-transitional zone in the southern Great Plains, USA. J. Hydrol. 2014, 513, 446–456. [Google Scholar] [CrossRef]
- Gervais, M.; Gyakum, J.R.; Atallah, E.; Tremblay, L.B.; Neale, R.B. How well are the distribution and extreme values of daily precipitation over North America represented in the community climate system model? A comparison to reanalysis, satellite, and gridded station data. J. Clim. 2014, 27, 5219–5239. [Google Scholar] [CrossRef]
- Delahaye, F. Analyse Comparative des Différents Produits Satellitaires D’estimation des Précipitations en Amazonie Bresilienne. Ph.D Thesis, Université Rennes, Rennes, France, 2013. [Google Scholar]
- Vila, D.A.; de Goncalves, L.G.G.; Toll, D.L.; Rozante, J.R. Statistical evaluation of combined daily gauge observations and rainfall satellite estimates over continental South America. J. Hydrometeorol. 2009, 10, 533–543. [Google Scholar] [CrossRef]
- Tan, M.; Ibrahim, A.; Duan, Z.; Cracknell, A.; Chaplot, V. Evaluation of six high-resolution satellite and ground-based precipitation products over Malaysia. Remote Sens. 2015, 7, 1504–1528. [Google Scholar] [CrossRef]
- Yang, X.; Yong, B.; Hong, Y.; Chen, S.; Zhang, X. Error analysis of multi-satellite precipitation estimates with an independent raingauge observation network over a medium-sized humid basin. Hydrol. Sci. J. 2015. [Google Scholar] [CrossRef]
- Yong, B.; Liu, D.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Ren, L.; Hong, Y. Global view of real-time TRMM multi-satellite precipitation analysis: Implication to its successor global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 96, 283–296. [Google Scholar] [CrossRef]
- Miao, C.; Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Duan, Q. Evaluation of the PERSIANN-CDR daily rainfall estimates in capturing the behavior of extreme precipitation events over China. J. Hydrometeorol. 2015, 16, 1387–1396. [Google Scholar] [CrossRef]
- Pereira Filho, A.J.; Carbone, R.E.; Janowiak, J.E.; Arkin, P.; Joyce, R.; Hallak, R.; Ramos, C.G.M. Satellite rainfall estimates over south America: Possible applicability to the water management of large watersheds. JAWRA J. Am. Water Resour. Assoc. 2010, 46, 344–360. [Google Scholar] [CrossRef]
- Rozante, J.R.; Moreira, D.S.; de Goncalves, L.G.G.; Vila, D.A. Combining TRMM and surface observations of precipitation: technique and validation over South America. Weather Forecast. 2010, 25, 885–894. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Bi, X.-Q.; Kong, X.-H. Observed diurnal cycle of summer precipitation over South Asia and East Asia based on CMORPH and TRMM satellite data. Atmos. Ocean. Sci. Lett. 2015, 8, 101. [Google Scholar]
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Gebregiorgis, A.; Xue, X.; Zhang, X. Inter-comparison of high-resolution satellite precipitation products over Central Asia. Remote Sens. 2015, 7, 7181–7212. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar]
- Moazami, S.; Golian, S.; Kavianpour, M.R.; Hong, Y. Comparison of PERSIANN and V7 TRMM Multi-satellite Precipitation Analysis (TMPA) products with rain gauge data over Iran. Int. J. Remote Sens. 2013, 34, 8156–8171. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Zulkafli, Z.; Buytaert, W.; Onof, C.; Manz, B.; Tarnavsky, E.; Lavado, W.; Guyot, J.-L. A comparative performance analysis of TRMM 3B42 (TMPA) Versions 6 and 7 for hydrological applications over Andean–Amazon river basins. J. Hydrometeorol. 2014, 15, 581–592. [Google Scholar] [CrossRef]
- Clarke, R.T.; Buarque, D.C.; de Paiva, R.C.D.; Collischonn, W. Issues of spatial correlation arising from the use of TRMM rainfall estimates in the Brazilian Amazon. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Tanaka, L.M.; Satyamurty, P.; Machado, L.A.T. Diurnal variation of precipitation in central Amazon Basin. Int. J. Climatol. 2014, 34, 3574–3584. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Huffman, G.J.; David, T. Bolvin TRMM and other Data Precipitation Data Set Documentation; NASA: Greenbelt, MD, USA, 2013. [Google Scholar]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite–based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Hammond, D.S. Tropical Forests of the Guiana Shield: Ancient Forests in a Modern World; CABI: Oxfordshire, UK, 2005. [Google Scholar]
- Bovolo, C.I.; Pereira, R.; Parkin, G.; Kilsby, C.; Wagner, T. Fine-scale regional climate patterns in the Guianas, tropical South America, based on observations and reanalysis data. Int. J. Climatol. 2012, 32, 1665–1689. [Google Scholar] [CrossRef]
- Beltrando, G. Les Climats: Processus, Variabilité et Risques; Armand Colin: Paris, France, 2011. [Google Scholar]
- Burroughs, W.J. L’encyclopédie du Climat; Delachaux et Niestlé: Lausanne, Switzerland, 2000. [Google Scholar]
- Marengo, J.A. Interannual variability of surface climate in the Amazon basin. Int. J. Climatol. 1992, 12, 853–863. [Google Scholar] [CrossRef]
- Marengo, J.A. Interannual variability of deep convection over the tropical South American sector as deduced from ISCCP C2 data. Int. J. Climatol. 1995, 15, 995–1010. [Google Scholar] [CrossRef]
- Satyamurty, P.; da Costa, C.P.W.; Manzi, A.O. Moisture source for the Amazon Basin: a study of contrasting years. Theor. Appl. Climatol. 2013, 111, 195–209. [Google Scholar] [CrossRef]
- Negri, A.J.; Anagnostou, E.N.; Adler, R.F. A 10-yr climatology of amazonian rainfall derived from passive microwave satellite observations. J. Appl. Meteorol. 2000, 39, 42–56. [Google Scholar] [CrossRef]
- Fitzjarrald, D.R.; Sakai, R.K.; Moraes, O.L.L.; Cosme de Oliveira, R.; Acevedo, O.C.; Czikowsky, M.J.; Beldini, T. Spatial and temporal rainfall variability near the Amazon-Tapajós confluence. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Buarque, D.C.; de Paiva, R.C.D.; Clarke, R.T.; Mendes, C.A.B. A comparison of Amazon rainfall characteristics derived from TRMM, CMORPH and the Brazilian national rain gauge network. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Buarque, D.C.; Clarke, R.T.; Collischonn, W.; Allasia, D.G. Reduced precipitation over large water bodies in the Brazilian Amazon shown from TRMM data: TRMM rainfall reduction Amazon Rivers. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Dos Santos, M.J.; Silva Dias, M.A.F.; Freitas, E.D. Influence of local circulations on wind, moisture, and precipitation close to Manaus City, Amazon Region, Brazil. J. Geophys. Res. Atmospheres 2014, 119, 233–249. [Google Scholar] [CrossRef]
- Cutrim, E.; Martin, D.W.; Rabin, R. Enhancement of cumulus clouds over deforested lands in Amazonia. Bull. Am. Meteorol. Soc. 1995, 76, 1801–1805. [Google Scholar] [CrossRef]
- Silva Dias, M.A.F.; Silva Dias, P.L.; Longo, M.; Fitzjarrald, D.R.; Denning, A.S. River breeze circulation in eastern Amazonia: Observations and modelling results. Theor. Appl. Climatol. 2004, 78, 111–121. [Google Scholar] [CrossRef]
- Pereira, R.; Bovolo, C.I.; Forsythe, N.; Pedentchouk, N.; Parkin, G.; Wagner, T. Seasonal patterns of rainfall and river isotopic chemistry in northern Amazonia (Guyana): From the headwater to the regional scale. J. South Am. Earth Sci. 2014, 52, 108–118. [Google Scholar] [CrossRef]
- Watson, D.F.; Philip, G.M. Triangle based interpolation. J. Int. Assoc. Math. Geol. 1984, 16, 779–795. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Gordon, A.D. A review of hierarchical classification. J. R. Stat. Soc. 1987, 150, 119–137. [Google Scholar] [CrossRef]
- Ghajarnia, N.; Liaghat, A.; Daneshkar Arasteh, P. Comparison and evaluation of high resolution precipitation estimation products in Urmia Basin-Iran. Atmos. Res. 2015, 158–159, 50–65. [Google Scholar] [CrossRef]
- Yong, B.; Hong, Y.; Ren, L.-L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving TRMM-based multisatellite real-time precipitation estimation methods and their impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Yong, B.; Ren, L.; Hong, Y.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Chen, X.; Wang, W.; Wen, Y. First evaluation of the climatological calibration algorithm in the real-time TMPA precipitation estimates over two basins at high and low latitudes: Validation of crucial algorithmic upgrade in NASA TMPA. Water Resour. Res. 2013, 49, 2461–2472. [Google Scholar] [CrossRef]
- NASA. Available online: ftp://disc2.nascom.nasa.gov/data/TRMM/Gridded/3B42_V7/ (accessed on 1 December 2015).
- NASA. Available online: ftp://disc2.nascom.nasa.gov/data/TRMM/Gridded/3B42RT/ (accessed on 1 December 2015).
- UCI. Available online: ftp://persiann.eng.uci.edu/pub/PERSIANN/tar_3hr/ (accessed on 1 December 2015).
- NOAA. Available online: http://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/RAW/ (accessed on 1 December 2015).
- Hidroweb. Available online: http://www.snirh.gov.br/hidroweb/ (accessed on 2 December 2015).
- Kummerow, C.; Hong, Y.; Olson, W.; Yang, S.; Adler, R.; McCollum, J.; Ferraro, R.; Petty, G.; Shin, D.-B.; Wilheit, T. Evolution of the Goddard profiling algorithm (GPROF) for rainfall estimatin from passive microwave sensors. J. Appl. Meteorol. 2001, 40, 1801–1820. [Google Scholar] [CrossRef]
- Warner, T.T.; Mapes, B.E.; Xu, M. Diurnal patterns of rainfall in northwestern south America. Part II: Model simulations. Mon. Weather Rev. 2003, 131, 813–829. [Google Scholar] [CrossRef]
- Gianotti, R.L.; Zhang, D.; Eltahir, E.A.B. Assessment of the regional climate model version 3 over the maritime continent using different cumulus parameterization and land surface schemes. J. Clim. 2012, 25, 638–656. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal analysis of TRMM-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Adler, R.F.; Negri, A.J.; Keehn, P.R.; Hakkarinen, I.M. Estimation of monthly rainfall over Japan and surrounding waters from a combination of low-orbit microwave and geosynchronous IR data. J. Appl. Meteorol. 1993, 32, 335–356. [Google Scholar] [CrossRef]
- Shepherd, J.M.; Grundstein, A.J.; Mote, T.L. An analysis of seasonal biases in satellite and reanalysis rainfall products in the Savannah River basin. Phys. Geogr. 2014, 35, 181–194. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Sharma, A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: Part 3−A nonparametric probabilistic forecast model. J. Hydrol. 2000, 239, 249–258. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D. Systematic anomalies over inland water bodies in satellite-based precipitation estimates. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D. A global map of uncertainties in satellite-based precipitation measurements: Uncertainties in precipitation data. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.-S.; Nasrollahi, N.; Hsu, K.; Sorooshian, S. Evaluation of satellite-based precipitation estimation over Iran. J. Arid Environ. 2013, 97, 205–219. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ringard, J.; Becker, M.; Seyler, F.; Linguet, L. Temporal and Spatial Assessment of Four Satellite Rainfall Estimates over French Guiana and North Brazil. Remote Sens. 2015, 7, 16441-16459. https://doi.org/10.3390/rs71215831
Ringard J, Becker M, Seyler F, Linguet L. Temporal and Spatial Assessment of Four Satellite Rainfall Estimates over French Guiana and North Brazil. Remote Sensing. 2015; 7(12):16441-16459. https://doi.org/10.3390/rs71215831
Chicago/Turabian StyleRingard, Justine, Melanie Becker, Frederique Seyler, and Laurent Linguet. 2015. "Temporal and Spatial Assessment of Four Satellite Rainfall Estimates over French Guiana and North Brazil" Remote Sensing 7, no. 12: 16441-16459. https://doi.org/10.3390/rs71215831
APA StyleRingard, J., Becker, M., Seyler, F., & Linguet, L. (2015). Temporal and Spatial Assessment of Four Satellite Rainfall Estimates over French Guiana and North Brazil. Remote Sensing, 7(12), 16441-16459. https://doi.org/10.3390/rs71215831







