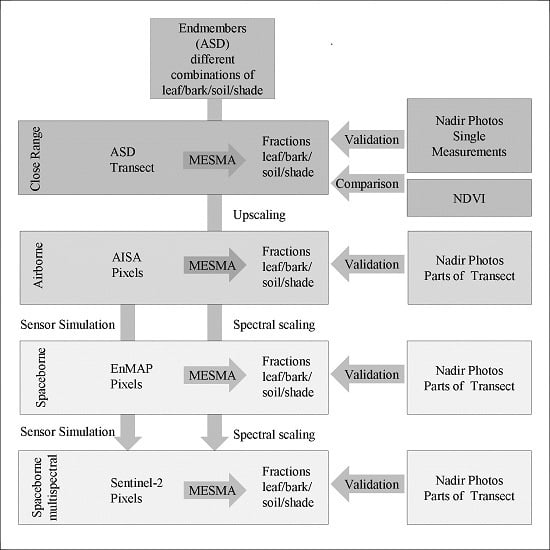
Spectral Unmixing of Forest Crown Components at Close Range, Airborne and Simulated Sentinel-2 and EnMAP Spectral Imaging Scale
Abstract
:1. Introduction
- (a)
- Does spectral unmixing have the potential to simultaneously estimate the fractional distribution of different canopy components, including exposed bark?
- (b)
- Does the inclusion of a bark endmember improve the accuracy of the unmixing process?
- (c)
- Can spectral unmixing methods achieve an enhanced estimate for leaf cover when compared to the NDVI in densely vegetated ecosystems?
- (d)
- What is the effect of different spectral scales on the unmixing process—Analytical Spectral Device (ASD), Airborne Imaging Spectrometer for Applications (AISA), Environmental Mapping and Analysis Program (EnMAP), Sentinel-2)?
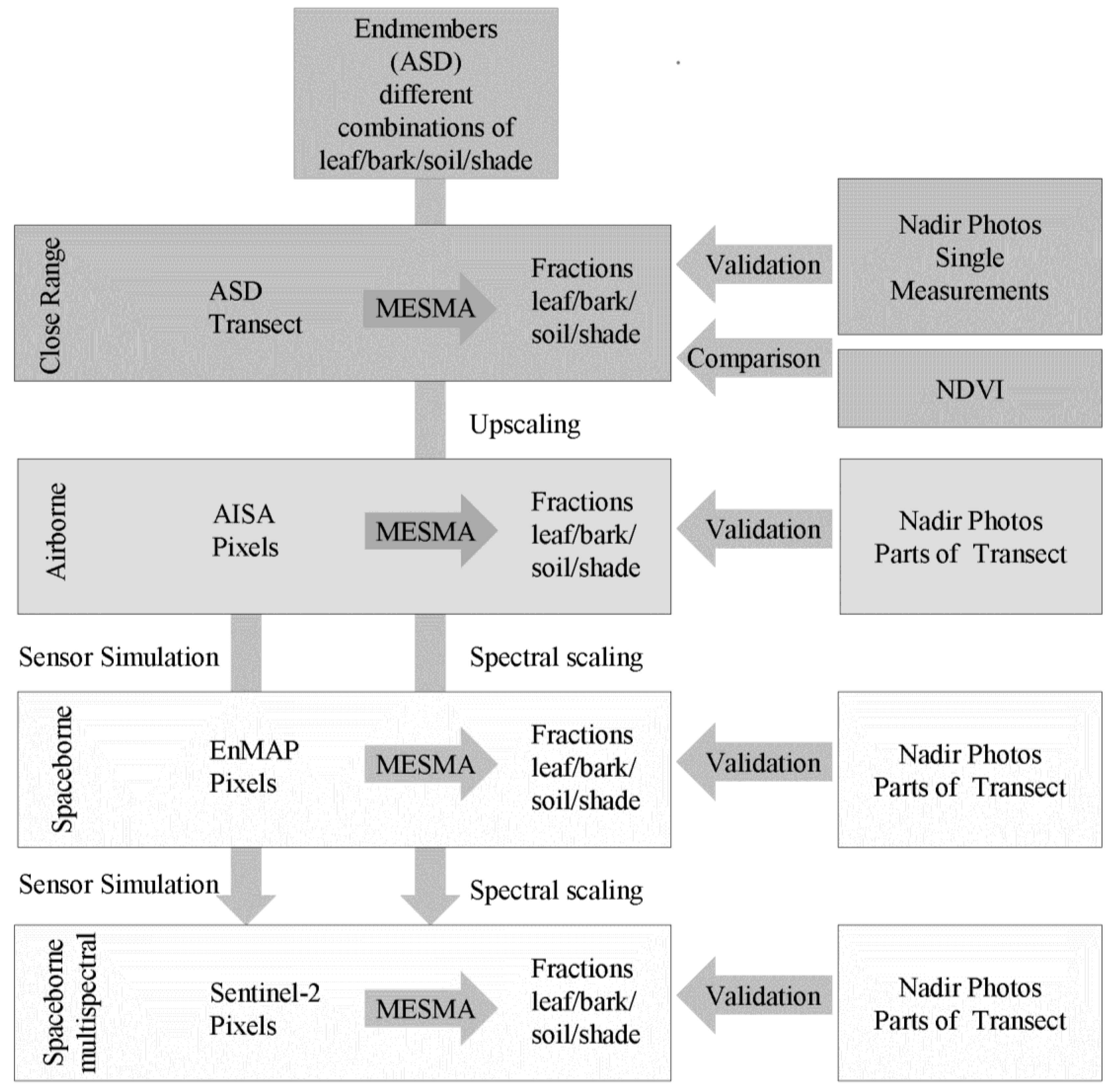
2. Materials and Methods
2.1. Study Area
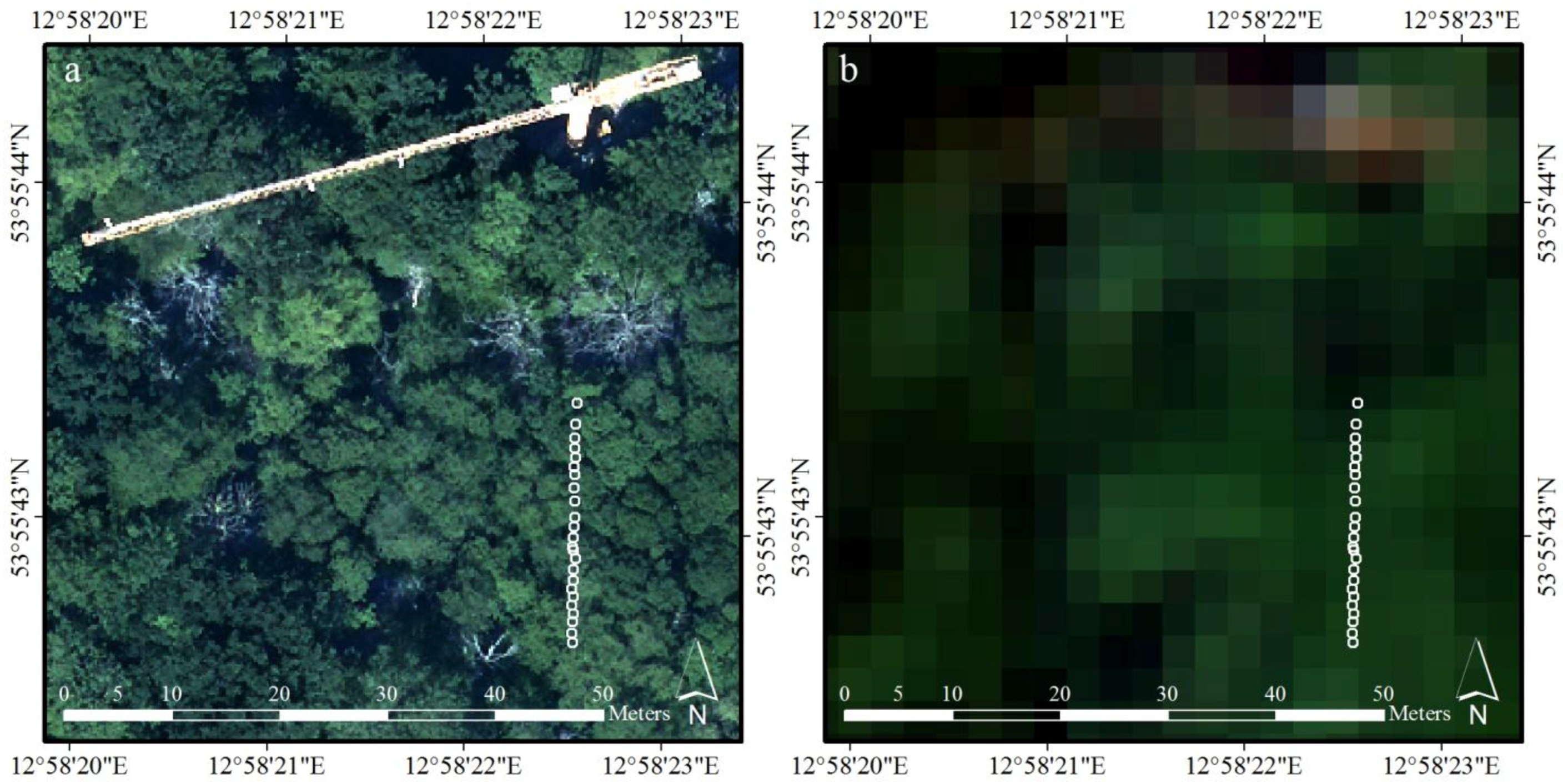
2.2. Data
| Sensor | ASD | AISA | EnMAP | Sentinel-2 |
|---|---|---|---|---|
| Number of bands (total) | 2151 | 367 | 242 | 13 |
| Number of bands used | 1727 | 286 | 200 | 10 |
| Spectral range (nm) | 350 to 2500 | 401 to 2500 | 423 to 2439 | 442 to 2194 |
| Radiometric resolution | 16 bit | 12 bit | 14 bit | 12 bit |
| Bandwidth (nm) | 3 to 8 * | 1.9 to 9.4 | 8.1 to 12.5 | 15 -180 |
| Ground sampling resolution | 1.4 m | 3 m | 3 m | 3 m |
| Origin of endmembers | in field (2011 to 2014) | simulated (ASD based) | simulated (ASD based) | simulated (ASD based) |
| Origin of transect | in field 15 June 2012 | airborne 29 June 2011 | simulated (AISA based) | simulated (AISA based) |
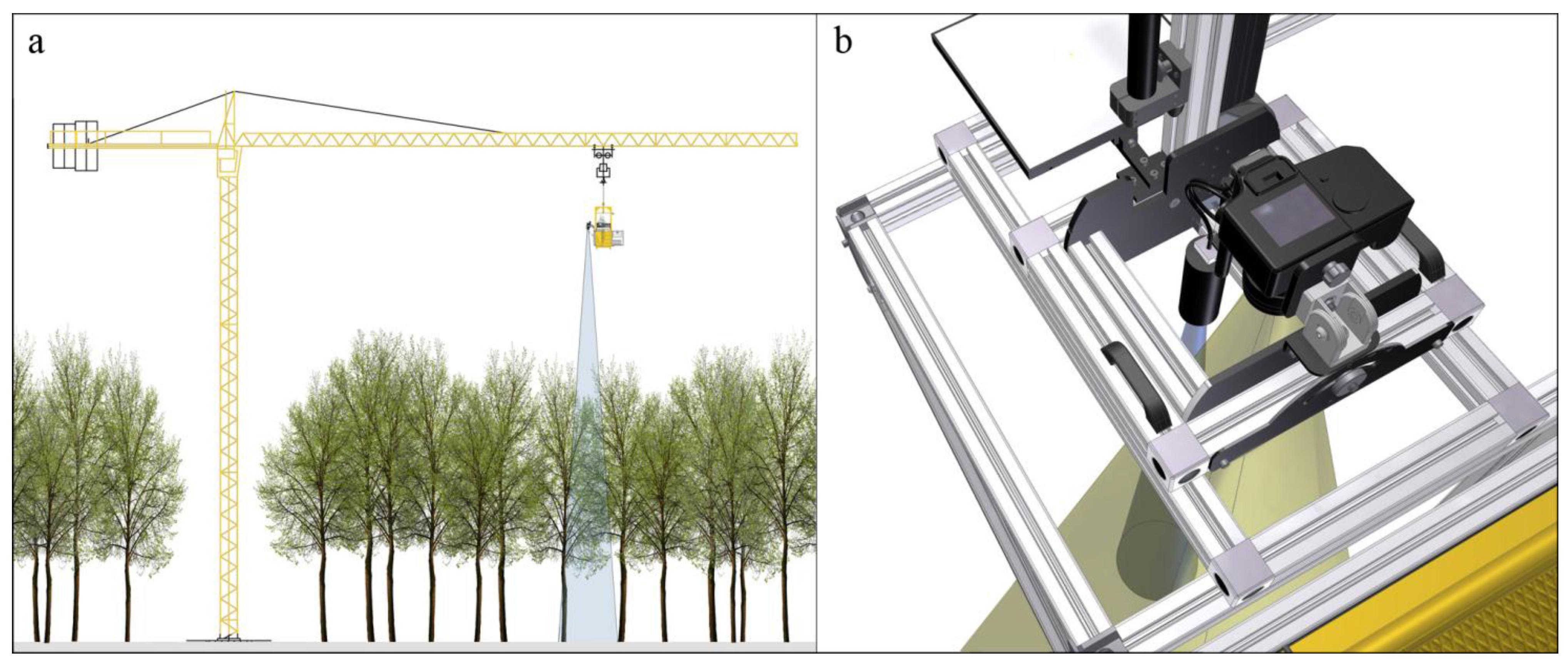
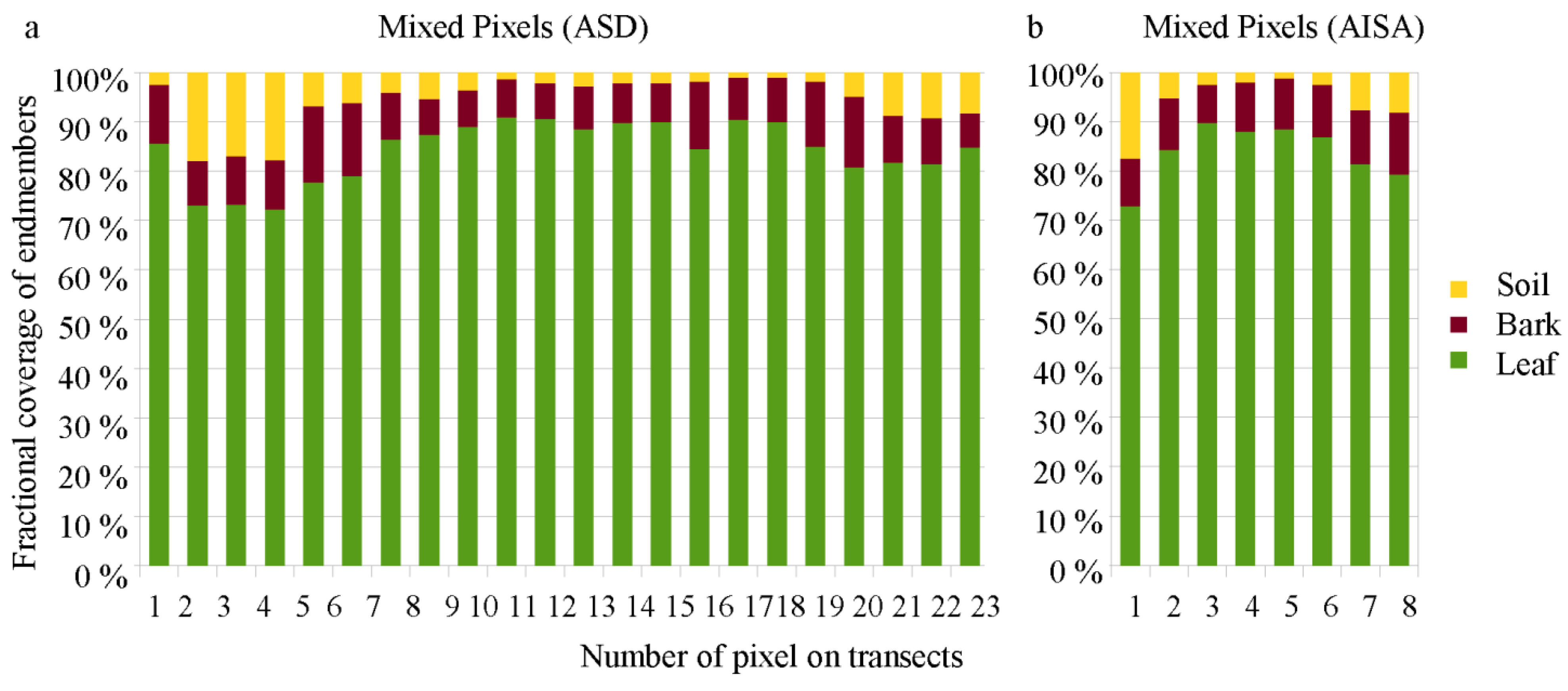
2.2.1. Mixed Pixel Spectra—Close Range ASD Data Set
2.2.2. Mixed Pixel Spectra—Airborne AISA Data Set
2.2.3. Mixed Pixel Spectra—Spectrally Simulated Spaceborne Data Sets
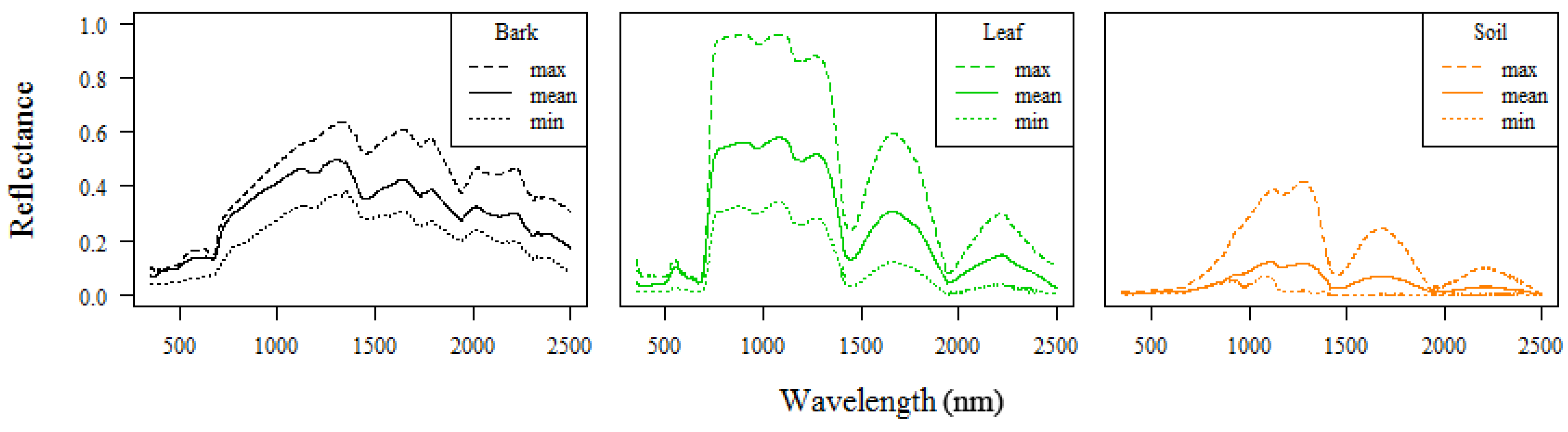
2.2.4. Endmember Spectra
2.2.5. Reference Fractions
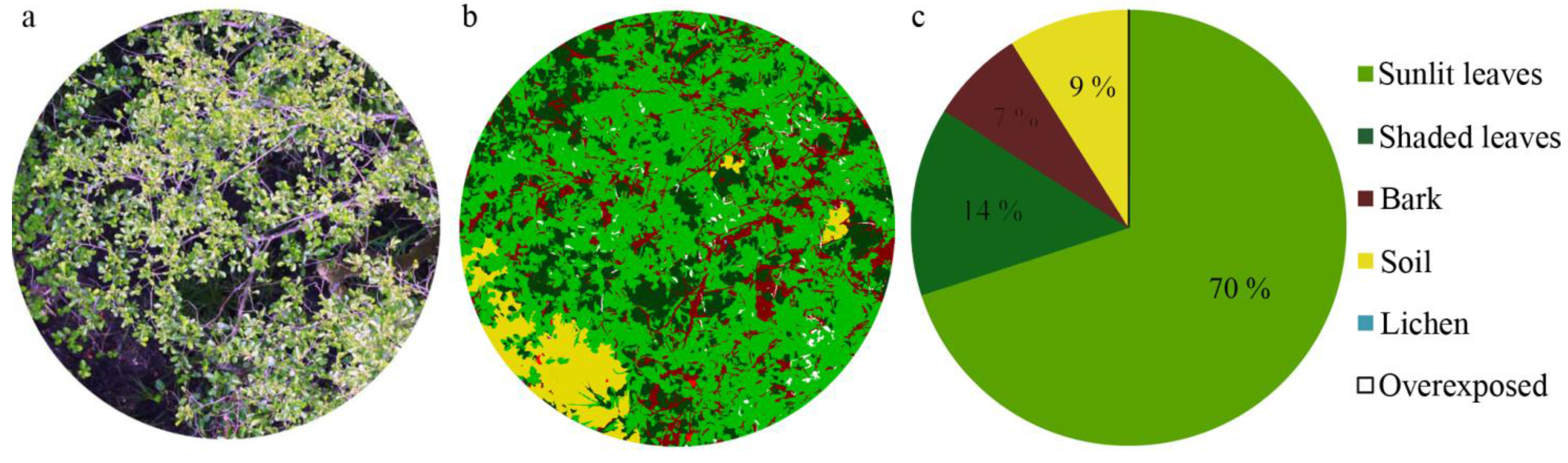
2.3. Spectral Unmixing
3. Results
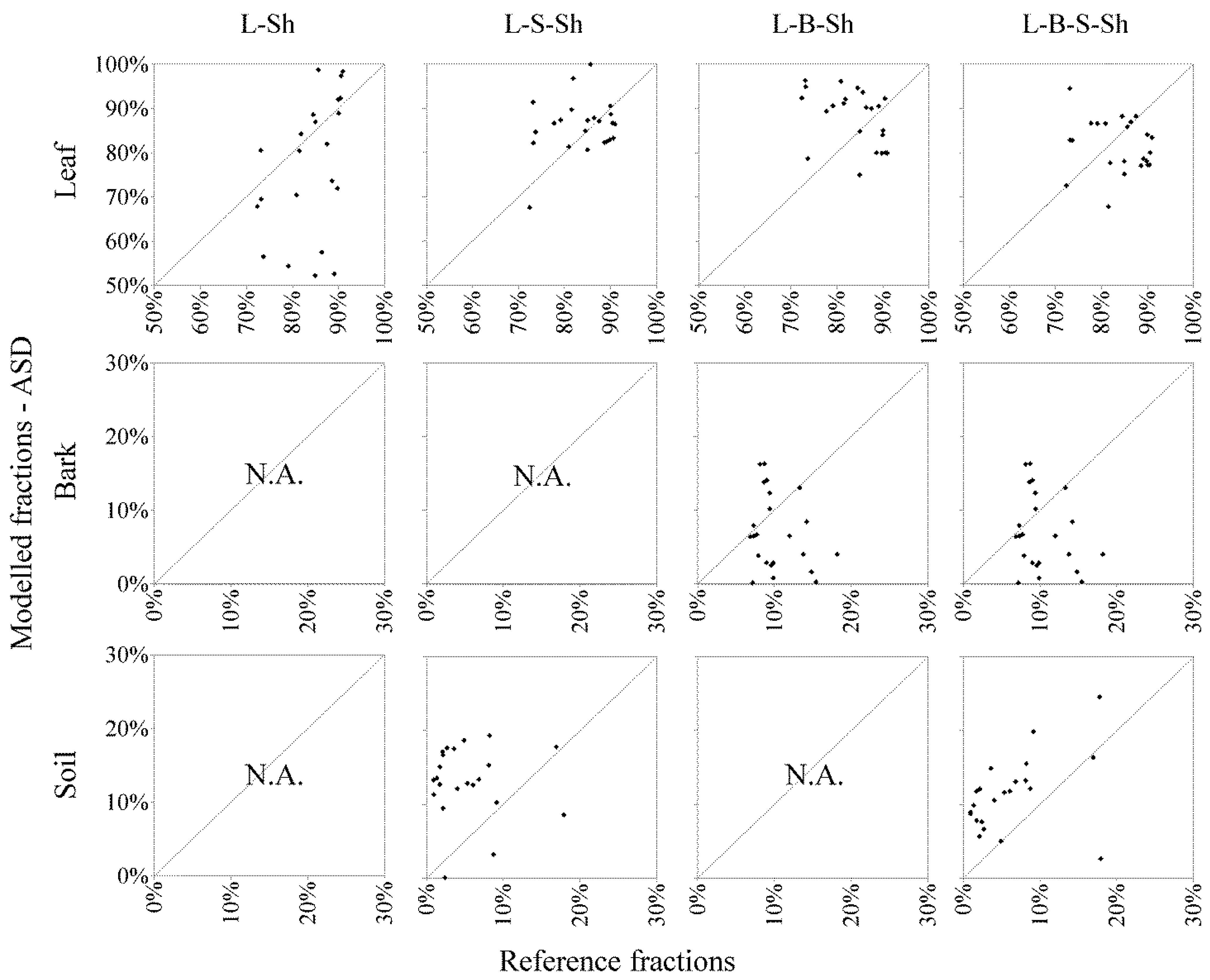
3.1. Close Range Data Set
| MESMA 2 EM | MESMA 3 EM | MESMA 3 EM | MESMA 4 EM | |
|---|---|---|---|---|
| Leaf-Shade L-Sh | Leaf-Soil-Shade L-S-Sh | Leaf-Bark-Shade L-B-Sh | Leaf-Bark-Soil-Shade L-B-S-Sh | |
| Leaf | 11.9% | 6.3% | 9.4% | 8.1% |
| Bark | N.A. | N.A. | 6.2% | 5.9% |
| Soil | N.A. | 9.6% | N.A. | 6.9% |
| Overall | 11.9% | 8.7% | 7.1% | 7.0% |
| Modelling RMSE | 0.0087 | 0.0055 | 0.0064 | 0.0051 |
| Complexity | 2 EM | 2-3 EM | 2-3-4 EM |
|---|---|---|---|
| Possible Models | LSh | LSh/LBSh/LSSh | LSh/LBSh/LSSh/LBSSh |
| Leaf | 11.9% | 7.6% | 7.9% |
| Bark | N.A. | 9.7% | 6.4% |
| Soil | N.A. | 5.7% | 6.3% |
| Overall | 11.9% | 8.6% | 6.9% |
| Models chosen | 23xLSh | 5xLBSh, 18xLSSh | 1xLBSh, 3xLSSh, 19xLBSSh |
| Modelling RMSE (mean) | 0.0087 | 0.0053 | 0.0050 |
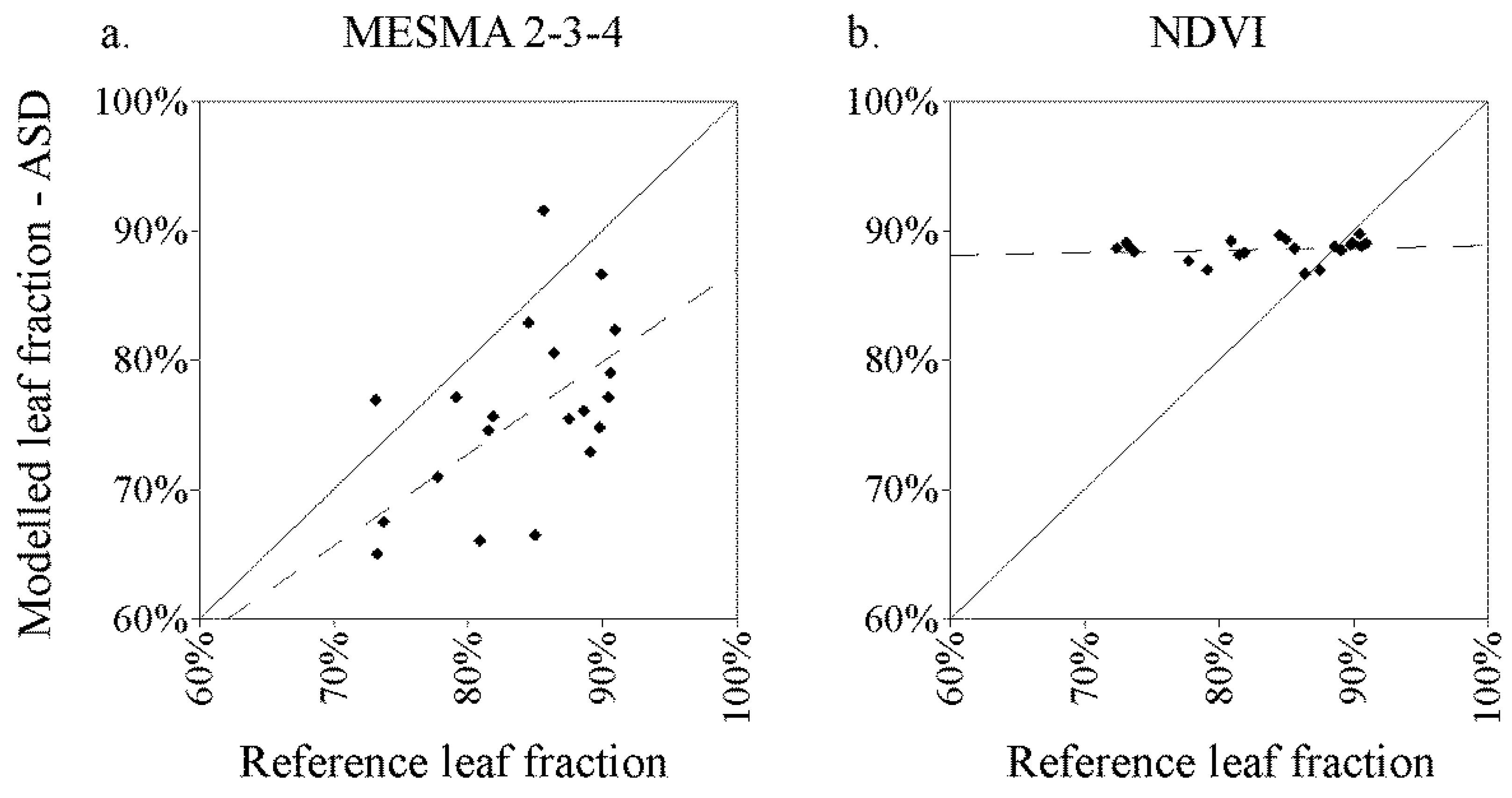
3.2. Airborne and Simulated Spaceborne Data Sets
| Sensor EM | AISA 2 EM LSh | AISA 3 EM LSSh | AISA 3 EM LBSh | AISA 4 EM LBSSh | EnMAP 2 EM LSh | EnMAP 3 EM LSSh | EnMAP 3 EM LBSh | EnMAP 4 EM LBSSh | Sentinel 2 EM LSh | Sentinel 3 EM LSSh | Sentinel 3 EM LBSh | Sentinel 4 EM LBSSh |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Leaf | 14.9% | 13.7% | 10.2% | 11.9% | 21.7% | 15.3% | 14.8% | 21.0% | 10.3% | 11.4% | 7.6% | 9.3% |
| Bark | N.A | N.A | 6.4% | 12,8% | N.A | N.A | 8.5% | 8.4% | N.A | N.A | 3.0% | 4.2% |
| Soil | N.A | 9.7% | N.A | 8.7% | N.A | 20.1% | N.A. | 0.28% | N.A | 6.3% | N.A. | 7.6% |
| Overall | 14.9% | 11.7% | 8.3% | 11.1% | 21.7% | 17.7% | 11.8% | 19.1% | 10.3% | 8.9% | 5.3% | 7.0% |
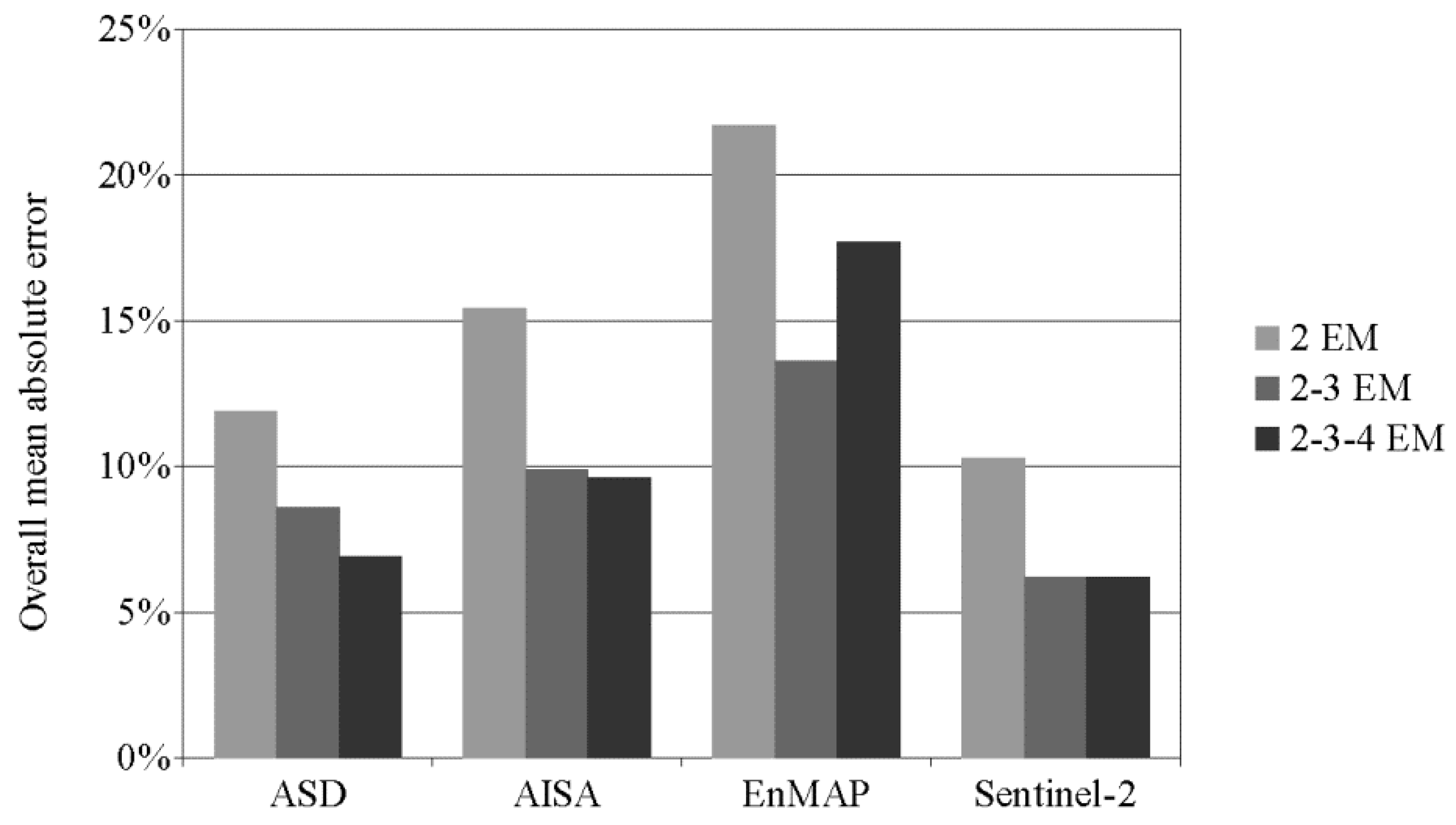
4. Discussions
4.1. Close Range Data Set
4.2. Airborne AISA Data Set
4.3. Spectrally Simulated EnMAP and Sentinel-2 Data Sets
5. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wessman, C.A. Remote sensing and the estimation of ecosystem parameters and functions. In Imaging Spectrometry—A Tool for Environmental Observations; Hill, J., Mégier, J., Eds.; Springer: Houten, The Netherlands, 1994; pp. 39–56. [Google Scholar]
- Peterson, D.L.; Hubbard, G.S. Scientific issues and potential remote-sensing requirements for plant biochemical content. J. Imaging Sci. Technol. 1992, 36, 446–456. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In NASA Special Publication 351; NASA: Washington, DC, USA, 1974; p. 309. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using Landsat TM images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint LiDAR and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Tillack, A.; Clasen, A.; Kleinschmit, B.; Förster, M. Estimation of the seasonal leaf area index in an alluvial forest using high-resolution satellite-based vegetation indices. Remote Sens. Environ. 2014, 141, 52–63. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Asner, G.P.; Vitousek, P.M. Remote analysis of biological invasion and biogeochemical change. Proc. Natl. Acad. Sci. USA 2005, 102, 4383–4386. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Hughes, R.F. Invasive species detection in Hawaiian rainforests using airborne imaging spectroscopy and LiDAR. Remote Sens. Environ. 2008, 112, 1942–1955. [Google Scholar] [CrossRef]
- Roberts, D.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R. Mapping chaparral in the Santa Monica Mountains using multiple endmember spectral mixture models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Youngentob, K.N.; Roberts, D.A.; Held, A.A.; Dennison, P.E.; Jia, X.; Lindenmayer, D.B. Mapping two Eucalyptus subgenera using multiple endmember spectral mixture analysis and continuum-removed imaging spectrometry data. Remote Sens. Environ. 2011, 115, 1115–1128. [Google Scholar] [CrossRef]
- Dudley, K.L.; Dennison, P.E.; Roth, K.L.; Roberts, D.A.; Coates, A.R. A multi-temporal spectral library approach for mapping vegetation species across spatial and temporal phenological gradients. Remote Sens. Environ. 2015, 167, 121–134. [Google Scholar] [CrossRef]
- Sonnentag, O.; Chen, J.M.; Roberts, D.A.; Talbot, J.; Halligan, K.Q.; Govind, A. Mapping tree and shrub leaf area indices in an ombrotrophic peatland through multiple endmember spectral unmixing. Remote Sens. Environ. 2007, 109, 342–360. [Google Scholar] [CrossRef]
- Somers, B.; Verbesselt, J.; Ampe, E.M.; Sims, N.; Verstraeten, W.W.; Coppin, P. Spectral mixture analysis to monitor defoliation in mixed-aged Eucalyptus globulus Labill plantations in southern Australia using Landsat5-TM and EO-1Hyperion data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 270–277. [Google Scholar] [CrossRef]
- Roberts, D.A.; Adams, J.B.; Smith, M.O. Green vegetation, non-photosynthetic vegetation and soils in AVIRIS data. Remote Sens Environ. 1993, 44, 255–270. [Google Scholar] [CrossRef]
- Asner, G.P.; Lobell, D.B. A biogeophysical approach for automated SWIR unmixing of soils and vegetation. Remote Sens. Environ. 2000, 74, 99–112. [Google Scholar] [CrossRef]
- Huete, A.R. Separation of soil-plant spectral mixtures by factor analysis. Remote Sens. Environ. 1986, 19, 237–251. [Google Scholar] [CrossRef]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in deserts: I. A regional measure of abundance from multispectral images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A. Species-level differences in hyperspectral metrics among tropical rainforest trees as determined by a tree-based classifier. Remote Sens. 2012, 4, 1820–1855. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Förster, M.; Bruzual-Alfonzo, H.; Clasen, A.; Kleinschmit, B. The utilization of GEOBIA for a hyperspectral mixture analysis of tree crown components. South-East. Eur. J. Earth Obs. Geomat. 2014, 3, 363–367. [Google Scholar]
- Bohlman, S. Hyperspectral remote sensing of exposed wood and deciduous trees in seasonal tropical forests. In Hyperspectral Remote Sensing of Tropical and Sub-Tropical Forests; CRC Press: Boca Raton, FL, USA, 2008; pp. 177–192. [Google Scholar]
- Yuan, H.; Ma, R.; Atzberger, C.; Li, F.; Loiselle, S.A.; Luo, J. Estimating forest fAPAR from multispectral Landsat-8 data using the invertible forest reflectance model INFORM. Remote Sens. 2015, 7, 7425–7446. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Bacour, C.; Poilvé, H.; Frangi, J.-P. Comparison of four radiative transfer models to simulate plant canopies reflectance: Direct and inverse mode. Remote Sens. Environ. 2000, 74, 471–481. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Wallace, J.; Macfarlane, C.; McJannet, D.; Ellis, T.; Grigg, A.; van Dijk, A. Evaluation of forest interception estimation in the continental scale Australian Water Resources Assessment—Landscape (AWRA-L) model. J. Hydrol. 2013, 499, 210–223. [Google Scholar] [CrossRef]
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol. 1996, 80, 135–163. [Google Scholar] [CrossRef]
- Förster, M.; Spengler, D.; Buddenbaum, H.; Hill, J.; Kleinschmit, B. A review of the combination of spectral and geometric modelling for the application in forest remote sensing. Photogramm. Fernerkund. Geoinf. 2010, 2010, 253–265. [Google Scholar] [CrossRef]
- Chen, X.; Vierling, L. Spectral mixture analyses of hyperspectral data acquired using a tethered balloon. Remote Sens. Environ. 2006, 103, 338–350. [Google Scholar] [CrossRef]
- Somers, B.; Cools, K.; Delalieux, S.; Stuckens, J.; van der Zande, D.; Verstraeten, W.W.; Coppin, P. Nonlinear Hyperspectral Mixture Analysis for tree cover estimates in orchards. Remote Sens. Environ. 2009, 113, 1183–1193. [Google Scholar] [CrossRef]
- Hilker, T.; Nesic, Z.; Coops, N.C.; Lessard, D. A New, Automated, multiangular radiometer instrument for tower-based observations of canopy reflectance (AMSPEC II). Instrum. Sci. Technol. 2010, 38, 319–340. [Google Scholar] [CrossRef]
- Gong, P.; Miller, J.R.; Spanner, M. Forest canopy closure from classification and spectral unmixing of scene components—Multisensor evaluation of an open canopy. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1067–1080. [Google Scholar] [CrossRef]
- Hufkens, K.; Bogaert, J.; Dong, Q.H.; Lu, L.; Huang, C.L.; Ma, M.G.; Che, T.; Li, X.; Veroustraete, F.; Ceulemans, R. Impacts and uncertainties of upscaling of remote-sensing data validation for a semi-arid woodland. J. Arid Environ. 2008, 72, 1490–1505. [Google Scholar] [CrossRef]
- Justice, C.; Belward, A.; Morisette, J.; Lewis, P.; Privette, J.; Baret, F. Developments in the “validation” of satellite sensor products for the study of the land surface. Int. J. Remote Sens. 2000, 21, 3383–3390. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Huete, A.R. Effects of standing litter on the biophysical interpretation of plant canopies with spectral indices. Remote Sens. Environ. 1996, 55, 123–138. [Google Scholar] [CrossRef]
- Numata, I.; Roberts, D.A.; Chadwick, O.A.; Schimel, J.; Sampaio, F.R.; Leonidas, F.C.; Soares, J.V. Characterization of pasture biophysical properties and the impact of grazing intensity using remotely sensed data. Remote Sens. Environ. 2007, 109, 314–327. [Google Scholar] [CrossRef]
- Gill, T.; Phinn, S. Estimates of bare ground and vegetation cover from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) short-wave-infrared reflectance imagery. J. Appl. Remote Sens. 2008, 2, 023511:1–023511:19. [Google Scholar] [CrossRef]
- Okin, G.S. Relative spectral mixture analysis—A multitemporal index of total vegetation cover. Remote Sens. Environ. 2007, 106, 467–479. [Google Scholar] [CrossRef]
- Plaza, A.; Martinez, P.; Perez, R.; Plaza, J. A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 650–663. [Google Scholar] [CrossRef]
- Gong, P.; Zhang, A. Noise effect on linear spectral unmixing. Geogr. Inf. Sci. 1999, 5, 52–57. [Google Scholar] [CrossRef]
- Asner, G.P.; Heidebrecht, K.B. Imaging spectroscopy for desertification studies: Comparing AVIRIS and EO-1 Hyperion in Argentina drylands. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1283–1296. [Google Scholar] [CrossRef]
- Zacharias, S.; Bogena, H.; Samaniego, L.; Mauder, M.; Fuß, R.; Pütz, T.; Frenzel, M.; Schwank, M.; Baessler, C.; Butterbach-Bahl, K.; et al. A network of terrestrial environmental observatories in Germany. Vadose Zone J. 2011, 10, 955–973. [Google Scholar] [CrossRef]
- Plaza, J.; Plaza, A. Comparative analysis of training strategies for neural network-based spectral unmixing of laboratory-simulated forest hyperspectral scenes. In Proceedings of the 2010 IAPR Workshop on Pattern Recognition in Remote Sensing (PRRS), Istanbul, Turkey, 22 August 2010; pp. 1–4.
- Fan, W.; Hu, B.; Miller, J.; Li, M. Comparative study between a new nonlinear model and common linear model for analysing laboratory simulated-forest hyperspectral data. Int. J. Remote Sens. 2009, 30, 2951–2962. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Segl, K.; Guanter, L.; Rogass, C.; Kuester, T.; Roessner, S.; Kaufmann, H.; Sang, B.; Mogulsky, V.; Hofer, S. EeteS—The EnMAP end-to-end simulation tool. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 522–530. [Google Scholar] [CrossRef]
- Segl, K.; Guanter, L.; Gascon, F.; Kuester, T.; Rogass, C.; Mielke, C. S2eteS: An end-to-end modeling tool for the simulation of Sentinel-2 image products. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5560–5571. [Google Scholar] [CrossRef]
- MacArthur, A.; MacLellan, C.J.; Malthus, T. The fields of view and directional response functions of two field spectroradiometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3892–3907. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Gillespie, A.R. Imaging Spectroscopy: Interpretation Based on Spectral Mixture Analysis; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Ball, J.E.; Kari, S.; Younan, N.H. Hyperspectral pixel unmixing using singular value decomposition. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 3253–3256.
- Dennison, P.E.; Halligan, K.Q.; Roberts, D.A. A comparison of error metrics and constraints for multiple endmember spectral mixture analysis and spectral angle mapper. Remote Sens. Environ. 2004, 93, 359–367. [Google Scholar] [CrossRef]
- Demarchi, L.; Canters, F.; Chan, J.C.; van de Voorde, T. Multiple endmember unmixing of CHRIS/Proba imagery for mapping impervious surfaces in urban and suburban environments. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3409–3424. [Google Scholar] [CrossRef]
- Breuer, L.; Eckhardt, K.; Frede, H.-G. Plant parameter values for models in temperate climates. Ecol. Model. 2003, 169, 237–293. [Google Scholar] [CrossRef]
- Galdos, F.V.; Álvarez, C.; García, A.; Revilla, J.A. Estimated distributed rainfall interception using a simple conceptual model and Moderate Resolution Imaging Spectroradiometer (MODIS). J. Hydrol. 2012, 468, 213–228. [Google Scholar] [CrossRef]
- Markham, B.L.; Townshend, J.R.G. Land cover classification accuracy as a function of sensor spatial resolution. In Proceedings of the International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 11–15 May 1981; pp. 1075–1090.
- Marceau, D.J.; Howarth, P.J.; Gratton, D.J. Remote sensing and the measurement of geographical entities in a forested environment. 1. The scale and spatial aggregation problem. Remote Sens. Environ. 1994, 49, 93–104. [Google Scholar] [CrossRef]
- Van der Meer, F. Analysis of spectral absorption features in hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2004, 5, 55–68. [Google Scholar] [CrossRef]
- Somers, B.; Delalieux, S.; Verstraeten, W.W.; van Aardt, J.A.N.; Albrigo, G.L.; Coppin, P. An automated waveband selection technique for optimized hyperspectral mixture analysis. Int. J. Remote Sens. 2010, 31, 5549–5568. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.-I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C. Vegetation structure retrieval in beech and spruce forests using spectrodirectional satellite data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 8–17. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clasen, A.; Somers, B.; Pipkins, K.; Tits, L.; Segl, K.; Brell, M.; Kleinschmit, B.; Spengler, D.; Lausch, A.; Förster, M. Spectral Unmixing of Forest Crown Components at Close Range, Airborne and Simulated Sentinel-2 and EnMAP Spectral Imaging Scale. Remote Sens. 2015, 7, 15361-15387. https://doi.org/10.3390/rs71115361
Clasen A, Somers B, Pipkins K, Tits L, Segl K, Brell M, Kleinschmit B, Spengler D, Lausch A, Förster M. Spectral Unmixing of Forest Crown Components at Close Range, Airborne and Simulated Sentinel-2 and EnMAP Spectral Imaging Scale. Remote Sensing. 2015; 7(11):15361-15387. https://doi.org/10.3390/rs71115361
Chicago/Turabian StyleClasen, Anne, Ben Somers, Kyle Pipkins, Laurent Tits, Karl Segl, Max Brell, Birgit Kleinschmit, Daniel Spengler, Angela Lausch, and Michael Förster. 2015. "Spectral Unmixing of Forest Crown Components at Close Range, Airborne and Simulated Sentinel-2 and EnMAP Spectral Imaging Scale" Remote Sensing 7, no. 11: 15361-15387. https://doi.org/10.3390/rs71115361
APA StyleClasen, A., Somers, B., Pipkins, K., Tits, L., Segl, K., Brell, M., Kleinschmit, B., Spengler, D., Lausch, A., & Förster, M. (2015). Spectral Unmixing of Forest Crown Components at Close Range, Airborne and Simulated Sentinel-2 and EnMAP Spectral Imaging Scale. Remote Sensing, 7(11), 15361-15387. https://doi.org/10.3390/rs71115361