The Use of Airborne and Mobile Laser Scanning for Modeling Railway Environments in 3D
Abstract
:1. Introduction
- (i)
- Building extraction and reconstructionThe methods for 3D building modeling rely heavily on data sources. Data from the field of photogrammetry, such as single images, stereo-images or multiple images, extract edge features or line-shaped objects, which provides significant benefits. However, planar feature extraction usually relies on texture recognition, which has considerable impacts on an object’s reflection, the light source, the angle of illumination, the position of the camera, etc. Therefore, it is more reliable to acquire planar features from laser scanning point clouds. However, the edge feature in point cloud scanning exhibits a saw-tooth shape and additional work is required to generalize the feature for the final line-shape acquisition. For building reconstruction, two techniques are usually applied: a model-driven approach and data-driven approach. Model-driven approaches construct the models by predefined primitives, whereas data-driven approaches utilize complex algorithms, such as plane detection, shape generalization, intersection line detection, to achieve the final model. A comparison between model-driven and data-driven methods has been conducted by Tarsha-Kurdi et al. [5]. According to their study, model-driven approaches rely on prior knowledge wherein people know a scene well and know what kind of building types are in a scene. Nevertheless, models based on this approach usually show less visual deformation compared to data-driven approaches. An advantage of data-driven approaches is that they do not require prior knowledge of a scene. Therefore, they can be applied to large unknown areas. Currently 3D models towards the whole world are going on [6]. It will require years until completion. Thus, automatic methods must still be developed and improved.Literature reviews on the methods of building extraction and reconstruction can be found by Wang [7], Hyyppa et al. [8], Baltsavias [9], Brenner [10], Kaartinen and Hyyppa [11], and Haala and Kada [12]. Wang [7] produced an overview of the methods according to different data sources. Hyyppa et al. [8] produced an overall review for the methods of building extraction and reconstruction from single to multiple data sources since the 1990s. Kaartinen and Hyyppa [11] collected building extraction methods from 11 research agencies in 4 testing areas. Input data contained airborne-based data and ground plans (for selected buildings). Building extraction methods were analyzed and evaluated from the aspects of the time consumed, level of automation, level of detail, geometric accuracy, and total relative building area and shape dissimilarity. Haala and Kada [12] reviewed building reconstruction approaches according to building structures, such as roofs and facades, in which the input data covered both airborne-based and ground-based data.In addition, Rutzinger [13] investigated the accuracy of data fusion of building walls and roofs from MLS and ALS, respectively, and verified their availabilities for 3D building modeling.According to the previous research work, it can be concluded that the use of aerial-based data and ground-based data can achieve 3D building models with a (i) high level of automation and (ii) high level of detail.
- (ii)
- Powerline and pylon modelingThe available approaches to modeling powerlines can be obtained from Melzer and Briese [14], McLaughlin [15], Jwa et al. [16], and Sohn et al. [17]. Melzer and Briese (2004) proposed a method for powerline extraction and modeling via ALS by using a 2D Hough transformation and 3D fitting methods. However, it was based on the assumption that the powerlines were parallel. In practical applications, the scenes are usually more complex. Jwa (2009) introduced a voxel-based piece-wise line detector (VPLD) approach for automatic powerline reconstruction using ALS data. This method was based on certain assumptions such as the transmission line not being disconnected within one span and the direction of the powerline not changing abruptly within a span. The latest contribution to powerline classification and reconstruction using ALS data was by Sohn et al. (2012); they used a Markov random field (MRF) classifier to discern the spatial context of linear and planar features, such as in a graphical model for powerline and building classification. They assumed that powerlines run through inhabited areas with many buildings. Powerline pylons were classified and showed the connection between powerlines.
- (iii)
- Pole detectionPole-like objects such as street lights or traffic lights are essential in railway environments. Studies about pole detection methods can be found in Brenner [18], Golovinskiy et al. [19], Lehtomäki et al. [20], Pu et al. [21], and Li and Elberink [22]. Golovinskiy et al. [19] utilized computer vision knowledge for object recognition (including poles) by the following four steps: locating, segmenting, characterizing, and classifying clusters of 3D points. The resulting recognition rate is 65%. Lehtomaki et al. [20] proposed an automatic method for pole-like object detection in MLS, and the algorithm is divided into four phases: (i) segment each profile into a group; (ii) remove the long group; (iii) cluster and merge the groups; and (iv) classify poles and non-poles according to their shape, length, orientation and point density in the local neighborhood of the cluster. The algorithm was evaluated and achieved a comparable accuracy, with a correctness of 81% and a detection possibility of 77.7%. Li and Elberink [22] proposed a five-step method of pole-like object detection. The accuracy of detecting pole-like objects was 72.4% and 75.1% in two different test datasets. However, most proposed methods were knowledge-based methods that required prior knowledge of the environment or scene.
- (iv)
- Road modelingStudies of road extraction usually use images ([23–25]), ALS ([26–28]) or both ([29,30]) as data sources. Currently, certain methods based on MLS data are also available: Goulette et al. [31], Kukko [32], Jaakkola et al. [33] and Pu et al. [21]. MLS provides direct information to acquire the positions of railroads if the trajectory of the MLS fits the center line of one of the railroads. Searching for parallel lines could be helpful for other railway environment extractions. In this paper, the goal was to produce a final visualization of railway environments. Therefore, the visualization of railroads was conducted by mapping orthophotos onto ground models, with railroads considered part of the ground.Additionally, currently 3D visualization has received considerable attention due to the large screen, the powerful processors and abundant memory as well as open operation system of the computer and the mobile devices, e.g., iPad, smartphone, or PDA [8]. However, as sensor technology continues to develop, it not only increases the number of point clouds but also the accuracy of data acquisition, although 3D models from a significant number of points would cause difficulties in the model post-processing, including model rendering and visualization, especially for dense ground points. Therefore, model simplification is required. Ground models are popularly called digital elevation models (DEMs), and they utilize raster format or vector format to represent terrain characteristics. Before the advent of ALS, the photogrammetric method was used as a primary method of DEM generation and included breakline extraction from stereo-images. DEM generation has primarily been in a vector format. ALS has become a very important method of DEM generation because of its rapid, accurate, and highly efficient data acquisition, especially over large survey areas. DEM is usually extracted from ALS as a raster. Raster DEMs present flat or undulated terrain as points with uniform spaces. Disadvantages include redundant points for flat terrain and inadequate representation in a changing or sloped area. Numerous methods for DEM simplification have been reported, and the main methods are as follows [34]: (i) working from a finer resolution of DEM to a coarse resolution for a point reduction method; (ii) reconstructing the terrain by a triangulated irregular network (TIN) method; (iii) filtering method; (iv) point-additive method; (v) point-subtractive method; (vi) feature-point method; and (vii) combination of the point-additive and feature-point methods [34]. This paper will present a novel and effective approach for ground point simplification that has adjustable parameters for the different levels of detail of the ground features. After ground point simplification, the reduction of the points can be up to 99.36% of the original number, and this approach is flexible for 3D visualization.In this paper, a complete procedure for railway environment modeling and visualization is addressed. The railway environment modeling contains object classifications and reconstructions of buildings, powerlines and poles. The different advantages of ALS and MLS are used in modeling the objects from different data sources. The primary focus is on building roof extraction from ALS, building facade extraction from MLS, complete building integration from ALS and MLS, powerline and pylon detection from ALS and ground model simplification for 3D visualization. The remainder of the paper is organized as follows: Section 2 introduces the data sources for railway environment modeling; Section 3 presents the modeling methods; Section 4 includes the result and discussion; and Section 5 offers the conclusions.
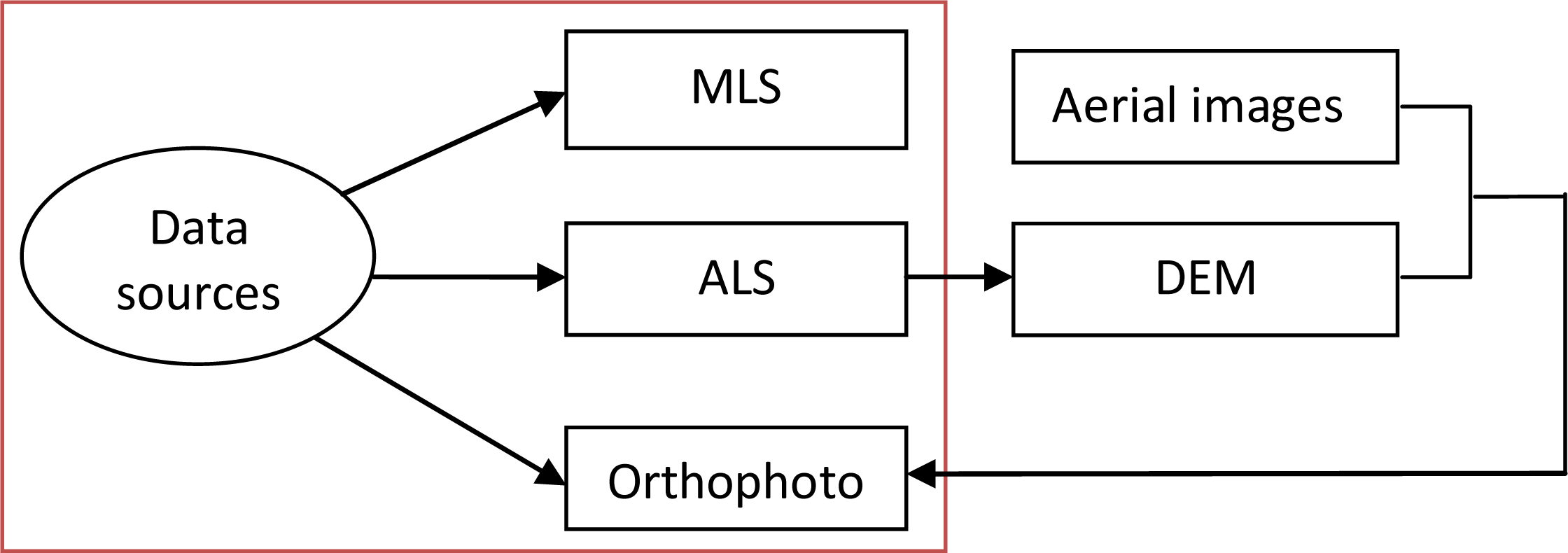
2. Materials
- (i)
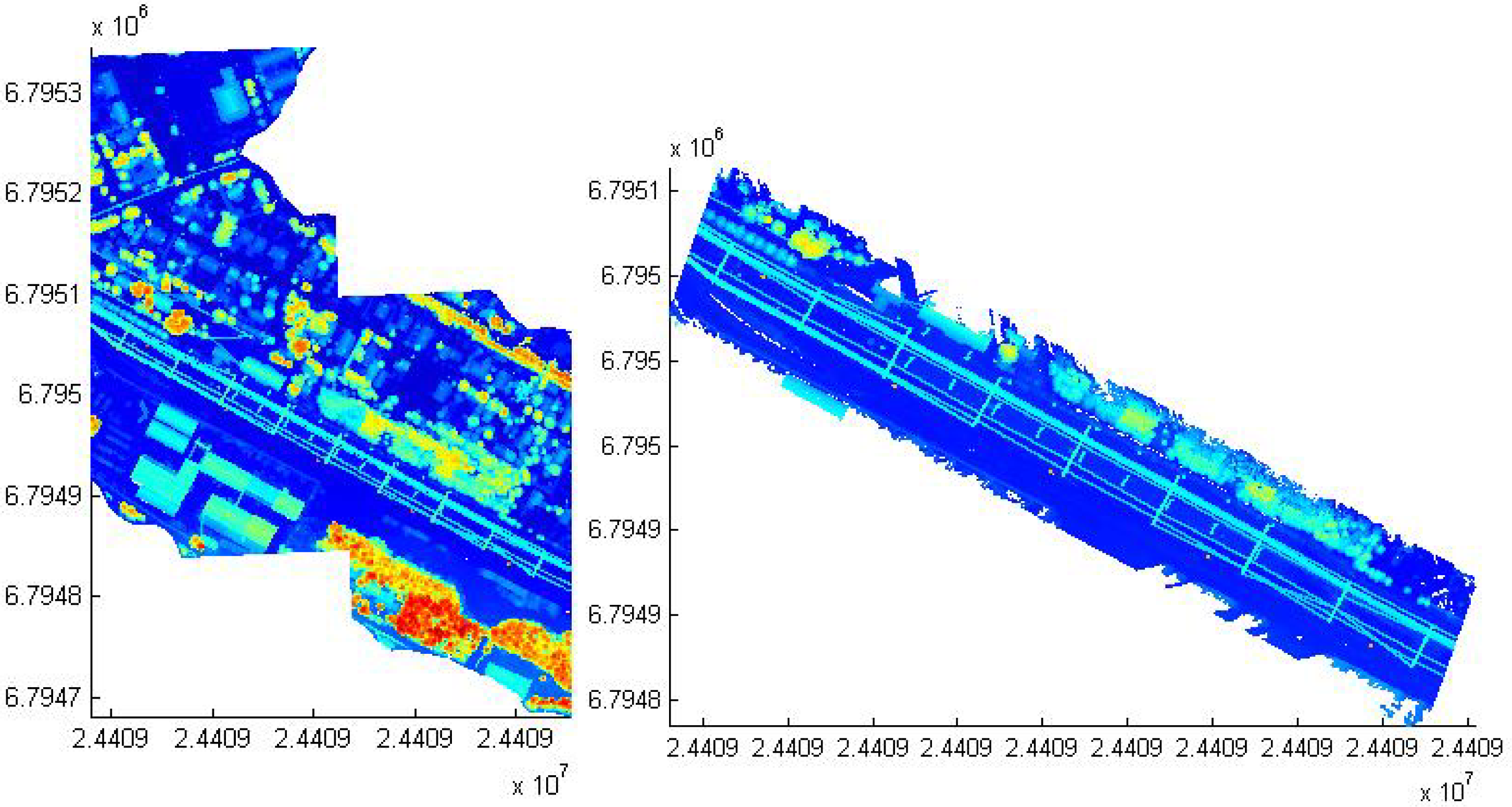
- ALS dataThe relative accuracy between individual flight lines has been verified. TerraMatch (Terrasolid software, Finland) was used for individual corrections for each flight line in XYZ, roll and mirror scale. Ground control points were used for reference. The report showed that after matching, the global statistics of total Root Mean Square (RMS) was 0.034 m.
- (ii)
- MLS dataThe accuracy of the final GNSS solution and INS trajectory was estimated at 3–5 cm and 5 cm or less, respectively, by comparing the results of the forward processing solution and the reverse processing solution. The different drive passes were matched together using tie lines, and the data were matched to the control points. The raw laser data and INS trajectories were combined together to produce a georeferenced point cloud. The average correction to match the control points in X, Y, Z was less than 10 cm and the maximum was up to 0.4 m.
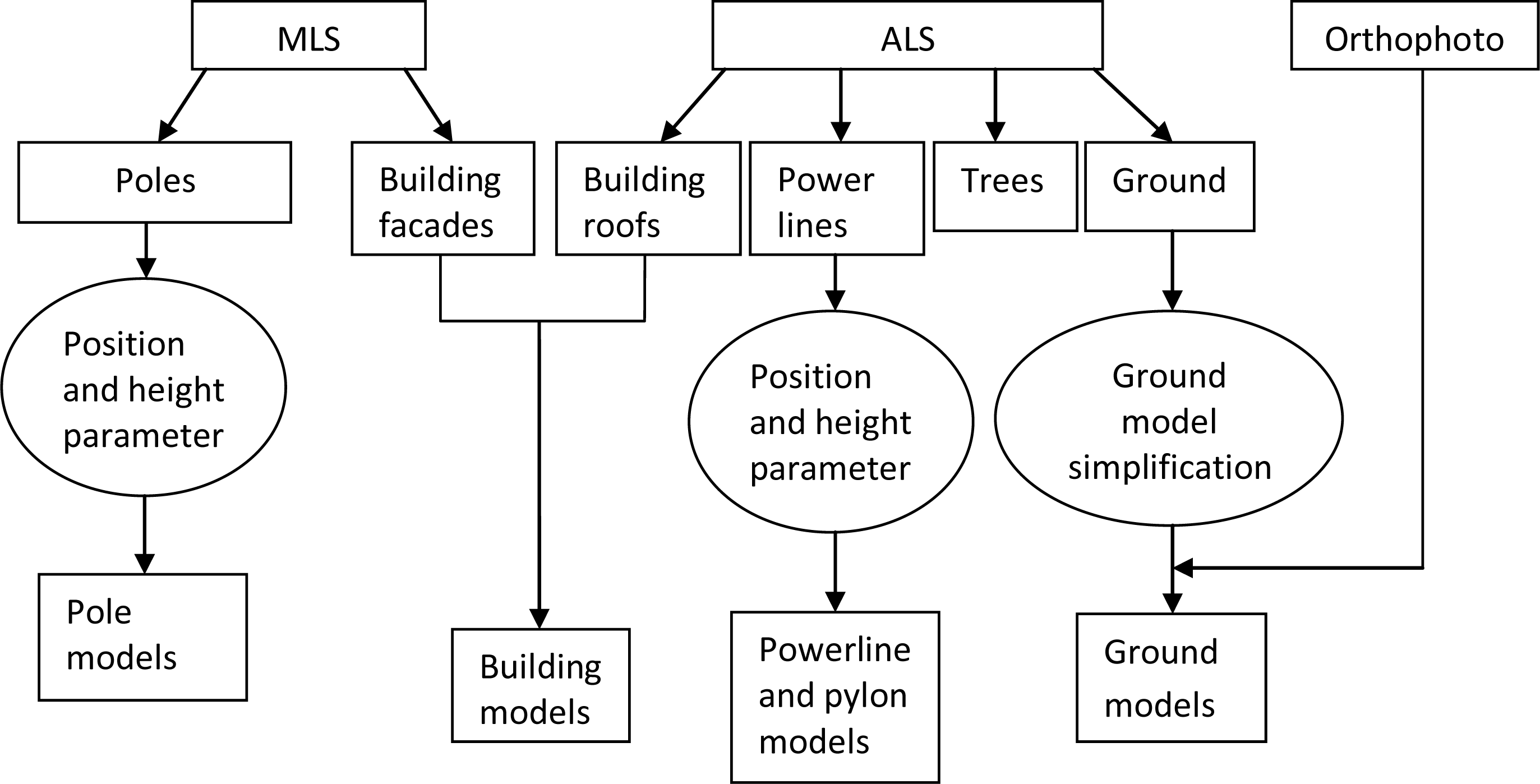
3. Modeling of Railway Environments
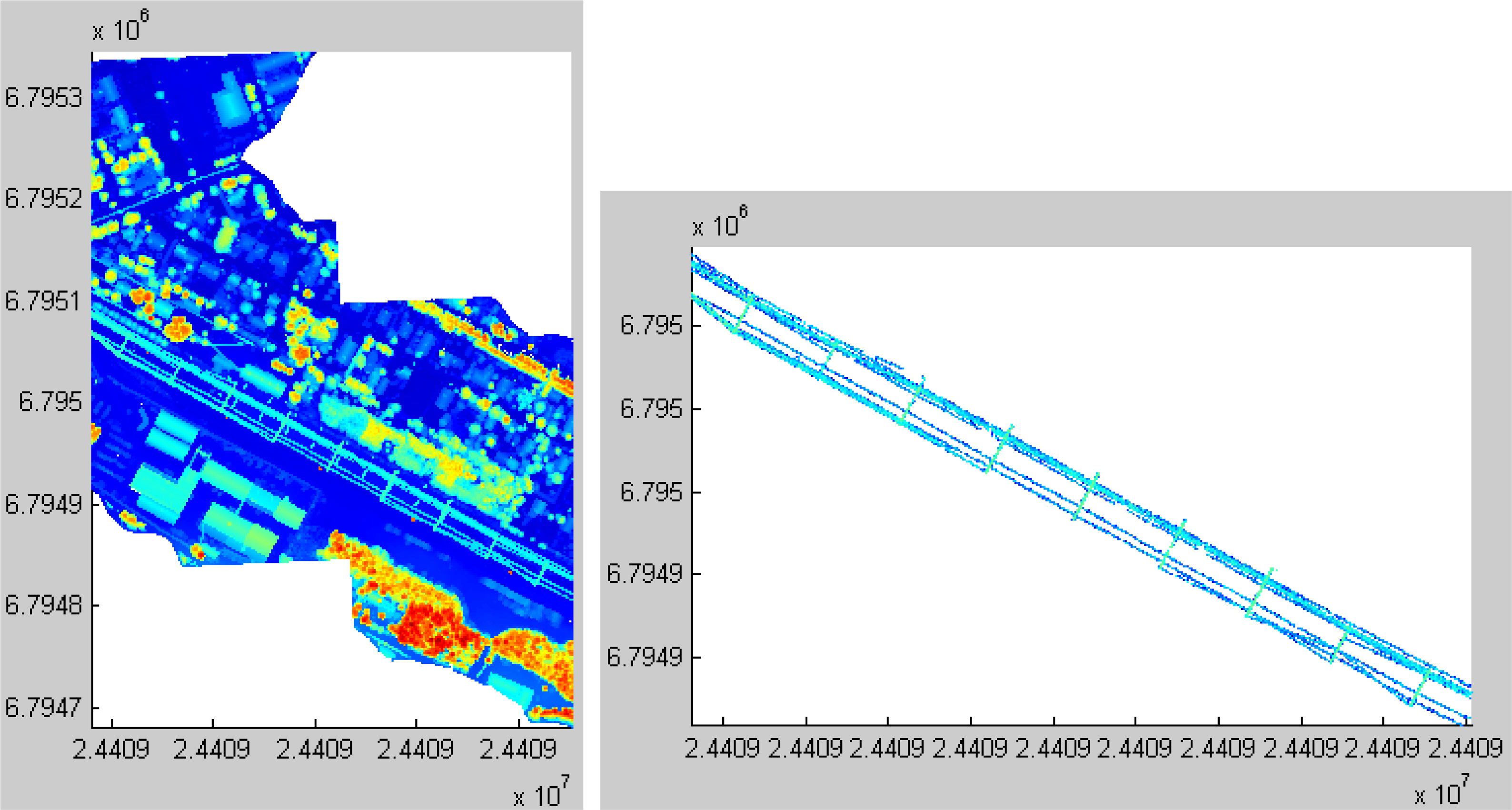
3.1. Object Extraction from ALS Point Cloud
3.1.1. Ground
3.1.2. Building roofs
- (i)
- Grid the data and separate the data into two sub-datasets (processing the points grid by grid): Dlower and Dupper, where Dlower refers to the points that their height differences from the lowest point of the grid are less than or equal to 2.5 m, Dupper is the points that their height differences from the lowest point of the grid are less than 2.5 m.
- (ii)
- Transform Dlower (–xy plane view) into a binary image and accept objects as 0 and no objects as 1.
- (iii)
- Process the binary image and remove the noise points by thresholding the parameters of image processing, which are the area and shape of each region.
- (iv)
- Transform the cleaned binary image back to a 3D point cloud (the reverse process in step (ii)).
- (v)
- Construct the TIN to remove the scattered noise points.
- (vi)
- Utilize histograms to find the clusters and remove the small cluster points.
3.1.3. Powerlines
- (i)
- Calculate the gradient for each point: , , where Z = F(x, y);
- (ii)
- Obtain points that satisfy the conditions: |Fx| ≥ T1 and |Fx| ≤ T2, and |Fy| ≥ T1 and |Fy| ≤ T2, where T1 < T2;
- (iii)
- Transform the 3D points into a 2D binary image and use the constraints in the image region properties to remove non-powerline related objects;
- (iv)
- Transform the derived powerline image into a 3D point cloud;
- (v)
- For pylon detection, grid the point cloud and count the number of points (Pcnt) in each grid; generate the binary image: when Pcnt ≥ T, label it as 1. Otherwise, label it as zero. T is the threshold for the number of the points.
- (vi)
- Transform the binary image back to a 3D point cloud for the resulting pylons.
- (vii)
- The heights and positions of the pylons are derived by calculating the height difference of each pylon and extracting the endings of each pylon.
3.1.4. Trees
3.2. Object Extraction from MLS Point Cloud
3.2.1. Building Facades
3.2.2. Poles
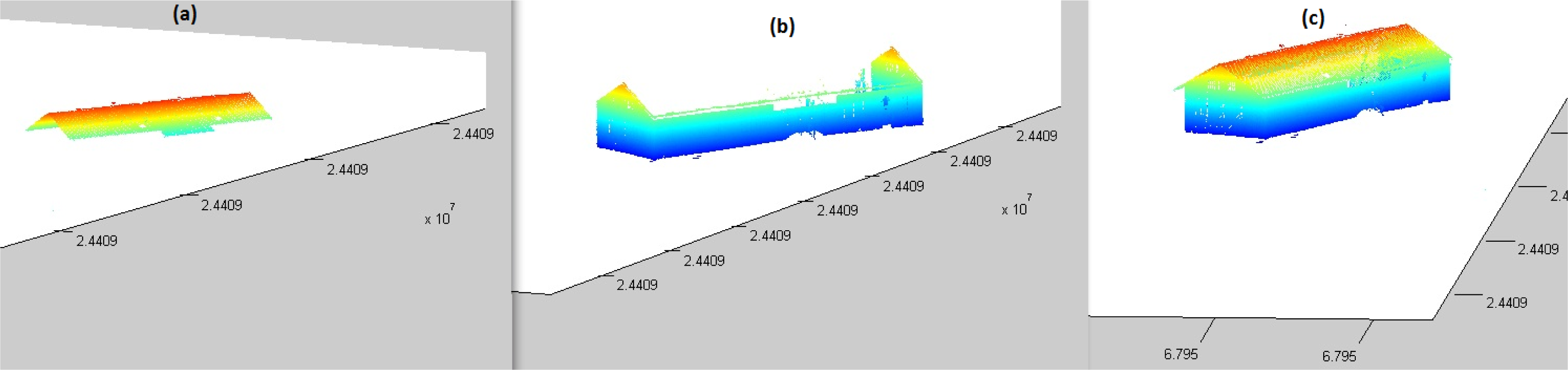
3.3. Object Fusion and Building Planar Separation
3.3.1. Complete Building Models
3.3.2. Planar Detection of Buildings
3.4. Ground Model
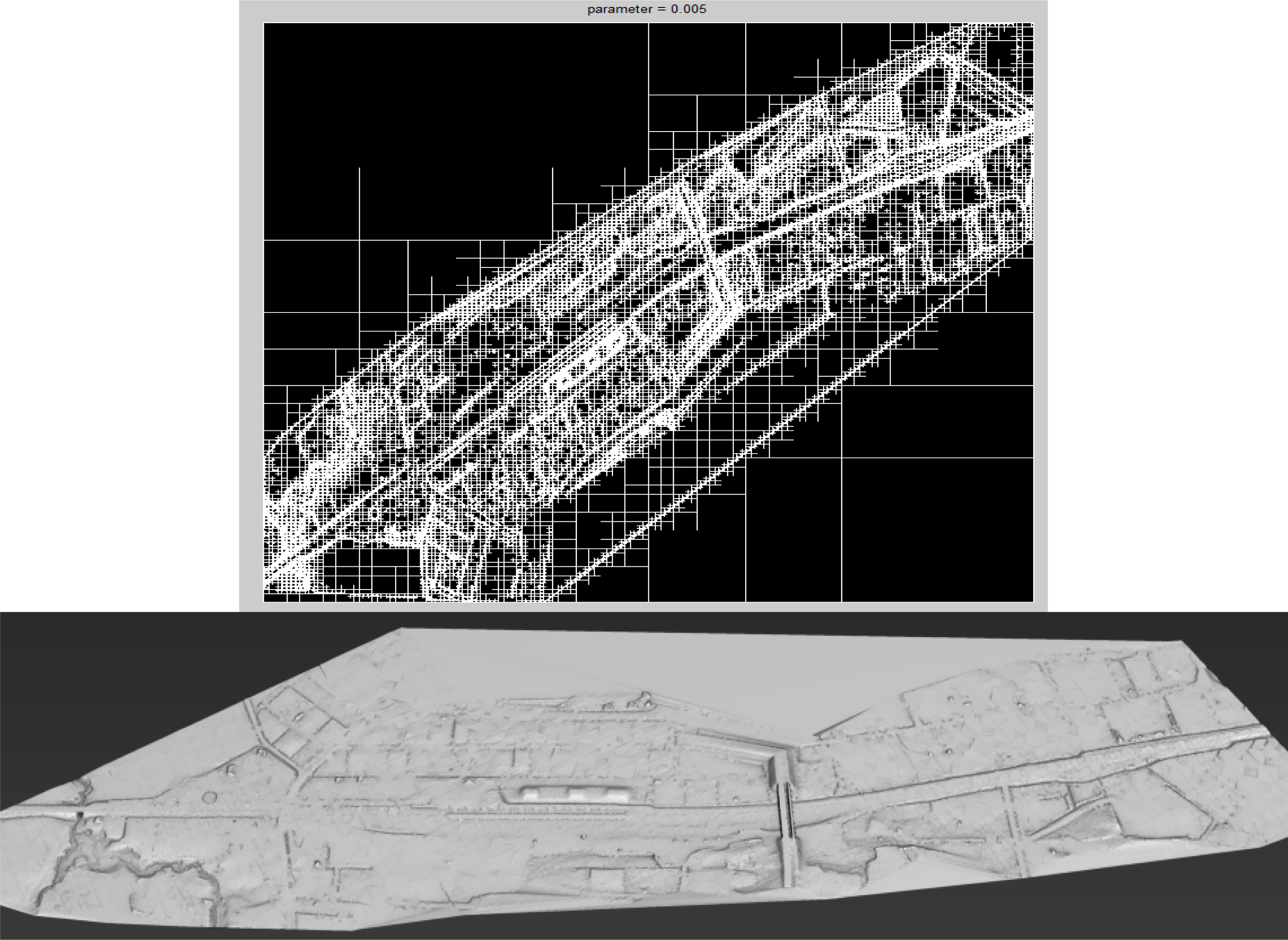
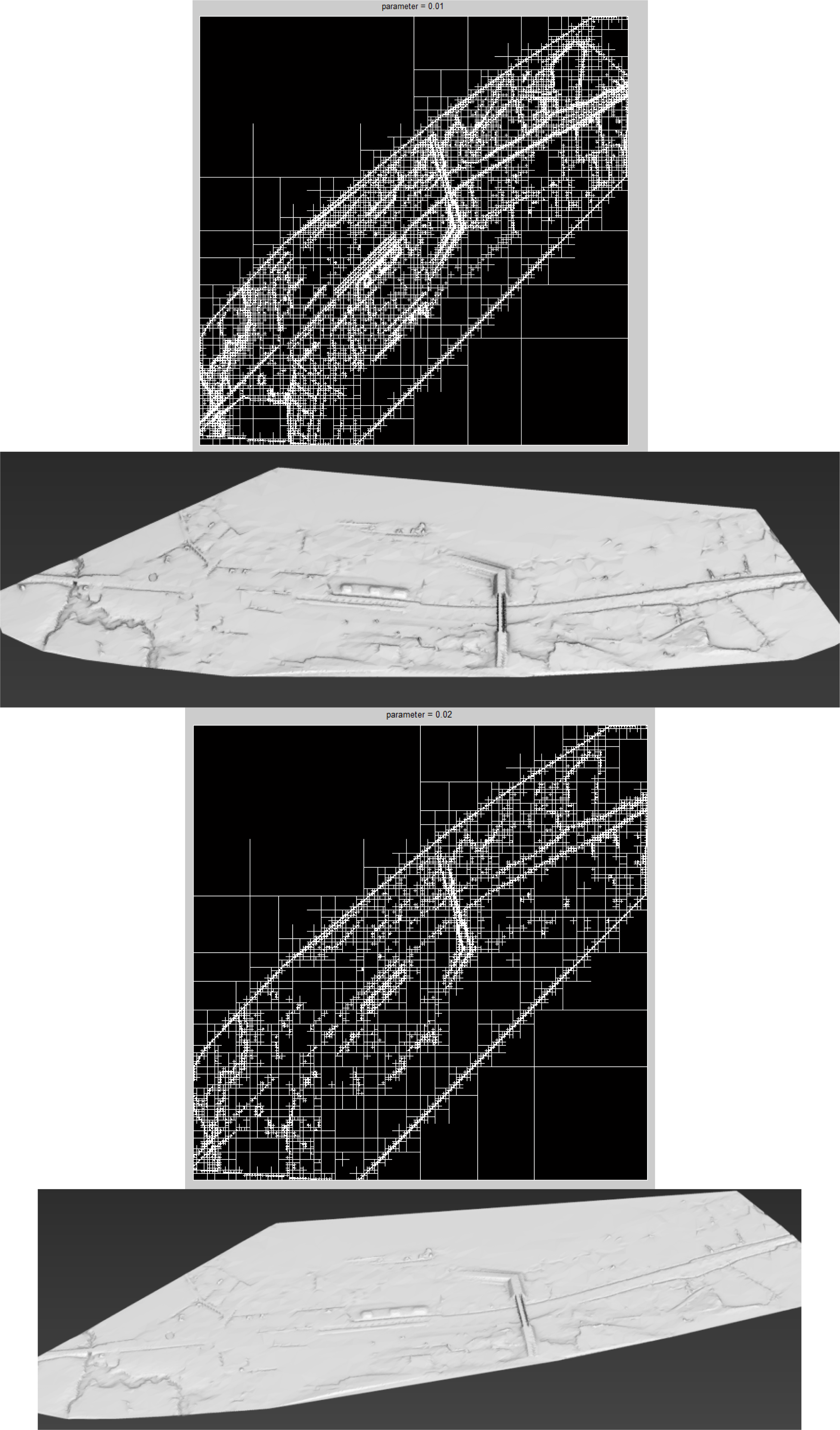
Ground Model Simplification
4. Results and Discussion
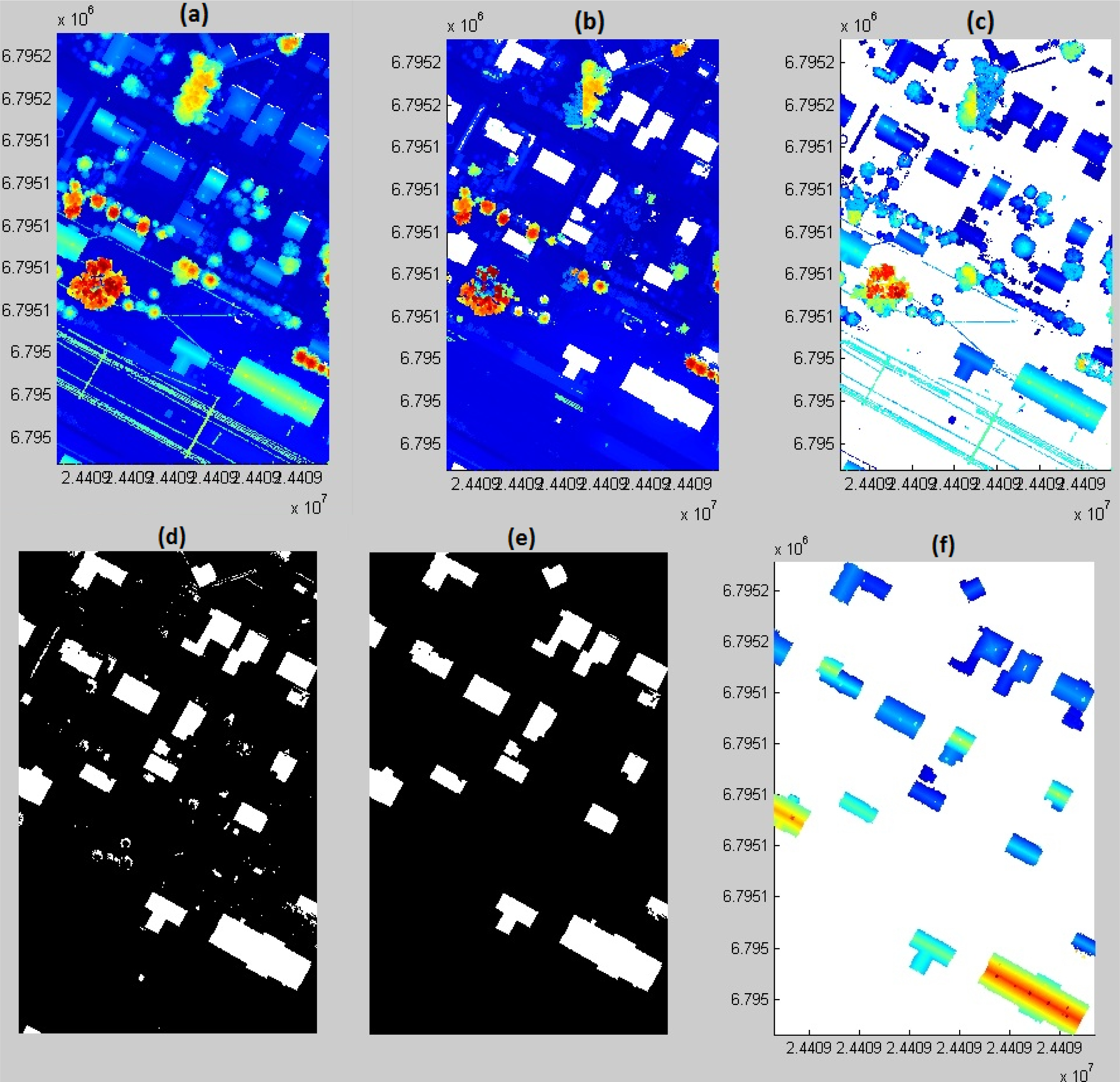
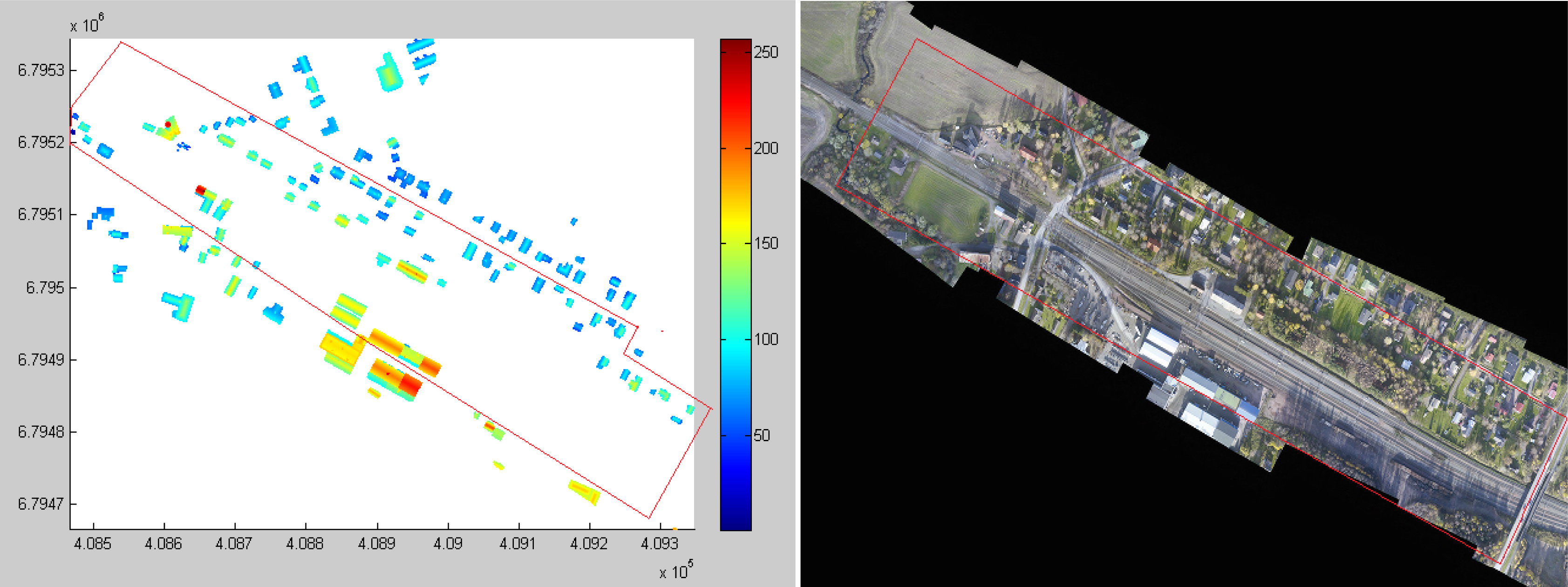
4.1. Building Classification Results
4.2. Powerlines and Pylons
4.3. Ground Model Simplification
5. Conclusions
- (i)
- An entire railway environment was successfully reconstructed from ALS and MLS datasets.
- (ii)
- Automatic algorithms for modeling buildings from both ALS and MLS data were developed. The accuracy of building detection from ALS is 93.44% for the test data.
- (iii)
- Powerlines and pylons were extracted from ALS data. An acceptable result was achieved because of the dense point cloud and clear cutoff edge between the powerlines and surrounding environments.
- (iv)
- An algorithm for ground model simplification has been proposed. The reduction of points was up to 99.36% of the original point size, which was beneficial for model post processing and 3D visualization. It was especially flexible because users can select the level of ground detail in different applications.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Railways and the Environment: Building on the Railways’ Environmental Strengths. Available online: http://www.cer.be/publications/brochures/brochures-details/railways-and-the-environment-building-on-the-railways-environmental-strengths/ (accessed on 7 February 2014).
- Railway Passenger Transport Industry: Market. Research Reports, Statistics and Analysis. Available online: http://www.reportlinker.com/ci02334/Railway-Passenger-Transport.html (accessed on 16 August 2013).
- RIEGL Website. Available online: http://www.riegl.com/ (accessed on 21 January 2014).
- Kukko, A.; Kaartinen, H.; Hyyppa, J.; Chen, Y. Multiplatform mobile laser scanning: Usability and performance. Sensors 2012, 12, 11712–11733. [Google Scholar]
- Model-Driven and Data-Driven Approaches Using Lidar Data: Analysis and Comparison. Available online: http://www.pf.bgu.tum.de/isprs/pia07/puba/PIA07_Tarsha-Kurdi_et_al.pdf (accessed on 7 February 2014).
- 3D City Map Website. Available online: http://www.computamaps.com/products/3Dcitymap.htm (accessed on 20 Noveber 2013).
- Wang, R. 3D building modeling using images and LiDAR: A review. Int. J. Image Data Fusion 2013, 4, 273–292. [Google Scholar]
- Hyyppa, J.; Zhu, L.; Liu, Z.; Kaartinen, H.; Jaakkola, A. 3D City Modeling and Visualization for Smart Phone Applications. In Ubiquitous Positioning and Mobile Location-Based Services in Smart Phones; Chen, R., Ed.; Chapter 10; IGI Global: Hershey, PA, USA, 2012. [Google Scholar]
- Baltsavias, E.P. Object extraction and revision by image analysis using existing geodata and knowledge: Current status and steps towards operational systems. ISPRS J. Photogramm. Remote Sens 2004, 58, 129–151. [Google Scholar]
- Brenner, C. Building reconstruction from images and laser scanning. Int. J. Appl. Earth Obs. Geoinf 2005, 6, 187–198. [Google Scholar]
- Kaartinen, H.; Hyyppa, J. EuroSDR-Project Commission 3 “Evaluation of Building Extraction”, Final Report; No. 50; EuroSDR Official Publication: Leuven, Belgium, 2006. [Google Scholar]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS J. Photogramm. Remote Sens 2010, 65, 570–580. [Google Scholar]
- Automatic Extraction of Vertical Walls from Mobile and Airborne. Available online: http://www.isprs.org/proceedings/xxxviii/3-w8/papers/p74.pdf (accessed on 7 February 2014).
- Extraction and Modeling of Powerlines from ALS Point Clouds. Available onlne: http://www.ipf.tuwien.ac.at/cb/publications/melzer_powerlines_OAGM_2004.pdf (accessed on 7 February 2014).
- McLaughlin, R.A. Extracting transmission lines from airborne LIDAR Data. IEEE Geosci. Remote Sens Lett 2006, 3, 222–226. [Google Scholar]
- Automatic 3D Powerline Reconstruction Using Airborne Lidar Data. Available online: http://www.isprs.org/proceedings/xxxviii/3-w8/papers/p105b.pdf (accessed on 7 February 2014).
- Automatic Powerline Scene Classification and Reconstruction Using Airborne Lidar Data. Available online: http://www.isprs-ann-photogramm-remote-sens-spatial-inf-sci.net/I-3/167/2012/isprsannals-I-3-167-2012.pdf (accessed on 7 February 2014).
- Extraction of Features from Mobile Laser Scanning Data for Future Driver Assistance System Advances in GIScience. Available online: http://link.springer.com/chapter/10.1007%2F978-3-642-00318-9_2 (accessed on 7 February 2014).
- Shape-Based Recognition of 3D Point Clouds in Urban Environments. Available online: http://www.cs.princeton.edu/~funk/iccv09.pdf (accessed on 7 February 2014).
- Lehtomaki, M.; Jaakkola, A.; Hyyppa, J.; Kukko, A.; Kaartinen, H. Detection of vertical pole-like objects in a road environment using vehicle-based laser scanning data. Remote Sens 2010, 2, 641–664. [Google Scholar]
- Pu, S.; Rutzinger, M.; Vosselman, G.; Elberink, S.O. Recognizing basic structures from mobile laser scanning data for road inventory studies. ISPRS J. Photogramm. Remote Sens 2011, 66, 28–39. [Google Scholar]
- Optimizing Detection of Road Furniture (Pole-Like Object) in Mobile Laser Scanner Data. Available online: http://www.itc.nl/library/papers_2013/msc/gfm/danli.pdf (accessed on 7 February 2014).
- Hay, G.J.; Castilla, G. Geographic Object-Based Image Analysis (GEOBIA). In Object-Based Image Analysis—Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G. J., Eds.; Chapter 1.4; Springer: Verlag, Berlin, Germany, 2008; pp. 81–92. [Google Scholar]
- Nussbaum, S.; Menz, G. Object-Based Image Analysis and Treaty Verification: New Approaches in Remote Sensing—Applied to Nuclear Facilities in Iran; Springer Verlag: Berlin, Germany, 2008. [Google Scholar]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens 2010, 65, 2–16. [Google Scholar]
- Clode, S.; Rottensteiner, F.; Kootsookos, P.; Zelniker, E. Detection and vectorisation of roads from LIDAR data. Photogramm. Eng. Remote Sens 2007, 73, 517–535. [Google Scholar]
- Assessing Image Segmentation Quality—Concepts, Methods and Application. Available online: http://www.isprs.org/proceedings/xxxviii/4-c1/sessions/Session2/6721_Neubert_Proc_pap.pdf (accessed on 7 February 2014).
- Boyko, A.; Funkhouser, T. Extracting roads from dense point clouds in large scale urban environment. ISPRS J. Photogramm. Remote Sens 2011, 66, S2–S12. [Google Scholar]
- Dong, J.; Zhuang, D.; Huang, Y.; Fu, J. Advances in multi-sensor data fusion: Algorithms and applications. Sensors 2009, 9, 7771–7784. [Google Scholar]
- Beger, R.; Gedrange, C.; Hecht, R.; Neubert, M. Data fusion of extremely high resolution aerial imagery and LIDAR data for automated railroad center line reconstruction. ISPRS J. Photogramm. Remote Sens 2011, 66, S40–S51. [Google Scholar]
- An Integrated On-Board Laser Range Sensing System for On-The-Way City and Road Modeling. Available online: http://www.isprs.org/proceedings/xxxvi/part1/Papers/T10-43.pdf (accessed on 7 February 2014).
- Kukko, A. Road Environment Mapper—3D Data Capturing with Mobile Mapping. Licentiate’s Thesis, Helsinki University of Technology, Espoo, Finland,. 2009; 158. [Google Scholar]
- Jaakkola, A.; Hyyppa, J.; Hyyppa, H.; Kukko, A. Retrieval algorithms for road surface modeling using laser-based mobile mapping. Sensors 2008, 8, 5238–5249. [Google Scholar]
- Zhou, Q.; Chen, Y. Generalisation of DEM for terrain analysis using a compound method. ISPRS J. Photogramm. Remote Sens 2011, 66, 38–45. [Google Scholar]
- VR Track Oy Website. Available online: http://www.vrgroup.fi/en/ (accessed on 7 February 2014).
- Yu, X.; Hyyppa, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on random forests technique. ISPRS J. Photogramm 2011, 66, 28–37. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with aerial laser scanner data. ISPRS J. Photogramm. Remote Sens 1998, 53, 193–203. [Google Scholar]
- DEM Generation from Laser Scanner Data Using Adaptive TIN Models. Available online: http://www.isprs.org/proceedings/xxxviii/7-C4/308_GSEM2009.pdf (accessed on 7 February 2014).
- Raber, G.T.; Jensen, J.R.; Schill, S.R.; Schuckman, K. Creation of Digital Terrain Models using an adaptive Lidar vegetation point removal process. Photogramm. Eng. Remote Sens 2002, 68, 1307–1316. [Google Scholar]
- Ma, R.; Meyer, W. DTM generation and building detection from Lidar data. Photogramm. Eng. Remote Sens 2005, 71, 847–854. [Google Scholar]
- Shan, J.; Sampath, A. Urban DEM generation from raw LiDAR data: A labeling algorithm and its performance. Photogramm. Eng. Remote Sens 2005, 71, 217–226. [Google Scholar]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne Lidar data: A review of critical issues. Remote Sens 2010, 2, 833–860. [Google Scholar]
- Hyyppa, J.; Hyyppa, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens 2008, 29, 1339–1366. [Google Scholar]
- Kaartinen, H.; Hyyppa, J.; Yu, X.; Vastaranta, M.; Hyyppa, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An international comparison of individual tree detection and extraction using airborne laser scanning. Remote Sens 2012, 4, 950–974. [Google Scholar]
- Zhu, L.; Hyyppa, J.; Kukko, A.; Kaartinen, H.; Chen, R. Photorealistic 3D city modeling from mobile laser scanning data. Remote Sens 2011, 3, 1406–1426. [Google Scholar]
- The Use of Mobile Laser Scanning Data and Unmanned Aerial Vehicle Images for 3D Model Reconstruction. Available online: http://www.int-arch-photogramm-remote-sens-spatial-inf-sci.net/XL-1-W2/419/2013/isprsarchives-XL-1-W2-419-2013.pdf (accessed on 7 February 2014).
- The 3D Hough Transform for Plane Detection in Point Clouds—A Review and A new Accumulator Design. Available online: http://link.springer.com/article/10.1007%2F3DRes.02%282011%293 (accessed on 7 February 2014).





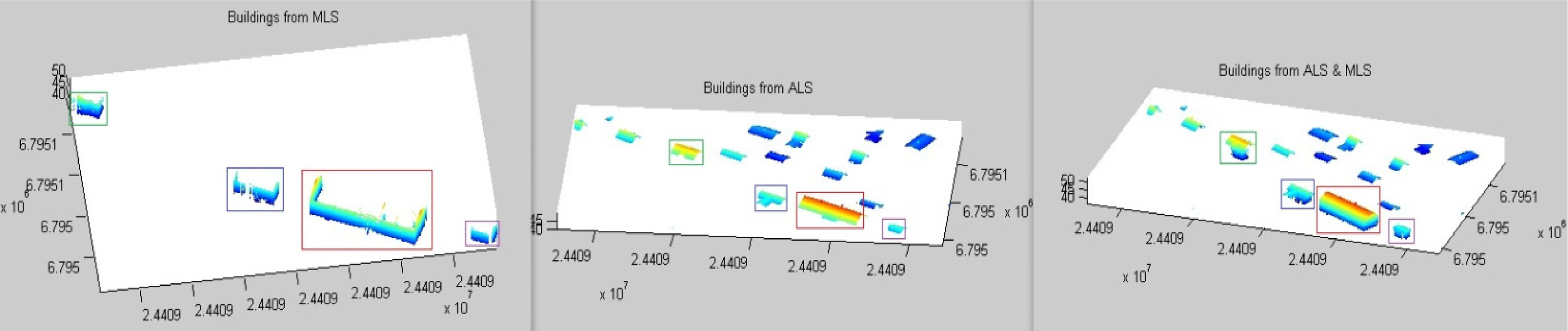


| Statistical Items | The Number of Objects on the Orthophoto | The Number of Objects from the Point Cloud | Detection Accuracy |
|---|---|---|---|
| Buildings from ALS | 61 | 57 | 93.44% |
| Walls from MLS | 10 | 10 | 100% |
| Powerline pylons | 20 | 20 | 100% |
| Number of Original Points | Number of Points after Simplification | Reduction Rate | |
|---|---|---|---|
| 0.005 | 6,890,129 | 252,339 | 96.34% |
| 0.01 | 181,232 | 97.37% | |
| 0.02 | 113,165 | 99.36% |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, L.; Hyyppa, J. The Use of Airborne and Mobile Laser Scanning for Modeling Railway Environments in 3D. Remote Sens. 2014, 6, 3075-3100. https://doi.org/10.3390/rs6043075
Zhu L, Hyyppa J. The Use of Airborne and Mobile Laser Scanning for Modeling Railway Environments in 3D. Remote Sensing. 2014; 6(4):3075-3100. https://doi.org/10.3390/rs6043075
Chicago/Turabian StyleZhu, Lingli, and Juha Hyyppa. 2014. "The Use of Airborne and Mobile Laser Scanning for Modeling Railway Environments in 3D" Remote Sensing 6, no. 4: 3075-3100. https://doi.org/10.3390/rs6043075
APA StyleZhu, L., & Hyyppa, J. (2014). The Use of Airborne and Mobile Laser Scanning for Modeling Railway Environments in 3D. Remote Sensing, 6(4), 3075-3100. https://doi.org/10.3390/rs6043075




