4.1. Point Source Data Analysis
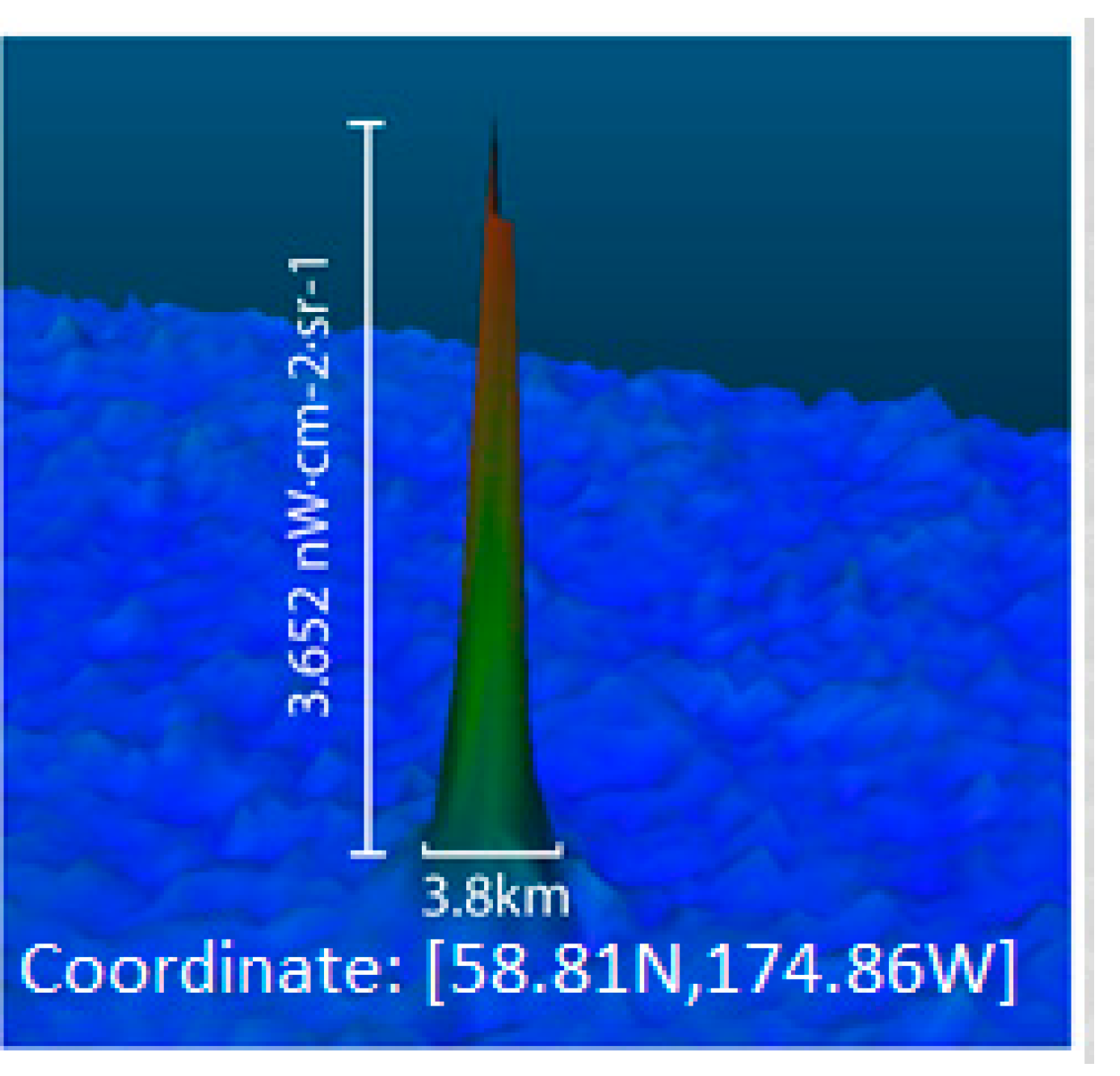
From the Bearing Sea crab-fishing vessel dataset, we found that although the vessel itself (about 34 meters × 10.4 meters) is much smaller than one VIIRS DNB pixel, there are actually 24 pixels illuminated in the DNB for this vessel, with a Gaussian like distribution (
Figure 5;
Table 1), and a maximum pixel radiance value of 3.652 nW∙cm
−2∙sr
−1, which is at the level of specified minimum radiance for the VIIRS DNB instrument. Since the actual DNB minimum detectable radiance is more than an order of magnitude smaller and the background ocean has little light, the vessel signal is clearly detected. This is very significant for search and rescue operations where the light intensity of the object is usually relatively small. The multiple pixel illumination could have been mis-interpreted as a point spread effect of the instrument, but this is not possible since the resolution of the instrument is 742 meters at full-width-half-max (FWHM), and as discussed later, there are indeed single points illuminated in the DNB datasets such as shown in other datasets for both fishing boats and city lights.
Figure 5.
3D view of the Bearing Sea crab vessel light (in satellite projection to avoid distortion).
Figure 5.
3D view of the Bearing Sea crab vessel light (in satellite projection to avoid distortion).
Table 1.
Radiant Power Calculation for the Crab Fishing Vessel.
Table 1.
Radiant Power Calculation for the Crab Fishing Vessel.
| | Value | Note |
|---|
| Total Radiance | 29.62 nW∙cm−2∙sr−1 | |
| # of illuminated pixels | 24 | |
| Atmospheric transmittance 1 | 95% | MODTRAN estimates |
| Radiant exitance | 171.65 W∙sr−1 | Equation (1) |
| Surface Lambertian reflection | 50% | Assumption |
| Total irradiance incident on surface | 1078.5W | Equations (1) and (2) |
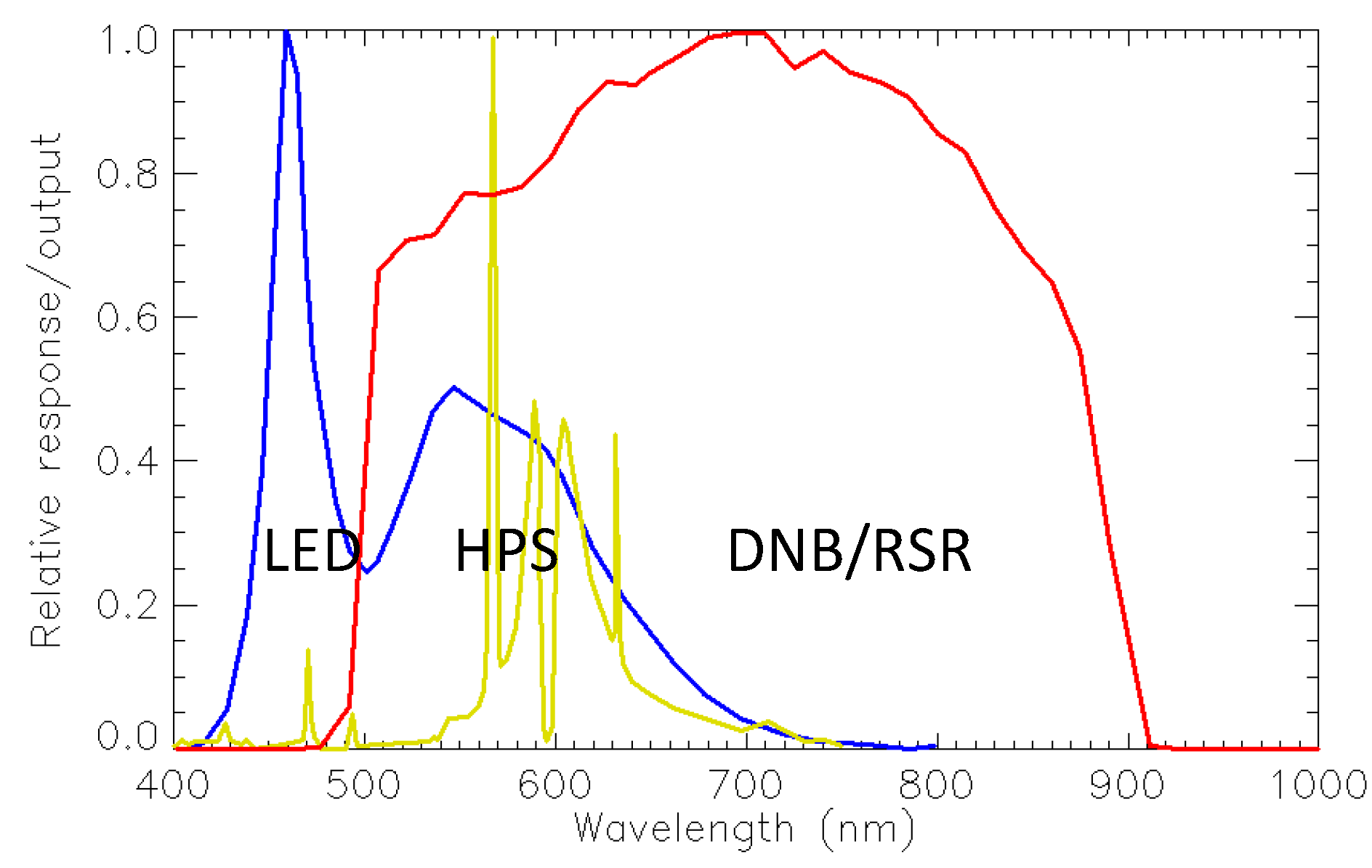
| Lamp electrical to Radiant Power conversion efficacy | 30% | Assume HPS; would be much higher for Tungsten |
| Estimated total electrical power used | 3.6kW | |
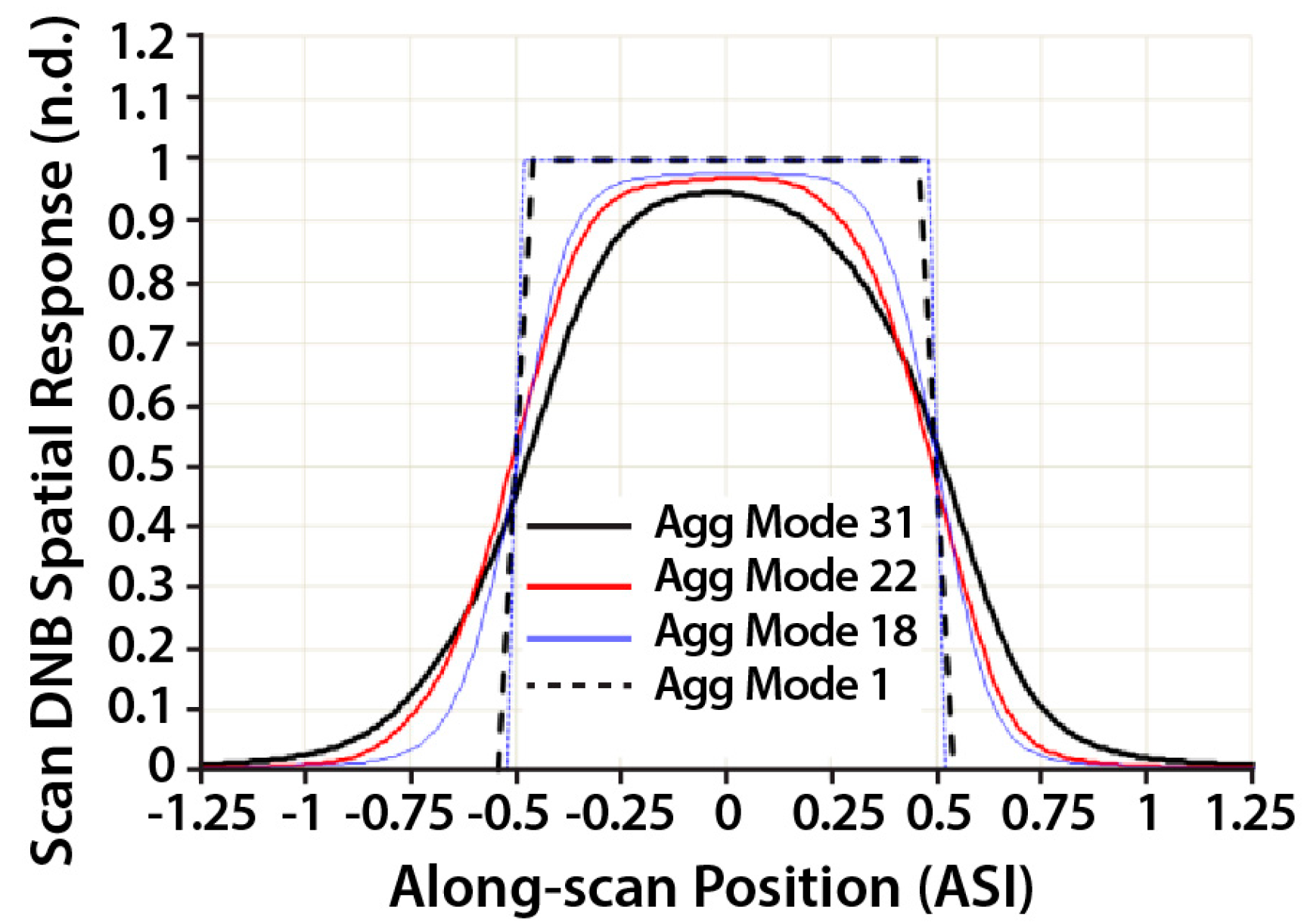
Since the vessel is not located near nadir on the DNB image, one possibility for the multiple pixel illumination is that the vessel light is in the corner of four DNB pixels which would illuminate about 8 pixels (worst case scenario) since the LSF along scan is responsive to ±1.25 pixels while a rectangular response is assumed in the track direction (
Figure 3). However, the 24 pixel illumination far exceeded the effect of the LSF and as a result, the alternative explanation is that a combination of near field scattering in the DNB instrument, and light scattering in the clouds have likely contributed to the illumination of a much large area. The symmetric pattern of the illuminated pixels also supports the hypothesis of scattering, since the LSF is not symmetric in the track and scan directions. To further verify this assumption, we analyzed the cloud optical thickness data for this granule [
20,
21]. The data shows that a mixture of ice and water clouds dominated the region at the time of DNB observation, which supports the hypothesis of cloud scattering. It is also possible that scattering would be different in water clouds
vs. ice clouds, which will require further analysis in the future. Another possible explanation is that there may have been multiple vessels at this location and time. However, detecting individual vessels within a group of contiguously illuminated pixels at 742 m resolution exceeded the spatial performance limit of the DNB. In addition, the ground truth data is not available in this case. Finally, it should be noted that the VIIRS DNB LSF on-orbit has not been fully verified. Additional work is also needed to derive a more solid LSF in both the scan and track directions.
Analysis of the light intensity of the fleet near the St. Paul Island (southeast of the trapped vessel) shows that there were many vessels in the area at the time, some with a similar level of radiance values with multiple pixel illumination, although vessels with radiances as low as 0.987 nW∙cm−2∙sr−1 with a single pixel illumination have also been detected. This compares to a background radiance of ~0.2 nW∙cm−2∙sr−1 which is for the ocean surface.
To estimate the light power from the fishing vessel, Equation (1) is used. Given the total radiance of the 24 pixels illuminated, we derive the radiant exitance of 171.65 W∙sr
−1. We further assume that the vessel surface has a reflection of 50% (possibly higher if there is snow), and the lamp used is assumed to be High Pressure Sodium (HPS) floodlights [
22], which have a 30% electrical to radiant conversion efficacy. The estimated total electrical power required would be about 3.6 kW. Alternatively, if the lamp type is Halogen-Tungsten, the electric power required could be lower because of its higher efficacy. It is noted that the floodlights in this case would be primarily used to illuminate the deck of the vessel for operations, in contrast to the squid fishing boats where the light is primarily used for attracting the fish. For comparison, we also analyzed sample lights for squid fishing boats in the Sea of Japan, which suggests that the light power (typically >130 nW∙cm
−2∙sr
−1) is many times higher than that of the crab fishing vessel analyzed here. This demonstrates that the light power calculations can potentially be used to obtain more information about the vessels and objects of interest.
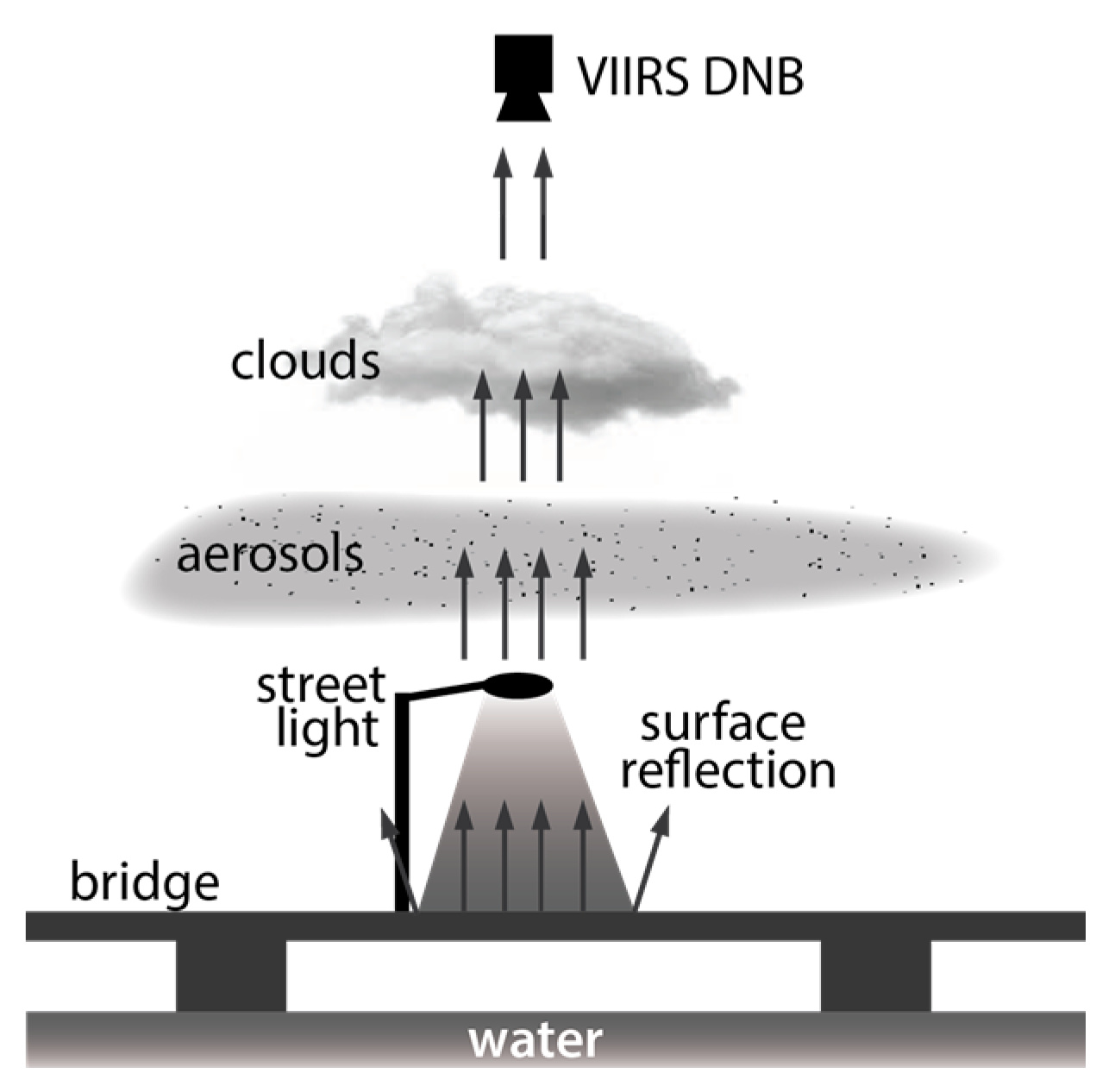
The vessel lights have strong signals for DNB and are very useful for tracking and identification, but unfortunately, they are mobile and therefore not suitable for long-term stability analysis for obvious reasons. Therefore, for long-term stability, we focused on the lights on bridges. The bridge lights have several advantages. First, bridges are above water, which has low reflectance and works well when used as background. Second, bridges are typically made of concrete with moderate level of reflectance in the DNB spectral range. Third, bridges are mostly illuminated at night. On the negative side, there are transient traffic lights contributing to the brightness. We assume that the contribution from the traffic is relatively constant long-term. In this study, we focus on the San Mateo bay bridge (
Figure 6) which is located between San Francisco and San Jose, California, and the Incheon airport bridge in South Korea.
Figure 6.
Nightlight from the San Mateo Bridge.
Figure 6.
Nightlight from the San Mateo Bridge.
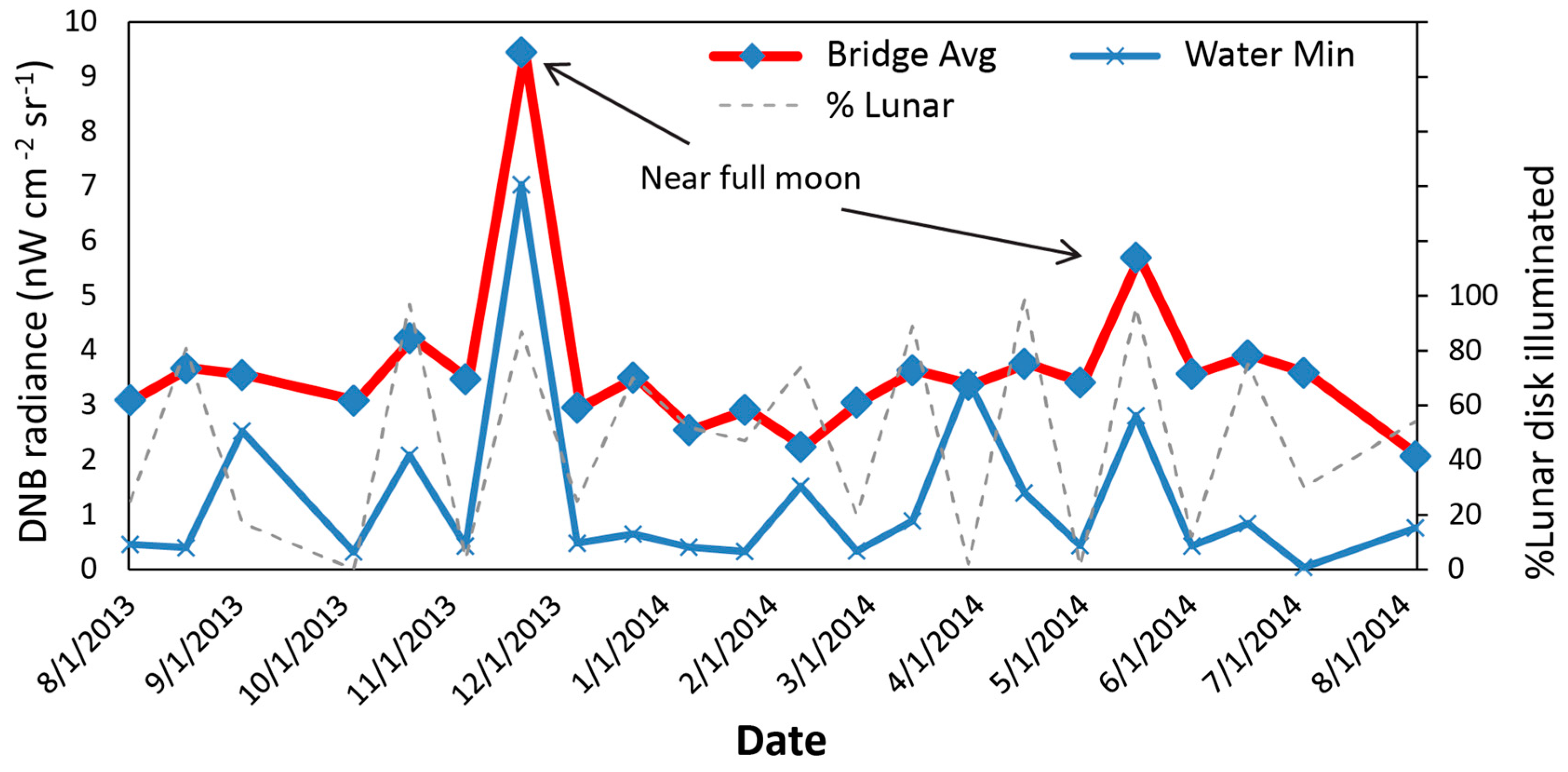
Figure 7 shows one-year pixel-level averaged radiance data over the San Mateo bridge. Several features can be seen in this time series. First, the largest spike in the time series occurred on 21 November 2013. We found that it was due to a combination of lunar illumination near fully moon and cloud cover, which has high reflection of moonlight at the time. The minimum radiance within the region (normally would be over water) is also high due to cloud cover and lunar illumination. A similar spike with a lower magnitude was found on 16 May 2014. This is likely due to a combination of two effects. There was a solar eclipse event on 29 April 2014, which contaminated the solar diffuser calibration data as well as the DNB offset data (the latter was collected during new moon around 29 April 2014). This contamination led to a positive bias in the calibration coefficients and calibrated radiances [
23]. Meanwhile, on 16 May 2014, it was near full moon and the reflected lunar radiance also contributed to the up spike.
Figure 7.
DNB over San Mateo bridge one-year time series with 16 day sampling interval (each data point for the radiance represents an average of 12 pixel taken along the bridge).
Figure 7.
DNB over San Mateo bridge one-year time series with 16 day sampling interval (each data point for the radiance represents an average of 12 pixel taken along the bridge).
Second, other than the moon illuminated cases, the radiance values for nearly all cases are in the range of 2–4 nW∙cm−2∙sr−1. This is lower than expected as discussed later, given the density of the light poles on the bridge. Third, the radiance values have a relatively large variability between the sampled pixels, and over time as well for the same pixel. This is likely due to various factors including traffic lights which are transient. Finally, the last data point in the time series (4 August 2014) appears to have much lower values than those of the previous points. This could be due to either dark clouds or calibration uncertainties because the DNB straylight correction lookup table (LUT) was not updated promptly in the summer of 2014. However, this will require further investigation with a longer time series.
The nominal radiance for the bridge from VIIRS DNB is 3.28 nW∙cm
−2∙sr
−1. To validate this value, we investigated the bridge lights on the San Mateo bridge from several sources. We excluded pixels near the shore on both sides of the bridge so only ~10 km of the bridge with 12 VIIRS DNB pixels are included in the analysis. From the DNB image, it is found that the angle between cross-scan and the bridge is 32 degrees. Therefore, the bridge segment length in each pixel is actually 875 m, and each pixel has 31.9 lamps, which include both sides of the bridge with a deck width of 25.9 meters. According to the California Department of Transportation (DOT), the light poles are 180 feet (or 54.86 meters) apart, and white LEDs have replaced the HPS lamps with equivalent power. Both LED and HPS are known to have an electrical to radiant power conversion efficacy of 30% [
24]. The lamp height is known to be 30 feet or 9.144 m. Given the geometry of the lamp setup, the solid angle of each lamp that the bridge surface intercepts the light is estimated to be 1.43 sr, while the lamp is assumed radiating into a 2 π space. As shown in
Table 2, the estimated DNB radiance would be 3.88 nW∙cm
−2∙sr
−1. This is more than 18% higher than the DNB observations. It also does not include lights contributed from the headlights of the cars and trucks on the bridge at the time (approximately 1:30 a.m., local time). We have verified all parameters used in the calculation and all results are consistently higher than the DNB observed radiances. The uncertainties in the calculations are dominated in the geometric factor and aerosol as discussed later.
Table 2.
San Mateo Bridge Light Radiance Validation.
Table 2.
San Mateo Bridge Light Radiance Validation.
| DNB OBSERVATION |
|---|
| Nominal radiance (pixel level) | 3.28 nW∙cm−2∙sr−1 | Radiance time series |
| Angle between DNB crosstrack and bridge | 32 degrees | Computed from DNB image |
| Bridge segment length within each DNB pixel at nadir | 875 m | Based on 32 degree angle above and 742 m pixel size |
| VALIDATION |
| LED Lamp Electrical Power | 310 W | Per lamp on east flat segment, or 400 W for the western high rise segment; California DOT |
| Radiant efficacy from electrical to optical power | 30% | Y. Zong, NIST |
| White LED % radiant power within DNB spectral range | 66% | Ratio of integration from typical white LED spectra and DNB spectral response |
| Radiant power to hemisphere | 9.77 W/sr | Uncertainties due to lack of specific details on the viewable angles |
| Lamp height | 9.144 m | California DOT |
| Solid angle of illuminated area (per lamp) | 1.43 sr | Computed based on lamp height, deck width, and Google map measurements; uncertainty due to actual area illuminated. |
| Radiant power intercepted by bridge | 13.92 W | Equations (2) |
| Surface Lambertian reflection | 18% | From AVIRIS spectral reflectance; uncertainty due to subpixel mixing at 16 m resolution. |
| Bridge reflected radiance per lamp | 0.798 W sr−1 | Equations (1) and (2) |
| Lamp spacing | 54.86 m | California DOT |
| #Lamps per pixel | 875/54.86 × 2 = 31.9 | |
| Radiance per DNB pixel | 4.62 E−5 W∙m−2∙sr−1 | Equations (1) and (2); Each pixel area 742 × 742 |
| Atmospheric transmittance | 0.84 | MODTRAN plus AERONET; uncertainty due to lack of in situ data |
| Predicted DNB radiance | 3.88 nW∙cm−2∙sr−1 | >13% higher than the nominal radiance from DNB observations |
The lights on the Incheon bridge are brighter (nominal value is 15 nW∙cm−2∙sr−1) for two reasons: (1) The spacing between lights are smaller (~15 m according google images) which leads to a higher density. (2) The lamps may have better efficacy and spectral coverage by the DNB. However, cloud is a major issue for the Incheon bridge and as a result, the one year time series with 16 day repeating cycle has many missing data points especially in the summer month.
Despite the calculated values are not exact, the results are encouraging. First of all, the one-year time series was able to reveal DNB LUT issues as discussed earlier. Secondly, the time series can be further refined with better in situ information about the lights. Third, it shows that a better light source can be specifically designed for DNB calibration use by taking a few simple steps, such as increasing the reflectance of the surface or radiating upward directly, fully capturing the lights from the source to avoid light loss, and using light bulbs with better radiant efficacy and spectral range. Therefore, with a light source specifically designed for DNB calibration monitoring such as using red LEDs, the light power needed to illuminate the DNB pixel at the 3 nW∙cm−2∙sr−1 level can be significantly reduced.
In contrast to the crab fishing vessel and bridge studies, the light intensity of Geneva city is much higher as expected. The main disadvantage in analyzing city lights is that the abundant light sources can cause significant cross pixel contamination in the samples. In other words, point source analysis using city lights is very difficult. Here we analyze the pixels with the maximum light intensity within the city to see if they are stable with the assumption that the maximum values are less contaminated by nearby pixels.
Table 3 shows the pixels with the maximum light intensity from selected sample dates.
Table 3.
The brightest pixels in Geneva city.
Table 3.
The brightest pixels in Geneva city.
| Dataset | Lat/Lon of the pixel | Radiance |
|---|
| 20140606_t0144510 | 46.222590/6.134870 | 383.677 nW∙cm−2∙sr−1 |
| 20140521_t0140214 | 46.222599/6.142890 | 279.319 nW∙cm−2∙sr−1 |
| 20140419_t0142441 | 46.223026/6.135354 | 504.672 nW∙cm−2∙sr−1 |
| 20140318_t0139254 | 46.2194791/6.140902 | 299.144 nW∙cm−2∙sr−1 |
| 20140313_t0135527 | 46.221821/6.137994 | 189.686 nW∙cm−2∙sr−1 |
Several phenomena are observed from the brightest light pixels in the Geneva city. First, the brightest pixels are mostly located in the Paquis Nation area along the Ave. De France, which is not too far from the World Meteorological Organization, as well as the IPCC (International Panel for Climate Change). Second, the brightest spots have typical values of greater than 180 nW∙cm
−2∙sr
−1. However, the brightest pixels are not always found in the same pixel location. For example, the 5 May 2014 dataset had the brightest point on the north side near the train station, while 16 days later, the brightest spot was found further south, and with a much different radiance value. The changing location of the brightest pixels can be due to several possibilities such as small geo-location differences in the pixel location between observations, but in any case the lights are not stable and may not be suitable for stability analysis intended for this study. This also suggests that the DNB spatial resolution is a limiting factor for urban light analysis. The DNB resolution can potentially be enhanced since inherently the DNB has higher spatial resolution at subpixel level before the aggregation [
10].
The alternative to city nightlight point source analysis is apparently using averaged city lights over a large geographic region such as the entire city. This type of analysis has been done in previous studies, which showed potentials [
25]. However, the issue with averaged light power for a region is that the absolute power calculated would be very difficult to validate. Additionally, as more efficient light bulbs are replacing the traditional types, this may introduce more uncertainties for regional analysis due to the mixing of light bulb types. This is also part of the reason that this study focuses on point source analysis.
4.3. Uncertainty Reduction
Based on the analysis in previous sections, it is clear that the nightlight point sources can potentially be good targets for the validation of DNB calibration stability and absolute accuracy at low radiances. The primary uncertainty in estimating the light power of point sources from the VIIRS DNB, and estimating the stability of the nightlights is the lack of sufficient ground truth. In the case of the fishing vessel, neither the deck surface reflectance nor the light bulb type is known which contributes to uncertainties in the calculations. Similar issues exist for the bridges, where the geometric factors require specific details such as lamp view angle and illuminated area on the bridge. In general, calculating radiometric quantities based on electrical power may not be reliable. In situ radiance measurement is essential in reducing the uncertainties. In addition, the effect of transient traffic lights is not included, and aerosols were not measured onsite.
Currently, it is difficult to separate the stability of the light source from the stability of the VIIRS DNB calibration. Atmospheric effects are simulated only partially (transmittance only), since currently models cannot incorporate artificial light source. The effect of scattering loss from aerosols, which has not been accounted for in this study, can be significant for nightlight point sources and may partially explain the low biases in the DNB observations. Finally, there are many other potential factors that could affect the uncertainties in the calculations, including but not limited to, residual straylight effects in the correction of DNB, air glow, and others.
These uncertainties raise the question about the accuracy that existing active light sources will allow us to achieve. It also points to the need for more accurate low light sources specifically designed for such purposes. This study shows that given the high sensitivity of the VIIRS DNB, it is quite feasible to design and install light sources which are well controlled and the accuracy well quantified. Our study shows that the light power required does not have to be high, depending on the type of light bulbs used. Good candidates include the latest power LEDs, which are known to be stable with low electrical power requirements. Red LEDs would be preferred over white LEDs for DNB due to its spectral range and better efficacy. Tungsten lamps have high electrical to radiant power efficacy and can also be an alternative.
Therefore, this study also serves as an initial assessment of the need and feasibility for developing an accurate active light source for VIIRS DNB calibration. Such a system would not only improve the low light calibration accuracy, but also the point spread function, as well as geolocation accuracy at night. This will potentially significantly improve the calibration accuracy and stability of the VIIRS DNB, which in turn will allow us to estimate environmental changes such as atmospheric variability as in aerosol retrievals at night, and potentially enable many other applications. In situ knowledge of the lamps and radiance measurements are essential to reduce uncertainties.