1. Introduction
Accurate forest information is required by a broad range of stakeholders to meet myriad information needs [
1]. For instance, government institutions require forest inventory information to meet reporting and planning responsibilities [
2]. Industrial forestry agencies require forest inventory data to make long term projection of volume, as well as to plan harvesting and field operations. Additionally, the roles of forests in regulating air quality, water flow, and climate regulation is well recognized [
3]. Therefore accurate information on forest composition and structure is necessary.
National Forest Inventories (NFI) have been established by most countries to monitor and report on forest resources for national and international purposes [
1]. In Canada the NFI is a key program of the Canadian Forest Service (CFS) dedicated to the production of information related to the structure and condition of Canada’s forests [
4]. Canada’s forest area occupies approximately 400 million ha [
5], representing an estimated 27.3 billion tonnes of biomass [
6]. This area includes 196.3 million ha of boreal forest [
6] for which limited coverage with aerial photography is available mainly due to financial and logistical constraints [
7]. Forests in the northern reaches of the boreal have low productivity and are accompanied by low densities of human population, and as a result, there is a lack of an operational imperative for air photo data collection and forest inventory development.
In Canada, forest stewardship responsibilities are primarily held by provinces and territories. Each jurisdiction has an inventory program to support planning and management activities. Federally, via a sample-based NFI, there is a process to standardize measures and definitions across jurisdictions and to support collection of additional data to ensure appropriate sample coverage and to support national and international reporting obligations [
2,
4]. The sample based inventory is a systematic survey of 2 × 2 km photo plots on a 20 km national grid. This configuration results in a 1% sample of Canada’s land mass. A subset of ground plots is also collected in support of quality control and calibration of photo plots as required. Photo plots are akin to subsets of polygon-based forest inventory data [
4]. In the southern portion of the country, where forests are more actively managed, photo plot information is typically acquired from manual interpretation of air photos. In the north, satellite data has been used to supply photo plot information, either from classified satellite imagery (a Landsat based land cover product [
8]) or, more recently, from Very High Spatial Resolution (VHSR, <1-m spatial resolution) WorldView or QuickBird imagery [
9]. National transects of Light Detection and Ranging (LiDAR) data have also been collected to provide field plot-like information over remote areas to enable model calibration and validation [
10]. Such data sources are intended to address the lack of inventory data in northern Canada and supplant the forest attribute estimates derived from look-up tables (LUT) developed as part of the Earth Observation for Sustainable Development of forests (EOSD) project [
8]. Furthermore these data sources are intended to enable greater consistency between the inventories of Canada’s northern and southern forests.
Characterization of a wide range of forest information such as stand type, crown closure, height, volume, and biomass with the use of optical satellite imagery has been proven feasible operationally for NFIs such as in northern Canada [
8,
11], Finland [
12] and Sweden [
13]. Airborne LiDAR also has a demonstrated ability to provide metrics from which accurate stand attribute estimates can be derived for large areas [
14,
15]. More specifically, LiDAR data has been used in sample-based protocols allowing the estimation of forest attributes outside the area covered by the LiDAR swath. Empirical and semi-empirical relationships were established between LiDAR metrics and other remote sensing-derived metrics from optical satellite imagery that enable a larger spatial coverage of the ground [
16,
17].
Falkowski
et al. [
9] proposed a series of recommendations, indicating the necessity to automate image processing techniques whenever possible, with manual interpretation of some difficult-to-capture parameters being considered when automation is not possible, inconsistent, or unreliable. Based on the framework proposed by Falkowski
et al. [
9], additional methodological developments have been undertaken towards automated attribute estimation requirements. For instance, Mora
et al. [
18] implemented a stand height estimation approach based upon an initial stand delineation procedure followed by calibration with photo-interpreted heights. This procedure used a segmentation method to create forest stands from VHSR imagery. Individual tree crown (ITC) isolation [
19] was then implemented to generate individual tree objects. To enable stand level attribution, the distributions of crown objects within segments were related to stand level measurements. Using the distribution of crown objects in the approach is intended to make the routine more robust to outliers and capitalize upon image spatial information. Algorithm development with a preference towards spatial information is aimed to reduce the reliance on spectral information (that can be influenced by the sensor used, calibration approach, acquisition date, and sun-surface-sensor geometry, as examples).
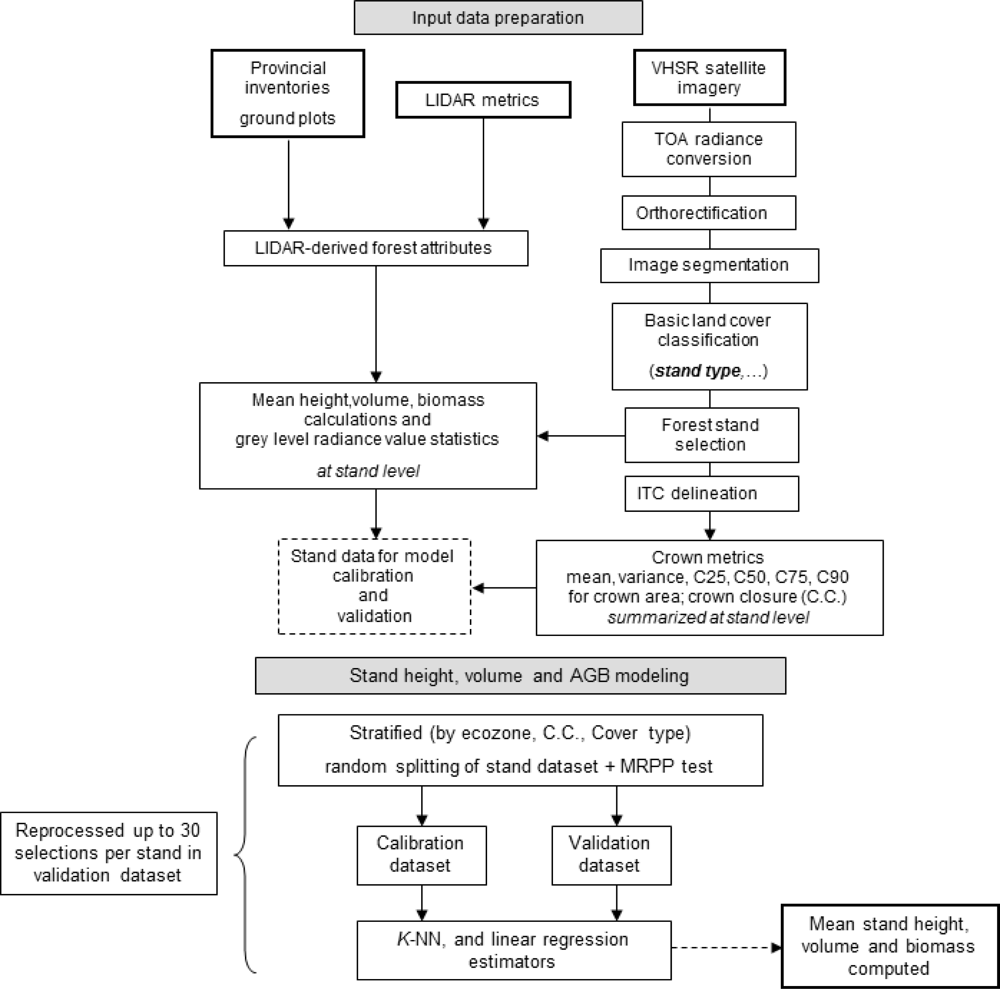
In this research we have focused on further development and extension of the Mora
et al. [
18] protocol to be calibrated and validated using airborne LiDAR-based stand heights in place of photo-interpreted heights. The relationship between LiDAR measures and stand structure is illustrated well in Frazer
et al. [
20]. Further, in this study we have aimed to expand the set of stand attributes predicted to make estimates of height, volume, and biomass. To meet these goals, we have developed a logic and processing chain that enables the extrapolation of structural characteristics from plot-calibrated LiDAR measures to statistical descriptions of segment constrained individual tree crowns. First, we build models relating LiDAR-derived metrics to the field measurements; we then apply the models to predict inventory attributes for all areas covered by the LiDAR acquisition, and then we build models relating image-derived metrics (including ITC metrics) to the LiDAR predictions. Finally, we apply the models to predict inventory attributes (including height, biomass, and volume) over the entire forested area of the imagery.
In this communication we demonstrate the logic and required processing chain designed to predict boreal forest stand height, volume, and biomass. A key innovation is the use of transects of LiDAR data to calibrate and independently validate the predicted forest structural outcomes. The use of LiDAR data in this manner allows for a larger sample size than is typically possible in the northern regions of Canada, as well as the independent validation of predicted stand level structural estimates. The accuracy of the model estimates are assessed by a comparison with independent stand height, volume, and biomass estimates derived from LiDAR-based models. Although the process described is in support of Canada’s sample-based NFI VHSR framework, the challenges identified are informative for stand-based forest inventories in general, especially areas not subject to systematic and regular inventory.
4. Discussion
In this study
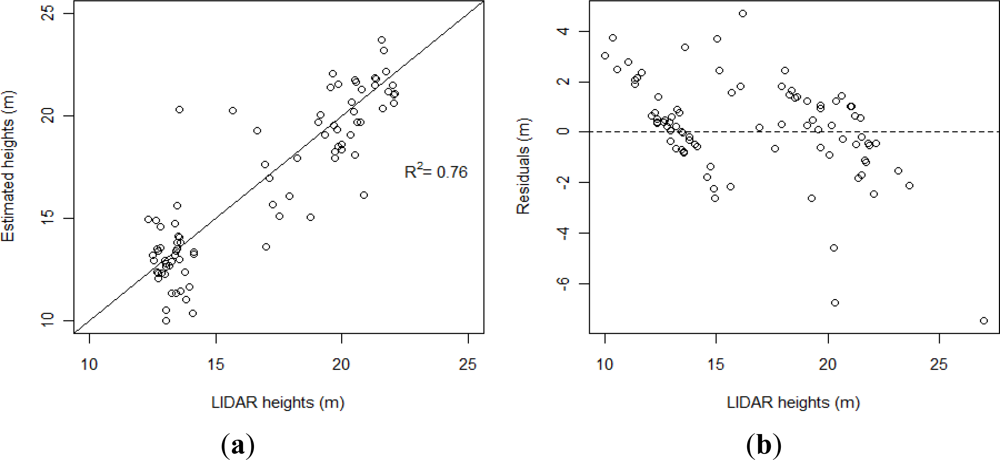
k-NN methods provided better results compared to the linear regression method for stand height estimation. Furthermore the influence of the distance calculation method on the results (
R2 and RMSE) was not found to be statistically significant (
t-test) (
Table 5). However the
k-NN method with the Mahalanobis distance provided the best results (
R2 = 0.76 and RMSE = 1.95 m (RMSE-% = 11.6). The performance of our best model compares favorably with the results of other studies modeling stand height with VHSR and discrete return LiDAR data. Chen
et al. [
17] built regression models based on spectral, texture, and shadow fraction metrics derived from multispectral QuickBird and LiDAR data in Quebec, Canada. Their best model provided a
R2 of 0.72 and a RMSE of 3.3 m (RMSE-% = 21). Peuhkurinen
et al. [
49] estimated mean stand height using stand-level spectral metrics derived from IKONOS imagery and k-most similar neighbors (K-MSN) approach, with an RMSE of 3.1 m. Wulder and Seemann [
16] estimated mean stand height using segmented Landsat-5 TM and LiDAR data with a
R2 of 0.67 and a RMSE of 3.3 m. Using regression, Maselli
et al. [
50] extended a sample of LiDAR-derived mean stand height estimates over 798 ha area using Landsat ETM+ data, resulting in an RMSE of 3.01 m.
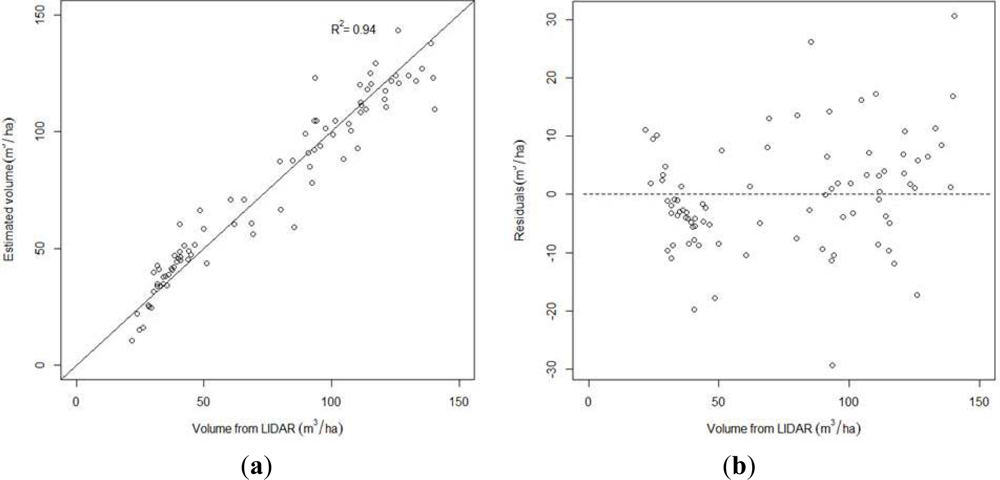
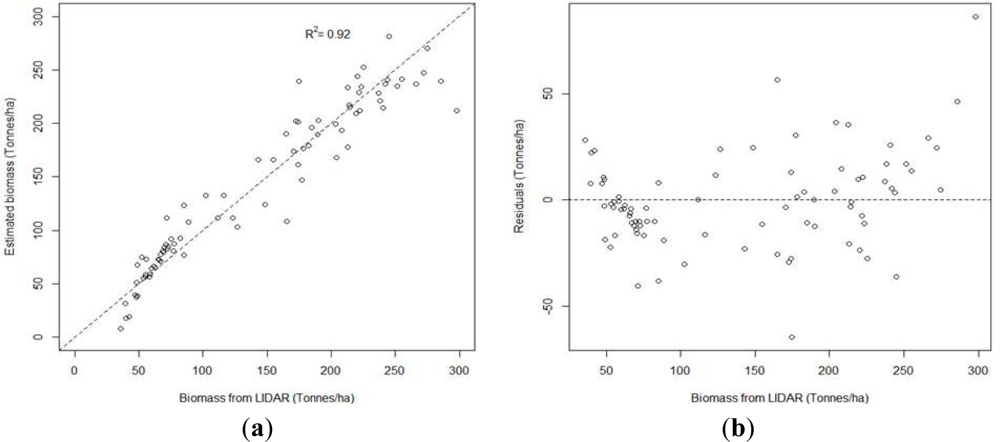
The best volume and AGB models compare well with models previously established in similar forest environments. Chen
et al. [
17] obtained a
R2 of 0.72 and a RMSE of 52.59 m
3/ha for the volume model and a
R2 of 0.72 and a RMSE of 39.5 tonnes/ha for the biomass. Hall
et al. [
11] proposed a method (BioSTRUCT: Biomass estimation from stand STRUCTure) to estimate a series of stand metrics for the EOSD initiative that represent the only consistent source of forest information in the north of Canada. Applied in Alberta, Canada, the regression models were built based on the same stand metrics used in our study (height, crown closure) but were derived from Landsat ETM+ and field plot data. In this study from Hall
et al. [
11], an adjusted
R2 of 0.71 was obtained with a RMSE of 74.7 m
3/ha for volume. For AGB an adjusted
R2 of 0.70 and a RMSE of 33.7 tonnes/ha were obtained. A similar approach for AGB estimation considering equivalent input metrics derived from LiDAR data has also been used by Næsset and Gobakken [
51] with canopy density (a measure of the proportion of laser echoes >2 m to the total number of echoes) replacing crown closure (
R2 = 0.88 and RMSE = 21%).
Errors in stand height, volume, and biomass estimates may be attributed to a number of factors. First, satisfactory model performances were reported by [
10] for the field-plot inventory attribute models (dominant height, gross stem volume and AGB) with
R2 values ranging from 0.76 to 0.84 and RMSE-% values ranging from 9 to 25. However, a greater number of field plots could have improved representation of the diverse forest conditions found throughout the Canadian boreal forests that were surveyed, and may have lead to improved model accuracies. Stand-level attribute models would have subsequently benefited from more accurate plot-level estimates. Second, as a result of the limited number of VHSR images collected in the study area, it was not possible to obtain images with equivalent acquisition conditions (off-nadir view angle notably). This causes variability in the results of the crown delineation procedure and in the stand-level grey-level statistics for the pool of images used to build a given model. Third, the relationship between crown diameter, DBH, and the estimated stand attributes [
52,
53] can be subject to alteration by a series of factors such as age and wind conditions. As a consequence, increased variability of the stand-level crown metrics used as model input can be expected. Due to a long distance to markets and relatively small trees, the study area has only limited harvesting activity with a stand structure that is largely the result of historic wildfire conditions. In addition, future applications should aim at considering satellite image acquisition angular conditions, rather than solely regional conditions (
i.e., ecozone-specific in this study case), for constraining algorithm development.
To mitigate these sources of error, we recommend the purchase of images with equivalent or as near-equivalent acquisition conditions, as possible. In addition, we recommend the use of a sufficient number of images per ecozone (≥3 from our experience) that intersect with the LiDAR transects to obtain sufficient stands for building statistically robust models, while ensuring representativeness of forest conditions. A similar reasoning should be applied to the location of the field plots used to calibrate the LiDAR data. Moreover, if stand type information is already available for the area of interest, one should check stand age, potential disturbances, and ensure a sufficient number of deciduous stands will be depicted by the VHSR and LiDAR data. This requirement may be difficult to fulfill for every ecozone in northern regions where the presence of deciduous trees may be rare. In addition, it is important to provide stand height, volume, and biomass values derived from an iterative process that aggregates multiple estimates to mitigate bias that could result from a single or a low number of random stand selections when calibration and validation datasets are generated.
Currently, when aiming to purchase VHSR imagery for national monitoring purposes we stipulate that the cloud cover tolerance over the actual 2 km × 2 km NFI photo plots is zero. Vendors are supplied with our national photo plot locations to interrogate the imagery for cloud-free status. We also limit the off nadir view angles to a maximum of 15 degrees. The view angle limitations are not specified based upon the particular look direction (that is, side to side versus fore/aft pointing). Combining these basic constraints serves to limit the number of scenes that can be obtained in a given year. While further specifying the desirable criteria for imagery suitable for inclusion in our processing chain, we are also mindful that tightening of the criteria will result in increased difficulty in obtaining imagery and our capacity to implement a sample based protocol. At present the yield of VHSR imagery on an annual basis is limited, and found to be below the number of images required to maintain our inventory reporting cycle.
In building towards this research, the capacity of VHSR imagery to capture forest inventory information was undertaken [
54]. We found that VHSR could be automatically segmented to produce spatial units akin to forest stand polygons and that an interpreter could label the stands in a manner similar to traditional photography [
18]. Following a review of the potential for automation of forest inventory practices using VHSR [
9], experimentation demonstrated the utility of within-stand crown objects for characterizing forest structural attributes [
18]. From this base research, a number of the components required of a framework for using VHSR imagery to provide otherwise unavailable information in support of the NFI were developed and aspects tested in this research. The current focus was upon stand height, volume, and biomass—a subset of attributes required for forest inventory and reporting.
Readers may note that the results achieved in this study using VHSR are similar to results achieved in other studies using Landsat (that is, RMSE ∼ 3 m, e.g., [
16,
50]). The question that then arises is therefore to what benefit is the cost and effort requirements of the VHSR approach presented herein, when the results are similar to results obtained using Landsat data? Moreover, a Landsat implementation to generate stand height would likely be simpler, more cost effective, and cover a larger area (with an image footprint of 185 km × 185 km rather than the approximate 10 km × 10 km of a typical VHSR image). Firstly, inventories require more than height (or volume and biomass for that matter), so the ability to interpret additional detailed information from VHSR imagery is an asset. While stand height, volume, and biomass do not constitute the entirety of an inventory, each is amongst the more important of the suite of attributes that are generated. Stand height information is important for management purposes and is indicative of site conditions, while volume is key to industrial forest management and biomass is a critical attribute for informing on forest function and carbon-related considerations. If an intimation of future recommendations can be suggested, it is that VHSR imagery (and related automated processing approaches) may remain focused on locations where jurisdiction-driven inventory programs persist, with the photo analogous data provided by the VHSR offering compatibility and similarity in the types of information generated. For areas that are not subject to regular management or monitoring activities, it is possible that the more limited suite of attributes that can be estimated from Landsat data will prove sufficient for many monitoring and reporting needs. Thus, a stratification of activity may be possible based upon the monitoring requirements associated with a given area. The ability to characterize large areas with Landsat data for a number of important forest inventory attributes may prove sufficient, although additional applications research and contextual consideration is required.
This work also encourages the further implementation of the protocol to other areas of Canada’s boreal forest. The research is aimed to determine if such an implementation for the north of Canada may offer an improved monitoring and reporting capacity. We propose that the approach demonstrated be considered to support other large-area jurisdictional or national level activities where similar characteristics are present. Further, large-area, wall-to-wall characterization with a high level of attribute detail are difficult to obtain, with sampling offering a practical, robust, and reliable alternative. Future global forest inventory programs may benefit from consideration of the framework and methods presented herein. We also note that depending on location and attributes required, wall-to-wall mapping with medium spatial resolution data (
i.e., Landsat), calibrated and validated with samples of LiDAR [
10], may provide analogous opportunities for systematic and repeatable monitoring and reporting activities.