Global Characterization of CO2 Column Retrievals from Shortwave-Infrared Satellite Observations of the Orbiting Carbon Observatory-2 Mission
Abstract
:1. Introduction
2. OCO Full Physics Retrieval Algorithm
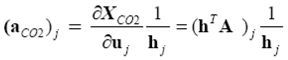
3. Simulation of OCO-2 Soundings
| Parameter | Range |
|---|---|
| Total tropospheric aerosol optical depth | 0., 0.01, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3 |
| Solar zenith angle (°) Nadir Mode Glint Mode | 10, 20, 30, 40, 50, 60, 65, 70, 75, 80, 85 10, 20, 30, 40, 50, 60, 65, 70, 75 |
| Surface type | Ocean, vegetation, desert, snow/ice (only nadir), savannah |
| Surface pressure (hPa) | 1,000, 900, 800, 700 |
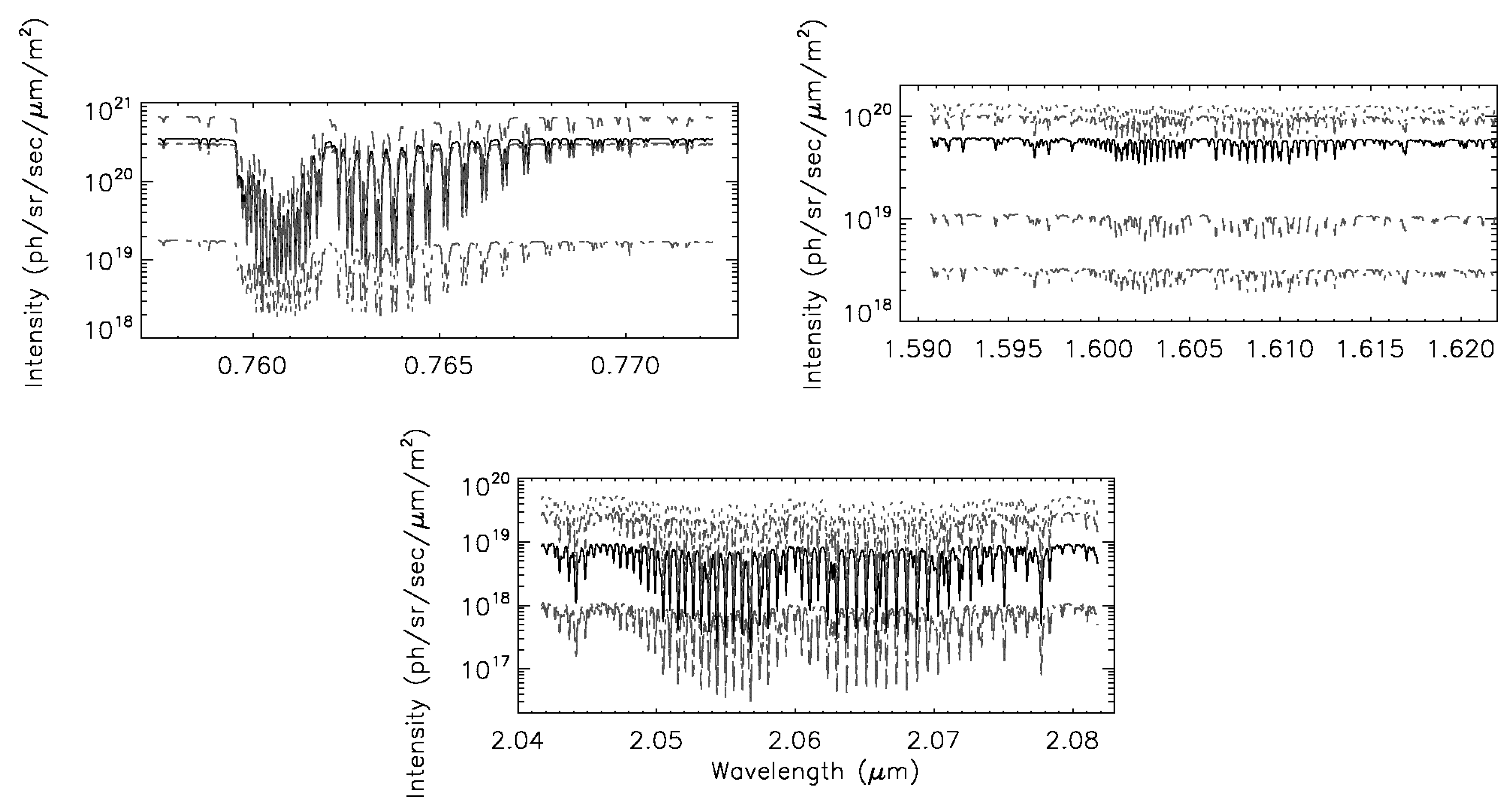
| Surface Type | O2 A-Band | 1.61 µm CO2 Band | 2.06 μm CO2 Band |
|---|---|---|---|
| Ocean | 166 | 81 | 32 |
| Vegetation | 814 | 440 | 166 |
| Desert | 750 | 652 | 448 |
| Snow/ice | 1,120 | 174 | 28 |
| Savannah | 758 | 570 | 328 |
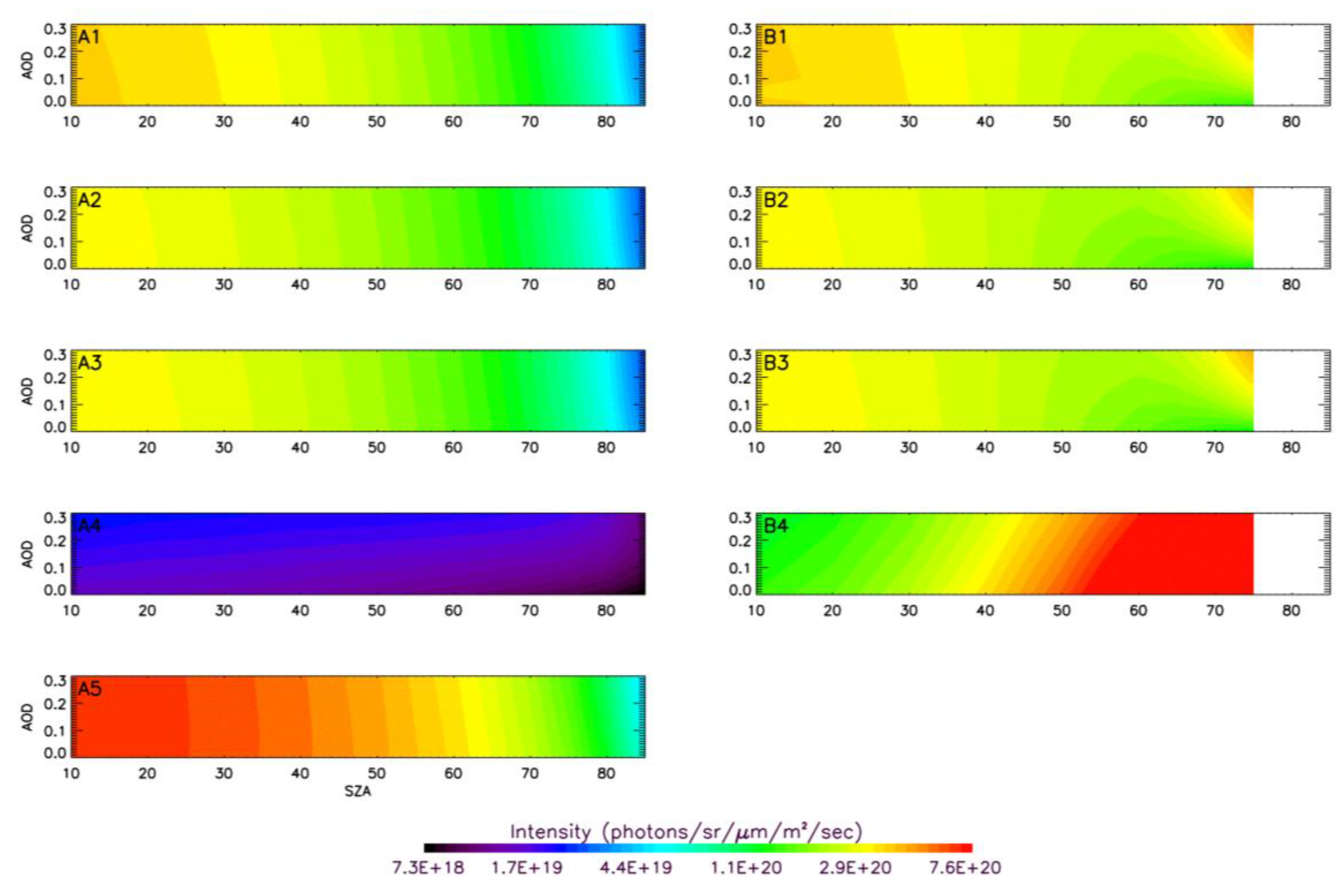
4. Characterization of Single-Sounding Errors and Averaging Kernels
4.1. XCO2 Retrieval Errors and Averaging Kernels as a Function of Key Parameters
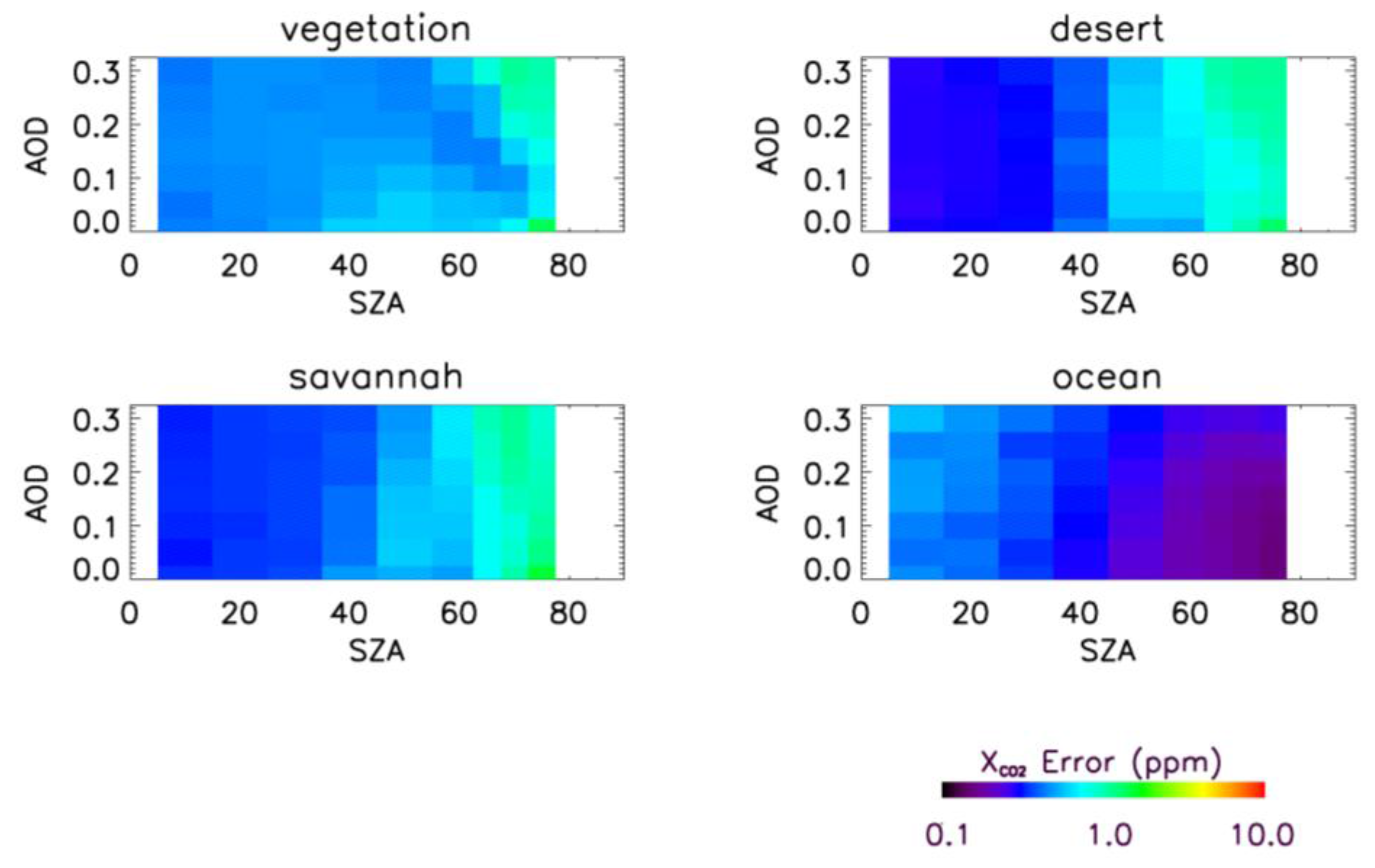
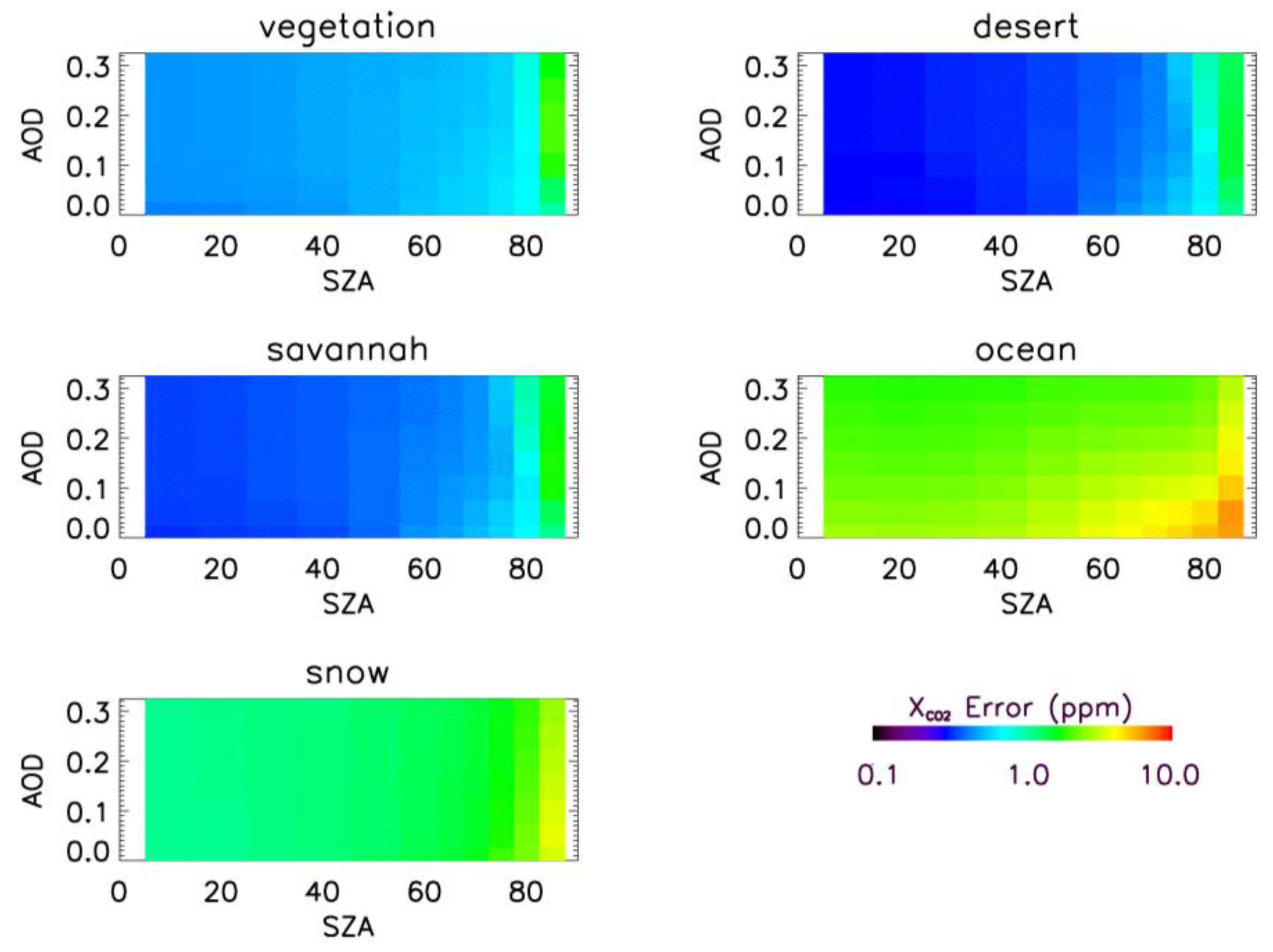
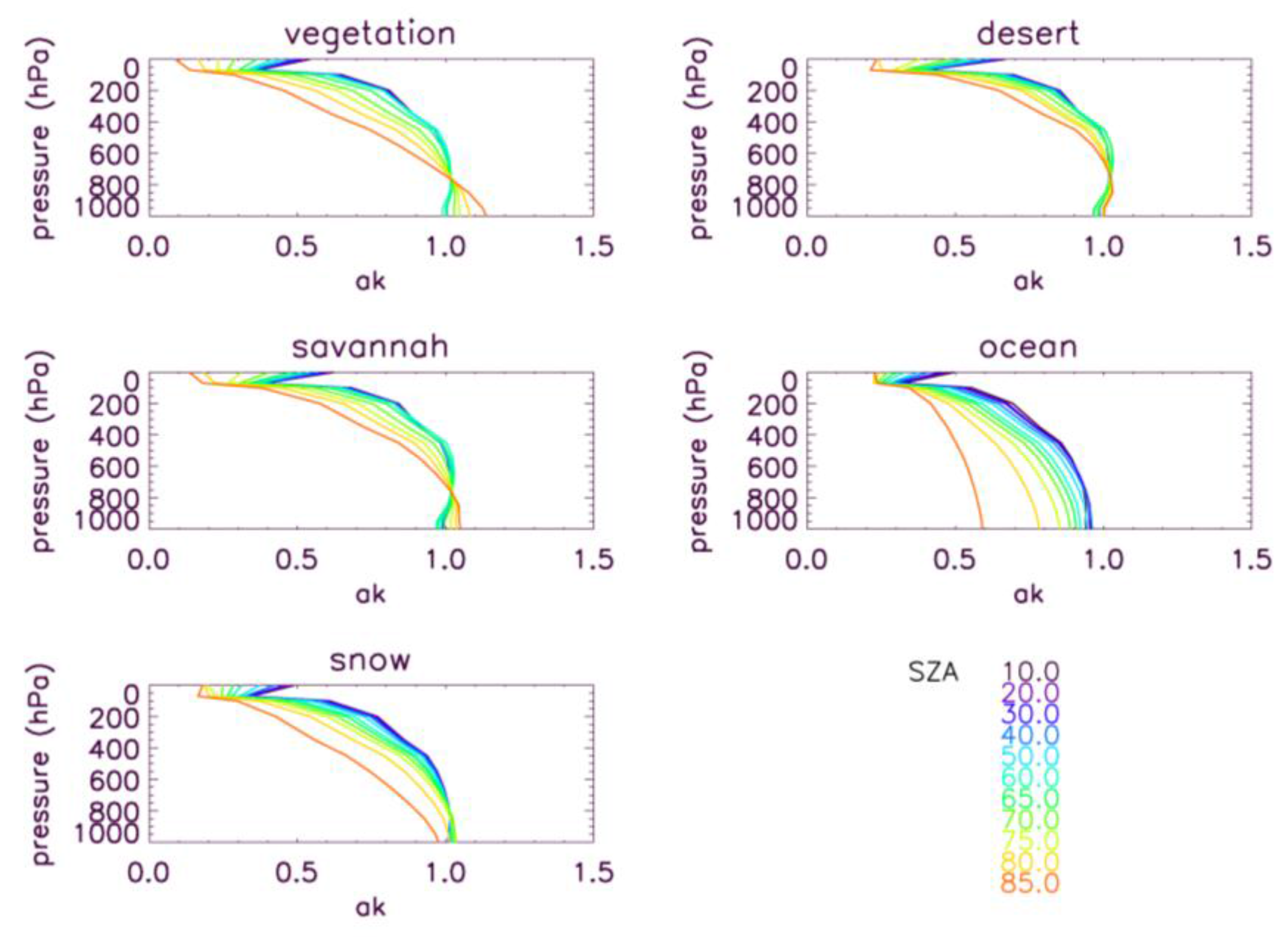
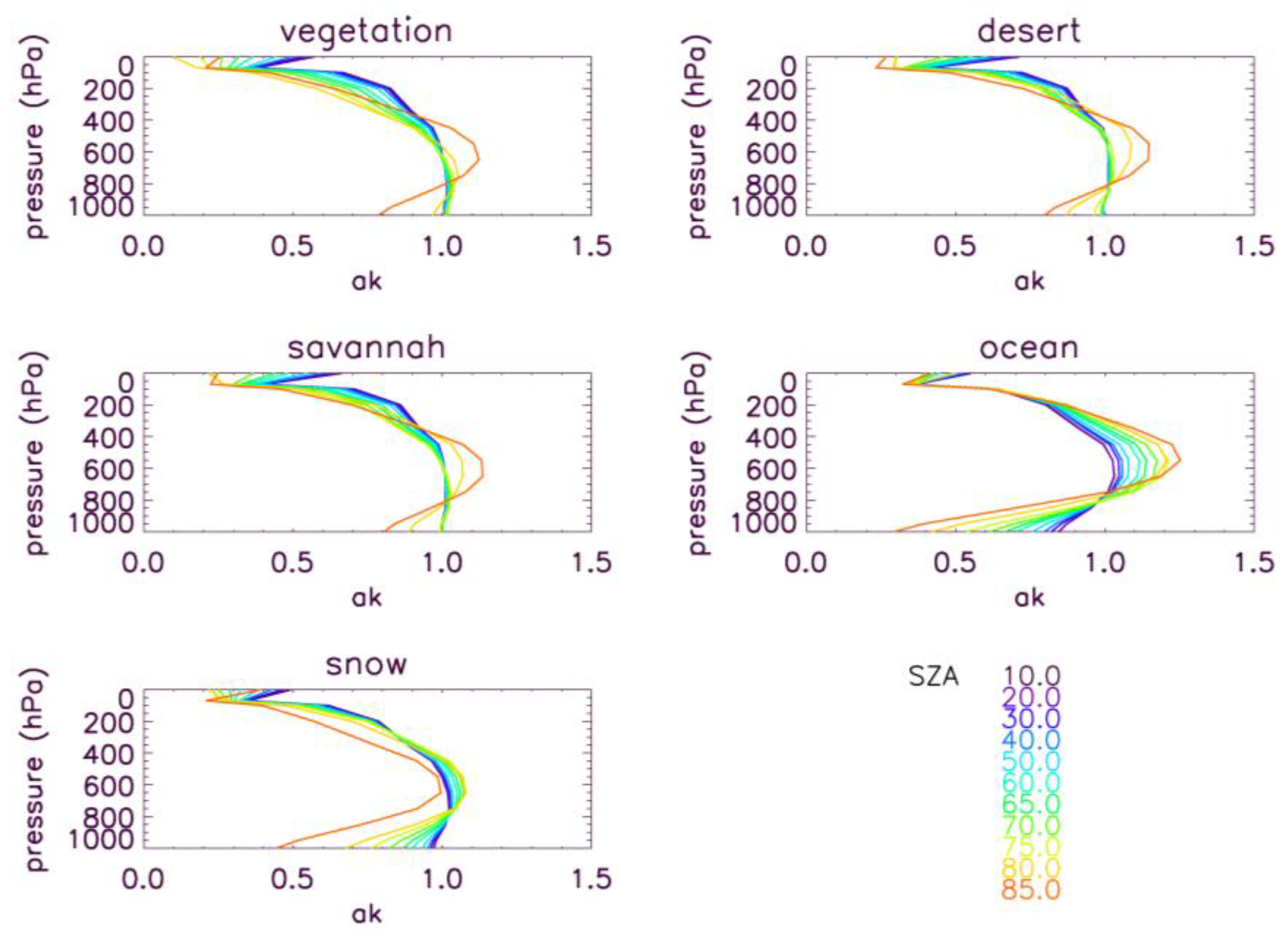
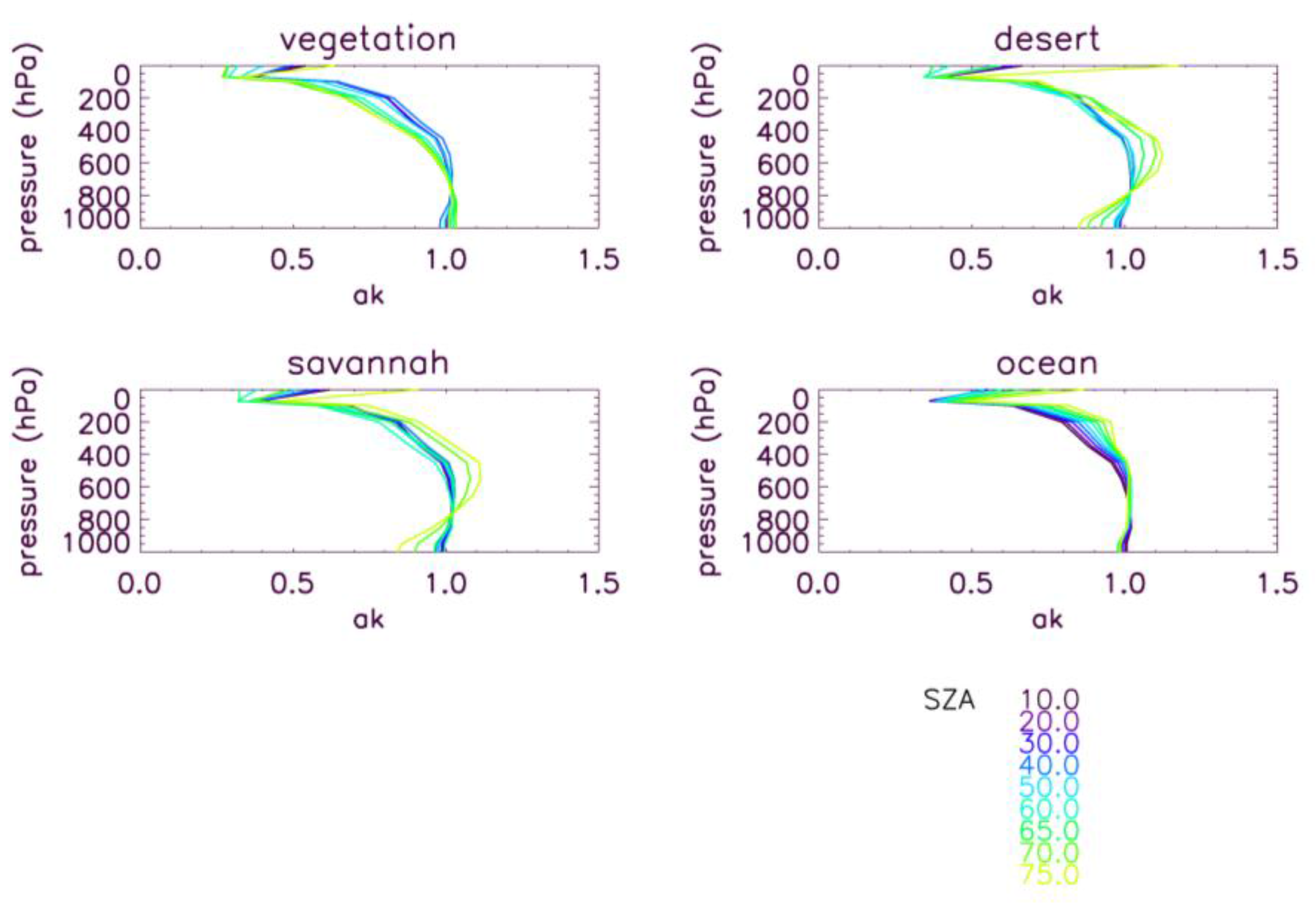
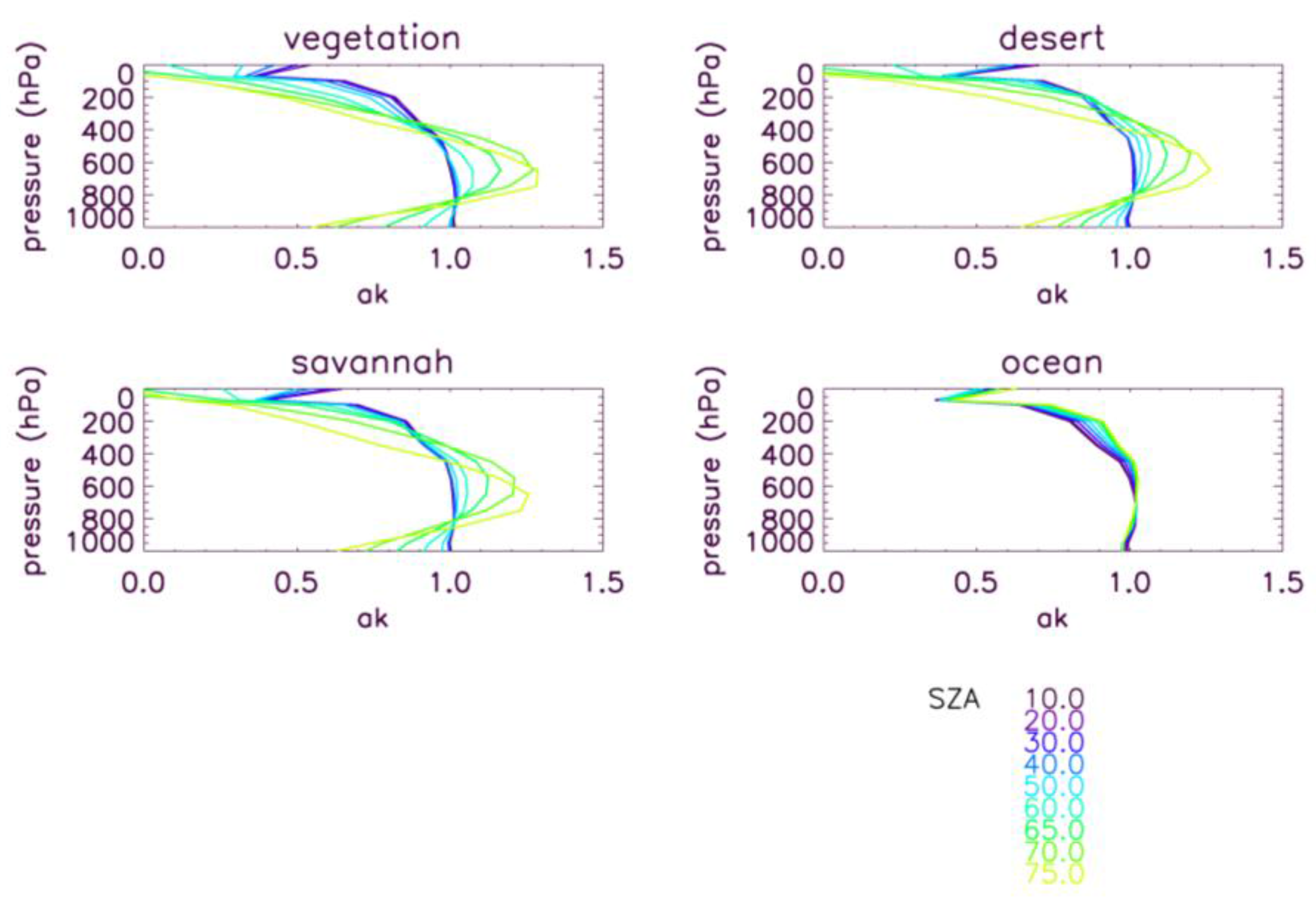

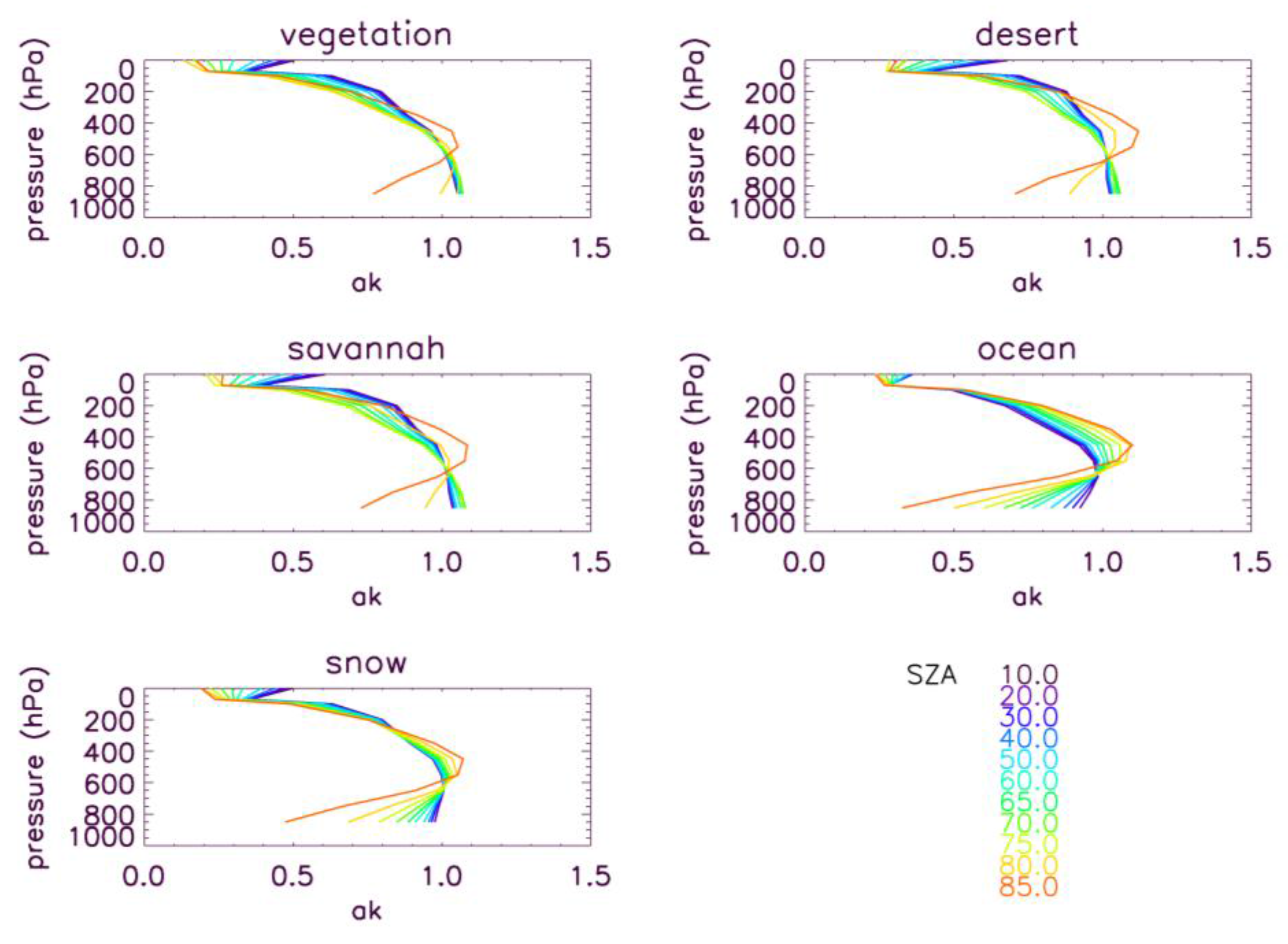
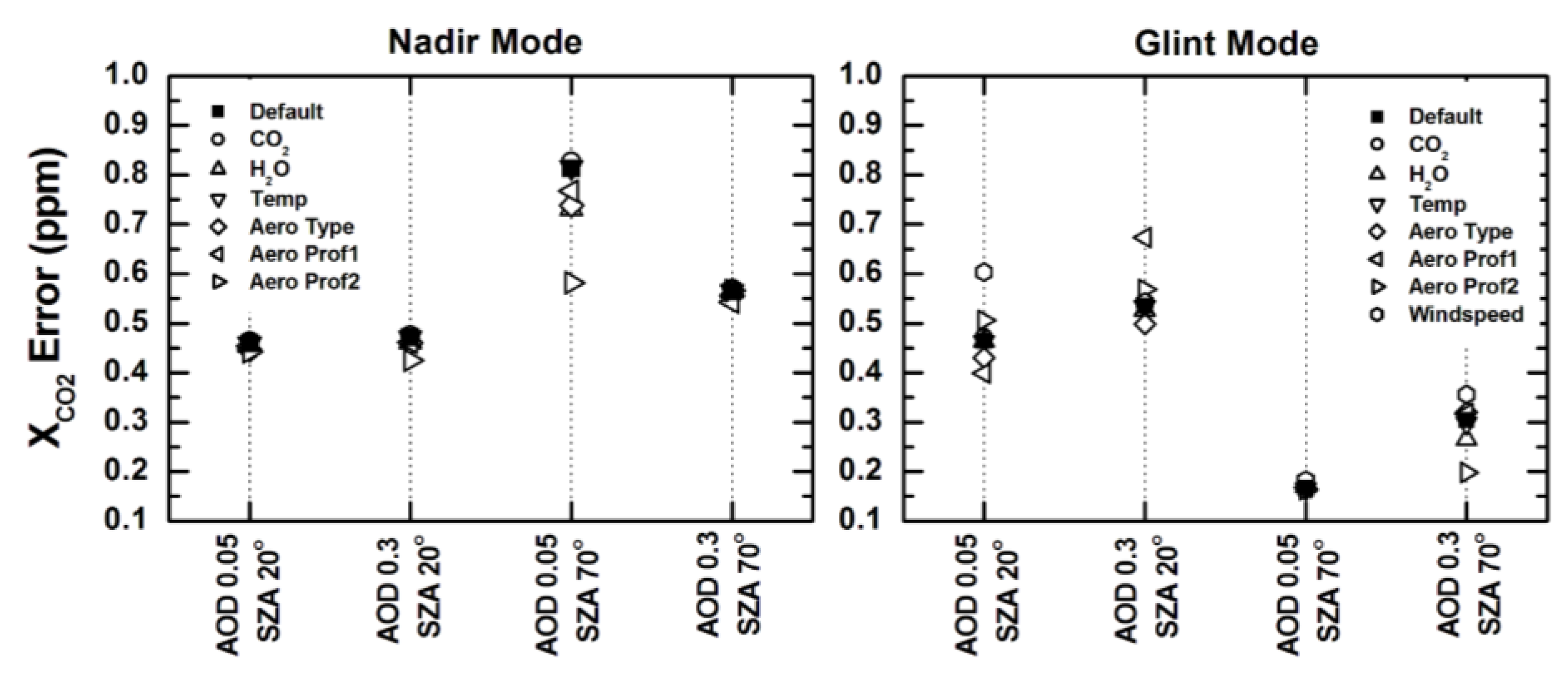
4.2. Sensitivity to Other Parameters
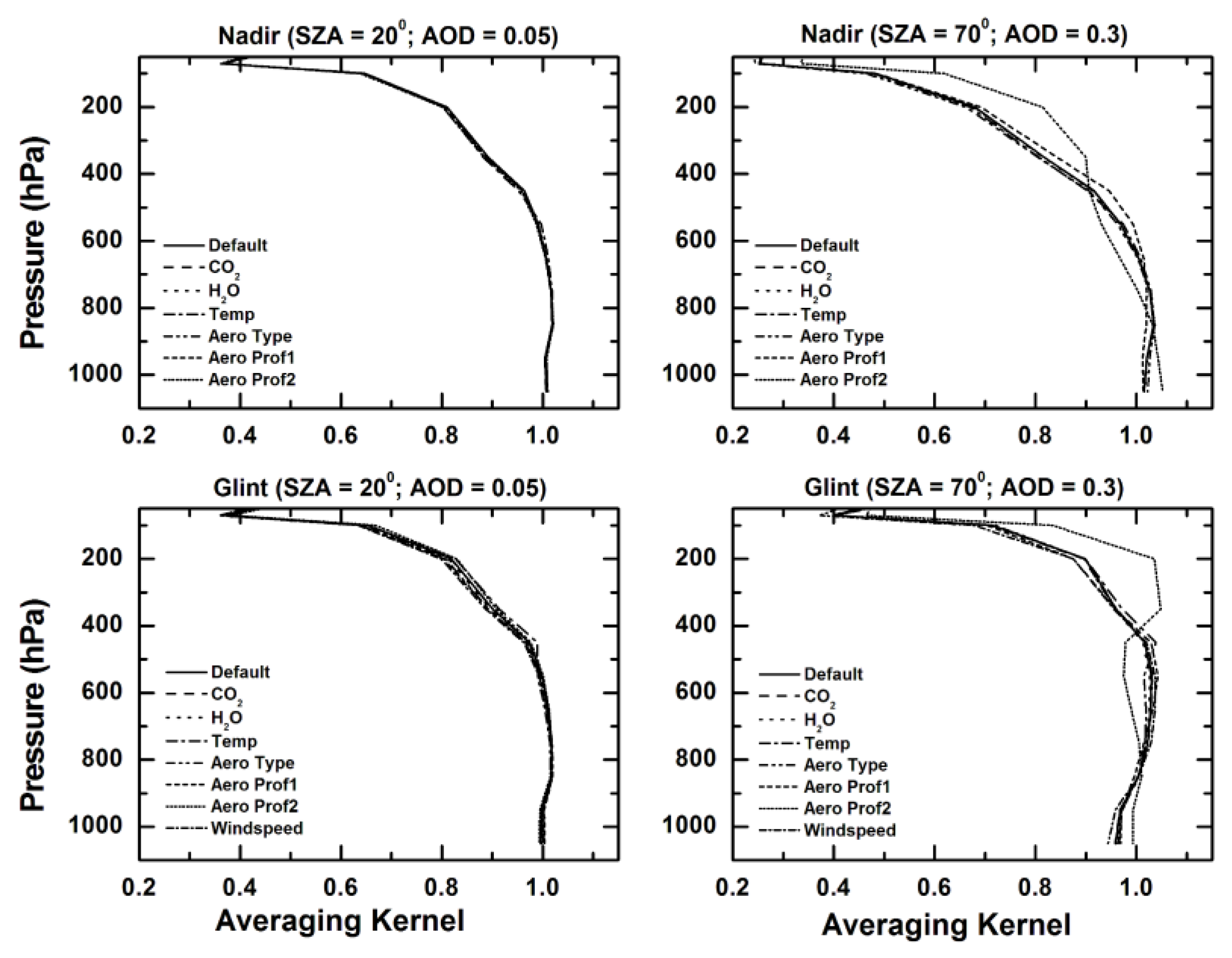
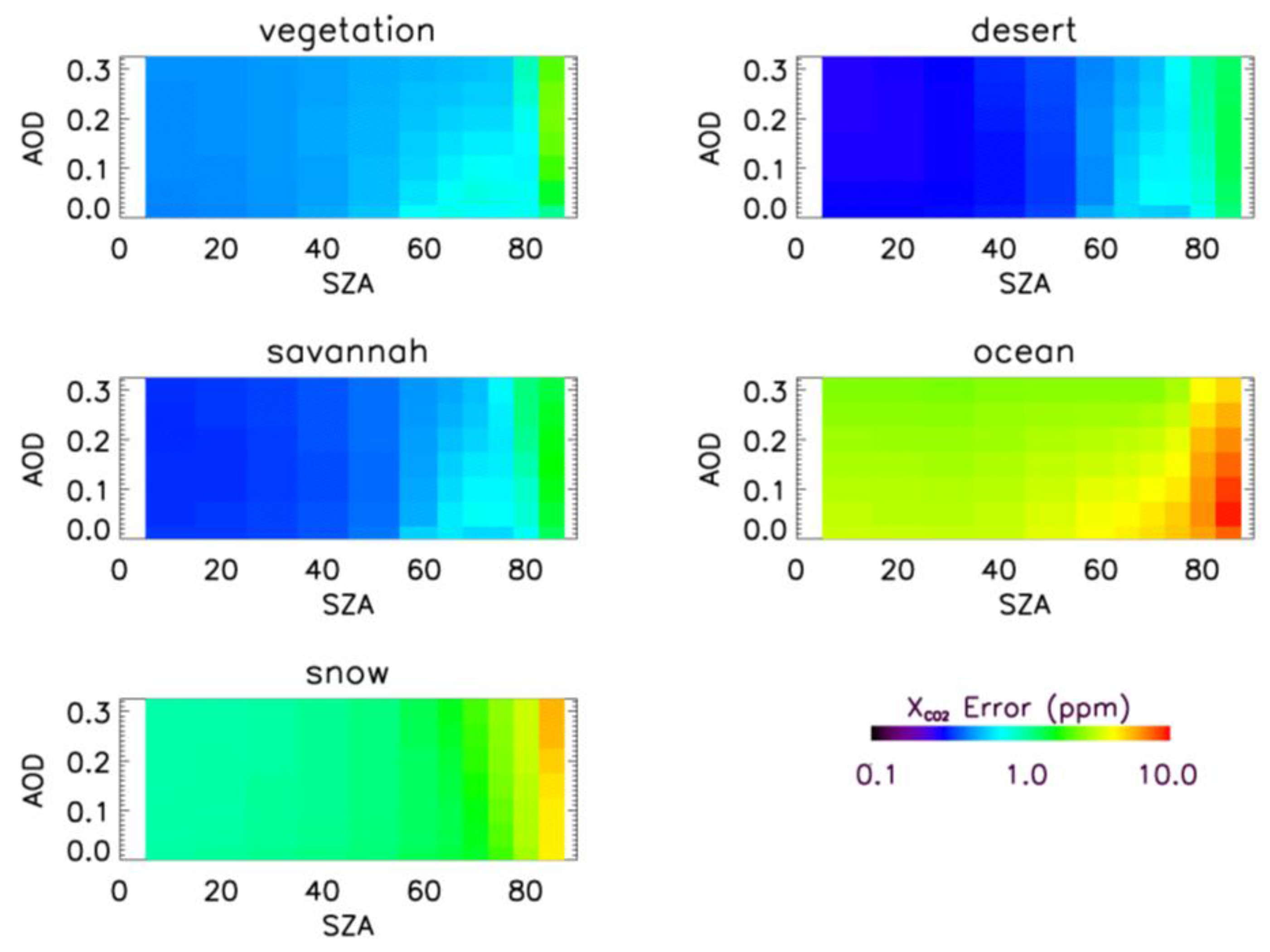
5. Global Distribution of XCO2 Errors
5.1. Aerosol and Surface Climatology
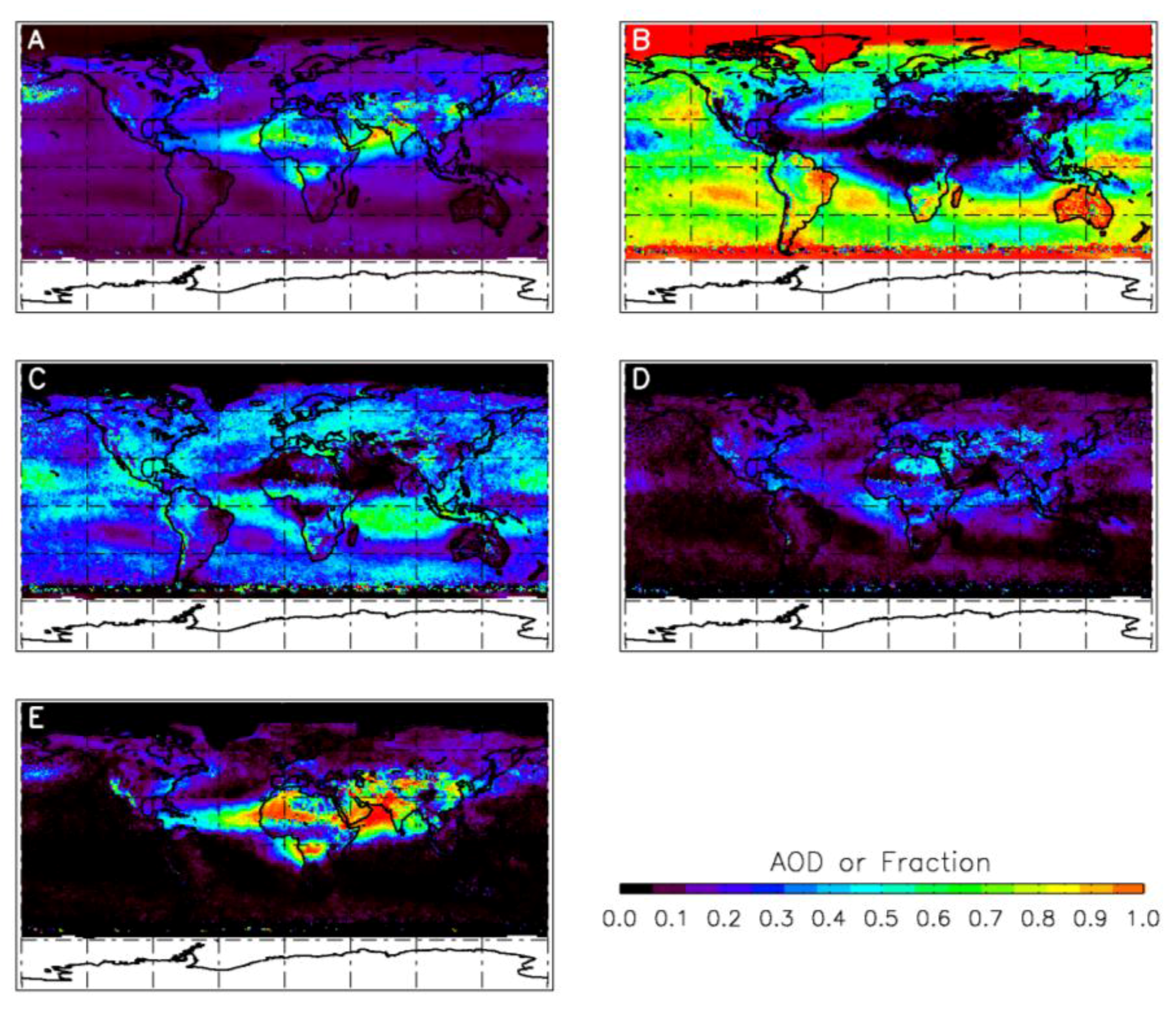
5.2. Spatio-Temporal Distribution of XCO2 Retrieval Errors
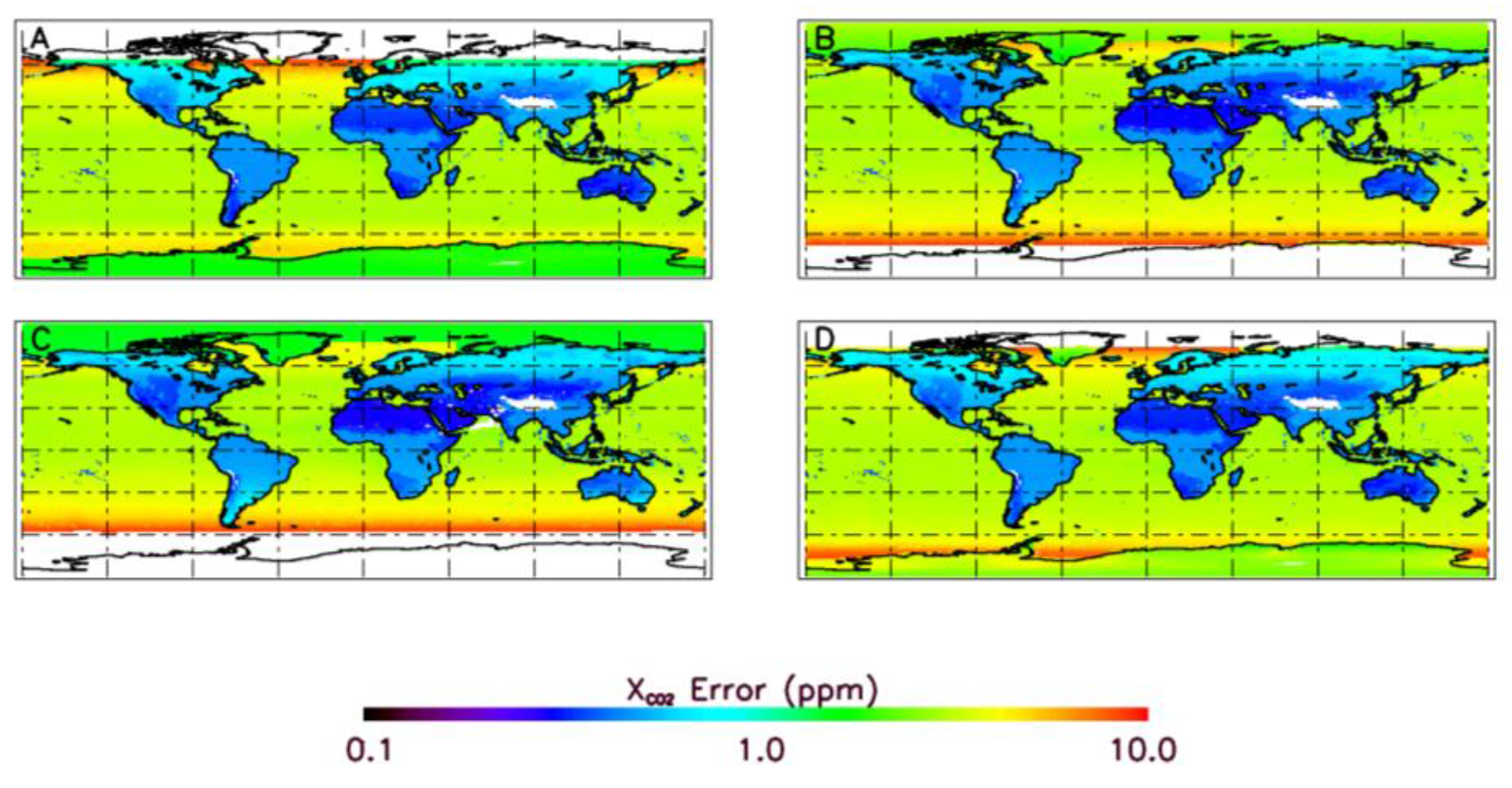
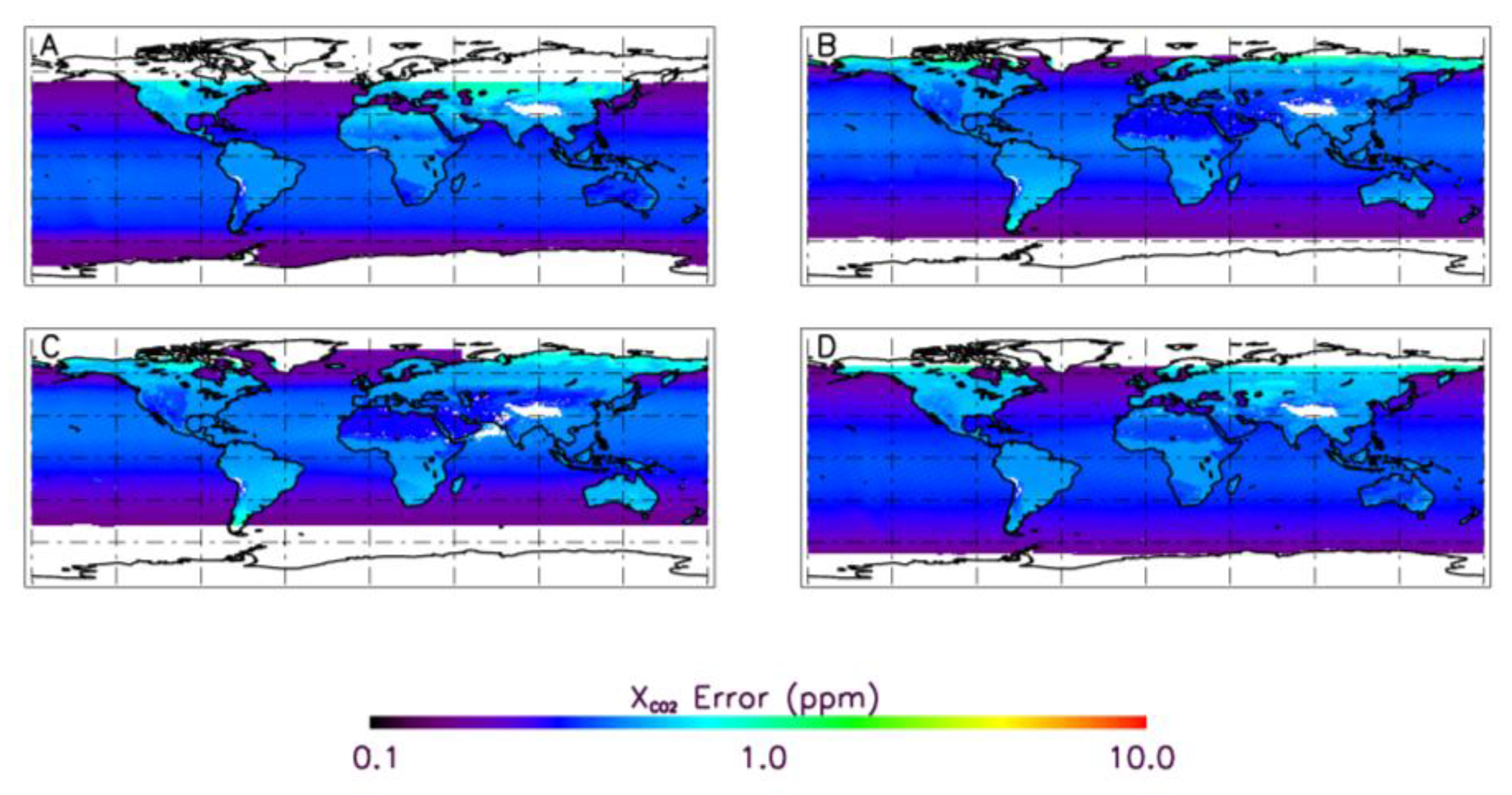
6. Cloud Climatology and Number of Cloud-Free OCO-2 Soundings
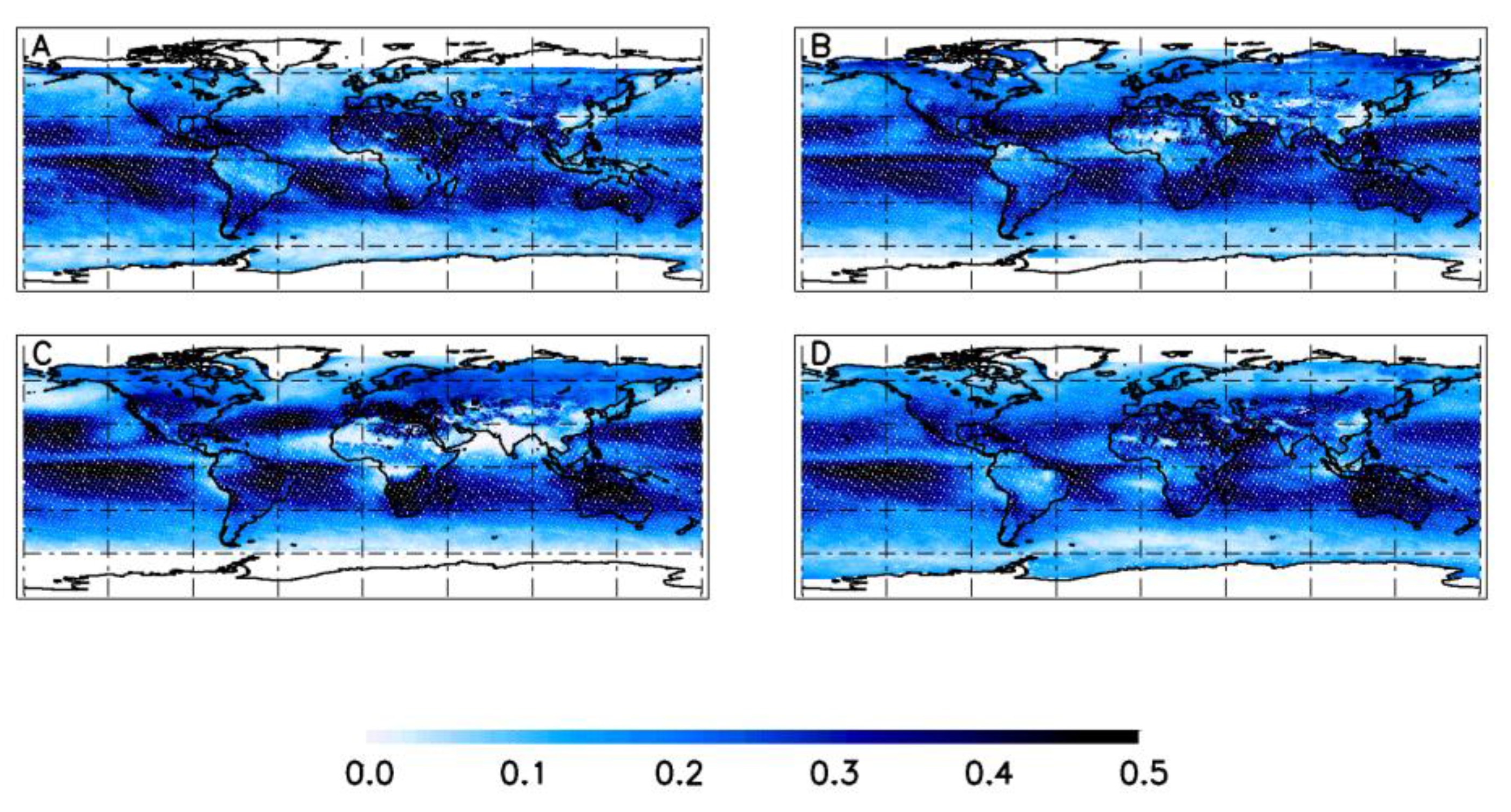
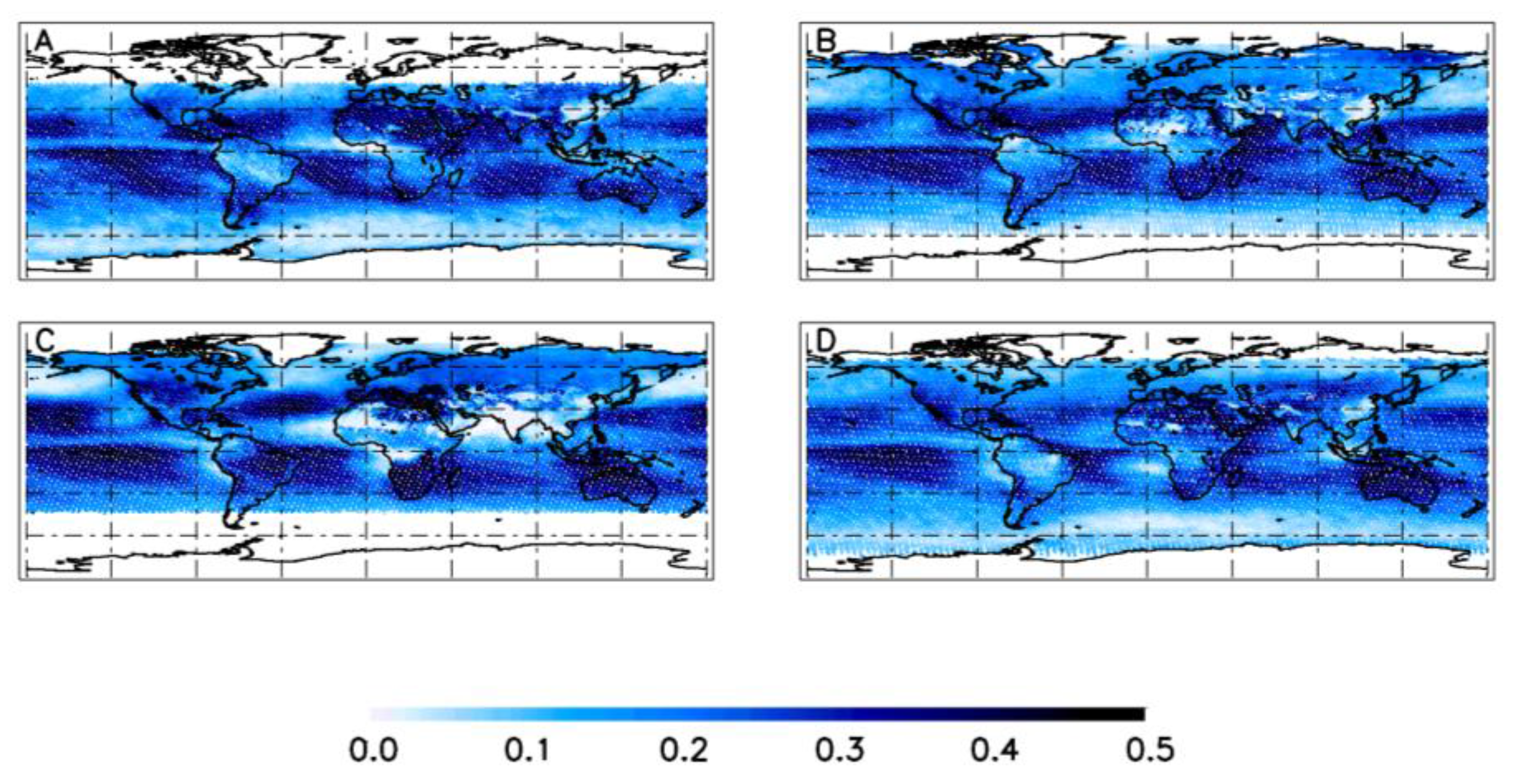
7. Summary and Discussion
| AOD/SZA (°) | Nadir Mode | Glint Mode | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.3 | 0.0 | 0.1 | 0.2 | 0.3 | |
| 10 | 0.447 (0.445) | 0.457 (0.473) | 0.463 (0.476) | 0.465 (0.474) | 0.439 (0.451) | 0.450 (0.481) | 0.456 (0.450) | 0.427 (0.479) |
| 30 | 0.473 (0.467) | 0.481 (0.495) | 0.486 (0.498) | 0.487 (0.495) | 0.491 (0.513) | 0.480 (0.495) | 0.477 (0.486) | 0.472 (0.470) |
| 50 | 0.572 (0.521) | 0.547 (0.532) | 0.537 (0.529) | 0.525 (0.523) | 0.617 (0.590) | 0.548 (0.541) | 0.468 (0.494) | 0.443 (0.461) |
| 70 | 0.727 (0.592) | 0.748 (0.579) | 0.630 (0.565) | 0.565 (0.553) | 0.705 (0.762) | 0.471 (0.450) | 0.837 (0.480) | 1.118 (0.569) |
| 80/75 | 0.769 (0.755) | 0.708 (0.715) | 0.796 (0.774) | 0.959 (0.832) | 1.375 (0.973) | 0.646 (0.469) | 0.906 (0.458) | 1.023 (0.484) |
| 85 | 1.147 (1.064) | 2.023 (1.888) | 2.478 (2.137) | 2.160 (1.762) | - | - | - | - |
| AOD/SZA (°) | Nadir Mode | Glint Mode | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.3 | 0.0 | 0.1 | 0.2 | 0.3 | |
| 10 | 0.301 (0.296) | 0.290 (0.305) | 0.283 (0.308) | 0.283 (0.309) | 0.295 (0.301) | 0.280 (0.304) | 0.281 (0.303) | 0.276 (0.313) |
| 30 | 0.310 (0.309) | 0.300 (0.322) | 0.298 (0.325) | 0.305 (0.325 | 0.310 (0.327) | 0.301 (0.325) | 0.308 (0.328) | 0.319 (0.325) |
| 50 | 0.356 (0.352) | 0.345 (0.361) | 0.359 (0.359) | 0.372 (0.356) | 0.524 (0.426) | 0.636 (0.426) | 0.618 (0.402) | 0.556 (0.371) |
| 70 | 0.596 (0.521) | 0.701 (0.465) | 0.623 (0.440) | 0.569 (0.445) | 0.975 (0.846) | 0.766 (0.729) | 0.971 (0.823) | 1.123 (0.899) |
| 80/75 | 0.750 (0.707) | 0.909 (0.684) | 1.035 (0.874) | 1.085 (0.976) | 1.306 (1.052) | 0.891 (0.757) | 1.034 (0.755) | 1.088 (0.745) |
| 85 | 1.242 (1.136) | 1.420 (1.556) | 1.427 (1.485) | 1.359 (1.386) | - | - | - | - |
| AOD/SZA (°) | Nadir Mode | Glint Mode | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.3 | 0.0 | 0.1 | 0.2 | 0.3 | |
| 10 | 0.342 (0.338) | 0.337 (0.355) | 0.335 (0.358) | 0.336 (0.357) | 0.335 (0.346) | 0.329 (0.356) | 0.332 (0.347) | 0.319 (0.362) |
| 30 | 0.357 (0.355) | 0.353 (0.374) | 0.354 (0.377) | 0.357 (0.376) | 0.366 (0.383) | 0.355 (0.377) | 0.355 (0.376) | 0.355 (0.369) |
| 50 | 0.429 (0.404) | 0.407 (0.413) | 0.410 (0.410) | 0.412 (0.405) | 0.530 (0.473) | 0.585 (0.461) | 0.539 (0.428) | 0.474 (0.393) |
| 70 | 0.630 (0.551) | 0.708 (0.505) | 0.619 (0.477) | 0.561 (0.472) | 1.029 (0.809) | 0.846 (0.718) | 1.051 (0.762) | 1.118 (0.819) |
| 80/75 | 0.769 (0.725) | 0.920 (0.689) | 1.128 (0.885) | 1.253 (1.020) | 1.570 (1.067) | 1.068 (0.672) | 0.958 (0.547) | 0.897 (0.533) |
| 85 | 1.380 (1.156) | 1.697 (1.803) | 1.729 (1.774) | 1.523 (1.592) | - | - | - | - |
| AOD/SZA (°) | Nadir Mode | Glint Mode | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.3 | 0.0 | 0.1 | 0.2 | 0.3 | |
| 10 | 3.435 (2.882) | 3.126 (2.397) | 2.839 (2.121) | 2.579 (1.914) | 0.464 (0.421) | 0.466 (0.445) | 0.530 (0.431) | 0.620 (0.460) |
| 30 | 3.296 (2.879) | 3.055 (2.425) | 2.787 (2.125) | 2.528 (1.912) | 0.364 (0.359) | 0.391 (0.363) | 0.421 (0.369) | 0.460 (0.374) |
| 50 | 3.738 (3.395) | 3.416 (2.829) | 3.024 (2.364) | 2.652 (2.049) | 0.241 (0.251) | 0.273 (0.256) | 0.312 (0.262) | 0.365 (0.271) |
| 70 | 4.847 (4.580) | 4.153 (3.461) | 3.346 (2.602) | 2.668 (2.147) | 0.163 (0.176) | 0.176 (0.178) | 0.231 (0.189) | 0.304 (0.212) |
| 80/75 | 6.180 (5.529) | 6.411 (3.899) | 5.517 (2.839) | 4.138 (2.384) | 0.149 (0.161) | 0.169 (0.166) | 0.227 (0.182) | 0.285 (0.210) |
| 85 | 7.899 (6.288) | 8.781 (5.311) | 6.774 (3.972) | 5.033 (3.185) | - | - | - | - |
| AOD/SZA (°) | Nadir Mode | |||
|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.3 | |
| 10 | 1.076 (1.132) | 1.051 (1.156) | 1.036 (1.166) | 1.029 (1.163) |
| 30 | 1.145 (1.193) | 1.104 (1.214) | 1.084 (1.221) | 1.077 (1.216) |
| 50 | 1.271 (1.335) | 1.220 (1.329) | 1.210 (1.320) | 1.226 (1.304) |
| 70 | 1.593 (1.655) | 1.716 (1.591) | 1.899 (1.562) | 2.049 (1.537) |
| 80/75 | 2.927 (2.500) | 3.081 (2.299) | 3.281 (2.094) | 3.406 (1.986) |
| 85 | 4.441 (3.480) | 4.564 (3.579) | 5.189 (3.158) | 5.778 (2.765) |
8. Conclusion
Acknowledgements
References
- Forster, P.; Ramaswamy, V.; Artaxo, P.; Berntsen, T.; Betts, R.; Fahey, D.W.; Haywood, J.; Lean, J.; Lowe, D.C.; Myhre, G.; Nganga, J.; Prinn, R.; Raga, G.; Schulz, M.; Van Dorland, R. Changes in atmospheric constituents and in radiative forcing. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK and New York, NY, USA, 2007. [Google Scholar]
- Gurney, K.R.; Law, R.M.; Denning, A.S.; Rayner, P.J.; Baker, D.; Bousquet, P.; Bruhwiler, L.; Chen, Y.-H.; Ciais, P.; Fan, S.; et al. Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models. Nature 2002, 415, 626–629. [Google Scholar] [CrossRef] [PubMed]
- Le Quere, C.; Raupach, M.R.; Canadell, J.G.; Marland, G.; et al. Trends in the sources and sinks of carbon dioxide. Nature Geoscience 2009, 2, 831–836. [Google Scholar] [CrossRef]
- Baker, D.F.; Doney, S.C.; Schimel, D.S. Variational data assimilation for atmospheric CO2. Tellus Ser. B 2006, 8, 359–365. [Google Scholar] [CrossRef]
- Baker, D.F.; Boesch, H.; Doney, S.C.; O’Brien, D.; Schimel, D.S. Carbon source/sink information provided by column CO2 measurements from the Orbiting Carbon Observatory. Atmos. Chem. Phys. 2010, 10, 4145–4165. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Boesch, H.; Dance, S. Estimating surface CO2 fluxes from space-borne CO2 dry air mole fraction observations using an ensemble Kalman Filter. Atmos. Chem. Phys. 2009, 9, 2619–2633. [Google Scholar] [CrossRef]
- Chevallier, F.; Breon, F.M.; Rayner, P.J. Contribution of the Orbiting Carbon Observatory to the estimation of CO2 sources and sinks: Theoretical study in a variational data assimilation framework. J. Geophys. Res. 2007, 112, D09307. [Google Scholar] [CrossRef]
- Houweling, S.; Hartmann, W.; Aben, I.; Schrijver, H.; Skidmore, J.; Roelofs, G.J.; Breon, F.M. Evidence of systematic errors in SCIAMACHY-observed CO2 due to aerosols. Atmos. Chem. Phys. 2005, 5, 3003–3013. [Google Scholar] [CrossRef]
- Rayner, P.J.; O’Brien, D. The utility of remotely sensed CO2 concentration data in surface source inversions. Geophys. Res. Lett. 2001, 28, 175–178. [Google Scholar] [CrossRef]
- Chedin, A.; Serrar, S.; Scott, N.A.; Crevoisier, C.; Armante, R. First global measurement of midtropospheric CO2 from NOAA polar satellites: Tropical zone. J. Geophys. Res. 2003, 108, 4581. [Google Scholar] [CrossRef]
- Matsueda, H.; Inoue, H.Y.; Ishii, M. Aircraft observation of carbon dioxide at 8–13 km altitude over the western Pacific from 1993 to 1999. Tellus Ser. B 2002, 54, 1–21. [Google Scholar] [CrossRef]
- Maddy, E.; Barnet, C.; Goldberg, M.; Sweeney, C.; Liu, X. CO2 retrievals from the Atmospheric Infrared Sounder: Methodology and validation. J. Geophys. Res. 2008, 113, D11. [Google Scholar]
- Chahine, M.; Barnet, C.; Olsen, E.T.; Chen, L.; Maddy, E. On the determination of atmospheric minor gases by the method of vanishing partial derivatives with application to CO2. Geophys. Res. Lett. 2005, 32, L22803. [Google Scholar] [CrossRef]
- Engelen, R.J.; McNally, A.P. Estimating atmospheric CO2 from advanced infrared satellite radiances within an operational fourdimensional variational (4D-Var) data assimilation system: Results and validation. J. Geophys. Res. 2005, 110, D18305. [Google Scholar] [CrossRef]
- Crevoisier, C.; Heilliette, S.; Chedin, A.; Serrar, S.; Armante, R.; Scott, N.A. Midtropospheric CO2 concentration retrieval from AIRS observations in the tropics. Geophys. Res. Lett. 2004, 31, L17106. [Google Scholar] [CrossRef]
- Crevoisier, C.; Chédin, A.; Matsueda, H.; Machida, T.; Armante, R.; Scott, N.A. First year of upper tropospheric integrated content of CO2 from IASI hyperspectral infrared observations. Atmos. Chem. Phys. 2009, 9, 4797–4810. [Google Scholar] [CrossRef]
- Chevallier, F.; Fisher, M.; Peylin, P.; Bousquet, S.S.; Breon, F.M.; Chedin, A.; Ciais, P. Inferring CO2 sources and sinks from satellite observations: Method and application to TOVS data. J. Geophys. Res. 2005, 110, D24309. [Google Scholar] [CrossRef]
- Chevallier, F.; Engelen, R.J.; Peylin, P. The contribution of AIRS data to the estimation of CO2 sources and sinks. J. Geophys. Res. 2005, 32, L23801. [Google Scholar] [CrossRef]
- Bovensmann, H.; Burrows, J.P.; Buchwitz, M.; Frerick, J.; Noel, S.; Rozanov, V.V.; Chance, K.V.; Goede, A.P.H. SCIAMACHY: Mission objectives and measurement modes. J. Atmos. Sci. 1999, 56, 127–150. [Google Scholar] [CrossRef]
- Burrows, J.P.; Holzle, E.; Goede, A.P.H.; Visser, H.; Fricke, W. SCIAMACHY—Scanning imaging absorption spectrometer for atmospheric chartography. Acta Astron. 1995, 35, 445–451. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Burrows, J.; Bovensmann, H.; Reuter, M.; Notholt, J. Three years of greenhouse gas column-averaged dry air mole fractions retrieved from satellite—Part 1: Carbon dioxide. Atmos. Chem. Phys. 2008, 8, 3827–3853. [Google Scholar] [CrossRef]
- Barkley, M.P.; Monks, P.S.; Frieß, U.; Mittermeier, R.L.; Fast, H.; Körner, S.; Heimann, M. Comparisons between SCIAMACHY atmospheric CO2 retrieved using (FSI) WFM-DOAS to ground based FTIR data and the TM3 chemistry transport model. Atmos. Chem. Phys. 2006, 6, 4483–4498. [Google Scholar] [CrossRef]
- Barkley, M.P.; Monks, P.S.; Hewitt, A.J.; Machida, T.; Desai, A.; Vinnichenko, N.; Nakazawa, T.; Yu Arshinov, M.; Fedoseev, N.; Watai, T. Assessing the near surface sensitivity of SCIAMACHY atmospheric CO2 retrieved using (FSI) WFM-DOAS. Atmos. Chem. Phys. 2007, 7, 3597–3619. [Google Scholar] [CrossRef]
- Boesch, H.; Toon, G.C.; Sen, B.; Washenfelder, R.A.; Wennberg, P.O.; Buchwitz, M.; de Beek, R.; Burrows, J.P.; Crisp, D.; Christi, M.; Connor, B.J.; Natraj, V.; Yung, Y.L. Space-based near-infrared CO2 measurements: Testing the Orbiting Carbon Observatory retrieval algorithm and validation concept using SCIAMACHY observations over Park Falls, Wisconsin. J. Geophys. Res. 2006, 111, D23. [Google Scholar]
- Palmer, P.I.; Barkley, M.P.; Monks, P.S. Interpreting the variability of CO2 columns over North America using a chemistry transport model: Application to SCIAMACHY data. Atmos. Chem. Phys. Dis. 2008, 8, 7339–7371. [Google Scholar] [CrossRef]
- Hamazaki, T.; Kaneko, Y.; Kuze, A.; Kondo, K. Fourier transform spectrometer for Greenhouse Gases Observing Satellite (GOSAT). Proc. SPIE 2005, 5659, 73–80. [Google Scholar]
- Washenfelder, R.A.; Toon, G.C.; Blavier, J.F.; Yang, Z.; Allen, N.T.; Wennberg, P.O.; Vay, S.A.; Matross, D.M.; Daube, B.C. Carbon dioxide column abundances at the Wisconsin Tall Tower site. J. Geophys. Res. 2006, 111, D22305. [Google Scholar] [CrossRef]
- Ohyama, H.; Morino, I.; Nagahama, T.; Machida, T.; Suto, H.; Oguma, H.; Sawa, Y.; Matsueda, H.; Sugimoto, N.; Nakane, H.; Nakagawa, K. Column-averaged volume mixing ratio of CO2 measured with ground-based Fourier transform spectrometer at Tsukuba. J. Geophys. Res. 2009, 114, D18303. [Google Scholar] [CrossRef]
- Machida, T.; Matsueda, H.; Sawa, Y.; Nakagawa, Y.; Hirotani, K.; Kondo, N.; Goto, K.; Nakazawa, T.; Ishikawa, K.; Ogawa, T. Worldwide measurements of atmospheric CO2 and other trace gas species using commercial airlines. J. Atmos. Oceanic Technol. 2008, 25, 1744–1754. [Google Scholar] [CrossRef]
- Public Release of Concentration Data (Carbon Dioxide and Methane) Analyzed from GOSAT Observational Data; NIES: Tsukuba, Japan, 2010; Available online: http://www.gosat.nies.go.jp/eng/result/result.htm (accessed on 5 March 2010).
- Crisp, D.; Atlas, R.M.; Breon, F.-M.; Brown, L.R.; Burrows, J.P.; Ciais, P.; Connor, B.J.; Doney, S.C.; Fung, I.Y.; Jacob, D.J.; et al. The Orbiting Carbon Observatory (OCO) Mission. Adv. Space Res. 2004, 34, 700–709. [Google Scholar] [CrossRef]
- Miller, C.E.; Crisp, D.; Decola, P.L.; Olsen, S.C.; Randerson, J.T.; Michalak, A.M.; Alkhaled, A.; Rayner, P.; Jacob, D.J.; Suntharalingam, P.; Jones, D.B.; et al. Precision requirements for space-based XCO2 data. J. Geophys. Res. 2007, 112, D10314. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific Publishing Co. Pte. Ltd: Hackensack, NJ, USA, 2000. [Google Scholar]
- Connor, B.J.; Boesch, H.; Toon, G.C.; Sen, B.; Miller, C.E.; Crisp, D. Orbiting carbon observatory: Inverse method and prospective error analysis. J. Geophys. Res. 2008, 113, D05305. [Google Scholar] [CrossRef]
- Spurr, R.; Christi, M. Linearization of the interaction principle: Analytic Jacobians in the “Radiant” model. J. Quant. Spectrosc. Radiat. Transfer 2007, 103, 431–446. [Google Scholar] [CrossRef]
- Christi, M.J.; Stephens, G.L. Retrieving profiles of atmospheric CO2 in clear sky and in the presence of thin cloud using spectroscopy from the near and thermal infrared: A preliminary case study. J. Geophys. Res. 2004, 109, D04316. [Google Scholar] [CrossRef]
- Spurr, R.J.D. A new approach to the retrieval of surface properties from earthshine measurements. J. Quant. Spectrosc. Radiat. Transfer 2004, 83, 15–46. [Google Scholar] [CrossRef]
- Natraj, V.; Spurr, R.; Boesch, H.; Jiang, Y.; Yung, Y. Evaluation of errors from neglecting polarization in the forward modeling of O-2 A band measurements from space, with relevance to CO2 column retrieval from polarization-sensitive instruments. J. Quant. Spectrosc. Radiat. Transfer 2007, 103, 245–259. [Google Scholar] [CrossRef]
- Natraj, V.; Boesch, H.; Spurr, R.; Yung, Y. Retrieval of X-CO2 from simulated Orbiting Carbon Observatory measurements using the fast linearized R-2OS radiative transfer model. J. Geophys. Res. 2008, 113, D11212. [Google Scholar] [CrossRef]
- Natraj, V.; Spurr, R.J.D. A fast linearized pseudo-spherical two orders of scattering model to account for polarization in vertically inhomogeneous scattering-absorbing media. J. Quant. Spectrosc. Radiat. Transfer 2007, 107, 263–293. [Google Scholar] [CrossRef]
- Geller, M. A High Resolution Atlas of the Infrared Spectrum of the Sun and the Earth Atmosphere from Space, volume III. Key to Identification of Solar Features from 650 to 4,800 cm-1; NASA Reference Publication 122; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Geller, M. Line identification in ATMOS solar spectra. In Laboratory and Astronomical High Resolution Spectra; Proceedings of ASP Conference No. 81; Brussels, Belgium, 29 August–2 September 1994, ASP Conference Series; Sauval, A.J., Blomme, R., Grevesse, N., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 1995; p. 81. [Google Scholar]
- Wallace, L.; Hinkle, K.; Livingston, W.C. An Atlas of the Photospheric Spectrum from 8,900 to 13,600 cm−1 (7350 to 11230 Å); NSO Technical Report; NSO: Tucson, AZ, USA, 1993. [Google Scholar]
- Livingston, W.; Wallace, L. An Atlas of the Solar Spectrum in the Infrared from 1,850 to 9,000 cm−1 (1.1 to 5.4 μm); NSO Technical Report; NSO: Tucson, AZ, USA, 1991. [Google Scholar]
- Cox, C.; Munk, W. Statistics of the sea surface derived from sun glitter. J. Mar. Res. 1954, 13, 198–227. [Google Scholar]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER Spectral Library Version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Arnold, G.T.; Tsay, S.C.; King, M.D.; Li, J.Y.; Soulen, P.F. Airborne spectral measurements of surface–atmosphere anisotropy for arctic sea ice and tundra. Int. J. Remote Sens. 2002, 23, 3763–3781. [Google Scholar] [CrossRef]
- Kahn, R.; Banerjee, P.; McDonald, D. Sensitivity of multiangle imaging to natural mixtures of aerosols over ocean. J. Geophys. Res. 2001, 106, D16. [Google Scholar] [CrossRef]
- de Rooij, W.A.; van der Stap, C.C.A.H. Expansion of Mie scattering matrices in generalized spherical functions. Astron. Astrophys. 1984, 131, 237–248. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D. Capabilities and limitations of a current Fortran implementation of the T-matrix method for randomly oriented, rotationally symmetric scatterers. J. Quant. Spectrosc. Radiat. Transfer 1998, 60, 309–324. [Google Scholar] [CrossRef]
- Olsen, S.C.; Randerson, J.T. Differences between surface and column atmospheric CO2 and implications for carbon cycle research. J. Geophys. Res. 2004, 109, D02301. [Google Scholar] [CrossRef]
- Breon, F.M.; O’Brien, D.; Spinhirne, J.D. Scattering layer statistics from space borne GLAS observations. Geophys. Res. Lett. 2005, 32, L22802. [Google Scholar] [CrossRef]
- Eguchi, N.; Yokota, T.; Inoue, G. Characteristics of cirrus clouds from ICESat/GLAS observations. Geophys. Res. Lett. 2007, 34, L09810. [Google Scholar] [CrossRef]
- Kuang, Z.; Margolis, J.; Toon, G.; Crisp, D.; Yung, Y. Spaceborne measurements of atmospheric CO2 by high-resolution NIR spectrometry of reflected sunlight: An introductory study. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Butz, A.; Hasekamp, O.P.; Frankenberg, C.; Aben, I. Retrievals of atmospheric CO2 from simulated space-borne measurements of backscattered near-infrared sunlight: Accounting for aerosol effects. Appl. Opt. 2009, 48(18), 3322–3336. [Google Scholar] [CrossRef]
- Marshak, A.; Wen, G.; Coakley, J.A., Jr.; Remer, L.A.; Loeb, N.G.; Cahalan, R.F. A simple model for the cloud adjacency effect and the apparent bluing of aerosols near clouds. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Le Quere, C.; Rödenbeck, C.; Buitenhuis, E.T.; Conway, T.J.; Langenfelds, R.; Gomez, A.; Labuschagne, C.; Ramonet, M.; Nakazawa, T.; Metzl, N.; et al. Saturation of the Southern ocean CO2 sink due to recent climate change. Science 2007, 316, 1735–1738. [Google Scholar] [CrossRef] [PubMed]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Boesch, H.; Baker, D.; Connor, B.; Crisp, D.; Miller, C. Global Characterization of CO2 Column Retrievals from Shortwave-Infrared Satellite Observations of the Orbiting Carbon Observatory-2 Mission. Remote Sens. 2011, 3, 270-304. https://doi.org/10.3390/rs3020270
Boesch H, Baker D, Connor B, Crisp D, Miller C. Global Characterization of CO2 Column Retrievals from Shortwave-Infrared Satellite Observations of the Orbiting Carbon Observatory-2 Mission. Remote Sensing. 2011; 3(2):270-304. https://doi.org/10.3390/rs3020270
Chicago/Turabian StyleBoesch, Hartmut, David Baker, Brian Connor, David Crisp, and Charles Miller. 2011. "Global Characterization of CO2 Column Retrievals from Shortwave-Infrared Satellite Observations of the Orbiting Carbon Observatory-2 Mission" Remote Sensing 3, no. 2: 270-304. https://doi.org/10.3390/rs3020270
APA StyleBoesch, H., Baker, D., Connor, B., Crisp, D., & Miller, C. (2011). Global Characterization of CO2 Column Retrievals from Shortwave-Infrared Satellite Observations of the Orbiting Carbon Observatory-2 Mission. Remote Sensing, 3(2), 270-304. https://doi.org/10.3390/rs3020270





