Performance Evaluation of Inherent Optical Property Algorithms and Identification of Potential Water Quality Indicators Using GCOM-C Data in Eutrophic Lake Kasumigaura, Japan
Abstract
1. Introduction
2. Materials and Methods
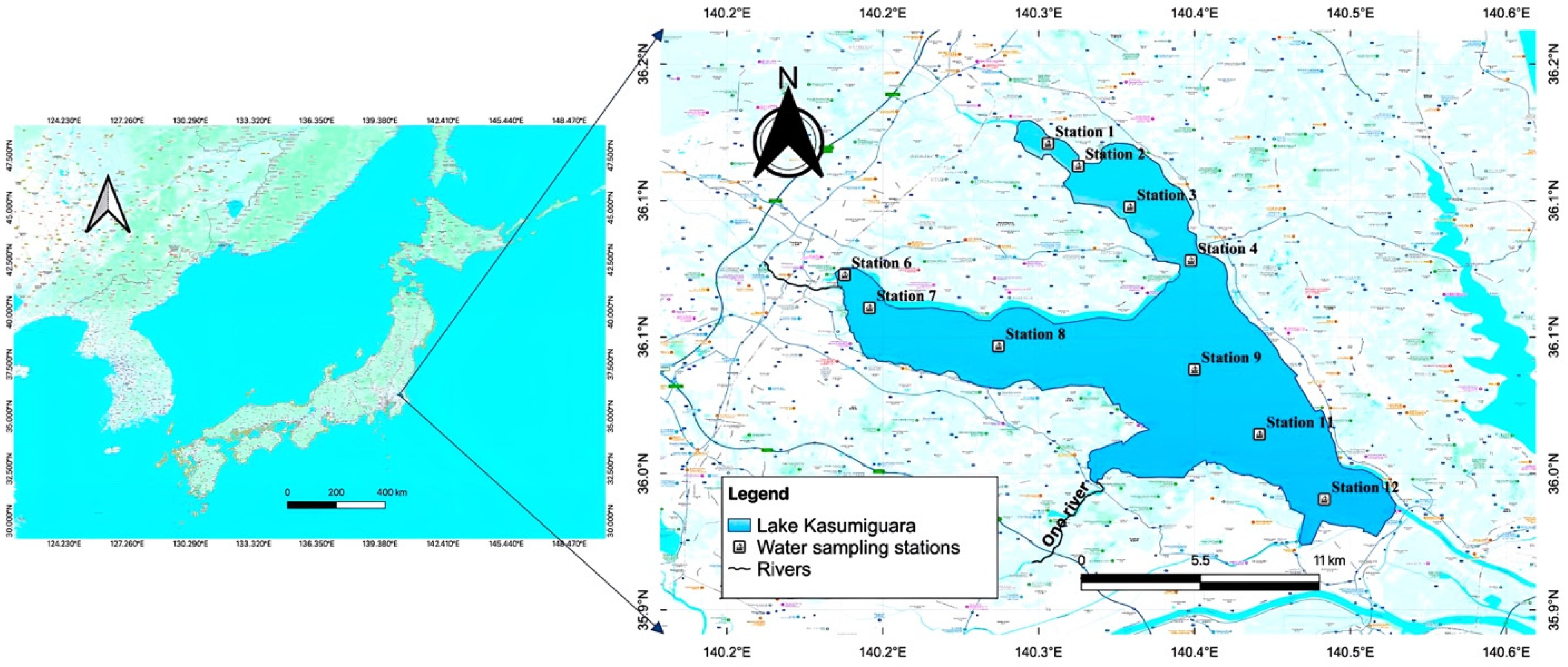
2.1. Study Area
2.2. Data Collection
2.2.1. Field Observations
2.2.2. Water Quality Dataset by the NIES
2.2.3. GCOM-C Satellite Imagery
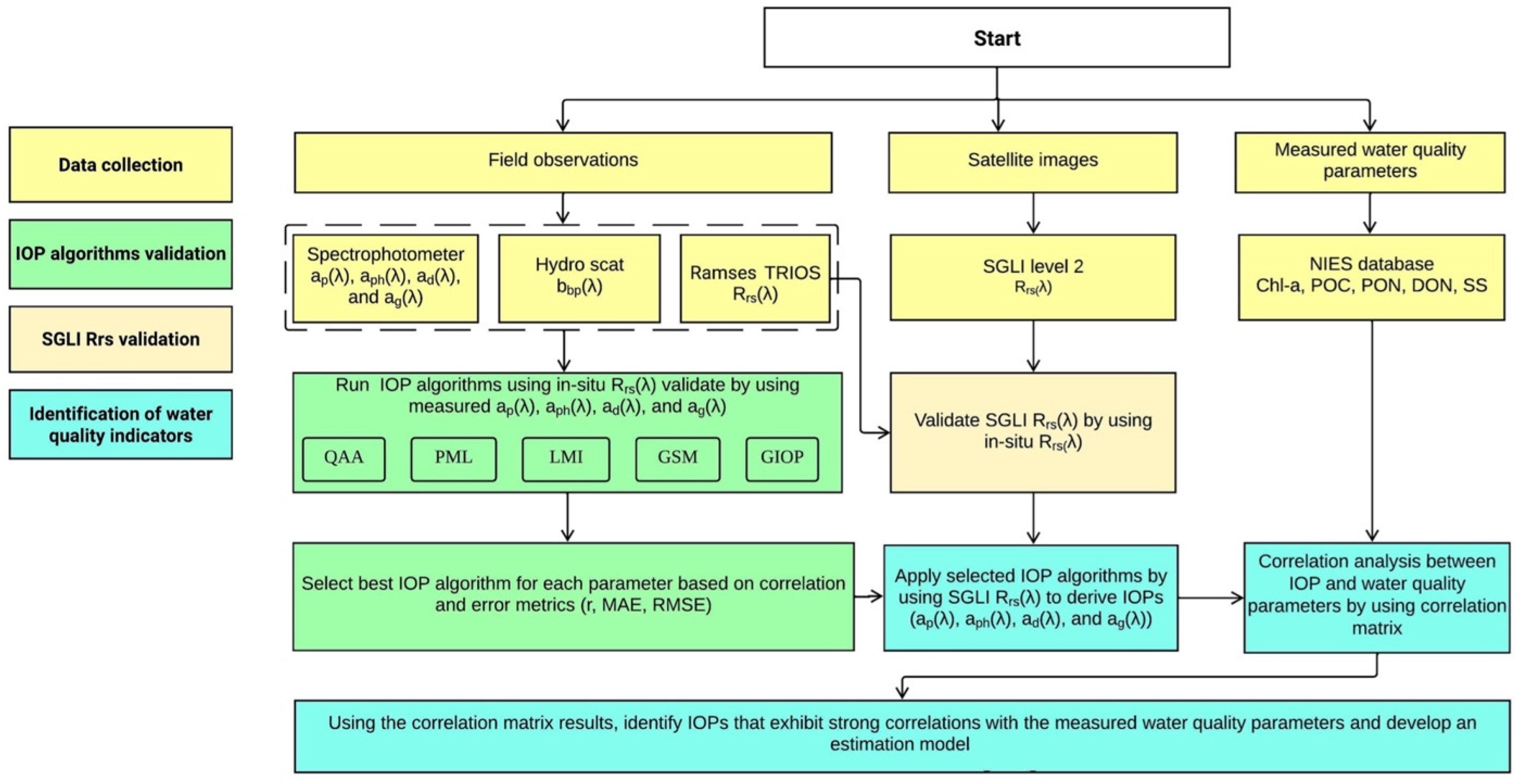
2.3. Study Design
2.4. Semi-Analytical IOP Algorithms
2.5. Accuracy Assessment of Inherent Optical Property Algorithms Using In Situ and Remote Sensing Data
| Measured IOP | Sample Size | Min | Max | Mean | Median | SD |
|---|---|---|---|---|---|---|
| ap (412 nm) | 24 | 0.93 | 1.97 | 1.63 | 1.69 | 0.34 |
| ap (443 nm) | 24 | 0.76 | 1.90 | 1.30 | 1.25 | 0.30 |
| ap (490 nm) | 24 | 0.41 | 1.14 | 0.74 | 0.71 | 0.19 |
| ap (530 nm) | 24 | 0.23 | 0.58 | 0.41 | 0.40 | 0.09 |
| ap (565 nm) | 24 | 0.16 | 0.40 | 0.28 | 0.27 | 0.06 |
| ap (670 nm) | 24 | 0.22 | 0.73 | 0.39 | 0.33 | 0.15 |
| aph (412 nm) | 24 | 0.28 | 0.99 | 0.57 | 0.51 | 0.23 |
| aph (443 nm) | 24 | 0.26 | 1.25 | 0.57 | 0.48 | 0.29 |
| aph (490 nm) | 24 | 0.12 | 0.69 | 0.31 | 0.25 | 0.19 |
| aph (530 nm) | 24 | 0.04 | 0.37 | 0.14 | 0.11 | 0.09 |
| aph (565 nm) | 24 | 0.01 | 0.24 | 0.08 | 0.06 | 0.06 |
| aph (670 nm) | 24 | 0.16 | 0.63 | 0.30 | 0.25 | 0.14 |
| aNAP (412 nm) | 24 | 0.075 | 2.164 | 1.180 | 1.512 | 0.793 |
| aNAP (443 nm) | 24 | 0.049 | 1.489 | 0.796 | 1.036 | 0.533 |
| aNAP (490 nm) | 24 | 0.031 | 0.967 | 0.506 | 0.637 | 0.342 |
| aNAP (530 nm) | 24 | 0.018 | 0.798 | 0.385 | 0.457 | 0.273 |
| aNAP (565 nm) | 24 | 0.013 | 0.729 | 0.309 | 0.345 | 0.230 |
| aNAP (670 nm) | 24 | 0.0002 | 0.606 | 0.203 | 0.215 | 0.173 |
| aCDOM (412 nm) | 24 | 0.593 | 1.548 | 1.088 | 1.114 | 0.288 |
| aCDOM (443 nm) | 24 | 0.429 | 1.109 | 0.757 | 0.785 | 0.192 |
| aCDOM (490 nm) | 24 | 0.255 | 0.621 | 0.442 | 0.462 | 0.111 |
| aCDOM (530 nm) | 24 | 0.165 | 0.377 | 0.279 | 0.293 | 0.067 |
| aCDOM (565 nm) | 24 | 0.121 | 0.282 | 0.195 | 0.204 | 0.045 |
| aCDOM (670 nm) | 24 | 0.049 | 0.204 | 0.083 | 0.080 | 0.031 |
3. Results
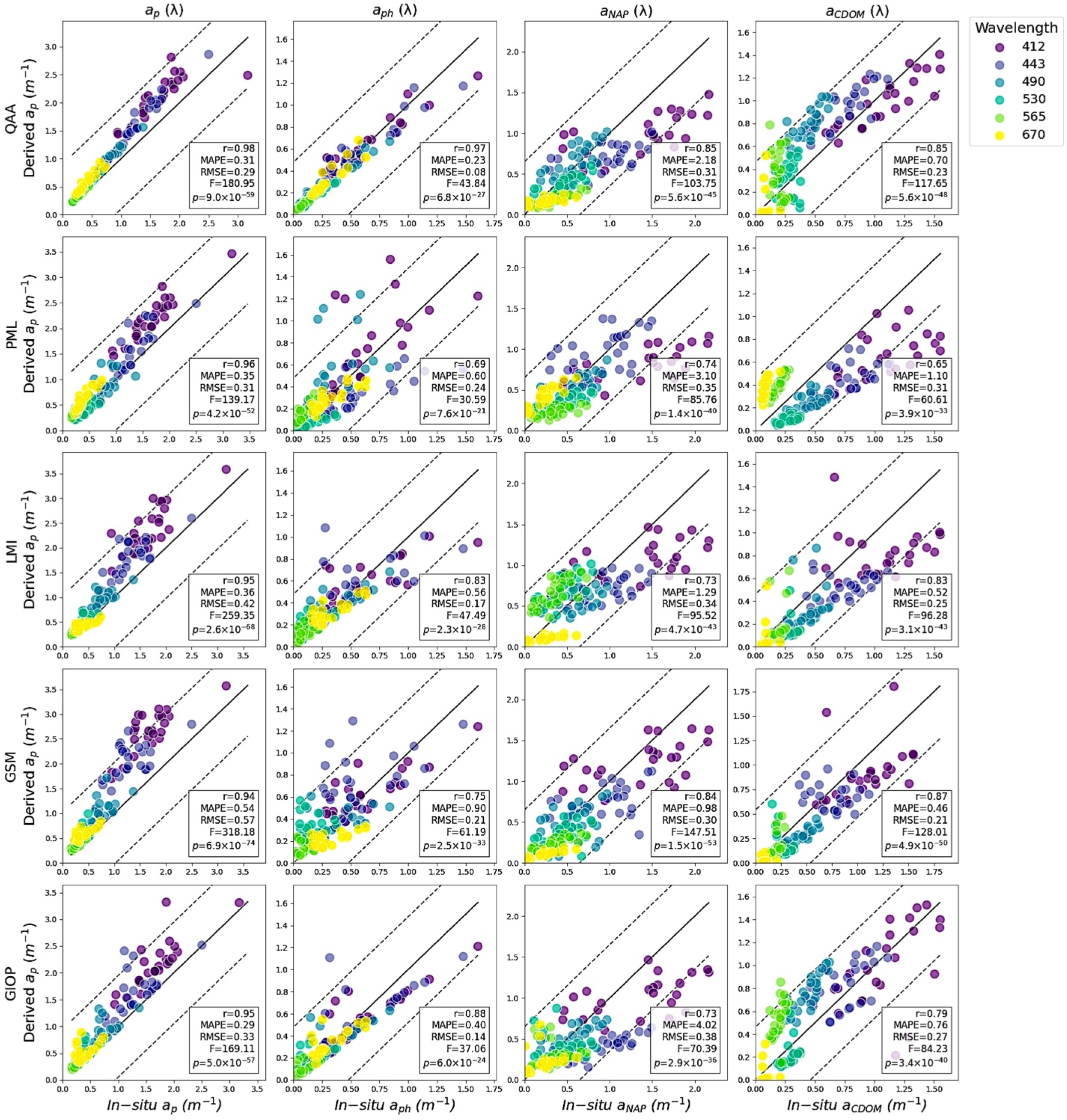
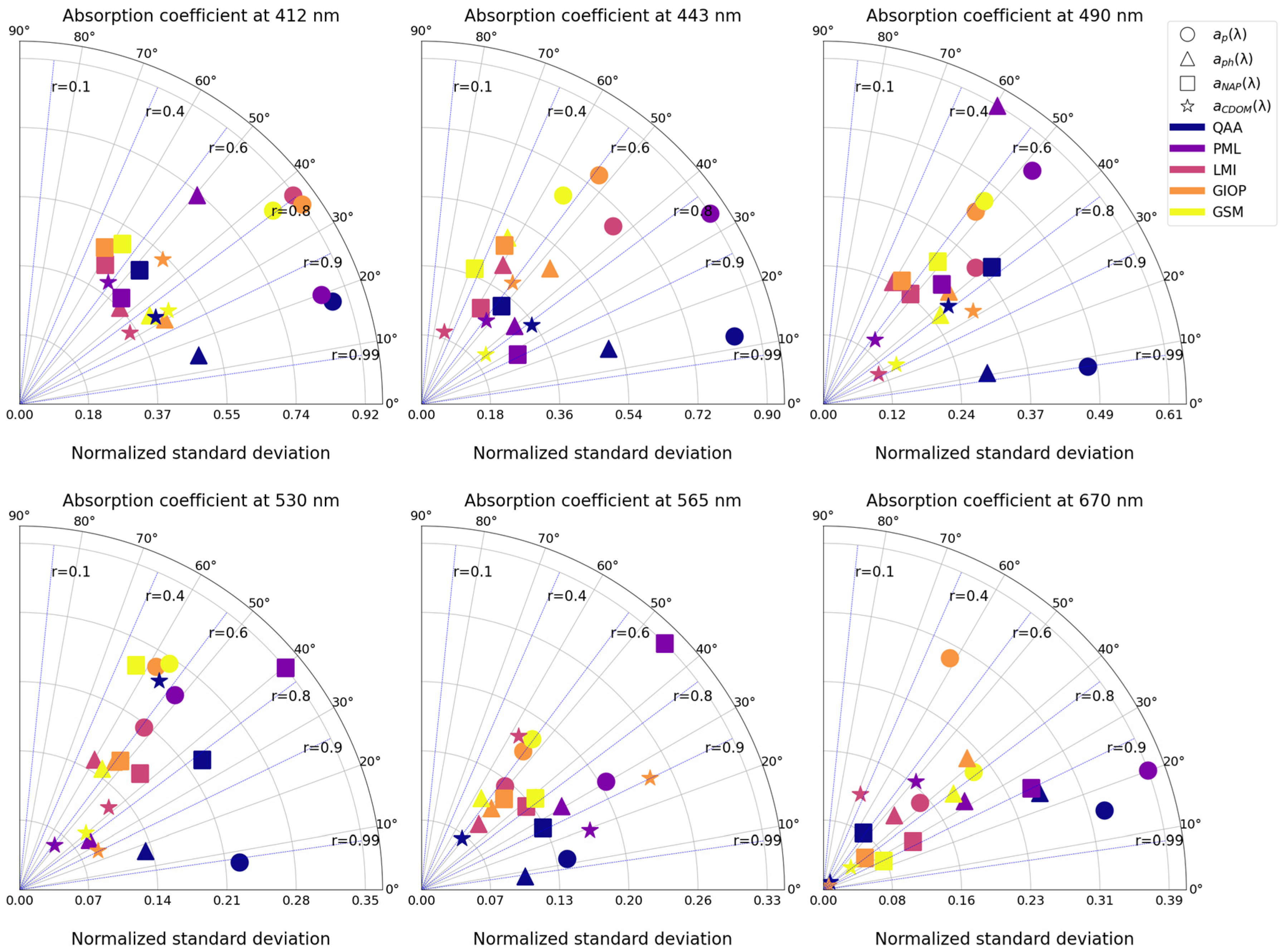
3.1. Comparative Analysis of IOP Algorithms
3.2. Accuracy Assessment of the GCOM-C/SGLI Satellite Imagery and In Situ Remote Sensing Reflectance
3.3. Correlation Between the Algorithm-Derived IOPs and the Measured Water Quality Parameters
4. Discussion
4.1. Performance Evaluation of IOP Algorithms and Validation of Rrs
4.2. Comparison of Phytoplankton Absorption and Chlorophyll a
4.3. Comparison of the Correlation Between Backscattering of Particles and Suspended Solids
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, C.; Song, C.; Wang, X.; Wang, Q.; Tao, H.; Wang, X.; Ma, Y.; Song, K. A novel total phosphorus concentration retrieval method based on two-line classification in lakes and reservoirs across China. Sci. Total Environ. 2024, 906, 167522. [Google Scholar] [CrossRef] [PubMed]
- Seegers, B.N.; Werdell, P.J.; Vandermeulen, R.A.; Salls, W.; Stumpf, R.P.; Schaeffer, B.A.; Owens, T.J.; Bailey, S.W.; Scott, J.P.; Loftin, K.A. Satellites for long-term monitoring of inland U.S. lakes: The MERIS time series and application for chlorophyll-a. Remote Sens. Environ. 2021, 266, 112685. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Shen, M.; Kutser, T.; Liu, M.; Qi, T.; Ma, J.; Ma, R.; Duan, H. What water color parameters could be mapped using MODIS land reflectance products: A global evaluation over coastal and inland waters. Earth-Science Rev. 2022, 232, 104154. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zhang, B.; Lee, Z.; Spyrakos, E.; Feng, L.; Liu, C.; Zhao, H.; Wu, Y.; Zhu, L.; et al. Changes of water clarity in large lakes and reservoirs across China observed from long-term MODIS. Remote Sens. Environ. 2020, 247, 111949. [Google Scholar] [CrossRef]
- Kapalanga, T.S.; Hoko, Z.; Gumindoga, W.; Chikwiramakomo, L. Remote-sensing-based algorithms for water quality monitoring in olushandja dam, north-central namibia. Water Supply 2021, 21, 1878–1894. [Google Scholar] [CrossRef]
- Krishna, S.; Ulloa, H.N.; Barbe, E.; Wüest, A. Disentangling the effects of climate change and reoligotrophication on primary production in a large lake. Aquat. Sci. 2023, 85, 16. [Google Scholar] [CrossRef]
- Ayala, A.I.; Mesman, J.P.; Jones, I.D.; de Eyto, E.; Jennings, E.; Goyette, S.; Pierson, D.C. Climate Change Impacts on Surface Heat Fluxes in a Deep Monomictic Lake. J. Geophys. Res. Atmos. 2023, 128, e2022JD038355. [Google Scholar] [CrossRef]
- Fathi, E.; Zamani-Ahmadmahmoodi, R.; Zare-Bidaki, R. Water quality evaluation using water quality index and multivariate methods, Beheshtabad River, Iran. Appl. Water Sci. 2018, 8, 210. [Google Scholar] [CrossRef]
- Holzbauer-Schweitzer, B.K.; Nairn, R.W. In-situ manipulations of aquatic optical depth and its effect on small unoccupied aerial systems–derived spectral reflectance. Drone Syst. Appl. 2022, 10, 427–443. [Google Scholar] [CrossRef]
- Najah, A.; Al-Shehhi, M.R. Performance of the Ocean Color Algorithms: QAA, GSM, and GIOP in Inland and Coastal Waters. Remote Sens. Earth Syst. Sci. 2021, 4, 235–248. [Google Scholar] [CrossRef]
- Betancur-Turizo, S.P.; González-Silvera, A.; Santamaría-del-ángel, E.; Tan, J.; Frouin, R. Evaluation of semi-analytical algorithms to retrieve particulate and dissolved absorption coefficients in Gulf of California optically complex waters. Remote Sens. 2018, 10, 1443. [Google Scholar] [CrossRef]
- Glukhovets, D. An Overview of the Special Issue on Seawater Bio-Optical Characteristics from Satellite Ocean Color Data. Remote Sens. 2023, 15, 1094. [Google Scholar] [CrossRef]
- van Oostende, M.; Hieronymi, M.; Krasemann, H.; Baschek, B. Global ocean colour trends in biogeochemical provinces. Front. Mar. Sci. 2023, 10, 1052166. [Google Scholar] [CrossRef]
- El Kassar, J.; Juhls, B.; Hieronymi, M.; Preusker, R.; Morgenstern, A.; Fischer, J.; Overduin, P.P. Optical remote sensing (Sentinel-3 OLCI) used to monitor dissolved organic carbon in the Lena River, Russia. Front. Mar. Sci. 2023, 10, 1082109. [Google Scholar] [CrossRef]
- Higa, H.; Sugahara, S.; Salem, S.I.; Nakamura, Y.; Suzuki, T. An estimation method for blue tide distribution in Tokyo Bay based on sulfur concentrations using Geostationary Ocean Color Imager (GOCI). Estuar. Coast. Shelf Sci. 2020, 235, 106615. [Google Scholar] [CrossRef]
- Salem, S.I.; Strand, M.H.; Higa, H.; Kim, H.; Kazuhiro, K.; Oki, K.; Oki, T. Evaluation of meris chlorophyll-a retrieval processors in a complex turbid lake kasumigaura over a 10-year mission. Remote Sens. 2017, 9, 1022. [Google Scholar] [CrossRef]
- Dalin, J. Estimation of Water Transparency from Remote Sensing Data Based on A New Underwater Visibility Theory. 2020. Available online: https://tsukuba.repo.nii.ac.jp/record/55096/files/DA09505.pdf (accessed on 5 September 2024).
- Chen, M.; Xiao, F.; Wang, Z.; Feng, Q.; Ban, X.; Zhou, Y.; Hu, Z. An Improved QAA-Based Method for Monitoring Water Clarity of Honghu Lake Using Landsat TM, ETM+ and OLI Data. Remote Sens. 2022, 14, 3798. [Google Scholar] [CrossRef]
- Higa, H.; Muto, M.; Salem, S.I.; Kobayashi, H.; Ishizaka, J.; Ogata, K.; Toratani, M.; Takahashi, K.; Maupin, F.; Victori, S. Optical Characterization of Coastal Waters with Atmospheric Correction Errors: Insights from SGLI and AERONET-OC. Remote Sens. 2024, 16, 3626. [Google Scholar] [CrossRef]
- Ahmed, M.; Mumtaz, R.; Anwar, Z.; Shaukat, A.; Arif, O.; Shafait, F. A Multi–Step Approach for Optically Active and Inactive Water Quality Parameter Estimation Using Deep Learning and Remote Sensing. Water 2022, 14, 2112. [Google Scholar] [CrossRef]
- Li, L.; Li, L.; Song, K.; Li, Y.; Tedesco, L.P.; Shi, K.; Li, Z. An inversion model for deriving inherent optical properties of inland waters: Establishment, validation and application. Remote Sens. Environ. 2013, 135, 150–166. [Google Scholar] [CrossRef]
- Kerrisk, G.; Drayson, N.; Ford, P.; Botha, H.; Anstee, J. Performance assessment of serial dilutions for the determination of backscattering properties in highly turbid waters. Limnol. Oceanogr. Methods 2023, 21, 243–258. [Google Scholar] [CrossRef]
- Zaneveld, R.; Barnard, A.; Lee, Z. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications. 2006. Available online: https://ioccg.org/reports/report5.pdf (accessed on 11 September 2024).
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. An Update of the Quasi-Analytical Algorithm (QAA_v5). Int. Ocean. Color Group Softw. Rep. 2009, 1, 1–9. [Google Scholar]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755. [Google Scholar] [CrossRef]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized Ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef] [PubMed]
- Jorge, D.S.F.; Loisel, H.; Jamet, C.; Dessailly, D.; Demaria, J.; Bricaud, A.; Maritorena, S.; Zhang, X.; Antoine, D.; Kutser, T.; et al. A three-step semi analytical algorithm (3SAA) for estimating inherent optical properties over oceanic, coastal, and inland waters from remote sensing reflectance. Remote Sens. Environ. 2021, 263, 112537. [Google Scholar] [CrossRef]
- Maritorena, S.; Siegel, D.A. Consistent merging of satellite ocean color data sets using a bio-optical model. Remote Sens. Environ. 2005, 94, 429–440. [Google Scholar] [CrossRef]
- Deng, L.; Zhou, W.; Cao, W.; Wang, G.; Zheng, W.; Xu, Z.; Li, C.; Yang, Y.; Xu, W.; Zeng, K.; et al. Evaluating semi-analytical algorithms for estimating inherent optical properties in the South China Sea. Opt. Express 2020, 28, 13155. [Google Scholar] [CrossRef]
- Smyth, T.J.; Moore, G.F.; Hirata, T.; Aiken, J. Semianalytical model for the derivation of ocean color inherent optical properties: Description, implementation, and performance assessment. Appl. Opt. 2006, 45, 8116–8131. [Google Scholar] [CrossRef]
- Hoge, F.E.; Lyon, P.E. Satellite retrieval of inherent optical properties by linear matrix inversion of oceanic radiance models: An analysis of model and radiance measurement errors. J. Geophys. Res. Ocean. 1996, 101, 16631–16648. [Google Scholar] [CrossRef]
- Hoge, F.E.; Lyon, P.E. New tools for the study of oceanic eddies: Satellite derived inherent optical properties. Remote Sens. Environ. 2005, 95, 444–452. [Google Scholar] [CrossRef]
- Chen, J.; Quan, W.; Duan, H.; Xing, Q.; Xu, N. An Improved Inherent Optical Properties Data Processing System for Residual Error Correction in Turbid Natural Waters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6596–6607. [Google Scholar] [CrossRef]
- Dall’olmo, G.; Gitelson, A.A. Absorption Properties of Dissolved and Particulate Matter in Turbid Productive Inland Lakes. In Proceedings of the Ocean Optics XVII, Montreal, QC, Canada, 9–13 October 2006; Available online: https://scispace.com/pdf/absorption-properties-of-dissolved-and-particulate-matt-er-38olblnet7.pdf (accessed on 6 October 2024).
- Xue, K.; Boss, E.; Ma, R.; Shen, M. Algorithm to derive inherent optical properties from remote sensing reflectance in turbid and eutrophic lakes. Appl. Opt. 2019, 58, 8549. [Google Scholar] [CrossRef]
- Xue, K.; Ma, R.; Shen, M.; Wu, J.; Hu, M.; Guo, Y.; Cao, Z.; Xiong, J. Horizontal and vertical migration of cyanobacterial blooms in two eutrophic lakes observed from the GOCI satellite. Water Res. 2023, 240, 120099. [Google Scholar] [CrossRef]
- Feng, C.; Zhu, Y.; Shen, A.; Li, C.; Song, Q.; Tao, B.; Zeng, J. Assessment of GCOM-C Satellite Imagery in Bloom Detection: A Case Study in the East China Sea. Remote Sens. 2023, 15, 691. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. A blended inherent optical property algorithm for global satellite ocean color observations. Limnol. Oceanogr. Methods 2019, 17, 377–394. [Google Scholar] [CrossRef]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.W.; Bricaud, A.; Brotas, V.; Ciotti, A.M.; Clementson, L.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining phytoplankton diversity from ocean color: A scientific roadmap for future development. Front. Mar. Sci. 2017, 4, 55. [Google Scholar] [CrossRef]
- Pegau, S.; Zunefeld, J.R.; Mitchell, B.G.; Muellel, J.L.; Kahru, M.; Wieland, J.; Stramska, M. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Rev. 4, Vol. IV: Inherent Optical Properties: Instruments, Characterisations, Field Measurements and Data Analysis Protocols. 2003. Available online: https://ntrs.nasa.gov/api/citations/20030093642/downloads/20030093642.pdf (accessed on 20 October 2024).
- Lee, Z.; Shang, S.; Wang, Y.; Wei, J.; Ishizaka, J. Nature of optical products inverted semianalytically from remote sensing reflectance of stratified waters. Limnol. Oceanogr. 2020, 65, 387–400. [Google Scholar] [CrossRef]
- Gilerson, A.; Herrera-Estrella, E.; Foster, R.; Agagliate, J.; Hu, C.; Ibrahim, A.; Franz, B. Determining the Primary Sources of Uncertainty in Retrieval of Marine Remote Sensing Reflectance from Satellite Ocean Color Sensors. Front. Remote Sens. 2022, 3, 857530. [Google Scholar] [CrossRef]
- Loisel, H.; Jorge, D.S.F.; Reynolds, R.A.; Stramski, D. A synthetic optical database generated by radiative transfer simulations in support of studies in ocean optics and optical remote sensing of the global ocean. Earth Syst. Sci. Data 2023, 15, 3711–3731. [Google Scholar] [CrossRef]
- Bi, S.; Hieronymi, M.; Röttgers, R. Bio-geo-optical modelling of natural waters. Front. Mar. Sci. 2023, 10, 1196352. [Google Scholar] [CrossRef]
- Kolluru, S.; Gedam, S.S.; Inamdar, A.B. Subcomponent inherent optical properties retrieval from total absorption coefficient and remote sensing reflectance measured in coastal waters. J. Earth Syst. Sci. 2021, 130, 159. [Google Scholar] [CrossRef]
- Jordan, T.M.; Dall'Olmo, G.; Tilstone, G.; Brewin, R.J.W.; Nencioli, F.; Airs, R.; Thomas, C.S.; Schlüter, L. A compilation of surface inherent optical properties and phytoplankton pigment concentrations from the Atlantic Meridional Transect. Earth Syst. Sci. Data 2025, 17, 493–516. [Google Scholar] [CrossRef]
- Fumenia, A.; Loisel, H.; Reynolds, R.A.; Stramski, D. Relationships between the concentration of particulate organic nitrogen and the inherent optical properties of seawater in oceanic surface waters. EGUsphere 2024, 2024, 1–41. [Google Scholar]
- Andrade, C.; Alcântara, E.; Bernardo, N.; Kampel, M. An assessment of semi-analytical models based on the absorption coefficient in retrieving the chlorophyll-a concentration from a reservoir. Adv. Space Res. 2019, 63, 2175–2188. [Google Scholar] [CrossRef]
- Houskeeper, H.F.; Draper, D.; Kudela, R.M.; Boss, E. Chlorophyll absorption and phytoplankton size information inferred from hyperspectral particulate beam attenuation. Appl. Opt. 2020, 59, 6765. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Wu, G. Satellite retrieval of oceanic particulate organic nitrogen concentration. Front. Mar. Sci. 2022, 9, 943867. [Google Scholar] [CrossRef]
- Koestner, D.; Stramski, D.; Reynolds, R.A. A Multivariable Empirical Algorithm for Estimating Particulate Organic Carbon Concentration in Marine Environments from Optical Backscattering and Chlorophyll-a Measurements. Front. Mar. Sci. 2022, 9, 941950. [Google Scholar] [CrossRef]
- Stramski, D.; Joshi, I.; Reynolds, R.A. Ocean color algorithms to estimate the concentration of particulate organic carbon in surface waters of the global ocean in support of a long-term data record from multiple satellite missions. Remote Sens. Environ. 2022, 269, 112776. [Google Scholar] [CrossRef]
- Kong, C.E.; Sathyendranath, S.; Jackson, T.; Stramski, D.; Brewin, R.J.W.; Kulk, G.; Jönsson, B.F.; Loisel, H.; Galí, M.; Le, C. Comparison of ocean-colour algorithms for particulate organic carbon in global ocean. Front. Mar. Sci. 2024, 11, 1309050. [Google Scholar] [CrossRef]
- Galí, M.; Falls, M.; Claustre, H.; Aumont, O.; Bernardello, R. Bridging the gaps between particulate backscattering measurements and modeled particulate organic carbon in the ocean. Biogeosciences 2022, 19, 1245–1275. [Google Scholar] [CrossRef]
- Kobayashi, H.; Toratani, M.; Matsumura, S.; Siripong, A.; Lirdwitayaprasit, T.; Jintasaeranee, P. Optical Properties of Inorganic Suspended Solids and Their Influence on Coastal Ocean Color Remote Sensing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 997–1001. [Google Scholar]
- Fuller, C.B.; Bonner, J.S.; Islam, M.S.; Ojo, T.; Page, C.A.; Kirkey, W.D. Estimating colloidal concentration using acoustic backscatter. IEEE Sens. J. 2013, 13, 4546–4555. [Google Scholar] [CrossRef]
- Sahin, C.; Verney, R.; Sheremet, A.; Voulgaris, G. Acoustic backscatter by suspended cohesive sediments: Field observations, Seine Estuary, France. Cont. Shelf Res. 2017, 134, 39–51. [Google Scholar] [CrossRef]
- Vergne, A.; Le Coz, J.; Berni, C. Some Backscatter Modeling Issues Complicating the Sonar-Based Monitoring of Suspended Sediments in Rivers. Water Resour. Res. 2023, 59, e2022WR032341. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Overview of the Application of Remote Sensing in Effective Monitoring of Water Quality Parameters. Remote Sens. 2023, 15, 1938. [Google Scholar] [CrossRef]
- Mitchell, C.; Cunningham, A.; McKee, D. Remote sensing of shelf sea optical properties: Evaluation of a quasi-analytical approach for the Irish Sea. Remote Sens. Environ. 2014, 143, 142–153. [Google Scholar] [CrossRef]
- Mizunoya, T.; Nozaki, N.; Singh, R.K. Impact of the municipal merger on watershed management: A study of Lake Kasumigaura, Japan. Asia-Pac. J. Reg. Sci. 2021, 5, 673–704. [Google Scholar] [CrossRef]
- Jeppesen, E.; Meerhoff, M.; Davidson, T.A.; Trolle, D.; Søndergaard, M.; Lauridsen, T.L.; Beklioglu, M.; Brucet, S.; Volta, P.; González-Bergonzoni, I.; et al. Climate change impacts on lakes: An integrated ecological perspective based on a multi-faceted approach, with special focus on shallow lakes. J. Limnol. 2014, 73 (Suppl. 1), 88–111. [Google Scholar]
- Oyama, Y.; Matsushita, B.; Fukushima, T.; Nagai, T.; Imai, A. A new algorithm for estimating chlorophyll-a concentration from multi-spectral satellite data in case II waters: A simulation based on a controlled laboratory experiment. Int. J. Remote Sens. 2007, 28, 1437–1453. [Google Scholar] [CrossRef]
- Oyama, Y.; Matsushita, B.; Fukushima, T.; Matsushige, K.; Imai, A. Application of spectral decomposition algorithm for mapping water quality in a turbid lake (Lake Kasumigaura, Japan) from Landsat TM data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 73–85. [Google Scholar] [CrossRef]
- Oyama, Y.; Matsushita, B.; Fukushima, T.; Chen, J.; Nagai, T.; Imai, A. Testing the spectral decomposition algorithm (SDA) for different phytoplankton species by a simulation based on tank experiments. Int. J. Remote Sens. 2010, 31, 1605–1623. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Kasuga, I.; Liu, M.; Katayama, H. Occurrence of antibiotic resistance genes as emerging contaminants in watersheds of Tama River and Lake Kasumigaura in Japan. In IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing: Bristol, UK, 2019; Volume 266. [Google Scholar]
- Higano, Y.; Sawada, T. The Dynamic Optimal Policy to Improve the Water Quality of Lake Kasumigaura. Stud. Reg. Sci. 1996, 26, 75–86. [Google Scholar] [CrossRef]
- Takamura, N.; Nakagawa, M. Photosynthesis and primary production in Lake Kasumigaura (Japan) monitored monthly since 1981. Ecol. Res. 2016, 31, 287. [Google Scholar] [CrossRef]
- Fukushima, T.; Arai, H. Regime shifts observed in Lake Kasumigaura, a large shallow lake in Japan: Analysis of a 40-year limnological record. Lakes Reserv. Sci. Policy Manag. Sustain. Use 2015, 20, 54–68. [Google Scholar] [CrossRef]
- MOE. MOE. 2023. Available online: https://www.env.go.jp/en/water/wq/lakes/origin.html (accessed on 1 July 2024).
- Lubac, B.; Loisel, H. Variability and classification of remote sensing reflectance spectra in the eastern English Channel and southern North Sea. Remote Sens. Environ. 2007, 110, 45–58. [Google Scholar] [CrossRef]
- Higa, H.; Ideno, R.; Salem, S.I.; Kobayashi, H. Uncertainty Analysis of Particle Backscattering Coefficient Measurement for Multiple Highly Turbid Water Areas in Ocean Color Remote Sensing. Sens. Mater. 2023, 35, 3807–3828. [Google Scholar] [CrossRef]
- HOBI Labs. HydroScat-6P Spectral Backscattering Sensor & Fluorometer User’s Manual. 2010. Available online: www.hobilabs.com (accessed on 25 October 2023).
- Babin, B.J.; Hardesty, D.M.; Suter, T.A. Color and shopping intentions: The intervening effect of price fairness and perceived affect. J. Bus. Res. 2003, 56, 541–551. [Google Scholar] [CrossRef]
- Neeley, A.R.; Mannino, A. (Eds.) IOCCG Protocol Series Ocean Optics & Biogeochemistry Protocols for Satellite Ocean Colour Sensor Validation Volume 1: Inherent Optical Property Measurements and Protocols: Absorption Coefficient; IOCCG Protocol Series; IOCCG: Dartmouth, NS, Canada, 2018. [Google Scholar]
- Kishino, M.; Takahashi, M.; Okami, N.; Ichimura, S. Estimation of the Spectral Absorption Coefficients of Phytoplankton In The Sea. Bull. Mar. Sci. 1985, 37, 634–642. [Google Scholar]
- Sosik, H.M.; Mitchell, B.G. Absorption, fluorescence, and quantum yield for growth in nitrogen-limited Dunaliella tertiolecta. Limnol. Oceanogr. 1991, 36, 910–921. [Google Scholar] [CrossRef]
- Yamashita, Y. Algorithm Description Ver. 1 (Vol. 1). Japan Aerospace Exploration Agency (JAXA). 2016. Available online: https://suzaku.eorc.jaxa.jp/GCOM_C/data/ATBD/ver2/V2ATBD_O3AB_CDOMa_Hirata.pdf (accessed on 25 February 2024).
- National Institute for Environmental Studies. Lake Kasumigaura Database, National Institute for Environmental Studies, Japan. 2016. Available online: https://db.cger.nies.go.jp/gem/moni-e/inter/GEMS/database/kasumi/contents/intro.html (accessed on 30 June 2024).
- Takamura, N.; Nakagawa, M.; Hanazato, T. Zooplankton abundance in the pelagic region of Lake Kasumigaura (Japan): Monthly data since 1980. Ecol. Res. 2017, 32. [Google Scholar] [CrossRef]
- National Institute for Environmental Studies. Lake Kasumigaura Database Interpretations of Observed Data. 2012. Available online: http://db.cger.nies.go.jp/gem/moni-e/inter/GEMS/database/kasumi/contents/database/datalist.html (accessed on 20 January 2024).
- Alvado, B.; Sòria-Perpinyà, X.; Vicente, E.; Delegido, J.; Urrego, P.; Ruíz-Verdú, A.; Soria, J.M.; Moreno, J. Estimating organic and inorganic part of suspended solids from sentinel 2 in different inland waters. Water 2021, 13, 2453. [Google Scholar] [CrossRef]
- Schartau, M.; Riethmüller, R.; Flöser, G.; van Beusekom, J.E.E.; Krasemann, H.; Hofmeister, R.; Wirtz, K. On the separation between inorganic and organic fractions of suspended matter in a marine coastal environment. Prog. Oceanogr. 2019, 171, 231–250. [Google Scholar] [CrossRef]
- Redfield, A.C. On the Proportions of Organic Derivatives in Sea Water and Their Relation to the Composition of Plankton. 1934. Available online: https://www.researchgate.net/publication/344709447 (accessed on 12 June 2024).
- Redfield, A.C. The biological control of chemical factors in the environment. Am. Sci. 1958, 46, 230A-221. [Google Scholar]
- Pinet, S.; Martinez, J.-M.; Ouillon, S.; Lartiges, B.; Villar, R.E. Variability of apparent and inherent optical properties of sediment-laden waters in large river basins–lessons from in situ measurements and bio-optical modeling. Opt. Express 2017, 25, A283. [Google Scholar] [CrossRef] [PubMed]
- Hoge, F.E.; Lyon, P.E.; Mobley, C.D.; Sundman, L.K. Radiative transfer equation inversion: Theory and shape factor models for retrieval of oceanic inherent optical properties. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Mobley, C. Remote-Sensing Retrieval of Oceanic Inherent Optical Properties by Inversion of the Radiative Transfer Equation. 2002. Available online: https://www.researchgate.net/publication/235033012 (accessed on 25 January 2024).
- Toratani, M.; Ogata, K.; Fukushima, H. SGLI Algorithm Theoretical Basis Document Atmospheric Correction Algorithm for Ocean Color. 2021. Available online: https://suzaku.eorc.jaxa.jp/GCOM_C/data/ATBD/ver3/V3ATBD_O2AB_NWLR_toratani.pdf (accessed on 24 July 2023).
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef]
- Fukushima’, H.; Toratani’, M.; Yamamiya’, S.; Mitom, Y. Atmospheric correction algorithms for adeos/octs ocean color data: Performance comparison based on ship and buoy measurements. Adv. Space Res. 2000, 25, 1015–1024. [Google Scholar] [CrossRef]
- Fukushima, H.; Toratani, M.; Murakami, H.; Deschamps, P.Y.; Frouin, R.; Tanaka, A. Evaluation of ADEOS-II GLI ocean color atmospheric correction using SIMBADA handheld radiometer data. J. Oceanogr. 2007, 63, 533–543. [Google Scholar] [CrossRef]
- Salem, S.I.; Toratani, M.; Higa, H.; Son, S.H.; Siswanto, E.; Ishizaka, J. Long-Term Evaluation of GCOM-C/SGLI Reflectance and Water Quality Products: Variability Among JAXA G-Portal and JASMES. Remote Sens. 2025, 17, 221. [Google Scholar] [CrossRef]
- Bailey, S.; He, X.; Jamet, C.; Ruddick, K.; Shanmugam, P.; Schroeder, T.; Stamnes, K.; Sterckx, S.; Steinmetz, F. IOCCG Technical Series Evaluation of Atmospheric Correction Algorithms over Turbid Waters Editors: Cédric Jamet Authors. 2019. Available online: https://ioccg.org/wp-content/uploads/2019/12/ioccg_atm-corr-report21nov2019.pdf (accessed on 28 June 2024).
- Gordon, H.R. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Hoge, F.E.; Wright, C.W.; Lyon, P.E.; Swift, R.N.; Yungel, J.K. Inherent optical properties imagery of the western North Atlantic Ocean: Horizontal spatial variability of the upper mixed layer. J. Geophys. Res. Ocean. 2001, 106, 31129–31140. [Google Scholar] [CrossRef]
- Lyon, P.E.; Hoge, F.E.; Wright, C.W.; Swift, R.N.; Yungel, J.K. Chlorophyll biomass in the global oceans: Satellite retrieval using inherent optical properties. Appl. Opt. 2004, 43, 5886–5892. [Google Scholar] [CrossRef]
- Werdell, P.J.; McKinna, L.I.; Boss, E.; Ackleson, S.G.; Craig, S.E.; Gregg, W.W.; Lee, Z.; Maritorena, S.; Roesler, C.S.; Rousseaux, C.S.; et al. An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 2018, 160, 186–212. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, Y.; Lee, Z.; Wang, D.; Chen, S.; Lai, W. A revision of NASA SeaDAS atmospheric correction algorithm over turbid waters with artificial Neural Networks estimated remote-sensing reflectance in the near-infrared. ISPRS J. Photogramm. Remote. Sens. 2022, 194, 235–249. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Q.; Wang, Y.; Zhang, Y. Evaluation of GOCI Remote Sensing Reflectance Spectral Quality Based on a Quality Assurance Score System in the Bohai Sea. Remote Sens. 2022, 14, 1075. [Google Scholar] [CrossRef]
- Guan, X.; Liu, Y. Bayesian Analysis for Fatigue Damage Prognostics and Remaining Useful Life Prediction. In Machine Learning and Knowledge Discovery for Engineering Systems Health Management; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012; pp. 203–243. [Google Scholar]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Słomska-Przech, K.; Panecki, T.; Pokojski, W. Heat maps: Perfect maps for quick reading? comparing usability of heat maps with different levels of generalization. ISPRS Int. J. Geo-Inf. 2021, 10, 562. [Google Scholar] [CrossRef]
- Simão, M.L.; Videiro, P.M.; Silva, P.B.A.; de Freitas Assad, L.P.; Sagrilo, L.V.S. Application of Taylor diagram in the evaluation of joint environmental distributions’ performances. Mar. Syst. Ocean Technol. 2020, 15, 151–159. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Salem, S.I.; Higa, H.; Kim, H.; Kazuhiro, K.; Kobayashi, H.; Oki, K.; Oki, T. Multi-algorithm indices and look-up table for chlorophyll-a retrieval in highly turbid water bodies using multispectral data. Remote Sens. 2017, 9, 556. [Google Scholar] [CrossRef]
- O'Shea, R.E.; Pahlevan, N.; Smith, B.; Boss, E.; Gurlin, D.; Alikas, K.; Kangro, K.; Kudela, R.M.; Vaičiūtė, D. A hyperspectral inversion framework for estimating absorbing inherent optical properties and biogeochemical parameters in inland and coastal waters. Remote Sens. Environ. 2023, 295, 113706. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations of light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Research. Ocean. 1998, 103, 33–64. [Google Scholar] [CrossRef]
- Rasse, R.; Dall’Olmo, G.; Graff, J.; Westberry, T.K.; van Dongen-Vogels, V.; Behrenfeld, M.J. Evaluating optical proxies of particulate organic carbon across the surface Atlantic ocean. Front. Mar. Sci. 2017, 4, 367. [Google Scholar] [CrossRef]
- Huang, C.; Jiang, Q.; Yao, L.; Yang, H.; Lin, C.; Huang, T.; Zhang, Y. Variation pattern of particulate organic carbon and nitrogen in oceans and inland waters. Biogeosciences 2018, 15, 1827–1841. [Google Scholar] [CrossRef]
- Schindler Wildhaber, Y.; Liechti, R.; Alewell, C. Organic matter dynamics and stable isotope signature as tracers of the sources of suspended sediment. Biogeosciences 2012, 9, 1985–1996. [Google Scholar] [CrossRef]
- Spencer, R.G.M.; Butler, K.D.; Aiken, G.R. Dissolved organic carbon and chromophoric dissolved organic matter properties of rivers in the USA. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Dadolahi, S.A.; Mohammad, A.H. Assessment of chromophoric dissolved organic matter and nutrient distribution in New Zealand rivers using satellite images. Appl. Ecol. Environ. Res. 2019, 17, 3575–3589. [Google Scholar] [CrossRef]
- Isada, T.; Abe, H.; Kasai, H.; Nakaoka, M. Dynamics of Nutrients and Colored Dissolved Organic Matter Absorption in a Wetland-Influenced Subarctic Coastal Region of Northeastern Japan: Contributions from Mariculture and Eelgrass Meadows. Front. Mar. Sci. 2021, 8, 711832. [Google Scholar] [CrossRef]
- Kobayashi, S.; Nakada, S.; Nakajima, M.; Yamamoto, K.; Akiyama, S.; Fuchi, M.; Hayashi, M.; Ishizaka, J. Visualization of the distribution of dissolved organic matter in Osaka Bay using a satellite ocean color sensor (COMS/GOCI). J. Water Environ. Technol. 2017, 15, 55–64. [Google Scholar] [CrossRef]
- Koliyavu, T.; Martias, C.; Singh, A.; Mounier, S.; Gérard, P.; Dupouy, C. Situ Variability of DOM in Relation with Biogeochemical and Physical Parameters in December 2017 in Laucala Bay (Fiji Islands) after a Strong Rain Event. J. Mar. Sci. Eng. 2021, 2021, 241. [Google Scholar] [CrossRef]
- Arellano, A.R.; Coble, P.G. Assessing carbon and nutrient inputs in a spring-fed estuary using fluorescence spectroscopy and discriminatory classification. Limnol. Oceanogr. 2015, 60, 789–804. [Google Scholar] [CrossRef]
- Doxaran, D.; Ehn, J.; Bélanger, S.; Matsuoka, A.; Hooker, S.; Babin, M. Optical characterisation of suspended particles in the Mackenzie River plume (Canadian Arctic Ocean) and implications for ocean colour remote sensing. Biogeosciences 2012, 9, 3213–3229. [Google Scholar] [CrossRef]
- Martinez-Vicente, V.; Land, P.E.; Tilstone, G.H.; Widdicombe, C.; Fishwick, J.R. Particulate scattering and backscattering related to water constituents and seasonal changes in the Western English Channel. J. Plankton Res. 2010, 32, 603–619. [Google Scholar] [CrossRef]
- Favareto, L.R.; Rudorff, N.; Kampel, M.; Frouin, R.; Röttgers, R.; Doxaran, D.; Murakami, H.; Dupouy, C. Bio-optical characterization and ocean colour inversion in the Eastern Lagoon of New Caledonia, South Tropical Pacific. Remote Sens. 2018, 10, 1043. [Google Scholar] [CrossRef]
- Ishizaka, J.; Yang, M.; Fujii, N.; Katano, T.; Hori, M.; Mine, T.; Saitoh, K.; Murakami, H. Use of AERONET-OC for validation of SGLI/GCOM-C products in Ariake Sea, Japan. J. Oceanogr. 2022, 78, 291–309. [Google Scholar] [CrossRef]
- Terrel, M.M.; Fukushima, T.; Matsushita, B.; Yoshimura, K.; Imai, A. Long-term light environment variability in Lake Biwa and Lake Kasumigaura, Japan: Modeling approach. Limnology 2012, 13, 237–252. [Google Scholar] [CrossRef]
- Miyazaki, T. Measuring the Water Quality of Lake Kasumigaura by LANDSAT. Remote Sensing. 1986. Available online: https://www.nies.go.jp/kanko/kenkyu/pdf/972089-1.pdf (accessed on 3 March 2024).
- Jaelani, L.M.; Matsushita, B.; Yang, W.; Fukushima, T. Evaluation of four MERIS atmospheric correction algorithms in Lake Kasumigaura, Japan. Int. J. Remote Sens. 2013, 34, 8967–8985. [Google Scholar] [CrossRef]
- Ogashawara, I.; Mishra, D.R.; Nascimento, R.F.F.; Alcântara, E.H.; Kampel, M.; Stech, J.L. Re-parameterization of a quasi-analytical algorithm for colored dissolved organic matter dominant inland waters. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 128–145. [Google Scholar] [CrossRef]
- Grunert, B.K.; Mouw, C.B.; Ciochetto, A.B. Deriving inherent optical properties from decomposition of hyperspectral non-water absorption. Remote Sens. Environ. 2019, 225, 193–206. [Google Scholar] [CrossRef]
- Kritten, L.; Preusker, R.; Brockmann, C.; Fincke, T.; Koponen, S.; Fischer, J. Water remote sensing reflectance from radiative transfer simulations on a global scale of Inherent Optical Properties. Earth Syst. Sci. Data Discuss. 2018, 2018, 1–14. [Google Scholar]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117, C01011. [Google Scholar] [CrossRef]
- Watanabe, F.; Mishra, D.R.; Astuti, I.; Rodrigues, T.; Alcântara, E.; Imai, N.N.; Barbosa, C. Parametrization and calibration of a quasi-analytical algorithm for tropical eutrophic waters. ISPRS J. Photogramm. Remote Sens. 2016, 121, 28–47. [Google Scholar] [CrossRef]
- Lewis, K.M.; Arrigo, K.R. Ocean Color Algorithms for Estimating Chlorophyll a, CDOM Absorption, and Particle Backscattering in the Arctic Ocean. J. Geophys. Res. Ocean. 2020, 125, e2019JC015706. [Google Scholar] [CrossRef]
- Woźniak, S.B.; Stramski, D.; Stramska, M.; Reynolds, R.A.; Wright, V.M.; Miksic, E.Y.; Cichocka, M.; Cieplak, A.M. Optical variability of seawater in relation to particle concentration, composition, and size distribution in the nearshore marine environment at Imperial Beach, California. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Stramski, D.; Bricaud, A.; Morel, A. Modeling the inherent optical properties of the ocean based on the detailed composition of the planktonic community. Appl. Opt. 2001, 40, 2929. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, M.S.; Boss, E.; Macdonald, J.B.; Pegau, W.S.; Barnard, A.H.; Zaneveld, J.R.V. A model for estimating bulk refractive index from the optical backscattering ratio and the implications for understanding particle composition in case I and case II waters. J. Geophys. Res. Ocean. 2001, 106, 14129–14142. [Google Scholar] [CrossRef]
- Cunningham, A.; Ramage, L.; McKee, D. Relationships between inherent optical properties and the depth of penetration of solar radiation in optically complex coastal waters. J. Geophys. Res. Ocean. 2013, 118, 2310–2317. [Google Scholar] [CrossRef]
- Xue, K.; Ma, R.; Duan, H.; Shen, M.; Boss, E.; Cao, Z. Inversion of inherent optical properties in optically complex waters using sentinel-3A/OLCI images: A case study using China’s three largest freshwater lakes. Remote Sens. Environ. 2019, 225, 328–346. [Google Scholar] [CrossRef]
- Tripathy, S.C.; Kerkar, A.U.; Sabu, P.; Padhi, S.K.; Pandi, S.R.; Sarkar, A.; Parli, B.V.; Mohan, R. Short-term time-series observations of phytoplankton light-absorption and productivity in Prydz Bay, coastal Antarctica. Front. Mar. Sci. 2024, 11, 1420179. [Google Scholar] [CrossRef]
- Wei, J.; Wang, M.; Mikelsons, K.; Jiang, L. Chlorophyll-Specific Absorption Coefficient of Phytoplankton in World Oceans: Seasonal and Regional Variability. Remote Sens. 2023, 15, 2423. [Google Scholar] [CrossRef]
- Murakami, H. Algorithm Theoretical Basis Document (ATBD) of GCOM-C Chlorophyll-a Concentration Algorithm (Version 2). Japan Aerospace Exploration Agency (JAXA). 2018. Available online: https://suzaku.eorc.jaxa.jp/GCOM_C/data/ATBD/ver2/V2ATBD_O3AB_Chla_Murakami.pdf (accessed on 10 May 2024).
- Bricaud, A.; Babin, M.; Morel, A.; Claustre, H. Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization. J. Geophys. Res. 1995, 100, 13321–13332. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Hu, C.; Lewis, M.; Arnone, R.; Li, Y.; Lubac, B. Time series of bio-optical properties in a subtropical gyre: Implications for the evaluation of interannual trends of biogeochemical properties. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Simis, S.; Zhang, Y. Validation of MERIS case-2 water products in lake taihu, China. GIScience Remote Sens. 2012, 49, 873–894. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Schroeder, T.; Clementson, L.A.; Brando, V.E.; Purcell, D.; Ford, P.; Williams, D.K.; Doxaran, D.; Anstee, J.; Thapar, N.; et al. Bio-optical properties of two neigboring coastal regions of tropical Northern Australia: The Van Diemen Gulf and Darwin Harbour. Front. Mar. Sci. 2017, 4, 114. [Google Scholar] [CrossRef]





| Channel | Center Wavelength (nm) | Bandwidth (nm) |
|---|---|---|
| VN1 | 380 | 10 |
| VN2 | 412 | 10 |
| VN3 | 443 | 10 |
| VN4 | 490 | 10 |
| VN5 | 530 | 20 |
| VN6 | 565 | 20 |
| VN7 | 673.5 | 20 |
| VN8 | 673.5 | 20 |
| VN9 | 763 | 12 |
| VN10 | 868.5 | 20 |
| VN11 | 868.5 | 20 |
| IOP Algorithm | Error Metrics | QAA | PML | LMI | GSM | GIOP |
|---|---|---|---|---|---|---|
| ap (λ) | MAPE | 0.31 | 0.35 | 0.36 | 0.54 | 0.29 |
| RMSE | 0.29 | 0.31 | 0.42 | 0.57 | 0.33 | |
| r | 0.98 | 0.96 | 0.95 | 0.94 | 0.95 | |
| F | 180.95 | 139.17 | 259.35 | 318.18 | 169.11 | |
| p-value | 8.9 × 10−59 | 4.2 × 10−52 | 2.6 × 10−68 | 6.9 × 10−74 | 4.9 × 10−57 | |
| % between ±30% to 1:1 | 91.81 | 85.83 | 79.31 | 75.04 | 85.97 | |
| aph (λ) | MAPE | 0.23 | 0.60 | 0.56 | 0.90 | 0.40 |
| RMSE | 0.08 | 0.24 | 0.17 | 0.21 | 0.14 | |
| r | 0.97 | 0.69 | 0.83 | 0.75 | 0.88 | |
| F | 43.84 | 30.59 | 47.49 | 61.19 | 37.06 | |
| p-value | 6.8 × 10−27 | 7.6 × 10−21 | 2.3 × 10−28 | 2.4 × 10−33 | 6.0 × 10−24 | |
| % between ±30% to 1:1 | 89.17 | 56.11 | 63.89 | 65.83 | 75.17 | |
| aNAP (λ) | MAPE | 2.18 | 3.10 | 1.29 | 0.98 | 4.02 |
| RMSE | 0.31 | 0.35 | 0.34 | 0.30 | 0.38 | |
| r | 0.85 | 0.74 | 0.73 | 0.84 | 0.73 | |
| F | 103.75 | 85.76 | 95.52 | 147.51 | 70.39 | |
| p-value | 5.5 × 10−45 | 1.3 × 10−40 | 4.7 × 10−43 | 1.5 × 10−53 | 2.9 × 10−36 | |
| % between ±30% to 1:1 | 74.19 | 69.58 | 61.25 | 75.53 | 62.03 | |
| aCDOM (λ) | MAPE | 0.70 | 0.10 | 0.52 | 0.46 | 0.76 |
| RMSE | 0.23 | 0.31 | 0.25 | 0.21 | 0.27 | |
| r | 0.85 | 0.65 | 0.83 | 0.87 | 0.79 | |
| F | 117.65 | 60.61 | 96.28 | 128.01 | 84.23 | |
| p-value | 5.6 × 10−48 | 3.8 × 10−33 | 3.1 × 10−43 | 4.9 × 10−50 | 3.4 × 10−40 | |
| % between ±30% to 1:1 | 71.25 | 52.50 | 66.67 | 73.33 | 59.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choto, M.; Higa, H.; Salem, S.I.; Siswanto, E.; Suzuki, T.; Mäll, M. Performance Evaluation of Inherent Optical Property Algorithms and Identification of Potential Water Quality Indicators Using GCOM-C Data in Eutrophic Lake Kasumigaura, Japan. Remote Sens. 2025, 17, 1621. https://doi.org/10.3390/rs17091621
Choto M, Higa H, Salem SI, Siswanto E, Suzuki T, Mäll M. Performance Evaluation of Inherent Optical Property Algorithms and Identification of Potential Water Quality Indicators Using GCOM-C Data in Eutrophic Lake Kasumigaura, Japan. Remote Sensing. 2025; 17(9):1621. https://doi.org/10.3390/rs17091621
Chicago/Turabian StyleChoto, Misganaw, Hiroto Higa, Salem Ibrahim Salem, Eko Siswanto, Takayuki Suzuki, and Martin Mäll. 2025. "Performance Evaluation of Inherent Optical Property Algorithms and Identification of Potential Water Quality Indicators Using GCOM-C Data in Eutrophic Lake Kasumigaura, Japan" Remote Sensing 17, no. 9: 1621. https://doi.org/10.3390/rs17091621
APA StyleChoto, M., Higa, H., Salem, S. I., Siswanto, E., Suzuki, T., & Mäll, M. (2025). Performance Evaluation of Inherent Optical Property Algorithms and Identification of Potential Water Quality Indicators Using GCOM-C Data in Eutrophic Lake Kasumigaura, Japan. Remote Sensing, 17(9), 1621. https://doi.org/10.3390/rs17091621








