SFRADNet: Object Detection Network with Angle Fine-Tuning Under Feature Matching

Abstract

Due to the distant acquisition and bird’s-eye perspective of remote sensing images, ground objects are distributed in arbitrary scales and multiple orientations. Existing detectors often utilize feature pyramid networks (FPN) and deformable (or rotated) convolutions to adapt to variations in object scale and orientation. However, these methods solve scale and orientation issues separately and ignore their deeper coupling relationships. When the scale features extracted by the network are significantly mismatched with the object, it is difficult for the detection head to effectively capture orientation of object, resulting in misalignment between object and bounding box. Therefore, we propose a one-stage detector—Scale First Refinement-Angle Detection Network (SFRADNet), which aims to fine-tune the rotation angle under precise scale feature matching. We introduce the Group Learning Large Kernel Network (GL²KNet) as the backbone of SFRADNet and employ a Shape-Aware Spatial Feature Extraction Module (SA-SFEM) as the primary component of the detection head. Specifically, within GL²KNet, we construct diverse receptive fields with varying dilation rates to capture features across different spatial coverage ranges. Building on this, we utilize multi-scale features within the layers and apply weighted aggregation based on a Scale Selection Matrix (SSMatrix). The SSMatrix dynamically adjusts the receptive field coverage according to the target size, enabling more refined selection of scale features. Based on precise scale features captured, we first design a Directed Guiding Box (DGBox) within the SA-SFEM, using its shape and position information to supervise the sampling points of the convolution kernels, thereby fitting them to deformations of object. This facilitates the extraction of orientation features near the object region, allowing for accurate refinement of both scale and orientation. Experiments show that our network achieves a mAP of 80.10% on the DOTA-v1.0 dataset, while reducing computational complexity compared to the baseline model.

1. Introduction

Remote sensing (RS) images often cover large areas with high spatial resolution, so they contain a large amount of ground object information in RS scenes. Object detection networks enable the accurate and rapid identification of ground objects from complex RS scenes, with widespread applications in urban development, geological disaster prevention and agricultural monitoring. However, due to the complexity of RS scenes and the multi-scale, multi-orientation characteristics of RS objects, efficiently modeling the morphological variations of these objects to meet the precise and rapid detection needs in RS contexts remains a prominent research topic.

Currently, RS object detectors are categorized into two types: two-stage and one-stage detectors. Two-stage detectors typically consist of a region proposal network (RPN) and a detection head. Detectors such as CAD-Net [1], Mask-OBB [2], ORPN [3], and APE [4] generate a series of anchors from feature maps of each stage of the RPN, and then preliminarily refine and classify these proposed anchors. In the second stage, the detection head performs operations such as ROIPooling or ROIAlign based on anchor regions to extract fine-grained features from feature maps, further classifying and precisely localizing anchors. In order to simplify the detection process and speed up the detection speed, the core goal of one-stage detectors such as O2-DNet [5] and DRN [6] is to extract features of the input RS images and proposed anchors of different sizes on feature maps, and complete the classification of the object and the positioning of the bounding box (BBox) at the detection head at one time, so as to achieve the purpose of rapid detection. However, one-stage detectors lack a positive-negative sample assignment mechanism and do not incorporate ROIPooling or ROIAlign operations. As a result, background noise is mixed into the subsequent extraction of orientation features, interfering with the detection results.

Compared to natural scenes, RS images possess broad fields of view and bird’s-eye perspectives, leading to object distributions at arbitrary scales and orientations. To address the significant differences in scales of object, traditional strategies predominantly employ feature pyramid networks (FPN) [7] or make improvements based on FPN [8]. Additionally, ignoring computational overhead, Transformer-based models leverage powerful global modeling capabilities, offering a novel approach to managing image scale disparities. STO-DETR [9] utilizes the Swin-Transformer as a backbone network to extract features from input images, accurately locating small objects among various scales of RS objects through the global modeling capability of the Transformer. FPNFormer [10] integrates the Transformer mechanism with feature pyramids, constructing a Transformer-based feature pyramid that mitigates inaccuracies in detection caused by significant scale differences in remote sensing objects by capturing global features across multiple scales. However, these multi-scale extraction methods are only improved for objects with obvious scale differences, and do not consider the difference between fine scales, which leads to the misalignment of scale features and objects, and it is easy to mix background noise in the subsequent orientation feature extraction. 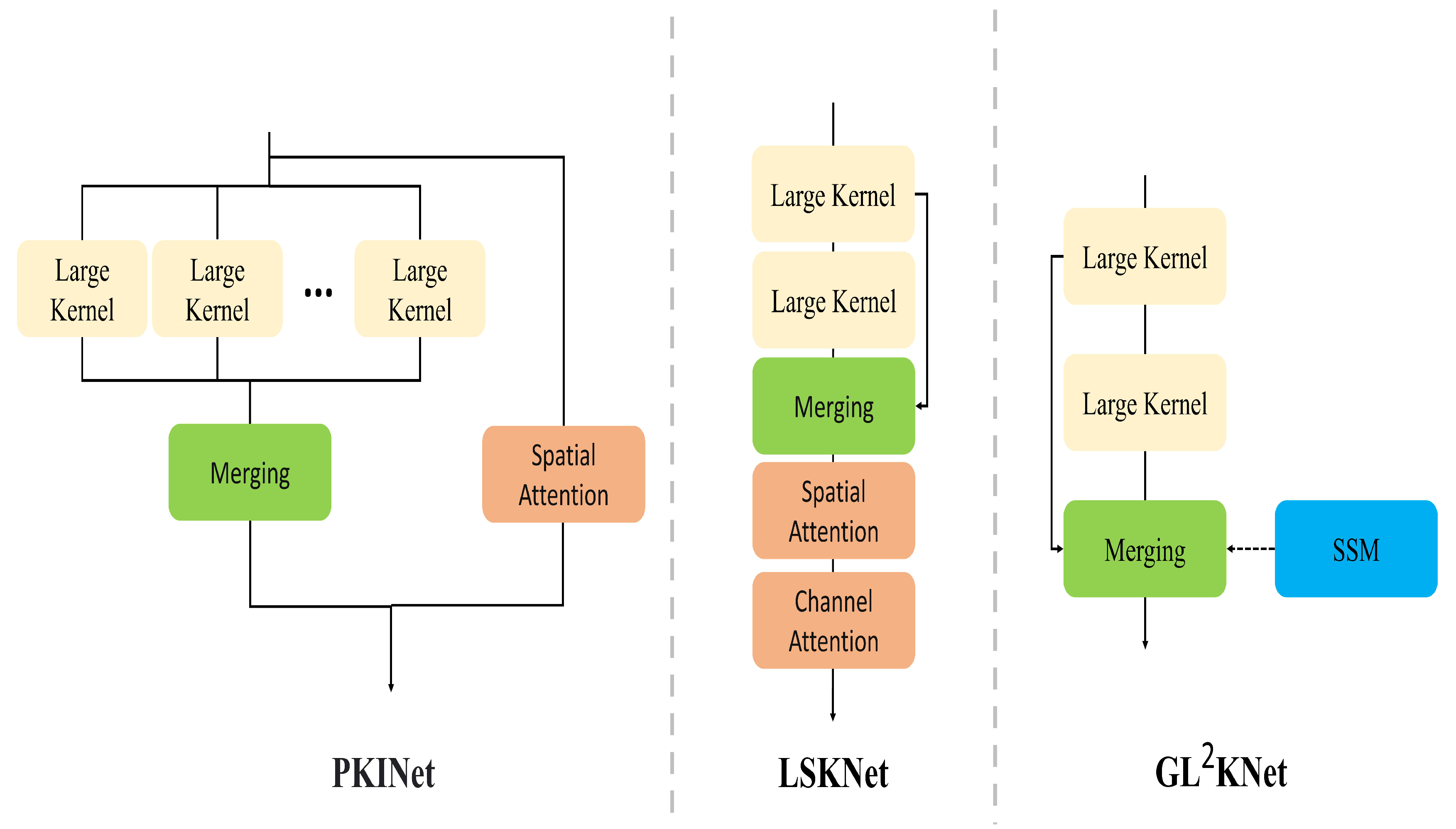Existing methods employing large-kernel convolutions [11,12] aim to address the issue of scale variation in object detection. These approaches often utilize attention mechanisms to capture multi-scale distribution differences. However, the additional attention mechanism increases the computational complexity in the inference stage and cannot meet the needs of real-time detection of remote sensing images.

We consider that in RS images, not only are there significant differences in object scales, but the multi-orientationality of objects also poses challenges for object detection. Some methods [13,14,15] utilize rotated anchors to locate objects in arbitrary orientations. However, achieving well spatial alignment between rotated anchors and RS objects is difficult, which can hinder the provision of sufficient orientation features for regression. Chen et al. [16] proposed a conversion algorithm from horizontal BBoxes to rotated ones to solve the detection of arbitrarily oriented dense objects in RS images. Unlike traditional methods that present many multi-rotated anchors, this approach rotates the proposed horizontal BBoxes to appropriate angles by calculating the relationship function between angles and distances. This results in higher-quality rotated anchors, facilitating subsequent positional corrections. Pu et al. [17] designed a rotational convolution that predicts the direction of rotation by adjusting the input conditional parameters and using a fully connected layer. This operation allows the convolution kernel to adapt to the rotation angle, so as to meet the feature extraction of the rotated object. However, the above-mentioned orientation feature extraction method is achieved by changing the position of the convolution kernel sampling points, and a single label cannot respond well to the direction changes of the object during supervised training, lacking strong supervision information. Adopting a dense angle rotation strategy will address the problem of increased parameter and computational complexity.

In summary, some existing RS object detection models recognize the differences in object scale and orientation and make targeted improvements. However, these methods treat scale and orientation issues separately, failing to consider the more profound correlation between them and neglecting the impact of scale on orientational representation. This oversight leads to spatial misalignment in RS object detection. Specifically, this misalignment can be categorized into the following three aspects:

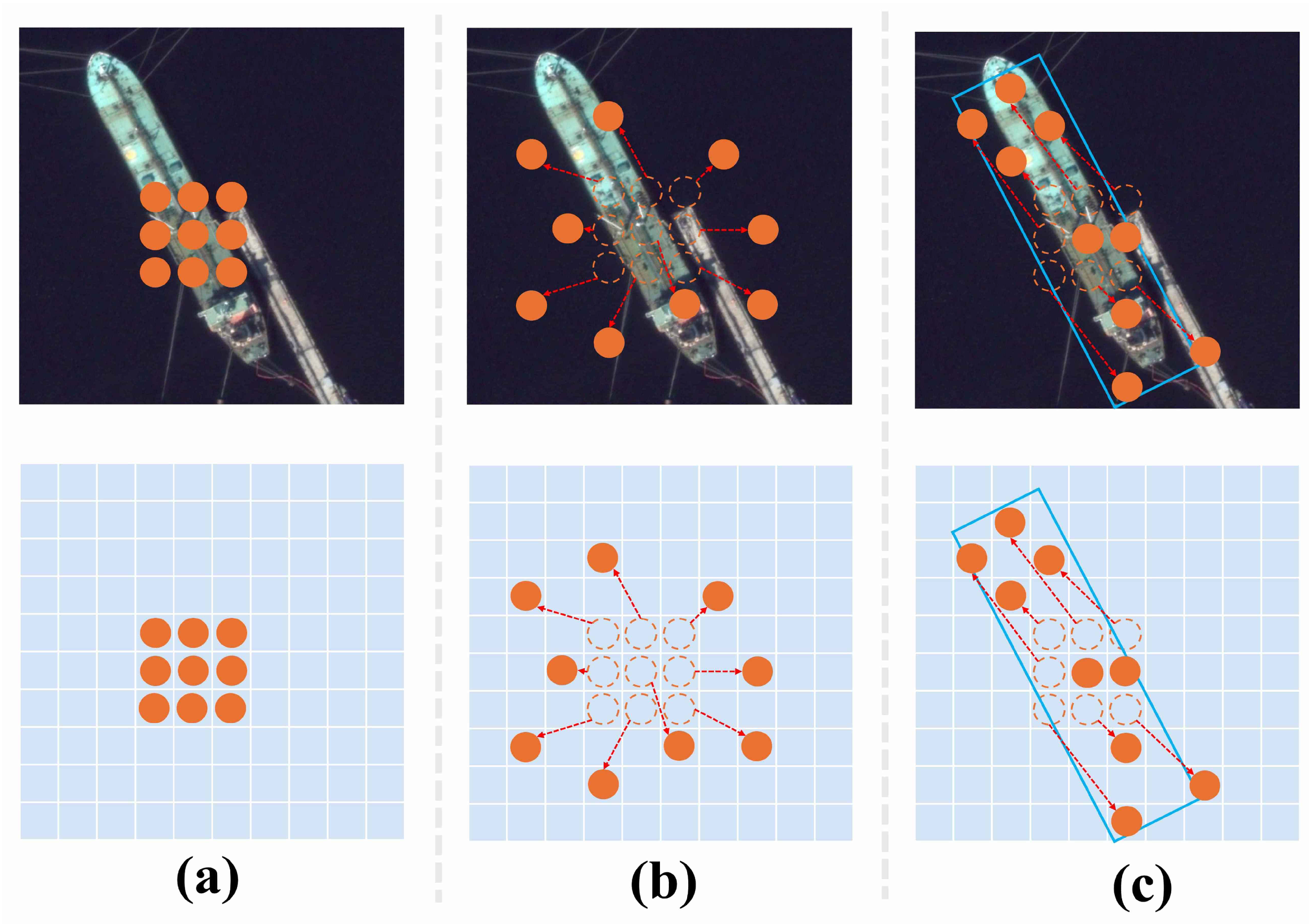
(a) Scale Misalignment: The scales of RS objects change progressively, particularly among different object types. For instance, as illustrated in Figure 1, the size discrepancies result in varying scales: the pixel areas of a car are approximately 20 × 20, while a yacht and a cargo ship occupy roughly 150 × 90 and 400 × 200 pixels, respectively. Current RS detectors typically construct FPNs that fuse fixed-level feature maps from the backbone. However, there may be three different pixel size differences among ship types, namely 400 × 200, 350 × 150, and 200 × 100. This could substantially increase the computational complexity if additional spatial pyramids are set up for these three scales. Moreover, using Transformers for global feature extraction may introduce significant background noise, which can negatively impact the subsequent refinement of anchors. Therefore, existing methods for handling scales have difficulty adapting to more subtle scale changes in RS scenarios.

(b) Relationship Between Scale Misalignment and Orientation: Inadequate precision in acquiring scale features can hinder the network’s ability to extract orientation features from the pyramid’s feature maps, resulting in inaccurate regression of the rotated BBoxes. As shown in Figure 1b, when the detection head receives an excessively large scale feature for positioning, these large-scale features encompass the object’s scale information and capture noise from the surrounding environment. This interference complicates the regression localization of the object, causing the predicted rotated BBox to include not only the object itself but also elements from the surrounding environment. Consequently, the orientation of the rotated BBox fails to reflect the object’s proper orientation. Conversely, when scale features are set too small, the receptive field cannot capture the overall contour characteristics of the object, leading to the absence of holistic orientation features. In this case, the predicted BBox is confined within the overall contour of the object, rendering the expressed rotated orientation unrepresentative of the object’s actual orientation.

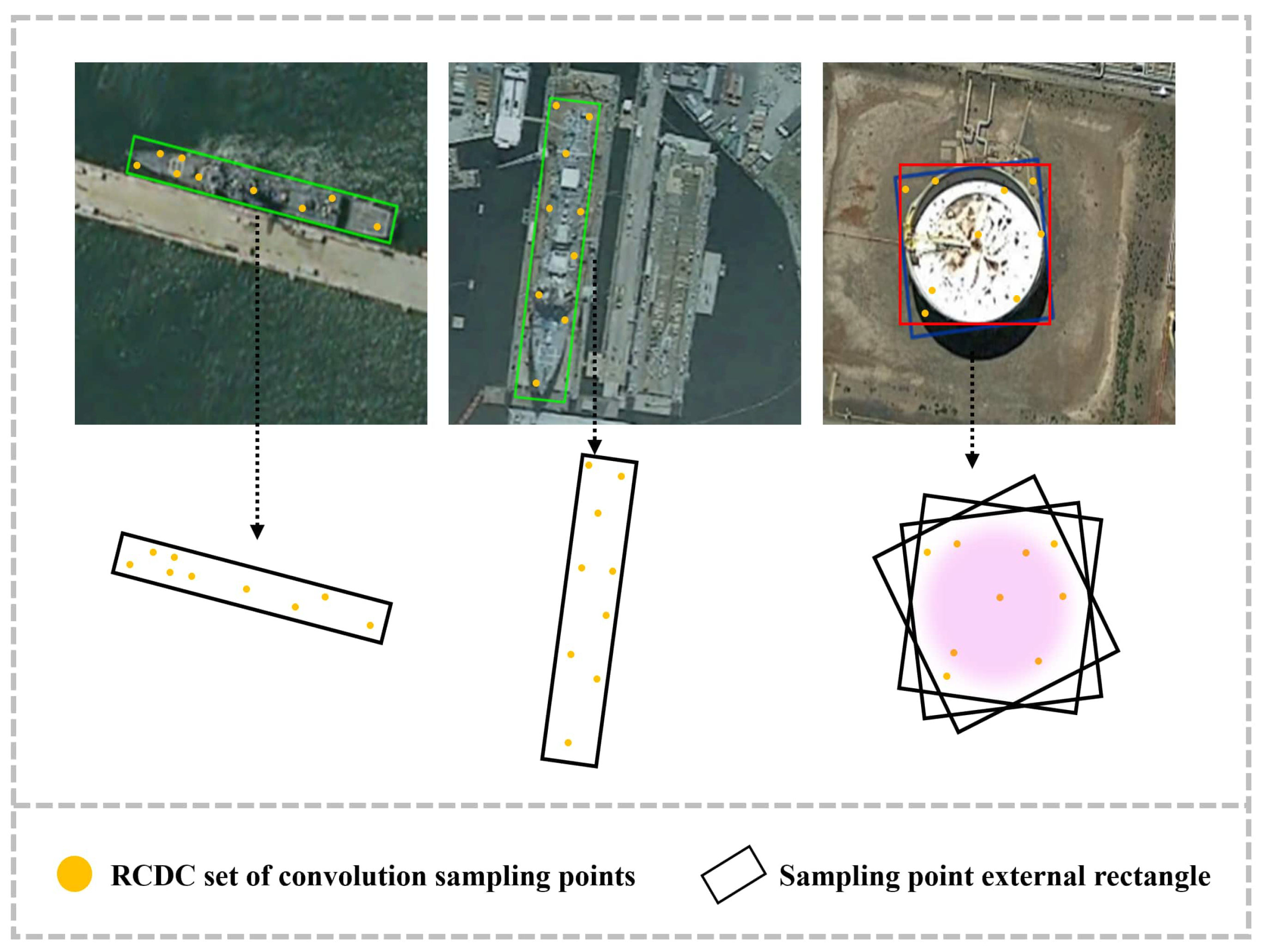
(c) Orientational Misalignment: Some existing deformable convolutions adapt to the direction of the object by changing the position of the sampling points of the convolution kernel, but the learning task is complex because the convolution kernel needs to learn the offset of any position on the complete feature map to determine the position of the sampling points. In addition, during training, the supervision provided by a single position and class label is limited, which cannot provide efficient supervision guidance for determining the sampling position of the convolutional kernel. As a result, the sampling locations can deviate significantly, introducing noise into the orientation features and interfering detection accuracy.

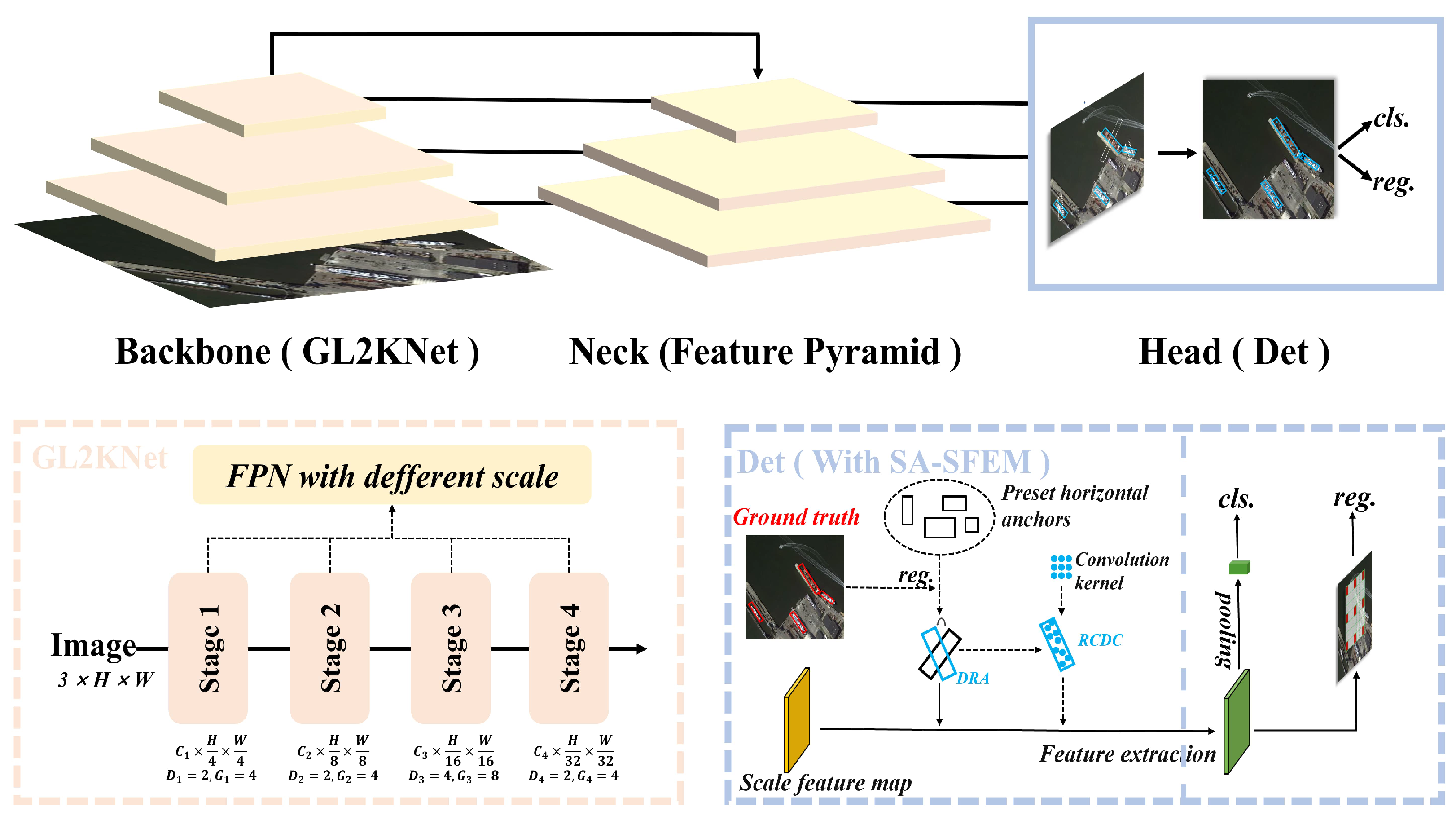
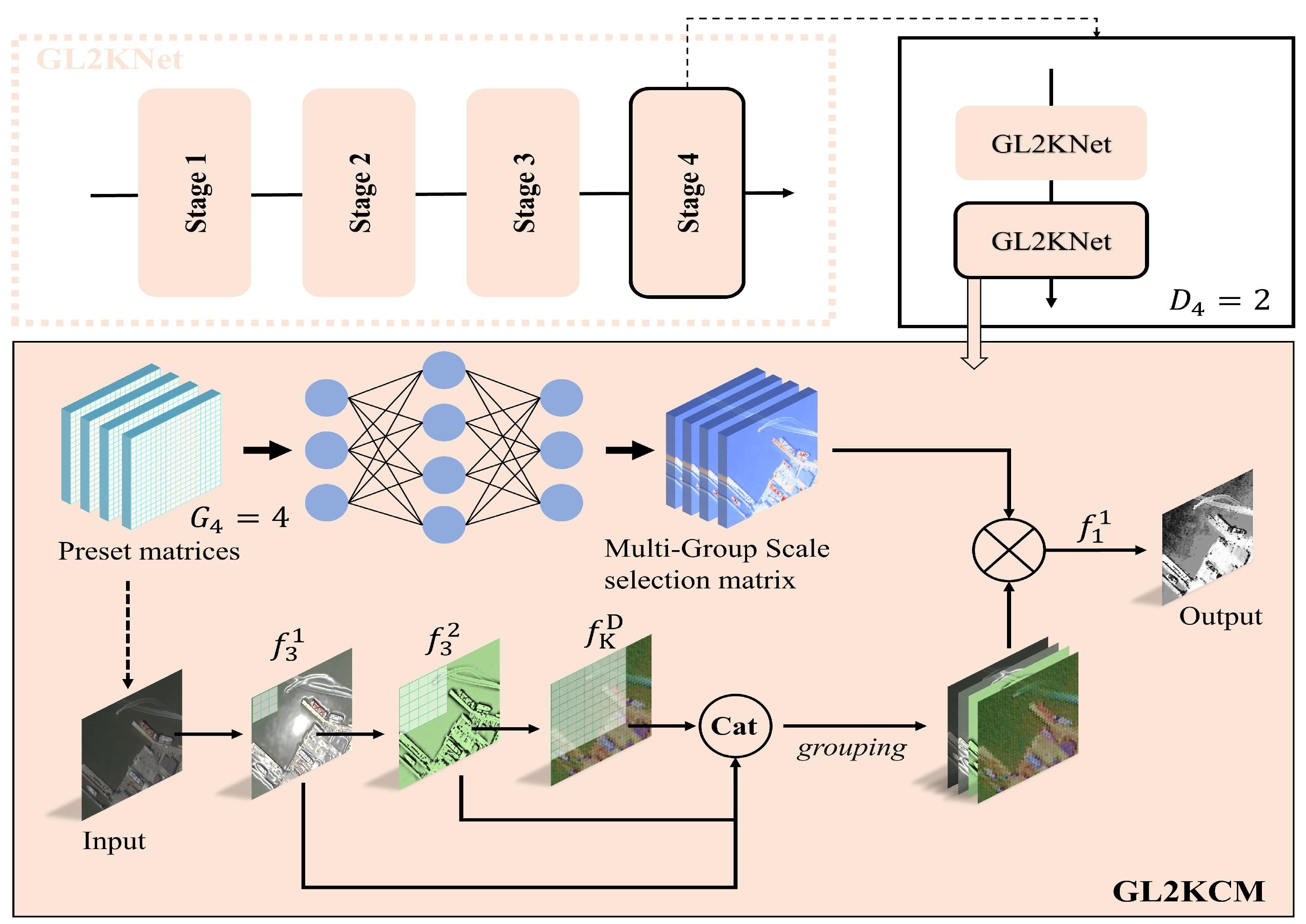
The analysis above shows that the key to resolving spatial misalignment in RS object detection lies in orientation refinement based on scale. To address the scale and orientation misalignment issues for objects, we propose the Scale First Refinement-Angle Detection Network (SFRADNet), which aims to resolve both scale and directional misalignment issues for arbitrarily oriented remote sensing targets. SFRADNet consists of two main components: the group learning large kernel network (GL²KNet) and the Shape-Aware Spatial Feature Extraction Module (SA-SFEM).The GL²KNet dynamically adjusts the receptive field coverage through inter-layer feature aggregation, addressing the issue of imprecise scale feature extraction for targets of arbitrary sizes. GL²KNet is constructed by stacking different numbers of Group Learning Large Kernel Convolution Modules (GL²KCMs) at various stages. Within each module, multiple layers of small dilated convolutional kernels are used to replace large convolutional kernels with the same receptive field, enabling the extraction of more refined scale features from the target’s neighborhood. Furthermore, Scale Selection Matrix (SSMatrix) is employed to capture spatial feature distribution differences at fine scales, followed by weighted fusion within the layer, achieving more accurate scale feature extraction. Unlike other large-kernel convolution methods, our model does not rely on attention mechanisms during inference, thereby avoiding the computational overhead associated with complex attention operations and maintaining high inference efficiency. Building upon the fine-scale features of the object, the SA-SFEM first performs preliminary refinements on horizontal anchors to form Directed Guide Boxes (DGBoxes). Utilizing the angular information from the DGBoxes, the convolution kernels are rotated accordingly, and uniform sampling is conducted based on the location and shape of the DGBoxes. the convolution kernel can dynamically change according to the shape of the object to form Region-Constrained Deformable Convolutions (RCDCs). RCDCs provide strong supervisory information during training, making them more sensitive to the object’s orientation and effectively alleviating orientational misalignment. The main contributions of this paper are as follows:

1.

We conduct a focused analysis and review of the phenomenon of multiple misalignments in current RS object detection, particularly how severe scale misalignment significantly impacts subsequent orientational alignment.

2.

To address the issue of imprecise scale feature extraction in current methods, we propose GL²KNet, a novel backbone capable of performing diversified and fine-grained modeling of targets at different scales. During the inference, GL²KNet eliminates the need for attention mechanisms and instead employs a SSMatrix for weighted feature fusion. This approach not only enhances the precision of scale feature extraction but also significantly improves inference efficiency, making it more suitable for real-time applications.

3.

We propose the SA-SFEM, which introduces a novel deformable convolution using DGBoxes as supervision. This allows the convolution kernel sampling points to better align with object morphology, improving orientation feature extraction and addressing the weak supervision of previous deformable convolutions. Additionally, it can be combined with the GL²KNet to enable accurate object detection with appropriately scale features.

The remainder of the paper is organized as follows. Section 2 reviews the related works and analyzes the existing problems. In Section 3, a detailed description of the proposed SFRADNet is presented. In Section 4, extensive experiments are conducted and the results are discussed. Conclusions are summarized in Section 5.

2. Related Works

Due to the arbitrary scale and multi-directional distribution of RS objects, conventional deep learning detectors struggle to locate and classify objects of varying scales and orientations accurately. To solve this issue, current mainstream approaches often adopt a decoupled strategy for improving either scale feature or orientation feature extraction independently rather than integrating these methods cohesively.

2.1. Scale Feature Extraction

In RS detection tasks, detectors often need to accommodate significant scale differences among objects. Previous studies have typically addressed this challenge by designing specific FPN, altering convolution structures, and employing attention mechanisms for the adaptive weighting of objects at different scales. NPMMR-Det [18] constructs a non-local excited pyramid attention mechanism and incorporates prior features of similar object profiles from a bird’s-eye view to guide the model in focusing on key features of the object while suppressing complex background noise, thereby refining the extraction of scale features. Li et al. [19] proposed an enhanced FPN based on multi-scale feature extraction for objects, which introduces inception blocks into the lateral connections of the FPN to improve the feature representation capability of the encoder and decoder. This approach better extracts features in layers to solve the variations of multi-scale objects in RS images. Pan et al. [6] introduced a feature selection module that adjusts the receptive field based on the shape and orientation of objects, allowing features to be transmitted to the detection head for precise detection.

Similarly, LO-Det [20] develops the CSA-DRF (Channel Separation-Aggregation and Dynamic Receptive Field) module for efficient feature extraction, where the DRF module employs stacked dilated convolutions to expand the receptive field, improving the capacity for global information extraction. The CSA module reduces the number of feature channels generated by convolutions, significantly lowering the computational complexity of the DRF. The CSA-DRF module ensures that the overall model maintains high accuracy in RS image detection while benefiting from lightweight architecture. SAHR-CapsNet [21] designs a high-resolution capsule network that integrates spatial and channel attention. In this network, the channel feature attention reflects the interdependencies among feature channels to adapt to multi-scale RS objects. The spatial feature attention computes global information through weighting to suppress background features. Combining these two attention mechanisms alleviates the challenges of extracting complex features from RS objects. SCRDet [22] introduces a multi-dimensional attention network that enables fixed feature maps to learn the significance between channels, representing foreground and background scores to suppress background information. This approach solve the issue of excessive noise potentially overwhelming object information, thereby reducing the rates of missed detections and false positives. However, the above methods are often structurally complex, computationally expensive, and unable to perform precise feature extraction for objects of arbitrary scales. These represent limitations in achieving accurate and rapid detection of RS objects.

In addition to the aforementioned methods for obtaining scale features, large-kernel convolutions have recently gained popularity as backbones for multi-scale feature extraction. For instance, PeLK [23] expands the receptive field of convolutions to a size of 101 × 101, enabling the extraction of larger-scale features on deep semantic feature maps that correspond to targets in the original image. Similarly, PKINet [12] utilizes an Inception module to capture features at different scales, where convolutional kernels of varying sizes operate in parallel within the module, followed by a spatial attention mechanism to filter out the most relevant scale features. LSKNet [11] employs sequential large-kernel convolutions and leverages both spatial and channel attention mechanisms to selectively express the appropriate scale of targets, achieving state-of-the-art results in various remote sensing tasks. In these large-kernel convolution methods, techniques such as dilated convolutions or kernel stacking are commonly used to reduce parameter counts and computational costs, while attention mechanisms are applied to filter out suitable features. However, the introduction of attention mechanisms necessitates additional computations for attention weights during inference, which seriously increases the computational complexity of the model.

When dealing with scale issues, we have taken advantage of the large-kernel network. We abandoned the traditional attention mechanism and used a SSMatrix to weight the multi-scale feature map of the large kernel convolution (Figure 2) to dynamically select the appropriate scale features. Our approach does not require attention during inference; instead, it uses a scale selectivity matrix to directly weight multi-scale features, avoiding an increase in computational complexity.

2.2. Orientation Feature Extraction

In addition to the accurate extraction of object scale features, it is also important to extract orientation features. Both affect the classification and localization ability of detectors. For the extraction of orientation features, the current mainstream detectors mainly focus on the improvement of the detection head, such as the improvement of the rotated anchors and the extraction optimization of fine-grained features. Ding et al. [24] proposed a supervised selection RoI learner that adjusts horizontal RoIs to rotated RoIs through supervised learning, addressing the misalignment between RoIs and objects. Traditionally, orientation-invariant feature extraction has been approached through spatial dimensions. ReDet [25] introduced a novel rotation-invariant RoI alignment method, incorporating an additional rotational dimension to ensure that rotated RoIs produce rotation-invariant features. R3Det [26] designs a feature refinement module (FRM) based on RetinaNet [27] to deal with the problem of feature misalignment caused by the change of BBox position. FRM encodes the position information of the current BBox to the corresponding feature points through pixel by pixel feature interpolation to realize feature reconstruction and alignment.

The quantity and quality of the generated rotated anchors are also a critical issue. Wang et al. [28] introduced a candidate region generation network that encodes the content of regions based on the shape of underlying anchors. Applying an adaptive scheme transforms the shapes of these anchors into features specific to individual locations, preventing a large number of uniformly generated anchors across the feature map. Liu et al. [29] proposed a high-quality anchor generation scheme, which constructed a nearly closed form of rotated BBox space. This scheme analyzes the possibility of the space covering the detection object, and selects a small number of potential anchors to make the whole detection process more accurate and fast.

Despite the above methods available for extracting orientational features, achieving a balance between speed and accuracy is a significant challenge. This is particularly true for deformable and rotated convolutions, which often consume substantial computational resources. The model’s overall computational burden increases, impacting its ability to perform real-time detection. Therefore, identifying efficient feature extraction methods that reduce unnecessary computations while maintaining detection accuracy has become a crucial focus in current research.

3. Method

3.1. Overall Structure

To address the challenges of spatial scale misalignment and orientation misalignment in RS object detection, existing detection networks often adopt a decoupled approach, improving either scale feature extraction or orientation feature extraction independently. This approach overlooks the impact of scale misalignment on orientation. Therefore, we propose a one-stage detection network that performs orientation feature extraction under the condition of precise scale feature matching: the Scale First ReFinement-Angle Detection Network (SFRADNet). SFRADNet fully considers the correlation between scale features and orientation. By hierarchically extracting scale features across different layers, it avoids the interference of background noise in the detection head, effectively mitigating spatial misalignment in remote sensing target detection.

In this section, we provide a detailed introduction to SFRADNet. As shown in Figure 3, the overall architecture consists of two main components: the Group Learning Large Kernel Network (GL²KNet) and a detection head equipped with a Shape-Aware Spatial Feature Extraction Module (SA-SFEM). To more accurately adapt to the scale variations of targets and ensure that scale features align with orientational changes, we design GL²KNet, which serves as the backbone of the detection model. GL²KNet is constructed by stacking Group Learning Large Kernel Convolution Modules (GL²KCM) at different stages. During detection, GL²KNet first extracts the fine-grained scale features of the target. These features are then fed into the detection head, where the SA-SFEM refines the position and classification of preset anchor boxes, enabling more accurate localization of multi-scale and multi-oriented RS objects.

As illustrated in Figure 3, GL²KNet adopts a hierarchical design, divided into four stages ($Stag{e}_1-Stag{e}_4$). Each stage contains GL²KCM with varying depths ($D_1-D_4$) and different group numbers ($G_1-G_4$). The specific configurations for each stage are as follows: Channel numbers: $\{C_1,C_2,C_3,C_4\}=\{64,128,256,512\}$, Depths: $\{D_1,D_2,D_3,D_4\}=\{2,2,4,2\}$, Group numbers: $\{G_1,G_2,G_3,G_4\}=\{4,4,8,4\}$.

The detection head of SFRADNet is built upon R³Det [26]. In R³Det, the original rotation refinement module is replaced with the Shape-Aware Spatial Feature Extraction Module (left side of the dashed line in the detection head in Figure 3). Additionally, an extra layer of large-kernel convolution is added to the regression branch to extract local information around the target, further enhancing the accuracy of target localization.

Group Learning Large Kernel Network

In RS detection tasks, the environment surrounding an object can provide helpful information about the object’s class or location. For instance, in vehicle and ship detection, it can be challenging for the detector to distinguish between these objects based solely on their shapes, colors, and sizes, as they are often similar, leading to confusion between vehicles and ships during detection. By leveraging the environmental information around vehicles or ships, the detector can better understand the object’s contextual information, aiding in classification during detection. Furthermore, different types of objects require contextual information in different size ranges. In traditional RS detectors, the receptive fields of neurons at each layer are designed to share the same fixed size, preventing neurons from adaptively adjusting their receptive field sizes according to the multiple scales of input information. This limitation hinders the precise extraction of fine-scale features for different object types.

Large-kernel convolution networks provide a reference for extracting scale features, but these structures often rely on operations such as attention mechanisms to filter scale features. This requires additional computation of attention weights for feature maps during the inference phase, which increases the computational complexity of the model. To effectively extract fine-grained scale features for targets of arbitrary sizes and improve detection efficiency, this paper proposes the Group Learning Large Kernel Network (GL²KNet), as illustrated in Figure 4.

The GL²KNet consists of four stages, each of which stacks a different number of Group Learning Large Kernel Convolution Modules (GL²KCM). Within the same stage, these modules share the same number of groups. First, we employ a large-kernel decomposition paradigm to decompose a theoretical large convolutional kernel into a series of smaller convolutional kernels with varying dilation rates. Since scale features are determined by the current receptive field, these decomposed smaller kernels are designed with appropriate dilation rates to meet the needs of different receptive field sizes. Furthermore, to efficiently filter features, our designed GL²KNet does not rely on the conventional attention mechanisms used in large-kernel convolutions. Instead, it utilizes multi-group Scale Selection Matrices (SSMatrices) to construct different spatial distribution features for the target. Each group of SSMatrices adaptively learns the weights of key points on the feature map, and these weights are used to filter feature maps across different channels. During the training phase, the SSMatrices of different groups self-learn the importance of feature maps through an additional neural network. During the inference phase, the scale selection matrices directly weight the feature maps using the learned weights, avoiding the parameter-heavy issues associated with attention mechanisms. This approach efficiently obtains more refined scale features suitable for the target. Specifically, the large-kernel decomposition paradigm follows these equations:

$$\begin{array}{c}{k}_i=k_{origin}+(k_{origin}-1)(D-1)\end{array}$$

(1)

$$\begin{array}{c}R{F}_i=\left\{\begin{array}{cc}{k}_i,& i=1\\ R{F}_{i-1}+(k_i-1)S,& i>1\end{array}\right.\end{array}$$

(2)

where i represents the i-th layer convolution, $k_i$ denotes the size of the convolutional kernel at the current layer, $k_{origin}$ represents the smaller convolutional kernel decomposed from the current layer, and D signifies the dilation rate of the smaller convolutional kernel. $R{F}_i$ corresponds to the receptive field of the current layer, while S indicates the stride of the convolution. In order to ensure the resolution of the feature map during the convolution process, padding follows $k_i-1$ in the convolution process.

The increase in the dilated rate of each small convolution kernel can cause changes in the theoretical large convolution kernel (Equation (1)), thereby causing changes in the current receptive field range (Equation (2)). For example, we stack a convolution with the original convolution kernel of 5 × 5 and a convolution kernel of 7 × 7 (the default step size is 1 and the dilated rate is 1), and the receptive field of the simulated theoretical kernel is 11; when the dilated rate is 2 and 3 respectively, the receptive field of the simulated theoretical kernel is 27. During this process, the number of sample points of the convolution kernel does not change, which will not cause an increase in the amount of parameters and calculations. Under the same amount of parameters, the long-distance context information captured by stacking small convolution kernels of two or more depths is richer.

We leverage large convolution kernels, which offer a broader receptive field compared to single small convolution kernels, thereby capturing more extensive long-range contextual information. However, successive convolutions can lead to a reduction in high-resolution features and an increase in low-resolution features. The diversity of scale features often resides across different resolution features. Low-resolution features encompass more semantic information, which aids in the recognition of overall categories; whereas high-resolution features contain more detailed information, facilitating the determination of object boundaries. For a detection head, acquiring well-defined object boundary features contributes to the precise localization of targets. To prevent the loss of high-resolution features, we integrate feature maps from different layers, simultaneously utilizing the semantic information from low-resolution features and the detailed information from high-resolution features, thereby enhancing the classification and localization capabilities of object detection.The equation is as follows:

$$\begin{array}{c}{X}_{i+1}=f_{k_{\mathrm{origin}1}}^{D_{i+1}}\left(X_i\right),i=[0,1,2,3,\dots ,n]\end{array}$$

(3)

where $x_i$ denotes the feature map of the input group learning the large-kernel convolution module. When $i=0$, $X_0$ represents the feature map of the input module; f signifies the large-kernel convolution operation of the current layer, D indicates the dilation rate of the convolutional kernel in use, and k represents the actual size of the convolutional kernel. To enhance the model’s focus on relevant contextual regions and improve detection capabilities, the model uses multiple scale-selective matrices to identify feature maps that best correspond to the target scale. First, we concatenate and then group the feature maps from different scales.

$$\begin{array}{c}\tilde{X}=Cat\left[X_1,X_2,X_3,\dots ,X_n\right]\end{array}$$

(4)

$$\begin{array}{c}{G}_j=Group(\tilde{X},N),j=1,2,3,4,\dots ,N\end{array}$$

(5)

where Cat denotes the operation of concatenating feature maps along the channel dimension, and $Group(\ast ,N)$ represents the grouping operator, where N is the set hyperparameter for the number of groups. $G_j$ signifies the feature maps after different groupings. For each group $G_j$, an H × W matrix is established, with sampling positions on the matrix generated randomly through a Gaussian distribution. We use a Multi-Layer Perceptron (MLP) to learn the importance weights of the feature maps in this group. This MLP network takes the scale-selective matrix as input and outputs a scalar weight $w_j$, indicating the significance of $G_j$ in the current task. During the training phase, the MLP network is optimized end-to-end along with the entire model. Through this approach, the model can adaptively adjust the contribution of each group of feature maps, thereby more effectively capturing task-relevant features.

$$\begin{array}{c}{w}_j=MLP\left(R_j\right)\end{array}$$

(6)

where $R_j$ represents the generated scale-selective matrix, $MLP(\ast )$ denotes the additional network, and $w_j$ signifies the generated weight. During the inference, this network is no longer utilized, instead, the feature maps of the group are directly weighted using the trained SSMatrix.

$$\begin{array}{c}\widetilde{G_j}=w_j·G_j\end{array}$$

(7)

where $\widetilde{G_j}$ denotes the weighted group feature maps. The rationale behind employing grouping in this process is to enhance the model’s generalization capability and its adaptability to features of different scales. Through the grouping operation, the model is able to process multiple feature subspaces in parallel, with each subspace independently learning its specific scale information, thereby circumventing the potential issue of feature ossification that may arise from single-scale selective convolution. To facilitate the interaction of information across different spaces, the weighted feature maps $\widetilde{G_j}$ from each group are ultimately fused via convolution operation.

$$\begin{array}{c}y=f_1^1\left(Cat\left[{\tilde{G}}_1,{\tilde{G}}_2\dots .{\tilde{G}}_N\right]\right)\end{array}$$

(8)

where, y represents the feature map output by the GL²KCM, and $f_1^1$ denotes a 1 × 1 convolution, which is utilized to further extract deep-level features.

3.2. Shape-Aware Spatial Feature Extraction Module

Misalignment in orientation significantly impacts detection accuracy in RS object detection. Objects in RS images are distributed in multiple orientations and non-uniformly, and current methods often rely on many anchors with various sizes to accommodate object appearance variations. However, the number of anchors grows geometrically with the preset rotation angles, leading to a decrease in detection speed as the number of anchors increases. Additionally, a higher number of anchors introduces more varied shapes, which significantly increases background noise, affecting the detector. Beyond the impact of proposed anchors, the subsequent feature extraction process also influences the classification and regression (localization) outcomes in the detection head. Applying specific convolution structures, such as rotational and deformable convolutions, to extract features is a common approach. However, using fixed-angle rotated convolutions struggles to align with object orientations accurately. Deformable convolutions require learning the offset at each position in the feature map. The network’s limited supervisory information may fail to guide the convolution kernel accurately, leading to sampling locations that deviate from the object and introducing background noise into orientation feature extraction.

To capture high-quality anchors and design deformable convolution with strong supervisory information that balances detection accuracy and speed, we propose the shape-aware spatial feature extraction module (SA-SFEM). SA-SFEM consists of two components: directed guide box (DGBox) and region-constrained deformable convolution (RCDC), with specific details shown in the section of Figure 3. First, after obtaining scale features from the backbone, horizontal anchors are proposed. Based on these horizontal anchors and backbone features, regression is performed to generate DGBoxes. Unlike two-stage detectors, classification of background/foreground is omitted during the inference stage to improve detection speed. DGBox serves as powerful supervisory information, guiding the convolution kernel to stretch and rotate, thereby forming the RCDC. As shown in Figure 5, the DGBoxes ensure that the sampling points of the RCDC convolution kernels align with the object’s orientation, allowing the RCDC to finely extract orientation features of objects, reducing background noise interference. Finally, multi-angle RCDCs are obtained by rotating RCDC, enabling orientation feature extraction and fusion during regression. This approach captures additional semantic information around the object, ensuring the precision of the regression task. Furthermore, the optimal rotated angle is selected to align with the object’s orientation. This alignment is then used for convolution feature extraction during the classification task, which improves the accuracy of classification.

3.2.1. Directed Guide Box

In anchor-based object detectors, the quality of proposed anchors directly determines the precision of subsequent classification and localization. The more accurate the proposed anchor, the higher the probability that the object will be contained, resulting to more precise classification and localization. Our anchors are constructed based on the scale features of the previous level. Initially, A anchors (where $A=5$) are proposed at each position on the deep-scale feature map. These anchors are represented as $(x_o,y_o,w_o,h_o,{\theta }_o)$, where $x^c,y^c$ are the center coordinates of different proposed anchors, $h^c,w^c$ are the height and width of the anchors, and ${\theta }^c$ is the anchor angle, initialized to 0, making the proposed anchors horizontal.

During training, we refine the anchors by adjusting them according to the ground truth (GT) to adapt to objects in various orientations. This process first calculates the overlap between proposed anchors and the GT, retaining anchors with IoU greater than 0.5. These retained anchors then pass through a classification network and a regression network. Unlike two-stage detectors, the classification distinguishes object classes in detail, and the regression network performs preliminary refinement of the proposed anchors. The above approach allows the model to dynamically learn the distribution of orientation for each class based on category labels, enabling anchors to adapt to the rotation range specific to each object category. In the inference stage, classification is skipped, and the DGBox is obtained by directly regressing the original proposed anchors using the trained parameters. Specifically, the DGBox’s parameter offsets received from the regression network are represented as $({\delta }_x,{\delta }_y,{\delta }_w,{\delta }_h,{\delta }_{\theta })$, with the regression process shown in Equations (9)–(11).

$$\begin{array}{c}{\delta }_x={\displaystyle \frac{x-x_o}{w_o}},{\delta }_y={\displaystyle \frac{y-y_o}{h_o}}\end{array}$$

(9)

$$\begin{array}{c}{\delta }_w=log\left({\displaystyle \frac{w}{w_o}}\right),{\delta }_h=log\left({\displaystyle \frac{h}{h_o}}\right)\end{array}$$

(10)

$$\begin{array}{c}{\delta }_{\theta }=tan\left(\theta -{\theta }_o\right)\end{array}$$

(11)

where $(x,y,w,h,\theta )$ represent the anchor parameters of the GT, $(x,y)$ are the center coordinates, w and h are the width and height of the actual BBox, and $\theta$ is the rotation angle. Moreover, the range for $\theta$ and ${\theta }_o$ are $(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}})$.

The entire DGBox generation process is trained using a composite loss function, as shown in the equation:

$$\begin{array}{c}L={\displaystyle \frac{1}{N}}\left({\displaystyle \sum _{i=1}^N}{L}_{cls}\left(c_i^{*},c_i\right)+{\displaystyle \sum _{i=1}^N}{L}_{reg}\left(l_i^{*},l_i\right)\right)\end{array}$$

(12)

where N is the number of proposed anchors; $L_{cls}$ is the classification loss, which uses Focal Loss [27]; and $L_{reg}$ is the regression loss, which uses Smooth L1. $c_i^{*}$ is the predicted class, $c_i$ is the ground truth class, $l_i^{*}$ is the predicted BBox, and $l_i$ is the GT.

3.2.2. Region-Constrained Deformable Convolution

RCDC is a type of deformable convolution guided by strong supervisory information. Unlike conventional deformable convolutions, RCDC undergoes stretching and rotation transformations based on a standard convolution, guided by a DGBox. Given a standard 3 × 3 convolution kernel for 2D, as shown in Figure 5a, the central coordinates are defined as $K_i=\left(x_i,y_i\right)$. The sampling locations of this 2D standard convolution are described as: $L(x,y)=\left\{x_{i+j},y_{i+k}|j,k\in (-1,0,1)\right\}$. In convention deformable convolutions (Figure 5b), the convolution kernel often shifts irregularly across the feature map, generating offsets $∆x$ and $∆y$. The coordinates of the resulting convolution kernel $L_o$ are expressed as shown in equation:

$$\begin{array}{c}\begin{array}{c}\hfill L_o(x,y)=\left\{x_{i+j\pm ∆x},y_{i+k\pm ∆y}\mid j,k\in (-1,0,1);\right.\left.∆x,∆y\in (0,1,2,\dots ,n)\right\}\end{array}\end{array}$$

(13)

where the offsets $∆x$ and $∆y$ are learned from the feature map, with n representing the deformable stretch range. Convention deformable convolution predicts the position of each pixel to determine the offset, resulting in a high computational overhead for supervising offset learning.

Additionally, due to the weak supervisory information and unordered nature of position predictions in convention deformable convolutions, alignment with the object is often inaccurate. This misalignment causes the convolution kernel to shift away from the object region, introducing substantial background noise during the convolution process.

To ensure that the positions of the deformable convolution kernel better align with the object and to strengthen the supervision in kernel deformation learning, we add regional constraints and offset angles on the convolution kernel offsets in deformable convolution (Figure 5c); This allows the kernel to deform within a specified range, aligning more closely with the object’s orientation. The regional constraint used is the DGBox, and the offset rotation of the convolution kernel in the rotation-aligned convolution is represented by Equation (14):

$$\begin{array}{c}{L}_d=\left(p+{\displaystyle \frac{(w,h)}{k}}\ast r\right)\ast R^T\left(\theta \right)\end{array}$$

(14)

where $p=(x,y)$ represents the original sampling point of the convolution kernel and also the center coordinate of the DGBox. k is the size of the convolution kernel, and $(w,h)$ are the width and height of the DGBox. r is a parameter that adjusts the scaling ratio, with its specific value learned during training. $R\left(\theta \right)={(cos\theta ,-sin\theta ;sin\theta ,cos\theta )}^T$ represents the rotation matrix. In the entire process, the convolution kernel first shifts within the constraints of the DGBox and then rotates according to $R\left(\theta \right)$, causing the sampling points of the convolution kernel to align closely with the object’s orientation.

4. Experiments

4.1. Datasets

Our experiments were conducted on three publicly available RS object detection datasets. (1) DOTA-v1.0 Dataset [30]: This dataset consists of many high-resolution RS images covering many scenes. It includes 2806 images with resolutions varying from 800 × 800 to 4000 × 4000 pixels, and it contains annotations for 15 different object categories, with each object annotated using a rotated BBox. (2) HRSC2016 Dataset [31]: This dataset is specifically designed for ship detection in high-resolution aerial images. The HRSC2016 dataset includes annotations for various types of ships, with each object annotated using a rotated BBox. (3) UCAS-AOD Dataset [32]: This dataset is a public dataset aimed at object detection in aerial images. The dataset mainly includes two objects: cars and airplanes, which contains 1510 high-resolution images, covering objects from multiple angles in complex RS scenes.

4.2. Implementation Details and Evaluation Metrics

4.2.1. Evaluation Metrics

In object detection tasks, different objects may appear at different positions in each image, and it is necessary to evaluate the classification and regression of the model. A single evaluation criterion cannot be directly used for object detection tasks. Therefore, we use the mean average precision (mAP) to measure the performance of the detection network. mAP is obtained by taking the average of the AP for each category. AP is the area under the P-R curve (precision-recall curve) for each category, where P represents the precision of the target and R represents the recall of the target. The expression of mAP is as follows:

$$\begin{array}{c}P={\displaystyle \frac{TP}{TP+FP}}\end{array}$$

(15)

$$\begin{array}{c}R={\displaystyle \frac{TP}{TP+FN}}\end{array}$$

(16)

$$\begin{array}{c}mAP={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{\int }_0^1{P}_i\left(R_i\right)d{R}_i\end{array}$$

(17)

where $TP, FP$, and $FN$ represent true positives, false positives, and false negatives in the confusion matrix. In the evaluation process, if the Intersection over Union (IoU) of the predicted BBox and the GT is greater than 0.5, the instance is judged as $TP$. P represents the precision of the model, and R represents the recall rate of the model. $P_i\left(R_i\right)$ represents the curve of precision and recall, with values ranging from $[0,1]$.

To comprehensively assess the performance of our model, we also analyzed its parameters (Params) and floating-point operations (FLOPs), which reflect the model’s size and computational complexity, respectively. Additionally, we measured the frames per second (FPS) on the DOTA dataset to assess the inference speed.

4.2.2. Implementation Details

We employ the proposed GL²KNet as the backbone network. The backbone network undergoes thorough pre-training on the ImageNet dataset. The entire training and inference process is conducted on a server equipped with the PyTorch-1.13.1 framework and two NVIDIA 3090 cards. During training, the model is optimized using the AdamW optimizer, with an initial learning rate of 1 × 10⁻⁴. The batch size is set to 8, and data augmentation strategies comprise random scaling, cropping, and rotating. To accurately detect objects, the confidence threshold for the detection head is set at 0.5. Additionally, we utilize R3Det as the baseline for ablation experiments. R3Det is an efficient, one-stage detector that is easily composable with other detection networks.

For these three public datasets, we referred to [11,33,34] and performed the following processing. Both DOTA-v1.0 and HRSC2016 datasets were released with predefined training, validation, and test splits, so we adhered to their official partitioning. For the UCAS-AOD dataset, we randomly divided it into training, validation, and test sets in a 5:2:3 ratio. During model training, we adopted differentiated strategies based on the characteristics of each dataset. For the large-scale and complex DOTA-v1.0 dataset—which contains numerous images with significant scale variations and diverse categories—we employed multi-scale cropping (682 × 682, 1024 × 1024, and 2048 × 2048) as a data augmentation method and trained the model for 12 epochs. In contrast, for the HRSC2016 and UCAS-AOD datasets, which have relatively uniform image sizes, we used a fixed input scale of 800 × 800 and 512 × 512, respectively. Additionally, since the processed HRSC2016 and UCAS-AOD datasets contained far fewer images than DOTA-v1.0, we extended their training to 36 epochs to ensure sufficient feature learning.

4.3. Ablation Experiment

To demonstrate the effectiveness of each component, we conducted extensive ablation experiments on the HRSC2016 and UCAS-AOD datasets, encompassing both the decoupling and inter-module coupling of SFRADNet. We proposed GL²KNet as the backbone for SFRADNet and compared it with mainstream backbones such as ResNet [35], Swin-Transformer [36], and the PKINet [12]. Additionally, we investigated the impact of different backbones combined with SA-SFEM on R3Det. Furthermore, we explored the internal parameters of GL²KNet, including the theoretical receptive field size of large-kernel convolutions, the number of stacked GL²KCMs at different stages, and the number of groups in the GL²KNet at various stages. Moreover, within the detection head, we compared RCDC with convention convolutions and deformable convolutions.

4.3.1. Different Backbones

Our ablation experiments were centered around employing various networks as the backbone of the model and applying the SA-SFEM module to the baseline model R3Det.

The HRSC2016 dataset encompasses vessels of various orientations and scales. The backbone in the detector generates feature maps of different scales at various stages, which are typically connected to an FPN structure to address the scale variations introduced by different targets. However, the traditional ResNet50 as a backbone has achieved only an 88.64% mAP. As can be seen from

Table 1. The impact of different backbones in SFRADNet on the HRSC2016 dataset.

Backbone	SA-SFEM	Pamrams (M)	GFLOPs	mAP (%)
ResNet-18	×	25.90	169.29	88.74
ResNet-50	×	41.58	200.92	89.42
ResNet-101	×	60.57	248.47	89.47
Swin-T	×	40.55	641.40	88.33
Swin-B	×	99.90	489.55	90.97
PKINet	×	40.38	219.13	91.04
GL2KNet	×	27.48	177.90	91.54
ResNet-18	√	20.21	104.03	89.18
ResNet-50	√	36.71	135.66	90.09
ResNet-101	√	55.70	183.21	91.11
Swin-T	√	35.68	380.76	89.04
Swin-B	√	95.02	228.91	91.52
PKINet	√	35.50	153.93	91.77
GL2KNet	√	22.61	112.64	92.81

, the introduction of GL²KNet has increased the mAP to 91.54%. Moreover, the heatmaps in Figure 6 reveal that the scale heatmaps of our designed GL²KNet more closely align with the actual size of the targets. ResNet fails to accurately localize the scale of the targets, while Swin-Transformer and PKINet, although capable of adapting to scale variations of targets of different sizes, introduce additional background noise. Consequently, GL²KNet acquires more refined scale features compared to other backbones, and it demonstrates that using only the FPN structure cannot finely extract the scale features of targets.

From Table 1, we also observe that when GL²Knet is utilized as the detector’s backbone in conjunction with SA-SFEM, the mAP increases by 1.34%. Furthermore, when other backbones are employed with the addition of SA-SFEM, there is also an improvement in detection accuracy, albeit to a lesser extent. We posit that this is due to SA-SFEM requiring more precise scale features as a prerequisite for the accurate extraction of directional features, and GL²Knet possesses the capability for such precise scale feature extraction. In contrast to other backbones, GL²Knet is able to achieve coupling with SA-SFEM.

On the UCAS-AOD dataset, our experiments yielded results similar to those mentioned above, as shown in

Table 2. The impact of different backbones in SFRADNet on the UCAS-AOD dataset.

Backbone	SA-SFEM	Pamrams (M)	GFLOPs	mAP (%)
ResNet-18	×	25.11	69.36	88.71
ResNet-50	×	41.60	82.30	89.55
ResNet-101	×	60.60	101.77	89.47
Swin-T	×	40.57	263.70	88.99
Swin-B	×	99.92	324.30	89.46
PKINet	×	40.37	89.78	89.84
GL2KNet	×	27.51	72.89	89.86
ResNet-18	√	20.24	42.67	88.97
ResNet-50	√	36.73	55.60	89.67
ResNet-101	√	55.72	75.08	89.59
Swin-T	√	35.70	156.91	89.74
Swin-B	√	95.04	217.52	89.81
PKINet	√	35.47	63.08	89.99
GL2KNet	√	22.63	46.19	90.23

. Compared to other backbones, GL²Knet achieved higher accuracy. When the SA-SFEM module was added, the detection accuracy of different backbones increased. The experimental results indicate that there is no conflict between the components, and the combination of scale feature and rotation feature extraction effectively avoids the multiple misalignment phenomena in rs object detection.

4.3.2. The Influence of GL²Knet’s Parameters on Detection Results

GL²KNet is composed of stacked GL²KCMs. The number of GL²KCMs at different stages in GL²KNet, the size of the convolution kernel’s receptive field, and the amount of group learning in the SSMatrix directly affect the experimental results. In this section, we explore the impact of hyperparameters in GL²KNet on the experiment.

Table 3. On the HRSC2016 dataset, the influence of the combination of GL²KCM convolution kernels on the experimental results. k represents the convolution kernel size, a represents the void rate.

Receptive Field	(k, a)	Pamrams (M)	GFLOPs	mAP (%)
15	(3,1)→(3,2)→(3,4)	24.57	116.25	91.47
17	(5,1) →(7,2)	22.61	112.64	91.53
27	(5,2) →(7,3)	22.61	112.64	92.81
29	(3,1) →(5,2) →(7,3)	24.70	116.86	92.07
35	(3,1) →(3,2) →(5,2) →(7,3)	25.56	118.36	91.89

and

Table 4. On the UCAS-AOD dataset, the influence of the combination of GL²KCM convolution kernels on the experimental results. k represents the convolution kernel size, a represents the void rate.

Receptive Field	(k, a)	Pamrams (M)	GFLOPs	mAP (%)
15	(3,1)→(3,2)→(3,4)	24.59	47.67	89.71
17	(5,1) →(7,2)	22.63	46.19	89.73
27	(5,2) →(7,3)	22.63	46.19	90.23
29	(3,1) →(5,2) →(7,3)	24.73	47.92	90.04
35	(3,1) →(3,2) →(5,2) →(7,3)	25.58	48.53	89.84

show that when the receptive field of the convolutional kernel is adjusted to 27, the highest evaluation metrics are achieved on both the HRSC2016 and UCAS-AOD datasets, at 92.81% and 90.23%, respectively. When the receptive field of the convolution kernel is adjusted to 15 or 17, the model’s ability to accurately perceive target boundaries is compromised due to the reduced range of the convolution kernel’s receptive field, leading to difficulties in scale feature extraction and a consequent decline in detection accuracy on both datasets. As the receptive field of the convolution kernel is gradually increased, the accuracy on both datasets also decreases to varying degrees. We think this is because an excessively large receptive field extends far beyond the target itself, introducing a significant amount of background noise into the extraction of target scale features. Additionally, increasing the receptive field also leads to an increase in the number of parameters and computational load. In summary, both excessively large and small receptive fields of the convolution kernel result in suboptimal detection performance. Through extensive experimentation, we have selected a receptive field size of 27 to meet our accuracy requirements in the detection process.

From

Table 5. The impact of the number of stacked GL²KCM at different stages of GL²KNet on the HRSC2016 dataset.

Number of Stacked GL2KCM	Pamrams (M)	GFLOPs	mAP (%)
$[1,1,1,1]$	15.76	95.72	91.86
$[2,2,2,2]$	20.77	108.03	92.51
$[2,2,3,2]$	21.69	110.33	92.45
$[2,2,4,2]$	22.69	112.64	92.81
$[2,3,4,2]$	22.98	116.40	92.61

and

Table 6. The impact of the number of stacked GL²KCM at different stages of GL²KNet on the UCAS-AOD dataset.

Number of Stacked GL2KCM	Pamrams (M)	GFLOPs	mAP (%)
$[1,1,1,1]$	15.78	39.26	89.74
$[2,2,2,2]$	20.79	44.30	89.82
$[2,2,3,2]$	21.71	45.25	90.10
$[2,2,4,2]$	22.63	46.19	90.23
$[2,3,4,2]$	23.00	47.73	90.01

, it is evident that the number of GL²KCM stacked at different stages in GL²KNet can influence the experimental results. When the number of stacked GL²KCMs is too low, the model’s feature extraction capability is insufficient. Increasing the number of stacked GL²KCMs enhance detection accuracy but also leads to an increase in the model’s computational load and number of parameters. When the number of stacked layers is excessively high, it can cause the model to overfit, adversely affecting the detection outcomes. Through experiments, we have determined the optimal combination of GL²KCMs numbers to be $[2,2,4,2]$.

The precise selection of scale features is determined by the SSMatrix. In G^L2Knet, the scale-selective matrices at different stages have varying numbers of groups.

Table 7. The impact of the number of groups in different stages of GL²KCM on the HRSC2016 dataset.

Number of Groups	Pamrams (M)	GFLOPs	mAP (%)
$[2,4,4,2]$	22.60	112.59	91.74
$[4,4,4,4]$	22.60	112.62	92.07
$[4,4,8,4]$	22.61	112.64	92.81
$[4,8,8,4]$	22.61	112.66	92.56
$[8,8,8,8]$	22.61	112.71	92.34

and

Table 8. The impact of the number of groups in different stages of GL²KCM on the UCAS-AOD dataset.

Number of Groups	Pamrams (M)	GFLOPs	mAP (%)
$[2,4,4,2]$	22.62	46.17	89.72
$[4,4,4,4]$	22.62	46.18	89.99
$[4,4,8,4]$	22.63	46.19	90.23
$[4,8,8,4]$	22.63	46.20	90.11
$[8,8,8,8]$	22.63	46.22	90.09

display the combinations of group numbers at different stages on the HRSC2016 and UCAS-AOD datasets, respectively. The results present the number of parameters, computational load, and detection accuracy during the model’s inference process. Changes in the number of groups have a minimal impact on the model’s parameter count and computational load, as the scale-selective matrix does not require additional attention operations during the inference phase; instead, it directly filters the feature maps using trained weights. Furthermore, we observe that the number of groups affects detection accuracy. Through multiple ablation experiments on both datasets, we have ultimately determined the number of groups at different stages to be $[4,4,8,4]$.

4.3.3. Impact of SA-SFEM’s RCDC on Detection Results

The SA-SFEM internally incorporates RCDC. This section primarily explores the impact of RCDC on detection. On the HRSC2016 dataset, when conventional convolution is employed, an mAP of 89.91% is achieved; when conventional deformable convolution is utilized, the mAP increases by 0.98%. With our designed RCDC, the mAP reaches 92.81%. We attribute this improvement to the fact that conventional convolution lacks the finesse in feature extraction, leading to suboptimal detection results. When RCDC is applied, the model is capable of learning richer semantic information and exhibits stronger feature representation capabilities. Additionally, as can be seen from

Table 9. The impact of convolution type on the experimental results of HRSC2016 dataset in SA-SFEM, the difference between RCDC and conventional convolution and deformable convolution.

Convolution Type	Pamrams (M)	mAP(%)
Conv3 × 3	25.55	89.91
Deformable	28.75	90.89
RCDC	22.61	92.81

, there is a significant reduction in the number of parameters when RCDC is used, meeting the requirement for model lightweighting. On the UCAS-AOD dataset,

Table 10. The impact of convolution type on the experimental results of UCAS-AOD dataset in SA-SFEM, the difference between RCDC and conventional convolution and deformable convolution.

Convolution Type	Pamrams (M)	mAP(%)
Conv3 × 3	26.01	89.17
Deformable	30.26	89.56
RCDC	22.63	90.23

presents results consistent with those from the HRSC2016 dataset experiments, further substantiating the effectiveness of RCDC.

4.4. Main Experiment

Results on the DOTA-v1.0 Dataset: Table 11 shows that DFTR-Net achieved the best AP for individual object categories, including BD, SV, SH, BC, ST, HA, and SP, with values of $85.45\%$, $81.75\%$, $88.56\%$, $87.31\%$, $87.59\%$, $78.54\%$, and $83.35\%$, respectively. Additionally, DFTR-Net outperforms other models with the best mAP of $80.10\%$. Compared to the state-of-the-art (SOTA) detector FCOSF [37], DFTR-Net achieves $1.51\%$ higher mAP. FCOSF effectively represents the rotated orientation of the objects by incorporating contour functions to introduce orientational information and output corresponding distance predictions. This allows FCOSF to adaptively adjust the direction of the Boundaring Boxes (BBoxes) based on object orientation, generating BBoxes that fit the object orientation. However, FCOSF’s orientation prediction faces interference when object scale is not clearly represented. As can be visually observed in Figure 7, the detection differences between FCOSF and our model are evident. When detecting objects with different scales, FCOSF’s BBoxes fail to properly reflect the object’s scale. For instance, the rotated BBoxes for the HA and TC do not accurately cover the object’s size and shape, leading to misalignment during subsequent orientational adjustments. Moreover, for the SV and LV, FCOSF does not accurately express the size and shape of individual objects, resulting in misalignment between the rotated BBox and the object. We analyze this phenomenon as stemming from FCOSF’s exclusive focus on modeling orientational features, while using traditional feature pyramid structures for scale feature extraction, which lacks finer-grained feature extraction. In contrast, SFRADNet first extracts more precise scale features from objects through the GL²KNet and uses RCDC in SA-SFEM to resolve the orientation issue, achieving optimal results.

In the DOTA-v1.0 dataset, RS objects exhibit significant scale differences. For example, the scale difference between HA and SH in the same image can be approximately 20 times. As shown in Figure 8A,J, SFRADNet can accurately detect these objects with vastly different scales. Furthermore, for objects like SH, where the scale changes gradually, Figure 8B demonstrates that SFRADNet can also achieve precise localization even when faced with fine-scale variations. We believe this is because SFRADNet can adapt to changes in any scale, enabling precise detection of objects across a wide range of scales. Additionally, SFRADNet maintains strong performance in orientational alignment. For instance, in Figure 8C, when dealing with densely distributed SV objects, the network can accurately detect each object, with the BBox direction aligning with the object’s orientation. This is achieved through the proposed SA-SFEM, which can form DGBoxes as predefined anchors under suitable scale matching. With the supervision provided by these DGBoxes, the convolution kernels undergo deformation, enabling the sampling points of the kernels to align with the object’s orientation and extract rich rotational features. This approach effectively prevents orientation misalignment during the detection process. We evaluated the benchmark performance (

Table 12. Benchmark test with image resolution of 1024 × 1024 on DOTA-v1.0 dataset.

Methods	Backbone	mAP (%)	FPS	Pamrams (M)	GFLOPs
O-RepPoints [38]	ResNet101	76.52	13.70	55.60	272.14
R3Det [26]	ResNet101	76.47	15.50	66.03	525.72
ORCNN-PKINet [12]	PKINet-S	78.39	12.00	43.09	227.00
R3Det-LSKNet [11]	LSKNet	78.08	17.60	33.39	412.38
SFRADNet (Ours)	GL2KNet	80.10	18.10	22.67	185.72

) at a resolution of 1024 × 1024. Compared to the baseline model R3Det [26], SFRADNet achieves significantly fewer parameters, lower computational costs, and faster inference speeds. Furthermore, when compared to point-set prediction methods [38], the two-stage detector O-RCNN and large-kernel networks [11,12] our proposed model maintains superior detection accuracy (highest mAP) while requiring fewer parameters and less computational overhead.

Table 11. Comparison results with advanced Dets on the DOTA-v1.0 dataset.

Methods	Backbone	PL	BD	BR	GTF	SV	LV	SH	TC	BC	ST	SBF	RA	HA	SP	HC	mAP (%)
ROI-Trans [24]	ResNet101	88.53	77.91	37.63	74.08	66.53	62.97	66.57	90.50	79.46	76.75	59.04	56.73	62.54	61.29	55.56	67.74
RSDet [39]	ResNet101	89.80	82.90	48.60	65.20	69.50	70.10	70.20	90.50	85.60	83.40	62.50	63.90	65.60	67.20	68.00	72.21
SCRNet [22]	ResNet101	89.98	80.65	52.09	68.36	68.36	60.32	72.41	90.85	87.94	86.86	65.02	66.68	66.25	68.24	65.21	72.61
R3Det [26]	ResNet101	89.80	83.77	48.11	66.77	78.76	83.27	87.84	90.82	85.38	85.51	65.67	62.68	67.53	78.56	72.62	76.47
Gridding-Vertex [40]	ResNet101	89.64	85.00	52.26	77.34	73.01	73.14	86.82	90.74	79.02	86.81	59.55	70.91	72.94	70.86	57.32	75.02
O2-DNet [5]	Hourglass-104	89.31	82.14	47.33	61.21	71.31	74.03	78.62	90.76	82.23	81.36	60.93	60.17	58.21	66.98	61.03	71.04
BBAVetors [41]	ResNet101	88.35	79.96	50.69	62.18	78.43	78.98	87.94	90.85	83.58	84.35	54.13	60.24	65.22	64.28	55.70	72.32
DRN [6]	Hourglass-104	89.71	82.34	47.22	64.10	76.22	74.43	85.84	90.57	86.18	84.89	57.65	61.93	69.30	69.63	58.48	73.23
CSL [42]	ResNet152	90.25	85.53	54.64	75.31	70.44	73.51	77.62	90.84	86.15	86.69	69.60	68.04	73.83	71.10	68.93	76.17
S2A-Net [43]	ResNet50	89.07	82.22	53.63	69.88	80.94	82.12	88.72	90.73	83.77	86.92	63.78	67.86	76.51	73.03	56.60	76.38
CFC-Net [44]	ResNet50	89.08	80.41	52.41	70.02	76.28	78.11	87.21	90.89	84.47	85.64	60.51	61.52	67.82	68.02	50.09	73.50
RIDet-O [45]	ResNet101	88.94	78.45	46.87	72.63	77.63	80.68	88.18	90.55	81.33	83.61	64.85	63.72	73.09	73.13	56.87	74.70
AO2-DETR [14]	ResNet50	87.13	85.43	65.87	74.69	77.46	84.13	86.19	90.23	81.14	86.56	56.04	70,48	75.47	78.30	72.66	75.89
DAL [46]	ResNet101	88.68	76.55	45.08	66.80	67.00	76.76	79.74	90.84	79.54	78.45	57.71	62.27	69.05	73.14	60.11	71.44
RetinaNet-GWD [47]	ResNet152	86.14	81.59	55.33	75.57	74.20	67.34	81.75	87.48	82.80	85.46	69.47	67.20	70.97	70.91	74.07	75.35
Center-Map [48]	ResNet101	80.83	84.41	54.60	70.25	77.66	78.32	87.19	90.66	84.89	85.27	56.46	69.23	74.13	71.56	66.06	76.03
O-Reppoints [38]	ResNet101	89.53	84.07	59.86	71.76	79.95	80.03	87.33	90.84	87.54	85.23	59.15	66.37	75.23	73.75	57.23	76.52
RFCOS-ABFL [49]	ResNet50	89.05	83.09	48.20	63.38	79.06	77.48	86.02	90.89	82.24	84.60	56.66	66.13	64.75	69.82	54.33	73.01
CFA [50]	ResNet101	89.26	81.72	51.81	67.17	79.99	78.25	84.46	790.77	83.40	85.54	54.86	67.75	73.04	70.24	64.96	75.05
FCOSF [37]	ResNet50	89.46	81.53	55.29	69.70	81.49	84.79	88.54	90.88	87.73	87.09	68.78	67.83	76.14	76.77	72.82	78.59
KLD [51]	ResNet50	88.91	85.23	53.64	81.23	78.20	76.99	84.58	89.50	86.84	86.38	71.69	68.06	75.95	72.23	75.42	78.32
ORCNN-PKINet [12]	PKINet-S	89.72	84.20	55.81	77.63	80.25	84.45	88.12	90.88	87.57	86.07	66.86	70.23	77.47	73.62	62.94	78.39
R3Det-LSKNet [11]	LSKNet-S	90.50	82.11	53.42	73.57	76.42	86.73	87.47	90.63	79.70	76.02	68.81	78.19	78.62	70.14	79.25	78.08
SFRADNet (Ours)	GL2KNet	89.44	85.45	58.96	78.54	81.75	84.64	88.56	90.85	87.31	87.59	66.89	70.22	78.54	83.35	69.46	80.10

Table 11. Comparison results with advanced Dets on the DOTA-v1.0 dataset.

Methods	Backbone	PL	BD	BR	GTF	SV	LV	SH	TC	BC	ST	SBF	RA	HA	SP	HC	mAP (%)
ROI-Trans [24]	ResNet101	88.53	77.91	37.63	74.08	66.53	62.97	66.57	90.50	79.46	76.75	59.04	56.73	62.54	61.29	55.56	67.74
RSDet [39]	ResNet101	89.80	82.90	48.60	65.20	69.50	70.10	70.20	90.50	85.60	83.40	62.50	63.90	65.60	67.20	68.00	72.21
SCRNet [22]	ResNet101	89.98	80.65	52.09	68.36	68.36	60.32	72.41	90.85	87.94	86.86	65.02	66.68	66.25	68.24	65.21	72.61
R3Det [26]	ResNet101	89.80	83.77	48.11	66.77	78.76	83.27	87.84	90.82	85.38	85.51	65.67	62.68	67.53	78.56	72.62	76.47
Gridding-Vertex [40]	ResNet101	89.64	85.00	52.26	77.34	73.01	73.14	86.82	90.74	79.02	86.81	59.55	70.91	72.94	70.86	57.32	75.02
O2-DNet [5]	Hourglass-104	89.31	82.14	47.33	61.21	71.31	74.03	78.62	90.76	82.23	81.36	60.93	60.17	58.21	66.98	61.03	71.04
BBAVetors [41]	ResNet101	88.35	79.96	50.69	62.18	78.43	78.98	87.94	90.85	83.58	84.35	54.13	60.24	65.22	64.28	55.70	72.32
DRN [6]	Hourglass-104	89.71	82.34	47.22	64.10	76.22	74.43	85.84	90.57	86.18	84.89	57.65	61.93	69.30	69.63	58.48	73.23
CSL [42]	ResNet152	90.25	85.53	54.64	75.31	70.44	73.51	77.62	90.84	86.15	86.69	69.60	68.04	73.83	71.10	68.93	76.17
S2A-Net [43]	ResNet50	89.07	82.22	53.63	69.88	80.94	82.12	88.72	90.73	83.77	86.92	63.78	67.86	76.51	73.03	56.60	76.38
CFC-Net [44]	ResNet50	89.08	80.41	52.41	70.02	76.28	78.11	87.21	90.89	84.47	85.64	60.51	61.52	67.82	68.02	50.09	73.50
RIDet-O [45]	ResNet101	88.94	78.45	46.87	72.63	77.63	80.68	88.18	90.55	81.33	83.61	64.85	63.72	73.09	73.13	56.87	74.70
AO2-DETR [14]	ResNet50	87.13	85.43	65.87	74.69	77.46	84.13	86.19	90.23	81.14	86.56	56.04	70,48	75.47	78.30	72.66	75.89
DAL [46]	ResNet101	88.68	76.55	45.08	66.80	67.00	76.76	79.74	90.84	79.54	78.45	57.71	62.27	69.05	73.14	60.11	71.44
RetinaNet-GWD [47]	ResNet152	86.14	81.59	55.33	75.57	74.20	67.34	81.75	87.48	82.80	85.46	69.47	67.20	70.97	70.91	74.07	75.35
Center-Map [48]	ResNet101	80.83	84.41	54.60	70.25	77.66	78.32	87.19	90.66	84.89	85.27	56.46	69.23	74.13	71.56	66.06	76.03
O-Reppoints [38]	ResNet101	89.53	84.07	59.86	71.76	79.95	80.03	87.33	90.84	87.54	85.23	59.15	66.37	75.23	73.75	57.23	76.52
RFCOS-ABFL [49]	ResNet50	89.05	83.09	48.20	63.38	79.06	77.48	86.02	90.89	82.24	84.60	56.66	66.13	64.75	69.82	54.33	73.01
CFA [50]	ResNet101	89.26	81.72	51.81	67.17	79.99	78.25	84.46	790.77	83.40	85.54	54.86	67.75	73.04	70.24	64.96	75.05
FCOSF [37]	ResNet50	89.46	81.53	55.29	69.70	81.49	84.79	88.54	90.88	87.73	87.09	68.78	67.83	76.14	76.77	72.82	78.59
KLD [51]	ResNet50	88.91	85.23	53.64	81.23	78.20	76.99	84.58	89.50	86.84	86.38	71.69	68.06	75.95	72.23	75.42	78.32
ORCNN-PKINet [12]	PKINet-S	89.72	84.20	55.81	77.63	80.25	84.45	88.12	90.88	87.57	86.07	66.86	70.23	77.47	73.62	62.94	78.39
R3Det-LSKNet [11]	LSKNet-S	90.50	82.11	53.42	73.57	76.42	86.73	87.47	90.63	79.70	76.02	68.81	78.19	78.62	70.14	79.25	78.08
SFRADNet (Ours)	GL2KNet	89.44	85.45	58.96	78.54	81.75	84.64	88.56	90.85	87.31	87.59	66.89	70.22	78.54	83.35	69.46	80.10

Results on the HRSC2016 Dataset: This dataset contains a large number of ships, with significant variations in aspect ratio, scale, and orientation. As shown in

Table 13. Comparison results with advanced Dets on the HRSC2016 dataset.

Methods	Backbone	mAP (%)
Rotated-RPN [53]	ResNet101	79.08
ROI-Transformer [24]	ResNet101	86.20
Gliding-Vertex [40]	ResNet101	88.20
OBD [54]	ResNet101	89.22
R3Det-DCL [55]	ResNet101	89.46
FPN-CSL [42]	ResNet101	89.62
RIDet [45]	ResNet101	89.63
R3Det-GWD [47]	ResNet101	89.85
RRD [56]	VGG16	84.30
BBAVector [41]	ResNet101	88.60
GRS-Det [52]	ResNet101	89.60
CFC-Net [44]	ResNet101	89.70
SFRADNet (Ours)	GL2KNet	92.65

, SFRADNet achieved the highest mAP of 92.65%. GRS-Det [52] is a dedicated ship detection network, and from the evaluation metrics, it is evident that SFRADNet outperforms this specific ship detector by 3.05% in terms of mAP. We visualized the results of ship detection, as shown in Figure 9. In Group B of Figure 9, ships of different scales are accurately distinguished by SFRADNet. Additionally, Group A of Figure 9 clearly demonstrates the multi- orientational distribution of ships, with SFRADNet accurately predicting the orientation of each ship. Group C of Figure 9 show the model’s ship detection capability in complex backgrounds. Given the presence of significant interference from the background, such as docks, coastlines, and other ships, which typically impact the precision of detection algorithms, our model shows remarkable robustness to interference, successfully detecting all ships. This objectively demonstrates the superior detection performance of our proposed network in RS object detection.

Results on the UCAS-AOD Dataset: The experimental results in

Table 14. Comparison results with advanced Dets on the UCAS-AOD dataset.

Methods	Backbone	mAP (%)
YOLOv3 [57]	Darknet53	82.08
R-RetinaNet [27]	ResNet50	87.57
FR-O [30]	ResNet50	88.36
RoI-Trans [24]	ResNet50	89.02
CFC-Net [44]	ResNet50	89.49
TIOE-Det [58]	ResNet50	89.49
DAL [46]	ResNet50	89.87
SFRADNet (Ours)	GL2KNet	90.23

show that SFRADNet achieves the best performance among the compared detectors, reaching an mAP of $90.18\%$. SFRADNet outperforms other one-stage detectors and even surpasses some advanced two-stage detectors, such as RoI-Trans [24]. The visual results from Group A in Figure 10 reveal that for objects with any orientation, the BBox orientation is aligned with the object’s orientation. Furthermore, SFRADNet can precisely localize objects such as cars and airplanes, which have large scale differences, indicating that our model can adapt to scale variations in the objects. In A-(3) of Figure 10, where cars are parked in a shadowed area, SFRADNet can accurately detect the cars despite the presence of shadows. The key to this ability lies in the application of convolution kernel stacking strategy in GL²KNet for modeling objects of arbitrary scale, which has a richer and more diverse receptive field than a single convolution kernel. This modeling approach effectively integrates the scale information of the object and the surrounding semantic information, thereby effectively identifying the object from shadow interference. In B-(3) of Figure 10, where there is a significant difference in lighting conditions compared to other images, SFRADNet is still able to accurately detect the airplane. This demonstrates the robustness of SFRADNet under varying lighting conditions.

4.5. Analysis

SFRADNet achieves high accuracy while maintaining a lightweight architecture, which we attribute to its fine-grained angle adjustment under precise scale matching. Specifically, SFRADNet first employs GL²KNet to dynamically align multi-scale features, followed by angle refinement to rotate bounding boxes into optimal positions. In contrast, other advanced detectors, such as R3Det [26] and ReDet [25], exhibit strong sensitivity to orientation prediction but lack the crucial prerequisite of accurate scale extraction. Moreover, compared to large-kernel convolution-based dynamic scale feature extractors like LSKNet [11] and PKINet [12], GL²KNet in SFRADNet achieves dynamic multi-scale feature selection with fewer parameters and lower computational costs. Another key distinction lies in angle alignment; unlike conventional approaches, our SA-SFEM module adopts RCDC for angle-aware localization. RCDC is a deformable convolution variant that incorporates region constraints, enabling it to adaptively adjust sampling points based on target orientation. As shown in Figure 11, for slender ship targets, RCDC’s sampling points are confined within the bounding box. The minimum enclosing rectangle of these sampling points precisely conforms to the target’s actual spatial distribution, which fundamentally accounts for RCDC’s superior feature extraction capability. Compared to standard deformable convolution and rotation-based convolution, RCDC ensures that sampling points better conform to object boundaries, thereby enhancing feature representation. Furthermore, since RCDC restricts sampling point prediction to a fixed region around the target, it avoids the computational overhead of per-pixel sampling point estimation in traditional deformable convolution, significantly reducing model complexity.

SFRADNet achieves lightweight and high accuracy, making it suitable for deployment on edge devices (e.g., drones). However, benchmark tests reveal that the proposed model exhibits certain limitations in real-time inference capability. As shown in Table 12, its inference speed on the DOTA dataset is comparable to that of LSKNet. We attribute this to the backbone network, GL²KNet: while it avoids the attention-based computations present in LSKNet, its SSMatrix relies on dynamic feature weighting through direct matrix multiplication, which introduces high computational complexity and hinders real-time performance. Furthermore, as illustrated in Figure 8E, SFRADNet predicts storage-tanks originally annotated with horizontal bounding boxes as rotated boxes. This phenomenon occurs because RCDC performs feature extraction by sampling points according to target shapes. For quasi-square objects, the minimum enclosing rectangle of sampling points can be represented as squares in multiple orientations. As demonstrated in Figure 11, when RCDC samples storage-tank targets, the enclosing rectangular region of sampling points degenerates into a square. These sampling points can represent square-oriented boxes in various directions, consequently leading to imprecise feature extraction for quasi-square targets by RCDC. This square-like problem remains an unsolved challenge in oriented object detection. In our future work, we plan to address this issue through approaches such as multi-expert decision mechanisms, where we may integrate both horizontal and oriented object detection models, delegating square-like targets to horizontal detection models for processing.

5. Conclusions

RS objects have the characteristics of arbitrary scale and multi-directional distribution. Existing detectors typically utilize FPN and deformable/rotated convolution to adapt to changes in object scale and orientation. However, these methods solve scale and orientation issues separately, ignoring their deeper coupling relationships. In this paper, we propose a one-stage detection network called Scale First-Refinement Angle Detection Network (SFRADNet) for detecting RS objects at arbitrary scale and orientation. The proposed network comprises two parts: the GL²KNet and the SA-SFEM. These two modules work synergistically to accurately classify and localize objects with arbitrary scales and multiple orientations in RS images. GL²Knet, serving as the backbone of SFRADNet, is composed of stacked GL²KCMs. Within the GL²KCM, we construct a diversity of receptive fields with varying dilation rates to capture features across different spatial coverage ranges, and then utilize a SSMatrix for diversified scale fusion. Compared to traditional large-kernel convolution networks, GL²KCM does not involve complex attention calculations during inference, significantly reducing the number of parameters and computational load. On the basis of obtaining precise scale features, we employ SA-SFEM for the extraction of orientational features. In SA-SFEM, a novel deformable convolution named RCDC is proposed, which uses DGBox as supervision information to guide the deformation of the convolution kernel sampling points. With the participation of RCDC, SA-SFEM shows exhibits heightened sensitivity to the object’s rotation angle, effectively mitigating orientation misalignment. Experimental results demonstrate the efficacy of the collaborative operation between these two modules. When compared to advanced detectors, our model achieves the highest mAP of $80.10\%$ on the DOTA-v1.0 dataset.

Although SFRADNet demonstrates superior detection performance with accurate angle alignment and scale matching across multiple datasets, along with a lightweight design, its real-time inference capability remains limited. In future work, we will continue to explore improvements in model efficiency and deployability on edge devices.