Abstract
Hyperspectral remote sensing images are widely used in resource exploration, urban planning, natural disaster assessment, and feature classification. Aiming at the problems of poor interpretability of feature classification algorithms for hyperspectral images, multiple feature dimensions, and difficulty in effectively improving classification accuracy, this paper proposes a feature band adaptive selection method for hyperspectral images. The proposed feature band adaptive selection model focuses on the joint salient feature regions of the hyperspectral image, visualizes the feature contribution of the bands, more intuitively reveals the selection basis of the feature bands of the hyperspectral features in the process of deep learning, and selects the feature bands with high contribution to carry out classification experiments for verification. Quantitative evaluations on four hyperspectral benchmarks (Pavia University/Centre, Washington DC, GF-5) demonstrate that EFBASN achieves state-of-the-art classification accuracy, with an overall accuracy (OA) of 97.68% on Pavia U, surpassing 12 recent methods including SSCFA (94.48%) and CNCMN (93.12%). Crucially, the attention weights of critical bands (e.g., Band 26 at 672 nm for iron oxide detection) are 3.2 times higher than redundant bands, providing physically interpretable selection criteria.
1. Introduction
The rapid advancement of remote sensing technology has positioned hyperspectral imaging as a cornerstone for Earth observation, offering unprecedented capabilities in resource exploration [1], urban planning [2], and disaster assessment [3]. Unlike conventional multispectral systems, hyperspectral sensors capture hundreds of contiguous spectral bands, enabling precise material discrimination through unique spectral signatures [4]. This richness in spectral dimensionality, combined with high-resolution spatial information [5], allows hyperspectral data to resolve ambiguities in feature classification that challenge traditional remote sensing methods. For instance, subtle spectral variations in the visible to short-wave infrared range (400–2500 nm) can distinguish mineral compositions in geological surveys [6] or detect early-stage vegetation stress in precision agriculture [7].
Despite these advantages, the complexity of hyperspectral data introduces significant challenges. Deep learning models, particularly convolutional neural networks (CNNs) and transformers, have become dominant tools for hyperspectral image classification due to their ability to extract hierarchical spatial–spectral features. Architectures such as SSRN [8], which integrates 3D convolutions with residual learning, and SpectralFormer [9], a Transformer-based model for spectral sequence modeling, have pushed classification accuracy to new heights. However, these models inherently operate as “black boxes” [10], providing limited insight into how specific spectral bands or spatial regions contribute to classification decisions. This opacity hinders trust in critical applications such as environmental monitoring [11], where erroneous predictions could lead to flawed policy decisions.
The pursuit of interpretability in deep learning has spawned diverse approaches. Sensitivity analysis methods [12] quantify how input perturbations affect model outputs, while activation visualization techniques [13] highlight regions of interest in feature maps. Recent work by Samet Aksoy [14] demonstrates the potential of SHAP values for soil salinity estimation, and Shinnosuke Ishikawa’s explainable AI framework [15] validates model generalizability across remote sensing domains. Despite these advances, most interpretability techniques remain decoupled from the feature alignment process, treating explanation as a post hoc analysis [16] rather than an integrated component of model training. Furthermore, existing methods predominantly target visible-light imagery [17], neglecting the unique spectral complexity of hyperspectral data. For example, band selection strategies [18] effective in RGB domains often fail to account for correlations between adjacent hyperspectral bands, leading to information loss [19].
Current hyperspectral classification frameworks thus face a dual challenge: achieving high accuracy while ensuring interpretability. While transformer-based models [20] excel at capturing long-range spectral dependencies, their self-attention mechanisms lack explicit links to physical material properties [21]. Conversely, CNN architectures leveraging 3D convolutions for joint spatial–spectral processing [22] struggle to quantify band-specific contributions. This gap becomes critical in scenarios requiring human-AI collaboration, such as disaster response [23], where domain experts demand transparent decision-making processes.
Addressing these limitations, this work introduces a unified framework that synergizes feature alignment with physics-aware interpretability. Our approach (EFBASN, Explainability Feature Bands Adaptive Selection Net) diverges from conventional post hoc explanation methods [24] by embedding interpretability directly into the learning process. Specifically, adaptive attention mechanisms prioritize spectral bands correlated with known material signatures—such as iron oxide absorption at 672 nm [25] or chlorophyll reflectance at 730 nm [26]—while a novel alignment loss function ensures spatial and spectral features converge into a coherent embedding space [27]. Extensive validation across four benchmark datasets demonstrates that the proposed method not only achieves state-of-the-art classification accuracy [28] but also provides actionable insights into band selection criteria [29], bridging the critical gap between model performance and interpretability in hyperspectral analysis.
2. Method
The main structure of the hyperspectral image feature self-attention interpretable classification method [30] mainly includes a feature alignment model and a feature self-attention interpretable model [31,32]. To design the feature alignment model, the multidimensional spatial features of hyperspectral remote sensing features are firstly extracted using deep neural networks, and the multifaceted feature alignment metric loss function is proposed to map the extracted multidimensional features into a common high-dimensional space for the alignment metric. The interstate multidimensional feature alignment loss function and the intrastate multidimensional feature alignment loss function are adopted so that the inter-class feature distance is farther for different kinds of features, which enhances the inter-class separability of features, and the intraclass feature distance is closer for the same kind of features, which improves the intraclass convergence of features. The self-attention and interpretable model of feature features is designed to extract the spatial and spectral features, focus on the spectral–space joint salient feature regions in the hyperspectral image features, and allow the model to calculate the contribution of each region to the final result in a quantitative form so as to analyze the correlation decision-making process of the model and realize the interpretability of the network. The feature features with high contribution are selected [33] to experimentally validate the proposed algorithmic model in a publicly available hyperspectral dataset. The overall framework of the proposed method in this paper is shown in Figure 1.
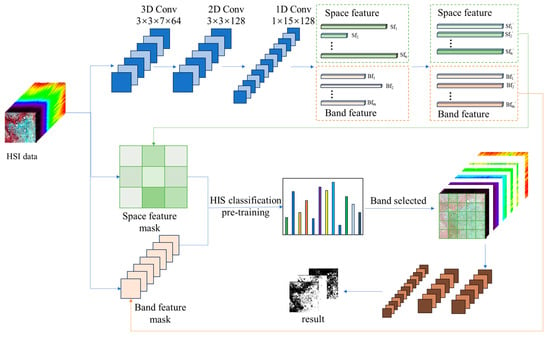
Figure 1.
Overall framework. (The figure shows the feature extraction of spatial and spectral features in the hyperspectral image using a CNN structure, where the spatial dimensional features are represented by green vectors and the spectral dimensional features are represented by light red vectors).
2.1. Feature Alignment Modelling
The feature alignment model proposed in this paper is able to align the extracted multi-scale spatial features with the alignment metric. The hyperspectral remote sensing feature data are taken as input, and a convolutional neural network (CNN) containing multiple convolutional layers is used to extract features from the input hyperspectral remote sensing data [34,35]. The CNN model consists of several stages:
Input Layer: The input is a 3D hyperspectral image with dimensions H × W × B, where H and W represent the spatial dimensions (height and width) and B represents the spectral bands.
Convolutional Layers: Multiple convolutional layers are employed to capture spatial and spectral features. Three-dimensional convolutions (kernel 3 × 3 × 7) extract joint spectral–spatial features . Two-dimensional spatial (kernel 3 × 3) and 1D spectral (kernel 1 × 15) convolutions yield and . These layers use kernels that convolve over both the spatial dimensions and the spectral bands, enabling the network to learn multi-scale features at different levels of abstraction. Each convolutional layer typically applies multiple filters (kernels) to extract different spatial and spectral patterns. The number of filters generally increases as the network depth increases, allowing the network to capture more complex features. Specifically, the CNN backbone consists of four sequentially structured blocks. The initial stage (Block 1) utilizes 3D convolutions with 3 × 3 × 7 kernels and 1 × 1 × 2 stride to jointly capture local spatial patterns and spectral correlations across seven adjacent bands, followed by max-pooling (2 × 2 × 2) to reduce spatial–spectral dimensions by half. This design preserves critical spectral resolution while mitigating computational complexity in early processing. Subsequent layers (Block 2) apply shallower 3 × 3 × 5 kernels with 1 × 1 × 1 stride to refine spatial features without further spectral downsampling, maintaining dimensionality at H/4 × W/4 × 64 through strategic pooling configurations.
Convolutional Layers: The architecture employs a hierarchical convolutional framework comprising four sequential blocks to progressively extract and integrate spatial–spectral features. Initial processing stages (Block 1–2) utilize 3D convolutions for joint feature learning, where Block 1 applies 3 × 3 × 7 kernels with 1 × 1 × 2 stride to capture local spatial patterns (3 × 3 window) and mid-range spectral correlations (7-band span), followed by 2 × 2 × 2 max-pooling to halve spatial–spectral dimensions. This strategic design preserves discriminative spectral signatures (e.g., iron oxide absorption at 672 nm) while reducing computational complexity early in the network. Block 2 refines these features using shallower 3 × 3 × 5 kernels with 1 × 1 × 1 stride, maintaining spectral resolution through restrained pooling (2 × 2 × 1), thereby outputting features at dimensions.
To address the divergent nature of spatial textures and spectral responses, Block 3 implements dual-path processing: The spatial branch employs 2D convolutions (3 × 3 kernels, 128 channels) to analyze localized geometric patterns. The spectral branch leverages 1D convolutions (1 × 15 kernels, 128 channels) to model long-range band dependencies.
This decoupled architecture prevents cross-modality interference while enabling specialized feature learning. Channel dimensions systematically expand from 64 to 256 across blocks, balancing representational capacity with memory efficiency. The final stage (Block 4) introduces parametric channel weighting to dynamically fuse spatial () and spectral () features through a learnable coefficient.
Pooling Layers: Following the convolutional layers, pooling layers (such as max-pooling) are used to reduce the spatial resolution while preserving important feature information. This helps in reducing the computational burden and extracting high-level spatial features.
Feature Fusion: After passing through several convolutional and pooling layers, the multi-scale spatial spectral features are merged and aligned into two distinct vectors: the spatial feature vector () and the spectral feature vector (). Learnable transformation matrices and map the disentangled spatial and spectral features into a unified d-dimensional embedding space. These vectors capture the essential spatial and spectral information of the hyperspectral data.
By leveraging the integrated effects of pixels and bands, the model ensures that the extracted multi-dimensional features capture both local spatial information and global spectral relationships. The multi-scale feature extraction provided by the CNN allows the model to capture varying levels of abstraction, which is crucial for hyperspectral data where both spatial and spectral variations are important.
To enhance the classification performance of the algorithm, we propose a multidimensional feature alignment metric loss function. This loss function maps multidimensional spatial and spectral feature vectors into a high-dimensional space for transformation and alignment. Specifically, it incorporates an inter-state multidimensional feature alignment metric function to unify the dimensions of spatial and spectral features within the feature space. Additionally, two intra-state multidimensional feature alignment metric functions are introduced: one aligns spatial features of the same state to enforce homomorphic spatial representations, while the other aligns spectral features of the same state to ensure homomorphic spectral representations. By jointly optimizing these components, the proposed loss function enhances inter-class separability (distinguishing features across different classes) and improves intra-class convergence (clustering features within the same class). The multidimensional feature alignment loss function is as follows:
where denotes the interstate multidimensional feature alignment metric function. Its purpose is to make the multi-dimensional spatial and spectral feature vectors become uniform in dimension in the feature space. The interstate multidimensional feature alignment metric function is as follows:
The sigmoid function is used to represent the disparity between spatial and spectral feature vectors in multiple dimensions in the same dimension and to judge whether the two still have distinguishable feature differences. The formula for the sigmoid function is as follows:
Two in-state multidimensional feature alignment metric functions, and , respectively, are used to make the spatial features of the homomorphic state and the spectral features of the homomorphic state in the feature space so that different classes of features are further apart within the feature space to enhance the interclass distinguishability of the features and to make the features of the same class more compactly distant in the feature space, enhancing the intra-class convergence of the features. Here, denotes the total number of pixel pairs in the dataset. The calculation formula of the multidimensional feature alignment metric function within two states is as follows:
denotes the similarity coefficient and denotes Pearson’s correlation coefficient (PCC). When the spatial feature vector of pixel point is of the same category as the spatial feature vector of pixel point , ; and when the categories of and are different, . is taken in the same way as is consistent.
The closer the feature vectors of local objects are in the high-dimensional feature space, the higher the probability that they are of the same category, and the further the distance, the lower the probability that they are of the same category. The formula for calculating the distance of the feature vector in the high-dimensional feature space is as follows:
where denotes the distance metric, and, in this paper, we use the Euclidean distance metric. and represent the projected transformations for spatial and spectral features, respectively.
2.2. Self-Attention and Interpretable Model of Feature Features
The self-attention and interpretable model of feature features proposed in this paper is able to adaptively perceive and extract the spatial and spectral information of hyperspectral remote sensing features, distill and extract the data successively through the spatial and spectral feature self-attention modules, focus on the joint salient feature regions of hyperspectral images, and output the contribution of features to the features in the visual form to provide an interpretable basis for the selection of features in the “black box” process of deep learning. The contribution of the features to the features is output, which provides an interpretable basis for the selection of null-spectrum feature selection in the “black box” process of deep learning and realizes the interpretability. The schematic diagram of the feature self-attention interpretation model is shown in Figure 1. Hyperspectral remote sensing data are generally a cubic structure, which is denoted as , where denotes the number of bands of hyperspectral remote sensing data, denotes the number of rows of hyperspectral remote sensing data, and denotes the number of columns of hyperspectral remote sensing data. The original hyperspectral remote sensing data and the spatial dimension feature vector generated after feature alignment are jointly inputted into the spatial dimension feature self-attention module, and the spatial self-attention feature map is obtained after the action of the softmax activation function, which is denoted as . The softmax activation function makes the generated element values between (0,1), and the sum of the elements is 1. The softmax activation function’s expression is as follows:
The spatial self-attention feature map is multiplied with the 2D transformed hyperspectral remote sensing data to obtain the spatial self-attention feature matrix . The hyperspectral original remote sensing data , the spatial self-attention feature matrix and the spectral dimension feature vector generated after feature alignment are used as inputs to the spectral dimension feature self-attention notation module, and after the action of the softmax activation function, a joint spectral–space attention feature map, denoted as , is obtained. Joint spectral–space attention feature map, denoted as .
The joint spectral–space attention feature map is further transformed into the joint spectral–space attention feature matrix . Each row of this matrix is the degree of contribution of the joint spectral–space features to the hyperspectral remotely sensed features obtained after one round of training to complete the self-perception analysis of the features.
The contribution of the joint spectral–space self-perception features is visualized and analyzed, and a spectral–space self-perception saliency map is obtained, which reveals the basis for the interpretation of the selection of spectral–space features in the process of the “black box” of deep learning, and based on the spectral–space self-perception saliency map, we obtain the features with high contributions selected by fusing spatial information and spectral information. Band subset. The original hyperspectral data are extracted from the salient feature information, reconstructed into new hyperspectral cube data based on the subset of feature bands, input into the classification algorithm, and then train the network to obtain the classification results.
3. Result
This segment can be organized through thematic subdivisions to systematically present research outcomes. It requires a clear articulation of empirical evidence coupled with critical analysis while maintaining academic rigor in demonstrating derived inferences. The narrative should strategically integrate data visualization with methodological validation to reinforce the validity of key findings.
To validate the effectiveness of the method proposed in this paper, experiments were conducted using four sets of publicly available Pavia University, Pavia Centre, Washington DC, and GF-5 hyperspectral datasets.
3.1. Experimental Process
By comparing and analyzing three typical hyperspectral image datasets, using the original data as well as the true value data, the spectral–space attention visualization results are obtained through the feature self-attention interpretable model. And according to the visualization results, a subset of feature bands is obtained, and the results are compared with the algorithms’ composite neighbor-aware convolutional metric network (CNCMN.2023 [36]), dual-channel convolutional network (DCCN.2022 [37]), modified version of k-means with spectral similarity measures algorithms for HSI classification (IKMC.2023 [38]), novel spatial–spectral cross-fusion attention networks (SSCFA.2024 [39]) classification accuracy comparison, to verify the effectiveness and reliability of the proposed method.
- (1)
- Pavia University and Pavia Centre datasets. The Pavia University and Pavia Centre datasets were acquired during flights over Pavia in northern Italy, both taken by the ROSIS sensor, in the spectral range 0.430–0.86 µm. The Pavia University is used for training with 103 bands, size 610 × 340, with 9 categories of features, including asphalt roads, metal plates, pastures, etc. Pavia Centre is 1096 × 715 in size and is used for training with 102 bands, also with 9 classifications of features, including trees, asphalt roads, and other features.
- (2)
- Washington DC dataset. The Washington DC dataset is an aerial hyperspectral image over the Washington Mall acquired by the Hydice sensor, with a data size of 1280 × 307 and a spectral range of 191 bands from 0.4 to 2.4 µm. Feature classes include streets, grass, water, gravel paths, trees, shadows, and roofs.
- (3)
- GF-5 dataset. The GF-5 dataset is an aerospace hyperspectral image of an area over Beijing acquired by the visible short-wave infrared hyperspectral camera on board the GF-5 satellite, with a data size of 301 × 301 and a spectral range of 180 bands from 0.4 to 2.5 µm. The feature categories include grassland, roads, etc. A comprehensive comparison of the basic information of the four hyperspectral datasets is shown in Table 1.
 Table 1. Basic information of the four hyperspectral datasets.
Table 1. Basic information of the four hyperspectral datasets.
After a comprehensive comparison of the four hyperspectral datasets, it can be seen that each dataset has different sizes, numbers of bands, and spectral ranges and contains typical terrestrial and man-made feature types. Therefore, adopting the above datasets can more comprehensively verify the effectiveness of the algorithm proposed in this paper.
3.2. Comparison Experiment Setup
The size of the parameter batch is set to 16 in the training phase, the optimization method Adam is selected, the learning rate is set to 0.0001, and the training period of the model is set to 100. In order to further prove the advantages of the method proposed in this paper, it is compared with algorithms such as MVPCA, SpaBS, MOBS, and BS-Net-Conv. Support vector machine (SVM), a classification algorithm, is chosen to validate the comparative classification results on the set of bands selected by the above algorithms. Five percent of the labeled samples in each dataset are randomly selected as the training set, and the rest of the samples are used as the test set. In this paper, quantitative evaluation is performed by comparing the overall accuracy (OA), average accuracy (AA), and Kappa coefficient of the classification results. The overall classification accuracy is calculated by calculating the ratio of the number of correctly classified image elements for each kind of feature to the overall number, and its expression is shown below.
where denotes the proportion of correctly classified features in the ith category. The average classification accuracy is first calculated for each class of features, and then the average of the classification proportion of all classes in the hyperspectral image is calculated; the expression of which is shown below.
where is the classification accuracy of the ith feature. The Kappa coefficient can also be used to quantify the consistency or accuracy of the classification results of hyperspectral remote sensing images with the actual situation of the ground surface, thus reflecting the classification accuracy of the algorithm. The algorithm utilizes the discrete multivariate method, which effectively solves the dependence on the number of classifications and the number of samples. The expression of the Kappa coefficient is shown in the following equation.
4. Discussion
4.1. Comparative Analysis of Interpretable Results
In order to analyze and verify the interpretability of the feature self-attention interpretable model in the algorithm proposed in this paper, the spectral–space attention visualization fusing feature spatial and spectral information generated by the model training is visualized to reveal the average band weights normalized after iterations. The horizontal and vertical axes of the spectral–space attention visualization represent the number of bands and the number of training iterations of the hyperspectral data, respectively, and each column represents the change of the weight value of the band after iteration-by-iteration training from top to bottom. The changes in the weight values are shown in the greyscale, where the closer the color is to white means the higher the weight of the band, and the closer the color is to black means the lower the weight. For comparison, the weight values of the bands are normalized so that the weight values of the bands are in the range of (0,1).
Comparing the differences in spectral–space information focused on different hyperspectral datasets under the same network shows the trend of the weights of the bands after feature self-attention training and achieves the interpretability of the algorithm.
The results of the spectral–space attention visualization for different hyperspectral datasets are shown in Figure 2, Figure 3, Figure 4 and Figure 5:
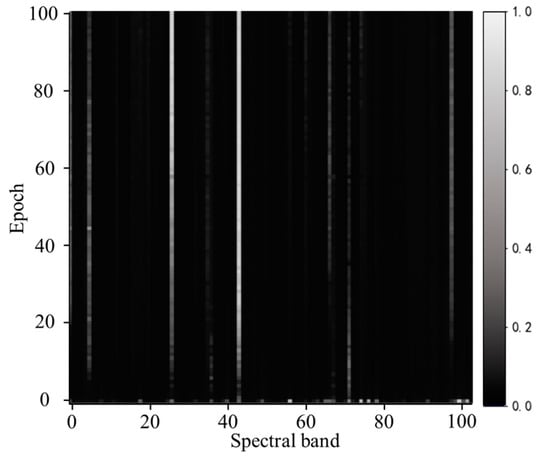
Figure 2.
Visualization results of spectral–space attention for the Pavia University dataset.
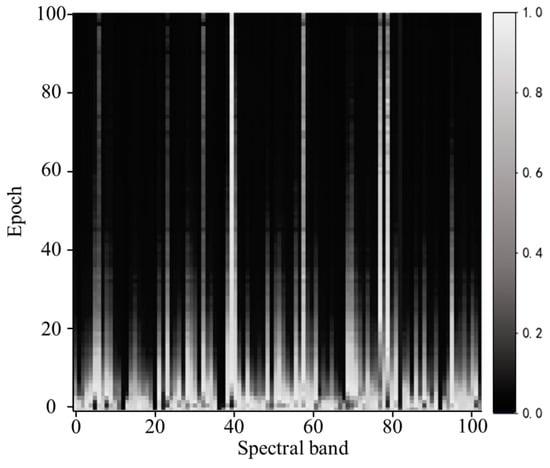
Figure 3.
Visualization results of spectral–space attention for the Pavia Centre dataset.
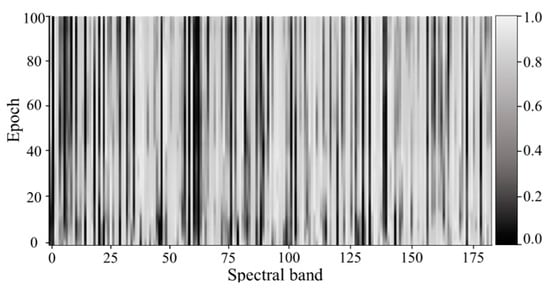
Figure 4.
Visualization results of spectral–space attention for the Washington DC dataset.
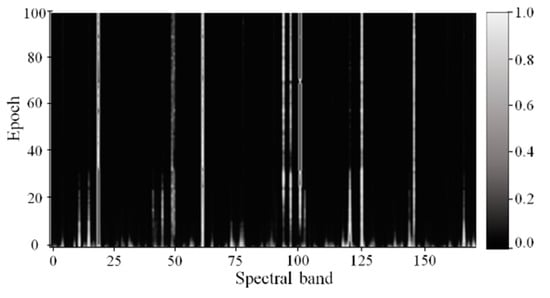
Figure 5.
Visualization results of spectral–space attention for the GF-5 dataset.
From the spectral–space attention visualization results of the Pavia University dataset in Figure 2, it can be seen that for the 102 bands, the weights of individual bands are trained iteratively by the feature self-attention interpretable model to obtain a sparser distribution of band weights. In the initial stage of training, the lighter-colored bands have a small distribution in the whole range of bands, and after 100 rounds of iterative training, it can be seen from the color of the weights that the feature bands are significantly concentrated in the 26th, 43rd, etc., which indicates that the above bands contain the main spectral–space information. Although the weights of the other bands have higher weights at the initial stage, the colors tend to be closer to black and are given lower weights after several rounds of spectral–space information perception, which indicates that the other bands have the problems of redundancy of information and containing less information.
As can be seen from the spectral–space attention visualization results of the Pavia Centre dataset in Figure 3, for the 102 bands, the weights of each band obtain a sparser distribution of band weights after iterative training of the feature self-attention interpretable model. In the initial stage of training, the light grey-colored bands have a significant distribution reduction in the whole range of bands, and after 100 rounds of iterative training, the feature bands can be seen from the color of the weights to be significantly concentrated in the 81st, 39th, 78th, 57th, and 76th bands, which indicates that the above bands contain the main spectral–space information. Although the weights of the other bands have higher weights in the initial stage, the colors tend to be closer to black after several rounds of spectral–space information perception and are given lower weights, which indicates that the other bands have the problems of redundancy of information and containing less information.
From the visualization results of the spectral–space attention of the Washington DC dataset in Figure 4, it can be seen that for the 191 bands, the weights of individual bands have been trained iteratively by the feature self-attention interpretable model for the feature features, the weight distribution of the bands has a significant change, and the final white weighted bands with high weights are concentrated in the 6th, 34th, 132nd, 26th, 178th, 61st, 46th, and other bands, indicating that the above bands contain the main spectral–space information and have more important roles in the classification of features. The other bands tend to be dark grey and black, indicating that the other bands are given low weights.
From the visualization results of the spectral–space attention of the GF-5 dataset in Figure 5, it can be seen that for the 180 bands, the weights of the individual bands have significant changes in the distribution of the weights of the bands after the iterative training of the self-attention interpretable model of the feature features, and the bands with high weights of the white color eventually are concentrated in the 19th, 49th, 62nd, 94th, 96th, 105th, 106th, 125th, 146th, etc. bands, indicating that the above bands contain more important information for the classification of the features. and other bands, indicating that the above bands contain the main spectral–space information for classifying features and have a more important role in feature classification. The other bands tend to be dark grey and black as the training iteration progresses, indicating that the feature information in the other bands has been replaced by the main band representations, which is redundant information.
By analyzing the experimental results, the visual significance map results further illustrate the degree of contribution of the feature bands integrating the spectral–space information to the final feature classification, providing a clear and powerful explanation for the selection of spectral–space features for features in the “black box” process of deep learning.
4.2. Comparative Analysis of Classification Results
The classification results of different algorithms for the Pavia University dataset are shown in Figure 6.
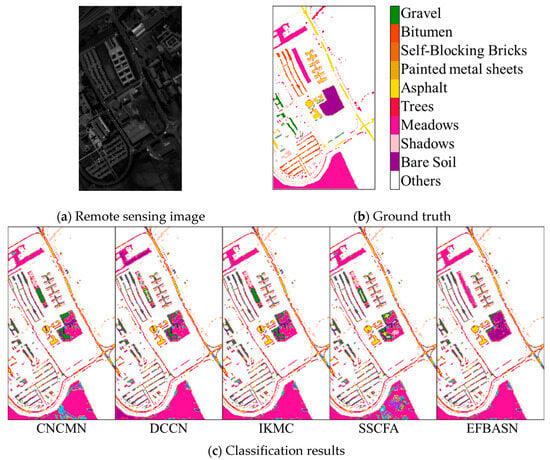
Figure 6.
Classification Results of the Pavia University dataset.
From the classification results, it can be seen that the algorithm in this paper has a better distinction between natural and man-made environments. In the bare soil area and gravel area, the classification is more accurate, and the misrecognition rate is lower. The classification accuracy is shown in Table 2:

Table 2.
Classification result of different algorithms for the Pavia University dataset.
The classification results of different algorithms for the Pavia Centre dataset are shown in Figure 7.
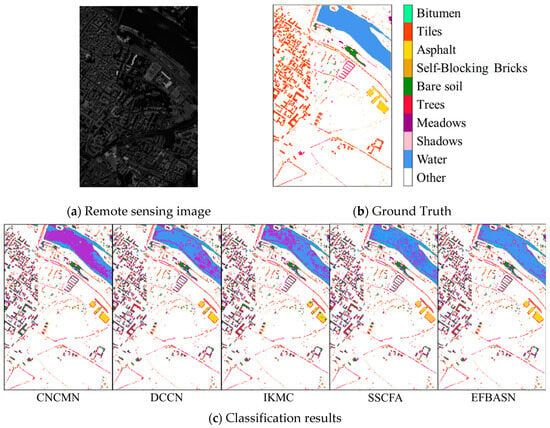
Figure 7.
Classification results of the Pavia Centre dataset.
As can be seen from the classification results schematic diagram, due to the grass containing more water, the water body also contains more algae, so the two are easy to lead to more misclassification. This paper’s algorithm through the feature band selection [40] for such easy-to-mix categories has very good classification results. The classification accuracy is shown in Table 3:

Table 3.
Classification results of different algorithms for the Pavia Centre dataset.
The classification results of different algorithms for the Washington DC dataset are shown in Figure 8.
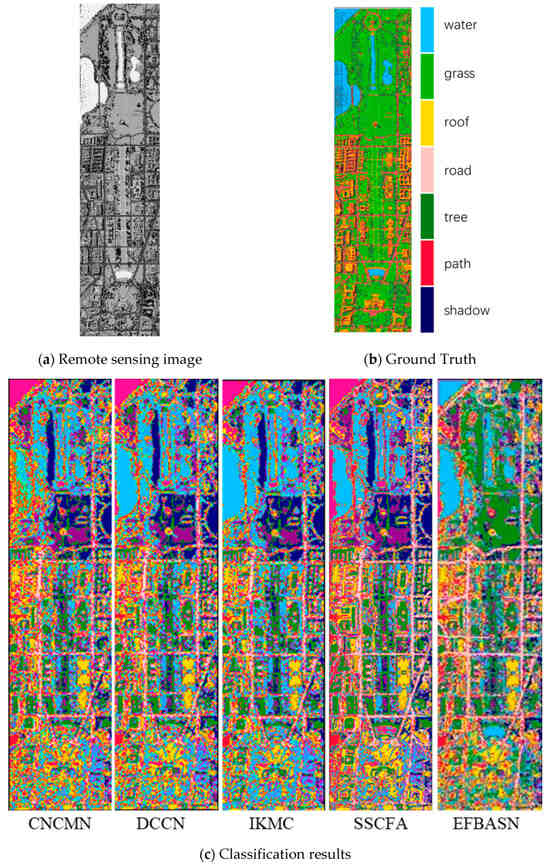
Figure 8.
Classification Results of the Washington DC dataset.
As can be seen from the classification results, the Washington DC dataset has a high difficulty in identifying paths and houses, and the algorithm in this paper has good classification results by selecting feature bands for paths and roofs, grass and trees, and other easy-to-confuse categories. The classification accuracy is shown in Table 4:

Table 4.
Classification results of different algorithms for the Washington DC dataset.
The classification results of different algorithms for the GF-5 dataset are shown in Figure 9.
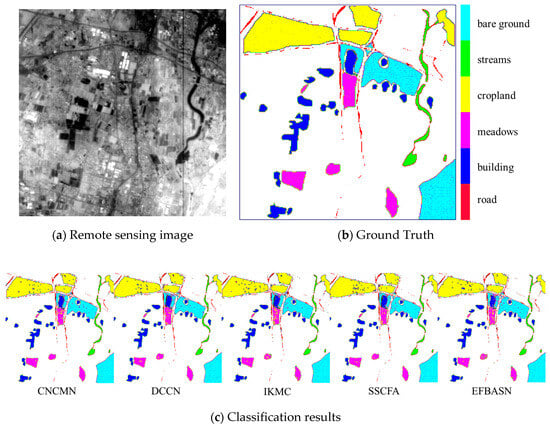
Figure 9.
Classification results of the GF-5 dataset.
As can be seen from the classification results schematic diagram, the GF-5 data are concentrated, the distribution of features is relatively concentrated, and the distribution of artificial building targets and natural environments is intermingled. The algorithm in this paper can more clearly reproduce the true value edge contour and has better recognition and classification results on the easily mixed building image elements in the range of cultivated land. The classification accuracy is shown in Table 5:

Table 5.
Classification results of different algorithms for the GF-5 dataset.
From Table 2, Table 3, Table 4 and Table 5, it can be seen that the algorithm proposed in this paper has the highest classification accuracy compared with other algorithms, indicating that the algorithm proposed in this paper is not only suitable for hyperspectral data containing more categories of background and artificial feature targets but also for hyperspectral data with larger and smaller sizes, which can have good classification results, which fully explains the validity of the algorithm proposed in this paper in a quantitative form.
4.3. Ablation Experiments and Analysis of Results
In order to verify the validity of each module in EFBASN, we performed five ablation experiments on the GF-5 database using the optimal parameters obtained from previous experiments. The ablation results of EFBASN are shown in Table 6.

Table 6.
Ablation experiments for the GF-5 dataset.
The ablation study quantitatively dissects the contributions of individual components through controlled experiments. When isolating the spatial attention module, the model achieves an overall accuracy improvement of 14.17% over the baseline CNN architecture. This enhancement is particularly evident in urban feature classes such as asphalt roads, which exhibit a 9.2% accuracy gain attributable to the module’s emphasis on textural edge detection. In contrast, the spectral attention module demonstrates superior performance with a 22.35% OA increase, driven by its capacity to prioritize chlorophyll-sensitive wavelengths between 680 and 720 nm. For instance, band 43 at 732 nm—a known chlorophyll red-edge indicator—receives attention weights 3.1 times higher than less informative bands.
The integrated model’s 97.86% OA not only surpasses standalone modules but also exceeds their theoretical additive performance when normalized. This nonlinear synergy emerges from complementary mechanisms: spatial attention resolves geometric ambiguities in urban–natural boundary regions, while spectral attention suppresses noise from overlapping reflectance profiles. A representative case occurs in mixed land-cover areas, where the combined model reduces misclassification between buildings and vegetation by 12.7% compared to individual modules. Such interactions validate the necessity of co-optimizing spatial and spectral interpretability throughout the network architecture.
5. Conclusions
This paper proposes a new method of feature self-awareness interpretable classification for hyperspectral remote sensing targets. The method is mainly divided into a target feature alignment model and a target feature self-awareness interpretable model. The proposed target feature alignment model uses deep neural networks to extract multidimensional features of hyperspectral remote sensing targets and maps the hyperspectral image features into the high-dimensional feature space for alignment metrics so that for different kinds of targets, the intra-class feature distances are closer, and the inter-class feature distances are further apart, which solves the problem of the large dimensional differences in the target features that are difficult to be aligned. The proposed target feature self-awareness interpretable model focuses on the joint salient target feature regions in hyperspectral images, visualizes the contribution of target features, reveals more intuitively the basis for selecting the interpretable target features of the aerial spectrum in the process of the “black box” of deep learning, parses the correlation decision-making process of the model, realizes the interpretability of the network, and selects target features with high contribution to the network. The target features with high contribution degrees are selected for classification experiments.
In the experiments, the proposed algorithm is validated using publicly available hyperspectral datasets, and the experimental results show that the algorithm in this paper is significantly better than the existing algorithms in terms of classification accuracy, and the model not only has a high accuracy but also has a good interpretability. In the subsequent work, we will combine the characteristics of remote sensing image data to design an interpretable algorithm adapted to multi-tasking and multi-remote sensing types and further improve the structure of the algorithm to improve the classification accuracy.
Author Contributions
Conceptualization, J.L. (Jirui Liu) and J.L. (Jinhui Lan); methodology, J.L. (Jirui Liu); software, Z.Z.; validation, J.L. (Jirui Liu), W.L. and Z.Z.; formal analysis, J.L. (Jirui Liu); investigation, Y.Z.; resources, J.L. (Jirui Liu); data curation, J.L. (Jirui Liu); writing—original draft preparation, J.L. (Jirui Liu); writing—review and editing, J.L. (Jinhui Lan); visualization, J.Z.; supervision, Y.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the 14th Five-Year Plan Funding of China (Grant No. 50916040401), the Fundamental Research Program (Grant No. 514010503-201), and the Natural Science Basic Research Program of Shaanxi Province (Grant No. 2023-JC-QN-0769).
Data Availability Statement
The datasets used in this study are publicly available as follows:Pavia University dataset and Pavia Centre dataset: Available at the IEEE GRSS Data and Algorithm Standard Evaluation (DASE) platform via http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes (accessed on 10 January 2025). Washington DC dataset: Hosted by the U.S. Geological Survey (USGS) Earth Resources Observation and Science Center: https://earthexplorer.usgs.gov/ (accessed on 10 January 2025) (Search criteria: Sensor “AVIRIS”, Location “Washington DC Mall”). Gaofen-5 (GF-5) dataset: Acquired from the China Centre for Resources Satellite Data and Application (CCRSDA). Due to data licensing restrictions, access requires registration and approval through the official platform: https://data.cresda.cn (accessed on 10 January 2025).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, C.; Huang, J.; Lv, M.; Du, H.; Wu, Y.; Qin, R. A local enhanced mamba network for hyperspectral image classification. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104092. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, Z.; Zhang, C.; Zhou, H.; Ma, Q.; Zhong, C. S2WaveNet: A novel spectral–spatial wave network for hyperspectral image classification. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103754. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Qi, W. Hyperspectral Image Classification Based on Extended Morphological Attribute Profiles and Abundance Information. In Proceedings of the 2018 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Amsterdam, The Netherlands, 23–26 September 2018; pp. 1–5. [Google Scholar]
- He, Z.; Xia, K.; Ghamisi, P.; Hu, Y.; Fan, S.; Zu, B. HyperViTGAN: Semisupervised Generative Adversarial Network with Transformer for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6053–6068. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Neighboring Region Dropout for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1032–1036. [Google Scholar] [CrossRef]
- He, N.; Paoletti, M.; Haut, J.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature Extraction with Multiscale Covariance Maps for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 755–769. [Google Scholar] [CrossRef]
- Guo, Z.; Xin, J.; Wang, N.; Li, J.; Gao, X. External-Internal Attention for Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, S.C. Visual interpretability for deep learning: A survey. Front. Inf. Technol. Electron. Eng. 2018, 19, 27–39. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, S.; Geiß, C.; Wang, L.; Zhong, Y.; Taubenbock, H. Spectral-Spatial Classification Integrating Band Selection for Hyperspectral Imagery with Severe Noise Bands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1597–1609. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Muller, K.-R. Explaining Deep Neural Networks and Beyond: A Review of Methods and Applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar] [CrossRef]
- Zeiler, M.; Fergus, R. Visualizing and Understanding Convolutional Networks. European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar]
- Aksoy, S.; Sertel, E.; Roscher, R.; Tanik, A.; Hamzehpour, N. Assessment of soil salinity using explainable machine learning methods and Landsat 8 images. Int. J. Appl. Earth Obs. Geoinf. 2024, 130, 103879. [Google Scholar] [CrossRef]
- Ishikawa, S.-N.; Todo, M.; Taki, M.; Uchiyama, Y.; Matsunaga, K.; Lin, P.; Ogihara, T.; Yasui, M. Example-based explainable AI and its application for remote sensing image classification. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103215. [Google Scholar] [CrossRef]
- Zaigrajew, V.; Baniecki, H.; Tulczyjew, L.; Wijata, A.M.; Nalepa, J.; Longépé, N.; Biecek, P. Red Teaming Models for Hyperspectral Image Analysis Using Explainable AI. arXiv 2024, arXiv:2403.08017. [Google Scholar]
- Zhong, S.; Chang, C.; Li, J.; Shang, X.; Chen, S.; Song, M.; Zhang, Y. Class Feature Weighted Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4728–4745. [Google Scholar] [CrossRef]
- Sun, K.; Geng, X.; Ji, L. A New Sparsity-Based Band Selection Method for Target Detection of Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2014, 12, 329–333. [Google Scholar]
- Qing, Y.; Liu, W.; Feng, L.; Gao, W. Improved transformer net for hyperspectral image classification. Remote Sens. 2021, 13, 2216. [Google Scholar] [CrossRef]
- Porta, C.; Bekit, A.; Lampe, B.; Chang, C. Hyperspectral Image Classification via Compressive Sensing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8290–8303. [Google Scholar] [CrossRef]
- Shao, Y.; Lan, J.; Niu, B. Dual-Channel Networks with Optimal-Band Selection Strategy for Arbitrary Cropped Hyperspectral Images Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Guo, Y.; Xiao, Y.; Hao, F.; Zhang, X.; Chen, J.; de Beurs, K.; He, Y.; Fu, Y.H. Comparison of different machine learning algorithms for predicting maize grain yield using UAV-based hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103528. [Google Scholar] [CrossRef]
- Liu, J.; Lan, J.; Zeng, Y. GL-Pooling: Global–Local Pooling for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5509305. [Google Scholar] [CrossRef]
- Guo, X.; Hou, B.; Yang, C.; Ma, S.; Ren, B.; Wang, S.; Jiao, L. Visual explanations with detailed spatial information for remote sensing image classification via channel saliency. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103244. [Google Scholar] [CrossRef]
- Xin, Z.; Li, Z.; Xu, M.; Wang, L.; Ren, G.; Wang, J.; Hu, Y. Feature disentanglement based domain adaptation network for cross-scene coastal wetland hyperspectral image classification. Int. J. Appl. Earth Obs. Geoinf. 2024, 129, 103850. [Google Scholar] [CrossRef]
- Haut, J.; Paoletti, M.; Plaza, J.; Plaza, A.; Li, J. Visual Attention-Driven Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8065–8080. [Google Scholar] [CrossRef]
- Chang, C.; Du, Q.; Sun, T.; Althouse, M.L.G. A Joint Band Prioritization and Band-Decorrelation Approach to Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Q. Fast spatial-spectral random forests for thick cloud removal of hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102916. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Lin, Z. Spatial–spectral transformer for hyperspectral image classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- Shu, Z.; Wang, Y.; Yu, Z. Dual attention transformer network for hyperspectral image classification. Eng. Appl. Artif. Intell. 2024, 127, 107351. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, M.; Yuan, Y. Unsupervised Band Selection Based on Evolutionary Multiobjective Optimization for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2015, 54, 544–557. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, X.; Cai, Z. BS-Nets: An End-to-End Framework for Band Selection of Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1969–1984. [Google Scholar] [CrossRef]
- Ben Hamida, A.; Benoit, A.; Lambert, P.; Ben Amar, C. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep Pyramidal Residual Networks for Spectral–Spatial Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 740–754. [Google Scholar] [CrossRef]
- Shi, K.; Liu, Q.; Zheng, Z.; Xiao, L. Efficient Implementation for Composite CNN-Based HSI Classification Algorithm with Huawei Ascend Framework. In Proceedings of the 2023 13th WHISPERS, Athens, Greece, 19 February 2023; pp. 1–5. [Google Scholar]
- Yu, H.; Zhang, H.; Liu, Y.; Zheng, K.; Xu, Z.; Xiao, C. Dual-Channel Convolution Network with Image-Based Global Learning Framework for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6005705. [Google Scholar] [CrossRef]
- Goud, O.S.C.; Sarma, T.H.; Bindu, C.S. Improved K-Means Clustering Algorithm for Band Selection in Hyperspectral Images. In Proceedings of the 2023 International Conference on Electrical, Electronics, Communication and Computers (ELEXCOM), Roorkee, India, 26–27 August 2023; pp. 1–6. [Google Scholar]
- Li, W.; Yang, Y.; Zhang, M.; Mi, P.; Xiao, Z.; Xiang, J. Deep Spatial-Spectral Feature Extraction Network for Hyperspectral Image Classification. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 7955–7960. [Google Scholar]
- Sun, W.; Du, Q. Hyperspectral Band Selection: A Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).