A Spatiotemporal U-Net-Based Data Preprocessing Pipeline for Sun-Synchronous Path Planning in Lunar South Polar Exploration
Abstract
1. Introduction
2. Data and Methods
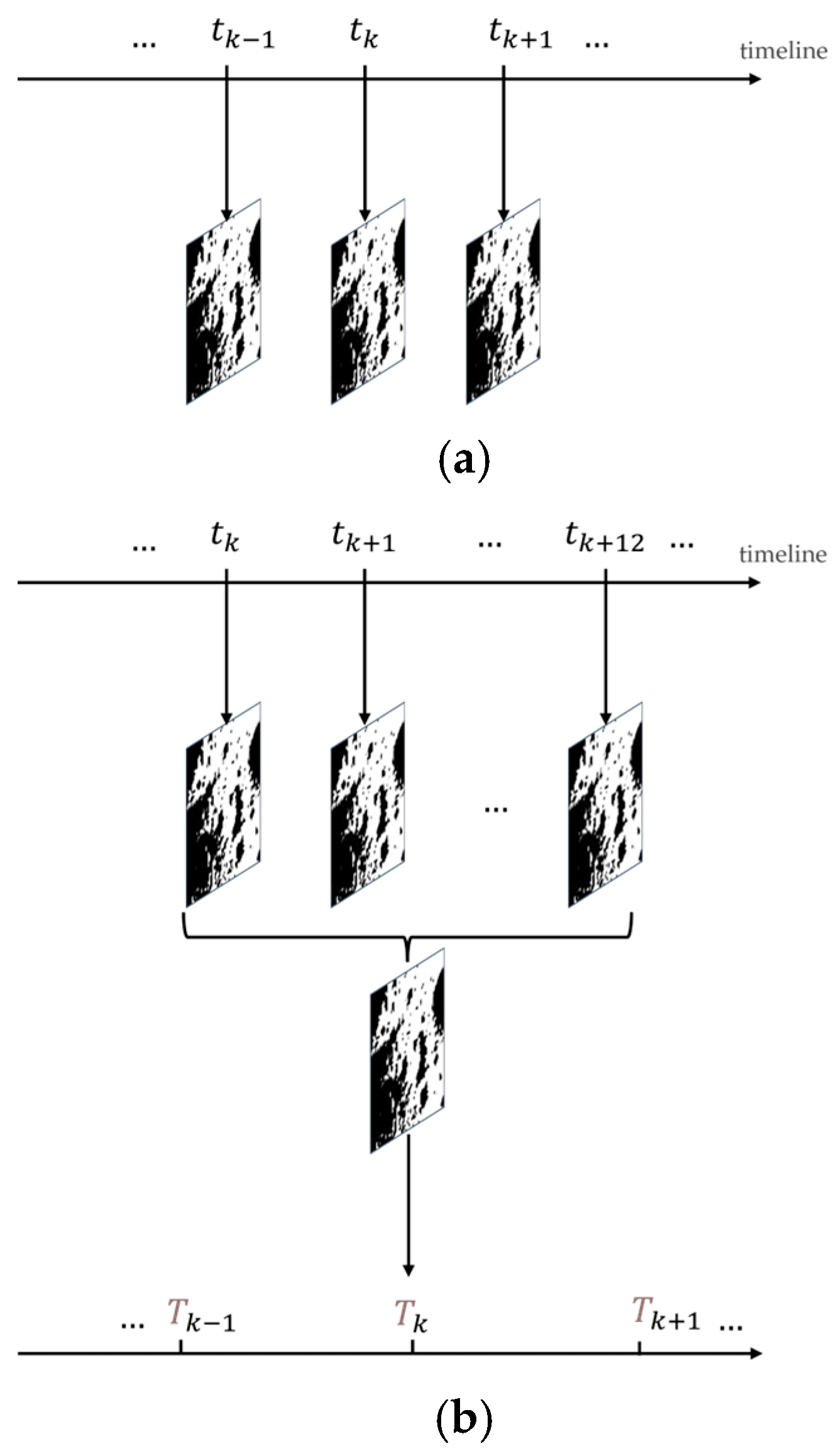
2.1. Datasets
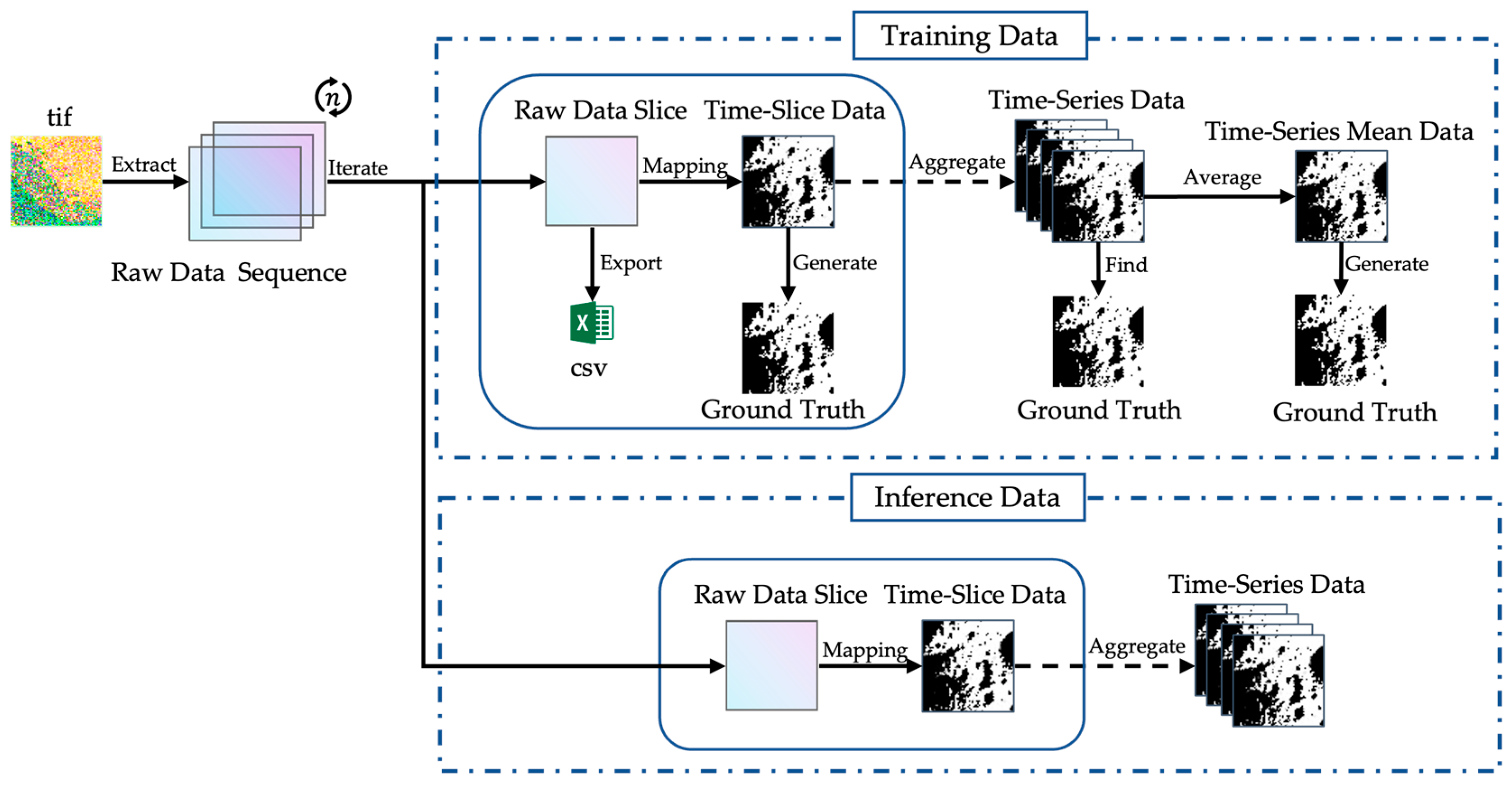
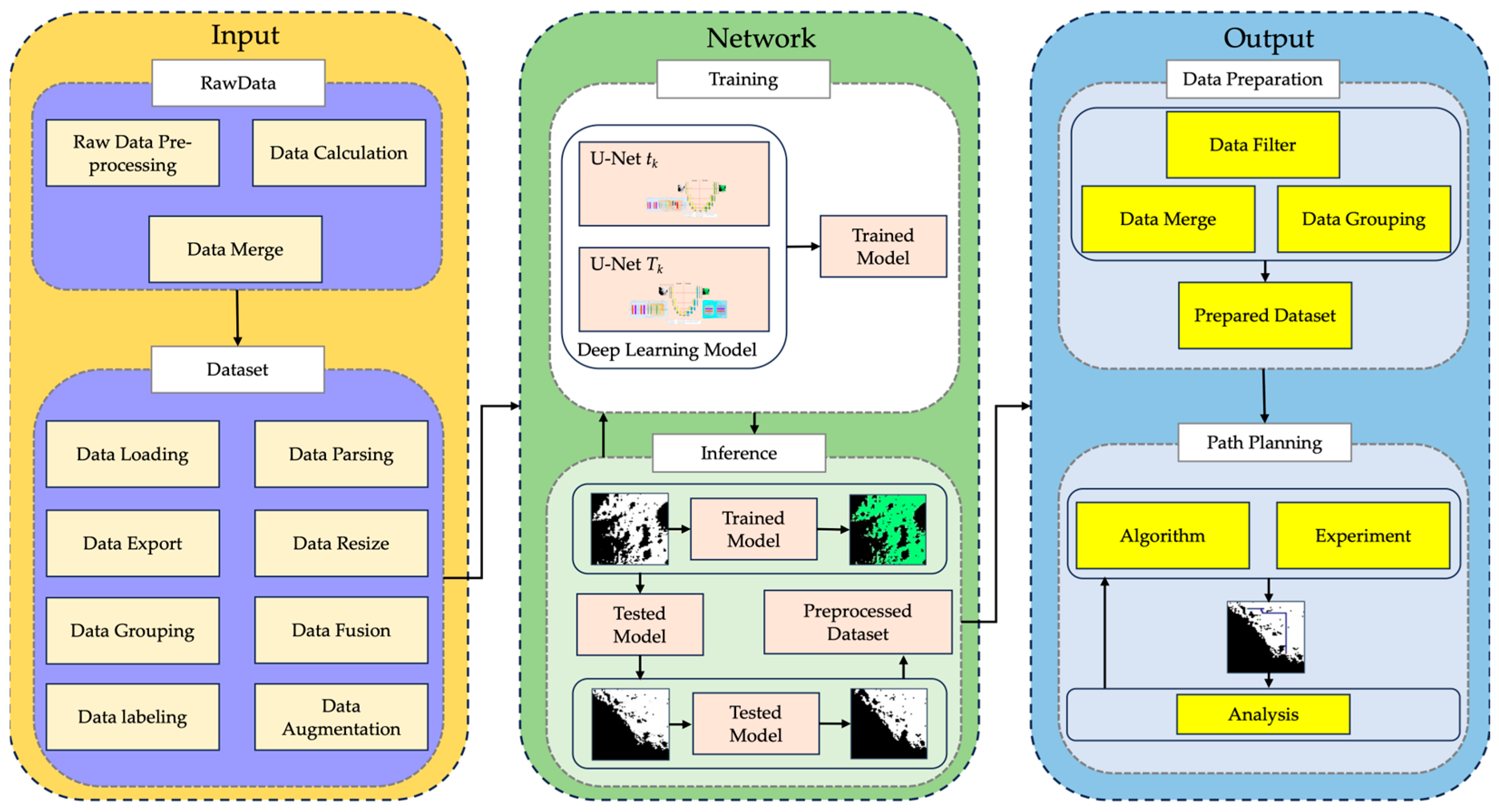
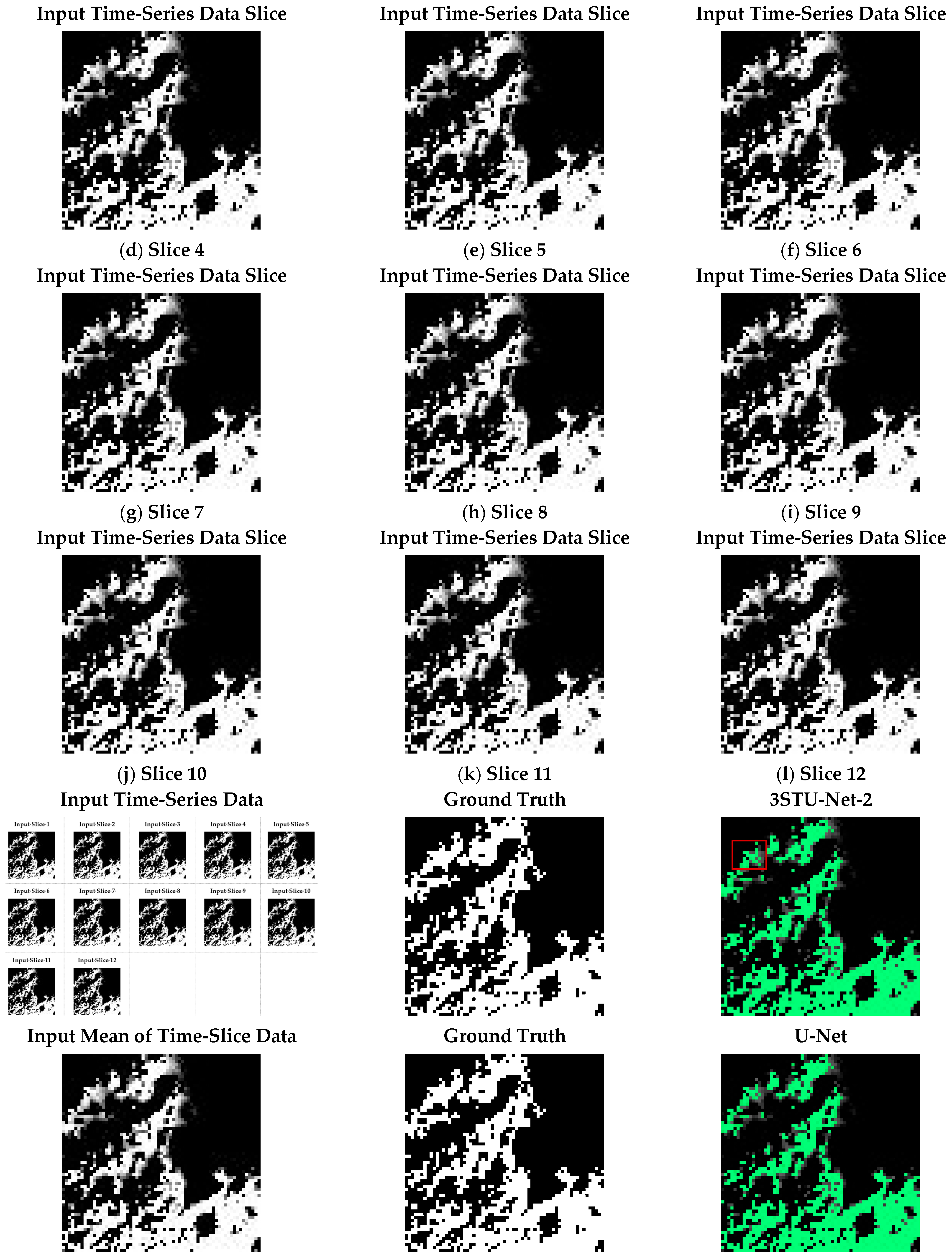
2.2. Data Preprocessing Pipeline
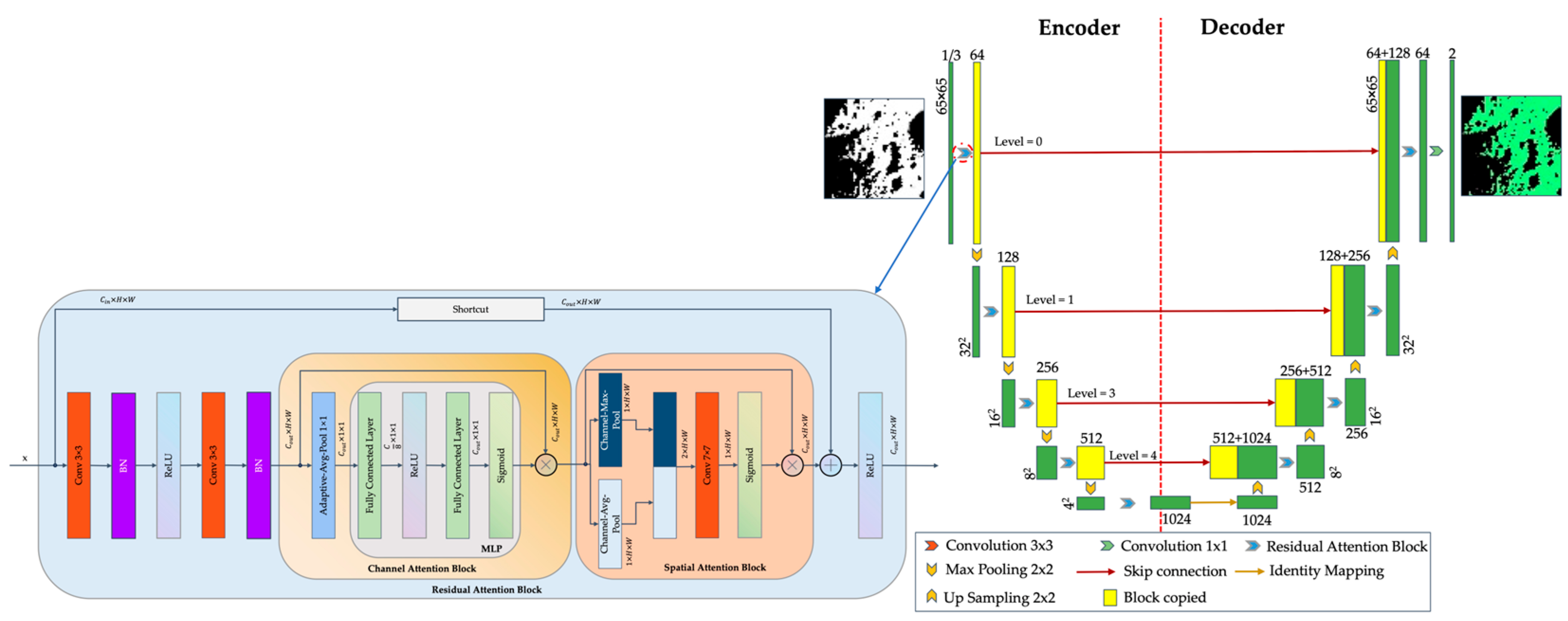
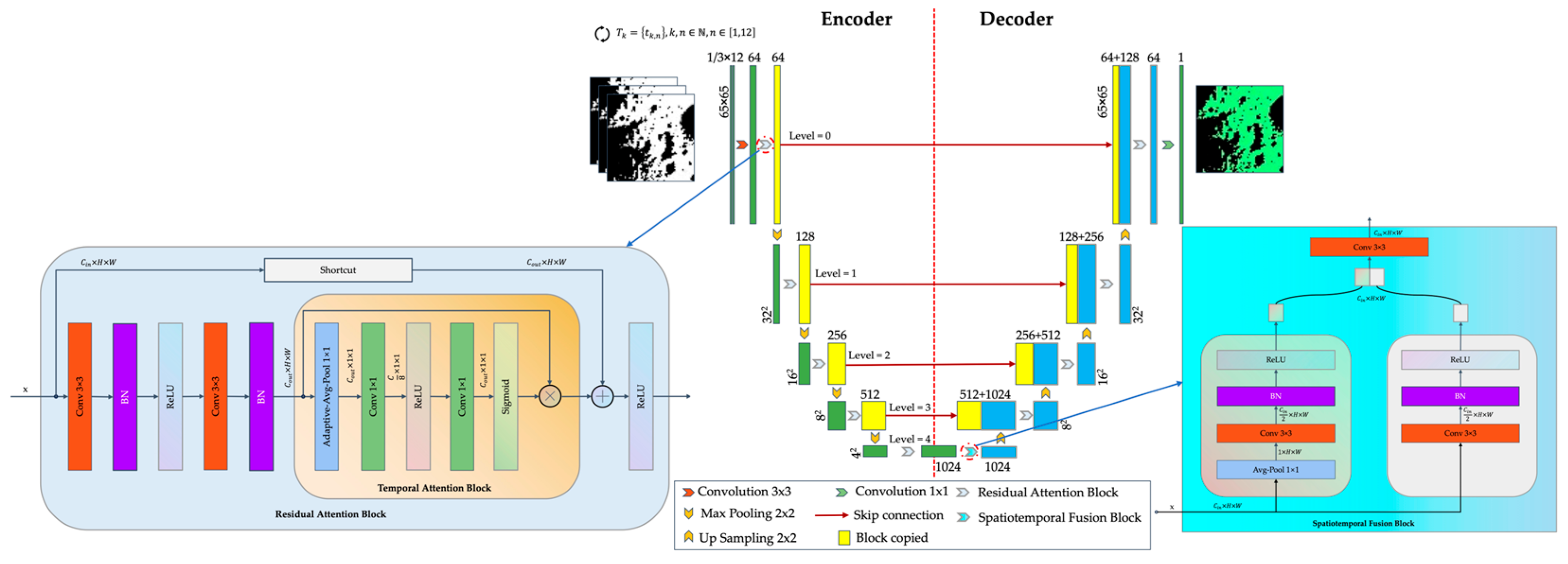
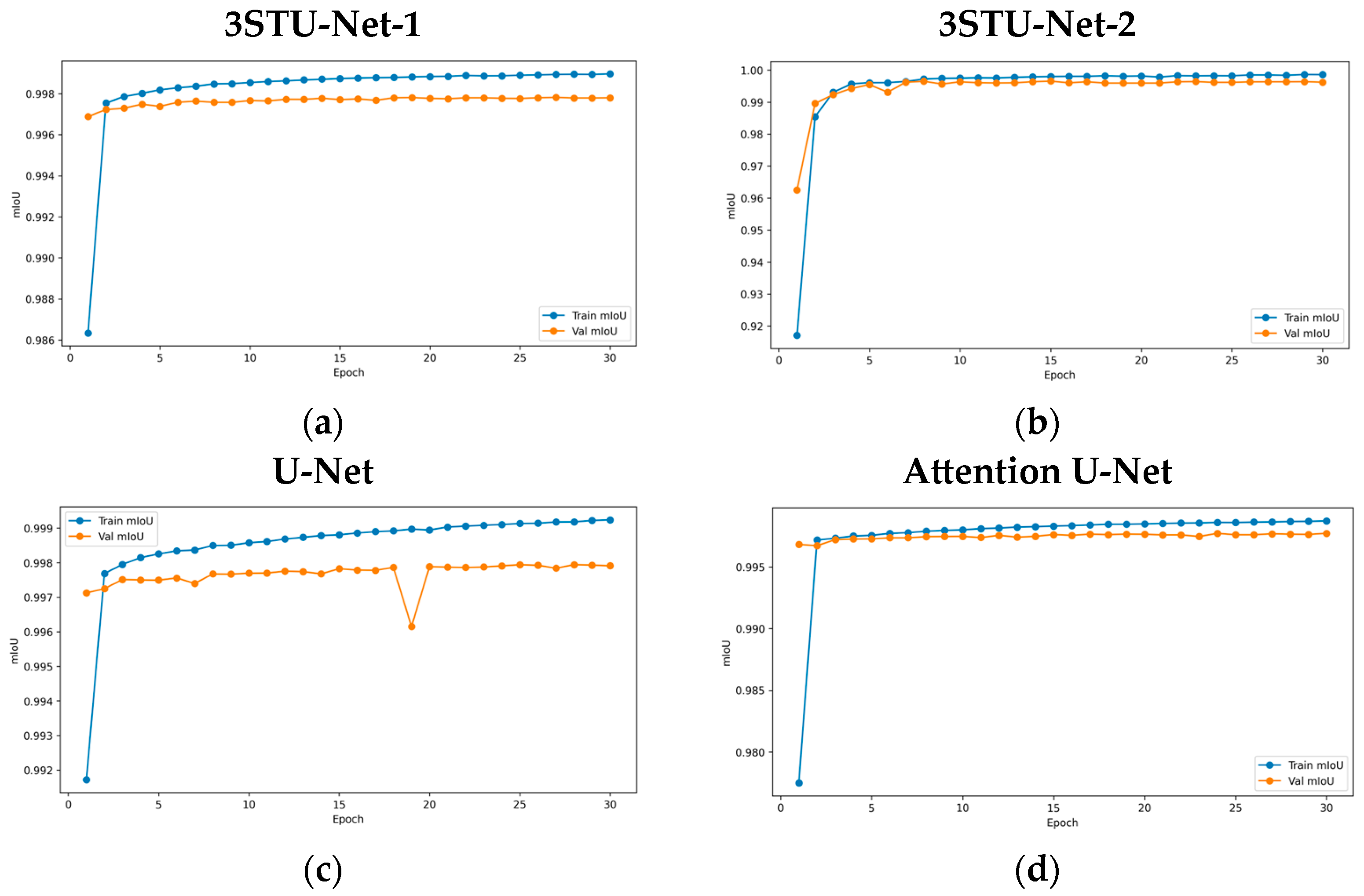
2.3. Sun-Synchronous Spatiotemporal U-Net (3STU-Net)
2.3.1. 3STU-Net-1 for Time-Slice 2.5D Data
- “Channel Attention” Block: This block serves to enhance the responses of significant feature channels. It employs adaptive average pooling to reduce the spatial dimensions of the input feature map to 1 × 1. Subsequently, it determines the channel weights through a Multi-Layer Perceptron block, which comprises two fully connected layers interspersed with a rectified linear unit and incorporates a Sigmoid function. During the forward propagation process, the input feature map is initially pooled and flattened. The channel weights are then derived from the fully connected layers. Ultimately, the weights are expanded to correspond with the original shape of the input and are multiplied element-wise with the input, thereby augmenting the feature representation of critical channels.
- “Spatial Attention” Block: This module executes average and maximum pooling operations on the input feature map within the channel dimension to optimize the extraction of static features. After the concatenation of the resultant outputs, it derives the weights via a 7 × 7 convolutional layer followed by the application of the Sigmoid function.
- “Residual Attention” Block: This block comprises two groups of 3 × 3 convolutional layers accompanied by a batch normalization layer interspersed with a rectified linear unit. Subsequently, it integrates the aforementioned two attention mechanisms and incorporates residual connections to enhance the model’s efficiency.
- The architecture’s encoder comprises “Down” modules that integrate a max-pooling layer alongside a “Residual Attention” block for down-sampling. This configuration methodically diminishes the dimensionality of the feature map while concurrently augmenting the channel count. In contrast, the decoder is structured with “Up” modules, which incorporate a transposed convolutional layer and a “Residual Attention” block to facilitate up-sampling. This process systematically enlarges the feature map’s dimensions whilst reducing the number of channels. During the up-sampling phase, the architecture adeptly addresses the discrepancies in size by concatenating the feature maps corresponding to the layers in the encoder. Ultimately, the “Out-Conv” module employs a 1 × 1 convolution to produce the segmentation results.
- The formula of the “Channel Attention” block is
- The formula of the “Spatial Attention” block is
- The formula of the “Residual Attention” block is
- The feature update formula for each level in the encoder is
2.3.2. 3STU-Net-2 for Time-Series 2.5D Data
- “Input Layer” block: This block enhances input features by using a 3 × 3 convolutional layer to convert input channels into 64 channels, extracting basic features such as edges and textures. It is then processed by a custom residual convolution block, known as the “Residual Attention” block, which will be introduced later. The residual connection alleviates the vanishing gradient problem and improves feature extraction.
- “Temporal Attention” Block: This block enhances feature extraction of time slices by replacing both the “Channel Attention” and “Spatial Attention” blocks. It utilizes the channel attention mechanism, beginning with adaptive average pooling to condense the input feature map to 1 × 1, obtaining global average features for each channel. Next, two 1 × 1 convolutional operations are performed, separated by a rectified linear unit. The first convolution reduces the channel count to one-eighth of the original, thereby lowering computational complexity. The second convolution restores the channel count to its original level. The Sigmoid function then maps the output to the range of [0, 1], producing attention weights for each channel. These weights are finally multiplied element-wise with the input feature map to enhance the important channel features.
- “Residual Attention” Block: This block enhances the temporal feature extraction ability of temporal slice data by employing a temporal attention mechanism alongside a residual connection. The primary modification involves replacing the original “Channel Attention” and “Spatial Attention” blocks with the “Temporal Attention” block, while other design elements remain unchanged.
- “Spatiotemporal Fusion” Block: This module fuses temporal and spatial features, connecting the encoder and decoder. In the temporal branch, the input feature map is averaged along the channel dimension to create a temporal feature map, which is processed through a 3 × 3 convolutional layer with a channel constraint of 1. This is followed by batch normalization and a rectified linear unit, resulting in a feature map with half the input channels. In contrast, the spatial branch retains its structures without the average pooling in the channel dimension, emphasizing static spatial features. Finally, the temporal and spatial feature maps are concatenated along the channel dimension and processed through another 3 × 3 convolutional layer for effective feature fusion.
- The designs of the other parts of the encoder and decoder of this architecture are the same as those for time-slice data. The improved “Residual Attention” block is placed in each layer for refined feature extraction. Ultimately, the “Out-Conv” module uses a 1 × 1 convolution to output the segmentation result.
- The encoder and decoder designs in this architecture mirror those used for time-slice data. Each layer incorporates an enhanced “Residual Attention” block for improved feature extraction. Ultimately, the “Out-Conv” module employs a 1 × 1 convolution to produce the segmentation results.
- The formula of the “Input Layer” block isis the output feature map of the input layer, represents the 3 × 3 convolutional operation, and represents the “Residual Attention” block operation, which we will discuss later. is the input of time-series data.
- The formula of the “Temporal Attention” block iswhere represents the global average pooling operation. represents the 1 × 1 convolutional operation. represents the rectified linear unit operation. represents the Sigmoid function to output the attention weight values to the range of [0, 1] and the results are represented as .
- The formula of the “Residual Attention” block isrepresents the rectified linear unit operation. represents the output feature map from the main path and represents output of the residual path. The formula of isrepresents the output feature map from the previous main path, and its formula iswhere represents the batch operation. represents the 3 × 3 convolutional operation. represents the element-wise multiplication operation. represents the “Temporal Attention” block operation. The formula of is
- The formula for the “Spatiotemporal Fusion” block is
- The feature update formula for each level in the encoder is
2.3.3. Loss Function
2.3.4. Assessment
2.4. Sun-Synchronous Spatiotemporal A* Path-Planning Algorithm (3ST-A*)
2.4.1. A* and Spatiotemporal A* (ST-A*)
2.4.2. 3ST-A*
- 1.
- Maps
- 2.
- Fixed Path Route
- 3.
- Cost Function
- 4.
- Assessment
3. Experiment Setup
3.1. 3STU-Net
3.2. 3ST-A*
4. Results and Discussion
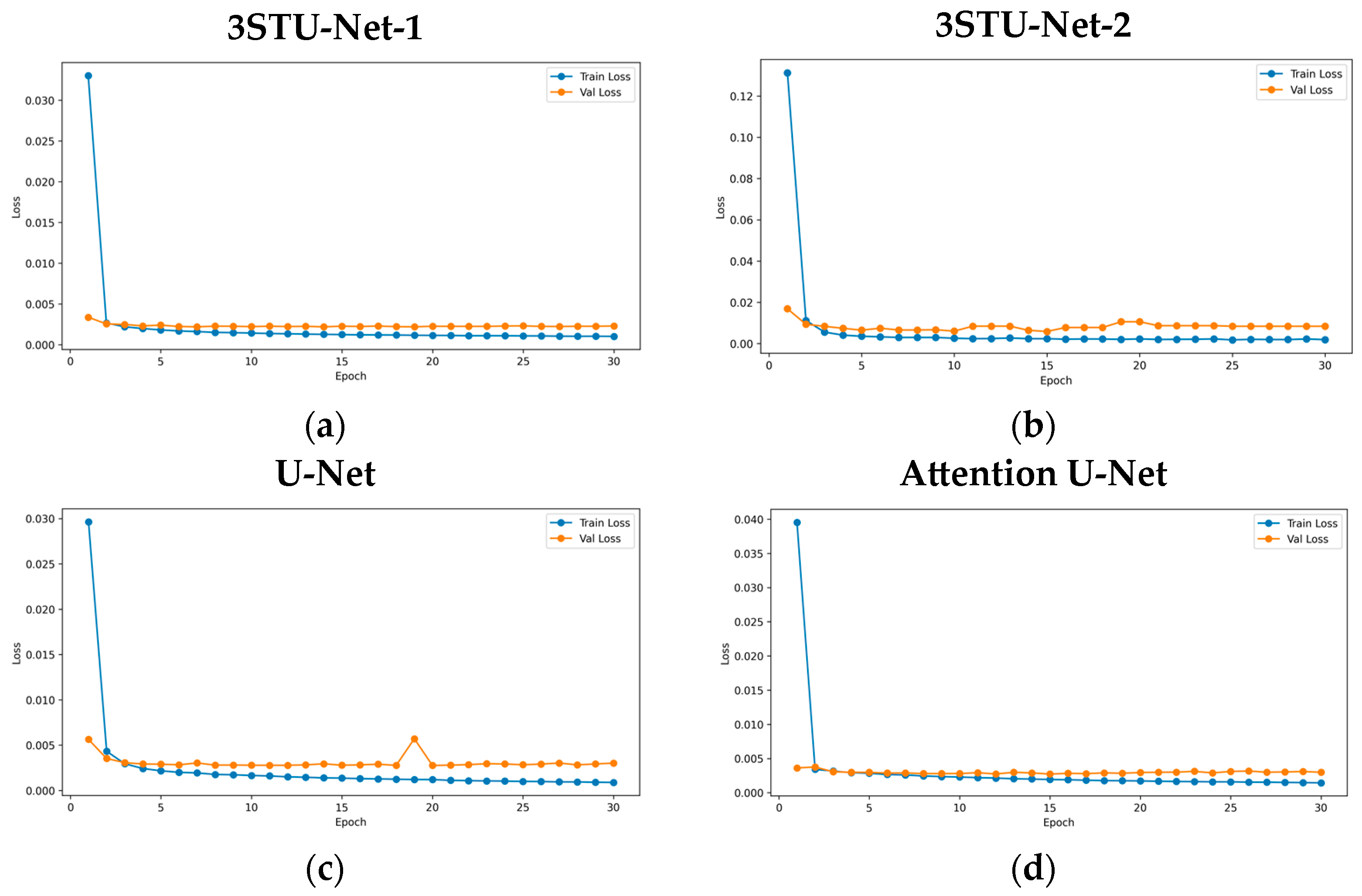
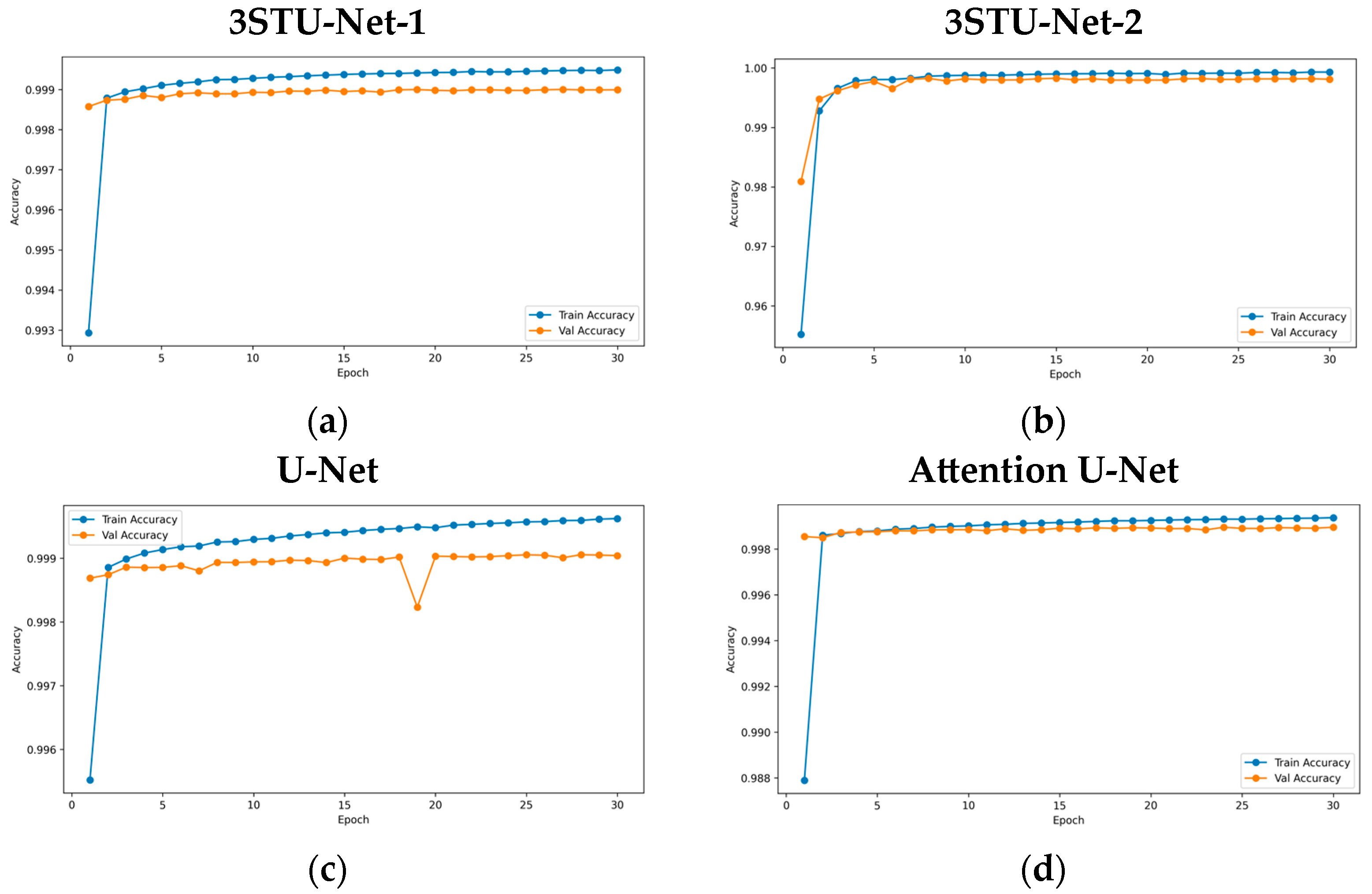
4.1. 3STU-Net Learning Results
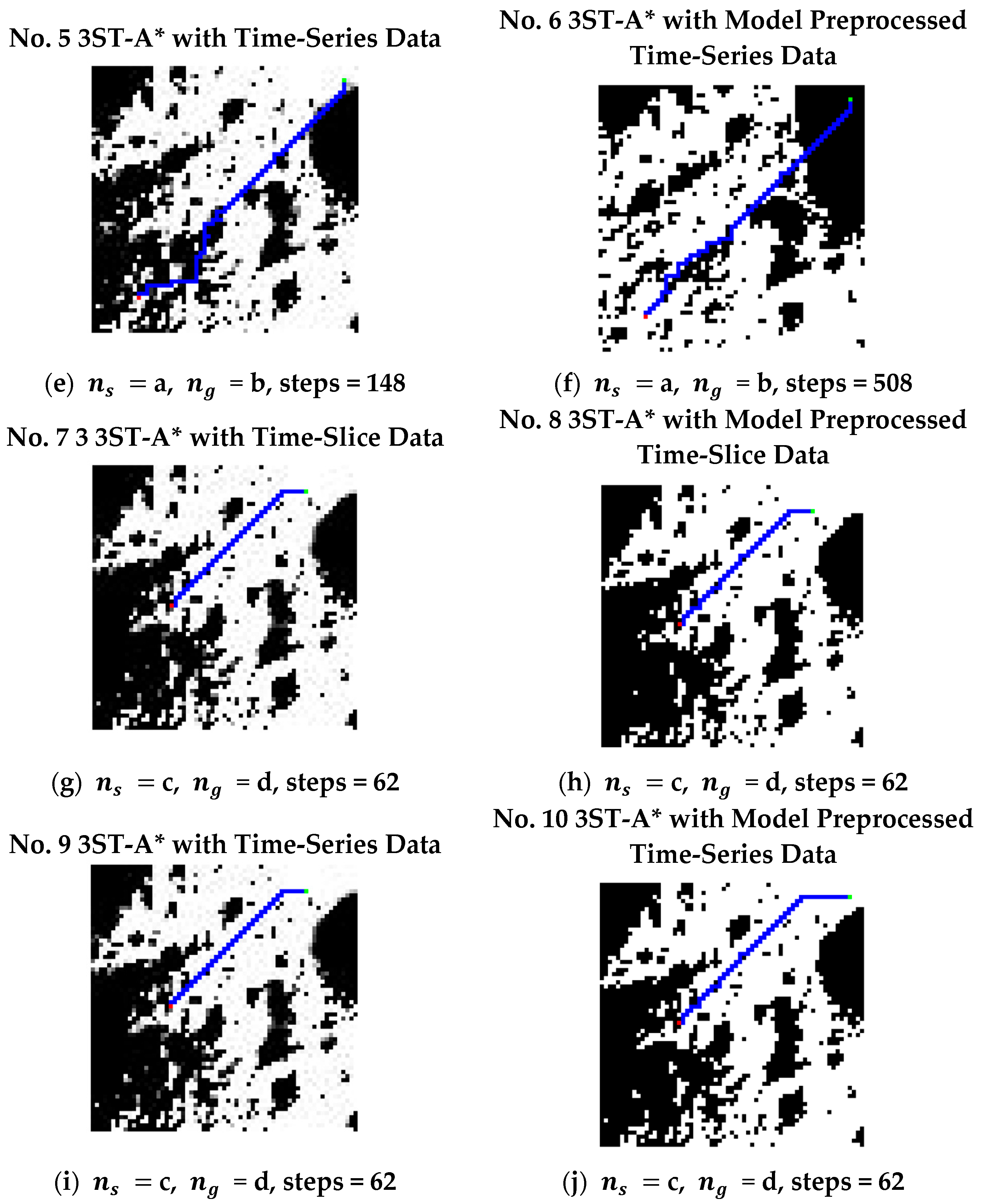
4.2. 3ST-A* Path Planning Results and Comparation
4.3. Discussion
5. Conclusions
- (1)
- A residual module enhances feature extraction for time-slice data through a channel attention mechanism.
- (2)
- Twelve consecutive time slices are used for time-series data, employing a residual attention module that combines a temporal attention block and spatiotemporal fusion block to minimize accuracy loss.
- (3)
- Performance in edge regions has improved compared to the original U-Net and Attention U-Net.
- (1)
- The algorithm integrates dynamic lighting and slope data as constraints in the heuristic function, limiting optimal conditions at each step.
- (2)
- Resetting the open set fixes the planned path, adapting to real-world lighting changes in polar regions and enhancing the algorithm’s practical value.
- (3)
- A comparison of the path-planning results between using the original data and the data segmented by 3STU-Net shows that the segmented data can ensure that each step of the planned path can obtain adequate sunlight.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| LSPR | Lunar South Polar Region |
| 2.5D/3D | 2.5 Dimension/3 Dimension |
| DEM | Digital Elevation Model |
| CE-7 | Chang’E 7 Mission |
| LUPEX | Lunar Polar Exploration |
| ILRS | International Lunar Research Station |
| PSRs | Permanent Shadow Regions |
| ROI | Region of Interest |
| SVF | Solar Visibility Factor |
References
- Flahaut, J.; Carpenter, J.; Williams, J.P.; Anand, M.; Crawford, I.A.; Van Westrenen, W.; Füri, E.; Xiao, L.; Zhao, S. Regions of interest (ROI) for future exploration missions to the lunar South Pole. Planet. Space Sci. 2020, 180, 104750. [Google Scholar] [CrossRef]
- Watson-Morgan, L.; Chavers, G.; Connolly, J.; Crowe, K.; Krupp, D.; Means, L.; Percy, T.; Polsgrove, T.; Turpin, J. NASA’s Initial and Sustained Artemis Human Landing Systems. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; pp. 1–11. [Google Scholar]
- Ishihara, Y.; Shimomura, T.; Nishitani, R.; Aida, M.; Mizuno, H. JAXA’s Mission Instruments in the ISRO-JAXA Joint Lunar Polar Exploration (LUPEX) Project—Overview and Developing Status. LPI Contrib. 2024, 3040, 1761. [Google Scholar]
- Wang, L.; Shen, G.; Zhang, H.; Hou, D.; Zhang, S.; Zhang, X.; Quan, Z.; Liao, J.; Ji, W.; Sun, Y. Design and Development of Energy Particle Detector on China’s Chang’E -7. Aerospace 2024, 11, 893. [Google Scholar] [CrossRef]
- Wu, W. International Lunar Research Station. Aerosp. China 2023, 24, 10–14. [Google Scholar]
- Wang, C.; Jia, Y.; Xue, C.; Lin, Y.; Liu, J.; Fu, X.; Xu, L.; Huang, Y.; Zhao, Y.; Xu, Y.; et al. Scientific objectives and payload configuration of the Chang’E-7 mission. Natl. Sci. Rev. 2024, 11, nwad329. [Google Scholar] [CrossRef]
- Boatwright, B.D.; Head, J.W. Shape-from-shading Refinement of LOLA and LROC NAC Digital Elevation Models: Applications to Upcoming Human and Robotic Exploration of the Moon. Planet. Sci. J. 2024, 5, 124. [Google Scholar] [CrossRef]
- Tong, X.H.; Huang, Q.; Liu, S.J.; Xie, H.; Chen, H.; Wang, Y.Q.; Xu, X.; Wang, C.; Jin, Y.M. A high-precision horizon-based illumination modeling method for the lunar surface using pyramidal LOLA data. Icarus 2023, 390, 115302. [Google Scholar] [CrossRef]
- Wang, J.; Ma, C.; Zhang, Z.; Wang, Y.; Peng, M.; Wan, W.; Feng, X.; Wang, X.; He, X.; You, Y. Lunar surface sampling feasibility evaluation method for Chang’E-5 mission. The International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2019, 42, 1463–1469. [Google Scholar]
- Okolie, C.J.; Smit, J.L. A systematic review and meta-analysis of Digital Elevation Model (DEM) fusion: Preprocessing, methods and applications. ISPRS J. Photogramm. Remote Sens. 2022, 188, 1–29. [Google Scholar] [CrossRef]
- Wu, X.; Huang, S.; Huang, G. Deep Reinforcement Learning-Based 2.5D Multi-Objective Path Planning for Ground Vehicles: Considering Distance and Energy Consumption. Electronics 2023, 12, 3840. [Google Scholar] [CrossRef]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-Net and Its Variants for Medical Image Segmentation: A Review of Theory and Applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Bilal, M.; Ali, G.; Iqbal, M.W.; Anwar, M.; Malik, M.S.A.; Abdul Kadir, R. Auto-Prep: Efficient and Automated Data Preprocessing Pipeline. IEEE Access 2022, 10, 107764–107784. [Google Scholar] [CrossRef]
- Li, P.; Chen, Z.; Chu, X.; Rong, K. DiffPrep: Differentiable Data Preprocessing Pipeline Search for Learning over Tabular Data. In Proceedings of the ACM on Management of Data, Association for Computing Machinery, New York, NY, USA, 1–2 June 2023; Volume 1, pp. 1–26. [Google Scholar]
- Li, C. Preprocessing Methods and Pipelines of Data Mining: An Overview. arXiv 2019, arXiv:1906.08510. [Google Scholar]
- Mutholib, A.; Abdul Rahim, N.; Surya Gunawan, T.; Kartiwi, M. Trade-Space Exploration with Data Preprocessing and Machine Learning for Satellite Anomalies Reliability Classification. IEEE Access 2025, 13, 35903–35921. [Google Scholar] [CrossRef]
- Vijayakumar, K.; Mohit, K.; Pooja; Darshan, M.; Tiwari, A. Boulders and Craters Detection Using Transfer Learning. SSRN Prepr. 2024. Available online: https://ssrn.com/abstract=5134413 (accessed on 22 April 2025).
- Fairweather, J.H.; Lagain, A.; Servis, K.; Benedix, G.K.; Kumar, S.S.; Bland, P.A. Automatic Mapping of Small Lunar Impact Craters Using LRO-NAC Images. Earth Space Sci. 2022, 9, e2021EA002177. [Google Scholar] [CrossRef]
- Liu, B.; Li, C.L.; Zhang, G.L.; Xu, R.; Liu, J.J.; Ren, X.; Tan, X.; Zhang, X.X.; Zuo, W.; Wen, W.B. Data processing and preliminary results of the Chang’e-3 VIS/NIR Imaging Spectrometer in-situ analysis. Res. Astron. Astrophys. 2014, 14, 1578–1594. [Google Scholar] [CrossRef]
- Thakur, K.; Gaurav, K.; Shubham, P.; Banerjee, P.; Kumar, B.; Mitra, D. Design and Implementation of Real-Time Image Retrieval System for De-Noising Space Images in Chandrayaan 3 Lunar Mission Using Autoencoders. In Proceedings of the 2024 7th International Conference on Contemporary Computing and Informatics (IC3I), Greater Noida, India, 18–20 September 2024. [Google Scholar]
- Afrosheh, S.; Askari, M. Fusion of Deep Learning and GIS for Advanced Remote Sensing Image Analysis. Remote Sensing 2024, 16, 123. [Google Scholar]
- Yang, H.; Xu, X.; Ma, Y.; Xu, Y.; Liu, S. CraterDANet: A Convolutional Neural Network for Small-Scale Crater Detection via Synthetic-to-Real Domain Adaptation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4600712. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, X.M.; Bruzzone, L.; Liu, B.; Liu, D.W.; Ren, X.; Benediktsson, J.A.; Liang, Y.C.; Yang, B.; Yin, M.H.; et al. Comprehensive mapping of lunar surface chemistry by adding Chang’e—5 samples with deep learning. Nat. Commun. 2023, 14, 7554. [Google Scholar] [CrossRef]
- Suo, J.; Long, H.; Ma, Y.; Zhang, Y.; Liang, Z.; Yan, C.; Zhao, R. Resource-Exploration-Oriented Lunar Rocks Monocular Detection and 3D Pose Estimation. Aerospace 2024, 12, 4. [Google Scholar] [CrossRef]
- Akagündüz, E.; Ulku, I. A Survey on Deep Learning-Based Architectures for Semantic Segmentation on 2D Images. J. Appl. Artif. Intell. 2022, 36, 2032924. [Google Scholar]
- Wu, C.H.; Yuan, Z. Image Segmentation and Object Detection of Lunar Landscape. Comput. Sci. 2020. Available online: https://cs230.stanford.edu/projects_winter_2020/reports/32601432.pdf (accessed on 22 April 2025).
- Ronneberger, O.; Fischer, P.; Brox, T. Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Azad, R.; Khodapanah Aghdam, E.; Rauland, A.; Jia, Y.; Haddadi Avval, A.; Bozorgpour, A.; Karimijafarbigloo, S.; Cohen, J.P.; Adeli, E.; Merhof, D. Medical Image Segmentation Review: The Success of U-Net. arXiv 2022, arXiv:2211.14830. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Granada, Spain, 20 September 2018; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2018. [Google Scholar]
- Oktay, O.; Schlemper, J.; Le Folgoc, L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Xu, W.; Deng, X.; Guo, S.; Chen, J.; Sun, L.; Zheng, X.; Xiong, Y.; Shen, Y.; Wang, X. High-Resolution U-Net: Preserving Image Details for Cultivated Land Extraction. Sensors 2020, 20, 4064. [Google Scholar] [CrossRef]
- Petrakis, G.; Partsinevelos, P. Lunar ground segmentation using a modified U-Net neural network. Mach. Vis. Appl. 2024, 35, 50. [Google Scholar] [CrossRef]
- Kanade, S.; Kande, S.; Wanare, A.; Kapadnis, J. Safe Lunar Surface Navigation: Leveraging U-Net and Semantic Segmentation for Obstacle Detection. Int. J. Res. Publ. Rev. 2023, 4, 2279–2284. [Google Scholar]
- Sinha, M.; Paul, S.; Ghosh, M.; Mohanty, S.N.; Pattanayak, R.M. Automated Lunar Crater Identification with Chandrayaan-2 TMC-2 Images using Deep Convolutional Neural Networks. Sci. Rep. 2024, 14, 8231. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del-Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef]
- Reda, M.; Onsy, A.; Haikal, A.Y.; Ghanbari, A. Path Planning Algorithms in the Autonomous Driving System: A Comprehensive Review. Robot. Auton. Syst. 2024, 174, 104630. [Google Scholar] [CrossRef]
- Richter, J.; Kolvenbach, H.; Valsecchi, G.; Hutter, M. Multi-Objective Global Path Planning for Lunar Exploration with a Quadruped Robot. In Proceedings of the 2024 International Conference on Space Robotics (iSpaRo), Luxembourg, 24–27 June 2024. [Google Scholar]
- Li, Y.; Huang, Z.; Xie, Y. Path planning of mobile robot based on improved genetic algorithm. In Proceedings of the 2020 3rd International Conference on Electron Device and Mechanical Engineering (ICEDME), Suzhou, China, 1–3 May 2020. [Google Scholar]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Meng, B.H.; Godage, I.S.; Kanj, I. RRT*-based path planning for continuum arms. IEEE Robot. Autom. Lett. 2022, 7, 6830–6837. [Google Scholar] [CrossRef] [PubMed]
- Xu, T. Recent advances in Rapidly-exploring Random Tree: A Review. Heliyon 2024, 10, e32451. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Rondao, D.; Aouf, N. Deep learning-based spacecraft relative navigation methods: A survey. Acta Astronaut. 2022, 191, 22–40. [Google Scholar] [CrossRef]
- Wang, Y.; Wan, W.; Gou, S.; Peng, M.; Liu, Z.; Di, K.; Li, L.C.; Yu, T.Y.; Wang, J.; Cheng, X. Vision-based decision support for rover path planning in the Chang’e-4 Mission. Remote Sens. 2020, 12, 624. [Google Scholar] [CrossRef]
- Silvestrini, S.; Piccinin, M.; Zanotti, G.; Brandonisio, A.; Bloise, I.; Feruglio, L.; Lunghi, P.; Lavagna, M.; Varile, M. Optical navigation for Lunar landing based on Convolutional Neural Network crater detector. Aerosp. Sci. Technol. 2022, 123, 107503. [Google Scholar] [CrossRef]
- Bickel, V.T.; Moseley, B.; Lopez-Francos, I.; Shirley, M. Peering into lunar permanently shadowed regions with deep learning. Nat. Commun. 2021, 12, 5607. [Google Scholar] [CrossRef]
- Feng, Y.; Li, H.; Tong, X.; Li, P.; Wang, R.; Chen, S.; Liu, S. Optimized Landing Site Selection at the Lunar South Pole: A Convolutional Neural Network Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 10998–11015. [Google Scholar] [CrossRef]
- Deng, X.; Jiao, T.; Qin, X.; Wang, Y.; Zheng, Q.; Hou, Z.; Li, W. Radiation Mapping based on DFS and Gaussian Process Regression. In Proceedings of the 2024 4th URSI Atlantic Radio Science Meeting (AT-RASC), Meloneras, Spain, 19–24 May 2024. [Google Scholar]
- Chen, G.; You, H.; Huang, Z.; Fei, J.; Wang, Y.; Liu, C. An Efficient Sampling-Based Path Planning for the Lunar Rover with Autonomous Target Seeking. Aerospace 2022, 9, 148. [Google Scholar] [CrossRef]
- Zhang, P.; Hua, Y.; Li, T. Dynamic Trajectory Planning and Tracking Algorithm of Lunar Rover with Updating Map Information. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022. [Google Scholar]
- Tang, Z.; Ma, H. An overview of path planning algorithms. IOP Conf. Ser. Earth Environ. Sci. 2021, 804, 022024. [Google Scholar] [CrossRef]
- Bai, J.H.; Oh, Y.J. Global Path Planning of Lunar Rover Under Static and Dynamic Constraints. Int. J. Aeronaut. Space Sci. 2020, 21, 1105–1113. [Google Scholar] [CrossRef]
- Peng, S.; Zeng, Q.; Li, C.; Su, Z.; Wan, G.; Liu, L. An Improved A* Algorithm for Multi-Environmental Factor Lunar Rover Path Planning. In Proceedings of the 2023 3rd International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Nanjing, China, 21–23 July 2023. [Google Scholar]
- Hu, R.; Zhang, Y.; Fan, L. Planning and analysis of safety-optimal lunar sun-synchronous spatiotemporal routes. Acta Astronaut. 2023, 204, 253–262. [Google Scholar] [CrossRef]
- Inoue, H.; Adachi, S. Spatio-Temporal Path Planning for Lunar Polar Exploration with Robustness against Schedule Delay. Trans. Jpn. Soc. Aeronaut. Space Sci. 2021, 64, 304–311. [Google Scholar] [CrossRef]
- Tanaka, T.; Malki, H. A Deep Learning Approach to Lunar Rover Global Path Planning Using Environmental Constraints and the Rover Internal Resource Status. Sensors 2024, 24, 844. [Google Scholar] [CrossRef]
- Margot, J.L. Topography of the Lunar Poles from Radar Interferometry: A Survey of Cold Trap Locations. Science 1999, 284, 1658–1660. [Google Scholar] [CrossRef]
- Noda, H.; Araki, H.; Goossens, S.; Ishihara, Y.; Matsumoto, K.; Tazawa, S.; Kawano, N.; Sasaki, S. Illumination conditions at the lunar polar regions by KAGUYA (SELENE) laser altimeter. Geophys. Res. Lett. 2008, 35, L24203. [Google Scholar] [CrossRef]
- Gläser, P.; Scholten, F.; De Rosa, D.; Marco Figuera, R.; Oberst, J.; Mazarico, E.; Neumann, G.A.; Robinson, M.S. Illumination conditions at the lunar south pole using high resolution Digital Terrain Models from LOLA. Icarus 2014, 243, 78–90. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Head, J.W. Improved LOLA elevation maps for south pole landing sites: Error estimates and their impact on illumination conditions. Planet. Space Sci. 2021, 203, 105119. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Jackson, G.B.; Cavanaugh, J.F.; Neumann, G.A.; Riris, H.; Sun, X.; Zellar, R.S.; Coltharp, C.; Connelly, J.; et al. The Lunar Orbiter Laser Altimeter Investigation on the Lunar Reconnaissance Orbiter Mission. Space Sci. Rev. 2010, 150, 209–241. [Google Scholar] [CrossRef]
- De Rosa, D.; Bussey, B.; Cahill, J.T.; Lutz, T.; Crawford, I.A.; Hackwill, T.; van Gasselt, S.; Neukum, G.; Witte, L.; McGovern, A.; et al. Characterisation of potential landing sites for the European Space Agency’s Lunar Lander project. Planet. Space Sci. 2012, 74, 224–246. [Google Scholar] [CrossRef]
- Speyerer, E.J.; Robinson, M.S. Persistently illuminated regions at the lunar poles: Ideal sites for future exploration. Icarus 2013, 222, 122–136. [Google Scholar] [CrossRef]
- Wei, G.; Li, X.; Zhang, W.; Tian, Y.; Jiang, S.; Wang, C.; Ma, J. Illumination conditions near the Moon’s south pole: Implication for a concept design of China’s Chang’E−7 lunar polar exploration. Acta Astronaut. 2023, 208, 74–81. [Google Scholar] [CrossRef]
- Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Torrence, M.H. Illumination conditions of the lunar polar regions using LOLA topography. Icarus 2011, 211, 1066–1081. [Google Scholar] [CrossRef]
- Acton, C.H. Ancillary data services of NASA’s navigation and ancillary information facility. Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Mao, A.; Mohri, M.; Zhong, Y. Cross-Entropy Loss Functions: Theoretical Analysis and Applications. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Zhao, R.; Qian, B.; Zhang, X.; Li, Y.; Wei, R.; Liu, Y.; Pan, Y. Rethinking Dice Loss for Medical Image Segmentation. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020. [Google Scholar]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Foeada, D.; Ghifaria, A.; Kusumaa, M.B.; Hanafiah, N.; Gunawan, E. A Systematic Literature Review of A* Pathfinding. Procedia Comput. Sci. 2021, 179, 507–514. [Google Scholar] [CrossRef]







| 1. | Initialization |
|---|---|
| Input: Region slope , Region illumination /, Start node , Goal node , Current node , Current node slope , Current node illumination /, Next chosen node illumination / | |
| Initialization: / | |
| 2. | Node Search and Path Planning |
| While True If is Add into Break and return planning path If / is not dark Add into Else Rechoose a new non-dark node Set For each neighbor of neighbors at / Add ) into If is empty Region illumination // // Stay, continue and begin the next iteration Region illumination // // | |
| 3. | End |
| Illumination Grid Condition Assessment | |||
|---|---|---|---|
| Dark | Weak | Bright | |
| SVF Value Range | / | /.75 | / |
| Slope Grid Condition Assessment | |||
| Forbidden | Good | ||
| Slope Value Range | |||
| Hyperparameter | Values |
|---|---|
| Learning Rate | 1 × 10−4 |
| Optimizer | Adam |
| Batch Size | 8 |
| Epochs | 30~800 |
| 0.3 | |
| 1 × 10−6 |
| No. | A* | 3ST-A* | Data Preprocessed Pipeline | |||||
|---|---|---|---|---|---|---|---|---|
| Time-Slice Data | 3STU-Net-1 Preprocessed | Tim-Series Data | 3STU-Net-2 Preprocessed | |||||
| 1 | ☑ | ☐ | ☑ | ☐ | ☐ | ☐ | ||
| 2 | ☑ | ☐ | ☐ | ☐ | ☑ | ☐ | ||
| 3 | ☐ | ☑ | ☑ | ☐ | ☐ | ☐ | ||
| 4 | ☐ | ☑ | ☑ | ☑ | ☐ | ☐ | ||
| 5 | ☐ | ☑ | ☐ | ☐ | ☑ | ☐ | ||
| 6 | ☐ | ☑ | ☐ | ☐ | ☑ | ☑ | ||
| 7 | ☐ | ☑ | ☑ | ☐ | ☐ | ☐ | ||
| 8 | ☐ | ☑ | ☑ | ☑ | ☐ | ☐ | ||
| 9 | ☐ | ☑ | ☐ | ☐ | ☑ | ☐ | ||
| 10 | ☐ | ☑ | ☐ | ☐ | ☑ | ☑ | ||
| Time-Slice Dataset | Time-Series Dataset (Time-Series Data Input) | Time-Series Dataset (Mean Data Input) | ||||
|---|---|---|---|---|---|---|
| Accuracy | Accuracy | Accuracy | ||||
| 3STU-Net-1 | 95.01 | 87.18 | - | - | - | - |
| 3STU-Net-2 | - | - | 96.43 | 91.83 | - | - |
| U-Net | 94.89 | 86.87 | - | - | 94.99 | 89.94 |
| Attention U-Net | 94.80 | 86.67 | - | - | 94.90 | 89.75 |
| No. | AG 1 | SG 2 | Total Steps | Planning Time (s) | NoI | NoS | Stay | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dark | Weak | Bright | Forbidden | Good | ||||||||
| 1 | a | b | A* | - | 104 | 23 | 20 | 23 | 61 | 0 | 104 | 0 |
| 2 | a | b | A* | - | 104 | 24 | 24 | 19 | 61 | 0 | 104 | 0 |
| 3 | a | b | 3ST-A* | - | 147 | 34 | 0 | 53 | 87 + 7R 3 | 0 | 147 | 1 |
| 4 | a | b | 3ST-A* | 3STU-Net-1 | 522 | 119 | 0 | 0 | 522 | 0 | 522 | 0 |
| 5 | a | b | 3ST-A* | - | 148 | 27 | 0 | 61 | 80 + 7R | 0 | 148 | 28 |
| 6 | a | b | 3ST-A* | 3STU-Net-2 | 508 | 126 | 0 | 0 | 508 | 0 | 508 | 0 |
| 7 | c | d | 3ST-A* | - | 62 | 11 | 0 | 3 | 59 | 0 | 62 | 0 |
| 8 | c | d | 3ST-A* | 3STU-Net-1 | 62 | 16 | 0 | 0 | 62 | 0 | 62 | 0 |
| 9 | c | d | 3ST-A* | - | 62 | 11 | 0 | 4 | 58 | 0 | 62 | 0 |
| 10 | c | d | 3ST-A* | 3STU-Net-2 | 62 | 14 | 0 | 0 | 62 | 0 | 62 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wei, G.; Zhang, H.; Lu, J.; Pang, F. A Spatiotemporal U-Net-Based Data Preprocessing Pipeline for Sun-Synchronous Path Planning in Lunar South Polar Exploration. Remote Sens. 2025, 17, 1589. https://doi.org/10.3390/rs17091589
Chen Y, Wei G, Zhang H, Lu J, Pang F. A Spatiotemporal U-Net-Based Data Preprocessing Pipeline for Sun-Synchronous Path Planning in Lunar South Polar Exploration. Remote Sensing. 2025; 17(9):1589. https://doi.org/10.3390/rs17091589
Chicago/Turabian StyleChen, Yang, Guangfei Wei, Hao Zhang, Jianfeng Lu, and Fuchuan Pang. 2025. "A Spatiotemporal U-Net-Based Data Preprocessing Pipeline for Sun-Synchronous Path Planning in Lunar South Polar Exploration" Remote Sensing 17, no. 9: 1589. https://doi.org/10.3390/rs17091589
APA StyleChen, Y., Wei, G., Zhang, H., Lu, J., & Pang, F. (2025). A Spatiotemporal U-Net-Based Data Preprocessing Pipeline for Sun-Synchronous Path Planning in Lunar South Polar Exploration. Remote Sensing, 17(9), 1589. https://doi.org/10.3390/rs17091589








