Abstract
Traditional high-precision satellite orbits rely on globally dense and evenly distributed ground tracking stations, while the accuracy of precise orbit determination (POD) based on a regional network cannot compare with that of a global network. Low Earth orbit (LEO) satellites can serve as space-based monitoring stations to compensate for this. In response to the current regional integrated POD that only resolves the ambiguities of ground stations, this paper proposes an ambiguity resolution (AR) strategy related to LEO satellites to enhance GPS orbit accuracy. A joint observation network is established using seven International GNSS Service (IGS) stations within China and 10 LEO satellites, including GRACE-C/D, LuTan1-A/B, SWARM-A/B/C, Sentinel-3A/B, and Sentinel-6A. Experiments are conducted and analyzed from three aspects: independent baseline selection, the common view time, and the wide-lane (WL) threshold of double-differenced ambiguity. The ambiguity fixing strategy is determined to be a combination of inter-satellite and satellite–ground baselines, a common view time of 5 min, and a WL ambiguity threshold of 0.2 cycles. Taking the final products released by the IGS as the reference, the GPS orbit accuracy in the along-track, cross-track, radial, and 1D RMS is 3.23, 2.74, 2.36, and 2.89 cm, respectively, which represents improvements of 9.3%, 12.5%, 10.9%, and 10.8% compared with the solution that only fixes the ambiguities of ground stations. This result demonstrates that, in regional integrated POD, further implementation of LEO satellite-related ambiguity fixing significantly improves GPS orbit accuracy. Given the limitation that most LEO satellites can only receive GPS satellite signals, in the future, as more LEO satellites gain access to GNSS observations, the ambiguity fixing strategy presented in this paper can provide an effective and feasible approach.
1. Introduction
Satellite orbits serve as the spatial reference for Global Navigation Satellite Systems (GNSSs) and form the critical foundation for achieving positioning, navigation, and timing (PNT) [1,2]. Traditional high-precision satellite orbits rely on densely and evenly distributed ground tracking stations worldwide [3,4,5]. Although the scientific community can utilize well-distributed global ground stations, some commercial operators and the BeiDou navigation satellite system (BDS) choose to build their own regional monitoring stations for the stability and reliability of the system [6]. However, relying solely on a regional network makes it challenging to obtain high-precision satellite orbits.
Thanks to the booming development of low Earth orbit (LEO) satellites, they can be used as space-based monitoring stations to achieve global tracking of GNSS satellites, greatly enhancing the observation geometry. This brings new possibilities for jointly processing ground station and LEO satellite observations to improve the GNSS satellite orbit accuracy. Many scholars have already verified that the inclusion of LEO satellites can significantly improve the orbit accuracy of the GPS or BDS [7,8,9,10]. For ground networks with a limited number of regional stations, Li et al. (2019) [11] demonstrated through simulation experiments that orbit determination becomes less dependent on ground stations when a large number of LEO satellites are used. With the assistance of 60 LEO satellites, centimeter-level GNSS satellite orbit accuracy can be achieved using observations from only eight regional stations. Based on actual data, Huang et al. (2020) [12] pointed out that the orbital configuration of LEO satellites has a greater impact on the GNSS orbit quality than the number of LEO satellites involved in precise orbit determination (POD). Using seven LEO satellites and 10 regional stations for an integrated solution, the GPS orbit accuracy in 1D RMS was approximately 5 cm. Li et al. (2024) [6] further optimized this, achieving a 3D RMS orbit accuracy of about 5.15 cm using six regional stations in China and 13 LEO satellites. However, the above studies only fixed the ambiguity of ground stations and did not implement ambiguity resolution (AR) related to LEO satellites, which greatly limited the performance of the integrated POD.
In the existing integer ambiguity resolution (IAR) theory, there are three different classes of integer estimators: the class of integer (I) estimators [13], the class of integer aperture (IA) estimators [14], and the class of integer equivariant (IE) estimators [15]. Among them, the best integer equivariant (BIE) estimator is the optimal estimator within the class of IE estimators in terms of the minimum mean square error (MSE), while the integer least-squares (ILS) estimator is the best in maximizing the probability of correct integer estimation within the smaller integer class [16]. However, these estimators require both the execution of a search process and an ambiguity decorrelation step to enhance the efficiency of this search. The rounding or sequential rounding estimator, although inferior to the integer least-squares solution, does not require a search and can be computed directly [17]. Generally, the ‘sequential integer rounding’ method, which is also referred to as the ‘integer bootstrapping’ method, is widely used in post-processing GNSS POD [18,19,20,21], primarily because the batch least-squares (LSQ) method is commonly used for parameter estimation. Since the variance–covariance matrix of the sequential conditional least-squares solution is diagonal, the probability of correct integer estimation of the bootstrapped solution can be computed exactly [17]. Following the previous work, this paper adopts a similar method for ambiguity resolution.
Furthermore, many scholars have conducted research on spaceborne LEO POD AR, providing valuable reference methods for fixing the ambiguities of LEO satellites. Kroes et al. (2005) [22] and Guo et al. (2020) [23] performed double-differenced ambiguity resolution (DD-AR) based on the formation-flying Gravity Recovery and Climate Experiment (GRACE) satellites, and the results showed that it could significantly improve the relative orbit accuracy of the satellites. Additionally, ambiguity research using ground stations and LEO satellites to form satellite–ground baselines has been proven to have a positive impact on LEO POD [24]. Jäggi et al. (2007) [25] further demonstrated that the inter-satellite and satellite–ground baseline combination solution involving GRACE-A, GRACE-B, and International GNSS Service (IGS) ground stations significantly improved the relative orbit accuracy compared to the satellite–ground baseline solution alone. However, due to the small number of successfully fixed satellite–ground baseline ambiguities, no improvement in absolute accuracy was observed. Based on this, Zhang et al. (2021) [26] further improved the narrow-lane fixation rate of satellite–ground baselines and proved that satellite–ground DD-AR and single-differenced ambiguity resolution (SD-AR) can achieve comparable absolute orbit accuracy. In light of the above ambiguity resolution methods, in the context of integrated POD, LEO satellites can serve as dynamic tracking stations to construct baselines between LEO satellites and between LEO satellites and ground stations to carry out DD-AR.
In summary, due to the sparse number of ground stations in the regional networks, the resulting number of ground DD ambiguities is limited. Therefore, it is of significant value to research the fixing of the ambiguities related to LEO satellites in integrated POD to enhance the orbit accuracy of GNSSs. This paper conducts a detailed analysis from three aspects—independent baseline selection, the common view time, and the threshold of DD ambiguity—in order to optimize the effectiveness of ambiguity resolution for LEO satellites. The organization of this paper is as follows. Section 2 provides the mathematical models employed in the integrated POD, the selected LEO satellites and ground station observations, the specific data processing strategies, and the experimental schemes. Subsequently, the results are analyzed and discussed from the three research perspectives, along with a comprehensive comparison of the experiments. Finally, conclusions are drawn.
2. Methodology
2.1. Mathematical Model
In the integrated POD processing, the ionosphere-free (IF) combination is commonly applied to eliminate the first-order ionospheric delay. Based on the pseudorange and carrier-phase observations for the ground stations and the LEO satellites, the IF combinations can be expressed as follows:
where and refer to the ground station and LEO satellite IF combination pseudorange, respectively, whereas and are the corresponding IF combination carrier-phase observations; and denote the IF combination geometric distances from the GPS satellite to the ground station receiver and LEO onboard receiver in meters, respectively; is the speed of light in a vacuum; , , and refer to the ground station receiver, LEO onboard receiver, and GPS satellite clock offsets in seconds, respectively; is the mapping function for tropospheric delay; and is the zenith delay of the tropospheric wet component for the ground station. , , and denote the IF combination pseudorange hardware delays at the ground station receiver, LEO onboard receiver, and GPS satellite sides in meters, respectively; , , and are the corresponding phase delays in meters; , , , and are the sum of noise and multipath errors for the pseudorange and phase IF combination observations in meters, respectively; and denotes the wavelength of the IF combination. and represent the integer ambiguity of the IF combination for ground stations and LEO satellites, respectively. In the IF combination, the existence of hardware biases for both the pseudorange and carrier phases contaminates the IF ambiguities, since they are functionally hard to isolate from the IF ambiguities. Therefore, the IF ambiguities have to be estimated as float values, which can be expressed as follows:
For the orbit model, the approximate initial epoch states of GNSS and LEO satellites are obtained from broadcast ephemerides and single-point positioning, respectively. The initial orbits of both the GNSS and LEO satellites are calculated using numerical integration, based on the equations of motion and the variational equations. The following conditions must be satisfied:
where is the state transition matrix, is the state vector of the GNSS or LEO satellites at epoch , and denotes the initial epoch state vector, including and associated with GNSS and LEO satellites, respectively. , , and are the GNSS satellites’ initial position, velocity, and dynamic model parameters, respectively. Similarly, , , and indicate the LEO satellites’ initial position, velocity, and dynamic model parameters, respectively. The dynamic parameters of GNSS satellites mainly refer to the coefficients of solar radiation pressure (SRP), whereas those of LEO satellites usually include coefficients of SRP, as well as atmosphere, drag, and empirical accelerations. In summary, for reduced-dynamic integrated POD, the parameters to be estimated can be expressed as follows:
According to Equations (1) and (3), accurate initial epoch states and dynamic model parameters of the GNSS and LEO satellites can be estimated simultaneously using ground station and LEO satellite onboard observations through the batch least-squares (LSQ) method. For detailed calculations, refer to [6,12,27]. After the float solution is completed, the float ambiguity parameters can be obtained. The DD-AR method can be used to fix the ambiguities between ground stations, between LEO satellites, and between LEO satellites and ground stations. For detailed algorithms, we suggest referring to [20,21,28]. After two additional estimations and orbit updating, the final orbits of the GNSS and LEO satellites are determined.
2.2. LEO Satellites and Ground Network
In this study, considering the limitations of data acquisition, the onboard GPS data from 10 LEO satellites were selected for the integrated POD. These LEO satellites were from four different missions: Gravity Recovery and Climate Experiment Follow-on (GRACE-FO) [29], LuTan [30], Sentinel [31,32], and Swarm [33,34]. To facilitate descriptions, these 10 LEO satellites are abbreviated as GRCC, GRCD, LT1A, LT1B, SE3A, SE3B, SE6A, SWMA, SWMB, and SWMC. The detailed information on the LEO satellites is summarized in Table 1. Figure 1 depicts the ground tracks of the ten LEO satellites on DOY 070, 2022, where LEO satellites in the same orbital plane are plotted in the same color. The ten LEO satellites can almost achieve global coverage.

Table 1.
Detailed information on the 10 LEO satellites.
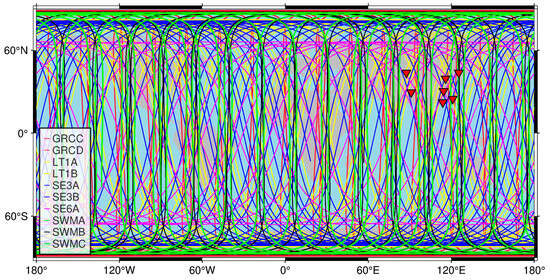
Figure 1.
Ground tracks of ten LEO satellites on DOY 070, 2022, and seven ground stations in China (red triangle).
In addition, seven IGS stations located within China, namely BJFS, CHAN, JFNG, HKSL, LHAZ, URUM, and TWTF, were selected for the regional network tracking. Their distribution is shown in Figure 1. The time period for the ground station data and onboard observations used was from day of year (DOY) 062 to 090 in 2022.
2.3. POD Processing Strategy
For the GPS and LEO integrated POD, Position and Navigation Data Analyst (PANDA) software is used for the data analysis. This software is capable of processing multiple techniques, including GNSSs, Satellite Laser Ranging (SLR), Inter-Satellite Links (ISLs), Precise Point Positioning (PPP), and other geodetic applications [35]. Table 2 presents the dynamic models used for the GPS and LEO satellites in the integrated POD, while Table 3 provides the observation models and estimated parameters. Considering the limited number of ground stations, the Earth rotation parameters were corrected directly with the product from the International Earth Rotation Service (IERS).

Table 2.
The dynamic models of the GPS and LEO satellites in the integrated POD.

Table 3.
The observation model and estimated parameters in the integrated POD.
2.4. Experimental Schemes
To investigate the impact of LEO satellite-related ambiguity fixing on orbit accuracy in integrated POD, this paper designed multiple experimental schemes, S1–S3, based on three main factors affecting LEO satellite ambiguity resolution: (1) independent baseline selection, (2) the ambiguity common view time, and (3) the ambiguity threshold, as detailed in Table 4. In each scheme, based on the principle of a single variable, only one influencing factor is analyzed, and the final ephemeris products released by IGS are used as a reference to evaluate the absolute orbit accuracy of GPS satellites. Among them, the baselines related to LEO satellites are divided into inter-satellite baselines between LEO satellites (abbreviated as LL) and satellite–ground baselines between LEO satellites and ground stations (abbreviated as LG). Through the experimental verification of schemes S1–S3, the comprehensive experiment S4 is implemented with the ambiguity resolution strategy, compared with the results involving only fixed ground station ambiguity, in order to explore the final improvement potential.

Table 4.
The regional integrated POD refinement schemes.
3. Results
3.1. Independent Baseline Selection
Baseline length is a basic condition for judging whether a baseline is usable, and as LEO satellites are dynamic tracking stations, the distances of inter-satellite baselines and satellite–ground baselines are constantly changing. Due to the poor conditions for constructing inter-satellite baselines between different orbital planes, only the inter-satellite baselines within the same orbital plane and satellite–ground baselines are studied.
Figure 2 shows the lengths of the inter-satellite baselines GRCC-GRCD, SWMA-SWMC, and LT1A-LT1B on DOY 070 of 2022. It can be seen that although the lengths of the three groups of inter-satellite baselines were constantly changing, the baseline length of GRCC-GRCD remained at 200~202 km and the SWMA-SWMC baseline length remained at 54~66 km, while LT1A-LT1B, due to its mission requirements, had a longer baseline length, remaining at 5345~5357 km. In addition, it should be noted that even though SE3A and SE3B were flying in the same orbit, they were 140° apart and could not meet the common view condition for DD-AR [26]. Taking GRCC/LT1A/SWMA/SE3A/SE6A as examples, Figure 3 shows the length of satellite–ground baselines formed with the ground station HKSL. The variations in length for these baselines were more drastic, ranging from 1000 km to 14,000 km. Based on the characteristics of baselines formed by LEO satellites, this paper focused on the selection of independent baselines related to LEOs, without limiting the lengths of inter-satellite baselines and satellite–ground baselines. Finally, all double-difference ambiguities on the selected independent baselines were further screened to identify independent double-difference ambiguities using the simple independence check algorithm from [45].
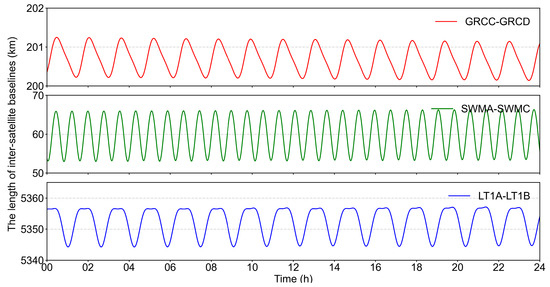
Figure 2.
The lengths of inter-satellite baselines for GRCC-GRCD, SWMA-SWMC, and LT1A-LT1B.
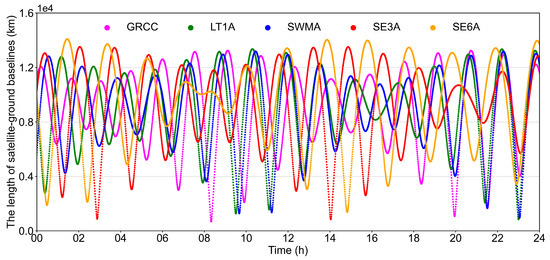
Figure 3.
The lengths of satellite–ground baselines for the GRCC, LT1A, SWMA, SE3A, and SE6A satellites with the HKSL station.
To verify the impact of independent baseline selection on integrated POD, we designed four schemes: only three inter-satellite baselines (GRCC-GRCD, LT1A-LT1B, and SWMA-SWMB), only ten satellite–ground baselines (ten LEO satellites with a ground station), a combination of three inter-satellite baselines and three satellite–ground baselines (GRCC, LT1A, and SWMA with a ground station), and a combination of three inter-satellite baselines and seven satellite–ground baselines (excluding those for GRCD, LT1B, and SWMB). These schemes were denoted by LL, LG10, LL + LG3, and LL + LG7, respectively. Due to the large number of satellites, statistical values of the orbit differences were computed to quantify the performance of each scheme. Figure 4 shows the along-track (A), cross-track (C), radial (R), and 1D RMS of the GPS satellite orbit differences compared with the IGS final products. Firstly, comparing the LL and LG10 solutions, their 1D RMS values of orbits are comparable, being 3.11 cm and 3.09 cm, respectively, as summarized in Table 5. However, it can be observed that the LL solution shows a more significant improvement in the along-track accuracy, while the LG10 solution more remarkably improves the cross-track accuracy. In addition, the LL + LG3 combined solution can further improve the accuracy of GPS orbits in all directions. Compared with the LL solution, the A/C/R/1D RMS improvements are approximately 2.6%, 5.3%, 2.4%, and 3.5%, respectively. With a further increase in the number of satellite–ground baselines, there is a notable improvement in the radial accuracy of GPS orbits. Compared with that of the LL + LG3 solution, the radial accuracy of the LL + LG7 solution is improved by about 2.4%. In summary, inter-satellite baselines can establish connections between LEO satellites, enhancing the relative orbit accuracy, while satellite–ground baselines can further strengthen the geometric constraints between LEO satellites and ground stations, improving the absolute orbit accuracy. Therefore, the combination of inter-satellite and satellite–ground baselines become a priority for enhancing GPS orbit accuracy.
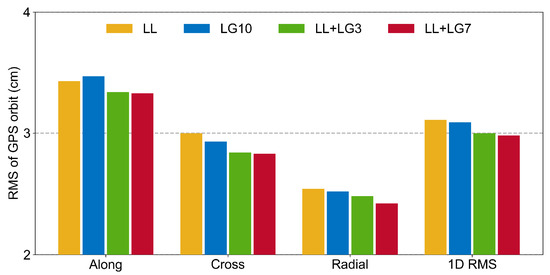
Figure 4.
The along-track, cross-track, radial, and 1D RMS of the GPS satellite orbit compared to the IGS final products of LL, LG10, LL + LG3, and LL + LG7 schemes.

Table 5.
Statistical results of the GPS orbit accuracy determined with different baseline selection solutions compared with the IGS final products (unit: cm).
3.2. Common View Time
The length of the common view time is one of the critical factors determining the difficulty of double-differenced ambiguity resolution. Figure 5 presents the cumulative distribution function of the common view time for independent DD ambiguities on inter-satellite (denoted by LL) and satellite–ground baselines (denoted by LG), using the ground station HKSL as an example. For the inter-satellite baselines, the average common view times for GRCC-GRCD, LT1A-LT1B, and SWMA-SWMC are 16.52, 18.38, and 28.91 min, respectively, with an average of 21.27 min. In contrast, the average common view times for all the satellite–ground baselines are relatively longer, ranging from 24.06 to 38.78 min, with an average of 27.92 min. This is due to the fact that, unlike stationary ground stations, LEO satellites travel at high speeds around the Earth, leading to shorter durations of GPS tracking arcs. A statistical analysis was conducted with thresholds of 5, 10, and 15 min; the percentages of excluded inter-satellite DD ambiguities were approximately 20.8%, 48.7%, and 73.8%, respectively, while those of the satellite–ground DD ambiguities were approximately 17.9%, 35.2%, and 55.1%, respectively.
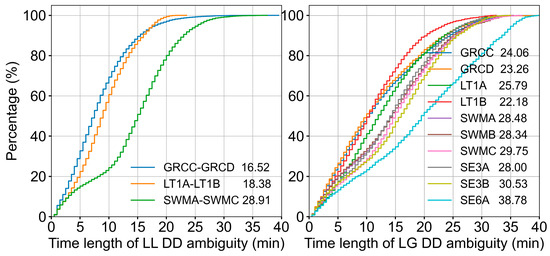
Figure 5.
Cumulative percentages of common view time lengths of DD ambiguities for LL (inter-satellite) and LG (satellite–ground) baselines from DOY 062 to 090.
To study the impact of the common view time of DD ambiguities related to LEO satellites on GPS orbit accuracy, based on the distribution characteristics of inter-satellite and satellite–ground DD ambiguities analyzed above, we discuss the inter-satellite (LL) and satellite–ground (LG) baselines separately and set the common view times to 5, 10, and 15 min, resulting in a total of six comparison experiments. The statistical results of the GPS orbits compared with IGS products in terms of the A, C, R, and 1D RMS are shown in Figure 6. For the inter-satellite baselines, as the common view time increases, the GPS orbit accuracy decreases sequentially in all directions. Compared with that of the LL-5 solution, the 1D RMS of the LL10 and LL15 solutions decreases by about 1.3% and 3.3%, respectively. The statistical results are shown in Table 6. Additionally, regarding the satellite–ground baselines, the impact of different common view times on the GPS orbit accuracy is relatively minor. Only the cross-track and 1D RMS values show a slight decrease as the common view time increases. In general, for ground baselines, the longer the common view time of DD ambiguities, the easier they are to fix. However, for baselines formed by LEO satellites, if the common view time is set too long, it may excessively eliminate the number of DD ambiguities, negatively impacting the accuracy of GPS orbits. Therefore, experiments have proven that a common view time of 5 min is the preferred choice.
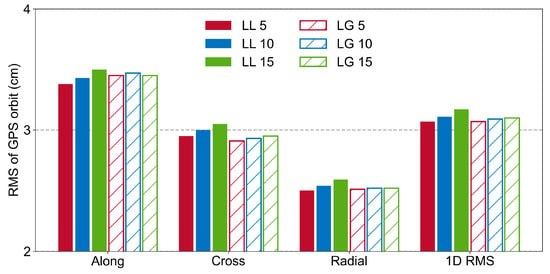
Figure 6.
The along-track, cross-track, radial, and 1D RMS of the GPS satellite orbit compared to the IGS final products with 5, 10, and 15 min common view times set in LL (inter-satellite) and LG (satellite–ground) schemes.

Table 6.
Statistical results of the GPS orbit accuracy determined with different common view times compared with the IGS final products (unit: cm).
3.3. Ambiguity Resolution Threshold
The distribution of ambiguity residuals is usually used as an important metric to assess the certainty of integer parameter estimation [46].
In the POD of traditional ground stations, in order to avoid the potential negative impact of incorrectly fixed ambiguities, rigorous thresholds of 0.15 cycles and 0.15 cycles are typically adopted to accept the rounded WL and NL ambiguities [47]. In the case of LEO POD AR, relatively conservative thresholds of 0.25 cycles and 0.15 cycles are commonly used [26]. To identify the ambiguity thresholds conducive to fixing the ambiguities of LEO satellites in integrated POD, we first analyzed the residual distribution of DD wide-lane (WL) and narrow-lane (NL) ambiguities for both inter-satellite and satellite–ground baselines. The residual distribution of WL ambiguities includes all ambiguities involved in the fixing process, while the residual distribution of NL ambiguities includes only those ambiguities obtained after successfully fixing the WL ambiguities. Figure 7 shows three inter-satellite baselines, while Figure 8 presents six satellite–ground baselines. It can be seen that for the WL and NL ambiguities, the average residuals of ambiguities for LL and LG are both less than 0.01 cycles, indicating that the integer property of the ambiguities has been restored. For the inter-satellite baselines, the distribution of WL residuals for the three baselines is approximately 86–92% within ±0.15 cycles and 95–99% within ±0.2 cycles. Among them, LT1A-LT1B exhibits the best distribution, followed by SWMA-SWMB, while GRCC-GRCD shows the worst distribution. The standard deviation (STD) of NL residuals is the smallest for SWMA-SWMB, followed by LT1A-LT1B, and that for GRCC-GRCD is the worst. As for satellite–ground baselines, the distribution of WL residuals within ±0.15 cycles is approximately 62% to 74%, while that within ±0.2 cycles is about 82% to 92%; these values are significantly lower than those of inter-satellite baselines. This indicates that there are many ambiguities between LEO satellites and ground stations that are difficult to fix. This phenomenon may be due to the large differences between the types of onboard receivers carried by LEO satellites and ground station receivers, which result in signal distortion biases (SDBs) affecting the WL ambiguity fixing rate [48,49]. We will conduct a detailed analysis in our subsequent research. For now, to prioritize ensuring that more ambiguities can participate in the resolution, the WL ambiguity threshold can be appropriately relaxed.
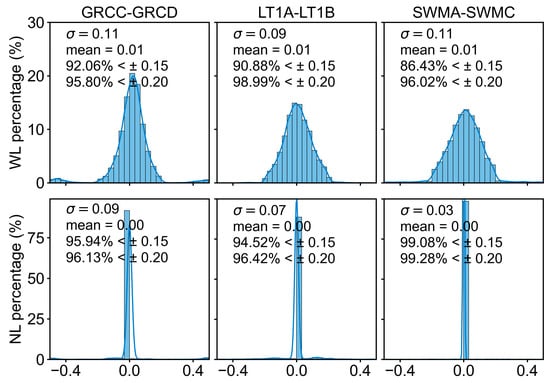
Figure 7.
Distributions of WL and NL ambiguity residuals for GRCC-GRCD, LT1A-LT1B, and SWMA-SWMC in the DD-AR solutions. The top row presents the distribution of WL ambiguity residuals, while the bottom row is that of NL ambiguity residuals.
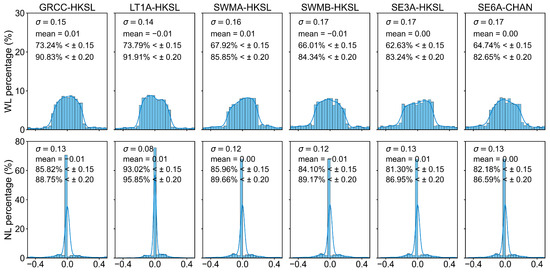
Figure 8.
Distributions of WL and NL ambiguity residuals for the different LEOs and ground stations in the DD-AR solutions. The top row presents the distribution of WL ambiguity residuals, while the bottom row is that of NL ambiguity residuals.
To study the impact of the ambiguity fixing thresholds of LEO satellites on the accuracy of GPS orbits, based on the distribution characteristics of the WL and NL ambiguity residuals derived above, the WL ambiguity thresholds were set to 0.15 and 0.2 cycles, while the NL ambiguity threshold remained at 0.15 cycles. Comparative experiments were conducted, with inter-satellite and ground-based baseline discussions discussed separately and referred to as LL and LG, respectively. Figure 9 illustrates the differences in GPS orbits and IGS final products in terms of the along-track, cross-track, radial, and 1D RMS, with statistical results shown in Table 7. For the LL solution, there was almost no change in the GPS orbit accuracy in the A/C/R directions before and after the adjustment of the ambiguity threshold. However, in the LG solution, slight improvements were observed in all directions. The speculation for this phenomenon is that although the WL ambiguity threshold was enlarged and the number of ambiguities involved in WL ambiguity fixing increased, the increase in the number of fixed NL ambiguities was not obvious.
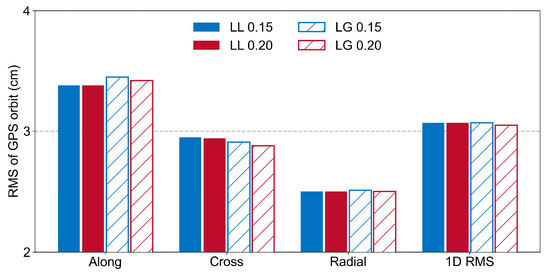
Figure 9.
The along-track, cross-track, radial, and 1D RMS of the GPS satellite orbit compared to the IGS final products with WL ambiguity thresholds of 0.15 and 0.2 cycles in LL (inter-satellite) and LG (satellite–ground) schemes.

Table 7.
Statistical results of the GPS orbit accuracy determined with different WL ambiguity thresholds compared with the IGS final products (unit: cm).
Therefore, we further present the total number of ambiguities and successfully fixed numbers of WL and NL ambiguities in the above four schemes, as shown in Figure 10. Table 8 provides the statistics of the number of ambiguities and the fixing rates of WL and NL ambiguities, where the NL fixing rate was calculated relative to the number of successfully fixed WL ambiguities. It can be seen that after the WL ambiguity threshold was increased from 0.15 to 0.2 cycles, the total number of ambiguities in the LL solution and the numbers of successfully fixed WL and NL ambiguities increased by approximately 2.7%, 3.6%, and 3.8%, respectively. However, the fixing rates for WL and NL ambiguities only increased by 0.8% and 0.2%, which aligns with the expectation that there was no improvement in the GPS orbit accuracy of the LL solution. For the LG solution, the numbers of successfully fixed WL and NL ambiguities increased by approximately 9.3% and 11.6%, respectively. The fixing rates for WL and NL ambiguities increased by 6.75% and 1.8%, which is also consistent with the expectation of a slight improvement in the orbit accuracy of the LG solution. In addition, comparing the LL and LG solutions revealed that although the total number of ambiguities for both was comparable, the number of successfully fixed WL and NL ambiguities in the LG solution was significantly lower than that in the LL solution. The reasoning for this is similar to that analyzed for the ambiguity residual distribution of satellite–ground baselines mentioned above. If the receiver bias issue is resolved in the future, the orbit accuracy should be further improved. In addition, due to the ambiguities of some LEO satellites potentially lacking integer properties, there may be certain limitations with integer bootstrapping estimators. In the future, it may be possible to try using algorithms such as least-squares ambiguity decorrelation adjustment (LAMBDA) [50], vectorial integer bootstrapping (VIB) [51], and best integer equivariant (BIE) [52]. Based on the results of this analysis, in the comprehensive experiment discussed in Section 3.4, it is recommended to prioritize setting the WL ambiguity threshold at 0.2 cycles.
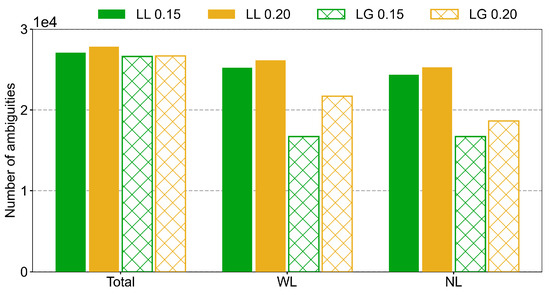
Figure 10.
The numbers of total and successfully fixed WL and NL ambiguities for LL and LG DD-AR solutions with different thresholds of WL ambiguity.

Table 8.
The numbers of total and fixed WL and NL ambiguities and fixing rates for LL and LG DD-AR solutions with different thresholds of WL ambiguity.
3.4. Comprehensive Experiment
Based on the above experimental results, we identified the preferred strategy for ambiguity fixing of LEO satellites in regional integrated POD, which involves the combination of inter-satellite and satellite–ground baselines, a 5 min common view time for DD ambiguities, and a threshold of 0.2 cycles for WL ambiguities. The final comprehensive experiment was conducted using this strategy (denoted by GRD + LEO AR) and compared with the scheme that only fixed the ambiguities of ground stations (denoted by GRD AR). Figure 11 illustrates the time series of differences in the along-track, cross-track, radial, and 1D RMS of the GPS orbits for the two schemes, which were compared with the IGS final products. There were three days of missing results, DOY 076, 083, and 089, due to the maneuvering of LEO satellites or poor data quality. It is worth noting that the GPS orbit accuracy of the GRD + LEO AR solution was superior to that of the GRD AR solution in all directions. Table 9 summarizes the statistical results of GPS orbit accuracy for all days, with improvements of 9.3%, 12.5%, 10.9%, and 10.8% in the along, cross, radial, and 1D RMS, respectively. The most significant improvement was in the cross direction, which is attributed to the seven satellite–ground baselines selected in the experiment. This correlates well with the findings in Section 3.1 that satellite–ground baselines significantly improve the cross-track accuracy. Moreover, this experimental result is based on real data, with fewer regional ground stations or LEO satellites selected, which is superior to the results of previous studies [12,53].
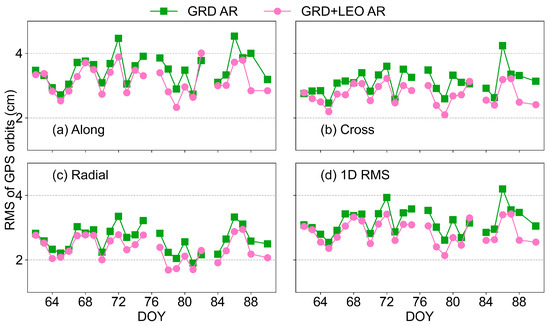
Figure 11.
Time series of the along-track, cross-track, radial, and 1D RMS of the GPS satellite orbit differences of GRD AR and GRD + LEO AR compared to the IGS final products from DOY 062 to 090 of 2022.

Table 9.
The statistical results of the GPS satellite orbit differences compared to the IGS final products from DOY 062 to 090 of 2022 (unit: cm).
In addition, Figure 12 shows the time series of the ambiguity fixing rates for LEO satellites, ground stations, and the total in the GRD + LEO AR solution; the statistical results for the 26 days are 81.44%, 93.23%, and 82.24%, respectively. The lower ambiguity fixing rate for LEO satellites is due to the low fixing rate of the satellite–ground baselines. If the receiver differential issue is resolved, the fixing rate will be further improved in the future. In summary, implementing ambiguity resolution related to LEO satellites in regional integrated POD significantly enhances the GPS orbit accuracy. Nie et al. (2025) [10] has already proven that LEO satellites can greatly improve the GPS accuracy of float solutions. In the ambiguity fixing process, the potential of LEO satellites should also be fully explored to maximize the performance of POD.
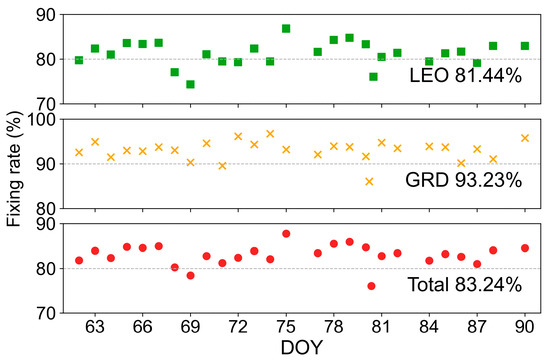
Figure 12.
Time series of the fixing rates of LEO satellites, ground stations, and the total for the GRD + LEO AR solution from DOY 062 to 090 of 2022.
4. Discussion
In this study, we selected seven IGS stations within China and 10 LEO satellites, including GRACE-C/D, LuTan1-A/B, SWARM-A/B/C, Sentinel-3A/B, and Sentinel-6A, to establish a regional integrated observation network and investigate the contribution of ambiguity resolution related to LEO satellites to GPS orbit accuracy. Comparative experiments were carried out sequentially from three aspects—independent baseline selection, the common view time, and the threshold of DD ambiguity—to analyze in detail the impact of each factor on GPS orbit accuracy.
Firstly, regarding the selection of independent baselines, inter-satellite baselines can establish connections between LEO satellites and improve the relative orbit accuracy, while satellite–ground baselines can further strengthen the geometric constraints between LEO satellites and ground stations, improving the absolute orbit accuracy. Therefore, the combination of inter-satellite and satellite–ground baselines were identified as the best choice for improving the orbit accuracy. Secondly, based on the distribution characteristics of the common view times of DD ambiguities for inter-satellite and satellite–ground baselines, it was found that setting the common view time too long resulted in excessive elimination of ambiguities, thereby reducing the GPS orbit accuracy. Consequently, a common view time of 5 min was verified to be the best choice. Next, in the ambiguity threshold experiments, it was observed that adjusting the WL ambiguity threshold from 0.15 cycles to 0.2 cycles resulted in comparable GPS orbit accuracy, which was consistent with the slight improvement in the NL fixing rate. In addition, the low fixing rate of satellite–ground baselines may be due to the significant differences in the types of receivers between LEO satellites and ground stations, which will be further investigated in future work.
Finally, a comprehensive experiment was conducted using the determined preferred ambiguity fixing strategy, with the final ephemeris products released by IGS as the reference. The GPS orbit accuracy presented improvements of 9.3%, 12.5%, 10.9%, and 10.8% in the along-track, cross-track, radial, and 1D RMS, respectively, compared with the solution that only fixed ground station ambiguities. This result demonstrates that further implementation of LEO-satellite-related ambiguity fixing significantly enhanced the accuracy of GPS orbits in the regional integrated POD. As more LEO satellites receive GNSS observations in the future, the ambiguity fixing strategy presented in this paper can provide an effective and feasible approach.
5. Conclusions
In the integrated precise orbit determination based on LEOs and regional stations, ambiguity resolution has great significance in improving orbit accuracy. In response to the current regional integrated POD that only resolves the ambiguities of ground stations, this paper proposes an AR strategy of LEO satellites to enhance GPS orbit accuracy.
Based on the characteristics of LEO satellites that are different from ground stations, this paper conducts detailed experimental analysis and determines the strategy from three aspects: independent baseline selection, double-difference ambiguity common view time, and ambiguity resolution threshold. Comprehensive experiments show that further implementation of LEO satellite-related ambiguity fixing can significantly improve the GPS orbit accuracy in regional integrated POD.
Given the limitation that most LEO satellites can only receive GPS satellite signals, in the future, as more LEO satellites gain access to GNSS observations, the ambiguity fixing strategy presented in this paper can provide an effective and feasible approach.
Author Contributions
X.L.: designed the research, processed the data, and wrote the paper; J.G.: outlined the paper’s framework and revised this paper; J.L. and S.X.: software implementation; Q.Z.: revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The IGS is gratefully acknowledged for providing the GPS tracking data. The numerical calculations in this study were performed on the supercomputing system at the Supercomputing Center of Wuhan University.
Conflicts of Interest
The authors declare no competing interests.
References
- Prol, F.S.; Ferre, R.M.; Saleem, Z.; Valisuo, P.; Pinell, C.; Lohan, E.S.; Elsanhoury, M.; Elmusrati, M.; Islam, S.; Celikbilek, K.; et al. Position, Navigation, and Timing (PNT) Through Low Earth Orbit (LEO) Satellites: A Survey on Current Status, Challenges, and Opportunities. IEEE Access 2022, 10, 83971–84002. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, Y.; Ren, X.; Jia, X.; Sun, B. Demand and Key Technology for a LEO Constellation as Augmentation of Satellite Navigation Systems. Satell. Navig. 2024, 5, 11. [Google Scholar] [CrossRef]
- Hackel, S.; Steigenberger, P.; Hugentobler, U.; Uhlemann, M.; Montenbruck, O. Galileo Orbit Determination Using Combined GNSS and SLR Observations. GPS Solut. 2015, 19, 15–25. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison. J. Geod. 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Wu, J.; Yuan, Y.; Xiong, Y.; Gong, X.; Wu, Z. Multi-GNSS Products and Services at iGMAS Wuhan Innovation Application Center: Strategy and Evaluation. Satell. Navig. 2022, 3, 20. [Google Scholar] [CrossRef]
- Li, K.; Tang, C.; Zhou, S.; Hu, X.; Zhou, X. High-Precision GPS Orbit Determination by Integrating the Measurements from Regional Ground Stations and LEO Onboard Receivers. Satell. Navig. 2024, 5, 27. [Google Scholar] [CrossRef]
- Zhu, S.; Reigber, C.; König, R. Integrated Adjustment of CHAMP, GRACE, and GPS Data. J. Geod. 2004, 78, 103–108. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Guo, J.; Yang, G.; Liao, M.; Ma, H.; Liu, J. Enhanced Orbit Determination for BeiDou Satellites with FengYun-3C Onboard GNSS Data. GPS Solut. 2017, 21, 1179–1190. [Google Scholar] [CrossRef]
- Li, M.; Wei, K.; Xu, T.; Shi, Y.; Wang, D. Enhanced Precise Orbit Determination for GPS and BDS-2/3 with Real LEO Onboard and Ground Observations. Measurement 2024, 224, 113912. [Google Scholar] [CrossRef]
- Nie, L.; Wang, J.; Tang, L.; Ge, H.; Ge, M.; Schuh, H. Impact of LEO Configuration on GPS Precise Orbit Determination with Un-Differenced Ambiguity Resolution. GPS Solut. 2025, 29, 28. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Ma, F.; Zhang, W.; Zhang, Q.; Qin, Y.; Zhang, H.; Meng, Y.; Bian, L. Integrated Precise Orbit Determination of Multi-GNSS and Large LEO Constellations. Remote Sens. 2019, 11, 2514. [Google Scholar] [CrossRef]
- Huang, W.; Männel, B.; Sakic, P.; Ge, M.; Schuh, H. Integrated Processing of Ground- and Space-Based GPS Observations: Improving GPS Satellite Orbits Observed with Sparse Ground Networks. J. Geod. 2020, 94, 96. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. An Optimality Property of the Integer Least-Squares Estimator. J. Geod. 1999, 73, 587–593. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Integer aperture GNSS ambiguity resolution. Artif. Satell. 2003, 38, 79–88. [Google Scholar]
- Teunissen, P.J.G. Theory of Integer Equivariant Estimation with Application to GNSS. J. Geod. 2003, 77, 402–410. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Massarweh, L. Theory for the Ambiguity Function Method: Probability Model and Global Solution. J. Geod. 2025, 99, 28. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping. J. Geod. 1998, 72, 606–612. [Google Scholar] [CrossRef]
- Dong, D.; Bock, Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California. J. Geophys. Res. 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 Km. J. Geophys. Res. 1989, 94, 10187–10203. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Guo, J.; Yang, C.; Zhao, Q. Near Real-Time Multi-GNSS Orbits, Clock and Observable-Specific Biases at Wuhan University. GPS Solut. 2024, 28, 191. [Google Scholar] [CrossRef]
- Li, J.; Guo, J.; Xu, S.; Zhao, Q. Undifferenced Ambiguity Resolution for Precise Multi-GNSS Products to Support Global PPP-AR. Remote Sens. 2025, 17, 1451. [Google Scholar] [CrossRef]
- Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE Baseline Determination Using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
- Guo, X.; Geng, J.; Chen, X.; Zhao, Q. Enhanced Orbit Determination for Formation-Flying Satellites Through Integrated Single- and Double-Difference GPS Ambiguity Resolution. GPS Solut. 2020, 24, 14. [Google Scholar] [CrossRef]
- Švehla, D.; Rothacher, M. Kinematic Orbit Determination of LEOs Based on Zero or Double-Difference Algorithms Using Simulated and Real SST GPS Data. In Vistas for Geodesy in the New Millennium; Ádám, J., Schwarz, K.P., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2002; Volume 125. [Google Scholar] [CrossRef]
- Jäggi, A.; Hugentobler, U.; Bock, H.; Beutler, G. Precise Orbit Determination for GRACE Using Undifferenced or Doubly Differenced GPS Data. Adv. Space Res. 2007, 39, 1612–1619. [Google Scholar] [CrossRef]
- Zhang, K.; Li, X.; Wu, J.; Yuan, Y.; Li, X.; Zhang, X.; Zhang, W. Precise Orbit Determination for LEO Satellites with Ambiguity Resolution: Improvement and Comparison. JGR Solid. Earth 2021, 126, e2021JB022491. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods, and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P. Improving Carrier-Phase Ambiguity Resolution in Global GPS Network Solutions. J. Geod. 2005, 79, 103–110. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Q.; Jiang, K.; Guo, X.; Lian, Y.; Li, M. Precise Orbit Determination of the LuTan Satellite Using GPS, BDS-2, and BDS-3 Signals. Meas. Sci. Technol. 2024, 35, 096314. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise Orbit Determination of the Sentinel-3A Altimetry Satellite Using Ambiguity-Fixed GPS Carrier Phase Observations. J. Geod. 2018, 92, 711–726. [Google Scholar] [CrossRef]
- Berzosa-Molina, J.; Peter, H.; Fernández, J.; Féménias, P. Copernicus Sentinel–3B—GPS L2C Tracking Tests During Commissioning Phase. Adv. Space Res. 2021, 68, 1023–1047. [Google Scholar] [CrossRef]
- Van den Ijssel, J.; Encarnação, J.; Doornbos, E.; Visser, P. Precise Science Orbits for the Swarm Satellite Constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Van den Ijssel, J.; Arnold, D. Reduced Dynamic and Kinematic Precise Orbit Determination for the Swarm Mission from 4 Years of GPS Tracking. GPS Solut. 2018, 22, 79. [Google Scholar] [CrossRef]
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar] [CrossRef]
- Shako, R.; Förste, C.; Abrikosov, O.; Bruinsma, S.; Marty, J.-C.; Lemoine, J.M.; Flechtner, F.; Neumayer, H.; Dahle, C. EIGEN-6C: A High-Resolution Global Gravity Combination Model Including GOCE Data. In Observation of the System Earth from Space—CHAMP, GRACE, GOCE and Future Missions; Flechtner, F., Sneeuw, N., Schuh, W.D., Eds.; Advanced Technologies in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions 2010; No.36 in IERS Technical Note; Verlag des Bundesamtes für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. FES2014 Global Ocean Tide Atlas: Design and Performance. Ocean. Sci. 2021, 17, 615–649. [Google Scholar] [CrossRef]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s New Solar Radiation Pressure Model for GNSS Orbit Determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef]
- Vielberg, K.; Kusche, J. Extended Forward and Inverse Modeling of Radiation Pressure Accelerations for LEO Satellites. J. Geod. 2020, 94, 43. [Google Scholar] [CrossRef]
- Bruinsma, S. The DTM-2013 Thermosphere Model. J. Space Weather. Space Clim. 2015, 5, A1. [Google Scholar] [CrossRef]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase Center Modeling for LEO GPS Receiver Antennas and Its Impact on Precise Orbit Determination. J. Geod. 2009, 83, 1145–1162. [Google Scholar] [CrossRef]
- Kouba, J. A Simplified Yaw-Attitude Model for Eclipsing GPS Satellites. GPS Solut. 2009, 13, 1–12. [Google Scholar]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Manuscr. Geod. 1993, 18, 91–98. [Google Scholar] [CrossRef]
- Mervart, L. Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System. Ph.D. Thesis, University of Berne, Bern, Switzerland, 1995. [Google Scholar]
- Teunissen, P.J.G. The Parameter Distributions of the Integer GPS Model. J. Geod. 2002, 76, 41–48. [Google Scholar] [CrossRef]
- Guo, J.; Wang, C.; Chen, G.; Xu, X.; Zhao, Q. BDS-3 Precise Orbit and Clock Solution at Wuhan University: Status and Improvement. J. Geod. 2023, 97, 15. [Google Scholar] [CrossRef]
- Shi, C.; Tian, Y.; Zheng, F.; Hu, Y. Accounting for Signal Distortion Biases for Wide-Lane and Narrow-Lane Phase Bias Estimation with Inhomogeneous Networks. Remote Sens. 2022, 14, 191. [Google Scholar] [CrossRef]
- Shu, B.; Lei, T.; Li, P.; Wang, L.; Huang, G.; Zhang, S.; Zhang, Q. Calibration of Inconsistent Receiver-Dependent Pseudorange Bias and Its Impact on Wide-Lane Ambiguity Fixing. GPS Solut. 2025, 29, 64. [Google Scholar] [CrossRef]
- Massarweh, L.; Verhagen, S.; Teunissen, P.J.G. New LAMBDA Toolbox for Mixed-Integer Models: Estimation and Evaluation. GPS Solut. 2025, 29, 14. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Massarweh, L.; Verhagen, S. Vectorial Integer Bootstrapping: Flexible Integer Estimation with Application to GNSS. J. Geod. 2021, 95, 99. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Best Integer Equivariant Estimation for Elliptically Contoured Distributions. J. Geod. 2020, 94, 82. [Google Scholar] [CrossRef]
- She, H.; Huang, G.; Wang, L.; Qin, Z.; Xie, S.; Lai, W.; Tian, J. A Simplified GNSS/LEO Joint Orbit Determination Method. Measurement 2024, 236, 115029. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).