A Comprehensive Review of Path-Planning Algorithms for Planetary Rover Exploration
Abstract
1. Introduction
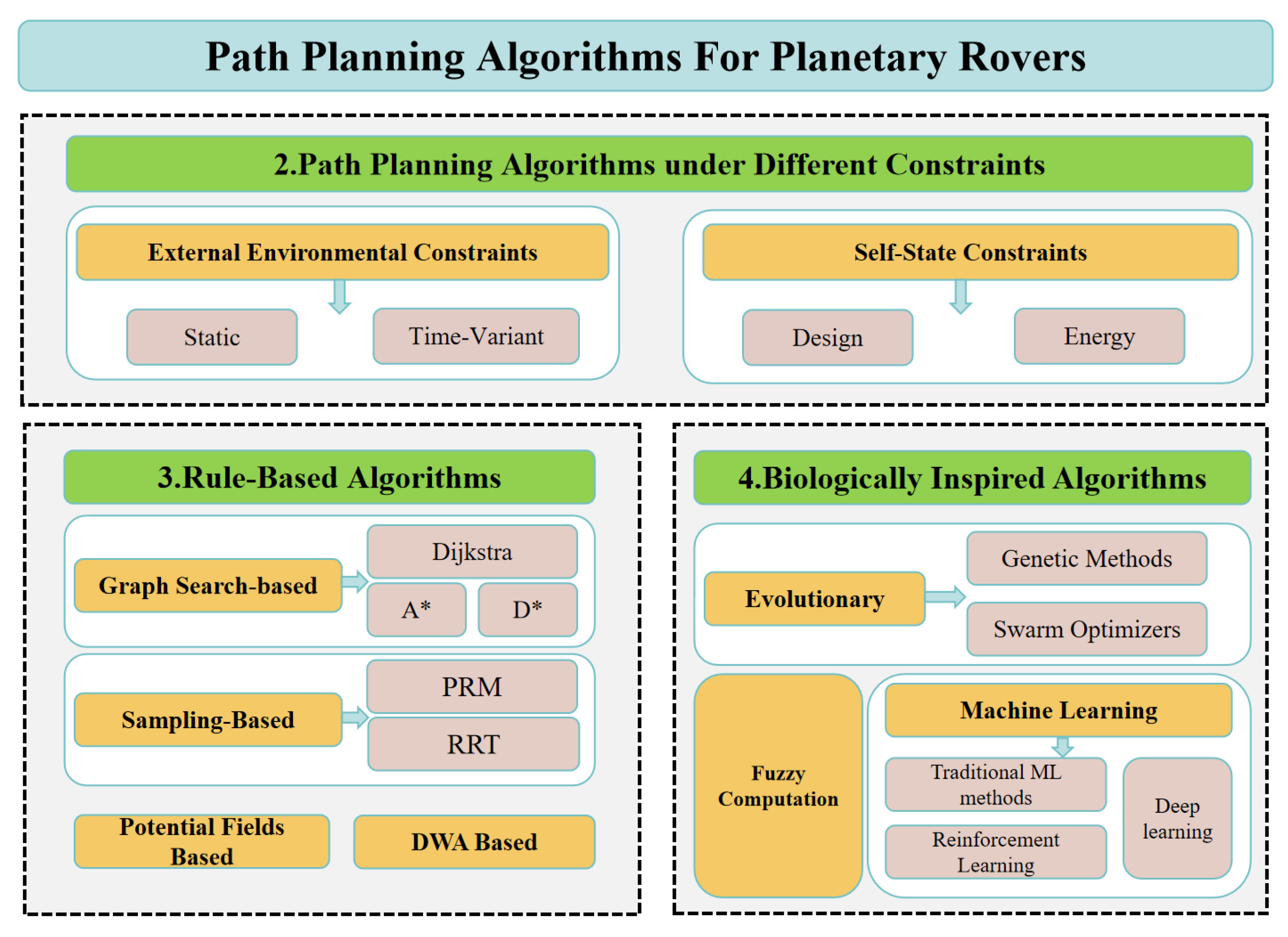
2. Path-Planning Algorithms Under Different Constraints
2.1. Algorithms Based on External Environmental Constraints
2.2. Algorithms Based on Self-State Constraints
3. Rule-Based Path-Planning Algorithms
3.1. Graph Search-Based Algorithms
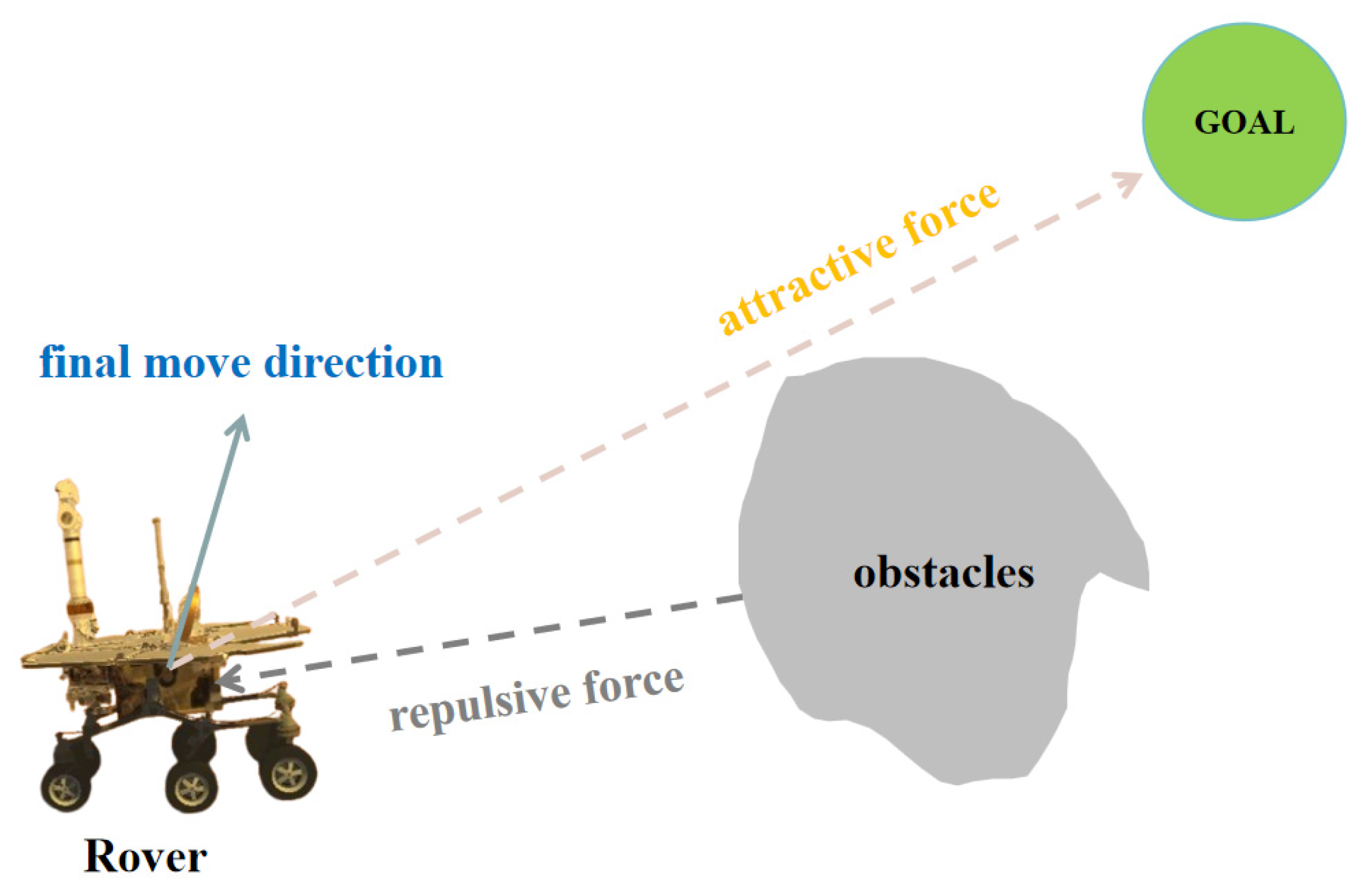
3.2. Potential Field-Based Algorithms
3.3. Sampling-Based Algorithms
3.4. Dynamic Window Approach
4. Biologically Inspired Path-Planning Algorithms
4.1. Algorithms Based on Evolutionary Learning
4.2. Algorithms Based on Fuzzy Computation
4.3. Machine Learning-Based Algorithms
4.3.1. Traditional Machine Learning Algorithms
4.3.2. Deep Learning-Based Algorithms
4.3.3. Reinforcement Learning-Based Algorithms
- The training of machine learning models needs to rely on a large amount of real data. However, the current amount of data on the extraterrestrial surface is extremely limited, which may lead to insufficient model generalization ability. In addition, the uncertainty of planetary surface environmental data (e.g., terrain, obstacles, soil properties, etc.) also increases the difficulty of model training.
- Machine learning models, due to the “black box” nature of the operation process and the lack of interpretability, may lead to unpredictable and unsafe behaviors of the planetary rover, which may be a greater risk, especially in critical missions.
- There are challenges in the migration ability and robustness of machine learning-based methods. In future deep space exploration missions, planetary rovers need to plan paths in different terrains, environments, and scientific objectives, and machine learning-based models may have the problem of superior modeling in specific environments but poor performance in real environments due to their strong dependence on training data.
- Machine learning algorithms have problems such as complex training processes and consumption of computational resources, especially when such algorithms are applied to autonomous path planning for planetary rovers, which is a considerable burden on the rover’s computational platform.
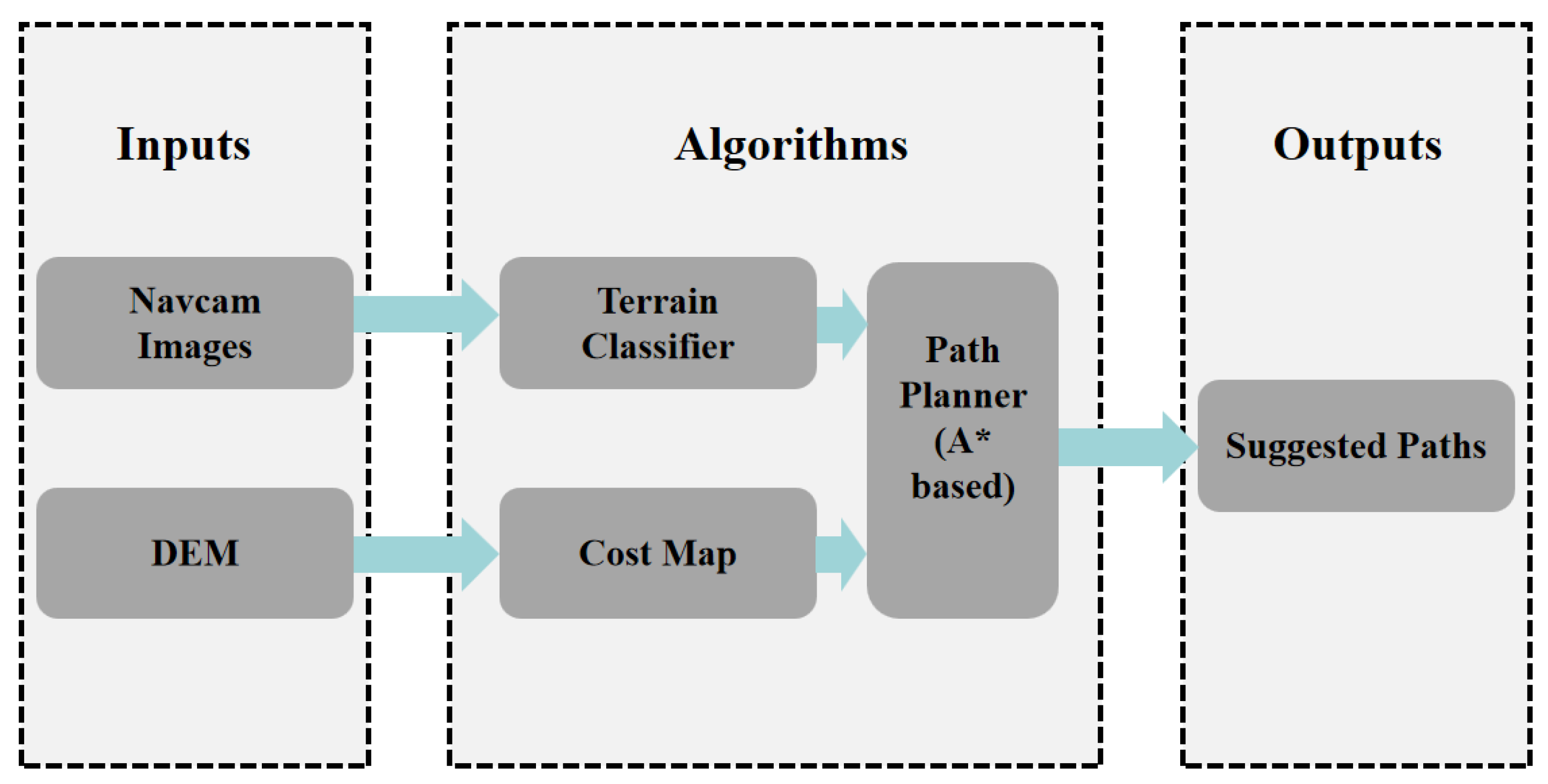
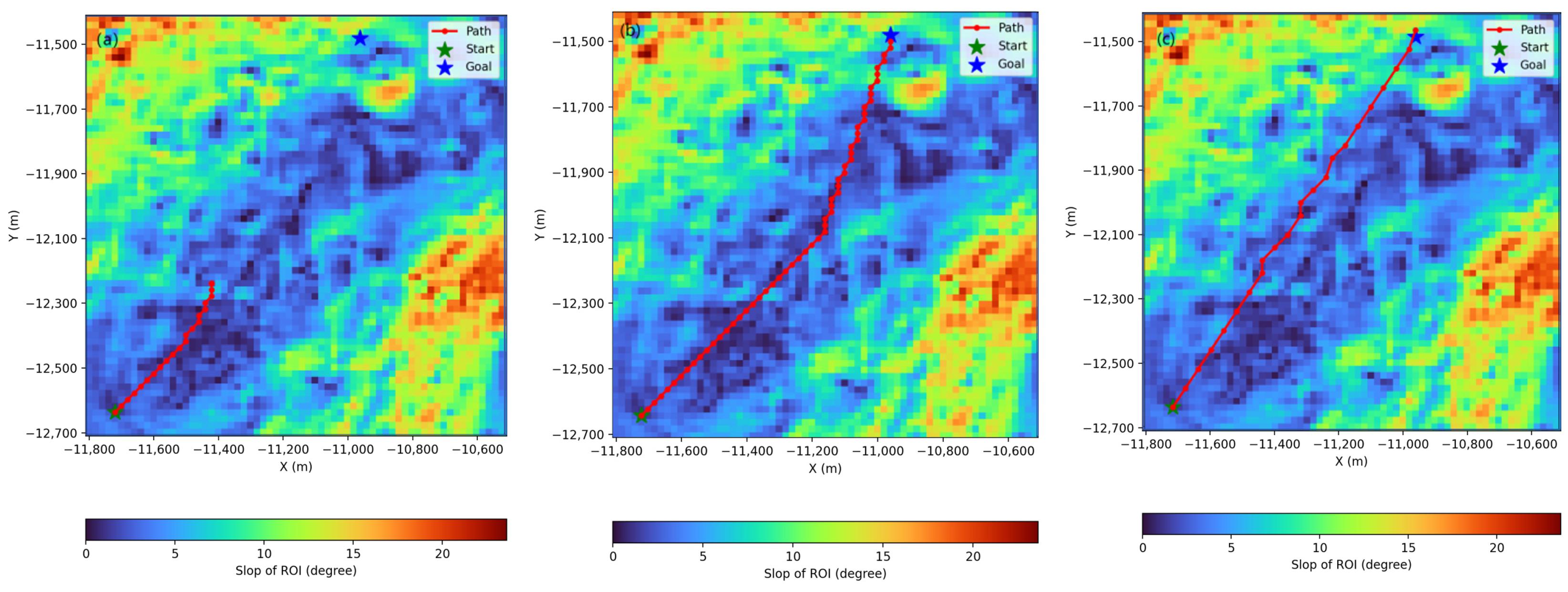
5. Discussion and Future Works
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vondrak, R.; Keller, J.; Chin, G.; Garvin, J. Lunar Reconnaissance Orbiter (LRO): Observations for lunar exploration and science. Space Sci. Rev. 2010, 150, 7–22. [Google Scholar] [CrossRef]
- Harvey, B. Soviet and Russian Lunar Exploration; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Li, C.; Wang, C.; Wei, Y.; Lin, Y. China’s present and future lunar exploration program. Science 2019, 365, 238–239. [Google Scholar] [CrossRef]
- Weiren, W.; Jizhong, L.; Yuhua, T.; Dengyun, Y.; Guobin, Y.; Zhe, Z. China lunar exploration program. J. Deep Space Explor. 2019, 6, 405–416. [Google Scholar]
- Dengyun, Y.; Xueying, W.; Weiren, W. Review of technology development for Chinese lunar exploration program. J. Deep Space Explor. 2016, 3, 307–314. [Google Scholar]
- Ding, L.; Zhou, R.; Yuan, Y.; Yang, H.; Li, J.; Yu, T.; Liu, C.; Wang, J.; Li, S.; Gao, H. A 2-year locomotive exploration and scientific investigation of the lunar farside by the Yutu-2 rover. Sci. Robot. 2022, 7, eabj6660. [Google Scholar] [CrossRef] [PubMed]
- Johnston, R.S.; Hull, W.E.; Dietlein, L.; Berry, C. Apollo missions. In Biomedical Results of Apollo; NASA: Washington, DC, USA, 1975; pp. 9–40. [Google Scholar]
- Grotzinger, J.P.; Crisp, J.; Vasavada, A.R.; Anderson, R.C.; Baker, C.J.; Barry, R.; Blake, D.F.; Conrad, P.; Edgett, K.S.; Ferdowski, B. Mars science laboratory mission and science investigation. Space Sci. Rev. 2012, 170, 5–56. [Google Scholar] [CrossRef]
- Farley, K.A.; Williford, K.H.; Stack, K.M.; Bhartia, R.; Chen, A.; de la Torre, M.; Hand, K.; Goreva, Y.; Herd, C.D.; Hueso, R. Mars 2020 mission overview. Space Sci. Rev. 2020, 216, 142. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, T.; Jia, Y.; Peng, S.; Yan, C. Zhurong: Features and mission of China’s first Mars rover. Innovation 2021, 2, 100121. [Google Scholar] [CrossRef]
- Smith, M.; Craig, D.; Herrmann, N.; Mahoney, E.; Krezel, J.; McIntyre, N.; Goodliff, K. The Artemis program: An overview of NASA’s activities to return humans to the moon. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–10. [Google Scholar]
- Wang, C.; Jia, Y.; Xue, C.; Lin, Y.; Liu, J.; Fu, X.; Xu, L.; Huang, Y.; Zhao, Y.; Xu, Y. Scientific objectives and payload configuration of the Chang’E-7 mission. Natl. Sci. Rev. 2024, 11, nwad329. [Google Scholar] [CrossRef]
- Wong, C.; Yang, E.; Yan, X.-T.; Gu, D. Adaptive and intelligent navigation of autonomous planetary rovers—A survey. In Proceedings of the 2017 NASA/ESA Conference on Adaptive Hardware and Systems (AHS), Pasadena, CA, USA, 24–27 July 2017; pp. 237–244. [Google Scholar]
- Yu, X.; Wang, P.; Zhang, Z. Learning-based end-to-end path planning for lunar rovers with safety constraints. Sensors 2021, 21, 796. [Google Scholar] [CrossRef]
- Sutoh, M.; Otsuki, M.; Wakabayashi, S.; Hoshino, T.; Hashimoto, T. The right path: Comprehensive path planning for lunar exploration rovers. IEEE Robot. Autom. Mag. 2015, 22, 22–33. [Google Scholar] [CrossRef]
- Yu, X.; Huang, Q.; Wang, P.; Guo, J. Comprehensive global path planning for lunar rovers. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 505–510. [Google Scholar]
- Takemura, R.; Ishigami, G. Traversability-based RRT* for planetary rover path planning in rough terrain with LIDAR point cloud data. J. Robot. Mechatron. 2017, 29, 838–846. [Google Scholar] [CrossRef]
- Bai, C.; Guo, J.; Guo, L.; Song, J. Deep multi-layer perception based terrain classification for planetary exploration rovers. Sensors 2019, 19, 3102. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, F.; Liu, C.; Zhang, Z.; Li, Q. Review of autonomous path planning for planetary rovers. Chin. J. Eng. 2024, 46, 2063–2075. [Google Scholar]
- Hoa, D.K.; Dung, L.; Dzung, N.T. Efficient determination of disparity map from stereo images with modified sum of absolute differences (SAD) algorithm. In Proceedings of the 2013 International Conference on Advanced Technologies for Communications (ATC 2013), Ho Chi Minh City, Vietnam, 16–18 October 2013; pp. 657–660. [Google Scholar]
- Chen, J.; Xing, Y.; Li, Z.; Mao, X.; Teng, B.; Liu, X.; Jia, Y.; Gu, P. Autonomous environment perception and obstacle avoidance technologies of Zhurong Mars rover. Sci. Sin. Technol. 2022, 52, 1186–1197. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Karaman, S.; Walter, M.R.; Perez, A.; Frazzoli, E.; Teller, S. Anytime motion planning using the RRT. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1478–1483. [Google Scholar]
- Han, W.-G.; Baek, S.-M.; Kuc, T.-Y. Genetic algorithm based path planning and dynamic obstacle avoidance of mobile robots. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 2747–2751. [Google Scholar]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic algorithm based approach for autonomous mobile robot path planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Wenyuan, Z.; Jifeng, G.; Chengchao, B. Adaptive Path Planning for Unmanned Planetary Rover with Dynamic Obstacle. In Proceedings of the 2019 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 17–19 October 2019; pp. 730–735. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Manteaux, T.; Rodríguez-Martínez, D.; Rajan, R.T. RAPF: Efficient path planning for lunar microrovers. arXiv 2024, arXiv:2405.16659. [Google Scholar]
- Bassil, Y. Neural network model for path-planning of robotic rover systems. arXiv 2012, arXiv:1204.0183. [Google Scholar]
- Zhang, J.; Xia, Y.; Shen, G. A novel learning-based global path planning algorithm for planetary rovers. Neurocomputing 2019, 361, 69–76. [Google Scholar] [CrossRef]
- Higa, S.; Iwashita, Y.; Otsu, K.; Ono, M.; Lamarre, O.; Didier, A.; Hoffmann, M. Vision-based estimation of driving energy for planetary rovers using deep learning and terramechanics. IEEE Robot. Autom. Lett. 2019, 4, 3876–3883. [Google Scholar] [CrossRef]
- Tanaka, T.; Malki, H. A Deep Learning Approach to Lunar Rover Global Path Planning Using Environmental Constraints and the Rover Internal Resource Status. Sensors 2024, 24, 844. [Google Scholar] [CrossRef] [PubMed]
- Park, B.-J.; Chung, H.-J. Deep reinforcement learning-based failure-safe motion planning for a 4-wheeled 2-steering lunar rover. Aerospace 2023, 10, 219. [Google Scholar] [CrossRef]
- Bai, J.H.; Oh, Y.-J. Global path planning of lunar rover under static and dynamic constraints. Int. J. Aeronaut. Space Sci. 2020, 21, 1105–1113. [Google Scholar] [CrossRef]
- Biesiadecki, J.J.; Maimone, M.W. The mars exploration rover surface mobility flight software driving ambition. In Proceedings of the 2006 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2006; p. 15. [Google Scholar]
- Jianxin, C.; Yan, X.; Baoyi, T.; Xiaoyan, M.; Xiang, L.; Yong, J.; Jin, Z.; Lei, W. Guidance, navigation and control technologies of Chang’E-3 lunar rover. Sci. Sin. 2014, 44, 461. [Google Scholar]
- Iagnemma, K.; Genot, F.; Dubowsky, S. Rapid physics-based rough-terrain rover planning with sensor and control uncertainty. In Proceedings of the Proceedings 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; pp. 2286–2291. [Google Scholar]
- Cunningham, C.; Amato, J.; Jones, H.L.; Whittaker, W.L. Accelerating energy-aware spatiotemporal path planning for the lunar poles. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4399–4406. [Google Scholar]
- Inoue, H.; Adachi, S. Spatio-temporal path planning for lunar polar exploration with robustness against schedule delay. Trans. Jpn. Soc. Aeronaut. Space Sci. 2021, 64, 304–311. [Google Scholar] [CrossRef]
- Brunner, M.; Fiolka, T.; Schulz, D.; Schlick, C.M. Design and comparative evaluation of an iterative contact point estimation method for static stability estimation of mobile actively reconfigurable robots. Robot. Auton. Syst. 2015, 63, 89–107. [Google Scholar] [CrossRef]
- Farritor, S.; Dubowsky, S. Genetic planning method and its application to planetary exploration. J. Dyn. Sys. Meas. Control 2002, 124, 698–701. [Google Scholar] [CrossRef]
- Goldberg, S.B.; Maimone, M.W.; Matthies, L. Stereo vision and rover navigation software for planetary exploration. In Proceedings of the Proceedings, IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; p. 5. [Google Scholar]
- Weih, R.C., Jr.; Mattson, T.L. Modeling slope in a geographic information system. J. Ark. Acad. Sci. 2004, 58, 100–108. [Google Scholar]
- Mahtab, A.; Narender, B.; Ajai. Satellite derived digital elevation model and terrain parameters—Generation, accuracy assessment and validation. J. Indian Soc. Remote Sens. 2003, 31, 19–24. [Google Scholar] [CrossRef]
- Bussey, D.B.J.; Spudis, P.D.; Robinson, M.S. Illumination conditions at the lunar south pole. Geophys. Res. Lett. 1999, 26, 1187–1190. [Google Scholar] [CrossRef]
- Plonski, P.A.; Tokekar, P.; Isler, V. Energy-efficient path planning for solar-powered mobile robots. J. Field Robot. 2013, 30, 583–601. [Google Scholar] [CrossRef]
- Kaplan, A.; Kingry, N.; Uhing, P.; Dai, R. Time-optimal path planning with power schedules for a solar-powered ground robot. IEEE Trans. Autom. Sci. Eng. 2016, 14, 1235–1244. [Google Scholar] [CrossRef]
- Lamarre, O.; Malhotra, S.; Kelly, J. Safe Mission-Level Path Planning for Exploration of Lunar Shadowed Regions by a Solar-Powered Rover. In Proceedings of the 2024 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2024; pp. 1–14. [Google Scholar]
- Staudinger, E.; Giubilato, R.; Schuster, M.J.; Pöhlmann, R.; Zhang, S.; Dömel, A.; Wedler, A.; Dammann, A. Terrain-aware communication coverage prediction for cooperative networked robots in unstructured environments. Acta Astronaut. 2023, 202, 799–805. [Google Scholar] [CrossRef]
- de Curtò, J.; de Zarzà, I.; Calafate, C.T. UWB and MB-OFDM for Lunar Rover Navigation and Communication. Mathematics 2023, 11, 3835. [Google Scholar] [CrossRef]
- Ohki, T. Online Slip Estimation for Mobile Robot Localization and Reactive Path Planning on Rough and Deformable Terrain. Ph.D. Thesis, Tohoku University, Sendai, Japan, 2013. [Google Scholar]
- Zhang, H.; Zhang, Y.; Yang, T. A survey of energy-efficient motion planning for wheeled mobile robots. Ind. Robot Int. J. Robot. Res. Appl. 2020, 47, 607–621. [Google Scholar] [CrossRef]
- Malenkov, M.; Volov, V. Wheel-walking propulsion unit of a planetary rover with active suspension. Russ. Eng. Res. 2017, 37, 1033–1040. [Google Scholar] [CrossRef]
- Moreland, S.; Skonieczny, K.; Wettergreen, D.; Asnani, V.; Creager, C.; Oravec, H. Inching locomotion for planetary rover mobility. In Proceedings of the 2011 Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–6. [Google Scholar]
- Creager, C.; Moreland, S.; Skonieczny, K.; Johnson, K.; Asnani, V.; Gilligan, R. Benefit of “Push-Pull” Locomotion for Planetary Rover Mobility. In Earth and Space 2012: Engineering, Science, Construction, and Operations in Challenging Environments; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 11–20. [Google Scholar]
- Ishigami, G.; Nagatani, K.; Yoshida, K. Path planning and evaluation for planetary rovers based on dynamic mobility index. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 601–606. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; ACM Books: New York, NY, USA, 2022; pp. 287–290. [Google Scholar]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3310–3317. [Google Scholar]
- Muñoz, P.; R-Moreno, M.D.; Castaño, B. 3Dana: A path planning algorithm for surface robotics. Eng. Appl. Artif. Intell. 2017, 60, 175–192. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, F.; Li, Q. An improved path planning and tracking control method for planetary exploration rovers with traversable tolerance. Biomim. Intell. Robot. 2025, 5, 100219. [Google Scholar] [CrossRef]
- Hong, Z.; Tu, B.; Tong, X.; Pan, H.; Zhou, R.; Zhang, Y.; Han, Y.; Wang, J.; Yang, S.; Ma, Z. A fast large-scale path planning method on lunar DEM using distributed tile pyramid strategy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 16, 344–355. [Google Scholar] [CrossRef]
- Nasuha, A.; Priambodo, A.; Pratama, G. Vortex artificial potential field for mobile robot path planning. J. Phys. Conf. Ser. 2022, 2406, 012001. [Google Scholar] [CrossRef]
- Hossain, M.A.; Ferdous, I. Autonomous robot path planning in dynamic environment using a new optimization technique inspired by bacterial foraging technique. Robot. Auton. Syst. 2015, 64, 137–141. [Google Scholar] [CrossRef]
- Diab, M.; Mohammadkarimi, M.; Rajan, R.T. Artificial Potential Field-Based Path Planning for Cluttered Environments. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; pp. 1–8. [Google Scholar]
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Lavalle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Technical Report; Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Hidalgo-Paniagua, A.; Bandera, J.P.; Ruiz-de-Quintanilla, M.; Bandera, A. Quad-RRT: A real-time GPU-based global path planner in large-scale real environments. Expert Syst. Appl. 2018, 99, 141–154. [Google Scholar] [CrossRef]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng, M.Q.H. Neural RRT*: Learning-based optimal path planning. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Zhang, F.; Li, N.; Xue, T.; Zhu, Y.; Yuan, R.; Fu, Y. An improved dynamic window approach integrated global path planning. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2873–2878. [Google Scholar]
- Chang, L.; Shan, L.; Jiang, C.; Dai, Y. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment. Auton. Robot. 2021, 45, 51–76. [Google Scholar] [CrossRef]
- Huiting, W.; Meng, Y.; Yuye, L.; Tao, H.; Bo, Z. Autonomous Navigation Path Planning Algorithm for Rovers in Lunar South Pole Surface. J. Deep Space Explor. 2023, 10, 598–607. [Google Scholar]
- Tianyi, Y.; Jiangtao, F.; Lichun, L.; Xiao, C. Study on path planning method of lunar rover. J. Deep Space Explor. 2019, 6, 384–390. [Google Scholar]
- Zhou, R.; Liu, Y.; Hong, Z.; Pan, H.; Zhang, Y.; Han, Y.; Tao, J. A Safe and Efficient Global Path-Planning Method Considering Multiple Environmental Factors of the Moon Using a Distributed Computation Strategy. Remote Sens. 2025, 17, 924. [Google Scholar] [CrossRef]
- Ono, M.; Fuchs, T.J.; Steffy, A.; Maimone, M.; Yen, J. Risk-aware planetary rover operation: Autonomous terrain classification and path planning. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–10. [Google Scholar]
- Ge, S.S.; Cui, Y.J. Dynamic motion planning for mobile robots using potential field method. Auton. Robot. 2002, 13, 207–222. [Google Scholar] [CrossRef]
- Raja, R.; Dutta, A.; Venkatesh, K.S. New potential field method for rough terrain path planning using genetic algorithm for a 6-wheel rover. Robot. Auton. Syst. 2015, 72, 295–306. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Sanchez-Ibanez, J.R.; Pérez-del-Pulgar, C.J.; García-Cerezo, A. Path planning for autonomous mobile robots: A review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.-S.; Man, K.-F.; Kwong, S.; He, Q. Genetic algorithms and their applications. IEEE Signal Process. Mag. 1996, 13, 22–37. [Google Scholar] [CrossRef]
- Lanfeng, Z.; Lina, Y.; Hua, F. Lunar Rover Path Planning Based on Comprehensive Genetic Algorithm Based on Slip Prediction. J. Phys. Conf. Ser. 2019, 1267, 012097. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, W.; Zhang, X.; Cao, T. Path planning of lunar robot based on dynamic adaptive ant colony algorithm and obstacle avoidance. Int. J. Adv. Robot. Syst. 2020, 17, 1729881419898979. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Peng, S.; Jia, Y. Global path planning for lunar rover based on Particle Swarm Optimization algorithm. In Proceedings of the 2011 IEEE 5th International Conference on Robotics, Automation and Mechatronics (RAM), Qingdao, China, 17–19 September 2011; pp. 83–88. [Google Scholar]
- Wang, L.; Liu, L.; Lu, X. Robot Path Planning Based on Generative Learning Particle Swarm Optimization. IEEE Access 2024, 12, 130063–130072. [Google Scholar] [CrossRef]
- Seraji, H.; Bon, B. Autonomous Navigation of Planetary Rovers: A Fuzzy Logic Approach; JPL Internal Document; Jet Propulsion Laboratory: Pasadena, CA, USA, 1998.
- Zavlangas, P.G.; Tzafestas, S.G. Motion control for mobile robot obstacle avoidance and navigation: A fuzzy logic-based approach. Syst. Anal. Model. Simul. 2003, 43, 1625–1637. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ji, Y.; Yamashita, A.; Asama, H. Fuzzy based traversability analysis for a mobile robot on rough terrain. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3965–3970. [Google Scholar]
- Brooks, C.A.; Iagnemma, K. Self-supervised terrain classification for planetary surface exploration rovers. J. Field Robot. 2012, 29, 445–468. [Google Scholar] [CrossRef]
- Otsu, K.; Ono, M.; Fuchs, T.J.; Baldwin, I.; Kubota, T. Autonomous terrain classification with co-and self-training approach. IEEE Robot. Autom. Lett. 2016, 1, 814–819. [Google Scholar] [CrossRef]
- Zhang, H.; Dai, X.; Sun, F.; Yuan, J. Terrain classification in field environment based on Random Forest for the mobile robot. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 6074–6079. [Google Scholar]
- Fan, L.; Yuan, J.; Zha, K. TerSeg: A dual-branch semantic segmentation network for Mars terrain and autonomous path planning. Expert Syst. Appl. 2025, 270, 126397. [Google Scholar] [CrossRef]
- Rothrock, B.; Kennedy, R.; Cunningham, C.; Papon, J.; Heverly, M.; Ono, M. Spoc: Deep learning-based terrain classification for mars rover missions. In AIAA SPACE 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016; p. 5539. [Google Scholar]
- Tamar, A.; Levine, S.; Abbeel, P.; Wu, Y.; Thomas, G. Value Iteration Networks. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Pflueger, M.; Agha, A.; Sukhatme, G.S. Rover-IRL: Inverse Reinforcement Learning with Soft Value Iteration Networks for Planetary Rover Path Planning. IEEE Robot. Autom. Lett. 2019, 4, 1387–1394. [Google Scholar] [CrossRef]
- Hu, T.; Cao, T.; Zheng, B.; Zhang, H.; Ni, M. Large-scale Autonomous Navigation and Path Planning of Lunar Rover via Deep Reinforcement Learning. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 2050–2055. [Google Scholar]
- Hu, R.; Zhang, Y. Fast path planning for long-range planetary roving based on a hierarchical framework and deep reinforcement learning. Aerospace 2022, 9, 101. [Google Scholar] [CrossRef]
- Ram, A.; Boone, G.; Arkin, R.; Pearce, M. Using genetic algorithms to learn reactive control parameters for autonomous robotic navigation. Adapt. Behav. 1994, 2, 277–305. [Google Scholar] [CrossRef]
- Lanfeng, Z.; Lina, Y.; Hua, F. Research on slip prediction path planning based on an ant colony algorithm. J. East China Norm. Univ. 2020, 2020, 72. [Google Scholar]
- Katiyar, S.; Dutta, A. PSO based path planning and dynamic obstacle avoidance in CG space of a 10 DOF Rover. In Proceedings of the 2021 5th International Conference on Advances in Robotics, Kanpur, India, 30 June–3 July 2021; pp. 1–6. [Google Scholar]
- Howard, A.; Seraji, H.; Werger, B. Fuzzy terrain-based path planning for planetary rovers. In Proceedings of the 2002 IEEE World Congress on Computational Intelligence. 2002 IEEE International Conference on Fuzzy Systems, Honolulu, HI, USA, 12–17 May 2002; pp. 316–320. [Google Scholar]
- Garcia, A.; Barrientos Cruz, A.; Medina, A.; Colmenarejo, P.; Mollinedo, L.; Rossi, C. 3D Path planning using a fuzzy logic navigational map for Planetary Surface Rovers. In Proceedings of the 11 th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, The Netherlands, 12–14 April 2011. [Google Scholar]
- Tarokh, M. Hybrid intelligent path planning for articulated rovers in rough terrain. Fuzzy Sets Syst. 2008, 159, 2927–2937. [Google Scholar] [CrossRef]
- Nampoothiri, M.H.; Vinayakumar, B.; Sunny, Y.; Antony, R. Recent developments in terrain identification, classification, parameter estimation for the navigation of autonomous robots. SN Appl. Sci. 2021, 3, 480. [Google Scholar] [CrossRef]
- Peijian, Y.; Linzhi, M.; Jinan, M.; Qiang, W.; Ying, L.; Yu, D.; Shuo, W. Suggestions on artificial intelligence technology application and development in deep space exploration. J. Deep Space Explor. 2019, 6, 303–316, 383. [Google Scholar]
- Estlin, T.A.; Bornstein, B.J.; Gaines, D.M.; Anderson, R.C.; Thompson, D.R.; Burl, M.; Castano, R.; Judd, M. Aegis automated science targeting for the mer opportunity rover. ACM Trans. Intell. Syst. Technol. 2012, 3, 1–19. [Google Scholar] [CrossRef]
- Moreira, I.; Rivas, J.; Cruz, F.; Dazeley, R.; Ayala, A.; Fernandes, B. Deep reinforcement learning with interactive feedback in a human–robot environment. Appl. Sci. 2020, 10, 5574. [Google Scholar] [CrossRef]
- Ono, M.; Rothrock, B.; Otsu, K.; Higa, S.; Iwashita, Y.; Didier, A.; Islam, T.; Laporte, C.; Sun, V.; Stack, K. Maars: Machine learning-based analytics for automated rover systems. In Proceedings of the 2020 IEEE aerospace conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–17. [Google Scholar]
- Yutong, J.; Zhang, S.; Bin, L.; Kaichang, D.; Bin, X.; Jing, N.; Chenxu, Z.; Gang, W. A robust method for large-scale route optimization on lunar surface utilizing a multi-level map model. Chin. J. Aeronaut. 2025, 38, 103388. [Google Scholar]
- Chen, Y.; Wei, G.; Zhang, H.; Lu, J.; Pang, F. A Spatiotemporal U-Net-Based Data Preprocessing Pipeline for Sun-Synchronous Path Planning in Lunar South Polar Exploration. Remote Sens. 2025, 17, 1589. [Google Scholar] [CrossRef]
- Endo, M.; Taniai, T.; Ishigami, G. Deep Probabilistic Traversability with Test-time Adaptation for Uncertainty-aware Planetary Rover Navigation. arXiv 2024, arXiv:2409.00641. [Google Scholar]
- Meng, S.; Wang, Y.; Yang, C.-F.; Peng, N.; Chang, K.-W. Llm-a*: Large language model enhanced incremental heuristic search on path planning. arXiv 2024, arXiv:2407.02511. [Google Scholar]
- Xiao, L.; Yamasaki, T. LLM-Advisor: An LLM Benchmark for Cost-efficient Path Planning across Multiple Terrains. arXiv 2025, arXiv:2503.01236. [Google Scholar]
- Doma, P.; Arab, A.; Xiao, X. LLM-Enhanced Path Planning: Safe and Efficient Autonomous Navigation with Instructional Inputs. arXiv 2024, arXiv:2412.02655. [Google Scholar]
- Zhao, Y.; Wu, Q.; Wang, Y.; Tai, Y.-W.; Tang, C.-K. Dynamic Path Navigation for Motion Agents with LLM Reasoning. arXiv 2025, arXiv:2503.07323. [Google Scholar]
- Daftry, S.; Abcouwer, N.; Del Sesto, T.; Venkatraman, S.; Song, J.; Igel, L.; Byon, A.; Rosolia, U.; Yue, Y.; Ono, M. Mlnav: Learning to safely navigate on martian terrains. IEEE Robot. Autom. Lett. 2022, 7, 5461–5468. [Google Scholar] [CrossRef]
- Lu, S.; Xu, R.; Li, Z.; Wang, B.; Zhao, Z. Lunar Rover Collaborated Path Planning with Artificial Potential Field-Based Heuristic on Deep Reinforcement Learning. Aerospace 2024, 11, 253. [Google Scholar] [CrossRef]
- Gläser, P.; Scholten, F.; De Rosa, D.; Figuera, R.M.; Oberst, J.; Mazarico, E.; Neumann, G.; Robinson, M. Illumination conditions at the lunar south pole using high resolution Digital Terrain Models from LOLA. Icarus 2014, 243, 78–90. [Google Scholar] [CrossRef]
- De Rosa, D.; Bussey, B.; Cahill, J.T.; Lutz, T.; Crawford, I.A.; Hackwill, T.; van Gasselt, S.; Neukum, G.; Witte, L.; McGovern, A. Characterisation of potential landing sites for the European Space Agency’s Lunar Lander project. Planet. Space Sci. 2012, 74, 224–246. [Google Scholar] [CrossRef]









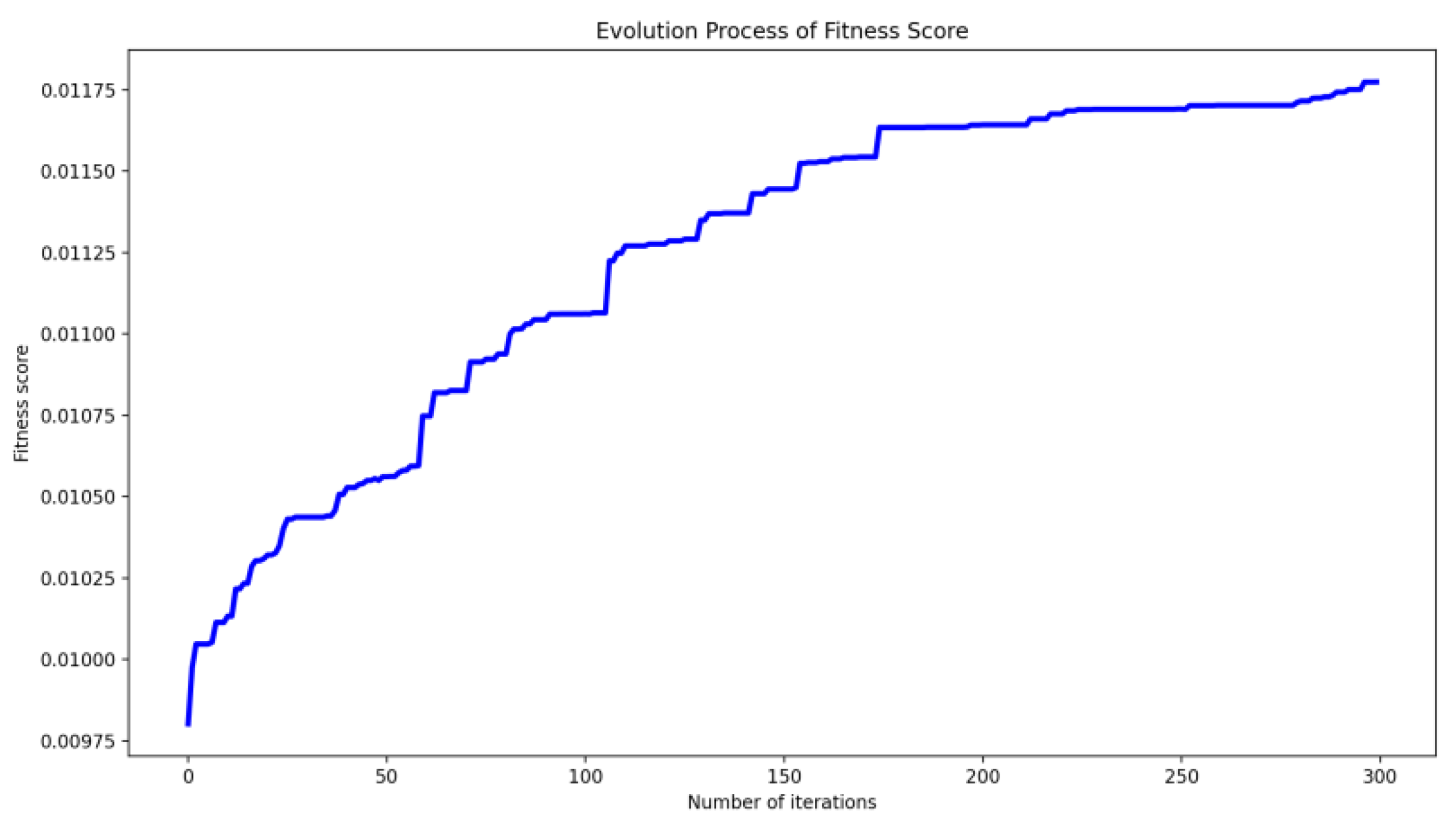
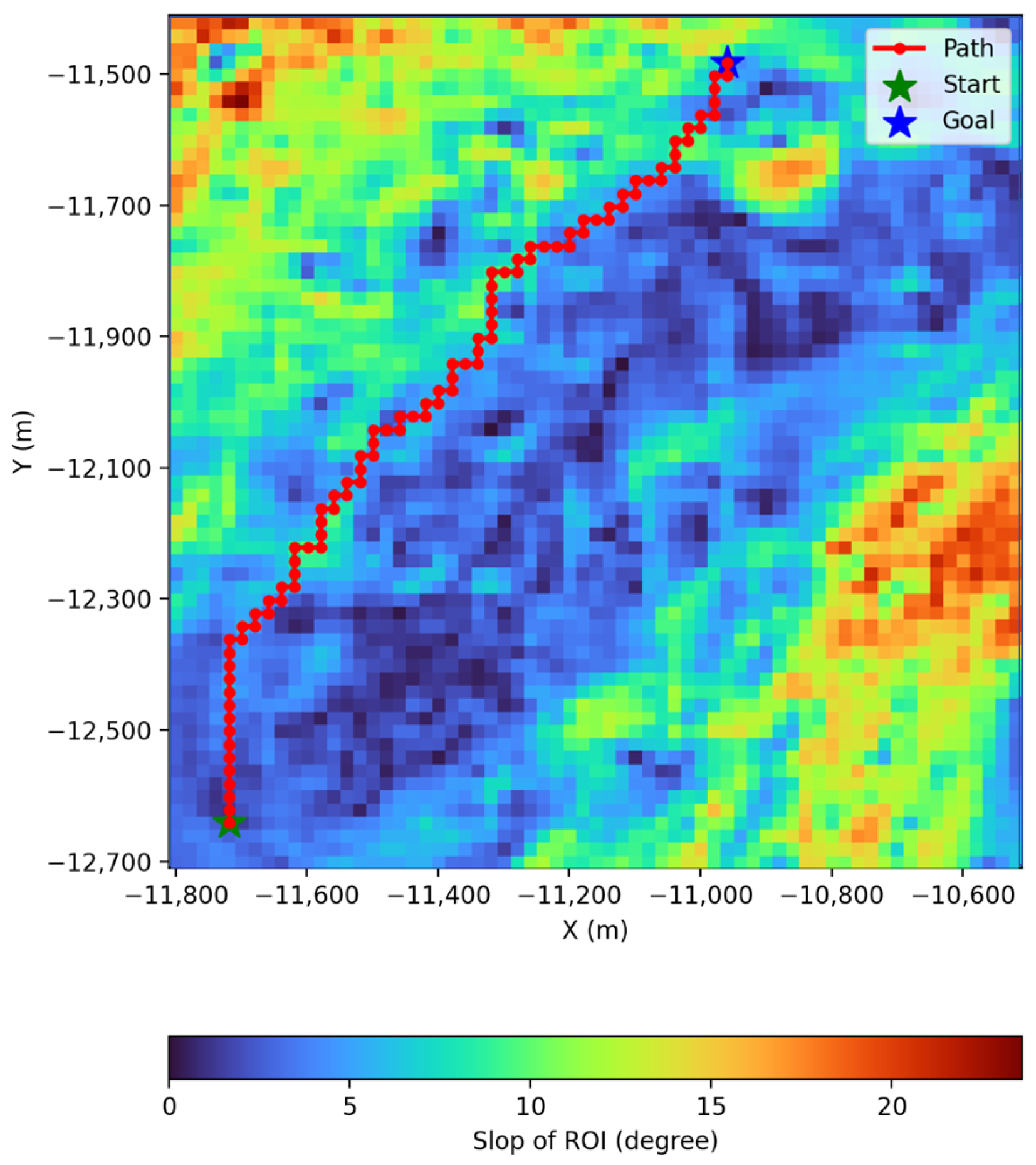

| External Environmental Constraints | Self-State Constraints | Concrete Algorithms | |||
|---|---|---|---|---|---|
| Publication | Static Constraints | Time-Varying Constraints | Structural Design Factors | Resource Constraints | |
| Bai et al. [34] | Slope | Lighting conditions | / | / | A* |
| Biesiadecki et al. [35] | Slope roughness | / | / | / | GESTALT |
| Chen et al. [36] | Terrain | / | Movement capabilities | / | Not mentioned |
| Iagnemma et al. [37] | Terrain roughness | / | Rover stability | / | A* |
| Sutoh et al. [15] | / | Insolation | Locomotion mechanism | / | Grid-based (e.g., Dijkstra’s algorithm) |
| Cunningham et al. [38] | / | Communication availability, illumination | / | Energy constraints | A* |
| INOUE et al. [39] | Slope | Illumination, communication | / | / | ROBUST-STP3R |
| Brunner et al. [40] | Rough terrain | / | Robot–terrain interaction | / | Not mentioned |
| Farritor et al. [41] | / | / | Wheel slip, vehicle stability | Power | Genetic algorithm |
| Tanaka et al. [32] | Slope | Illumination, temperature | / | Thermal, power status | Reinforcement learning algorithm |
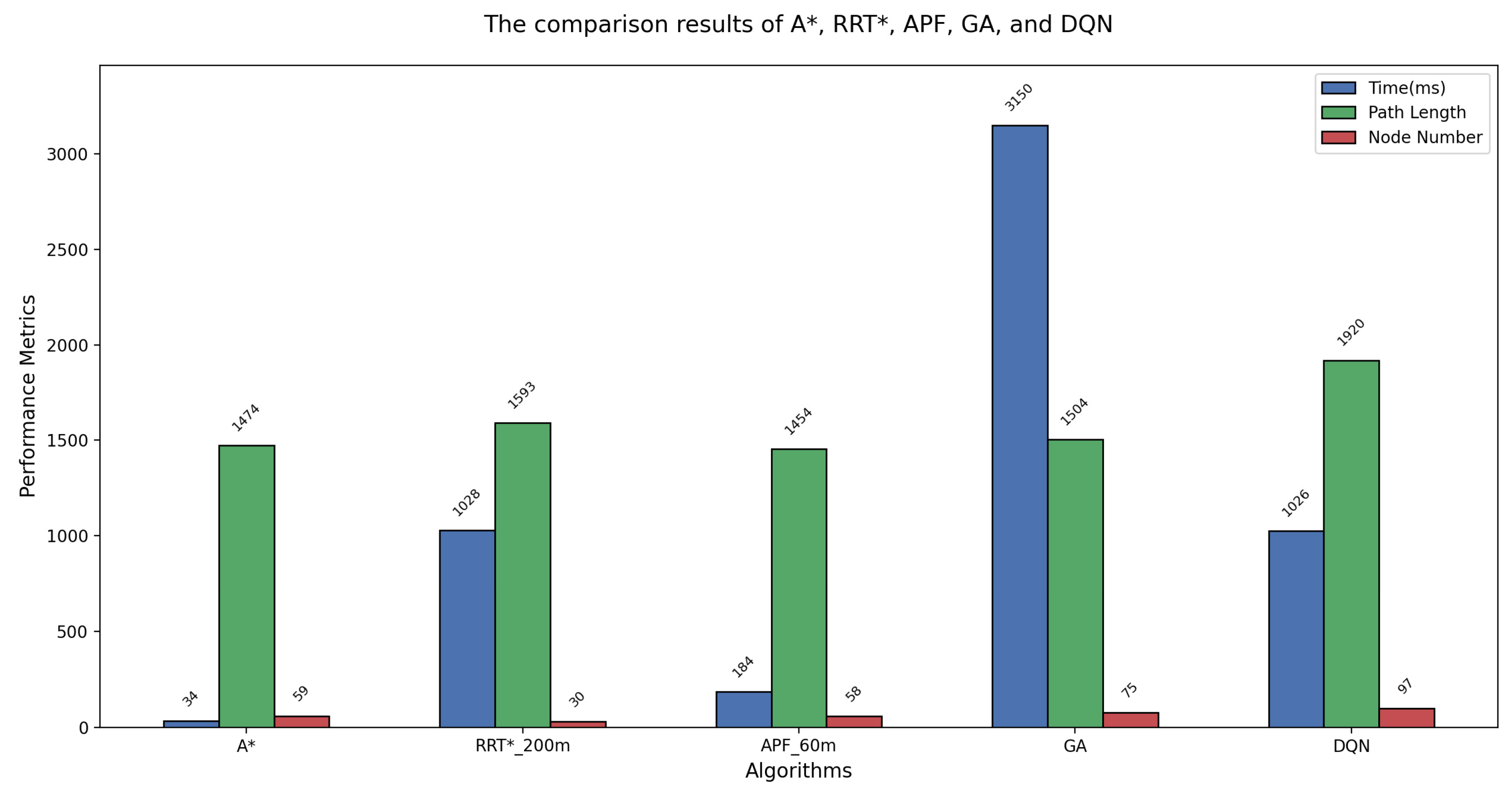
| Algorithms | Parameter Settings | Computation Time (ms) | Path Length (m) | Generated Node Number |
|---|---|---|---|---|
| A* | / | 34 | 1474 | 59 |
| RRT* | Initial parameter set to 200 m | 453 | 1623 | 11 |
| Initial parameter set to 100 m | 567 | 1609 | 19 | |
| Initial parameter set to 60 m | 1028 | 1593 | 30 | |
| APF | Step size set to 20 m | / | / | / |
| Step size set to 30 m | 184 | 1454 | 58 | |
| Step size set to 60 m | 88 | 1426 | 23 | |
| GA | Iterations set to 300 | 3150 | 1504 | 75 |
| DQN | / | 1026 | 1920 | 97 |
| Different Types of Algorithms | Advantages | Disadvantages | ||
|---|---|---|---|---|
| Rule-based Path-Planning Algorithms | Graph Search-based Algorithms | Simple | lower computational efficiency | |
| Potential Field-based Algorithms | 1. High computational efficiency. 2. Good real-time performance. 3. Suitable for dynamic environments. | Easy to get stuck in local minima. | ||
| Sampling-based Algorithms | Suitable for high-dimensional complex environments | 1. Slower convergence rates. 2. Sensitive to initial solutions. | ||
| Dynamic Window Approach | 1. High computational efficiency. 2. Good real-time performance. 3. Suitable for dynamic environments. | Easy to get stuck in local minima. | ||
| Biologically Inspired Path-Planning Algorithms | Evolutionary Learning | Strong adaptability to dynamic environments | 1. High consumption of computational resources. 2. Slower convergence speeds. | |
| Fuzzy Computation | Simple | Lack adaptability to complex dynamic environments. | ||
| Machine Learning-based Algorithms | Traditional Machine Learning Algorithms | Good environmental adaptability | 1. Require a large amount of data to train the models. 2. Significant computational resources and poor interpretability. 3. May lead to issues with path safety and model generalization | |
| Deep Learning-based Algorithms | Powerful feature extraction and processing capabilities | |||
| Reinforcement Learning-based Algorithms | Achieving end-to-end path planning | |||
| Category | Optimality | Completeness | Deterministic | Resource Requirement |
|---|---|---|---|---|
| Graph Search | optimal | Yes | Yes | Depends on graph size |
| APF | Sub-optimal | Not ensured | Yes | Low |
| Sampling-based | Asymptotical | Not ensured | No | Depends on sampling density and environmental complexity |
| DWA | Sub-optimal | Not ensured | Yes | Medium |
| Evolutionary Learning | Heuristic | Not ensured | No | Medium |
| Fuzzy Computation | Heuristic | Not ensured | No | Low |
| Machine Learning | Heuristic | Not ensured | No | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Q.; Wei, G. A Comprehensive Review of Path-Planning Algorithms for Planetary Rover Exploration. Remote Sens. 2025, 17, 1924. https://doi.org/10.3390/rs17111924
Miao Q, Wei G. A Comprehensive Review of Path-Planning Algorithms for Planetary Rover Exploration. Remote Sensing. 2025; 17(11):1924. https://doi.org/10.3390/rs17111924
Chicago/Turabian StyleMiao, Qingliang, and Guangfei Wei. 2025. "A Comprehensive Review of Path-Planning Algorithms for Planetary Rover Exploration" Remote Sensing 17, no. 11: 1924. https://doi.org/10.3390/rs17111924
APA StyleMiao, Q., & Wei, G. (2025). A Comprehensive Review of Path-Planning Algorithms for Planetary Rover Exploration. Remote Sensing, 17(11), 1924. https://doi.org/10.3390/rs17111924








