SSHFormer: Optimizing Spectral Reconstruction with a Spatial–Spectral Hybrid Transformer

Abstract

Reconstructing hyperspectral images (HSIs) from RGB images is an effective technique to overcome the high cost of spectrometers. Recently, Transformers have shown potential in capturing long-range dependencies for spectral reconstruction. However, few Transformer models attempt to simultaneously capture both spatial and spectral correlations in HSIs. Within this study, we introduce an integrated spatial–spectral hybrid Transformer (SSHFormer) framework designed to capture the interplay between spatial and spectral features in HSIs, with the aim of incrementally enhancing the fidelity of the reconstructed HSIs. In SSHFormer, we propose a spatial–spectral multi-head self-attention (SSMA) mechanism, which utilizes dilated convolution to extract non-local spatial features while maintaining parameter efficiency and applies the attention mechanism to the channel dimension to model inter-spectral correlations. Additionally, a 3D feedforward network (3DFFN) is proposed for SSHFormer, which leverages 3D convolution to fuse the spatial and spectral information, enabling more comprehensive feature extraction. Experimental results demonstrate that our SSHFormer achieves state-of-the-art (SOTA) performance on public datasets.

1. Introduction

Imaging systems can capture how light is distributed across various narrow spectral bands in a scene. Hyperspectral images (HSIs) provide detailed light intensity information in narrow spectral bands, while RGB images contain light intensity information in wide spectral bands. Recent works have demonstrated that the spectral reflectivity or radiometric distribution of HSIs can be predicted from RGB images, which presents a promising approach for acquiring HSIs at a lower cost. This technology has diverse applications, including remote sensing [1,2,3,4,5], medical imaging [6,7,8,9,10], object detection [11,12,13,14,15,16], and materials science [17,18,19,20].

In spectral reconstruction, intrinsic spectral and spatial relationships between RGB images and HSIs are often overlooked, leading to distortions or inaccuracies in the reconstructed HSIs. Despite recent advancements, existing Transformer-based methods in hyperspectral image reconstruction still face significant limitations. These methods struggle with computational cost and scalability when dealing with high-dimensional hyperspectral data. While Transformers excel at capturing long-range dependencies, their performance deteriorates as the dimensionality of the hyperspectral data increases, leading to high memory and computational requirements. This makes it difficult to efficiently process large-scale HSI datasets.

To overcome these fundamental limitations, we propose an innovative cascaded spatial–spectral hybrid Transformer (SSHFormer) framework, specifically engineered to capture and represent the complex spatial–spectral correlations inherent in HSIs. Our framework distinguishes itself from conventional Transformer architectures through its novel spatial–spectral attention mechanism, which achieves remarkable computational efficiency while preserving high reconstruction fidelity. The framework’s sophisticated multi-scale fusion mechanism enables precise preservation of spectral details across different scales, substantially enhancing the quality of reconstructed images. This design allows for efficient processing of high-dimensional data while maintaining exceptional reconstruction accuracy.

Although there have been advancements in Transformer models for hyperspectral image reconstruction, previous approaches have not adequately addressed the scalability and computational efficiency challenges when handling high-dimensional hyperspectral data. By introducing a targeted approach that balances long-range dependency modeling with computational efficiency, our work bridges this gap and offers a more efficient and accurate solution for spectral reconstruction tasks.

It has been demonstrated that HSIs exhibit both inter-spectral correlations [21,22] and non-local spatial similarity [23]. By utilizing inter-spectral correlations, the robustness and accuracy of spectral reconstruction can be enhanced. To this end, we introduce the spectral-wise multi-head self-attention (S-MSA) mechanism to capture inter-spectral correlations. In S-MSA, each spectral band is considered as an individual feature, and the attention mechanism computes the relationships between these bands, effectively modeling inter-spectral dependencies. Additionally, we utilize dilated convolution to capture non-local spatial similarity. Dilated convolution can expand the receptive field without increasing parameters compared to traditional convolution, thereby better capturing long-range dependencies. By incorporating S-MSA and dilated convolution, we develop a spatial–spectral multi-head self-attention (SSMA) mechanism that can capture both spectral and spatial correlations.

Furthermore, fusing spectral and spatial information is crucial for accurate reconstruction. Although the feedforward network (FFN) is a key component in Transformers, most modern Transformers focus on the design of attention mechanisms, often neglecting the design of the FFN. Three-dimensional convolution has demonstrated superior inductive bias for fusing spatial and channel information. Therefore, we propose a 3DFFN to fuse spatial and channel information by incorporating 3D convolution into FFN, thereby enhancing the performance of HSI reconstruction.

We propose a cascaded SSHFormer framework for spectral reconstruction that effectively models spectral-spatial correlations of HSIs. Our framework features two innovations: (1) an SSMA mechanism with dilated convolution and S-MSA for feature extraction, and (2) a 3DFFN using 3D convolution for information fusion. Experiments show that SSHFormer achieves state-of-the-art performance with reduced computational requirements.

The essence of our contributions is as outlined below:

• We present a cascaded SSHFormer for spectral reconstruction, which models both spectral and spatial correlations of HSIs and progressively improves the quality of reconstructed HSIs.
• We propose an SSMA mechanism to employ inter-spectral correlations and non-local spatial similarities.
• We design a novel 3DFFN for SSHFormer, which simultaneously fuses the spectral and spatial information of HSIs.
• The proposed SSHFormer surpasses state-of-the-art (SOTA) methods with lower memory and computational costs on public datasets.

2. Materials and Methods

2.1. Related Work

2.1.1. Spectral Reconstruction

Traditional spectral reconstruction approaches predominantly rely on handcrafted priors. Zhang et al. [24] introduced an HSI reconstruction method based on extending data sparsity, which effectively captures the inherent sparsity of spectral signatures. Arad et al. [25] introduced a sparse coding method aimed at creating a dictionary that maps HSI signals to their corresponding RGB image representations, demonstrating the effectiveness of dictionary learning in spectral reconstruction. Aeschbacher et al. [26] suggested employing a relatively shallow learning model for specific spectra to achieve spectral reconstruction, which showed promising results on controlled scenarios. However, these model-driven approaches face several limitations. Handcrafted priors struggle to capture complex spectral variations, making these methods less effective in natural, diverse scenes. Additionally, they often exhibit poor generalization, with performance degrading significantly in unseen scenarios with changing lighting conditions or material properties. Furthermore, their rigid feature extraction mechanisms lack adaptability, preventing them from effectively learning complex spectral–spatial dependencies from data.

In recent times, drawing motivation from the remarkable achievements of deep learning, convolutional neural networks (CNNs) have been utilized to develop mapping algorithms that translate an RGB image into an HSI. For instance, Xiong et al. [27] introduced an integrated HSCNN model aimed at reconstructing HSIs from both RGB and measurement images, which leverages the complementary information from multiple sources. Shi et al. [28] developed a deep residual network, HSCNN-R, utilizing enhanced residual blocks to facilitate gradient flow and enable deeper network architectures. Zhang et al. [29] developed a hybrid network with pixel-aware depth-functional capabilities for modeling the reconstruction from RGB images to HSIs, which adaptively adjusts the network’s behavior based on local image characteristics. Despite these advancements, CNN-based approaches still face fundamental challenges. Their limited receptive field, due to the reliance on localized convolutional filters, makes it difficult to capture long-range dependencies in both spectral and spatial dimensions. Moreover, they struggle to model non-local similarities effectively, as spectral features often exhibit self-similarity across different spatial locations, which CNNs fail to explicitly account for. Additionally, many CNN architectures treat spectral bands as independent features, neglecting the global spectral relationships that are crucial for accurate reconstruction.

2.1.2. Vision Transformer

Vision Transformer (ViT) [30] successfully extends techniques from natural language processing to computer vision tasks. The model effectively captures both local and global image characteristics by dividing the image into several smaller patches and treating them as visual tokens. It then employs a self-attention mechanism to analyze these patches, thereby enhancing feature extraction and enabling the model to capture long-range dependencies that are difficult for CNNs to model.

As an extension of ViT, Swin Transformer [31] combines the self-attention mechanism of Transformers with the hierarchical feature extraction ability of CNNs, introducing a sliding window mechanism and hierarchical design. This architecture effectively reduces the computational complexity and makes the model adapt to images of different scales. The sliding window mechanism computes self-attention within non-overlapping local regions while enabling interaction between windows through shifted window partitioning. The hierarchical structure progressively expands the receptive field across multiple stages, allowing for feature extraction at different scales and maintaining computational efficiency.

Transformers have also been introduced into HSI reconstruction with promising results. Cai et al. proposed a reconstruction model MST++ [21] based on Vision Transformer, which effectively captures the global correlation between different spectral bands using its global attention mechanism and achieves superior performance in spectral fidelity. Zamir et al. proposed Restormer [32], an efficient Transformer-based image restoration network through the interaction of local and global features, demonstrating the potential of self-attention mechanisms in image restoration tasks. These Transformer-based models overcome the shortcomings of traditional CNN methods in capturing long-range dependence, and exhibit stronger generalization ability and higher reconstruction accuracy.

While Transformer-based models show strong potential in HSI reconstruction, their high computational cost and lack of inherent spectral–spatial inductive bias limit scalability and generalization. Unlike CNNs, which leverage local connectivity, Transformers process images as token sequences, potentially missing fine-grained spectral correlations. Moreover, most existing approaches focus on global spectral dependencies while overlooking non-local spatial similarities, which are crucial for robust spectral reconstruction.

2.1.3. 3D Convolution in Spectral Analysis

Three-dimensional convolution has emerged as a powerful tool for analyzing multi-dimensional data, particularly in spectral imaging applications. Unlike 2D convolution, which operates on spatial dimensions only, 3D convolution processes both spatial and spectral dimensions simultaneously, making it particularly suitable for HSI analysis. Ji et al. [33] pioneered the use of 3D CNNs for video analysis, demonstrating their effectiveness in capturing spatio-temporal correlations. This concept has been adapted for HSI processing, where the temporal dimension is replaced by the spectral dimension. Roy et al. [34] proposed a 3D CNN architecture for HSI classification that effectively leverages both spatial and spectral information. Chen et al. [35] developed a hybrid 2D-3D CNN framework that combines the advantages of both convolution types for HSI feature extraction. These works demonstrate the potential of 3D convolution in capturing the intricate relationships between spatial and spectral dimensions in HSI data, motivating our design of the 3DFFN module.

2.2. Method

2.2.1. Challenges and Motivations

Before delving into the specific methodology, it is essential to analyze the key challenges faced by traditional approaches in hyperspectral image reconstruction: (1) Limited receptive field: Traditional convolutions struggle to capture long-range spatial dependencies, impacting reconstruction quality in complex regions. (2) Feature decoupling: Existing methods often process spatial and spectral features separately, overlooking their intrinsic correlations and leading to suboptimal results. (3) Computational inefficiency: Expanding the receptive field typically requires deep stacking, increasing computational overhead and limiting practical deployment.

To address these challenges, our proposed SSHFormer framework incorporates several innovative designs: (1) A hybrid design combining dilated convolution and attention mechanisms, capturing broad contextual information efficiently without excessive parameters. (2) A 3DFFN module that jointly models spatial–spectral features, preserving their intricate relationships for more comprehensive representations. (3) Depth-wise separable architectures, optimizing computational efficiency while maintaining strong feature extraction capabilities.

These design choices form the foundation of our SSHFormer framework, which will be detailed in the following sections. Our approach represents a significant advancement in addressing the limitations of existing methods while maintaining practical efficiency considerations.

2.2.2. Mathematical Model of Spectral Reconstruction

Spectral reconstruction aims to recover a high-dimensional hyperspectral image (HSI) from a low-dimensional RGB image. This process can be formulated as reconstructing an HSI $I_{HSI}\in R^{C\times H\times W}$ from an RGB image $I_{RGB}\in R^{3\times H\times W}$, where C represents the number of spectral bands in $I_{HSI}$, and $H\times W$ denotes its spatial dimensions. The relationship between RGB images and HSIs can be described by the following imaging model:

$$I_{RGB}(r,h,w)=\sum _{c=1}^C{\mathrm{\Phi }}_{r,c}{I}_{HSI}(c,h,w)+\epsilon (r,h,w),$$

(1)

where $\mathrm{\Phi }\in {\mathbb{R}}^{3\times C}$ represents the spectral response matrix of the RGB camera sensor, with ${\mathrm{\Phi }}_{r,c}$ denoting the response of the r-th RGB channel ($r\in \{1,2,3\}$) to the c-th spectral band ($c\in \{1,...,C\}$). The term $\epsilon (r,h,w)\in {\mathbb{R}}^{3\times H\times W}$ represents the measurement noise. The spectral response function $\mathrm{\Phi }$ characterizes how the camera’s RGB sensors respond to different wavelengths of light.

The spectral reconstruction process can be expressed as an inverse problem:

$$I_{HSI}=f\left(I_{RGB};\theta \right)+n,$$

(2)

where $f(·;\theta )$ represents a parameterized non-linear mapping function typically modeled by deep neural networks, and n denotes reconstruction error that may occur due to information loss or model approximation. This inverse problem is inherently ill-posed due to the significant dimension gap between input and output (from 3 to C spectral bands, where C typically ranges from 20 to 200 in hyperspectral images).

The mapping function f can be implemented using deep learning models, which learn to recover the lost spectral information by exploiting the following:

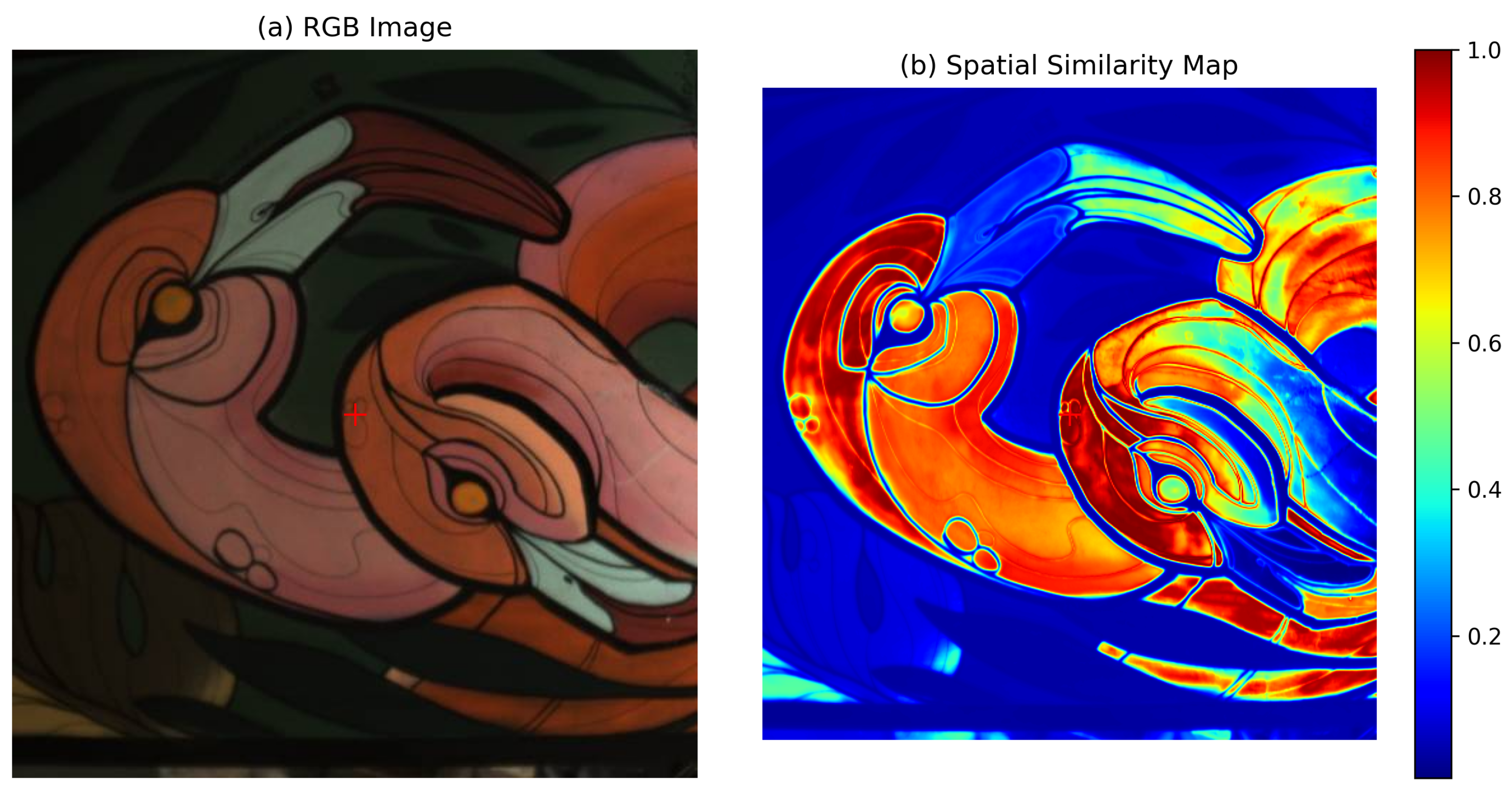
(1) Spectral Correlations: Adjacent spectral bands typically exhibit strong correlations, as illustrated in Figure 1b.

$$R_{spec}(b_i,b_j)={\displaystyle \frac{{\sum }_{h,w}(I_{HSI}(i,h,w)-{\mu }_i)(I_{HSI}(j,h,w)-{\mu }_j)}{\sqrt{{\sum }_{h,w}{(I_{HSI}(i,h,w)-{\mu }_i)}^2}\sqrt{{\sum }_{h,w}{(I_{HSI}(j,h,w)-{\mu }_j)}^2}}},$$

(3)

where $R_{spec}$ measures the Pearson correlation coefficient between spectral bands $b_i$ and $b_j$, $I_{HSI}(i,h,w)$ and $I_{HSI}(j,h,w)$ are the pixel values of the bands $b_i$ and $b_j$ at position $(h,w)$, and ${\mu }_i$ and ${\mu }_j$ are the mean values of bands $b_i$ and $b_j$, respectively.

(2) Spatial Dependencies: Natural images often contain recurring patterns and self-similarities at different spatial locations. These spatial dependencies, illustrated in Figure 2b, can be expressed as follows:

$$R_{spat}\left(p_1,p_2\right)=\sum _{c=1}^C{∥I_{HSI}\left(c,p_1\right)-I_{HSI}\left(c,p_2\right)∥}_2^2,$$

(4)

where $R_{spat}$ measures the similarity between spatial positions $p_1$ and $p_2$.

The quality of reconstruction can be evaluated using various metrics:

(1) Mean Relative Absolute Error (MRAE):

$$MRAE={\displaystyle \frac{1}{CHW}}\sum _{c,h,w}{\displaystyle \frac{\left|I_{HSI}\left(c,h,w\right)-f\left(I_{RGB}\right)\left(c,h,w\right)\right|}{\left|I_{HSI}\left(c,h,w\right)\right|}}$$

(5)

MRAE measures the relative pixel-wise differences between the reconstructed and ground truth HSIs. This metric is particularly useful when dealing with varying intensity levels across different spectral bands, as it normalizes the error by the ground truth value. A lower MRAE indicates better reconstruction quality.

(2) Root Mean Square Error (RMSE):

$$RMSE=\sqrt{{\displaystyle \frac{1}{CHW}}\sum _{c,h,w}{\left(I_{HSI}\left(c,h,w\right)-f\left(I_{RGB}\right)\left(c,h,w\right)\right)}^2}$$

(6)

RMSE provides a measure of the absolute differences between predicted and actual values, with larger errors being penalized more heavily due to the squared term. This metric is sensitive to outliers and gives a good indication of reconstruction accuracy in the original data scale.

(3) Peak Signal-to-Noise Ratio (PSNR):

$$PSNR=10{log}_{10}\left({\displaystyle \frac{MA{X}_I^2}{MSE}}\right)$$

(7)

where $MSE$ is the mean squared error and $MA{X}_I$ is the maximum possible pixel value. PSNR is widely used in image processing to assess the quality of reconstruction, with higher values indicating better quality. It is expressed in decibels (dB) and is particularly useful when comparing results across different datasets.

These metrics provide complementary perspectives on the reconstruction quality, with MRAE focusing on relative errors, RMSE on absolute differences, and PSNR on the signal-to-noise ratio.

2.2.3. Overall Architecture

The proposed SSHFormer framework comprises several key components designed for hyperspectral image reconstruction from RGB images. The overall architecture is illustrated in Figure 3, consisting of three main stages: initial noise purification, feature extraction and transformation, and progressive spectral reconstruction.

First, a Non-Local Purification Module (NPM) [36] is employed to remove unwanted noise from RGB images. The NPM utilizes a hierarchical pyramid structure to capture multi-scale information. By leveraging non-local information, the module adapts and adjusts pixel values based on the surrounding context, removes artifacts through multi-scale feature aggregation, and provides cleaner input features for subsequent spectral reconstruction.

Following the NPM, a Spatial–Spectral U-shaped network (SSU) is constructed, incorporating Spatial–Spectral Attention Blocks (SSABs) to process and enhance the image data. Multiple SSUs are then cascaded to progressively improve the quality and visual fidelity of reconstructed HSIs.

As shown in Figure 3a, the complete SSHFormer architecture consists of an initial NPM for noise reduction, two 3 × 3 convolution layers for feature extraction, N cascaded SSUs for progressive reconstruction, and global residual connections to facilitate gradient flow during training.

The structure of the SSU is detailed in Figure 3b. Each SSU comprises an embedding layer, an encoder path, a bottleneck, a decoder path, and a mapping layer. Both embedding and mapping layers are implemented as 3 × 3 convolution layers for initial feature transformation and final spectral reconstruction, respectively.

The encoder path consists of three stages, each performing downsampling through 4 × 4 strided convolution followed by $N_1$, $N_2$, and $N_3$ SSABs for the respective stages. The bottleneck contains $N_4$ SSABs for comprehensive feature processing. The decoder mirrors the encoder structure but uses 2 × 2 strided transposed convolution for upsampling. Skip connections between corresponding encoder and decoder levels prevent information loss during downsampling operations.

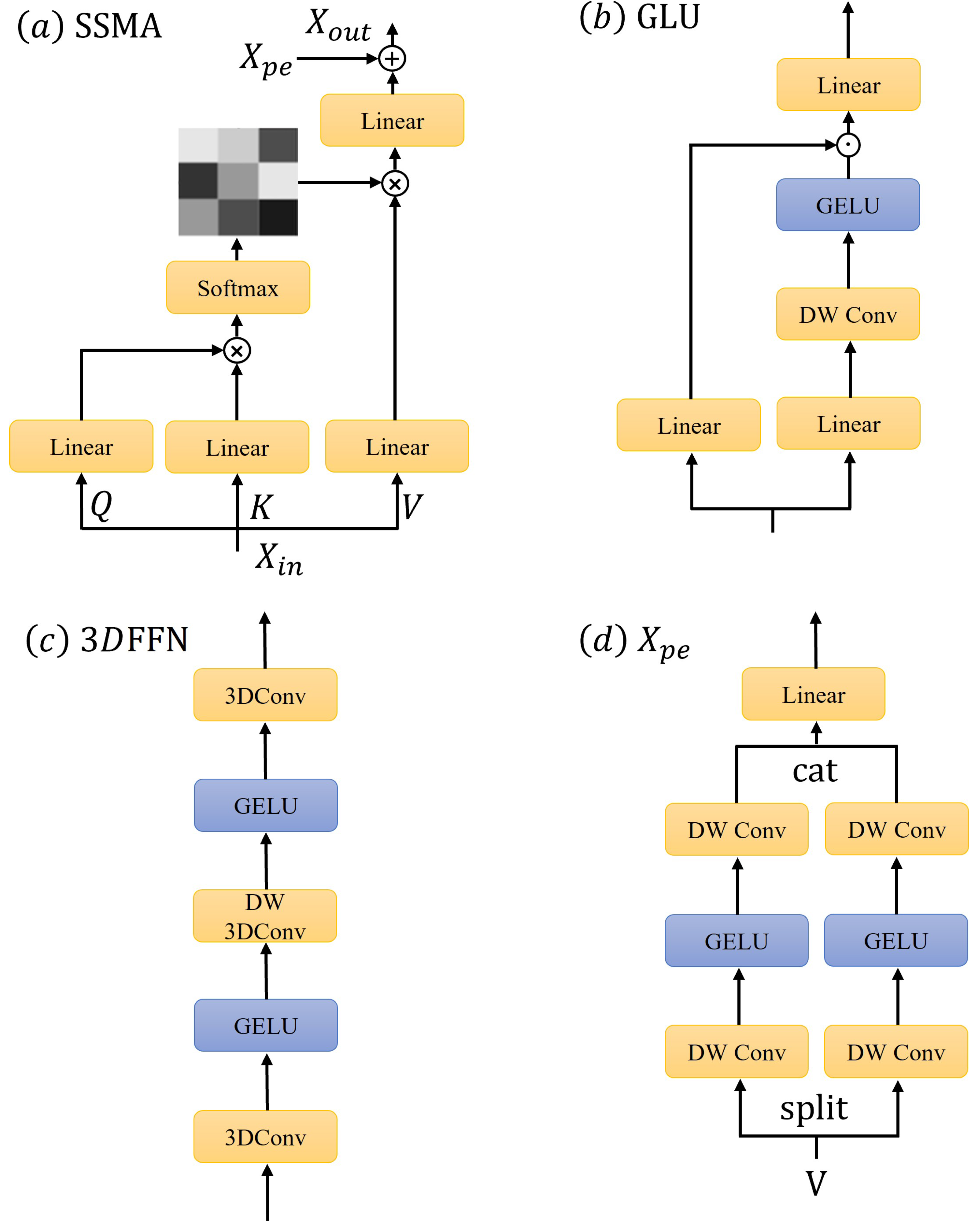
The SSAB, illustrated in Figure 3c, is designed to effectively process both spatial and spectral information. Its core structure includes an SSMA module for joint spatial–spectral attention, a Gated Linear Unit (GLU) [37] for adaptive feature gating, a 3DFFN for feature transformation, and LayerNorm with residual connections for stable training.

The mathematical formulation of SSAB can be expressed as a sequence of transformations with residual connections:

$$Z_l^{\prime }=SSMA\left(Z_{l-1}\right)+Z_{l-1},$$

(8)

where $Z_{l-1}$ represents the input features at layer l, and $SSMA(·)$ denotes the spatial–spectral multi-head attention operation. The residual connection $+Z_{l-1}$ helps maintain gradient flow during training.

$$Z_l^{\prime \prime }=GLU\left(LN\left(Z_l^{\prime }\right)\right)+Z_l^{\prime },$$

(9)

where $LN(·)$ represents the Layer Normalization operation that stabilizes the feature distribution, and $GLU(·)$ is the Gated Linear Unit that adaptively controls information flow through the network.

$$Z_l=3DFFN\left(LN\left(Z_l^{\prime \prime }\right)\right)+Z_l^{\prime \prime },$$

(10)

where $3DFFN(·)$ denotes the 3D FeedForward Network that jointly processes spatial and spectral information. The complete transformation sequence can be summarized as follows:

$$Z_l={\mathcal{F}}_{SSAB}\left(Z_{l-1}\right)={\mathcal{F}}_{3DFFN}\circ {\mathcal{F}}_{GLU}\circ {\mathcal{F}}_{SSMA}\left(Z_{l-1}\right),$$

(11)

where ∘ denotes function composition, and ${\mathcal{F}}_{SSAB}$ represents the complete SSAB transformation.

The dimensions of the intermediate features are preserved throughout these operations: $Z_{l-1},Z_l^{\prime },Z_l^{\prime \prime },Z_l\in {\mathbb{R}}^{C\times H\times W}$, where C denotes the number of channels, and H and W represent the spatial height and width.

Each component serves a specific purpose in the SSAB:

• SSMA captures long-range dependencies in both spatial and spectral domains.
• GLU performs adaptive feature selection through its gating mechanism.
• 3DFFN enables efficient fusion of spatial–spectral information.
• Layer Normalization and residual connections ensure stable training and effective gradient propagation.

It is worth noting that the downsampling operation utilized by the SSHFormer framework offers several advantages over conventional methods. Unlike traditional approaches that typically double the number of channels during downsampling, SSHFormer maintains the number of channels while effectively halving the spatial resolution. This innovative approach significantly reduces the model’s parameters, leading to a more efficient architecture. By maintaining the channel count, SSHFormer ensures that the rich spectral information is preserved, which is crucial for accurate hyperspectral image reconstruction. Additionally, this method enhances computational efficiency, allowing for faster processing times and reduced memory usage, making it particularly suitable for large-scale applications and real-time processing scenarios. The streamlined architecture not only facilitates easier deployment on resource-constrained devices but also contributes to the overall robustness and scalability of the model.

2.2.4. Spatial–Spectral Multi-Head Self-Attention

Based on our analysis of traditional methods’ limitations, we present the design rationale for the SSMA module. The multi-head attention mechanism serves as the core structure for several key reasons: First, its ability to simultaneously focus on multiple feature subspaces makes it particularly effective for handling complex spectral relationships. Second, the incorporation of dilated convolutions enables the expansion of the receptive field while maintaining parameter efficiency. Third, compared to traditional convolutional methods, this approach demonstrates superior capability in capturing long-range dependencies. These combined properties allow the SSMA module to effectively address the inherent limitations of conventional approaches, particularly their restricted receptive fields and feature separation issues.

The SSMA mechanism, depicted in Figure 4a, is a core component of the SSAB, designed to capture complex dependencies across both spatial and spectral dimensions. The process begins by reshaping the input $X_{in}\in R^{H\times W\times C}$ into a sequence of tokens $X\in R^{HW\times C}$. This transformation facilitates the application of attention mechanisms by treating each spatial location as a token.

Subsequently, the query (Q), key (K), and value (V) matrices are derived from the input tokens through linear transformations:

$$Q=W^{Q}X,K=W^{K}X,V=W^{V}X,$$

(12)

where $W^Q,W^K,$ and $W^V$ are learnable weight matrices. These matrices are then partitioned into N heads along the channel dimension, resulting in $Q=\left[Q_1,\dots ,Q_N\right]$, $K=\left[K_1,\dots ,K_N\right]$, and $V=\left[V_1,\dots ,V_N\right]$. Each head has a dimensionality of $d={\displaystyle \frac{C}{N}}$, allowing the model to attend to information from multiple representation subspaces.

The attention mechanism for each head is computed as follows:

$$Att{n}_j\left(Q_j,K_j,V_j\right)=V_j·\mathrm{Softmax}\left({\displaystyle \frac{K_j^T{Q}_j}{{\alpha }_j}}\right),$$

(13)

where ${\alpha }_j$ is a trainable scaling factor that adjusts the magnitude of the dot product between K and Q before the softmax operation, ensuring numerical stability and effective gradient flow.

The outputs from all heads are concatenated and linearly transformed to produce the final output:

$$X_{out}=\left({\mathrm{Concat}}_{j=1}^N\left(Att{n}_j\left(Q_j,K_j,V_j\right)\right)\right)W+X_{pe},$$

(14)

where $W\in R^{C\times C}$ is a learnable projection matrix. The positional encoding $X_{pe}$, shown in Figure 4d, is integrated to provide spatial context, enhancing the model’s ability to capture positional information without increasing computational complexity. This is achieved by incorporating dilated convolutions, which expand the receptive field.

The positional encoding $X_{pe}$ is computed by splitting V into two parts along the spectral dimension: $V=\left[V^1,V^2\right]$. The encoding is then expressed as follows:

$$X_{pe}=f\left(\mathrm{Concat}\left(f_1\left(V^1\right),f_2\left(V^2\right)\right)\right),$$

(15)

where $f_1$ consists of two depthwise 3 × 3 convolution layers followed by a GELU activation, and $f_2$ comprises two depthwise dilated 3 × 3 convolution layers with a dilation rate of three and a GELU activation. The function $f\left(·\right)$ is a linear projection layer that consolidates the processed features into the positional encoding.

This sophisticated attention mechanism allows the SSMA to effectively model intricate spatial–spectral relationships, enhancing the overall performance of the SSHFormer framework in hyperspectral image reconstruction tasks.

2.2.5. Gated Linear Unit

The GLU is an advanced activation mechanism that enhances neural network expressiveness through a sophisticated gating mechanism. Originally introduced in [37] for language modeling, GLU has proven effective across various deep learning applications, particularly in image processing and spectral reconstruction tasks.

As illustrated in Figure 4b, GLU operates by splitting the input feature into two components. The general mathematical formulation of GLU is given by the following:

$$GLU\left(x\right)=x\odot \sigma (Wx+b)$$

(16)

where x represents the input feature, ⊙ denotes element-wise multiplication, $\sigma$ is the sigmoid activation function, and W and b are learnable parameters. This gating mechanism enables selective feature propagation, effectively filtering out less relevant information while preserving crucial features. The design’s ability to modulate information flow also helps mitigate vanishing gradient issues in deep architectures.

The GLU mechanism shares conceptual similarities with the gating structures in recurrent neural networks (LSTM and GRU), where gates control information retention. In our hyperspectral image processing context, GLU enhances the model’s ability to capture complex spectral–spatial relationships through improved non-linear feature representation. For clarity, it should be noted that while our implementation leverages the core idea of GLU, it is based on the convolutional variant. This distinction is important because the convolutional GLU is tailored to exploit local contextual information, making it particularly well suited for image and spectral data where spatial locality is critical.

2.2.6. Spatial–Spectral Fusion Feedforward Network

The 3DFFN module is designed with 3D convolutions to efficiently fuse spatial and spectral information. This design choice is motivated by three key factors: 3D convolutions naturally process spatial and spectral data simultaneously, maintain better feature continuity than cascaded 2D convolutions, and use depthwise separable operations to reduce computational complexity.

The 3DFFN, depicted in Figure 4c, is a critical component of the SSAB, designed to effectively integrate spatial and spectral information. This network architecture leverages the power of 3D convolutions to process data across three dimensions: height, width, and spectral depth.

The 3DFFN comprises two GELU (Gaussian Error Linear Unit) activation layers, a depthwise 3D convolution (3DConv) with a kernel size of 3 × 3 × 3, and two pointwise 3D convolutions. The inclusion of 3DConv extends the capabilities of traditional 2D convolutions by incorporating an additional depth dimension, which is essential for capturing the intricate relationships present in hyperspectral data.

The 3D convolution operation aggregates visual information across both spatial and spectral domains, allowing the network to abstract features across multiple dimensions (spatial and spectral). This multi-dimensional feature abstraction is crucial for capturing detailed textures and structures that are often present in hyperspectral images. By processing data in three dimensions, the 3DFFN can effectively model the complex interactions between different spectral bands and spatial locations, leading to more accurate and robust feature representations.

Furthermore, the use of depthwise convolutions in the 3DFFN reduces the computational complexity while maintaining the ability to capture essential features. This efficiency is particularly beneficial for large-scale hyperspectral datasets, where computational resources can be a limiting factor.

The pointwise 3D convolutions serve to refine the features extracted by the depthwise 3DConv, ensuring that the final output is both rich in detail and computationally efficient. This combination of depthwise and pointwise convolutions allows the 3DFFN to balance the trade-off between computational efficiency and feature richness, making it an ideal choice for hyperspectral image processing tasks.

Overall, the 3DFFN enhances the SSHFormer framework’s ability to process and interpret complex hyperspectral data, contributing to improved performance in tasks such as classification, segmentation, and reconstruction.

3. Results

3.1. Datasets and Implementation Details

To comprehensively evaluate the effectiveness of our proposed network, we conducted experiments on two well-established hyperspectral datasets, ensuring fairness and consistency across all experimental conditions.

The first dataset was sourced from the NTIRE 2022 Spectral Recovery Challenge [38]. This dataset comprises 1000 pairs of RGB images and their corresponding HSIs. The dataset was meticulously divided into training, validation, and test sets with an 18:1:1 ratio, ensuring a robust evaluation framework. Each HSI in this dataset has a spatial resolution of 482 × 512 pixels and includes 31 spectral bands, covering wavelengths from 400 nm to 700 nm. This wide spectral range allows for a detailed analysis of the spectral recovery capabilities of our network.

The second dataset, known as CAVE [39], consists of 32 HSIs, each with 31 spectral bands spanning the same wavelength range of 400 nm to 700 nm. For our experiments, we randomly selected 20 HSIs for training, 6 for validation, and 6 for testing. This selection strategy ensures that the model is trained on a diverse set of scenes, enhancing its generalization ability across different spectral and spatial contexts.

In terms of implementation, our network was developed using the PyTorch 1.8.0 framework, which provides a flexible and efficient platform for deep learning research. We utilized NVIDIA GPUs to accelerate the training process, allowing for rapid experimentation and fine-tuning of model parameters. The training was conducted with a batch size of 16, and the learning rate was initially set to 0.001, with a decay factor applied every 10 epochs to ensure convergence.

Data augmentation techniques, such as random cropping, flipping, and rotation, were employed to increase the diversity of the training data and prevent overfitting. These techniques are crucial for enhancing the robustness of the model, enabling it to perform well on unseen data. For reproducibility, the following hyperparameters were used for data augmentation: images were randomly cropped to a size of $128\times 128$ pixels, with a $0.5$ probability of horizontal and vertical flipping, and rotation angles randomly chosen from the set [0°,90°,180°,270°].

To ensure fairness in all experiments, we maintained consistent training and evaluation protocols across both datasets. This included using the same data augmentation strategies, training parameters, and evaluation metrics. By standardizing these aspects, we ensured that the performance comparisons between different models and datasets were unbiased and reliable. Additionally, for each comparative method, we employed the best-performing learning rate as reported in the original papers to ensure optimal training conditions.

The experimental setup incorporates multiple datasets, a standardized training framework, and systematic data augmentation techniques to ensure comprehensive evaluation of hyperspectral image reconstruction performance.

During training, RGB images were linearly scaled to the range [0, 1] by the min–max normalization, followed by cropping RGB images and corresponding HSIs into 128 × 128 pixel patches. We set the batch size to 16, and Adam optimizer was utilized for parameter optimization, setting ${\beta }_1=0.9$ and ${\beta }_2=0.999$. To augment the training data, random cropping, rotations, and flipping were applied. The learning rate was set to 0.0004, and we trained for 300 epochs. Our proposed SSHFormer was implemented using the PyTorch framework, and the first dataset was trained on a single NVIDIA RTX 4090 GPU. In the implementation, we set $N_1=N_2=N_3=N_4=1,C=31$. During testing, the RGB images were also scaled to the [0, 1] range using the min–max normalization.

3.2. Quantitative Results

We conducted comprehensive comparisons between our proposed SSHFormer and SOTA methods, including both specialized spectral reconstruction algorithms (HSCNN+ [28], MST++ [21]) and advanced natural image reconstruction models (MPRNet [40], Restormer [32], HINet [41]). The quantitative results are presented in

Table 1. Performance comparison on NTIRE 2022 HSI dataset. (↓ indicates performance degradation, ↑ indicates performance improvement, and bold represents the best performance.)

Method	Params (M)	FLOPs (G)	MRAE ↓	RMSE ↓	PSNR ↑
HSCNN+	4.65	304.45	0.3813	0.0580	26.31
HINet	5.21	31.04	0.2067	0.0294	32.49
MPRNet	3.62	101.59	0.1752	0.0262	33.85
Restormer	15.11	93.77	0.1778	0.0261	33.85
MST++	1.62	23.05	0.1713	0.0254	34.10
SSHFormer	0.92	21.47	0.1657	0.0243	34.39

and

Table 2. Performance comparison on CAVE dataset. (↓ indicates performance degradation, ↑ indicates performance improvement, and bold represents the best performance.)

Method	Params (M)	FLOPs (G)	MRAE ↓	RMSE ↓	PSNR ↑
HSCNN+	4.65	304.45	0.2314	0.0642	25.06
HINet	5.21	31.04	0.1757	0.0370	29.28
MPRNet	3.62	101.59	0.1748	0.0283	31.18
Restormer	15.11	93.77	0.1703	0.0276	31.41
MST++	1.62	23.05	0.1712	0.0277	31.40
SSHFormer	0.92	21.47	0.1634	0.0277	31.66

.

The experimental results demonstrate that SSHFormer consistently outperforms existing SOTA methods while maintaining significantly lower computational requirements in terms of both parameters and FLOPs. Specifically, when compared to HSCNN+, our SSHFormer achieves a remarkable improvement of 8.08 dB in PSNR while utilizing only 19.78% (0.92 M vs. 4.65 M) of the parameters and 7.05% (21.47 G vs. 304.45 G) of the FLOPs. Similarly, compared to HINet, SSHFormer demonstrates superior performance with a 1.9 dB improvement in PSNR while requiring merely 17.66% (0.92 M vs. 5.21 M) of the parameters and 69.17% (21.47 G vs. 31.04 G) of the computational resources.

Furthermore, our model shows consistent superiority across different evaluation metrics. In terms of MRAE and RMSE, SSHFormer achieves the lowest values among all compared methods, indicating its superior ability in preserving both spectral and spatial information. The performance advantage is particularly notable on the challenging NTIRE 2022 HSI dataset, where SSHFormer achieves a PSNR of 34.39 dB, surpassing the second-best method MST++ by 0.29 dB while using only 56.79% of its parameters.

Moreover, we conducted extensive validation on the CAVE dataset to evaluate SSHFormer’s performance in real-world scenarios. The experimental results demonstrate that SSHFormer excels not only in hyperspectral image reconstruction but also in handling practical challenges including sensor noise and illumination variations. These findings on the CAVE dataset provide strong evidence for SSHFormer’s robustness and practical utility in real-world applications.

The comprehensive evaluation results confirm that SSHFormer achieves superior reconstruction quality while maintaining exceptional computational efficiency. This dual advantage of high performance and low resource requirements makes SSHFormer particularly well suited for practical applications where both accuracy and efficiency are paramount.

3.3. Qualitative Results

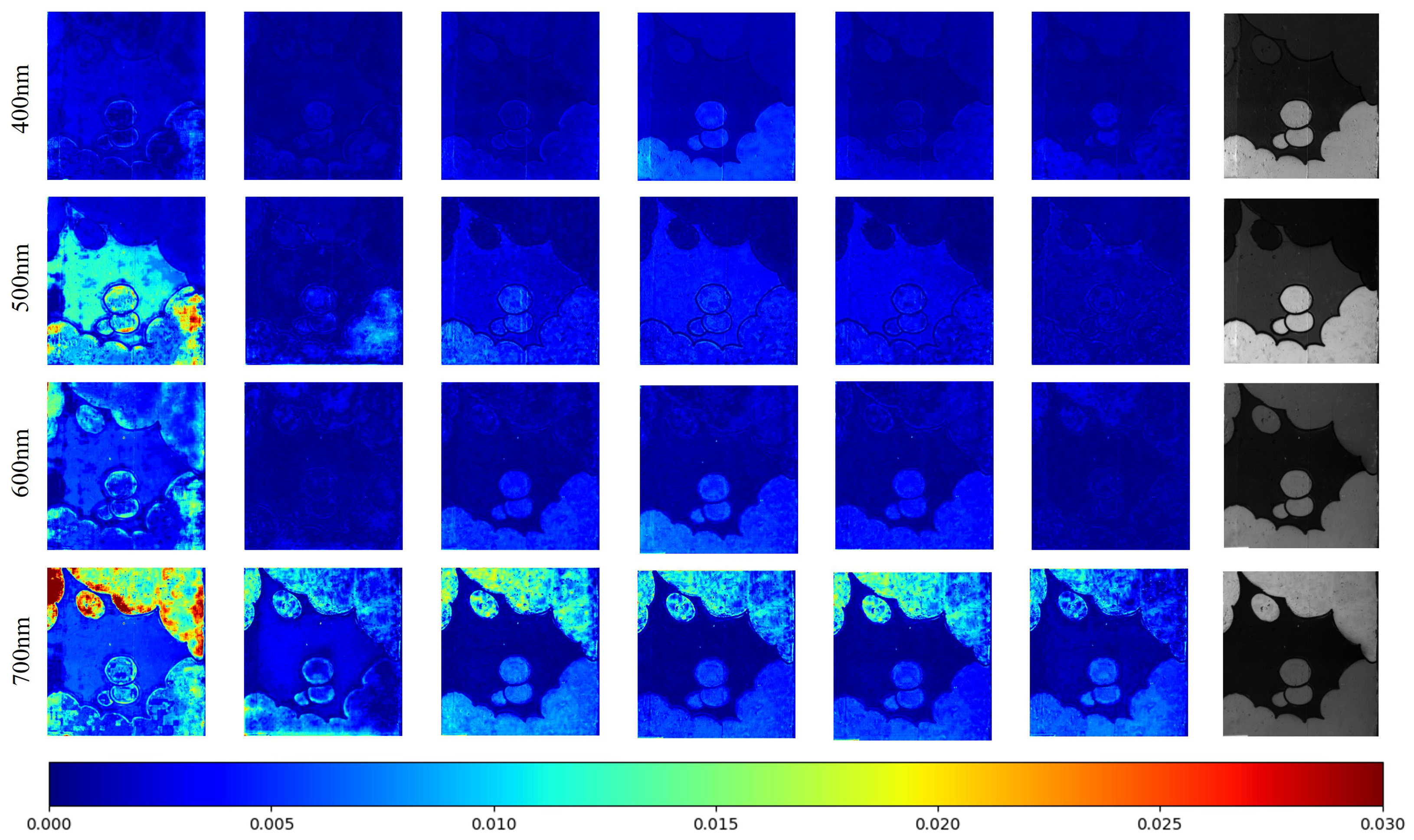
Figure 5 and Figure 6 illustrate a detailed visual comparison through absolute error heat maps across multiple spectral bands. Our evaluation focuses on the ARAD_1K dataset, specifically examining wavelengths at 400, 500, 600, and 700 nm. The visualizations present residual maps between reconstructed spectral bands from six different models—five state-of-the-art approaches and our proposed SSHFormer—with the ground truth (GT) bands shown in the rightmost column for reference. To enhance visualization clarity, we scaled the absolute error by a factor of 1/10, creating a more smoother color gradient while preserving the relative error distribution between different methods.

These absolute error heat maps offer a clear visualization of reconstruction accuracy across the spatial domain, with darker regions representing smaller reconstruction errors and thus higher accuracy. Our analysis reveals that SSHFormer achieves remarkable consistency in preserving both structural and textural fidelity, producing reconstructions that closely mirror the GT. While most competing methods demonstrate acceptable performance at intermediate wavelengths (400 nm and 500 nm), their reconstruction quality deteriorates noticeably at spectral extremes. In contrast, SSHFormer maintains exceptional reconstruction accuracy across the entire spectral range, showcasing its robust and consistent performance regardless of wavelength.

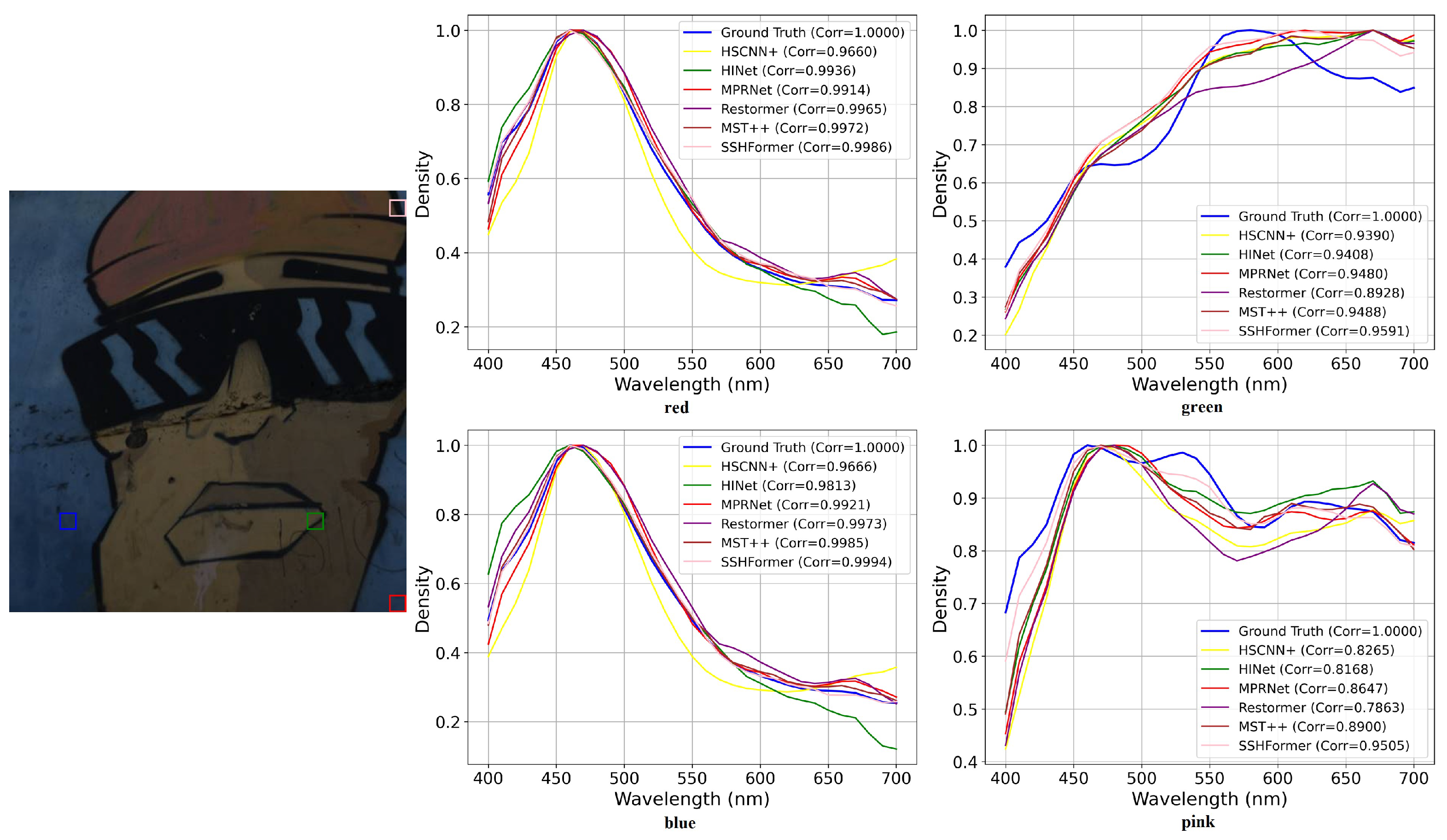
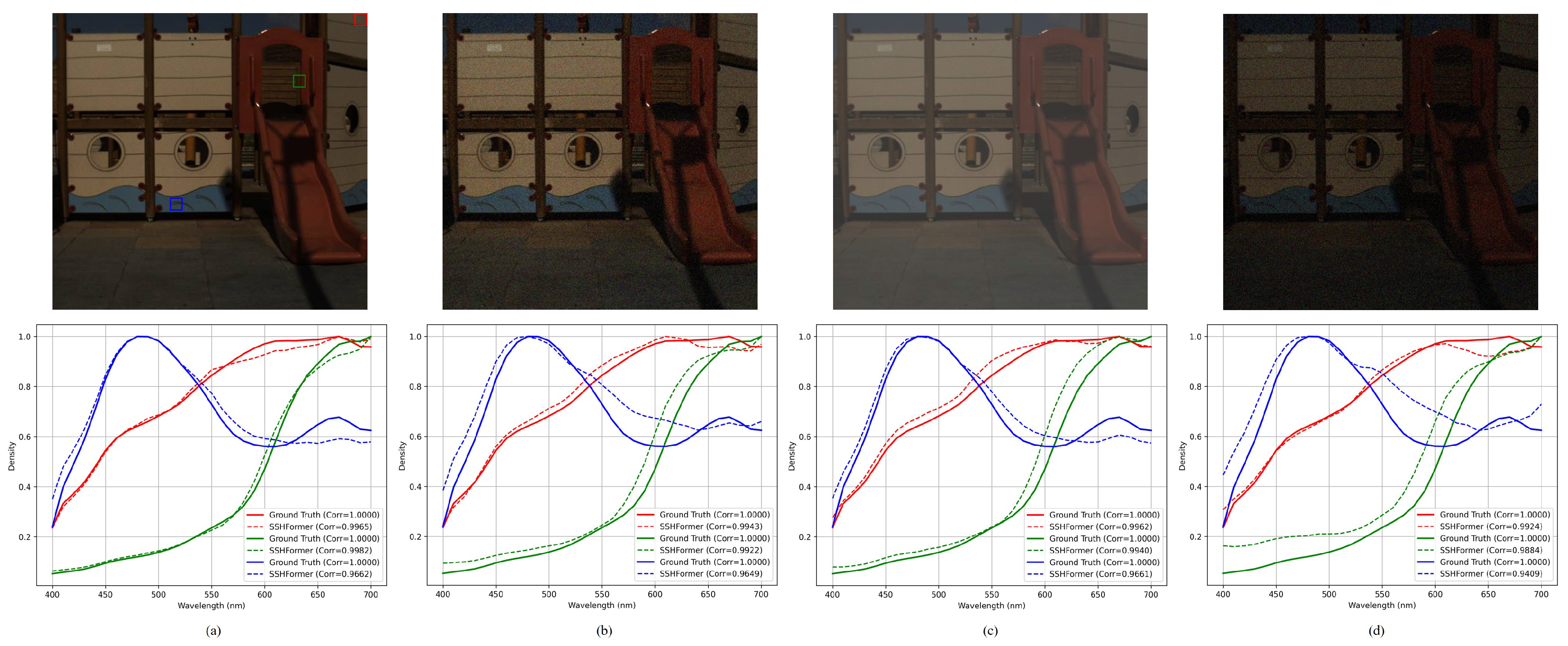
Figure 7 provides a detailed analysis of the ARAD_1K_0917 dataset, showing an original RGB image on the left with four representative regions of interest (ROIs) highlighted by colored bounding boxes, while the right side displays the mean spectral curves of these regions for comprehensive comparison between ground truth spectra and reconstruction results from leading methods (HSCNN+, HINet, MPRNet, Restormer, MST++, and our proposed SSHFormer). The y-axis “Density” represents the normalized spectral signature within each ROI region.

The results demonstrate SSHFormer’s exceptional performance in spectral reconstruction across all examined regions. Our method exhibits remarkable consistency in accurately reproducing the ground truth spectral signatures, surpassing the capabilities of existing approaches. While conventional methods like HSCNN+ and HINet show notable inconsistencies, particularly in higher wavelength ranges, SSHFormer maintains exceptional stability throughout the entire spectral range. This advantage becomes particularly evident in the bottom-right spectral plot, which represents a challenging region where competing methods show significant deviations from the ground truth. Furthermore, SSHFormer demonstrates remarkable adaptability across varying surface characteristics, successfully preserving intricate spectral details while maintaining reconstruction reliability. These comprehensive results clearly establish SSHFormer’s superior capability in minimizing spectral distortions and maintaining consistency across diverse scene elements.

Figure 8 illustrates the model’s robustness under various challenging conditions. In ideal scenarios, the model demonstrates exceptional reconstruction capabilities. When exposed to individual perturbations such as Gaussian noise (mean 0, std 0.05) or brightness variations (brightness factor 0.5), it maintains remarkable stability while preserving critical image features. However, when confronted with simultaneous disturbances (both noise and brightness adjustments), the model exhibits more noticeable performance degradation. This finding highlights opportunities for enhancing the model’s resilience to complex, multi-factor perturbations. Despite these challenging conditions, the model maintains acceptable reconstruction quality, demonstrating its inherent robustness. Future improvements could focus on strengthening the model’s ability to handle multiple concurrent disturbances, particularly in scenarios involving combined noise interference and illumination variations.

3.4. Ablation Experiments

To thoroughly evaluate the effectiveness of our proposed SSHFormer framework, we conducted comprehensive ablation experiments on the NTIRE 2022 HSI dataset. The baseline model was constructed by removing two key components: the SSMA and the 3DFFN from the complete SSHFormer architecture.

Decomposition and Ablation Study. We performed a systematic decomposition analysis to quantitatively assess the contribution of each architectural component. The experimental results are presented in

Table 3. Ablation study of different modules. (Bold represents the best performance.)

Method	Baseline	Baseline + SSMA	Baseline + SSMA + 3DFFN
Params(M)	0.90	0.92	0.92
FLOPs(G)	20.51	20.97	21.47
MRAE	0.1691	0.1671	0.1657
RMSE	0.0254	0.0251	0.0243

. Our baseline model, which implements only the basic network structure, achieved an MRAE of 0.1691. Through progressive incorporation of key components, we observed significant performance improvements:

First, adding the SSMA module to the baseline model resulted in a reduction of 0.0020 in MRAE. This improvement demonstrates SSMA’s effectiveness in capturing complex spatial–spectral correlations within the data. The self-attention mechanism enables the model to focus on relevant spectral features while maintaining spatial context, leading to more accurate spectral reconstruction.

Subsequently, incorporating the 3DFFN module further reduced the MRAE by 0.0044. This substantial improvement highlights the crucial role of 3DFFN in feature fusion and enhancement. The 3D convolution operations effectively integrate spatial and spectral information, enabling more comprehensive feature extraction and refinement.

In addition to these components, we also investigated the impact of varying the stage number $N_S$ on the performance metrics. As shown in

Table 4. Ablation study of stage number. (Bold represents the best performance.)

${\mathit{N}}_{\mathit{S}}$	1	2	3	4
MRAE	0.1764	0.1711	0.1657	0.1704
RMSE	0.0267	0.0259	0.0243	0.0253
Params(M)	0.31	0.62	0.92	1.22
FLOPs(G)	7.57	14.52	21.47	28.42

, MRAE and RMSE improve as the stage number increases from 1 to 3, with the best performance observed at $N_S=3$ (MRAE: 0.1657, RMSE: 0.0243). However, when increasing to four stages, the performance slightly degrades (MRAE: 0.1704, RMSE: 0.0253), indicating diminishing returns beyond three stages. This suggests that three stages provide an optimal balance between model capacity and performance, as additional stages do not contribute to better reconstruction quality but instead lead to increased computational overhead. The corresponding increase in parameters (from 0.31 M to 1.22 M) and FLOPs (from 7.57 G to 28.42 G) with each additional stage further justifies our choice of $N_S=3$ as the optimal configuration.

The complete SSHFormer framework, combining both SSMA and 3DFFN, achieves optimal performance by leveraging their complementary strengths. SSMA’s ability to model long-range dependencies and 3DFFN’s effective feature fusion mechanism work synergistically to achieve the following: 1. extract rich spectral information from RGB inputs; 2. maintain spatial consistency across different spectral bands; 3. enhance fine detail preservation in the reconstructed images; and 4. improve overall reconstruction accuracy.

These results validate our architectural design choices and demonstrate that each component contributes significantly to the model’s performance. The SSMA module primarily enhances the model’s ability to capture spectral correlations, while the 3DFFN strengthens feature representation and fusion capabilities. Together, they enable SSHFormer to achieve superior performance in hyperspectral image reconstruction tasks.

4. Discussion

Our experimental results demonstrate that SSHFormer achieves superior performance in hyperspectral image reconstruction while maintaining computational efficiency. This success can be attributed to several key factors in our design. First, the SSMA module effectively captures complex spatial–spectral correlations, enabling accurate spectral reconstruction from RGB inputs. The multi-head self-attention mechanism allows the model to focus on relevant spectral features while preserving spatial context, leading to more precise spectral recovery. Second, the 3DFFN module provides efficient feature fusion and enhancement, contributing to improved detail preservation and overall reconstruction quality. The combination of depthwise and pointwise 3D convolutions enables effective processing of both spatial and spectral information while keeping computational costs low.

The significant reduction in computational requirements (using only 19.78% of HSCNN+’s parameters and 7.05% of its FLOPs) while achieving better performance (8.08 dB improvement in PSNR) represents a substantial advancement in efficient hyperspectral image reconstruction. Our approach demonstrates that carefully designed architectural components can simultaneously improve performance and reduce computational demands. This efficiency makes SSHFormer particularly suitable for practical applications where computational resources are limited, such as real-time remote sensing, mobile device-based spectral imaging, and rapid medical diagnosis systems.

However, there are several aspects that warrant further investigation. While SSHFormer demonstrates excellent performance on current benchmark datasets, its scalability to larger spectral ranges and higher spatial resolutions needs further exploration. The current architecture, though efficient, may require adaptations to handle increased data dimensionality effectively. Additionally, the model’s robustness to various types of noise and different lighting conditions could be enhanced through more advanced training strategies and data augmentation techniques. Environmental factors such as atmospheric conditions, sensor noise, and varying illumination can significantly impact reconstruction quality in real-world applications.

Looking forward, promising research directions include extending the framework to other spectral imaging modalities, investigating physics-informed neural network designs, and developing adaptive mechanisms that can adjust the model’s behavior based on specific application requirements. The integration of physical principles could provide additional constraints and guidance for the reconstruction process, potentially improving accuracy and generalization. Furthermore, adaptive mechanisms could enable the model to optimize its performance for different scenarios, such as prioritizing spatial detail in some cases and spectral accuracy in others. These advancements could further expand the applications of hyperspectral imaging in various domains while maintaining computational efficiency, particularly in emerging fields such as precision agriculture, environmental monitoring, and biomedical imaging.

5. Conclusions

In this paper, we proposed SSHFormer, an efficient Transformer-based framework for hyperspectral image reconstruction. Our approach effectively addresses the challenges of capturing both spatial and spectral correlations while maintaining computational efficiency. The key contributions of our work include the novel SSMA module and the efficient 3DFFN design.

The SSMA module introduces a sophisticated mechanism for modeling inter-spectral correlations through the combination of dilated convolution and Spatial Multi-head Self-Attention (S-MSA). This design enables effective capture of non-local spatial features while preserving crucial spectral relationships, leading to more accurate spectral reconstruction. The dilated convolution expands the receptive field efficiently, while S-MSA enables global context modeling across different spectral bands.

Furthermore, our proposed 3DFFN leverages three-dimensional convolutions to achieve effective fusion of spatial and spectral information. This design choice proves crucial for enhancing the quality of reconstructed HSIs, as demonstrated by our comprehensive experimental results. The 3DFFN’s ability to process spatial and spectral information simultaneously contributes significantly to the model’s superior performance.

Extensive experiments on benchmark datasets demonstrate that SSHFormer outperforms existing state-of-the-art methods while requiring substantially fewer computational resources. Specifically, our model achieves an 8.08 dB improvement in PSNR compared to HSCNN+ while using only 19.78% of its parameters. These results validate the effectiveness of our architectural design choices and demonstrate the potential of efficient Transformer-based approaches in hyperspectral image reconstruction.

The success of SSHFormer opens up new possibilities for practical applications in fields requiring efficient and accurate spectral imaging, such as remote sensing, medical diagnosis, and environmental monitoring. Our work provides a solid foundation for future research in efficient hyperspectral image reconstruction and demonstrates the potential of carefully designed neural architectures in addressing complex imaging challenges.