Infrared Small Target Detection Based on Entropy Variation Weighted Local Contrast Measure

Abstract

Infrared small target detection plays a crucial role in fields such as remote sensing and surveillance. However, during long-distance imaging, factors such as atmospheric attenuation lead to a low signal-to-clutter ratio for the targets, making their features difficult to extract effectively. Additionally, in complex background environments, background components that resemble the target morphology highly interfere with detection tasks. Therefore, infrared weak small target detection in complex backgrounds faces challenges of low detection accuracy and high false alarm rates. To solve the above difficulties, a novel entropy variation weighted local contrast measure (EVWLCM) is proposed. Firstly, a target saliency enhancement method based on a family of generalized Gaussian functions is introduced, which accurately characterizes the grayscale distribution states of various targets in infrared images. Secondly, a novel adaptive weighting strategy based on local joint entropy variation characteristics is suggested. Specifically, the spatial grayscale distribution difference between the target and the background is effectively perceived, enhancing the target while suppressing the background. Finally, experimental results on real infrared images show that EVWLCM outperforms existing methods on both public and private datasets. Additionally, the average processing speed of EVWLCM is 34 frames per second, which meets the requirements for real-time scenarios.

1. Introduction

Infrared imaging technology has significant research value due to its characteristics of all-weather operation, strong concealment, and long-distance detection capability. Particularly in the thermal infrared region (3 μm to 14 μm), infrared imaging can effectively capture the thermal radiation signals of objects and is widely applied in fields such as remote sensing, space surveillance, and public safety [1]. However, infrared small targets, such as UAVs, are affected by long-range imaging during the detection process, resulting in a limited number of pixels occupied by these targets on the image plane, which leads to a lack of structural and textural information. Furthermore, complex background clutter, such as forests, broken clouds, bright buildings, and pixel-sized noise with high brightness (PNHB), further degrades the target’s signal-to-clutter ratio (SCR). Due to the characteristics of infrared weak small targets in infrared remote sensing imaging, accurate detection of targets in complex scenarios is an important research challenge.

In recent years, the research progress of infrared small target detection methods is remarkable, and several types of detection methods have been proposed. These include low-rank decomposition-based detection methods, deep-learning-based detection methods, and saliency-based detection methods. These three types of methods are described below.

The low-rank decomposition method based on optimization theory is one of the research hotspots, transforming the target detection problem into an optimization challenge of low-rank matrix recovery [2,3,4]. For instance, Gao et al. [5] constructed an infrared patch image (IPI) model that leverages the non-local autocorrelation of the background to recover low-rank backgrounds. However, the sparse clutter in the complex background is easily decomposed incorrectly, leading to a high false alarm rate. Based on this, Dai et al. [6] introduced the singular value partial sum constraint in the model (NIPPS) to enhance the ability to suppress complex background. Dai et al. [7] proposed a reweighted infrared patch tensor model (RIPT) that incorporates local structural information into the non-local detection model, achieving improved suppression of strong edges. To further utilize the spatial structure information, Zhu et al. [8] designed a regularization term based on the morphological characteristics of the target (TCTHR). However, such methods require extensive iterative computations, making it challenging to meet the real-time demands of practical applications.

With the advancements in hardware computing power and the abundance of datasets, deep-learning-based methods for detecting infrared weak small targets achieve success [9,10,11,12]. Zhao et al. [13] applied Convolutional Neural Networks (CNNs) to the task of infrared small target detection, transforming the detection problem into a binary classification problem of target and background. Considering the limited pixel features of small targets and the loss of target information in deep networks, Hou et al. [14] combined handcrafted features with deep features to construct a target feature extraction framework (RISTD-Net). Zuo et al. [15] employed an attention mechanism to enhance the focus on target information in different feature layers (AFFPN). Li et al. [16] implemented repeated fusion and interaction of features from different network layers (DNA-NET), which enhanced the richness of target feature extraction. However, such methods rely on a large number of datasets for model training, and when the distribution of test data differs greatly from that of the training data, the network performance degrades significantly [17].

With the development of human visual system (HVS) research, saliency-based methods make a series of achievements in infrared small target detection. Owing to their advantages such as low data dependency, ease of model implementation, and strong interpretability, these methods hold substantial research in practical applications. Chen et al. [18] considered that the target’s grayscale value is higher than its surrounding background and constructed a nine-cell window to compute the local contrast (LCM) to enhance the target saliency. On this basis, Han et al. [19] proposed a joint computation formula combining ratio and difference to enhance the target while suppressing clutter (RLCM). Wei et al. [20] calculated grayscale differences in fixed directions (MPCM), based on the observation that targets have similar grayscale distributions in various directions. Furthermore, Han et al. [21] took into account the Gaussian-like shape distribution of the targets and performed Gaussian filtering on the central cell (TLLCM) to enhance weak targets that are submerged in a bright background. Shanraki et al. [22] constructed an eight-branch window to calculate the grayscale difference extending outward from the target center (BLCM), based on the targets’ grayscale gradient characteristics. Based on the discontinuity of the target grayscale distribution in local areas, Wu et al. [23] constructed dual-layer background cells around the central cell of the template (DNGM) and computed the product of gradient differences between dual neighborhoods to enhance target contrast as much as possible. Zhou et al. [24] fused local contrast and local gradient information to jointly compute the saliency map (MLCGM) and constructed a four-direction computational model to reduce the interference of bright background information near the target. Ye et al. [25] introduced a method based on size-aware local contrast measurement (SALCM). By employing single-event signal decomposition and adaptive target size estimation, they achieved precise detection of infrared targets in complex backgrounds. However, this approach has limited generalization ability for weak targets. While these prior hypothesis-based methods have achieved improved target enhancement, they may inadvertently over-enhance clutter and noise due to similar distribution characteristics in complex scenarios.

To further improve the performance of detection methods, an increasing number of methods utilize the statistical properties of local regions to calculate adaptive weights for contrast enhancement, making great advances in target enhancement and background suppression [26,27]. To strengthen the suppression effect of strong clutter edges, Liu et al. [28] presented weighted local contrast (WLCM), using the grayscale distribution characteristics of clutter edges to design weighting factors. To improve the false alarm suppression within strong clutter, Du et al. [29] introduced a homogeneity weighted local contrast measure (HWLCM), utilizing the homogeneity of the background around the target to calculate the standard deviation as a weight. To further suppress the background edges, Han et al. [30] suggested a weighted strengthened local contrast measure (WSLCM), adopting an improved region intensity level (IRIL) to independently compute the complexity and difference between the target and background. Wei et al. [31] proposed a weighted local ratio-difference contrast (WLRDC), which is based on the anisotropy of the target’s grayscale distribution and calculates the difference in grayscale statistical information between the central region and its neighboring multi-directions as the weight map to reduce the false alarm rate. To weaken the interference of PNHB, Zhao at al. [32] proposed the energy-weighted local uncertainty metric (ELUM), introducing the energy difference between the target and background to design an energy weighting factor. Hao et al. [33] proposed an infrared small target detection method based on multi-directional gradient filtering and adaptive size estimation. By dynamically optimizing the target size through sine curve fitting and suppressing background interference with multi-directional morphological filtering, they significantly improved detection accuracy in complex scenarios. However, this method struggles with detecting low-contrast targets. Xu et al. [34] proposed a method based on local contrast weighted multi-directional derivatives (LCWMDs). Through the use of multi-directional derivative penalty factors from the facet model and a three-layer dual local contrast fusion model, they effectively achieved precise detection of infrared small targets in complex backgrounds. However, this method still faces challenges with the generalization capability for targets at different scales. The above methods tend to consider the information of the target or background individually, neglecting the joint distribution information between the target and background. Consequently, they have limited effectiveness in suppressing highly complex clutter, such as forests, broken clouds, and bright buildings, that exist in complex scenarios.

To address the issues of erroneous enhancement of non-target components and the challenges of suppressing complex clutter, a novel entropy variation weighted local contrast measure (EVWLCM) is proposed, which enhances the robustness of detection methods in complex backgrounds. Specifically, the contributions presented in this paper are as follows:

(1)

To effectively characterize target morphology, a family of two-dimensional generalized Gaussian functions is introduced. Gaussian targets and Gaussian-like targets are significantly enhanced, improving the detection ability for dark and weak targets.

(2)

To fully utilize the prior information of the target and background structures, a new nested window is proposed to estimate the local joint entropy variation. The difference in grayscale distribution changes between target and background regions is characterized, enhancing the weak target while suppressing interference from strong clutter.

The remainder of this paper is organized as follows. In Section 2, we describe the proposed EVWLCM in detail. In Section 3, we provide the evaluation metrics and datasets used in the experiments, followed by ablation experiments and comparison experiments. In Section 4, we discuss the relevant characteristics and results of the method proposed. In Section 5, we present the conclusions.

2. Methods

The overall flowchart of the proposed algorithm is shown in Figure 1. Firstly, a generalized Gaussian filter is applied to enhance small targets, and the multi-directional local contrast of the enhanced central sub-block and its surrounding sub-blocks is computed for each pixel. Then, a novel nested window is constructed to compute the local joint entropy variation of the target and its surrounding background for weighting the multi-directional local contrast. Subsequently, max pooling is performed on the saliency maps to obtain the final saliency map. Finally, real target extraction is achieved by adaptive threshold segmentation.

2.1. Generalized Gaussian Weighted Local Contrast

Due to atmospheric attenuation and the performance limitations of infrared imaging systems, targets such as UAVs usually have low SCR when imaged at long distances, making it difficult to separate target signals from the background. Therefore, there is an urgent need for effective target enhancement. Matched filtering is an effective enhancement method that focuses on selecting the optimal filter that closely matches the target morphology. However, most of the existing target saliency-based detection methods rely on the classical two-dimensional Gaussian function for filtering, which is unable to adapt to the infrared targets with diverse morphologies in real scenes. This prior assumption tends to enhance the PNHB, which leads to an increase in the false alarm rate.

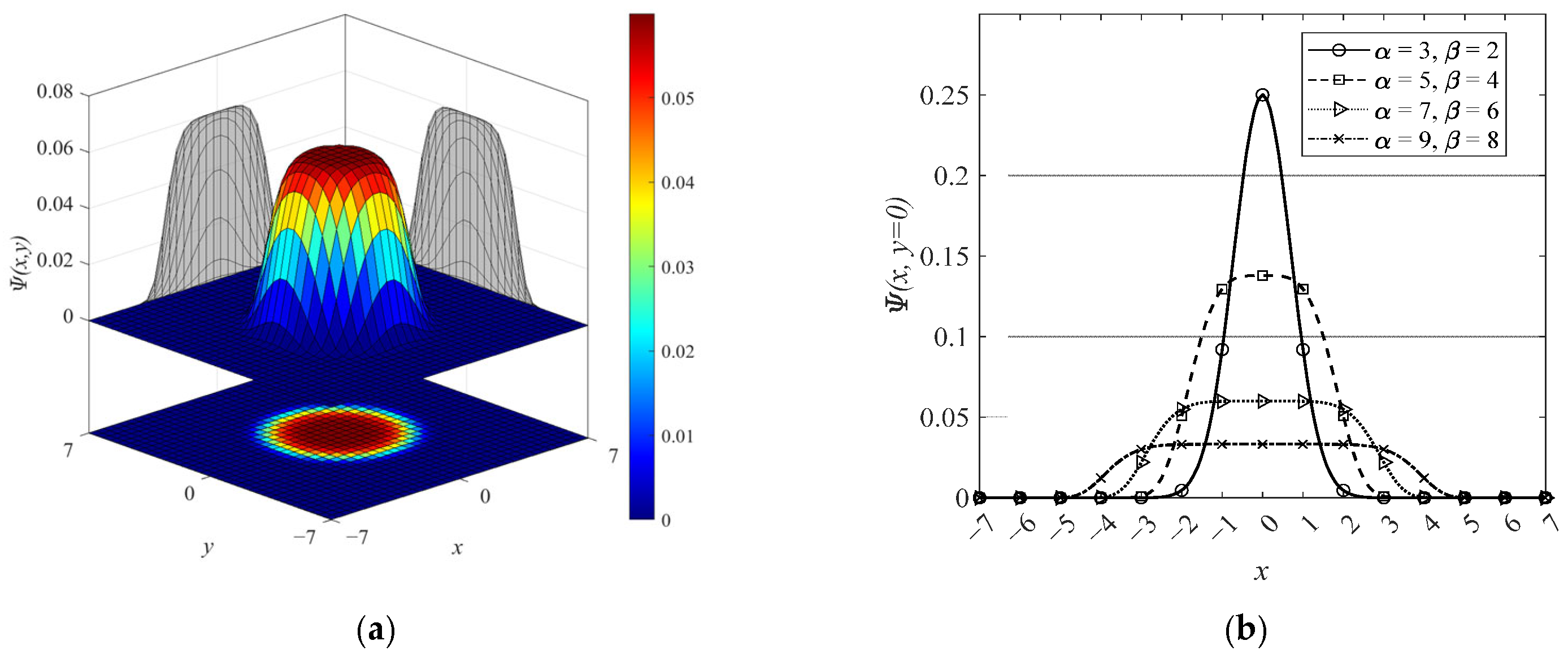
To effectively enhance targets with various morphological distributions, we note that the sizes of infrared small targets in real images typically range from 2 × 2 to 9 × 9 pixels. Moreover, the grayscale distribution of IR small targets generally shows the strongest intensity at the central pixel, with neighboring pixels exhibiting similar intensity. Based on these characteristics, a generalized Gaussian distribution model is introduced to represent the targets. The design of the generalized Gaussian function family inherits the basic ideas of the scale space theory, but its adjustable parameters (α, β) distinguish it from the fixed-shape Gaussian kernel of SIFT, allowing it to more flexibly adapt to targets of various shapes. As shown in Figure 2a, a typical two-dimensional generalized Gaussian function features a flat-topped center, with the grayscale values decreasing from the central region outward. Moreover, due to variations in parameter values, the shape and width of the generalized Gaussian function can be adjusted. The slices of the two-dimensional generalized Gaussian function family at different parameter values are illustrated in Figure 2b.

A family of two-dimensional generalized Gaussian functions is used to enhance small targets. The filtered image is represented as follows:

$$L(i,j)={\displaystyle \sum _{x=-c}^c{\displaystyle \sum _{y=-c}^c\mathsf{\Psi }(x,y)I(i+x,j+y)}}$$

(1)

$$\mathsf{\Psi }\left(x,y\right)={\displaystyle \frac{1}{C}}\exp \left(-{\left({\displaystyle \frac{\left|x-x_0\right|}{\alpha }}\right)}^{\beta }-{\left({\displaystyle \frac{\left|y-y_0\right|}{\alpha }}\right)}^{\beta }\right)$$

(2)

where $L(i,j)$ represents the gray value at the pixel $(i,j)$ after filtering with the family of generalized Gaussian functions. $x_0$ and $y_0$ denote the central positions in the $x$ and $y$ directions, respectively, both of which are set to 0. C is the normalization coefficient. $\alpha$ is the scale parameter that controls the width of the distribution, and $\beta$ is the shape parameter that controls the form of the distribution. By adjusting $\alpha$ and $\beta$, the generalized Gaussian function can describe various morphological distributions. Therefore, the introduction of the generalized Gaussian function allows for a more realistic and accurate representation of different targets in infrared images, thereby enhancing the adaptability of the method to Gaussian and Gaussian-like targets.

Beyond the morphological priors of infrared targets, their grayscale typically exhibits a consistent decreasing trend in all directions. In contrast, the grayscale distribution of background clutter, such as edges, shows anisotropy. Based on this characteristic, grayscale differences in multiple directions can be utilized to enhance targets while suppressing background clutter.

To calculate the differential properties of the grayscale distribution in different directions, the sliding window (SW) used in this paper is evenly divided into nine sub-blocks, as shown in Figure 3. The center cell $\left(\mathrm{T}\right)$ captures target grayscale information, while the eight surrounding cells ${(\mathrm{B}}_{\mathrm{n}})$ gather background grayscale information. Subsequently, generalized Gaussian filtering is applied to the central cell to enhance the energy of the targets.

The generalized Gaussian weighted local contrast (WGLCM) is calculated by filtering the infrared image using a generalized Gaussian function family and calculating the grayscale differences between the central and surrounding regions. The specific calculation formula is presented as follows:

$$\mathrm{WGLCM}(i,j)=\underset{n=1,\dots ,4}{\min }\left(d_n\cdot d_{n+4}\right)$$

(3)

$$d_n(i,j)=L_T(i,j)-M_{B_n}(i,j)$$

(4)

where $d_n$ is the grayscale difference in the $n$ direction, $L_T(i,j)$ represents the grayscale value at the pixel location $(i,j)$ after enhancement of the central region using the family of generalized Gaussian functions. $M_{B_n}$ is the mean grayscale value of all pixels in the $B_n$. The generalized Gaussian function models the target’s grayscale distribution by varying the scale parameter α and the shape parameter β. Leveraging the energy aggregation characteristics of real targets, we apply the generalized Gaussian function family to filter the input infrared images, thereby enhancing targets of various shapes. Subsequently, we compute the local contrast in the processed images to derive the WGLCM, which effectively amplifies the target signal.

2.2. Local Joint Entropy Variation Weighted Map Calculation

While the WGLCM can enhance weak targets, it encounters limitations in clutter suppression when the scene contains background elements with shapes highly similar to the infrared targets.

In infrared images, background regions typically exhibit a stable gray distribution and their entropy values remain relatively stable. However, the presence of targets changes this distribution, leading to an expanded range of grayscale and a notable increase in entropy. Therefore, entropy variations can be utilized to distinguish the target from the background.

Based on the above analysis, a novel nested window is designed to characterize the entropy variation effect. The nested window consists of a cross window (CW) and a hollow window (HW), as illustrated in Figure 1c. The CW is a window used to measure the local entropy of the target and adjacent background regions. The HW is a window used to measure the local entropy of the background region surrounding the target. When the sliding window is positioned in the target region, the CW is capable of covering both target and background pixels, resulting in a high entropy value due to the significant heterogeneity of the two components. Additionally, the center of the cross window contains the target pixels and the four pointed corners contain the background pixels. This balanced distribution of pixels facilitates more accurate local entropy information statistics. Conversely, the HW only covers the background pixels, leading to a low entropy value due to the low complexity of the grayscale distribution in a homogeneous background region. Therefore, the ratio of the two windows can be utilized to measure the likelihood of a target being present in a given area.

The local joint entropy variation (LJEV) is a feature value calculated as the ratio of entropy within the cross window and hollow window regions. The formula of LJEV is as follows:

$$\mathrm{LJEV}(i,j)={\displaystyle \frac{CE(i,j)}{\max (HE(i,j),\zeta )}}$$

(5)

$$CE(i,j)=-{\displaystyle \sum _{m=1}^{S_1}{p}_m\cdot {\log }_2{p}_m}$$

(6)

$$HE(i,j)=-{\displaystyle \sum _{n=1}^{S_2}{p}_n\cdot {\log }_2{p}_n}$$

(7)

where $CE(i,j)$ represents the local entropy of the cross window centered at pixel $(i,j)$, while $HE(i,j)$ denotes the local entropy of the hollow window centered at the same pixel. $\zeta$ is a predefined constant to prevent division by zero. $p_m$ is the probability of the $m\mathrm{th}$ gray level occurring within the cross window, and $p_n$ is the probability of the $n\mathrm{th}$ gray level occurring within the hollow window. Additionally, $S_1$ and $S_2$ represent the number of gray levels present in the corresponding sub-regions. The nested window structure is utilized to characterize the entropy variation features. Specifically, the CW quantifies the higher entropy values arising from the pronounced grayscale differences between the target and background, while the HW captures the lower entropy values due to the uniform grayscale distribution within the background regions. The ratio of these two window measurements effectively quantifies the grayscale distribution differences between the target and background. A high LJEV value reflects the local entropy increase caused by the target, suppressing the uniform background.

Weighted maps under various scenarios are shown in Figure 4. The presence of a target increases the information richness of CW, resulting in a larger $CE$. Furthermore, when the grayscale distribution of the background surrounding the target is more uniform, the $HE$ becomes smaller. In such cases, $\mathrm{LJEV}$ at the center pixel is significantly larger. In contrast, in highly complex large-area clutters, such as broken clouds, forests, and building edges, both the CW and HW contain background pixels with complex gray distribution. Hence, the entropy values within two windows are high and closely aligned, with the $\mathrm{LJEV}$ approaching 1, preventing the clutter from being incorrectly enhanced.

2.3. Multi-Scale Local Contrast Calculation

After obtaining the $\mathrm{WGLCM}$ and $\mathrm{LJEV}$, the entropy variation weighted local contrast measure (EVWLCM) is obtained by multiplying the WGLCM and LJEV:

$$\mathrm{EVWLCM}(i,j)=\mathrm{LJEV}(i,j)\cdot \mathrm{WGLCM}(i,j)$$

(8)

Considering the varying sizes of targets in infrared images, multiple scales are used to measure the saliency. The final saliency map is selected by the max pooling operation:

$$\mathrm{EVWLCM}=\max (0,{\mathrm{EVWLCM}}_l), l=3,5,7,9$$

(9)

where $l$ denotes the window size, with four scales selected for measuring target saliency.

2.4. Threshold Operation

The following is a brief analysis of the EVWLCM results for the pixel located at $(i,j)$ in different regions.

(1).

If $(i,j)$ is true target center, the generalized Gaussian functions enhance the target specifically, so the $\mathrm{WGLCM}$ is large. The $\mathrm{LJEV}$ will be large for the complex grayscale distribution in the target’s region. Therefore, the $\mathrm{EVWLCM}$ is a large value.

(2).

If $(i,j)$ is smooth background, the $\mathrm{WGLCM}$ is small due to the uniform grayscale. Since the low complexity of grayscale distribution, $\mathrm{LJEV}\approx 1$. The $\mathrm{EVWLCM}$ is a small value that will not disturb the detection.

(3).

If $(i,j)$ is complex clutter, such as forests or buildings. This type of area has a similar grayscale distribution to the target, and the $\mathrm{WGLCM}$ is relatively large. Due to the strong similarity in grayscale distribution between the cross window and hollow window, $\mathrm{LJEV}\approx 1$, preventing the enhancement of clutter. Therefore, the $\mathrm{EVWLCM}$ is lower than the real target and will not disturb the detection.

After obtaining the EVWLCM, adaptive threshold segmentation [35] is used to extract the real target

$$Th={\mu }_{\mathrm{EVWLCM}}+k\times {\sigma }_{\mathrm{EVWLCM}}$$

(10)

where ${\mu }_{\mathrm{EVWLCM}}$ and ${\sigma }_{\mathrm{EVWLCM}}$ are the mean and variance of the $\mathrm{EVWLCM}$, respectively. $k$ is a given constant, and our experiments show that 0.6 to 0.8 is appropriate. The overall process of the method in this paper is shown in Algorithm 1.

Algorithm 1. Detection steps of the proposed EVWLCM method

Input: Infrared image I, the size of sliding window, parameters $\alpha$, $\beta$ and l

Output: Detection result

1: Calculate a family of generalized Gaussian functions using Equation (2).

2: Filter the input image using a family of generalized Gaussian functions.

3: for i = 1:row do

4:  for j = 1:col do

5:   Calculate the WGLCM map using Equations (3) and (4).

6:   Calculate the LJEV map using Equations (5)–(7).

7:   Obtain EVWLCMl by using Equation (8).

8:  end for

9: end for

10: Obtain EVWLCM using Equation (9).

11: Obtain the detection result using Equation (10).

3. Experimental Results

To validate the effectiveness of the proposed method, this section details the evaluation metrics, datasets, and experimental results. The detection performance of various methods is evaluated through both qualitative and quantitative analyses. For comparison, eight state-of-the-art detection methods are selected: MPCM, RLCM, WLDM [36], HBMLCM, TLLCM, WSLCM, BLCM, and ELUM. The parameter settings for each method follow the recommendations provided by their authors.

3.1. Evaluation Metrics

To quantitatively evaluate the performance of various detection algorithms, three widely used evaluation metrics are employed: the signal-to-clutter ratio gain (SCRG), the background suppression factor (BSF), and the receiver operating characteristic curve (ROC).

The signal-to-clutter ratio gain (SCRG) [37] characterizes the ability of an algorithm to enhance targets. The larger the SCRG, the stronger the target enhancement performance of the detection method. Definitions are as follows:

$$\mathrm{SCRG}={\displaystyle \frac{{\mathrm{SCR}}_{\mathrm{out}}}{{\mathrm{SCR}}_{\mathrm{in}}+\mathrm{c}}}$$

(11)

$$\mathrm{SCR}={\displaystyle \frac{\left|{\mathsf{\mu }}_{\mathrm{t}}-{\mathsf{\mu }}_{\mathrm{b}}\right|}{{\mathsf{\delta }}_{\mathrm{b}}}}$$

(12)

where ${\mathsf{\mu }}_{\mathrm{t}}$ and ${\mathsf{\mu }}_{\mathrm{b}}$ represent the average gray values of the target region and the surrounding neighboring background region, respectively. ${\mathsf{\delta }}_b$ denotes the variance in gray values of the surrounding background area. ${\mathrm{SCR}}_{\mathrm{in}}$ and ${\mathrm{SCR}}_{\mathrm{out}}$ stand for the SCR of the original image and the processed image, respectively. $c$ is a small constant introduced to avoid division by zero.

The background suppression factor (BSF) represents the method’s ability to suppress the background. A higher BSF value indicates better background suppression performance. Definitions are as follows:

$$\mathrm{BSF}={\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{in}}}{{\mathsf{\sigma }}_{\mathrm{out}}+\mathrm{c}}}$$

(13)

where ${\mathsf{\sigma }}_{\mathrm{in}}$ and ${\mathsf{\sigma }}_{\mathrm{out}}$ are the standard deviations of the original image and processed image.

Furthermore, the receiver operating characteristic (ROC) curve [38] is introduced as an assessment metric to count and compare the performance of different detection algorithms. The ROC curve provides an objective measure for evaluating the performance of various algorithms, with the true positive rate (TPR) as the vertical axis and the false positive rate (FPR) as the horizontal axis. Definitions are as follows:

$$\mathrm{TPR}={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{true}\mathrm{detections}}{\mathrm{Number}\mathrm{of}\mathrm{actual}\mathrm{targets}}}$$

(14)

$$\mathrm{FPR}={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{false}\mathrm{alarm}\mathrm{detected}\mathrm{pixels}}{\mathrm{Number}\mathrm{of}\mathrm{all}\mathrm{pixels}}}$$

(15)

The ROC curve illustrates the trade-off between TPR and FPR. The closer the ROC curve is to the top-left corner, the better the detection performance.

3.2. Datasets

To verify the effectiveness and superiority of the proposed method, performance evaluation experiments were conducted on four real infrared image datasets, including three public datasets and one private dataset. The targets in these datasets range in size from 2 × 2 to 9 × 9 pixels. Figure 5 illustrates a schematic diagram of typical scenes from the datasets. Dataset 1 [39] contains 300 images, featuring complex buildings and dense forest clutter. Dataset 2 [40] consists of 376 images, with high-brightness clouds and complex structures. Dataset 3 [16] includes 589 images, with background interference such as bright and complex buildings, fragmented clouds, and dense forests. Dataset 4 is a private dataset captured in our laboratory, comprising 618 frames with complex background clutter, including illuminated clouds and highlighted buildings.

Specifically, to demonstrate the method’s capability in detecting weak targets, Dataset 5 is constructed by selecting infrared images from the aforementioned four datasets with target SCR < 6. Typical scenes from Dataset 5 are shown in Figure 6. The background contains clouds, forests, complex buildings, and multiple types of background components at the same time. Detailed information about all datasets is summarized in

Table 1. Details of the datasets.

Dataset	Frames	Target Type	Resolution	Target Number	Target Size	Target SCR	Background Description
1	300	aircraft	640 × 512	1	5 × 5 to 9 × 9	1.38 to 64.7	complex buildings, clouds, forest
2	376	aircraft	320 × 240, 324 × 324	1 to 6	2 × 2 to 9 × 9	1.8 to 359.6	complex buildings, thick forest
3	589	aircraft	480 × 359, 250 × 250	1 to 9	2 × 2 to 9 × 9	1.7 to 153.0	buildings, complex clouds, forest
4	618	UAV	640 × 512	1	3 × 3 to 7 × 7	4.2 to 136.4	bright clouds, buildings
5	547	aircraft, UAV	320 × 240, 640 × 512	1 to 5	2 × 2 to 9 × 9	1.7 to 5.9	complex buildings, clouds, forest

.

3.3. Ablation Experiments

To verify the design effectiveness of each component represented in the formula, we conducted ablation experiments on all datasets. Experimental validation was performed using multi-directional local contrast measure (LCM), Gaussian weighted local contrast measure (GLCM), generalized Gaussian weighted local contrast measure (WGLCM), and the entropy variation weighted local contrast measure (EVWLCM) proposed in this paper. Specifically, the LCM is defined as the contrast value obtained by directly calculating the grayscale statistical differences between the central region and its surrounding blocks in eight adjacent directions of the original infrared image. The GLCM is defined as the contrast value calculated by filtering the infrared image with a Gaussian function and calculating the grayscale statistical differences between the central region and its surrounding blocks in eight adjacent directions. The average SCRG and BSF values obtained from the ablation experiments are presented in

Table 2. Mean SCRG of the ablation experiments.

Dataset	LCM	GLCM	WGLCM	EVWLCM
1	185.29	189.88	190.01	541.24
2	368.01	365.11	368.98	641.45
3	171.65	174.56	176.01	830.67
4	646.85	647.50	653.79	674.56
5	772.44	768.15	782.27	1351.23

and

Table 3. Mean BSF of the ablation experiments.

Dataset	LCM	GLCM	WGLCM	EVWLCM
1	14.66	14.65	16.97	1154.01
2	88.33	94.22	105.20	1439.71
3	53.50	56.59	60.90	1946.75
4	15.79	15.94	16.02	2067.66
5	22.94	23.38	24.16	1860.10

, respectively. Figure 7 displays the ROC curves of each method across various datasets. It can be observed that each module contributes to improving the overall performance of the proposed method.

LCM calculates the contrast between the target and background directly using the mean grayscale value of the target region. However, it lacks appropriate enhancement strategies based on prior information for weak targets, resulting in limited target gain capability. Moreover, relying solely on contrast information makes it difficult to suppress interference from complex clutter in challenging scenes, leading to a high false alarm rate. Consequently, LCM achieves the lowest SCRG and BSF values, and its ROC curve is positioned in the lower-right region compared to the other methods.

GLCM is based on the prior assumption that the morphological distribution of infrared small targets follows a Gaussian shape, and it enhances targets through Gaussian filtering. While this approach can improve the detection of Gaussian-shaped targets, this prior assumption often fails to accurately represent the grayscale distribution of various targets. As a result, GLCM exhibits limited enhancement capability for small targets.

In contrast to LCM and GLCM, WGLCM introduces a family of generalized Gaussian weighting functions to better adapt to the morphological distributions of Gaussian-shaped and Gaussian-like targets in real infrared images. As a result, its performance metrics consistently surpass those of both LCM and GLCM.

Furthermore, EVWLCM builds upon WGLCM by incorporating a local joint entropy variation weighting term, significantly suppressing interference from complex background clutter. Consequently, the proposed method achieves remarkable improvements across various quantitative evaluation metrics, with the ROC curves for all datasets positioned in the upper-left corner.

3.4. Qualitative Analyses and Quantitative Comparisons

To perform a qualitative analysis of the methods’ detection performance. Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 present the detection results of various detection methods in different scenarios. The red-marked boxes indicate the real target areas, while the green-marked boxes show that the method fails to detect the target. The yellow ellipses highlight residual background clutter. In scene 1 and scene 2, MPCM relies on grayscale differences between the central region and its surroundings, enhancing targets located in deep space while having many false alarms for complex buildings. RLCM uses a combination of ratio and difference to measure contrast but struggles with weak target detection in complex backgrounds. TLLCM, WSLCM, and ELUM incorporate target energy distribution characteristics to enhance target saliency. However, they erroneously amplify detector noise and fluctuating backgrounds in deep space, leading to missed detections. WLDM and HBMLCM improve target saliency to some extent but fail to adequately suppress complex backgrounds, resulting in numerous false alarms at building edges. Additionally, their weak target enhancement capability remains limited. BLCM leverages grayscale distribution differences between the target and noise, calculating grayscale variations from the center to the surroundings in different directions. While it suppresses some noise points, it neglects complex background suppression. In contrast, the proposed EVWLCM effectively enhances targets while suppressing complex background clutter. In scene 1, there is a large area of buildings. Since the building areas do not satisfy the Gaussian prior and Gaussian-like prior, the calculated WGLCM value is relatively low. At the same time, both the cross window and hollow window contain buildings with complex grayscale distributions, resulting in higher entropy values for both, with the LJEV value approaching 1. At this point, the saliency values of the background region are significantly lower than those of the target region. In scene 2, there are areas of trees and railings. For the large area of trees, the grayscale distributions within both the cross window and hollow window are relatively complex, resulting in a ratio close to 1, which prevents the erroneous enhancement of tree clutter. Similarly, for the densely distributed railing area, when measuring local entropy values using the cross window and hollow window, both values are high and the ratio approaches 1, ensuring that they do not interfere with target detection.

In scene 3, MPCM and RLCM utilize grayscale differences between the target and background for enhancement. However, the forested scene contains substantial clutter with grayscale distributions similar to the target, leading to high false alarm rates. TLLCM and WSLCM consider the target’s morphological distribution characteristics, achieving effective enhancement but inadvertently amplifying forest clutter with similar morphologies. HBMLCM focuses on grayscale statistical differences between the target and background across different directions, resulting in poor suppression of complex clutter. WLDM suppresses the background by measuring grayscale distribution complexity in local regions but performs poorly in suppressing strong edge areas with high grayscale complexity. BLCM relies on grayscale differences across multiple directional branches, making it difficult to distinguish targets from similarly distributed clutter. ELUM ignores grayscale distribution differences between the target and edge regions, leading to high false alarms at edges. In forested scenes, EVWLCM effectively enhances the target while suppressing the forest clutter. In scene 3, there is a large area of forest, where the complexity of the grayscale distribution of the clutter is high. The entropy values measured within the cross window and hollow window are both large, resulting in the LJEV close to 1. Therefore, the saliency values of the clutter in the scene are not mistakenly enhanced.

In scene 4, while all methods successfully detect the target, the proposed EVWLCM not only enhances the target but also achieves the best background suppression performance by considering both target and background characteristics. In scene 4, there are complex buildings, and, since most of these buildings do not conform to the prior Gaussian distribution, their WGLCM is much smaller than that of the target. Furthermore, due to the similarity in the grayscale distribution of the building areas, the LJEV measured using nested windows is small. Therefore, the product of the WGLCM and LJEV is very small, which means that the background areas do not interfere with target detection.

In scene 5, numerous bright corners within buildings have grayscale distributions similar to the target, causing clutter interference that is prone to incorrect enhancement, as seen in MPCM, RLCM, HBMLCM, and ELUM. Additionally, TLLCM and WSLCM mistakenly enhance the PNHB. WLDM fails to suppress the strong edges in the scene. BLCM provides limited target enhancement, causing the target to be submerged in the complex background. The proposed EVWLCM refines the energy distribution assumption of the target, enabling better differentiation between the target and similarly distributed clutter and reducing the risk of incorrect clutter enhancement. Furthermore, the EVWLCM introduces an entropy-based weighting map that accounts for spatial distribution differences between the target and background, effectively suppressing high brightness backgrounds. Consequently, the EVWLCM demonstrates robust detection performance for weak targets under strong clutter. In scene 5, there are large areas of complex buildings. Although the brightness of the buildings is high, due to their large area and similar grayscale distribution, the entropy values measured in the cross window and the hollow window within the nested windows are close, resulting in the LJEV close to 1. Therefore, the complex buildings are not mistakenly enhanced.

Scene 6 represents a complex surface scenario with tree clutter. MPCM and RLCM only consider the differences in grayscale statistics within local regions, making it difficult to effectively suppress the complex background. WLDM, HBMLCM, and ELUM ignore the grayscale distribution characteristics at the background edges, resulting in a high number of false alarms at complex edges. Since there is spotty clutter in the trees that resembles the target’s grayscale distribution, TLLCM and WSLCM enhance the target signal using a Gaussian distribution prior but erroneously enhance the tree clutter in the background. BLCM only considers the grayscale decline characteristics of the target in multiple directions to distinguish between the target and the background, neglecting the suppression of complex clutter, and therefore exhibits insufficient background suppression ability. In contrast, the EVWLCM enhances the target based on shape priors while producing almost no false alarms in the scene. For complex background areas, when measuring local entropy variation characteristics using nested window, both the CW and HW contain similar background regions with complex grayscale distributions. The entropy ratio calculated between the two results in a small LJEV weight. This LJEV can effectively perceive the joint grayscale distribution differences between the target and the background, thereby reducing clutter interference.

To demonstrate the superiority of the proposed method,

Table 4. Average SCRG of different methods.

Dataset	MPCM	RLCM	WLDM	HBMLCM	TLLCM	WSLCM	BLCM	ELUM	EVWLCM
1	9.76	110.01	8.04	31.70	232.06	316.22	223.67	6.84	541.24
2	7.96	414.46	23.88	68.01	286.03	574.03	352.27	50.21	641.45
3	10.81	425.86	8.02	52.58	59.91	794.19	53.11	6.92	830.67
4	12.14	609.31	55.79	152.10	467.86	687.84	19.57	54.98	674.56
5	9.70	910.81	38.12	153.97	602.37	1270.61	190.01	67.60	1351.23

and

Table 5. Average BSF of different methods.

Dataset	MPCM	RLCM	WLDM	HBMLCM	TLLCM	WSLCM	BLCM	ELUM	EVWLCM
1	9.33	19.07	9.42	19.43	39.68	768.92	254.16	21.17	1154.01
2	9.33	48.09	54.53	60.64	60.64	1265.29	570.23	153.06	1439.71
3	22.25	28.69	14.91	85.59	37.67	1516.86	111.85	34.42	1946.75
4	12.32	28.31	6.10	70.34	46.88	551.56	80.32	83.25	2067.66
5	12.71	12.48	8.76	62.27	21.97	692.91	209.72	49.89	1860.10

present the average SCRG and BSF values for each detection method across five datasets. The bolded entries in the tables indicate the maximum SCRG and BSF values. For datasets 1, 2, 3, and 5, the proposed method achieved optimal target enhancement and background suppression capabilities. In dataset 4, since WSLCM assumes that the target follows a standard Gaussian distribution, and the target morphology in dataset 4 is closer to an ideal Gaussian model, WSLCM’s SCRG is relatively high. However, due to the presence of clutter with similar shapes in the scene, WSLCM is unable to effectively suppress similar morphological noise in complex backgrounds, resulting in a lower BSF. The proposed method effectively amplifies the target signal by considering its energy distribution. Furthermore, it utilizes a weighting map based on the entropy variation characteristics of local regions to suppress complex backgrounds. Consequently, the proposed EVWLCM achieves a balance between target enhancement and background suppression. These results indicate that the proposed EVWLCM delivers optimal overall detection performance

Figure 14 displays the ROC curves of nine detection methods across five datasets. It is evident that the ROC curve of the proposed method consistently lies in the upper-left corner compared to the other methods, indicating that it achieves the lowest false-positive rate while maintaining a high detection rate, thus demonstrating comprehensive optimal detection performance. MCPM, RLCM, and HBMLCM mainly rely on grayscale difference characteristics between the target and background, resulting in limited enhancement capability for weak targets. BLCM utilizes the grayscale variation characteristics of targets on different directional branches to distinguish targets from noise but is easily interfered by corner-like clutter in complex backgrounds. WLDM and HBMLCM lack sufficient consideration for clutter suppression in their design, making them less adaptable to various complex scenarios and resulting in poor robustness. The WSLCM enhances targets based on Gaussian distributions and incorporates background grayscale distribution information for suppression, enabling it to suppress strong edges. However, it is prone to incorrectly enhancing bright noise points in the scene, leading to overall detection performance inferior to that of the EVWLCM. TLLCM relies on grayscale differences between layers within a three-layer window to enhance targets, making it challenging to suppress backgrounds with complex grayscale distributions. ELUM introduces target energy distribution information to design a weighting factor; however, the presence of numerous bright corner points in the scene increases the risk of incorrect clutter enhancement. Based on the above analysis, existing methods struggle to achieve a good balance between detection rate and false alarm rate. This is primarily due to the presence of corner points in complex scenes that resemble target distributions, exhibiting high contrast and leading to incorrect enhancement by these methods. In contrast, the method proposed in this paper considers the joint distribution characteristics of targets and backgrounds, thereby achieving considers detection performance.

3.5. Algorithm Computational Time

In addition to analyzing detection performance, real-time capability is also crucial for infrared small target detection. We have compiled the average computation time of the methods, as shown in

Table 6. Comparison of average computing time (in seconds) of the methods.

	MPCM	RLCM	WLDM	HBMLCM	TLLCM	WSLCM	BLCM	ELUM	EVWLCM
Time/s	0.04	0.86	4.43	0.02	0.76	1.54	0.06	0.02	0.03

. The experimental results indicate that for infrared images of size 512 × 640, on a computer with an Intel i9 14900K processor, the average processing speed of EVWLCM is 34 frames per second, which meets the requirements for real-time scenarios.

4. Discussion

Existing saliency-based detection methods exhibit strong detection capabilities for data with a high SCR and relatively simple scenarios. Nevertheless, their efficiency in detecting dark and weak targets decreases significantly in complex scenes, such as those containing buildings, cloud clutter, and forest clutter. Some classic local contrast methods, such as MPCM and RLCM, primarily rely on the grayscale difference between the target and the background. When the target’s SCR is low and it is submerged in a complex background, the grayscale difference between the target and the background diminishes, resulting in low saliency values and an increased likelihood of missed detections. This highlights considerable potential for algorithmic improvement.

To enhance the ability of the algorithms to detect dim and small targets, some methods introduce prior features for target enhancement. For instance, TLLCM and WSLCM leverage the Gaussian distribution prior characteristics of targets to filter infrared images and then compute the grayscale distribution differences between the target and the background. These algorithms have improved the detection capability for weak small targets. While these algorithms improve detection capabilities for weak small targets, real targets often deviate from prior assumptions. Consequently, clutter with similar morphological distributions to targets, such as high-brightness corners in buildings, forest clutter, broken clouds, and PNHB, is also mistakenly enhanced, leading to a higher false alarm rate.

To improve clutter suppression, some methods employ weighted functions combined with contrast information for target detection, such as WLDM, WSLCM, and ELUM. However, when designing the weight map, these algorithms either calculate it using individual target energy information or multi-directional grayscale information, or they specifically design it based on edge grayscale background distribution information in the scene. These approaches neglect the joint grayscale distribution information between the target and the background, resulting in poor adaptability to different scenarios.

The method proposed in this paper optimizes the target shape distribution assumptions while incorporating joint grayscale distribution information between the target and the background. It integrates target shape priors, multi-directional contrast information, and joint entropy variation information between target and the background. As can be seen from Figure 10, the proposed algorithm adapts effectively to different complex scenarios while maintaining robust detection performance for weak small targets. Additionally, we have compiled the average computation time for all detection methods. The average processing speed of the EVWLCM is 34 frames per second, which meets the requirements for real-time scenarios.

The EVWLCM relies on traditional features of weak infrared targets, taking into full account the morphological characteristics of infrared small targets as well as the differences in spatial gray distribution between the targets and the background. It exhibits strong robustness against weak targets in complex backgrounds such as cloud, dense forests, and highlighted buildings. However, in extremely complex scenarios, the gray distribution of extremely weak targets (0 < SCR < 2) in infrared images is blurred. At this point, the detection capability of the EVWLCM, which relies on traditional features of weak infrared targets, is relatively limited. In future research, we will collect a large amount of high-quality labeled sample data to extract more representative deep features using deep learning methods, and we will combine these with the features extracted by the EVWLCM to achieve more efficient and accurate real-time detection.

5. Conclusions

This paper proposes a novel entropy variation weighted local contrast method (EVWLCM) based on a generalized Gaussian function family and local joint entropy variation, enhancing targets while effectively suppressing the background. The experimental results indicate that the EVWLCM achieves high detection rates and low false alarm rates under various complex backgrounds. Notably, for low SCR targets (SCR ≤ 6) in complex scenes, the proposed method achieves the highest values for both SCRG and BSF, with its ROC curves consistently positioned in the upper-left corner. These results indicate that the proposed algorithm is highly adaptable to the detection of infrared weak targets in diverse complex scenarios. Furthermore, through the analysis of algorithm runtime, the EVWLCM achieves a good balance between detection capability and real-time performance. In future work, for extremely weak targets (0 < SCR < 2) in infrared images, the EVWLCM may exhibit relatively poor detection capability due to the ambiguity in the target’s grayscale distribution. We will subsequently collect a large number of high-quality annotated sample data and utilize deep-learning-based methods to extract more representative deep features, combining them with the features extracted by the EVWLCM to achieve more efficient and accurate real-time detection.