Next Article in Journal
Case Study on the Use of an Unmanned Aerial System and Terrestrial Laser Scanner Combination Analysis Based on Slope Anchor Damage Factors
Previous Article in Journal
A Deep Learning Method for Land Use Classification Based on Feature Augmentation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 8
10.3390/rs17081399
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Characterizing Seasonal Variation of the Atmospheric Mixing Layer Height Using Machine Learning Approaches

by
Yufei Chu
1,*,
Guo Lin
2,3,
Min Deng
4,
Hanqing Guo
5 and
Jun A. Zhang
2,3
1
School of Marine and Atmospheric Sciences, Stony Brook University, New York, NY 11790, USA
2
NOAA/AOML/Hurricane Research Division, Miami, FL 33149, USA
3
Cooperative Institute for Marine and Atmospheric Studies, University of Miami, Miami, FL 33149, USA
4
Brookhaven National Laboratory, Environmental and Climate Sciences Department, Upton, NY 11793, USA
5
Electrical and Computer Engineering, University of Hawaii at Manoa, Honolulu, HI 96822, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(8), 1399; https://doi.org/10.3390/rs17081399
Submission received: 21 February 2025 / Revised: 27 March 2025 / Accepted: 9 April 2025 / Published: 14 April 2025
Browse Figures
Versions Notes

Abstract

As machine learning becomes more integrated into atmospheric science, XGBoost has gained popularity for its ability to assess the relative contributions of influencing factors in the atmospheric boundary layer height. To examine how these factors vary across seasons, a seasonal analysis is necessary. However, dividing data by season reduces the sample size, which can affect result reliability and complicate factor comparisons. To address these challenges, this study replaces default parameters with grid search optimization and incorporates cross-validation to mitigate dataset limitations. Using XGBoost with four years of data from the atmospheric radiation measurement (ARM) (Southern Great Plains (SGP) C1 site, cross-validation stabilizes correlation coefficient fluctuations from 0.3 to within 0.1. With optimized parameters, the R value can reach 0.81. Analysis of the C1 site reveals that the relative importance of different factors changes across seasons. Lower tropospheric stability (LTS, ~0.53) is the dominant factor at C1 throughout the year. However, during DJF, latent heat flux (LHF, 0.44) surpasses LTS (0.22). In SON, LTS (0.58) becomes more influential than LHF (0.18). Further comparisons among the four long-term SGP sites (C1, E32, E37, and E39) show seasonal variations in relative importance. Notably, during JJA, the differences in the relative importance of the three factors across all sites are lower than in other seasons. This suggests that boundary layer development in the summer is not dominated by a single factor, reflecting a more intricate process likely influenced by seasonal conditions such as enhanced convective activity, higher temperatures, and humidity, which collectively contribute to a balanced distribution of parameter impacts. Furthermore, the relative importance of LTS gradually increases from morning to noon, indicating that LTS becomes more significant as the boundary layer approaches its maximum height. Consequently, the LTS in the early morning in autumn exhibits greater relative importance compared to other seasons. This reflects a faster development of the mixing layer height (MLH) in autumn, suggesting that it is easier to retrieve the MLH from the previous day during this period. The findings enhance understanding of boundary layer evolution and contribute to improved boundary layer parameterization.

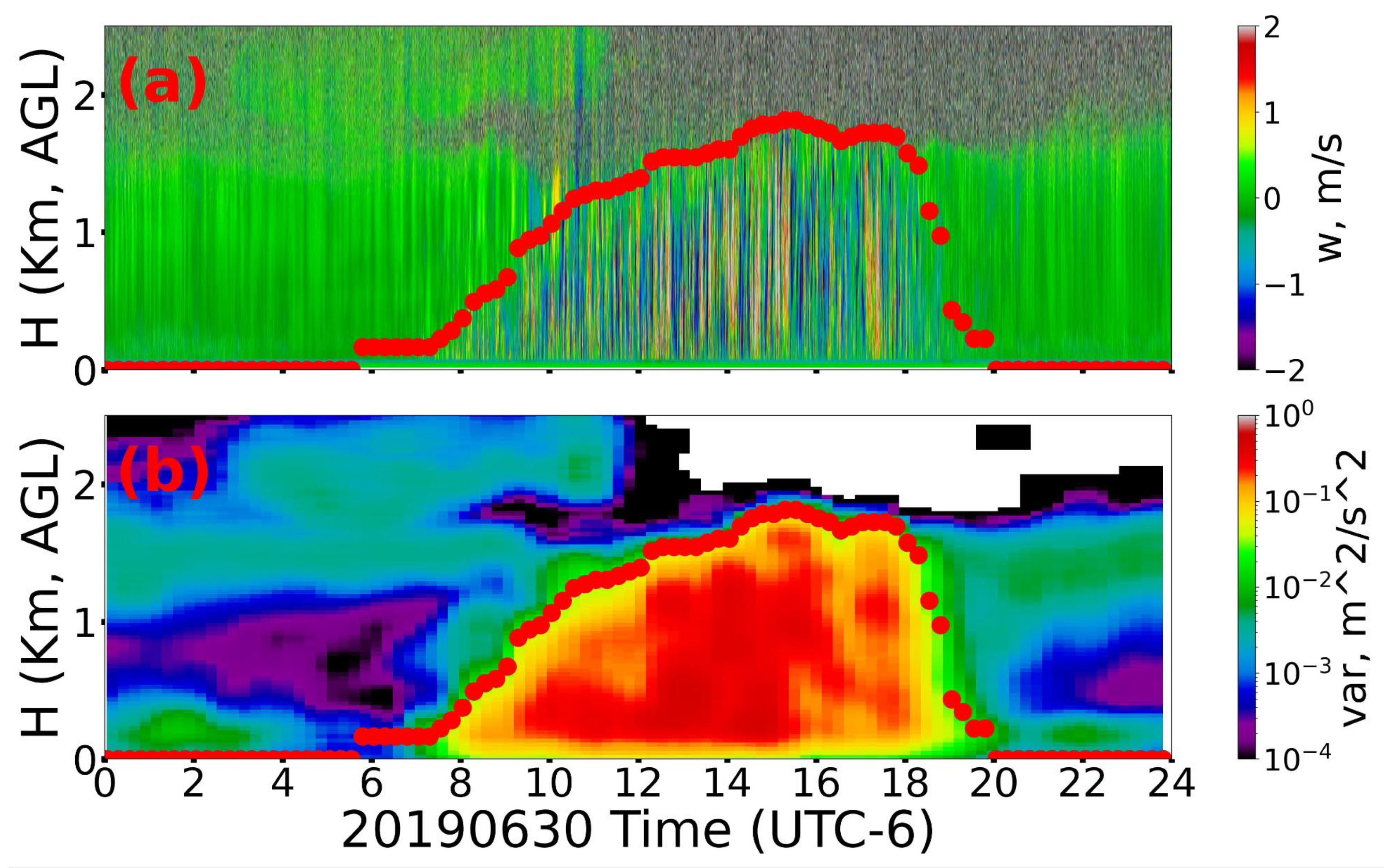
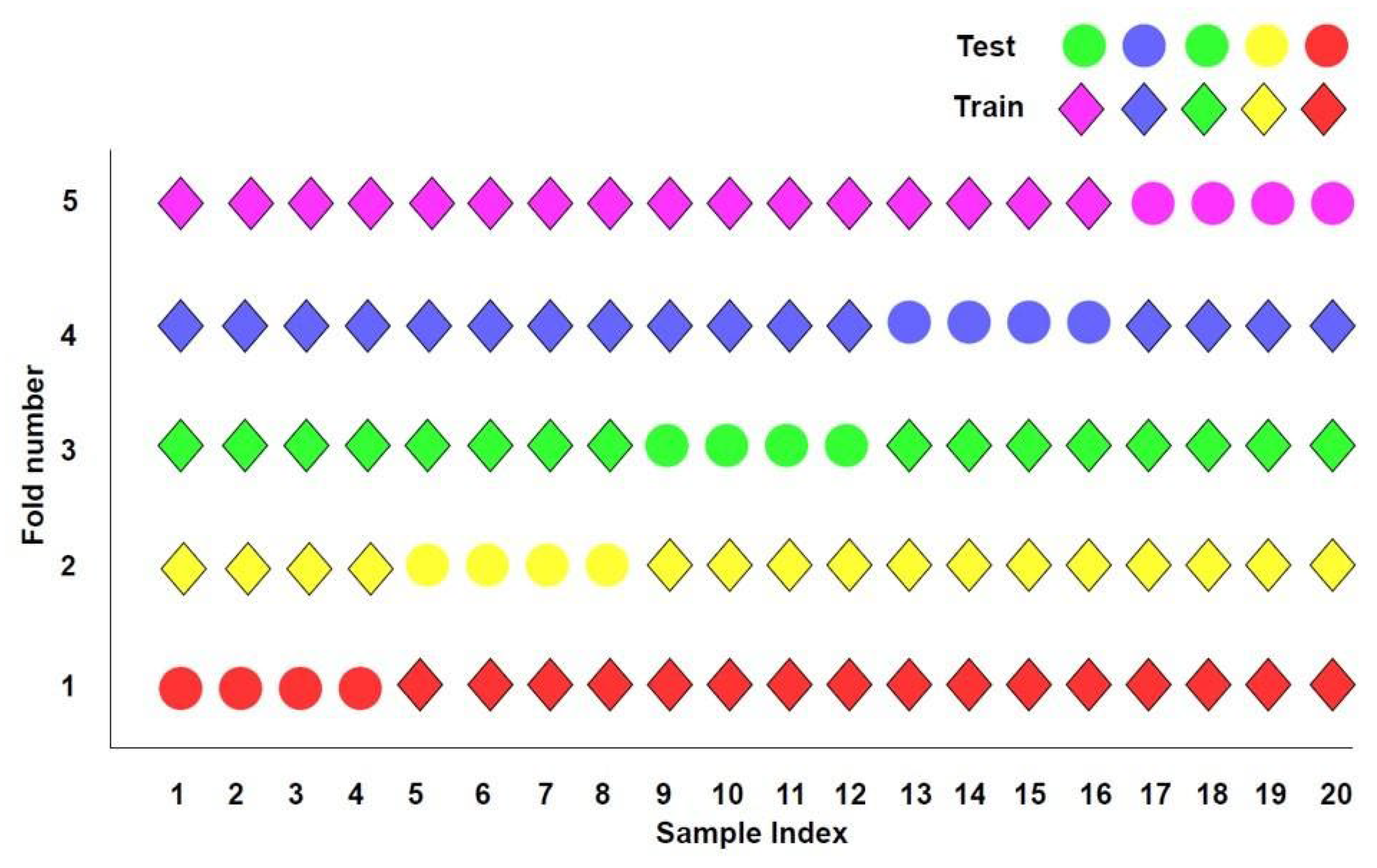
1. Introduction

With the rapid advancement of machine learning, its application in atmospheric science has expanded significantly [1,2,3]. Machine learning has become a powerful tool for analyzing and predicting complex atmospheric processes that traditional methods struggle to model. These techniques have improved our ability to understand and forecast dynamic atmospheric phenomena, particularly within the atmospheric boundary layer (ABL) [4,5,6]. The ABL plays a critical role in the Earth’s climate system through the exchange of momentum, heat, and moisture between the surface and the free atmosphere [7,8]. These exchanges in ABL directly affect the hydrological cycle, radiation balance, weather patterns, climate dynamics, and air quality. Accurate characterizing the ABL is essential for various applications, including weather forecasting, climate modeling, and pollution control [9,10,11]. However, predicting ABL behavior remains challenging due to its complexity from sensitivity to surface conditions and interactions with the broader atmosphere [8,10].
Recent advancements in machine learning have led to the development of new methods for addressing these challenges in atmospheric science studies. Models such as XGBoost and neural networks have proven effective in analyzing the impacts of meteorological parameters on the mixing layer height (MLH), a key indicator of ABL evolution [12,13,14]. These models are well-suited for handling large datasets and capturing complex, nonlinear relationships, making them effective tools for studying ABL processes. Despite these successes, most studies have relied on single field experiments or annual datasets from specific sites [15,16,17]. While these studies provide useful insights, they often overlook significant seasonal variations in ABL dynamics. It is well established that factors influencing the ABL vary by season due to changes in solar radiation, surface heating, and atmospheric stability [18,19,20].
To capture seasonal variations accurately, data need to be segmented by season. However, this approach reduces the dataset size, which may compromise the reliability of results [21,22]. Atmospheric observations are costly and logistically complex, limiting the availability of long-term, high-quality datasets. As a result, obtaining sufficient data for detailed seasonal analysis is challenging [11,23,24,25,26]. Extending the observation period can help increase the dataset size. However, it may introduce systematic errors due to instrument aging, changes in detection models, or component replacements, all of which affect data consistency [27,28]. Thus, more data do not always lead to better results. The difficulty of long-term data collection and consistency issues further complicate the issue. Researchers continue to explore ways to maximize the effectiveness of limited datasets.
To address these challenges, our study aims to integrate cross-validation with extreme gradient boosting (XGBoost) to analyze the seasonal impacts. Cross-validation is a robust statistical technique that enhances model reliability by partitioning the dataset into multiple folds, ensuring that the model is trained and tested on different subsets. Grid search optimization identifies the optimal parameter settings for the dataset, reducing errors associated with default parameters. This approach maximizes the use of available data and mitigates the risk of overfitting, thereby improving the generalizability of the results [29,30,31,32]. Building on this foundation, our study aims to provide a more refined understanding of seasonal variations in the factors influencing MLH, offering valuable insights into future atmospheric research and modeling.
Numerous meteorological factors influence ABL development, leading many studies to use dozens of input parameters. Excessive data can increase measurement errors, and if boundary layer variations can be simulated using the fewest possible parameters, these errors can be minimized. To quantify and distinguish the varying degrees of influence among these input parameters, we introduce the concept of ‘relative importance’, which serves as a metric to assess their contributions to the model’s predictive performance. Based on the boundary layer theory, both thermodynamic forcing (through buoyancy production) and shear production are key drivers of turbulence, with their relative contributions varying depending on conditions [7,10]. To capture seasonal variations in key influencing factors, this study adopts a streamlined approach by selecting sensible heat flux (SHF), latent heat flux (LHF), and lower tropospheric stability (LTS) as input variables, with the mixed layer height (MLH) as the output. This selection is guided by the boundary layer theory, where thermodynamic processes and heat flux contributions provide a physical constraint for estimating CBLH. Specifically, these parameters reflect the atmospheric heat absorption and stability dynamics that govern boundary layer development, as opposed to relying on numerous parameters without such constraints [7,10]. Additionally, our study applies cross-validation to analyze multi-year lidar data from the atmospheric radiation measurement (ARM) Southern Great Plains (SGP) site [13,33,34].
Therefore, this study focuses on heat fluxes (SHF, LHF) and LTS, utilizing the XGBoost algorithm to predict MLH and analyze the relative contributions of these factors. The structure of this paper is as follows: Section 2 introduces the dataset used, along with the cross-validation and XGBoost methods. Section 3 validates the consistency of the results obtained using the XGBoost method alone and the combined approach of cross-validation and XGBoost. Section 4 investigates the influence of various factors on the mixed layer height (MLH) at the four ARM Southern Great Plains (SGP) sites (C1, E32, E37, E79) across different seasons, employing a combination of cross-validation and the XGBoost method. Subsequently, we compare the relative influence factors and their variations at different times of day across seasons, further informed by analyses of wind direction and SHAP value. Finally, this paper concludes with a conclusion.

2. Materials and Methods

2.1. ARM SGP Site Datasets and MLH

The DOE Atmospheric ARM SGP supersite contains five observational sites in Oklahoma for multiple-year ground-based observations (Table 1). Since 2016, the DOE ARM SGP supersite has provided a comprehensive dataset covering surface fluxes, radiation, atmospheric profiles, and detailed PBL observations [33]. This study utilizes multi-year (2016–2019) vertical wind data from Doppler lidar, along with SHF, LHF, and LTS measurements, as summarized in Table 1.
All Doppler lidars (DLs) used in this study are Halo Photonics Stream Line models that operate at a wavelength of 1.5 microns. The algorithm for determining MLH, developed by Chu et al. [34], is applied to the multiple-year vertical wind dataset. This algorithm effectively identifies the MHL, even with underlying challenges such as variation of turbulent eddy scales, the influence of gravity waves on velocity variance estimates, and the limitations of fixed variance threshold methods. The process begins with wavelet analysis to assess whether large-scale turbulence eddies dominate on a given day. This assessment covers all heights to construct a 2D vertical velocity variance profile by isolating the power spectrum within a specific frequency range corresponding to turbulence eddy size. Dynamic thresholds are then applied to this reconstructed variance profile, ensuring accurate MLH determination.
To characterize the daily cycle, this study leverages a variety of instruments and their respective measured quantities. For instance, the Atmospheric Emitted Radiance Interferometer (AERI) measures downward infrared spectra to derive temperature and water vapor profiles. The radiosonde (sonde) captures vertical profiles of temperature, humidity, and wind speed during its ascent. The Eddy correlation flux measurement system (ECOR) or the energy balance Bowen ratio (EBBR) system quantifies surface sensible and latent heat fluxes. Collectively, these instruments provide comprehensive observational data to underpin the analysis.
A typical daily cycle of MLH is shown in Figure 1 to visually illustrate the boundary layer development process. After sunrise, the ground heats up under sunlight, which in turn warms the atmosphere and generates turbulence. This turbulence, as seen in the vertical wind field data in Figure 1, causes the ML to rise gradually. By the afternoon (~15:00 UTC-6), MLH reaches its maximum altitude at approximately 1.8 km and fluctuates near this peak. After sunset, turbulence decreases, leading to the rapid dissipation of the ML. The bottom subplot of Figure 1 presents the variance of the vertical wind field, calculated using the previously described algorithm. The solid red dots indicate the MLHs determined by the method introduced in this study. Note that the data used in this study are limited to clear or non-precipitating high-cloud scenarios and do not include rainy or low-cloud days.
Although the C1 site lacks direct heat flux measurement instruments, the nearby E14 site, located within 1km and equipped with ECOR, provides comparable heat flux measurements. LTS is defined as the difference in potential temperature (θ) between the free troposphere (700 hPa) and the surface (~1000 hPa). LTS can be calculated using sounding data and the AERI. Previous research has demonstrated that LTS measurements obtained from AERI and radiosonde data are equivalent [13]. To avoid drift issues associated with sounding data, this study primarily relies on AERI data.
To compare SHF and LHF across different sites, the empirical substitution method proposed by Chu et al. [13] is applied to convert EBBR values into ECOR-equivalent values. Specifically, at the E32 site, where ECOR measurements are unavailable and only EBBR flux data are provided [35], we use the relationship HF_ECOR = 0.83 × HF_EBBR + 21.77 W/m2 to ensure consistency in flux comparisons across sites. The same study’s approach is followed to calculate LTS from AERI data at the C1, E32, E37, and E39 sites collected between 2016 and 2019. The dataset for machine learning is selected from the ARM sites C1, E32, E37, and E39, covering the period from 2016 to 2019. This dataset includes Doppler lidar vertical wind field data, heat flux measurements (ECOR/EBBR), and LTS values (AERI). After preprocessing, we selected LTS at 5:30 AM (UTC-6) and the cumulative SHF and LHF from sunrise to 11:30 AM as input features, with the MLH at 11:30 AM serving as the true output data for this machine learning study. This selection is motivated by the following: the heat flux at 11:30 AM represents the cumulative heat supplied by SHF and LHF from sunrise to that time, whereas LTS at 5:30 AM reflects the amount of heat required to lift the boundary layer to a specific height from early morning to midday, consistent with thermodynamic principles. For a convenient and accurate comparison, we selected days with complete MLH data available across all four sites for the analysis.

2.2. XGBoost Method

Among the various machine learning techniques, ensemble methods such as boosting have proven particularly effective in atmospheric detection applications. The evolution of the MLH is a complex process influenced by numerous factors, with many of these interactions being non-linear [1,3,17]. Therefore, machine learning holds significant potential for advancing research in the ABL field.
XGBoost integrates gradient boosting techniques with advanced optimization algorithms to deliver a highly efficient model capable of capturing both linear and non-linear relationships among variables. It employs decision trees as base learners—simple tree-like structures that split data based on feature thresholds—to iteratively refine predictions. In this process, XGBoost minimizes prediction errors by calculating the gradient of a loss function (e.g., mean squared error) and adjusting the model step-by-step to better fit the data, a technique known as gradient boosting. To illustrate, each new decision tree focuses on correcting the residuals (errors) of the previous trees, progressively improving the overall prediction accuracy. Additionally, XGBoost incorporates regularization techniques, such as L1 (Lasso) and L2 (Ridge) penalties, which constrain the complexity of the decision trees to prevent overfitting, thereby maintaining model robustness even in complex scenarios with noisy or high-dimensional data. Widely recognized for its effectiveness, XGBoost has become a popular machine learning method, celebrated for constructing accurate and computationally efficient predictive models [31,32]. For a visual representation of its workflow and parameter impacts, readers are referred to Section 2.4.
In most existing atmospheric science literature, XGBoost is typically used with its default parameters. The n_estimators parameter refers to the number of trees to be trained in the XGBoost model. Each tree works to correct the errors of the previous tree, which gradually reduces the overall error. If the n_estimators parameter is set too low, the model may underfit because it lacks sufficient trees to capture the complex patterns in the data. Conversely, if set too high, the model may overfit, as it might overly capture the noise in the training data. Typically, the n_estimators parameter is adjusted through cross-validation to find a balance between underfitting and overfitting. A common starting point is 100–200, which can be gradually increased to observe the effects [13,31].
The learning_rate parameter controls the contribution of each tree to the final model prediction. It determines the step size during each boosting process, or the degree to which each tree influences the final model. A small learning rate means that each tree has a smaller impact on the final prediction, which requires more trees (higher n_estimators) are needed to achieve the same level of fit. A large learning rate allows the model to converge faster but might skip the optimal solution. A typical starting point is 0.1, with adjustments made based on model performance. Smaller learning rates (e.g., 0.01) usually result in a more stable model but require a higher n_estimators parameter [36].
The max_depth parameter controls the maximum depth of each tree or the number of layers the tree can grow. Deeper trees are capable of capturing more complex patterns. However, deeper trees are more prone to overfitting. Shallow trees might fail to capture the complex relationships in the data, leading to underfitting. Starting with a smaller depth (e.g., 3 or 5) and gradually increasing while observing model performance is recommended. Typically, a depth between 3 and 10 is considered suitable [36].
In this study, we utilized the XGBoost package within Python 3.11’s machine learning framework to conduct our analyses. The XGBoost models were designed to investigate the relationships between MLH and key explanatory variables such as SHF, LHF, and LTS. The model was initialized with a default setup of 100 decision trees with a learning rate of 0.1 and a maximum depth of 3. The dataset was split into training and testing subsets, with two-thirds used for training and one-third for testing, ensuring a robust validation process. This setup allowed us to assess the model’s accuracy in predicting MLH. The importance of each explanatory variable was determined by its selection frequency during the XGBoost process, weighted by the improvement each partition contributed. At each iteration, predictions from the current sequence of trees informed the fitting of the subsequent tree, progressively improving model accuracy and stability.

2.3. Cross-Validation

Cross-validation is a widely used statistical technique in machine learning and data science for evaluating the performance and generalizability of predictive models. Unlike traditional methods that rely on a single training–testing split, cross-validation offers a more robust and reliable assessment of a model’s ability to perform on unseen data. This approach is particularly valuable when dealing with limited datasets, as it maximizes the effective use of available data. The core concept of cross-validation involves dividing the dataset into multiple subsets or “folds”, where each fold serves as a testing set while the remaining folds are used for training. One of the main benefits of cross-validation is its effectiveness in reducing overfitting. By training the model on various data subsets and validating it on unseen portions, cross-validation helps prevent the model from becoming overly specialized to a particular subset, which can otherwise result in poor performance on new data. Additionally, this technique provides insights into the variability of the model’s performance, contributing to a better understanding of its stability and robustness [37].
A common method for model evaluation is k-fold cross-validation, where the dataset is divided into k equally sized folds. The model is trained on k−1 of these folds and validated on the remaining fold. This process is repeated k times, with each fold serving as the validation set exactly once. The model’s performance is then averaged across the k iterations, yielding a comprehensive evaluation metric that reflects the model’s ability to generalize to unseen data. For example, as illustrated in Figure 2, consider a dataset of 20 subsets with the k-fold number set to 5. In the first iteration, subsets 1–4 are used as the test group, while subsets 5–20 serve as the Train group. In the second iteration, subsets 5–8 are designated as the test group, with subsets 1–4 and 9–20 as the Train group. This process is repeated for all 5 iterations, and the final result is obtained by averaging the performance across these iterations.
To assess the effectiveness of different parameter configurations, the scoring metric in cross-validation or grid search (e.g., GridSearchCV) often uses the negative mean squared error (neg_mean_squared_error). Mean squared error (MSE) is a common measure in regression models that quantifies the average squared difference between the predicted and actual values. Formula [38] is as follows:
M S E = 1 n ∑ i = 1 n y i − y ^ i 2
where y i represents the actual values, y ^ i represents the predicted values, and n denotes the number of samples. In GridSearchCV, a higher score indicates a better model; however, MSE is inherently a non-negative value where lower values are preferred. To reconcile this with the scoring requirements of GridSearchCV, MSE is converted into its negative counterpart (neg_mean_squared_error). This transformation allows the hyperparameter tuning process to select the parameter combination that maximizes this score, which effectively corresponds to minimizing the MSE.

2.4. Cross-Validation Combined with XGBoost

In this study, when developing models to predict MLH or to assess the impact of SHF, LHF, and TS on boundary layer development, cross-validation is employed to rigorously evaluate the model’s performance across different subsets of the data. The cross-validation and XGBoost workflow utilized in this study is illustrated in Figure 3.
  • Firstly, we collected heat flux data, DL vertical wind field data, and AERI temperature data as described in Section 2.1.
  • Based on the collected data and the algorithm outlined in Section 2.1, we preprocessed the cumulative SHF and LHF at 11:30, LTS at 5:30, and MLH at 11:30 for each day. Additionally, data from rainy and low-cloud days were excluded.
  • The cross-validation setup was executed using Python’s scikit-learn library, employing the KFold and cross_val_score functions. The data were partitioned into several folds (KFold with n_splits), with shuffling enabled (shuffle = True) and a fixed random seed (random_state = 42) to ensure reproducibility. This scheme was designed to rigorously evaluate the model’s performance across different subsets of the data.
  • Next, we initialized the machine learning model using the XGBRegressor from the XGBoost library. The model was configured with 100 estimators (or more), a learning rate of 0.1, and a maximum depth of 3 (or more), while the random state was also set to 42 to maintain consistency across experiments. The model was then trained.
  • The model was evaluated using the procedure. For each fold, the training and testing sets were derived based on the indices provided by the KFold split. The model was trained on the training set, and predictions were made on the testing set. The model’s performance was assessed by calculating the MSE and the coefficient of determination (R) for each fold.
  • The overall performance of the model was determined by averaging the MSE and R2 scores across all folds. If the results met the predefined criteria (minimum mean absolute error, MAE) for model performance, the configuration was finalized and saved. Otherwise, the cross-validation setup was reconfigured, and the process was repeated to achieve optimal model performance.
Fortunately, we can use GridSearchCV to identify the optimal combination of hyperparameters. When utilizing GridSearchCV, the commonly used default hyperparameters in param_grid are typically set as ‘n_estimators’: [50, 100, 200], ‘learning_rate’: [0.01, 0.1, 0.2], and ‘max_depth’: [3, 5, 7]. GridSearchCV conducts an exhaustive search across the specified parameter values. For each combination, it trains the model, performs cross-validation, and evaluates performance using the selected scoring metric, such as neg_mean_squared_error. This process iterates through all the hyperparameter combinations specified in param_grid. In the example above, it would assess 3 × 3 × 3 = 27 different combinations. The optimal combination is then selected based on the results from Equation (1). The selection of candidate hyperparameters is tailored to the characteristics of our dataset. For details, refer to Section 3.1.

3. Validation of the Two Methods Using the ARM Site Dataset

3.1. Impact of Different Parameter Settings on the Results of the XGBoost Algorithm

To examine the impact of different XGBoost parameters on the results, we tested various parameter combinations, as shown in Table 2. The range of n_estimators is 50–400, learning_rate varies from 0.01 to 0.5, and max_depth ranges from 3 to 9. In Table 2, the leftmost column, labeled “Group”, represents comparisons where only one parameter is adjusted while the others remain constant. Groups 1–3 compare the effects of n_estimators, learning_rate, and max_depth, respectively. Groups 4 and 5 involve manual tuning to identify the optimal parameter combination.
From Group 1, we observe that the correlation coefficient R2 increases as the number of estimators (n_estimators) increases. In this case, learning_rate and max_depth are fixed at 0.1 and 3, respectively. As the n_estimators parameter increases from 50 to 300, R improves from 0.60 to 0.73. Additionally, LTS decreases while SHF and LHF increase as the n_estimators parameter increases. Although a higher n_estimators parameter improves R, considering that the number of sampling days in this study is under 1000, setting n_estimators too high is not recommended. To balance performance and computational efficiency, it should remain below 200.
Group 2 shows that the correlation coefficient R2 increases as the learning_rate rises. In this case, n_estimators and max_depth are fixed at 100 and 3, respectively. As learning_rate increases from 0.01 to 0.5, R2 improves from 0.48 to 0.78. This trend is expected, as R2 is the lowest (0.48) when learning_rate is set to 0.01. Additionally, as learning_rate increases, the relative influence of LTS decreases, while SHF and LHF gain more importance. Since our sample size is under 1000, we do not recommend using a very low learning_rate. To maintain model efficiency and accuracy, it should be kept above 0.1.
Group 3 demonstrates that the correlation coefficient R2 increases as max_depth increases. In this case, n_estimators and learning_rate are fixed at 200 and 0.3, respectively. As max_depth increases from 3 to 9, R improves from 0.79 to 0.84. However, the change in R becomes minimal (less than 0.05) when max_depth increases from 5 to 9. Similarly, the relative influence of LTS, SHF, and LHF shows only slight variations. Since our sample size is under 1000, we do not recommend setting max_depth too high. To balance performance and computational efficiency, it should be kept below 7.
The objective of Group 4 is to evaluate the impact of varying other parameters while keeping max_depth fixed at 5. The results show that when n_estimators is set to 400, the difference in R2 between the learning_rate values of 0.1 and 0.5 is less than 0.01. However, when n_estimators is set to 100, the change in R2 between the same learning_rate values is slightly larger, at less than 0.08. Additionally, the difference in R2 between the parameter combinations (n_estimators, learning_rate) = (400, 0.1) and (100, 0.5) is also less than 0.01. This indicates that the relationship between R2 and these parameters is not strictly linear, and different parameter combinations can yield similar results. However, while R values may be comparable, slight differences remain in the relative influence of LTS, SHF, and LHF.
Group 5 builds on Group 4 by varying the max depth, further confirming that the relationship between the correlation coefficient R2 and the parameters is not linear, and different combinations can produce similar results. Therefore, it is necessary to carefully select XGBoost hyperparameters rather than simply using the default settings.

3.2. Impact of Different Cross-Validation Parameter Settings on the Results of the XGBoost Algorithm

The results in Section 3.1 indicate that different XGBoost parameters significantly affect the outcomes. The default hyperparameters are typically set as ‘n_estimators’: [50, 100, 200], ‘learning_rate’: [0.01, 0.1, 0.2], and ‘max_depth’: [3, 5, 7]. The results obtained using these default parameters are shown in Table 3 under ‘Default Parameters’. The results show that although the value of R does not change significantly (less than 0.01) as N splits vary from 3 to 12, the R2 value remains around 0.6. Further analysis revealed that although we set ‘learning_rate’, i.e., [0.01, 0.1, 0.2], and ‘max_depth’, i.e., [3, 5, 7], the learning rate actually selected was 0.01. This is because the software tends to select a smaller learning rate by default to prevent overfitting. However, due to the limited sample size in this study, a smaller learning rate may prevent finding the optimal solution. Additionally, to prevent overfitting, the number of estimators (n_estimators) should not be set too high, so we need to set a larger learning rate. Moreover, the relationship between MLH (mixing layer height) and LTS, SHF, and LHF is a complex nonlinear relationship, so we also set the learning rate to be above 0.3.
The results obtained using the optimized hyperparameters are presented in Table 3 under ‘Optimized Parameters’, showing improved performance. Based on the results from Section 3.1 and the default parameters, and considering the specifics of this dataset, the hyperparameters were set as ‘n_estimators’: [50, 100, 200], ‘learning_rate’: [0.3, 0.5, 0.7], and ‘max_depth’: [5, 7, 9]. The results show that the R value is 0.83 when n_splits is 3, and it remains around 0.81 within the range of 3–15. Additionally, the relative influence factors for LTS, SHF, and LHF are 0.50, 0.28, and 0.22, respectively. This indicates that due to the small sample size, increasing the number of splits beyond a certain point does not affect the final averaged results.
The effect of different K values on the correlation coefficient R2 is minimal; however, the impact on the relative importance of influencing factors is more pronounced. As illustrated in Table 3, the R2 values for K = 3 and K = 5 are 0.83 and 0.81, respectively, with a relative error of approximately ~0.02. In contrast, the variation in LHF can reach up to 0.09. This indicates that the choice of K values significantly influences the results, highlighting inconsistencies in performance across different datasets. Based on this evaluation, we determined that K = 3 provided the optimal performance among the tested values (3, 5, 7, 9, 12, 15) and, thus, it was consistently adopted in subsequent analyses, including Section 4. A possible explanation for this could be the seasonal variation in the relative importance of influencing factors. However, a prerequisite for studying the relative importance of seasonal variations is that the model must be sufficiently accurate, meaning the correlation coefficient (R2) should be adequately high, typically exceeding 0.8. Only when the model achieves such accuracy does the analysis of relative importance gain credibility.

4. Relative Influence Factors Across Different Seasons

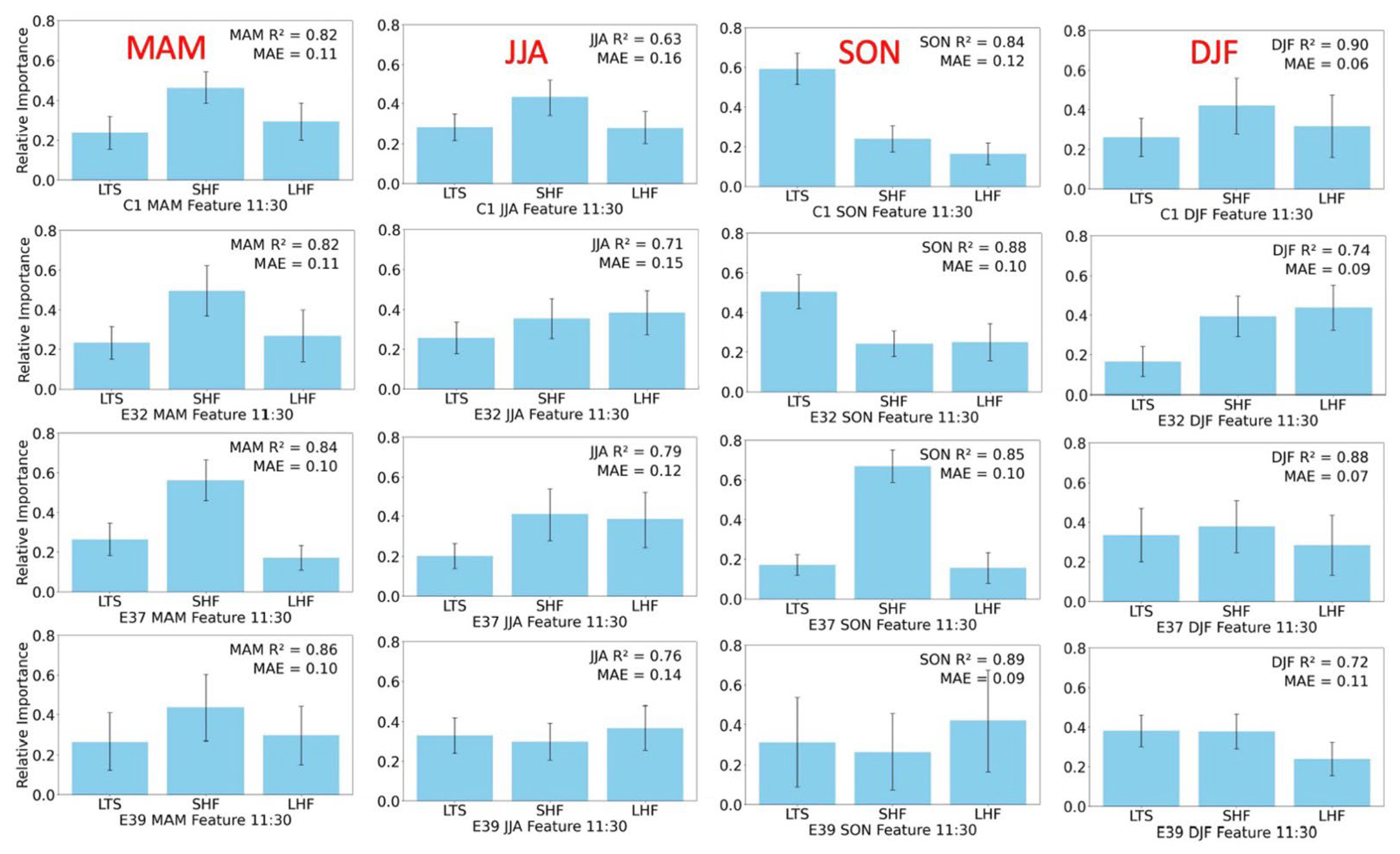
To compare the relative influence factors of LTS, LHF, and SHF across different seasons, we applied the optimized parameters to the SGP sites. Since the dataset becomes smaller when divided by season, we now choose K = 3, as shown in the first row of Figure 4. And the hyperparameters for individual seasons were set as follows: ‘n_estimators’: [50, 100, 200], ‘learning_rate’: [0.1, 0.3, 0.5], and ‘max_depth’: [3, 5, 7]. The dataset is divided into four seasons. DJF represents December, January, and February for winter; MAM represents March, April, and May for spring; JJA represents June, July, and August for summer; SON represents September, October, and November for autumn. To further compare the spatiotemporal variations across different sites and seasons, we combined and analyzed the seasonal data from C1, E32, E37, and E39, as presented in Figure 4. The first row corresponds to the C1 site, the second row to the E32 site, the third row to the E37 site, and the fourth row to the E39 site. Additionally, the first column represents DJF (winter), the second column represents MAM (spring), the third column represents JJA (summer), and the last column represents SON (autumn).
The relative influence of key atmospheric factors varies significantly across seasons, deviating notably from the annual trends. At the C1 site, LTS dominates in SON, reaching a relative importance of 0.6, whereas in other seasons, SHF becomes the primary factor (MAM: 0.5, JJA: 0.42, DJF: 0.4). Since JJA and SON contain more data points compared to DJF, LTS appears as the dominant factor in the annual analysis with value approximately 0.5 (Table 3). Additionally, during JJA, the relative contributions of LTS, SHF, and LHF are more balanced, with differences within 0.2, indicating a more equitable contribution of all three factors to ML development. In contrast, SON exhibits a more pronounced variation, with differences reaching up to 0.4, reinforcing the seasonal dependence of ML evolution. Comparing Table 3, the annual correlation coefficient at C1 is 0.83, whereas the seasonal values in Figure 4 are 0.90 for DJF, 0.82 for MAM, 0.84 for SON, and only 0.63 for JJA, indicating substantial seasonal variations. Although JJA contains more data points than MAM, it exhibits a lower R², suggesting that a greater proportion of boundary layer development in summer is influenced by other meteorological factors or that the controlling mechanisms are more complex during this season.
From the perspective of ABL evolution theory, a higher MLH generally corresponds to a greater influence from LTS, further confirming that MLH reaches its peak during SON. Additionally, C1 and E37 exhibit stronger LTS influences compared to E32 and E39, particularly in SON and JJA, suggesting greater sensitivity to stability-driven mechanisms at these locations. However, the variance in relative importance at E39 is notably larger, especially in SON, due to the significantly smaller dataset of only 70 samples, compared to 125 samples at C1. This suggests that dataset size has a considerable impact on the reliability of the results.
These results also highlight the need to consider the impact of MAE and dataset quality. Winter (DJF) consistently shows the lowest MAE values (<0.1), largely due to the inherently lower MLH during this season. In contrast, JJA exhibits the highest MAE values, partially because of the stronger turbulent-driven force in summer, leading to greater variability of MLH in model performance. SON and JJA have relatively high MAE values, with E32 in JJA reaching up to 0.16, indicating greater model uncertainty during these seasons. If an annual model were used, the MAE would exceed 0.15 (not explicitly shown in this study), highlighting the site-specific variations in feature importance and reinforcing the role of LTS in boundary layer growth, particularly in SON and JJA. The discrepancies in MAE and R² values across sites emphasize the necessity of further research into localized atmospheric processes affecting MLH variability. These findings suggest that ML development is highly sensitive to seasonal and regional variations in stability, surface fluxes, and local meteorological conditions.

5. Discussion

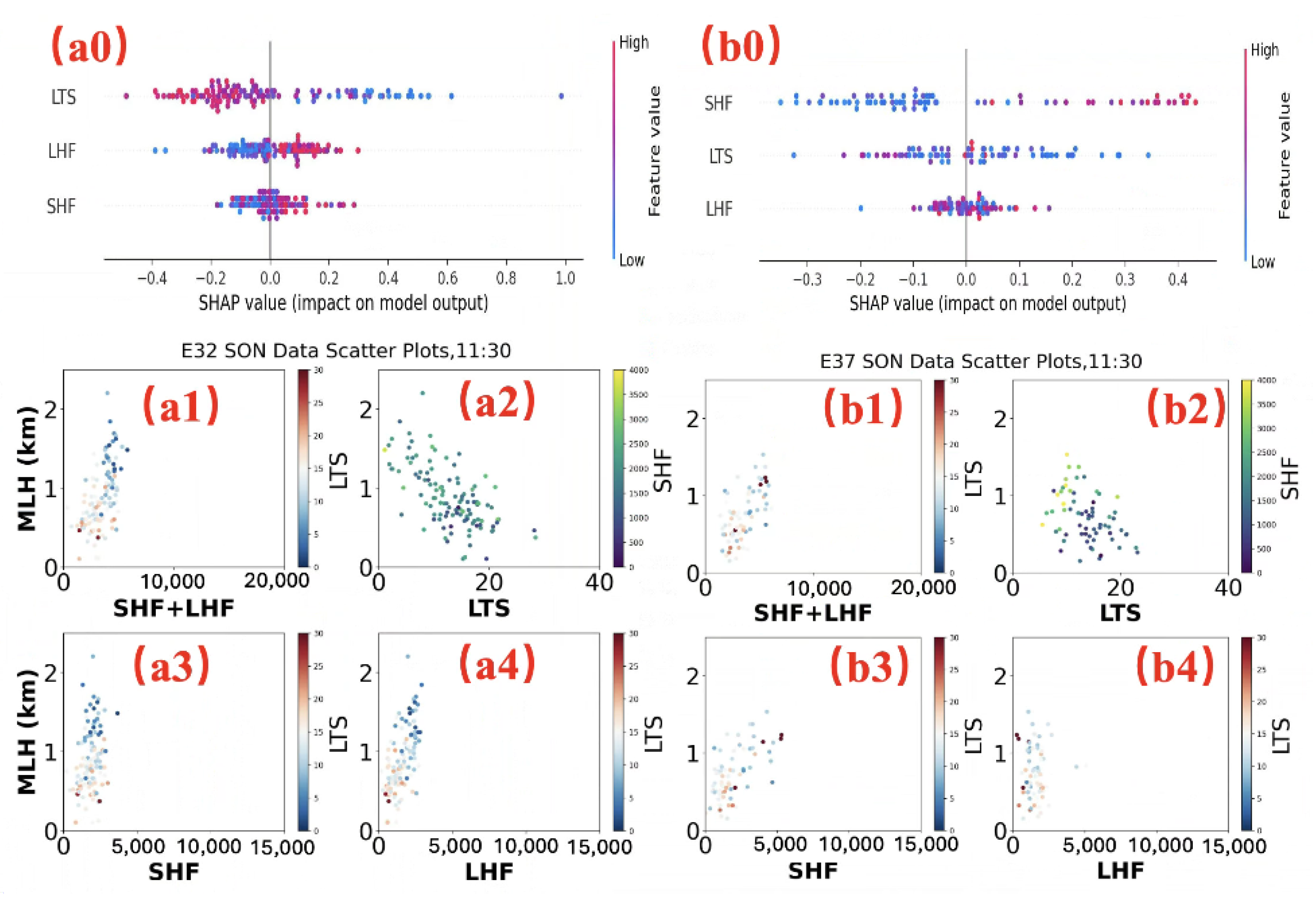
To interpret the results shown in Figure 4, where LTS is the dominant factor at E32 during SON, while SHF is the dominant factor at E37, we employed SHAP (SHapley Additive exPlanations) [39,40], a widely-used tool for interpreting machine learning model predictions. SHAP, rooted in Shapley values from game theory, explains model outputs by attributing contributions to each feature. These SHAP values quantify the impact of each feature on the prediction, allowing researchers to elucidate the model’s decision-making process, identify key contributing factors, and improve model performance. Specifically, positive SHAP values reflect a feature’s positive contribution to the MLH, a value of 0 indicates no influence and negative SHAP values signify a negative contribution, where an increase in the feature value reduces MLH. The results derived from our model are illustrated in Figure 5, where (a0) and (b0) depict the SHAP value beeswarm [39] plots for the E32 and E37 sites, respectively. And the a1–a4, and b1–b4 are the scatter plots of SHF, LHF, and LTS with MLH for the E32 and E37 sites, respectively.
Figure 5(a0) shows a predominantly negative correlation between LTS and SHAP values. Similarly, Figure 5(a2) also indicates a negative correlation, though it is less pronounced than in Figure 5(a0). Additionally, Figure 5(a0) reveals a positive correlation between LHF and SHAP values, a trend further supported by the scatter plot in Figure 5(a4). In contrast, Figure 5(b0) demonstrates that the correlation between LHF and SHAP values at the E37 site is weaker than at the E32 site, a pattern also reflected in Figure 5(b4). Meanwhile, Figure 5(b0) highlights a positive correlation between SHF and SHAP values, which is confirmed by the scatter plot in Figure 5(b3). However, the relationship between SHF and SHAP values in Figure 5(a0) is less evident, as shown in the scatter plot in Figure 5(a3). Notably, Figure 5(a1,5b1) demonstrate that the combined SHF and LHF exhibit a positive correlation with MLH. Specifically, at the ARM SGP sites, such as E37 and E32, which are approximately 57 km apart, these findings highlight the influence of local parameters (SHF and LHF) over broader meteorological conditions, as LTS remains relatively consistent across sites while SHF and LHF vary significantly. While the total SHF + LHF remains similar, the distribution between SHF and LHF is largely influenced by local factors.
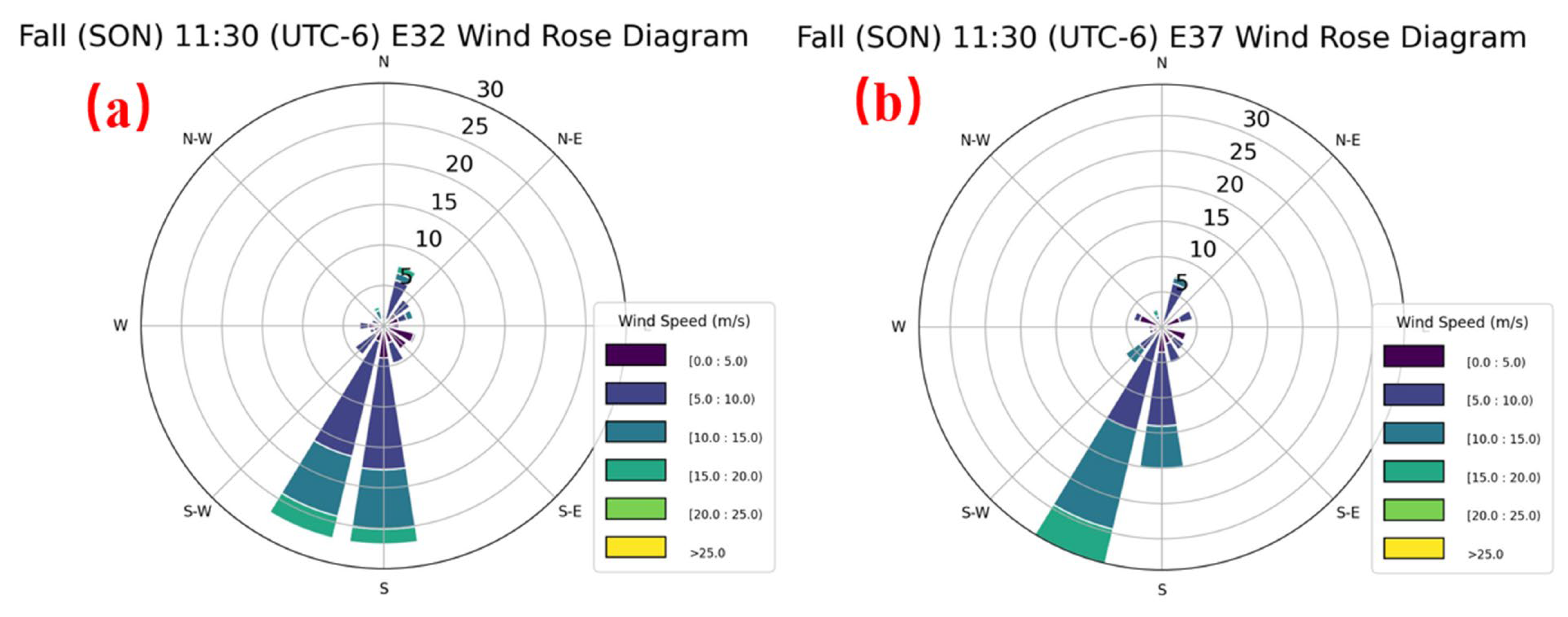
By analyzing the SHAP values of the model, we can clearly understand how the differences in relative influencing factors between different sites are determined. However, further investigation is needed to identify the underlying causes of these differences. In addition to local factors, wind direction appears to correlate with relative impact factors. To examine this relationship, wind rose diagrams were generated for each site across different seasons, using data over identical day counts as in Figure 5, with results presented in Figure 6. By comparing Figure 4 and Figure 6, we aim to clarify certain differences in relative impact factors. By comparing Figure 4 and Figure 6, we seek to elucidate differences in relative influence factors across sites and seasons. As depicted in Figure 4, during the SON season, LHF is more influential at site E32 (~0.50), whereas SHF predominates at site E37 (>0.60). Analysis of wind direction in Figure 7 indicates that, at E32 during SON, winds primarily originate from the south (180 ± 15°) and southwest (210 ± 15°), each with a probability of approximately 27%. At E37, southwest winds (210 ± 15°) occur with a higher probability (>30%), significantly exceeding the 15% probability of south winds (180 ± 15°). This difference suggests that south winds, which are typically more humid, enhance latent heat flux (LHF), whereas south-southwest winds, often drier, contribute less moisture. Consequently, LHF remains relatively stable at approximately 0.35 during JJA, likely reflecting the influence of prevailing humid south winds in the summer season.
The discussion above demonstrates the effectiveness of machine learning in analyzing the relative impacts of factors such as SHF, LHF, and LTS on boundary layer processes. However, the analysis focused on wind direction as an example to explore seasonal variations in relative impact factors across different locations. ABL drivers are inherently complex and dynamic, and thus, focusing solely on instantaneous values of SHF, LHF, and LTS is insufficient. Future research should incorporate additional boundary layer parameters and investigate how these factors interact dynamically to influence boundary layer development over time.
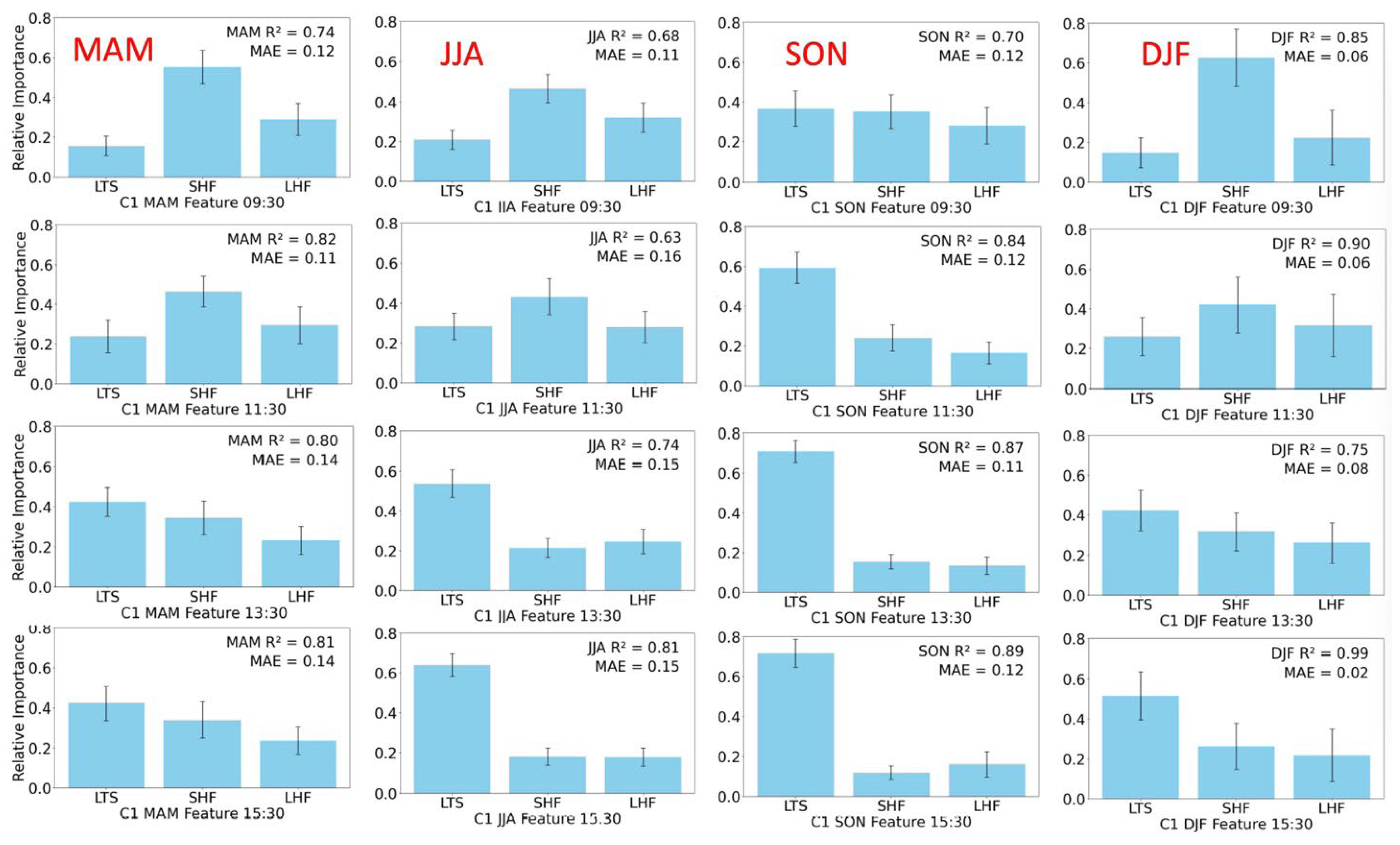
To further investigate the variations in relative importance across different seasons and time points, we analyze the changes at specific hours throughout the day. As shown in Figure 7, we evaluate four distinct time points from 9:30 AM to 3:30 PM, sampled at two-hour intervals across all four seasons. A notable trend is observed in the relative importance of LTS, which gradually increases from the morning to the afternoon across all seasons. Taking JJA as an example, the relative importance of LTS starts at approximately 0.2 at 9:30, increases to 0.28 at 11:30, reaches 0.4 at 13:30, and further rises to 0.6 at 15:30. This suggests that as the ABL develops, the role of LTS becomes increasingly significant. Initially, the ABL is less influenced by LTS, but as it grows towards the ABL top, a higher LTS necessitates a stronger flux-driven mechanism. This observation aligns well with ABL evolution theories, as discussed in the published literature on ABL [7,13,18].
Moreover, the SON season exhibits distinct characteristics. At 9:30 AM, the relative importance of LTS is close to 0.4, significantly higher than the other three seasons, where it remains below 0.2. This indicates that during autumn, the boundary layer reaches its top more rapidly. Conversely, in winter (DJF), the LTS at 9:30 AM is below 0.2, and despite a steady increase throughout the day, it only reaches approximately 0.4 at 3:30 PM. This suggests that during spring (MAM), the MLH encounters greater resistance in reaching the previous day’s boundary layer top. Additionally, comparing JJA and SON, the LTS during summer starts at 0.2 at 09:30 AM and increases to 0.6 at 3:30 PM, consistently lower than its autumn counterpart at corresponding time points. While summer exhibits stronger heat flux and a lower average LTS, the ascent rate of the ABL remains slower than in autumn. The reason for this phenomenon is that the relative importance of LTS gradually increases from morning to noon, indicating that LTS becomes more critical as the ABL approaches its maximum height. This occurs because further growth beyond the boundary layer top requires significantly more energy, and LTS represents the thermal energy needed to reach this threshold [9]. Consequently, the LTS at 9:30 in autumn (SON) exhibits greater relative importance compared to other seasons. This reflects a more rapid development of the MLH in autumn, suggesting that residual layers from precipitation may facilitate easier attainment of the ABL height from the previous day. Thus, Figure 7 provides valuable insights into the seasonal evolution of the ABL.
An interesting observation in DJF is that the MAE values remain below 0.1, with some as low as 0.02, while the R² values range from 0.75 to 0.99. Despite these seemingly favorable metrics, the error bars for relative importance are larger than those of other seasons, indicating significant fluctuations in model predictions. This instability is primarily attributed to data limitations: despite employing K-fold cross-validation, the effective data sample for DJF remains small, with only 60 days of observations, whereas JJA contains 156 days. Consequently, the model in DJF leads to higher variance in importance scores.

6. Conclusions

This study integrates XGBoost and cross-validation to analyze the relative importance of ABL driving factors in atmospheric research. While XGBoost has been applied in this field, it often relies on default parameters. Additionally, due to the challenges of acquiring long-term, multi-parameter meteorological data, it has not been widely used to study seasonal variations in driving factor importance. To address this, we focus on key thermodynamic drivers of the boundary layer, selecting LTS, SHF, and LHF as primary influencing factors. We use Doppler lidar vertical wind field data to derive MLH as an indicator of CBL evolution. This study examines the effects of different parameter settings and optimizes hyperparameters based on the actual research dataset. Without cross-validation, the correlation coefficient R2 from different XGBoost models fluctuates significantly, ranging from 0.47 to 0.83, with relative influence factors varying by more than 0.10. When cross-validation is applied with default parameters, the R2 value remains stable across different splits, but factor importance still varies by over 0.10, with only around 0.60. By using optimized parameters, both R and relative influence factors remain stable within a 0.03 range, achieving an R2 value of 0.81. Based on these results, we analyzed seasonal variations in relative influence factors at the C1 site, providing insights for applying similar methods in atmospheric studies.
Subsequently, the results of different seasons demonstrate significant seasonal variations in the relative influence of key atmospheric factors, deviating from the annual trends. While LTS dominates in summer at the C1 site (0.6), SHF plays a more dominant role in other seasons (MAM: 0.5, JJA: 0.42, DJF: 0.4). The increased number of data points in JJA and SON causes LTS to appear as the dominant factor in the annual analysis (~0.5, Table 3). However, seasonal differences are evident, with JJA exhibiting a lower R2 (0.63) despite having more data points, indicating that ABL development in summer is influenced by additional meteorological factors or more complex controlling mechanisms. Notably, during JJA, the differences in the relative importance of the three factors across all sites are low. This suggests that boundary layer development in summer is not dominated by a single factor, indicating a more complex process likely influenced by seasonal conditions such as enhanced convective activity, elevated temperatures, and increased humidity. These factors collectively contribute to a more balanced distribution of parameter impacts. However, these interpretations remain speculative and require further validation. MLH variations further confirm that its peak occurs in SON, where LTS plays a stronger role, particularly at C1 and E37. E39 shows a more balanced contribution from LTS, SHF, and LHF, but its higher variance, especially in SON, suggests that dataset size significantly impacts result reliability. Additionally, MAE values and dataset quality must be considered, as DJF consistently shows the lowest MAE (<0.1) due to inherently lower MLH, while JJA exhibits the highest MAE (~0.16 at E32), if an annual model were used, MAE would exceed 0.15, reflecting greater model uncertainty. These findings highlight the necessity of further research into localized atmospheric processes affecting ABL dynamics, as ABL evolution is highly sensitive to seasonal and regional variations in stability, surface fluxes, and local meteorological conditions.
We further analyzed the differences between E32 and E37 during autumn (SON) using SHAP and explored potential reasons for the discrepancies between the two sites through wind direction analysis with WIND ROSE figures. These findings highlight the intuitive and significant role that SHAP can play in considering the seasonal variations of influencing factors when analyzing different locations. Later, XGBoost expanded upon this by attempting to quantify the relative influence of different parameters on ABL development [13]. In this study, we integrate XGBoost with cross-validation to explain the relative influencing factors of various parameters on ABL development across different seasons.
Our analysis reveals significant seasonal variations in the relative importance of LTS in ABL evolution. Across all seasons, the LTS importance increases from morning to afternoon, with JJA rising from 0.2 at 09:30 AM to 0.6 at 3:30 PM, indicating its growing influence as the boundary layer develops. SON exhibits the highest LTS importance at 09:30 AM (~0.4), suggesting a faster ABL growth compared to other seasons. In contrast, DJF shows the lowest LTS values in the morning (<0.2), with a slower increase throughout the day, implying greater difficulty in reaching the previous day’s ABL top. Additionally, DJF exhibits potential overfitting issues, with MAE values consistently below 0.1 (as low as 0.02) and R² ranging from 0.75 to 0.99, likely due to a limited dataset (60 days vs. 156 days in JJA). These findings highlight the role of LTS in ABL dynamics and emphasize the need for more extensive wintertime data to improve model robustness.
To the authors’ knowledge, this study represents the first application of machine learning to investigate the relative importance of various meteorological parameters on ABL development across different locations and seasons. This study not only examines the relative importance of influencing factors at the C1 site throughout the year and across seasons but also compares their variations across multiple ARM SGP sites. Additionally, an attempt is made to use wind direction to distinguish differences in relative impact factors between sites. However, a more detailed investigation is needed to understand the specific differences in ABL evolution and the seasonal variations in influencing factors across the four sites [13]. Since this study investigates changes in the relative importance of parameters, it can provide valuable insights for refining machine learning frameworks in the future and contribute to developing models that approach or exceed the performance of traditional PBL schemes.
Despite certain limitations, such as focusing only on thermodynamic influences while neglecting dynamical factors, and without considering the full ABL evolution process, this study serves as an exploratory application of machine learning in atmospheric research. It highlights the importance of incorporating domain-specific scientific principles into machine learning tools like XGBoost to optimize parameters and ensure accurate results. This study initially focuses on thermodynamic parameters, acknowledging that the omission of dynamical factors (e.g., wind shear, advection) limits the theoretical foundation of the model. These dynamical factors play a critical role, particularly when the MLH nears the boundary layer top, where their absence may amplify discrepancies between predictions and observations. Nevertheless, the current approach can be extended to incorporate additional boundary layer drivers, such as wind speed, wind direction, terrain, vegetation, water vapor, and cloud properties [41,42,43,44,45,46]. Future research should integrate these dynamical factors to enhance the model’s theoretical robustness and predictive accuracy, as suggested by recent studies on gravity waves, wind shear, and stratospheric disturbances. Additionally, integrating machine learning with numerical models can provide a more comprehensive understanding of boundary layer dynamics [47].

Author Contributions

Conceptualization, Y.C.; methodology, Y.C.; software, H.G. and Y.C.; data curation, Y.C.; writing—original draft preparation, Y.C. and G.L.; writing—review and editing, Y.C., G.L., M.D. and J.A.Z.; visualization, H.G. and Y.C.; supervision, Y.C.; project administration, Y.C.; funding acquisition, Y.C. and J.A.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the U.S. Department of Energy, Office of Science, Atmospheric System Research (DOE-ASR) program under grant DE-SC0020171, the National Science Foundation (NSF) under grants AGS-1917693 and AGS-2211308, and the National Oceanic and Atmospheric Administration (NOAA) under grants NA22OAR4050669D, NA22OAR4590174, and NA22OAR4590178.

Data Availability Statement

Data were obtained from the Atmospheric Radiation Measurement (ARM) user facility, a U.S. Department of Energy (DOE) Office of Science user facility managed by the biological and environmental research program. The ARM SGP dataset is accessible at https://doi.org/10.2172/1253897; additional data can be provided upon request by contacting the authors.

Acknowledgments

The authors sincerely thank Emily Roberts from the School of Marine and Atmospheric Sciences (SOMAS) at Stony Brook University for her valuable assistance in improving the English grammar and writing of this manuscript. The authors would like to extend their sincere appreciation to Zhien Wang from SOMAS at Stony Brook University for his insightful discussions and invaluable guidance throughout the course of this research. His expertise and mentorship have been instrumental in shaping the direction and quality of our work.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Dueben, P.D.; Schultz, M.G.; Chantry, M.; Gagne, D.J.; Hall, D.M.; McGovern, A. Challenges and benchmark datasets for machine learning in the atmospheric sciences: Definition, status, and outlook. Artif. Intell. Earth Syst. 2022, 1, e210002. [Google Scholar] [CrossRef]
  2. Elith, J. Machine learning, random forests, and boosted regression trees. In Quantitative Analyses in Wildlife Science; Johns Hopkins University Press: St. Baltimore, MD, USA, 2019; pp. 281–297. [Google Scholar]
  3. Arcomano, T.; Szunyogh, I.; Pathak, J.; Wikner, A.; Hunt, B.R.; Ott, E. A machine learning-based global atmospheric forecast model. Geophys. Res. Lett. 2020, 47, e2020GL087776. [Google Scholar] [CrossRef]
  4. Brenowitz, N.D.; Beucler, T.; Pritchard, M.; Bretherton, C.S. Interpreting and stabilizing machine-learning parametrizations of convection. J. Atmos. Sci. 2020, 77, 4357–4375. [Google Scholar] [CrossRef]
  5. Wang, L.Y.; Tan, Z.M. Deep learning parameterization of the tropical cyclone boundary layer. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003034. [Google Scholar] [CrossRef]
  6. Summa, D.; Vivone, G.; Franco, N.; D’Amico, G.; De Rosa, B.; Di Girolamo, P. Atmospheric boundary layer height: Inter-comparison of different estimation approaches using the Raman lidar as benchmark. Remote Sens. 2023, 15, 1381. [Google Scholar] [CrossRef]
  7. Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 13. [Google Scholar]
  8. Lin, G.; Wang, Z.; Ziegler, C.; Hu, X.M.; Xue, M.; Geerts, B.; Chu, Y. A comparison of convective storm inflow moisture variability between the Great Plains and the southeastern United States using multiplatform field campaign observations. J. Atmos. Ocean. Technol. 2023, 40, 539–556. [Google Scholar] [CrossRef]
  9. Lin, G.; Wang, Z.; Chu, Y.; Ziegler, C.L.; Hu, X.M.; Xue, M.; DeGraw, J. Airborne measurements of scale-dependent latent heat flux impacted by water vapor and vertical velocity over heterogeneous land surfaces during the CHEESEHEAD19 campaign. J. Geophys. Res. Atmos. 2024, 129, e2023JD039586. [Google Scholar] [CrossRef]
  10. Lee, X. Fundamentals of Boundary-Layer Meteorology; Springer: Cham, Switzerland, 2018; Volume 256. [Google Scholar]
  11. Wang, Z.; Menenti, M. Challenges and opportunities in Lidar remote sensing. Front. Remote Sens. 2021, 2, 641723. [Google Scholar] [CrossRef]
  12. Wulfmeyer, V.; Pineda, J.M.V.; Otte, S.; Karlbauer, M.; Butz, M.V.; Lee, T.R.; Rajtschan, V. Estimation of the surface fluxes for heat and momentum in unstable conditions with machine learning and similarity approaches for the LAFE data set. Bound.-Layer Meteor. 2023, 186, 337–371. [Google Scholar] [CrossRef]
  13. Chu, Y.; Wang, Z.; Deng, M.; Lin, G.; Xue, L.; Li, W.; Shin, H.H. The Spatial and Temporal Variability of the Planetary Boundary Layer at the ARM SGP Supersite. In Proceedings of the AGU Fall Meeting, Chicago, IL, USA, 12–16 December 2022; p. A35K-1601. [Google Scholar]
  14. Beamesderfer, E.R.; Biraud, S.C.; Brunsell, N.A.; Friedl, M.A.; Helbig, M.; Hollinger, D.Y.; Richardson, A.D. The Role of Surface Energy Fluxes in Determining Mixing Layer Heights. Agric. For. Meteorol. 2023, 342, 109687. [Google Scholar] [CrossRef]
  15. He, S.; Li, X.; DelSole, T.; Ravikumar, P.; Banerjee, A. Sub-seasonal climate forecasting via machine learning: Challenges, analysis, and advances. Proc. AAAI Conf. Artif. Intell. 2021, 35, 169–177. [Google Scholar] [CrossRef]
  16. Han, W.; Zhang, X.; Wang, Y.; Wang, L.; Huang, X.; Li, J.; Wang, Y. A survey of machine learning and deep learning in remote sensing of geological environment: Challenges, advances, and opportunities. ISPRS J. Photogramm. Remote Sens. 2023, 202, 87–113. [Google Scholar] [CrossRef]
  17. Geer, A.J. Learning earth system models from observations: Machine learning or data assimilation? Philos. Trans. R. Soc. A 2021, 379, 20200089. [Google Scholar] [CrossRef]
  18. Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
  19. Vogelezang, D.H.; Holtslag, A.A. Evaluation and model impacts of alternative boundary-layer height formulations. Bound.-Layer Meteorol. 1996, 81, 245–269. [Google Scholar] [CrossRef]
  20. Vautard, R.; Yiou, P.; Van Oldenborgh, G.J. Decline of fog, mist and haze in Europe over the past 30 years. Nat. Geosci. 2009, 2, 115–119. [Google Scholar] [CrossRef]
  21. Geerken, R.A. An algorithm to classify and monitor seasonal variations in vegetation phenologies and their inter-annual change. ISPRS J. Photogramm. Remote Sens. 2009, 64, 422–431. [Google Scholar] [CrossRef]
  22. Kramar, V.; Alchakov, V. Time-series forecasting of seasonal data using machine learning methods. Algorithms 2023, 16, 248. [Google Scholar] [CrossRef]
  23. Beamish, A.; Raynolds, M.K.; Epstein, H.; Frost, G.V.; Macander, M.J.; Bergstedt, H.; Wagner, J. Recent trends and remaining challenges for optical remote sensing of Arctic tundra vegetation: A review and outlook. Remote Sens. Environ. 2020, 246, 111872. [Google Scholar] [CrossRef]
  24. Dubovik, O.; Schuster, G.L.; Xu, F.; Hu, Y.; Bösch, H.; Landgraf, J.; Li, Z. Grand challenges in satellite remote sensing. Front. Remote Sens. 2021, 2, 619818. [Google Scholar] [CrossRef]
  25. Zhang, Y.; Li, Z.; Bai, K.; Wei, Y.; Xie, Y.; Zhang, Y.; Li, D. Satellite remote sensing of atmospheric particulate matter mass concentration: Advances, challenges, and perspectives. Fundam. Res. 2021, 1, 240–258. [Google Scholar] [CrossRef]
  26. Chen, Q.; Xie, Y.; Guo, S.; Bai, J.; Shu, Q. Sensing system of environmental perception technologies for driverless vehicles: A review of state of the art and challenges. Sens. Actuators A Phys. 2021, 319, 112566. [Google Scholar] [CrossRef]
  27. von Engeln, A.; Teixeira, J. A planetary boundary layer height climatology derived from ECMWF reanalysis data. J. Clim. 2013, 26, 657–673. [Google Scholar] [CrossRef]
  28. Thorne, P.W.; Parker, D.E.; Tett, S.F.; Jones, P.D.; McCarthy, M.; Coleman, H.; Brohan, P. Revisiting radiosonde upper air temperatures from 1958 to 2002. J. Geophys. Res. Atmos. 2005, 110, D18105. [Google Scholar] [CrossRef]
  29. Smyth, P. Model selection for probabilistic clustering using cross-validated likelihood. Stat. Comput. 2000, 10, 63–72. [Google Scholar] [CrossRef]
  30. Sagi, O.; Rokach, L. Approximating XGBoost with an interpretable decision tree. Inf. Sci. 2021, 572, 522–542. [Google Scholar] [CrossRef]
  31. Zhao, W.P.; Li, J.; Zhao, J.; Zhao, D.; Lu, J.; Wang, X. XGB model: Research on evaporation duct height prediction based on XGBoost algorithm. Radioengineering 2020, 29, 81–93. [Google Scholar] [CrossRef]
  32. Ramraj, S.; Uzir, N.; Sunil, R.; Banerjee, S. Experimenting XGBoost algorithm for prediction and classification of different datasets. Int. J. Control Theory Appl. 2016, 9, 651–662. [Google Scholar]
  33. Krishnamurthy, R.; Newsom, R.K.; Chand, D.; Shaw, W.J. Boundary Layer Climatology at ARM Southern Great Plains; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2021; No. PNNL-30832. [Google Scholar]
  34. Chu, Y.; Wang, Z.; Xue, L.; Deng, M.; Lin, G.; Xie, H.; Wang, Y. Characterizing warm atmospheric boundary layer over land by combining Raman and Doppler lidar measurements. Opt. Express 2022, 30, 11892–11911. [Google Scholar] [CrossRef]
  35. Tang, S.; Xie, S.; Zhang, M.; Tang, Q.; Zhang, Y.; Klein, S.A.; Sullivan, R.C. Differences in Eddy-Correlation and Energy-Balance Surface Turbulent Heat Flux Measurements and Their Impacts on the Large-Scale Forcing Fields at the ARM SGP Site. J. Geophys. Res. Atmos. 2019, 124, 3301–3318. [Google Scholar] [CrossRef]
  36. Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
  37. Welbanks, L.; McGill, P.; Line, M.; Madhusudhan, N. On the application of Bayesian leave-one-out cross-validation to exoplanet atmospheric analysis. Astron. J. 2023, 165, 112. [Google Scholar] [CrossRef]
  38. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, E. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  39. Ponce-Bobadilla, A.V.; Schmitt, V.; Maier, C.S.; Mensing, S.; Stodtmann, S. Practical Guide to SHAP Analysis: Explaining Supervised Machine Learning Model Predictions in Drug Development. Clin. Transl. Sci. 2024, 17, e70056. [Google Scholar] [CrossRef] [PubMed]
  40. Huang, L.; Zhao, X.; Liu, Y.; Yang, P. Analysis of the Atmospheric Duct Existence Factors in Tropical Cyclones Based on the SHAP Interpretation of Extreme Gradient Boosting Predictions. Remote Sens. 2022, 14, 3952. [Google Scholar] [CrossRef]
  41. de Arruda Moreira, G.; Sánchez-Hernández, G.; Guerrero-Rascado, J.L.; Cazorla, A.; Alados-Arboledas, L. Estimating the Urban Atmospheric Boundary Layer Height from Remote Sensing Applying Machine Learning Techniques. Atmos. Res. 2022, 266, 105962. [Google Scholar] [CrossRef]
  42. Liu, X.; Xu, J.; Yue, J.; Liu, A.H. Gravity-wave-perturbed wind shears derived from SABER temperature observations. Atmos. Chem. Phys. 2020, 20, 14437–14456. [Google Scholar] [CrossRef]
  43. He, Y.; Zhu, X.; Sheng, Z.; He, M. Resonant waves play an important role in the increasing heat waves in Northern Hemisphere mid-latitudes under global warming. Geophys. Res. Lett. 2023, 50, e2023GL104839. [Google Scholar] [CrossRef]
  44. Liu, X.; Xu, J.; Yue, J.; Vadas, S.L.; Becker, E. Orographic primary and secondary gravity waves in the middle atmosphere from 16-year SABER observations. Geophys. Res. Lett. 2019, 46, 4512–4522. [Google Scholar] [CrossRef]
  45. Kang, M.; Chun, H.; Son, S.; Garcia, R.R.; An, S.; Park, S. Role of tropical lower stratosphere winds in quasi-biennial oscillation disruptions. Sci. Adv. 2022, 8, eabm7229. [Google Scholar] [CrossRef]
  46. He, Y.; Zhu, X.; Sheng, Z.; He, M. Identification of stratospheric disturbance information in China based on the round-trip intelligent sounding system. Atmos. Chem. Phys. 2024, 24, 3839–3856. [Google Scholar] [CrossRef]
  47. Shin, H.H.; Xue, L.; Li, W.; Firl, G.; D’Amico, D.F.; Muñoz-Esparza, D.; Vogelmann, A.M. Large-scale forcing impact on the development of shallow convective clouds revealed from LASSO large-eddy simulations. J. Geophys. Res. Atmos. 2021, 126, e2021JD035208. [Google Scholar] [CrossRef]
Remotesensing 17 01399 g001
Figure 1. The ARM SGP C1 site’s 20190630 daily evolution of MLH (red dots), (a) vertical wind speed, (b) variance of vertical wind speed.
Figure 1. The ARM SGP C1 site’s 20190630 daily evolution of MLH (red dots), (a) vertical wind speed, (b) variance of vertical wind speed.
Remotesensing 17 01399 g001
Remotesensing 17 01399 g002
Figure 2. Illustration of the cross-validation principle. Circles represent the test dataset, while diamonds indicate the training dataset. The five different colors correspond to the five distinct fold schemes applied in the cross-validation process.
Figure 2. Illustration of the cross-validation principle. Circles represent the test dataset, while diamonds indicate the training dataset. The five different colors correspond to the five distinct fold schemes applied in the cross-validation process.
Remotesensing 17 01399 g002
Remotesensing 17 01399 g003
Figure 3. The workflow of cross-validation and XGBoost for boundary layer parameter validation.
Figure 3. The workflow of cross-validation and XGBoost for boundary layer parameter validation.
Remotesensing 17 01399 g003
Remotesensing 17 01399 g004
Figure 4. Comparison of relative influence factors across different seasons at ARM SGP sites: C1 site (first row), E32 site (second row), E37 site (third row), and E39 site (fourth row). Seasons are denoted as DJF (December, January, February), MAM (March, April, May), JJA (June, July, August), and SON (September, October, November). Here, R represents the correlation coefficient, and K denotes the number of cross-validation splits. The relative importance of each factor is derived from the XGBoost model using a cross-validation (CV) approach, with uncertainty intervals calculated as the standard deviation of importance scores across all CV folds.
Figure 4. Comparison of relative influence factors across different seasons at ARM SGP sites: C1 site (first row), E32 site (second row), E37 site (third row), and E39 site (fourth row). Seasons are denoted as DJF (December, January, February), MAM (March, April, May), JJA (June, July, August), and SON (September, October, November). Here, R represents the correlation coefficient, and K denotes the number of cross-validation splits. The relative importance of each factor is derived from the XGBoost model using a cross-validation (CV) approach, with uncertainty intervals calculated as the standard deviation of importance scores across all CV folds.
Remotesensing 17 01399 g004
Remotesensing 17 01399 g005
Figure 5. The SHAP analysis evaluates the contributions of various relative influencing factors at the E32 and E37 sites during autumn (SON). Panels (a0,b0) depict the SHAP value beeswarm plots for the E32 and E37 sites, respectively, illustrating the distribution and impact of each feature on predictions. Panels (a1–a4,b1–b4) present scatter plots of sensible heat flux (SHF), latent heat flux (LHF), and lower tropospheric stability (LTS) against mixed layer height (MLH) for the E32 and E37 sites, respectively (Units: LTS in K; SHF and LHF in W/m2).
Figure 5. The SHAP analysis evaluates the contributions of various relative influencing factors at the E32 and E37 sites during autumn (SON). Panels (a0,b0) depict the SHAP value beeswarm plots for the E32 and E37 sites, respectively, illustrating the distribution and impact of each feature on predictions. Panels (a1–a4,b1–b4) present scatter plots of sensible heat flux (SHF), latent heat flux (LHF), and lower tropospheric stability (LTS) against mixed layer height (MLH) for the E32 and E37 sites, respectively (Units: LTS in K; SHF and LHF in W/m2).
Remotesensing 17 01399 g005
Remotesensing 17 01399 g006
Figure 6. Wind rose diagrams at the E32 and E37 sites during SON (September, October, November) around 11:30 (UTC-6): (a) E32 site, (b) E37 site.
Figure 6. Wind rose diagrams at the E32 and E37 sites during SON (September, October, November) around 11:30 (UTC-6): (a) E32 site, (b) E37 site.
Remotesensing 17 01399 g006
Remotesensing 17 01399 g007
Figure 7. Comparison of relative influence factors across different seasons at different time points: 9:30 (first row), 11:30 (second row), 13:30 (third row), 15:30 (fourth row). The first column corresponds to MAM, the second to JJA, the third to SON, and the fourth to DJF (DJF: December, January, February; MAM: March, April, May; JJA: June, July, August; SON: September, October, November). R represents the correlation coefficient, while MAE denotes the Mean Absolute Errors.
Figure 7. Comparison of relative influence factors across different seasons at different time points: 9:30 (first row), 11:30 (second row), 13:30 (third row), 15:30 (fourth row). The first column corresponds to MAM, the second to JJA, the third to SON, and the fourth to DJF (DJF: December, January, February; MAM: March, April, May; JJA: June, July, August; SON: September, October, November). R represents the correlation coefficient, while MAE denotes the Mean Absolute Errors.
Remotesensing 17 01399 g007
Table 1. Data provided by the ARM SGP C1 site used in this article.
Table 1. Data provided by the ARM SGP C1 site used in this article.
SitesDetection Instruments or Secondary Processed DatasetsDatasetNote
C1Doppler lidarsgpdlfptc1.b1Raw data
AERIsgpaerioe1turnC1.c1Raw data
SondesgpsondewnpnC1.b1Raw data
E14ECORsgp30qcecorE14.s1Raw data
E32Doppler lidarSgpdlfptE32.b1Raw data
AERIsgpaerioe1turnE32.c1Raw data
E37Doppler lidarSgpdlfptE37.b1Raw data
AERIsgpaerioe1turnE37.c1Raw data
E39Doppler lidarSgpdlfptE39.b1Raw data
AERIsgpaerioe1turnE39.c1Raw data
Other *MLHBased on Doppler lidar dataPreprocessed data
LTSBased on AERI dataPreprocessed data
* The MLH and LTS data processing methods are described in the text.
Table 2. Effect of different parameter settings using XGBoost on calculating the relative importance of correlated parameters for MLH.
Table 2. Effect of different parameter settings using XGBoost on calculating the relative importance of correlated parameters for MLH.
XGBoost ParametersModel Results
GroupN EstimatorLearning RateMax DepthLTSSHFLHFR2
1500.130.600.230.170.60
1000.130.570.260.170.64
2000.130.510.290.200.70
3000.130.500.300.200.73
21000.0130.670.220.110.48
1000.130.570.260.170.64
1000.330.500.300.200.74
1000.530.490.270.240.78
32000.330.500.280.220.79
2000.350.470.290.240.83
2000.370.480.280.240.84
2000.390.490.290.220.84
44000.150.490.290.220.83
4000.550.440.300.260.84
1000.550.470.300.230.83
1000.150.520.270.210.75
51000.170.550.260.190.81
1000.550.470.300.230.83
1000.530.490.280.230.78
2000.530.470.290.240.82
Table 3. Effect of different K settings using XGBoost on calculating the relative importance of correlated parameters for MLH with default parameters.
Table 3. Effect of different K settings using XGBoost on calculating the relative importance of correlated parameters for MLH with default parameters.
GroupN SplitsLTSSHFLHFR2
Default
parameters		30.600.230.170.60
50.510.290.200.60
70.490.300.210.60
90.490.300.210.60
120.510.280.210.60
150.510.280.210.60
Optimized
parameters		30.530.340.130.83
50.500.280.220.81
70.500.280.220.81
90.500.280.220.81
120.500.280.220.81
150.500.280.220.81
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chu, Y.; Lin, G.; Deng, M.; Guo, H.; Zhang, J.A. Characterizing Seasonal Variation of the Atmospheric Mixing Layer Height Using Machine Learning Approaches. Remote Sens. 2025, 17, 1399. https://doi.org/10.3390/rs17081399

AMA Style

Chu Y, Lin G, Deng M, Guo H, Zhang JA. Characterizing Seasonal Variation of the Atmospheric Mixing Layer Height Using Machine Learning Approaches. Remote Sensing. 2025; 17(8):1399. https://doi.org/10.3390/rs17081399

Chicago/Turabian Style

Chu, Yufei, Guo Lin, Min Deng, Hanqing Guo, and Jun A. Zhang. 2025. "Characterizing Seasonal Variation of the Atmospheric Mixing Layer Height Using Machine Learning Approaches" Remote Sensing 17, no. 8: 1399. https://doi.org/10.3390/rs17081399

APA Style

Chu, Y., Lin, G., Deng, M., Guo, H., & Zhang, J. A. (2025). Characterizing Seasonal Variation of the Atmospheric Mixing Layer Height Using Machine Learning Approaches. Remote Sensing, 17(8), 1399. https://doi.org/10.3390/rs17081399

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop