Spatiotemporal Dynamics and Future Projections of Carbon Use Efficiency on the Mongolian Plateau: A Remote Sensing and Machine Learning Approach
Abstract
1. Introduction
2. Materials and Methods
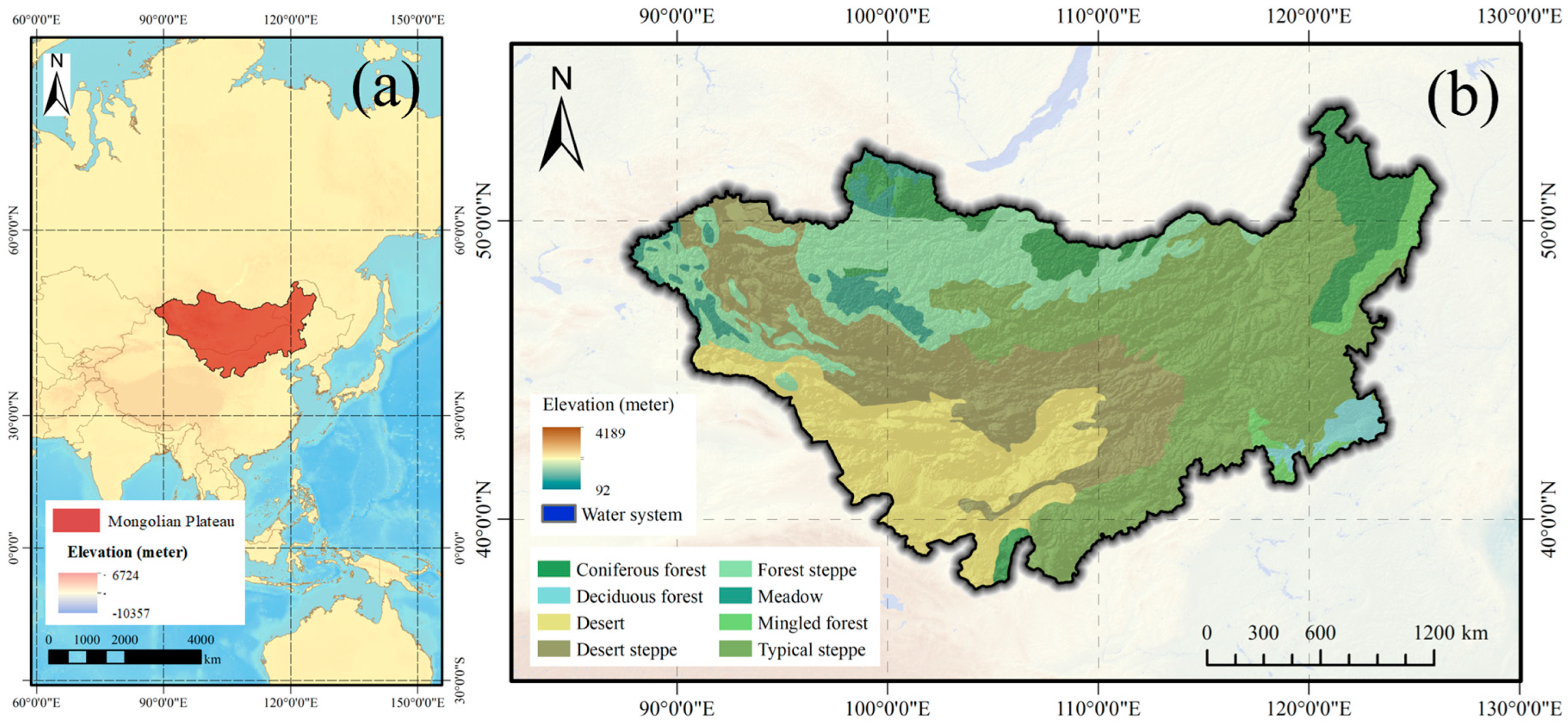
2.1. Study Area
2.2. Data Source
2.2.1. Climate Data
2.2.2. Remote Sensing Data
2.2.3. Topographic Data
2.2.4. CMIP6 Climate Data
2.3. Methodology
2.3.1. Carbon Use Efficiency
2.3.2. Trend Analysis
2.3.3. Hurst Exponent
2.3.4. Mann–Kendall (M-K) Mutation Test
2.3.5. GeoDetector
2.3.6. Machine Learning
- (1)
- Random forest regression
- (2)
- Lasso regression (L1 regularization)
- (3)
- Elastic net regression
- (4)
- Support vector regression (SVR)
3. Results
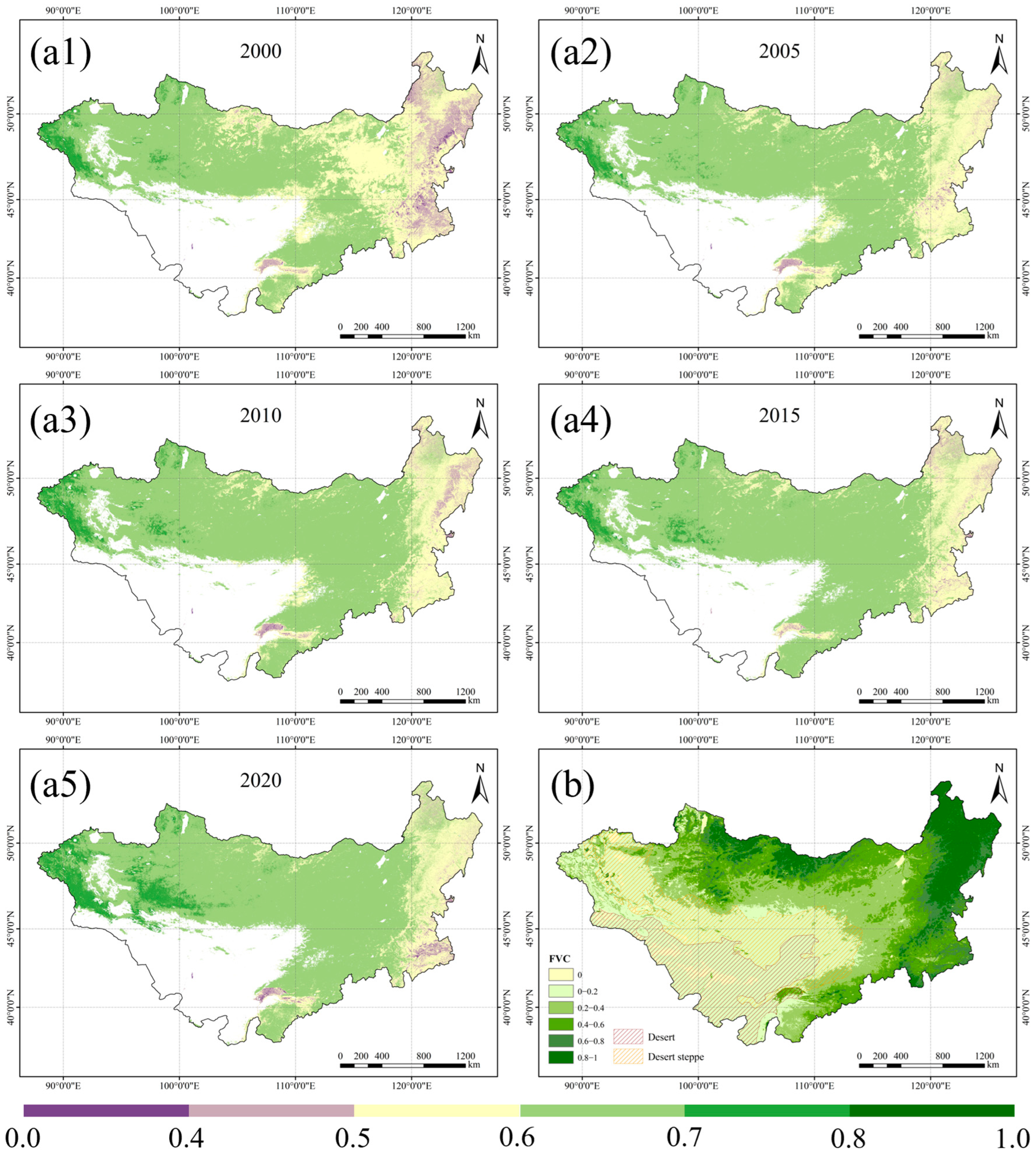
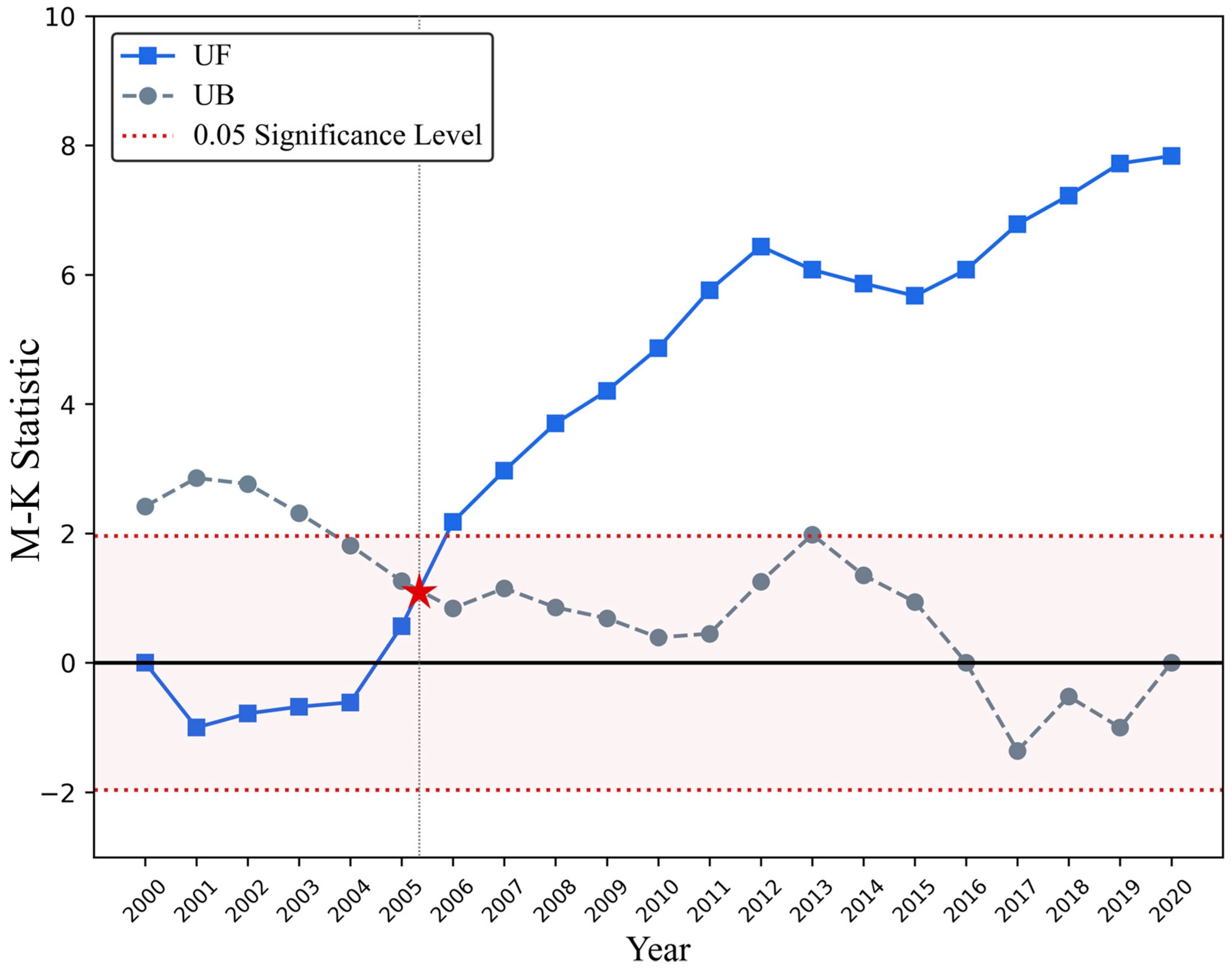
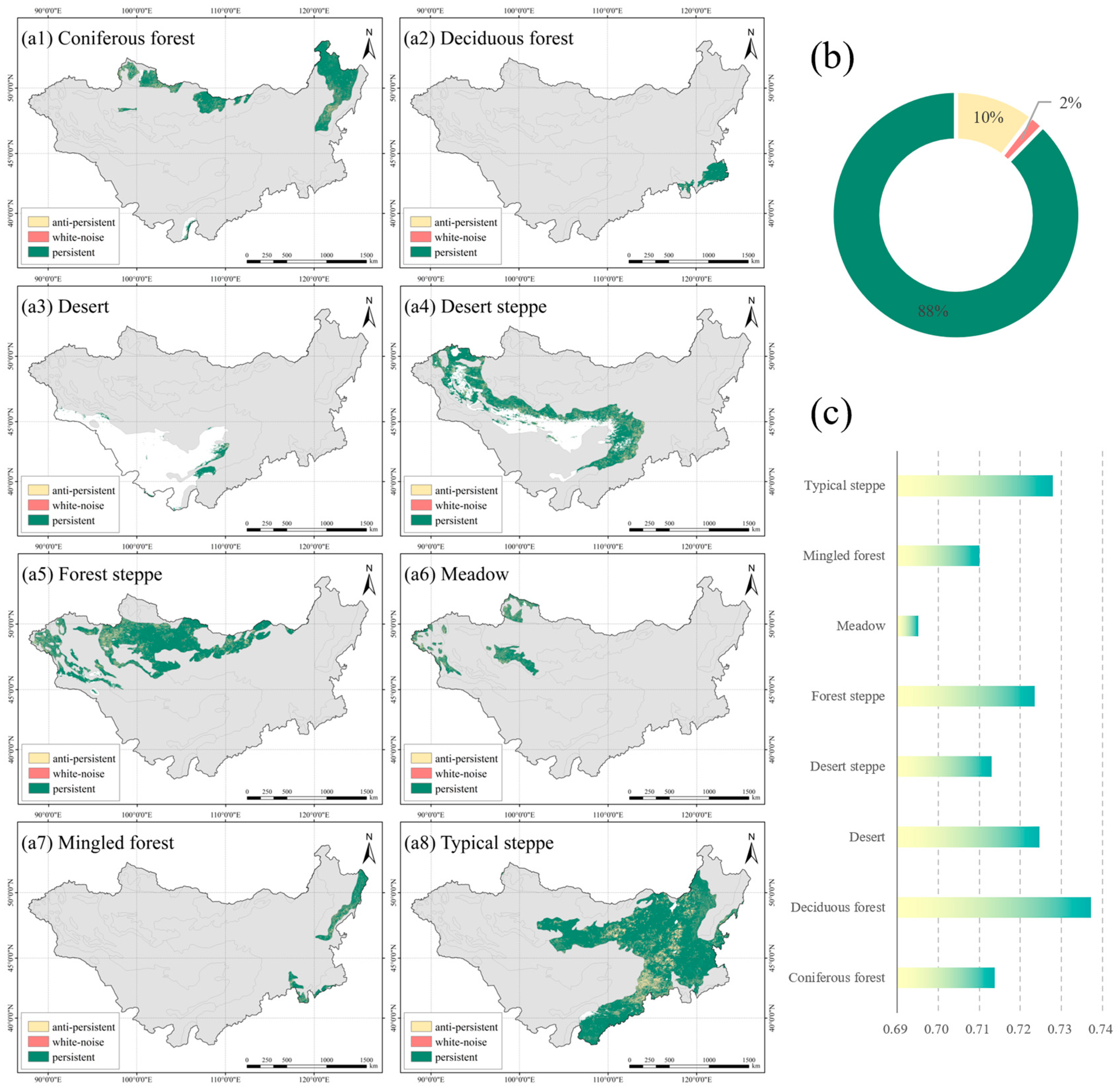
3.1. Spatiotemporal Distribution Characteristics of CUE
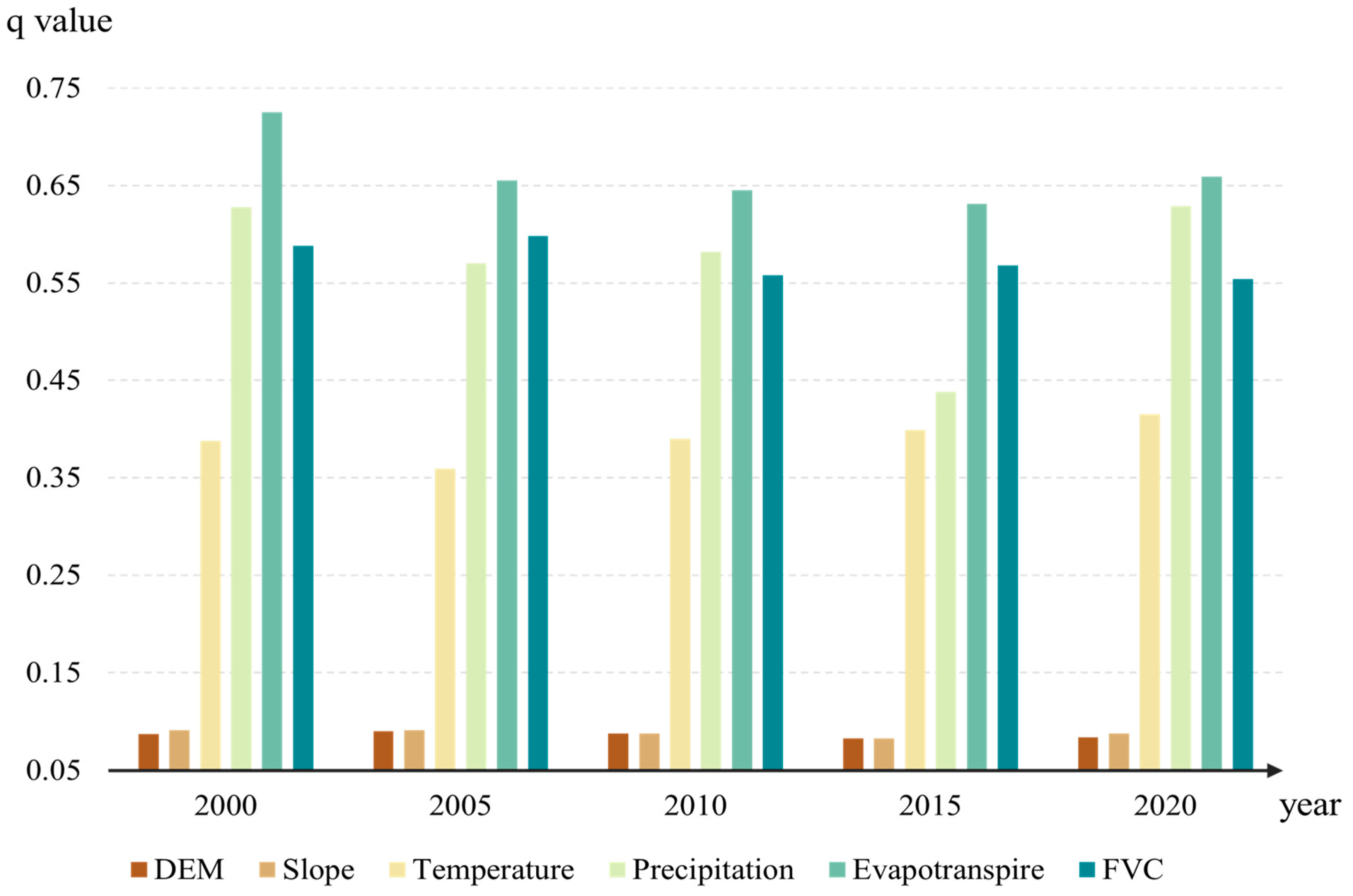
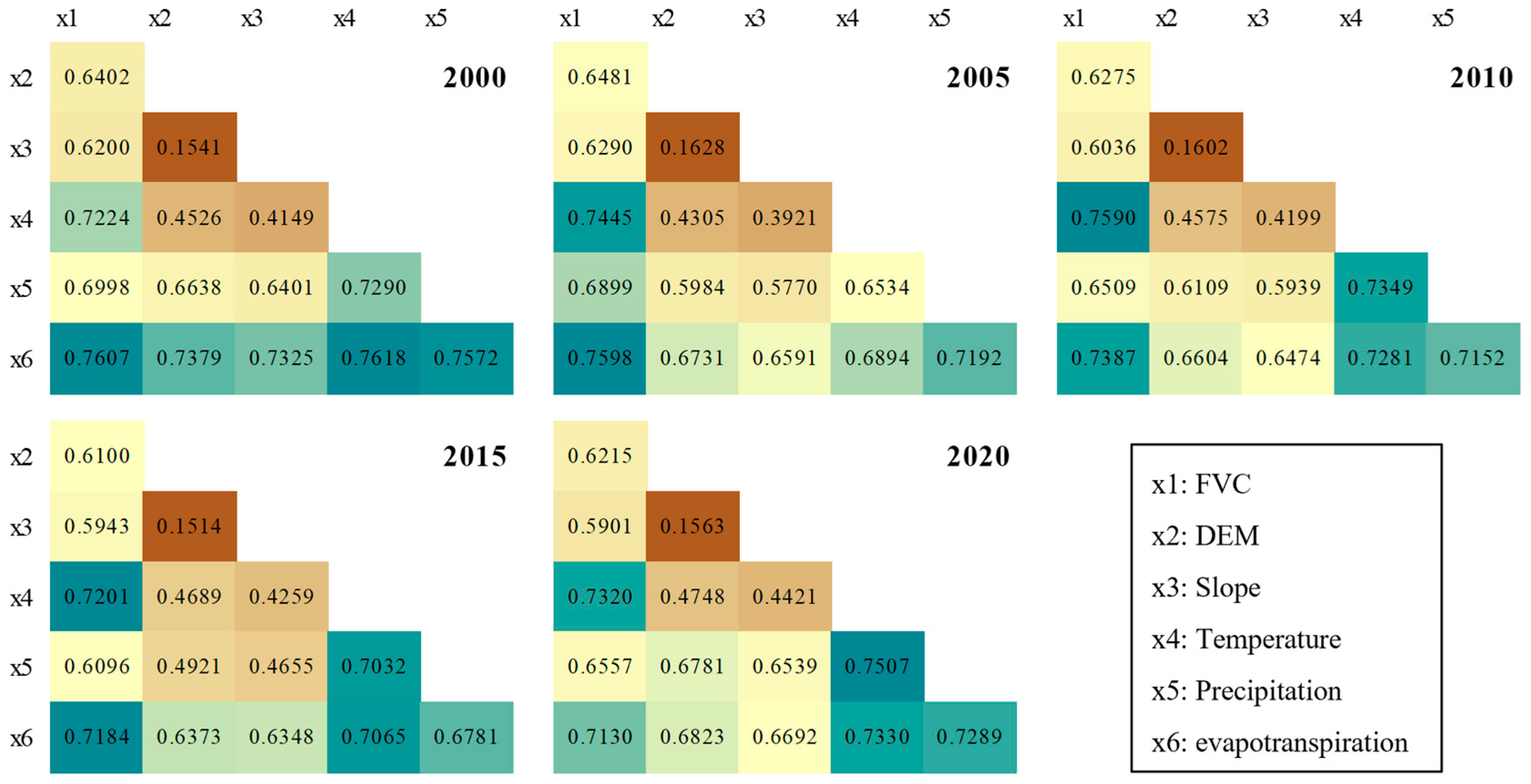
3.2. Analysis of CUE Driving Factors Based on GeoDetector
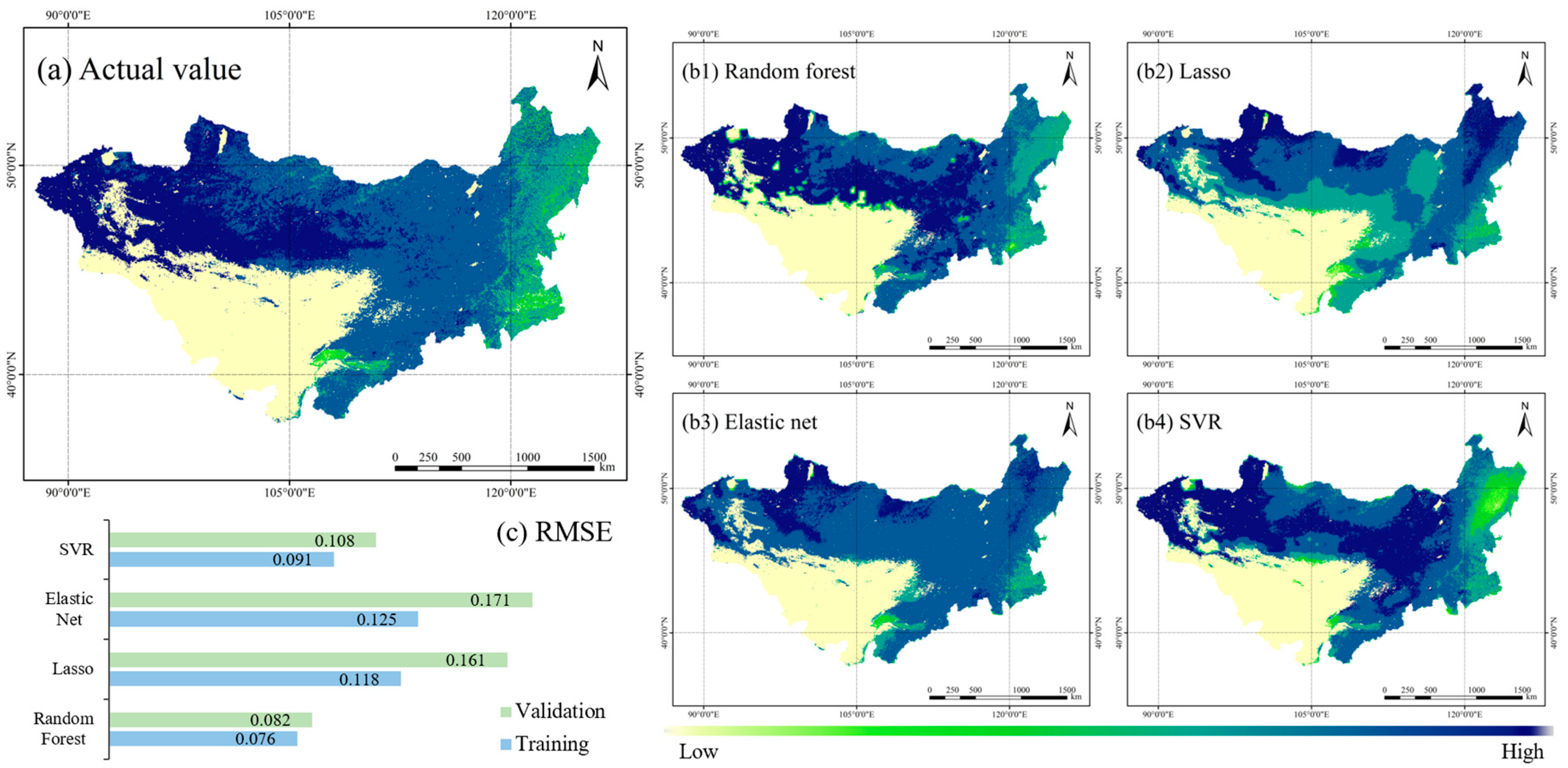
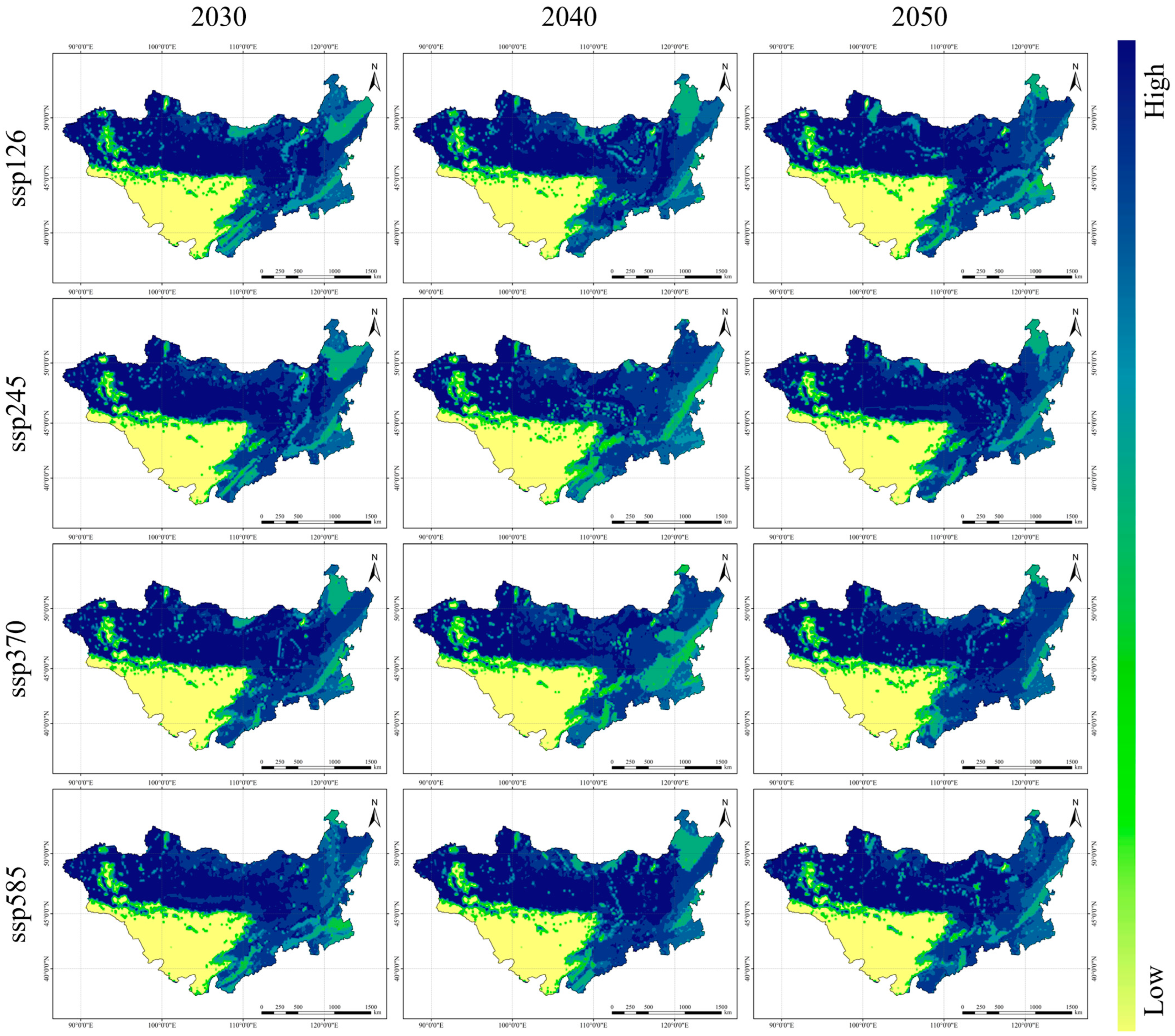
3.3. Future Trend Prediction of CUE Using Machine Learning
4. Discussion
4.1. Spatiotemporal Patterns of CUE and Its Driving Mechanisms
4.2. Future Evolution Trends of CUE Under Different Climate Scenarios
4.3. Study Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kabir, M.; Habiba, U.E.; Khan, W.; Shah, A.; Rahim, S.; Rios-Escalante, P.R.D.l.; Farooqi, Z.-U.-R.; Ali, L.; Shafiq, M. Climate Change Due to Increasing Concentration of Carbon Dioxide and Its Impacts on Environment in 21st Century; a Mini Review. J. King Saud Univ. Sci. 2023, 35, 102693. [Google Scholar] [CrossRef]
- Holmgren, M.; Stapp, P.; Dickman, C.; Gracia, C.; Graham, S. Extreme Climatic Events Shape Arid and Semiarid Ecosystems. Front. Ecol. Environ. 2006, 4, 87–95. [Google Scholar] [CrossRef]
- Reichstein, M.; Bahn, M.; Ciais, P.; Frank, D.; Mahecha, M.D.; Seneviratne, S.I.; Zscheischler, J.; Beer, C.; Buchmann, N.; Frank, D.C.; et al. Climate Extremes and the Carbon Cycle. Nature 2013, 500, 287–295. [Google Scholar] [CrossRef]
- Farrelly, D.J.; Everard, C.D.; Fagan, C.C.; McDonnell, K.P. Carbon Sequestration and the Role of Biological Carbon Mitigation: A Review. Renew. Sustain. Energy Rev. 2013, 21, 712–727. [Google Scholar] [CrossRef]
- Govind, A.; Kumari, J. Understanding the Terrestrial Carbon Cycle: An Ecohydrological Perspective. Int. J. Ecol. 2014, 2014, 712537. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Wang, Q.; Du, X.; Li, J.; Gang, C.; Zhou, W.; Wang, Z. Evaluating the Responses of Net Primary Productivity and Carbon Use Efficiency of Global Grassland to Climate Variability along an Aridity Gradient. Sci. Total Environ. 2019, 652, 671–682. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, B.J. Carbon Use Efficiency, and Net Primary Productivity of Terrestrial Vegetation. Adv. Space Res. 2000, 26, 1105–1108. [Google Scholar] [CrossRef]
- Babst, F.; Friend, A.D.; Karamihalaki, M.; Wei, J.; Arx, G.V.; Papale, D.; Peters, R.L. Modeling Ambitions Outpace Observations of Forest Carbon Allocation. Trends Plant Sci. 2021, 26, 210–219. [Google Scholar] [CrossRef]
- Curtis, P.S.; Vogel, C.S.; Gough, C.M.; Schmid, H.P.; Su, H.-B.; Bovard, B.D. Respiratory Carbon Losses and the Carbon-use Efficiency of a Northern Hardwood Forest, 1999–2003. New Phytol. 2005, 167, 437–456. [Google Scholar] [CrossRef]
- Zanotelli, D.; Montagnani, L.; Manca, G.; Tagliavini, M. Net Primary Productivity, Allocation Pattern and Carbon Use Efficiency in an Apple Orchard Assessed by Integrating Eddy Covariance, Biometric and Continuous Soil Chamber Measurements. Biogeosciences 2013, 10, 3089–3108. [Google Scholar] [CrossRef]
- Peichl, M.; Brodeur, J.J.; Khomik, M.; Arain, M.A. Biometric and Eddy-Covariance Based Estimates of Carbon Fluxes in an Age-Sequence of Temperate Pine Forests. Agric. For. Meteorol. 2010, 150, 952–965. [Google Scholar] [CrossRef]
- Verlinden, M.S.; Broeckx, L.S.; Zona, D.; Berhongaray, G.; De Groote, T.; Camino Serrano, M.; Janssens, I.A.; Ceulemans, R. Net Ecosystem Production and Carbon Balance of an SRC Poplar Plantation during Its First Rotation. Biomass Bioenergy 2013, 56, 412–422. [Google Scholar] [CrossRef]
- Street, L.E.; Subke, J.-A.; Sommerkorn, M.; Sloan, V.; Ducrotoy, H.; Phoenix, G.K.; Williams, M. The Role of Mosses in Carbon Uptake and Partitioning in Arctic Vegetation. New Phytol. 2013, 199, 163–175. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, G.; Yang, J.; Wimberly, M.C.; Zhang, X.; Tao, J.; Jiang, Y.; Zhu, J. Climate-driven Global Changes in Carbon Use Efficiency. Glob. Ecol. Biogeogr. 2014, 23, 144–155. [Google Scholar] [CrossRef]
- Kwon, Y.; Larsen, C.P.S. Effects of Forest Type and Environmental Factors on Forest Carbon Use Efficiency Assessed Using MODIS and FIA Data across the Eastern USA. Int. J. Remote Sens. 2013, 34, 8425–8448. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, A. The Response of Terrestrial Vegetation Carbon Use Efficiency to Global Environmental Changes. Glob. Planet. Change 2024, 240, 104537. [Google Scholar] [CrossRef]
- Fang, L.; Gao, R.; Wang, X.; Liu, T. Isotopes-Based Characterization of Precipitation Compositions and Atmospheric Water Vapor Sources over Typical Eurasian Steppes in South Mongolian Plateau. J. Hydrol. 2022, 615, 128724. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, J.; Zheng, Y.; Li, S.; Zhou, Y. Increased Carbon Uptake and Water Use Efficiency in Global Semi-Arid Ecosystems. Environ. Res. Lett. 2020, 15, 034022. [Google Scholar] [CrossRef]
- Gang, C.; Wang, Z.; Chen, Y.; Yang, Y.; Li, J.; Cheng, J.; Qi, J.; Odeh, I. Drought-Induced Dynamics of Carbon and Water Use Efficiency of Global Grasslands from 2000 to 2011. Ecol. Indic. 2016, 67, 788–797. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, Q.; Avirmed, B.; Wang, Y.; Orgilbold, M.; Cui, H.; Liu, Y.; Lian, J. The Relationship between Structure and Ecosystem Services of Forest and Grassland Based on Pattern Analysis Method: A Case Study of the Mongolian Plateau. Sci. Total Environ. 2024, 948, 174700. [Google Scholar] [CrossRef]
- Cai, Q.; Chen, W.; Chen, S.; Xie, S.-P.; Piao, J.; Ma, T.; Lan, X. Recent Pronounced Warming on the Mongolian Plateau Boosted by Internal Climate Variability. Nat. Geosci. 2024, 17, 181–188. [Google Scholar] [CrossRef]
- Wang, J.; Li, K.; Hong, M.; Shao, Y.; Sun, Z.; Liu, M.; Li, F.; Su, Y.; Jia, Q.; Liu, Y.; et al. Long-Term Land Cover Dataset of the Mongolian Plateau Based on Multi-Source Data and Rich Sample Annotations. Earth Syst. Sci. Data Discuss. 2024. preprint. [Google Scholar] [CrossRef]
- Janz, L.; Odsuren, D.; Bukhchuluun, D. Transitions in Palaeoecology and Technology: Hunter-Gatherers and Early Herders in the Gobi Desert. J. World Prehistory 2017, 30, 1–80. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, J.; He, C.; Fang, X. The Speed, Scale, and Environmental and Economic Impacts of Surface Coal Mining in the Mongolian Plateau. Resour. Conserv. Recycl. 2021, 173, 105730. [Google Scholar] [CrossRef]
- Lu, H.; Wang, X.; Wang, X.; Chang, X.; Zhang, H.; Xu, Z.; Zhang, W.; Wei, H.; Zhang, X.; Yi, S.; et al. Formation and Evolution of Gobi Desert in Central and Eastern Asia. Earthm Sci. Rev. 2019, 194, 251–263. [Google Scholar] [CrossRef]
- Dore, M.H.I. Climate Change and Changes in Global Precipitation Patterns: What Do We Know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, X.; Herzschuh, U. Asynchronous Evolution of the Indian and East Asian Summer Monsoon Indicated by Holocene Moisture Patterns in Monsoonal Central Asia. Earth-Sci. Rev. 2010, 103, 135–153. [Google Scholar] [CrossRef]
- Tolika, K. On the Analysis of the Temporal Precipitation Distribution over Greece Using the Precipitation Concentration Index (PCI): Annual, Seasonal, Monthly Analysis and Association with the Atmospheric Circulation. Theor. Appl. Climatol. 2019, 137, 2303–2319. [Google Scholar] [CrossRef]
- Xia, Y.; Dan, D.; Liu, H.; Zhou, H.; Wan, Z. Spatiotemporal Distribution of Precipitation over the Mongolian Plateau during 1976–2017. Atmosphere 2022, 13, 2132. [Google Scholar] [CrossRef]
- Jia, Q.; Gao, X.; Jiang, Z.; Li, H.; Guo, J.; Lu, X.; Yonghong Li, F. Sensitivity of Temperate Vegetation to Precipitation Is Higher in Steppes than in Deserts and Forests. Ecol. Indic. 2024, 166, 112317. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Z.; Han, G.; Schellenberg, M.P.; Wu, Q.; Gu, C. Grazing Induced Changes in Plant Diversity Is a Critical Factor Controlling Grassland Productivity in the Desert Steppe, Northern China. Agric. Ecosyst. Environ. 2018, 265, 73–83. [Google Scholar] [CrossRef]
- Wu, D.; Wu, H.; Zhao, X.; Zhou, T.; Tang, B.; Zhao, W.; Jia, K. Evaluation of Spatiotemporal Variations of Global Fractional Vegetation Cover Based on GIMMS NDVI Data from 1982 to 2011. Remote Sens. 2014, 6, 4217–4239. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Tebaldi, C.; Debeire, K.; Eyring, V.; Fischer, E.; Fyfe, J.; Friedlingstein, P.; Knutti, R.; Lowe, J.; O’Neill, B.; Sanderson, B.; et al. Climate Model Projections from the Scenario Model Intercomparison Project (ScenarioMIP) of CMIP6. Earth Syst. Dyn. 2021, 12, 253–293. [Google Scholar] [CrossRef]
- Jimenez, D.A.; Menapace, A.; Zanfei, A.; Pinto, E.J.d.A.; Brentan, B. Assessing Downscaling Techniques for Frequency Analysis, Total Precipitation and Rainy Day Estimation in CMIP6 Simulations over Hydrological Years. Hydrol. Earth Syst. Sci. 2024, 28, 1981–1997. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Guo, M.; Li, J.; He, H.; Xu, J.; Jin, Y. Detecting Global Vegetation Changes Using Mann-Kendal (MK) Trend Test for 1982–2015 Time Period. Chin. Geogr. Sci. 2018, 28, 907–919. [Google Scholar] [CrossRef]
- Yang, H.; Yu, J.; Xu, W.; Wu, Y.; Lei, X.; Ye, J.; Geng, J.; Ding, Z. Long-Time Series Ecological Environment Quality Monitoring and Cause Analysis in the Dianchi Lake Basin, China. Ecol. Indic. 2023, 148, 110084. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, R.; Xue, C.; Xia, Z. Ecological Sensitivity Evaluation and Explanatory Power Analysis of the Giant Panda National Park in China. Ecol. Indic. 2023, 146, 109792. [Google Scholar] [CrossRef]
- Han, J.; Dalaibaatar, E. A Study on the Influencing Factors of China’s Ecological Footprint Based on EEMD–GeoDetector. Sustainability 2023, 15, 6680. [Google Scholar] [CrossRef]
- Liu, X.; Lai, Q.; Yin, S.; Bao, Y.; Tong, S.; Adiya, Z.; Sanjjav, A.; Gao, R. Spatio-Temporal Patterns and Control Mechanism of the Ecosystem Carbon Use Efficiency across the Mongolian Plateau. Sci. Total Environ. 2024, 907, 167883. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Wang, J.; Ge, Y.; Xu, C. An Optimal Parameters-Based Geographical Detector Model Enhances Geographic Characteristics of Explanatory Variables for Spatial Heterogeneity Analysis: Cases with Different Types of Spatial Data. GISci. Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Tredennick, A.T.; Hooker, G.; Ellner, S.P.; Adler, P.B. A Practical Guide to Selecting Models for Exploration, Inference, and Prediction in Ecology. Ecology 2021, 102, e03336. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection Via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Basak, D.; Pal, S.; Patranabis, D.C. Support Vector Regression. Neural Inf. Process. 2007, 11, 203–224. [Google Scholar]
- Wang, G.; Huang, Y.; Wei, Y.; Zhang, W.; Li, T.; Zhang, Q. Climate Warming Does Not Always Extend the Plant Growing Season in Inner Mongolian Grasslands: Evidence From a 30-Year In Situ Observations at Eight Experimental Sites. JGR Biogeosci. 2019, 124, 2364–2378. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Zhou, L.; Zhu, B.; Tan, K.; Tao, S. Changes in Vegetation Net Primary Productivity from 1982 to 1999 in China. Glob. Biogeochem. Cycles 2005, 19, 2004GB002274. [Google Scholar] [CrossRef]
- Khalifa, M.; Elagib, N.A.; Ribbe, L.; Schneider, K. Spatio-Temporal Variations in Climate, Primary Productivity and Efficiency of Water and Carbon Use of the Land Cover Types in Sudan and Ethiopia. Sci. Total Environ. 2018, 624, 790–806. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Piao, S.; Li, X.; Chen, A.; Qin, D. Global Patterns of Vegetation Carbon Use Efficiency and Their Climate Drivers Deduced from MODIS Satellite Data and Process-Based Models. Agric. Meteorol. 2018, 256–257, 150–158. [Google Scholar] [CrossRef]
- Ewing, S.A.; Sutter, B.; Owen, J.; Nishiizumi, K.; Sharp, W.; Cliff, S.S.; Perry, K.; Dietrich, W.; McKay, C.P.; Amundson, R. A Threshold in Soil Formation at Earth’s Arid Hyperarid Transition. Geochim. Cosmochim. Acta 2006, 70, 5293–5322. [Google Scholar] [CrossRef]
- Ryo, M.; Rillig, M.C. Statistically Reinforced Machine Learning for Nonlinear Patterns and Variable Interactions. Ecosphere 2017, 8, e01976. [Google Scholar] [CrossRef]


| Variable Name | Unit |
|---|---|
| Digital Elevation Model (DEM) | Meter (m) |
| Surface Slope | Degree (°) |
| Temperature | Kelvin (K) |
| Precipitation | Millimeter (mm) |
| Evapotranspiration | Millimeter (mm) |
| Fractional vegetation cover (FVC) | Percentage (%) |
| Year | Minimum | Maximum | Mean | Median | Std | IQR |
|---|---|---|---|---|---|---|
| 2000 | 0.0246 | 0.8041 | 0.6055 | 0.6134 | 0.0649 | 0.0728 |
| 2005 | 0.0067 | 0.8060 | 0.6280 | 0.6339 | 0.0500 | 0.0613 |
| 2010 | 0.0086 | 0.8000 | 0.6305 | 0.6393 | 0.0529 | 0.0556 |
| 2015 | 0.0098 | 0.8043 | 0.6360 | 0.6487 | 0.0516 | 0.0483 |
| 2020 | 0.0240 | 0.8042 | 0.6433 | 0.6570 | 0.0554 | 0.0558 |
| Model | Training RMSE | Validation RMSE | Training MAE | Validation MAE | Training R2 | Validation R2 |
|---|---|---|---|---|---|---|
| Random Forest | 0.076 | 0.082 | 0.052 | 0.058 | 0.91 | 0.88 |
| Lasso | 0.118 | 0.161 | 0.085 | 0.112 | 0.75 | 0.68 |
| Elastic Net | 0.125 | 0.171 | 0.090 | 0.120 | 0.73 | 0.65 |
| SVR | 0.091 | 0.108 | 0.065 | 0.075 | 0.85 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Yu, Q.; Avirmed, B.; Wang, Y.; Zhao, J.; Sun, W.; Cui, H.; Chi, B.; Long, J. Spatiotemporal Dynamics and Future Projections of Carbon Use Efficiency on the Mongolian Plateau: A Remote Sensing and Machine Learning Approach. Remote Sens. 2025, 17, 1392. https://doi.org/10.3390/rs17081392
Yang X, Yu Q, Avirmed B, Wang Y, Zhao J, Sun W, Cui H, Chi B, Long J. Spatiotemporal Dynamics and Future Projections of Carbon Use Efficiency on the Mongolian Plateau: A Remote Sensing and Machine Learning Approach. Remote Sensing. 2025; 17(8):1392. https://doi.org/10.3390/rs17081392
Chicago/Turabian StyleYang, Xinyu, Qiang Yu, Buyanbaatar Avirmed, Yu Wang, Jikai Zhao, Weijie Sun, Huanjia Cui, Bowen Chi, and Ji Long. 2025. "Spatiotemporal Dynamics and Future Projections of Carbon Use Efficiency on the Mongolian Plateau: A Remote Sensing and Machine Learning Approach" Remote Sensing 17, no. 8: 1392. https://doi.org/10.3390/rs17081392
APA StyleYang, X., Yu, Q., Avirmed, B., Wang, Y., Zhao, J., Sun, W., Cui, H., Chi, B., & Long, J. (2025). Spatiotemporal Dynamics and Future Projections of Carbon Use Efficiency on the Mongolian Plateau: A Remote Sensing and Machine Learning Approach. Remote Sensing, 17(8), 1392. https://doi.org/10.3390/rs17081392






