A Robust InSAR-DEM Block Adjustment Method Based on Affine and Polynomial Models for Geometric Distortion
Abstract
1. Introduction
2. Methods
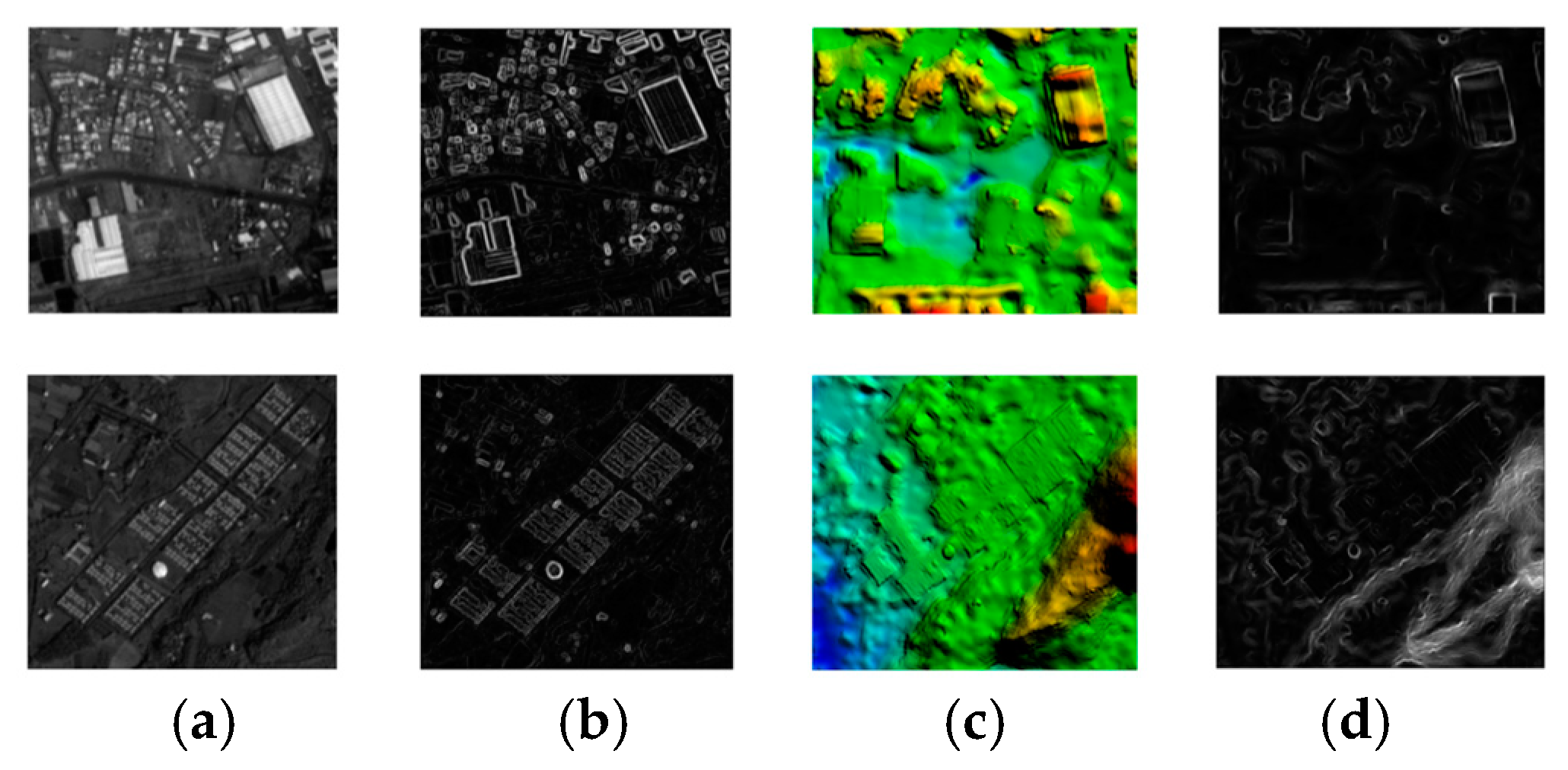
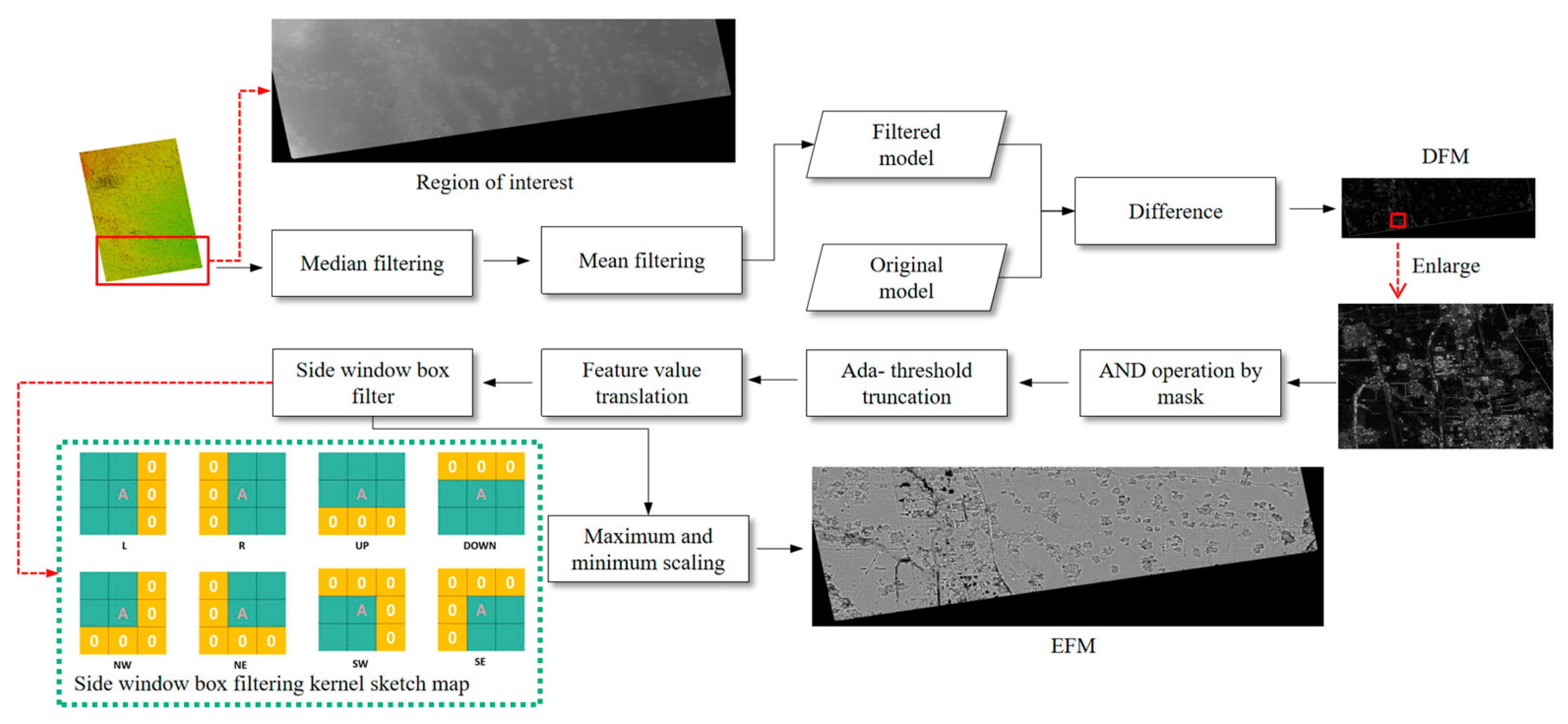
2.1. InSAR-DEM Enhanced Feature Map Construction Method
2.2. Point Extraction Method on Adaptive Threshold EFM
2.3. Construction of 296-Dimensional InSAR-DEM Feature Descriptors
2.4. Establishment of a Planar Registration Model
2.5. Establishment of the Elevation Adjustment Model
3. Experiments
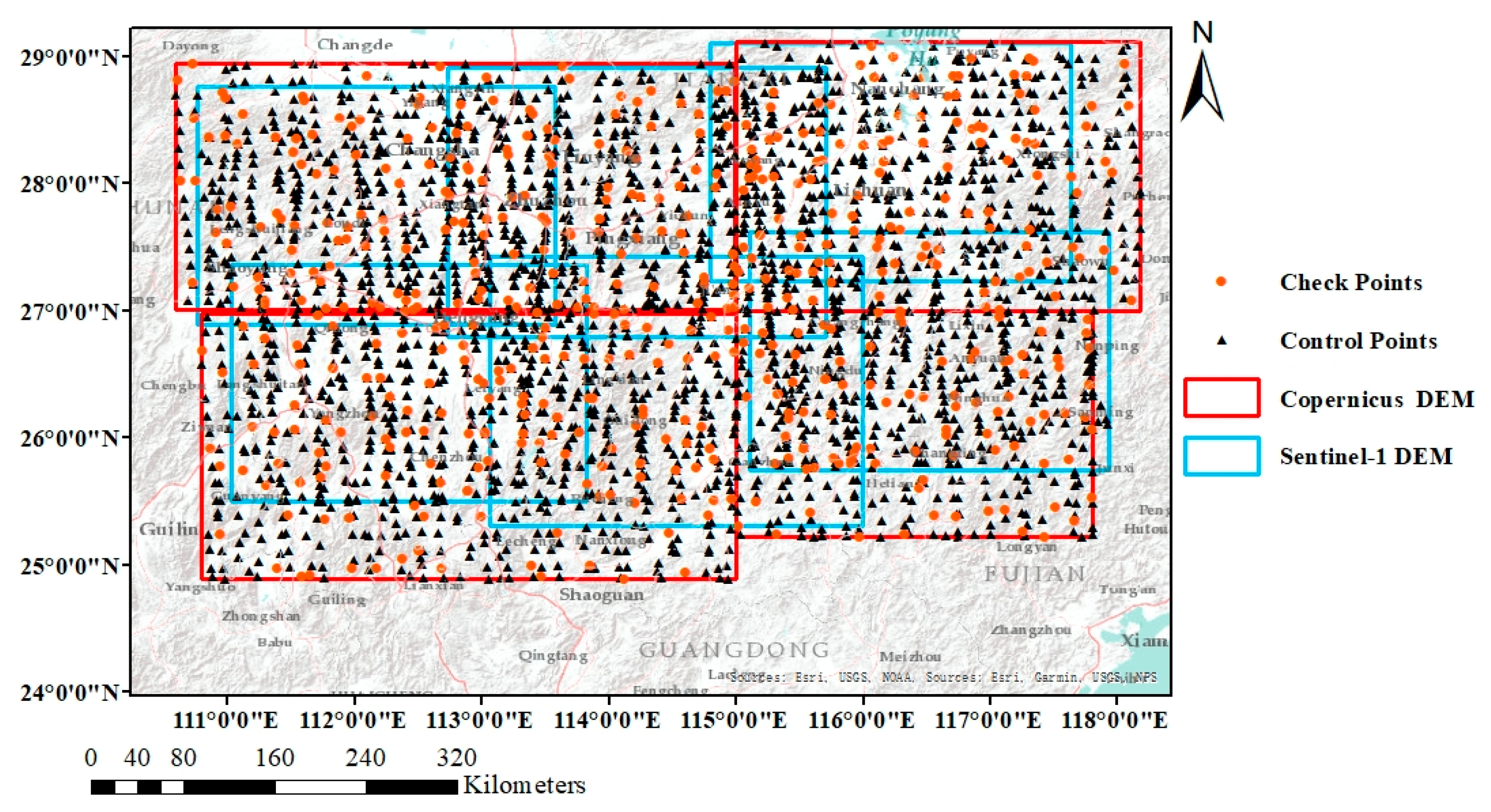
Research Region
4. Results
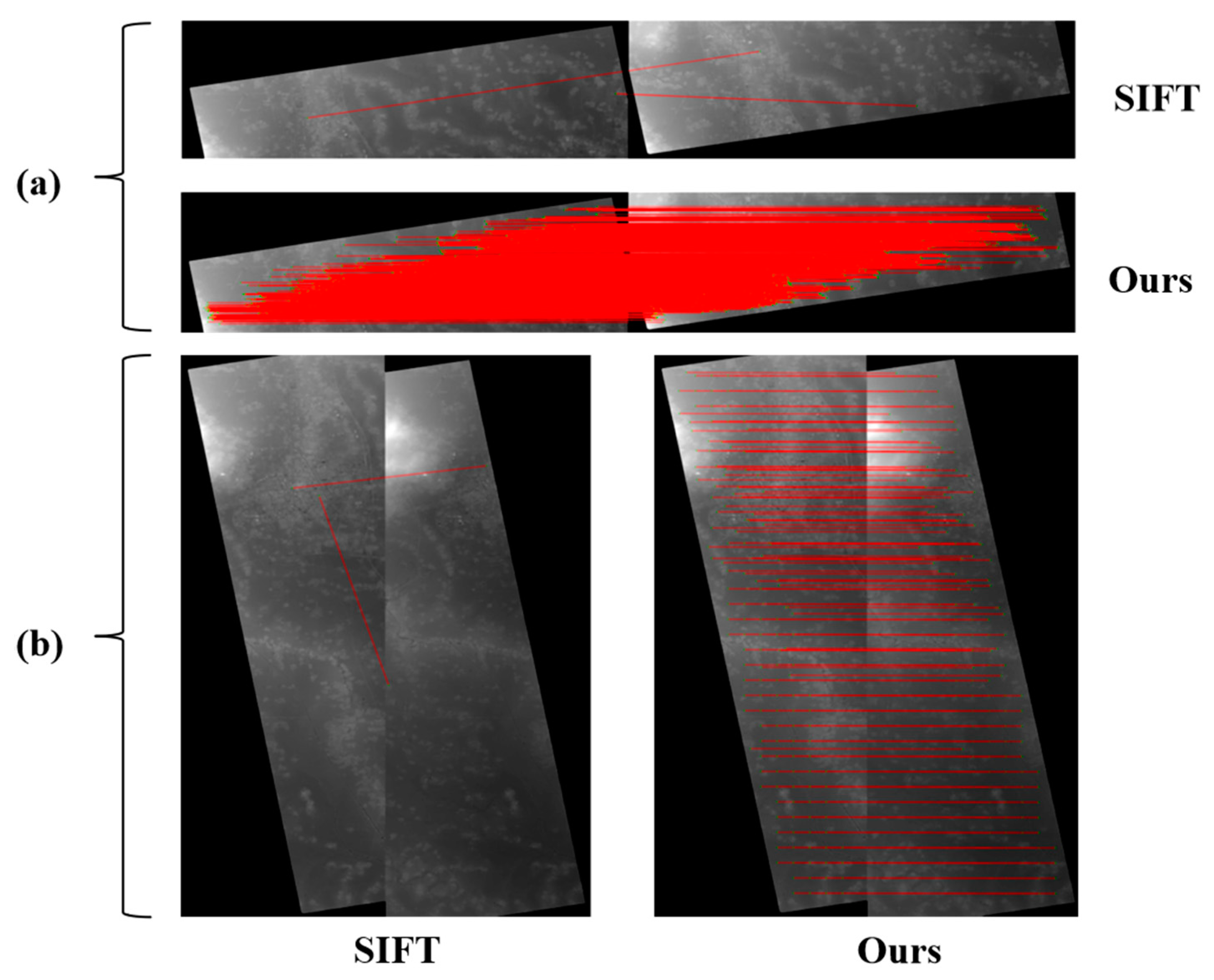
4.1. Keypoint Extraction and Matching
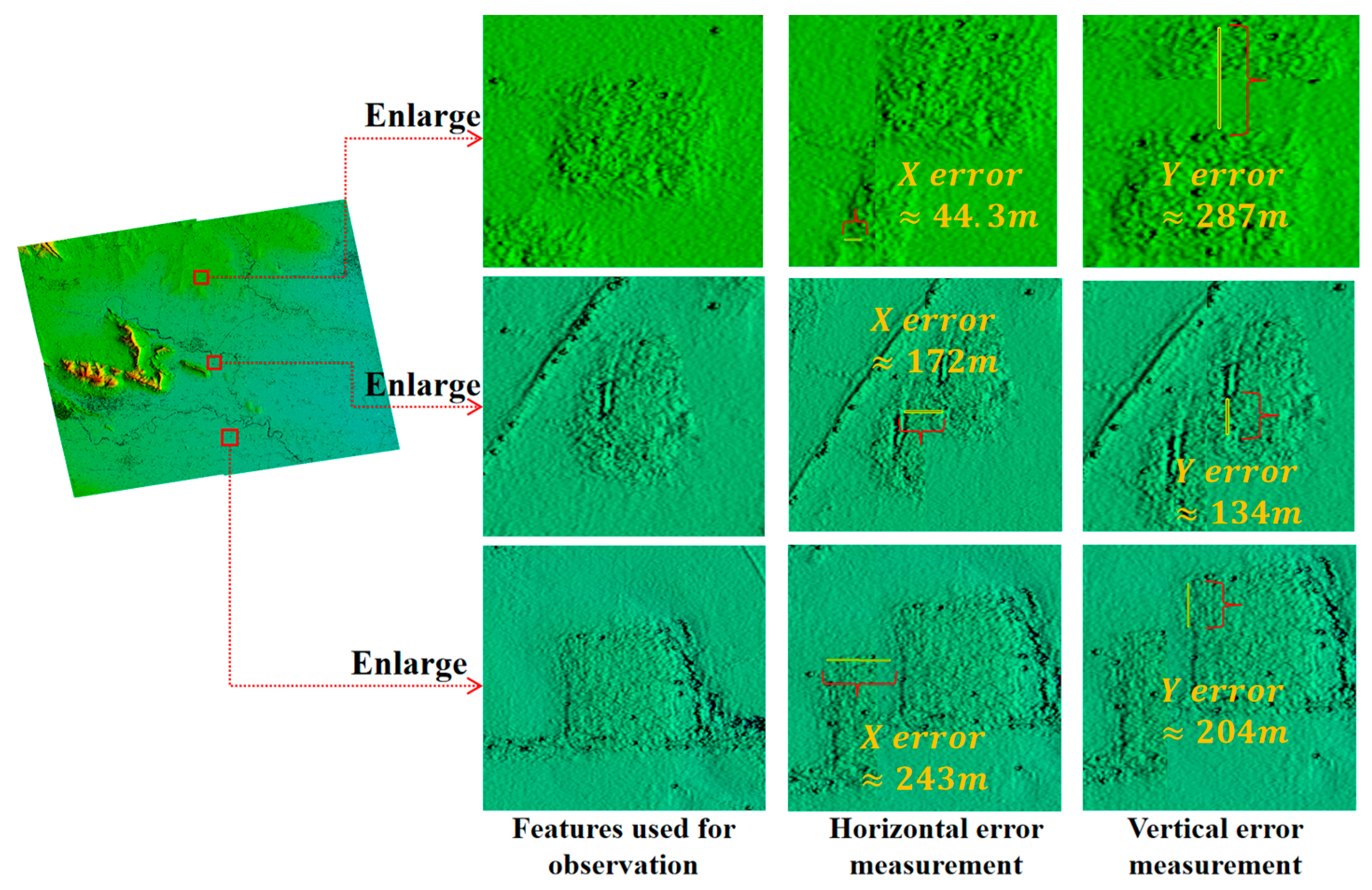
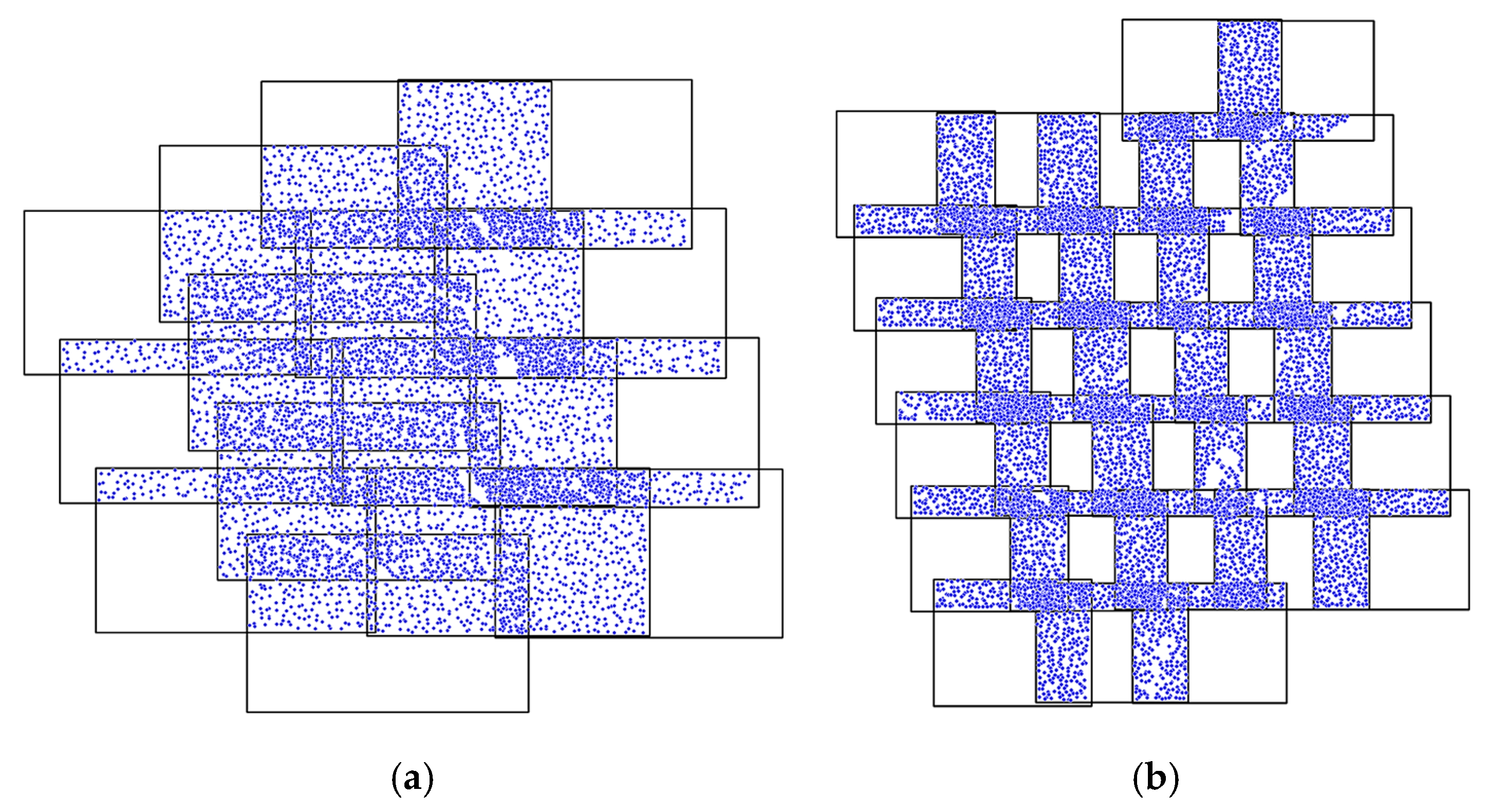
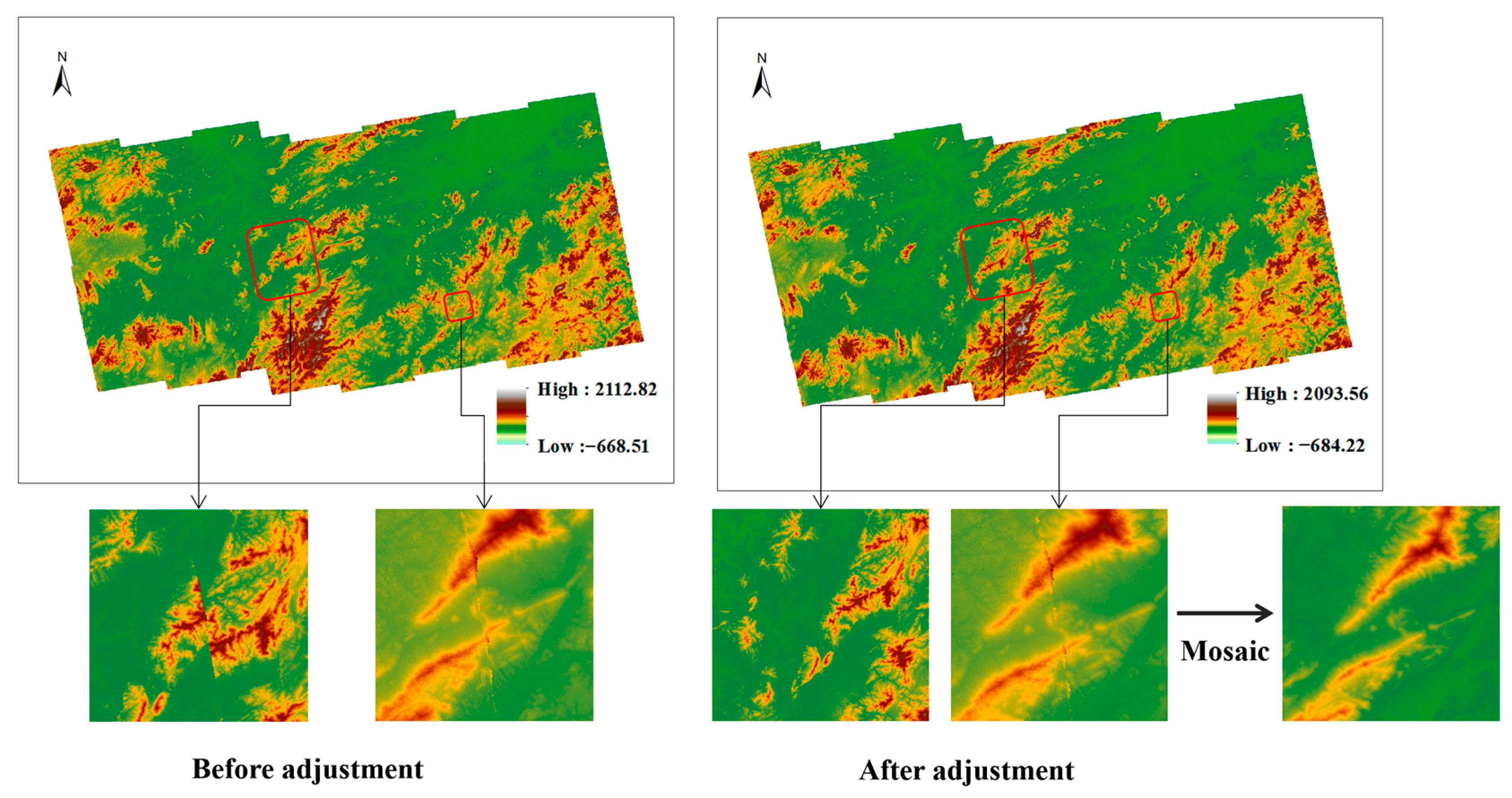
4.2. InSAR-DEM Block Adjustment Experiments and Comparisons
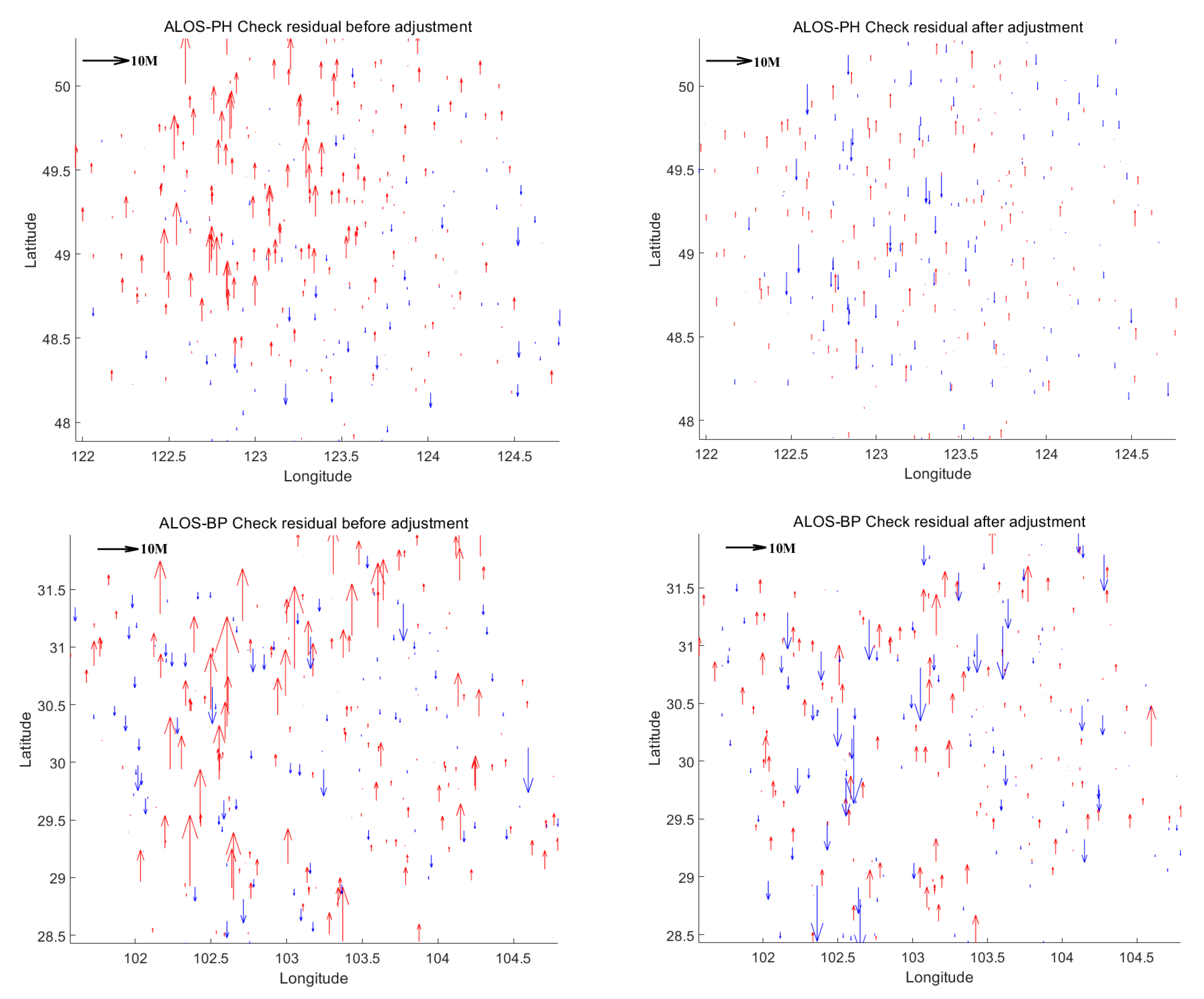
4.3. InSAR-DEM Block Adjustment
5. Discussion
- (1)
- Using the histogram of oriented gradients to describe features:The most typical characteristic of DEM is weak texture. For matching issues with weak-textured remote sensing images, feature fusion in the spatial and frequency domains is an advanced method [39]. This paper adopts the concept of edge-preserving filtering in the spatial domain but does not perform feature processing on DEM in the frequency domain. The reason is that images primarily rely on optical or radar sensors for data acquisition, and these sensors capture images based on the physical principles of light or radar waves, which have wave-like physical properties. Therefore, phase consistency can be used to detect feature edges. A similar choice is made in feature description work. We refer to the GIFT descriptor structure, but instead of using multi-level Log-Gabor filter responses as sampling points [40], which are based on phase principles, we use orientation gradient histograms, which are more suitable for describing DEM features.
- (2)
- Selection of Filters: When selecting edge-preserving filters, the traditional edge-preserving filters include bilateral filtering, guided filtering, and weighted least squares filtering. The effectiveness of bilateral filtering is closely related to the thresholds in both the spatial and intensity domains, making it difficult to set effectively on BFI. When weighted least squares filtering is applied to BFI with pixel quantities in the tens of millions to billions, the size of the differential operator matrix can reach billions, resulting in an unacceptable computational burden. Guided filtering requires a guidance image as a reference, making it difficult to apply to BFI. Therefore, we use an improved box filter based on the side-window filtering principle to further remove chaotic textures while preserving edge characteristics.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ICESat-2 | Ice, Cloud and land Elevation Satellite-2 |
| ICESat | Ice, Cloud and land Elevation Satellite |
| DEM | Digital Elevation Models |
| CopDEM | Copernicus InSAR-DEM |
| EFM | Enhanced Feature Map |
| DFM | Difference feature map |
| BFI | Background-free feature image |
| MFM | Median filter map |
| MMFM | Mean filtering on the median filter map |
| GIFT | Geometric and intensity-invariant feature transformation |
| SIFT | Scale-invariant feature transformation |
| NCC | Normalized Cross-Correlation |
| KNN | K-Nearest Neighbor |
References
- Crosetto, M. Calibration and validation of SAR interferometry for DEM generation. ISPRS J. Photogramm. Remote Sens. 2002, 57, 213–227. [Google Scholar] [CrossRef]
- Gesch, B.; Muller, J.; Farr, T.G. The shuttle radar topography mission-Data validation and applications. Photogramm. Eng. Remote Sens. 2006, 72, 233. [Google Scholar]
- Wang, Q. Research on High-Efficiency and High-Precision Processing Techniques of Spaceborne Interferometric Synthetic Aperture Radar. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2011. [Google Scholar]
- Gonszález, J.H.; Bachmann, M.; Krieger, G.; Fiedler, H. Development of the TanDEM-X calibration concept: Analysis of systematic errors. IEEE Trans. Geosci. Remote Sens. 2009, 48, 716–726. [Google Scholar] [CrossRef]
- Curlander, J.C. Location of spaceborne SAR imagery. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 359–364. [Google Scholar] [CrossRef]
- Montazeri, S.; Rodríguez González, F.; Zhu, X.X. Geocoding error correction for InSAR point clouds. Remote Sens. 2018, 10, 1523. [Google Scholar] [CrossRef]
- Fisher, P.F.; Tate, N.J. Causes and consequences of error in digital elevation models. Prog. Phys. Geogr. 2006, 30, 467–489. [Google Scholar] [CrossRef]
- Gong, J.; Li, Z.; Zhu, Q.; Sui, H.; Zhou, Y. Effects of various factors on the accuracy of DEMs: An intensive experimental investigation. Photogramm. Eng. Remote Sens. 2000, 66, 1113–1117. [Google Scholar]
- Xijuan, Y.; Chunming, H.; Changyong, D.; Yinghui, Z. Mathematical model of airborne InSAR block adjustment. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 59–63. [Google Scholar]
- Wessel, B.; Gruber, A.; Huber, M.; Roth, A. TanDEM-X: Block adjustment of interferometric height models. In Proceedings of the ISPRS Hannover Workshop “High-Resolution Earth Imaging for Geospatioal Information”, Hannover, Germany, 2–5 June 2009; International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. pp. 1–6. [Google Scholar]
- Zhang, X.; Xie, B.; Liu, S.; Tong, X.; Ding, R.; Xie, H.; Hong, Z. A Two-Step Block Adjustment Method for DSM Accuracy Improvement with Elevation Control of ICESat-2 Data. Remote Sens. 2022, 14, 4455. [Google Scholar] [CrossRef]
- Hong, Z.-H.; Sun, P.-F.; Zhou, R.-Y.; Tong, X.-H.; Feng, Y.-J.; Liu, S.-J. Fast mosaicking method of InSAR-generated multi-stripe digital elevation model. J. Infrared Millim. Waves 2022, 41, 493–500. [Google Scholar]
- Wang, R.; Lv, X.; Zhang, L. A novel three-dimensional block adjustment method for spaceborne InSAR-DEM based on general models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3973–3987. [Google Scholar] [CrossRef]
- Arefi, H.; Reinartz, P. Accuracy enhancement of ASTER global digital elevation models using ICESat data. Remote Sens. 2011, 3, 1323–1343. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and terrain height retrievals with ICESat-2: A first look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Li, B.; Xie, H.; Liu, S.; Tong, X.; Tang, H.; Wang, X. A method of extracting high-accuracy elevation control points from ICESat-2 altimetry data. Photogramm. Eng. Remote Sens. 2021, 87, 821–830. [Google Scholar] [CrossRef]
- Moudrý, V.; Gdulová, K.; Gábor, L.; Šárovcová, E.; Barták, V.; Leroy, F.; Špatenková, O.; Rocchini, D.; Prošek, J. Effects of environmental conditions on ICESat-2 terrain and canopy heights retrievals in Central European mountains. Remote Sens. Environ. 2022, 279, 113112. [Google Scholar] [CrossRef]
- Li, B.; Xie, H.; Liu, S.; Xi, Y.; Liu, C.; Xu, Y.; Ye, Z.; Hong, Z.; Weng, Q.; Sun, Y. A high-quality global elevation control point dataset from ICESat-2 altimeter data. Int. J. Digit. Earth 2024, 17, 2361724. [Google Scholar] [CrossRef]
- Rosenholm, D.; TORLEGARD, K. Three-dimensional absolute orientation of stereo models using digital elevation models. Photogramm. Eng. Remote Sens. 1988, 54, 1385–1389. [Google Scholar]
- Streutker, D.R.; Glenn, N.F.; Shrestha, R. A slope-based method for matching elevation surfaces. Photogramm. Eng. Remote Sens. 2011, 77, 743–750. [Google Scholar] [CrossRef]
- Ravanbakhsh, M.; Fraser, C. DEM registration based on mutual information. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 187–191. [Google Scholar] [CrossRef]
- Li, Z.; Bethel, J. DEM registration, alignment and evaluation for SAR interferometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 111–116. [Google Scholar]
- Jurie, F.; Dhome, M. A simple and efficient template matching algorithm. In Proceedings of the Eighth IEEE International Conference on Computer Vision ICCV, Vancouver, BC, Canada, 7–14 July 2001; pp. 544–549. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-modal image matching based on radiation-variation insensitive feature transform. IEEE Trans. Image Process. 2019, 29, 3296–3310. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Y.; Wan, Y.; Liu, X.; Yan, X.; Li, J. Multi-modal remote sensing image matching considering co-occurrence filter. IEEE Trans. Image Process. 2022, 31, 2584–2597. [Google Scholar] [CrossRef]
- Hirt, C. Artefact detection in global digital elevation models (DEMs): The Maximum Slope Approach and its application for complete screening of the SRTM v4. 1 and MERIT DEMs. Remote Sens. Environ. 2018, 207, 27–41. [Google Scholar] [CrossRef]
- Hu, Z.; Gui, R.; Hu, J.; Fu, H.; Yuan, Y.; Jiang, K.; Liu, L. InSAR digital elevation model void-filling method based on incorporating elevation outlier detection. Remote Sens. 2024, 16, 1452. [Google Scholar] [CrossRef]
- Lecours, V.; Devillers, R.; Edinger, E.N.; Brown, C.J.; Lucieer, V.L. Influence of artefacts in marine digital terrain models on habitat maps and species distribution models: A multiscale assessment. Remote Sens. Ecol. Conserv. 2017, 3, 232–246. [Google Scholar] [CrossRef]
- Hirt, C.; Kuhn, M.; Claessens, S.; Pail, R.; Seitz, K.; Gruber, T. Study of the Earth’ s short-scale gravity field using the ERTM2160 gravity model. Comput. Geosci. 2014, 73, 71–80. [Google Scholar] [CrossRef]
- Huber, M.; Gruber, A.; Wessel, B.; Breunig, M.; Wendleder, A. Validation of tie-point concepts by the DEM adjustment approach of TanDEM-X. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 23–30 July 2010; pp. 2644–2647. [Google Scholar]
- Li, Z.; Shen, H.; Weng, Q.; Zhang, Y.; Dou, P.; Zhang, L. Cloud and cloud shadow detection for optical satellite imagery: Features, algorithms, validation, and prospects. ISPRS J. Photogramm. Remote Sens. 2022, 188, 89–108. [Google Scholar] [CrossRef]
- Koschan, A.; Abidi, M. Detection and classification of edges in color images. IEEE Signal Process. Mag. 2005, 22, 64–73. [Google Scholar] [CrossRef]
- Yin, H.; Gong, Y.; Qiu, G. Side window filtering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8758–8766. [Google Scholar]
- Marešová, J.; Gdulová, K.; Pracná, P.; Moravec, D.; Gábor, L.; Prošek, J.; Barták, V.; Moudrý, V. Applicability of data acquisition characteristics to the identification of local artefacts in global digital elevation models: Comparison of the Copernicus and TanDEM-X DEMs. Remote Sens. 2021, 13, 3931. [Google Scholar] [CrossRef]
- Datla, R.; Mohan, C.K. A novel framework for seamless mosaic of Cartosat-1 DEM scenes. Comput. Geosci. 2021, 146, 104619. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Cattani, C.; Cui, Q.; Liu, S. Diffusion-based image inpainting forensics via weighted least squares filtering enhancement. Multimed. Tools Appl. 2021, 80, 30725–30739. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, Y.; Zhang, L. POS-GIFT: A geometric and intensity-invariant feature transformation for multimodal images. Inf. Fusion 2024, 102, 102027. [Google Scholar] [CrossRef]



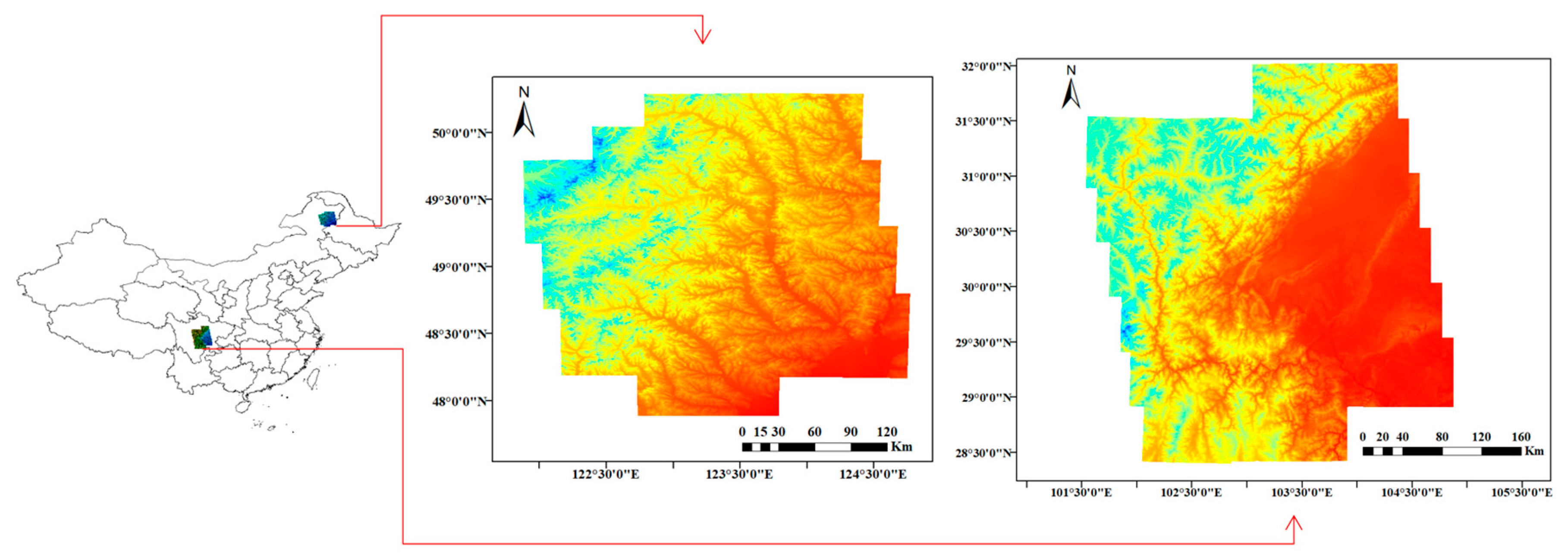





| Research Region | Elevation Range | Area (km2) | Image Size (Pixels × Pixels) | Terrain |
|---|---|---|---|---|
| ALOS-PH | 170–1415 m | 56,418 | 17,424 × 20,907 | Flat terrain and hills |
| ALOS-BP | 224–7405 m | 129,830 | 29,390 × 27,086 | Mountains and basins |
| DEM Number | Orbital Position | Overlapping Area (Pixels) | Number of Points Before (Enhance) | Number of Points After (Enhance) |
|---|---|---|---|---|
| DEM-Figure 8a(left) | Along | 5277 | 22,466 | |
| DEM-Figure 8a(right) | Along | 5988 | 22,094 | |
| DEM-Figure 8b(left) | Vertical | 21,237 | 56,318 | |
| DEM-Figure 8b(right) | Vertical | 9541 | 78,174 |
| After (m) | After (m) | After (m) | After (m) | |
|---|---|---|---|---|
| Data | ALOS-PH | ALOS-PH | ALOS-BP | ALOS-BP |
| Method | sliding window | Ours | sliding window | Ours |
| X RMSE | 2.656971 | 2.040121 | 2.166357 | 1.535620 |
| Y RMSE | 2.344169 | 1.910933 | 1.242834 | 0.910042 |
| XY MEAN | 2.798351 | 2.316631 | 1.723684 | 1.188659 |
| The number of TPs | 5363 | 6620 | 9414 | 9768 |
| TPs matching time (second) | 2106.27 | 2481.41 | 3967.8 | 4655.59 |
| Before (m) | After (m) | After (m) | Before (m) | After (m) | After (m) | |
|---|---|---|---|---|---|---|
| Data | ALOS-PH | ALOS-PH | ALOS-PH | ALOS-BP | ALOS-BP | ALOS-BP |
| Method | sliding window | sliding window | Ours | sliding window | sliding window | Ours |
| Height-ABS | 2.156771 | 1.837497 | 1.729699 | 4.456939 | 4.293428 | 4.215460 |
| Height-RMSE | 3.086416 | 2.578077 | 2.268726 | 6.807942 | 6.435393 | 6.111026 |
| Height-MAX | 11.673828 | 9.721665 | 8.131412 | 35.339111 | 32.825108 | 30.146499 |
| Height-MIN | 0.001465 | 0.012924 | 0.014138 | 0.004364 | 0.006792 | 0.004192 |
| Before | After (m) | After (m) | After (m) | |
|---|---|---|---|---|
| Data | Sentinel | Sentinel | Sentinel (Second) | Sentinel (Second) |
| Method | Ours | Ours | sliding window | Ours |
| X RMSE | 137.18337 | 6.660747 | 7.163181 | 6.844605 |
| Y RMSE | 32.527578 | 4.445506 | 5.002840 | 4.366544 |
| XY MEAN | 83.414873 | 5.876839 | 6.657243 | 5.713693 |
| Before (m) | After (m) | Before (m) | After (m) | Before (m) | After (m) | |
|---|---|---|---|---|---|---|
| Data | Sentinel& CopDEM | Sentinel& CopDEM | Sentinel | Sentinel | CopDEM | CopDEM |
| Height-ABS | 14.611961 | 6.604417 | 19.352163 | 10.076845 | 10.490046 | 3.584915 |
| HeightRMSE | 19.018838 | 10.291855 | 24.362027 | 14.183206 | 12.655347 | 4.806659 |
| HeightMAX | 93.140530 | 68.818319 | 93.140530 | 68.818319 | 41.209506 | 25.76232 |
| Height-MIN | 0.0228270 | 0.0023850 | 0.0623359 | 0.0023850 | 0.0228269 | 0.052466 |
| Before (m) | After (m) | After (Without TPs) | |
|---|---|---|---|
| Data | Sentinel | Sentinel | Sentinel |
| Height-ABS | 19.352163 | 10.076845 | 10.627355 |
| HeightRMSE | 24.362027 | 14.183206 | 14.554168 |
| HeightMAX | 93.140530 | 68.818319 | 68.818319 |
| Height-MIN | 0.0623359 | 0.0023850 | 0.063000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Z.; He, Z.; Pan, H.; Tang, Z.; Zhou, R.; Zhang, Y.; Han, Y.; Tao, J. A Robust InSAR-DEM Block Adjustment Method Based on Affine and Polynomial Models for Geometric Distortion. Remote Sens. 2025, 17, 1346. https://doi.org/10.3390/rs17081346
Hong Z, He Z, Pan H, Tang Z, Zhou R, Zhang Y, Han Y, Tao J. A Robust InSAR-DEM Block Adjustment Method Based on Affine and Polynomial Models for Geometric Distortion. Remote Sensing. 2025; 17(8):1346. https://doi.org/10.3390/rs17081346
Chicago/Turabian StyleHong, Zhonghua, Ziyuan He, Haiyan Pan, Zhihao Tang, Ruyan Zhou, Yun Zhang, Yanling Han, and Jiang Tao. 2025. "A Robust InSAR-DEM Block Adjustment Method Based on Affine and Polynomial Models for Geometric Distortion" Remote Sensing 17, no. 8: 1346. https://doi.org/10.3390/rs17081346
APA StyleHong, Z., He, Z., Pan, H., Tang, Z., Zhou, R., Zhang, Y., Han, Y., & Tao, J. (2025). A Robust InSAR-DEM Block Adjustment Method Based on Affine and Polynomial Models for Geometric Distortion. Remote Sensing, 17(8), 1346. https://doi.org/10.3390/rs17081346









