A Multi-Directional Pyranometer (CUBE-i) for Real-Time Direct and Diffuse Solar Irradiance Decomposition
Abstract
1. Introduction
2. DNI Estimation Model Using Five-Directional Global Irradiance
2.1. Review on Decomposition Methods
2.1.1. -Based Empirical Models
2.1.2. Multi-Directional Irradiance-Based Numerical Model
2.2. Development Pyranometer Model
2.2.1. Analysis of Cubic Directional Irradiance
2.2.2. DNI Estimation Model Derivation with DNN Application
| Model | Error Metrics | |||
|---|---|---|---|---|
| RMSE [W/m2] | nRMSE [%] | MBE [W/m2] | R2 [-] | |
| Model 1 | 69.2 | 10.3 | 0.24 | 0.967 |
| Model 2 | 67.5 | 10.0 | −1.15 | 0.968 |
| Model 3 | 69.0 | 10.3 | −1.41 | 0.967 |
| Model 4 | 65.7 | 9.8 | −0.28 | 0.970 |
| Model 5 | 74.5 | 11.1 | −0.28 | 0.961 |
| Model 6 | 20.2 | 8.2 | −1.30 | 0.997 |
3. Development of CUBE-i Method
3.1. Development of DNI Estimation Process of CUBE-i
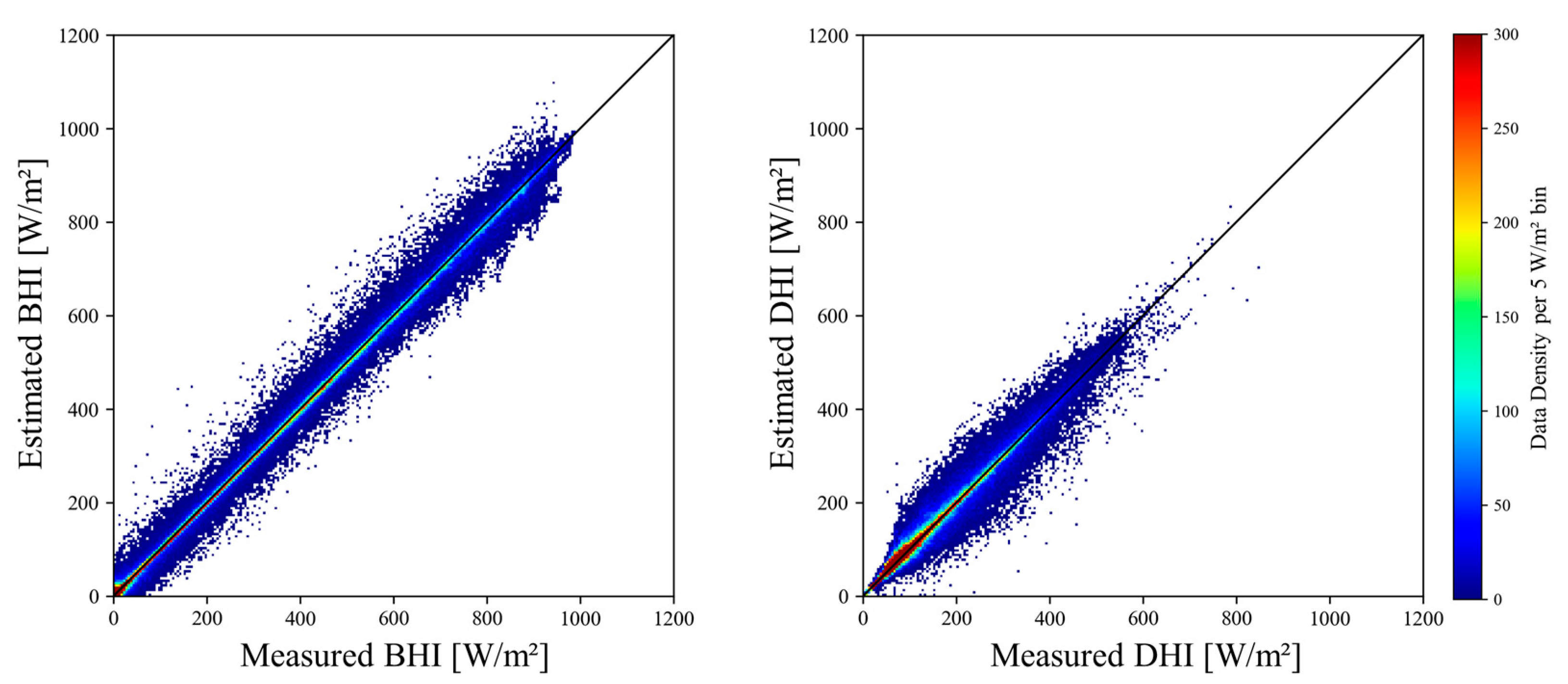
3.2. Computation of Direct and Diffuse Irradiance
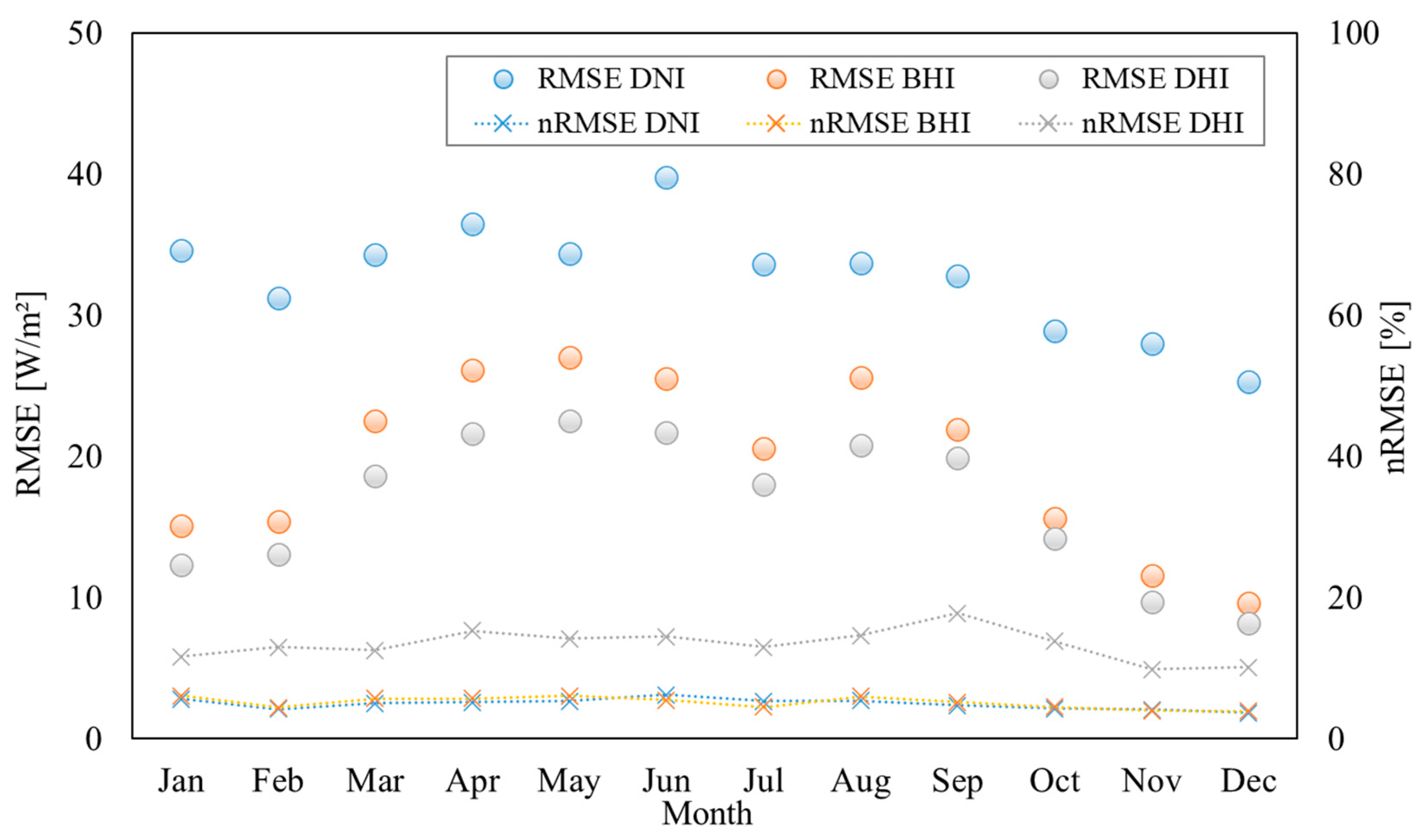
3.2.1. Estimation Results for Multi-Directional Irradiance
| Data Range | Error Metrics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | ||
| All data | R2 [-] | 0.997 | 0.998 | 0.997 | 0.997 | 0.997 | 0.995 | 0.996 | 0.997 | 0.997 | 0.998 | 0.998 | 0.998 |
| RMSE [W/m2] | 18.3 | 17.8 | 20.0 | 22.3 | 22.3 | 26.8 | 23.1 | 20.8 | 21.5 | 18.0 | 15.2 | 13.7 | |
| nRMSE [%] | 10.7 | 7.4 | 8.7 | 8.7 | 8.3 | 9.3 | 7.7 | 8.9 | 7.2 | 7.0 | 7.5 | 6.9 | |
| MAE [W/m2] | 6.6 | 6.8 | 8.6 | 9.0 | 9.9 | 10.9 | 9.8 | 9.1 | 8.9 | 7.6 | 5.7 | 5.1 | |
| MBE [W/m2] | −0.03 | −0.64 | −1.75 | −1.30 | −2.03 | −2.63 | −3.08 | −1.27 | −1.71 | −2.20 | −0.14 | 0.86 | |
| Above 10 W/m2 | R2 [-] | 0.990 | 0.990 | 0.990 | 0.988 | 0.990 | 0.985 | 0.988 | 0.989 | 0.988 | 0.991 | 0.993 | 0.993 |
| RMSE [W/m2] | 34.6 | 31.2 | 34.3 | 36.5 | 34.4 | 39.8 | 33.6 | 33.7 | 32.8 | 28.9 | 28.0 | 25.3 | |
| nRMSE [%] | 5.6 | 4.2 | 5.0 | 5.2 | 5.3 | 6.2 | 5.3 | 5.4 | 4.7 | 4.3 | 4.1 | 3.7 | |
| MAE [W/m2] | 23.2 | 20.5 | 24.6 | 23.1 | 22.6 | 23.3 | 20.2 | 22.9 | 20.2 | 19.4 | 18.7 | 16.8 | |
| MBE [W/m2] | −0.63 | −2.66 | −6.16 | −4.72 | −5.84 | −6.58 | −7.03 | −4.50 | −4.70 | −6.16 | −1.08 | 2.58 | |
| Data range | Error Metrics | BHI () | |||||||||||
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | ||
| All data | R2 [-] | 0.997 | 0.998 | 0.997 | 0.997 | 0.997 | 0.997 | 0.998 | 0.997 | 0.997 | 0.998 | 0.999 | 0.999 |
| RMSE [W/m2] | 7.7 | 8.6 | 12.8 | 15.6 | 17.1 | 16.8 | 13.8 | 15.3 | 14.0 | 9.5 | 6.1 | 5.0 | |
| nRMSE [%] | 12.2 | 7.9 | 10.2 | 9.7 | 9.7 | 8.4 | 6.7 | 10.1 | 8.2 | 7.5 | 7.8 | 7.6 | |
| MAE [W/m2] | 2.5 | 2.9 | 4.9 | 5.7 | 6.7 | 7.0 | 5.9 | 5.9 | 5.2 | 3.5 | 2.0 | 1.6 | |
| MBE [W/m2] | 0.01 | −0.33 | −1.14 | −0.91 | −1.38 | −0.76 | −1.01 | −0.37 | −0.75 | −0.81 | 0.05 | 0.37 | |
| Above 10 W/m2 | R2 [-] | 0.991 | 0.995 | 0.992 | 0.992 | 0.993 | 0.993 | 0.995 | 0.992 | 0.993 | 0.995 | 0.996 | 0.996 |
| RMSE [W/m2] | 15.1 | 15.4 | 22.5 | 26.1 | 27.0 | 25.5 | 20.6 | 25.6 | 21.9 | 15.6 | 11.6 | 9.6 | |
| nRMSE [%] | 6.1 | 4.4 | 5.7 | 5.7 | 6.1 | 5.5 | 4.5 | 6.0 | 5.2 | 4.5 | 4.0 | 3.9 | |
| MAE [W/m2] | 9.4 | 9.2 | 14.6 | 15.3 | 16.1 | 15.5 | 12.6 | 15.8 | 12.4 | 9.4 | 7.1 | 5.7 | |
| MBE [W/m2] | −0.18 | −1.31 | −4.11 | −3.36 | −4.15 | −2.26 | −2.57 | −1.80 | −2.27 | −2.42 | −0.12 | 1.29 | |
| Data range | Error Metrics | DHI () | |||||||||||
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | ||
| All data | R2 [-] | 0.988 | 0.986 | 0.987 | 0.979 | 0.980 | 0.978 | 0.980 | 0.979 | 0.973 | 0.982 | 0.993 | 0.991 |
| RMSE [W/m2] | 7.7 | 8.6 | 12.8 | 15.6 | 17.1 | 16.8 | 13.8 | 15.3 | 14.0 | 9.5 | 6.1 | 5.0 | |
| nRMSE [%] | 18.6 | 19.8 | 18.2 | 21.0 | 18.8 | 18.8 | 16.9 | 19.8 | 25.2 | 20.6 | 15.5 | 16.4 | |
| MAE [W/m2] | 2.5 | 2.9 | 4.9 | 5.7 | 6.7 | 7.0 | 5.9 | 5.9 | 5.2 | 3.5 | 2.0 | 1.6 | |
| MBE [W/m2] | −0.01 | 0.33 | 1.14 | 0.91 | 1.38 | 0.76 | 1.01 | 0.37 | 0.75 | 0.81 | −0.05 | −0.37 | |
| Above 10 W/m2 | R2 [-] | 0.975 | 0.973 | 0.978 | 0.965 | 0.966 | 0.963 | 0.963 | 0.964 | 0.953 | 0.964 | 0.986 | 0.979 |
| RMSE [W/m2] | 12.3 | 13.1 | 18.6 | 21.6 | 22.5 | 21.7 | 18.0 | 20.8 | 19.9 | 14.2 | 9.7 | 8.2 | |
| nRMSE [%] | 11.6 | 13.0 | 12.5 | 15.3 | 14.2 | 14.5 | 13.0 | 14.6 | 17.8 | 13.8 | 9.8 | 10.1 | |
| MAE [W/m2] | 6.5 | 6.8 | 10.3 | 10.9 | 11.7 | 11.6 | 10.0 | 10.9 | 10.5 | 7.9 | 5.2 | 4.3 | |
| MBE [W/m2] | −0.02 | 0.77 | 2.41 | 1.73 | 2.40 | 1.26 | 1.71 | 0.68 | 1.50 | 1.80 | −0.12 | −0.99 | |
| Data Range | Error Metrics | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| E | S | W | N | E | S | W | N | ||
| All data | R2 [-] | 0.998 | 0.998 | 0.996 | 0.985 | 0.993 | 0.989 | 0.987 | 0.998 |
| RMSE [W/m2] | 7.6 | 9.8 | 9.4 | 2.9 | 7.6 | 9.8 | 9.4 | 2.9 | |
| nRMSE [%] | 9.7 | 9.3 | 17.1 | 64.9 | 11.0 | 14.2 | 14.8 | 5.3 | |
| MAE [W/m2] | 2.2 | 3.3 | 2.3 | 0.2 | 2.2 | 3.3 | 2.3 | 0.2 | |
| MBE [W/m2] | −0.52 | −0.28 | −0.47 | −0.13 | 0.52 | 0.28 | 0.47 | 0.13 | |
| Above 10 W/m2 | R2 [-] | 0.995 | 0.995 | 0.990 | 0.952 | 0.981 | 0.976 | 0.975 | 1.000 |
| RMSE [W/m2] | 17.0 | 17.9 | 23.3 | 13.0 | 10.8 | 14.0 | 11.7 | 1.3 | |
| nRMSE [%] | 4.2 | 5.0 | 6.8 | 14.4 | 7.6 | 9.8 | 8.9 | 1.2 | |
| MAE [W/m2] | 10.7 | 10.6 | 13.2 | 4.4 | 4.5 | 6.8 | 4.4 | 0.3 | |
| MBE [W/m2] | −3.06 | −1.28 | −3.53 | −2.81 | 1.05 | 0.56 | 0.74 | 0.1 | |
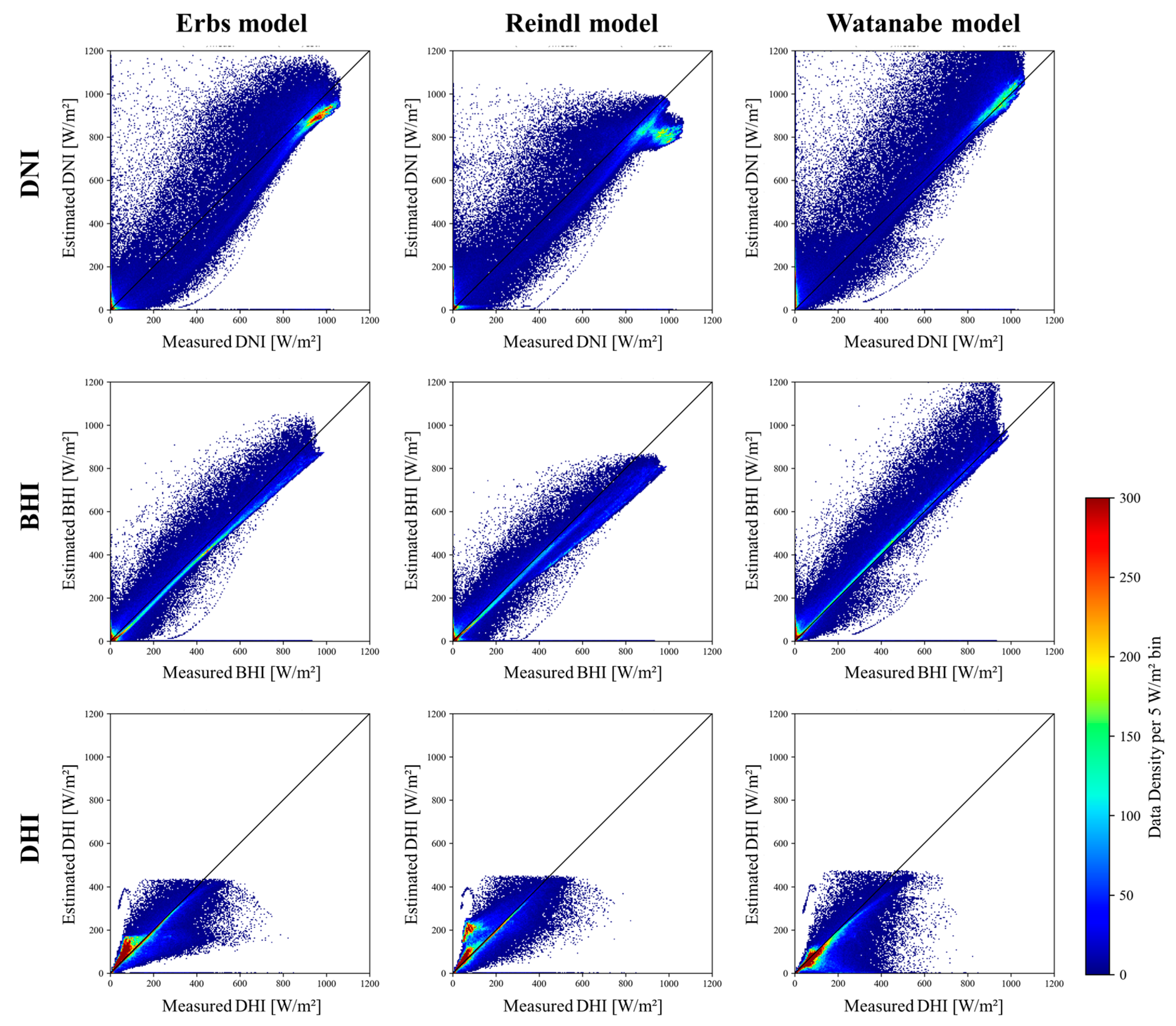
3.2.2. Comparison with Existing Decomposition Models
| Data Range | Error Metrics | ||||
|---|---|---|---|---|---|
| Erbs | Reindl | Watanabe | CUBE-i | ||
| All data | R2 [-] | 0.943 | 0.937 | 0.913 | 0.997 |
| RMSE [W/m2] | 90.8 | 95.0 | 111.9 | 20.2 | |
| nRMSE [%] | 36.7 | 38.4 | 45.2 | 8.2 | |
| MAE [W/m2] | 38.7 | 43.9 | 44.6 | 8.1 | |
| MBE [W/m2] | −1.55 | −12.33 | 35.36 | −1.3 | |
| Above 10 W/m2 | R2 [-] | 0.820 | 0.800 | 0.738 | 0.990 |
| RMSE [W/m2] | 137.6 | 145.0 | 166.1 | 33.1 | |
| nRMSE [%] | 20.5 | 21.6 | 24.7 | 4.9 | |
| MAE [W/m2] | 94.9 | 106.7 | 98.4 | 21.2 | |
| MBE [W/m2] | −14.7 | −45.97 | 73.24 | −4.25 | |
| Data range | Error Metrics | ||||
| Erbs | Reindl | Watanabe | CUBE-i | ||
| All data | R2 [-] | 0.967 | 0.956 | 0.950 | 0.997 |
| RMSE [W/m2] | 44.8 | 51.6 | 54.8 | 12.5 | |
| nRMSE [%] | 32.6 | 37.5 | 39.9 | 9.1 | |
| MAE [W/m2] | 17.6 | 22.0 | 20.1 | 4.5 | |
| MBE [W/m2] | −0.84 | −10.36 | 14.78 | −0.56 | |
| Above 10 W/m2 | R2 [-] | 0.924 | 0.898 | 0.887 | 0.994 |
| RMSE [W/m2] | 74.4 | 85.9 | 90.4 | 21.0 | |
| nRMSE [%] | 18.9 | 21.8 | 22.9 | 5.3 | |
| MAE [W/m2] | 46.9 | 59.2 | 49.8 | 12.2 | |
| MBE [W/m2] | −5.8 | −33.6 | 34.64 | −2.05 | |
| Data range | Error Metrics | ||||
| Erbs | Reindl | Watanabe | CUBE-i | ||
| All data | R2 [-] | 0.816 | 0.743 | 0.705 | 0.983 |
| RMSE [W/m2] | 40.6 | 48.0 | 51.5 | 12.5 | |
| nRMSE [%] | 66.3 | 78.3 | 84.0 | 20.4 | |
| MAE [W/m2] | 17.2 | 21.7 | 19.7 | 4.5 | |
| MBE [W/m2] | −0.68 | 8.84 | −16.3 | 0.56 | |
| Above 10 W/m2 | R2 [-] | 0.673 | 0.543 | 0.475 | 0.969 |
| RMSE [W/m2] | 58.2 | 68.8 | 73.8 | 17.9 | |
| nRMSE [%] | 46.3 | 54.7 | 58.7 | 14.2 | |
| MAE [W/m2] | 35.4 | 44.5 | 40.5 | 9.2 | |
| MBE [W/m2] | −1.36 | 18.21 | −33.43 | 1.16 | |
4. Discussions and Limitations
4.1. Impact of Multi-Sensor Errors
4.2. Regional Adaptability and Validation
4.3. Installation Requirements
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GHI | Global horizontal irradiance, W/m2 |
| BHI | Beam horizontal irradiance, W/m2 |
| DHI | Diffuse horizontal irradiance, W/m2 |
| DNI | Direct normal irradiance, W/m2 |
| MSE | Mean squared error |
| RMSE | Root mean squared error |
| nRMSE | Normalized root mean squared error |
| MBE | Mean bias error |
| MAE | Mean absolute error |
Nomenclature
| Symbols | |
| Julian day | |
| Solar irradiance, W/m2 | |
| Extraterrestrial radiant flux, W/m2 | |
| Solar constant, W/m2 | |
| Clearness index | |
| Greek letters | |
| Solar altitude angle, rad | |
| Solar azimuth angle relative to the surface normal of the pyranometer, rad | |
| Incident angle between solar beam and the surface normal of the pyranometer, rad | |
| Subscripts | |
| circ | Circumsolar zone |
| Diffuse components | |
| Direct components | |
| DN | Direct normal |
| dome | Isotropic sky dome |
| g | Global |
| Directional identifier of the pyranometer (E, S, W, N) | |
| refl | Reflected |
| ribn | Horizontal ribbon |
| Etc. | |
| Vertical direction on horizontal plane | |
| Vertical direction on tilted plane | |
References
- Sakti, A.D.; Ihsan, K.T.N.; Anggraini, T.S.; Shabrina, Z.; Sasongko, N.A.; Fachrizal, R.; Aziz, M.; Aryal, J.; Yuliarto, B.; Hadi, P.O.; et al. Multi-Criteria Assessment for City-Wide Rooftop Solar PV Deployment: A Case Study of Bandung, Indonesia. Remote Sens. 2022, 14, 2796. [Google Scholar] [CrossRef]
- Lee, D.S.; Jo, J.H. Application of Simple Sky and Building Models for the Evaluation of Solar Irradiance Distribution at Indoor Locations in Buildings. Build. Environ. 2021, 197, 107840. [Google Scholar] [CrossRef]
- Hou, M.; Aviv, D.; Chatterjee, A.; Teitelbaum, E.; Rida, M.; Meggers, F.; Khovalyg, D. Resolving Indoor Shortwave and Longwave Human Body Irradiance Variations for Mean Radiant Temperature and Local Thermal Comfort. Energy Build. 2023, 301, 113581. [Google Scholar] [CrossRef]
- Lee, D.S.; Jo, J.H. Measuring and Implementing Mean Radiant Temperature in Buildings: Technical Review. Renew. Sustain. Energy Rev. 2025, 207, 114908. [Google Scholar] [CrossRef]
- Arens, E.; Hoyt, T.; Zhou, X.; Huang, L.; Zhang, H.; Schiavon, S. Modeling the Comfort Effects of Short-Wave Solar Radiation Indoors. Build. Environ. 2015, 88, 3–9. [Google Scholar] [CrossRef]
- Kwon, S.J.; Jo, J.H.; Lee, D.S. Proposal of Three Methods for Deriving Representative Mean Radiant Temperatures Considering Zone Spatial Distributions. Energies 2024, 17, 5221. [Google Scholar] [CrossRef]
- Lee, D.; Cho, Y.H.; Jo, J.H. Assessment of Control Strategy of Adaptive Façades for Heating, Cooling, Lighting Energy Conservation and Glare Prevention. Energy Build. 2021, 235, 110739. [Google Scholar] [CrossRef]
- Xiong, J.; Tzempelikos, A. Model-Based Shading and Lighting Controls Considering Visual Comfort and Energy Use. Sol. Energy 2016, 134, 416–428. [Google Scholar] [CrossRef]
- Lee, D.S.; Koo, S.H.; Seong, Y.B.; Jo, J.H. Evaluating Thermal and Lighting Energy Performance of Shading Devices on Kinetic Façades. Sustainability 2016, 8, 883. [Google Scholar] [CrossRef]
- Huang, X.; Hayashi, K.; Matsumoto, T.; Tao, L.; Huang, Y.; Tomino, Y. Estimation of Rooftop Solar Power Potential by Comparing Solar Radiation Data and Remote Sensing Data—A Case Study in Aichi, Japan. Remote Sens. 2022, 14, 1742. [Google Scholar] [CrossRef]
- Dumka, U.C.; Kosmopoulos, P.G.; Ningombam, S.S.; Masoom, A. Impact of Aerosol and Cloud on the Solar Energy Potential over the Central Gangetic Himalayan Region. Remote Sens. 2021, 13, 3248. [Google Scholar] [CrossRef]
- López, G.; Gueymard, C.A.; Polo, J.; Alonso-Montesinos, J.; Marzo, A.; Martín-Chivelet, N.; Ferrada, P.; Escalona-Llaguno, M.I.; Batlles, F.J. Increasing the Resolution and Spectral Range of Measured Direct Irradiance Spectra for PV Applications. Remote Sens. 2023, 15, 1675. [Google Scholar] [CrossRef]
- Kirimtat, A.; Tasgetiren, M.F.; Brida, P.; Krejcar, O. Control of PV Integrated Shading Devices in Buildings: A Review. Build. Environ. 2022, 214, 108961. [Google Scholar] [CrossRef]
- Ito, R.; Lee, S. Performance Enhancement of Photovoltaic Integrated Shading Devices with Flexible Solar Panel Using Multi-Objective Optimization. Appl. Energy 2024, 373, 123866. [Google Scholar] [CrossRef]
- Suhaimi, M.F.B.; Kim, W.G.; Cho, C.W.; Lee, H. Impact of Solar Radiation on Human Comfort in a Vehicle Cabin: An Analysis of Body Segment Mean Radiant Temperature. Build. Environ. 2023, 245, 110849. [Google Scholar] [CrossRef]
- Kim, E.S.; Yun, S.H.; Park, C.Y.; Heo, H.K.; Lee, D.K. Estimation of Mean Radiant Temperature in Urban Canyons Using Google Street View: A Case Study on Seoul. Remote Sens. 2022, 14, 260. [Google Scholar] [CrossRef]
- Park, C.Y.; Lee, D.K.; Krayenhoff, E.S.; Heo, H.K.; Ahn, S.; Asawa, T.; Murakami, A.; Kim, H.G. A Multilayer Mean Radiant Temperature Model for Pedestrians in a Street Canyon with Trees. Build. Environ. 2018, 141, 298–309. [Google Scholar] [CrossRef]
- Olpenda, A.S.; Stereńczak, K.; Bȩdkowski, K. Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities. Remote Sens. 2018, 10, 694. [Google Scholar] [CrossRef]
- Prasad, A.A.; Taylor, R.A.; Kay, M. Assessment of Direct Normal Irradiance and Cloud Connections Using Satellite Data over Australia. Appl. Energy 2015, 143, 301–311. [Google Scholar] [CrossRef]
- Luo, H.; Han, Y.; Lu, C.; Yang, J.; Wu, Y. Characteristics of Surface Solar Radiation under Different Air Pollution Conditions over Nanjing, China: Observation and Simulation. Adv. Atmos. Sci. 2019, 36, 1047–1059. [Google Scholar] [CrossRef]
- Orgill, J.F.; Hollands, K.G.T. Correlation Equation for Hourly Diffuse Radiation on a Horizontal Surface. Sol. Energy 1977, 19, 357–359. [Google Scholar] [CrossRef]
- Erbs, D.G.; Klein, S.A.; Duffie, J.A. Estimation of the Diffuse Radiation Fraction for Hourly, Daily and Monthly-Average Global Radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Watanabe, T.; Urano, Y.; Hayashi, T. Procedures for Separating Direct and Diffuse Insolation on a Horizontal Surface and Prediction of Insolation on Tilted Surfaces. Trans. Archit. Inst. Japan 1983, 330, 96–108. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffle, J.A. Diffuse Fraction Correlations. Sol. Energy 1991, 47, 311–312. [Google Scholar] [CrossRef]
- Louche, A.; Notton, G.; Poggi, P.; Simonnot, G. Correlations for Direct Normal and Global Horizontal Irradiation on a French Mediterranean Site. Sol. Energy 1991, 46, 261–266. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Zelenka, A. Making Full Use of The Clearness Index for Parameterizing Hourly Insolation Conditions. Sol. Energy 1990, 45, 111–114. [Google Scholar] [CrossRef]
- Perez, R.R.; Ineichen, P.; Maxwell, E.L.; Seals, R.D.; Zelenka, A. Dynamic Global-to-Direct Irradiance Conversion Models. ASHRAE Trans. 1992, 98, 354–369. [Google Scholar]
- Maxwell, E.L. A Quasi-Physical Model for Converting Hourly Global Horizontal to Direct Normal Insolation. Sol. Energy Res. Inst. 1987, 1–55. Available online: https://www.nrel.gov/docs/legosti/old/3087.pdf (accessed on 6 April 2025).
- Steinmuller, B. The Two-Solarimeter Method for Insolation on Inclined Surface. Sol. Energy 1980, 25, 449–460. [Google Scholar] [CrossRef]
- Lamm, L.O.; Adler, C.G. A New Method for the Determination of Direct Insolation. Sol. Energy 1987, 39, 109–112. [Google Scholar] [CrossRef]
- Faiman, D.; Zemel, A. A Method for Monitoring Insolation in Remote Regions. Sol. Energy 1987, 38, 327–333. [Google Scholar] [CrossRef]
- Faiman, D.; Feuermann, D.; Ibbetson, P.; Zemel, A. A Multipyranometer Instrument for Obtaining the Solar Beam and Diffuse Components, and the Irradiance on Inclined Planes. Sol. Energy 1992, 48, 253–259. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling Daylight Availability and Irradiance Components from Direct and Global Irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- Faiman, D.; Feuermann, D.; Zemel, A. Site-Independent Algorithm for Obtaining the Direct Beam Insolation from a Multipyranometer Instrument. Sol. Energy 1993, 50, 53–57. [Google Scholar] [CrossRef]
- Brito, M.C.; e Silva, R.A.; Elsayed, A.M.; Pó, M. Estimating Global Irradiance on Tilted Surfaces Using a Cubic Multi-Directional Pyranometer Array. J. Renew. Sustain. Energy 2022, 14, 013704. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Ruiz-Arias, J.A. Extensive Worldwide Validation and Climate Sensitivity Analysis of Direct Irradiance Predictions from 1-Min Global Irradiance. Sol. Energy 2016, 128, 1–30. [Google Scholar] [CrossRef]
- Yang, D. Estimating 1-Min Beam and Diffuse Irradiance from the Global Irradiance: A Review and an Extensive Worldwide Comparison of Latest Separation Models at 126 Stations. Renew. Sustain. Energy Rev. 2022, 159, 112195. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook-Fundamentals (SI); American Society of Heating, Refrigerating and Air-Conditioning Engineers: Peachtree Corners, GA, USA, 2017. [Google Scholar]
- Bertrand, C.; Vanderveken, G.; Journée, M. Evaluation of Decomposition Models of Various Complexity to Estimate the Direct Solar Irradiance over Belgium. Renew. Energy 2015, 74, 618–626. [Google Scholar] [CrossRef]
- Wang, Z. How Frequent Should We Measure the Indoor Thermal Environment. Build. Environ. 2022, 222, 109464. [Google Scholar] [CrossRef]
- Baltazar, J.C.; Sun, Y.; Haberl, J. Improved Methodology to Evaluate Clear-Sky Direct Normal Irradiance with a Multi-Pyranometer Array. Sol. Energy 2015, 121, 123–130. [Google Scholar] [CrossRef]
- NREL Measurement and Instrumentation Data Center (MIDC). Available online: https://midcdmz.nrel.gov/apps/sitehome.pl?site=BMS (accessed on 15 January 2025).
- Alizamir, M.; Shiri, J.; Fard, A.F.; Kim, S.; Gorgij, A.R.D.; Heddam, S.; Singh, V.P. Improving the Accuracy of Daily Solar Radiation Prediction by Climatic Data Using an Efficient Hybrid Deep Learning Model: Long Short-Term Memory (LSTM) Network Coupled with Wavelet Transform. Eng. Appl. Artif. Intell. 2023, 123, 106199. [Google Scholar] [CrossRef]
- Wang, F.; Yu, Y.; Zhang, Z.; Li, J.; Zhen, Z.; Li, K. Wavelet Decomposition and Convolutional LSTM Networks Based Improved Deep Learning Model for Solar Irradiance Forecasting. Appl. Sci. 2018, 8, 1286. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Zhang, J.; Shi, J.; Gao, B.; Liu, W. Hybrid Deep Neural Model for Hourly Solar Irradiance Forecasting. Renew. Energy 2021, 171, 1041–1060. [Google Scholar] [CrossRef]
- Alkahtani, H.; Aldhyani, T.H.H.; Alsubari, S.N. Application of Artificial Intelligence Model Solar Radiation Prediction for Renewable Energy Systems. Sustainability 2023, 15, 6973. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Lee, H. Enhancing the Performance of Solar Radiation Decomposition Models Using Deep Learning. J. Korean Sol. Energy Soc. 2023, 43, 73–86. [Google Scholar] [CrossRef]
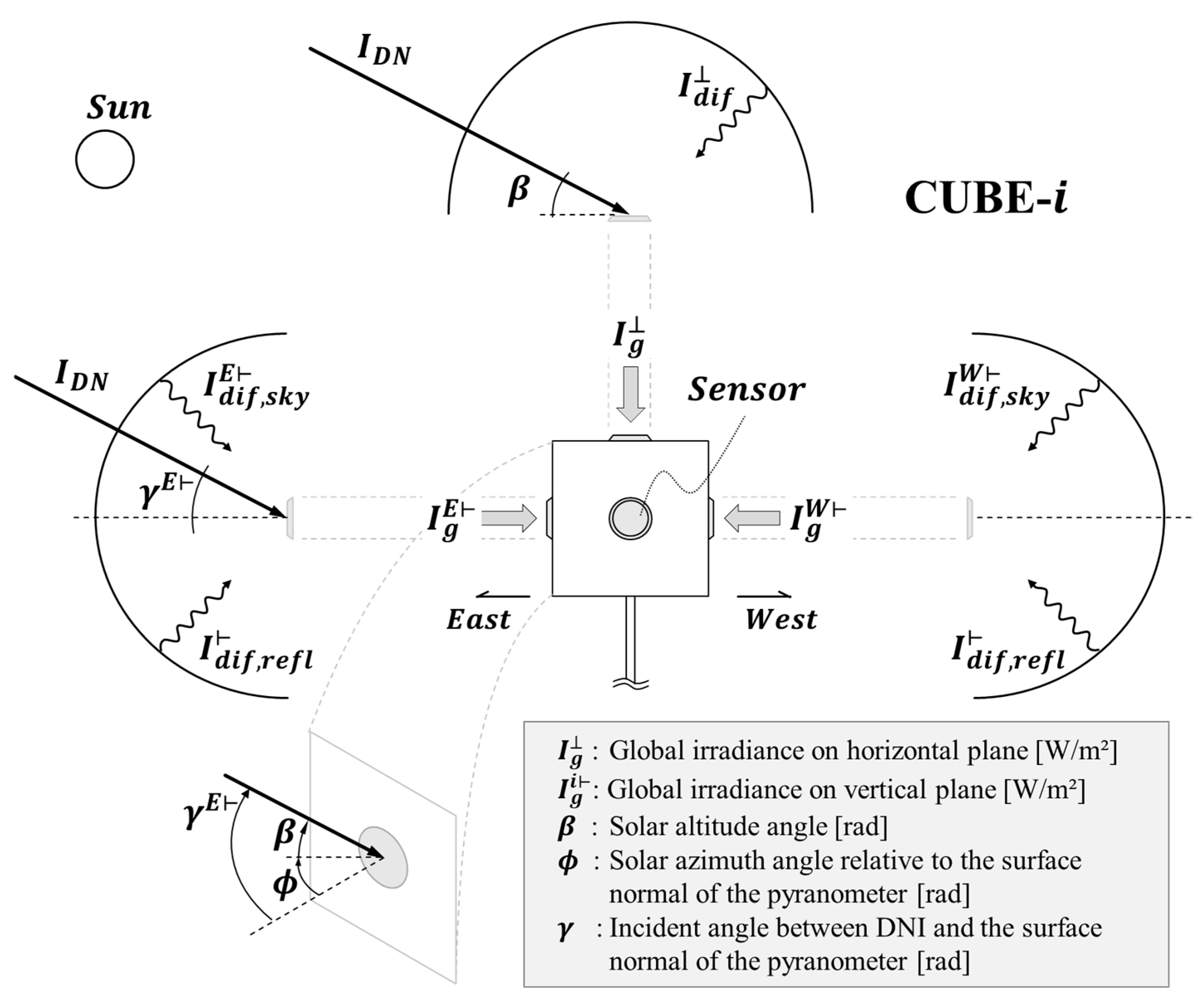
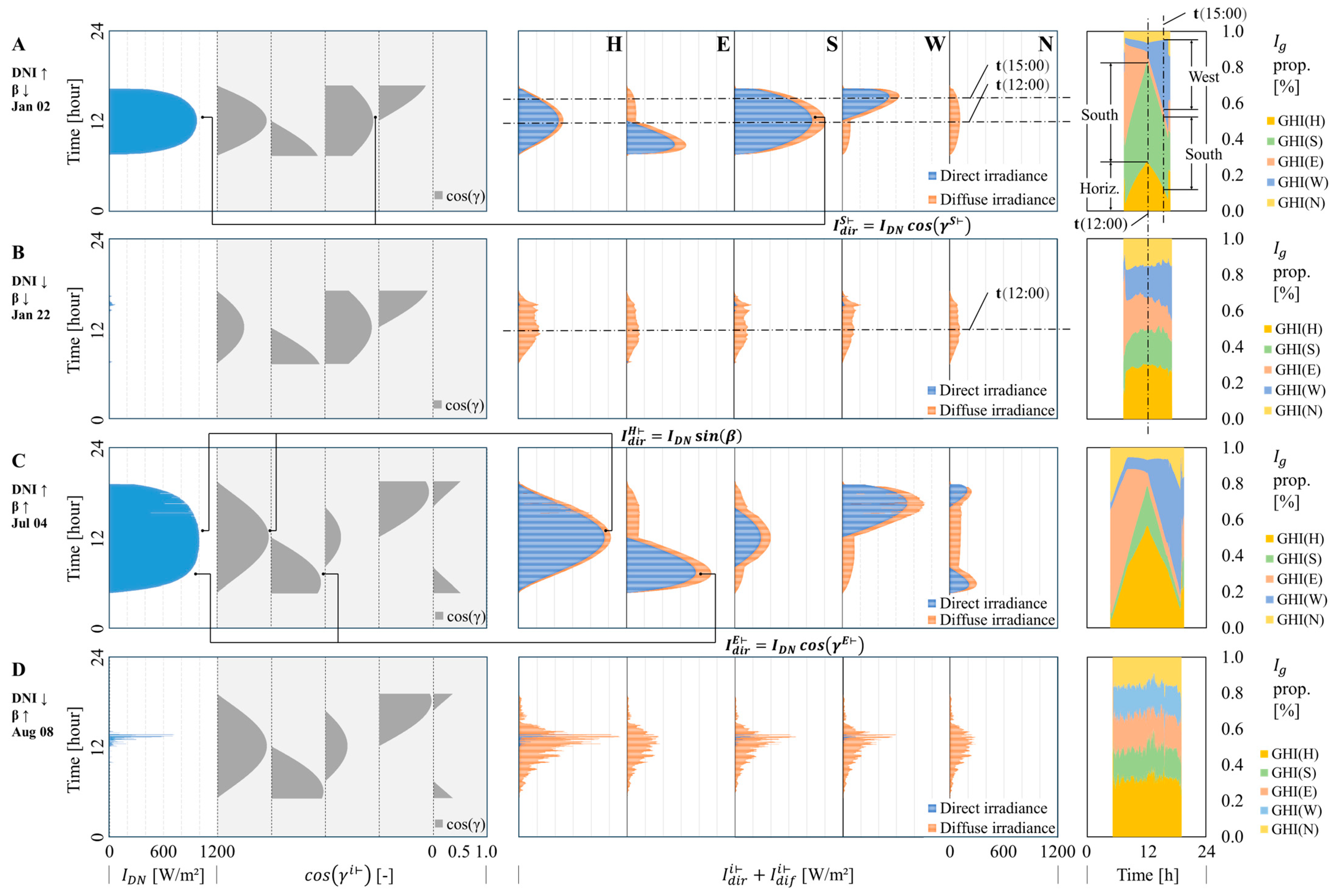
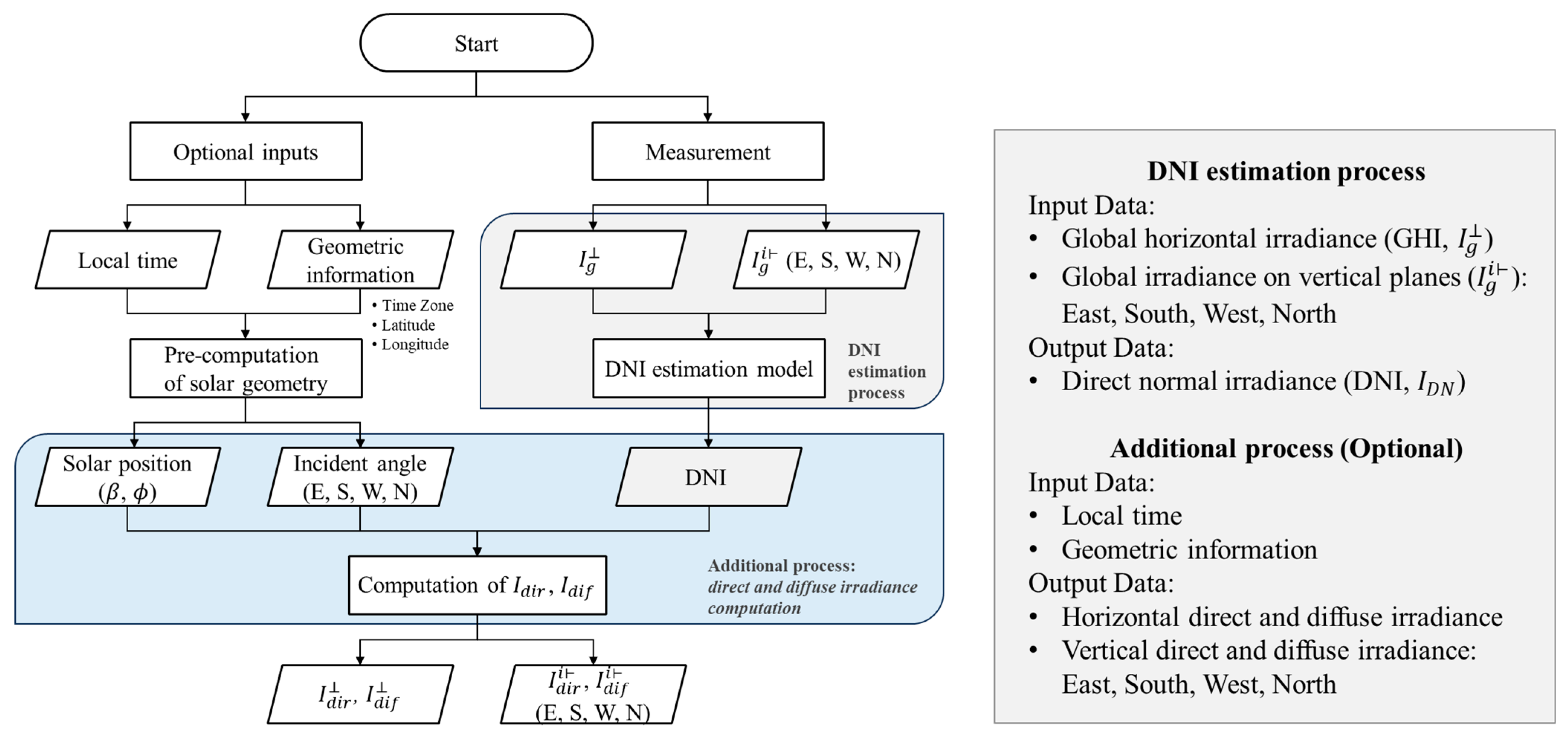
| Category | Specification | |
|---|---|---|
| Site information | Location | Colorado (USA) |
| Latitude | 39.742 | |
| Longitude | −105.18 | |
| Time zone | −7 | |
| Measurement | Measurement period | 1 year (2024) |
| CMP 22 | ||
| LI-200 | ||
| CHP 1-1 | ||
| Model | Input Variables |
|---|---|
| Model 1 | |
| Model 2 | |
| Model 3 | |
| Model 4 | —E, W |
| Model 5 | —S, N |
| Model 6 | —E, W, S, N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.-S. A Multi-Directional Pyranometer (CUBE-i) for Real-Time Direct and Diffuse Solar Irradiance Decomposition. Remote Sens. 2025, 17, 1336. https://doi.org/10.3390/rs17081336
Lee D-S. A Multi-Directional Pyranometer (CUBE-i) for Real-Time Direct and Diffuse Solar Irradiance Decomposition. Remote Sensing. 2025; 17(8):1336. https://doi.org/10.3390/rs17081336
Chicago/Turabian StyleLee, Dong-Seok. 2025. "A Multi-Directional Pyranometer (CUBE-i) for Real-Time Direct and Diffuse Solar Irradiance Decomposition" Remote Sensing 17, no. 8: 1336. https://doi.org/10.3390/rs17081336
APA StyleLee, D.-S. (2025). A Multi-Directional Pyranometer (CUBE-i) for Real-Time Direct and Diffuse Solar Irradiance Decomposition. Remote Sensing, 17(8), 1336. https://doi.org/10.3390/rs17081336






