Downscaling and Gap-Filling GRACE-Based Terrestrial Water Storage Anomalies in the Qinghai–Tibet Plateau Using Deep Learning and Multi-Source Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Methods
2.3. Model Test
3. Results
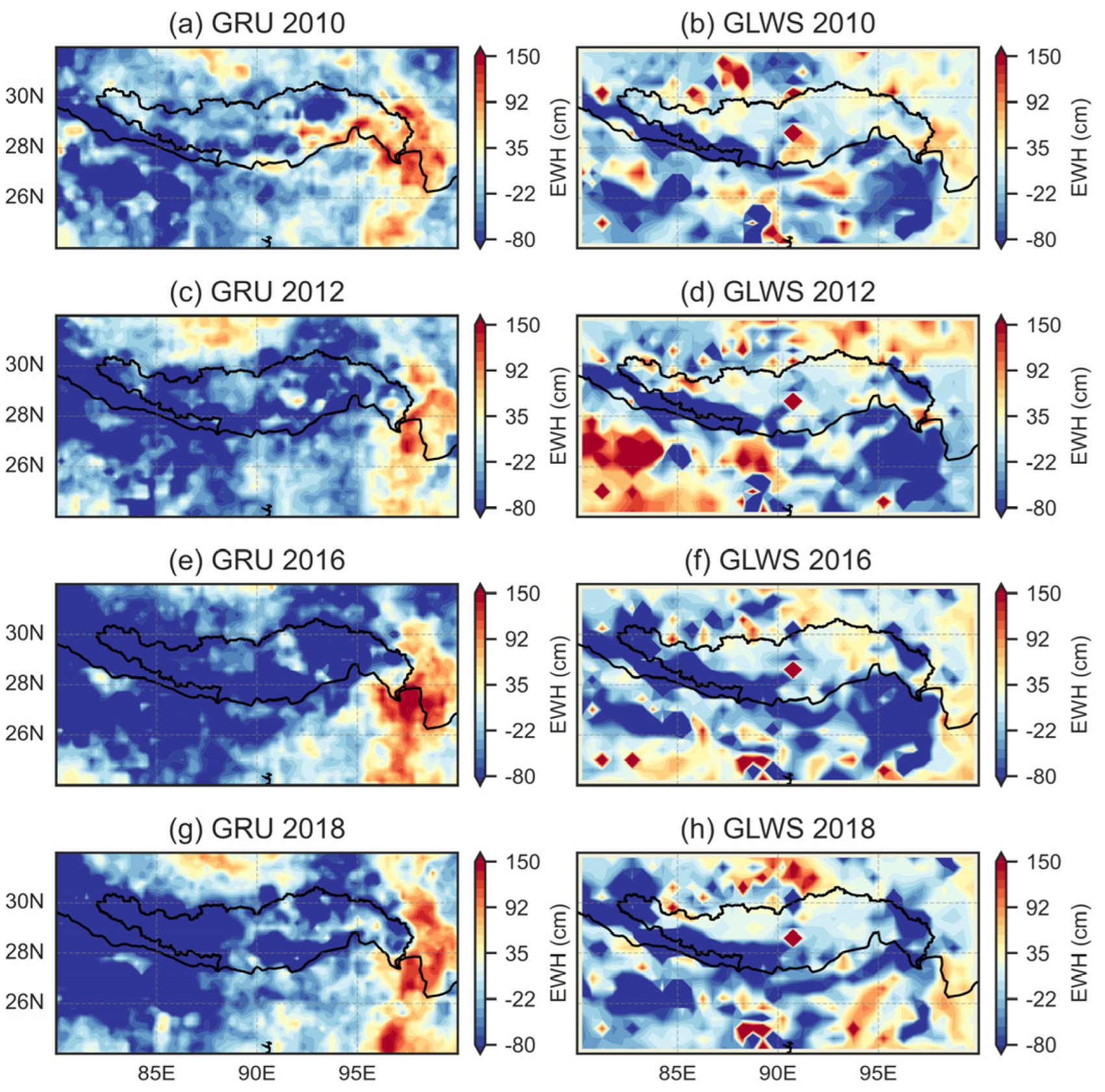
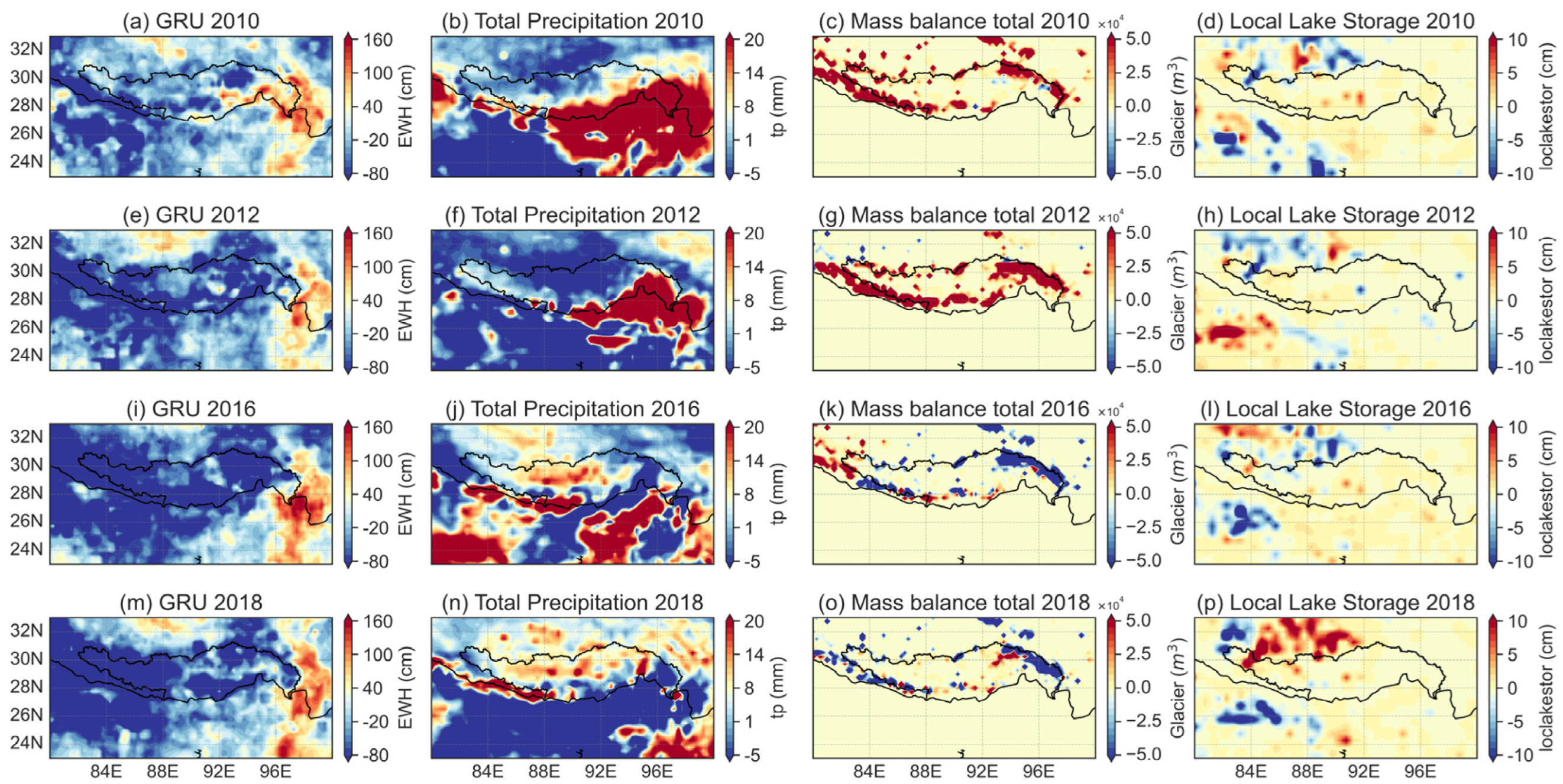
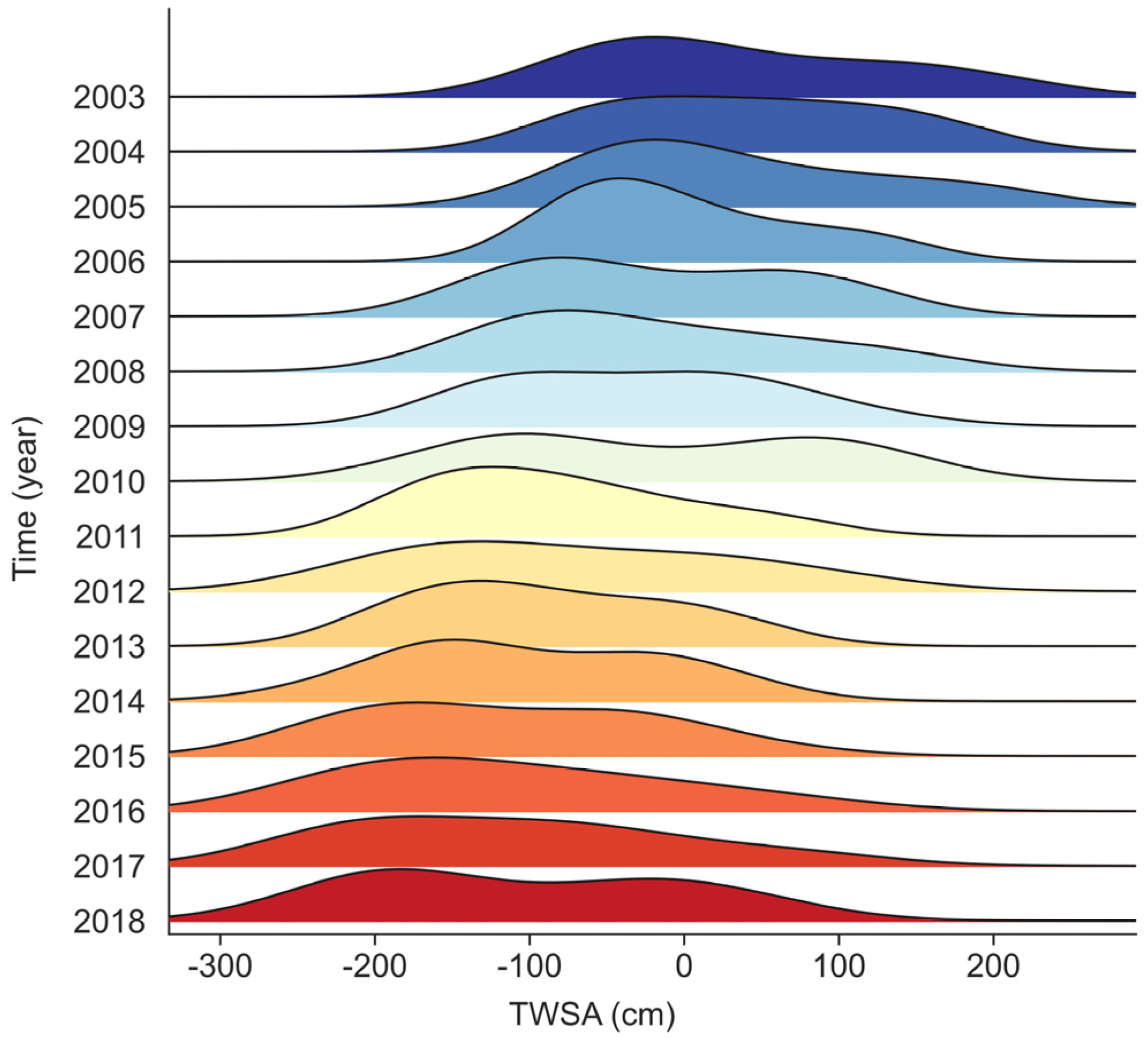
3.1. Spatiotemporal Characteristics of Downscaling TWSA on the QTP
3.2. TWSA Time Series of 12 Sub-Basins in the QTP
3.3. Gap Filling in GRACE/GRACE-FO Mission Data
4. Discussion
4.1. The Differences Between GRU-Derived TWSA and Mascon Models
4.2. Representative Area-Brahmaputra Basin
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GRACE | Gravity Recovery and Climate Experiment |
| GRACE-FO | Gravity Recovery and Climate Experiment and its Follow-On |
| QTP | Qinghai–Tibet Plateau |
| CSR | Center for Space Research |
| JPL | Jet Propulsion Laboratory |
| GSFC | Goddard Spaceflight Center |
| GLWS2.0 | Global Land Water Storage Dataset release 2 |
| TWSA | Terrestrial Water Storage Anomalies |
| GLDAS | Global Land Data Assimilation System |
| WGHM | WaterGAP Global Hydrology Model |
| PyGEM | Python Glacier Evolution Model |
| ERA5 | European Centre for Medium-Range Weather Forecasts Reanalysis v5 |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| GLEAM | Global Land Evaporation Amsterdam Model |
| CNRD | China Natural Runoff Dataset |
| GRU | Gated Recurrent Unit |
| MSE | Mean Squared Error |
| RMSE | Root Mean Square Error |
| EWH | Equivalent Water Height |
| CC | Correlation coefficient |
| NDVI | Normalized Difference Vegetation Index |
References
- Chen, T.; Pan, Y.; Ding, H.; Jiao, J.; He, M. Investigating Terrestrial Water Storage Variation and Its Response to Climate in Southeastern Tibetan Plateau Inferred through Space Geodetic Observations. J. Hydrol. 2024, 640, 131742. [Google Scholar] [CrossRef]
- Wang, G.; He, Y.; Huang, J.; Guan, X.; Wang, X.; Hu, H.; Wang, S.; Xie, Y. The Influence of Precipitation Phase Changes on the Recharge Process of Terrestrial Water Storage in the Cold Season over the Tibetan Plateau. J. Geophys. Res. Atmos. 2022, 127, e2021JD035824. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Hu, Q.; Liu, J. Responses of Terrestrial Water Storage to Climate Variation in the Tibetan Plateau. J. Hydrol. 2020, 584, 124652. [Google Scholar] [CrossRef]
- Beveridge, A.K.; Harig, C.; Simons, F.J. The Changing Mass of Glaciers on the Tibetan Plateau, 2002–2016, Using Time-Variable Gravity from the GRACE Satellite Mission. J. Geod. Sci. 2018, 8, 83–97. [Google Scholar] [CrossRef]
- Cheng, T.F.; Chen, D.; Wang, B.; Ou, T.; Lu, M. Human-Induced Warming Accelerates Local Evapotranspiration and Precipitation Recycling over the Tibetan Plateau. Commun. Earth Environ. 2024, 5, 388. [Google Scholar] [CrossRef]
- Lei, Y.; Li, R.; Letu, H.; Shi, J. Seasonal Variations of Recharge–Storage–Runoff Process over the Tibetan Plateau. J. Hydrometeorol. 2023, 24, 1619–1633. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different Glacier Status with Atmospheric Circulations in Tibetan Plateau and Surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, H.D. Asia’s Shrinking Glaciers Protect Large Populations from Drought Stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Bridget, R.S.; Michael, E.M.; Li, X.; Tian, F.; Sun, Z.; Wang, G. Water Loss over the Tibetan Plateau Endangers Water Supply Security for Asian Populations. Nat. Clim. Chang. 2022, 12, 785–786. [Google Scholar]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to Understanding Climate Change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Xu, Y.-P.; Yu, H.; Huang, Y.; Guo, Y. Monitoring the Extreme Flood Events in the Yangtze River Basin Based on GRACE and GRACE-FO Satellite Data. Hydrol. Earth Syst. Sci. 2022, 26, 5933–5954. [Google Scholar] [CrossRef]
- Zhang, G.; Bolch, T.; Chen, W.; Crétaux, J.-F. Comprehensive Estimation of Lake Volume Changes on the Tibetan Plateau during 1976–2019 and Basin-Wide Glacier Contribution. Sci. Total Environ. 2021, 772, 145463. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Su, F.; Li, Y.; Tong, K. Changes in Terrestrial Water Storage During 2003–2014 and Possible Causes in Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 2909–2931. [Google Scholar] [CrossRef]
- Deng, H.; Pepin, N.C.; Liu, Q.; Chen, Y. Understanding the Spatial Differences in Terrestrial Water Storage Variations in the Tibetan Plateau from 2002 to 2016. Clim. Chang. 2018, 151, 379–393. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation of Satellite Precipitation Retrievals and Their Potential Utilities in Hydrologic Modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Y.; Zhang, G.; Yang, K.; Zhou, T.; Wang, J.; Shum, C.K. What Controls Lake Contraction and Then Expansion in Tibetan Plateau’s Endorheic Basin Over the Past Half Century? Geophys. Res. Lett. 2022, 49, e2022GL101200. [Google Scholar] [CrossRef]
- Iqbal, N.; Hossain, F.; Lee, H.; Akhter, G. Satellite Gravimetric Estimation of Groundwater Storage Variations Over Indus Basin in Pakistan. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3524–3534. [Google Scholar] [CrossRef]
- Mo, S.; Zhong, Y.; Forootan, E.; Mehrnegar, N.; Yin, X.; Wu, J.; Feng, W.; Shi, X. Bayesian Convolutional Neural Networks for Predicting the Terrestrial Water Storage Anomalies during GRACE and GRACE-FO Gap. J. Hydrol. 2022, 604, 127244. [Google Scholar] [CrossRef]
- Foroumandi, E.; Nourani, V.; Jeanne Huang, J.; Moradkhani, H. Drought Monitoring by Downscaling GRACE-Derived Terrestrial Water Storage Anomalies: A Deep Learning Approach. J. Hydrol. 2023, 616, 128838. [Google Scholar] [CrossRef]
- Lyu, Y.; Yong, B. A Novel Double Machine Learning Strategy for Producing High-Precision Multi-Source Merging Precipitation Estimates Over the Tibetan Plateau. Water Resour. Res. 2024, 60, e2023WR035643. [Google Scholar] [CrossRef]
- Yazdian, H.; Salmani-Dehaghi, N.; Alijanian, M. A Spatially Promoted SVM Model for GRACE Downscaling: Using Ground and Satellite-Based Datasets. J. Hydrol. 2023, 626, 130214. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Cui, Y.; Cui, Y.; Xu, Y.; Hora, T.; Zaveri, E.; Rodella, A.-S.; Bai, L.; Long, D. Spatial Downscaling of GRACE-Derived Groundwater Storage Changes across Diverse Climates and Human Interventions with Random Forests. J. Hydrol. 2024, 640, 131708. [Google Scholar] [CrossRef]
- Qian, N.; Gao, J.; Li, Z.; Yan, Z.; Feng, Y.; Yan, Z.; Yang, L. Bridging the Terrestrial Water Storage Anomalies between the GRACE/GRACE-FO Gap Using BEAST+GMDH Algorithm. Remote Sens. 2024, 16, 3693. [Google Scholar] [CrossRef]
- Yin, W.; Zhang, G.; Han, S.-C.; Yeo, I.-Y.; Zhang, M. Improving the Resolution of GRACE-Based Water Storage Estimates Based on Machine Learning Downscaling Schemes. J. Hydrol. 2022, 613, 128447. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Irrgang, C.; Saynisch-Wagner, J.; Dill, R.; Boergens, E.; Thomas, M. Self-Validating Deep Learning for Recovering Terrestrial Water Storage from Gravity and Altimetry Measurements. Geophys. Res. Lett. 2020, 47, e2020GL089258. [Google Scholar] [CrossRef]
- Tao, H.; Al-Sulttani, A.H.; Salih, S.Q.; Mohammed, M.K.A.; Khan, M.A.; Beyaztas, B.H.; Ali, M.; Elsayed, S.; Shahid, S.; Yaseen, Z.M. Development of High-Resolution Gridded Data for Water Availability Identification through GRACE Data Downscaling: Development of Machine Learning Models. Atmos. Res. 2023, 291, 106815. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Yuan, D.-N. GRACE-FO. GRACEFO_L2_CSR_MONTHLY_0062. Ver. 6.2. PO.DAAC, CA, USA. (RL06.2). 2023. Available online: https://podaac.jpl.nasa.gov/dataset/GRACEFO_L2_CSR_MONTHLY_0062 (accessed on 4 March 2024).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2023. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=documentation (accessed on 4 March 2024).
- Rounce, D.; Hock, R.; Maussion, F. Global PyGEM-OGGM Glacier Projections with RCP and SSP Scenarios. (HMA2_GGP, Version 1); NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, Colorado, USA, 2022; Available online: https://nsidc.org/data/hma2_ggp/versions/1 (accessed on 4 March 2024).
- Pan, F.; Jiang, L.; Wang, G.; Pan, J.; Huang, J.; Zhang, C.; Cui, H.; Yang, J.; Zheng, Z.; Wu, S.; et al. MODIS Daily Cloud-Gap-Filled Fractional Snow Cover Dataset of the Asian Water Tower Region (2000–2022). Earth Syst. Sci. Data 2024, 16, 2501–2523. [Google Scholar] [CrossRef]
- Vermote, E.F.; Wolfe, R.E. MOD09GQ MODIS/Terra Surface Reflectance Daily L2G Global 250m SIN Grid V061; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2021. Available online: https://lpdaac.usgs.gov/products/mod09gqv061/ (accessed on 4 March 2024).
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-Based Land Evaporation and Root-Zone Soil Moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Gou, J.; Miao, C.; Duan, Q.; Tang, Q.; Di, Z.; Liao, W.; Wu, J.; Zhou, R. Sensitivity Analysis-based Automatic Parameter Calibration of the VIC Model for Streamflow Simulations over China. Water Resour. Res. 2020, 56, e2019WR025968. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Cáceres, D.; Eisner, S.; Flörke, M.; Herbert, C.; Niemann, C.; Peiris, T.A.; Popat, E.; Portmann, F.T.; Reinecke, R.; et al. The Global Water Resources and Use Model WaterGAP v2.2d: Model Description and Evaluation. Geosci. Model Dev. 2021, 14, 1037–1079. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved Methods for Observing Earth’s Time Variable Mass Distribution with GRACE Using Spherical Cap Mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Loomis, B.D.; Luthcke, S.B.; Sabaka, T.J. Regularization and Error Characterization of GRACE Mascons. J. Geod. 2019, 93, 1381–1398. [Google Scholar] [CrossRef]
- Gerdener, H.; Kusche, J.; Schulze, K.; Döll, P.; Klos, A. The Global Land Water Storage Data Set Release 2 (GLWS2.0) Derived via Assimilating GRACE and GRACE-FO Data into a Global Hydrological Model. J. Geod. 2023, 97, 73. [Google Scholar] [CrossRef]
- Tong, J.; Shi, Z.; Jiao, J.; Yang, B.; Tian, Z. Glacier Mass Balance and Its Impact on Land Water Storage in the Southeastern Tibetan Plateau Revealed by ICESat-2 and GRACE-FO. Remote Sens. 2024, 16, 1048. [Google Scholar] [CrossRef]
- Niranjannaik, M.; Kumar, A.; Beg, Z.; Singh, A.; Swarnkar, S.; Gaurav, K. Groundwater Variability in a Semi-Arid River Basin, Central India. Hydrology 2022, 9, 222. [Google Scholar] [CrossRef]
- Li, N.; Cuo, L.; Zhang, Y.; Flerchinger, G.N. Diurnal Soil Freeze-Thaw Cycles and the Factors Determining Their Changes in Warming Climate in the Upper Brahmaputra Basin of the Tibetan Plateau. J. Geophys. Res. Atmos. 2024, 129, e2023JD040369. [Google Scholar] [CrossRef]
- Wang, C.; Shi, H.; Hu, H.; Wang, Y.; Xi, B. Properties of Cloud and Precipitation over the Tibetan Plateau. Adv. Atmos. Sci. 2015, 32, 1504–1516. [Google Scholar] [CrossRef]
- Gao, G.; Zhao, J.; Wang, J.; Zhao, G.; Chen, J.; Li, Z. Spatiotemporal Variation and Driving Analysis of Groundwater in the Tibetan Plateau Based on GRACE Downscaling Data. Water 2022, 14, 3302. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, H.; Steffen, H.; Jiang, L.; Shen, Q.; Jia, L.; Su, Z.; Wang, W.; Deng, F.; Qiao, B.; et al. Two Decades of Terrestrial Water Storage Changes in the Tibetan Plateau and Its Surroundings Revealed through GRACE/GRACE-FO. Remote Sens. 2023, 15, 3505. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, Y.; Guan, Q.; Du, Q.; Zhang, Z.; Zhang, J.; Zhang, E. Exploring Future Trends of Precipitation and Runoff in Arid Regions under Different Scenarios Based on a Bias-Corrected CMIP6 Model. J. Hydrol. 2024, 630, 130666. [Google Scholar] [CrossRef]
- Xie, X.; He, B.; Guo, L.; Miao, C.; Zhang, Y. Detecting Hotspots of Interactions between Vegetation Greenness and Terrestrial Water Storage Using Satellite Observations. Remote Sens. Environ. 2019, 231, 111259. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Lutz, A.F.; Andrade, M.; Bahl, A.; Biemans, H.; Bolch, T.; Hyde, S.; Brumby, S.; Davies, B.J.; Elmore, A.C.; et al. Importance and Vulnerability of the World’s Water Towers. Nature 2020, 577, 364–369. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Felfelani, F.; Satoh, Y.; Boulange, J.; Burek, P.; Gädeke, A.; Gerten, D.; Gosling, S.N.; Grillakis, M.; Gudmundsson, L.; et al. Global Terrestrial Water Storage and Drought Severity under Climate Change. Nat. Clim. Chang. 2021, 11, 226–233. [Google Scholar] [CrossRef]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global Analysis of Spatiotemporal Variability in Merged Total Water Storage Changes Using Multiple GRACE Products and Global Hydrological Models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Yi, S.; Sneeuw, N. Filling the Data Gaps Within GRACE Missions Using Singular Spectrum Analysis. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021227. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Dong, Q.; Wang, Z.; Zhang, H.; Liu, X. Bridging the Gap between GRACE and GRACE-FO Using a Hydrological Model. Sci. Total Environ. 2022, 822, 153659. [Google Scholar] [CrossRef]
- Haddeland, I.; Clark, D.B.; Franssen, W.; Ludwig, F.; Voß, F.; Arnell, N.W.; Bertrand, N.; Best, M.; Folwell, S.; Gerten, D.; et al. Multimodel Estimate of the Global Terrestrial Water Balance: Setup and First Results. J. Hydrometeorol. 2011, 12, 869–884. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, S.; Sun, W. Continuous Estimates of Glacier Mass Balance in High Mountain Asia Based on ICESat-1,2 and GRACE/GRACE Follow-On Data. Geophys. Res. Lett. 2021, 48, e2020GL090954. [Google Scholar] [CrossRef]
- An, L.; Wang, J.; Huang, J.; Pokhrel, Y.; Hugonnet, R.; Wada, Y.; Cáceres, D.; Müller Schmied, H.; Song, C.; Berthier, E.; et al. Divergent Causes of Terrestrial Water Storage Decline Between Drylands and Humid Regions Globally. Geophys. Res. Lett. 2021, 48, e2021GL095035. [Google Scholar] [CrossRef]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A Spatially Resolved Estimate of High Mountain Asia Glacier Mass Balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting Patterns of Early Twenty-First-Century Glacier Mass Change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of Scaled GRACE Terrestrial Water Storage Estimates. Water Resour. Res. 2012, 48, 2011WR011453. [Google Scholar] [CrossRef]
- Mankin, J.S.; Diffenbaugh, N.S. Influence of Temperature and Precipitation Variability on Near-Term Snow Trends. Clim. Dyn. 2015, 45, 1099–1116. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The State and Fate of Himalayan Glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef]
- Girotto, M.; De Lannoy, G.J.M.; Reichle, R.H.; Rodell, M. Assimilation of Gridded Terrestrial Water Storage Observations from GRACE into a Land Surface Model: Grace Assimilation into a Land Surface Model. Water Resour. Res. 2016, 52, 4164–4183. [Google Scholar] [CrossRef]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Save, H. GRACE Satellite Monitoring of Large Depletion in Water Storage in Response to the 2011 Drought in Texas. Geophys. Res. Lett. 2013, 40, 3395–3401. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Toward a Complete Himalayan Hydrological Budget: Spatiotemporal Distribution of Snowmelt and Rainfall and Their Impact on River Discharge. J. Geophys. Res. Earth Surf. 2010, 115, F3. [Google Scholar] [CrossRef]
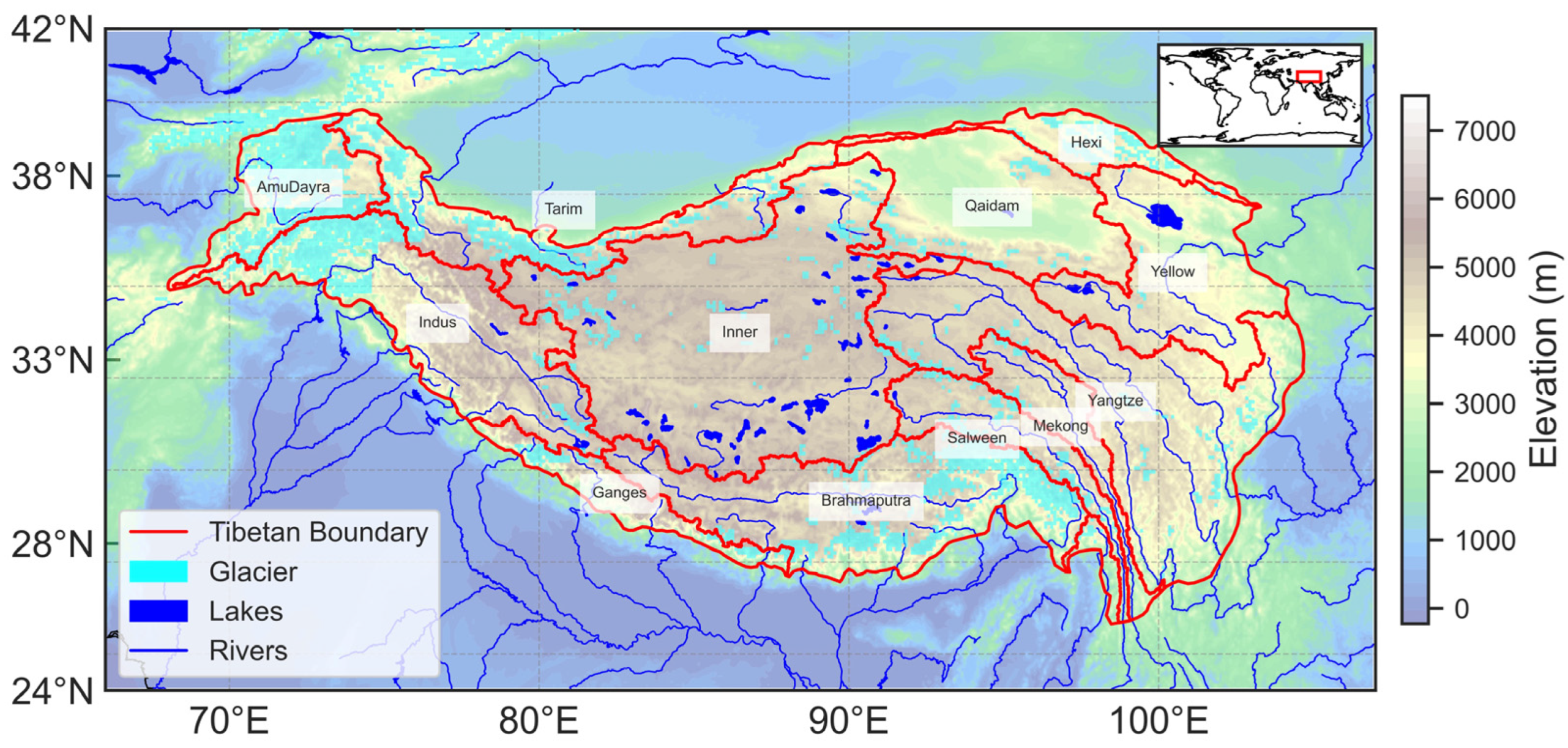



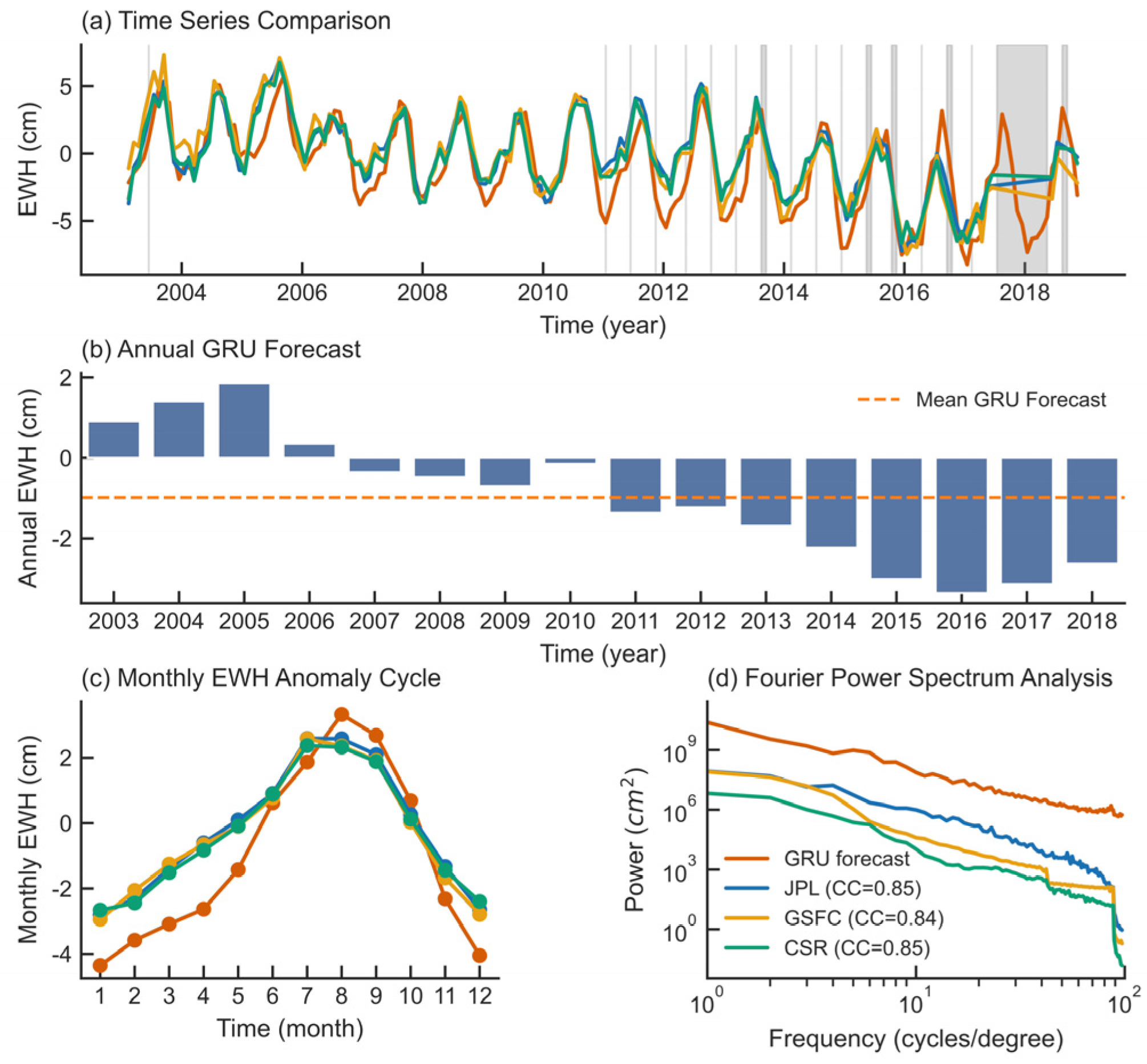
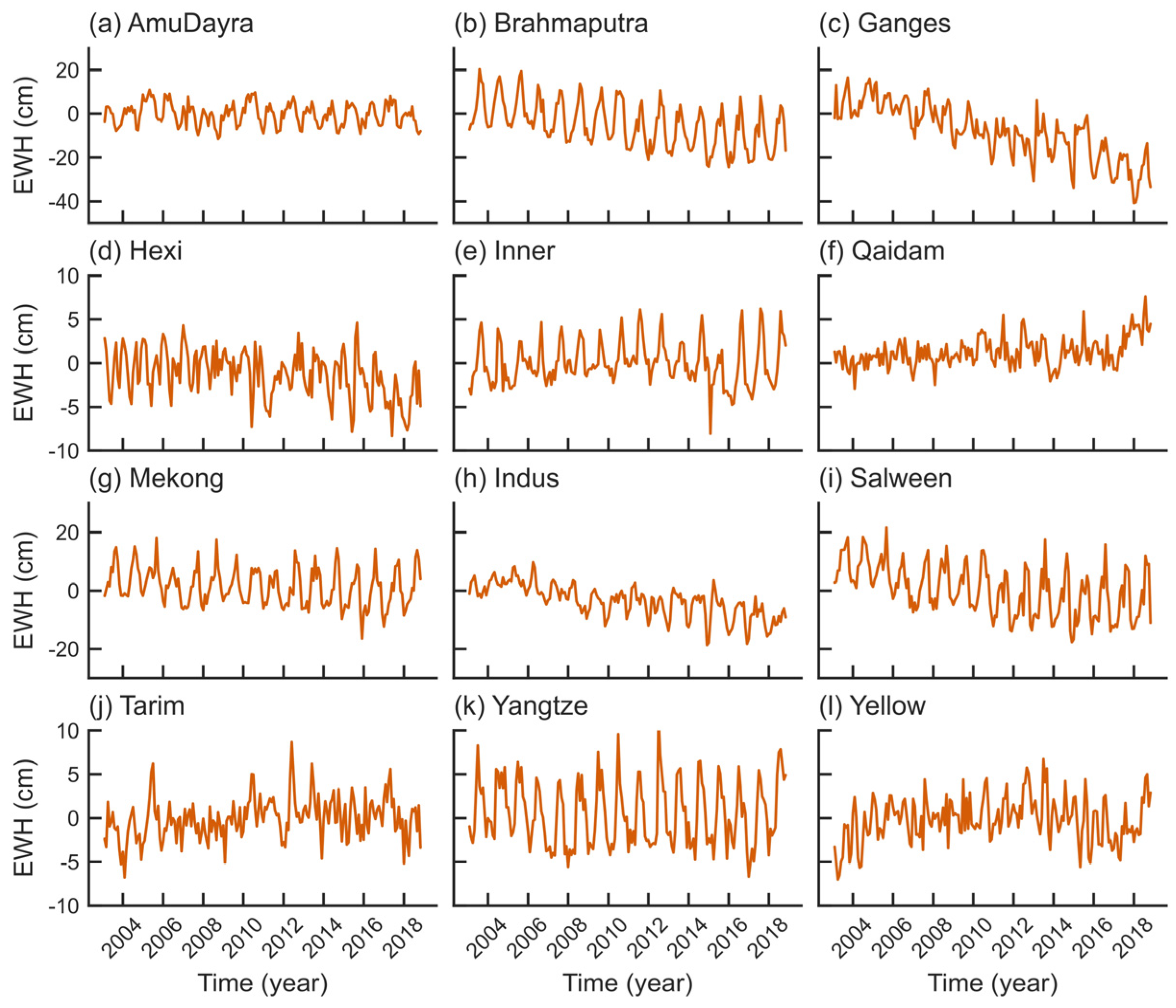


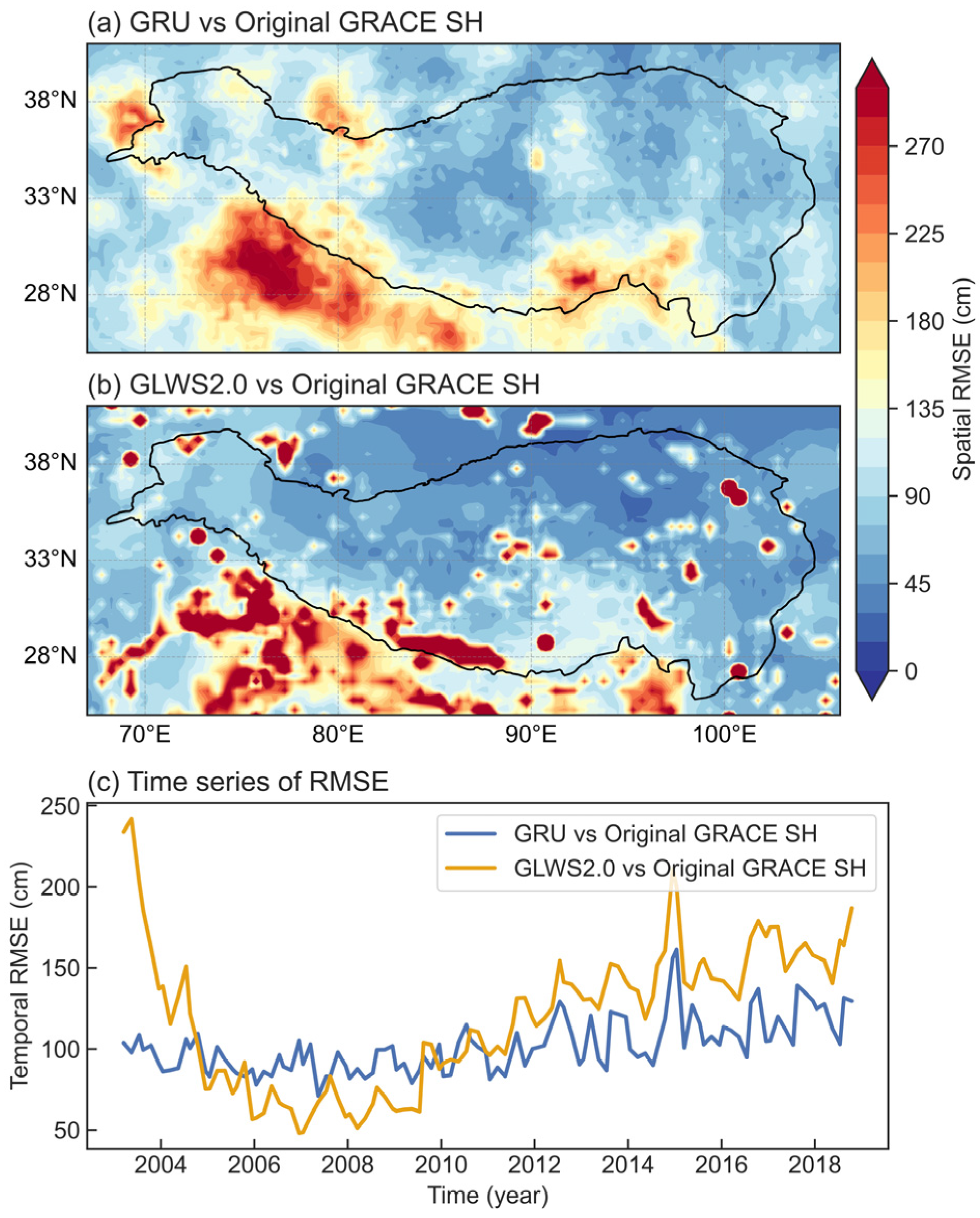

| Data Item | Solutions | Resolution | Time Range | Data Source (DOI) | |
|---|---|---|---|---|---|
| Spatial | Temporal | ||||
| Glacier mass balance | PyGEM | 0.1° | Monthly | January 2000–December 2100 | 10.5067/H118TCMSUH3Q |
| Snow cover | MODIS | 0.005° | Daily | February 2000–Present | 10.11888/Cryos.tpdc.272503 |
| Soil moisture | GLDAS | 0.25° | Monthly | January 1948–Present | 10.5067/SXAVCZFAQLNO |
| Groundwater storage | WGHM | 0.5° | Monthly | January 1902–December 2019 | 10.1594/PANGAEA.948461 |
| Lake water storage | WGHM | 0.5° | Monthly | January 1902–December 2019 | 10.1594/PANGAEA.948461 |
| Precipitation | ERA5 | 0.25° | Monthly | January 1940–Present | 10.24381/cds.f17050d7 |
| Evapotranspiration | GLEAM | 0.25° | Monthly | January 2003–December 2022 | 10.5194/gmd-10-1903-2017 |
| Temperature | MODIS | 0.25° | Monthly | March 2000–Present | 10.5067/MODIS/MOD11C3.006 |
| Streamflow | CNRD | 0.25° | Monthly | January 1961–December 2018 | 10.11888/Atmos.tpdc.272864 |
| TWSA | CSR-SH # CSR-M * JPL-M GSFC-M | 1~3° | Monthly | April 2002–Present | 10.5067/GRGSM-20C06 10.18738/T8/UN91VR 10.5067/TEMSC-3JC634 10.1007/s00190-019-01252-y |
| TWS | GLWS2.0 | 0.5 | Monthly | January 2003–December 2019 | 10.1594/PANGAEA.954742 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, L.; Chen, C.; Peng, Z. Downscaling and Gap-Filling GRACE-Based Terrestrial Water Storage Anomalies in the Qinghai–Tibet Plateau Using Deep Learning and Multi-Source Data. Remote Sens. 2025, 17, 1333. https://doi.org/10.3390/rs17081333
Chen J, Wang L, Chen C, Peng Z. Downscaling and Gap-Filling GRACE-Based Terrestrial Water Storage Anomalies in the Qinghai–Tibet Plateau Using Deep Learning and Multi-Source Data. Remote Sensing. 2025; 17(8):1333. https://doi.org/10.3390/rs17081333
Chicago/Turabian StyleChen, Jun, Linsong Wang, Chao Chen, and Zhenran Peng. 2025. "Downscaling and Gap-Filling GRACE-Based Terrestrial Water Storage Anomalies in the Qinghai–Tibet Plateau Using Deep Learning and Multi-Source Data" Remote Sensing 17, no. 8: 1333. https://doi.org/10.3390/rs17081333
APA StyleChen, J., Wang, L., Chen, C., & Peng, Z. (2025). Downscaling and Gap-Filling GRACE-Based Terrestrial Water Storage Anomalies in the Qinghai–Tibet Plateau Using Deep Learning and Multi-Source Data. Remote Sensing, 17(8), 1333. https://doi.org/10.3390/rs17081333









