Spectrum Sharing Design for Integrated Aeronautical Communication and Radar System
Abstract
1. Introduction
1.1. Related Works
1.1.1. Studies on RCC
1.1.2. Studies on ISAC
1.2. Motivation and Contributions
- We investigate an integrated transmission framework for an aeronautical communication and radar system in which MIMO is utilized at the ground base station (GBS) and the ACS to facilitate a flexible, multiple access scheme enabling inter-aircraft interference suppression, and NOMA is deployed to realize dual-spectrum sharing between the communication and the navigation avionic devices without interference. Given the proposed framework, we formulate a weighted achievable sum rate and the sensing SCNR maximization problem. Aiming for the joint optimization of the GBS-transmitted BF, the airborne receivers’ BFs, as well as the power allocation, the minimum operation requirements of both the communication and radar functions are guaranteed.
- A practical A2G MIMO channel model accounting for the AC dynamics is proposed. This model considers both the AC position and attitude to characterize the steering directions. A rotation matrix is constructed with the AC attitude represented by Euler angles (i.e., heading angle, pitch angle, and roll angle) to derive an equivalent position (EP) given the AC’s current position. Consequently, the realistic angle-of-arrivals (AoAs)/angle-of-departures (AoDs) can be obtained by leveraging the geometrical information.
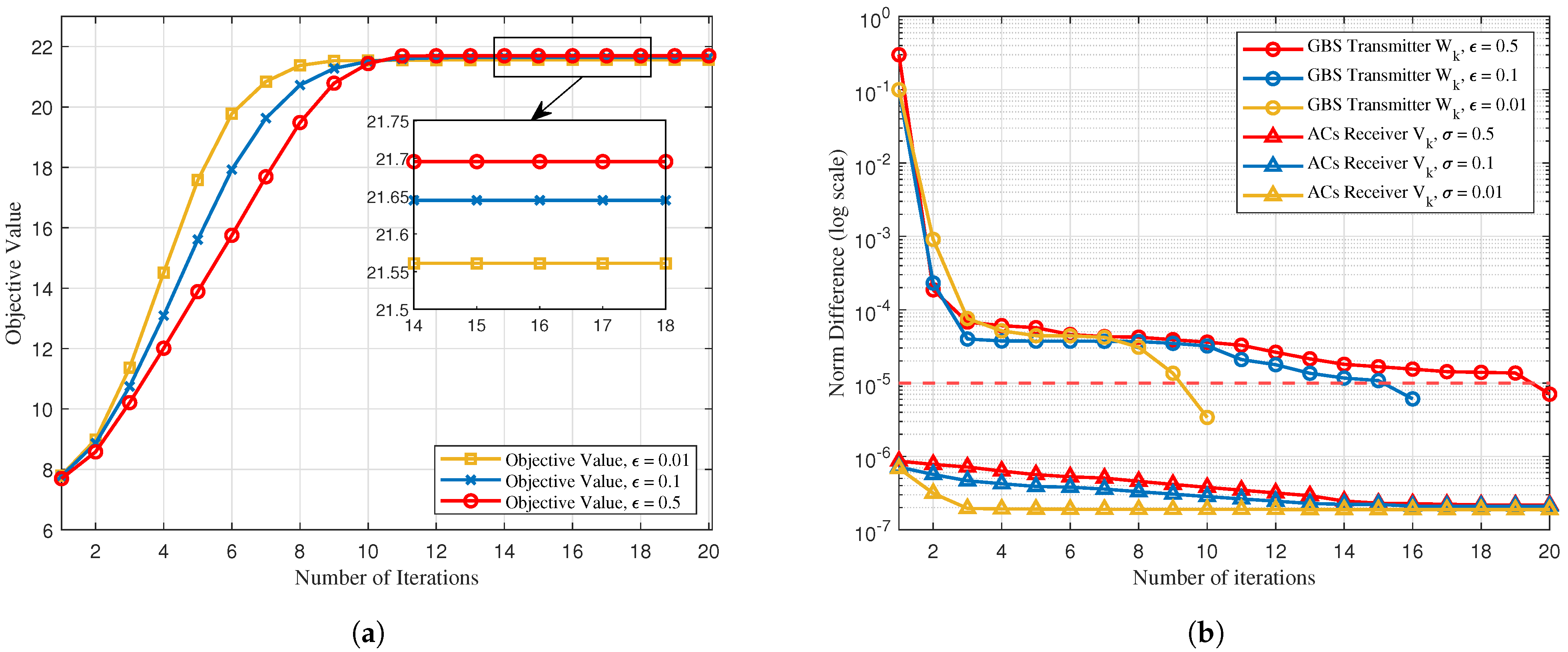
- We develop an alternating optimization (AO) algorithm solved alternatively, where the original problem is decomposed into two subproblems. By combining the GBS transmit BF and the power allocation subproblems, we construct the auxiliary variables, which incorporate the optimization variables to simplify the optimization process. Afterwards, the penalty-based method is invoked to handle the non-convex constraint for the covariance matrix of BF. For the airborne receivers’ BF design, we effectively solve them by utilizing the sequential rank-one constraint relaxation (SROCR) while fixing the other optimization variables.
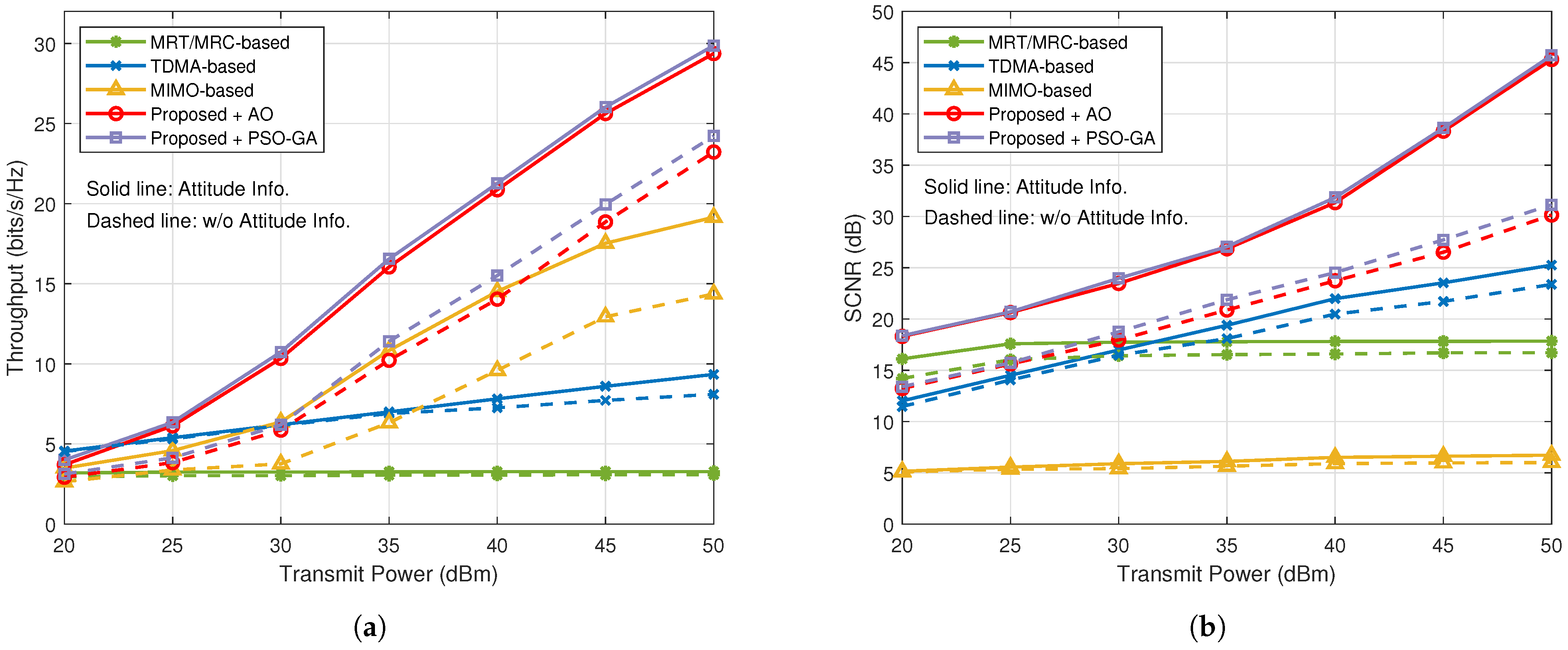
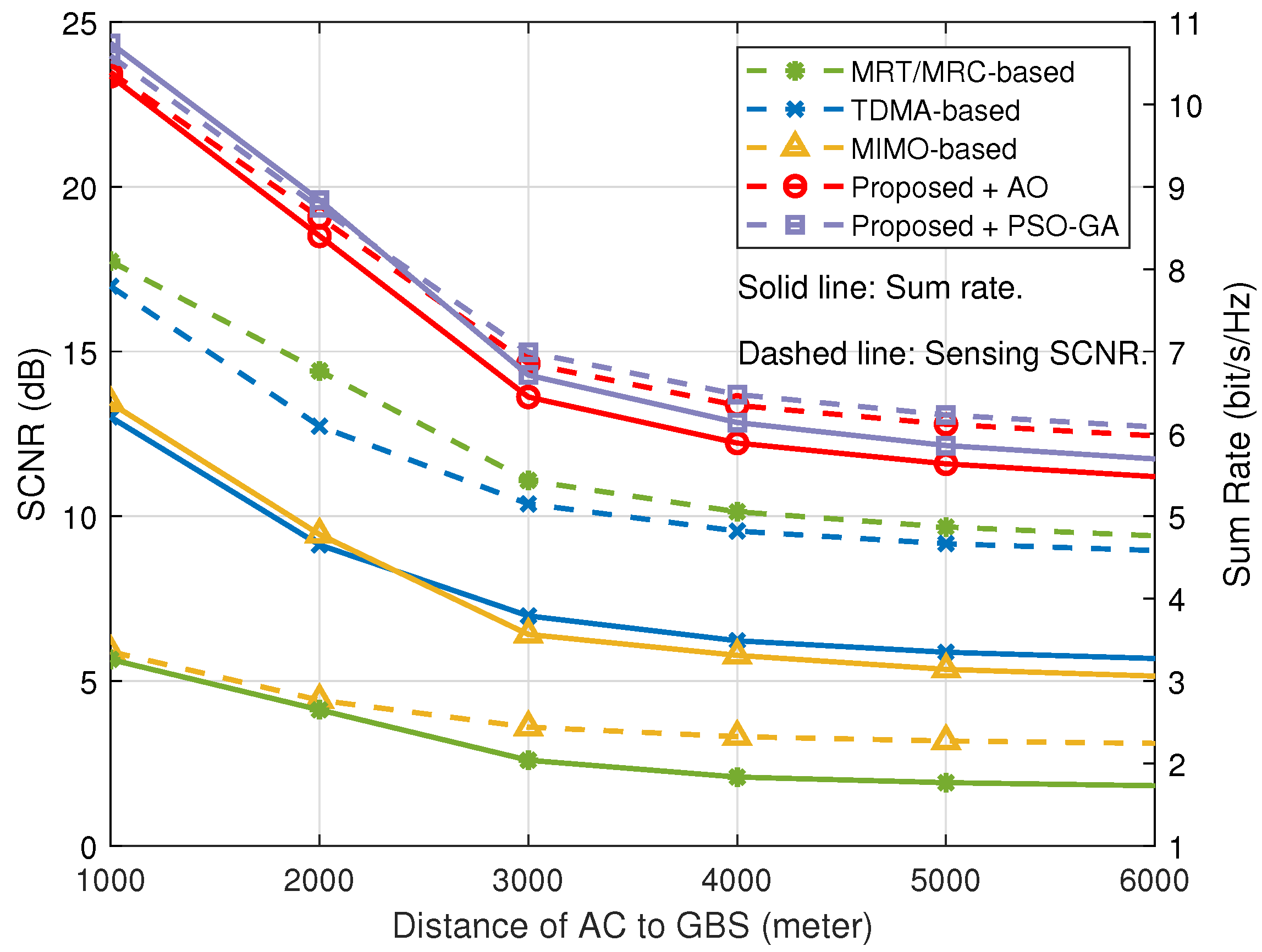
- Numerical results indicate that the proposed algorithm outperforms benchmark schemes in terms of both the sum rate and the sensing performance for the dual-function of communication and radar. It is demonstrated that the proposed NOMA-motivated MIMO IACRS schemes significantly improve A2G datalink performance, enabling the ACS to receive messages while maintaining high-quality radar detection. Furthermore, the system performance gain becomes significant when the AC’s attitude is considered.
1.3. Organization and Notation
2. System Model and Problem Formulation
2.1. System Description
2.2. Channel Model
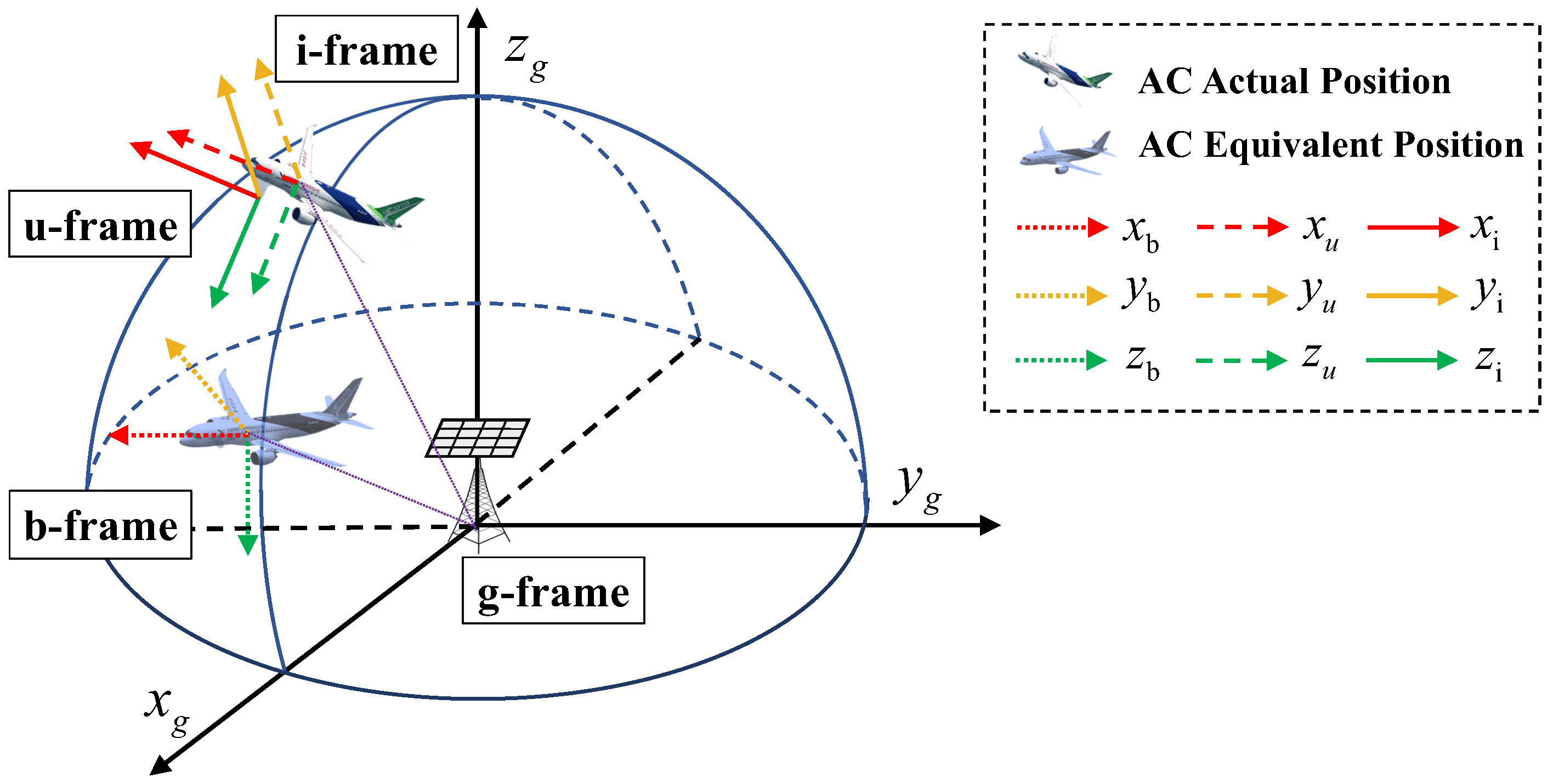
2.3. Coordinate Transformation
- The GBS geodetic coordinate frame (g-frame): Its origin is chosen as the center of gravity of the GBS-UPA, and its axes and are aligned with the directions of east and north, respectively. The axis is perpendicular to the ground surface pointing upwards, thus completing a right-handed coordinate frame. We assume that the row and column of the GBS-UPA are aligned with the axes and , respectively.
- The AC body coordinate frame (b-frame): Its origin is the AC center of gravity (ACCG). The axes , , and are aligned with its longitudinal (forward), lateral (right), and vertical (downward) direction, respectively, which are parallel to , , and , respectively.
- The inertial reference frame (i-frame): Its origin coincides with the ACCG, and its axes (roll axis) and (pitch axis)align along the directions of the AC’s head and starboard wing, respectively. And its axis (yaw axis) points downward, completing a right-handed coordinate frame.
- The AC-UPA coordinate frame (u-frame): Its origin is chosen as the AC-UPA center of gravity. The axes and are aligned with the row and column of the AC-UPA, respectively. The axis is perpendicular to the plane spanned by the axes and . We assume that the axes , , and are parallel to , , and , respectively. On the basis of the relationship of the u-frame and the i-frame, the u-frame would be consistent with the i-frame when the attitude of the AC changes.
2.4. Problem Formulation
3. AO-Based Alternative Optimization Algorithm
3.1. GBS’ Transmit BFs Design and Power Allocation
| Algorithm 1 Penalty-based approach to solve the joint transmit BF design and power allocation subproblem (35). |
|
3.2. ACS Receiver BFs’ Design
| Algorithm 2 SROCR method for solving the receiver BF design subproblem (43). |
3.3. Complexity Analysis
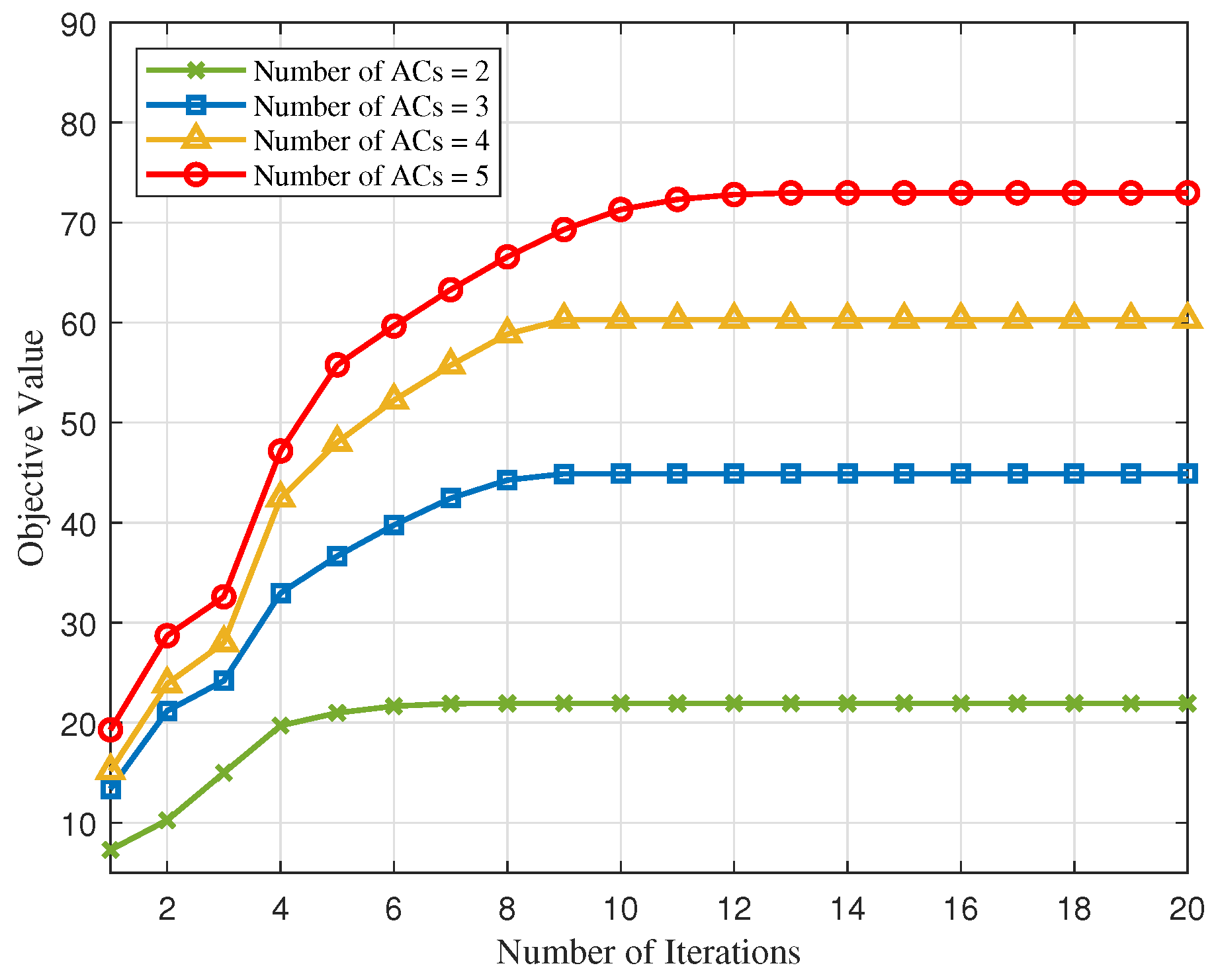
4. Results
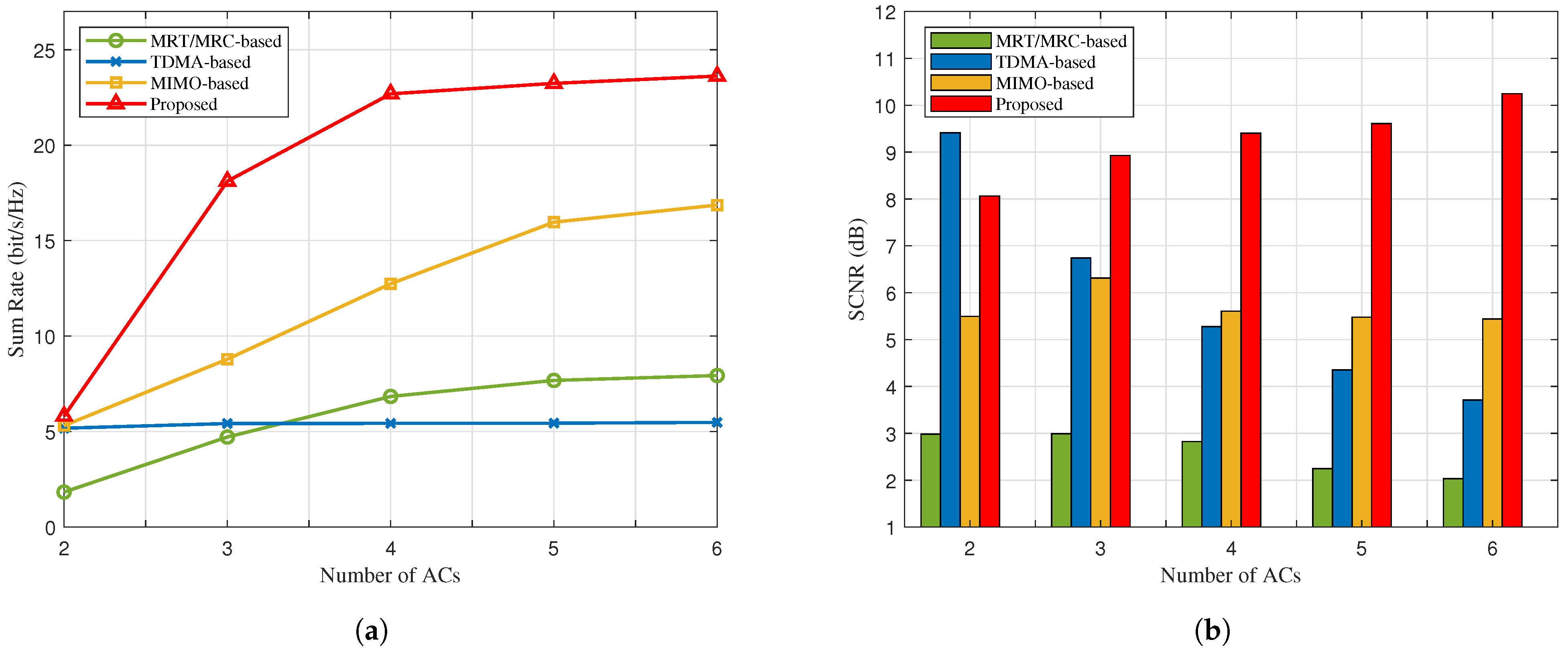
- TDMA-based dual-function scheme: In this scheme, the GBS with multi-antenna successively transmits dedicated messages and interrogation-detecting signal to the ACS over time slots, employing one common BF. Accordingly, for the TDMA-based scheme, the sensing SCNR at the k-th AC is given byand the corresponding achievable rate for the k-th AC isThe problem of maximizing the sum of and can be solved using the SCA algorithm as there are no inter-aircraft or inter-function interference terms involved.
- MIMO-based dual-function scheme: In this scheme, the MIMO-only GBS transmits communication data to the ACS, employing distinct BFs, which are also simultaneously utilized for the detection of the ACS. Notably, each AC directly receives its intended signal while treating the signals for other ACS as interference without the assistance of SIC, which means a low level of integration. Therefore, the sensing SCNR and the sum rate for the transmitted signal at the AC are similar, with (3) and (7), respectively.
- MRT/MRC-based dual-function scheme: In this scheme, the system model is the same as the proposed integrated framework, while using a linear transmitter and receiver, a maximum-ratio transmission/maximum-ratio combining (MRT/MRC) [40]. Hence, the approximate closed-form expressions of the transmit BFs of GBS and the receiver BFs of the ACS can be obtained.
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Zhang, J. Aeronautical Mobile Communication: The Evolution from Narrowband to Broadband. Engineering 2021, 7, 431–434. [Google Scholar] [CrossRef]
- Schnell, M.; Epple, U.; Shutin, D.; Schneckenburger, N. LDACS: Future aeronautical communications for air-traffic management. IEEE Commun. Mag. 2014, 52, 104–110. [Google Scholar] [CrossRef]
- Neji, N.; de Lacerda, R.; Azoulay, A.; Letertre, T.; Outtier, O. Survey on the Future Aeronautical Communication System and Its Development for Continental Communications. IEEE Trans. Veh. Technol. 2013, 62, 182–191. [Google Scholar]
- Xiao, Z.; Zhu, L.; Liu, Y.; Yi, P.; Zhang, R.; Xia, X.G.; Schober, R. A Survey on Millimeter-Wave Beamforming Enabled UAV Communications and Networking. IEEE Commun. Surv. Tutor. 2022, 24, 557–610. [Google Scholar]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Wu, D.O.; Xia, X.G. 3-D Beamforming for Flexible Coverage in Millimeter-Wave UAV Communications. IEEE Wirel. Commun. Lett. 2019, 8, 837–840. [Google Scholar]
- Chen, Z.; Tang, J.; Zhang, X.Y.; So, D.K.C.; Jin, S.; Wong, K.K. Hybrid Evolutionary-Based Sparse Channel Estimation for IRS-Assisted mmWave MIMO Systems. IEEE Trans. Wirel. Commun. 2022, 21, 1586–1601. [Google Scholar]
- Luong, N.C.; Lu, X.; Hoang, D.T.; Niyato, D.; Kim, D.I. Radio Resource Management in Joint Radar and Communication: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 780–814. [Google Scholar]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal Multiple Access for 5G and Beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Wu, D.O.; Xia, X.G. Millimeter-Wave NOMA with User Grouping, Power Allocation and Hybrid Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5065–5079. [Google Scholar]
- Zheng, L.; Lops, M.; Eldar, Y.C.; Wang, X. Radar and Communication Coexistence: An Overview: A Review of Recent Methods. IEEE Signal Process. Mag. 2019, 36, 85–99. [Google Scholar]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated Sensing and Communications: Toward Dual-Functional Wireless Networks for 6G and Beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Zhang, A.; Rahman, M.L.; Huang, X.; Guo, Y.J.; Chen, S.; Heath, R.W. Perceptive Mobile Networks: Cellular Networks with Radio Vision via Joint Communication and Radar Sensing. IEEE Veh. Technol. Mag. 2021, 16, 20–30. [Google Scholar] [CrossRef]
- Sturm, C.; Zwick, T.; Wiesbeck, W. An OFDM System Concept for Joint Radar and Communications Operations. In Proceedings of the VTC Spring 2009—IEEE 69th Vehicular Technology Conference, Barcelona, Spain, 26–29 April 2009; IEEE: New York, NY, USA, 2009; pp. 1–5. [Google Scholar]
- Agrawal, N.; Darak, S.J.; Bader, F. Spectral Coexistence of LDACS and DME: Analysis via Hardware Software Co-Design in Presence of Real Channels and RF Impairments. IEEE Trans. Veh. Technol. 2020, 69, 9837–9848. [Google Scholar] [CrossRef]
- Sturm, C.; Wiesbeck, W. Waveform Design and Signal Processing Aspects for Fusion of Wireless Communications and Radar Sensing. Proc. IEEE 2011, 99, 1236–1259. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, L.; Masouros, C.; Li, A.; Luo, W.; Petropulu, A. Toward Dual-functional Radar-Communication Systems: Optimal Waveform Design. IEEE Trans. Signal Process. 2018, 66, 4264–4279. [Google Scholar] [CrossRef]
- Mahal, J.A.; Khawar, A.; Abdelhadi, A.; Clancy, T.C. Spectral Coexistence of MIMO Radar and MIMO Cellular System. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 655–668. [Google Scholar] [CrossRef]
- Qian, J.; Lops, M.; Zheng, L.; Wang, X.; He, Z. Joint System Design for Coexistence of MIMO Radar and MIMO Communication. IEEE Trans. Signal Process. 2018, 66, 3504–3519. [Google Scholar] [CrossRef]
- Zhou, Q.; Gong, Y.; Nallanathan, A. Radar-Aided Beam Selection in MIMO Communication Systems: A Federated Transfer Learning Approach. IEEE Trans. Veh. Technol. 2024, 73, 12172–12177. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Zhang, L.; Liu, B.; Xu, H.X. Joint Power, Bandwidth, and Subchannel Allocation in a UAV-Assisted DFRC Network. IEEE Internet Things J. 2025. Early Access. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Liu, B. Joint Customer Assignment, Power Allocation, and Subchannel Allocation in a UAV-Based Joint Radar and Communication Network. IEEE Internet Things J. 2024, 11, 29643–29660. [Google Scholar] [CrossRef]
- Qiao, Y.; Niu, Y.; Han, Z.; Xiong, L.; Wang, N.; Quek, T.Q.S.; Ai, B. Resource Allocation for ISAC and HRLLC in UAV-Assisted HSR System with a Hybrid PSO-Genetic Algorithm. IEEE Internet Things J. 2025, 12, 6790–6804. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. MU-MIMO Communications with MIMO Radar: From Co-Existence to Joint Transmission. IEEE Trans. Wirel. Commun. 2018, 17, 2755–2770. [Google Scholar] [CrossRef]
- Dong, F.; Wang, W.; Hu, Z.; Hui, T. Low-Complexity Beamformer Design for Joint Radar and Communications Systems. IEEE Commun. Lett. 2021, 25, 259–263. [Google Scholar] [CrossRef]
- Chen, L.; Liu, F.; Wang, W.; Masouros, C. Joint Radar-Communication Transmission: A Generalized Pareto Optimization Framework. IEEE Trans. Signal Process. 2021, 69, 2752–2765. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Arora, A.; Chatzinotas, S.; Ottersten, B. Joint Transmit Waveform and Receive Filter Design for Dual-Function Radar-Communication Systems. IEEE J. Sel. Areas Commun. 2021, 15, 1378–1392. [Google Scholar]
- Zhao, J.; Gao, F.; Wu, Q.; Jin, S.; Wu, Y.; Jia, W. Beam Tracking for UAV Mounted SatCom on-the-Move with Massive Antenna Array. IEEE J. Sel. Areas Commun. 2018, 36, 363–375. [Google Scholar] [CrossRef]
- Zhu, J.; Li, W.; Wong, K.K.; Jin, T.; An, K. Waveform Design of DFRC System for Target Detection in Clutter Environment. IEEE Signal Process. Lett. 2023, 30, 1517–1521. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Du, Y.; Chen, Y.; Yu, F.R. Generalized Transceiver Beamforming for DFRC with MIMO Radar and MU-MIMO Communication. IEEE J. Sel. Areas Commun. 2022, 40, 1795–1808. [Google Scholar]
- Wang, Z.; Liu, Y.; Mu, X.; Ding, Z.; Dobre, O.A. NOMA Empowered Integrated Sensing and Communication. IEEE Commun. Lett. 2022, 26, 677–681. [Google Scholar] [CrossRef]
- Mu, X.; Liu, Y.; Guo, L.; Lin, J.; Hanzo, L. NOMA-Aided Joint Radar and Multicast-Unicast Communication Systems. IEEE J. Sel. Areas Commun. 2022, 40, 1978–1992. [Google Scholar] [CrossRef]
- Ouyang, C.; Liu, Y.; Yang, H. Revealing the Impact of SIC in NOMA-ISAC. IEEE Wirel. Commun. Lett. 2023, 12, 1707–1711. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint Radar and Communication Design: Applications, State-of-the-Art, and the Road Ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar]
- Chen, C.Y.; Vaidyanathan, P.P. MIMO Radar Waveform Optimization with Prior Information of the Extended Target and Clutter. IEEE Trans. Signal Process. 2009, 57, 3533–3544. [Google Scholar]
- Ogbe, D.; Love, D.J.; Rebholz, M.; Bidigare, T.P. Efficient Channel Estimation for Aerial Wireless Communications. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2774–2785. [Google Scholar]
- Cao, P.; Thompson, J.; Poor, H.V. A sequential constraint relaxation algorithm for rank-one constrained problems. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August 2017–2 September 2017; pp. 1060–1064. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Dinh, Q.T.; Diehl, M. Local Convergence of Sequential Convex Programming for Nonconvex Optimization; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Tian, Y.; He, X.; Xu, Y.; Wan, L.; Ye, B. 4D Trajectory Optimization of Commercial Flight for Green Civil Aviation. IEEE Access 2020, 8, 62815–62829. [Google Scholar]
- Li, Y.; Fan, P.; Leukhin, A.; Liu, L. On the Spectral and Energy Efficiency of Full-Duplex Small-Cell Wireless Systems with Massive MIMO. IEEE Trans. Veh. Technol. 2017, 66, 2339–2353. [Google Scholar]

| Considering Factor | [27] | [28] | [29] | [30,31] | Proposed |
|---|---|---|---|---|---|
| Multi-aircraft communication | ✓ | ✓ | ✓ | ✓ | ✓ |
| Multi-aircraft sensing | × | ✓ | ✓ | ✓ | ✓ |
| Radar interference cancellation | × | × | × | ✓ | ✓ |
| Deployment of NOMA | × | × | × | multiple-user access in communication | co-located dual-function coordination |
| DME-like sensing requirement | × | × | ✓ but not mentioned | × | ✓ |
| Aircraft attitude | ✓ | × | × | × | ✓ |
| Parameter | Symbol | Value | Parameter | Symbol | Value |
|---|---|---|---|---|---|
| Antenna spacing | d | Flight range | m | ||
| Roll angle range | 1 | Pitch angle range | |||
| Yaw angle range | Rician factor | 9 | |||
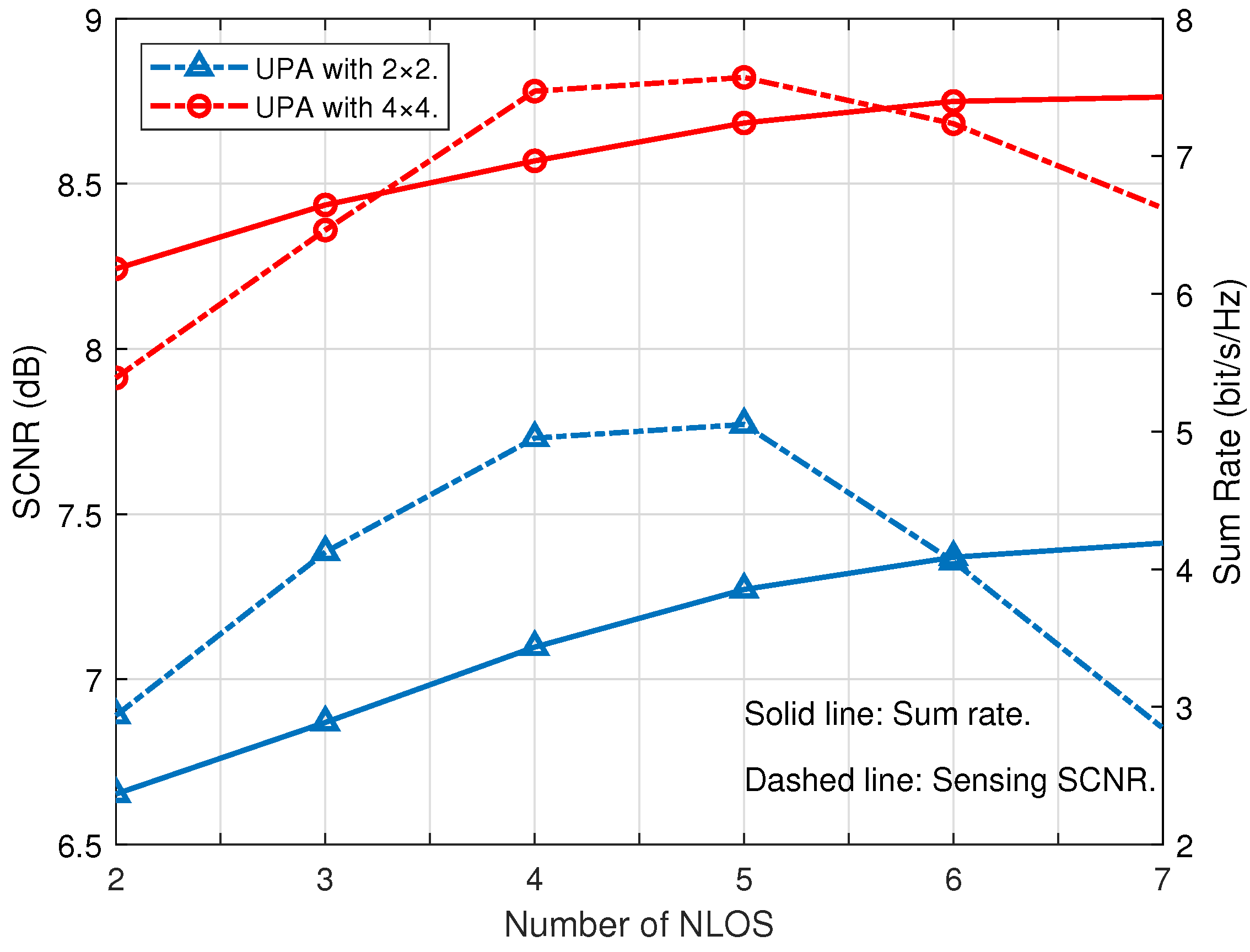
| Number of NLOS | L | 2 | Regularization parameters | 0.5, 0.5 | |
| Receiver power at k-th AC | 30 dBm | Transmit power at GBS | 30 dBm | ||
| Path loss reference | 32.6 dB | large-scale fading gain | |||
| Max path delay | Delay distribution | ||||
| Required data rate | 0.5 bit/s/Hz | Required SCNR | 1 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Zhao, J.; Zhou, Q.; Zhu, Y.; Cai, K. Spectrum Sharing Design for Integrated Aeronautical Communication and Radar System. Remote Sens. 2025, 17, 1208. https://doi.org/10.3390/rs17071208
Yu L, Zhao J, Zhou Q, Zhu Y, Cai K. Spectrum Sharing Design for Integrated Aeronautical Communication and Radar System. Remote Sensing. 2025; 17(7):1208. https://doi.org/10.3390/rs17071208
Chicago/Turabian StyleYu, Lanchenhui, Jingjing Zhao, Quan Zhou, Yanbo Zhu, and Kaiquan Cai. 2025. "Spectrum Sharing Design for Integrated Aeronautical Communication and Radar System" Remote Sensing 17, no. 7: 1208. https://doi.org/10.3390/rs17071208
APA StyleYu, L., Zhao, J., Zhou, Q., Zhu, Y., & Cai, K. (2025). Spectrum Sharing Design for Integrated Aeronautical Communication and Radar System. Remote Sensing, 17(7), 1208. https://doi.org/10.3390/rs17071208






