Assessment of the Potential of Spaceborne GNSS-R Interferometric Altimetry for Monthly Marine Gravity Anomaly

Abstract

The Earth’s time-variable gravity field holds significant research and application value. However, satellite gravimetry missions such as GRACE and GRACE-FO face limitations in spatial resolution when detecting monthly gravity fields, while traditional radar altimeters lack the observational efficiency needed for monthly gravity anomaly inversion. These limitations hinder further exploration and application of the Earth’s time-variable gravity field. Leveraging its advantages, such as rapid global coverage, high revisit frequency, and low cost for constellation formation, spaceborne GNSS-R technology holds the potential to address the observational efficiency gaps of traditional radar altimeters. This study presents the first assessment of the capability of spaceborne GNSS-R interferometric altimetry for high spatial resolution monthly marine gravity anomaly inversion through simulations. The results indicate that under the PARIS Operational scenario of a single GNSS-R satellite (a spaceborne GNSS-R interferometric altimetry scenario proposed by Martin-Neira), a 30′ grid resolution marine gravity anomaly can be inverted with an accuracy of 4.93 mGal using one month of simulated data. For a dual-satellite constellation, the grid resolution improves to 20′, achieving an accuracy of 4.82 mGal. These findings underscore the promise of spaceborne GNSS-R interferometric altimetry technology for high spatial resolution monthly marine gravity anomaly inversion.

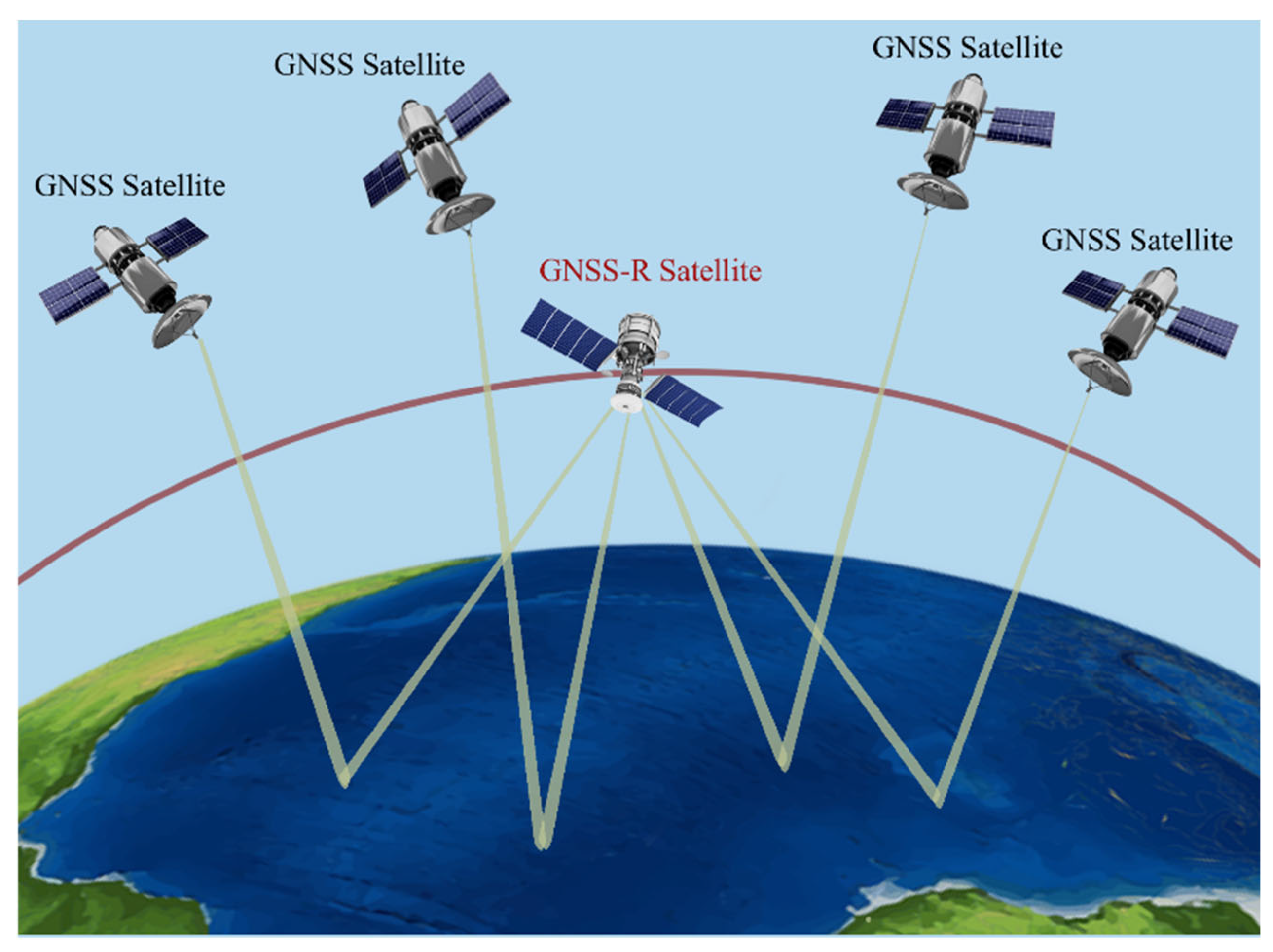
1. Introduction

The Earth’s gravitational field is a vital physical quantity in Earth sciences, providing valuable insights into the Earth’s mass distribution, density, and internal structure. Its spatio-temporal variations enable us to understand and track dynamic processes of material transport and exchange within the Earth’s system [1]. With approximately 71% of the Earth’s surface covered by oceans, the recovery of marine gravity field is essential for building a comprehensive Earth gravity field model. The time-variable marine gravity field is crucial for studying changes in the Earth’s system and engineering applications, such as the water cycle, climate change, movement of materials within the Earth, and energy development [2]. Additionally, the higher the resolution of the marine time-variable gravity field, the more information it provides about dynamic processes in the Earth’s system. Therefore, obtaining high-resolution, time-varying information about the marine gravity field is essential for both research and applications in Earth sciences.

In 1969, Wolff proposed the GRACE mission concept, employing inter-satellite ranging measurements between two low Earth co-orbiting satellites to observe the Earth’s time-variable gravity field [3]. At present, GRACE/GRACE-FO serve as the primary tools for detecting the global gravity variation, having continuously provided the monthly Earth’s gravity field data for over two decades [4]. These missions have significantly advanced the monitoring and understanding of global environmental changes, encompassing variations in ground-water storage [5], deformation caused by earthquakes [6], sea level rise [7], deep ocean currents [8], and ocean heat content [9]. However, the orbital configuration of GRACE/GRACE-FO satellites (~500 km satellite altitude, ~220 km inter-satellite distance) fundamentally limits the spatial resolution of their derived time-variable gravity fields to hundreds of kilometers [10]. Furthermore, the accuracy of the gravity field degrades significantly with increasing spherical harmonic degree, as high-degree coefficients dominated by noise [11]. To mitigate the impact of strong longitudinal stripes and random noises, spatial filtering is required, further reducing the spatial resolution of GRACE/GRACE-FO time-variable gravity data [12]. Currently, the monthly gravity field products from GFZ GRACE Release 06 (RL06) solutions are truncated at spherical harmonic degrees of 60 and 96 [13], corresponding to spatial resolutions of approximately 330 km and 220 km (half-wavelength) [14], respectively. Consequently, the coarse spatial resolution of the gravity field products provided by GRACE/GRACE-FO satellites hinders further research and applications of time-variable gravity fields [15,16].

Marine gravity anomalies from satellite altimetry have greatly improved the accuracy and spatial resolution of static marine gravity anomaly results [17,18,19,20], allowing for a better understanding of deep-sea seabed topography and structure [21,22,23]. However, due to the satellite’s limited view confined to the nadir and the high cost of constructing large-scale constellations, traditional radar altimeters struggle to achieve rapid global coverage and revisiting capabilities [24]. As a result, radar altimeter data are mainly used for inverting static marine gravity anomaly rather than for time-variable marine gravity fields, due to their insufficient observational efficiency. In 2021, Li et al. first utilized the yearly marine time-variable gravity field from radar altimetry, revealing the undersea volcano magma mass motions of the Izu-Bonin arcs near Japan. However, it was also pointed out that the low time resolution of altimetry-derived marine time-variable gravity fields makes it challenging to study rapidly evolving volcanic systems [25]. In 2023, Guo et al. verified the feasibility of deriving high spatial resolution monthly marine time-variable gravity anomaly from CryoSat-2 altimetry data. However, there may be no data within the window when the calculation window was less than 60′. Therefore, despite the resulting grid resolution for the monthly marine time-variable gravity anomaly being 3′, a 60′ calculation window was used due to insufficient data from the radar altimeter, leading to a poor overall resolution [26].

The spaceborne Global Navigation Satellite System Reflectometry (GNSS-R) is a passive remote sensing technique that can receive multiple reflected signals from GNSS satellites simultaneously, covering wide swathes. This allows for advantages such as large data volume, low power consumption, low cost for constellation formation, and rapid global coverage and revisiting capabilities [27]. Figure 1 shows the diagram of spaceborne GNSS-R observations. The concept of utilizing GNSS reflections for remote sensing was initially proposed by Hall in 1988 [28] and later expanded by Martin-Neira in 1993 with the PARIS concept (Passive Reflectometry and Interferometry System), which combines GNSS direct and reflected signals for altimetry [29]. At present, multiple spaceborne GNSS-R missions are in orbit [30,31,32,33,34,35], and have been successfully applied in various fields such as sea surface wind speed [36,37], sea ice [38,39], and soil moisture [40,41]. Sea surface height (SSH) altimetry is one of the most promising and challenging applications of GNSS-R, which can complement existing technologies such as radar satellites [42]. However, spaceborne GNSS-R altimetry technology still faces many challenges in practical applications. On one hand, most existing Spaceborne GNSS-R missions do not specifically target SSH altimetry; the altimetry accuracy is relatively poor due to the use of low bandwidth signals [43,44,45]. On the other hand, although carrier-phase altimetry experiments on PRETY and Spire satellites have achieved centimeter-level precision, the stringent observation conditions and insufficient effective observation rates remain significant challenges [46,47,48,49].

The spaceborne GNSS-R interferometric processing technique, proposed by Martin-Neira in 2011, is currently considered to be the most feasible spaceborne altimetry mode for spaceborne GNSS-R altimetry. By incoherently integrating power waveforms from multiple samples, the proposed PARIS IOD and Operational spaceborne GNSS-R missions can achieve decimeter-level sea surface height measurements with a 100-km along-track spatial resolution [50]. Subsequent studies have confirmed the stable performance of spaceborne GNSS-R interferometric altimetry in both accuracy and observation efficiency [51,52]. Meanwhile, the European Space Agency (ESA) proposed the GEROS-ISS mission [53], which, although not yet implemented, has significantly advanced GNSS-R interferometric altimetry. In 2016, Martin-Neira introduced the “Cookie” satellite constellation concept, analyzing its potential for networked observations [27]. Additionally, the feasibility of near real-time target detection from a constellation of GNSS-R has been demonstrated [54], offering even better temporal resolution than SWOT in mesoscale ocean observations [55]. This technology has shown significant potential for ocean circulation monitoring, positioning it as a valuable complement to traditional radar altimetry [56]. Furthermore, scholars also have pointed out that GNSS-R SSH altimetry products will become an important data source for global marine gravity anomaly inversion [57,58].

However, detecting short-wavelength marine gravity fields requires higher altimetry spatial resolution, yet increasing the GNSS-R along-track spatial resolution reduces the number of incoherent integrations, thereby decreasing altimetric accuracy. In 2018, Li et al. systematically analyzed the impact of incoherent integration and post-integration waveforms on the accuracy of interferometric altimetry [59]. Furthermore, studies indicate that the minimum spatial resolution of spaceborne GNSS-R altimetry footprints is approximately 10 km [55]. In 2024, our previous work demonstrated through simulations that PARIS can achieve high-precision inversion of marine vertical deflection (referred to as the deflection of vertical, DOV, another parameter for describing the gravity field) with a 10 km along-track resolution. Moreover, it is further speculated that its global coverage and revisit capabilities may contribute to the inversion of high-spatial resolution marine time-variable gravity fields [60].

Based on our previous work [60], this paper aims to assess the potential contribution of spaceborne GNSS-R interferometric altimetry technology in improving the current spatial resolution and accuracy of marine time-variable gravity fields. Specifically, it evaluates the precision of global monthly marine gravity anomaly inversion using one month of simulated data at various resolutions. Additionally, the impact of dual-satellite constellation observations and different instrument configurations on the accuracy of monthly marine gravity anomaly inversion will be analyzed.

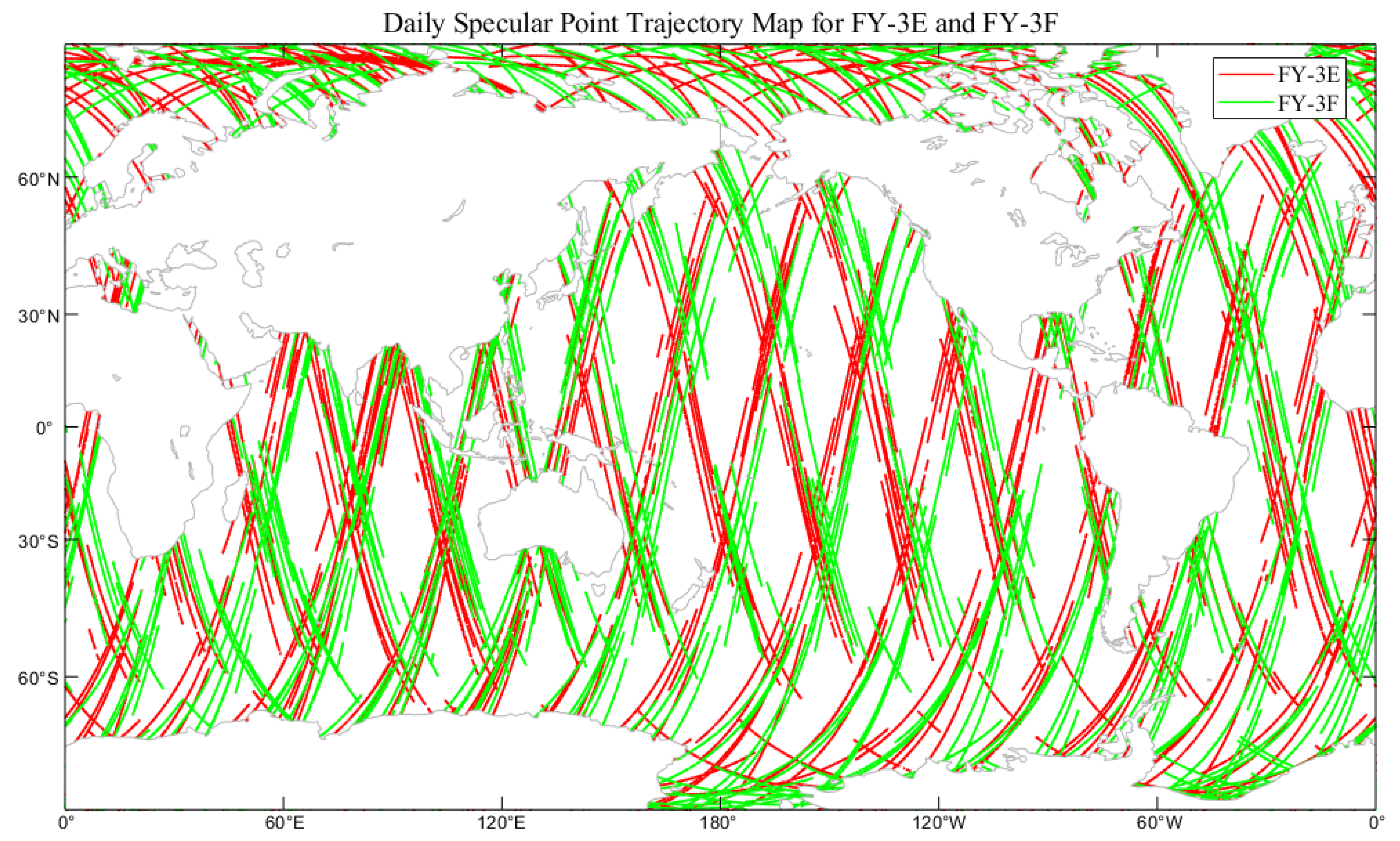
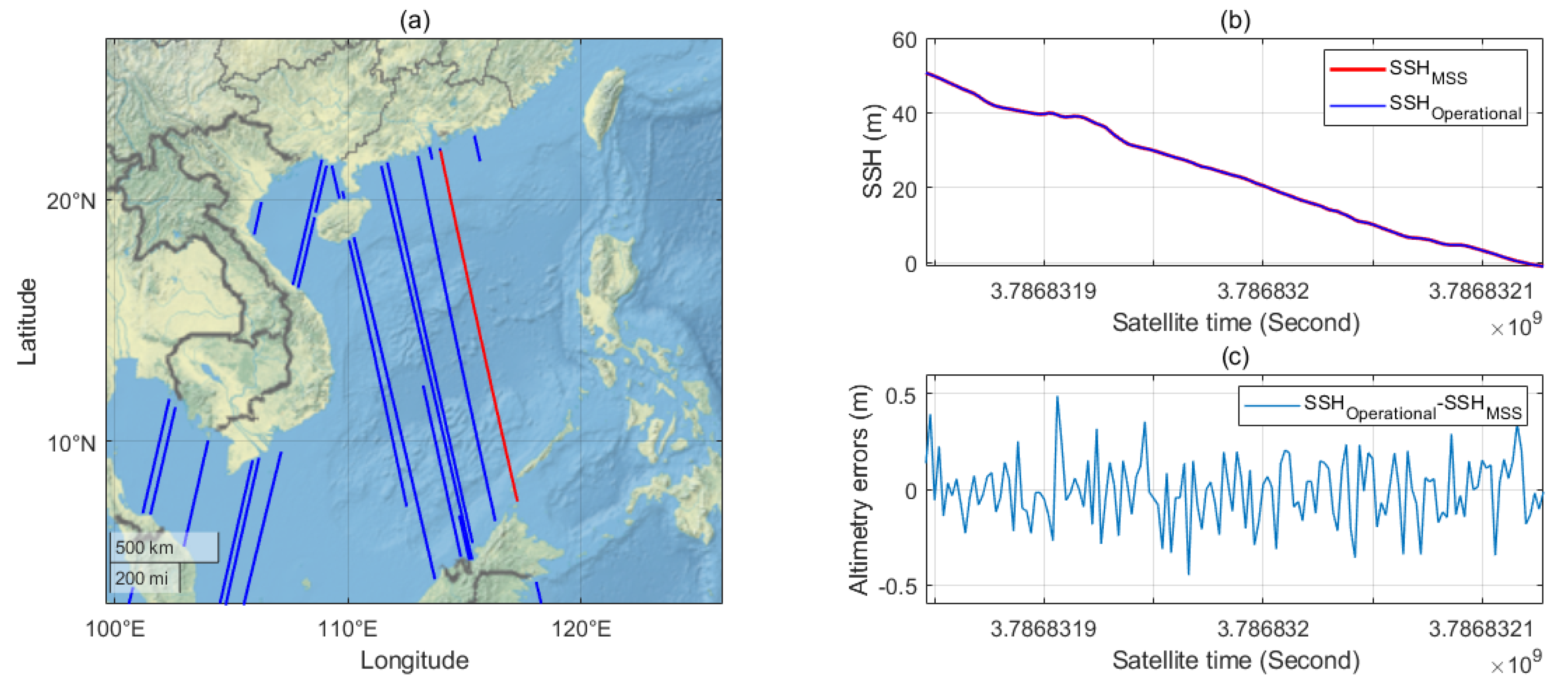
2. Experimental Data

To simulate spaceborne GNSS-R SSH interferometric altimetry data, the GNSS-R specular point trajectory data from the FY-3E and FY-3F satellites were utilized as input. The FY-3E and FY-3F satellites were launched in July 2021 and August 2023, respectively, and have formed a three-satellite constellation observation with the FY-3G satellite, which was launched in April 2023 [61]. All of these satellites carry the GNOS-II payload, which is capable of receiving GNSS reflection signals from the earth’s surface through eight signal-receiving channels, including GPS, BDS, and GALILEO. However, compared to the FY-3G satellite with an orbital altitude of 407 km and an inclination angle of 50°, the FY-3E and FY-3F satellites are more ideal for global SSH observations with an orbital altitude of 836 km and an inclination angle of 98.75°, aligning with the orbit parameters of geodetic missions. Therefore, the Level 2 (L2) GNSS-R specular points trajectory of FY-3E/F satellites in October 2023 are utilized to evaluate the ability to detect global monthly marine gravity anomalies through spaceborne GNSS-R interferometry altimetry.

Figure 2 displays the daily trajectory map of specular points for FY-3E and FY-3F. It can be observed that the specular points trajectories of these two satellites are adjacent, which allows them to complement each other and improve the coverage of spaceborne GNSS-R through constellation observation. In addition, due to strict data control and filtering of L2 data, the number of observation strips of each satellite does not always reach the maximum observable number. After calculation, in the selected L2 data for October 2023, FY-3E satellite utilized an average of 3.5 channels out of 8 channels, while FY-3F utilized an average of 3.8 channels.

In recent years, spaceborne GNSS-R interferometric altimetry performance and methodologies have been extensively studied and optimized. However, the PARIS interferometric altimetry performance model proposed by Martin-Neira (2011) remains the most classic and representative achievement in this field [50]. Therefore, this study adopts it as the theoretical foundation and a typical representation of GNSS-R interferometric altimetry performance. According to the error budget table analyzed by Martin-Neira, the antenna gain for PARIS in IOD and Operational scenarios are 23 dBi and 30 dBi, respectively, with orbital altitudes of 800 km and 1500 km. After incoherently integrating power waveforms from multiple samples and considering correction accuracies for instrument noise, ionosphere, troposphere, electromagnetic bias, skewness bias, and orbit, the altimetry accuracy can reach 17.5 cm and 7.5 cm at the edge of a swath with a 100 km along-track resolution. This altimetric performance can meet the detection requirements of its main target of ocean mesoscale studies.

To meet the detection requirements for high-frequency information of gravity field, the minimum along-track resolution (10 km) achieved by spaceborne GNSS-R interferometric altimetry should be taken as the parameter. Based on the altimetry accuracy proposed by Martin-Neira for a 100 km along-track resolution and its relationship with along-track resolution, the altimetry accuracy for the IOD and Operational scenarios at a 10 km along-track resolution can be extrapolated. Additionally, Martin-Neira’s error budget table omits the impact of geophysical error corrections such as tide correction and inverted barometer correction, which are crucial for gravity field inversion. Referring to the geophysical correction error budgets of radar altimeters, this study sets the correction accuracy for geophysical errors at 3 cm [62]. Furthermore, the orbital altitude of FY-3E/F differs from that of PARIS IOD and Operational scenarios, and orbital altitude significantly affects the detection efficiency and altimetry accuracy of GNSS-R. Therefore, this study recalculated the altimetry accuracy of PARIS based on the error budget table proposed by Martin-Neira, taking into account the impact of the orbital altitude of FY-3E/F, 10 km along-track resolution, and geophysical error correction. The results showed that at the orbit altitude of FY-3E/F, the altimetry accuracy for IOD ${\sigma }_{IOD}$ and Operational scenarios ${\sigma }_{Operational}$ are 41.52 cm and 16.17 cm, respectively, with a 10 km along-track resolution. Figure 3 illustrates the process of simulating spaceborne GNSS-R altimetry data, while the detailed calculation process can be found in our previous work [60].

Prior to simulating sea surface height (SSH) data for spaceborne GNSS-R interferometric altimetry, sparse sampling was applied to the specular point trajectory data of the FY-3E and FY-3F satellites. This approach was adopted to address the 5.6 km ground spacing between adjacent along-track specular points of FY-3E/F satellites, which is below the minimum achievable along-track resolution (10 km) for spaceborne GNSS-R interferometric altimetry. The sparse sampling ensures the independence between adjacent sampling points along the track, thereby eliminating data redundancy. As shown in Figure 4, the minimum sampling distance was set at 10 km.

To simulate SSH in spaceborne GNSS-R interferometric altimetry, the DTU21MSS model from the Technical University of Denmark (DTU) was selected as the input mean sea surface (MSS) model. With a grid resolution of 1 arc-minute, the DTU21MSS model is significantly finer than the 10 km spatial resolution achievable by spaceborne GNSS-R interferometric altimetry, except in polar regions. To accurately represent the impact of the spatial resolution of spaceborne GNSS-R interferometry on the SSH observations, the average SSH within the spatial resolution of spaceborne GNSS-R interferometry was employed as the background field. As shown in Figure 4, a 10 km × 10 km specular reflection area was constructed with each spaceborne GNSS-R specular point as the center, and the reflection area was resampled into points with a 2 km interval. The SSH value at each resampling point within the reflection area was calculated by interpolating with the DTU21MSS model, and the average SSH of all resampling points within the reflection area was calculated as the average MSS within the specular reflection area $MS{S}_{Sp\_area}$.

At a single point, the altimetry accuracy can also be seen as the difference error between spaceborne GNSS-R SSH interferometric altimetry results and the true SSH. Furthermore, in practical scenarios, the altimetry errors of adjacent points along the track are generally correlated. However, from a global and long-term observation perspective, the distribution of all altimetry errors follows a normal distribution. Therefore, in the evaluation of the global monthly marine gravity field recovered by spaceborne GNSS-R interferometric altimetry, altimetry errors can be assigned to all points based on the central limit theorem. This is achieved by generating a random number from a normal distribution with a mean of 0 and a standard deviation of altimetry accuracy (41.52 cm for the IOD scenario and 16.17 cm for the Operational scenario). Lastly, the final simulated results of spaceborne GNSS-R interferometric altimetry results $SS{H}_{GNSS-R}$ will be determined by adding altimetry errors ${\epsilon }_{altimetry}$ to the $MS{S}_{Sp\_area}$.

$$SS{H}_{GNSS-R}=MS{S}_{Sp\_area}+{\epsilon }_{altimetry}=SS{H}_{MSS}+{\epsilon }_{area}+{\epsilon }_{altimetry}$$

(1)

where $SS{H}_{MSS}$ represents the sea surface height at the center point of the GNSS-R specular reflection, while ${\epsilon }_{area}$ denotes the difference between the mean sea surface height $MS{S}_{Sp\_area}$ within the GNSS-R altimetry resolution and $SS{H}_{MSS}$. The difference ${\epsilon }_{area}$ reflects the impact of GNSS-R altimetry resolution on the altimetry results and is referred to as the representativeness error in the [55].

Figure 5 provides an example of the simulated SSH altimetry results for an Operational track. Figure 5b shows the variations of the simulated Operational SSH altimetry results and the true SSH (using the MSS as the true SSH) along the red track in Figure 5a, while Figure 5c displays the differences between the simulated Operational SSH altimetry results and the true SSH. It can be observed that the simulated Operational SSH $SS{H}_{Operational}$ follows a similar trend as the true sea surface height $SS{H}_{MSS}$, but with an error term compared to the true SSH. As shown in Figure 5c, the error term corresponds to the simulated spaceborne GNSS-R interferometric altimetry error, which includes both representativeness errors ${\epsilon }_{area}$ and altimetric errors ${\epsilon }_{altimetry}$.

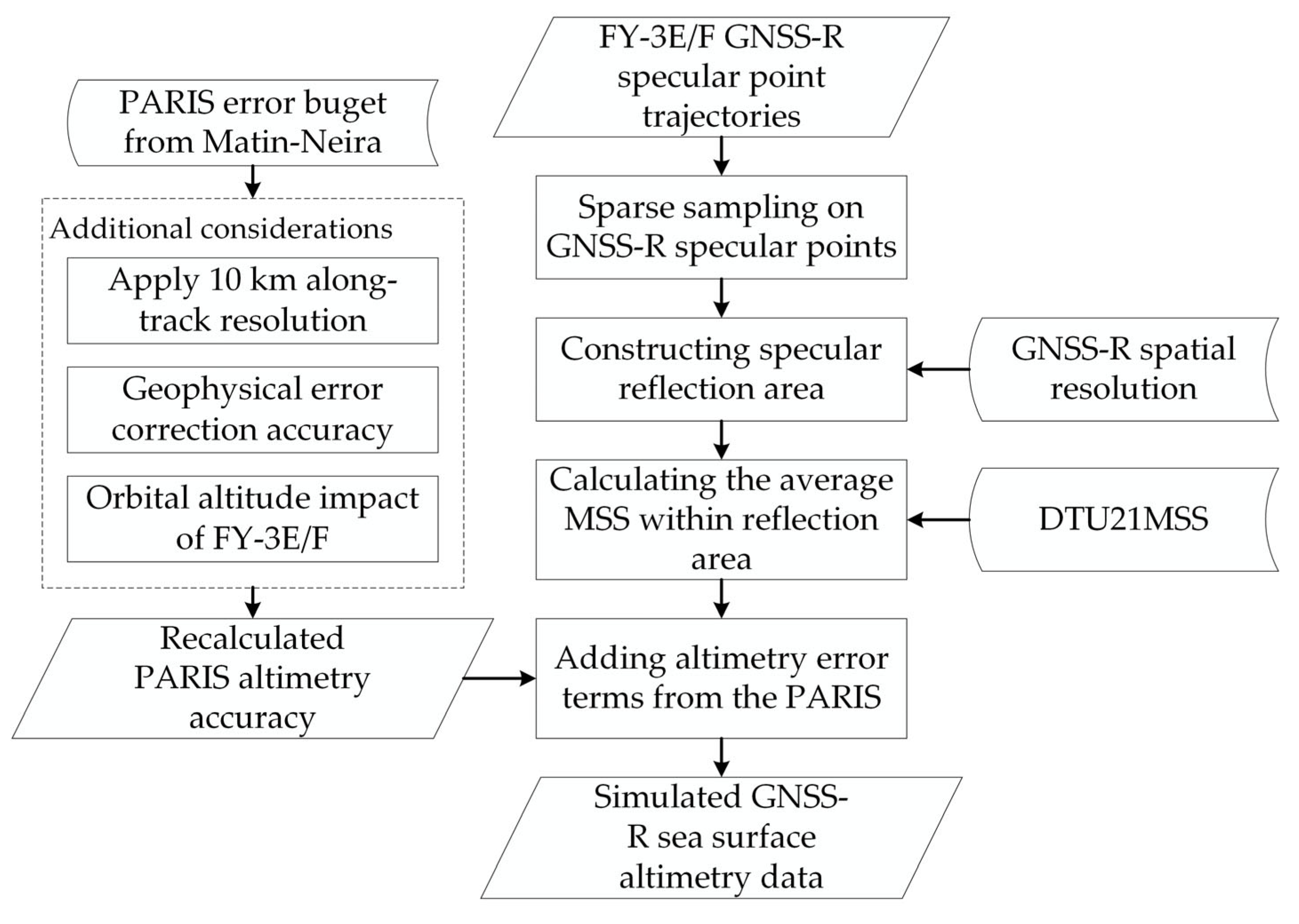
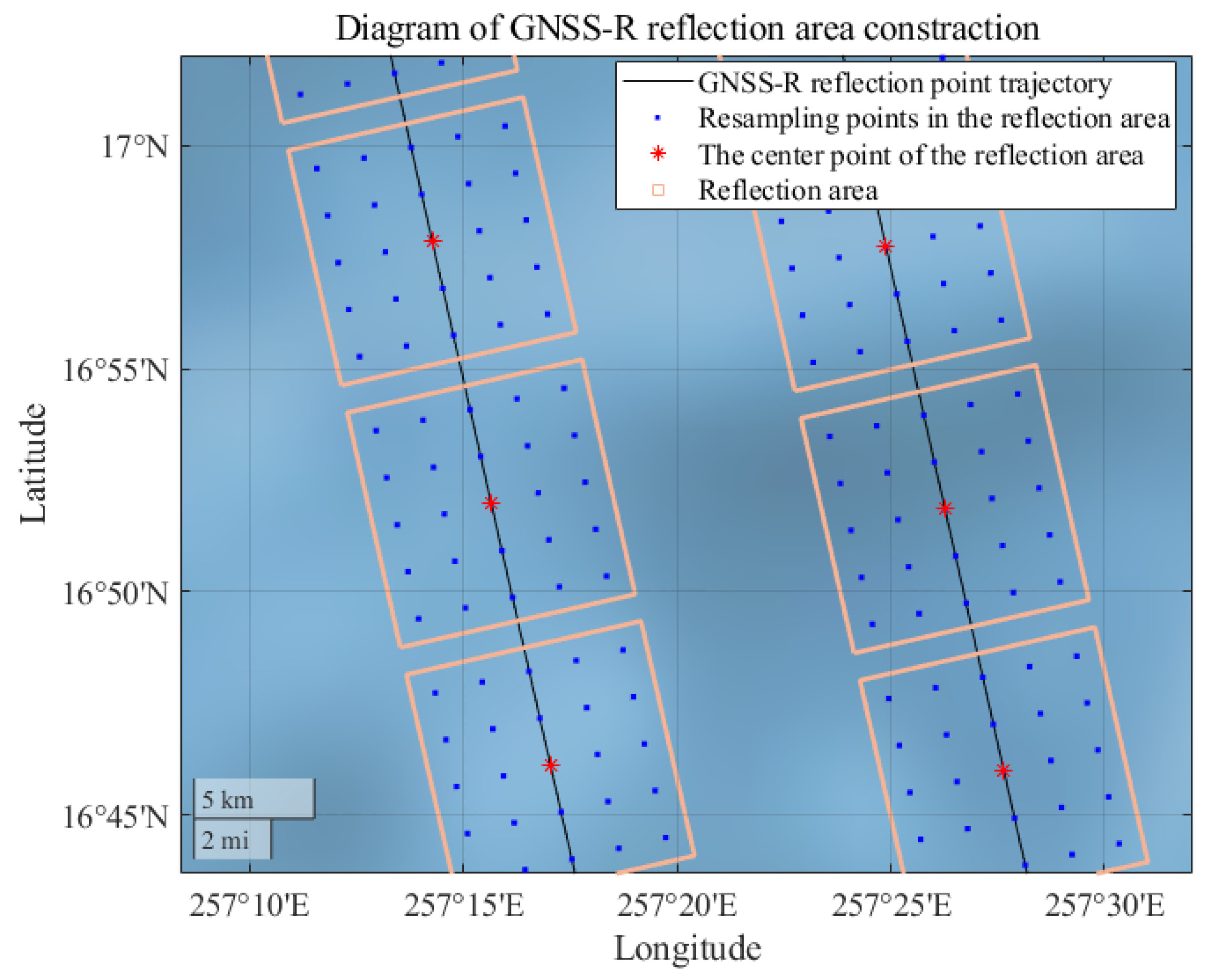
3. Methodology

The inverse Vening Meinesz method is a commonly used method for gravity anomalies inversion using vertical deflections. Therefore, prior to calculating the gravity anomalies, the gridded vertical deflection components must first be derived from the simulated spaceborne GNSS-R SSH altimetry results in Section 2. Additional filtering was applied to the simulated data, removing points with errors greater than 3 times the value of the altimetry accuracy $\sigma$. Since the gravity anomaly inversion relies on the geoid height N, where $N=MSS-DTU$, the MDT_CNES_CLS_18_global model obtained from AVISO was subtracted from the simulated SSH to eliminate the influence of mean dynamic topography (MDT) and obtain the simulated geoid height. The gridded geoid surface is then obtained by gridding the geoid heights of all simulated altimetry points in a month. Finally, the vertical deflection on the grid (i,j) can be calculated using Equations (2) and (3) for the north–south ξ(i,j) and east–west directions $\eta$(i,j), respectively. This algorithm not only improves efficiency but has also been verified for accuracy and applicability [63,64].

$$\xi \left(i,j\right)=-{\displaystyle \frac{1}{R}}{\displaystyle \frac{\left(N_{i+1}-N_i\right)}{\left({\phi }_{i+1}-{\phi }_i\right)}}$$

(2)

$$\eta \left(i,j\right)=-{\displaystyle \frac{1}{Rcos{\phi }_i}}{\displaystyle \frac{\left(N_{j+1}-N_j\right)}{\left({\lambda }_{j+1}-{\lambda }_j\right)}}$$

(3)

where $R$ is the Earth’s mean radius, $N$ is the mean geoid height at the grid point, and $\phi$ and $\lambda$ represent the latitude and longitude of the grid point, respectively.

In 1997, Hwang derived the Inverse Vening Meinesz formula, which converts vertical deflections into gravity anomalies by utilizing the gradient of the H function, as Equations (4) and (5).

$$\Delta \mathrm{g}(p)={\displaystyle \frac{{\gamma }_0}{4\pi }}{\displaystyle {\iint }_{\sigma }{H}^{\prime }({\xi }_q\cos {\alpha }_{qp}+{\eta }_q\sin {\alpha }_{qp})d{\sigma }_q}$$

(4)

$$H^{\prime }={\displaystyle \frac{\mathrm{d}H}{d{\psi }_{pq}}}=-{\displaystyle \frac{\cos \frac{{\psi }_{pq}}{2}}{2{\sin }^2\frac{{\psi }_{pq}}{2}}}+{\displaystyle \frac{\cos \frac{{\psi }_{pq}}{2}\left(3+2\sin \frac{{\psi }_{pq}}{2}\right)}{2\sin \frac{{\psi }_{pq}}{2}\left(1+\sin \frac{{\psi }_{pq}}{2}\right)}}$$

(5)

where the average gravity of the Earth ${\gamma }_0={\displaystyle \frac{GM}{R^2}}$, $H^{\prime }$ is the gradient of the H function, and p and q are two points on the sphere. ${\alpha }_{qp}$ and ${\psi }_{pq}$ represent the azimuth and spherical distance between the two points and can be calculated using Equations (6) and (7).

$$\tan {\alpha }_{qp}={\displaystyle \frac{-\cos {\varphi }_p\sin \Delta {\lambda }_{qp}}{-\sin \left({\varphi }_q-{\varphi }_p\right)+2\sin {\varphi }_q\cos {\varphi }_p{\sin }^2\frac{\Delta {\lambda }_{qp}}{2}}}$$

(6)

$${\sin }^2\left({\displaystyle \frac{{\psi }_{qp}}{2}}\right)={\sin }^2\left({\displaystyle \frac{\Delta {\varphi }_{qp}}{2}}\right)+{\sin }^2\left({\displaystyle \frac{\Delta {\lambda }_{qp}}{2}}\right)\cos {\varphi }_q\cos {\varphi }_p$$

(7)

where $\Delta {\varphi }_{qp}={\varphi }_q-{\varphi }_p$, $\Delta {\lambda }_{qp}={\lambda }_q-{\lambda }_p$, ${\varphi }_p$ and ${\varphi }_q$ represent the latitude of points p and q, while ${\lambda }_p$ and ${\lambda }_q$ represent the longitude of point p and q.

Additionally, Hwang considered latitude differences and used a one-dimensional Fast Fourier Transform (1D FFT) for global gravity field calculations, making the theoretical framework more rigorous:

$$\begin{array}{l}\Delta g_{{\varphi }_p}\left({\lambda }_p\right)={\displaystyle \frac{{\gamma }_0\Delta \varphi \Delta \lambda }{4\pi }}{\displaystyle \sum _{{\varphi }_q={\varphi }_1}^{{\varphi }_n}{\displaystyle \sum _{{\lambda }_q={\lambda }_1}^{{\lambda }_n}{H}^{\prime }\left(\Delta {\lambda }_{qp}\right)\times \left({\xi }_{\cos }\cos {\alpha }_{qp}+{\eta }_{\cos }\sin {\alpha }_{qp}\right)}}\\ ={\displaystyle \frac{{\gamma }_0\Delta \varphi \Delta \lambda }{4\pi }}{F}_1^{-1}\times \left\{{\displaystyle \sum _{{\varphi }_q={\varphi }_1}^{{\varphi }_n}\left[F_1\right.}\left(H^{\prime }\left(\Delta {\lambda }_{qp}\right)\cos {\alpha }_{qp}\right)F_1\left({\xi }_{\cos }\right)\right.\\ +\left.F_1\left(H^{\prime }\left(\Delta {\lambda }_{qp}\right)\sin {\alpha }_{qp}\right)F_1\left({\eta }_{\cos }\right)\right\}\end{array}$$

(8)

where ${\xi }_{\cos }=\xi \cos \varphi$, ${\eta }_{\cos }=\eta \cos \varphi$, and $\Delta \varphi$ and $\Delta \lambda$ represent the grid spacing in the latitude and longitude directions, respectively.

However, when the spherical distance ${\psi }_{pq}=0$, the kernel function will be singular. Therefore, the innermost zone effect must be considered, which can be calculated using Equation (9):

$$g_0={\displaystyle \frac{s_0{\gamma }_0}{2}}\left({\xi }_y+{\eta }_x\right)$$

(9)

$${\mathrm{s}}_0={\left({\displaystyle \frac{\Delta \varphi \Delta \lambda }{\pi }}\right)}^{{\displaystyle \frac{1}{2}}}$$

(10)

where ${\mathrm{s}}_0$ is the innermost zone, ${\xi }_y={\displaystyle \frac{\partial \xi }{\partial y}}$, and ${\eta }_x={\displaystyle \frac{\partial \eta }{\partial x}}$.

It should be noted that the grid DOV calculated from the simulated data is only available for the marine region. However, since the gravity of the land area also affects the long-wave component of the marine gravity field, the DOV resolved by the EGM2008 model is used to fill the missing values in the land area before calculating the marine gravity anomaly. It can be seen that we did not use the remove–restore method to restore the long-wave component of the marine gravity field for the residual gravity anomalies [19], but instead used the total vertical deflection to invert the gravity anomalies. While both methods aim to recover the long-wave component of the gravity field, the remove–restore method is unable to effectively suppress noise in the simulation scenarios. On the other hand, using total vertical deflection for gravity anomaly inversion allows for a better assessment of the potential of utilizing spaceborne GNSS-R interferometric altimetry in simulation gravity field inversion.

Lastly, the gravity anomaly model EGM2008, released by the National Geospatial-Intelligence Agency (NGA), is employed as the true gravity anomaly values. These reference values are then compared with the gravity anomaly results calculated using the simulated data in a month. The EGM2008 model provides up to 2159 degrees and 2190 orders of spherical harmonic coefficients, which can be used to calculate gravity anomaly results with a spatial resolution of up to 5′ × 5′ using spherical harmonic functions, as shown in Figure 6. By using different maximum spherical harmonic coefficients for expansion orders, we can obtain gravity anomaly results with different grid resolutions and compare them with the simulated gravity anomaly results at corresponding resolutions. The relationship between the order of maximum spherical harmonic coefficients and spatial resolution can be described by Equation (11):

$$\Omega ={180}^{\circ }/n$$

(11)

where n is the maximum degree of the spherical harmonic coefficients used, and $\Omega$ is the corresponding resolution of the model.

4. Results and Discussion

4.1. Assessment of Monthly Marine Gravity Field Recovered a Single GNSS-R Satellite

To explore the feasibility of using spaceborne GNSS-R interferometric altimetry for monthly marine gravity anomaly inversion, this study first simulated GNSS-R SSH interferometric altimetry data based on one-month trajectories from the FY-3E satellite and then inverted the monthly global marine gravity anomaly within latitudes between ±80°. Based on our previous research, spaceborne GNSS-R has the advantages of rapid coverage and revisits, which can compensate for the poor accuracy of single altimetry and obtain high-precision global marine vertical deflections. As the accuracy of vertical deflections directly affects the accuracy of gravity anomaly inversion, it can be expected that altimetry accuracy and revisits are also important factors affecting the accuracy of marine gravity anomaly inversion using spaceborne GNSS-R interferometric altimetry. Altimetry accuracy depends on instrument performance and error correction accuracy, which can be demonstrated through simulations using PARIS IOD and Operational scenarios. When the time period is fixed to one month, the size of the grid used is the key factor affecting the number of revisits. Therefore, the accuracy of monthly gravity anomaly simulations was evaluated for grid sizes of 10′, 15′, 20′, 25′, and 30′ under both PARIS IOD and Operational scenarios. The results are shown in

Table 1. Evaluation of monthly gravity anomaly simulation for single PARS IOD and Operational satellite with different grid resolution.

Grid Resolution	Scenarios	Mean (mGal)	RMS (mGal)	Coverage Rate	Revisits
10′	IOD	−0.06	28.37	72.62%	2.34
	Operational	0.05	13.22
15′	IOD	−0.06	14.34	84.31%	5.27
	Operational	−0.07	8.09
20′	IOD	−0.08	8.98	89.83%	9.39
	Operational	−0.08	6.15
25′	IOD	−0.09	6.77	91.14%	14.68
	Operational	−0.09	5.36
30′	IOD	−0.10	5.70	91.91%	21.14
	Operational	−0.11	4.93

, which reflects the ability of spaceborne GNSS-R interferometric altimetry to invert monthly marine gravity anomaly.

According to Table 1, at a grid resolution of 10′, the inversion accuracy is poor in both the IOD and Operational scenarios, at 28.37 mGal and 13.22 mGal, respectively. The superior accuracy of the Operational scenario highlights its advantage over the IOD scenario, primarily due to the insufficient coverage rate (72.62%) and low average revisits (2.34 times) of a single spaceborne GNSS-R satellite at this resolution. However, in the Operational scenario, the inversion accuracy reaches within 10 mGal at a grid resolution of 15′ or finer, and within 5 mGal at a grid resolution of 30′, specifically 4.93 mGal. In the IOD scenario, the accuracy reaches within 10 mGal at a grid resolution of 20′ or finer. In conclusion, the accuracy of monthly gravity field inversion is significantly influenced by the accuracy of GNSS-R interferometric altimetry under the observation of a single satellite.

Furthermore, Guo et al. used CryoSat-2 conventional radar altimeter data to successfully invert the monthly gravity anomaly, achieving an accuracy of 5.063 mGal with a 60′ search radius [26]. Comparing this to the Operational scenario’s inversion accuracy of 4.93 mGal at a grid resolution of 30′, and the IOD scenario’s accuracy of 5.7 mGal, it can be seen that the inverted gravity field from spaceborne GNSS-R interferometric altimetry can achieve comparable accuracy at a finer spatial resolution.

Figure 7 shows the 30′ monthly marine gravity anomaly inverted using simulated interferometric altimetry data from a single GNSS-R satellite in the Operational scenario. Despite some gaps in the 30′ marine gravity field, most marine areas are covered, as shown in Figure 7. According to Table 1, the coverage rate at this resolution reaches 91.91%, with an average revisit rate of 21.14. Additionally, it can be observed that there are significantly fewer detection gaps in the Indian Ocean and Western Pacific regions compared to other areas. This is due to the presence of IGSO satellites from BeiDou Navigation Satellite System (BDS-2 and BDS-3) in these regions, resulting in a higher spatial coverage range for the BDS signals received by FY-3E in these areas [65].

Additionally, it is worth noting that the coverage rate and average revisits of spaceborne GNSS-R observations increase as the grid resolution decreases, resulting in improved monthly marine gravity field inversion accuracy (RMS). Furthermore, at a grid resolution of 25′, spaceborne GNSS-R achieves a coverage rate of over 90%, specifically 91.14%, with an average of 14.68 revisits. Compared to radar altimeters, spaceborne GNSS-R offers superior global coverage due to its ability to conduct multiple track observations over the ocean. This is more efficient than traditional radar altimeters, which can only observe at nadir points. Additionally, the wide-swath observations of spaceborne GNSS-R overcomes the limitations of repetitive orbits in non-geodetic measurements, a common issue with traditional radar altimeters. Therefore, spaceborne GNSS-R interferometric altimetry has a natural advantage in high spatial resolution time-variable gravity fields compared to radar altimeters.

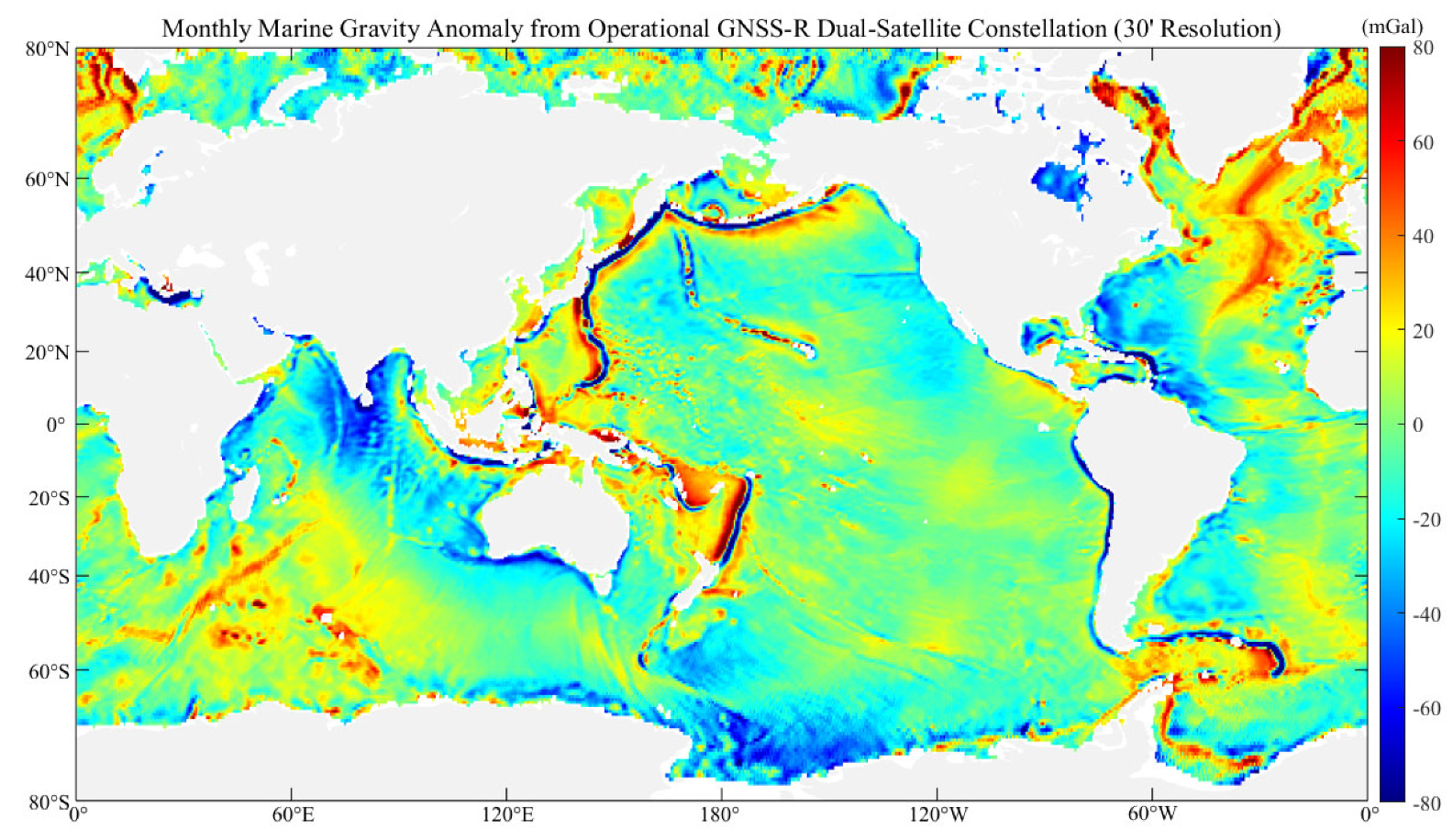
4.2. Assessment of Monthly Marine Gravity Field from Dual Satellite Constellation

Compared to radar altimeters, spaceborne GNSS-R payloads have the advantages of low power consumption, low weight, low cost, and low size, making them highly suitable for constellation formation [54]. Therefore, this study leverages the specular points trajectories of FY-3E and FY-3F to simulate GNSS-R interferometric altimetry data from a dual-satellite constellation for monthly marine gravity anomaly inversion. Still using a 30′ resolution as an example, Figure 8 presents the inversion results of the monthly marine gravity field in the Operational dual-satellite constellation scenario. Compared to single-satellite results, the dual-satellite constellation significantly reduces data gaps and enhances coverage.

Furthermore, the accuracy of the monthly marine gravity anomaly inversion in the dual-satellite GNSS-R interferometric altimetry constellation was evaluated, with results shown in

Table 2. Evaluation of monthly gravity anomaly simulation for PARS IOD and Operational dual-satellite constellation with different grid resolutions.

Grid Resolution	Scenarios	Mean (mGal)	RMS (mGal)	Coverage Rate	Revisits
10′	IOD	−0.04	20.35	87.83%	4.81
	Operational	0.04	9.73
15′	IOD	−0.07	9.87	91.45%	10.83
	Operational	−0.06	5.93
20′	IOD	−0.08	6.52	92.24%	19.28
	Operational	−0.08	4.82
25′	IOD	−0.09	5.22	92.46%	30.16
	Operational	−0.09	4.44
30′	IOD	−0.10	4.68	92.50%	43.43
	Operational	−0.10	4.27

. It can be observed that the dual-satellite constellation improves the coverage rate, revisits, and inversion accuracy of the monthly marine gravity anomaly compared to the single-satellite. At a 15′ grid resolution, the GNSS-R dual-satellite constellation observations can achieve a coverage rate of over 90%, reaching 91.45%, with average revisits of 10.83 times. The monthly marine gravity anomaly inversion accuracy is better than 10 mGal in both the IOD and Operational scenarios, reaching 9.87 mGal and 5.93 mGal, respectively. At a 20′ grid resolution, the accuracy in the Operational dual-satellite constellation scenario is better than 5 mGal, specifically 4.82 mGal. In the IOD scenario, at a 30′ grid resolution, the accuracy also surpasses 5 mGal, reaching 4.68 mGal. Compared to single-satellite observations, the dual-satellite constellation not only improves inversion accuracy but also narrows the accuracy gap between the IOD and Operational scenarios with increasing revisits. Therefore, GNSS-R constellations are crucial in improving the precision of monthly marine gravity anomaly inversion using spaceborne GNSS-R interferometric altimetry.

However, at 10′ grid resolution, the Operational monthly marine gravity anomaly accuracy significantly surpasses that of the IOD scenario, whether with a single satellite or a dual-satellite constellation. This is due to the fact that as spatial resolution increases, the reduction in average revisits is approximately proportional to the square of the grid resolution enhancement. For example, the average number of revisits at a 10′ grid is approximately one-fourth of that at a 20′ grid resolution. Therefore, despite high monthly revisits and accuracy of the monthly marine gravity field at a 20′ grid resolution, when inverting the monthly gravity field at higher resolutions like 10′ or 5′, the ability to enhance average revisits and improve inversion accuracy by increasing the number of networked satellites or reflection channels is limited. At this stage, the influence of altimetry accuracy becomes more pronounced.

5. Conclusions

This study utilized simulation to invert global monthly marine gravity anomalies using sea surface specular point trajectories from the FY-3E and FY-3F satellites over one month. The altimetry performance of PARIS IOD and Operational satellite GNSS-R interferometric altimetry missions, proposed by Martin-Neira, served as examples. The potential contribution of spaceborne GNSS-R interferometric altimetry to global monthly time-variable gravity field inversion was assessed based on coverage, revisit frequency, and inversion accuracy. The main conclusions are as follows:

• Spaceborne GNSS-R interferometric altimetry technology allows for high-resolution and precise inversion of monthly marine gravity anomaly, enhancing the spatial resolution of current time-variable gravity field products. In the single GNSS-R satellite Operational scenario, the accuracy of monthly marine gravity anomaly inversion on a 30′ grid can reach 4.93 mGal.
• Considering the low cost of constellation formation features of spaceborne GNSS-R technology, a dual-satellite constellation simulation experiment was conducted. The dual-satellite constellation improves the spatial resolution of time-variable gravity fields that can be inverted with the same level of accuracy. For example, in an Operational dual-satellite constellation scenario with a 5 mGal precision requirement for gravity field inversion, a dual-satellite constellation can invert a global monthly marine gravity anomaly on a 20′ grid, achieving an accuracy of 4.82 mGal.
• Increasing the number of revisits can compensate for the precision limitations of spaceborne GNSS-R interferometric altimetry, thereby enhancing the accuracy of the monthly marine gravity anomaly. It is worth noting that our study utilized only two GNSS-R satellites, each with fewer than four effective channels. Future improvements could involve increasing the number of satellites in the constellation or observation channels to enhance monthly coverage and average revisits.
• When inverting the global monthly marine gravity anomaly at a resolution finer than 10′, the precision of the inversion is significantly impacted by the accuracy of spaceborne GNSS-R interferometric altimetry. As the grid resolution improves, the need for high spatial resolution observations grows approximately proportional to the square of the grid resolution enhancement. Beyond a certain threshold, relying solely on increasing the number of satellites for network observations will also make it difficult to achieve sufficient revisits within a month. Therefore, enhancing the accuracy of spaceborne GNSS-R interferometric altimetry becomes particularly important at this stage.

In recent years, spaceborne GNSS-R technology has rapidly advanced and is expected to provide higher-quality sea surface altimetry data in the future. With advantages such as multi-track observations, low-cost constellation formation, and rapid global coverage and revisiting capabilities, it presents a promising tool for high-resolution monthly marine gravity anomaly inversion. This will complement the time-variable gravity field data from gravity satellites, advancing research and applications in Earth’s time-variable gravity fields.