Three-Dimensional Ice-Flow Recovery from Ascending–Descending DInSAR Pairs and Surface-Parallel Flow Hypothesis: A Simplified Implementation in SNAP Software
Abstract
1. Introduction
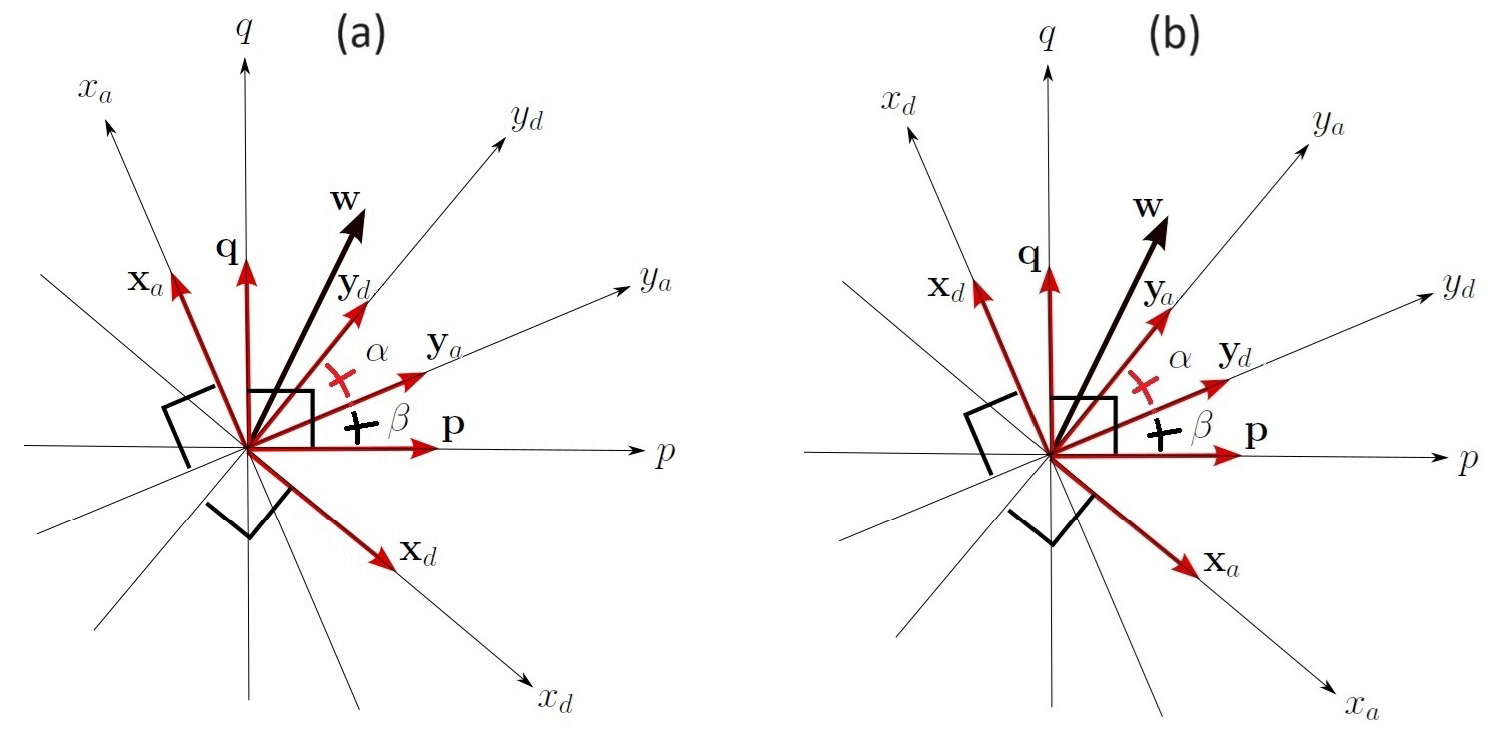
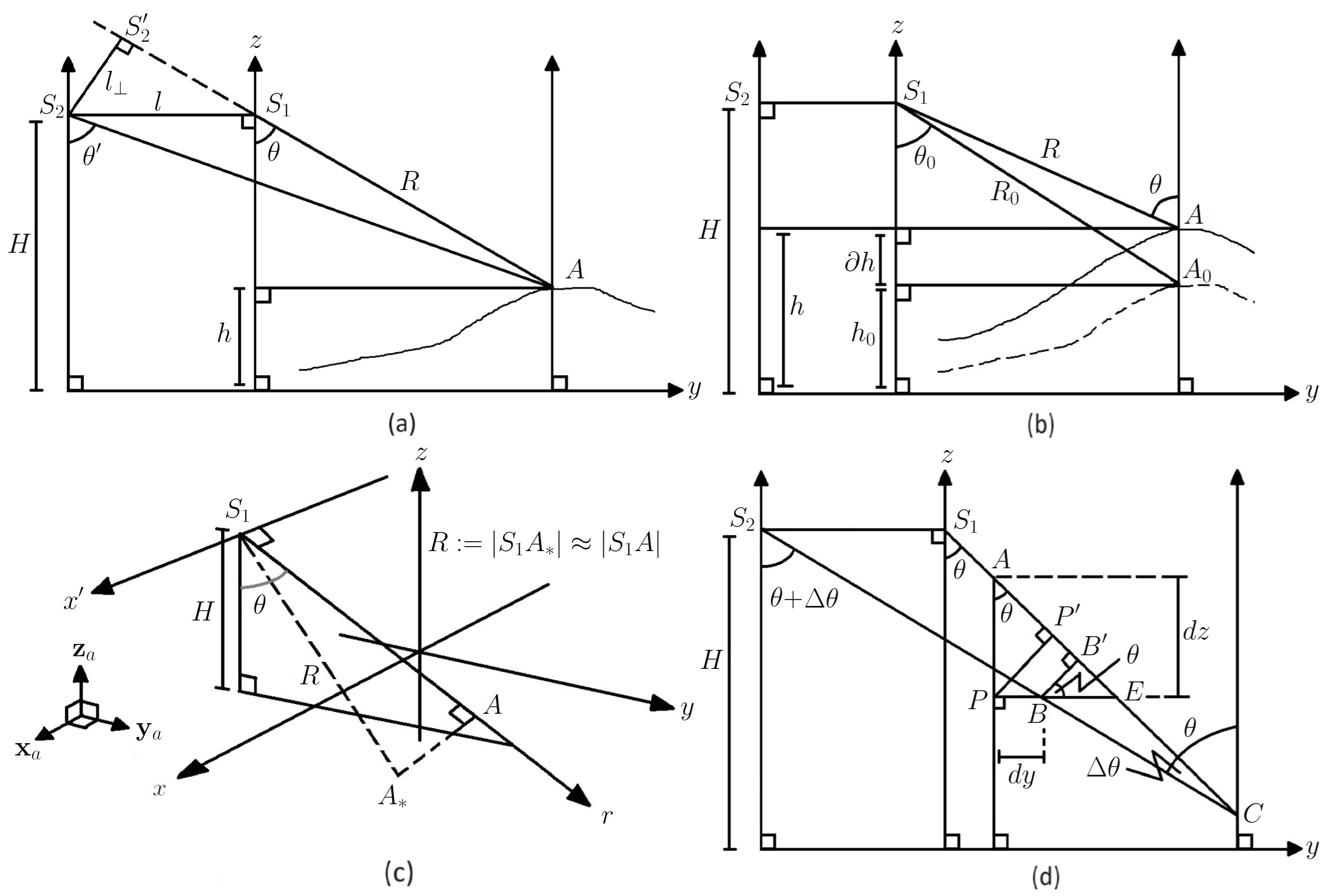
2. Horizontal Velocity Vector in Terms of Ascending and Descending Data
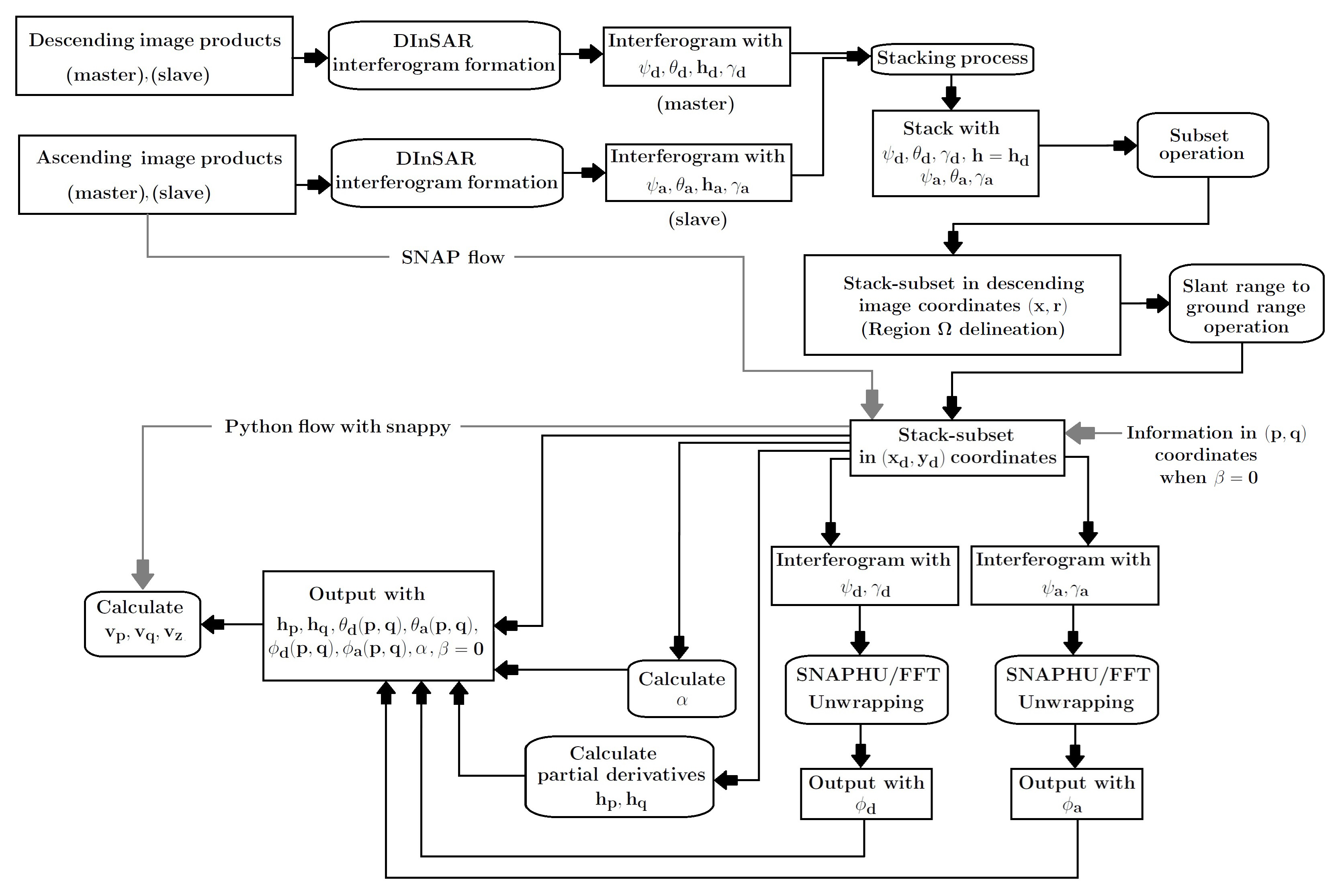
3. Method Proposed and Real Data Experiment: Velocity Vector Estimation
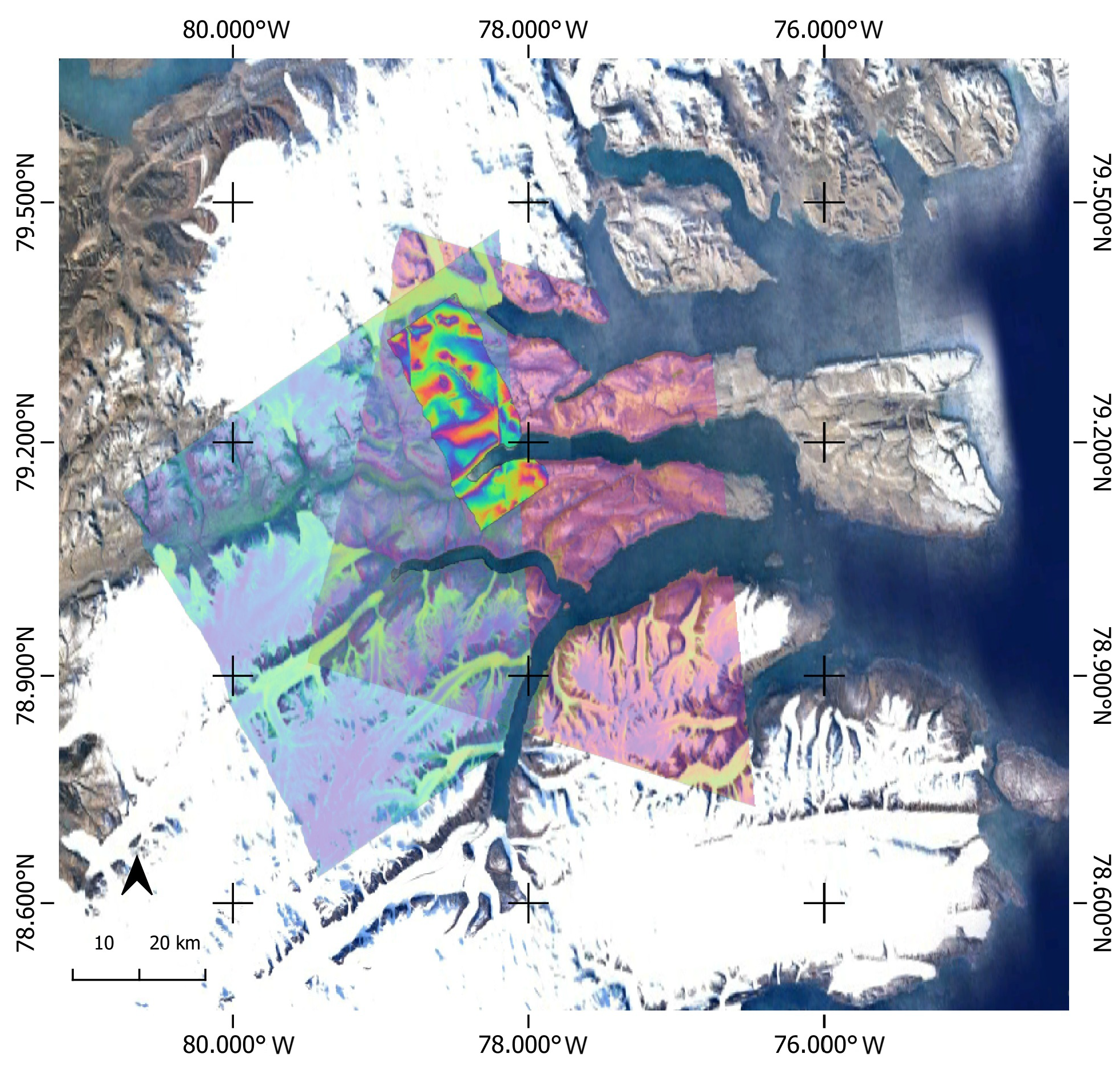
3.1. Materials and Methods
3.2. Estimated Angle and General Processing Flow Description
3.3. Velocity Components’ Estimation
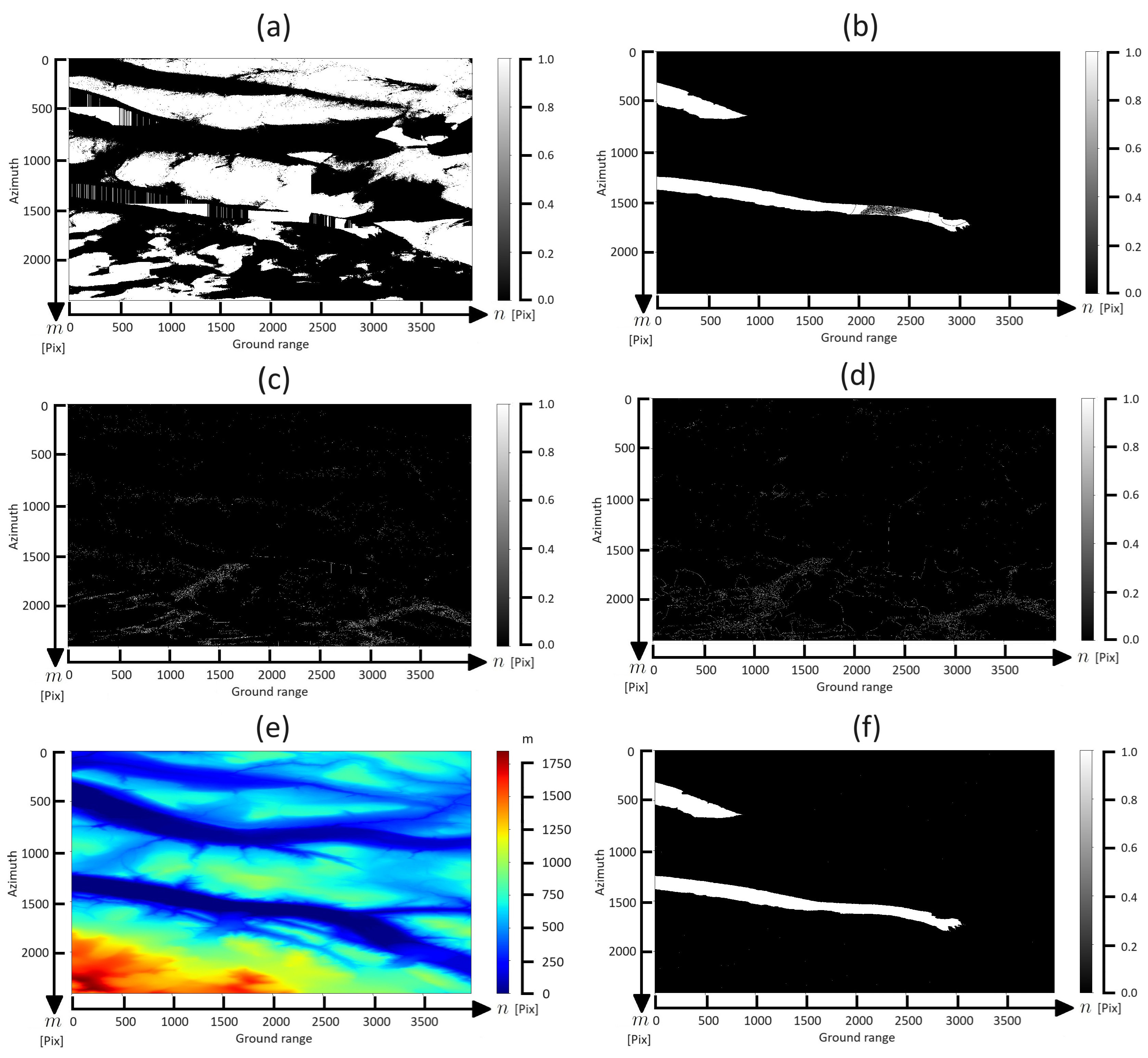
3.4. SPF Limitations and General SAR Data Details
4. Simulated Experiment: Accuracy Analysis
4.1. Synthetic Data Generation
4.2. Errors Achieved by Different Ascending–Descending Across-Track Angles
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAR | Synthetic aperture radar |
| JKF | Joughin, Kwok, and Fahnestock |
| SNAP | Sentinel application platform |
| InSAR | Interferometric SAR |
| DInSAR | Differential InSAR |
| DEM | Digital elevation model |
| SPF | Surface-parallel flow |
| LOS | Line of sight |
| IW | Interferometric wide swath |
| SLC | Single-look complex |
| SNAPHU | Statistical cost network flow algorithm for phase unwrapping |
| FFT | Fast Fourier transform |
Appendix A. SAR Data and Its Relation with LOS Displacement
Appendix A.1. DInSAR Signals and Their Deformation Phases
Appendix A.2. Deformation Phase and Its Relation with Ground Range and Vertical Displacements
Appendix B. Results Achieved from the Unwrapping Stage
References
- Hewitt, I.J.; Schoof, C. Models for polythermal ice sheets and glaciers. Cryosphere 2017, 11, 541–551. [Google Scholar] [CrossRef]
- Soto, V. Bedrock outcropping in the accumulation zone of the largest glacier in Mexico (Glaciar Norte of Citlaltépetl), as evidence of a possible accelerated extinction. J. Mt. Sci. 2023, 20, 338–354. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers; Academic Press: New York, NY, USA, 2010. [Google Scholar]
- Goldstein, R.M.; Engelhardt, H.; Kamb, B.; Frolich, R.M. Satellite radar interferometry for monitoring ice sheet motion: Application to an Antarctic ice stream. Science 1993, 262, 1525–1530. [Google Scholar] [PubMed]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar]
- Joughin, I.R.; Kwok, R.; Fahnestock, M.A. Interferometric estimation of three-dimensionl ice-flow using ascending and descending passes. IEEE Trans. Geosci. Remote Sens. 1998, 36, 25–37. [Google Scholar]
- Shi, Y.; Liu, G.; Wang, X.; Liu, Q.; Shum, C.; Bao, J.; Mao, W. Investigating the intra-annual dynamics of Kunlun glacier in The West Kunlun Mountains, China, from ascending and descending Sentinel-1 SAR observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1272–1282. [Google Scholar]
- Whitehead, K.; Moorman, B.J.; Wainstein, P. Determination of variations in glacier surface movements through high resolution interferometry; Bylot Island, Canada. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. II–230–II–233. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, C.; Dongchen, E.; Wang, Z. A baseline-combination method for precise estimation of ice motion in Antarctica. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5790–5797. [Google Scholar]
- Yang, Z.; Li, Z.; Zhu, J.; Preusse, A.; Hu, J.; Feng, G.; Yi, H.; Papst, M. An alternative method for estimating 3-D large displacements of mining areas from a single SAR amplitude pair using offset tracking. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3645–3656. [Google Scholar]
- Kumari, S.; Ramsankaran, R.; Walker, J.P. Impact of window size in remote sensing based glacier feature tracking- a study on Chhota Shigri Glacier, Western Himalayas, India. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 4175–4178. [Google Scholar] [CrossRef]
- Samsonov, S.; Dille, A.; Dewitte, O.; Kervyn, F.; d’Oreye, N. Satellite interferometry for mapping surface deformation time series in one, two and three dimensions: A new method illustrated on a slow-moving landslide. Eng. Geol. 2019, 266, 105471. [Google Scholar]
- Chang, Z.; Wang, Y.; Qian, S.; Zhu, J.; Wang, W.; Liu, X.; Yu, J. An approach for retrieving complete three-dimensional ground displacement components from two parallel-track InSAR measurements. J. Geod. 2020, 94, 1–12. [Google Scholar]
- Murray, K.D.; Lohman, R.B.; Kim, J.; Holt, W.E. An alternative approach for constraining 3D-displacements with InSAR, applied to a fault-bounded groundwater entrainment field in California. J. Geophys. Reseacrh: Solid Earth 2021, 126, e2020JB021137. [Google Scholar]
- Andersen, J.K.; Boncori, J.P.M.; Ander, K. Connectivity approach for detecting unreliable DInSAR ice velocity measurements. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar]
- Ren, K.; Yao, X.; Li, R.; Zhou, Z.; Yao, C.; Jiang, S. 3D displacement and deformation mechanism of deep-seated gravitational slope deformation revealed by InSAR: A case study in Wudongde Reservoir, Jinsha River. Landslides 2022, 19, 2159–2175. [Google Scholar]
- Kumar, V.; Hogda, K.A.; Larsen, Y. Across-track and multi-aperture InSAR for 3-D glacier velocity estimation of the Siachen Glacier. Remote Sens. 2023, 15, 4794. [Google Scholar] [CrossRef]
- Sánchez-Gámez, P.; Navarro, F.J. Glacier surface velocity retrieval using D-InSAR and offset tracking techniques applied to ascending and descending passes of Sentinel-1 data for Southern Ellesmere Ice Caps, Canadian Arctic. Remote Sens. 2017, 9, 442. [Google Scholar] [CrossRef]
- Braun, A.; Veci, L. Sentinel-1 Toolbox: TOPS Interferometry Tutorial; ESA-SkyWatch Space Applications Inc.: Online, 2021; Available online: https://sentinel.esa.int/web/sentinel/toolboxes/sentinel-1/tutorials (accessed on 3 March 2025).
- Fahrland, E.; Paschko, H.; Jacob, P.; Kahabka, H. Copernicus DEM Product Handbook; AIRBUS Defence and Space: Online, 2022. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar]
- Sharma, A. Getting Started with SNAP Toolbox in Python; Towards Data Science: Online, 2020; Available online: https://medium.com/towards-data-science/getting-started-with-snap-toolbox-in-python-89e33594fa04 (accessed on 3 March 2025).
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar]
- Téllez-Quiñones, A.; Chi-Couoh, D.B.; Gamboa-Salazar, L.B.; Legarda-Sáenz, R.; Valdiviezo-Navarro, J.C.; León-Rodríguez, M. Two-dimensional phase unwrapping based on Fourier transforms and the Yukawa potential spectrum. J. Opt. Soc. Am. A 2023, 40, 692–702. [Google Scholar]
- Hanssen, R.F. Radar Interferometry, Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Mohr, J.J.; Reeh, N.; Madsen, S.N. Three-dimensional glacial flow and surface elevation measured with radar interferometry. Nature 1998, 391, 273–276. [Google Scholar]
- Straozzi, T.; Luckman, A.; Murray, T.; Werner, C.L. Glacier motion estimation using offset-tracking procedures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2384–2391. [Google Scholar]
- Bailo, D.; Paciello, R.; Michalek, J.; Cocco, M.; Freda, C.; Jefferey, K.; Atakan, K. The EPOS multi-disciplinary Data Portal for integrated access to solid Earth science datasets. Sci Data 2023, 10, 784. [Google Scholar] [CrossRef] [PubMed]
- Fallourd, R.; Vernier, F.; Yan, Y.; Trouve, E.; Bolon, P.; Nicolas, J.-M. Alpine glacier 3D displacement derived from ascending and descending TerraSAR-X images on Mont-Blanc test site. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A Review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Téllez-Quiñones, A.; Salazar-Garibay, A.; Valdiviezo-Navarro, J.C.; Hernandez-Lopez, F.; Silván-Cárdenas, J.L. DInSAR method applied to dual-pair interferograms with Sentinel-1 data: A study case on inconsistent unwrapping outputs. Int. J. Remote Sens. 2020, 41, 4662–4681. [Google Scholar]
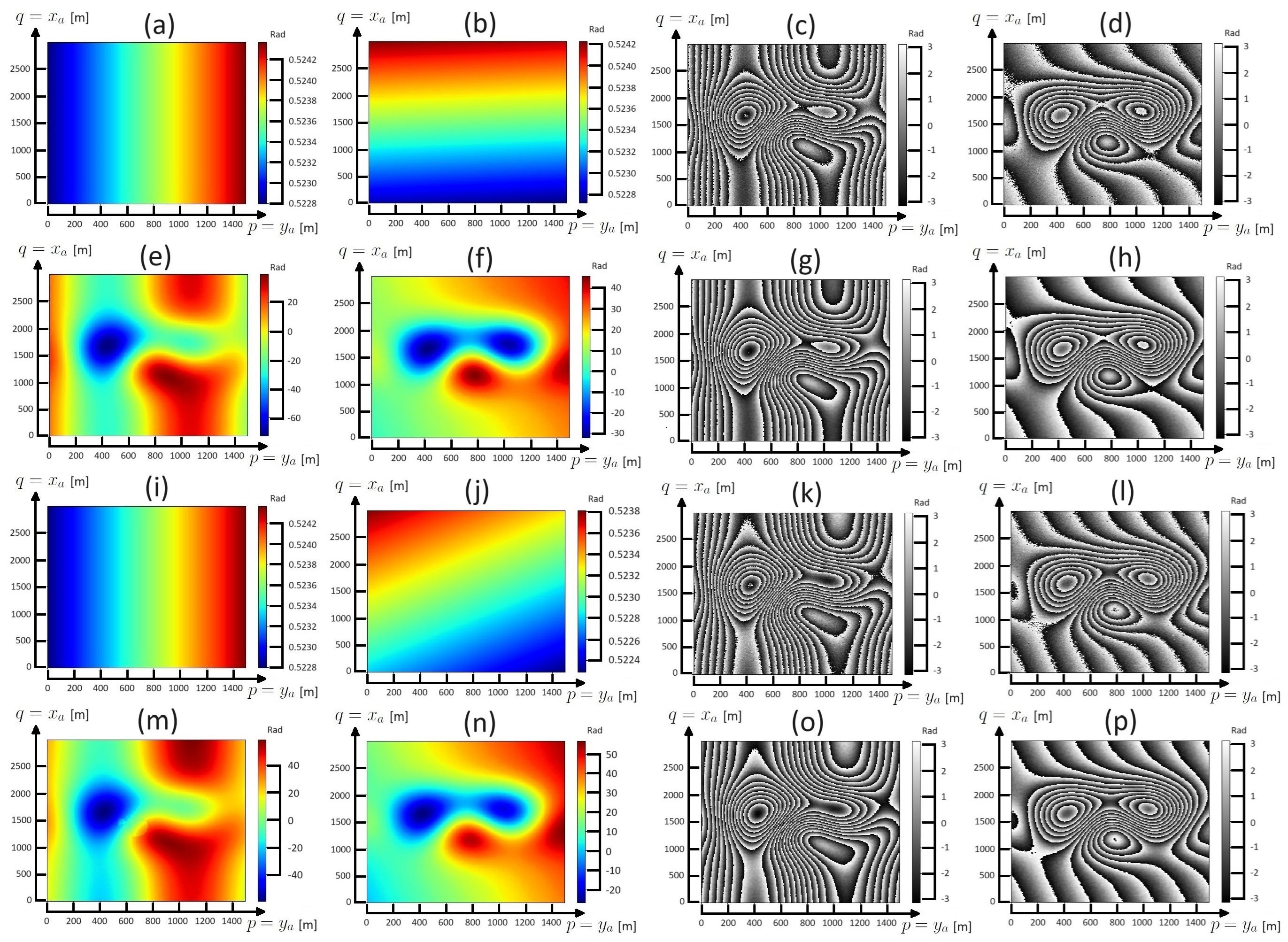
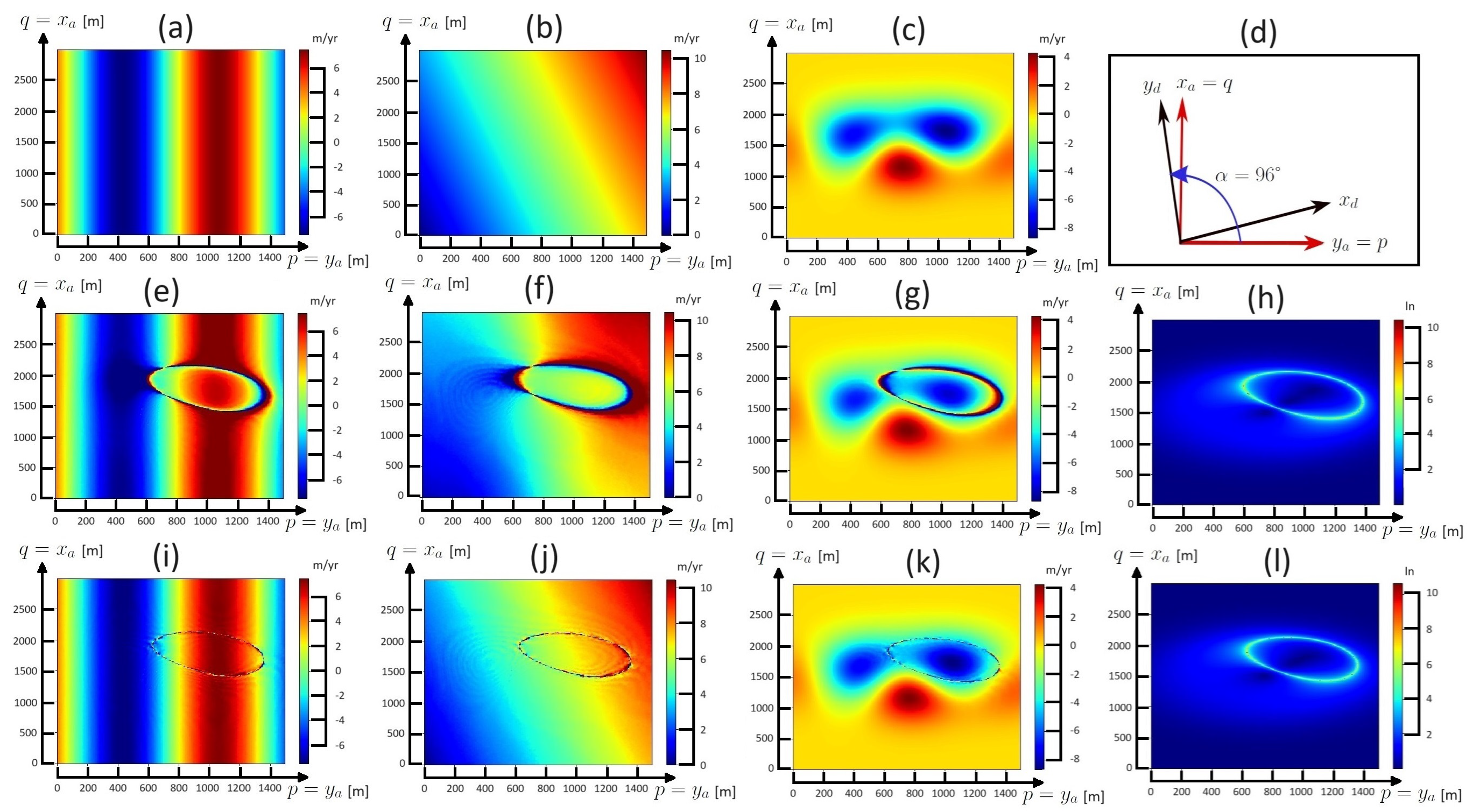

| JKF ← Prop. | JKF ← Prop. | JKF ← Prop. | JKF ← Prop. |
|---|---|---|---|
| Interferogram | Acquisition Date | Baseline | Sub-Swath and Bursts |
|---|---|---|---|
| 29/Feb/2016 (descending) | 30.7 [m] | IW2-Bursts 7-8-9 | |
| 12/Mar/2016 (descending) | |||
| 04/Mar/2016 (ascending) | 47.06 [m] | IW1-Bursts 4-5-6 | |
| 16/Mar/2016 (ascending) |
| Interferogram | Acquisition Date | Baseline | Sub-Swath and Bursts |
|---|---|---|---|
| 22/Jan/2017 (ascending) | 16.84 [m] | IW1-Bursts 4-5-6 | |
| 03/Feb/2017 (ascending) | |||
| 30/Jan/2017 (descending) | 92.56 [m] | IW2-Bursts 7-8-9 | |
| 11/Feb/2017 (descending) |
| Equation | ||||||
|---|---|---|---|---|---|---|
| 96 | Equation (15) | 0.1518 | 0.1161 | 0.2250 | 0.0047 | 0.0075 |
| Equation (11) | 0.0424 | 0.0323 | 0.0646 | |||
| 100 | Equation (15) | 0.2027 | 0.1557 | 0.2980 | 0.0073 | 0.0045 |
| Equation (11) | 0.0356 | 0.0274 | 0.0562 | |||
| 135 | Equation (15) | 0.4741 | 0.3098 | 0.5981 | 0.0076 | 0.0039 |
| Equation (11) | 0.0259 | 0.0252 | 0.0597 |
| Equation | ||||||
|---|---|---|---|---|---|---|
| 96 | Equation (15) | 0.1311 | 0.1123 | 0.2125 | 0.0425 | 0.0116 |
| Equation (11) | 0.0913 | 0.0664 | 0.1296 | |||
| 100 | Equation (15) | 0.3079 | 0.1918 | 0.4168 | 0.1321 | 0.0252 |
| Equation (11) | 0.2097 | 0.1289 | 0.2956 | |||
| 135 | Equation (15) | 0.5228 | 0.3199 | 0.6366 | 0.0982 | 0.0067 |
| Equation (11) | 0.1725 | 0.1129 | 0.2835 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Téllez-Quiñones, A.; Salazar-Garibay, A.; Cruz-Sánchez, B.I.; Carlos-Martínez, H.; Valdiviezo-Navarro, J.C.; Soto, V. Three-Dimensional Ice-Flow Recovery from Ascending–Descending DInSAR Pairs and Surface-Parallel Flow Hypothesis: A Simplified Implementation in SNAP Software. Remote Sens. 2025, 17, 1168. https://doi.org/10.3390/rs17071168
Téllez-Quiñones A, Salazar-Garibay A, Cruz-Sánchez BI, Carlos-Martínez H, Valdiviezo-Navarro JC, Soto V. Three-Dimensional Ice-Flow Recovery from Ascending–Descending DInSAR Pairs and Surface-Parallel Flow Hypothesis: A Simplified Implementation in SNAP Software. Remote Sensing. 2025; 17(7):1168. https://doi.org/10.3390/rs17071168
Chicago/Turabian StyleTéllez-Quiñones, Alejandro, Adán Salazar-Garibay, Beatriz I. Cruz-Sánchez, Hugo Carlos-Martínez, Juan C. Valdiviezo-Navarro, and Victor Soto. 2025. "Three-Dimensional Ice-Flow Recovery from Ascending–Descending DInSAR Pairs and Surface-Parallel Flow Hypothesis: A Simplified Implementation in SNAP Software" Remote Sensing 17, no. 7: 1168. https://doi.org/10.3390/rs17071168
APA StyleTéllez-Quiñones, A., Salazar-Garibay, A., Cruz-Sánchez, B. I., Carlos-Martínez, H., Valdiviezo-Navarro, J. C., & Soto, V. (2025). Three-Dimensional Ice-Flow Recovery from Ascending–Descending DInSAR Pairs and Surface-Parallel Flow Hypothesis: A Simplified Implementation in SNAP Software. Remote Sensing, 17(7), 1168. https://doi.org/10.3390/rs17071168






