Harnessing InSAR and Machine Learning for Geotectonic Unit-Specific Landslide Susceptibility Mapping: The Case of Western Greece
Abstract
1. Introduction
2. Materials and Methods
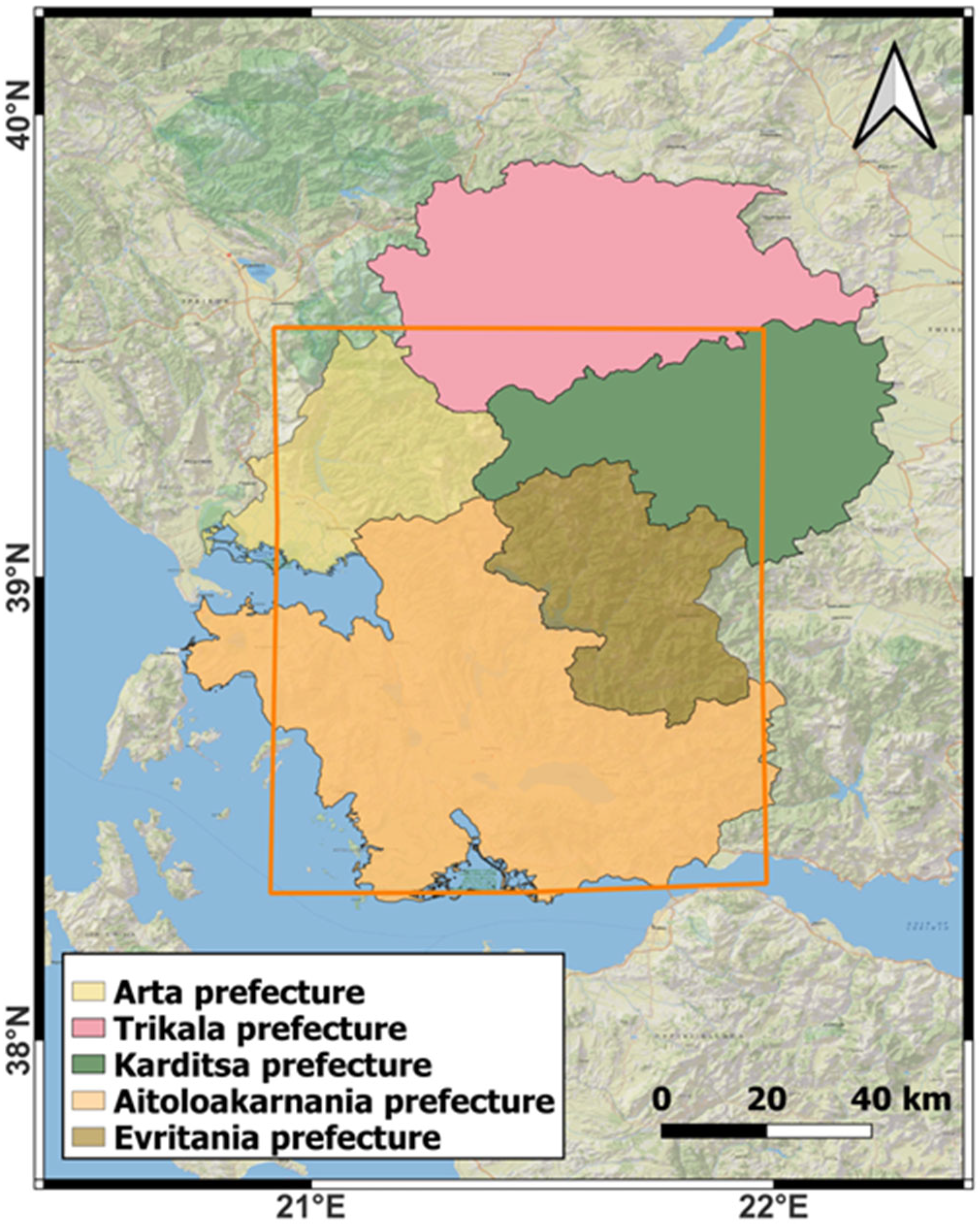
2.1. The Study Area
2.2. Landslide Inventory
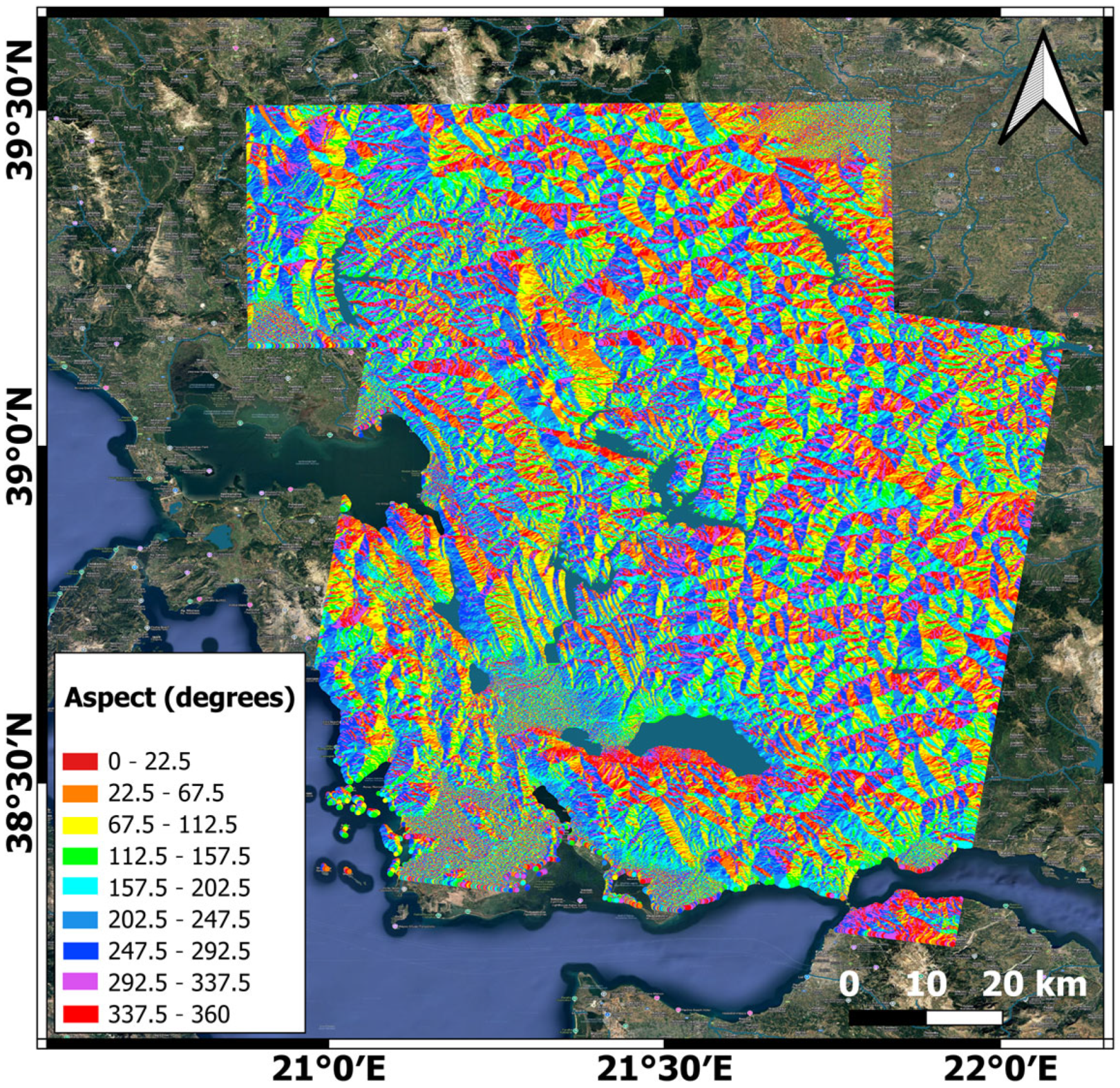
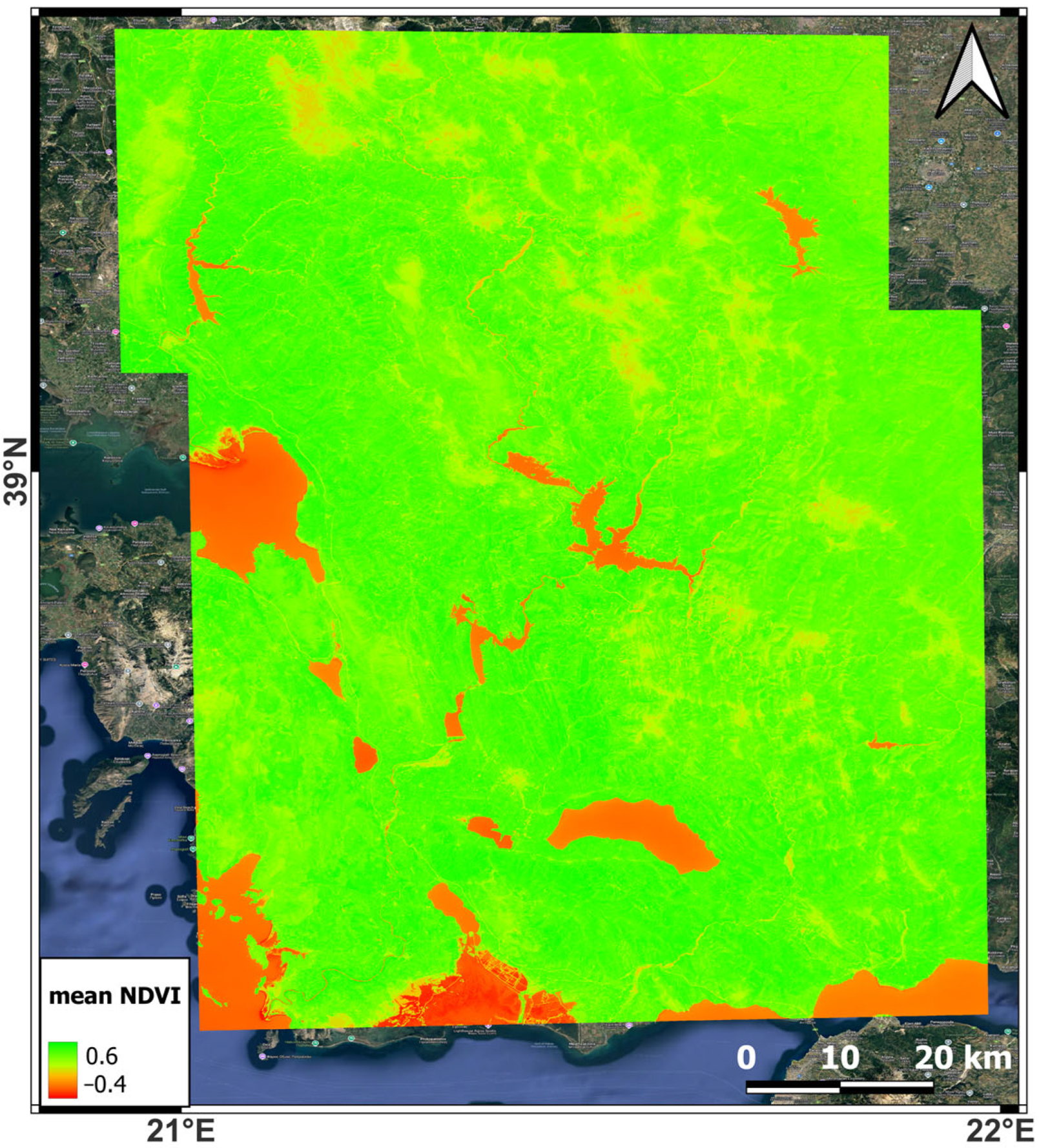
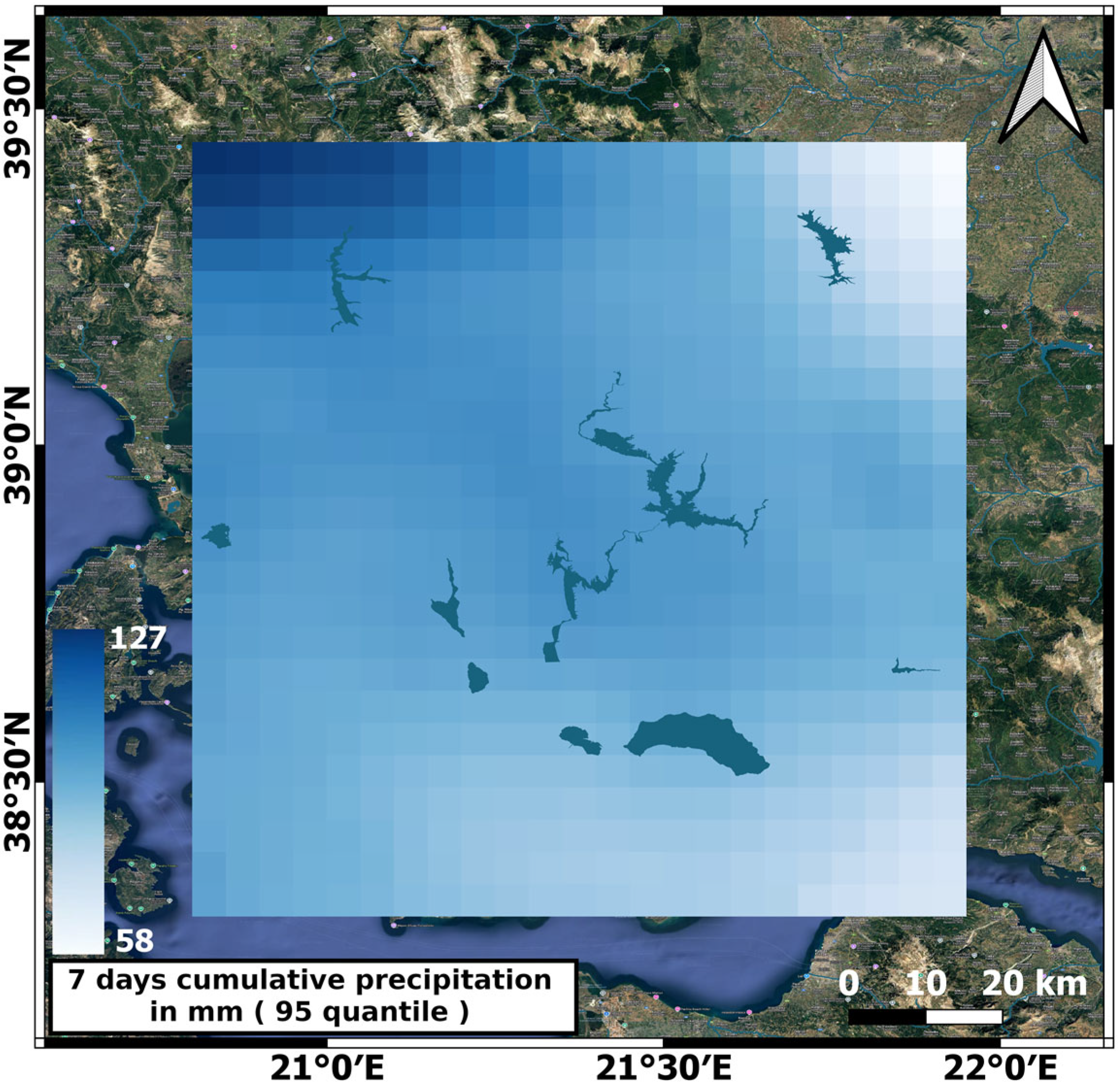
2.3. Landslide Causal Factors
2.4. Machine Learning Pipeline
2.4.1. Problem Formulation and Algorithm
2.4.2. Feature Selection and Preprocessing
2.4.3. Dataset Split for Training, Validation and Testing, and Hyperparameterization
2.4.4. Train/Validation Test Datasets Visualization
3. Results
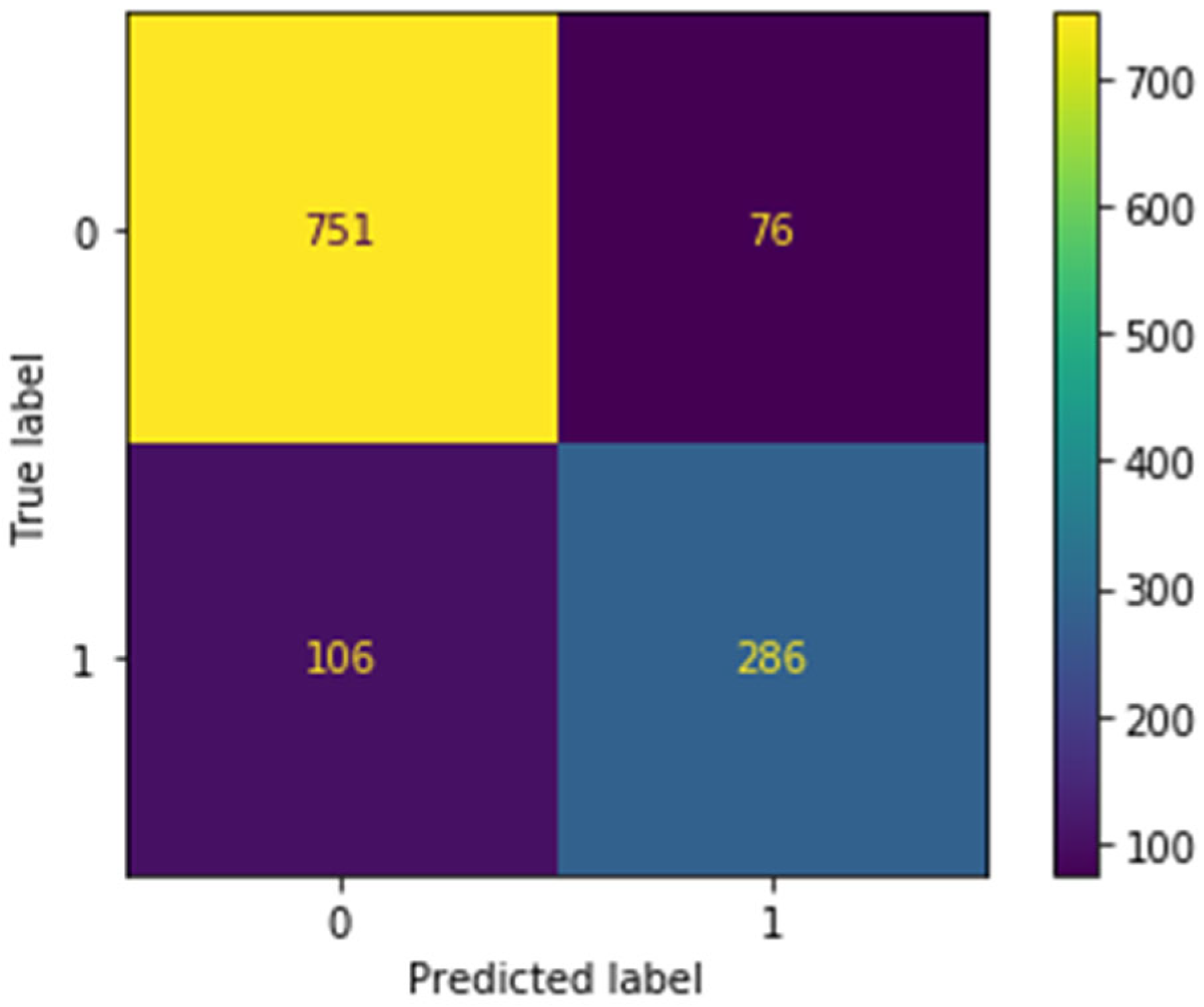
3.1. Results for Main Split Setting
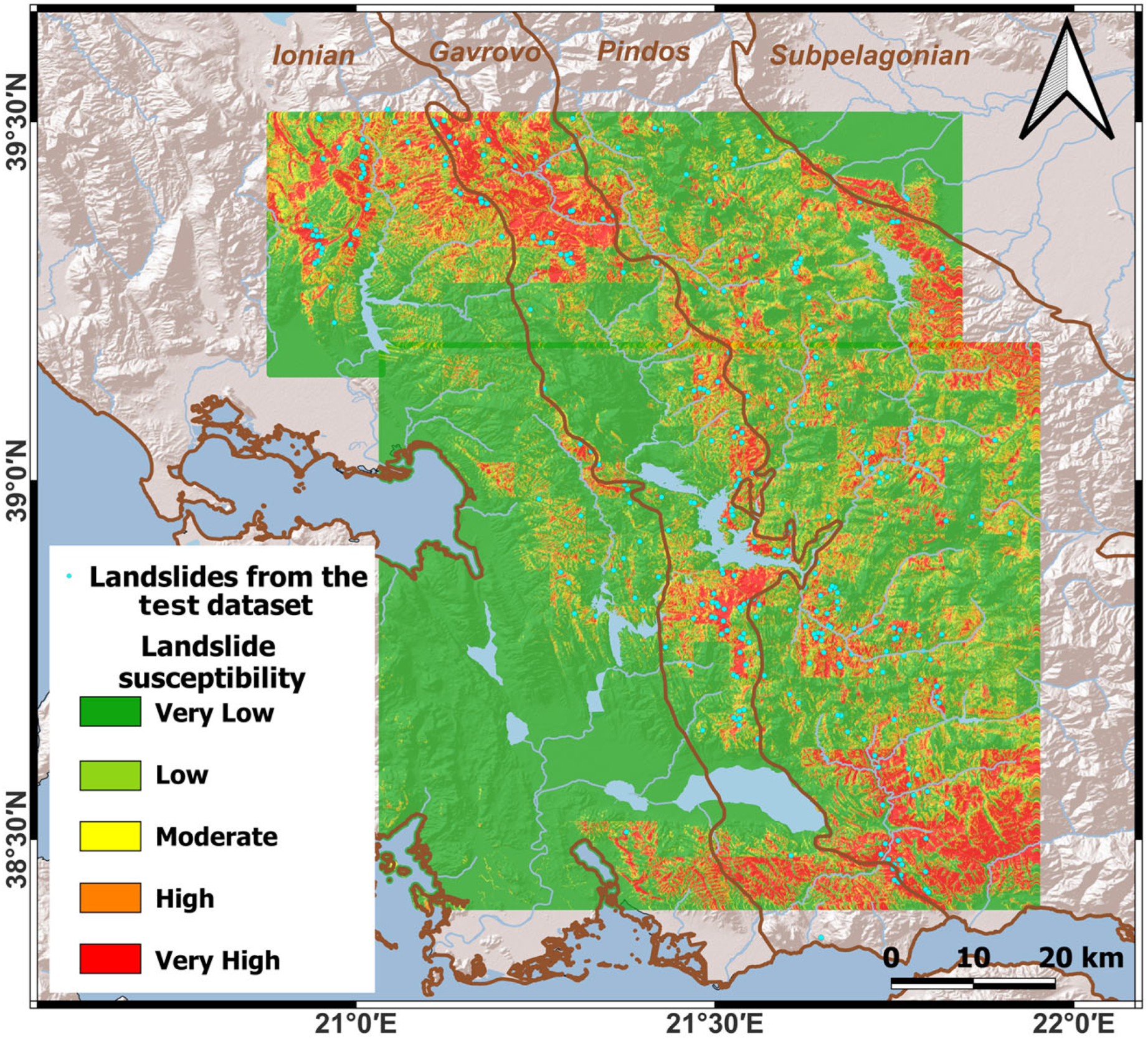
3.2. Results for Test Split in Remote Area
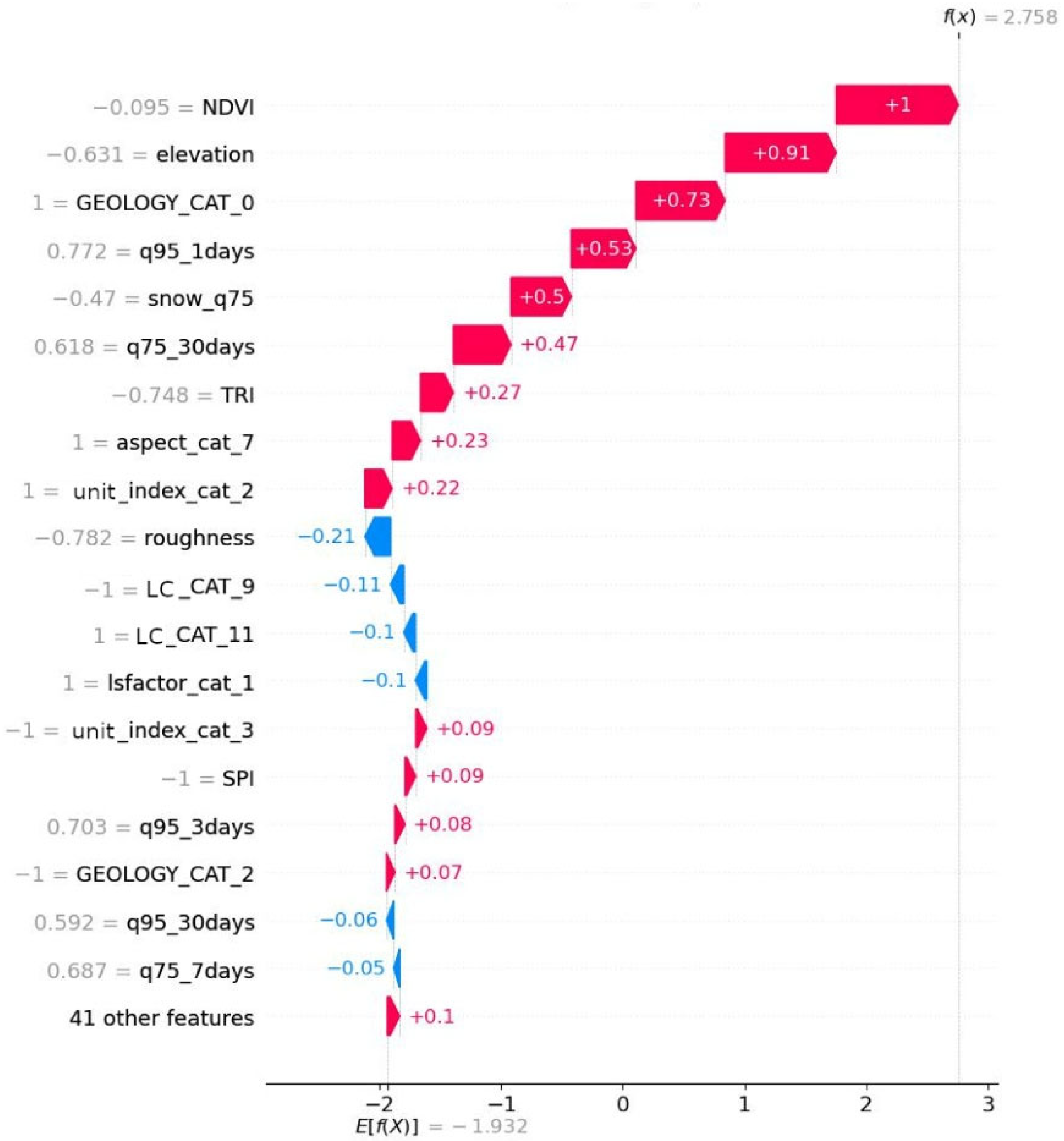
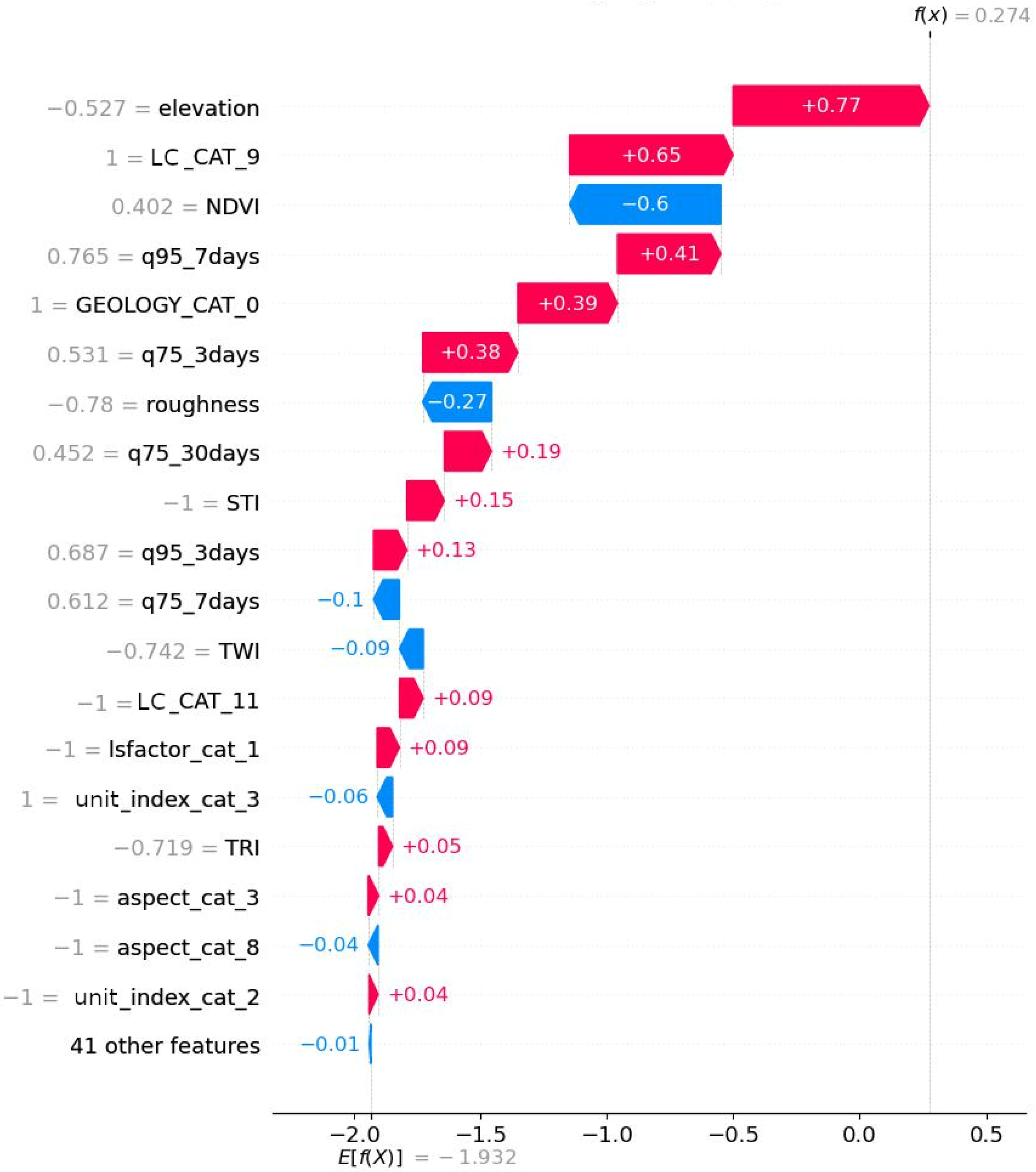
3.3. SHAP Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Slope Value | Class | Model Feature |
|---|---|---|
| 0 ≤ x ≤ 20° | 1 | slope_cat_1 |
| 20° < x ≤ 40° | 2 | slope_cat_2 |
| 40° < x ≤ 60° | 3 | slope_cat_3 |
| 60° < x ≤ 80° | 4 | slope_cat_4 |
| 80° < x | 5 | slope_cat_5 |
| Aspect Value | Class | Aspect of Elevation | Model Feature |
|---|---|---|---|
| x = −1 | 1 | Flat | aspect_cat_1 |
| 0° ≤ x ≤ 22.5° | 2 | North | aspect_cat_2 |
| 22.5° < x ≤ 67.5° | 3 | Northeast | aspect_cat_3 |
| 67.5° < x ≤ 112.5° | 4 | East | aspect_cat_4 |
| 112.5° < x ≤ 157.5° | 5 | Southeast | aspect_cat_5 |
| 157.5° < x ≤ 202.5° | 6 | South | aspect_cat_6 |
| 202.5° < x ≤ 247.5° | 7 | Southwest | aspect_cat_7 |
| 247.5° < x ≤ 292.5° | 8 | West | aspect_cat_8 |
| 292.5° < x ≤ 337.5° | 9 | Northwest | aspect_cat_9 |
| 337.5° < x ≤ 360° | 2 | North | aspect_cat_2 |
| Geology Category | Class | Model Feature |
|---|---|---|
| Flysch | 0 | GEOLOGY_CAT_0 |
| Alluvial deposits | 1 | GEOLOGY_CAT_1 |
| Limestones | 2 | GEOLOGY_CAT_2 |
| Fine-grained igneous rock Mesozoic | 3 | GEOLOGY_CAT_3 |
| Schist-Cherts | 4 | GEOLOGY_CAT_4 |
| LS Factor | Class | Model Feature |
|---|---|---|
| 0 ≤ x ≤ 4 | 1 | lsfactor_cat_1 |
| 5 ≤ x ≤ 8 | 2 | lsfactor_cat_2 |
| 9 ≤ x ≤ 12 | 3 | lsfactor_cat_3 |
| 13 ≤ x ≤ 16 | 4 | lsfactor_cat_4 |
| 17 ≤ x ≤ 20 | 5 | lsfactor_cat_5 |
| 21 ≤ x ≤ 24 | 6 | lsfactor_cat_6 |
| 25 ≤ x ≤ 28 | 7 | lsfactor_cat_7 |
| 29 ≤ x | 8 | lsfactor_cat_8 |
| Corine LU/LC Level 2 | Code 1 | Model Feature |
|---|---|---|
| Heterogeneous agricultural areas | 9 | LC_CAT_9 |
| Forests | 10 | LC_CAT_10 |
| Open spaces with little or no vegetation | 13 | LC_CAT_13 |
| Scrub and/or herbaceous vegetation associations | 11 | LC_CAT_11 |
| Pastures | 8 | LC_CAT_8 |
| Water bodies | 16 | LC_CAT_16 |
| Non-irrigated arable land | 4 | LC_CAT_4 |
| Industrial, commercial, and transport units | 1 | LC_CAT_1 |
| Permanently irrigated land | 5 | LC_CAT_5 |
| Permanent crops | 7 | LC_CAT_7 |
| Urban fabric | 0 | LC_CAT_0 |
| Inland wetlands | 14 | LC_CAT_14 |
| Mine, dump, and construction sites | 3 | LC_CAT_3 |
| Coastal wetlands | 15 | LC_CAT_15 |
| Rice fields | 6 | LC_CAT_6 |
| Geotectonic Unit | Category 1 | Model Feature |
|---|---|---|
| Gavrovo | 2 | unit_index_cat_2 |
| Ionios | 3 | unit_index_cat_3 |
| Pindos | 8 | unit_index_cat_8 |
Appendix B



References
- Koukis, G.; Sabatakakis, N.; Nikolaou, N.; Loupasakis, C. Landslide hazard zonation in Greece. In Landslides; Springer: Berlin/Heidelberg, Germany, 2005; pp. 291–296. [Google Scholar]
- Koukouvelas, I.; Nikolakopoulos, K.; Zygouri, V.; Kyriou, A. Post-seismic monitoring of cliff mass wasting using an unmanned aerial vehicle and field data at Egremni, Lefkada Island, Greece. Geomorphology 2020, 367, 107306. [Google Scholar] [CrossRef]
- El Kamali, M.; Papoutsis, I.; Loupasakis, C.; Abuelgasim, A.; Omari, K.; Kontoes, C. Monitoring of land surface subsidence using persistent scatterer interferometry techniques and ground truth data in arid and semi-arid regions, the case of Remah, UAE. Sci. Total Environ. 2021, 776, 145946. [Google Scholar] [CrossRef] [PubMed]
- Alatza, S.; Papoutsis, I.; Paradissis, D.; Kontoes, C.; Papadopoulos, G.A. Multi-Temporal InSAR Analysis for Monitoring Ground Deformation in Amorgos Island, Greece. Sensors 2020, 20, 338. [Google Scholar] [CrossRef]
- Sykioti, O.; Kontoes, C.; Elias, P.; Briole, P.; Sachpazi, M.; Paradissis, D.; Kotsis, I. Ground deformation at Nisyros volcano (Greece) detected by ERS-2 SAR differential interferometry. Int. J. Remote Sens. 2003, 24, 183–188. [Google Scholar] [CrossRef]
- Kontoes, C.; Loupasakis, C.; Papoutsis, I.; Alatza, S.; Poyiadji, E.; Ganas, A.; Psychogyiou, C.; Kaskara, M.; Antoniadi, S.; Spanou, N. Landslide Susceptibility Mapping of Central and Western Greece, Combining NGI and WoE Methods, with Remote Sensing and Ground Truth Data. Land 2021, 10, 402. [Google Scholar] [CrossRef]
- Nefros, C.; Alatza, S.; Loupasakis, C.; Kontoes, C. Persistent Scatterer Interferometry (PSI) Technique for the Identification and Moni-toring of Critical Landslide Areas in a Regional and Mountainous Road Network. Remote Sens. 2023, 15, 1550. [Google Scholar] [CrossRef]
- Aslan, G.; Foumelis, M.; Raucoules, D.; De Michele, M.; Bernardie, S.; Cakir, Z. Landslide Inventory Mapping and Monitoring Using Persistent Scatterer Interferometry (PSI) Technique in the French Alps. Remote Sens. 2020, 12, 1305. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Y.; Ge, D.; Deng, Y.; Wang, R. InSAR Study of Landslides: Early Detection, Three-Dimensional, and Long-Term Surface Displacement Estimation—A Case of Xiaojiang River Basin, China. Remote Sens. 2022, 14, 1759. [Google Scholar] [CrossRef]
- Ohki, M.; Abe, T.; Tadono, T.; Shimada, M. Landslide detection in mountainous forest areas using polarimetry and interferometric coherence. Earth Planets Space 2020, 72, 67. [Google Scholar] [CrossRef]
- Tzouvaras, M.; Danezis, C.; Hadjimitsis, D.G. Small Scale Landslide Detection Using Sentinel-1 Interferometric SAR Coherence. Remote Sens. 2020, 12, 1560. [Google Scholar] [CrossRef]
- Ma, P.; Cui, Y.; Wang, W.; Lin, H.; Zhang, Y.; Zheng, Y. Landslide Movement Monitoring with InSAR Technologies. In Landslides; IntechOpen: London, UK, 2022. [Google Scholar] [CrossRef]
- Hussain, S.; Pan, B.; Afzal, Z.; Ali, M.; Zhang, X.; Shi, X.; Ali, M. Landslide detection and inventory updating using the time-series InSAR approach along the Karakoram Highway, Northern Pakistan. Sci. Rep. 2023, 13, 7485. [Google Scholar] [CrossRef]
- Smail, T.; Abed, M.; Mebarki, A.; Lazecky, M. Earthquake-induced landslide monitoring and survey by means of InSAR. Nat. Hazards Earth Syst. Sci. 2022, 22, 1609–1625. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Handwerger, A.L.; Agram, P.; Kirschbaum, D.B. InSAR-based detection method for mapping and monitoring slow-moving landslides in remote regions with steep and mountainous terrain: An application to Nepal. Remote Sens. Environ. 2020, 249, 111983. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Y.; Ge, D.; Deng, Y.; Wang, R. Insar Driven Landslide Detection and Monitoring Based on Small Baseline Sets: A Case Study of Jinsha River Valley (Dongchuan Section). In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 8388–8391. [Google Scholar] [CrossRef]
- Ma, Z.; Mei, G.; Piccialli, F. Machine learning for landslides prevention: A survey. Neural Comput. Appl. 2021, 33, 10881–10907. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support Vector Machines for Landslide Susceptibility Mapping: The Staffora River Basin Case Study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S.-M.; Jung, H.-S. A Support Vector Machine for Landslide Susceptibility Mapping in Gangwon Province, Ko-rea. Sustainability 2017, 9, 48. [Google Scholar] [CrossRef]
- Xu, K.; Zhao, Z.; Chen, W.; Ma, J.; Liu, F.; Zhang, Y.; Ren, Z. Comparative study on landslide susceptibility mapping based on different ratios of training samples and testing samples by using RF and FR-RF models. Nat. Hazards Res. 2024, 4, 62–74. [Google Scholar] [CrossRef]
- Park, S.; Kim, J. Landslide Susceptibility Mapping Based on Random Forest and Boosted Regression Tree Models, and a Comparison of Their Performance. Appl. Sci. 2019, 9, 942. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A Comprehensive Assessment of XGBoost Algorithm for Landslide Susceptibility Mapping in the Upper Basin of Ataturk Dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Badola, S.; Varun, M.; Surya, P. Landslide susceptibility mapping using XGBoost machine learning method. In Proceedings of the 2023 International Conference on Machine Intelligence for GeoAnalytics and Remote Sensing (MIGARS), Hyderabad, India, 27–29 January 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Hussain, M.A.; Chen, Z.; Zheng, Y.; Shoaib, M.; Shah, S.U.; Ali, N.; Afzal, Z. Landslide Susceptibility Mapping Using Machine Learning Algorithm Validated by Persistent Scatterer In-SAR Technique. Sensors 2022, 22, 3119. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Predictive Performances of Ensemble Machine Learning Algorithms in Landslide Susceptibility Mapping Using Random Forest, Extreme Gradient Boosting (XGBoost) and Natural Gradient Boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar] [CrossRef]
- Sahin, E.K. Comparative analysis of gradient boosting algorithms for landslide susceptibility mapping. Geocarto Int. 2020, 37, 2441–2465. [Google Scholar] [CrossRef]
- Karantanellis, E.; Marinos, V.; Vassilakis, E.; Hölbling, D. Evaluation of Machine Learning Algorithms for Object-Based Mapping of Landslide Zones Using UAV Data. Geosciences 2021, 11, 305. [Google Scholar] [CrossRef]
- Ferreira, Z.; Almeida, B.; Costa, A.C.; do Couto Fernandes, M.; Cabral, P. Insights into landslide susceptibility: A comparative evaluation of multi-criteria analysis and machine learning techniques. Geomatics. Nat. Hazards Risk 2025, 16, 2471019. [Google Scholar] [CrossRef]
- Ngo, P.T.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef] [PubMed]
- Dahim, M.; Alqadhi, S.; Mallick, J. Enhancing landslide management with hyper-tuned machine learning and deep learning models: Predicting susceptibility and analyzing sensitivity and uncertainty. Front. Ecol. Evol. 2023, 11, 1108924. [Google Scholar] [CrossRef]
- Kainthura, P.; Sharma, N. Hybrid machine learning approach for landslide prediction, Uttarakhand, India. Sci. Rep. 2022, 12, 20101. [Google Scholar] [CrossRef]
- Sheng, M.; Zhou, J.; Chen, X.; Teng, Y.; Hong, A.; Liu, G. Landslide Susceptibility Prediction Based on Frequency Ratio Method and C5.0 Decision Tree Model. Front. Earth Sci. 2022, 10, 918386. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Clague, J.J.; Jaafari, A.; Chen, W.; Nguyen, H. Landslide Susceptibility Mapping Using Machine Learning Algorithms and Remote Sensing Data in a Tropical Environment. Int. J. Environ. Res. Public Health 2020, 17, 4933. [Google Scholar] [CrossRef]
- Nikparvar, B.; Thill, J.-C. Machine Learning of Spatial Data. ISPRS Int. J. Geo-Inf. 2021, 10, 600. [Google Scholar] [CrossRef]
- Apostolakis, A.; Girtsou, S.; Giannopoulos, G.; Bartsotas, N.S.; Kontoes, C. Estimating Next Day’s Forest Fire Risk via a Complete Machine Learning Methodology. Remote Sens. 2022, 14, 1222. [Google Scholar] [CrossRef]
- Sabatakakis, N.; Koukis, G.; Vassiliades, E.; Lainas, S. Landslide susceptibility zonation in Greece. Nat. Hazards 2013, 65, 523–543. [Google Scholar]
- Kilias, A. The Hellenides: A multiphase deformed orogenic belt, its structural architecture, kinematics and geotectonic setting during the Alpine orogeny: Comression vs Extension the dynamic peer for the orogen making. A synthesis. J. Geol. Geosci. 2021, 15, 2021. [Google Scholar]
- Mountrakis, D.; Sapountzis, E.; Kilias, A.; Elefteriadis, G.; Christofides, G. Paleogeographic conditions in the western Pelagonian margin in Greece during the initial rifting of the continental area. Can. J. Earth Sci. 1983, 20, 1673–1681. [Google Scholar]
- Mountrakis, D. Γεωλογια και Γεωτεκτονικη Εξελιξη της Ελλαδας; University Studio Press: Thessaloniki, Greece, 2010; p. 374. [Google Scholar]
- Doutsos, T.; Kokkalas, S. Stress and deformation patterns in the Aegean region. J. Struct. Geol. 2001, 23, 455–472. [Google Scholar]
- Kassaras, I. Study of the geodynamics in Aitoloakarnania (W. Greece) based on joint seismological and GPS data. In Proceedings of the 33rd ESC General Assembly, Moscow, Russia, 19–24 August 2012. [Google Scholar]
- Dermitzakis, M.D.; Papanikolaou, D.J. Paleogeography and geodynamics of the Aegean region during the Neogene. Ann. Geol. Pays Hell. 1981, 30, 245–289. [Google Scholar]
- Koukouvelas, I.; Aydin, A. Fault structure and related basins of the North Aegean Sea and its surroundings. Tectonics 2002, 21, 10-1–10-17. [Google Scholar]
- Marinos, V.; Papathanassiou, G.; Vougiouka, E.; Karantanellis, E. Towards the Evaluation of Landslide Hazard in the Mountainous Area of Evritania, Central Greece. In Engineering Geology for Society and Territory—Volume 2; Lollino, G., Giordan, D., Crosta, G.B., Corominas, J., Azzam, R., Wasowski, J., Sciarra, N., Eds.; Springer: Cham, Switzerland, 2015; pp. 989–993. [Google Scholar]
- Delibasis, N.; Karydis, P. Recent earthquake activity in Trichonis region and its tectonic significance. Ann. Geophys. 1977, 30, 19–81. [Google Scholar]
- Papoutsis, I.; Kontoes, C.; Alatza, S.; Apostolakis, A.; Loupasakis, C. InSAR Greece with Parallelized Persistent Scatterer Interferometry: A National Ground Motion Service for Big Copernicus Sentinel-1 Data. Remote Sens. 2020, 12, 3207. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Skilodimou, H.D.; Bathrellos, G.D.; Koskeridou, E.; Soukis, K.; Rozos, D. Physical and Anthropogenic Factors Related to Landslide Activity in the Northern Peloponnese, Greece. Land 2018, 7, 85. [Google Scholar] [CrossRef]
- Papathanassiou, G.; Valkaniotis, S.; Ganas, A. Spatial patterns, controlling factors, and characteristics of landslides triggered by strike-slip faulting earthquakes: Case study of Lefkada island, Greece. Bull. Eng. Geol. Environ. 2021, 80, 3747–3765. [Google Scholar] [CrossRef]
- Nefros, C.; Tsagkas, D.S.; Kitsara, G.; Loupasakis, C.; Giannakopoulos, C. Landslide Susceptibility Mapping under the Climate Change Impact in the Chania Regional Unit, West Crete, Greece. Land 2023, 12, 154. [Google Scholar] [CrossRef]
- Argyriou, A.V.; Polykretis, C.; Teeuw, R.M.; Papadopoulos, N. Geoinformatic Analysis of Rainfall-Triggered Landslides in Crete (Greece) Based on Spatial Detection and Hazard Mapping. Sustainability 2022, 14, 3956. [Google Scholar] [CrossRef]
- Hellenic National Meteorological Service (HNMS). Climate Atlas of Greece 1971–2000. 2016. Available online: http://climatlas.hnms.gr/sdi/ (accessed on 8 March 2025).
- Clerici, A.; Perego, S.; Tellini, C.; Vescovi, P. A GIS-based automated procedure for landslide susceptibility mapping by the Conditional Analysis method: The Baganza valley case study (Italian Northern Apennines). Environ. Geol. 2006, 50, 941–961. [Google Scholar] [CrossRef]
- Meten, M.; PrakashBhandary, N.; Yatabe, R. Effect of Landslide Factor Combinations on the Prediction Accuracy of Landslide Susceptibility Maps in the Blue Nile Gorge of Central Ethiopia. Geoenviron. Disasters 2015, 2, 9. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses; Agriculture Handbook, n. 537, Agriculture Research Service; US Department of Agriculture: Washington, DC, USA, 1978.
- Henriques, C.; Zêzere, J.; Marques, F. The role of the lithological setting on the landslide pattern and distribution. Eng. Geol. 2015, 189, 17–31. [Google Scholar] [CrossRef]
- Peduzzi, P. Landslides and vegetation cover in the 2005 North Pakistan earthquake: A GIS and statistical quantitative approach. Nat. Hazards Earth Syst. Sci. 2010, 10, 623–640. [Google Scholar] [CrossRef]
- Digital Elevation Model over Europe (EU-DEM). Available online: https://www.eea.europa.eu/data-and-maps/data/eu-dem (accessed on 25 November 2024).
- LS-Factor (Slope Length and Steepness Factor) for the EU. Available online: https://esdac.jrc.ec.europa.eu/content/ls-factor-slope-length-and-steepness-factor-eu (accessed on 3 November 2023).
- Copernicus Corine Land Cover 2018. Available online: https://land.copernicus.eu/en/products/corine-land-cover/clc2018 (accessed on 25 November 2024).
- EGDI 1:1 Million Pan-European Surface Geology. Available online: https://egdi.geology.cz/record/basic/5f7db57f-6e84-4484-835f-706b0a010833 (accessed on 3 November 2023).
- ERA5-Land Hourly Data from 1950 to Present. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=overview (accessed on 25 November 2024).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Krassakis, P.; Ioannidou, A.; Tsangaratos, P.; Loupasakis, C. Landslide Susceptibility Mapping of the Aitoloakarnania and Evrytania regional units, Western Greece, updated with the extensive catastrophic of Winter 2015. In Proceedings of the ICED2020: 1st International Conference on Environmental Design, Athens, Greece, 24–25 October 2020. [Google Scholar] [CrossRef]
- Bathrellos, G.; Koukouvelas, I.; Skilodimou, H.; Nikolakopoulos, K.; Vgenopoulos, A. Landslide causative factors evaluation using GIS in the tectonically active Glafkos River area, northwestern Peloponnese, Greece. Geomorphology 2024, 461, 109285. [Google Scholar] [CrossRef]



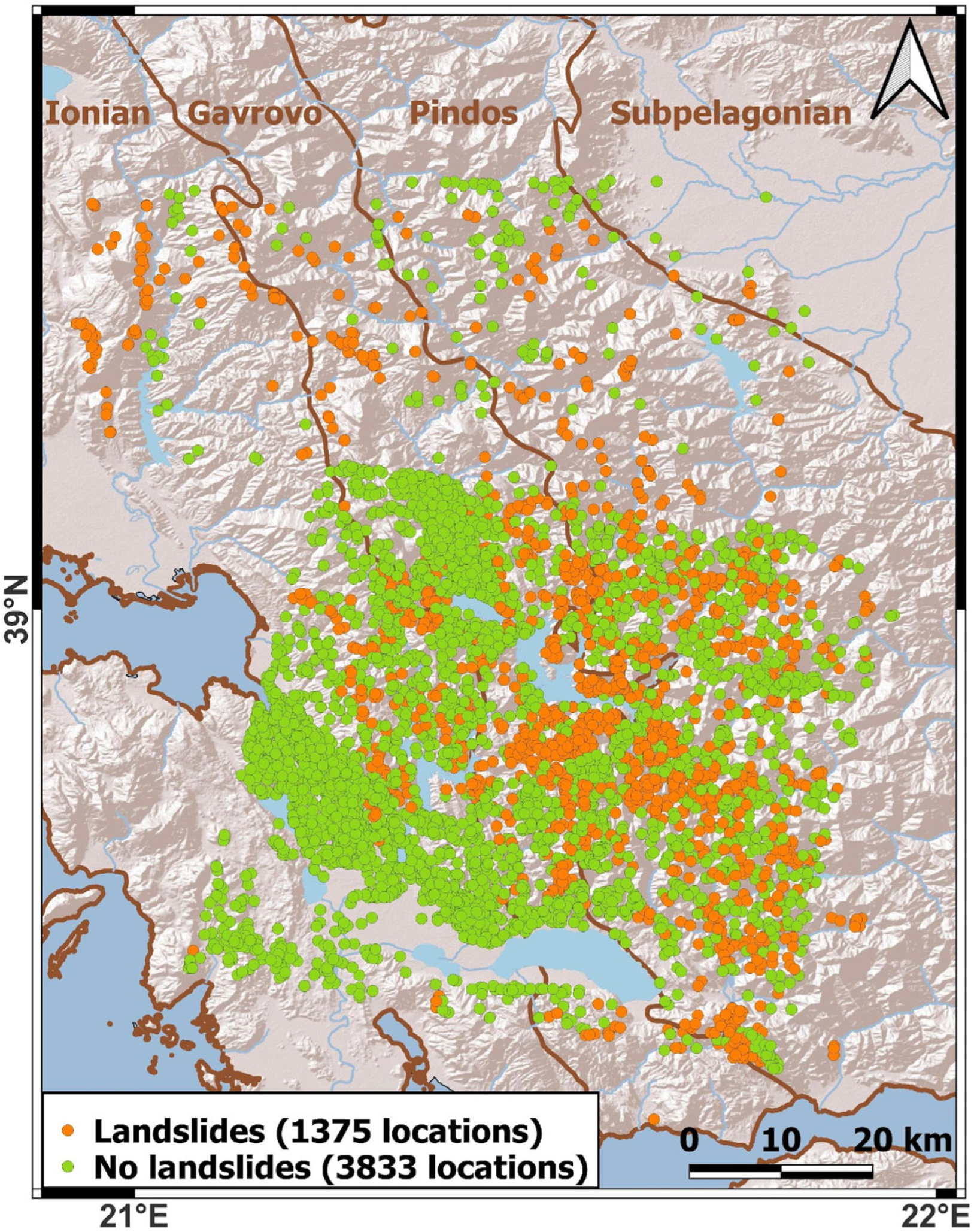
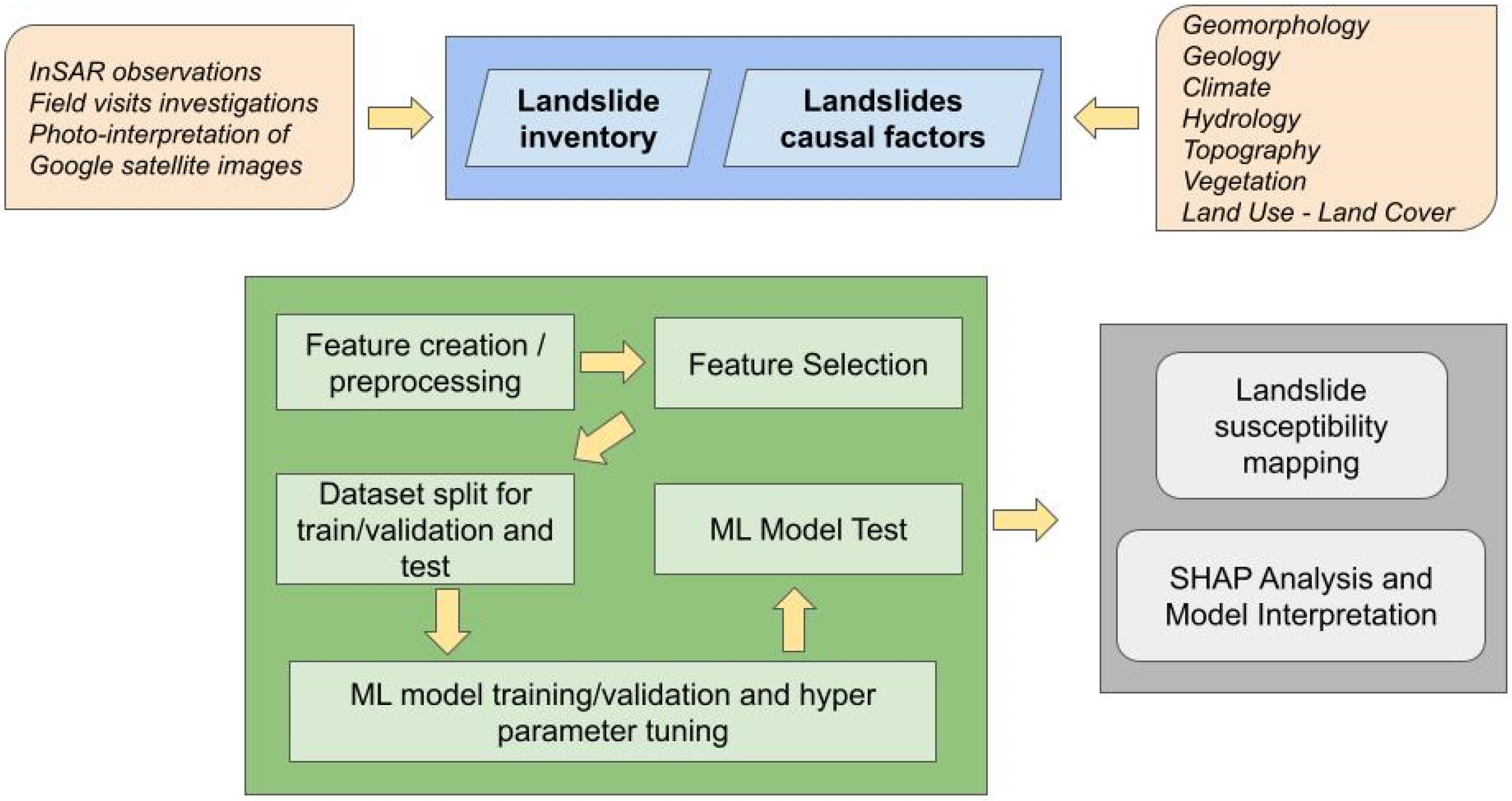

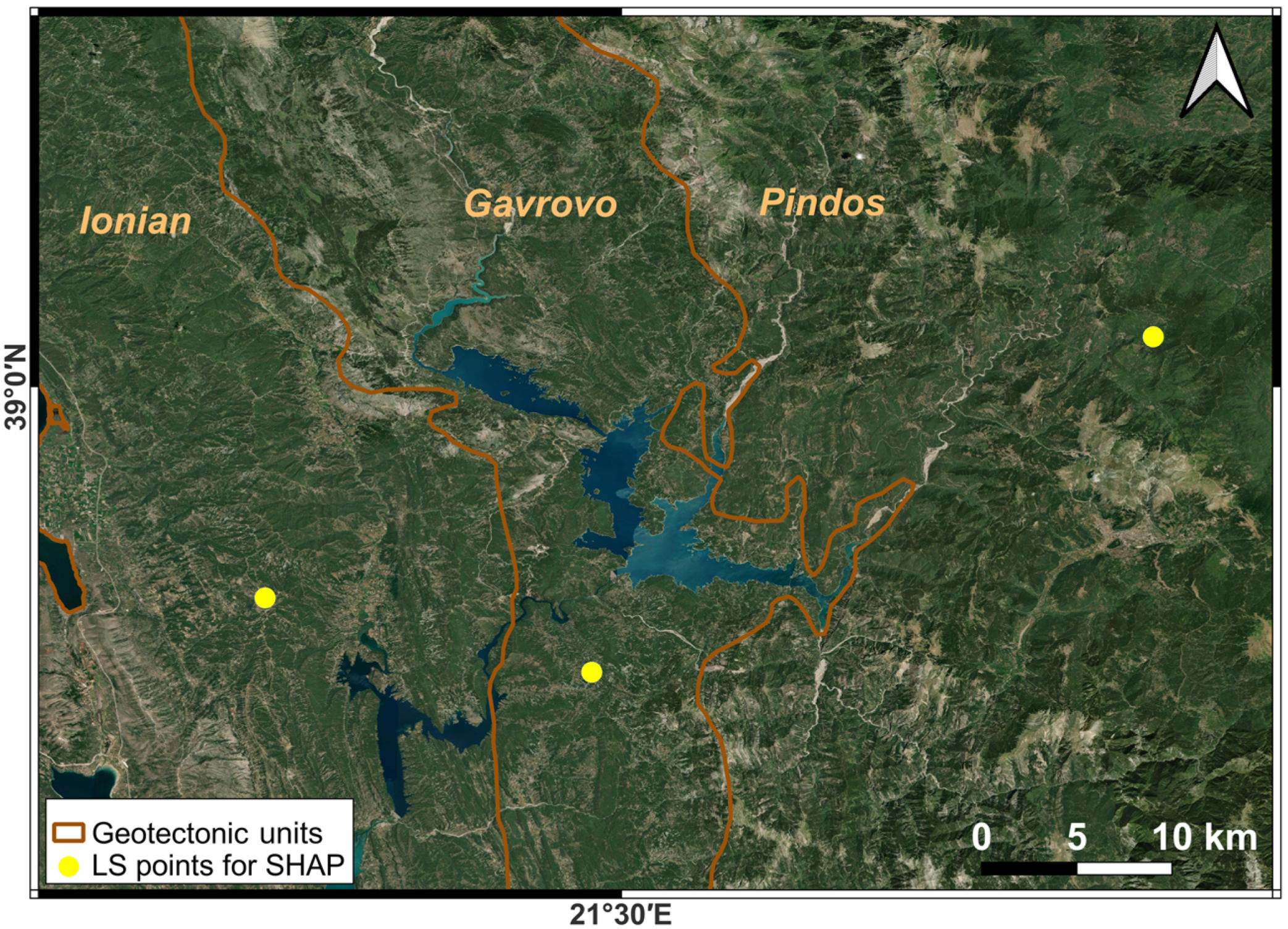

| No of LS Points | Source |
|---|---|
| 642 | Kontoes et al. [6] |
| 704 | Visual inspection of satellite images |
| 2354 | InSAR Greece product [47] |
| Category | Model Parameters | Feature Code Name |
|---|---|---|
| Geomorphology | Elevation | elevation (numerical) |
| Roughness | roughness (numerical) | |
| Aspect | aspect (one-hot class) | |
| Slope | slope (one-hot class) | |
| Geology | LS factor | lsfactor (one-hot class) |
| Surface Lithology | GEOLOGY (one-hot class) | |
| Geotectonic unit | unit_index (one-hot class) | |
| Climate | Snow melt | snow_q75 (numerical) |
| Precipitation | q95_1days, q95_3days, q95_7days, q95_30days, q75_1days, etc. (numerical) | |
| Hydrology and Topography | Sediment Transport Index | STI (numerical) |
| Topographic Wetness Index | TWI (numerical) | |
| Terrain Ruggedness Index | TRI (numerical) | |
| Stream Power Index | SPI (numerical) | |
| Vegetation | Normalized Difference Vegetation Index | NDVI (numerical) |
| Land use–Land cover | Land use–Land cover | LC (one-hot class) |
| Score Metric | Precision | Recall | F1 | Support | Accuracy | MCC |
|---|---|---|---|---|---|---|
| No Landslide | 0.88 | 0.91 | 0.89 | 827 | 0.85 | 0.65 |
| Landslide | 0.79 | 0.73 | 0.76 | 392 |
| Dataset | Score Metric | Precision | Recall | F1 | Accuracy | MCC |
|---|---|---|---|---|---|---|
| Buffered | No Landslide | 0.73 | 0.46 | 0.56 | 0.71 | 0.38 |
| Landslide | 0.70 | 0.88 | 0.78 | |||
| Unbuffered | No Landslide | 0.67 | 0.43 | 0.53 | 0.57 | 0.17 |
| Landslide | 0.51 | 0.74 | 0.60 |
| LS Points | Aspect (Degrees) | Slope (Degrees) | Geology | Land Use/Land Cover |
|---|---|---|---|---|
| LS Ionios | 157.5–202.5 | 0–20 | Flysch | Heterogeneous agricultural areas |
| LS Gavrovo | 202.5–247.5 | 0–20 | Flysch | Scrub and/or herbaceous vegetation associations |
| LS Pindos | 247.5–292.5 | 0–20 | Flysch | Heterogeneous agricultural areas |
| Pindos | Gavrovo | Ionios | |
|---|---|---|---|
| No. of the grid’s high LS susceptible points | 2,050,717 (44%) | 1,578,546 (34%) | 1,007,408 (22%) |
| Unit area within the AOI (in km2) | 3474 | 6490 | 6958 |
| Grid’s high LS susceptible points/km2 | 590 | 243 | 145 |
| No. of the Grid’s High LS Susceptible Points | Geological Formations Area Within the AOI (in km2) | Grid’s High LS Susceptible Points/km2 | |
|---|---|---|---|
| Flysch | 3,269,571 | 7665 | 426 |
| Limestones | 1,820,270 | 5927 | 307 |
| Alluvial deposits | 299,332 | 1842 | 162 |
| Schist-cherts | 327,211 | 502 | 651 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alatza, S.; Apostolakis, A.; Loupasakis, C.; Kontoes, C.; Kokkalidou, M.; Bartsotas, N.S.; Christopoulos, G. Harnessing InSAR and Machine Learning for Geotectonic Unit-Specific Landslide Susceptibility Mapping: The Case of Western Greece. Remote Sens. 2025, 17, 1161. https://doi.org/10.3390/rs17071161
Alatza S, Apostolakis A, Loupasakis C, Kontoes C, Kokkalidou M, Bartsotas NS, Christopoulos G. Harnessing InSAR and Machine Learning for Geotectonic Unit-Specific Landslide Susceptibility Mapping: The Case of Western Greece. Remote Sensing. 2025; 17(7):1161. https://doi.org/10.3390/rs17071161
Chicago/Turabian StyleAlatza, Stavroula, Alexis Apostolakis, Constantinos Loupasakis, Charalampos Kontoes, Martha Kokkalidou, Nikolaos S. Bartsotas, and Georgios Christopoulos. 2025. "Harnessing InSAR and Machine Learning for Geotectonic Unit-Specific Landslide Susceptibility Mapping: The Case of Western Greece" Remote Sensing 17, no. 7: 1161. https://doi.org/10.3390/rs17071161
APA StyleAlatza, S., Apostolakis, A., Loupasakis, C., Kontoes, C., Kokkalidou, M., Bartsotas, N. S., & Christopoulos, G. (2025). Harnessing InSAR and Machine Learning for Geotectonic Unit-Specific Landslide Susceptibility Mapping: The Case of Western Greece. Remote Sensing, 17(7), 1161. https://doi.org/10.3390/rs17071161







