Research on Universal Time/Length of Day Combination Algorithm Based on Effective Angular Momentum Dataset
Abstract
1. Introduction
2. Datasets
2.1. UT1 Dataset
2.2. LOD Dataset
2.3. EAM Dataset
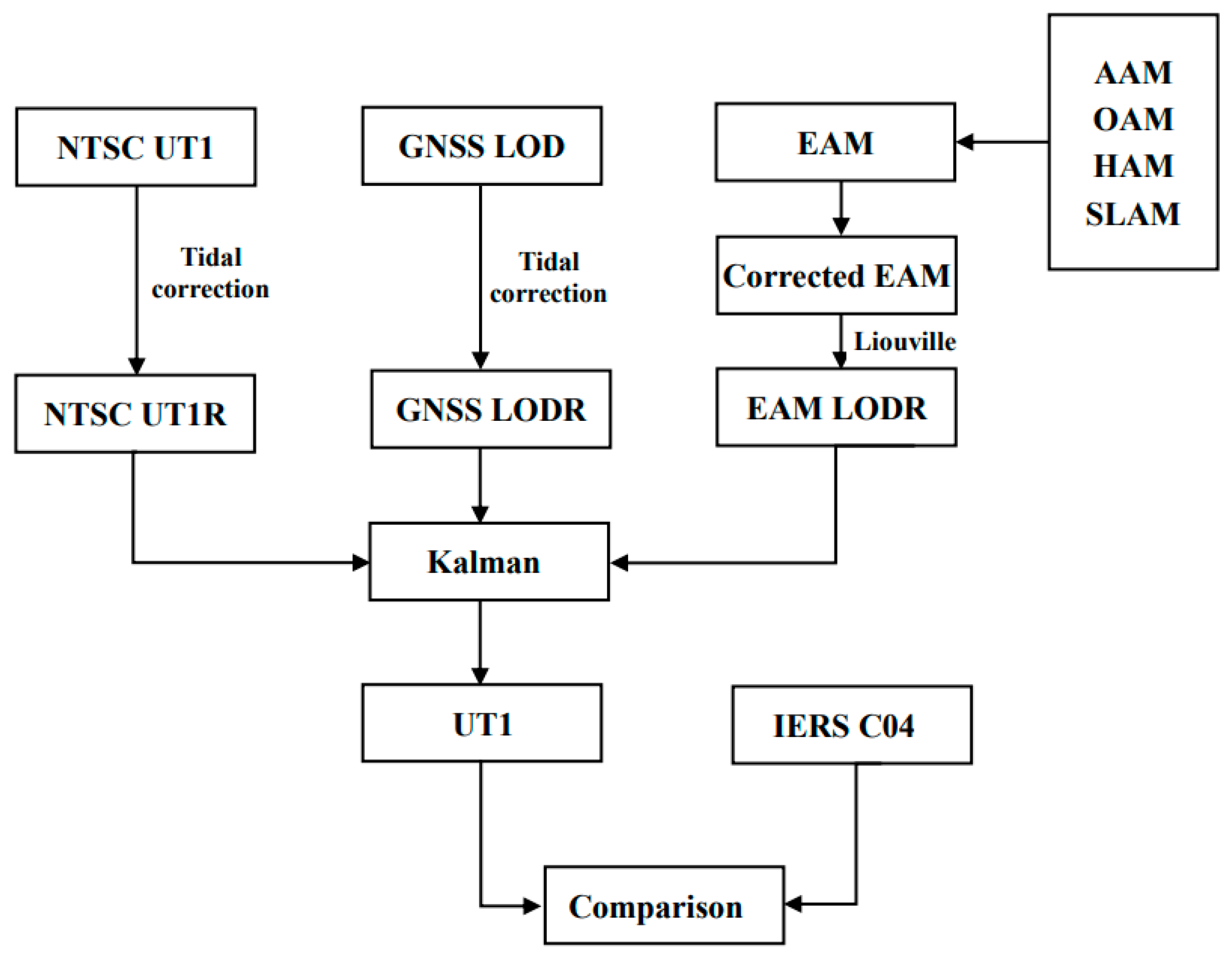
3. Method
3.1. Data Preprocessing
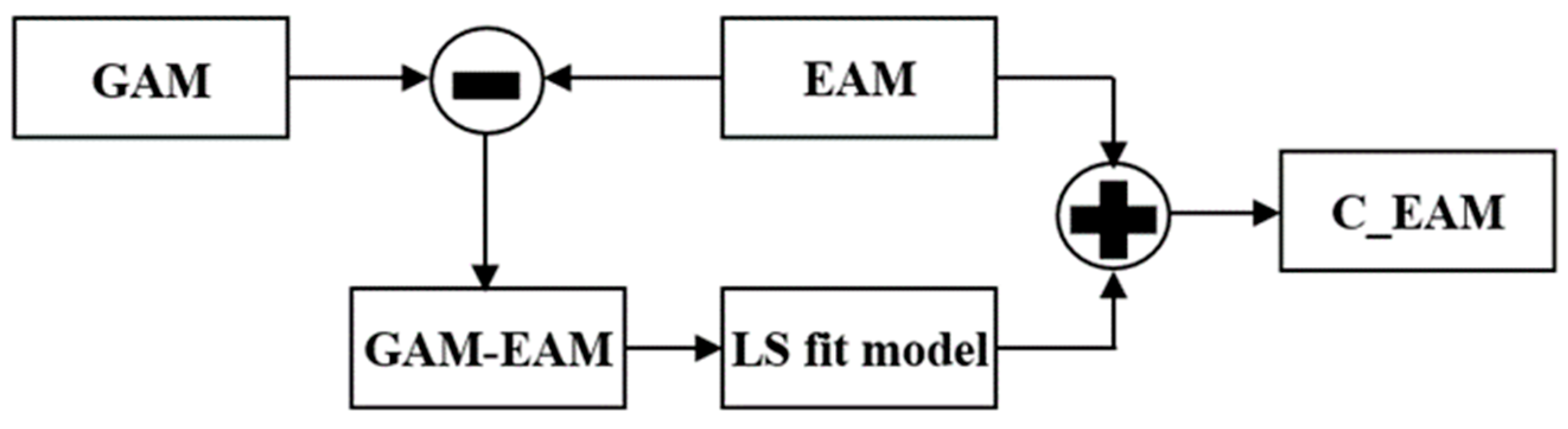
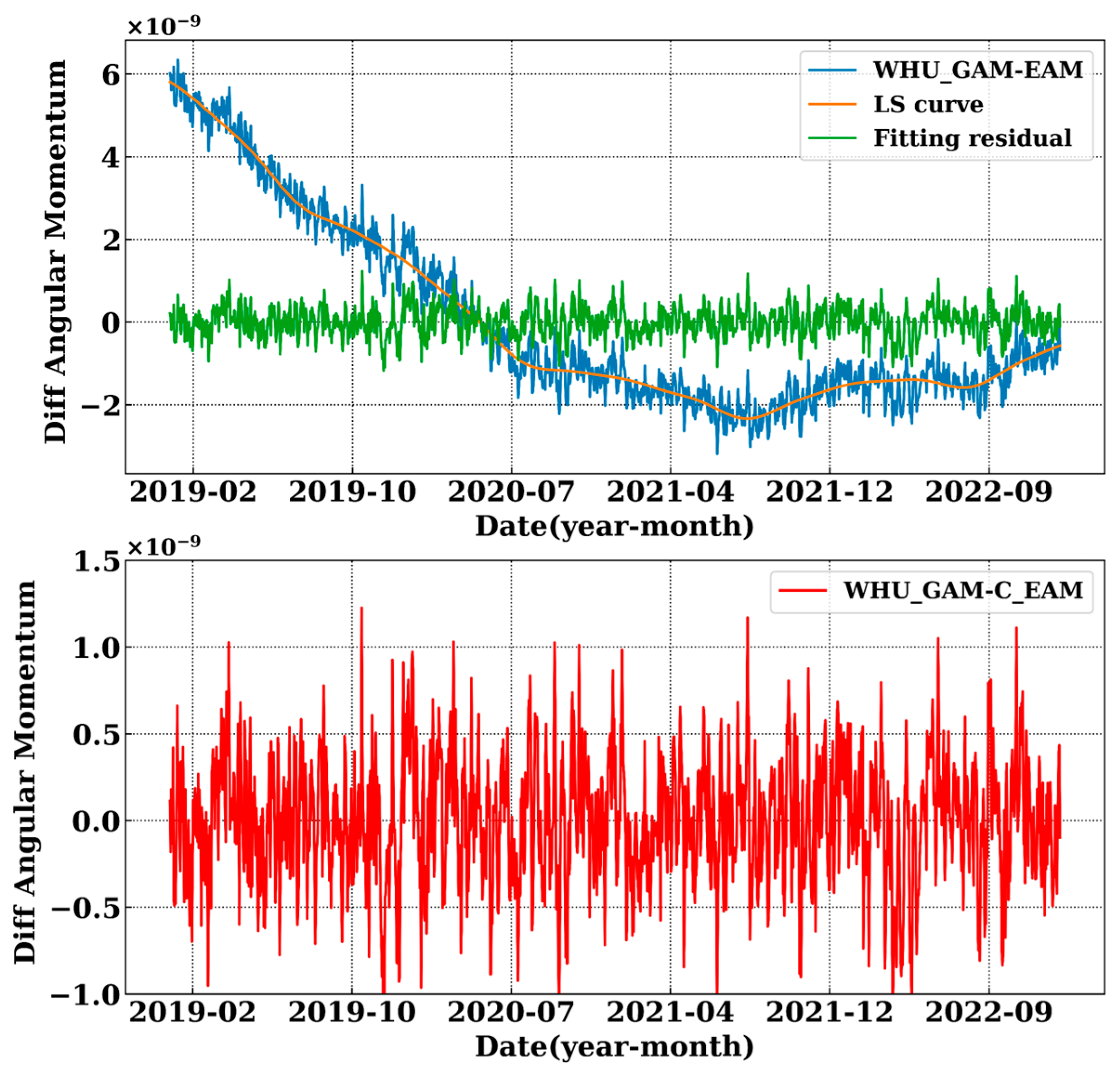
3.1.1. LOD System Bias
3.1.2. Differences Between EAM and LODR
3.2. Kalman Combination Algorithm
4. Evaluation
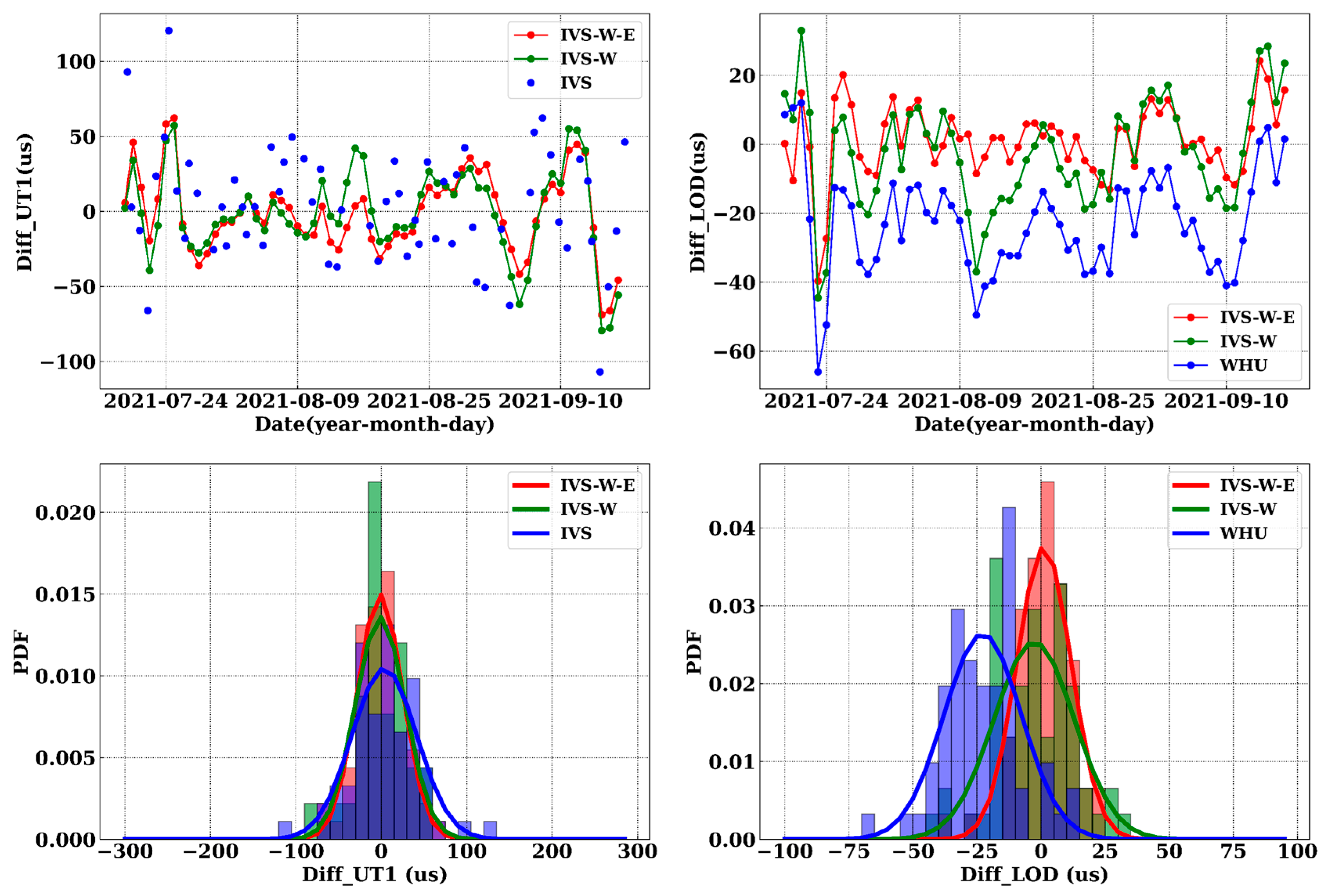
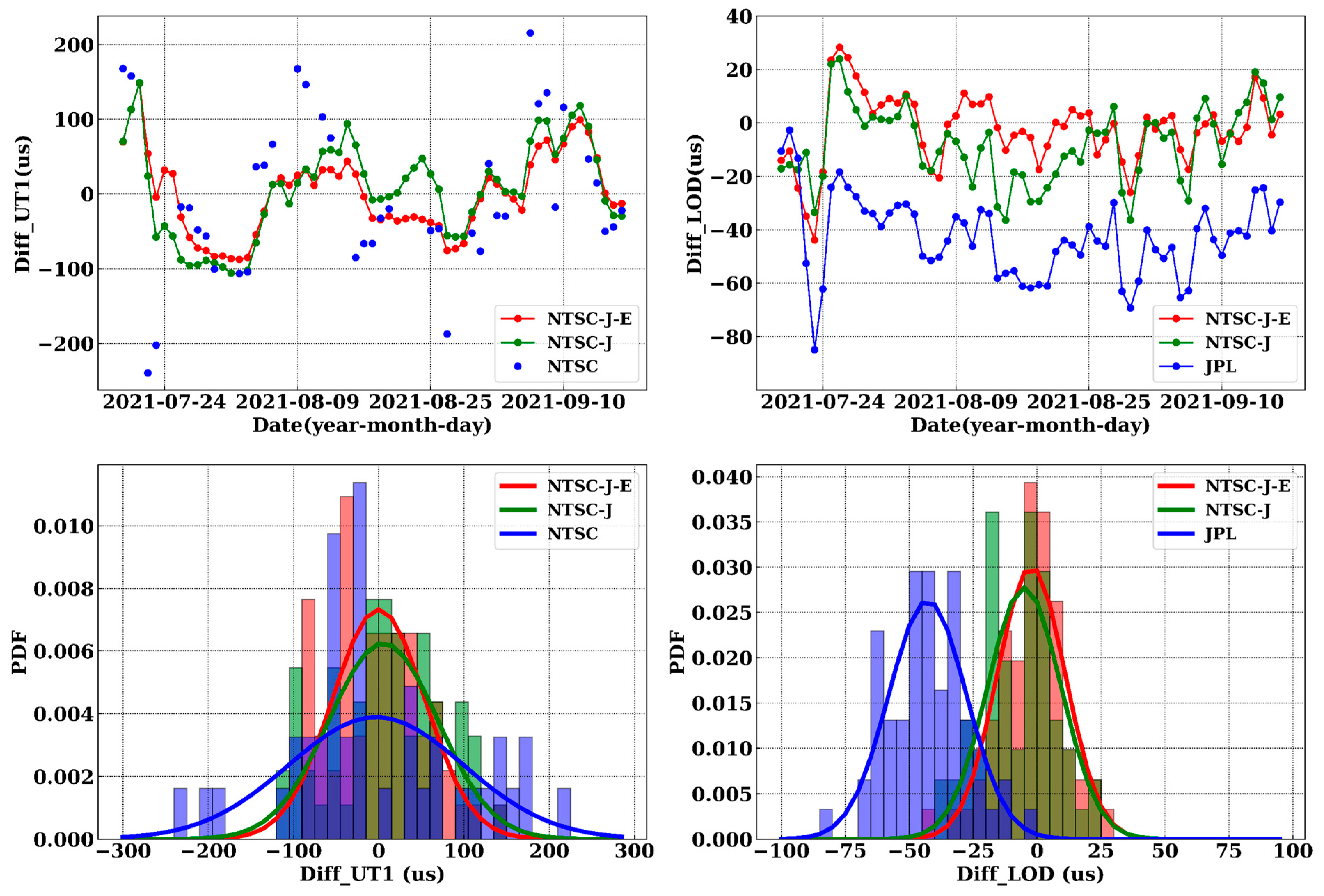
4.1. Comparison with C04 UT1/LOD
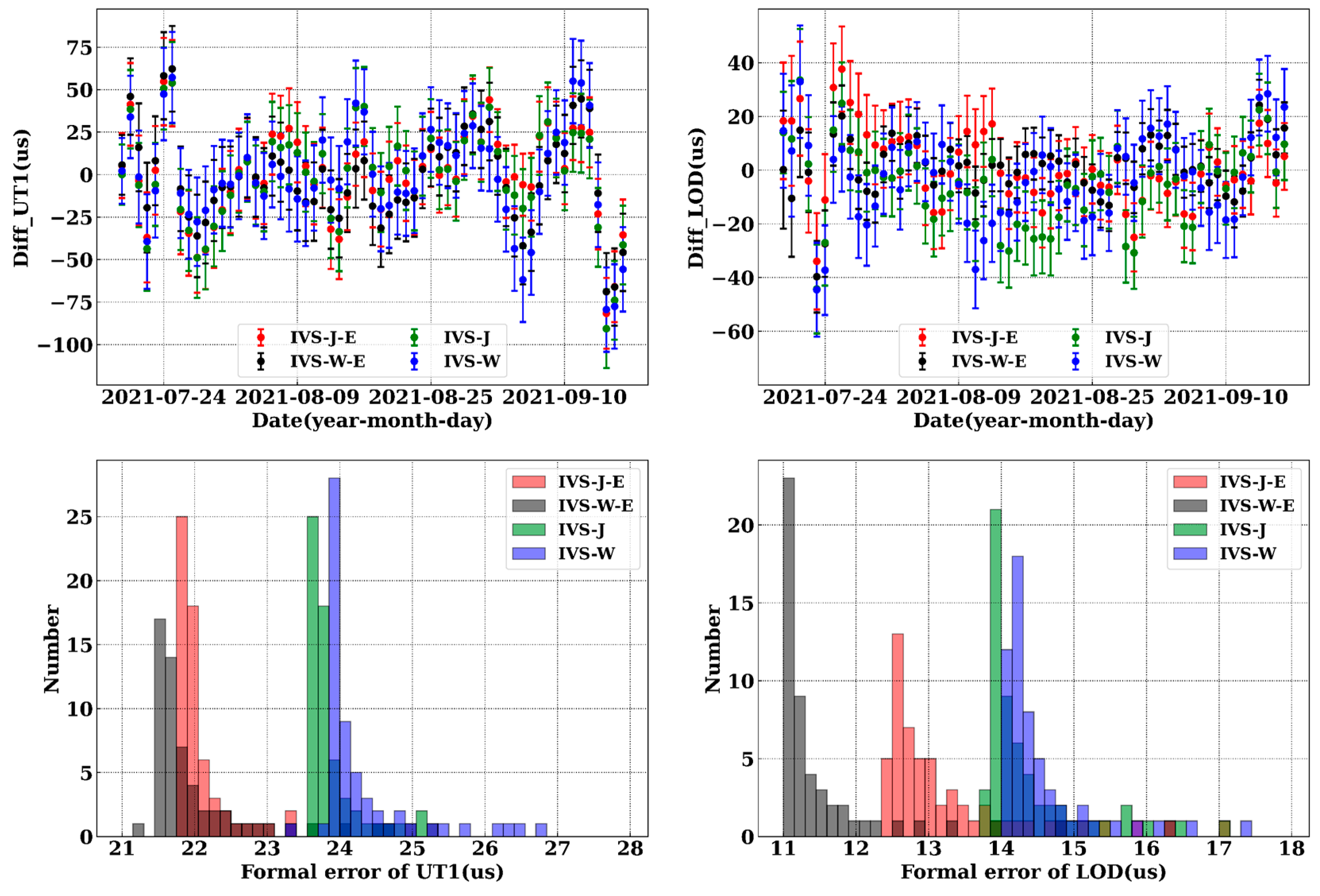
4.1.1. Combination of IVS with JPL/WHU and EAM
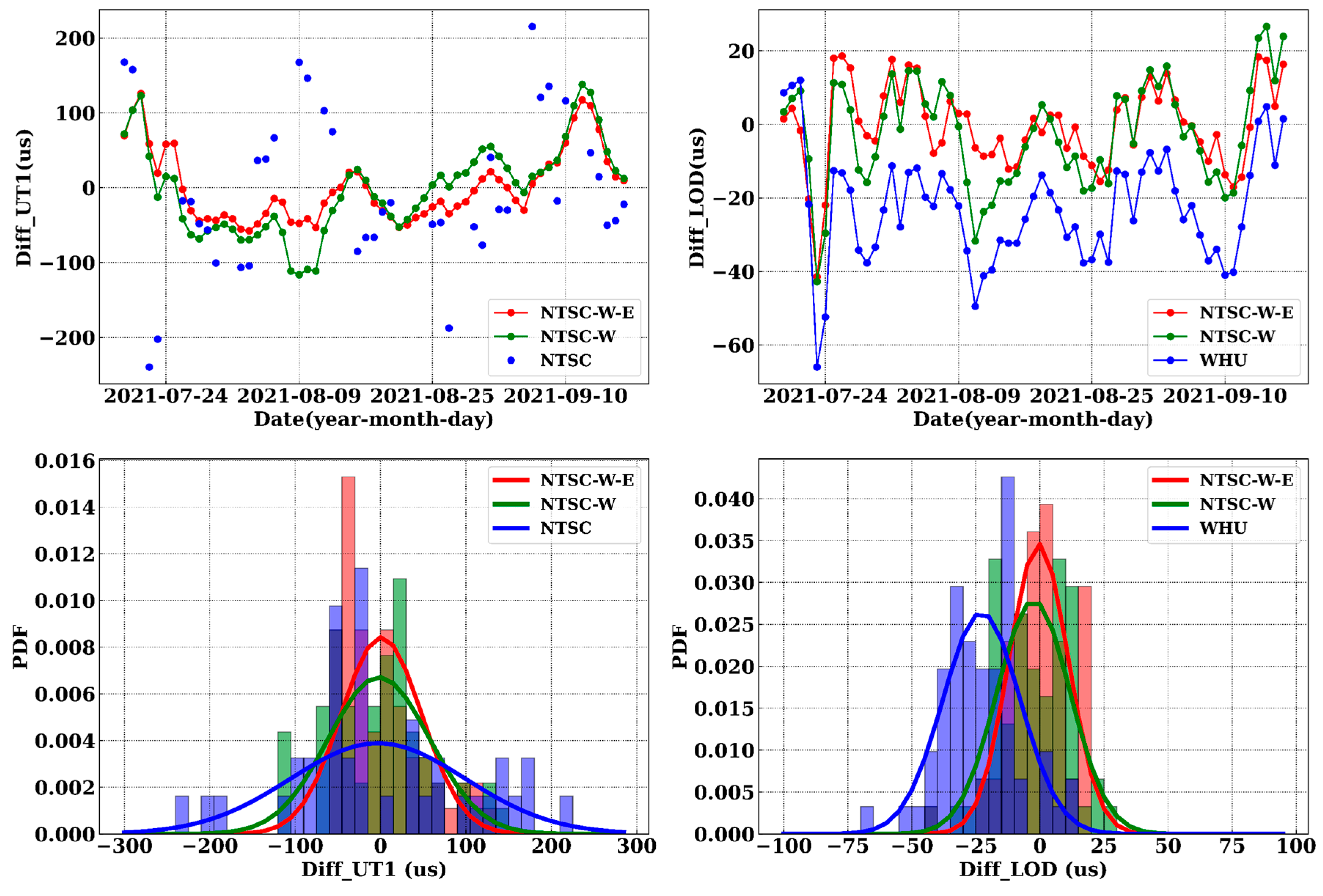
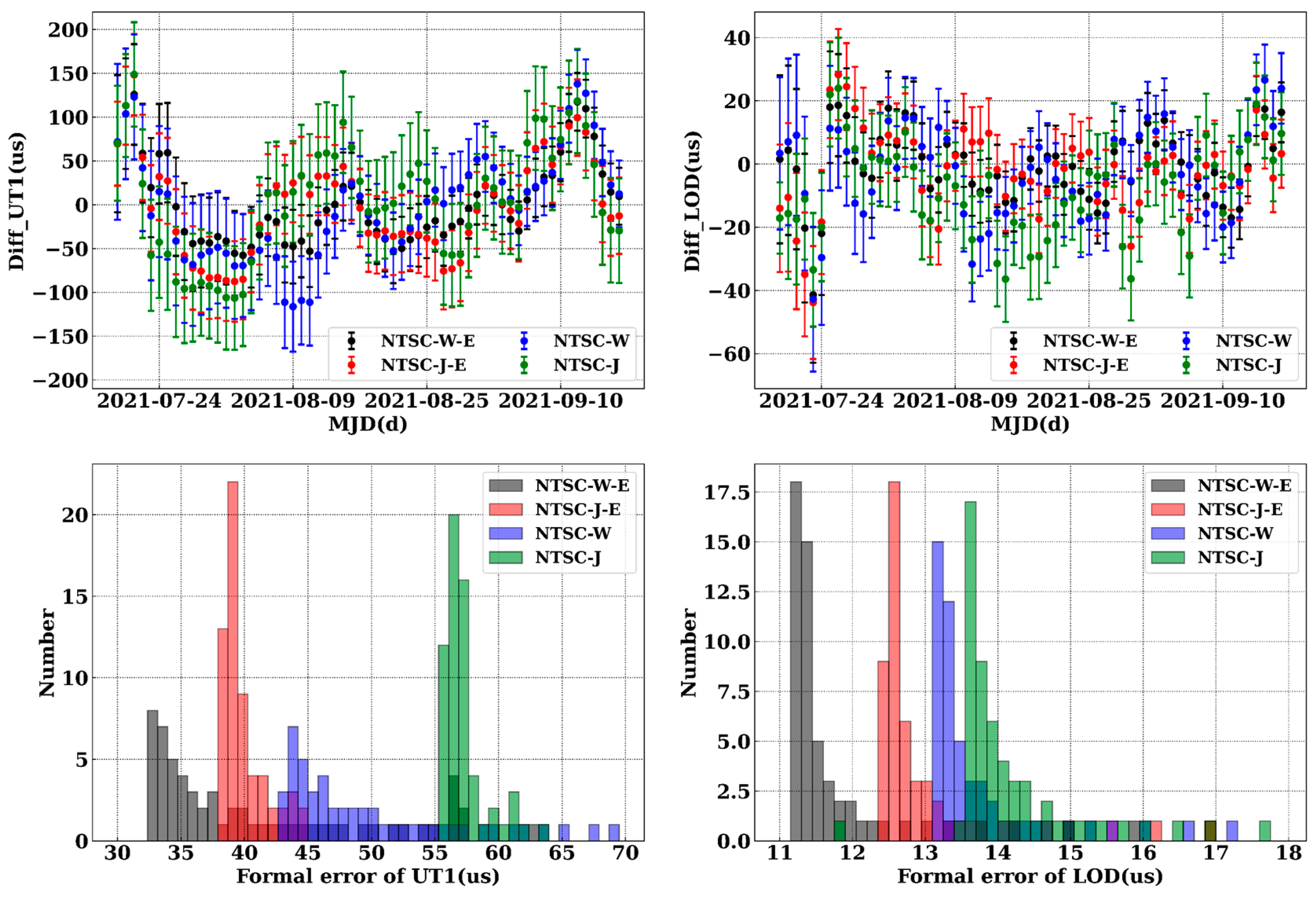
4.1.2. Combination of NTSC with JPL/WHU and EAM
4.2. UT1/LOD Uncertainty
5. Discussion
5.1. The Combination of IVS and NTSC UT1
5.2. Time Resolution of Input Datasets
5.3. Prospects
- (a)
- The development of an updated Kalman filter with the ability to handle multiple UT1, LOD, and EAM inputs, which can be used to combine and evaluate more UT1, LOD, and EAM results from multiple analysis centers;
- (b)
- The design of a Kalman filter tool that can also integrate the polar motion components with the VLBI, GNSS, and EAM datasets as inputs (the X and Y components of the AAM show strong correlation and consistent periodicity with the PMX and PMY, respectively);
- (c)
- Investigations and estimations of the uncertainties of the EAM dataset to enhance the combination and prediction of EOPs.
6. Conclusions
- (a)
- The 11-parameter combination algorithm improved the accuracy of the UT1 data by over 30%, with the accuracy of the UT1 dataset from the NTSC increasing by nearly 54%, and the accuracy of the intensive observation UT1 dataset from the IVS improving by approximately 30%;
- (b)
- Compared to using only the GNSS and VLBI datasets, the inclusion of the EAM dataset yields superior combination results, characterized by higher accuracy, better stability, and more concentrated outcomes. Particularly for UT1 input datasets with high uncertainty, the EAM dataset can enhance the UT1 combination accuracy by 10 µs;
- (c)
- The formal uncertainty, measured by the square root of the diagonal elements of the covariance matrix, demonstrates that the Kalman combination model exhibits high reliability and rationality;
- (d)
- Validation through eight combination scenarios confirmed the algorithm’s strong applicability to input datasets. The higher the accuracy of the input dataset, the greater the combination accuracy; for datasets with lower accuracy, the improvement is more pronounced;
- (e)
- The combination algorithm not only corrects the systematic biases in the LOD but also effectively enhances the accuracy of LOD data.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Petti, G.; Luzum, B. IERS Conventions 2010; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; Available online: https://www.researchgate.net/publication/235112142 (accessed on 1 January 2025)ISBN 3-89888-989-6.
- Gambis, D.; Luzum, B. Earth rotation monitoring, UT1 determination and prediction. Metrologia 2011, 48, 165–170. [Google Scholar] [CrossRef]
- Nastula, J.; Chin, T.M.; Gross, R.; Śliwińska, J.; Wińska, M. Smoothing and predicting celestial pole offsets µsing a Kalman filter and smoother. J. Geod. 2020, 94, 2–17. [Google Scholar] [CrossRef]
- Nilsson, T.; Böhm, J.; Schuh, H. Sub-diurnal earth rotation variations observed by VLBI. Artif. Satell. 2010, 45, 49–55. [Google Scholar] [CrossRef]
- Nilsson, T.; Böhm, J.; Schuh, H. Universal time from VLBI single-baseline observations during CONT08. J. Geod. 2011, 85, 415–423. [Google Scholar] [CrossRef]
- Nilsson, T.; Heinkelmann, R.; Karbon, M.; Raposo-Pulido, V.; Soja, B.; Schuh, H. Earth orientation parameters estimated from VLBI during the CONT11 campaign. J. Geod. 2014, 88, 491–502. [Google Scholar] [CrossRef]
- Byram, S.; Hackman, C. High-precision GNSS orbit, clock and EOP estimation at the United States Naval Observatory. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Mireault, Y.; Kouba, J. IGS Earth rotation parameters. GPS Solut. 1999, 3, 59–72. [Google Scholar] [CrossRef]
- Coulot, D.; Pollet, A.; Collilieux, X.; Berio, P. Global optimization of core station networks for space geodesy: Application to the referencing of the SLR EOP with respect to ITRF. J. Geod. 2010, 84, 31–50. [Google Scholar] [CrossRef]
- Pavlov, D. Role of lunar laser ranging in realization of terrestrial, lunar, and ephemeris reference frames. J. Geod. 2020, 94, 5. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The international laser ranging service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Willis, P.; Fagard, H.; Ferrage, P.; Lemoine, F.G.; Noll, C.E.; Noomen, R.; Otten, M.; Ries, J.C.; Rothacher, M.; Soudarin, L.; et al. The international DORIS service (IDS): Toward maturity. Adv. Space Res. 2010, 45, 1408–1420. [Google Scholar] [CrossRef]
- Moreaux, G.; Lemoine, F.G.; Capdeville, H.; Kuzin, S.; Otten, M.; Štěpánek, P.; Willis, P.; Ferrage, P. The international DORIS service contribution to the 2014 realization of the international terrestrial reference frame. Adv. Space Res. 2016, 58, 2479–2504. [Google Scholar] [CrossRef]
- Angermann, D.; Seitz, M.; Drewes, H. Analysis of the DORIS contributions to ITRF2008. Adv. Space Res. 2010, 46, 1633–1647. [Google Scholar] [CrossRef]
- Taller, D.; Krugel, M.; Rothache, M.; Tesmer, V.; Schmid, R.; Angermann, D. Combined Earth orientations parameters based on Homogeneous and continuous VLBI and GPS dhata. J. Geod. 2007, 81, 529–541. [Google Scholar] [CrossRef]
- Bizouard, C.; Gambis, D. The combined solution C04 for Earth orientation parameters consistent with international terrestrial reference frame 2005. In Proceedings of the International Association of Geodesy Symposium, Munich, Germany, 9–14 October 2009; pp. 265–270. [Google Scholar] [CrossRef]
- Artz, T.; Bernhard, L.; Nothnagel, A.; Steigenberger, P.; Tesmer, S. Methodology for the combination of sub-daily Earth rotation from GPS and VLBI observations. J. Geod. 2012, 86, 221–239. [Google Scholar] [CrossRef]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.-Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geod. 2019, 93, 621–633. [Google Scholar] [CrossRef]
- Ratcliff, J.T.; Gross, R.S. Combinations of Earth Orientation Measurements: SPACE2018, COMB2018, and POLE2018; JPL Publication 19-7; National Aeronautics and Space Administration: Washington, DC, USA, 2019; Available online: https://www.researchgate.net/publication/336778776 (accessed on 1 January 2025).
- Kehm, A.; Hellmers, H.; Blossfeld, M.; Dill, R.; Angermann, D.; Seitz, F.; Hugentobler, U.; Dobslaw, H.; Thomas, M.; Thaller, D.; et al. Combination strategy for consistent final, rapid and predicted Earth rotation parameters. J. Geod. 2023, 97, 3. [Google Scholar] [CrossRef]
- He, B.; Wang, X.Y.; Hu, X.G.; Zhao, Q.-H. Combination of terrestrial reference frames based on space geodetic techniques in SHAO: Methodology and main issues. Res. Astron. Astrophys. 2017, 17, 89. [Google Scholar] [CrossRef]
- Schoenemann, E.; Springer, T.; Otten, M.; Mayer, V.; Bruni, S.; Enderle, W.; Zandbergen, R. Status of ESA’s independent Earth orientation parameter products. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. EGU 2020-17154. [Google Scholar] [CrossRef]
- Gambis, D.; Biancale, R.; Carlucci, T.; Lemoine, J.; Marty, J.; Bourda, G.; Charlot, P.; Loyer, S.; Lalanne, T.; Soudarin, L.; et al. Combination of Earth Orientation Parameters and Terrestrial Frame at the Observation Level. Int. Assoc. Geod. Symp. 2009, 134, 3–9. [Google Scholar] [CrossRef]
- Wang, J.G.; Ge, M.R.; Glaser, S. Impact of Tropospheric Ties on UT1-UTC in GNSS and VLBI Integrated Solution of in tensive Sessions. J. Geophys. Res-Solid Earth 2022, 127, e2022JB025228. [Google Scholar] [CrossRef]
- Davis, M.; Carter, M.S.; Dieck, C.; Stamatakos, N. The IERS Rapid Service/Prediction Centre UT1−UTC Combined Solution: Present and Future Contributions. In Proceedings of the 24th Meeting of the European VLBI Group for Geodesy and Astrometry, Las Palmas de Gran Canaria, Spain, 17–19 March 2019; pp. 184–189. [Google Scholar]
- Schindelegger, M.; Bohm, J.; Salstein, D. High resolution atmospheric angular momentum functions related to Earth rotation parameters during CONT08. J. Geod. 2011, 85, 425–433. [Google Scholar] [CrossRef]
- Hide, R.; Birch, N.T.; Morrison, L.V.; Shea, D.J.; White, A.A. Atmospheric angular momentum fluctuations and changes in the length of the day. Nature 1980, 286, 114–117. [Google Scholar] [CrossRef]
- Eubanks, T.M.; Steppe, J.A.; Dickey, J.O.; Callahan, P.S. A spectral-analysis of the Earth’s angular momentum budget. J. Geophys. Res. 1985, 90, 5385–5404. [Google Scholar] [CrossRef]
- Rosen, R.D.; Salstein, D.A.; Wood, T.M. Discrepancies in the Earth atmosphere angular momentum budget. J. Geophys. Res.-Solid Earth Planets 1990, 95, 265–279. [Google Scholar] [CrossRef]
- Mound, J.E.; Buffett, B.A. Detection of a gravitational oscillation in length-of-day. Earth Planet. Sc. Lett. 2006, 243, 383–389. [Google Scholar] [CrossRef]
- Niedzielski, T.; Kosek, W. Prediction of UT1–UTC, LOD and AAM by combination of least-squares and multivariate stochastic methods. J. Geod. 2008, 82, 83–92. [Google Scholar] [CrossRef]
- Freedman, A.P.; Steppe, J.A.; Dickey, J.O.; Eubanks, T.M.; Sung, L.Y. The short-term prediction of universal time and length of day µsing atmospheric angular momentum. J. Geophys. Res. Solid Earth 1994, 99, 6981–6996. [Google Scholar] [CrossRef]
- Gross, R.S.; Fukumori, I.; Menemenlis, D.; Gegout, P. Atmospheric and oceanic excitation of length-of-day variations during 1980–2000. J Geophys Res Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Guo, J.Y.; Li, Y.B.; Dai, C.; Shum, C. A technique to improve the accuracy of Earth orientation prediction algorithms based on least squares extrapolation. J. Geodyn. 2013, 70, 36–48. [Google Scholar] [CrossRef]
- Rekier, J.; Chao, B.F.; Chen, J.; Dehant, V.; Rosat, S.; Zhu, P. Earth’s Rotation: Observations and Relation to Deep Interior. Surv. Geophys. 2022, 43, 149–175. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Ye, R.; Cheng, X.; Zhang, S. Research on Methods to Improve Length of Day Precision by Combining with Effective Angular Momentum. Remote Sens. 2024, 16, 722. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y.; Yao, D.; Liu, J.; Nan, K.; Ma, L.; Cheng, X.; Yang, X.; Zhang, S. Research on UT1-UTC and LOD Prediction Algorithm Based on Denoised EAM Dataset. Remote Sens. 2023, 15, 4654. [Google Scholar] [CrossRef]
- Nothnagel, A.; Schnell, D. The impact of errors in polar motion and nutation on UT1 determinations from VLBI intensive observations. J. Geod. 2008, 82, 863–869. [Google Scholar] [CrossRef]
- Yao, D.; Wu, Y.W.; Zhang, B.; Sun, J.; Sun, Y.; Xu, S.-J.; Liu, J.; Ma, L.-M.; Gong, J.-J.; Yang, Y.; et al. The NTSC VLBI System and its application in UT1 measurement. Res. Astron. Astrophys. 2020, 20, 153–162. [Google Scholar] [CrossRef]
- Dill, R.; Dobslaw, H.; Thomas, M. Improved 90-day Earth orientation predictions from angular momentum forecasts of atmosphere, ocean, and terrestrial hydrosphere. J. Geod. 2019, 93, 287–295. [Google Scholar] [CrossRef]
- Dobslaw, H.; Dill, R.; Grötzsch, A.; Brzezinski, A.; Thomas, M. Seasonal polar motion excitation from numerical models of atmosphere, ocean, and continental hydrosphere. J. Geophys. Res. 2010, 115, 406. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Fischer, N.; Haak, H.; Lohmann, K.; Marotzke, J.; Matei, D.; Mikolajewicz, U.; Notz, D.; von Storch, J.S. Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI-Earth system model. J. Adv. Model. Earth Syst. 2013, 5, 422–446. [Google Scholar] [CrossRef]
- Hagemann, S.; Dumenil, L. A parametrization of the waterflow for the global scale. Clim. Dyn. 1998, 14, 17–31. [Google Scholar] [CrossRef]
- Tamisiea, M.E.; Hill, E.M.; Ponte, R.M.; Davis, J.L.; Velicogna, I.; Vinogradova, N.T. Impact of self-attraction and loading on the annual cycle in sea level. J. Geophys. Res-Oceans 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Dobslaw, H.; Dill, R. Predicting Earth orientation changes from global forecasts of atmosphere hydrosphere dynamics. Adv. Space Res. 2018, 61, 1047–1054. [Google Scholar] [CrossRef]
- Chao, B.F.; Chung, W.Y.; Shih, Z.; Hsieh, Y. Earth’s rotation variations: A wavelet analysis. Terra Nova 2014, 26, 260–264. [Google Scholar] [CrossRef]
- Ding, H.; Chao, F. Application of Stabilized AR-z Spectrum in Harmonic Analysis for Geophysics. J. Geophys. Res. Solid Earth 2018, 123, 8249–8259. [Google Scholar] [CrossRef]
- Ray, R.D.; Erofeeva, S.Y. Long-period tidal variations in the length of day. J. Geophys. Res. Solid Earth 2014, 119, 1498–1509. [Google Scholar] [CrossRef]
- Morabito, D.D.; Eubanks, T.M.; Steppe, J.A. Kalman filtering of Earth orientation changes. In The Earth’s Rotation and Reference Frames for Geodesy and Geodynamics; Babcock, A.K., Wilkins, G.A., Eds.; Kluwer Acad: Norwell, MA, USA, 1988; pp. 257–267. [Google Scholar] [CrossRef]
- Gross, R.S.; Eubanks, T.M.; Steppe, J.A.; Freedman, A.P.; Dickey, J.O.; Runge, T.F. A Kalman-filter-based approach to combining independent Earth-orientation series. J. Geod. 1988, 72, 215–235. [Google Scholar] [CrossRef]


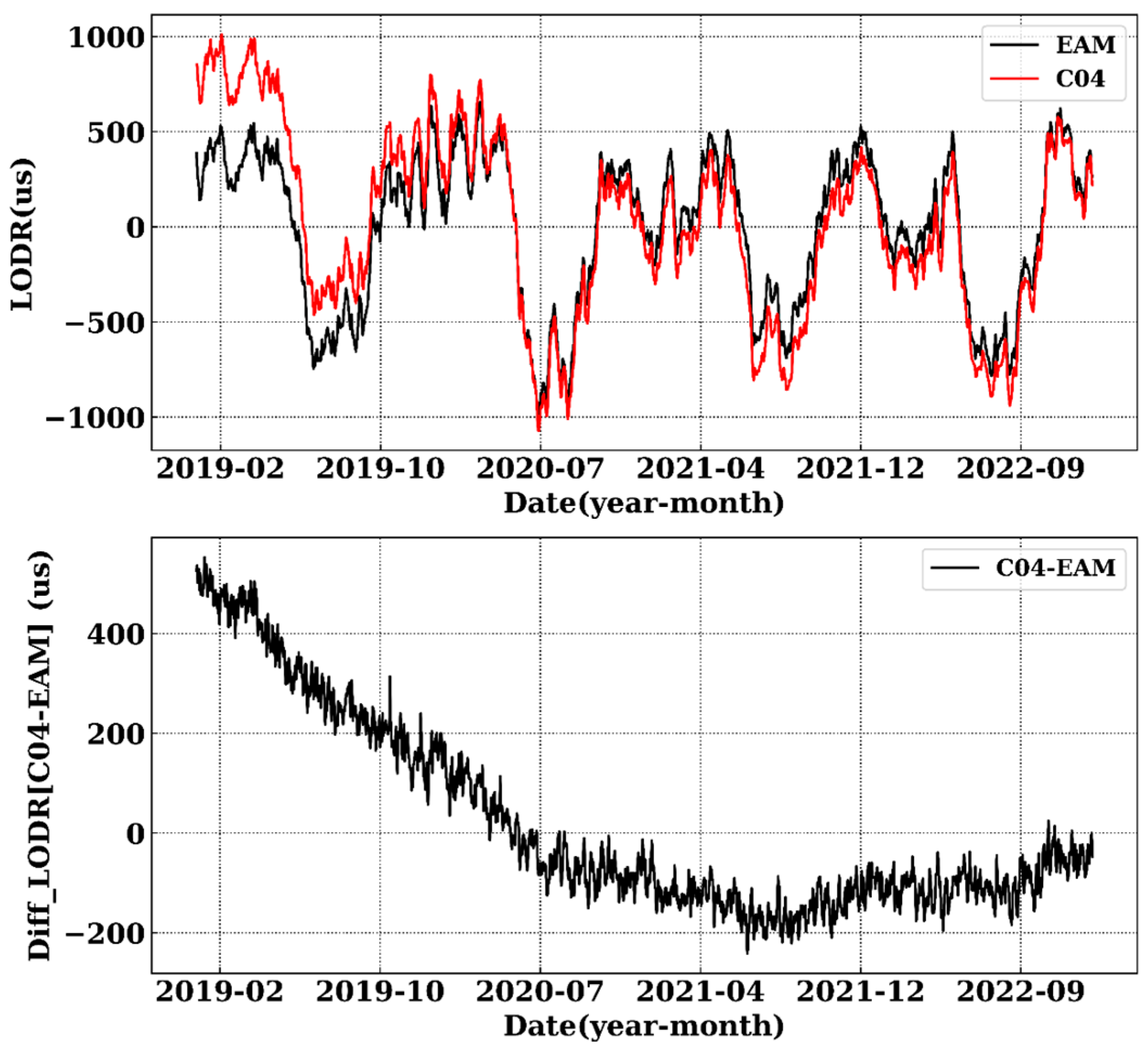
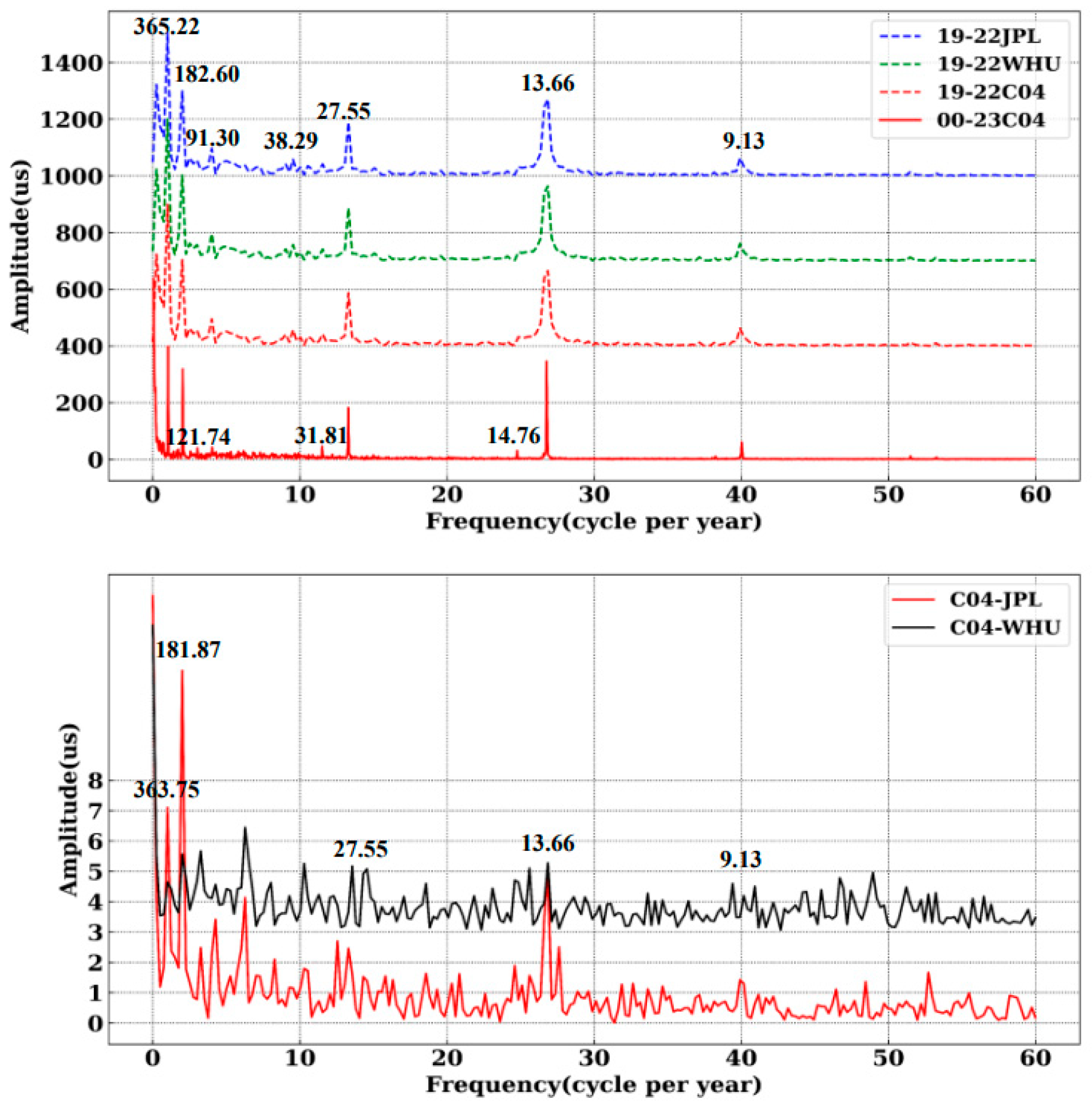

| UT1 | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
|---|---|---|---|---|---|---|
| IVS | 39.58 | 38.66 | 8.51 | 9.84 | 122.95 | −180.26 |
| NTSC | 102.32 | 101.67 | −11.36 | −25.65 | 215.29 | −239.59 |
| LOD | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
|---|---|---|---|---|---|---|
| JPL | 41.39 | 23.30 | −34.21 | −34.13 | 95.51 | −98.46 |
| WHU | 29.95 | 21.81 | −20.51 | −20.31 | 86.21 | −99.64 |
| Period (days) | 4 y JPL (µs) | 4 y WHU (µs) | 4 y C04 (µs) | 23 y C04 (µs) |
|---|---|---|---|---|
| 9.13 | 63.07 | 61.35 | 61.80 | 60.70 |
| 13.66 | 270.07 | 263.49 | 265.12 | 346.47 |
| 14.76 | -- | -- | -- | 30.97 |
| 27.55 | 189.35 | 186.52 | 187.09 | 182.38 |
| 31.81 | 41.64 | 41.29 | 41.91 | 45.65 |
| 38.29 | 57.25 | 57.24 | 56.61 | -- |
| 91.30 | 96.39 | 96.25 | 95.15 | 42.68 |
| 121.74 | 55.52 | 56.78 | 55.86 | 40.05 |
| 182.60 | 298.79 | 302.12 | 303.91 | 318.45 |
| 365.22 | 505.66 | 500.57 | 499.20 | 399.21 |
| … | … | … |
| Period (days) | C04, JPL Amplitude (µs) | C04, WHU Amplitude (µs) |
|---|---|---|
| 33.92 | 20.17 | |
| 7.46 | 1.36 | 1.95 |
| 9.13 | 1.42 | 1.59 |
| 13.66 | 4.91 | 2.28 |
| 27.55 | 2.45 | 2.17 |
| 58.20 | 4.13 | 3.44 |
| 85.59 | 3.41 | 1.56 |
| 121.33 | 2.48 | 1.68 |
| 181.87 | 11.62 | 2.57 |
| 363.75 | 7.10 | 1.65 |
| … | … | … |
| UT1 | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
| IVS-J-E | 26.97 | 26.97 | 0.05 | 2.52 | 54.74 | −81.68 |
| IVS-W-E | 26.67 | 26.64 | −1.40 | −1.46 | 62.24 | −68.90 |
| IVS-J | 28.17 | 28.17 | −0.09 | 2.38 | 54.00 | −90.65 |
| IVS-W | 28.37 | 28.35 | −1.08 | −3.18 | 57.18 | −79.45 |
| IVS | 38.33 | 38.16 | 3.61 | 2.91 | 120.38 | −106.95 |
| LOD | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
| IVS-J-E | 13.54 | 13.48 | 1.35 | −1.45 | 37.59 | −33.93 |
| IVS-W-E | 10.68 | 10.62 | 1.12 | 1.81 | 24.18 | −39.66 |
| IVS-J | 15.28 | 15.12 | −2.23 | 0..03 | 36.48 | −41.25 |
| IVS-W | 15.37 | 15.14 | −2.71 | −2.20 | 32.92 | −44.52 |
| JPL | 45.41 | 15.16 | −42.81 | −43.7 | −2.70 | −85.00 |
| WHU | 27.35 | 15.11 | −22.79 | −22.30 | 12.00 | −66.00 |
| UT1 | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
| NTSC-J-E | 54.42 | 54.42 | −0.13 | −3.86 | 148.24 | −87.67 |
| NTSC-W-E | 47.36 | 47.35 | 1.02 | −14.49 | 125.80 | −57.78 |
| NTSC-J | 64.09 | 63.86 | 5.51 | 6.27 | 148.55 | −106.55 |
| NTSC-W | 59.49 | 59.46 | −1.79 | 3.60 | 137.84 | −116.36 |
| NTSC | 102.69 | 102.65 | −3.00 | −22.20 | 215.30 | −239.60 |
| LOD | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
| NTSC-J-E | 13.47 | 13.27 | −2.28 | −1.38 | 28.29 | −43.84 |
| NTSC-W-E | 11.54 | 11.53 | −0.48 | 0.40 | 18.59 | −41.44 |
| NTSC-J | 14.68 | 14.38 | −2.98 | −0.73 | 28.99 | −31.43 |
| NTSC-W | 14.55 | 14.33 | −2.49 | −1.08 | 26.60 | −42.76 |
| JPL | 45.41 | 15.16 | −42.81 | −43.7 | −2.70 | −85.00 |
| WHU | 27.35 | 15.11 | −22.79 | −22.30 | 12.00 | −66.00 |
| PRODUCT | UT1/µs | LOD/µs | ||
|---|---|---|---|---|
| RMS w.r.t. C04 | Kalman Uncertainties | RMS w.r.t. C04 | Kalman Uncertainties | |
| IVS-J-E | 26.97 | 22.30 | 13.54 | 13.92 |
| IVS-W-E | 26.67 | 21.92 | 10.68 | 11.03 |
| IVS-J | 28.17 | 24.70 | 15.28 | 14.70 |
| IVS-W | 28.37 | 24.27 | 15.27 | 14.12 |
| NTSC-J-E | 54.42 | 42.95 | 13.47 | 12.59 |
| NTSC-W-E | 47.36 | 35.47 | 11.54 | 11.12 |
| NTSC-J | 64.09 | 55.22 | 14.68 | 14.29 |
| NTSC-W | 59.49 | 49.81 | 14.55 | 13.92 |
| UT1 | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
| IVS-NTSC-W-E | 25.59 | 25.49 | 2.22 | 3.34 | 59.42 | −59.54 |
| IVS-W-E | 26.67 | 26.64 | −1.40 | −1.46 | 62.24 | −68.90 |
| IVS-NTSC | 39.43 | 39.08 | 5.18 | 2.35 | 90.34 | −95.70 |
| IVS | 38.33 | 38.16 | 3.61 | 2.91 | 120.38 | −106.95 |
| LOD | RMS (µs) | STD (µs) | MEAN (µs) | MEDIAN (µs) | MAX. (µs) | MIN. (µs) |
| IVS-NTSC-W-E | 10.77 | 10.77 | −0.08 | 0.23 | 22.69 | −42.93 |
| IVS-W-E | 10.68 | 10.62 | 1.12 | 1.81 | 24.18 | −39.66 |
| WHU | 27.35 | 15.11 | −22.79 | −22.30 | 12.00 | −66.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wu, Y.; Yao, D.; Liu, J.; Nan, K.; Zhang, Z.; Wang, W.; Duan, X.; Ma, L.; Yang, H.; et al. Research on Universal Time/Length of Day Combination Algorithm Based on Effective Angular Momentum Dataset. Remote Sens. 2025, 17, 1157. https://doi.org/10.3390/rs17071157
Li X, Wu Y, Yao D, Liu J, Nan K, Zhang Z, Wang W, Duan X, Ma L, Yang H, et al. Research on Universal Time/Length of Day Combination Algorithm Based on Effective Angular Momentum Dataset. Remote Sensing. 2025; 17(7):1157. https://doi.org/10.3390/rs17071157
Chicago/Turabian StyleLi, Xishun, Yuanwei Wu, Dang Yao, Jia Liu, Kai Nan, Zewen Zhang, Weilong Wang, Xuchong Duan, Langming Ma, Haiyan Yang, and et al. 2025. "Research on Universal Time/Length of Day Combination Algorithm Based on Effective Angular Momentum Dataset" Remote Sensing 17, no. 7: 1157. https://doi.org/10.3390/rs17071157
APA StyleLi, X., Wu, Y., Yao, D., Liu, J., Nan, K., Zhang, Z., Wang, W., Duan, X., Ma, L., Yang, H., Qiao, H., Yang, X., Li, X., & Zhang, S. (2025). Research on Universal Time/Length of Day Combination Algorithm Based on Effective Angular Momentum Dataset. Remote Sensing, 17(7), 1157. https://doi.org/10.3390/rs17071157






