2.1. Analysis of Strong Straylight
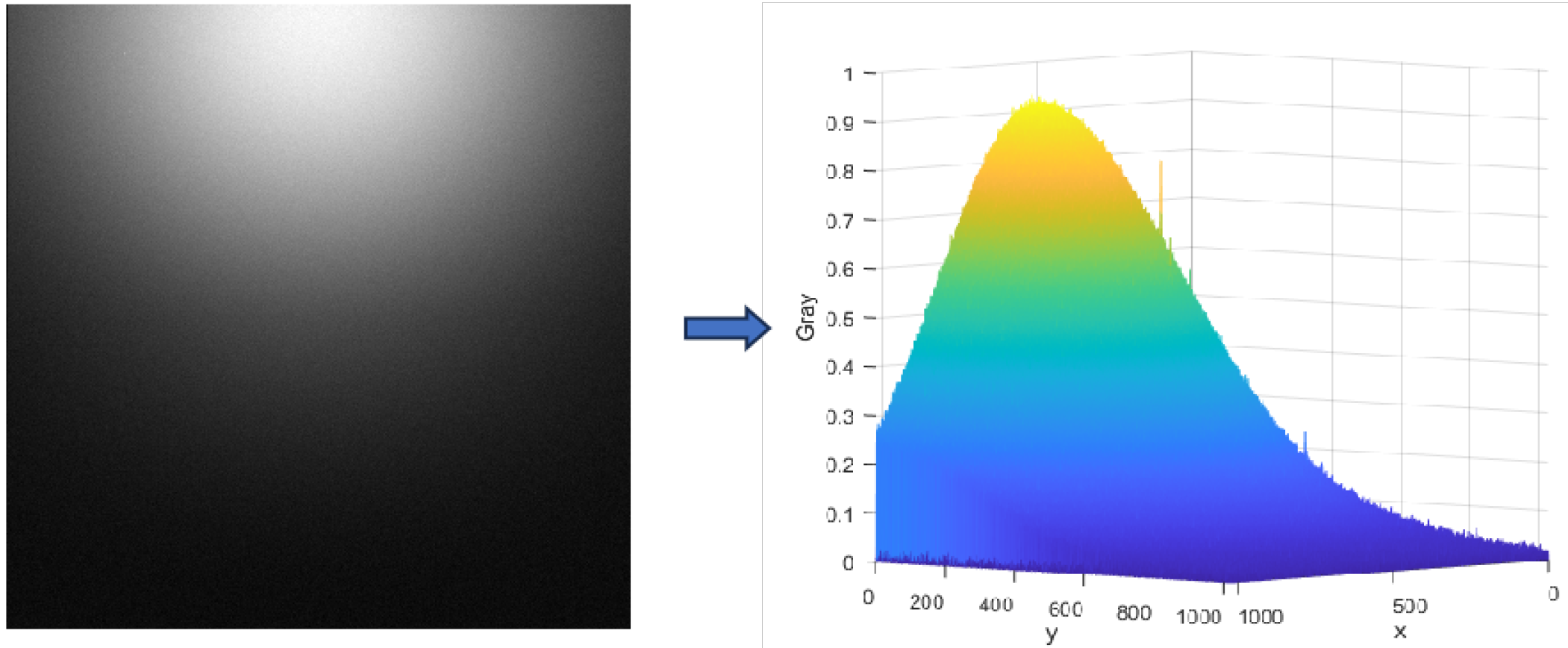
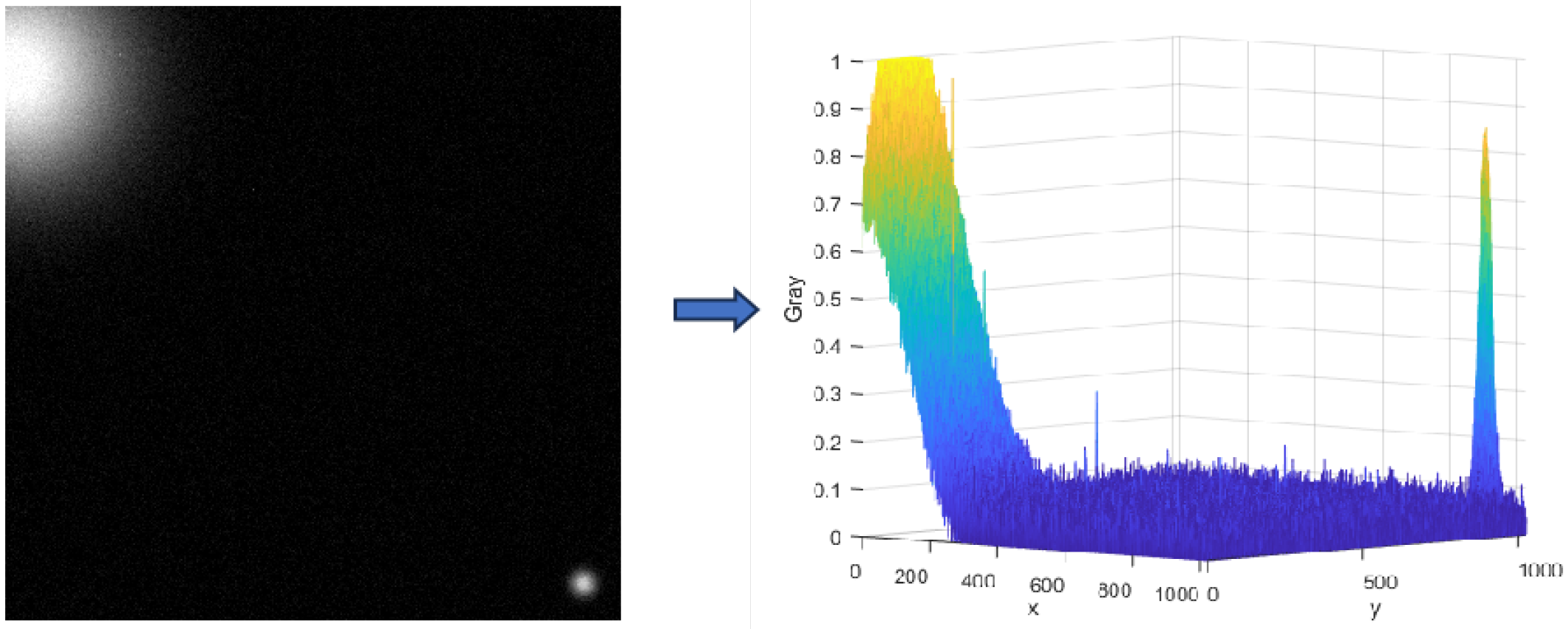
Straylight, including sunlight, moonlight, and Earth-atmosphere light, causes interference with star trackers. Straylight can cause local or overall brightness in the star tracker’s images, resulting in a higher background value and certain star points being veiled. The following equation describes the imaging characteristics of star pictures [
25,
26] when noise and straylight background interference are presented:
In the equation, represents the pixel value at position in the star image, denotes the pixel value of the star at position , is the straylight background at position in the star image, and denotes the noise at position .
2.1.1. Star Sensor System Noise
The noise in star sensor images is mostly caused by device noise during operation and background noise from the star field. The imaging process is influenced by a variety of noise sources, including readout noise, dark current noise, and shot noise, due to inherent faults in the star sensor’s CCD sensing components [
27,
28]. Readout noise refers to the uncertainty created during the process of reading electrons from the camera, such as thermal mobility of electrons within the device, reset of the readout amplifier, and analog-to-digital conversion (ADC). Dark current noise is caused by thermally produced electrons within the silicon layer of the camera chip, which are expressed as pixels. It is mostly caused by thermal excitation in semiconductors and is random in both space and time, dependent on the material quality and manufacturing method of the camera chip. Thermal pixels in star sensor images are created mostly by displacement damage from high-energy particles or muons in space radiation that strike the image sensor. This causes charge leakage in certain pixels on the device, resulting in higher dark signals and worse charge transfer efficiency.
2.1.2. Strong Straylight Noise
For a star sensor, the wavelength of light that can be imaged by its sensing element is fixed,
is a constant. Let the transmission coefficient be
. The atmospheric scattering light radiation intensity model can be approximated as [
29]:
In the equation, denotes the radiation intensity of atmospheric scattered light, represents the solar radiation intensity, is the scattering angle, is the phase function, and l is the scattering path length. is the transmission coefficient. Because solar radiation intensity is constant, the radiation intensity of atmospheric scattered light is determined solely by the scattering angle and path length. As a result, the intensity of terrestrial glow impacting star point imaging is affected by both the scattering angle and the scattering route length.
Geometric relationships show that within a local pixel neighborhood, the scattering path length of the terrestrial light in the atmosphere varies continuously and monotonically. Because the fluctuation in the scattering path length is substantially smaller than the overall route length, it is reasonable to assume that the scattering path length along the x and y directions of the star field varies linearly. As a result, a plane model can be used to estimate the scattering path length of light in the atmosphere within the immediate area. A background grayscale model for the immediate region can be created using the linear connection between the incident light intensity and the pixel imaging gray scale in a star sensor.
In the equation, represents the grayscale value of the pixel, K is a constant proportional coefficient determined by the star sensor’s hardware parameters, denotes the terrestrial glow radiation model from the previous equation, and is the initial background grayscale value.
When the sun approaches the sun sensor’s baffle avoidance angle, solar straylight noise can have a substantial impact on the star sensor’s operation. The windows around the star image point are all small. Within this narrow range, the energy distribution of solar straylight can be modeled as simple linear ramp noise. The collected energy of the pixels
is the sum of a constant threshold and the ramp function, represented as [
30].
In the equation, and are the slopes in the row direction (x-direction) and column direction (y-direction), respectively; is the background energy threshold; b is the y-intercept of the ramp; and represents the effective starlight energy value of the pixel.
The centroid truth value is located on a pixel, and its integral coordinate is , which is the geometric center point of the pixel, and the window is opened around , and the truth offset relative to the pixel center point is defined as and , and then the centroid line coordinates (x and y are equivalent) under the background of solar straylight.
2.3. Saliency Detection Algorithm
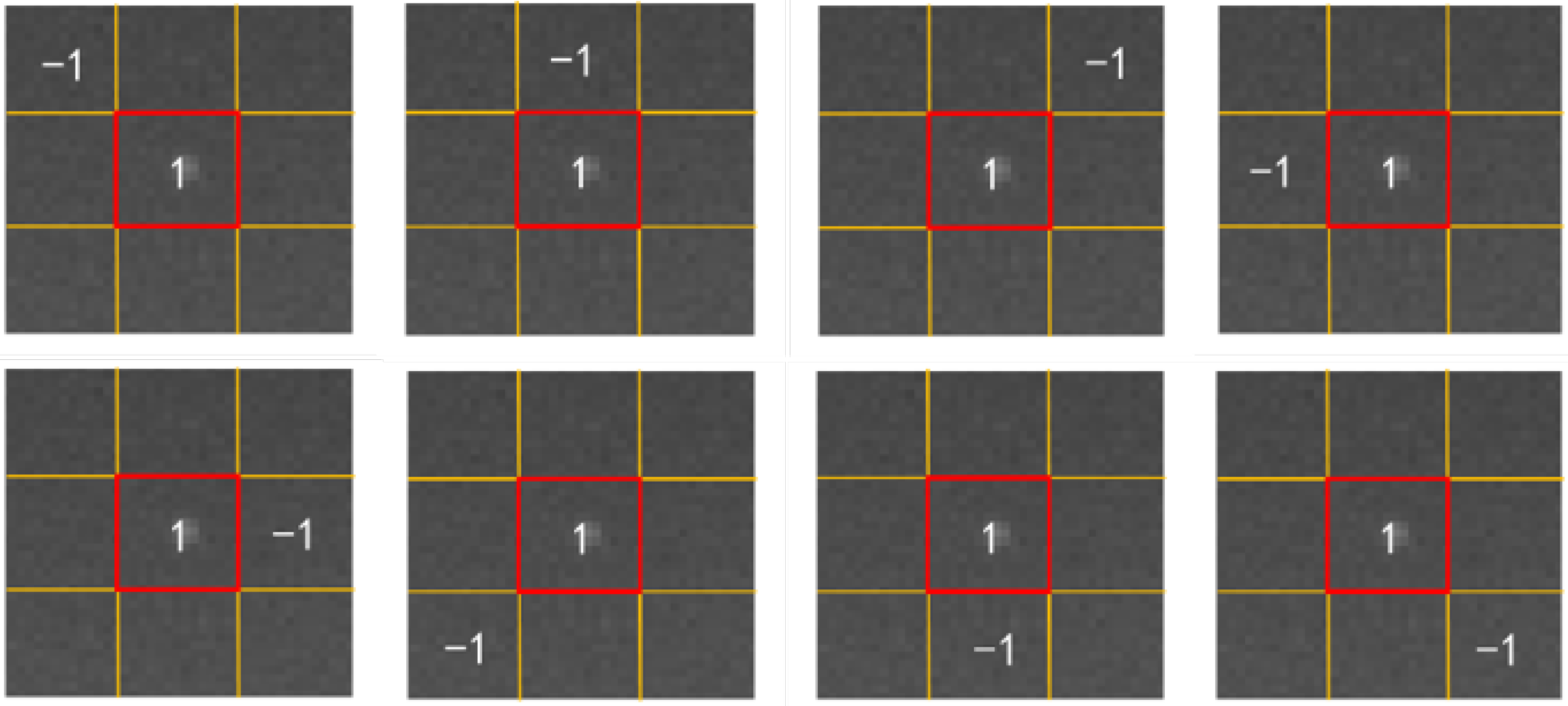
The star point extraction algorithm suggested in this chapter, which is based on multi-directional gradient local contrast enhancement, is principally inspired by the saliency detection MPCM algorithm. As a result, the purpose of this section is to describe how the MPCM algorithm works. The classic local contrast algorithm (LCM), first proposed by Chen, is a weak target identification algorithm designed for the human vision system. The LCM algorithm calculates each pixel’s local contrast value by discriminating between the weak target region and the background region and then comparing each pixel with its neighbors.
Figure 5 shows the definitions for the target and background regions. Here,
w represents the current frame image,
u denotes the target region, and
v signifies the moving scanning window within the image.
Figure 6 depicts the LCM algorithm, which uses a sliding window to travel pixel by pixel across the image from left to right and top to bottom. Each window is divided into 9 (3 × 3) sub-windows, with the middle red rectangular position representing the target’s likely location.
Figure 6 depicts the region dividing method used to perform local contrast calculations.
First, calculate the maximum grayscale value
at the central region “0”, as follows:
In the equation, represents the grayscale value of the k pixel in region 0, and N denotes the number of pixels within the region.
Next, for the eight surrounding small regions (1 to 8) near the central region “0”, calculate the average grayscale value for each of these small regions, as follows:
In the equation, represents the grayscale value of the k pixel in the i small region among the eight neighboring regions, while denotes the total number of pixels in the i small region.
Therefore, the contrast value
for the central small region and each of the neighboring small regions can be obtained as follows:
Finally, the local contrast LCM value
C can be computed as follows:
The larger the value of C, the greater the likelihood that the central region contains the target. The analysis is as follows: If the central region is the target, then , which results in . If the central region is not the target, then , which results in .
In the PCM(Possibilistic C-means) algorithm, to define the proposed measure, a nested structure is illustrated as shown in
Figure 7. First, the sliding window is divided into two parts: the center red rectangular box, denoted as
T, where the target is likely to appear, and the surrounding part, which represents the background. To measure local contrast more accurately, the surrounding background part is divided into 8 patches
, where
. This method aims to enhance the target and suppress the background. The definition of the PCM algorithm is as follows:
The difference between the target sub-window
T and the background sub-window
can be defined as follows:
In the equation,
d represents the degree of difference between the target and the background. There are various methods for calculating
d; this paper uses the mean difference method as follows:
In the equation, and represent the mean pixel values of the target region and the background sub-region, respectively.
Building on the above, a local contrast measure at a certain scale is further introduced to effectively describe the prominence of small targets in complex backgrounds. For small targets, the grayscale intensity within the region often differs significantly from the surrounding background. To quantitatively describe this property, this paper proposes the following definition:
In the equation, indicates the difference between the reference patch and the background patch in the i direction. We can see that when and have the same sign, . This means that the intensity of the central putative target region is either greater or less than that of the background patches. As a result, it can be used to assess the properties of the target region.
In dim target enhancement, the contrast between the target and background regions should be as high as possible.
Figure 8 shows the minimal distance between the reference sub-window and the surrounding background sub-window, which can be used to measure contrast. To calculate a sub-window-based contrast measure (PCM) on a given scale, follow these steps:
where
represents the coordinates of the reference center pixel.
where
N is the width and height of the image, and
rounds
down to the nearest integer less than or equal to
. The PCM algorithm workflow is as follows:
(1) Calculate the mean grayscale value of the target sub-window.
(2) Apply the 8 filters, as shown in the figure, to each background sub-window to obtain the background-reduced image.
(3) Compute the local contrast of the image using the following formula:
(4) Slide the window across the entire image until the whole image is processed, and output the saliency contrast map
C, calculated using the following formula:
In practical applications, the size of small targets is often not predetermined. Therefore, the window size should be as close as possible to the actual size of the small target. According to the definition of the MPCM algorithm, the calculation formula is as follows:
where
represents the local contrast map at multiple scales, with
l indicating different scales of the sub-window,
L being the maximum scale, and
p and
q representing the number of rows and columns in the contrast map, respectively.
From the definition of MPCM, it is clear that it is straightforward and suitable for parallel computation. From the above formula, if
for all
i in the target region, then
T is a bright target; otherwise,
T is a dark target. Based on this property, MPCM has two special cases. If only bright targets are present in the known application scenario, then it is as follows:
where
. Similarly, the following formulas can be derived for dark targets:
MPCM can benefit both bright and dark targets. Using the MPCM algorithm, a mean filtering operation can be used as a preprocessing step. This procedure serves to successfully suppress visual clutter and noise, enhancing target recognition accuracy. Mean filtering smoothes out the image, lessening the effect of local noise on future processing. This enables the MPCM algorithm to more accurately identify target regions in complicated backdrops. The MPCM algorithm’s primary role in target detection is to increase the saliency of the target region while suppressing background interference. Because the target zone is brighter than the background, MPCM can improve its brightness attributes at various scales. This enhancement makes the target more visible in the image, increasing the accuracy of target detection. When
and
have opposite signs, the contrast drops. When
and
have the same sign, we have
From the formula, it is clear that the larger T is, the greater becomes. This means that when T is a target, the contrast value increases significantly. Conversely, when T is background, it resembles the surrounding module. In this case, the contrast approaches zero, indicating that the method can enhance the target while suppressing the background.
2.4. Star Point Centroid Calculation
2.4.1. Star Map Enhancement
Although a star field is composed of discrete pixels in a two-dimensional space, due to the relative continuity of pixel grayscale values in the local area, the star field can typically be considered as a two-dimensional surface. In the theory of differential calculus for single-variable functions, curvature is often used to represent the degree of bending of a point on a surface. Suppose that there is a point
on the surface
y, and this point
has second-order derivative characteristics. The curvature of this point on the surface can be expressed as
where
is the horizontal gradient of pixel point
,
is the vertical gradient of pixel point
, and
is the first derivative of pixel point
.
where
is the second derivative of the horizontal direction of pixel point
,
is the second derivative of the vertical direction of pixel point
,
is the second derivative of the mixed direction of pixel point
, and
is the second derivative of pixel point
.
where
S represents the curvature value at the point
,
denotes the second-order derivative at this point on the surface, and
represents the first-order derivative at this point on the surface.
The curvature of a point on an image can be represented as a combination of the second-order and first-order derivatives in a certain direction on the surface at that point. Considering the discrete nature in the digital domain, the spatial curvature at a point on the image can be comprehensively represented using the first-order and second-order derivative values in four directions: 0°, 90°, 180°, and 270°.
In this paper, the facet model proposed by Haralick is used to describe the star field. First, let R = {−2, −1, 0, 1, 2} and C = {−2, −1, 0, 1, 2} be the index sets for symmetric neighborhoods. The pixel values within a 5 × 5 neighborhood can be used to represent the current center pixel, and can be expressed by the following formula:
where
represents the discrete orthogonal polynomial basis, and
satisfies
.
where
represents the combination coefficient, and each combination coefficient
for a pixel
in the star field is unique. Therefore, the expression for the combination coefficient
can be obtained using the least squares fitting of the polynomial orthogonality characteristics, as follows:
A portion of the variables can be represented using the weight coefficient
, as follows:
Thus, the combination coefficient
can be expressed as
where the combination coefficient
is represented by the convolution of the weight coefficient
and the star field, with the weight coefficient
determined based on the characteristics of
.
Combining the principles of directional derivative calculation, the first-order and second-order derivatives of the pixel
along the direction vector
can be expressed as
where
represents the angle between the direction vector
and the horizontal direction of the image.
The preceding formula demonstrates that the computing cost of the second-order derivative is lowered from O(2N) to O(N) when compared with the first-order derivative. As a result, in the following methods provided in this work, only the second-order derivative will be employed to represent the image’s curvature information.
Local contrast enhancement is conducted on the star points in the star field using the second-order derivatives derived at angles of 0°, 90°, 180°, and 270°. The goal of local contrast enhancement is to emphasize the properties of the star points while minimizing interference from complicated backgrounds. Prior to local contrast augmentation, a feature analysis of the star points’ second-order derivatives is performed.
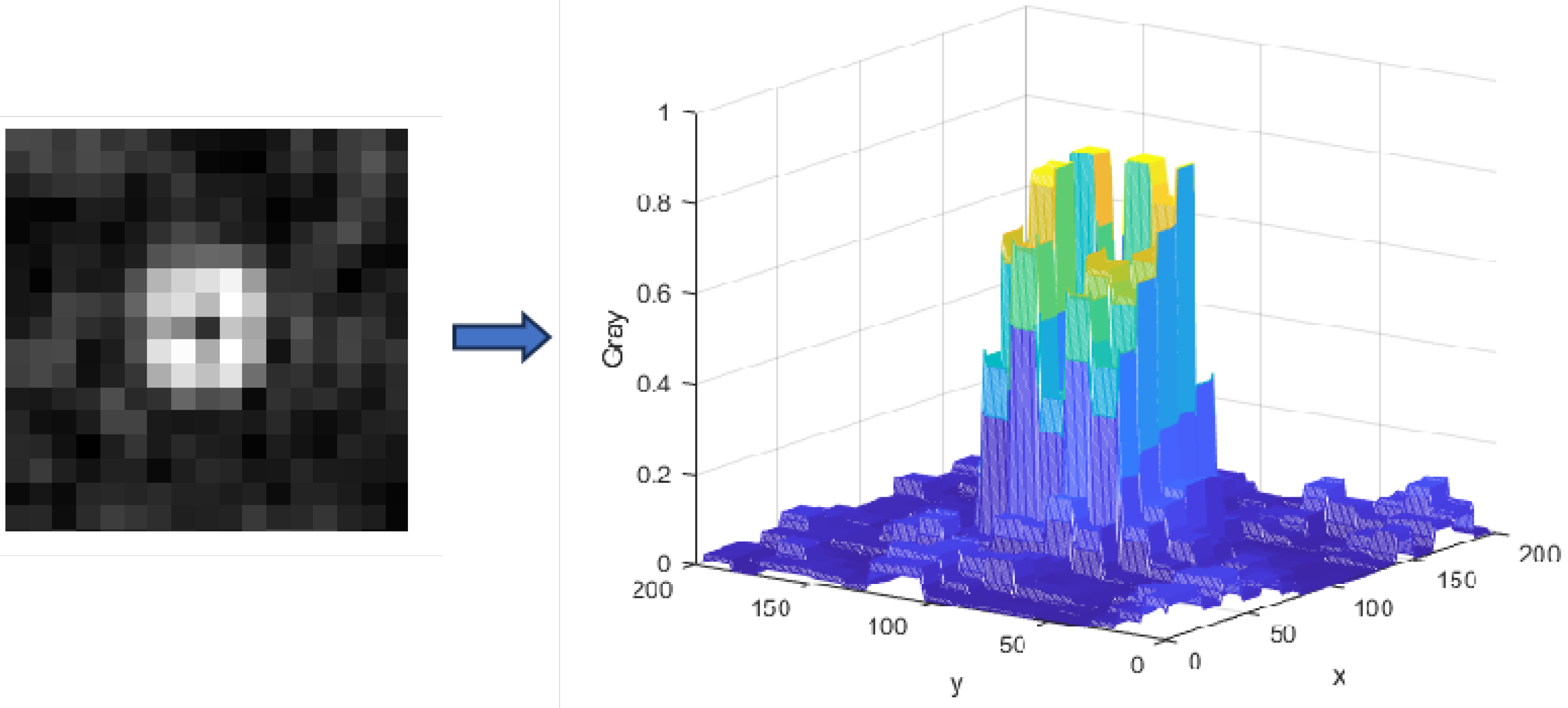
Figure 9 shows the local star field processed using second-order derivatives in the 0°, 90°, 180°, and 270° directions, top to bottom and left to right. In the red rectangle box is a partial enlarged image of the star points after gradient enhancement. The graphic clearly shows that the directional second-order derivative approach improves the local star field while efficiently suppressing interference from intense straylight. Each augmented star field image significantly improves the visibility of star points in all four directions, facilitating the implementation of following star point identification algorithms. Furthermore, this approach remains robust in the presence of significant straylight contamination, which is typical in astronomical photography. It increases not just the visibility of star points but also the overall quality of the star field by decreasing unwanted noise interference.
To address the concerns raised, we offer an improved star point centroid localization approach designed specifically for star maps influenced by severe straylight interference. The suggested method begins with a multi-directional gradient improvement of the star map, which successfully mitigates the effects of intense straylight.
Figure 10 shows how gradient images of the star map in four directions—0°, 90°, 180°, and 270°—are combined to create a locally enhanced star map. This multi-directional gradient enhancement increases the prominence of the star points, which improves their detection capabilities.
2.4.2. Star Detection
Currently, local contrast enhancement algorithms based on the human visual system can successfully extract faint star points that are difficult to separate from background noise, considerably enhancing star point identification capabilities. However, these techniques continue to face hurdles in actual applications requiring high-precision centroid localization of star points. Although dim star points can be effectively retrieved, their energy distribution patterns are frequently disturbed, making precise centroid extraction challenging. As illustrated in
Figure 11, the overemphasis on local information during the execution of local contrast enhancement algorithms can result in irregular energy distributions of star points, upsetting their original distribution. This disturbance not only alters the overall form of the star points, but also complicates and makes the subsequent centroid extraction process more complex. Centroid extraction, an important step in star point analysis, has a substantial impact on subsequent star point analysis and categorization.
In the enhanced star map, the MPCM algorithm is used for initial star point extraction. By performing connected component analysis on the enhanced star map and combining it with threshold segmentation, noise is effectively filtered out, and coarse localization of the star points is achieved.
2.4.3. Star Point Centroid Localization
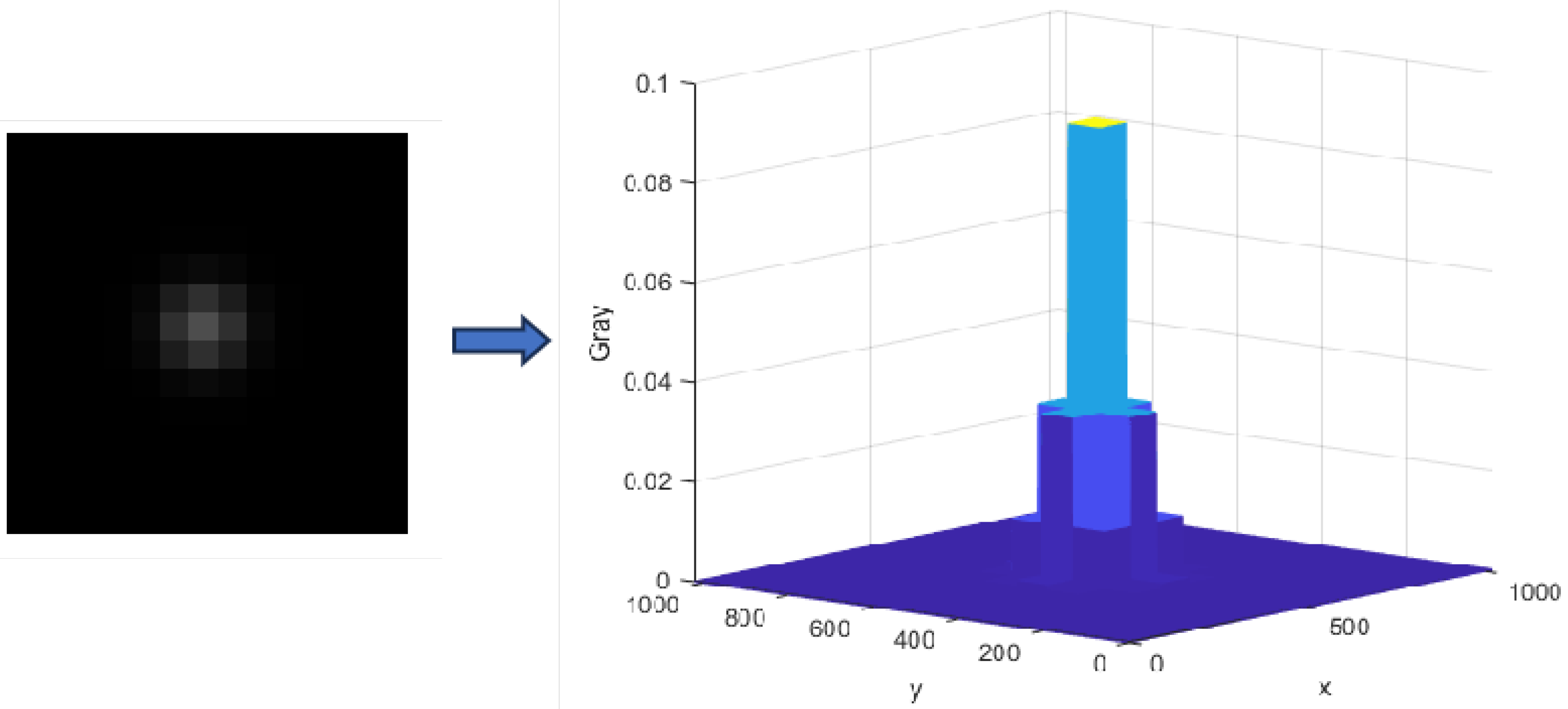
As illustrated in
Figure 12, the intensity distribution of an initial star point imaged on a star tracker is obtained by convolving the intensity distribution function with the optical system’s point spread function. In the ideal model, the star is considered a point target. To achieve higher centroid localization accuracy, the optical system of the star tracker often employs defocusing methods to spread the star spots on the imaging surface to a range of 3 × 3 to 5 × 5 pixels [
31].
where
is the total energy of the star radiated to the imaging plane during the camera exposure time,
denotes the coordinates of the star’s center on the imaging plane, and
represents the diffusion radius of the Gaussian point spread function, indicating the concentration of the star image’s energy.
As shown in
Figure 13, the enhanced star map has an energy distribution pattern with low intensity in the center and high intensity at the edges, which can be approximated as a Gaussian-like distribution near the starting star point. However, due to camera system noise and significant straylight noise, the energy distribution of the improved star map may be compromised to some extent.
In order to overcome this problem, we process the 3 × 3 pixel neighborhood around each star point. As shown in the following formula, the gray values in the eighth neighborhood of the pixel with the lowest energy are arranged from small to large (
), and the variance of the pixels in the eighth neighborhood is calculated. The maximum gray value and the sub-maximum gray value in the eighth neighborhood are subtracting variance. The minimum gray value and the sub-small gray value plus variance can reduce the influence of noise on centroid calculation and improve the accuracy of star centroid localization.
In the equation, is the variance of the eighth neighborhood; , , , and are respectively the maximum gray value in the eighth neighborhood, the sub-major gray value, the maximum gray value after compensation, and the sub-major gray value after compensation; and , , , and are respectively the minimum gray value in the eight neighborhood, the sub-small gray value, the minimum gray value after compensation, and the sub-small gray value after compensation.
This method integrates the star point’s energy distribution characteristics and noise compensation strategy, significantly enhancing the accuracy and reliability of star point detection under strong straylight interference.
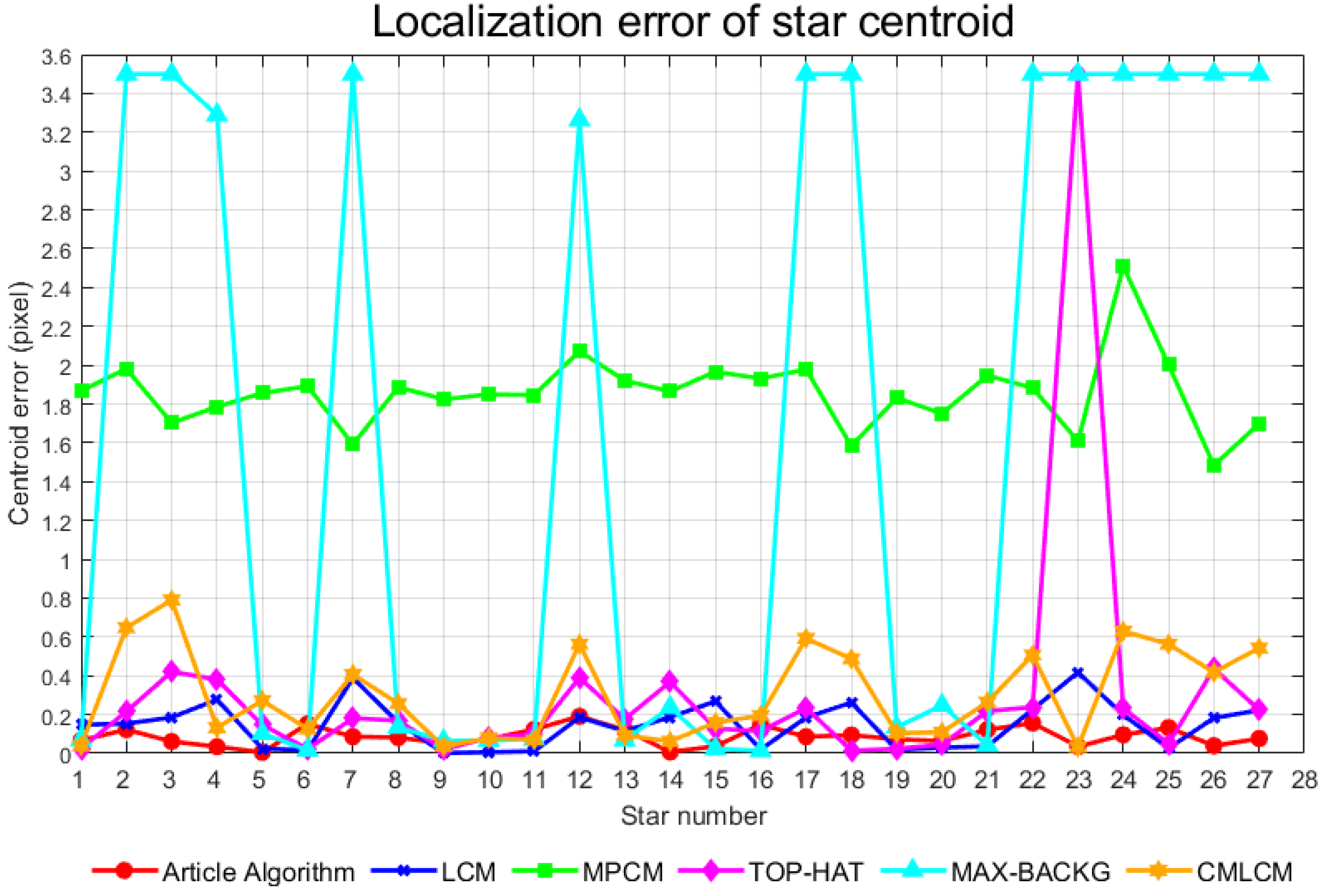
Gaussian fitting, the weighted centroid approach, and the threshold-based centroid method are popular algorithms for extracting star centroids [
32,
33,
34,
35,
36]. The star points after picture enhancement are difficult to fit to compute the center of mass using the Gaussian approach. The weighted centroid approach has low anti-interference ability. The threshold-based centroid method is simple to develop and has excellent anti-noise properties, making it ideal for centroid extraction in this work. As a result, we use the threshold-based centroid approach to calculate centroid values. This approach works by using the gray value of the target pixels within the star picture region to weight their coordinates. The formula for this procedure is provided by
In the formula, represents the pixel coordinates; denotes the pixel gray value; T is the local background threshold for the star point; indicates the coordinates of the top-left pixel of the target star image window; represents the coordinates of the bottom-right pixel of the target star image window, which should encompass all valid pixels covered by the star image point; and is the estimated value of the star image point’s centroid , with subpixel accuracy.
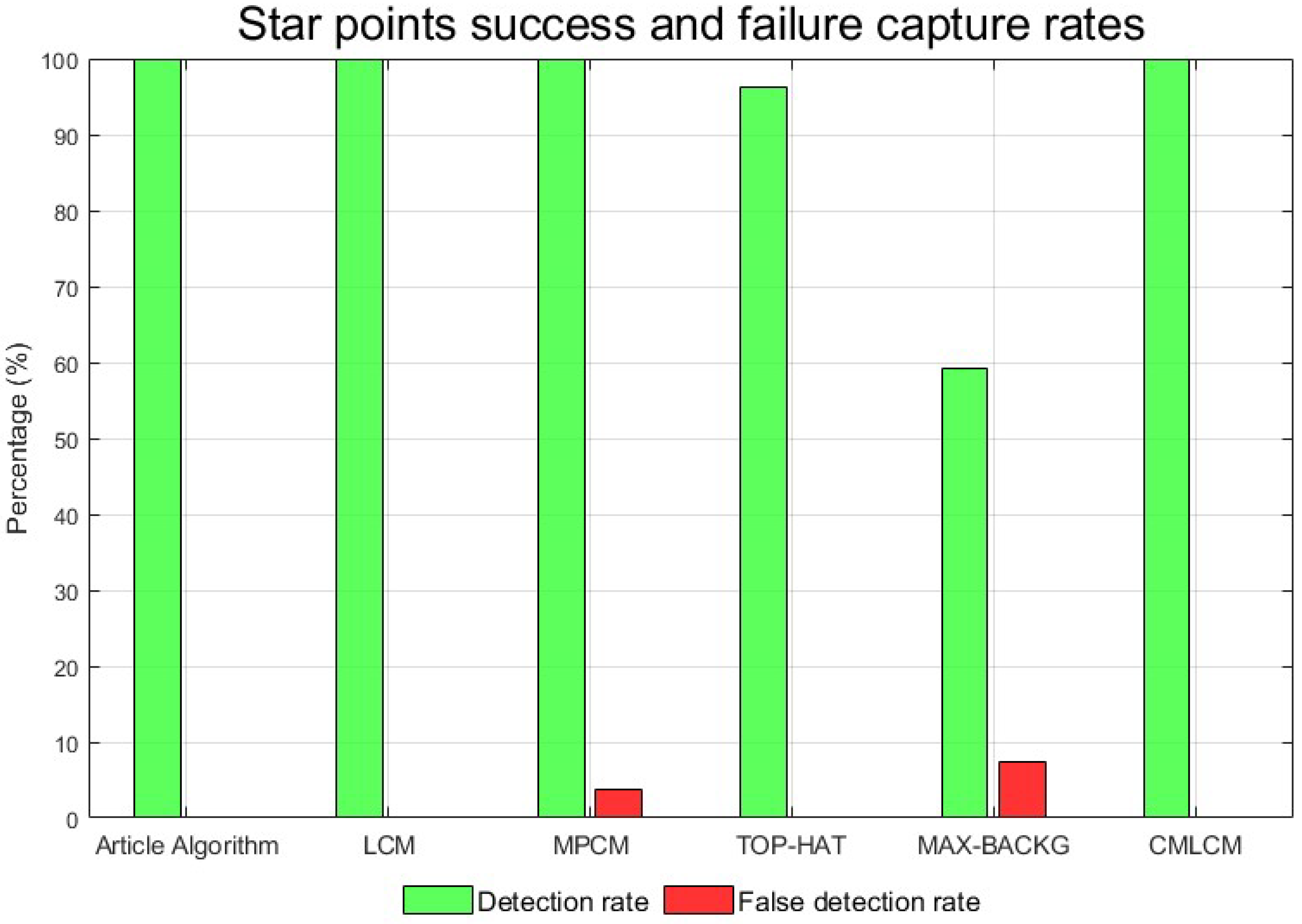
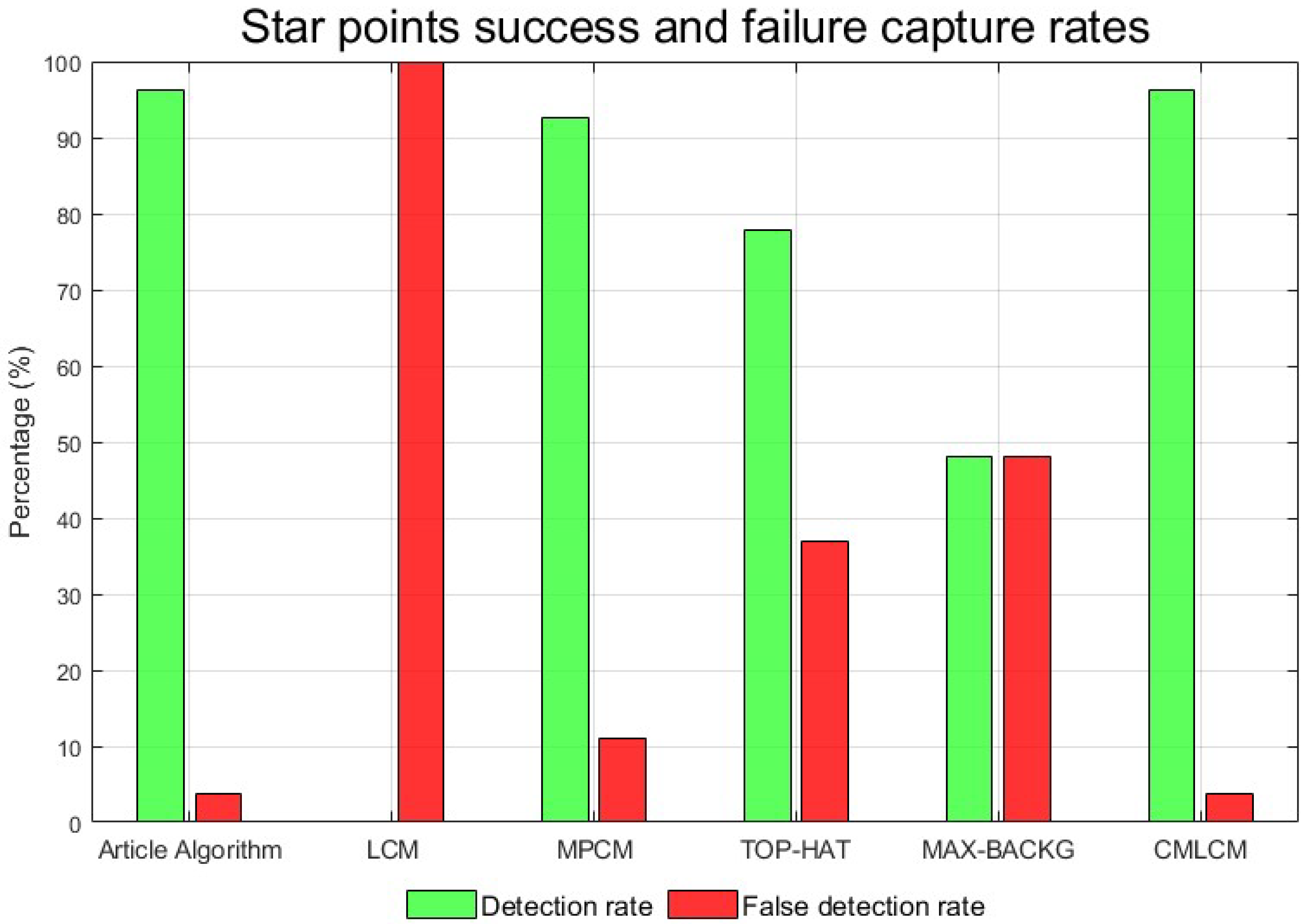
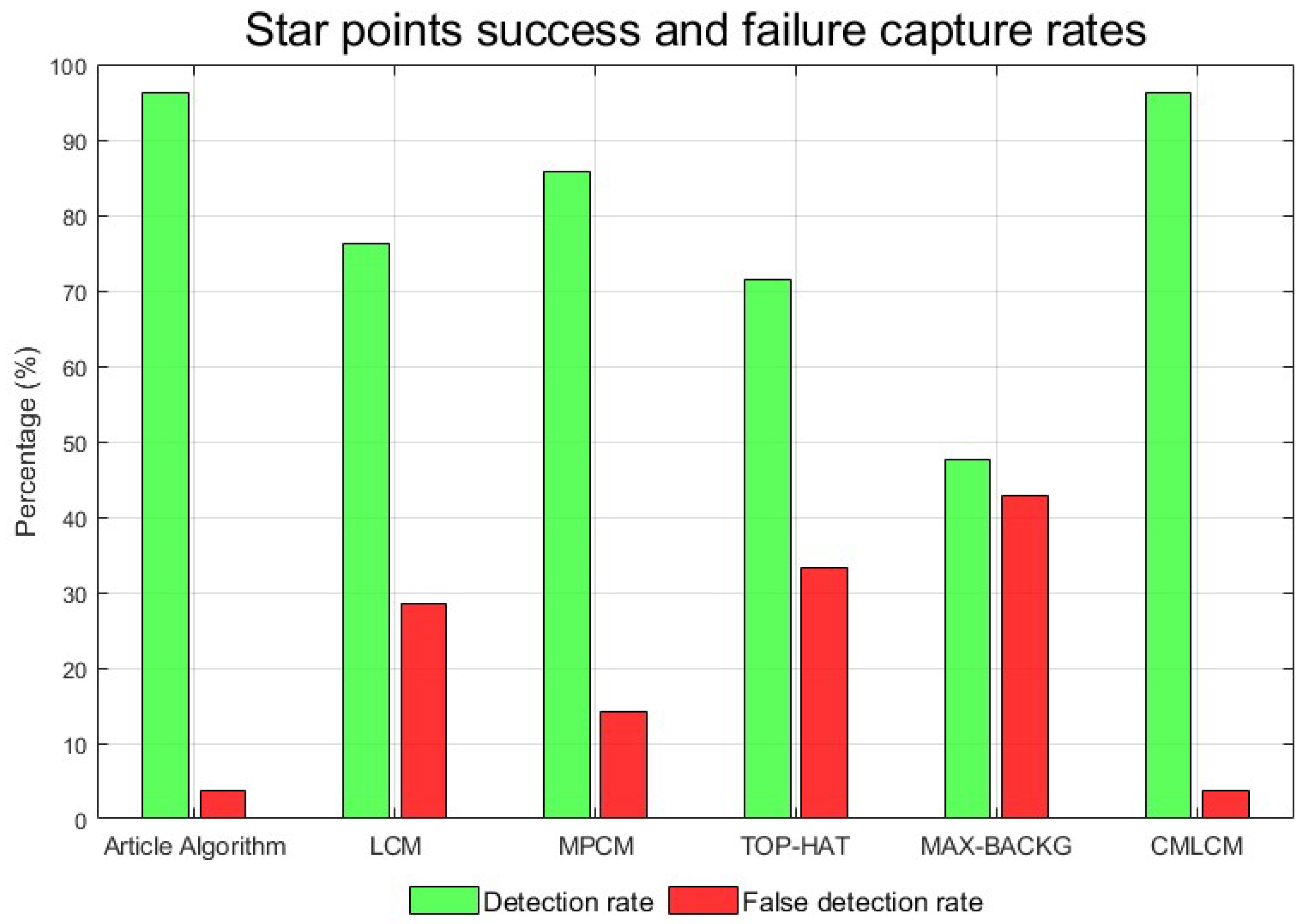
For star maps with strong straylight interference, traditional algorithms (TOP-HAT, MAX-BACKG) rely on accurate background modeling and reasonable processing of the highlighted areas in the image. When straylight introduces a wide range of high-light interference in the image, the two methods may not be able to effectively separate the target and straylight, resulting in poor target recognition or an enhancement effect. Therefore, the algorithm in this paper first introduces a multi-directional gradient to locally enhance the star map under strong straylight interference, enhance the difference degree between the target and the strong straylight background, and improve the subsequent star point extraction rate. Classical significance testing algorithms (LCM, MPCM) are affected by background changes, luminance distribution distortion, and local contrast failure. These problems often lead to inaccurate extraction of salient regions, possibly misinterpreting straylight as the target region, or failing to accurately identify the true target. The CMLCM algorithm first enhanced the image of the star map under the interference of strong straylight, and then extracted the star points directly through the LCM algorithm and threshold segmentation. In this way, the energy distribution of the star points obtained by direct processing was broken, resulting in the low accuracy of star centroid positioning. First, this algorithm makes the enhanced star energy distribution as close as possible to Gaussian distribution by means of four-way gradient local star energy enhancement, and determines the star neighborhood position distribution by the rough extraction of centroid positioning, and introduces the star local neighborhood gray compensation mechanism to further improve the star energy distribution so as to achieve high-precision positioning of a star centroid.