Multi-Timescale Validation of Satellite-Derived Global Horizontal Irradiance in Côte d’Ivoire
Abstract
1. Introduction
2. Materials and Methods
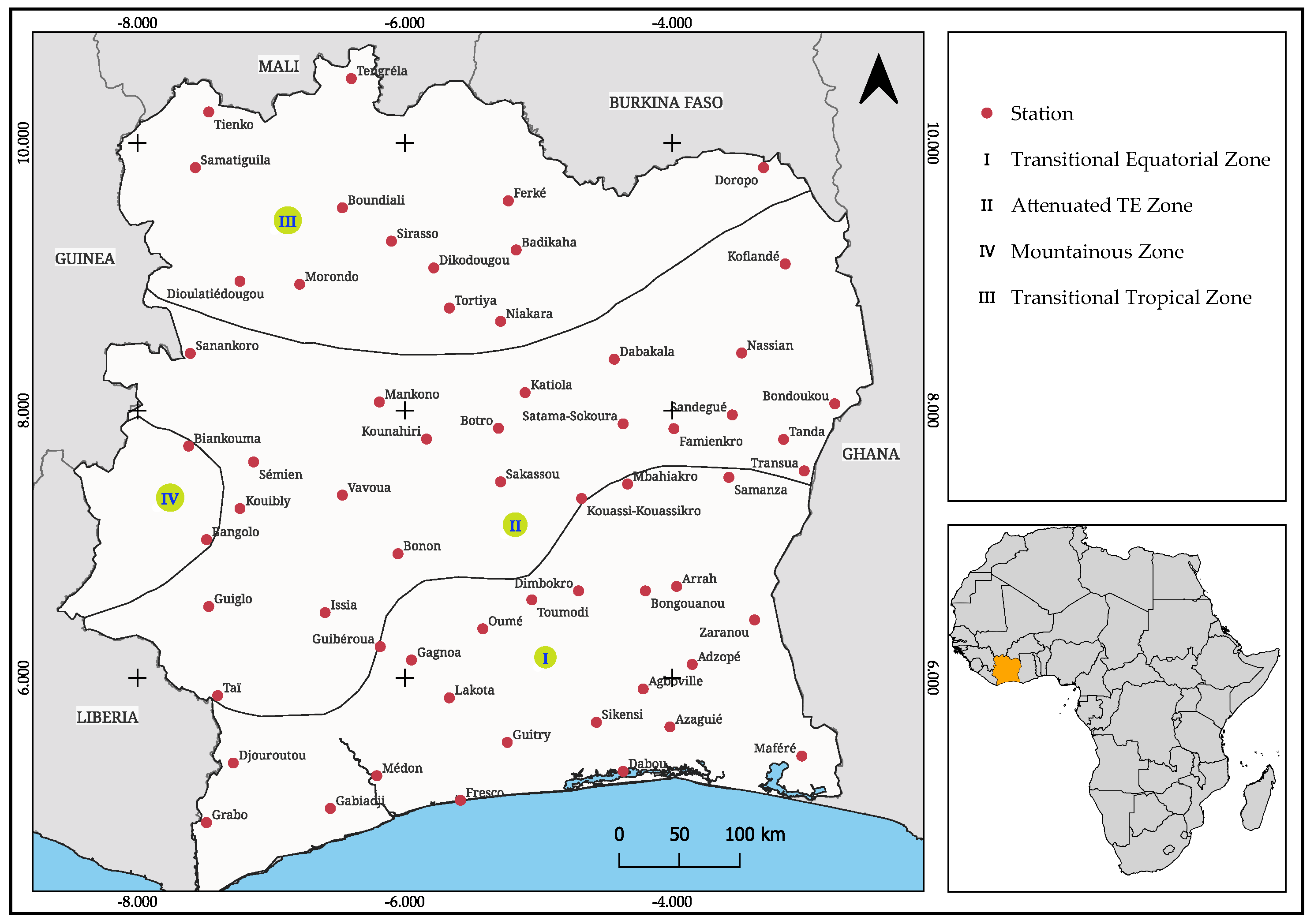
2.1. Study Area
2.2. Satellite and Reanalysis Datasets
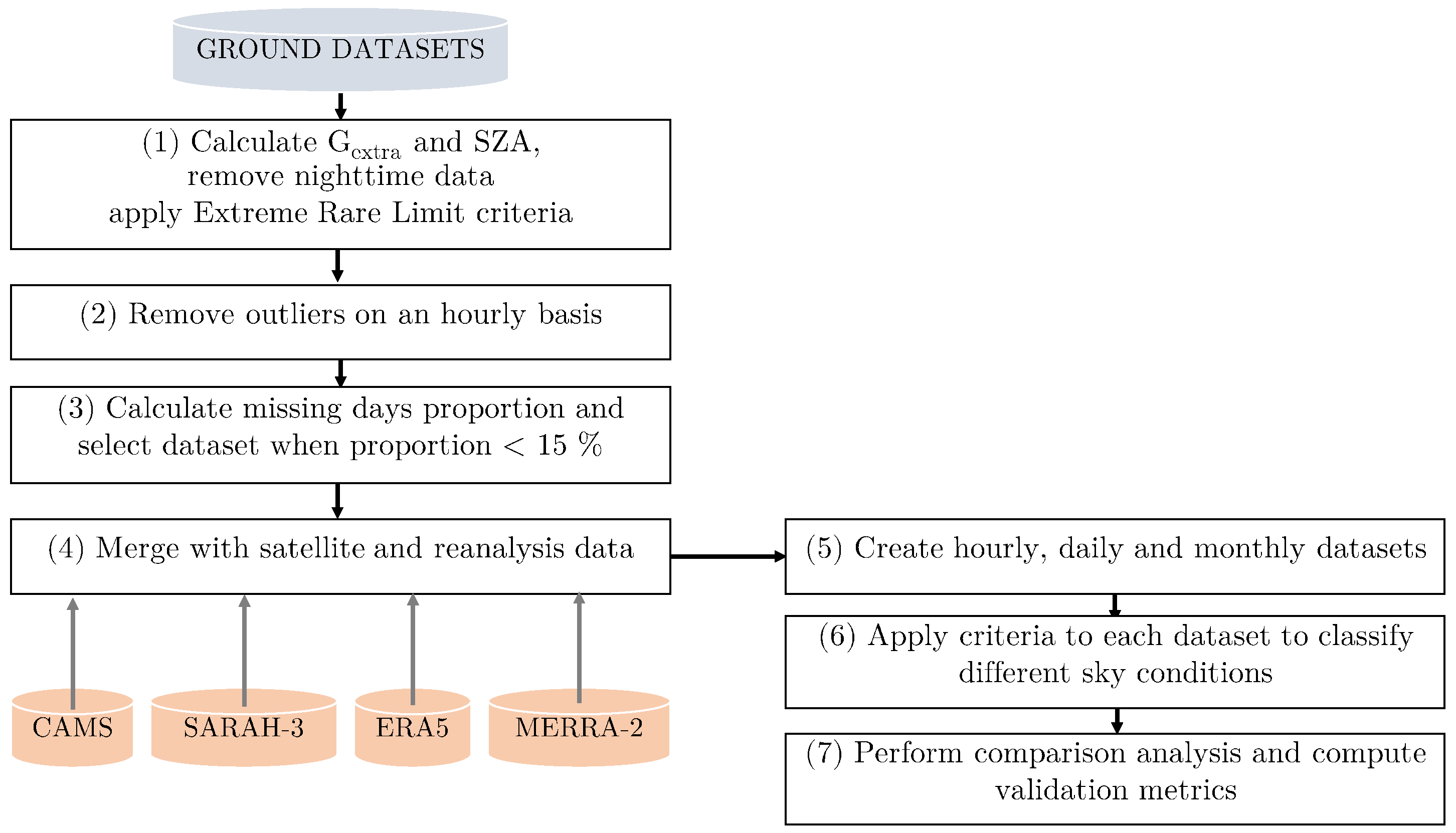
2.3. Quality Control of Ground Measurements Database
2.4. Classification of Sky Conditions
2.5. Validation Metrics
2.6. Data Aggregation
3. Results
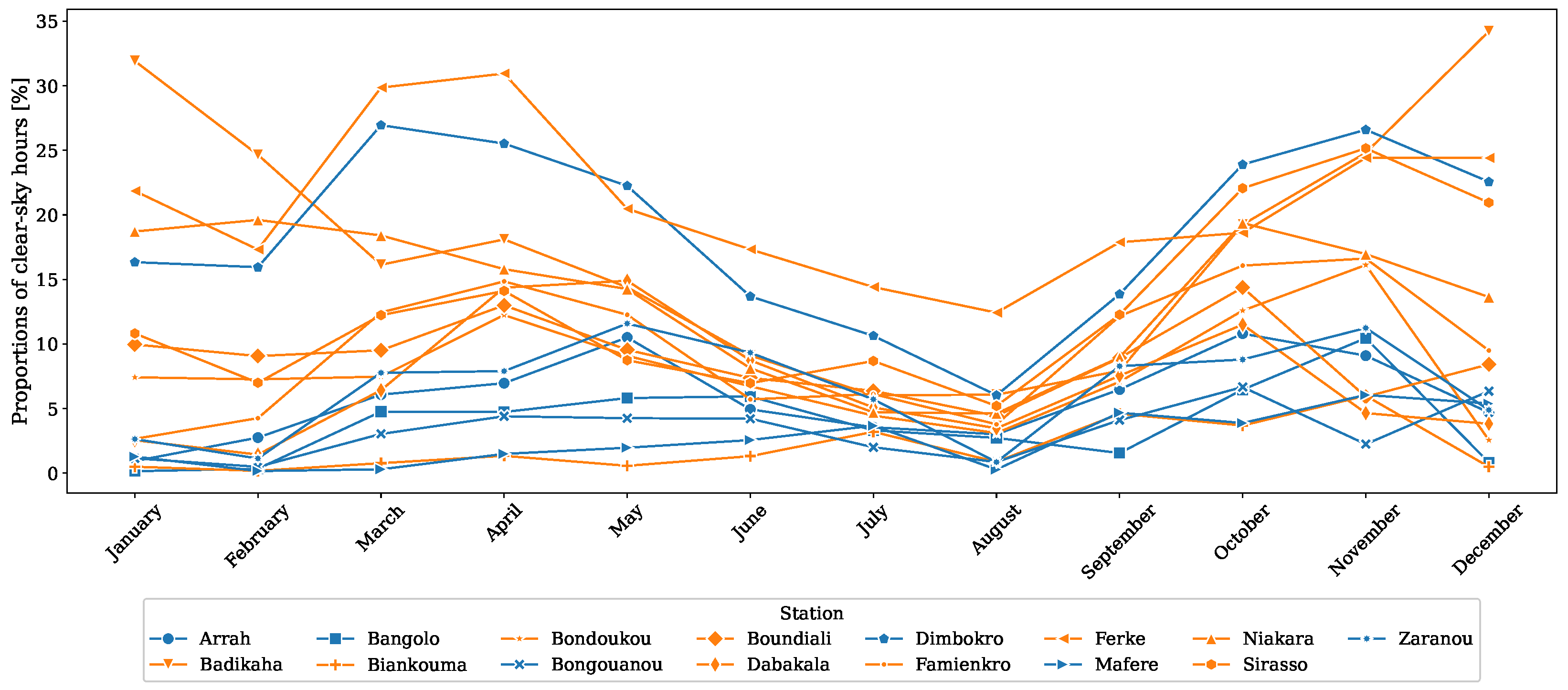
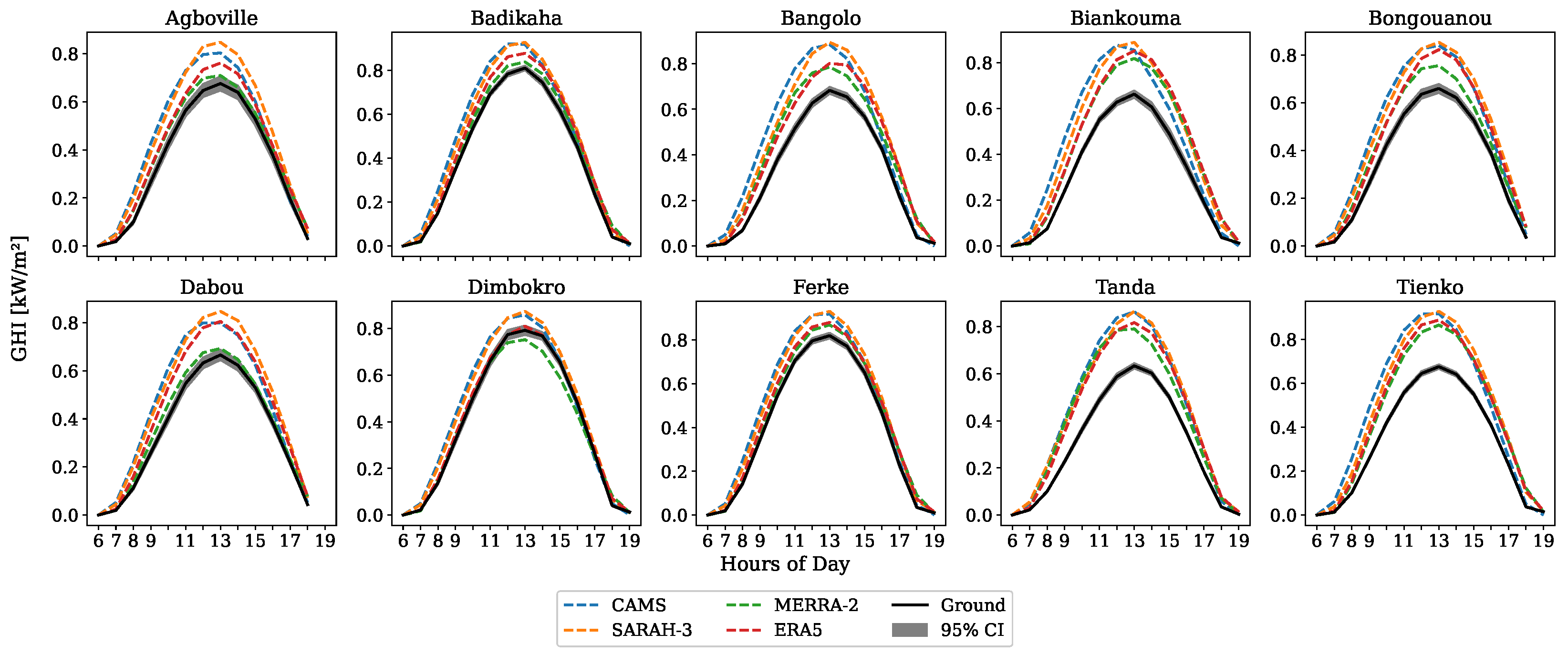
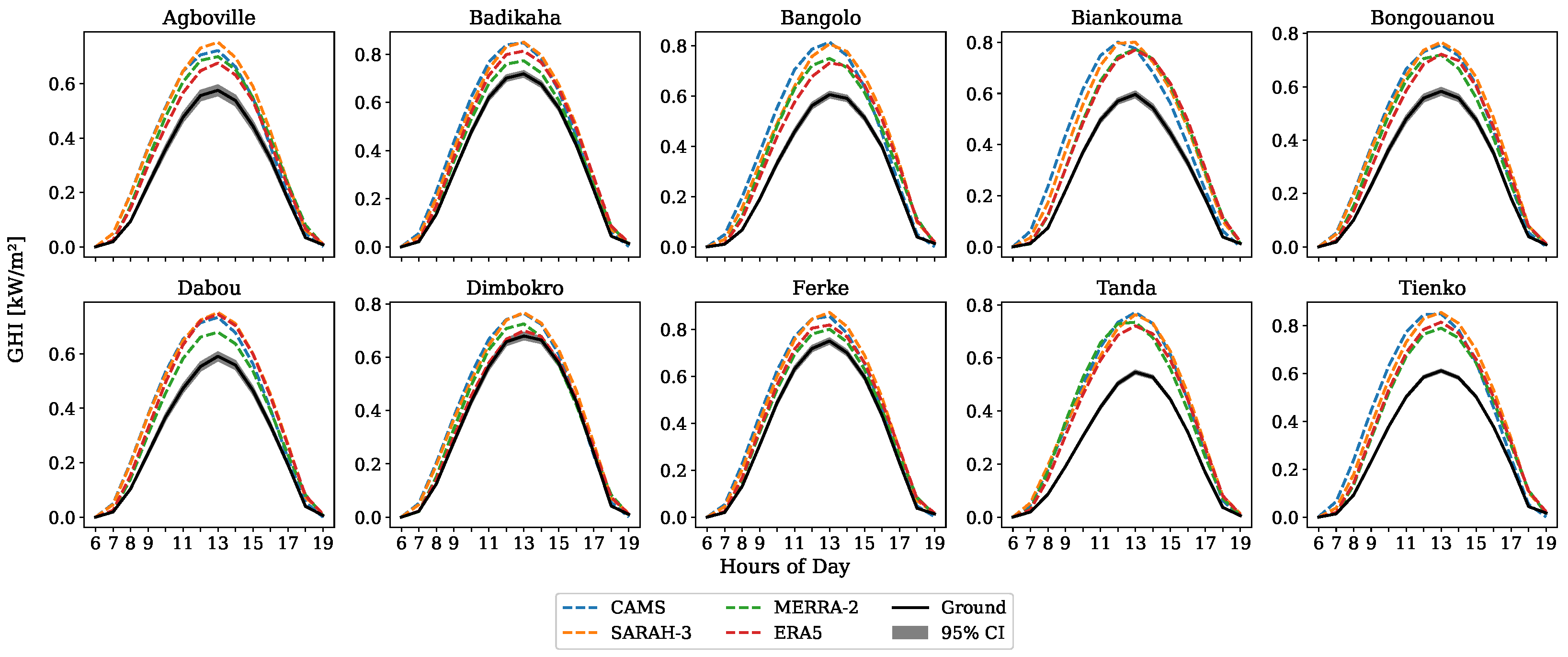
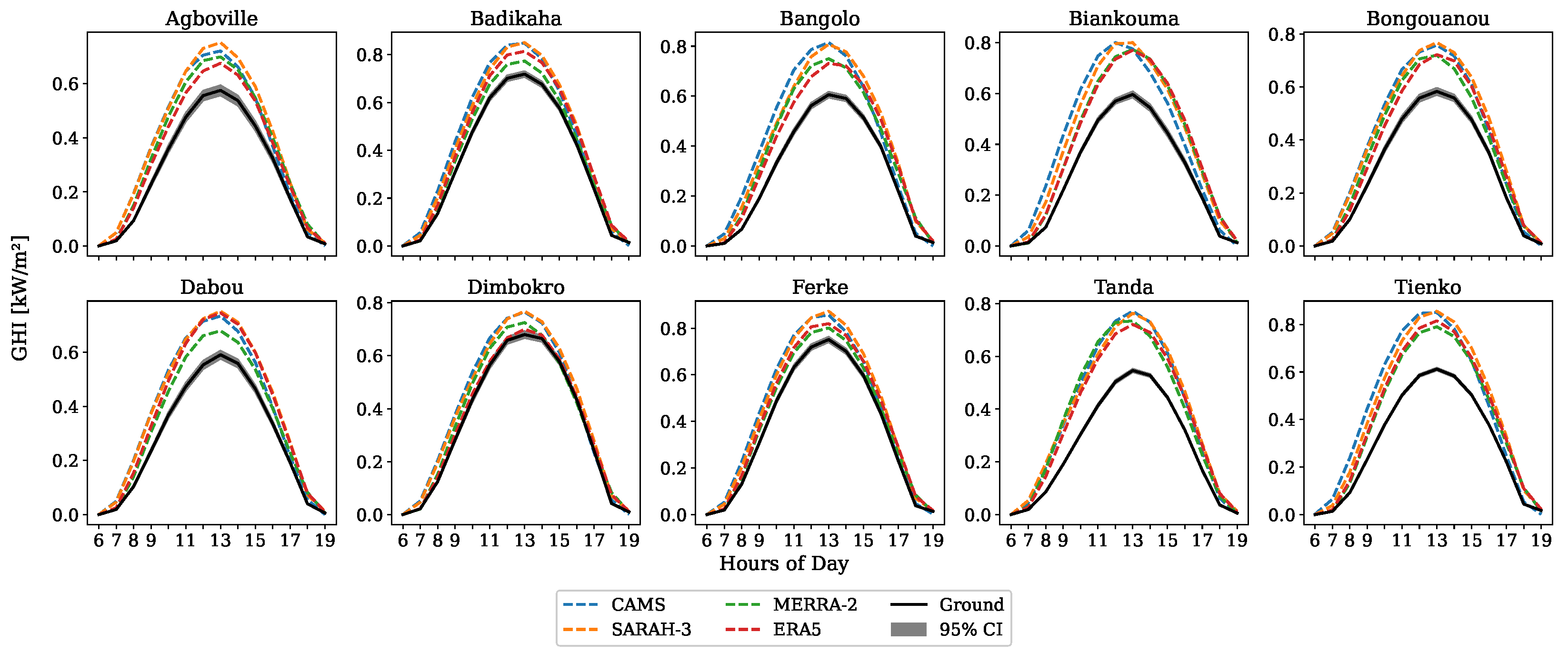
3.1. Clear-Sky Conditions
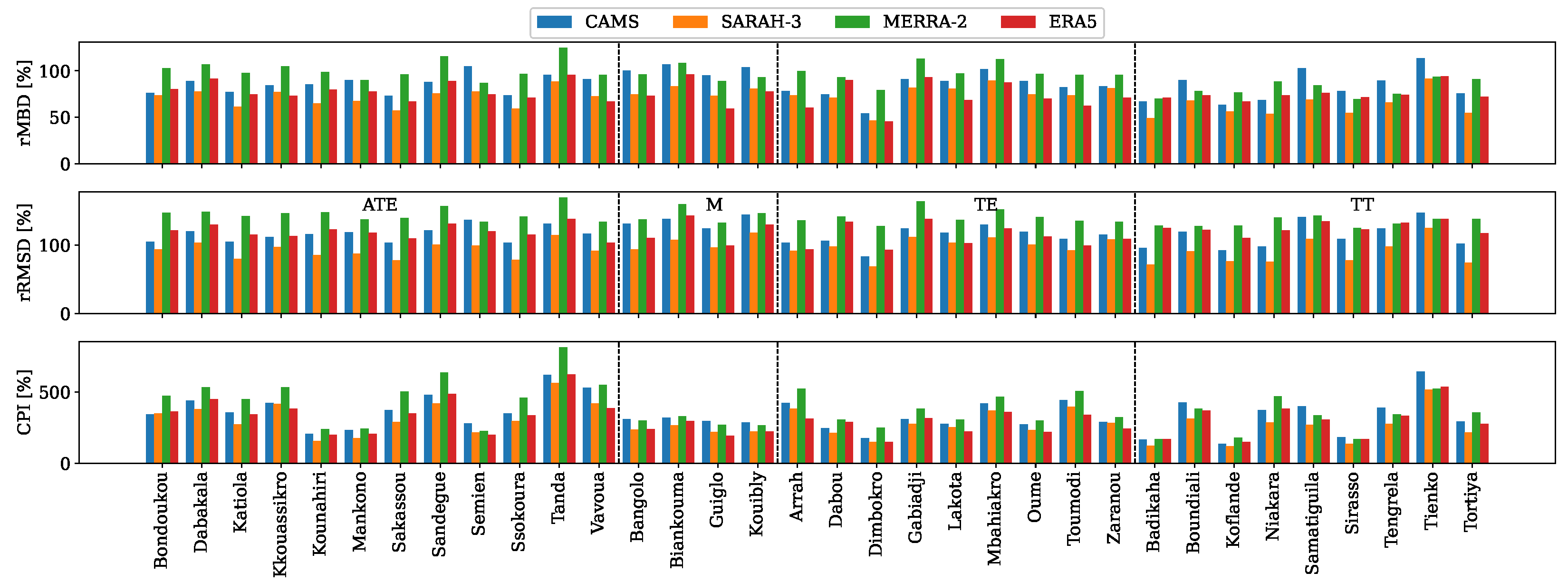
3.2. Performance Evaluation Across Different Timescales
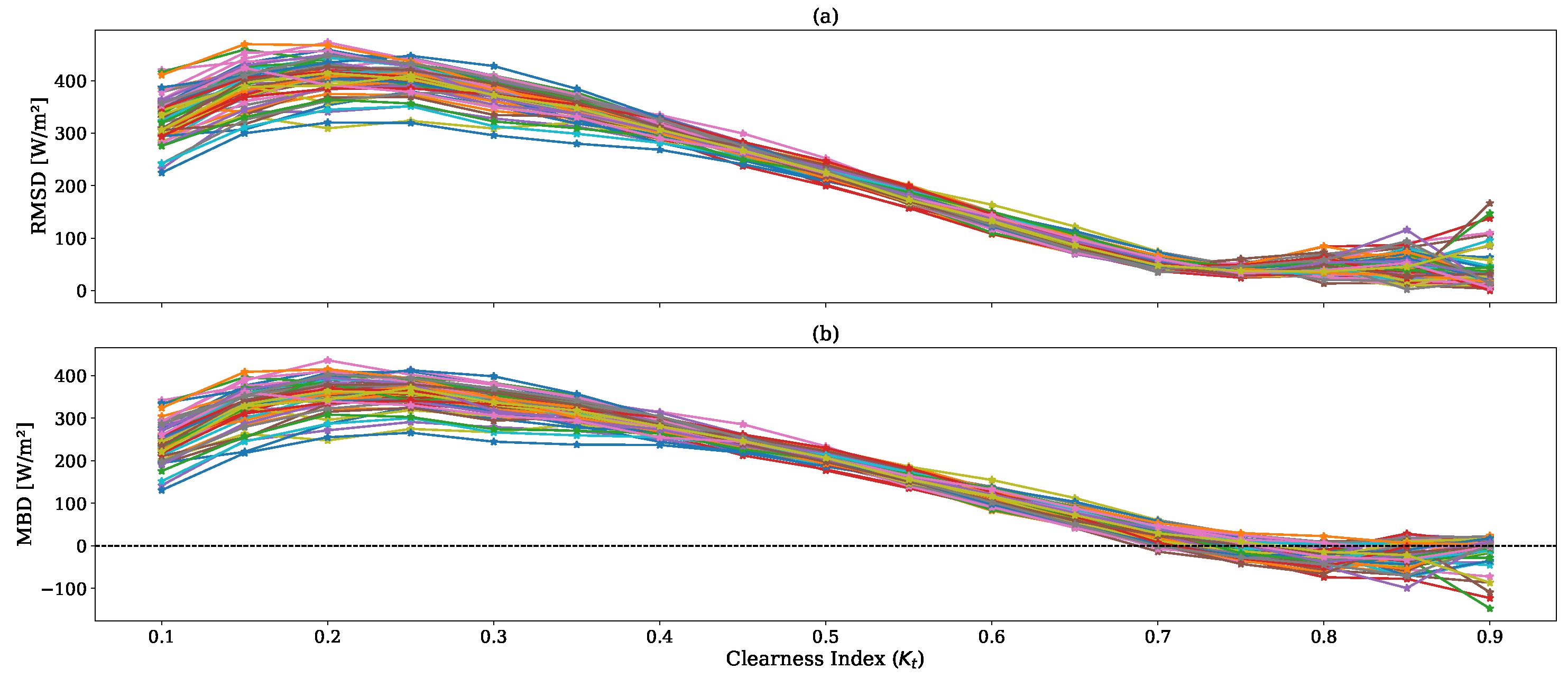
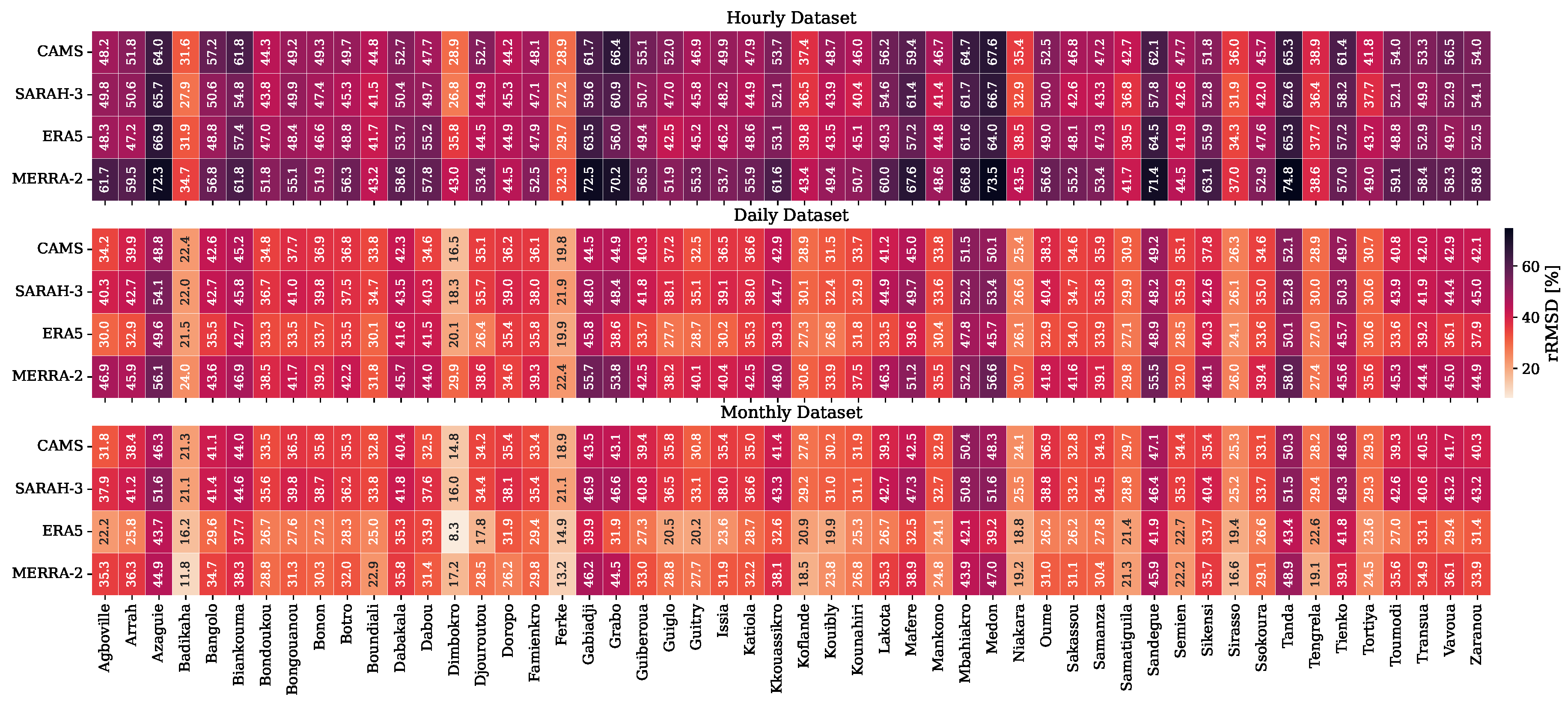
3.2.1. Performance Evaluation of Hourly Datasets
3.2.2. Performance Evaluation of Daily Datasets
3.2.3. Performance Evaluation of Monthly Datasets
3.2.4. Comparison Across Temporal Scales
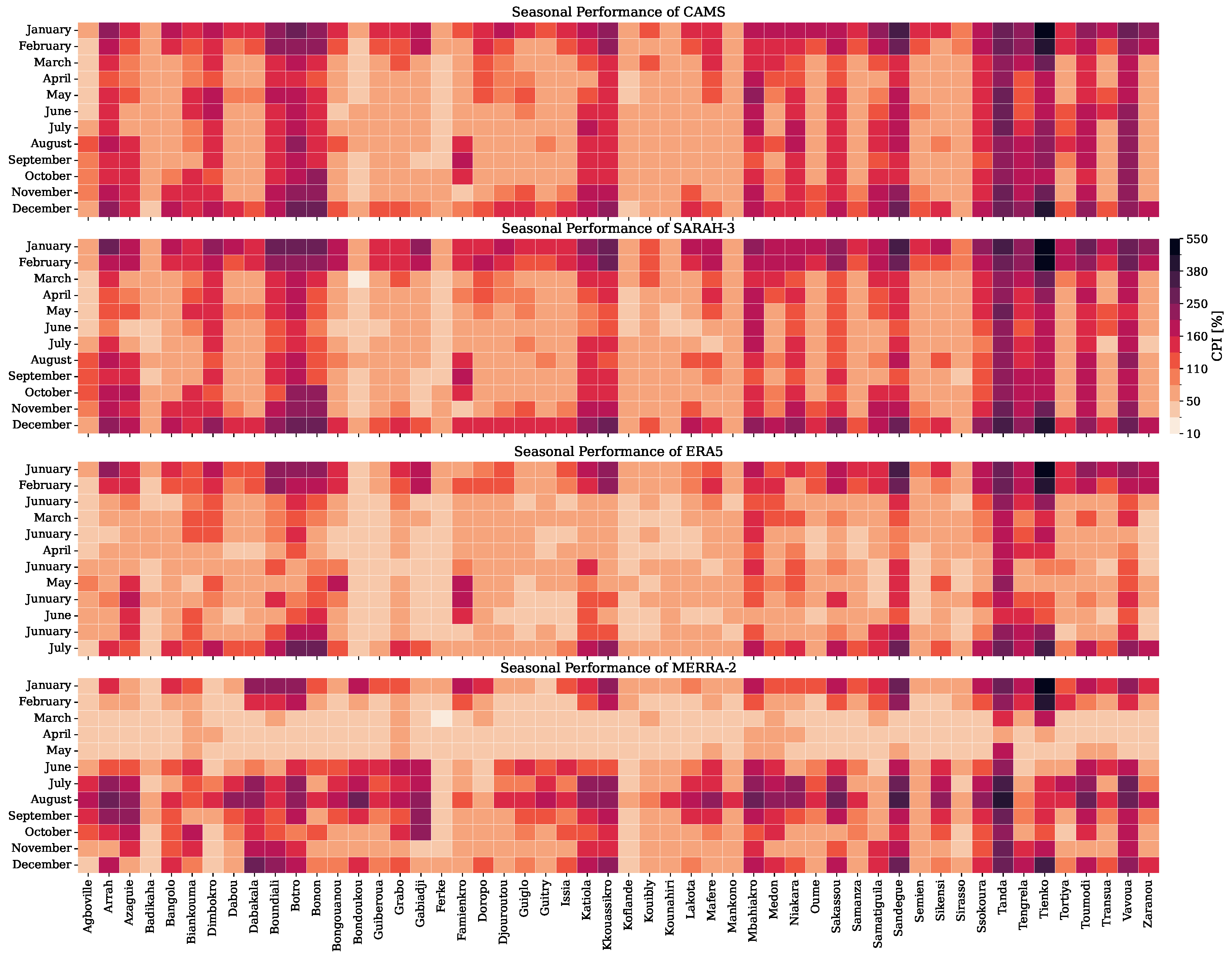
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ackah, I.; Asiama, R.K.; Ohene, A.O.; Essuman, V.A.; Eshun, M.E.; Owusu, C.; Nyarko, P. The Gains and Pains of the Energy Transition: A Perspective on Sub-Saharan Africa. In Energy Regulation in Africa: Dynamics, Challenges, and Opportunities; Ackah, I., Gatete, C., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 453–472. [Google Scholar] [CrossRef]
- Official Website of the Ministry of Petroleum, Energy and Renewable Energies of Côte d’Ivoire. Available online: https://www.energie.gouv.ci/ (accessed on 4 February 2025).
- ISO 9060:2018; Solar Energy—Specification and Classification of Instruments for Measuring Hemispherical Solar and Direct Solar Radiation, 2nd ed. International Organization for Standardization: Geneva, Switzerland, 2018. Available online: https://www.iso.org/standard/67464.html (accessed on 10 February 2025).
- Iturbide, P.; Alonso-Suarez, R.; Ronchetti, F. An Analysis of Satellite-Based Machine Learning Models to Estimate Global Solar Irradiance at a Horizontal Plane. In Proceedings of the Cloud Computing, Big Data & Emerging Topics; Springer: Cham, Switzerland, 2023; pp. 118–128. [Google Scholar]
- Jain, S.; Singh, C.; Tripathi, A.K. A Flexible and Effective Method to Integrate the Satellite-Based AOD Data into WRF-Solar Model for GHI Simulation. J. Indian Soc. Remote Sens. 2021, 49, 2797–2813. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, Y.; Zhang, Y.; Terzija, V. Quantitative synergy assessment of regional wind-solar energy resources based on MERRA reanalysis data. Appl. Energy 2018, 216, 172–182. [Google Scholar] [CrossRef]
- Psiloglou, B.; Kambezidis, H.; Kaskaoutis, D.; Karagiannis, D.; Polo, J. Comparison between MRM simulations, CAMS and PVGIS databases with measured solar radiation components at the Methoni station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Palmer, D.; Blanchard, R. Evaluation of High-Resolution Satellite-Derived Solar Radiation Data for PV Performance Simulation in East Africa. Sustainability 2021, 13, 1852. [Google Scholar] [CrossRef]
- Sawadogo, W.; Bliefernicht, J.; Fersch, B.; Salack, S.; Guug, S.; Diallo, B.; Ogunjobi, K.; Nakoulma, G.; Tanu, M.; Meilinger, S.; et al. Hourly global horizontal irradiance over West Africa: A case study of one-year satellite- and reanalysis-derived estimates vs. in situ measurements. Renew. Energy 2023, 216, 119066. [Google Scholar] [CrossRef]
- Mendyl, A.; Mabasa, B.; Bouzghiba, H.; Weidinger, T. Calibration and Validation of Global Horizontal Irradiance Clear Sky Models against McClear Clear Sky Model in Morocco. Appl. Sci. 2023, 13, 320. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Anderson, K.; Hansen, C.; Holmgren, W.; Jensen, A.; Mikofski, M.; Driesse, A. pvlib python: 2023 project update. J. Open Source Softw. 2023, 8, 5994. [Google Scholar] [CrossRef]
- Kenny, D.; Fiedler, S. Which gridded irradiance data is best for modelling photovoltaic power production in Germany? Sol. Energy 2022, 232, 444–458. [Google Scholar] [CrossRef]
- Mathews, D.; Ó Gallachóir, B.; Deane, P. Systematic bias in reanalysis-derived solar power profiles & the potential for error propagation in long duration energy storage studies. Appl. Energy 2023, 336, 120819. [Google Scholar] [CrossRef]
- Khan, M.U.; Jama, M.A. Evaluation and correction of solar irradiance in Somaliland using ground measurements and global reanalysis products. Heliyon 2024, 10, e35256. [Google Scholar] [CrossRef] [PubMed]
- Potisomporn, P.; Adcock, T.A.; Vogel, C.R. Evaluating ERA5 reanalysis predictions of low wind speed events around the UK. Energy Rep. 2023, 10, 4781–4790. [Google Scholar] [CrossRef]
- Frank, C.W.; Wahl, S.; Keller, J.D.; Pospichal, B.; Hense, A.; Crewell, S. Bias correction of a novel European reanalysis data set for solar energy applications. Sol. Energy 2018, 164, 12–24. [Google Scholar] [CrossRef]
- Tong, L.; He, T.; Ma, Y.; Zhang, X. Evaluation and intercomparison of multiple satellite-derived and reanalysis downward shortwave radiation products in China. Int. J. Digit. Earth 2023, 16, 1853–1884. [Google Scholar] [CrossRef]
- Claver Kakou, K.P.; Laouali, D.; Aka, B.; Osei, J.A.; Franck Kassi Ette, N.; Frey, G. Validation of Satellite-derived Daily Sunshine Duration Estimates Against Campbell-Stokes Sensor Measurements in Côte d’Ivoire. In Proceedings of the 2024 IEEE International Humanitarian Technologies Conference (IHTC), Bari, Italy, 27–30 November 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Kouassi, A.M.; Kouao, J.M.; Kouakou, K. Intra-annual characterization of climate variability in Ivory Coast. Bull. de l’Association de Géographes Français 2022, 99, 289–306. [Google Scholar] [CrossRef]
- Dajuma, A.; Yahaya, S.; Touré, S.; Diedhiou, A.; Adamou, R.; Konaré, A.; Sido, M.; Golba, M. Sensitivity of Solar Photovoltaic Panel Efficiency to Weather and Dust over West Africa: Comparative Experimental Study between Niamey (Niger) and Abidjan (Côte d’Ivoire). Comput. Water Energy Environ. Eng. 2016, 5, 123–147. [Google Scholar] [CrossRef]
- Soro, T.D.; Koné, M.; N’Dri, A.B.; N’Datchoh, E.T. Identified Main Fire Hotspots and Seasons in Côte d’Ivoire (West Africa) Using MODIS Fire Data. S. Afr. J. Sci. 2021, 117, 1–13. [Google Scholar] [CrossRef]
- Nassa, R.; Kouassi, A.; Toure, M. Sensitivity of Statistical Models for Extremes Rainfall Adjustment Regarding Data Size: Case of Ivory Coast. J. Water Resour. Prot. 2021, 13, 654–674. [Google Scholar] [CrossRef]
- Tie, A.G.B.; Konan, B.; Brou, Y.T.; Issiaka, S.; Fadika, V.; Srohourou, B. Estimation des pluies exceptionnelles journalières en zone tropicale: Cas de la Côte d’Ivoire par comparaison des lois lognormale et de Gumbel. Hydrol. Sci. J. 2007, 52, 49–67. [Google Scholar] [CrossRef]
- Santé, N.; N’Go, Y.A.; Soro, G.E.; Meledje, N.H.; Goula, B.T.A. Characterization of Meteorological Droughts Occurrences in Côte d’Ivoire: Case of the Sassandra Watershed. Climate 2019, 7, 60. [Google Scholar] [CrossRef]
- Global Solar Atlas. Côte d’Ivoire Solar Resource Data. 2023. Available online: https://globalsolaratlas.info/download/cote-d-ivoire (accessed on 16 October 2024).
- Qu, Z.; Oumbe, A.; Blanc, P.; Espinar, B.; Gesell, G.; Gschwind, B.; Klüser, L.; Lefèvre, M.; Saboret, L.; Schroedter-Homscheidt, M.; et al. Fast radiative transfer parameterisation for assessing the surface solar irradiance: The Heliosat-4 method. Meteorol. Z. 2017, 26, 33–57. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Azam, F.; Betcke, J.; Hanrieder, N.; Lefèvre, M.; Saboret, L.; Saint-Drenan, Y.M. Surface solar irradiation retrieval from MSG/SEVIRI based on APOLLO Next Generation and HELIOSAT-4 methods. Contrib. Atm. Sci./Meteorol. Z. 2022, 31, 455–476. [Google Scholar] [CrossRef]
- CAMS Gridded Solar Radiation. Available online: https://ads.atmosphere.copernicus.eu/datasets/cams-gridded-solar-radiation?tab=overview (accessed on 12 November 2024).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present. 2023. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=overview (accessed on 12 November 2024). [CrossRef]
- Global Modeling and Assimilation Office (GMAO). MERRA-2 tavg1_2d_rad_Nx: 2d, 1-Hourly, Time-Averaged, Single-Level, Assimilation, Radiation Diagnostics V5.12.4, 2015. Digital Science Data. Available online: https://cmr.earthdata.nasa.gov/search/concepts/C1276812851-GES_DISC.html (accessed on 12 November 2024). [CrossRef]
- Pfeifroth, U.; Kothe, S.; Drücke, J.; Trentmann, J.; Schröder, M.; Selbach, N.; Hollmann, R. Surface Radiation Data Set-Heliosat (SARAH)-Edition 3. 2023. Available online: https://navigator.eumetsat.int/product/EO:EUM:DAT:0863 (accessed on 12 November 2024). [CrossRef]
- World Meteorological Organization. Technical Note N° 172; Technical Report WMO-No. 554; World Meteorological Organization: Geneva, Switzerland, 1981. [Google Scholar]
- Agence Française de Développement. Étude des Besoins et Stratégie de Développement des Services Climatiques Dans le Domaine de L’agriculture en Côte d’Ivoire: Cartographie du Réseau National D’observation. 2022. Available online: https://www.prospect-cs.be/extranet/?voir=one-project&projectid=1236 (accessed on 10 February 2025).
- Konate, D.; Didi, S.R.; Dje, K.B.; Diedhiou, A.; Kouassi, K.L.; Kamagate, B.; Paturel, J.E.; Coulibaly, H.S.J.P.; Kouadio, C.A.K.; Coulibaly, T.J.H. Observed Changes in Rainfall and Characteristics of Extreme Events in Côte d’Ivoire (West Africa). Hydrology 2023, 10, 104. [Google Scholar] [CrossRef]
- Espinar, B.; Blanc, P.; Wald, L.; Hoyer-Lick, C.; Schroedter-Homscheidt, M.; Wanderer, T. Controlling the quality of measurements of meteorological variables and solar radiation. From sub-hourly to monthly average time periods. In Proceedings of the EGU General Assembly 2012, European Geosciences Union, Vienna, Austria, 22–27 April 2012; pp. 22–27. [Google Scholar]
- Long, C.N.; Dutton, E.G. BSRN Global Network recommended QC tests, V2.x. 2010. Available online: https://hdl.handle.net/10013/epic.38770.d001 (accessed on 15 November 2024).
- Remund, J.; Müller, S.; Schmutz, M.; Barsotti, D.; Graf, P.; Cattin, R. Handbook Part II: Theory; Meteotest AG: Bern, Switzerland, 2017. [Google Scholar]
- Younes, S.; Claywell, R.; Muneer, T. Quality control of solar radiation data: Present status and proposed new approaches. Energy 2005, 30, 1533–1549. [Google Scholar] [CrossRef]
- Duarte, L.V.; Formiga, K.T.M.; Costa, V.A.F. Comparison of Methods for Filling Daily and Monthly Rainfall Missing Data: Statistical Models or Imputation of Satellite Retrievals? Water 2022, 14, 3144. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The solar radiation climate of Athens: Variations and tendencies in the period 1992–2017, the brightening era. Sol. Energy 2018, 173, 328–347. [Google Scholar] [CrossRef]
- Younes, S.; Muneer, T. Clear-sky classification procedures and models using a world-wide data-base. Appl. Energy 2007, 84, 623–645. [Google Scholar] [CrossRef]
- Ianetz, A.; Lyubansky, V.; Setter, I.; Kriheli, B.; Evseev, E.G.; Kudish, A.I. Inter-comparison of different models for estimating clear sky solar global radiation for the Negev region of Israel. Energy Convers. Manag. 2007, 48, 259–268. [Google Scholar] [CrossRef]
- Reindl, D.; Beckman, W.; Duffie, J. Diffuse fraction correlations. Sol. Energy 1990, 45, 1–7. [Google Scholar] [CrossRef]
- Li, D.H.; Lam, J.C. An analysis of climatic parameters and sky condition classification. Build. Environ. 2001, 36, 435–445. [Google Scholar] [CrossRef]
- Kuye, A.; Jagtap, S. Analysis of solar radiation data for Port Harcourt, Nigeria. Sol. Energy 1992, 49, 139–145. [Google Scholar] [CrossRef]
- Gueymard, C.A. A review of validation methodologies and statistical performance indicators for modeled solar radiation data: Towards a better bankability of solar projects. Renew. Sustain. Energy Rev. 2014, 39, 1024–1034. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Espinar, B.; Ramírez, L.; Drews, A.; Beyer, H.G.; Zarzalejo, L.F.; Polo, J.; Martín, L. Analysis of different comparison parameters applied to solar radiation data from satellite and German radiometric stations. Sol. Energy 2009, 83, 118–125. [Google Scholar] [CrossRef]
- Hansen, C.W.; Holmgren, W.F.; Tuohy, A.; Sharp, J.; Lorenzo, A.T.; Boeman, L.J.; Golnas, A. The Solar Forecast Arbiter: An Open Source Evaluation Framework for Solar Forecasting. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019; pp. 2452–2457. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service. ERA5-Land Post-Processed Daily-Statistics from 1950 to Present. 2024. Available online: https://cds.climate.copernicus.eu/datasets/derived-era5-land-daily-statistics?tab=overview (accessed on 12 February 2025). [CrossRef]
- Roesch, A.; Wild, M.; Ohmura, A.; Dutton, E.G.; Long, C.N.; Zhang, T. Assessment of BSRN radiation records for the computation of monthly means. Atmos. Meas. Tech. 2011, 4, 339–354. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Climatological Practices, 2018 ed.; Number WMO-No. 100; World Meteorological Organization (WMO): Geneva, Switzerland, 2018. [Google Scholar]
- Trentmann, J. Algorithm Theoretical Baseline Document: Meteosat Solar Surface Radiation and Effective Cloud Albedo Climate Data Records - Heliosat SARAH-3: The MAGICSOL Method Applied for the Generation of SARAH-3. Atbd, EUMETSAT, CM SAF. 2023. Available online: https://www.cmsaf.eu/SharedDocs/Literatur/document/2023/saf_cm_dwd_atbd_sarah_3_5_pdf.html (accessed on 12 February 2025).
- Petty, M.D. Calculating and Using Confidence Intervals for Model Validation. In Proceedings of the Fall Simulation Interoperability Workshop 2012, Orlando, FL, USA, 10–14 September 2012. [Google Scholar]
- Biagne, R.; Gnagbo, A.; Kouamé, F. Dynamic of the vegetation and climatic variables in Dimbokro Department, Central Côte d’Ivoire. Sci. Vie Terre Agron. 2021, 9, 81–89. [Google Scholar]
- Sianturi, Y.; Marjuki; Sartika, K. Evaluation of ERA5 and MERRA2 reanalyses to estimate solar irradiance using ground observations over Indonesia region. AIP Conf. Proc. 2020, 2223, 020002. [Google Scholar] [CrossRef]
- Peng, X.; She, J.; Zhang, S.; Tan, J.; Li, Y. Evaluation of Multi-Reanalysis Solar Radiation Products Using Global Surface Observations. Atmosphere 2019, 10, 42. [Google Scholar] [CrossRef]
- Babar, B.; Graversen, R.; Boström, T. Solar radiation estimation at high latitudes: Assessment of the CMSAF databases, ASR and ERA5. Sol. Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Sazib, N.; Zhang, Y.; Rientjes, T. Effect of Bias Correction of Satellite-Rainfall Estimates on Runoff Simulations at the Source of the Upper Blue Nile. Remote Sens. 2014, 6, 6688–6708. [Google Scholar] [CrossRef]
- Danso, D.K.; Anquetin, S.; Diedhiou, A.; Adamou, R. Cloudiness Information Services for Solar Energy Management in West Africa. Atmosphere 2020, 11, 857. [Google Scholar] [CrossRef]
- Clauzel, L.; Anquetin, S.; Lavaysse, C.; Bergametti, G.; Bouet, C.; Siour, G.; Lapere, R.; Marticorena, B.; Thomas, J. Solar radiation estimation in West Africa: Impact of dust conditions during the 2021 dry season. Atmos. Chem. Phys. 2025, 25, 997–1021. [Google Scholar] [CrossRef]
- Danso, D.K.; Anquetin, S.; Diedhiou, A.; Kouadio, K.; Kobea, A.T. Daytime low-level clouds in West Africa–occurrence, associated drivers, and shortwave radiation attenuation. Earth Syst. Dyn. 2020, 11, 1133–1152. [Google Scholar] [CrossRef]
- Kniffka, A.; Knippertz, P.; Fink, A.H. The role of low-level clouds in the West African monsoon system. Atmos. Chem. Phys. 2019, 19, 1623–1647. [Google Scholar] [CrossRef]
- Danso, D.K.; Anquetin, S.; Diedhiou, A.; Lavaysse, C.; Kobea, A.; Touré, N.E. Spatio-temporal variability of cloud cover types in West Africa with satellite-based and reanalysis data. Q. J. R. Meteorol. Soc. 2019, 145, 3715–3731. [Google Scholar] [CrossRef]
- Copernicus Atmosphere Monitoring Service Documentation. Available online: https://atmosphere.copernicus.eu/documentation (accessed on 11 February 2025).
- Gnamien, S.; Liousse, C.; Keita, S.; Siélé, S.; Bahino, J.; Gardrat, E.; Kassamba-Diaby, M.; Ochou, A.; Yoboué, V. Chemical characterization of urban aerosols in Abidjan and Korhogo (Côte d’Ivoire) from 2018 to 2020 and the identification of their potential emission sources. Environ. Sci. Atmos. 2023, 3, 1741–1757. [Google Scholar] [CrossRef]
- Liu, D.; Lu, Y.; Wang, L.; Zhang, M.; Qin, W.; Feng, L.; Wang, Z. Performance evaluation of different cloud products for estimating surface solar radiation. Atmos. Environ. 2025, 344, 121023. [Google Scholar] [CrossRef]
- Wang, P.; Westrhenen, R.; Meirink, J.F.; Veen, S.; Knap, W. Surface solar radiation forecasts by advecting cloud physical properties derived from Meteosat Second Generation observations. Sol. Energy 2018, 177, 47–58. [Google Scholar] [CrossRef]
- Goessling, H.F.; Rackow, T.; Jung, T. Recent global temperature surge intensified by record-low planetary albedo. Science 2025, 387, 68–73. [Google Scholar] [CrossRef]
- Bahino, J.; Giordano, M.; Beekmann, M.; Yoboué, V.; Ochou, A.; Galy-Lacaux, C.; Liousse, C.; Hughes, A.; Nimo, J.; Lemmouchi, F.; et al. Temporal variability and regional influences of PM2.5 in the West African cities of Abidjan (Côte d’Ivoire) and Accra (Ghana). Environ. Sci. Atmos. 2024, 4, 468–487. [Google Scholar] [CrossRef]

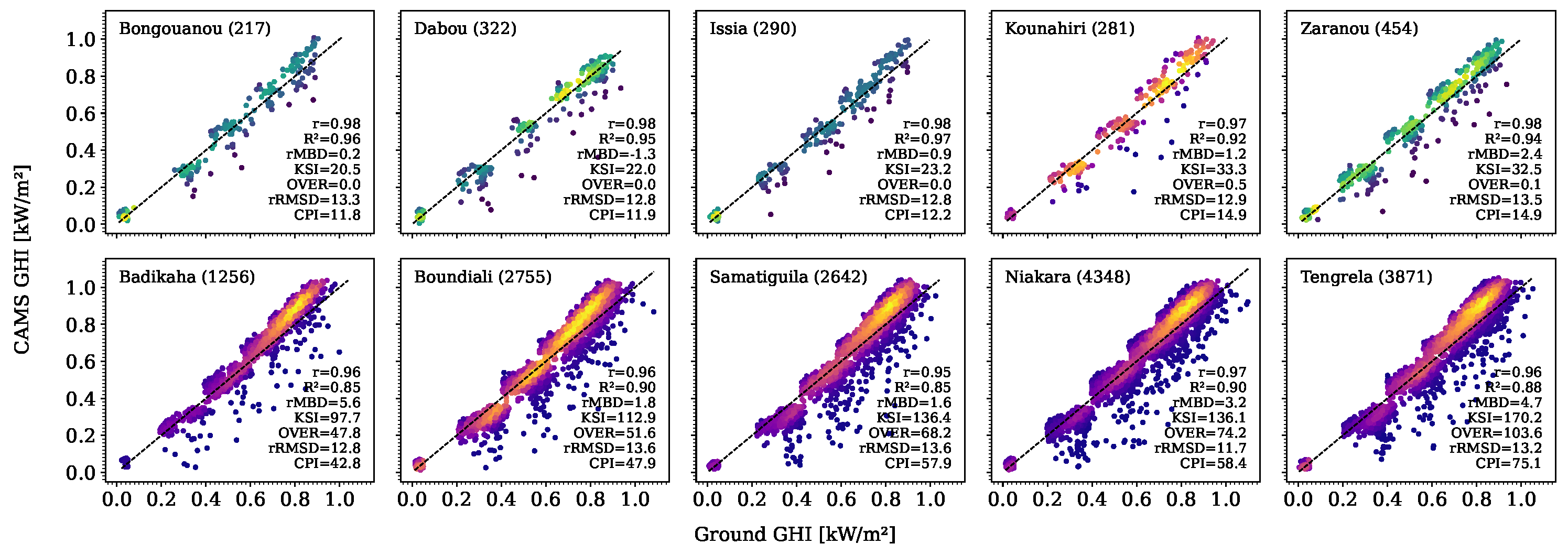

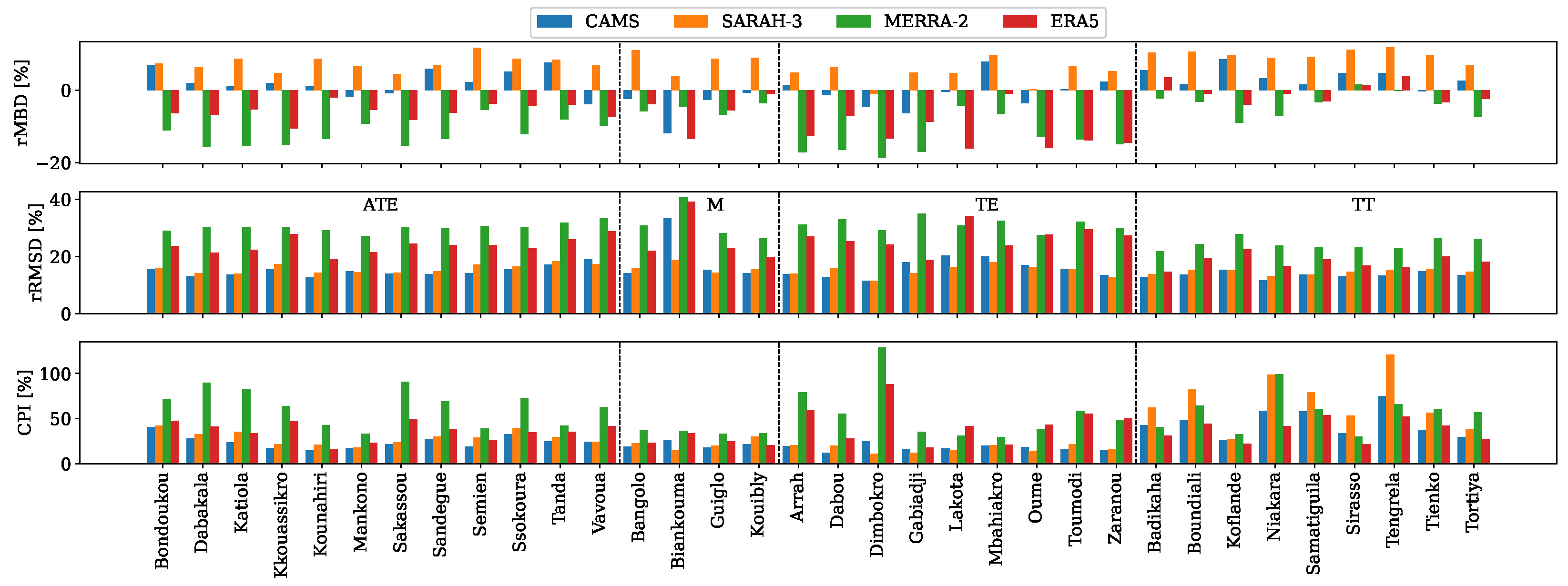
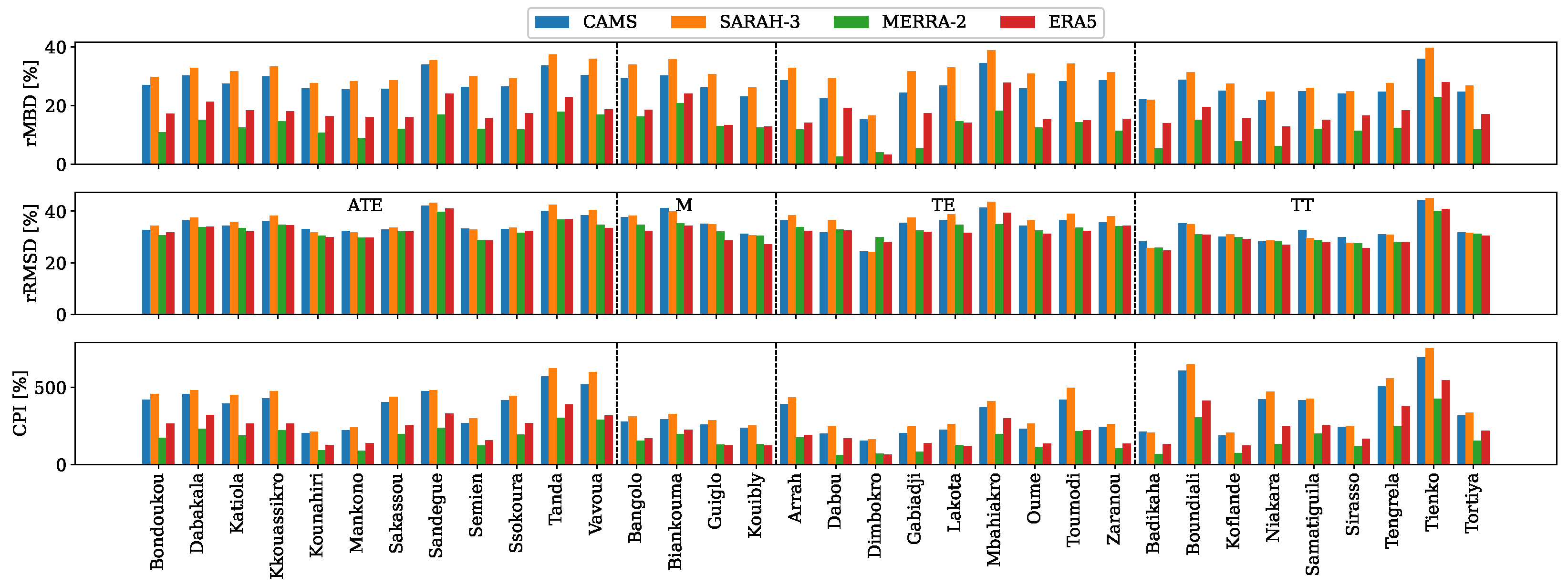
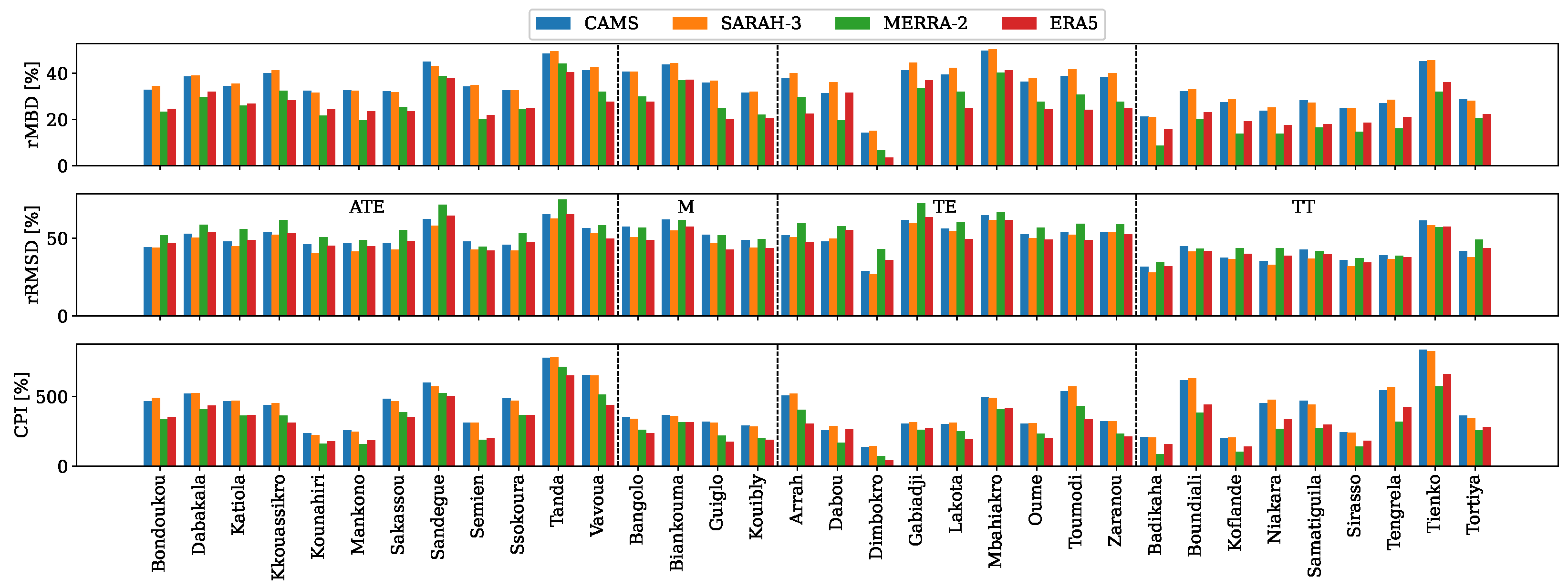
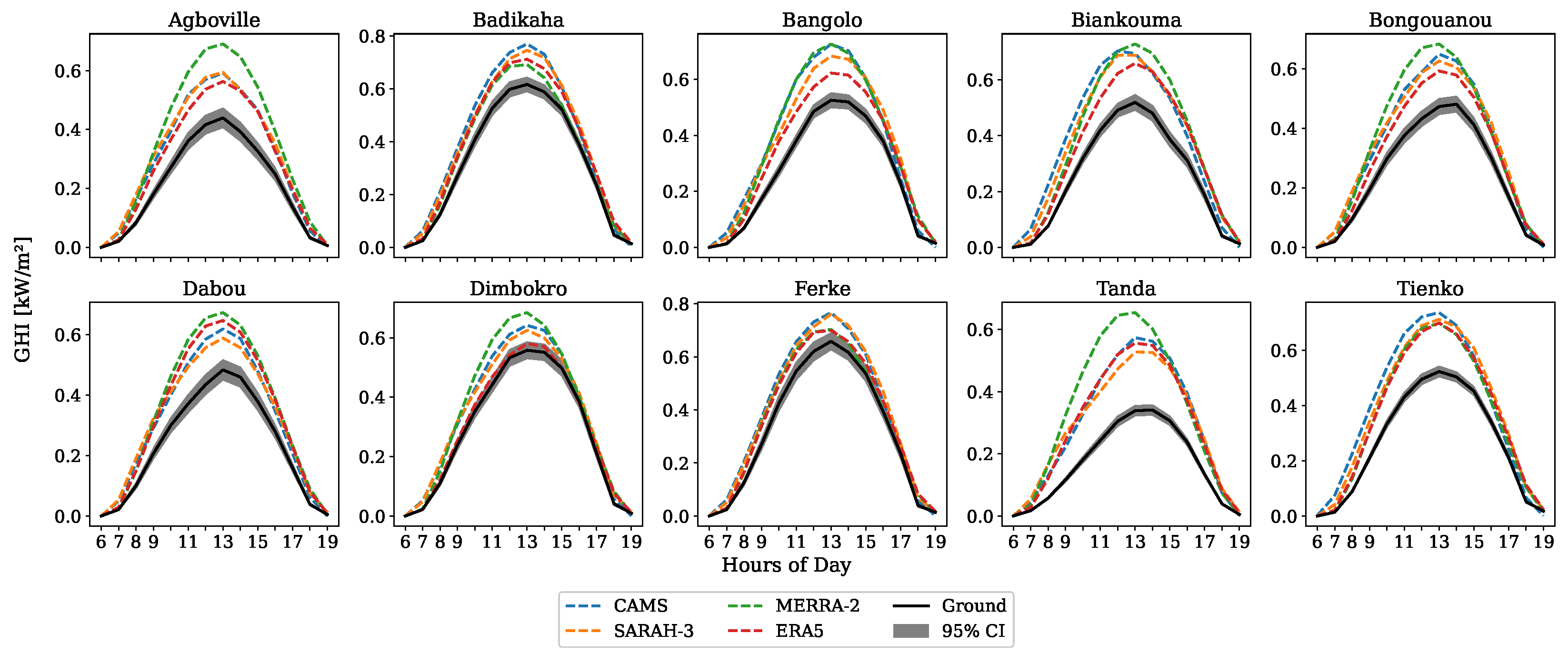
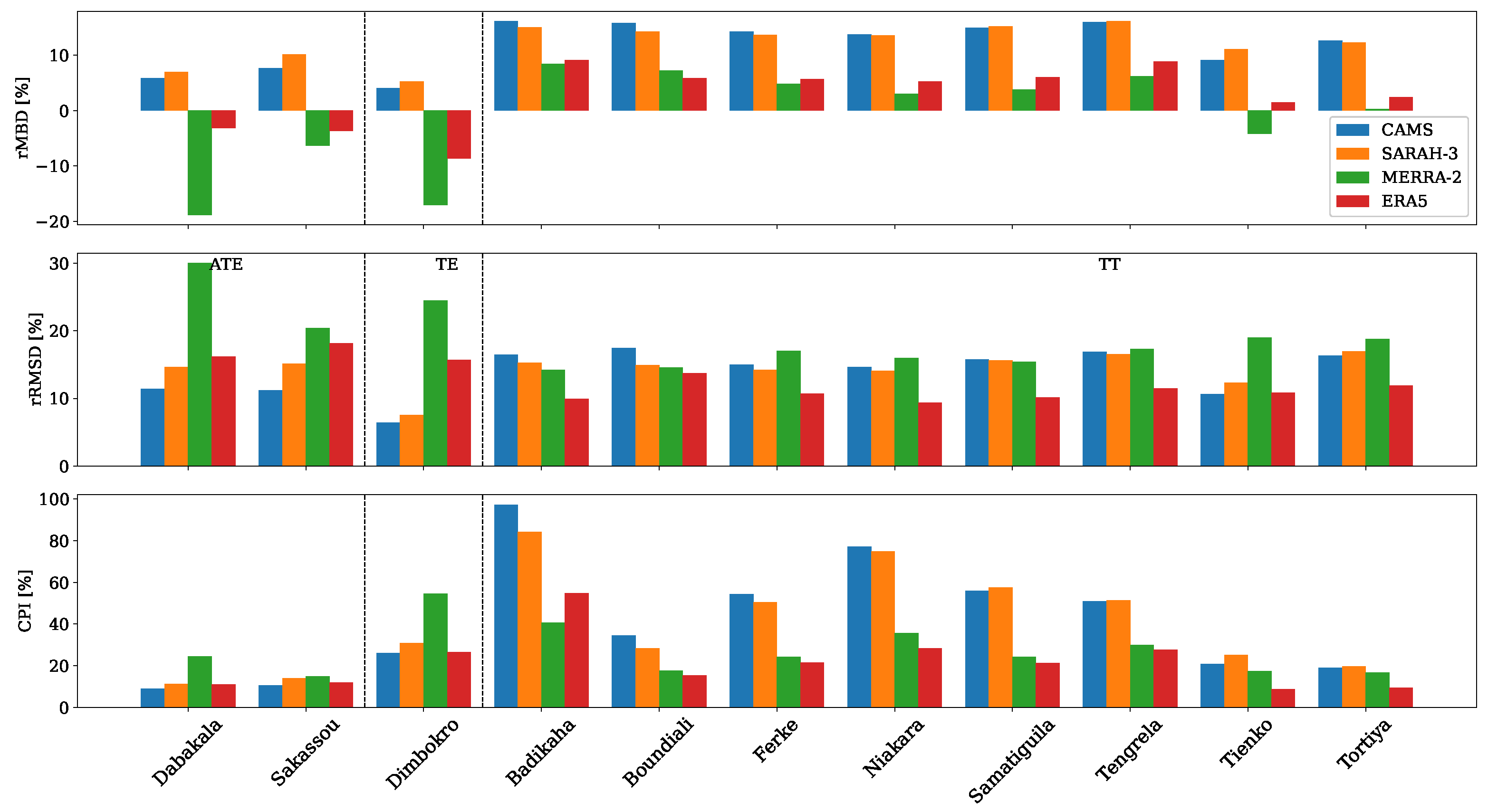
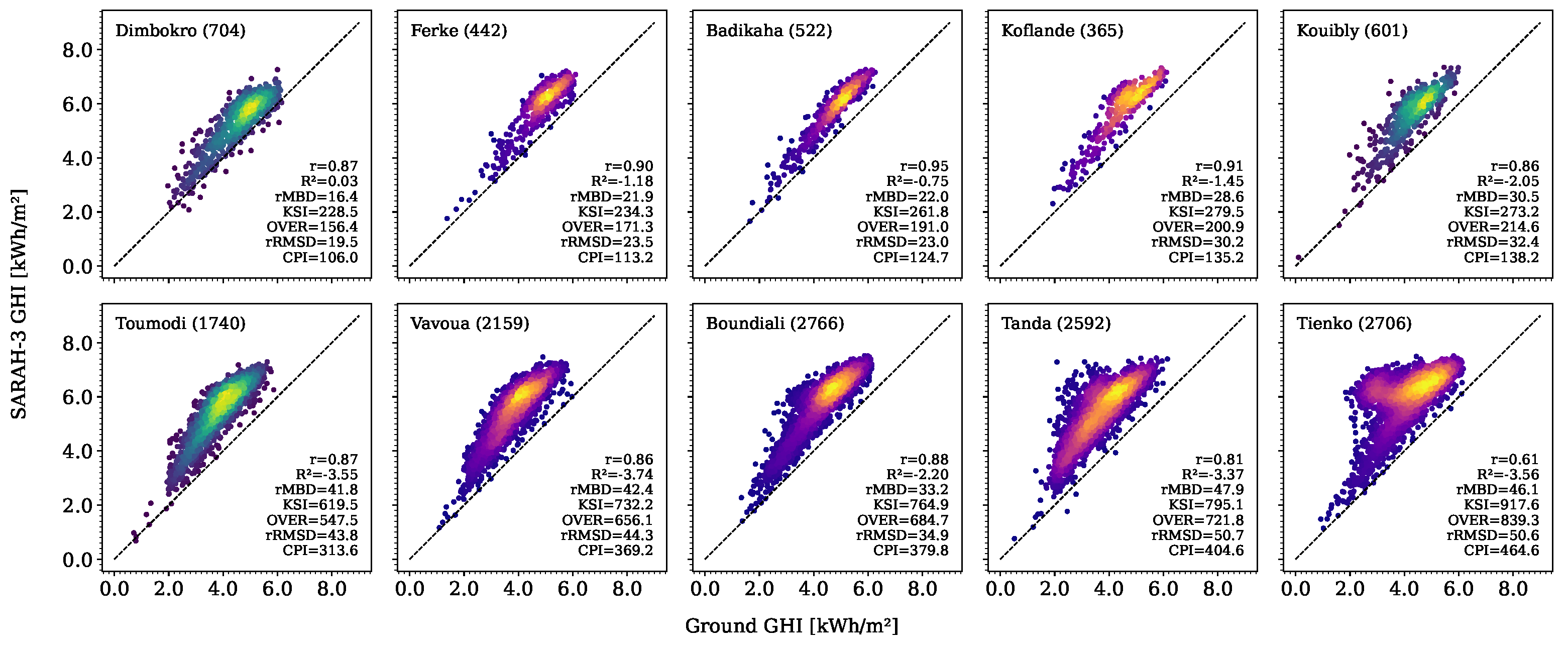
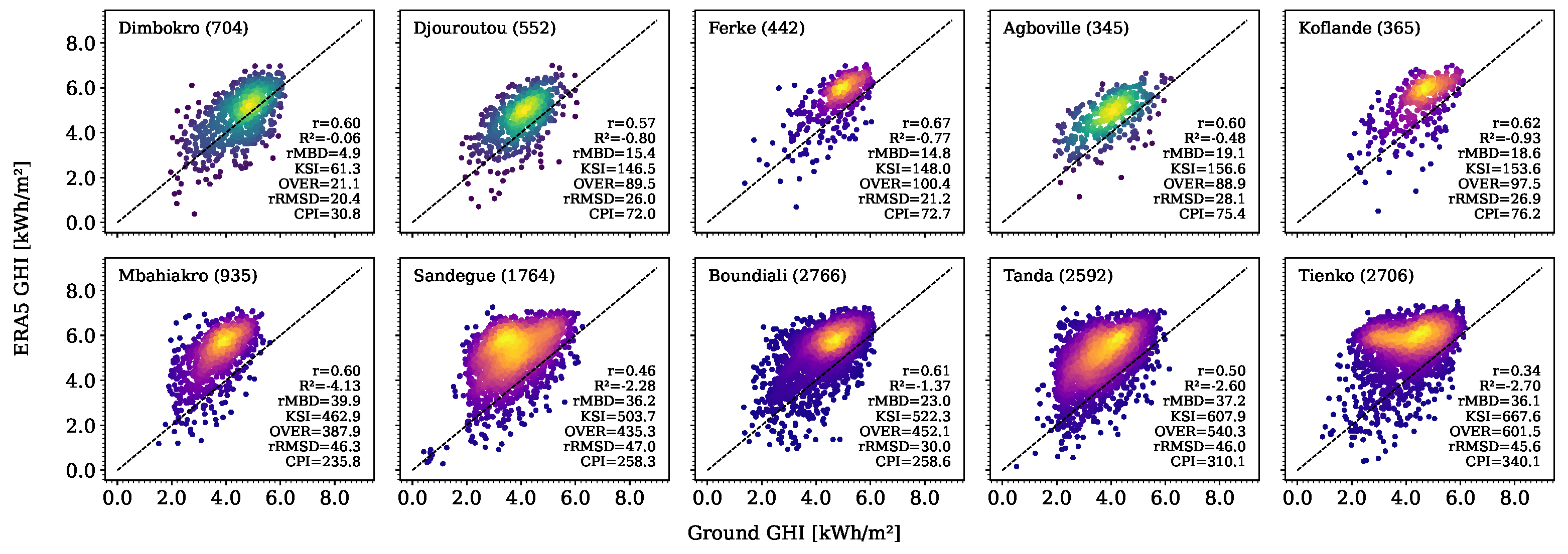
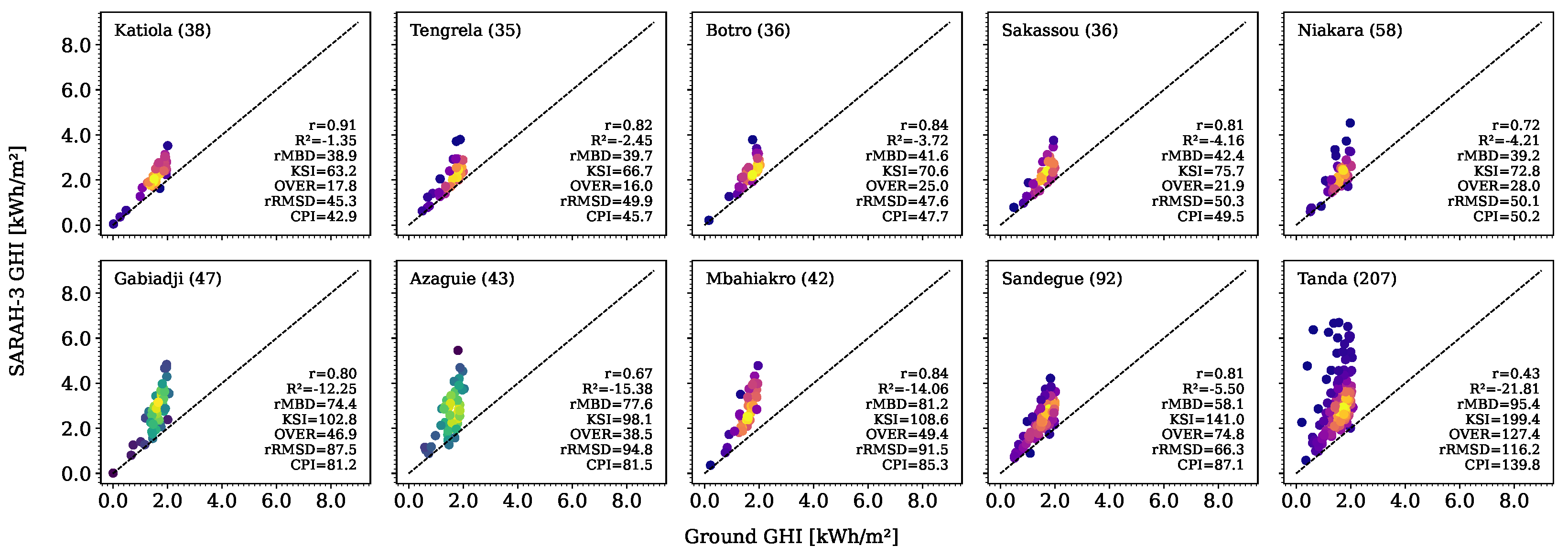
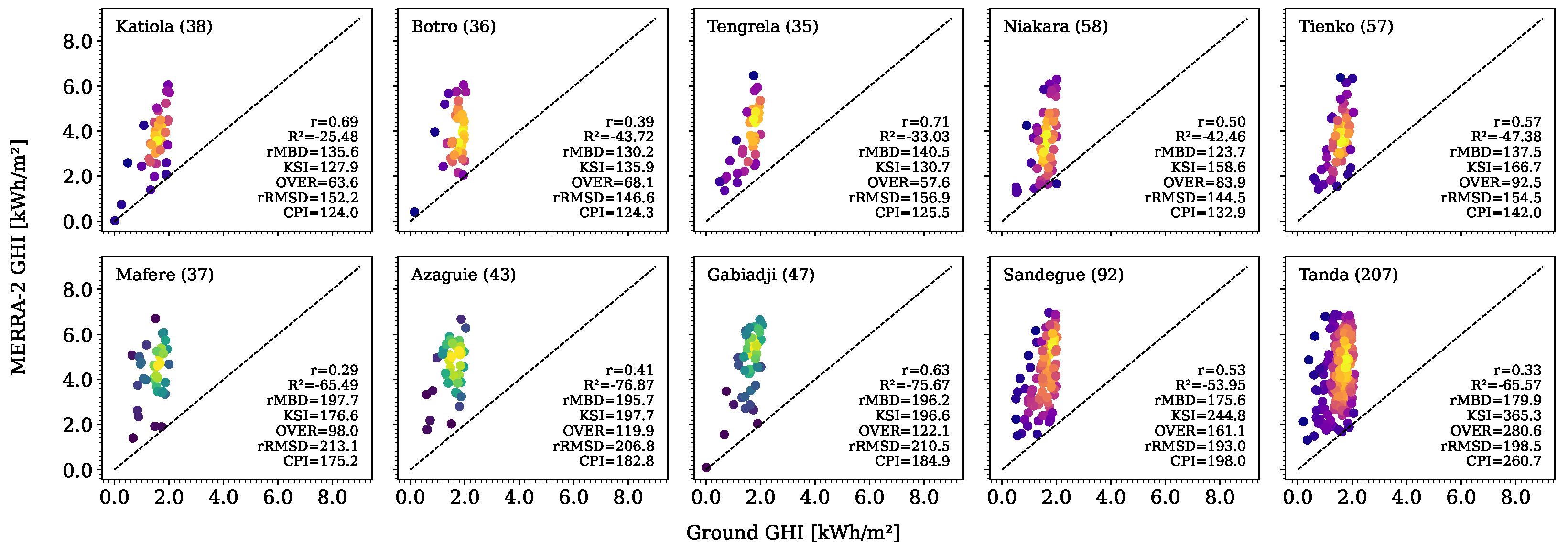
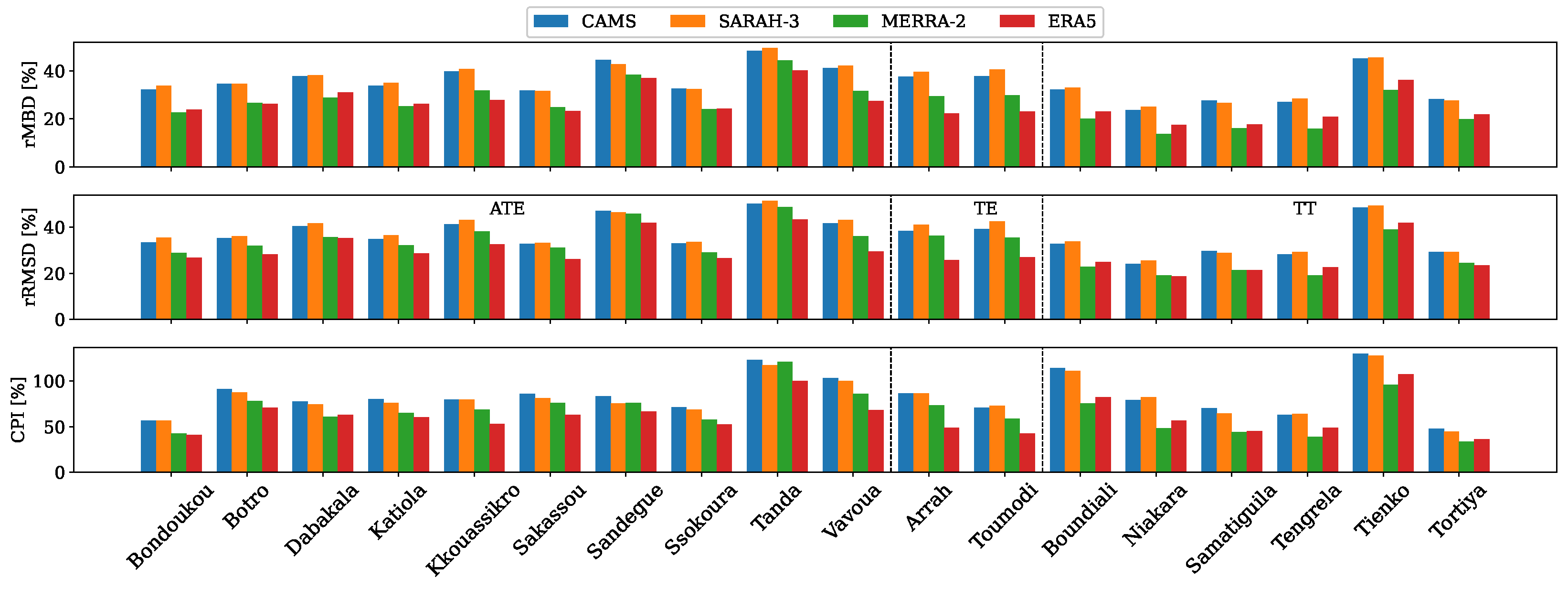
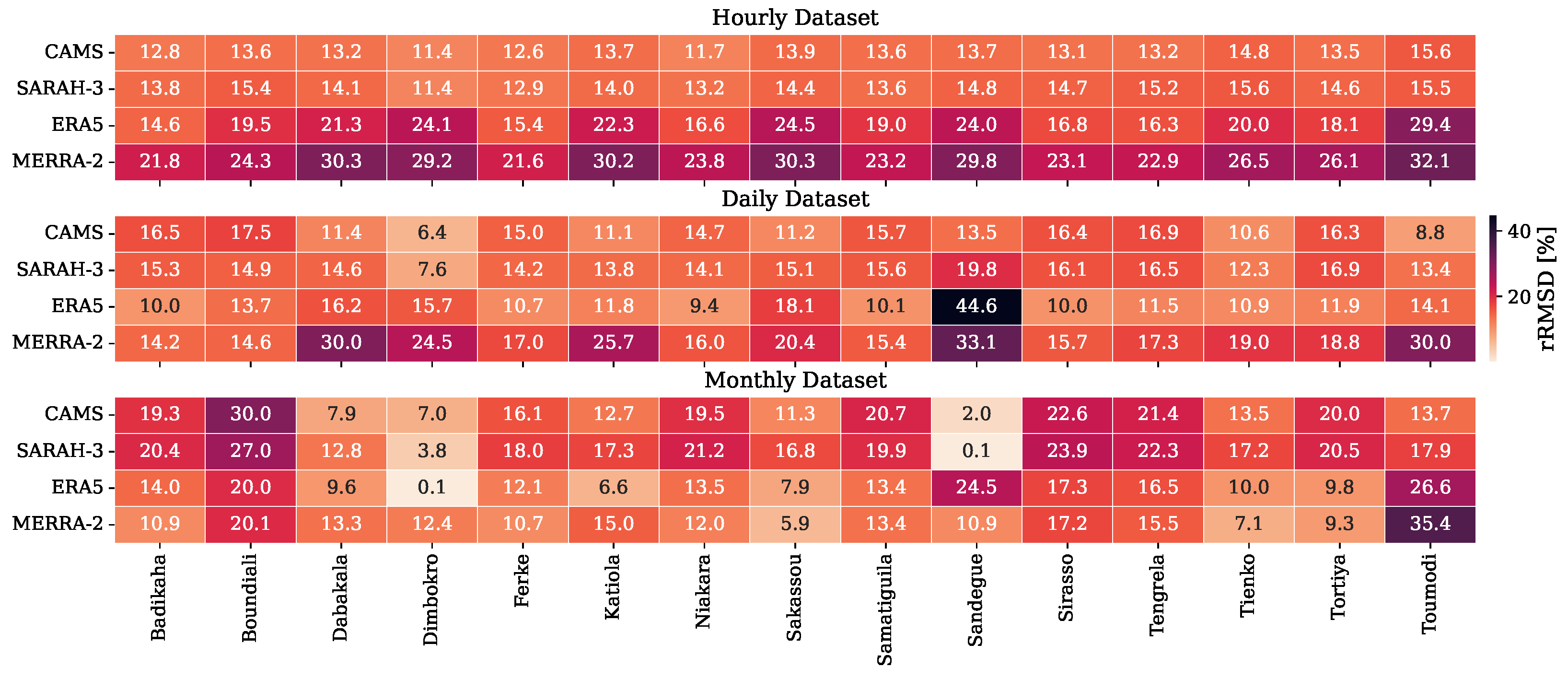
| Station | Lat | Long | Period | Md [%] | Station | Lat | Long | Period | Md [%] |
|---|---|---|---|---|---|---|---|---|---|
| Agboville | 5.9 | −4.2 | 24 November 2022/27 November 2023 | 4.6 | Koflande | 9.1 | −3.1 | 12 November 2022/29 November 2023 | 10.7 |
| Arrah | 6.6 | −3.9 | 20 July 2019/29 November 2023 | 9.2 | Kouibly | 7.3 | −7.2 | 18 October 2022/25 June 2024 | 9.4 |
| Azaguie | 5.6 | −4.0 | 25 November 2022/11 June 2024 | 5.7 | Kounahiri | 7.8 | −5.8 | 08 March 2023/09 April 2024 | 10.3 |
| Badikaha | 9.2 | −5.1 | 05 October 2022/25 June 2024 | 14.1 | Lakota | 5.8 | −5.7 | 15 October 2022/09 April 2024 | 8.5 |
| Bangolo | 7.0 | −7.4 | 17 October 2022/25 June 2024 | 7.9 | Mafere | 5.4 | −3.0 | 26 November 2022/25 June 2024 | 3.8 |
| Biankouma | 7.7 | −7.6 | 05 October 2022/25 June 2024 | 12.5 | Mankono | 8.0 | −6.2 | 07 March 2023/18 June 2024 | 10.4 |
| Bondoukou | 8.0 | −2.7 | 13 April 2019/17 June 2024 | 12.6 | Mbahiakro | 7.4 | −4.3 | 04 October 2022/11 June 2024 | 6.6 |
| Bongouanou | 6.6 | −4.2 | 28 November 2022/25 June 2024 | 3.8 | Medon | 5.3 | −6.2 | 02 December 2022/17 June 2024 | 5.1 |
| Bonon | 6.9 | −6.0 | 16 October 2022/11 June 2024 | 6.6 | Niakara | 8.7 | −5.3 | 11 August 2016/25 June 2024 | 8.2 |
| Botro | 7.8 | −5.3 | 19 April 2019/17 June 2024 | 11.5 | Oume | 6.4 | −5.4 | 11 November 2022/25 June 2024 | 11.8 |
| Boundiali | 9.5 | −6.4 | 17 August 2016/25 June 2024 | 13.3 | Sakassou | 7.5 | −5.3 | 18 April 2019/17 June 2024 | 14.8 |
| Dabakala | 8.3 | −4.4 | 24 April 2019/17 June 2024 | 14.3 | Samanza | 7.5 | −3.6 | 27 November 2022/25 June 2024 | 6.6 |
| Dabou | 5.3 | −4.3 | 25 November 2022/11 June 2024 | 9.4 | Samatiguila | 9.8 | −7.6 | 21 May 2019/19 June 2024 | 13.5 |
| Dimbokro | 6.6 | −4.7 | 08 April 2022/19 June 2024 | 9.7 | Sandegue | 7.9 | −3.5 | 13 April 2019/17 June 2024 | 7.3 |
| Djouroutou | 5.3 | −7.2 | 01 December 2022/11 June 2024 | 8.2 | Semien | 7.6 | −7.1 | 18 October 2022/25 June 2024 | 10.0 |
| Doropo | 9.8 | −3.3 | 10 November 2022/11 June 2024 | 9.0 | Sikensi | 5.7 | −4.6 | 23 November 2022/25 June 2024 | 5.2 |
| Famienkro | 7.8 | −3.9 | 27 November 2022/11 June 2024 | 5.7 | Sirasso | 9.3 | −6.1 | 13 October 2022/25 June 2024 | 13.3 |
| Ferke | 9.5 | −5.2 | 06 October 2022/05 April 2024 | 14.1 | Ssokoura | 7.9 | −4.4 | 12 July 2019/18 June 2024 | 12.7 |
| Gabiadji | 5.0 | −6.5 | 30 November 2022/25 June 2024 | 12.2 | Tanda | 7.8 | −3.2 | 28 September 2016/11 June 2024 | 5.1 |
| Grabo | 4.9 | −7.4 | 01 December 2022/25 June 2024 | 9.1 | Tengrela | 10.5 | −6.4 | 18 August 2016/08 June 2024 | 12.3 |
| Guiberoua | 6.2 | −6.2 | 12 November 2022/25 June 2024 | 7.6 | Tienko | 10.2 | −7.5 | 05 October 2016/225 June 2024 | 8.3 |
| Guiglo | 6.5 | −7.4 | 22 October 2022/25 June 2024 | 9.3 | Tortiya | 8.8 | −5.7 | 13 May 2019/11 October 2022 | 14.4 |
| Guitry | 5.5 | −5.2 | 14 October 2022/25 June 2024 | 5.5 | Toumodi | 6.6 | −5.0 | 27 May 2019/18 June 2024 | 10.8 |
| Issia | 6.5 | −6.6 | 11 October 2022/25 June 2024 | 6.9 | Transua | 7.5 | −3.0 | 07 November 2022/25 June 2024 | 5.4 |
| Katiola | 8.1 | −5.1 | 23 April 2019/29 July 2023 | 12.3 | Vavoua | 7.4 | −6.5 | 31 May 2018/25 June 2024 | 10.3 |
| Kkouassikro | 7.3 | −4.7 | 16 July 2019/21 April 2024 | 12.0 | Zaranou | 6.4 | −3.4 | 05 November 2022/25 June 2024 | 6.5 |
| Sky | Zone | CAMS | ERA5 | MERRA-2 | SARAH-3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CPI | rRMSD | rMBD | CPI | rRMSD | rMBD | CPI | rRMSD | rMBD | CPI | rRMSD | rMBD | ||
| All | TE | 1414.4 | 53.9 | 37.6 | 1003.9 | 51.0 | 25.4 | 1092.4 | 59.9 | 28.5 | 1473.8 | 52.9 | 40.1 |
| TT | 1435.8 | 44.8 | 30.7 | 1075.3 | 42.8 | 22.6 | 884.5 | 45.0 | 19.1 | 1455.8 | 41.4 | 31.1 | |
| M | 676.2 | 54.8 | 37.7 | 466.8 | 48.1 | 26.1 | 508.4 | 54.9 | 28.1 | 671.2 | 49.0 | 38.1 | |
| ATE | 1683.4 | 52.8 | 37.7 | 1294.9 | 51.4 | 27.9 | 1331.5 | 58.6 | 29.5 | 1682.3 | 49.2 | 38.0 | |
| Clear | TE | 42.7 | 15.4 | 173.4 | 27.3 | 211.4 | 30.8 | 43.9 | 14.5 | 3.1 | |||
| TT | 153.3 | 13.3 | 2.9 | 108.1 | 18.0 | 176.8 | 24.0 | 236.8 | 14.6 | 9.8 | |||
| M | 34.4 | 15.9 | 36.4 | 22.3 | 57.3 | 28.7 | 41.3 | 15.6 | 8.9 | ||||
| ATE | 72.7 | 15.0 | 2.1 | 122.3 | 23.3 | 220.8 | 29.6 | 97.2 | 15.5 | 7.3 | |||
| Cloudy | TE | 1227.5 | 35.6 | 27.0 | 715.8 | 31.7 | 14.3 | 557.3 | 32.9 | 10.8 | 1422.3 | 37.9 | 32.1 |
| TT | 1389.7 | 33.6 | 26.4 | 975.5 | 30.2 | 17.8 | 670.4 | 30.7 | 12.7 | 1508.6 | 32.9 | 28.7 | |
| M | 554.4 | 36.3 | 27.1 | 343.6 | 30.7 | 17.1 | 321.0 | 33.1 | 15.6 | 623.2 | 36.0 | 31.6 | |
| ATE | 1479.3 | 35.9 | 28.6 | 974.7 | 33.1 | 18.0 | 728.5 | 33.6 | 13.9 | 1634.2 | 37.1 | 32.1 | |
| Overcast | TE | 1563.9 | 113.2 | 83.9 | 1363.7 | 110.3 | 72.7 | 1740.1 | 140.6 | 98.5 | 1458.5 | 101.7 | 77.5 |
| TT | 1359.6 | 132.1 | 95.1 | 1146.7 | 132.6 | 81.4 | 1200.1 | 139.8 | 87.6 | 1056.0 | 109.5 | 74.0 | |
| M | 713.9 | 134.1 | 101.4 | 537.9 | 121.1 | 76.8 | 641.9 | 144.2 | 96.9 | 566.2 | 103.5 | 78.0 | |
| ATE | 1700.4 | 117.2 | 86.0 | 1557.6 | 118.4 | 77.9 | 1944.0 | 146.0 | 103.2 | 1499.4 | 95.0 | 72.3 | |
| Model | rMBD [%] | rRMSD [%] | KSI [%] | OVER [%] | CPI [%] | r | ||
|---|---|---|---|---|---|---|---|---|
| CAMS | Min | 0.1 (Cl) | 11.4 (Cl) | 11.5 (Cl) | 0 (Cl) | 11.8 (Cl) | 0.8 (Cd) | −2.7 (Ov) |
| Max | 113.3 (Ov) | 147.0 (Ov) | 1661.9 (Al) | 1566.3 (Al) | 837.8 (Al) | 1.0 (Cl) | 1.0 (Cl) | |
| Mean | 36.7 | 53.9 | 498.7 | 424.7 | 257.8 | 0.9 | 0 | |
| SARAH-3 | Min | 0.2 (Cl) | 11.4 (Cl) | 18.6 (Cl) | 0 (Cl) | 10.9 (Cl) | 0.8 (Ov) | −1.7 (Ov) |
| Max | 91.7 (Ov) | 124.7 (Ov) | 1644.4 (Al) | 1549.5 (Al) | 827.6 (Al) | 1.0 (Cl) | 1.0 (Cl) | |
| Mean | 36.3 | 48.5 | 500.9 | 426.2 | 256.0 | 0.9 | 0.2 | |
| ERA5 | Min | 0.8 (Cl) | 14.6 (Cl) | 26.9 (Cl) | 0 (cl) | 16.3 (Cl) | 0.7 (Cd) | −2.5 (Ov) |
| Max | 96.2 (Ov) | 143.0 (Ov) | 1315.4 (Al) | 1222.3 (Al) | 663.0 (Al) | 1.0 (Cl) | 0.9 (Cl) | |
| Mean | 27.6 | 55.4 | 384.2 | 306.5 | 200.4 | 0.8 | 0 | |
| MERRA-2 | Min | 0.2 (Cl) | 21.6 (Cl) | 39.5 (Cl) | 0.1 (Cl) | 23.8 (Cl) | 0.6 (Cd) | −4.2 (Ov) |
| Max | 124.6 (Ov) | 168.9 (Ov) | 1505.9 (Ov) | 1414.5 (Ov) | 814.6 (Ov) | 0.9 (Cl) | 0.9 (Cl) | |
| Mean | 30.7 | 64.2 | 397.7 | 320.1 | 211.5 | 0.8 | −0.3 |
| Model | rMBD [%] | rRMSD [%] | KSI [%] | OVER [%] | CPI [%] | r | ||
|---|---|---|---|---|---|---|---|---|
| CAMS | Min | 4.1 (Cl) | 6.4 (Cl) | 12.9 (Cl) | 0 (Cl) | 8.9 (Cl) | 0.5 (Ov) | −25.8 (Ov) |
| Max | 106.7 (Ov) | 126.0 (Ov) | 907.8 (Cd) | 829.3 (Cd) | 459.3 (Cd) | 1.0 (Cl) | 1.0 (Cl) | |
| Mean | 37.3 | 40.4 | 344.6 | 275.8 | 175.3 | 0.9 | −3.1 | |
| SARAH-3 | Min | 5.2 (Cl) | 7.6 (Cl) | 15.7 (Cl) | 0 (Cl) | 11.2 (Cl) | 0.4 (Ov) | −21.8 (Cl) |
| Max | 95.4 (Ov) | 116.2 (Ov) | 917.6 (Cd) | 839.3 (Cd) | 464.6 (Cd) | 1.0 (Cl) | 1.0 (Cl) | |
| Mean | 37.3 | 41.1 | 349.3 | 281.2 | 178.2 | 0.8 | −3.1 | |
| ERA5 | Min | 1.4 (Cl) | 9.4 (Cl) | 11.5 (Cl) | 0 (cl) | 8.7 (Cl) | −0.2 (Ov) | −62.6 (Ov) |
| Max | 139.3 (Ov) | 162.1 (Ov) | 667.6 (Al) | 601.5 (Cd) | 340.1 (Cd) | 1.0 (Cl) | 0.9 (Cl) | |
| Mean | 34.3 | 45.0 | 256.5 | 193.8 | 135.1 | 0.6 | −5.4 | |
| MERRA-2 | Min | 0.3 (Cl) | 14.2 (Cl) | 18.4 (Cl) | 0 (Cl) | 14.8 (Cl) | 0 (Cd) | −120.2 (Ov) |
| Max | 197.7 (Ov) | 213.1 (Ov) | 687.5 (Al) | 610.0 (Al) | 353.4 (Al) | 0.9 (Cl) | 0.9 (Cl) | |
| Mean | 41.5 | 57.4 | 261.5 | 195.2 | 142.8 | 0.3 | −10.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakou, P.-C.K.; Laouali, D.; Aka, B.; Osei, J.A.; Ette, N.F.K.; Frey, G. Multi-Timescale Validation of Satellite-Derived Global Horizontal Irradiance in Côte d’Ivoire. Remote Sens. 2025, 17, 998. https://doi.org/10.3390/rs17060998
Kakou P-CK, Laouali D, Aka B, Osei JA, Ette NFK, Frey G. Multi-Timescale Validation of Satellite-Derived Global Horizontal Irradiance in Côte d’Ivoire. Remote Sensing. 2025; 17(6):998. https://doi.org/10.3390/rs17060998
Chicago/Turabian StyleKakou, Pierre-Claver Konin, Dungall Laouali, Boko Aka, Janet Appiah Osei, Nicaise Franck Kassi Ette, and Georg Frey. 2025. "Multi-Timescale Validation of Satellite-Derived Global Horizontal Irradiance in Côte d’Ivoire" Remote Sensing 17, no. 6: 998. https://doi.org/10.3390/rs17060998
APA StyleKakou, P.-C. K., Laouali, D., Aka, B., Osei, J. A., Ette, N. F. K., & Frey, G. (2025). Multi-Timescale Validation of Satellite-Derived Global Horizontal Irradiance in Côte d’Ivoire. Remote Sensing, 17(6), 998. https://doi.org/10.3390/rs17060998









