Multi-Layer LEO Constellation Optimization Based on D-NSDE Algorithm

Abstract

Low-Earth-orbit (LEO) satellites have unique advantages in communication, navigation, and remote sensing due to their low orbit, strong landing signal strength, and low launch cost. However, the optimization of the design of LEO constellations to obtain the optimal configuration to meet different missions faces great challenges. Traditional multi-objective optimization algorithms often struggle with designing constellations involving composite functions due to various constraints, which can result in premature termination and local optimality issues. This paper introduces a dynamic parameter-based non-dominated sorting differential evolution (D-NSDE) algorithm to obtian better solutions, which is capable of dynamically adjusting the boundary of feasible solutions and modifying operators according to the iteration process to mitigate these constraints. Additionally, we model a composite LEO constellation with multiple layers, constructing 2-/3-/4-layer configurations, and we include constraints from the third-generation BeiDou Navigation Satellite System (BDS-3) navigation constellations. Subsequently, we employ the D-NSDE algorithm to solve the corresponding multi-objective optimization problems and derive the optimal solution set. The results demonstrate that D-NSDE can generate complete and multi-level solution sets under diverse constraint conditions, with 75% of D-NSDE algorithm optimization solutions being able to achieve seamless positioning for 95% of global coverage. Furthermore, the PDOP median values are 5.12/4.23/2.97 without BDS-3 navigation constraints and 1.38/1.44/1.51 with BDS-3 navigation constraints. Additionally, simulation experiments conducted on standard function test sets confirm that the solution sets produced by the D-NSDE algorithm exhibit favorable distribution and convergence performance better than the Non-dominated Sorting Genetic Algorithm (NSGA)-III.

1. Introduction

The Global Navigation Satellite System (GNSS) satellite system has experienced rapid development in recent years and has found extensive applications in fields including navigation, positioning, and timing. GNSS provides all-time, continuous, and high-precision positioning, navigation, and timing (PNT) services with substantial economic and military defense implications [1]. Nevertheless, limitations such as weak signal strength in indoor and signal-restricted areas, susceptibility to interference, and extended convergence time for navigation and positioning restrict the applicability of GNSS [2]. Studies suggest that augmenting GNSS with LEO satellites can effectively overcome these constraints in GNSS applications [3,4].

Moreover, progress in satellite launch technology has significantly decreased launch expenses [5], facilitating the extensive deployment of LEO satellites. LEO satellites, with their lower orbital altitudes, offer benefits such as reduced signal attenuation and stronger ground signal power, leading to widespread attention. Many commercial entities, countries, and regions have launched or planned LEO satellite constellations, such as Iridium Satellite, OneWeb, O3b, Starlink, and China’s ’GW’ and Microspace LEO constellations [6]. As LEO satellite systems evolve, the functions of these constellations have expanded from basic mobile communications to encompass a diverse range of composite functions, including broadband access, space-based Internet of Things (IoT), and GNSS navigation enhancement and positioning [7]. The design of a satellite constellation directly affects its performance by determining the structure and parameters of each satellite orbit, such as orbital altitude and satellite quantity. As of January 2024, due to frequent human space activities, there are 28,363 active spacecraft, defunct spacecraft, and space debris globally (https://www.space-track.org#ssr, accessed on 24 March 2024), as depicted in Figure 1. The existence of these objects poses a specific threat to the safety and long-term viability of the space environment, leading to the inaccessibility of a significant portion of near-Earth orbital space. Additionally, excessively low orbital altitudes subject satellites to gravitational and atmospheric drag forces, as well as to the presence of Van Allen radiation belts. These factors impact both the lifespan and orbit precision of satellites and create difficulties for constellation design.

Research on optimizing LEO satellite constellations has garnered considerable focus, with numerous academics utilizing heuristic algorithms to improve their design. Xu et al. applied the Non-dominated Sorting Genetic Algorithm (NGSA)-II and MOEA/D algorithms to create a LEO constellation tailored for global multi-GNSS-R observations [8]. Ma et al. introduced a multi-objective weighted function and used a genetic algorithm to design a LEO navigation constellation for worldwide applications [9]. Guan [10], Liu [11], and Teng [12] utilized the NSGA-III algorithm to craft a hybrid walker constellation to enhance GNSS capabilities. Melaku and Kim used the NSGA-II algorithm to develop a cubic satellite constellation system for global Earth observation and regional disaster monitoring [13]. Deng et al. independently devised a multi-objective optimization algorithm for constructing a two-layer walker LEO navigation constellation [14]. Such algorithms have achieved good results when the objective function is relatively simple and there are no additional constraints involved.

However, the design of a composite navigation and communication integrated LEO constellation is a novel and complex LEO application. Currently, unresolved issues persist in the design of this composite constellation. Current technological conditions limit the integration of navigation and communication signals in a composite integrated LEO constellation of navigation and communication. Embracing an integrated navigation and communication solution will unavoidably lead to increased satellite mass and power consumption, contradicting the benefits of low-cost and large-scale operations for LEO satellites [15]. In addition, it amplifies the complexity and cost of the receiver terminal design. A multi-layered constellation design offers the advantage of covering the same Earth area while requiring fewer satellites [16], improving continuous communication between ground terminals and satellites, and achieving enhanced observation geometry and ranging accuracy. The constellation optimization method mentioned above mainly focuses on obtaining a good solution set in the feasible region. Nevertheless, the design of the composite low-orbit satellite constellation encounters several constraints, including altitude, the number of satellites, restrictions on navigation and communication functions, and others, which result in a non-continuous feasible domain in decision space—hiding the feasible solution in the boundary of the domain—and the constraint condition, hindering the acquisition of an optimal set of solutions.

This paper utilizes a heterogeneous constellation, comprising both communication and navigation satellites, to formulate composite LEO satellite constellations. Initially, this section presents the structure of the heterogeneous constellation, establishes a communication/navigation constellation model, and collaboratively designs the constellation with the BDS-3 system. Following the identification of decision variables and objective functions, the design issue is converted into a constrained multi-objective optimization problem (CMOP), which is then addressed using an optimization algorithm to derive the optimal constellation parameters.

Then, we have developed a new multi-objective optimization algorithm that takes into account multiple constraints. Our algorithm progressively converges to the Pareto front over several iterations, facilitating the optimized design of a composite navigation and communication integrated low-Earth-orbit constellation while satisfying diverse constraints, such as satellite numbers and altitudes, and ensuring satisfactory performance metrics.

The subsequent sections of this paper are structured as follows: Section 2 presents CMOP and the non-dominated sorting differential evolution (D-NSDE) algorithm, alongside the assessment metrics for evaluating algorithm performance. The acquired solution sets are evaluated against a standard set of problem functions. In Section 3, the application of the proprietary algorithm to address CMOP is outlined. Section 4 details the modeling of the multi-layer LEO satellite constellation optimization problem as a CMOP, along with providing specifics on the experimental setup and results. Lastly, Section 5 serves as the conclusion of this paper.

2. Constrained Many-Objective Optimization Problems (CMaOPs) and Constraint-Handling Techniques

The optimization problem of LEO constellations can be considered a traditional multi-objective optimization problem. Nevertheless, the key challenge in designing composite multi-layer LEO constellations is in formulating the constellation issue as a CMaOPs, which takes into account the varied constraints linked to each individual constellation. This section provides an overview of the concept of CMaOPs and traditional approaches, penalty function, utilized for addressing CMaOPs.

2.1. CMOP

Balancing multiple conflicting objectives while satisfying constraints is recognized as a CMOP. If the problem covers four or more objectives, it is identified as a CMaOP [17]. Mathematically, CMaOPs can be depicted as minimizing m objective functions while considering a set of constraints. The mathematical expression for them is as follows.

$$\begin{array}{cc}\hfill & \min F\left(\mathbf{x}\right)={(f_1\left(\mathbf{x}\right),f_2\left(\mathbf{x}\right),\cdots ,f_m\left(\mathbf{x}\right))}^T\hfill \\ \hfill & s.t.\left\{\begin{array}{c}{g}_j\left(\mathbf{x}\right)\le 0,j=1,\cdots ,l\hfill \\ \mathbf{x}={(x_1,x_2,\cdots ,x_D)}^T\in \mathbb{Z}\hfill \end{array}\right.\hfill \end{array}$$

(1)

where $\mathbb{Z}$ denotes the decision space, $\mathbf{x}$ denotes the solution vector in the decision space with a dimension of D, $F\left(\mathbf{x}\right)$ denotes the objective vector and $g_j\left(\mathbf{x}\right)$ denotes the inequality constraints. l denotes the number of inequality constraints. The decision vector can be discrete or continuous.

2.2. Constraint-Handling Techniques

Within CMaOPs, penalty function methods are frequently utilized to direct the iterative progression of solution vectors. The value of the constraint violation function (CV) $cv(\cdot )$ is used to assess the constraint violations within the objective function. The mathematical expression is as follows:

$$cv\left(\mathbf{x}\right)={\displaystyle \frac{1}{q}}\sum _{i=1}^q{\displaystyle \frac{G_i\left(\mathbf{x}\right)}{{max}_{\mathbf{x}\in {\mathcal{P}}_0}\left\{G_i\left(\mathbf{x}\right)\right\}}}$$

(2)

$$G_i\left(\mathbf{x}\right)=max\{g_i\left(\mathbf{x}\right),0\},i=1,2,\dots ,q$$

(3)

where ${\mathcal{P}}_0$ refers to the initial population, while $G_i\left(\mathbf{x}\right)$ denotes the degree of constraint violation for each solution. Using constraint penalty techniques, the feasibility of a solution can be assessed. A solution exhibiting a CV value of 0 indicates feasibility, while a non-zero CV value denotes an infeasible solution.

Consequently, for any two solutions of CMaOPs, as shown in Figure 2, ${\mathbf{x}}_{\mathbf{1}}$ and ${\mathbf{x}}_{\mathbf{2}}$ have the following cases:

• ${\mathbf{x}}_{\mathbf{1}}$ and ${\mathbf{x}}_{\mathbf{2}}$ are feasible while ${\mathbf{x}}_{\mathbf{1}}$ Pareto dominates ${\mathbf{x}}_{\mathbf{2}}$.
• ${\mathbf{x}}_{\mathbf{1}}$ and ${\mathbf{x}}_{\mathbf{2}}$ are feasible, and ${\mathbf{x}}_{\mathbf{1}}$ non-dominates ${\mathbf{x}}_{\mathbf{2}}$.
• ${\mathbf{x}}_{\mathbf{1}}$ and ${\mathbf{x}}_{\mathbf{2}}$ are infeasible, but the CV value of ${\mathbf{x}}_{\mathbf{1}}$ is smaller than ${\mathbf{x}}_{\mathbf{2}}$.
• ${\mathbf{x}}_{\mathbf{1}}$ is feasible while ${\mathbf{x}}_{\mathbf{2}}$ is infeasible.

3. D-NSDE Algorithm

Prior research has illustrated the efficacy of employing NSGA-III for optimizing satellite constellations in unconstrained settings, attributed to its hyperplane reference framework for multi-objective optimization. Nevertheless, when constraints are present, the iteration and optimization capabilities of NSGA-III are limited, leading to susceptibility to local optima. To tackle these constraints of designing composite multi-layer LEO constellations, we propose the D-NSDE algorithm, which preserves the hyperplane reference framework while integrating dynamic reference planes and operators. This approach enables the adjustment of operators and reference planes continuously during the iteration process, effectively overcoming the problem of NSGA-III being stuck in local optima when constraints are present.

3.1. Dynamic $\epsilon$-Feasible Solution

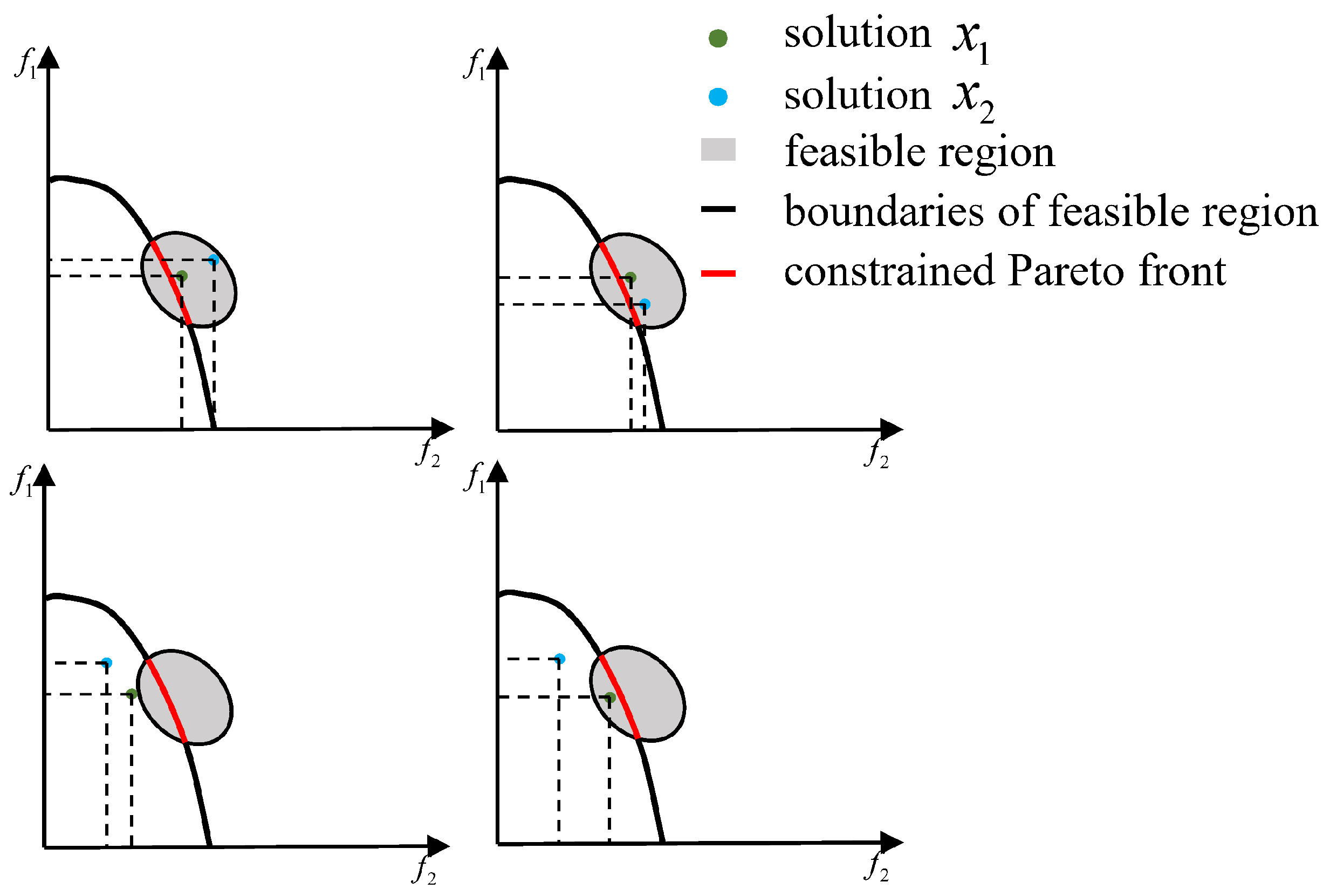
Depending solely on constraint violation as the guiding factor in population evolution may cause premature convergence of the population within a limited feasible region. Moreover, restricting selections to the feasible region may significantly reduce population diversity. In scenarios where the feasible region comprises multiple disconnected parts, there is a risk of overlooking specific solution sets, potentially resulting in the absence of certain Pareto-optimal solutions.

Hence, when addressing CMaOPs, both feasible and infeasible solutions are essential, as the latter can facilitate the population’s traversal of infeasible regions, as illustrated in Figure 3. Nevertheless, not all infeasible solutions contribute positively to population evolution. Permitting an excessive number of infeasible solutions can enlarge the search space and squander computational resources. Moreover, specific deceptive infeasible solutions can result in the population becoming ensnared in local optima.

We employ a dynamic $\epsilon$ parameter that enables the utilization of diverse infeasible solutions during various stages of population evolution. This approach aids in achieving balance between constraint satisfaction, diversity, and convergence performance. More specifically, an individual is deemed feasible if its degree of constraint violation is below $\epsilon$. When $\epsilon$ tends towards 0, the constraint form aligns with that employed in the COP method.

From this, it can be deduced that the combination of the aforementioned constraint-handling techniques with dynamic $\epsilon$ parameters results in the following scenarios during offspring selection $cv\left({\mathbf{x}}_{\mathbf{1}}\right)$:

• If $cv\left({\mathbf{x}}_{\mathbf{1}}\right)\le \epsilon$, $cv\left({\mathbf{x}}_{\mathbf{2}}\right)\le \epsilon$, and $cv\left({\mathbf{x}}_{\mathbf{1}}\right)$ Pareto dominates $cv\left({\mathbf{x}}_{\mathbf{2}}\right)$, then choose $cv\left({\mathbf{x}}_{\mathbf{1}}\right)$.
• If $cv\left({\mathbf{x}}_{\mathbf{1}}\right)\le \epsilon$, $cv\left({\mathbf{x}}_{\mathbf{2}}\right)>\epsilon$, then choose $cv\left({\mathbf{x}}_{\mathbf{1}}\right)$.
• If $cv\left({\mathbf{x}}_{\mathbf{1}}\right)>\epsilon$, $cv\left({\mathbf{x}}_{\mathbf{2}}\right)>\epsilon$, and $cv\left({\mathbf{x}}_{\mathbf{1}}\right)<cv\left({\mathbf{x}}_{\mathbf{2}}\right)$, then choose $cv\left({\mathbf{x}}_{\mathbf{1}}\right)$.

The relaxation of dynamic $\epsilon$-feasible solution values is accomplished through an exponential function within the simulated annealing algorithm [18]. The calculation formula of dynamic $\epsilon$-feasible solution values is provided below.

$${\epsilon }_i^{\left(t\right)}=A_{i}exp\left[-{\left(t/B_i\right)}^{cp}\right]-\delta ,i=1,2,\dots ,q$$

(4)

where $\delta$ is a small value ($1\times {10}^{-8}$), and $cp$ is the constant parameter that controls the trend of $\epsilon$ decrease (set at 5). In order to ensure that the initial population can reach $\epsilon$ feasible, we select the maximum constraint violation value of the population in each iteration as the initial constraint boundary. The maximum value ensures that the initial population contains at least some $\epsilon$-feasible solutions, allowing the algorithm to start from a feasible region and gradually improve these solutions.

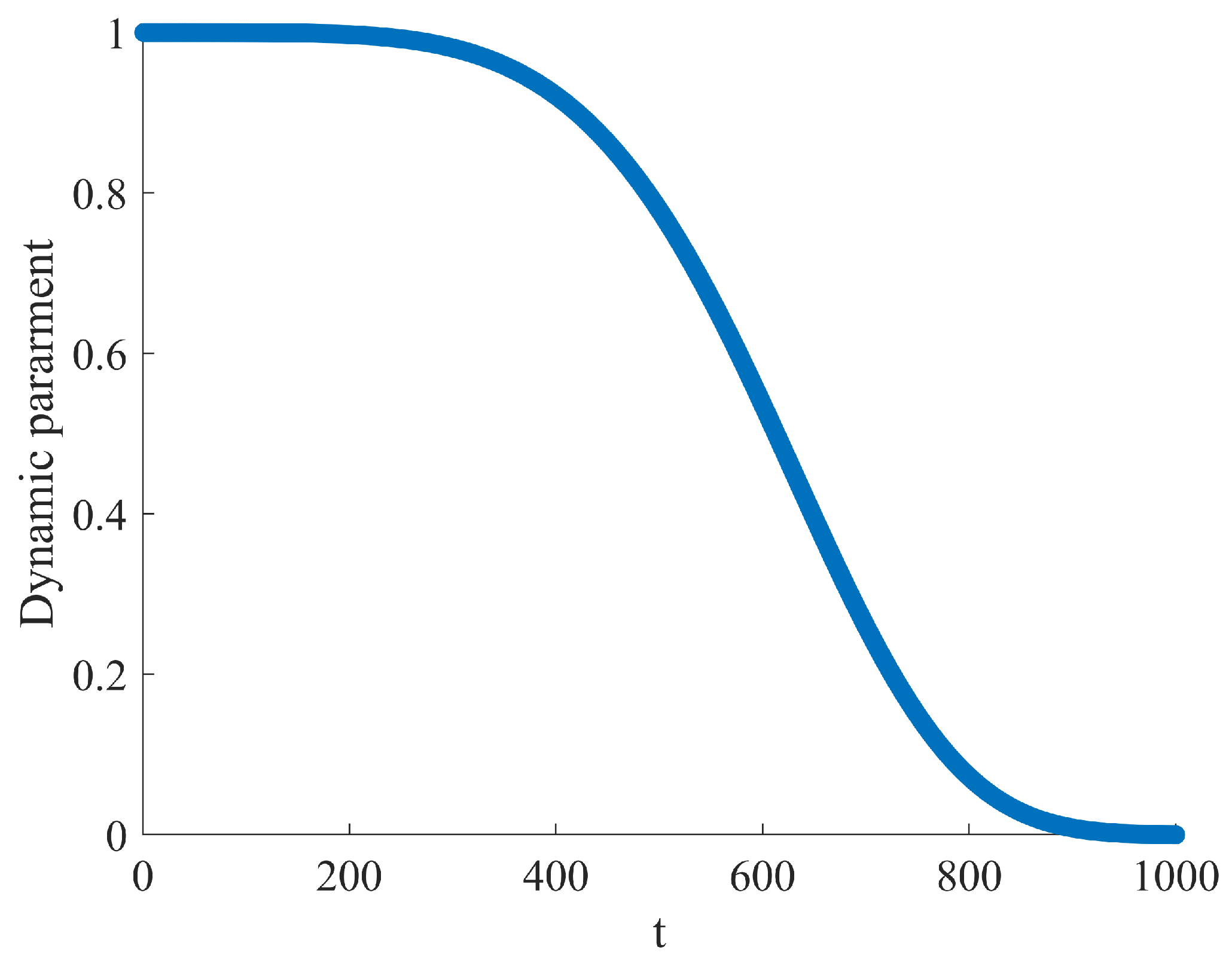
As the iterations process in Figure 4, the dynamic $\epsilon$ value gradually shrinks to 0. It can be deduced that

$$t=0,{\epsilon }_i^0=max\in \left\{Gi\left(x\right)\right\},i=1,2,\cdots ,q$$

(5)

$$t=T,{\epsilon }_i^T=0,i=1,2,\cdots ,q$$

(6)

$A_i$ and $B_i$ can be deduced as follows:

$$\left\{\begin{array}{c}{A}_i={\epsilon }_i^{\left(0\right)}+\delta \hfill \\ B_i={\displaystyle \frac{T}{\sqrt[cp]{ln\left(\frac{{\epsilon }_i^{\left(0\right)}+\delta }{\delta }\right)}}}\hfill \end{array}\right.$$

(7)

where $A_i$ represents the initial $\epsilon$ value plus a small offset $\delta$ to ensure positivity; $B_i$ is a scaling factor that determines the rate at which $\epsilon$ decreases over iterations. $A_i$ controls the starting point of the $\epsilon$ value for the i-th constraint, while $B_i$ controls how quickly $\epsilon$ decreases. A larger $B_i$ value means a slower decrease in $\epsilon$, allowing the algorithm to explore a broader range of solutions in the early stages and gradually focus on more feasible solutions as iterations progress.

Thus, the CMaOP is transformed into a CMaOP based on $\epsilon$-feasible solutions, which can be formulated as follows:

$$\begin{array}{cc}\hfill & minimize(f_1\left(\mathbf{x}\right),\dots ,f_m\left(\mathbf{x}\right),c\nu \left(\mathbf{x}\right))\hfill \\ \hfill & subjectto:g\left(\mathbf{x}\right)\le {\epsilon }^{\left(t\right)}\hfill \\ \hfill & where:{\epsilon }^{\left(t\right)}=({\epsilon }_1^{\left(t\right)},\dots ,{\epsilon }_q^{\left(t\right)}),t=0,1,\dots ,T\hfill \end{array}$$

(8)

where ${\epsilon }^{\left(t\right)}$ denotes the dynamic boundary; the solution where $g\left(\mathbf{x}\right)\le {\epsilon }^{\left(t\right)}$ is referred to as an $\epsilon$-feasible solution, where t denotes the iteration number. The constraint boundary of feasible solutions decreases with the increase in the iteration number, ultimately converging to 0.

3.2. Dynamic DE Operator

Compared with GA operators of NSGA-III, DE operators possess rotation invariance, which implies that the convergence contour of DE operators rotates along with the search space. It does not imply that DE operators are consistently superior to GA operators. However, when dealing with an uncertain Pareto front, the use of DE operators is a preferable option [19,20].

To handle such uncertain Pareto fronts, we select the DE operators DE/rand/1 and DE/best/1 [20], and we utilize dynamic $\epsilon$ parameters to regulate the operator direction during population iteration. The formulation for this approach is presented below.

$$\left\{\begin{array}{cc}{o}_d={\mathbf{x}}_{\mathbf{1}\mathbf{d}}+F·({\mathbf{x}}_{\mathbf{2}\mathbf{d}}-{\mathbf{x}}_{\mathbf{3}\mathbf{d}})\hfill & \hfill 1\le d\le DwithprobabilityCR\ast (1-\epsilon )\\ or\hfill \\ o_d={\mathbf{x}}_{\mathbf{1}\mathbf{d}\left(\mathbf{best}\right)}+F·({\mathbf{x}}_{\mathbf{2}\mathbf{d}}-{\mathbf{x}}_{\mathbf{3}\mathbf{d}})\hfill & \hfill 1\le d\le DwithprobabilityCR\ast \epsilon \\ & \\ o_d={\mathbf{x}}_{\mathbf{1}\mathbf{d}\left(\mathbf{best}\right)}\hfill & \hfill 1\le d\le Dwithprobability1-CR\end{array}\right.$$

(9)

where F denotes the multiplier that controls the amplification of the difference between ${\mathbf{x}}_{\mathbf{2}}$ and ${\mathbf{x}}_{\mathbf{3}}$, $CR$ denotes the parameter that controls the differential probability. When $\epsilon$ is high (in the early iterations), the algorithm is more likely to use the DE/rand/1 operator, which promotes exploration by generating new solutions based on the differences of random individuals. This helps the algorithm explore a broader search range and avoid premature convergence. As $\epsilon$ decreases (in the later iterations), the algorithm is more likely to use the DE/best/1 operator, which focuses on exploitation by generating new solutions based on the best individual found so far. This helps the algorithm to converge faster to the optimal solution. The dynamic probability $\epsilon$ is adjusted over iterations to ensure that the algorithm can adaptively switch between exploration and exploitation, thereby improving the search efficiency and convergence speed.

3.3. Flow of the Algorithm D-NSDE

D-NSDE integrates the non-dominated sorting algorithm, dynamic $\epsilon$ feasible solution parameter, and dynamic DE operators from the NSGA-III algorithm, with a critical emphasis on the dynamic $\epsilon$ parameter, which is specifically designed for addressing CMaOPs. The overview of the algorithm’s process is illustrated in Algorithm 1, followed by a detailed step-by-step procedure outlined below.

Algorithm 1: General flow of D-NSDE.

1. Generate an initial population $p_0$, population size = N a. Randomly generate N individuals within the decision variable range b. Evaluate the objective functions and constraint violation (CV) values for each individual 2. The initial value of the dynamic $\epsilon$ parameter is set during initialization, $\epsilon ={\epsilon }_0$, iteration t = 0 a. Set the initial dynamic $\epsilon$ parameter ${\epsilon }_i^0=max\in \left\{Gi\left(x\right)\right\}$ b. Set the iteration counter t = 0 While Iteration termination not satisfied do    Update the dynamic $\epsilon$ parameter using the formula: $\epsilon ={\epsilon }_{t+1}$ 3.    Generate the mating pool by Tournament Selection and dynamic DE operator,        population size = $2N$        a. For each individual in the population, select two parents using tournament selection        b. Apply the dynamic DE operator to generate offspring individuals:           - With probability CR * (1 −$\epsilon$), use DE/rand/1           - With probability CR * $\epsilon$, use DE/best/1           - With probability 1 − CR, use the best individual        c. Evaluate the objective functions and CV values for the offspring individuals        d. Combine the parent and offspring populations into a combined population        e. Perform non-dominated sorting on the combined population        f. Select the top N individuals based on the non-dominated sorting and reference-point-based elitist selection 4.    Update the population $p_{t+1}$ by Reference-Point-Based Non-dominated Sorting of       NSGA-III from mating pool, population size = N       a. Increment the iteration counter t = t + 1 end 5. Return non-dominated solutions.

Step 1:

Initialization

The population is initialized by randomly generating N individuals within the range of the values of the decision variables. For each individual in the population, objective function values and CV values are computed. Subsequently, the initial value of the dynamic $\epsilon$ parameter is calculated based on the initial CV values.

Step 2:

Dynamic parameter control

Throughout the iteration process, the dynamic parameter $\epsilon$ is adjusted in accordance with the progress of population iteration denoted by t. This dynamic parameter $\epsilon$ gradually diminishes to facilitate convergence.

Step 3:

Generate population offspring

The population p from the preceding iteration is utilized to derive the parent population through a binary selection method. Subsequently, the dynamic $\epsilon$-controlled DE operator is utilized to produce an equivalent number of offspring individuals, resulting in a set size of $2N$ at this juncture.

Step 4:

Update population

The objective function values and CV values of the entire population are calculated, followed by partitioning the population into three sets: strictly feasible solution, $\epsilon$ feasible solution, and infeasible solution. Non-dominated sorting and reference point-based elitist selection are utilized to select individuals from the strictly feasible solution set. If the population size is less than N, individuals with smaller CV values are subsequently selected from the $\epsilon$ feasible solution set to reach N.

Step 5:

Iteration

Return to Step 2 and repeat the remaining steps until the algorithm terminates.

4. Analysis of Test Set Function Results

To evaluate the performance of the D-NSDE algorithm, our initial step involves comparing it with NSGA-III in the CEC Test Functions (CF) suite, the Ma-Wang (MW) [17] suite and the Deb–Thiele–Laumanns–Zitzler (DTLZ) suite [19,21,22]. These test sets encompass benchmark functions that feature a minimum of three objective functions.

Using the Common Test Platform (CTP) test suite framework, the CF test suite and the test set were crafted. Within the CF test set, a non-linear PF is evident in the decision space, featuring a CPF distinguished by disconnected geometric shapes. Introducing variable linkages within the CF test set poses challenges for algorithms to converge effectively when tackling CF problems. The Zhou–Xiang–He (ZXH)_CF suite, an extension of the CF suite, incorporates infeasible obstacles near the optimal solution, leading to inter-relationships between position and distance variables. Simultaneously, it limits the optimal region within the feasible space, resulting in the generation of Pareto fronts exhibiting diverse shapes.

The Constraint (C)-DTLZ test suite is developed as an extension of the unconstrained DTLZ test problem [23]. It incorporates two types of constraints from the CF series and introduces a novel constraint that renders the entire UPF infeasible, consequently yielding a CPF defined by the boundaries of the feasible region. In the case of (Dynamic Constraint) DC-DTLZ [24], local optima are strategically positioned within the infeasible region, thereby increasing the likelihood of algorithms becoming ensnared in these local optimal regions and being unable to transition into the feasible region.

Additionally, the MW test suite encompasses four distinct constraint types: (1) the unconstrained PF aligns with the constrained PF; (2) the constrained PF is entirely nested within the unconstrained PF; (3) the constrained PF exhibits partial overlap with the unconstrained PF while remaining partially non-overlapping; and (4) the constrained PF is entirely disjoint from the unconstrained PF.

4.1. Performance Metrics

To evaluate the performance of various algorithms in these test sets, we used two commonly used metrics in our experimental analysis: inverted generational distance (IGD) [25] and hypervolume (HV) [26].

IGD represents the average distance from the true non-dominated solution set and can be expressed as follows:

$$\mathrm{IGD}(P^{*},P)={\displaystyle \frac{{\displaystyle \sum _{\mathbf{x}\in P^{*}}}dis(\mathbf{x},\mathbf{P})}{|P^{*}|}}$$

(10)

where $P^{*}$ denotes the true PF and P is the solution. $dis$ denotes the Euclidean distance between a solution x and its nearest point in the true solution set. In other words, a lower IGD value means that the solutions are nearer to the true solution set and demonstrate a favorable distribution. Using this metric, we can assess both the convergence and the diversity of solutions.

Hypervolume (HV) refers to the volume of the objective space enclosed by the obtained solution set and a reference point $z^r$. Its mathematical expression is defined as

$$\mathrm{VOL}\left(\bigcup _{x\in P}[x_1,z_1^r]\times \cdots \times [x_m,z_m^r]\right)$$

(11)

where VOL denotes the Lebesgue measure. A higher HV value indicates a better dominance relationship. The reference point is typically chosen as the worst value for each objective function on the PF, and in our experiments, we set the reference point as (1.1, 1.1, …) after normalization.

4.2. Analysis of Test Set Function Results

The parameter settings for the NSGA-III and D-NSDE algorithms are as follows: For NSGA-III, simulated binary crossover (SBX): crossover probability PC = 0.9, distribution index $\mathsf{\eta }$c = 30. For polynomial mutation (PM): mutation probability PM = 1/n, distribution index $\mathsf{\eta }$m = 20 [27]. For D-NSDE, the crossover rate (CR) is set to 0.2, and the mutation rate (F) is set to 0.5.

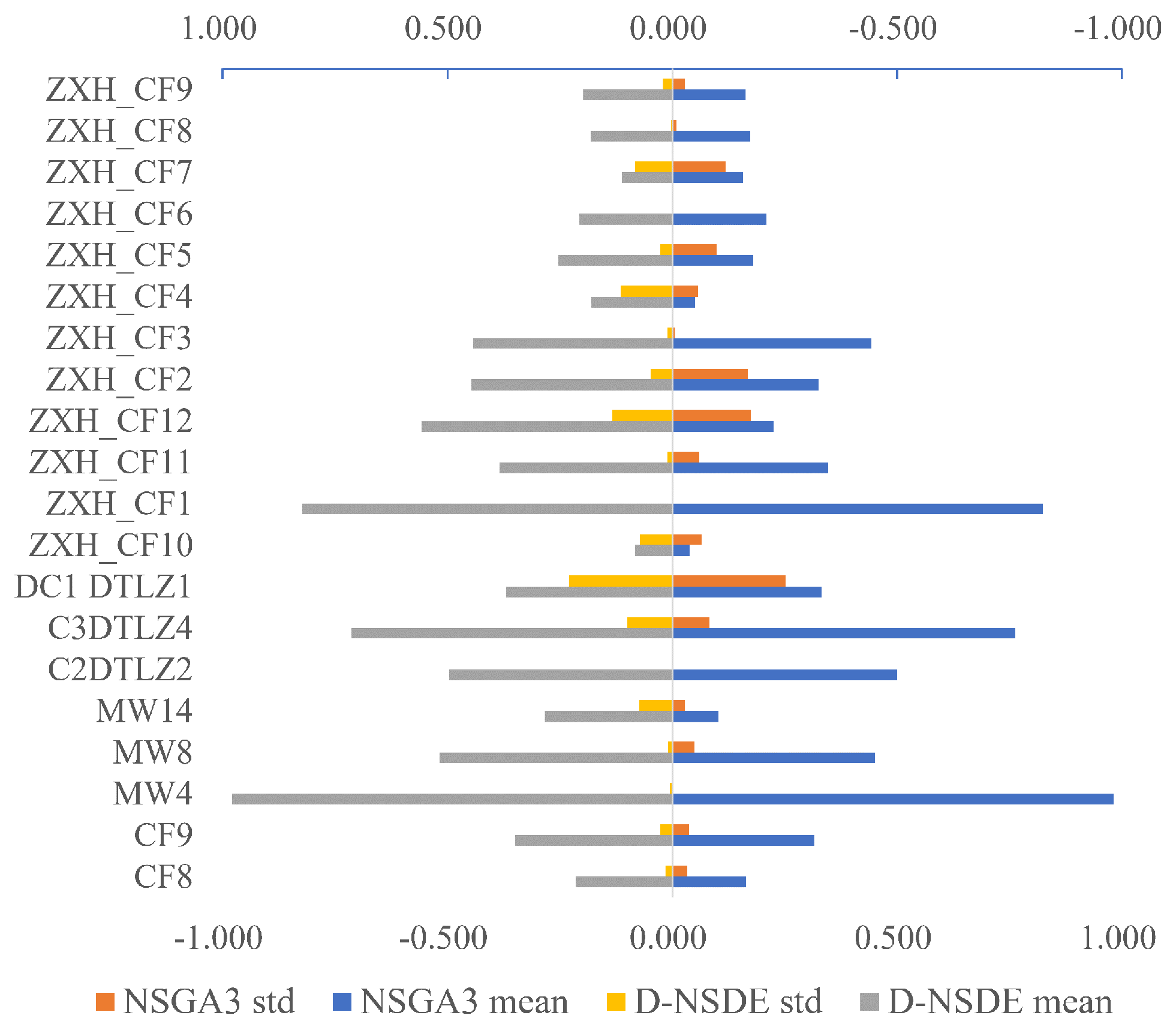
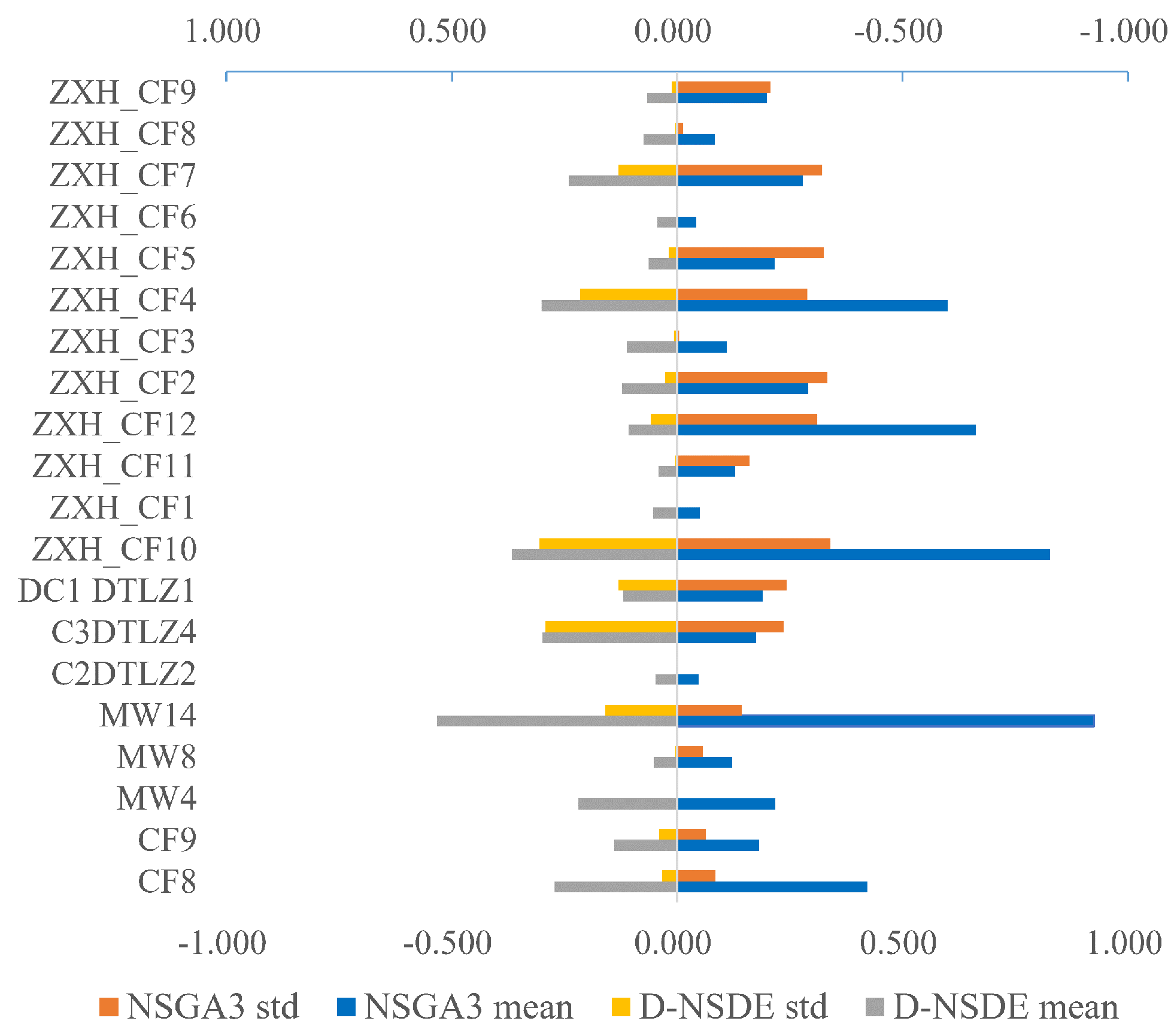
The population size is set to 100, and the number of evaluations is set to 30,000. To reduce randomness, all algorithms are independently run 50 times. Figure 5 and Figure 6 illustrate the precise average and standard deviation values of the IGD and HV metrics in 50 experimental runs, as follows:

It is evident that, for the majority of the selected test problems, the D-NSDE algorithm exhibits superior mean and standard deviation values compared to NSGA-III when evaluated using the HV metric in Figure 5. In particular, for the ZXH_CF problem series, the solution sets obtained by D-NSDE demonstrate significantly higher average and standard deviation values compared to NSGA-III. This highlights D-NSDE’s proficiency in identifying feasible solutions for non-linear Pareto optimal problems within the decision space, where NSGA-III faces challenges. In the case of the DTLZ problem series, D-NSDE performs similarly to NSGA-III in terms of average performance, but its standard deviation surpasses that of NSGA-III. This suggests that when infeasible non-intersecting solutions are present within the feasible region of DTLZ problems, D-NSDE exhibits greater stability in finding the optimal solution compared to NSGA-III.

As shown in Figure 6, the results obtained from the IGD metric clearly demonstrate that the D-NSDE algorithm consistently outperforms the NSGA-III algorithm across nearly all examined problems. This finding serves to reaffirm that, across various constraint-based test problems, the D-NSDE algorithm not only excels in identifying solution sets with superior feasibility but also guarantees their favorable distribution characteristics.

Through a longitudinal comparison across various test problems, the D-NSDE algorithm exhibits substantial performance enhancements within the ZXH_CF series when contrasted with other test scenarios. This observation highlights how the incorporation of four distinct constraints in the ZXH_CF series empowers the D-NSDE algorithm not only to achieve a high-quality set of feasible solutions but also to maintain a desirable distribution among the obtained feasible solution set.

While the D-NSDE algorithm demonstrates significant performance on the ZXH_CF test problems, it exhibits negligible disparities compared to the NSGA-III algorithm on the DTLZ test problems. This can be attributed to the fact that the feasible region of the chosen DTLZ problem series constitutes only a small portion of the infeasible region. As a result, both algorithms might have inadequate discriminative abilities when navigating through the infeasible region.

5. Experiments to Optimize LEO Constellations

5.1. LEO Constellation Model

Walker constellations are configurations of satellites evenly distributed in space, all having the same semi-major axis, inclination, eccentricity and argument of perigee. This design is prevalent in modern LEO satellite systems. A Walker constellation is specified by N/P/F, where N is the total satellite count, P is the number of orbital planes, S is the number of satellites per plane (S = N/P) and F is the phase factor reflecting the satellite positions across adjacent planes, ranging from 0 to P−1. This paper’s LEO satellite constellation uses Walker modes, including a regional communication layer and 1-/2-/3-layer global navigation constellations, labeled C1/C2/C3, respectively. Additionally, BDS-3 is included with similar Walker mode settings, noted as C4/C5/C6 for all three schemes. C1 and C4 feature single-layer low-Earth-orbit regional communication and navigation constellations. C2 and C5 have single-layer low-Earth-orbit regional communication constellations and double-layer low-Earth-orbit navigation constellations. C3 and C6 consist of single-layer low-Earth-orbit communication constellations and three-layer low-Earth-orbit navigation constellations. In composite constellations, to ensure less signal transmission attenuation and global coverage of navigation signals, communication constellations are placed at the lowest orbital level, with navigation constellations distributed above them. Also, C4, C5, and C6 add BDS-3 as a constraint for the medium-Earth-orbit navigation constellation.

5.2. Communication/Navigation (Com-Nav) LEO Constellation Objective Function

5.2.1. Communications Performance Evaluation

Regional communication constellations aim to achieve complete satellite coverage within a designated area, termed single coverage. The quality of coverage in these constellations is evaluated using performance metrics such as the percentage of coverage, the maximum coverage gap, the average coverage gap, and the time-averaged gap.

This research uses the percentage of coverage as a key performance metric for communication constellations. The percentage of coverage is calculated by dividing the time it takes for a specific regional grid point to be covered by one or more satellites by the total duration of the simulation. A ground point is considered covered when a satellite is visible within the defined elevation angle constraint, and it is deemed uncovered when the angle exceeds this limit. The interval during which the satellite remains visible is called the satellite visibility time.

5.2.2. Navigation Performance Evaluation

The positioning accuracy of LEO constellations is generally assessed using dilution of precision (DOP) values, which depend on the geometry between the ground station and visible satellites. Therefore, position accuracy can be represented as

$$\sigma =GDOP·{\sigma }_{UERE}$$

(12)

The geometric dilution of precision (GDOP) value can be expressed as follows:

$$GDOP=\sqrt{trace\left\{{\left[{\left({\mathbf{H}}^k\right)}^T{\mathbf{H}}^k\right]}^{-1}\right\}}.$$

(13)

Within the Earth-centered coordinate system, the matrix $\mathbf{H}$ consists of observational values satisfying specific conditions. The pseudo-range error factor ${\sigma }_{UERE}$ mainly includes satellite clock bias, ionospheric and atmospheric errors, receiver noise, and multi-path effects.

Two primary goals are central to optimizing the low Earth orbit. The first objective aims to achieve a specified percentage of satellite coverage within a region defined by latitudes [0, 60] and longitudes [60, 140]. Here, coverage percentages are averaged across 60 strategically selected observation points. The second objective aims to improve navigation performance globally. This is carried out by dividing the global region into a 5° × 5° grid to compute the maximum GDOP value at each point on the grid. For this purpose, a fixed satellite cutoff elevation angle of 7° is used, considering Earth’s J2 term during orbit integration, with an integration time of 60 s. The mathematical formulation is as follows:

$$Fitnes{s}_1=av{g}_{t\in (0.T_P)}av{g}_{F\in (0.P-1)}av{g}_{r_{Pe}Earth}coverage(r_P,t,c)/T_p$$

(14)

$$Fitnes{s}_2={max}_{t\in (0.T_P)}{max}_{F\in (0.P-1)}{max}_{r_{Pe}Earth}GDOP(r_P,t,c)$$

(15)

$T_P$ denotes the duration of the satellite coverage, $r_P$ indicates the subdivided grid points, and c symbolizes the assessed satellite constellation.

Furthermore, considering the total cost of the satellite system, the number of satellites in the constellation is taken as the third objective function.

$$Fitnes{s}_3=\sum _{n=1}^3{s}_n\times p_n$$

(16)

Given the adoption of a multi-layer satellite configuration to establish the low-Earth-orbit constellation, the objective functions for the satellite orbit altitudes of each layer are designated as the fourth to seventh objectives.

$$Fitnes{s}_{4\sim 7}=altitude{s}_{1\sim 4}$$

(17)

5.3. Decision Space

This study employs the Walker model for the design of LEO constellations, setting the parameters of the satellites in each layer as decision variables. Considering the influence of the Van Allen radiation belt on these satellites, the decision variables and space are detailed in the

Table 1. Range of decision variables.

	${\mathit{S}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$	${\mathit{INCL}}_{\mathit{i}}$	${\mathit{H}}_{\mathit{i}}$
C1/C4	1/1	1/1	45°/0°	500/500
	15/30	15/20	90°/90°	1500/1500
C2/C5	1/1/1	1/1/1	45°/0°/50°	500/500/500
	15/30/30	15/20/20	90°/60°/110°	1500/1500/1500
C3/C6	1/1/1/1	1/1/1/1	45°/0°/30°/70°	500/500/500/500
	15/30/30/30	15/20/20/20	90°/50°/80°/110°	1500/1500/1500/1500

. The set of essential optimized parameters for the constellation is $X_C=\{S_i,P_i,INC{L}_i,H_i\}$, where C represents distinct constellations and i refers to the layers of the composite constellation. Considering the Van Allen radiation belts, the constellation’s altitude is set between 500 and 1500 km. This range reduces signal attenuation, increases ground signal power, and reduces operational costs. Orbital inclination, satellite number, and orbit number are shaped by constellation design, coverage, and performance needs, ensuring uniform and reliable coverage.

5.4. Constraint Condition

In contrast to “hard” constraints in decision making, supplementary constraints offer greater flexibility. Our dynamic parameter settings initially permit these constraints to be overlooked, accommodating a broader spectrum of solutions. Subsequently, the parameters are refined to reinforce a stricter adherence to these constraints. To improve solution diversity and address issues such as low-Earth-orbit object interference and the effects of the Van Allen radiation belts, these supplementary constraints are introduced.

• The communication constellation is placed at the lowest altitude by minimizing the decision variable related to its height, compared to other layers, ensuring it is the lowest in the constellation;
• A total satellite count cap of 400 is enforced to adhere to the constraint on the number of satellites, ensuring manageable and feasible satellite operations;
• A multi-layer navigation constellation is designed with altitudes incrementally increasing from S1 to S3, optimizing satellite performance in coverage and reliability;
• Integrating the BDS-3 system is necessary to enhance the navigation capabilities of C4/C5/C6, thereby improving navigation accuracy while serving as a constraint to augment the overall navigation performance of the satellite constellation.

5.5. Analysis of LEO Constellation Results

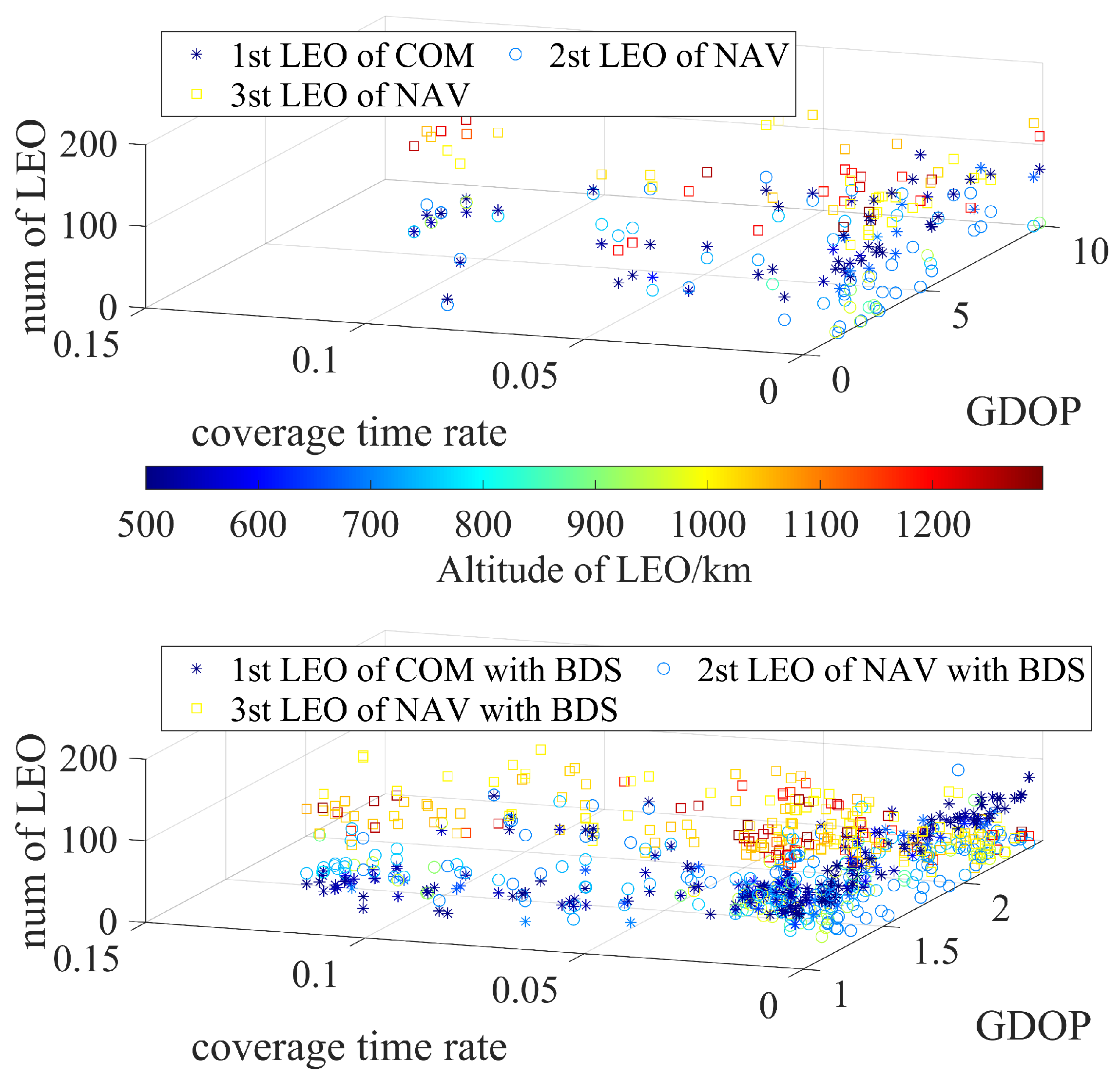
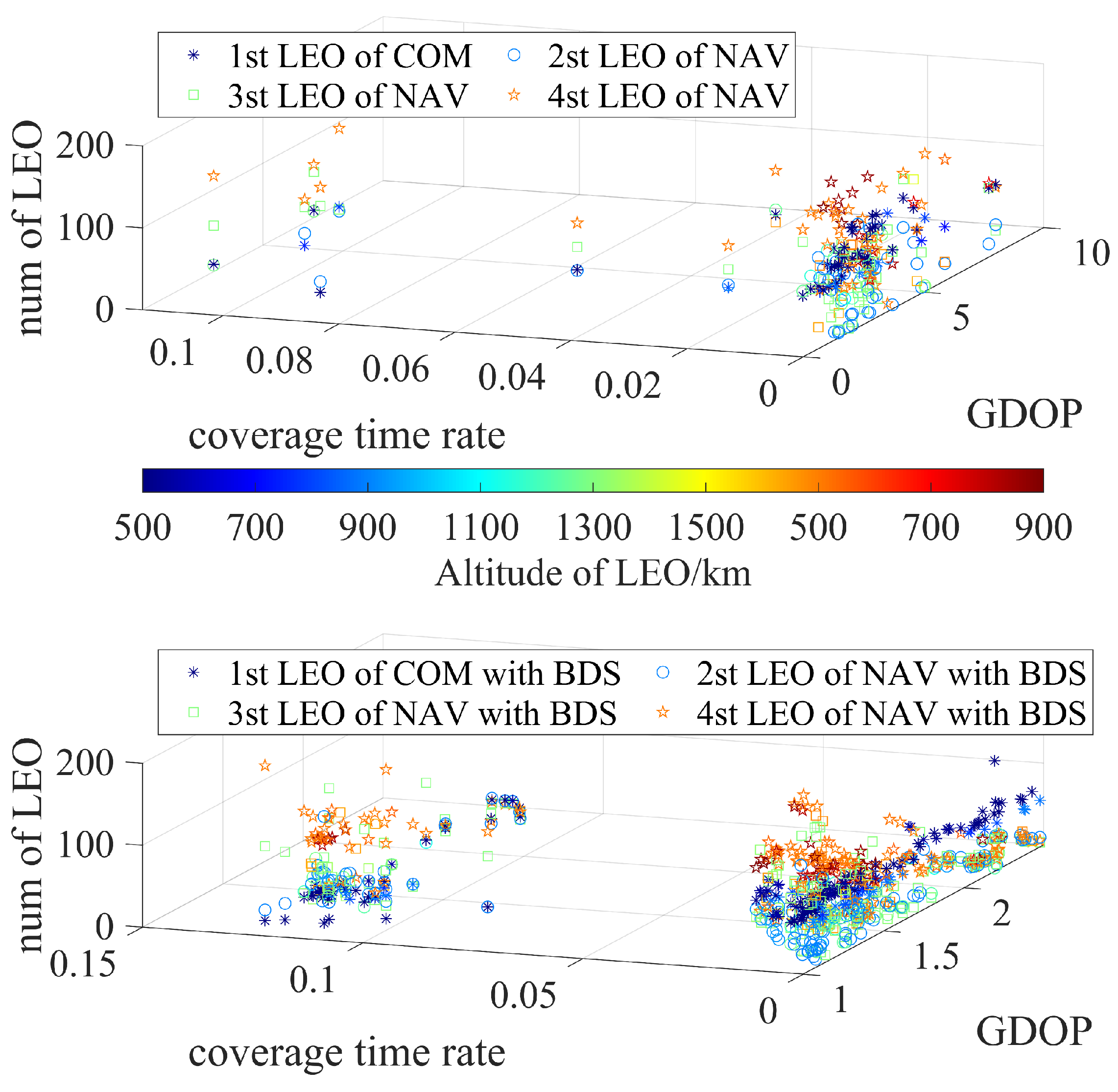
After establishing the objective function, the decision variables and constraints, we converted the composite Com-Nav LEO constellation into CMaOPs. We approached the problem using D-NSDE with parameters from testing functions. For each constellation type (C1/C2/C3/C4/C5/C6), the optimization was executed ten times, implementing parallel computing to reduce computational time. The distribution of the final solution set is illustrated in Figure 7, Figure 8 and Figure 9.

The results reveal a clear “layered” effect in orbits due to the effective implementation of the D-NSDE algorithm. This algorithm ensures that solutions evade infeasible regions, leading to a varied and well-spread collection of solutions. The figures further show that solution sets for nearby orbit heights create smooth surfaces, showcasing the D-NSDE algorithm’s excellent convergence ability.

Compared to Figure 7 and Figure 8, Figure 9 exhibits a denser distribution. This is due to the increased complexity of the four-layer composite low-Earth-orbit constellations depicted by C3 / C6, which involve 16 decision variables and added constraints, resulting in a larger infeasible area and thus a denser solution set. The results indicate that for regional communication constellations, the solution set remains relatively uniform, with most feasible solutions located within a similar region, aside from infeasible ones. This occurs because, despite the additional constraints, the convergence performance of the solution set remains unaffected. In particular, a regional communication constellation with under 100 satellites can achieve a 90% coverage rate.

Incorporating BDS-3 constraints into the navigation constellations C4/C5/C6 results in a noticeably more concentrated solution set than the more dispersed C1/C2/C3. This shows that these additional constraints significantly improve the convergence performance of the solutions.

The D-NSDE algorithm determined the configuration parameters for the composite Com-Nav LEO constellations, which were subsequently evaluated for Com-Nav performance. The results are depicted in the box plots of Figure 10a–c.

The GDOP values for C1/C2/C3, which include only LEO constellations, are greater compared to C4/C5/C6, which incorporate BDS-3 constraints. The GDOP for C1/C2/C3 is more varied, with median values around 5, 4, and 3, respectively, and 75th percentile values of approximately 7 for C1/C2 and under 5 for C3. These results indicate that single-layer structures with LEO constellations perform better than multi-layer structures. In contrast, for C4 / C5 / C6, introducing BDS-3 constraints reduces their median GDOP to 1–2, with similar 75th percentile values, showing marked improvement and consistency in navigation performance. This underscores the value of integrating the appropriate constraints to identify optimal solutions.

Communication constellations C1 to C6 share a single-layer design with the same additional constraints, leading to similar communication performance, with the 75th percentile of solutions close to 95%. In particular, C3 and C6 exhibit more stable performance, likely due to more decision variables. This stability impacts constraints on low-Earth-orbit navigation constellations, resulting in a limited and more focused set of feasible solutions for communication constellations in a low Earth orbit.

Figure 11a–f illustrate the typical configurations for each LEO satellite constellation solution set, with their parameters detailed in

Table 2. Parameters of LEO constellation.

		Configuration	Inclination (Deg)	Altitude (km)	Coverage	GDOP
C1	COM	W63/7/1	61.5	788	96.9%
	NAV	W160/10/1	86.7	1220		3.5
C2	COM	W77/7/4	60	700	98.6%
	NAV	W7/7/1	34.3	900		2.6
		W196/14/2	86.6	1200
C3	COM	W99/9/3	69.7	700	99.8%
	NAV	W84/14/2	24.9	900		2.2
		W70/10/1	69.8	1100
		W140/14/1	78.7	1500
C4	COM	W54/9/2	60.8	955	96.4%
	NAV	W150/10/1	113.2	1256		1.5
C5	COM	W104/8/4	65.1	700	99.6%
	NAV	W27/9/1	23.4	907		1.2
		W225/15/2	68.4	1200
C6	COM	W98/7/2	68.4	707	99.8%
	NAV	W45/15/1	22.3	1056		1.1
		W9/3/1	53.5	1100
		W210/14/4	83.8	1308

. The mean coverage percentages for C1, C2, and C3 are 96.9%, 98.6%, and 99.8%, respectively, with peak GDOP values of 3.5, 2.6, and 2.2. By incorporating BDS-3 constraints, C4, C5 and C6 achieve an average coverage of 96.4%, 99.6%, and 99.8%, while reducing the maximum GDOP to 1.5, 1.2, and 1.1. This solution set highlights that the integration of a single-layer communication and dual-layer navigation constellation results in reduced objectives and superior communication and navigation performance.

6. Conclusions

We introduce D-NSDE, designed to tackle interactions between objectives and constraints in a multi-dimensional objective space. This algorithm dynamically adjusts constraint boundaries and operator forms during the population iteration, guided by the population’s iteration status. By incorporating dynamic parameters, it adeptly manages a wide spectrum of infeasible regions. For many-objective optimization problems with constraints, it adeptly balances convergence, diversity, and constraint violation, yielding superior solutions. Standard benchmark tests reveal that our algorithm surpasses NSGA-III in IGD and HV, demonstrating excellent performance.

We devised a model for the Com-Nav LEO constellation, featuring a navigation segment structured as a composite constellation with one to three layers. By establishing decision variables and objective functions, we reformulate these into a multi-objective optimization problem with additional constraints. This approach yields a set of satellite configuration parameters that exhibit well-distributed and convergent properties. An analysis of the coverage of the communication constellation indicates that about 95% of the solutions reside within the 75th percentile range. Adding constraints to the navigation LEO constellation markedly improves satellite navigation performance, reducing the 75th percentile GDOP from three to seven to between one and two. This reduction demonstrates the effectiveness of the constraints in enhancing convergence performance and solution diversity achieved by the D-NSDE algorithm.

In summary, D-NSDE excels at balancing various objectives within the Com-Nav LEO constellation domain, yielding high-quality solutions. However, practical constellation design requires additional constraints. For example, assessing the cost of navigation and communication constellations should extend beyond the altitude and number of satellites, taking into account the precise characteristics of the payload. Furthermore, as low-Earth orbit communication/navigation/remote sensing constellations evolve, potential composite payloads add complexity, requiring multiple performance metrics to be evaluated.