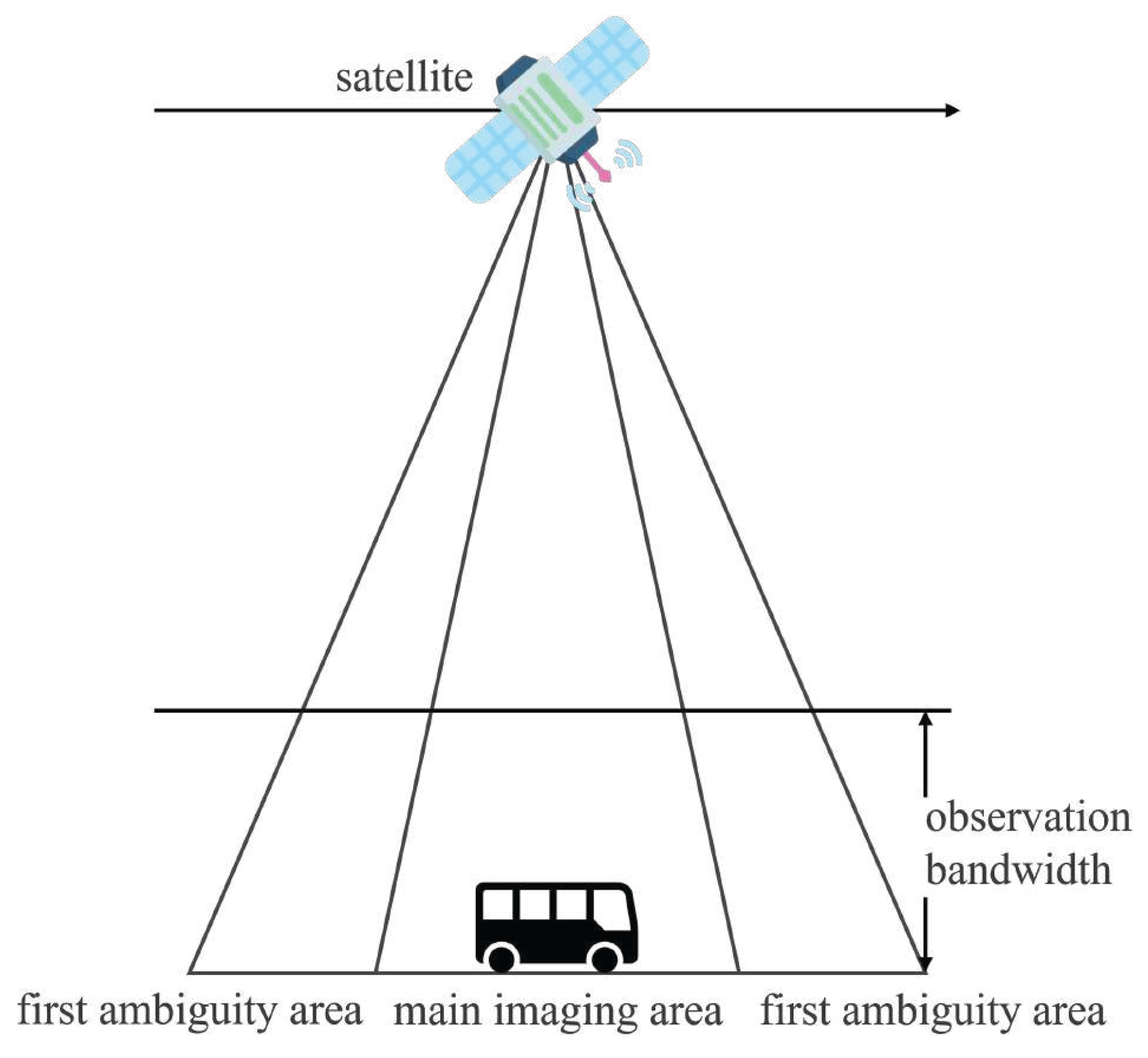
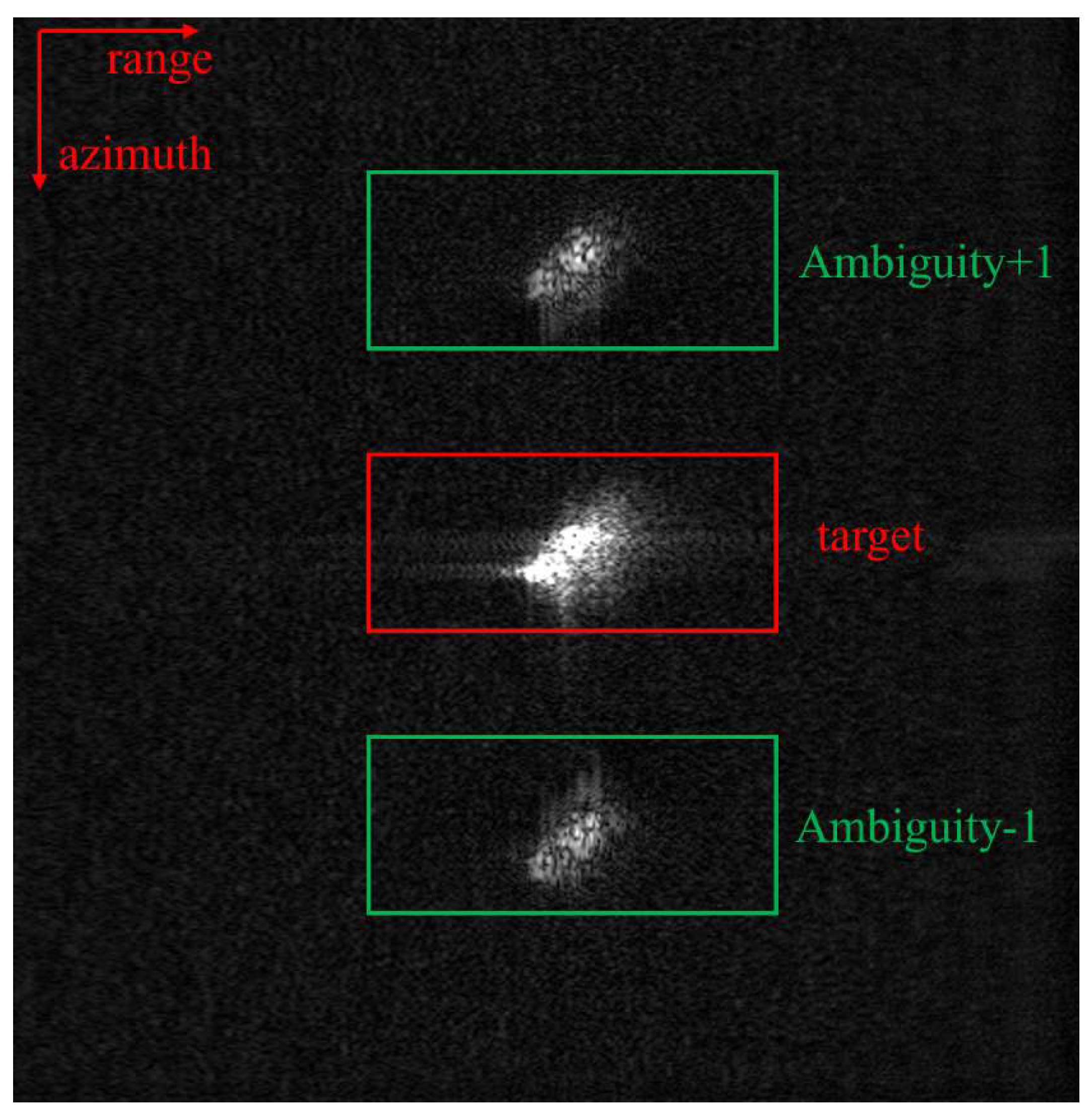
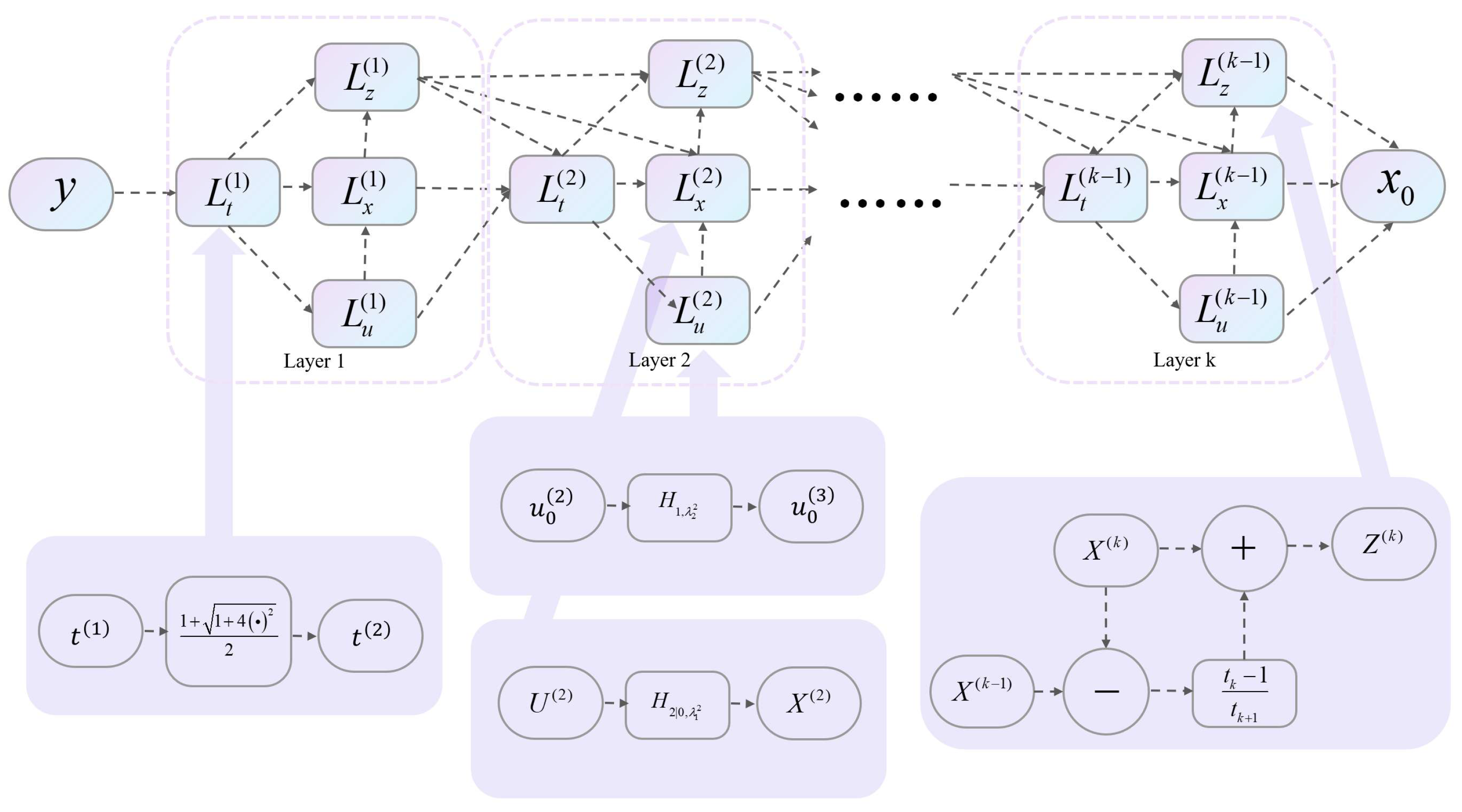
1. Introduction
High-resolution synthetic aperture radar (SAR) imaging algorithms have recently earned significant attention in the field of SAR imaging. However, due to the constraints imposed by the Nyquist sampling theorem [
1], achieving high-resolution wide-format imaging requires higher sampling rates. The SAR imaging problem, viewed as an inverse problem, can potentially overcome this limitation through the application of compressed sensing theory [
2,
3]. The first proposed application of compressed sensing theory to SAR imaging algorithms was made by [
4]. Subsequent work by [
5,
6,
7] further enhanced sparse synthetic aperture radar algorithms. Additionally, compressed sensing algorithms have been applied in the fields of inverse synthetic aperture radar imaging [
8,
9] and three-dimensional imaging [
10,
11,
12]. Compared to traditional SAR imaging methods, sparse SAR imaging algorithms can reduce the number of samples. However, most of these algorithms operate in the time domain, overlooking or failing to account for azimuth–distance coupling. As a result, they suffer from high computational complexity and memory usage, making them challenging to apply to large-scale scenes or wide-format imaging. Reference [
13] proposed an approximated observation-based sparse SAR imaging algorithm that can significantly reduce computational and temporal complexities. This approach maintains consistency in computational complexity and matched filtering algorithms.
In practice, traditional sparse synthetic aperture radar imaging algorithms often require manual parameter tuning. This means that the parameters must be readjusted for different imaging scenarios, and the entire tuning process is heavily reliant on manual experience. In recent years, SAR imaging based on deep learning has been widely used [
14,
15,
16,
17,
18], leveraging deep learning for adaptive parameter adjustment. Reference [
19] introduced the concept of a sparse unfolding network by leveraging the properties of neural networks. This method replaces the iterative process of the original algorithm with a multi-layer neural network, which is used to automatically train and adjust the parameters that would traditionally need manual fine-tuning, ensuring that the parameters are selected optimally. In recent years, deep unfolding networks have found applications in sparse synthetic aperture radar imaging. In [
20], a joint range migration and sparse reconstruction network for 3D millimeter-wave imaging was introduced. In [
15,
21], a SAR imaging framework based on the depth-expanded network of ISTA was proposed and successfully applied to passive SAR. However, these methods are limited in their ability to effectively utilize the structural information inherent in SAR signals and therefore cannot address issues such as range ambiguity and azimuth ambiguity.
Since the energy of azimuth ambiguity cannot be ignored in practical applications, it is essential to pay attention to azimuth ambiguity suppression in sparse SAR imaging. Existing ambiguity suppression algorithms can be broadly categorized into three types: those that directly or indirectly utilize the filtering results of filters [
22,
23], sparse reconstruction-based algorithms [
24,
25,
26], and those that use regions with less ambiguity for imaging [
27,
28]. Whether the filter results are directly applied to imaging or used as part of the a priori knowledge, accurate spectral information is critical. Although filtering can effectively mitigate spectral aliasing in certain regions, it often leads to adverse effects on the spectrum in the primary region as well. Sparse reconstruction-based methods, on the other hand, typically involve complex, large-scale computations. These approaches often require manual parameter tuning, making them highly sensitive to user input and limiting their adaptability. Due to the inherent characteristics of radar system imaging, identifying regions with minimal ambiguity proves to be a challenging task. Consequently, the practical implementation of algorithms that rely on these less ambiguous regions for imaging faces substantial obstacles.
Based on this, in this paper, we investigate the cause of azimuthal ambiguity and introduce group sparse constraints to reformulate the SAR imaging model. We employ the compressed sensing algorithm for sparse reconstruction and leverage a network structure to train the parameters that would typically require manual adjustment, significantly mitigating the issue of insufficiently accurate manual tuning. Additionally, a self-supervised algorithm is introduced to address the problem of traditional neural network-based imaging algorithms being overly dependent on existing datasets. The entire algorithm is built upon the chirp scaling algorithm. This choice is motivated by the fact that, under the assumption of a small oblique viewing angle, the chirp scaling algorithm can perform range migration correction more accurately through phase multiplication, rather than interpolation. This is in contrast to the distance Doppler algorithm, which relies on interpolation to handle range migration in the distance–time–azimuth–frequency domain (distance Doppler domain). While the Omega-K algorithm can provide more precise results, it demands more computational resources and is not suitable for large-scale scene imaging [
29].
The main contributions of this article are as follows:
(1) Sparse expansion of the iterative process: The iterative process of traditional algorithms is sparsely expanded, and a deep unfolded network is introduced for adaptive training of parameters. This approach addresses the challenges of large computational load, slow processing speed, and poor generalization inherent in traditional algorithms.
(2) Self-supervised imaging network: A self-supervised imaging network structure is designed to tackle the problem of insufficient datasets. This network eliminates the need for manual parameter adjustments and enhances the network’s adaptability to different imaging scenes.
(3) Structural sparsity for azimuthal ambiguity suppression: The concept of structural sparsity is introduced, and the lq-norm is applied for azimuthal ambiguity suppression, leading to further improvements in imaging quality. A joint loss function, combining structural sparsity and principal view clarity, is formulated to achieve azimuthal ambiguity suppression while maintaining robustness against noise.
This method is evaluated using both simulated point targets and real datasets. The experimental results highlight the effectiveness of the algorithm in reducing side-lobes and enhancing target features, demonstrating its potential for tackling challenges in large-scale imaging scenarios.
The rest of this article is organized as follows.
Section 2 presents the SAR signal model and three kinds of sparse SAR imaging methods. In
Section 3, both simulation experiments and real data experiments results are presented. Finally, the conclusions are drawn in
Section 5.
3. Results
In this chapter, we analyze the performance of the SAAS-Net on point target simulation experiments and real data experiments. Since the proposed imaging network is formed by sparse SAR imaging based on ISTA with the chirp-scaling operator, we compare our network with CS-IST, ISTA-Net, and CS-IST-AAS.
3.1. Simulation Experiments and Results
We designed a point-target simulation experiment to test the effectiveness of the network proposed in this paper in terms of orientation ambiguity suppression.
Table 1 shows the necessary radar imaging parameters for the simulation experiment, where there is 60% undersampling in the azimuth direction. We used the CS-IST algorithm, CS-IST-AAS algorithm, ISTA-Net, and SAAS-Net for point target imaging. The imaging results are shown in
Figure 8.
In the imaging results, the longitudinal direction is the azimuthal direction, and the transverse direction is the range direction. In contrast, the ISTA-Net algorithm in
Figure 8b can weaken the azimuth ambiguity to a certain degree. The ambiguity phenomenon is eliminated in
Figure 8c,d. Comparing
Figure 8a to
Figure 8b, since
Figure 8b uses a deep unfolding network with the theoretically optimal parameters, the imaging result is better than in
Figure 8a, which completely relies on manual parameter tuning. Similarly, the imaging result of
Figure 8d is slightly better than
Figure 8c. At the same time, the algorithms in
Figure 8c,d add structural sparsity constraints, and from the perspective of the signal model and the causes of azimuth ambiguity, they suppress azimuth ambiguity. Therefore, compared to the algorithms in
Figure 8a,b, they show a significant suppression effect on azimuth ambiguity.
This indicates that SAAS-Net can significantly reduce the side-lobes, which leads to the more accurate reconstruct results. And, the proposed network has better azimuth ambiguity suppression capabilities.
For quantitative comparison, a Monte Carlo experiment was conducted, and the Peak Side-Lobe Ratio (PSNR), Integral Side-Lobe Ratio (ISLR), and mean Azimuth Ambiguity Signal Ratio (AASR) along the azimuth detection were used to evaluate the imaging quality. The formulae for these evaluation parameters are given below. The results are shown in
Table 2.
Here, A represents the amplitude and S represents the amplitude spectrum.
Monte Carlo experiments further demonstrate the effectiveness of the ambiguity suppression algorithm proposed in this paper for azimuthal ambiguity suppression. In addition, utilizing the unfolding network training, the imaging quality is higher than that of the traditional algorithm because better iteration parameters can be obtained.
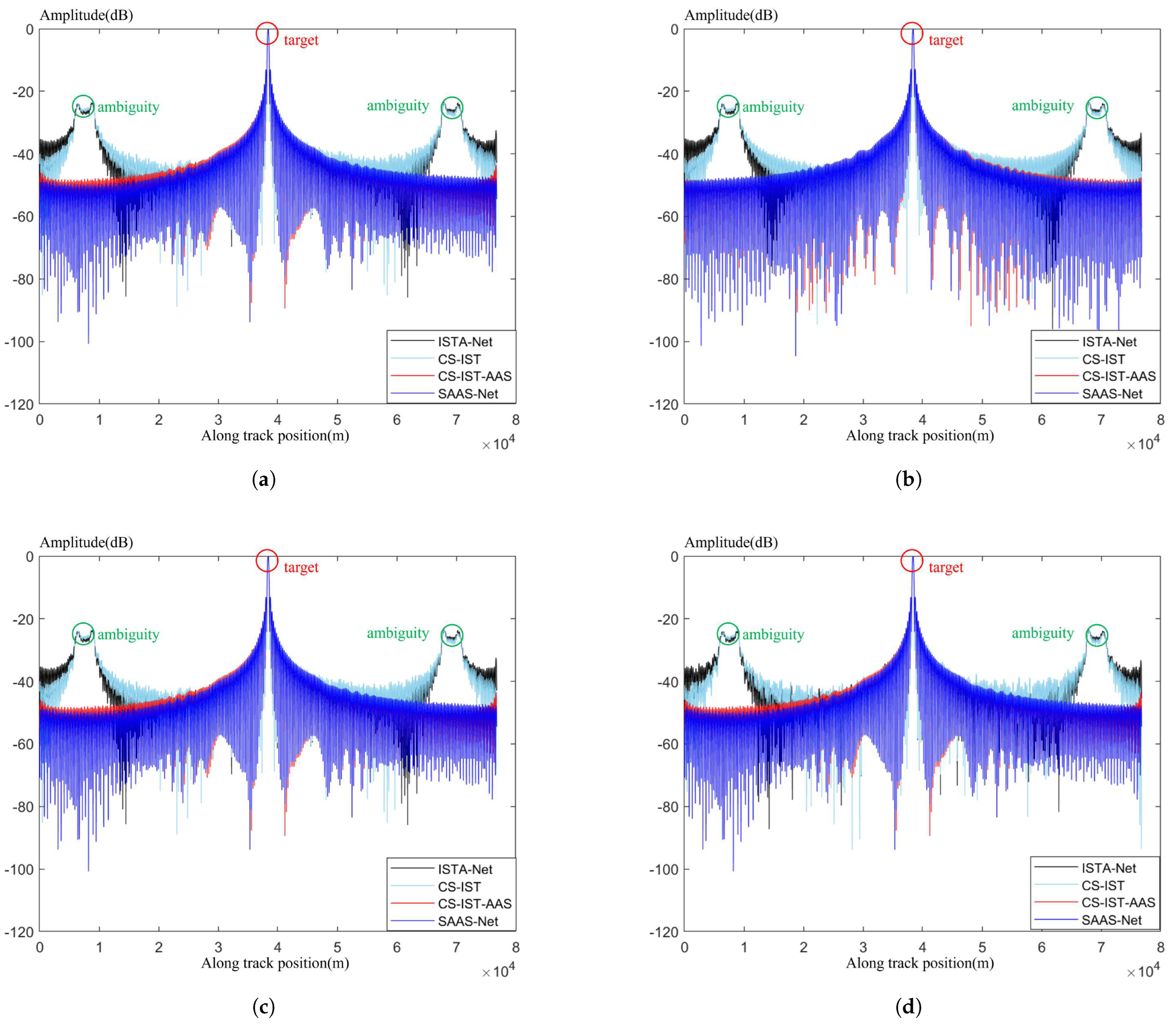
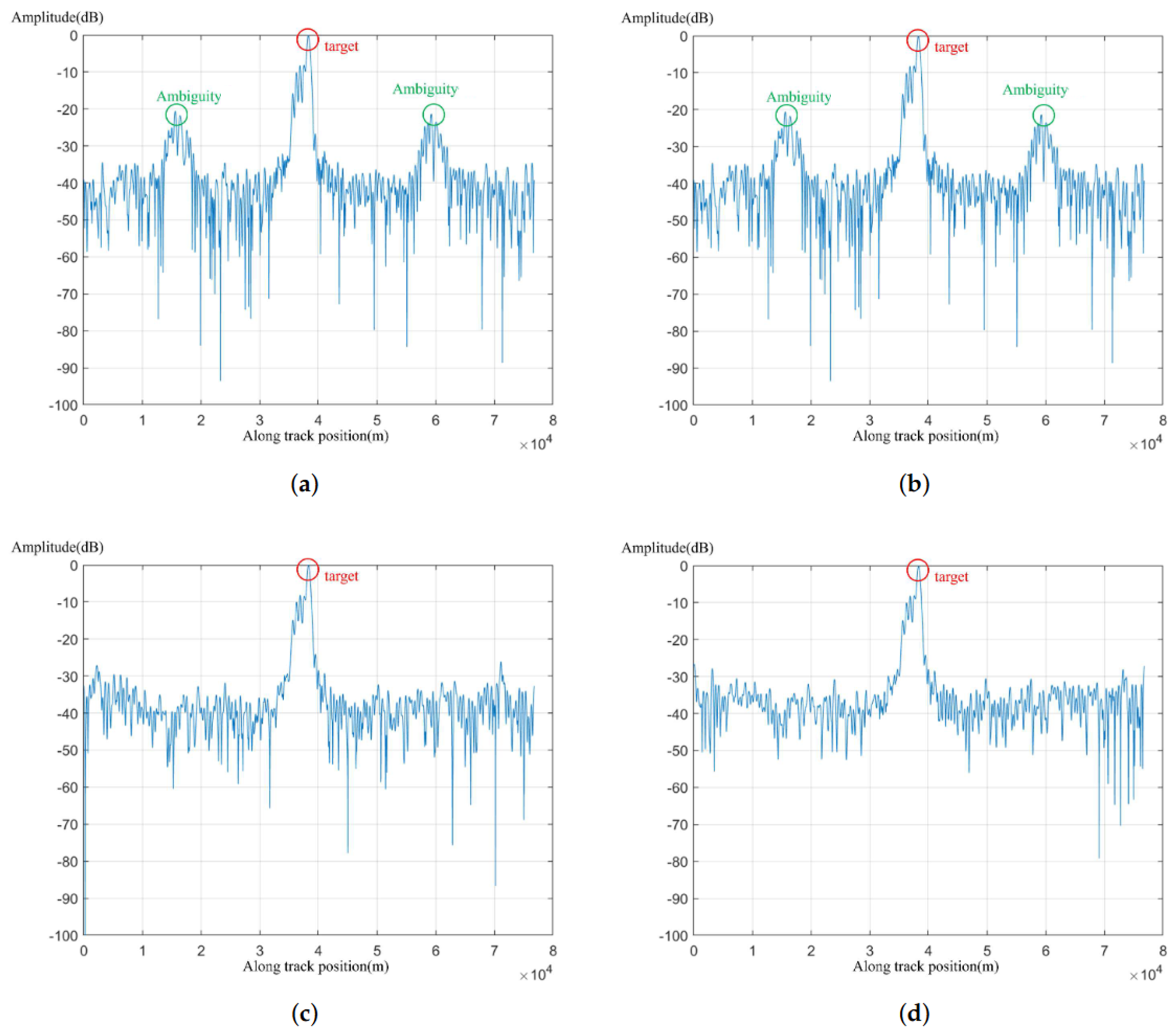
To better show the imaging effectiveness of the algorithms, we located the point of maximum value and conducted interpolation 16 times. The interpolated azimuthal slice is shown in
Figure 9. This indicates that both the CS-IST-AAS algorithm and SAAS-Net can significantly reduce the side-lobes. In the results of CS-IST and ISTA-Net, there are two side peaks on the left and right sides of the main peak, which is known as azimuth ambiguity. This occurs due to an insufficient sampling rate in the azimuth direction, causing part of the main observation area’s spectrum to fold into the ambiguous region, thereby creating ambiguous energy. In the azimuth spectrum, this will appear as two symmetric peaks.
The azimuthal results show that the algorithm proposed in this paper significantly reduces the azimuthal side-lobe, achieving the best suppression of azimuthal ambiguity rings. CS-IST-AAS also has some effect on ambiguity ring suppression. The CS-IST and ISTA-Net algorithms, on the other hand, do not perform additional sparse optimization of the azimuthal direction and thus suffer from spectral aliasing in the azimuthal direction when the azimuthal direction is undersampled. In the process of gradually reducing the sampling rate, the algorithm in this paper is relatively less affected, and the side flap suppression effect is relatively good. In the comparative experiment, 5 dB noise, 10 dB noise, 20 dB noise, and no noise were added, respectively. The results of the azimuthal frequency spectrum indicate that although the waveform underwent some changes after the addition of noise, the main viewing area and the ambiguity area could still be clearly distinguished, further confirming the robustness of the algorithm presented in this paper.
To further demonstrate the effectiveness of the method, imaging experiments with multiple point targets were designed. In
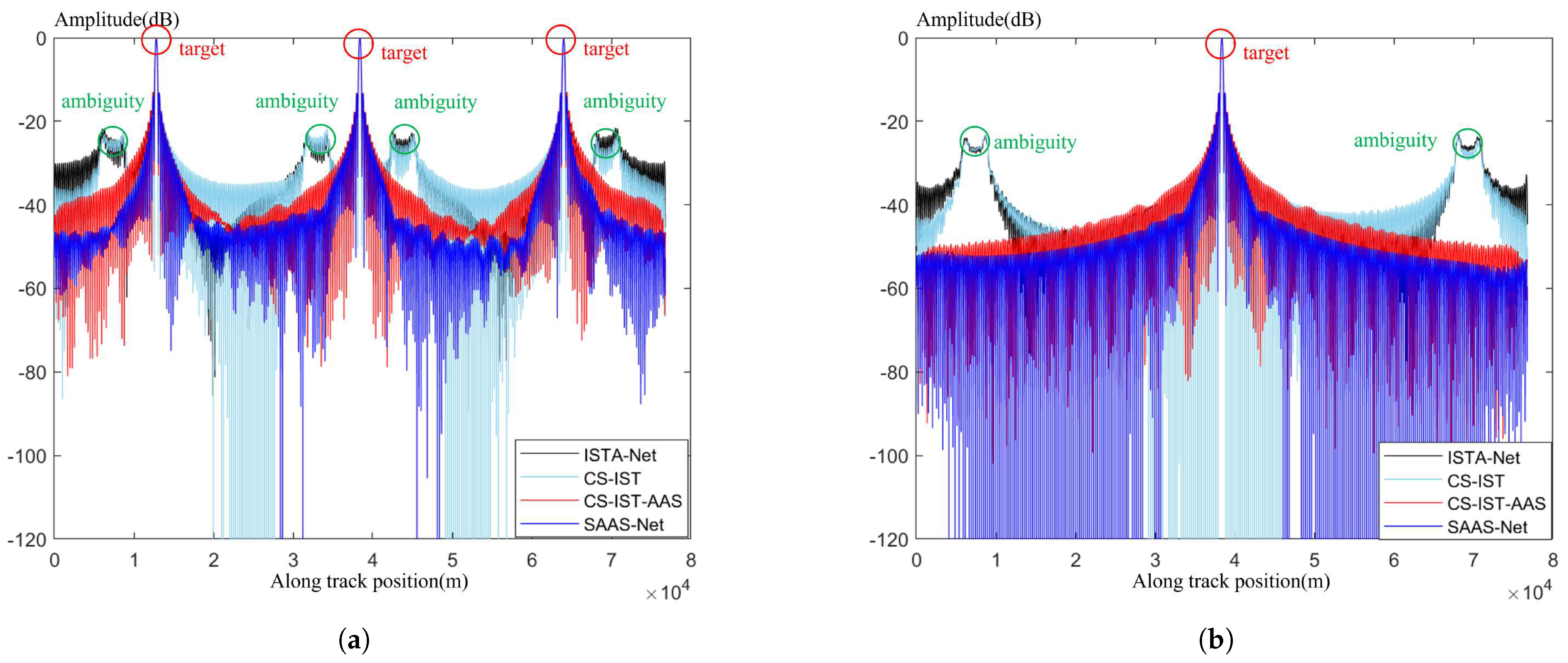
Figure 10a, sparse imaging of three point targets uniformly distributed in the azimuth direction was performed, while in
Figure 10b, sparse imaging of three point targets uniformly distributed in the range direction was carried out. It can be observed that, whether in the azimuth or range direction, SAAS-Net performs well in suppressing azimuthal ambiguity. Meanwhile, although the imaging effect of CS-IST-AAS is similar to that of SAAS-Net in single point target imaging experiments, in the imaging process of multiple point targets, SAAS-Net exhibits a significantly stronger suppression effect on side-lobes compared to CS-IST-AAS.
To show the effectiveness of the sampling pattern generated by our proposed network, we selected the same scene under 30% undersampling, 70% undersampling, and 90% undersampling and calculated the AASR at this point. The results of the experiments are shown in
Table 3 in order to further demonstrate the superiority of this paper’s algorithm in azimuthal ambiguity suppression.
3.2. Real Data Experiments and Results
The data we used were sourced from the imaging results of the Gaofen-3 satellite on 30 March 2019, at 22:12:43. We used four algorithms, CS-IST, CS-IST-AAS, ISTA-Net, and SAAS-Net, to image the actual data. The imaging results are shown in
Figure 11.
We selected an area with two ships for sparse SAR imaging. It can be observed that due to undersampling in the azimuth direction, both the conventional CS-IST algorithm and the ISTA-Net algorithm suffered from severe azimuth ambiguity, with artifacts appearing above or below the target ship. The presence of artifacts in the imaging scene is almost invisible in the imaging results using proposed method as well as the CS-IST-AAS algorithm. The imaging quality of the proposed algorithm and CS-IST-AAS was suppressed. In order to further compare the imaging results of these algorithms, the AASR and Frames Per Minute (FPM) of these four algorithms were compared. The results are shown in
Table 4. It can be seen that the ambiguity suppression effect of proposed algorithm in the azimuthal direction was not significantly different from that of the CS-IST-AAS algorithm. At the same time, the imaging speed was much higher than that of the CS-IST-AAS algorithm.
In order to compare the imaging quality of these algorithms, we calculated their AASR. At the same time, we also compared the imaging speed of these algorithms. The results are shown in
Table 4. The algorithm in this paper had a comparable ambiguity suppression effect with the CS-IST-AAS algorithm, and the computational speed was improved by about 800 times compared to the CS-IST-AAS algorithm. Therefore, SAAS-Net can realize fast imaging with azimuthal ambiguity suppression.
We sliced the azimuthal direction of the real data. It can be seen in
Figure 12 that the azimuthal side-lobes were significantly reduced in the algorithm of this paper and CS-IST-AAS, and the other two algorithms had significant ambiguity energy in the azimuthal direction.
We conducted comparative experiments using ISTA-net and the proposed network at undersampling rates of 80%, 60%, and 30%, adding 20 dB of noise throughout the experiment. The results are presented in
Figure 13. We chose a region with a single ship to perform sparse SAR imaging.
There are three ships that can be seen in
Figure 13a. In fact, the center portion represents the actual ship that was imaged, while the ships above and below are artifacts were due to azimuthal ambiguity. At a undersampling rate of 80%, artifacts in the upper and lower vessels due to orientation ambiguity were visible with ISTA-net, while these ambiguity artifacts were barely noticeable in the proposed network. At a undersampling rate of 60%, the artifacts in ISTA-net became more prominent, and a slight artifact also appeared in the proposed network. At a undersampling rate of 30%, both algorithms exhibited clear artifacts, but the ambiguity energy in the proposed network remained significantly lower than that in ISTA-net, demonstrating the effectiveness of the proposed algorithm in suppressing ambiguity energy in the azimuth direction. This demonstrates that the algorithm presented in this paper effectively suppresses ambiguity energy in the azimuth direction. At the same time, the algorithm in this paper is robust to noise.
To further investigate the imaging performance of the algorithm in complex scenes, an imaging experiment was conducted with a scene containing 13 ships. In this complex scene, some targets are closely connected, and the real targets of some objects are close to the ghost images of other real targets. The imaging results are shown in
Figure 14. It can be observed that both the SAAS-Net and CS-IST-AAS algorithms effectively suppress azimuthal ambiguity, while the imaging results of the ISTA-Net and CS-IST algorithms show obvious ghost images. This further confirms the effectiveness of the algorithm presented in this paper.
In order to further demonstrate the structural properties of the SAAS-Net, we show the imaging outputs for each layer of the imaging process in
Figure 15. There are three ships in the imaging area. It can be seen that when there is one iterative layer, the outline of the imaging gradually appears, but it still has significant azimuth ambiguity. With the increase in the number of iterative layers, the imaging quality gradually improves. It reaches the highest quality when there are five iterative layers, after which the change is no longer obvious.
As a result, the network essentially reaches convergence by the fifth layer, and with the overall network structure being relatively shallow, the training process can be completed quickly, thereby further enhancing imaging efficiency. Meanwhile, 20 dB of Gaussian noise was added in this experiment, and the imaging results were still clear. This also proves the robustness of the proposed algorithm.
4. Discussion
We proposed the Self-supervised Azimuth Ambiguity Suppression Network (SAAS-Net), a novel algorithm designed to effectively suppression azimuth ambiguity in sparse SAR imaging. Through comprehensive simulation and real data experiments, we demonstrated the superior performance of SAAS-Net in terms of both azimuth ambiguity suppression and computational efficiency.
The experimental results clearly indicate that SAAS-Net can significantly reduce azimuth ambiguity, outperforming traditional algorithms in terms of both suppression effectiveness and processing speed. While conventional methods rely heavily on intricate computations, SAAS-Net leverages group sparsity to effectively address azimuth ambiguity, leading to a more efficient and accurate solution. Additionally, in the scenario with multiple point targets, the imaging performance of SAAS-Net was slightly better than that of the CS-IST-AAS algorithm. The algorithm’s ability to maintain high performance while achieving faster processing times highlights its practical potential for real-time SAR imaging applications.
We also conducted experiments under undersampling conditions to investigate the algorithm’s robustness when the azimuth sampling rate was insufficient. As expected, azimuth ambiguity was still observed under low sampling rates. However, the results clearly showed that SAAS Net significantly mitigated the impact of this ambiguity compared to traditional methods. While some residual ambiguity remained, the suppression capabilities of SAAS Net were evident, suggesting its robustness even in challenging conditions of insufficient sampling.
5. Conclusions
Azimuth ambiguity remains a significant challenge in SAR imaging, severely affecting image quality and hindering the performance of conventional SAR applications. Limited by the azimuth sampling rate, azimuth ambiguity becomes particularly problematic in sparse SAR imaging scenarios. To address this issue, this article proposed SAAS-Net, a novel sparse SAR imaging unfolded network designed to suppress azimuth ambiguity efficiently. We introduced a unique encoder–decoder network structure within SAAS-Net, where the encoder generates reference imaging results and facilitates a self-supervised training process, while the decoder is responsible for the actual imaging procedure. This architecture enables SAAS-Net to learn from data directly, optimizing the parameters through end-to-end training. As a result, the network adapts automatically without requiring complex manual tuning, making the process both efficient and user-friendly. The core advantage of SAAS-Net lies in its ability to suppress azimuth ambiguity, even under undersampling conditions, thus preserving the inherent benefits of sparse SAR imaging. This solution not only enhances the quality of the resulting images but also accelerates the entire imaging process, reducing computational costs without sacrificing accuracy. To validate the effectiveness of SAAS-Net, we conducted imaging experiments on both simulated and real datasets. The results clearly demonstrate the efficiency of our proposed algorithm in suppressing azimuth ambiguity, achieving better performance than traditional methods. Moreover, the algorithm’s ability to handle undersampled data and still produce high-quality imaging results underscores its robustness in SAR applications, where undersampling and noisy conditions are often encountered.
In summary, the proposed SAAS-Net algorithm presents a preliminary exploration into addressing azimuth ambiguity in sparse SAR imaging. Preliminary experimental results indicate that the method exhibits certain robustness under undersampled conditions and noise interference, offering a new technical approach to improving sparse SAR imaging quality. However, the algorithm’s generalizability to highly complex real-world scenarios—such as extreme undersampling or dynamic target environments—still requires further validation. Future work will focus on refining the network architecture, exploring its adaptability across broader operational scenarios.