A Big Data Approach for the Regional-Scale Spatial Pattern Analysis of Amazonian Palm Locations
Abstract
1. Introduction
- (1)
- Test our hypothesis. : Palms are randomly distributed on a regional scale. : Palms are clustered on a regional scale.
- (2)
- Investigate the pattern in the distribution of palms using appropriate statistical techniques.
- (3)
- Determine the correlation between palm distribution and environmental features, including cation exchange capacity, distance to drainage channels, elevation, nitrogen content, pH of soil water, sand content, slope, and the volume of the soil water.
- (4)
- Construct a logistic regression to identify multivariate responses to the presence or absence of palm features.
- (5)
- Compare the results from our model of remotely sensed palm locations with published ground-based palm ecological studies.
2. Materials and Methods
2.1. Elevation Model and Its Derivatives
2.2. Soil Data
2.3. Pattern Analysis
- (1)
- Reasonably attribute clustering to parent–child effects;
- (2)
- Make connections concerning inter-species competition.
2.4. Juxtaposition of Traditional vs. Nontraditional Pattern Analysis
2.5. Logistic Regression for Covariate Response to the Presence of Palms
3. Results
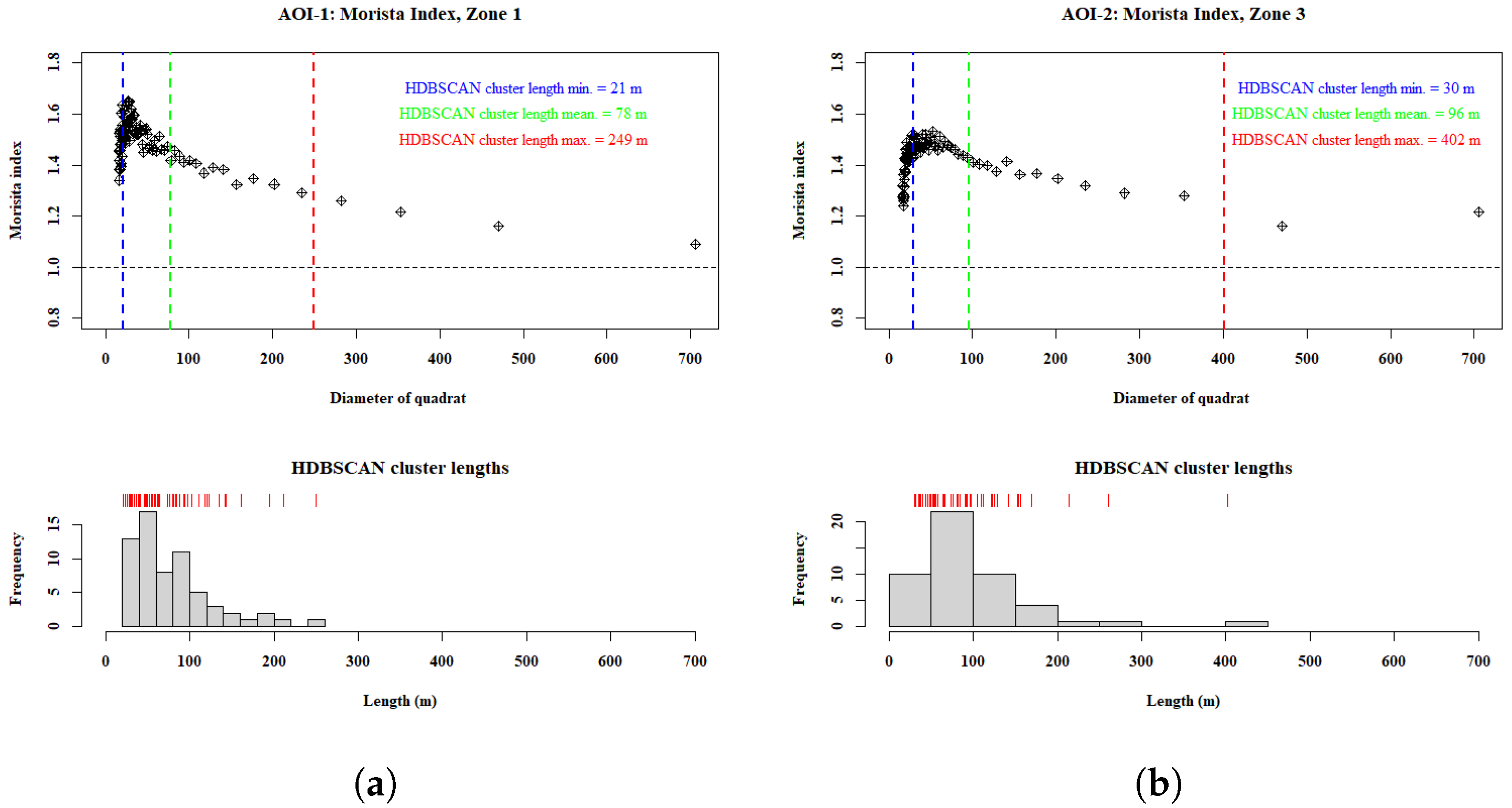
3.1. HDBSCAN
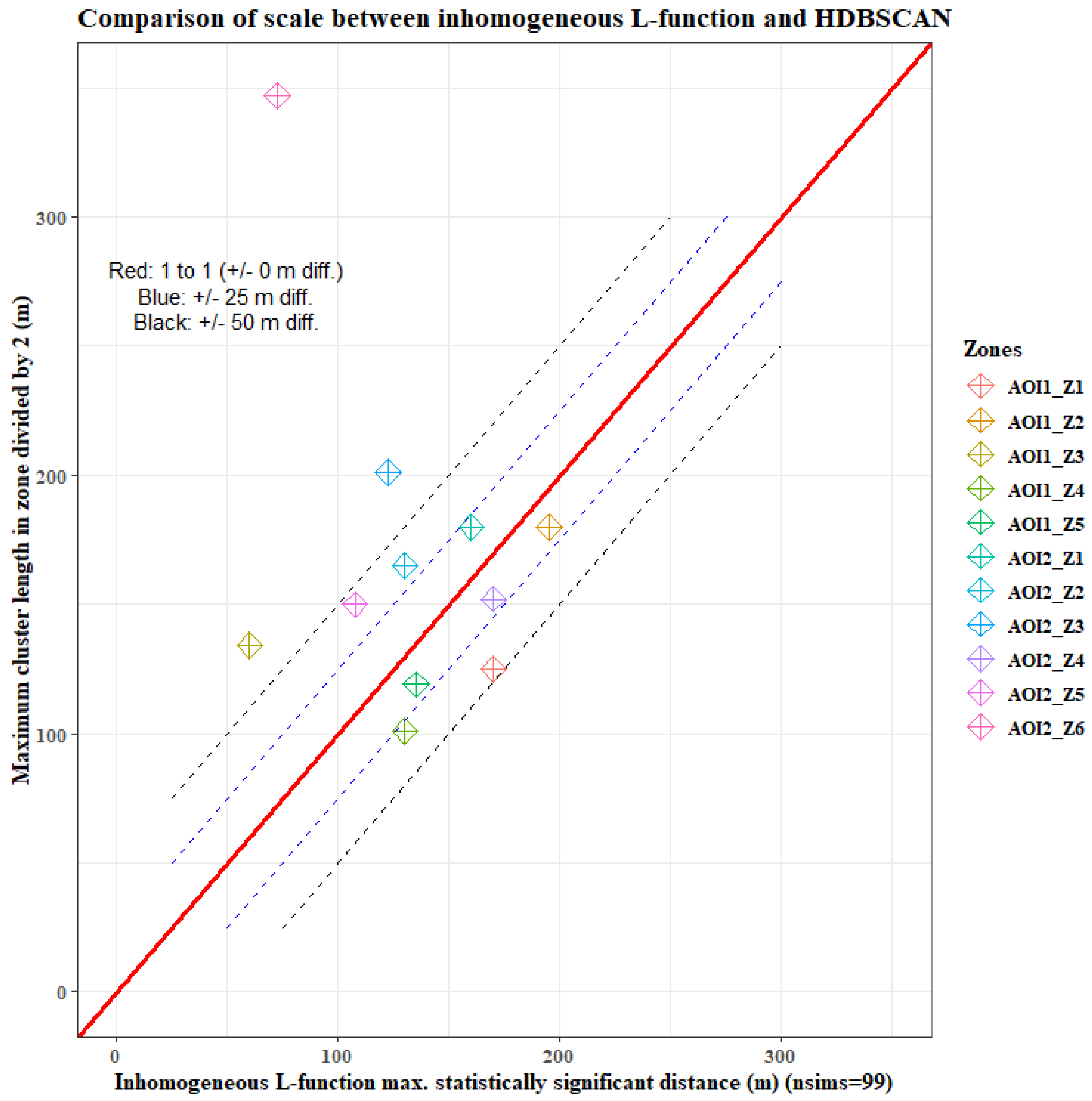
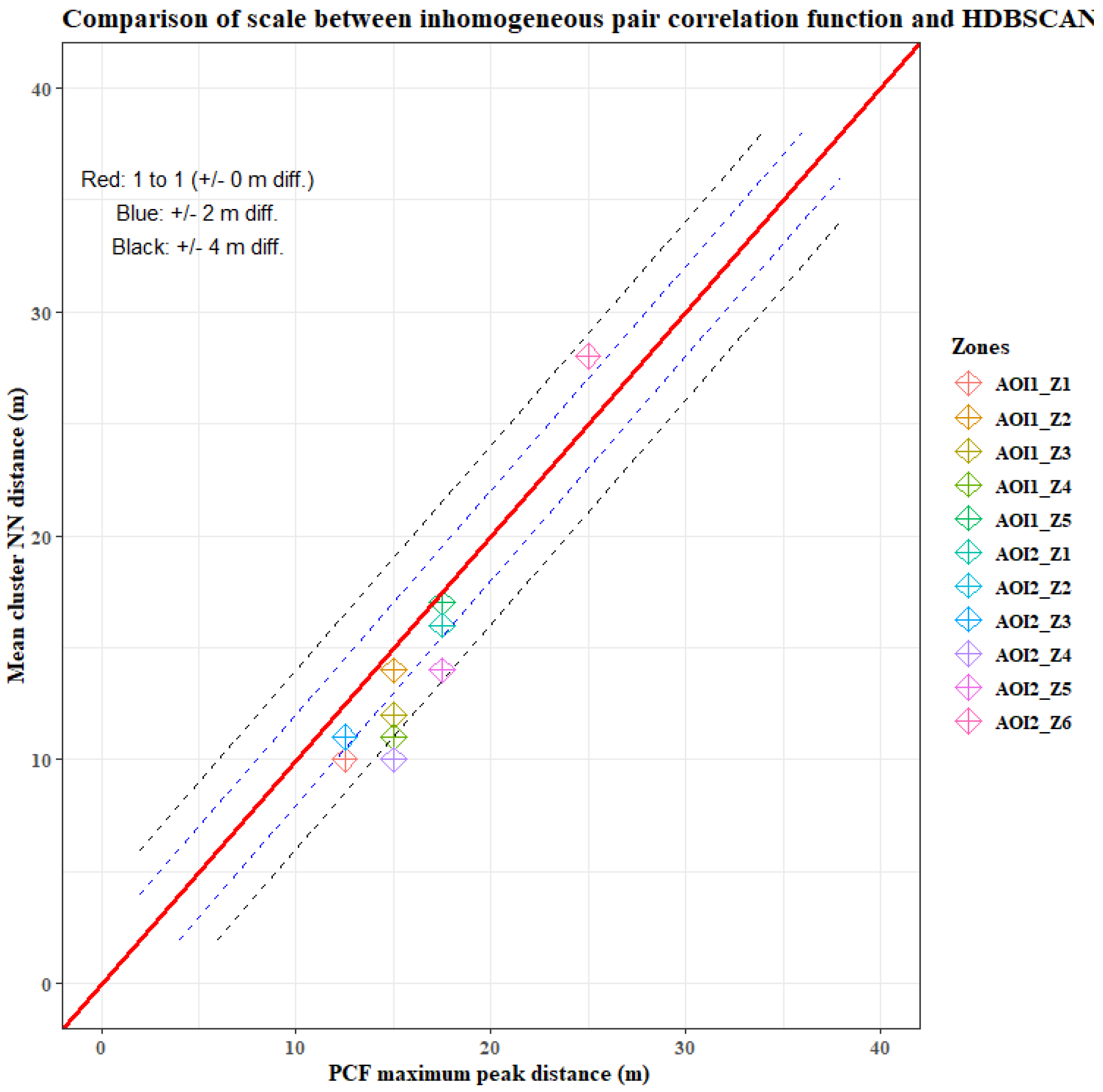
3.2. Spatial Point Pattern Analysis
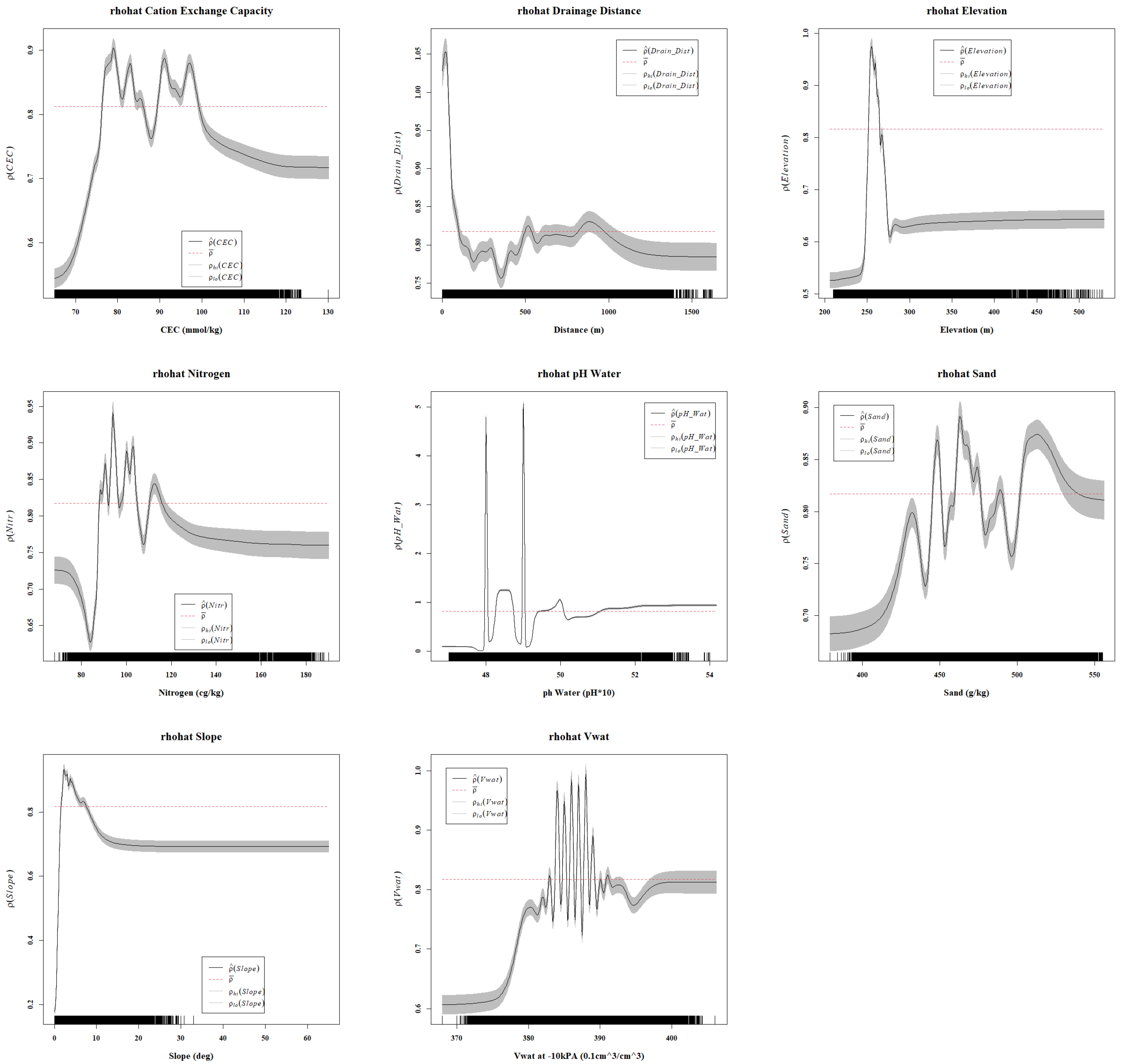
3.3. Logistic Regression Model
3.3.1. AOI-1
3.3.2. AOI-2
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Macía, M.J.; Armesilla, P.J.; Cámara-Leret, R.; Paniagua-Zambrana, N.; Villalba, S.; Balslev, H.; Pardo-de Santayana, M. Palm Uses in Northwestern South America: A Quantitative Review. Bot. Rev. 2011, 77, 462–570. [Google Scholar] [CrossRef]
- Ozanne, C.M.P.; Cabral, C.; Shaw, P.J. Variation in Indigenous Forest Resource Use in Central Guyana. PLoS ONE 2014, 9, e102952. [Google Scholar] [CrossRef][Green Version]
- Cummings, A.R.; Read, J.M. Drawing on traditional knowledge to identify and describe ecosystem services associated with Northern Amazon’s multiple-use plants. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2016, 12, 39–56. [Google Scholar] [CrossRef]
- Silva, J.Z.D.; Reis, M.S.D. Consumption of Euterpe edulis fruit by wildlife: Implications for conservation and management of the Southern Brazilian Atlantic Forest. An. Acad. Bras. Ciências 2019, 91, e20180537. [Google Scholar] [CrossRef]
- Valencia, R.; Foster, R.B.; Villa, G.; Condit, R.; Svenning, J.C.; Hernández, C.; Romoleroux, K.; Losos, E.; Magård, E.; Balslev, H. Tree species distributions and local habitat variation in the Amazon: Large forest plot in eastern Ecuador. J. Ecol. 2004, 92, 214–229. [Google Scholar] [CrossRef]
- Dalling, J.W.; Schnitzer, S.A.; Baldeck, C.; Harms, K.E.; John, R.; Mangan, S.A.; Lobo, E.; Yavitt, J.B.; Hubbell, S.P. Resource-based habitat associations in a neotropical liana community. J. Ecol. 2012, 100, 1174–1182. [Google Scholar] [CrossRef]
- Giroldo, A.B.; Nascimento, A.R.T.; Silva, P.P.F.; Pinho Júnior, G.V. Population structure and density of Attalea phalerata Mart. ex Spreng. (Arecaceae) in a semideciduous forest. Rev. Árvore 2012, 36, 637–645. [Google Scholar] [CrossRef]
- Baldeck, C.A.; Harms, K.E.; Yavitt, J.B.; John, R.; Turner, B.L.; Valencia, R.; Navarrete, H.; Davies, S.J.; Chuyong, G.B.; Kenfack, D.; et al. Soil resources and topography shape local tree community structure in tropical forests. Proc. R. Soc. B Biol. Sci. 2013, 280, 20122532. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, L.; Cintra, R.; Castilho, C.; Pereira, O.; Pimentel, T. Influences of forest structure and landscape features on spatial variation in species composition in a palm community in central Amazonia. J. Trop. Ecol. 2014, 30, 565–578. [Google Scholar] [CrossRef]
- Salm, R.; Prates, A.; Simões, N.R.; Feder, L. Palm community transitions along a topographic gradient from floodplain to terra firme in the eastern Amazon. Acta Amaz. 2015, 45, 65–74. [Google Scholar] [CrossRef][Green Version]
- Jucker, T.; Bongalov, B.; Burslem, D.F.R.P.; Nilus, R.; Dalponte, M.; Lewis, S.L.; Phillips, O.L.; Qie, L.; Coomes, D.A. Topography shapes the structure, composition and function of tropical forest landscapes. Ecol. Lett. 2018, 21, 989–1000. [Google Scholar] [CrossRef] [PubMed]
- Muscarella, R.; Bacon, C.D.; Faurby, S.; Antonelli, A.; Kristiansen, S.M.; Svenning, J.C.; Balslev, H. Soil fertility and flood regime are correlated with phylogenetic structure of Amazonian palm communities. Ann. Bot. 2019, 123, 641–655. [Google Scholar] [CrossRef] [PubMed]
- Zuleta, D.; Russo, S.E.; Barona, A.; Barreto-Silva, J.S.; Cardenas, D.; Castaño, N.; Davies, S.J.; Detto, M.; Sua, S.; Turner, B.L.; et al. Importance of topography for tree species habitat distributions in a terra firme forest in the Colombian Amazon. Plant Soil 2020, 450, 133–149. [Google Scholar] [CrossRef]
- Duque, A.; Cavelier, J.; Posada, A. Strategies of Tree Occupation at a Local Scale in terra firme Forests in the Colombian Amazon. Biotropica 2003, 35, 20–27. [Google Scholar] [CrossRef]
- Kristiansen, T.; Svenning, J.C.; Pedersen, D.; Eiserhardt, W.L.; Grández, C.; Balslev, H. Local and regional palm (Arecaceae) species richness patterns and their cross-scale determinants in the western Amazon. J. Ecol. 2011, 99, 1001–1015. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Flores, O.; Bourland, N.; Doucet, J.L.; Fétéké, R.F.; Pasquier, A.; Hardy, O.J. Spatial aggregation of tropical trees at multiple spatial scales. J. Ecol. 2011, 99, 1373–1381. [Google Scholar] [CrossRef]
- Law, R.; Illian, J.; Burslem, D.F.R.P.; Gratzer, G.; Gunatilleke, C.V.S.; Gunatilleke, I.A.U.N. Ecological information from spatial patterns of plants: Insights from point process theory. J. Ecol. 2009, 97, 616–628. [Google Scholar] [CrossRef]
- Ben-Said, M. Spatial point-pattern analysis as a powerful tool in identifying pattern-process relationships in plant ecology: An updated review. Ecol. Process. 2021, 10, 56. [Google Scholar] [CrossRef]
- Ripley, B.D. Modelling Spatial Patterns. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 172–212. [Google Scholar] [CrossRef]
- Besag, J. Discussion on Dr Ripley’s Paper. J. R. Stat. Soc. Ser. B Stat. Methodol. 1977, 39, 193–195. [Google Scholar] [CrossRef]
- Stoyan, D.; Stoyan, H. Fractals, Random Shapes and Point Fields. Methods of Geometrical Statistics; John Wiley & Sons: Chichester, UK, 1994. [Google Scholar]
- Wiegand, T.; Moloney, K.A. Rings, circles, and null-models for point pattern analysis in ecology. Oikos 2004, 104, 209–229. [Google Scholar] [CrossRef]
- Velázquez, E.; Martínez, I.; Getzin, S.; Moloney, K.A.; Wiegand, T. An evaluation of the state of spatial point pattern analysis in ecology. Ecography 2016, 39, 1042–1055. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Almeida, D.R.A.d.; Papa, D.d.A.; Minervino, J.B.S.; Veras, H.F.P.; Formighieri, A.; Santos, C.A.N.; Ferreira, M.A.D.; Figueiredo, E.O.; Ferreira, E.J.L. Individual tree detection and species classification of Amazonian palms using UAV images and deep learning. For. Ecol. Manag. 2020, 475, 118397. [Google Scholar] [CrossRef]
- Wagner, F.H.; Dalagnol, R.; Tagle Casapia, X.; Streher, A.S.; Phillips, O.L.; Gloor, E.; Aragão, L.E.O.C. Regional Mapping and Spatial Distribution Analysis of Canopy Palms in an Amazon Forest Using Deep Learning and VHR Images. Remote Sens. 2020, 12, 2225. [Google Scholar] [CrossRef]
- Arce, L.S.D.; Osco, L.P.; Arruda, M.d.S.d.; Furuya, D.E.G.; Ramos, A.P.M.; Aoki, C.; Pott, A.; Fatholahi, S.; Li, J.; Araújo, F.F.d.; et al. Mauritia flexuosa palm trees airborne mapping with deep convolutional neural network. Sci. Rep. 2021, 11, 19619. [Google Scholar] [CrossRef] [PubMed]
- Cui, K.; Shao, Z.; Larsen, G.; Pauca, V.; Alqahtani, S.; Segurado, D.; Pinheiro, J.; Wang, M.; Lutz, D.; Plemmons, R.; et al. PalmProbNet: A Probabilistic Approach to Understanding Palm Distributions in Ecuadorian Tropical Forest via Transfer Learning. In Proceedings of the 2024 ACM Southeast Conference, Marietta, GA, USA, 18–20 April 2024. [Google Scholar]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed.; Pearson Education Inc.: Boston, MA, USA, 2007. [Google Scholar]
- Jawak, S.D.; Luis, A.J. A Comprehensive Evaluation of PAN-Sharpening Algorithms Coupled with Resampling Methods for Image Synthesis of Very High Resolution Remotely Sensed Satellite Data. Adv. Remote Sens. 2013, 2, 332–344. [Google Scholar] [CrossRef]
- Tobler, W. Measuring spatial resolution. In Proceedings of the Proceedings, Land Resources Information Systems Conference, Beijing, China, 25–28 May 1987; pp. 12–16. [Google Scholar]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; De Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Granville, J.J. Life forms and growth strategies of Guianan palms as related to their ecology. Bull. L’institut Français D’études Andin. 1992, 21, 533–548. [Google Scholar] [CrossRef]
- Drouillard, M.J.; Cummings, A.R. Regional-Scale Detection of Palms Using VHR Satellite Imagery and Deep Learning in the Guyanese Rainforest. Remote Sens. 2024, 16, 4642. [Google Scholar] [CrossRef]
- Valeriano, M.M.; Kuplich, T.M.; Storino, M.; Amaral, B.D.; Mendes, J.N.; Lima, D.J. Modeling small watersheds in Brazilian Amazonia with shuttle radar topographic mission-90m data. Comput. Geosci. 2006, 32, 1169–1181. [Google Scholar] [CrossRef]
- Hack, J.T. Studies of Longitudinal Stream Profiles in Virginia and Maryland; Series: Professional Paper; US Government Printing Office: Washington, DC, USA, 1957; Volume 294.
- Poggio, L.; de Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing soil information for the globe with quantified spatial uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Turek, M.E.; Poggio, L.; Batjes, N.H.; Armindo, R.A.; De Jong Van Lier, Q.; De Sousa, L.; Heuvelink, G.B. Global mapping of volumetric water retention at 100, 330 and 15 000 cm suction using the WoSIS database. Int. Soil Water Conserv. Res. 2023, 11, 225–239. [Google Scholar] [CrossRef]
- Normand, S.; Vormisto, J.; Svenning, J.C.; Grández, C.; Balslev, H. Geographical and Environmental Controls of Palm Beta Diversity in Paleo-Riverine Terrace Forests in Amazonian Peru. Plant Ecol. 2006, 186, 161–176. [Google Scholar] [CrossRef]
- Baddeley, A.; Turner, R. Modelling Spatial Point Patterns in R. In Case Studies in Spatial Point Process Modeling; Baddeley, A., Gregori, P., Mateu, J., Stoica, R., Stoyan, D., Eds.; Series Title: Lecture Notes in Statistics; Springer: New York, NY, USA, 2006; Volume 185, pp. 23–74. [Google Scholar] [CrossRef]
- Cressie, N.; Read, T.R.C. Multinomial Goodness-of-Fit Tests. J. R. Stat. Soc. Ser. B (Methodol.) 1984, 46, 440–464. [Google Scholar] [CrossRef]
- Morista, M. Measuring of dispersion of individuals and analysis of the distributional patterns. Jpn. J. Ecol. 1961, 11, 252. [Google Scholar] [CrossRef]
- Baddeley, A.J.; Møller, J.; Waagepetersen, R. Non- and semi-parametric estimation of interaction in inhomogeneous point patterns. Stat. Neerl. 2000, 54, 329–350. [Google Scholar] [CrossRef]
- Pommerening, A.; Stoyan, D. Edge-correction needs in estimating indices of spatial forest structure. Can. J. For. Res. 2006, 36, 1723–1739. [Google Scholar] [CrossRef]
- Ohser, J. On estimators for the reduced second moment measure of point processes. Ser. Stat. 1983, 14, 63–71. [Google Scholar] [CrossRef]
- Campello, R.J.G.B.; Moulavi, D.; Zimek, A.; Sander, J. Hierarchical Density Estimates for Data Clustering, Visualization, and Outlier Detection. ACM Trans. Knowl. Discov. Data 2015, 10, 1–51. [Google Scholar] [CrossRef]
- Rui, X.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef]
- Chadoeuf, J.; Goulard, M.; Pellerin, S. A Gibbs point process on a finite series of circles:the insertion of the primary roots of maize around the stem. J. Appl. Stat. 1993, 20, 177–185. [Google Scholar] [CrossRef]
- Stoyan, D. Statistical Inference for a Gibbs Point Process of Mutually Non-Intersecting Discs. Biom. J. 1989, 31, 153–161. [Google Scholar] [CrossRef]
- Agterberg, F.P. Automatic contouring of geological maps to detect target areas for mineral exploration. J. Int. Assoc. Math. Geol. 1974, 6, 373–395. [Google Scholar] [CrossRef]
- McFadden, D. Conditional Logit Analysis of Qualitative Choice Behavior; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Hensher, D.A.; Stopher, P.R. (Eds.) Behavioural Travel Modelling; Routledge: London, UK, 2021. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-Valverde, A.; Real, R. AUC: A misleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Balslev, H.; Kahn, F.; Millan, B.; Svenning, J.C.; Kristiansen, T.; Borchsenius, F.; Pedersen, D.; Eiserhardt, W.L. Species Diversity and Growth Forms in Tropical American Palm Communities. Bot. Rev. 2011, 77, 381–425. [Google Scholar] [CrossRef]
- Eiserhardt, W.L.; Svenning, J.C.; Kissling, W.D.; Balslev, H. Geographical ecology of the palms (Arecaceae): Determinants of diversity and distributions across spatial scales. Ann. Bot. 2011, 108, 1391–1416. [Google Scholar] [CrossRef]
- Kristiansen, T.; Svenning, J.C.; Eiserhardt, W.L.; Pedersen, D.; Brix, H.; Munch Kristiansen, S.; Knadel, M.; Grández, C.; Balslev, H. Environment versus dispersal in the assembly of western Amazonian palm communities. J. Biogeogr. 2012, 39, 1318–1332. [Google Scholar] [CrossRef]
- Schietti, J.; Emilio, T.; Rennó, C.D.; Drucker, D.P.; Costa, F.R.; Nogueira, A.; Baccaro, F.B.; Figueiredo, F.; Castilho, C.V.; Kinupp, V.; et al. Vertical distance from drainage drives floristic composition changes in an Amazonian rainforest. Plant Ecol. Divers. 2014, 7, 241–253. [Google Scholar] [CrossRef]
- Granville, J.J. Phytogeographical Characteristics of the Guianan Forests. Taxon 1988, 37, 578–594. [Google Scholar] [CrossRef]
- Balslev, H.; Eiserhardt, W.; Kristiansen, T.; Pedersen, D.; Grandez, C. Palms and Palm Communities in the Upper Ucayali River Valley-a Little-Known Region in the Amazon Basin. Palms 2010, 54, 1–16. [Google Scholar]
- Smith, N. Palms and People in the Amazon; Geobotany Studies; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Brum, H.D.; Souza, A.F. Flood disturbance and shade stress shape the population structure of açaí palm Euterpe precatoria, the most abundant Amazon species. Botany 2020, 98, 147–160. [Google Scholar] [CrossRef]
- Rennó, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J.; Waterloo, M.J. HAND, a new terrain descriptor using SRTM-DEM: Mapping terra-firme rainforest environments in Amazonia. Remote Sens. Environ. 2008, 112, 3469–3481. [Google Scholar] [CrossRef]

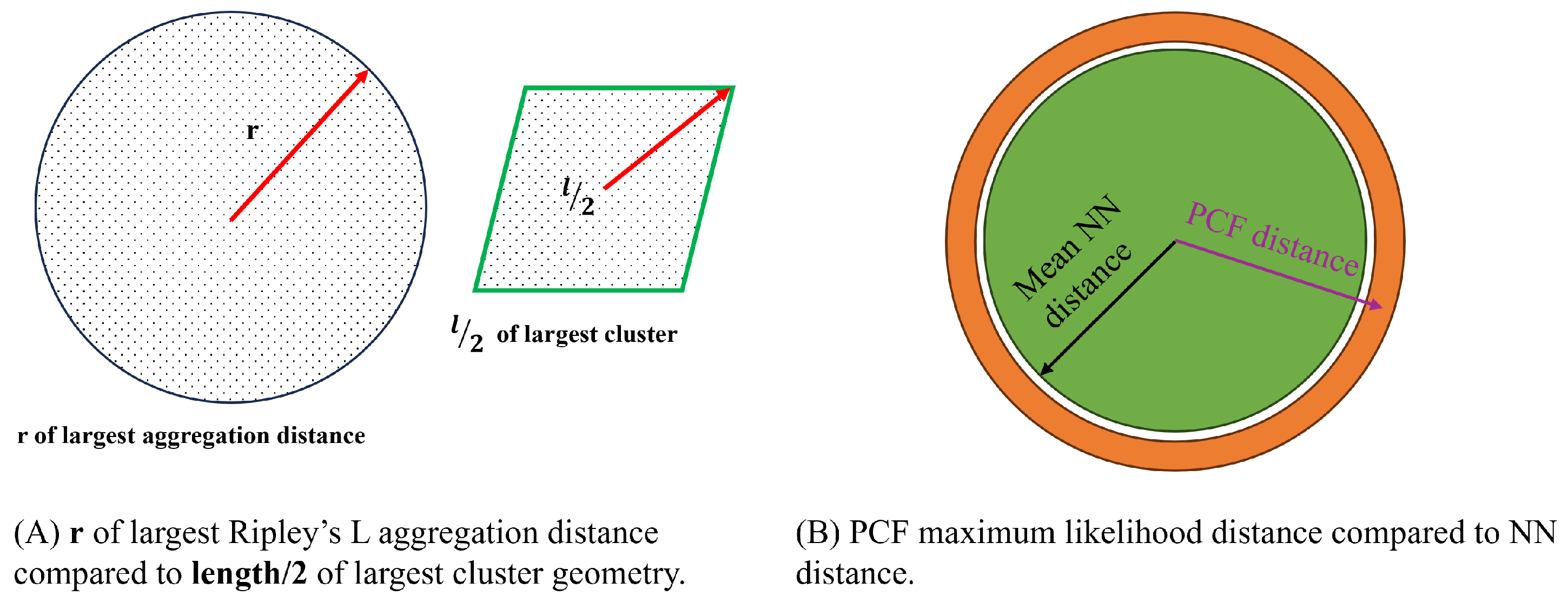
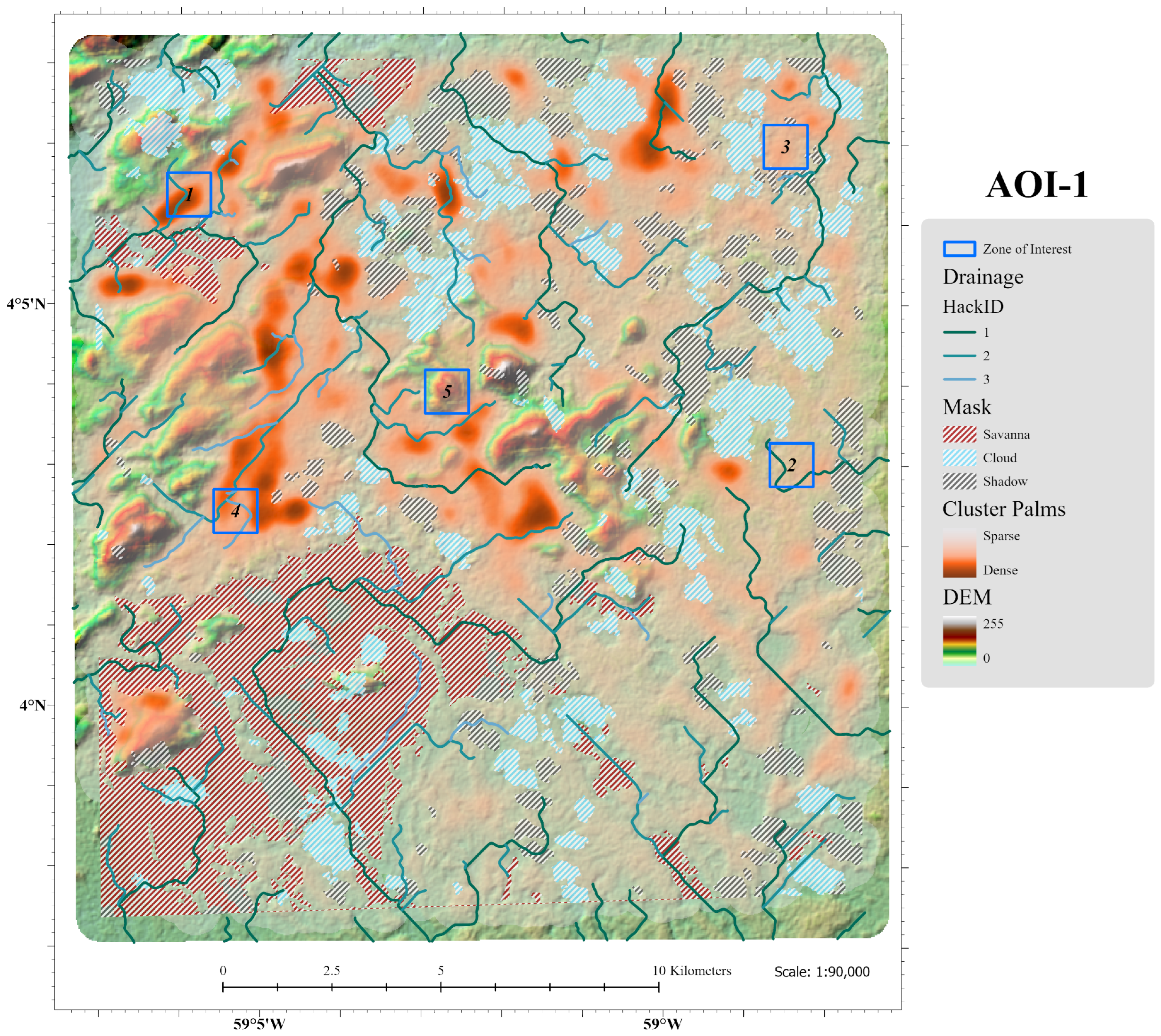
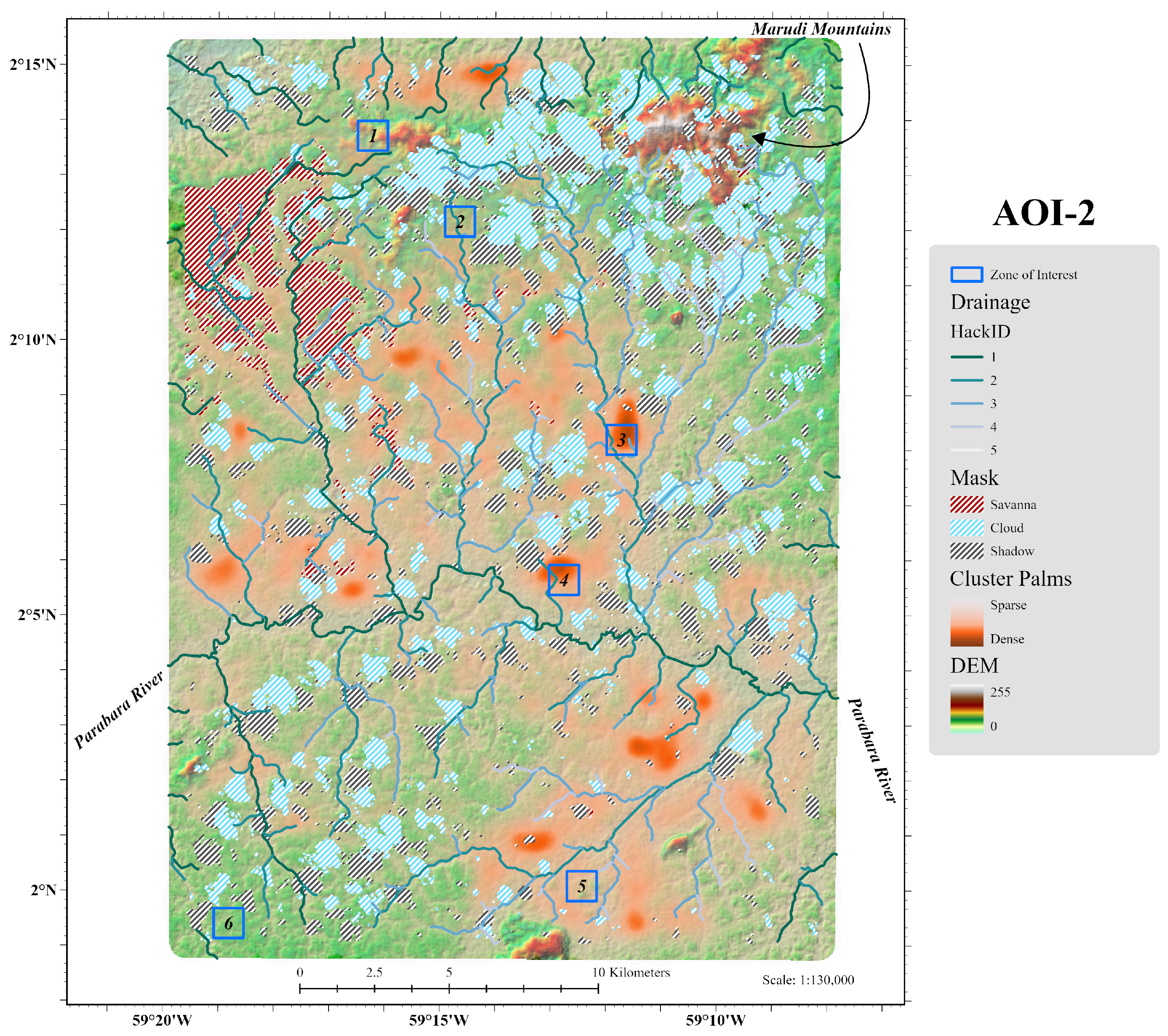
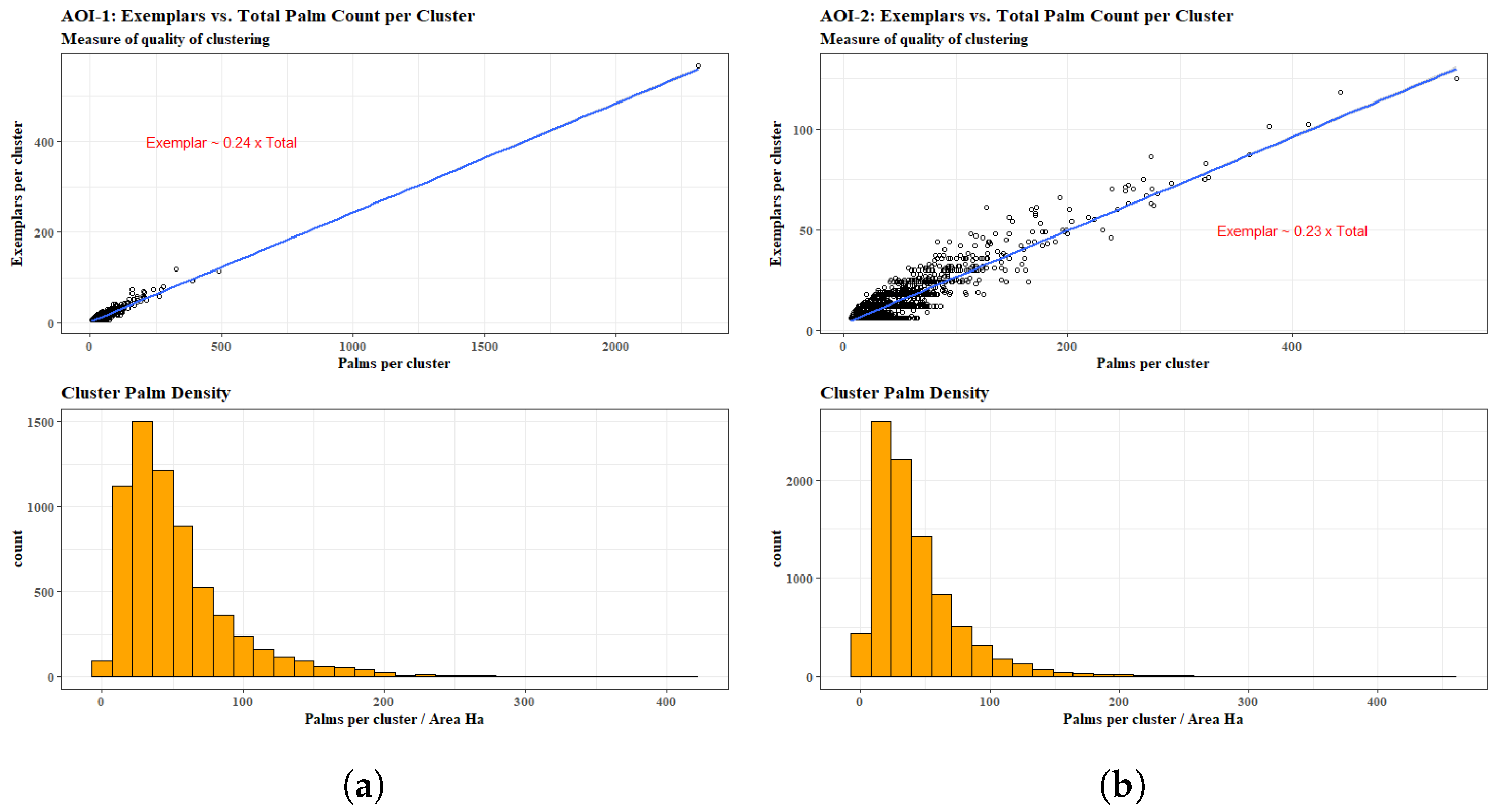

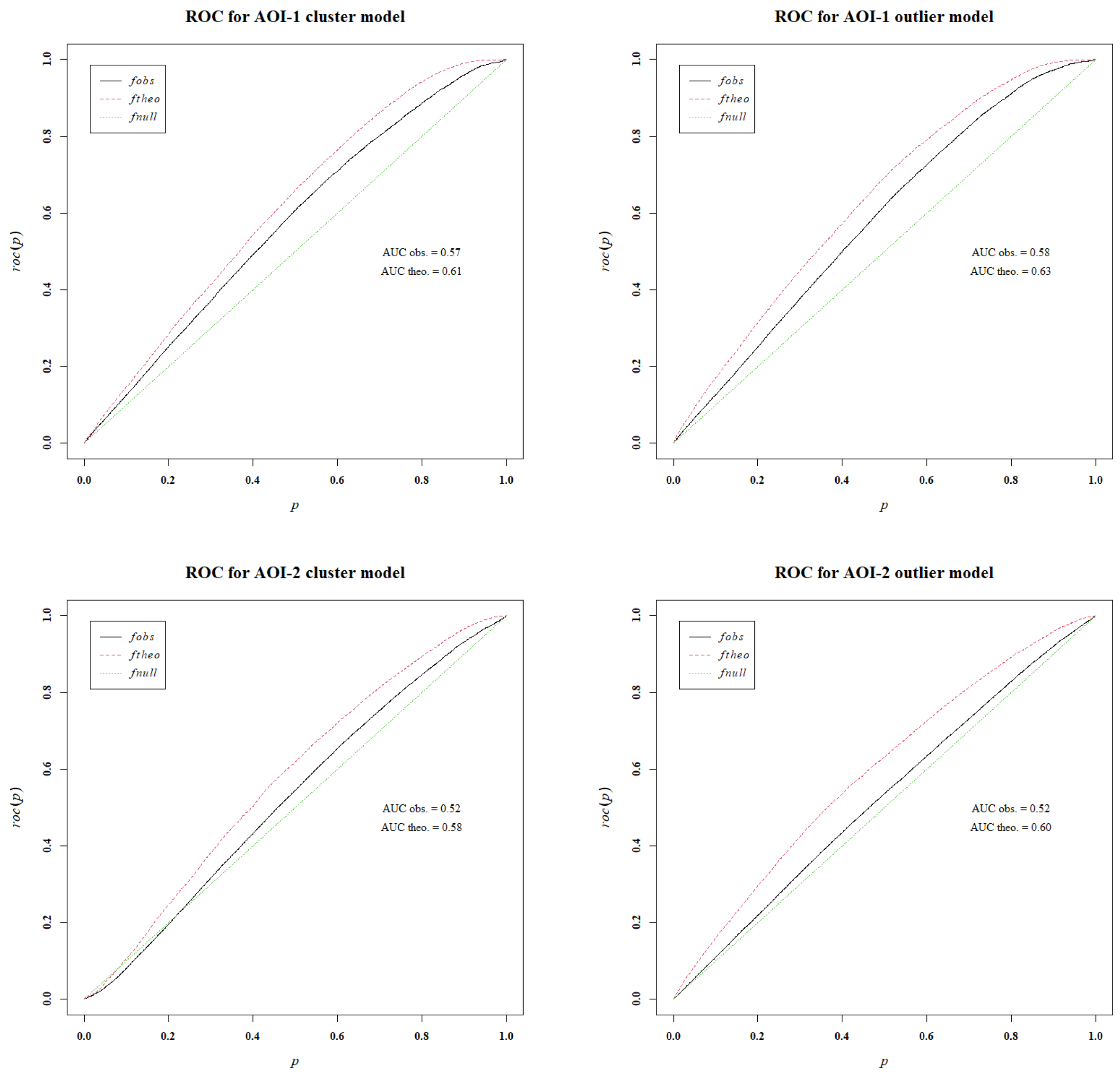

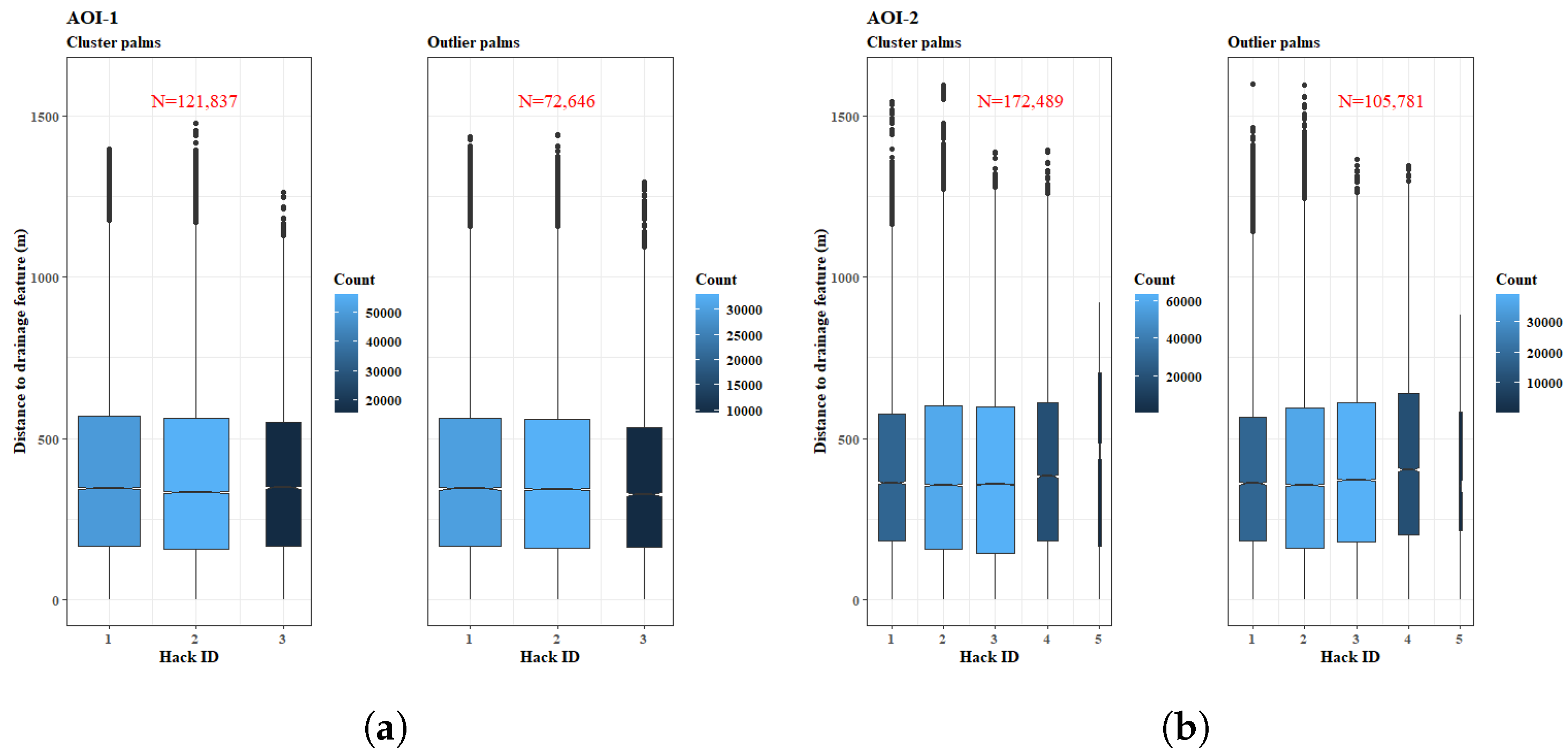

| AOI-1 Cluster Model | AOI-1 Outlier Model | |||||||
|---|---|---|---|---|---|---|---|---|
| Estimate | Std. Error | z value | Pr(>|z|) | Estimate | Std. Error | z value | Pr(>|z|) | |
| CEC | 0.1865 | 0.0060 | 31.14 | *** | 0.3091 | 0.0062 | 49.92 | *** |
| Drain_Dist | −0.0406 | 0.0053 | −7.61 | *** | −0.0951 | 0.0056 | −17.04 | *** |
| Elevation | 0.0693 | 0.0066 | 10.43 | *** | −0.0057 | 0.0070 | −0.81 | |
| Nitrogen | 0.0291 | 0.0071 | 4.09 | *** | −0.0086 | 0.0073 | −1.17 | |
| pH_Wat | −0.1922 | 0.0067 | −28.83 | *** | −0.2709 | 0.0071 | −38.27 | *** |
| Sand | 0.0605 | 0.0054 | 11.24 | *** | 0.0214 | 0.0056 | 3.85 | *** |
| Slope | −0.1670 | 0.0069 | −24.27 | *** | −0.0717 | 0.0069 | −10.35 | *** |
| Vwat | 0.0760 | 0.0068 | 11.10 | *** | 0.0990 | 0.0072 | 13.67 | *** |
| AOI-2 Cluster Model | AOI-2 Outlier Model | |||||||
| Estimate | Std. Error | z value | Pr(>|z|) | Estimate | Std. Error | z value | Pr(>|z|) | |
| CEC | −0.0255 | 0.0040 | −6.33 | *** | −0.0134 | 0.0042 | −3.21 | ** |
| Dep_Dist | 0.0330 | 0.0040 | 8.27 | *** | 0.0295 | 0.0041 | 7.16 | *** |
| Elevation | −0.3911 | 0.0078 | −50.44 | *** | −0.1477 | 0.0070 | −20.98 | *** |
| Nitr | -0.0707 | 0.0045 | −15.84 | *** | −0.0799 | 0.0048 | −16.79 | *** |
| pH_Wat | 0.0544 | 0.0046 | 11.88 | *** | −0.0939 | 0.0049 | −19.12 | *** |
| Sand | 0.0635 | 0.0046 | 13.69 | *** | 0.1514 | 0.0048 | 31.47 | *** |
| Slope | −0.0264 | 0.0049 | −5.41 | *** | −0.0993 | 0.0052 | −19.10 | *** |
| Vwat | 0.0032 | 0.0046 | 0.69 | −0.0504 | 0.0048 | −10.59 | *** | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drouillard, M.J.; Cummings, A.R. A Big Data Approach for the Regional-Scale Spatial Pattern Analysis of Amazonian Palm Locations. Remote Sens. 2025, 17, 784. https://doi.org/10.3390/rs17050784
Drouillard MJ, Cummings AR. A Big Data Approach for the Regional-Scale Spatial Pattern Analysis of Amazonian Palm Locations. Remote Sensing. 2025; 17(5):784. https://doi.org/10.3390/rs17050784
Chicago/Turabian StyleDrouillard, Matthew J., and Anthony R. Cummings. 2025. "A Big Data Approach for the Regional-Scale Spatial Pattern Analysis of Amazonian Palm Locations" Remote Sensing 17, no. 5: 784. https://doi.org/10.3390/rs17050784
APA StyleDrouillard, M. J., & Cummings, A. R. (2025). A Big Data Approach for the Regional-Scale Spatial Pattern Analysis of Amazonian Palm Locations. Remote Sensing, 17(5), 784. https://doi.org/10.3390/rs17050784









