Sparse Magnetization Vector Inversion Based on Modulus Constraints
Abstract
1. Introduction
2. Methods
2.1. Theory of Magnetization Vector Inversion
2.2. Inversion Based on Modulus Constraints
2.3. Improvement for Gradient Terms
3. Synthetic Examples
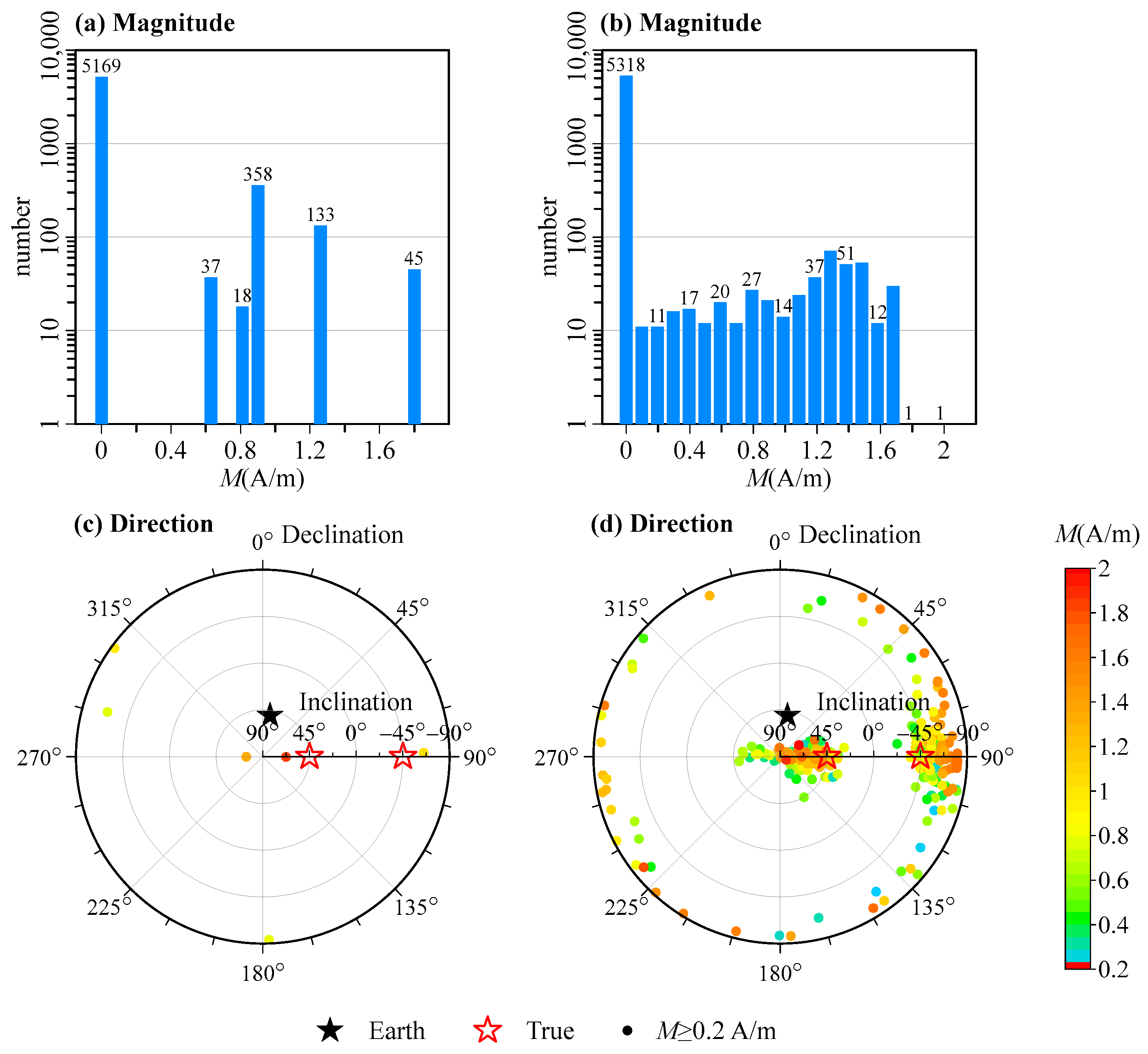
3.1. Combined Cube Models
3.2. Combined Dipping Dyke Models
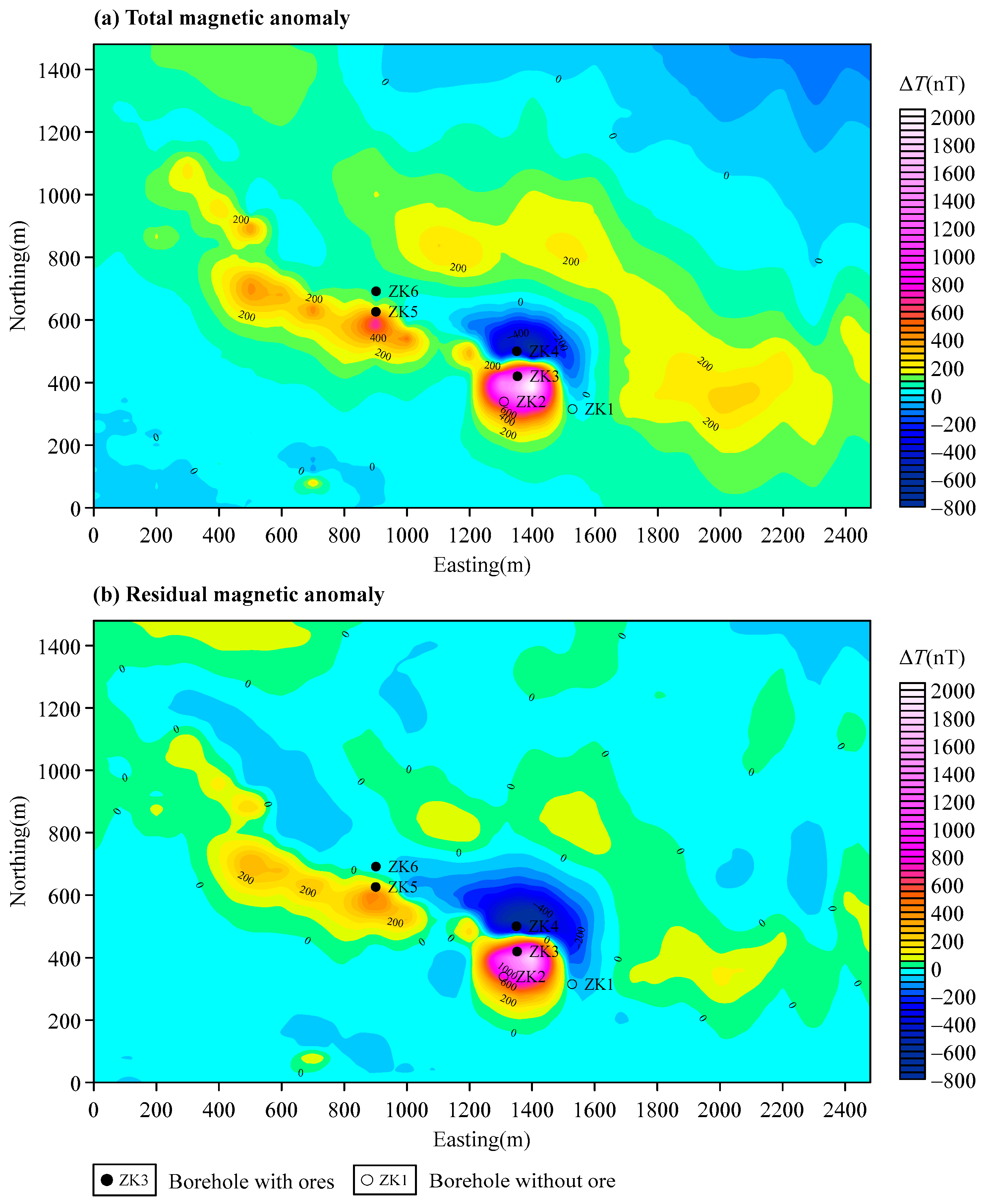
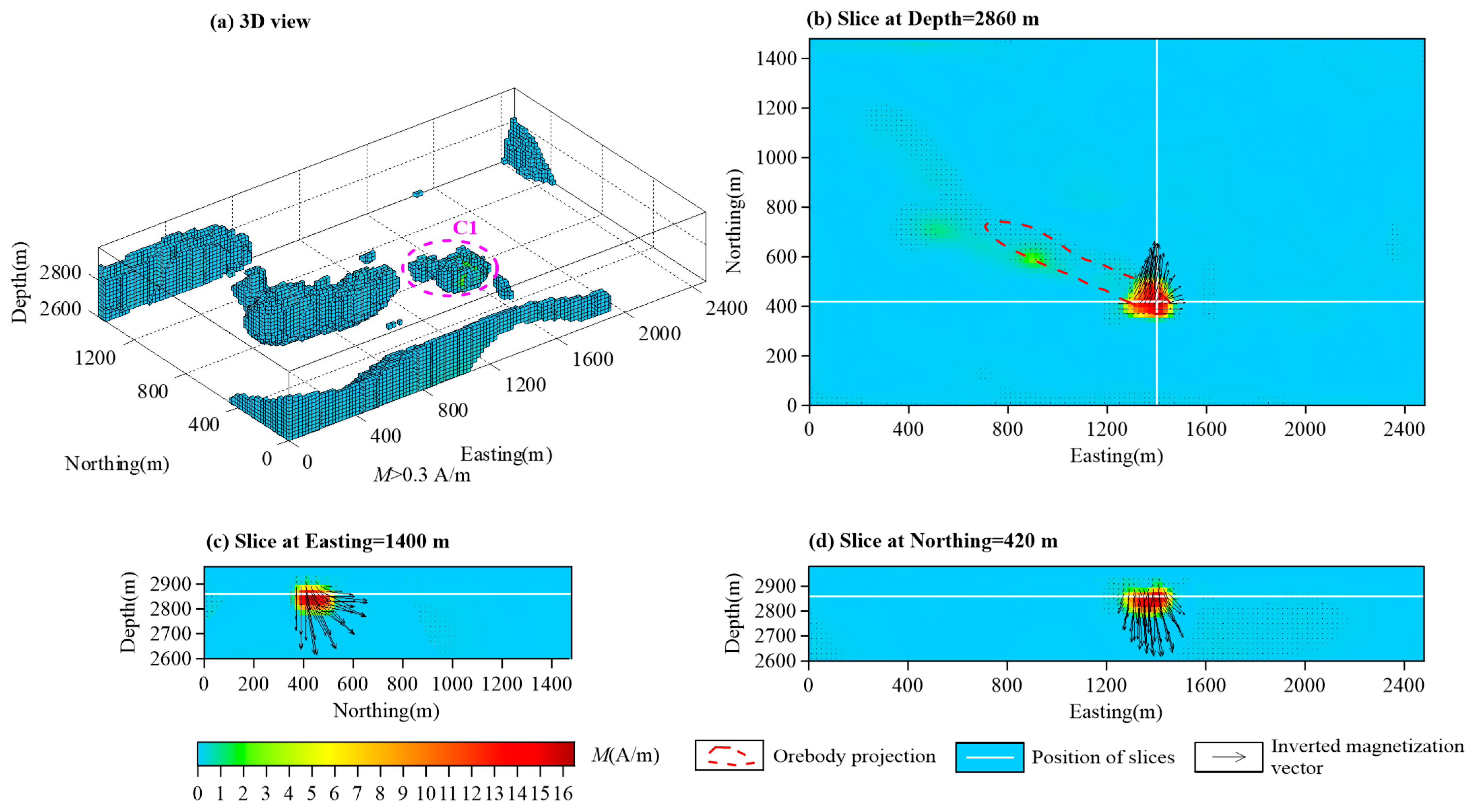
4. Field Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baniamerian, J.; Liu, S.; Hu, X.; Fedi, M.; Chauhan, M.S.; Abbas, M.A. Separation of magnetic anomalies into induced and remanent magnetization contributions. Geophys. Prospect. 2020, 68, 2320–2342. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Zuo, B.; Zhang, H.; Geng, M.; Ou, Y.; Yang, T.; Vatankhah, S. Susceptibility and remanent magnetization inversion of magnetic data with a priori information of the Köenigsberger ratio. Geophys. J. Int. 2020, 221, 1090–1109. [Google Scholar] [CrossRef]
- Liu, S.; Fedi, M.; Hu, X.; Baniamerian, J.; Wei, B.; Zhang, D.; Zhu, R. Extracting Induced and Remanent Magnetizations From Magnetic Data Modeling. J. Geophys. Res. Solid Earth 2018, 123, 9290–9309. [Google Scholar] [CrossRef]
- Li, Y.; Sun, J.; Li, S.; Leão-Santos, M. A paradigm shift in magnetic data interpretation: Increased value through magnetization inversions. Lead. Edge 2021, 40, 89–98. [Google Scholar] [CrossRef]
- Lelievre, P.G.; Oldenburg, D.W. A 3D total magnetization inversion applicable when significant, complicated remanence is present. Geophysics 2009, 74, L21–L30. [Google Scholar] [CrossRef]
- Wang, M.Y.; Di, Q.Y. Magnetization Vector Tomography. CT Theory Appl. 2000, 9, 48–50. [Google Scholar]
- Wang, M.Y.; Di, Q.Y.; Xu, K.; Wang, R. Magnetization vector inversion equations and 2D forward and inversed model study. Chin. J. Geophys. 2004, 47, 528–534. [Google Scholar]
- Kubota, R.; Uchiyama, A. Three-dimensional magnetization vector inversion of a seamount. Earth Planets Space 2005, 57, 691–699. [Google Scholar] [CrossRef]
- Elllis, R.G.; de Wet, B.; Macleod, I.N. Inversion of Magnetic Data from Remanent and Induced Sources. ASEG Ext. Abstr. 2012, 1–4. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Liu, T.; Feng, J.; Gao, W.; Qiu, L. Magnetization vector imaging for borehole magnetic data based on magnitude magnetic anomaly. Geophysics 2013, 78, D429–D444. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Xi, Y.; Liu, T.; Xu, S. 2D sequential inversion of total magnitude and total magnetic anomaly data affected by remanent magnetization. Geophysics 2015, 80, K1–K12. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.Y.; Zhang, H.L.; Geng, M.X.; Zuo, B.X. 3D Magnetization Vector Inversion of Magnetic Data: Improving and Comparing Methods. Pure Appl. Geophys. 2017, 174, 4421–4444. [Google Scholar] [CrossRef]
- Fournier, D. A Cooperative Magnetic Inversion Method with Lp-Norm Regularization. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2015. [Google Scholar]
- Zhdanov, M.S.; Čuma, M.; Wilson, G.A.; Polomé, L. 3D magnetization vector inversion for SQUID-based full tensor magnetic gradiometry. In Proceedings of the 2012 SEG Annual Meeting, Las Vegas, NV, USA, 4–9 November 2012; SEG Technical Program Expanded Abstracts. pp. 1–5. [Google Scholar]
- Queitsch, M.; Schiffler, M.; Stolz, R.; Rolf, C.; Meyer, M.; Kukowski, N. Investigation of three-dimensional magnetization of a dolerite intrusion using airborne full tensor magnetic gradiometry (FTMG) data. Geophys. J. Int. 2019, 217, 1643–1655. [Google Scholar]
- Ma, G.; Zhao, Y.; Xu, B.; Li, L.; Wang, T. High-Precision Joint Magnetization Vector Inversion Method of Airborne Magnetic and Gradient Data with Structure and Data Double Constraints. Remote Sens. 2022, 14, 2508. [Google Scholar] [CrossRef]
- Meng, Q.F. Research on High Precision Joint Inversion Method of Gravity and Magnetic with Undulating Terrain. Ph.D. Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Wang, T.; Ma, G.; Meng, Q.; Wang, T.; Jiang, Z. Joint Inversion Method of Gravity and Magnetic Data with Adaptive Zoning Using Gramian in Both Petrophysical and Structural Domains. Surv. Geophys. 2024, 45, 1291–1330. [Google Scholar] [CrossRef]
- Ou, Y.; Feng, J. Joint magnetization vector inversion of surface and borehole magnetic data. In Proceedings of the International Workshop and Gravity, Electrical & Magnetic Methods and Their Applications, Chengdu, China, 19–22 April 2015; pp. 73–76. [Google Scholar]
- Li, Y.; Sun, J. 3D magnetization inversion using fuzzy c-means clustering with application to geology differentiation. Geophysics 2016, 81, J61–J78. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y. Magnetization clustering inversion—Part 1: Building an automated numerical optimization algorithm. Geophysics 2018, 83, J61–J73. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y. Magnetization clustering inversion—Part 2: Assessing the uncertainty of recovered magnetization directions. Geophysics 2019, 84, J17–J29. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhdanov, M.S.; Čuma, M. Inversion of TMI data for the magnetization vector using Gramian constraints. In SEG Technical Program Expanded Abstracts 2015; Society of Exploration Geophysicists: Houston, TX, USA, 2015; pp. 1602–1606. [Google Scholar]
- Jorgensen, M.; Zhdanov, M.S.; Parsons, B. 3D Focusing Inversion of Full Tensor Magnetic Gradiometry Data with Gramian Regularization. Minerals 2023, 13, 851. [Google Scholar] [CrossRef]
- Fournier, D.; Heagy, L.J.; Oldenburg, D.W. Sparse magnetic vector inversion in spherical coordinates. Geophysics 2020, 85, J33–J49. [Google Scholar] [CrossRef]
- Ghalehnoee, M.H.; Ansari, A. Compact magnetization vector inversion. Geophys. J. Int. 2022, 228, 1–16. [Google Scholar] [CrossRef]
- Fournier, D.; Oldenburg, D.W. Inversion using spatially variable mixed ℓp norms. Geophys. J. Int. 2019, 218, 268–282. [Google Scholar] [CrossRef]
- Shi, X.; Geng, H.; Liu, S. Magnetization Vector Inversion Based on Amplitude and Gradient Constraints. Remote Sens. 2022, 14, 5497. [Google Scholar] [CrossRef]
- Xie, R.; Xiong, S.; Duan, S.; Luo, Y.; Wang, P. 2.5D magnetization vector inversion of vector magnetic data. Geophysics 2023, 88, G135–G144. [Google Scholar] [CrossRef]
- Ou, Y.; Lü, Q.; Yan, J.; Jia, D.; Li, Y. Enhancements for stabilizing functional in potential field inversion to recover sparse models with reasonable values and dipping structures. J. Appl. Geophys. 2023, 218, 105187. [Google Scholar] [CrossRef]
- Farquharson, C.G. Constructing piecewise-constant models in multidimensional minimum-structure inversions. Geophysics 2008, 73, K1–K9. [Google Scholar] [CrossRef]
- Sun, J.; Fournier, D. Understanding total variation regularization: Why can it recover dipping structures? Geophys. Prospect. 2023, 72, 424–434. [Google Scholar] [CrossRef]
- González, G.; Kolehmainen, V.; Seppänen, A. Isotropic and anisotropic total variation regularization in electrical impedance tomography. Comput. Math. Appl. 2017, 74, 564–576. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Feng, C.Y.; Zhao, Y.M.; Li, D.X.; Liu, J.N.; Xiao, Y.; Li, G.C.; Ma, S.C. Skarn Types and Mineralogical Characteristics of the Fe-Cu-polymetallic Skarn Deposits in the Qimantage Area, Western Qinghai Province. Acta Geol. Sin. 2011, 85, 1108–1115. [Google Scholar]
- Zhao, Y.M.; Feng, C.Y.; Li, D.X.; Liu, J.N.; Xiao, Y.; Yu, M.; Ma, S.C. Metallogenic setting and mineralization-alteration characteristics of major skarn Fe-polymetallic deposits in Qimantag area, western Qinghai Province. Miner. Depos. 2013, 32, 1–19. [Google Scholar]
- Ou, Y.; Feng, J.; Zhao, Y.; Jia, D.Y.; Gao, W.L. Forward modeling of magnetic data using the finite volume method with a simultaneous consideration of demagnetization and remanence. Chin. J. Geophys. 2018, 61, 4635–4646. [Google Scholar]
- Li, Y.; Oldenburg, D.W. Separation of regional and residual magnetic field data. Geophysics 1998, 63, 431–439. [Google Scholar] [CrossRef]
- Li, Z.; Yao, C. An Investigation of lp-Norm Minimization for the Artifact-Free Inversion of Gravity Data. Remote Sens. 2023, 15, 3465. [Google Scholar] [CrossRef]
- Liu, G.Y.; Zhao, Y.L.; Lin, G.; He, A.Q.; Wang, Z.S.; Li, Z. Preliminary analysis of prospecting potential in the western Zaohuohe iron polymetallic ore deposit area in eastern Kunlun belt. Miner. Explor. 2017, 8, 559–567. [Google Scholar]

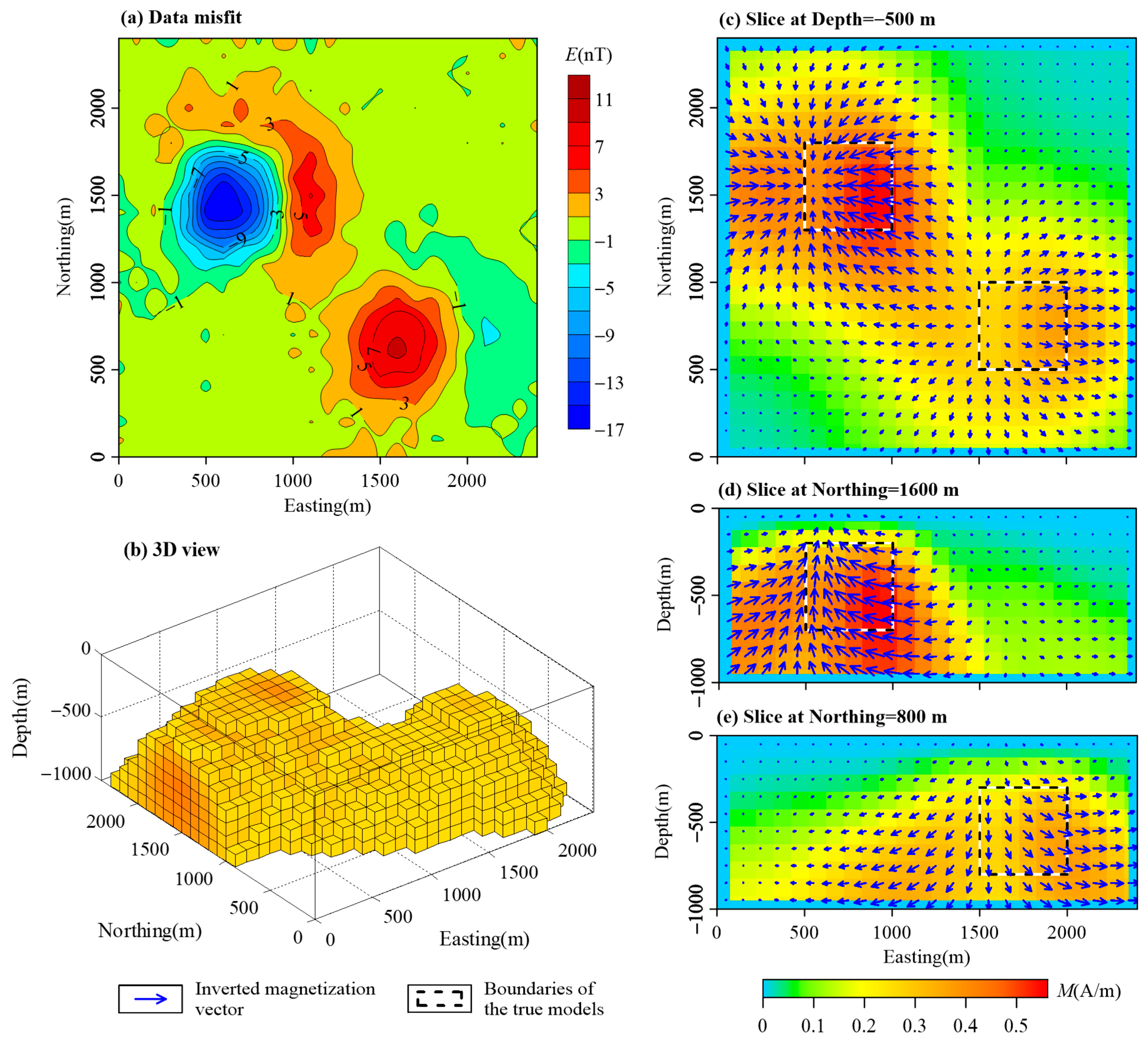
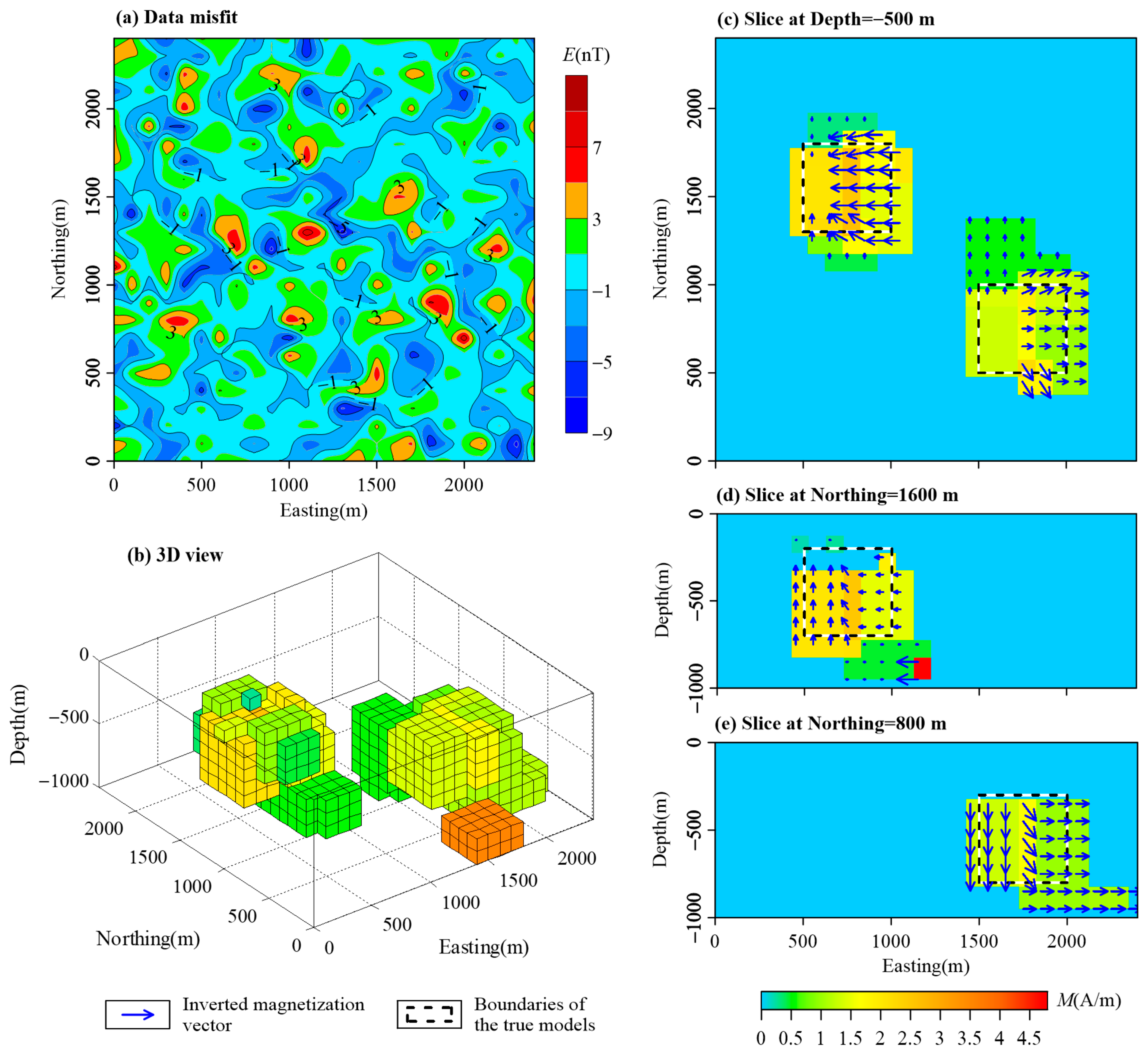
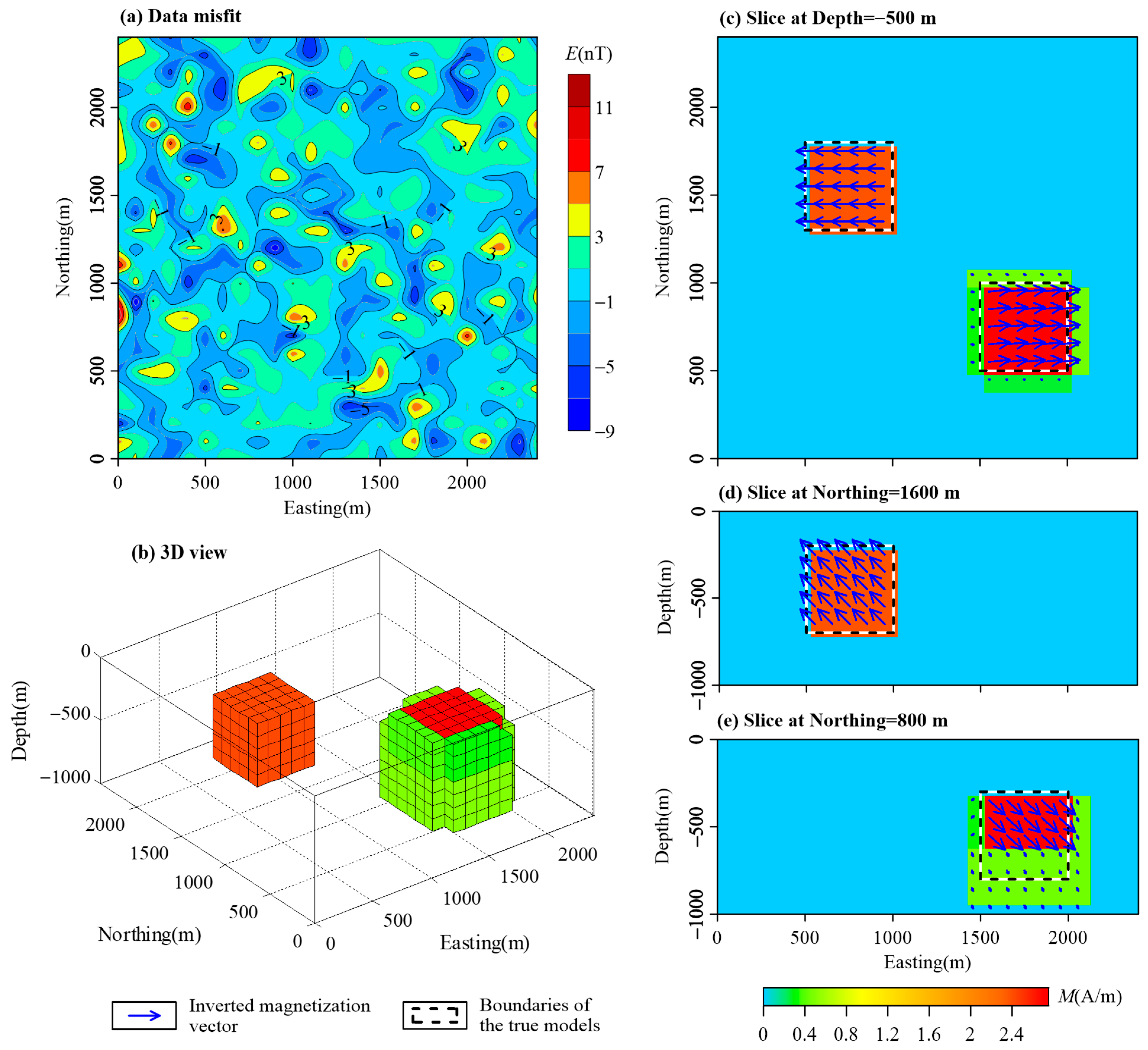
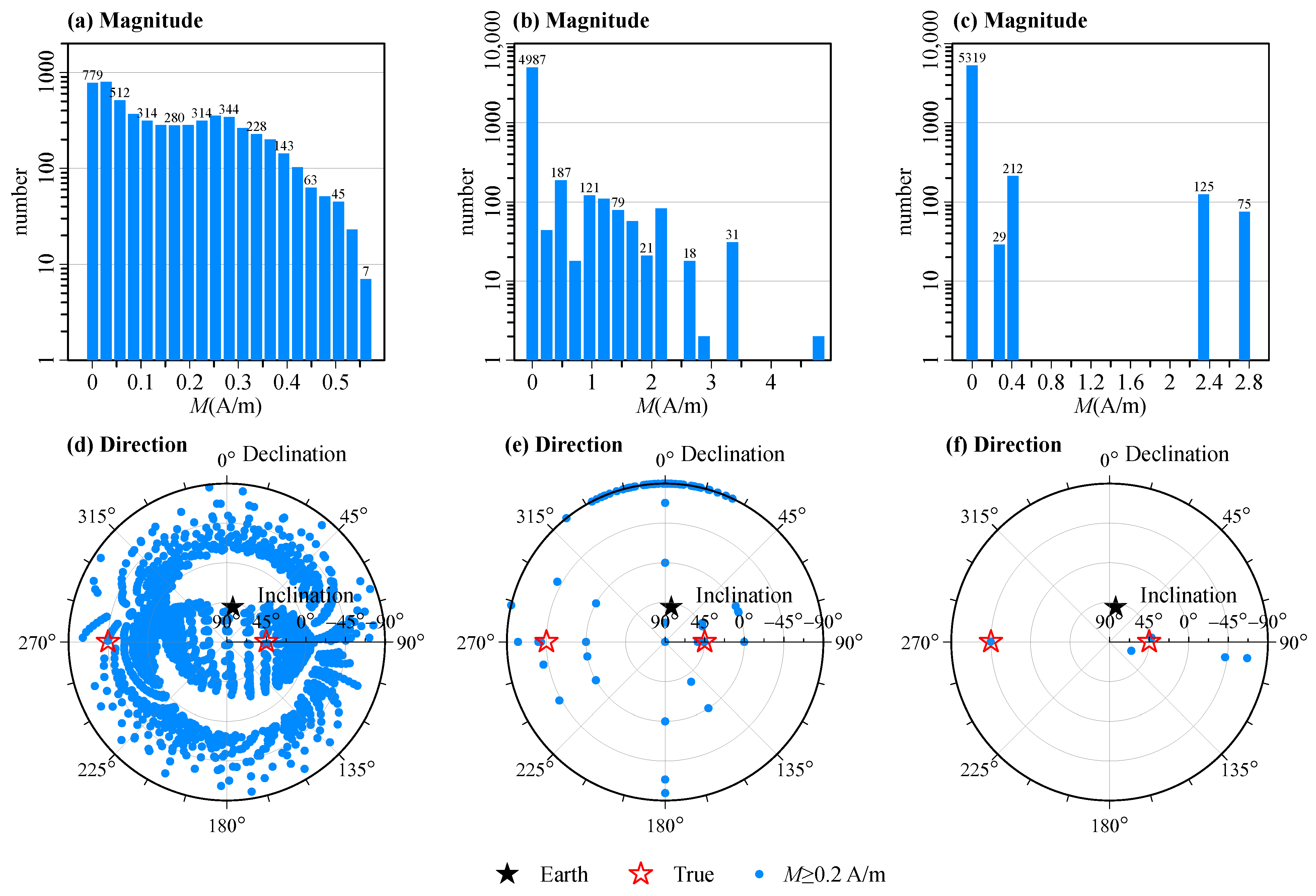


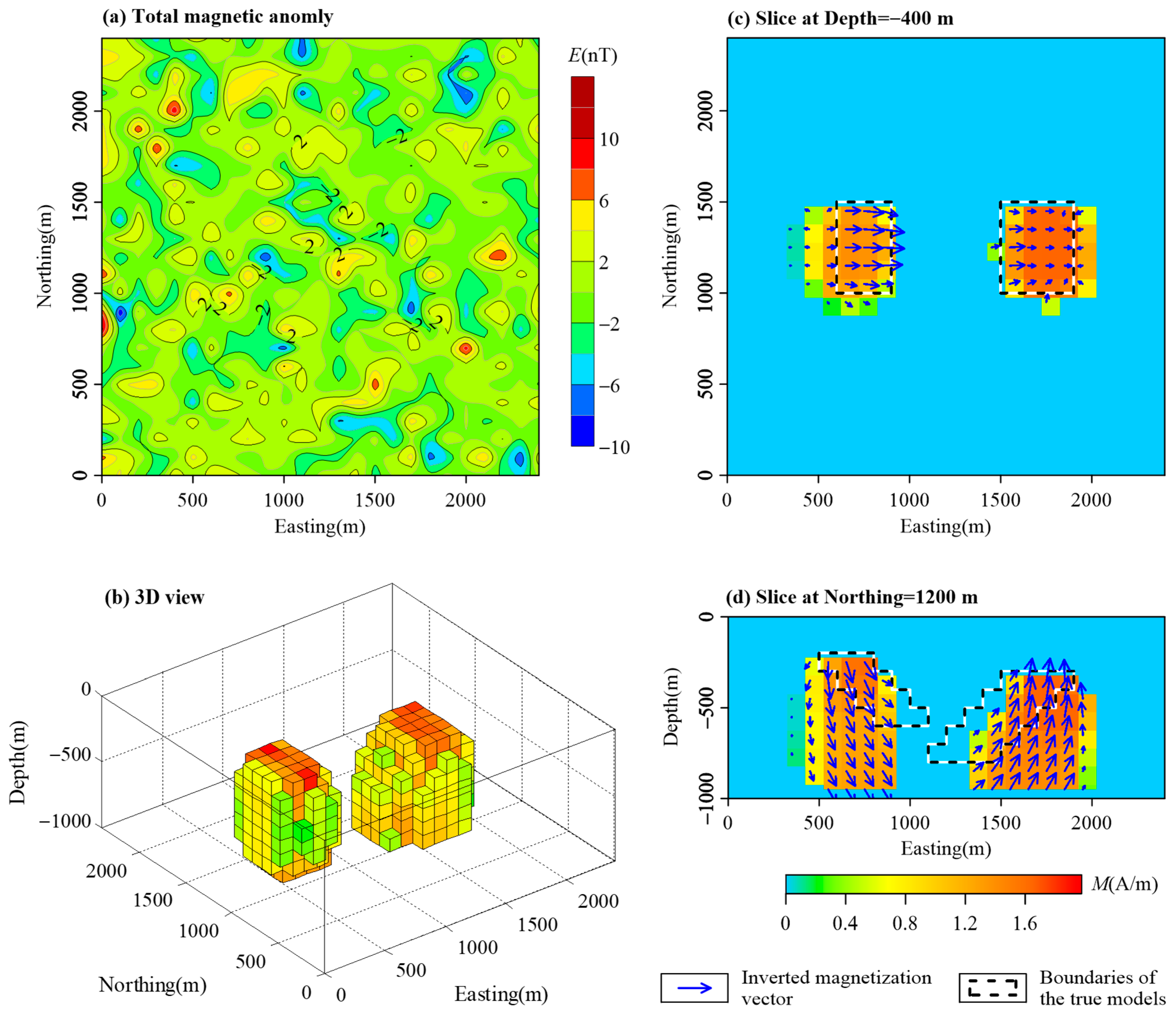

| Name | East Range (m) | North Range (m) | Vertical Range (m) | Magnetization Intensity (A/m) | Magnetization Inclination (°) | Magnetization Declination (°) |
|---|---|---|---|---|---|---|
| A | [1500, 2000] | [500, 1000] | [−300, −800] | 2.387 | 45 | 90 |
| B | [500, 1000] | [1300, 1800] | [−200, −700] | 2.387 | −45 | 270 |
| C | [600, 900] | [1000, 1500] | [−200, −600] | 2.387 | 45 | 90 |
| D | [1500, 1900] | [1000, 1500] | [−300, −800] | 2.387 | −45 | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Y.; Lü, Q.; Zhang, J.; Yang, Y.; Jia, D.; Li, Y.; Zhai, J.; Jiang, Z. Sparse Magnetization Vector Inversion Based on Modulus Constraints. Remote Sens. 2025, 17, 597. https://doi.org/10.3390/rs17040597
Ou Y, Lü Q, Zhang J, Yang Y, Jia D, Li Y, Zhai J, Jiang Z. Sparse Magnetization Vector Inversion Based on Modulus Constraints. Remote Sensing. 2025; 17(4):597. https://doi.org/10.3390/rs17040597
Chicago/Turabian StyleOu, Yang, Qingtian Lü, Jie Zhang, Yi Yang, Dingyu Jia, Yang Li, Jinghong Zhai, and Zhengzhong Jiang. 2025. "Sparse Magnetization Vector Inversion Based on Modulus Constraints" Remote Sensing 17, no. 4: 597. https://doi.org/10.3390/rs17040597
APA StyleOu, Y., Lü, Q., Zhang, J., Yang, Y., Jia, D., Li, Y., Zhai, J., & Jiang, Z. (2025). Sparse Magnetization Vector Inversion Based on Modulus Constraints. Remote Sensing, 17(4), 597. https://doi.org/10.3390/rs17040597






