Exploring the Long-Term Relationship Between Thermospheric ∑O/N2 and Solar EUV Flux
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
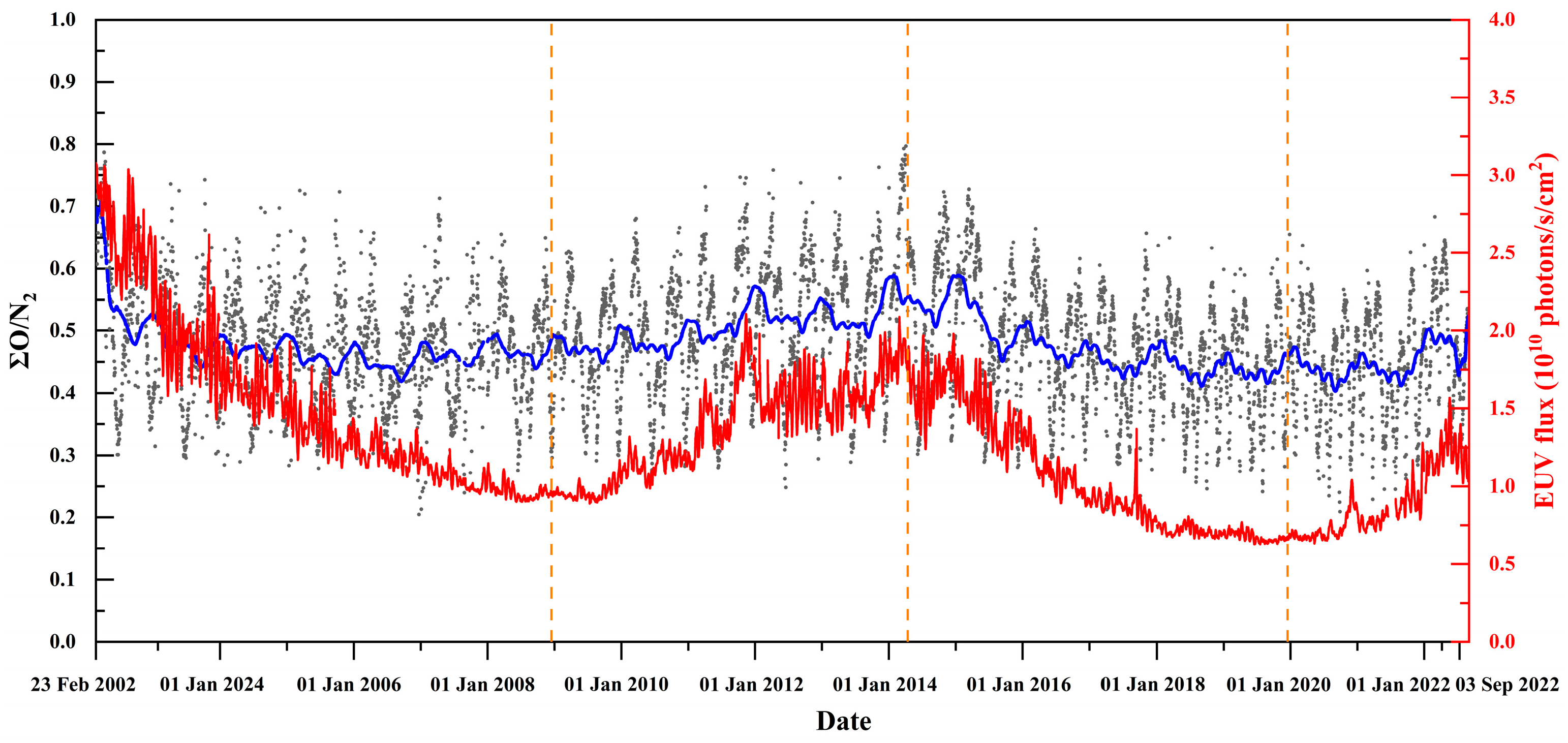
3. Results
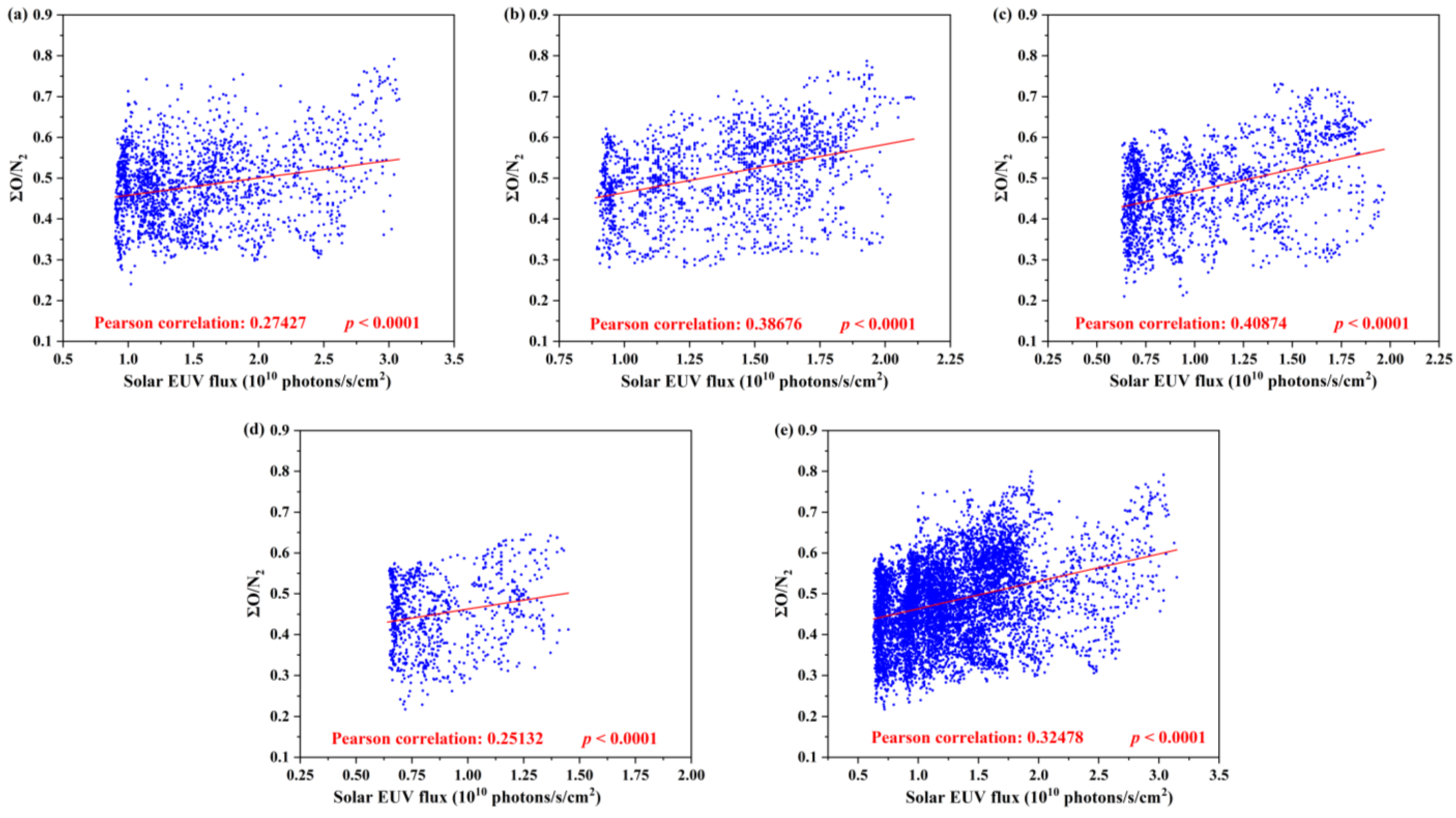
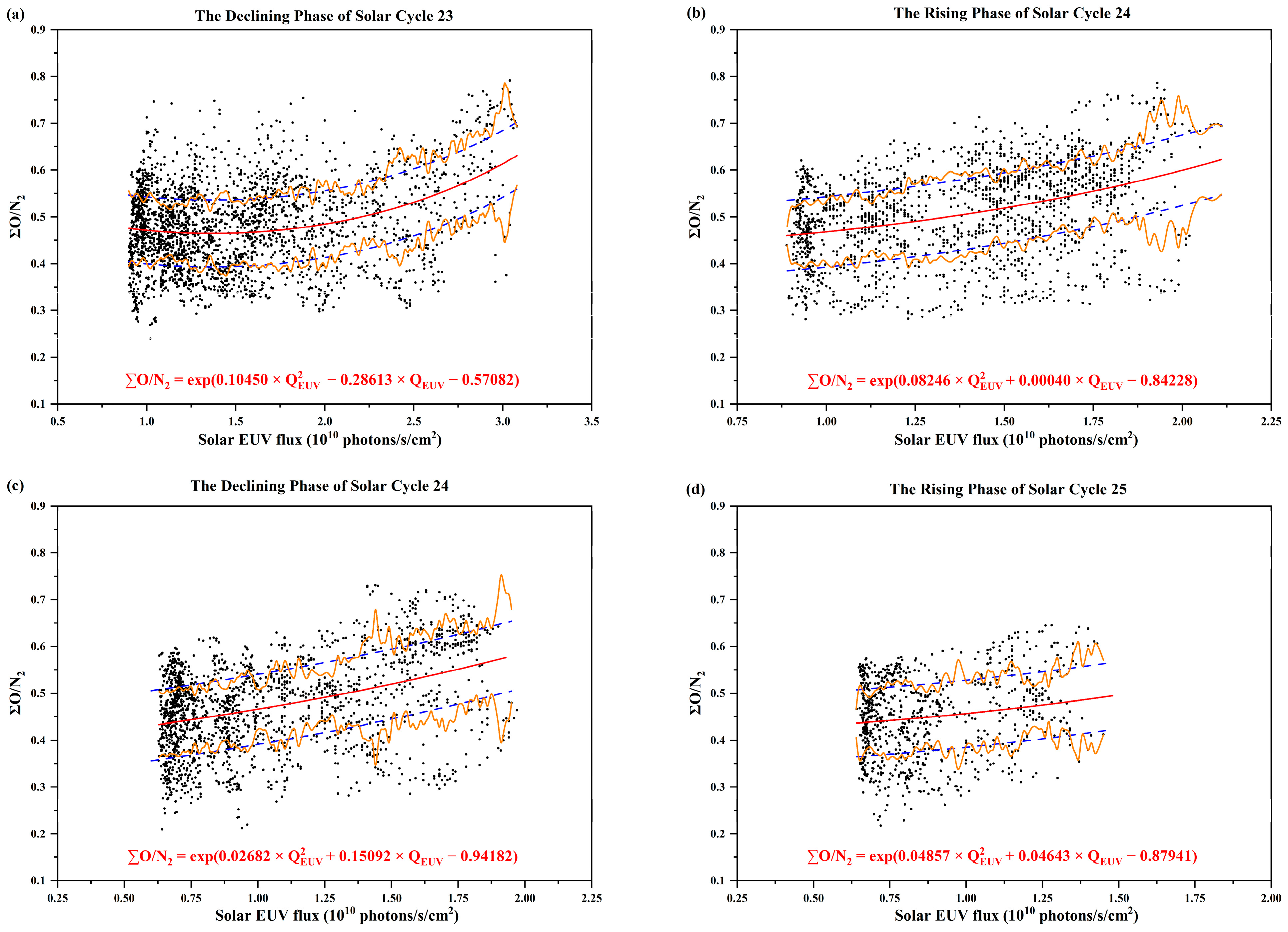
3.1. Correlation Analysis Results
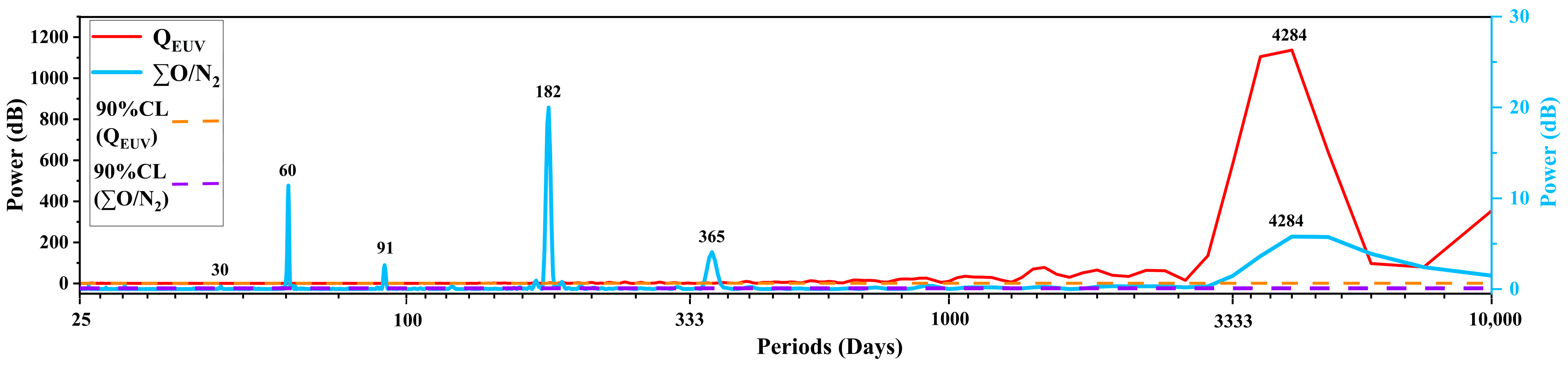
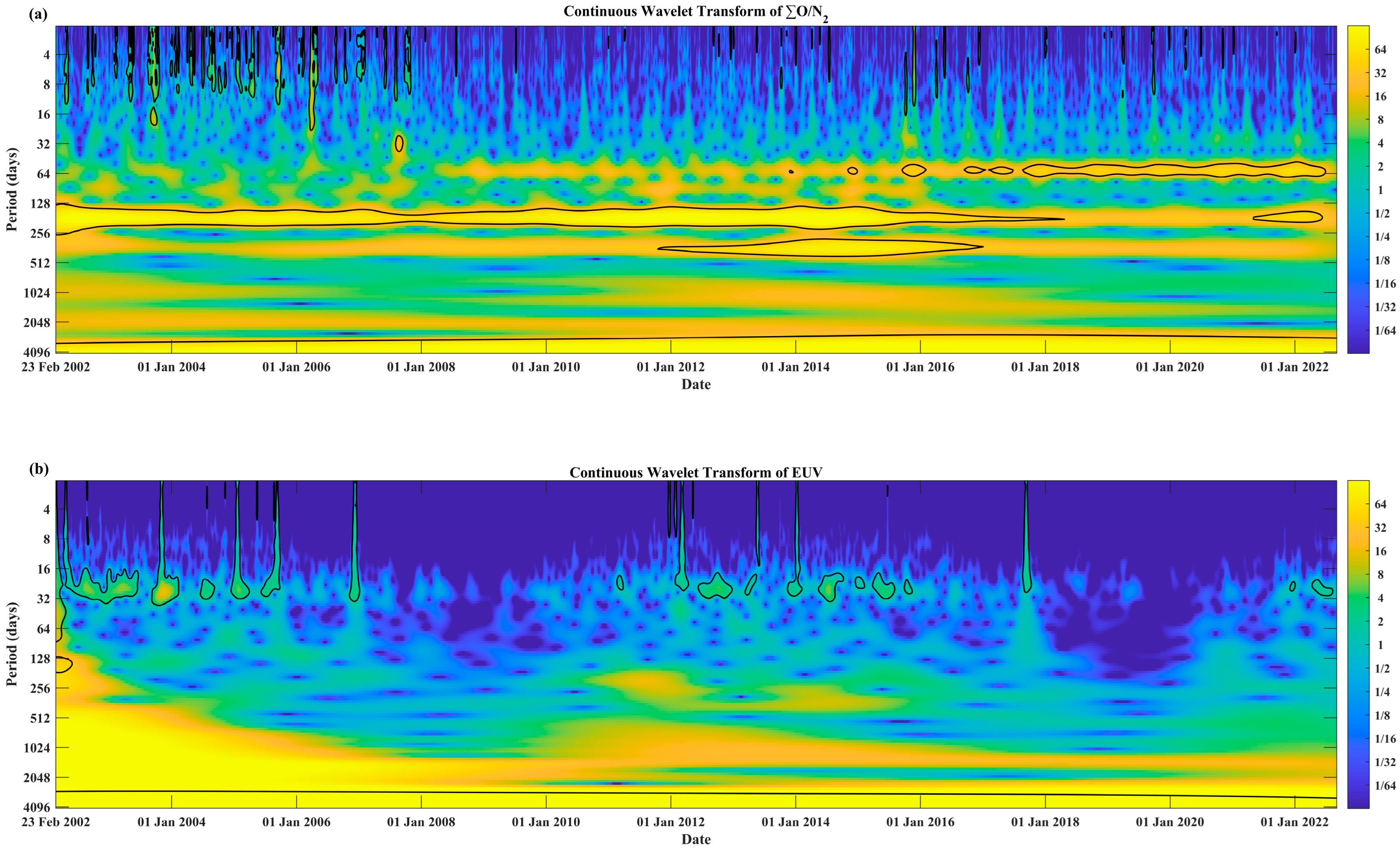
3.2. Periodic Component Analysis Results
4. Discussion
5. Conclusions
- (1)
- During the declining phase of Solar Cycle 23, throughout Solar Cycle 24, and in the initial phase of Solar Cycle 25, ∑O/N2 and QEUV exhibit a positive correlation. This correlation is mainly due to QEUV influencing atmospheric chemical processes, atmospheric circulation, and wave effects, which, in turn, lead to changes in ∑O/N2.
- (2)
- Comparing different solar activity periods, the mean QEUV of Solar Cycle 23 is higher than that of Solar Cycle 24. The mean ∑O/N2 is higher during the rising phase of Solar Cycle 24 and lower during the descending phases of Solar Cycle 23 and Solar Cycle 24.
- (3)
- During the descending phase of Solar Cycle 23 and the entire Solar Cycle 24, the changes in ∑O/N2 caused by QEUV variations reach about 30% of the mean ∑O/N2 during the same period.
- (4)
- The periodic components with higher coherence between ∑O/N2 and QEUV include the 27-day, annual, and 11-year periodic components. During the rising phase of Solar Cycle 24, the coherence between the annual components is stronger.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ∑O/N2 | Column O/N2 ratio |
| QEUV | Solar extreme ultraviolet radiation flux |
| EUV | Extreme ultraviolet |
| GUVI | Global Ultraviolet Imager |
| TIMED | Thermosphere, Ionosphere, Mesosphere Energetics and Dynamics |
| SEM | Solar EUV Monitor |
| SOHO | Solar and Heliospheric Observatory |
| LBH | Lyman–Birge Hopfield bands |
| LBHS | LBH short band |
| LBHL | LBH long band |
| LT | Local time |
| TEXO | Exospheric temperature |
| FUV | Far ultraviolet |
References
- Strickland, D.J.; Evans, J.S.; Paxton, L.J. Satellite remote sensing of thermospheric O/N2 and solar EUV: 1. Theory. J. Geophys. Res. Space Phys. 1995, 100, 12217–12226. [Google Scholar] [CrossRef]
- Zhang, Y.; Paxton, L.J.; Morrison, D.; Wolven, B.; Kil, H.; Meng, C.; Mende, S.B.; Immel, T.J. O/N2 changes during 1–4 October 2002 storms: IMAGE SI-13 and TIMED/GUVI observations. J. Geophys. Res. Space Phys. 2004, 109, A10308. [Google Scholar] [CrossRef]
- Crowley, G.; Reynolds, A.; Thayer, J.P.; Lei, J.; Paxton, L.J.; Christensen, A.B.; Zhang, Y.; Meier, R.R.; Strickland, D.J. Periodic modulations in thermospheric composition by solar wind high-speed streams. Geophys. Res. Lett. 2008, 35, L21106. [Google Scholar] [CrossRef]
- Khan, J.; Younas, W.; Khan, M.; Amory-Mazaudier, C. Climatology of O/N2 Variations at Low-and Mid-Latitudes during Solar Cycles 23 and 24. Atmosphere 2022, 13, 1645. [Google Scholar] [CrossRef]
- Yu, T.; Cai, X.; Ren, Z.; Li, S.; Pedatella, N.; He, M. Investigation of the ΣO/N2 depletion with latitudinally tilted equatorward boundary observed by GOLD during the geomagnetic storm on April 20, 2020. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030889. [Google Scholar] [CrossRef]
- Cai, X.; Burns, A.G.; Wang, W.; Qian, L.; Solomon, S.C.; Eastes, R.W.; McClintock, W.E.; Laskar, F.I. Investigation of a neutral “tongue” observed by GOLD during the geomagnetic storm on May 11, 2019. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028817. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wang, C.; Chen, T.; Wang, Y.L.; Tan, A.; Wu, T.S.; Germany, G.A.; Wang, W. Global patterns ofJoule heating in the high-latitude ionosphere. J. Geophys. Res. 2005, 110, A12208. [Google Scholar] [CrossRef]
- Qian, L.; Yu, W.; Pedatella, N.; Yue, J.; Wang, W. Hemispheric asymmetry of the annual and semiannual variation of thermospheric composition. J. Geophys. Res. Space Phys. 2023, 128, e2022JA031077. [Google Scholar] [CrossRef]
- Yu, T.; Ren, Z.; Le, H.; Wan, W.; Wang, W.; Cai, X.; Li, X. Seasonal variation of O/N2 on different pressure levels from GUVI limb measurements. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027844. [Google Scholar] [CrossRef]
- Qian, L.; Solomon, S.C.; Kane, T.J. Seasonal variation of thermospheric density and composition. J. Geophys. Res. Space Phys. 2009, 114, A01312. [Google Scholar] [CrossRef]
- Zhang, Y.; England, S.; Paxton, L.J. Thermospheric composition variations due tononmigrating tides and their effect on ionosphere. Geophys. Res. Lett. 2010, 37, L17103. [Google Scholar] [CrossRef]
- Burns, A.G.; Killeen, T.L.; Wang, W.; Roble, R.G. The solar-cycle-dependent response of the thermosphere to geomagnetic storms. J. Atmos. Sol. Terr. Phys 2004, 66, 1–14. [Google Scholar] [CrossRef]
- Floyd, L.; Newmark, J.; Cook, J.; Herring, L.; McMullin, D. Solar EUV and UV spectral irradiances and solar indices. J. Atmos. Sol.-Terr. Phys. 2005, 67, 3–15. [Google Scholar] [CrossRef]
- Thiemann, E.M.B.; Dominique, M. PROBA2 LYRA occultations: Thermospheric temperature and composition, sensitivity to EUV forcing, and comparisons with Mars. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029262. [Google Scholar] [CrossRef]
- Evans, J.S.; Strickland, D.J.; Huffman, R.E. Satellite remote sensing of thermospheric O/N2 and solar EUV: 2. Data analysis. J. Geophys. Res. Space Phys. 1995, 100, 12227–12233. [Google Scholar] [CrossRef]
- Meier, R.R.; Picone, J.M.; Drob, D.; Bishop, J.; Emmert, J.T.; Lean, J.L.; Stephan, A.W.; Strickland, D.J.; Christensen, A.B.; Paxton, L.J.; et al. Remote sensing of Earth’s limb by TIMED/GUVI: Retrieval of thermospheric composition and temperature. Earth Space Sci. 2015, 2, 1–37. [Google Scholar] [CrossRef]
- Zhang, Y.; Paxton, L.J. Long-term variation in the thermosphere: TIMED/GUVI observations. J. Geophys. Res. Space Phys. 2011, 116, A00H02. [Google Scholar] [CrossRef]
- Smith, A.K.; Marsh, D.R.; Mlynczak, M.G.; Mast, J.C. Temporal variations of atomic oxygen in the upper mesosphere from SABER. J. Geophys. Res. Atmos. 2010, 115, D18309. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.J. The “thermospheric spoon”: A mechanism for the semiannual density variation. J. Geophys. Res. Space Phys. 1998, 103, 3951–3956. [Google Scholar] [CrossRef]
- Akmaev, R.A. Simulation of large-scale dynamics in the mesosphere and lower thermosphere with the Doppler-spread parameterization of gravity waves: 1. Implementation and zonal mean climatologies. J. Geophys. Res. Atmos. 2001, 106, 1193–1204. [Google Scholar] [CrossRef]
- Akmaev, R.A. Simulation of large-scale dynamics in the mesosphere and lower thermosphere with the Doppler-spread parameterization of gravity waves: 2. Eddy mixing and the diurnal tide. J. Geophys. Res. Atmos. 2001, 106, 1205–1213. [Google Scholar] [CrossRef]
- Meier, R.R. The thermospheric column O/N2 ratio. J. Geophys. Res. Space Phys. 2021, 126, e2020JA029059. [Google Scholar] [CrossRef]
- Strickland, D.J.; Evans, J.S.; Correira, J. Comment on “Long-term variation in the thermosphere: TIMED/GUVI observations” by Y. Zhang and L.J. Paxton. J. Geophys. Res. Space Phys. 2012, 117, A07302. [Google Scholar] [CrossRef]
- Comberiate, J.; Paxton, L.J. Global Ultraviolet Imager equatorial plasma bubble imaging and climatology, 2002–2007. J. Geophys. Res. Space Phys. 2010, 115, A04305. [Google Scholar] [CrossRef]
- Kamalabadi, F.; Comberiate, J.M.; Taylor, M.J.; Pautet, P.-D. Estimation of electron densities in the lower thermosphere from GUVI 135.6 nm tomographic inversions in support of SpreadFEx. Ann. Geophys. 2009, 27, 2439–2448. [Google Scholar] [CrossRef]
- Christensen, A.B.; Paxton, L.J.; Avery, S.; Craven, J.; Crowley, G.; Humm, D.C.; Kil, H.; Meier, R.R.; Meng, C.I.; Morrison, D.; et al. Initial observations with the Global Ultraviolet Imager (GUVI) in the NASA TIMED satellite mission. J. Geophys. Res. Space Phys. 2003, 108, 553–559. [Google Scholar] [CrossRef]
- Paxton, L.J.; Christensen, A.B.; Humm, D.C.; Ogorzalek, B.S.; Pardoe, C.T.; Morrison, D.; Weiss, M.B.; Crain, W.; Lew, P.H.; Mabry, D.J.; et al. Global ultraviolet imager (GUVI): Measuring composition and energy inputs for the NASA Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) mission. Proc. SPIE Int. Soc. Opt. Eng. 1999, 3756, 265–276. [Google Scholar] [CrossRef]
- Strickland, D.J.; Meier, R.R.; Walterscheid, R.L.; Craven, J.D.; Christensen, A.B.; Paxton, L.J.; Morrison, D.; Crowley, G. Quiet-time seasonal behavior of the thermosphere seen in the far ultraviolet dayglow. J. Geophys. Res. Space Phys. 2004, 109, A01302. [Google Scholar] [CrossRef]
- Roble, R.G. Energetics of the mesosphere and thermosphere. In The Upper Mesosphere and Lower Thermosphere: A Review of Experiment and Theory; Springer: Dordrecht, The Netherlands, 1995; pp. 1–21. [Google Scholar] [CrossRef]
- Hovestadt, D.; Hilchenbach, M.; Bürgi, A.; Klecker, B.; Laeverenz, P.; Scholer, M.; Grünwaldt, H.; Axford, W.I.; Livi, S.; Marsch, E.; et al. CELIAS-charge, element and isotope analysis system for SOHO. In The SOHO Mission; Fleck, B., Domingo, V., Poland, A., Eds.; Springer: Dordrecht, The Netherlands, 1995; pp. 159–163. [Google Scholar] [CrossRef]
- Judge, D.L.; McMullin, D.R.; Ogawa, H.S.; Hovestadt, D.; Klecker, B.; Hilchenbach, M.; Möbius, E.; Canfield, L.R.; Vest, R.E.; Watts, R.; et al. First Solar EUV Irradiances Obtained from SOHO by the Celias/Sem. Sol. Phys. 1998, 177, 161–173. [Google Scholar] [CrossRef]
- Judge, D.L.; McMullin, D.R.; Ogawa, H.S. Absolute solar 30.4 nm flux from sounding rocket observations during the solar cycle 23 minimum. J. Geophys. Res. Space Phys. 1999, 104, 28321–28324. [Google Scholar] [CrossRef]
- Judge, D.; Ogawa, H.; McMullin, D.; Gangopadhyay, P.; Pap, J. The SOHO CELIAS/SEM EUV database from SC23 minimum to the present. Adv. Space Res. 2002, 29, 1963–1968. [Google Scholar] [CrossRef]
- Yu, T.; Ren, Z.; Yu, Y.; Yue, X.; Zhou, X.; Wan, W. Comparison of reference heights of O/N2 and ∑O/N2 based on GUVI dayside limb measurement. Space Weather. 2020, 18, e2019SW002391. [Google Scholar] [CrossRef]
- Dang, T.; Wang, W.; Burns, A.; Dou, X.; Wan, W.; Lei, J. Simulations of the ionospheric annual asymmetry: Sun-Earth distance effect. J. Geophys. Res. Space Phys. 2017, 122, 6727–6736. [Google Scholar] [CrossRef]
- Lei, J.; Dou, X.; Burns, A.; Wang, W.; Luan, X.; Zeng, Z.; Xu, J. Annual asymmetry in thermospheric density: Observations and simulations. J. Geophys. Res. Space Phys. 2013, 118, 2503–2510. [Google Scholar] [CrossRef]
- Yue, J.; Jian, Y.; Wang, W.; Meier, R.; Burns, A.; Qian, L.; Jones, M.; Wu, D.L.; Mlynczak, M. Annual and semiannual oscillations of thermospheric composition in TIMED/GUVI limb measurements. J. Geophys. Res. Space Phys. 2019, 124, 3067–3082. [Google Scholar] [CrossRef]
- Jones, M., Jr.; Emmert, J.T.; Drob, D.P.; Picone, J.M.; Meier, R.R. Origins of the thermosphere-ionosphere semiannual oscillation: Reformulating the “thermospheric spoon” mechanism. J. Geophys. Res. Space Phys. 2018, 123, 931–954. [Google Scholar] [CrossRef]
- Gasperini, F.; Hagan, M.E.; Zhao, Y. Evidence of tropospheric 90-day oscillations in the thermosphere. Geophys. Res. Lett. 2017, 44, 10125–10133. [Google Scholar] [CrossRef]
- Gasperini, F.; Liu, H.; Gan, Q. Madden-Julian Oscillation (MJO) Effects in the GOLD O/N2 and Swarm-C neutral density during 2018–2019? ESS Open Arch. 2020. [Google Scholar] [CrossRef]
- Forbes, J.M.; Bruinsma, S.; Lemoine, F.G. Solar rotation effects on the thermospheres of Mars and Earth. Science 2006, 312, 1366–1368. [Google Scholar] [CrossRef] [PubMed]
- Lei, J.; Thayer, J.P.; Forbes, J.M.; Wu, Q.; She, C.; Wan, W.; Wang, W. Ionosphere response to solar wind high-speed streams. Geophys. Res. Lett. 2008, 35, L19105. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Le, H.; Zhang, H. Discrepant responses of the global electron content to the solar cycle and solar rotation variations of EUV irradiance. Earth Planets Space 2015, 67, 80. [Google Scholar] [CrossRef]
- Elias, A.G.; de Haro Barbás, B.F.; Medina, F.D.; Zossi, B.S. On the Correlation between EUV Solar Radiation Proxies and their Long-Term Association. In Proceedings of the Thirteenth Workshop “Solar Influences on the Magnetosphere, Ionosphere and Atmosphere”; Bulgarian Academy of Sciences: Sofia, Bulgaria, 2021. e-ISSN 2367-7570. Available online: https://ui.adsabs.harvard.edu/link_gateway/2021simi.conf...20E/doi:10.31401/WS.2021.proc (accessed on 2 February 2025).
- Elias, A.G.; Martinis, C.R.; de Haro Barbas, B.F.; Medina, F.D.; Zossi, B.S.; Fagre, M.; Duran, T. Comparative analysis of extreme ultraviolet solar radiation proxies during minimum activity levels. Earth Planet. Phys. 2023, 7, 540–547. [Google Scholar] [CrossRef]
- Hussain, A.; Cao, J.; Ali, S.; Ullah, W.; Muhammad, S.; Hussain, I.; Abbas, H.; Hamal, K.; Sharma, S.; Akhtar, M.; et al. Wavelet coherence of monsoon and large-scale climate variabilities with precipitation in Pakistan. Int. J. Climatol. 2022, 42, 9950–9966. [Google Scholar] [CrossRef]
- Zhang, Y.; Paxton, L.J. Reply to comment by D.J. Strickland et al. on “Long-term variation in the thermosphere: TIMED/GUVI observations”. J. Geophys. Res. Space Phys. 2012, 117, A07304. [Google Scholar] [CrossRef]
- Swenson, G.R.; Vargas, F.; Jones, M.; Zhu, Y.; Kaufmann, M.; Yee, J.H.; Mlynczak, M. Intra-Annual Variation of Eddy Diffusion (kzz) in the MLT, From SABER and SCIAMACHY Atomic Oxygen Climatologies. J. Geophys. Res. Atmos. 2021, 126, e2021JD035343. [Google Scholar] [CrossRef] [PubMed]
- Malhotra, G.; Ridley, A.J.; Marsh, D.R.; Wu, C.; Paxton, L.J.; Mlynczak, M.G. Impacts of lower thermospheric atomic oxygen on thermospheric dynamics and composition using the global ionosphere thermosphere model. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027877. [Google Scholar] [CrossRef]
- Wang, J.C.; Yue, J.; Wang, W.; Qian, L.; Wu, Q.; Wang, N. The lower thermospheric winter-to-summer meridional circulation: 1. Driving mechanism. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030948. [Google Scholar] [CrossRef]
- Judge, D.; Ogawa, H.; McMullin, D.; Gangopadhyay, P. The SoHO CELIAS/SEM data base. Phys. Chem. Earth Part C Sol. Terr. Planet. Sci. 2000, 25, 417–420. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xiao, C.; Li, K.; Wang, Z.; Wu, X.; Yu, Y.; Xiao, L. Exploring the Long-Term Relationship Between Thermospheric ∑O/N2 and Solar EUV Flux. Remote Sens. 2025, 17, 574. https://doi.org/10.3390/rs17040574
Li H, Xiao C, Li K, Wang Z, Wu X, Yu Y, Xiao L. Exploring the Long-Term Relationship Between Thermospheric ∑O/N2 and Solar EUV Flux. Remote Sensing. 2025; 17(4):574. https://doi.org/10.3390/rs17040574
Chicago/Turabian StyleLi, Hao, Cunying Xiao, Kuan Li, Zewei Wang, Xiaoqi Wu, Yang Yu, and Luo Xiao. 2025. "Exploring the Long-Term Relationship Between Thermospheric ∑O/N2 and Solar EUV Flux" Remote Sensing 17, no. 4: 574. https://doi.org/10.3390/rs17040574
APA StyleLi, H., Xiao, C., Li, K., Wang, Z., Wu, X., Yu, Y., & Xiao, L. (2025). Exploring the Long-Term Relationship Between Thermospheric ∑O/N2 and Solar EUV Flux. Remote Sensing, 17(4), 574. https://doi.org/10.3390/rs17040574






