Interplanetary Magnetic Field Bx Effect on Field-Aligned Currents in Different Local Times

Abstract

This study explores the impact of the radial interplanetary magnetic field (IMF) on the strength and latitude of peak field-aligned currents (FACs). FACs are derived through vector magnetic field observations of the Swarm satellite mission. The analysis examines how the responses of FACs to radial IMF vary according to local time, season, and hemisphere. In the dawn and noon–midnight sectors, which are primarily influenced by westward auroral electrojets, the Northern Hemisphere (NH) exhibits stronger poleward FACs (FACp) when the IMF cone angle is ≥135° and weaker FACp when the cone angle is ≤45°. In contrast, the Southern Hemisphere (SH) shows the opposite response to the IMF Bx polarity. The effect of IMF Bx is more pronounced during summer than winter, especially in the noon-to-midnight sector, while its influence on FACs is more significant during the dawn period in winter. The latitude of FACs is most strongly affected by IMF Bx around noon and midnight. A relationship is observed between FAC density and latitude in response to IMF Bx, with stronger FACp occurring at lower latitudes.

1. Introduction

Field-aligned currents (FACs) flow along geomagnetic field lines and play a crucial role in the transfer of energy and momentum between the magnetosphere and the ionosphere [1,2,3]. On the dawn side, current sheets at higher latitudes (lower latitudes) flow downward into (upward out of) the ionosphere, forming R1 (R2) FACs. Conversely, on the dusk side, R1 (R2) FACs flow outward from (into) the ionosphere. The interplanetary magnetic field (IMF) significantly influences the spatial distribution and strength of FACs [4,5,6,7,8]. Among the three components of IMF, IMF Bz is dominant in shaping the development and characteristics of FACs. For a southward IMF (Bz < 0), both R1 and R2 FACs intensify and extend into lower latitudes. However, for a northward IMF (Bz > 0), R1 and R2 FACs weaken, and two additional current sheets, known as NBZ currents, emerge in the polar cap region.

Moreover, IMF By drives dawn–dusk and hemispheric asymmetries in FACs. When IMF By is dominant, two current systems with opposite polarities form in the noontime cusp region, known as DPY FACs. The DPY FACs located on the polar and equatorward sides are referred to as midday R0 and midday R1 FACs, respectively. For positive (negative) IMF By, the midday R0 (R1) FACs flow outward from (into) the Northern Hemisphere (NH) and inward to (out of) the Southern Hemisphere (SH).

To account for the combined effects of IMF By and Bz on FACs, the merging electric field Em has been proposed in the literature [9]. Em is regarded as significant in indicating the effectiveness of solar wind energy and momentum input into the magnetosphere. The intensities and latitudes of FACs have been shown to be well controlled by Em [5]. Notably, Em reflects the direction of IMF Bz but remains symmetric with respect to the polarity of IMF By. Recent studies, however, have highlighted local time and hemispheric asymmetries in the high-latitude current system in relation to the orientation of IMF By [10,11]. These studies show that at dusk and noon, when the auroral electrojet is eastward, NH (SH) FACs are greater when IMF By < 0 (By > 0). In contrast, at dawn, midnight, and noon, when the auroral electrojet is westward, NH (SH) FACs are more intense for IMF By > 0 (By < 0). Additionally, when the auroral electrojet is eastward, FACs are positioned at a higher latitude for positive (negative) IMF By, whereas FACs associated with westward auroral electrojet exhibit the opposite trend.

As outlined above, previous studies have primarily focused on the effects of IMF By and Bz on FACs characteristics. However, several studies have indicated that IMF Bx can significantly influence magnetospheric topology, the reconnection rate, and the potential difference across the ionosphere [12,13]. As a result, the energy released from magnetospheric reconnection may alter the intensity and distribution of FACs. Wang et al. (2024) [14] documented the impact of IMF Bx on the position and magnitude of the peak strength in the auroral electrojet. Specifically, within the midnight sector, the westward electrojet in the NH strengthens when IMF Bx is negative, while in the SH, the westward electrojet intensifies when IMF Bx is positive. This effect is more pronounced during the local winter season. Using multi-satellite and ground-based observations, Laundal et al. (2018) [15] showed that the polarity of IMF Bx can alter FACs and ionospheric equivalent currents by up to 10% under southward IMF Bz conditions. Their study relied on average distribution maps of auroral currents, sorted based on different IMF components. The simple average not accounting for the variation in current position may introduce errors. Shue et al. (2002) [16] observed that under similar IMF By conditions with a southward IMF, auroral power in the hemisphere is higher for negative Bx values compared to positive Bx values. This asymmetry in auroral power, influenced by the polarity of Bx, is evident in the seasons of summer and winter. Reistad et al. (2014) [17] noticed some significant imbalances in the responses of aurora intensity to IMF Bx in both hemispheres. Specifically, auroral brightness is higher in the 15–19 MLT sector when IMF Bx is negative in the NH, whereas in the SH, auroral brightness is stronger in the 16–20 MLT sector when IMF Bx is positive. These findings suggest that IMF Bx may similarly influence FACs. However, the effects of IMF Bx on FACs across different local times and hemispheres remain unclear, warranting further detailed investigation.

This study provides a statistical analysis of the influence of IMF Bx on the modulation of FACs using six years of Swarm satellite observations. We systematically investigate how the polarity of IMF Bx governs the peak current densities and magnetic latitude distributions of FACs. Our analysis specifically explores the local time dependence, seasonal variability, and interhemispheric asymmetries in FAC responses to IMF Bx forcing. Section 2 shows the data processing methods employed in this study, and Section 3 outlines the statistical results. Section 4 discusses these results, and Section 5 concludes with a summary.

2. Materials and Methods

The Swarm satellite constellation was launched by the European Space Agency (ESA, Paris, France) on 22 November 2013. It consists of three nearly identical spacecraft: Swarm A, Swarm B, and Swarm C. The primary goal of this mission is to conduct an in-depth study of the Earth’s geomagnetic environment, which includes the main geomagnetic field, the crustal magnetic field, and the currents in the ionosphere and magnetosphere. Swarm A and Swarm C orbit together at approximately 450 km above the Earth’s surface, maintaining a longitudinal separation of about 1.4°, while Swarm B operates independently at a higher altitude of around 510 km. The three satellites share a nearly identical orbital inclination of 87.4°. By utilizing polar orbits, the Swarm satellites provide comprehensive coverage of the auroral regions, enabling them to collect global data on FACs every 133 days.

This study utilized vector magnetic field data from the Swarm A and C satellites to invert FACs. Based on the geometric relationship between the two Swarm satellites, FACs can be derived using Ampère’s integral law, defined as ${\mathrm{j}}_{\parallel }={\displaystyle \frac{1}{{\mu }_{0}A\sin \left(i\right)}}\oint Bdl$, where μ₀ is the vacuum permeability, i is the magnetic field inclination, and B is the horizontal perturbation magnetic field generated by the FACs [18]. To compute the perturbation magnetic field B, the CHAOS-6 model (developed by DTU Space, Kongens Lyngby, Denmark) was utilized to remove the internal geomagnetic field. The integral is performed along the closed quadrilateral, which is constructed from four consecutive positions of the two satellites and includes the orbit segments of Swarm A and C, as well as the connecting lines between them (see Figure 1 of Ritter et al., 2013 [19]). Here, dl represents a line element along the integration path, while A denotes the area of the closed quadrilateral formed by the four observation points. Considering the radial distance between the Swarm A and C satellites, a 20 s low-pass filter was applied to the FACs, effectively suppressing Alfvén waves and other small-scale current structures. This filtering process allowed for extracting large-scale FACs (spatial scale > 150 km). In the following analysis, FACs emanating from the ionosphere were considered positive, while those moving inward toward the ionosphere were considered negative. FACs with absolute values below 50 A/m² were excluded from the analysis.

The Polar Electrojet (PEJ) refers to intense horizontal currents flowing in the ionospheric E-layer (~110 km altitude) within the auroral zones, oriented perpendicular to both the electric and magnetic fields. In the dusk sector, the PEJ flows eastward along the auroral belt, while in the dawn sector, it flows westward. These currents are driven by the convection electric field and are closely linked to FACs and auroral activity. In this study, PEJ intensity is derived from Swarm scalar magnetic field data. The PEJ is modeled as a series of infinite line currents spaced 1° apart in the ionospheric E-layer (110 km). The observed total field residuals are then inverted using an iterative least-squares fitting approach to determine the strength of each line current [20].

In this study, we used the polar electrojet (PEJ) to organize FACs. Swarm A scalar magnetic field data were utilized to derive the PEJ, conceptualized as an ensemble of linear currents extending infinitely within the ionospheric E-layer, spaced 1° apart. Using the least-squares fitting method, the residuals of the measured total magnetic field were processed to determine the intensity of each individual linear current. The calculation formula was defined as follows: I = (G^TAG)⁻¹ GΔF. In this formula, A is a weighting matrix used to prevent oscillatory results caused by adjacent line currents, while G is a matrix composed of known parameters such as satellite positions and the magnetic field model. To eliminate the ring current effect, the horizontal current intensity at ±50° magnetic latitude (MLat) was set to zero, and the current intensity along the orbit was shifted by an equal amount [20,21].

This study examined the six-year period from 17 April 2014 to 16 April 2020, using FAC observations from both the Swarm A and Swarm C satellites. To investigate the impacts of solar wind and IMF on the current system, OMNI solar wind and IMF data (NASA Goddard Space Flight Center, Greenbelt, MD, USA) at a 1 min resolution were employed. To align the time trajectories of FACs and IMF data, a 15 min moving average was applied to the OMNI data, and a 20 min delay was introduced to account for the propagation time from the bow shock to the ionosphere. The criteria for selecting dominant IMF Bx cases were based on the IMF cone angle, which is the angle between the direction of the IMF and the X-axis of the Geocentric Solar Magnetospheric (GSM) coordinate system, using the following formula: $\mathsf{\theta }=\arccos {\displaystyle \frac{{\mathrm{B}}_{\mathrm{x}}}{\sqrt{{\mathrm{B}}_{\mathrm{x}}^2+{\mathrm{B}}_{\mathrm{y}}^2+{\mathrm{B}}_{\mathrm{z}}^2}}}$. Specifically, θ < 45° or θ > 135° indicates that the IMF Bx component is primarily directed toward the Sun or the Earth. Therefore, in this study, we used an IMF cone angle ≤ 45° to represent periods with dominant positive IMF Bx values and an IMF cone angle ≥ 135° to represent periods with dominant negative IMF Bx values. Using this angle criterion helped us to isolate the IMF Bx effect from other components of the IMF, preventing the potential contamination of the results due to the Parker spiral configuration of the IMF.

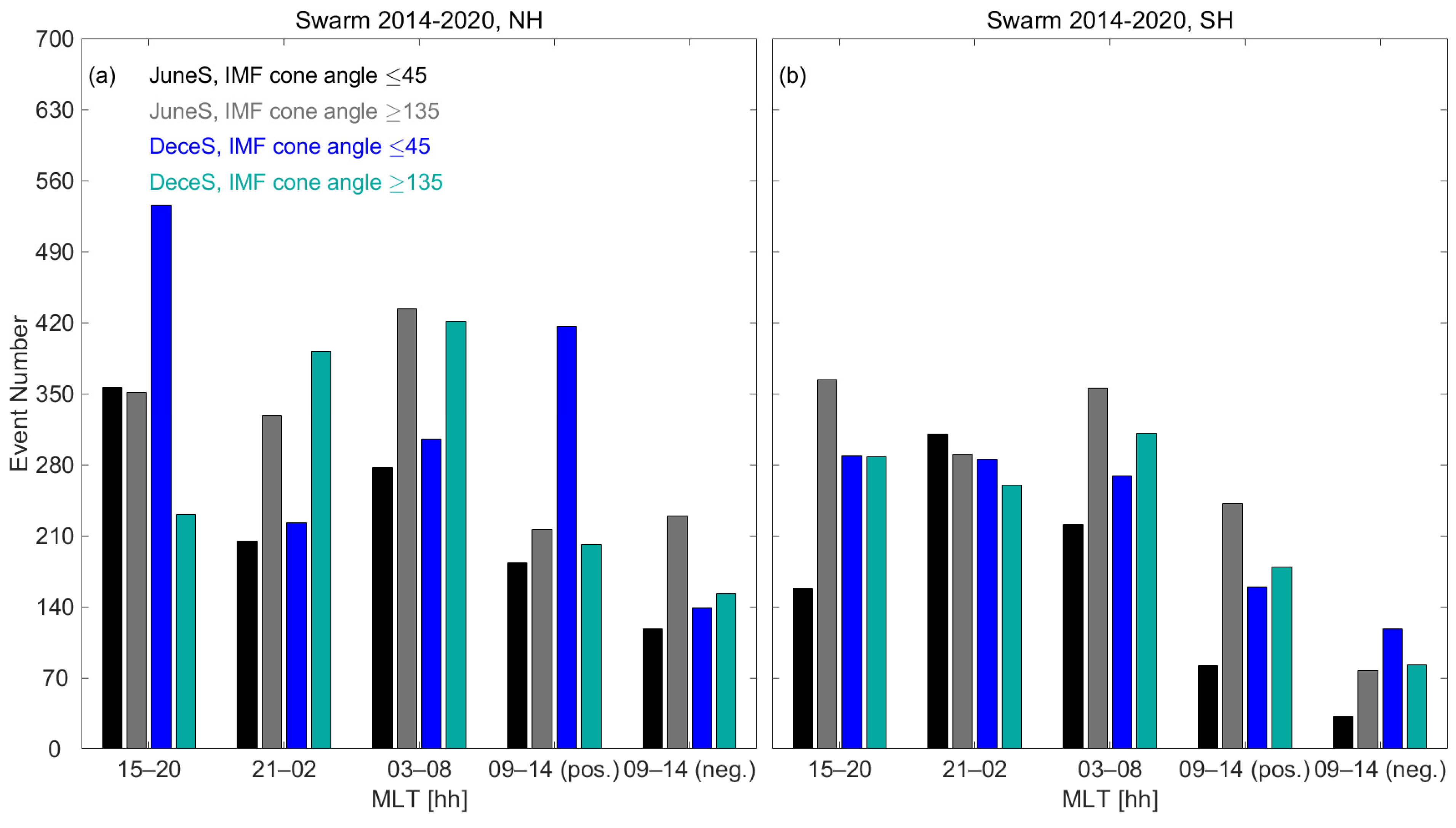
Figure 1 shows the distribution of auroral crossings, categorized by hemisphere, season, and local time. Local time is divided into four distinct intervals, 15–20, 21–02, 03–08, and 09–14 MLT, with each interval spanning six hours, consistent with the methodology described by Wang et al. (2024) [11]. To examine seasonal variation, the data are grouped into two distinct periods: the June solstice (±66 days around 1 July) and the December solstice (±66 days around January 1). The orientation of the PEJ in the 09–14 MLT sector is influenced by IMF By orientation. Consequently, the 09–14 MLT sector is further divided into eastward and westward PEJs (positive and negative PEJs).

There are a higher number of events in the NH, with each local time interval generally containing at least 100 occurrences. In contrast, the SH suffers from significant under-sampling in many high-latitude regions, mainly due to the large displacement of its geomagnetic pole. Such displacement is more pronounced in the SH, where the geographic and geomagnetic poles are more widely separated than in the NH. This spatial difference affects the detection and frequency of FAC events in the SH. However, each MLT sector in the SH still typically records more than 30 events, ensuring adequate statistical reliability for the analysis.

3. Results

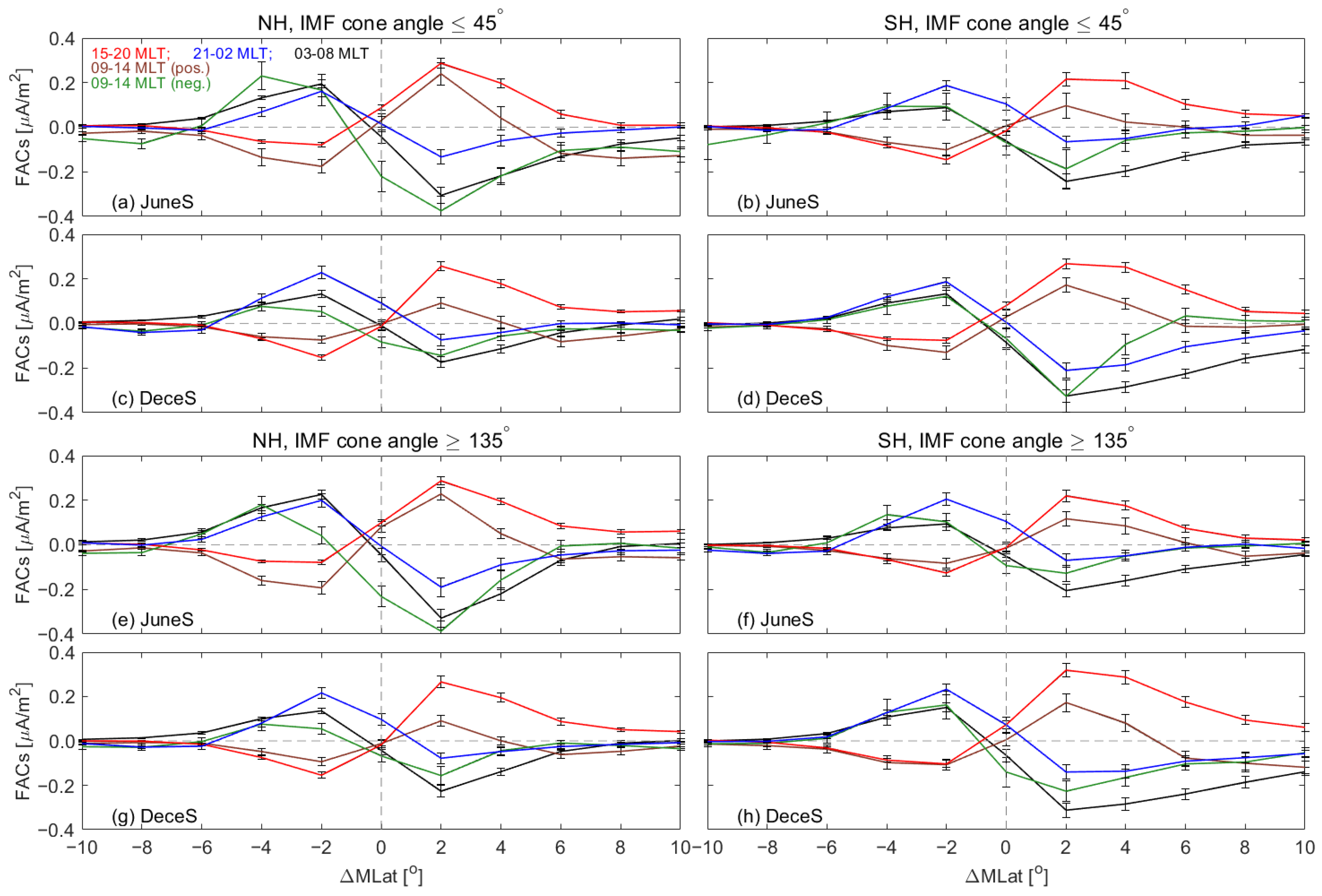
This study utilized the superposed location analysis method to analyze FACs. The FAC data were averaged over a reference latitude range of −10° to 10°, with a 2° ΔMLat bin size. The reference latitude (ΔMLat = 0°) was defined by the location of the peak PEJ, where negative values represent equatorward regions, and positive values represent poleward regions relative to the reference latitude. Figure 2 displays the latitudinal distribution of FACs during periods when the IMF cone angle is ≤45° and ≥135°. Each subfigure contains five colors, which correspond to specific MLT sectors. All data are categorized by season and hemisphere.

In the 15–20 MLT sector, a prominent presence of upward FACs is observed on the polar side of the reference latitude, alongside significant downward FACs on the equatorward side. These observations are consistent with the typical characteristics of R1 and R2 FACs, as well as eastward PEJ currents at dusk. At 21–02 MLT sector, the downward FACs are poleward of the westward PEJ, while the upward FACs are equatorward of it. Typically, three distinct current sheets appear around midnight, closely associated with abrupt changes in the electric field and current direction at the Harang discontinuity. This discontinuity causes the central FACs to flow outward from the ionosphere, while FACs on both sides flow inward, forming this specific current distribution pattern. At the 03–08 MLT sector, typical FACs suggest downward R1 (upward R2) currents centered around the westward PEJ. Meanwhile, at the MLT sector of 09–14, one can observe the midday R1 FACs at lower latitudes and midday R0 FACs at higher latitudes, with the current directions influenced by the orientation of IMF By. Prominent upward or downward R0 FACs and downward or upward R1 FACs co-occur with eastward or westward PEJ, depending on the orientation of IMF By and subsequent PEJ.

In this study, we use the labels FACp for FACs located on the polar side and FACe for those on the equatorial side. This terminology helps to clarify and deepen our understanding of these phenomena. Specifically, FACp denotes R1 FACs, whereas FACe denotes R2 FACs during dusk and dawn. In the MLT sector of 09–14, we use FACp to represent R0 FACs at noon, while FACe represents noontime R1 FACs. In the MLT sector of 21–02, FACp denotes the current entering the ionosphere, whereas FACe denotes the current leaving the ionosphere. This naming scheme enhances our ability to identify and analyze FAC characteristics across different times and locations.

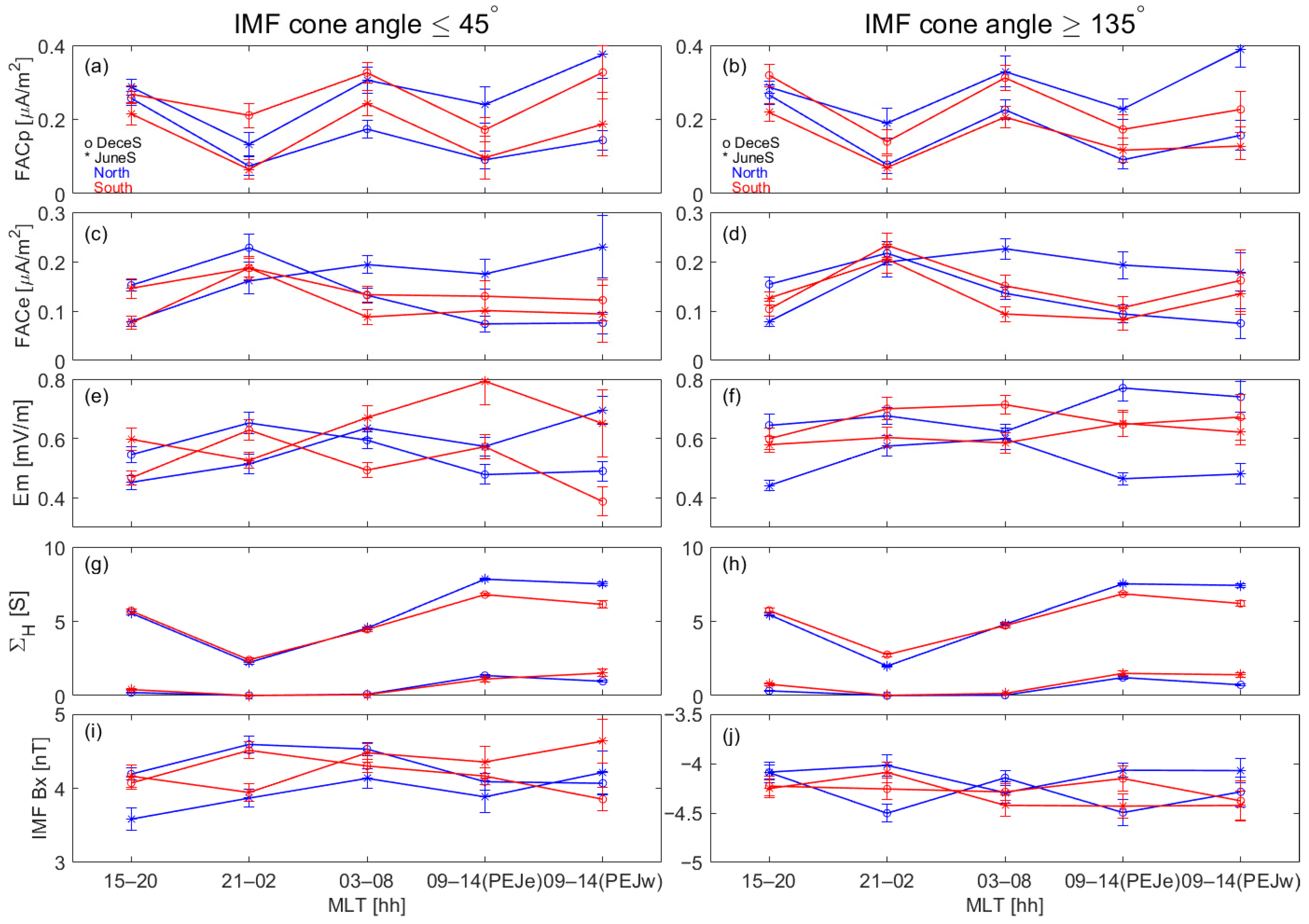
Figure 3 shows the maximum values of FACp and FACe, as observed during the June (marked with asterisks) and December (marked with circles) solstices, for IMF cone angles ≤ 45° and ≥135° across five local time sectors. Additionally, the bottom two panels of Figure 3 present the zonal variations in Em, ionospheric conductivity (Σ_H), and IMF Bx for comparison. The data corresponding to Figure 3 are provided in

Table 1. The data of the absolute peak strengths of FACp, FACe, merging electric field, Em, ionospheric conductivity ΣH, and IMF Bx for an IMF cone angle ≤ 45° across the 15–20 MLT, 21–02 MLT, 03–08 MLT, 09–14 MLT (PEJe), and 09–14 MLT (PEJw) sectors during the JuneS and DeceS in both hemispheres.

Local Time	15–20 MLT				21–02 MLT				03–08 MLT				09–14 MLT (PEJe)				09–14 MLT (PEJw)
Hemisphere	NH		SH		NH		SH		NH		SH		NH		SH		NH		SH
Season	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS
FACp [μA/m2]	0.29	0.26	0.22	0.27	0.13	0.07	0.06	0.21	0.31	0.17	0.24	0.33	0.24	0.09	0.10	0.17	0.38	0.14	0.19	0.33
FACe [μA/m2]	0.08	0.15	0.15	0.08	0.16	0.23	0.19	0.19	0.19	0.13	0.09	0.13	0.18	0.07	0.10	0.13	0.23	0.08	0.09	0.12
Em [mV/m]	0.45	0.55	0.60	0.47	0.51	0.65	0.53	0.63	0.64	0.60	0.67	0.49	0.57	0.48	0.79	0.57	0.70	0.49	0.65	0.39
ΣH [S]	5.55	0.20	0.40	5.70	2.23	0	0	2.41	4.55	0.08	0.06	4.46	7.83	1.35	1.11	6.79	7.50	0.96	1.52	6.12
IMF Bx [nT]	3.58	4.19	4.16	4.07	3.87	4.59	3.94	4.51	4.13	4.52	4.48	4.30	3.89	4.09	4.36	4.17	4.21	4.07	4.64	3.85

and

Table 2. The data of the absolute peak strengths of FACp, FACe, merging electric field, Em, ionospheric conductivity Σ_H, and IMF Bx for an IMF cone angle ≥ 135° across the 15–20 MLT, 21–02 MLT, 03–08 MLT, 09–14 MLT (PEJe) and 09–14 MLT (PEJw) sectors during the JuneS and DeceS in both hemispheres.

Local Time	15–20 MLT				21–02 MLT				03–08 MLT				09–14 MLT (PEJe)				09–14 MLT (PEJw)
Hemisphere	NH		SH		NH		SH		NH		SH		NH		SH		NH		SH
Season	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS	JuneS	DeceS
FACp [μA/m2]	0.29	0.27	0.22	0.32	0.19	0.08	0.07	0.14	0.33	0.23	0.21	0.31	0.23	0.09	0.12	0.17	0.39	0.16	0.13	0.23
FACe [μA/m2]	0.08	0.15	0.13	0.10	0.20	0.22	0.21	0.23	0.23	0.14	0.10	0.15	0.19	0.09	0.08	0.11	0.18	0.07	0.13	0.16
Em [mV/m]	0.44	0.64	0.58	0.60	0.57	0.68	0.60	0.70	0.60	0.62	0.59	0.71	0.46	0.77	0.65	0.65	0.48	0.74	0.62	0.67
ΣH [S]	5.46	0.31	0.76	5.73	1.99	0	0.01	2.75	4.8	0.02	0.14	0.47	7.51	1.21	1.49	6.84	7.41	0.72	1.40	6.19
IMF Bx [nT]	−4.09	−4.09	−4.25	−4.23	−4.02	−4.50	−4.09	−4.26	−4.29	−4.14	−4.42	−4.29	−4.07	−4.50	−4.43	−4.15	−4.07	−4.29	−4.42	−4.38

. For each peak PEJ event, the mean Em and ionospheric Hall conductivity values due to sunlight are calculated [22]. The average value of Em remains below 0.8 mV/m, indicating a relatively quiet study period.

In the dusk sector, as shown in Figure 3a,b, and Table 1 and Table 2, the intensities of FACp during the local summer are higher than those during the local winter. This is mainly due to the ionospheric conductivity effect, as illustrated in Figure 3g,h. The seasonal variation in FACe (Figure 3c,d) shows an opposite trend to the conductivity driven by sunlight but follows a pattern similar to that of Em (Figure 3e,f), suggesting that FACe is more influenced by Em. In the dawn sector, both FACp and FACe are impacted by conductivity, with values larger in summer than in winter (Figure 3a–d). It is notable that the seasonal difference in conductivity is more pronounced than that in the FACs, likely due to the counteracting influence of Em (Figure 3e,f).

In the 21–02 MLT region, the downward FACs (FACp, Figure 3a,b) exhibit significant seasonal fluctuations in two hemispheres, with stronger intensities in summer compared to those in winter. This increase in FACp during summer is primarily due to changes in ionospheric conductivity (Figure 3g,h). Enhanced solar radiation leads to an increase in electron densities, which increases conductivity and, in turn, increases the FACp intensity. This pattern is consistent across both hemispheres, with FACp being stronger during local summer. On the other hand, upward FACs (FACe, Figure 3c,d) show greater intensity in winter than in summer, which may be attributed to energetic particle precipitation effects. According to Newell et al. (1996) [23], high-energy electron precipitation associated with upward FACs can be suppressed at night by solar illumination. This ionospheric feedback effect may reduce the influence of solar radiation on upward FACs during night, a finding also supported by Wang et al. (2005) [4]. In the Southern Hemisphere (SH), the seasonal variation in FACe is relatively small, likely influenced more by changes in ionospheric conductivity due to particle precipitation than by solar illumination alone. In the MLT sector of 09–14, both FACs are notably stronger in summer than in winter (Figure 3a,b). This trend aligns with changes in ionospheric conductivity, indicating that in the midday sector, the intensity of FACs is primarily governed by solar-illuminated conductivity.

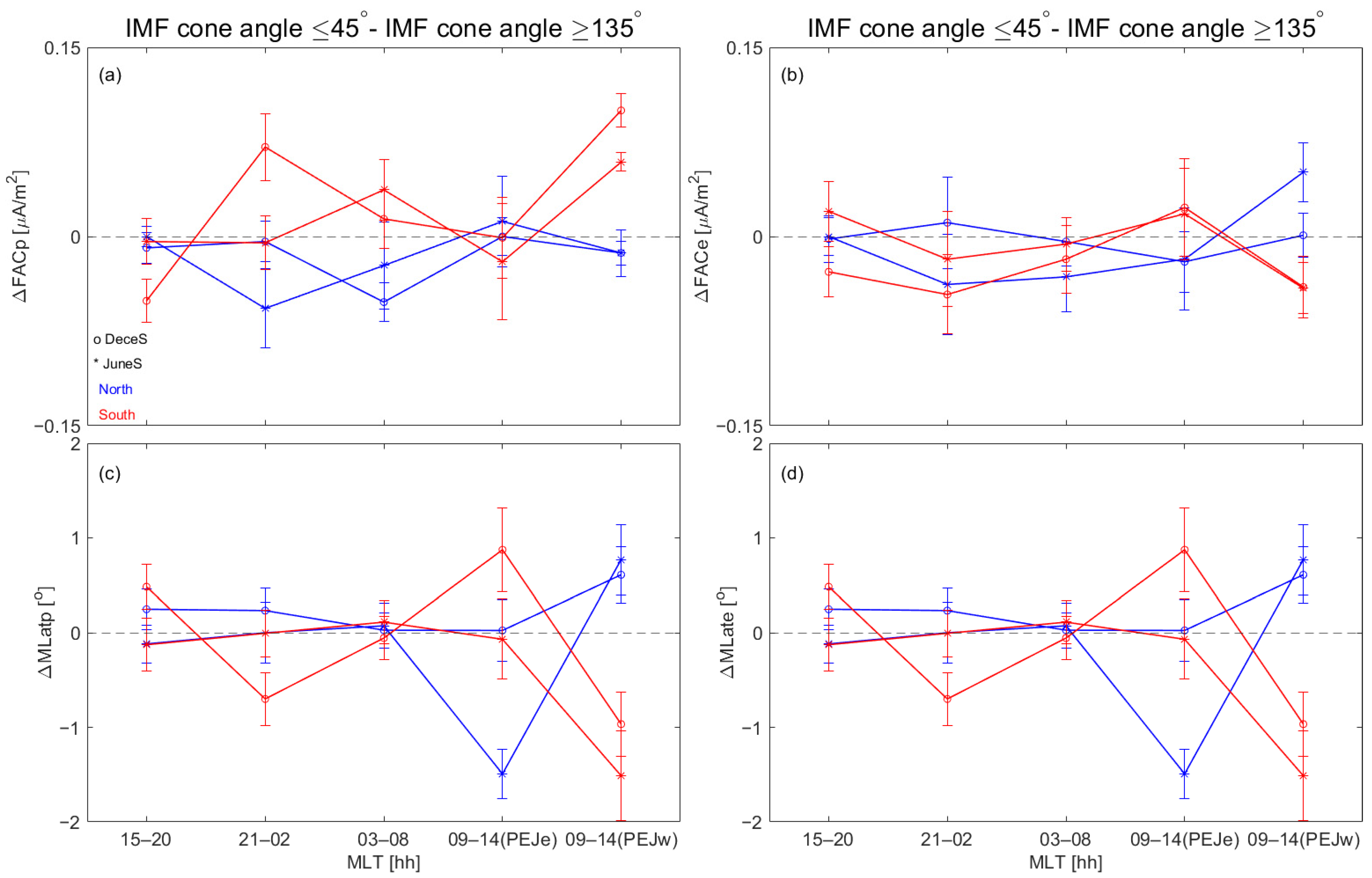
Figure 4 illustrates the differences in FAC strength and latitude between cases where the IMF cone angle is ≤45° and ≥135°. A positive value indicates a stronger current and a higher latitude when the IMF cone angle is ≤45° (i.e., IMF Bx > 0) compared to when the IMF cone angle is ≥135° (i.e., IMF Bx < 0). The June solstice is marked with an asterisk, and the December solstice is marked with a circle. Blue lines represent the Northern Hemisphere, while red lines represent the Southern Hemisphere. In MLT sectors dominated by westward PEJ (MLTs of 21–02, 03–08, and 09–14 with PEJw), the FACp intensity exhibits a stronger dependence on IMF Bx compared to sectors occupied by eastward electrojets (i.e., MLTs of 15–20 and 09–14 with PEJe).

In the 21–02 MLT sector, both FACp and FACe responses are more pronounced during the local summer than the local winter, with FACe showing weaker responses than FACp during the summer. In JuneS, the NH exhibits a larger ∆FACp for IMF cone angles ≥ 135° compared to those ≤45°. Conversely, in DeceS, the SH shows a greater ∆FACp for IMF cone angles ≤ 45° than for those ≥ 135°. In both hemispheres during the local summer, ∆FACe is generally stronger for IMF cone angles ≥ 135° than for those ≤45°.

In the 03–08 MLT sector, the response of FACp is more pronounced during local winter than the summer, while the response of FACe is not significant. In the south, FACp is greater for IMF cone angles ≤ 45° than for angles ≥ 135°, whereas in the NH, FACp is greater for IMF cone angles ≥ 135° than for those ≤45°. At 09–14 MLT, with westward electrojet (PEJw), the SH (NH) FACp shows higher values for IMF cone angles ≤ 45° (≥135°). However, FACe exhibits the opposite response to IMF Bx polarity.

As shown in the bottom panel of Figure 4, the impact of the IMF cone angles on the latitudes of FACs is mainly concentrated around noon and midnight, with smaller effects on the dawn and dusk sides. The changes in MLatp and MLate are quite similar in response to IMF cone angles. In the 09–14 and 21–02 MLT sectors with westward PEJ (PEJw), NH FACs are at a higher latitude for an IMF cone angle ≤ 45° than for an angle ≥ 135°. However, in the noon sector with eastward PEJ (PEJe), when the IMF cone angle ≥ 135°, north FACs tend to be situated at a higher latitude, whereas for an IMF cone angle ≤ 45°, south FACs shift to a higher latitude.

4. Discussion

This study leverages over six years of observational data (2014–2020) from dual Swarm satellites to examine how the polarity of the IMF Bx, as characterized by IMF cone angles, affects the peak density and magnetic latitude of FACs. While previous research has highlighted the significant roles played by IMF By and Bz in shaping the polar current system (e.g., [4,5,6,7,8]), our focus is specifically on isolating the effect of IMF Bx. To minimize the influence of the other IMF components (By and Bz), we select IMF cone angles of ≤45° and ≥135°, which correspond to periods dominated by IMF Bx > 0 and Bx < 0, respectively.

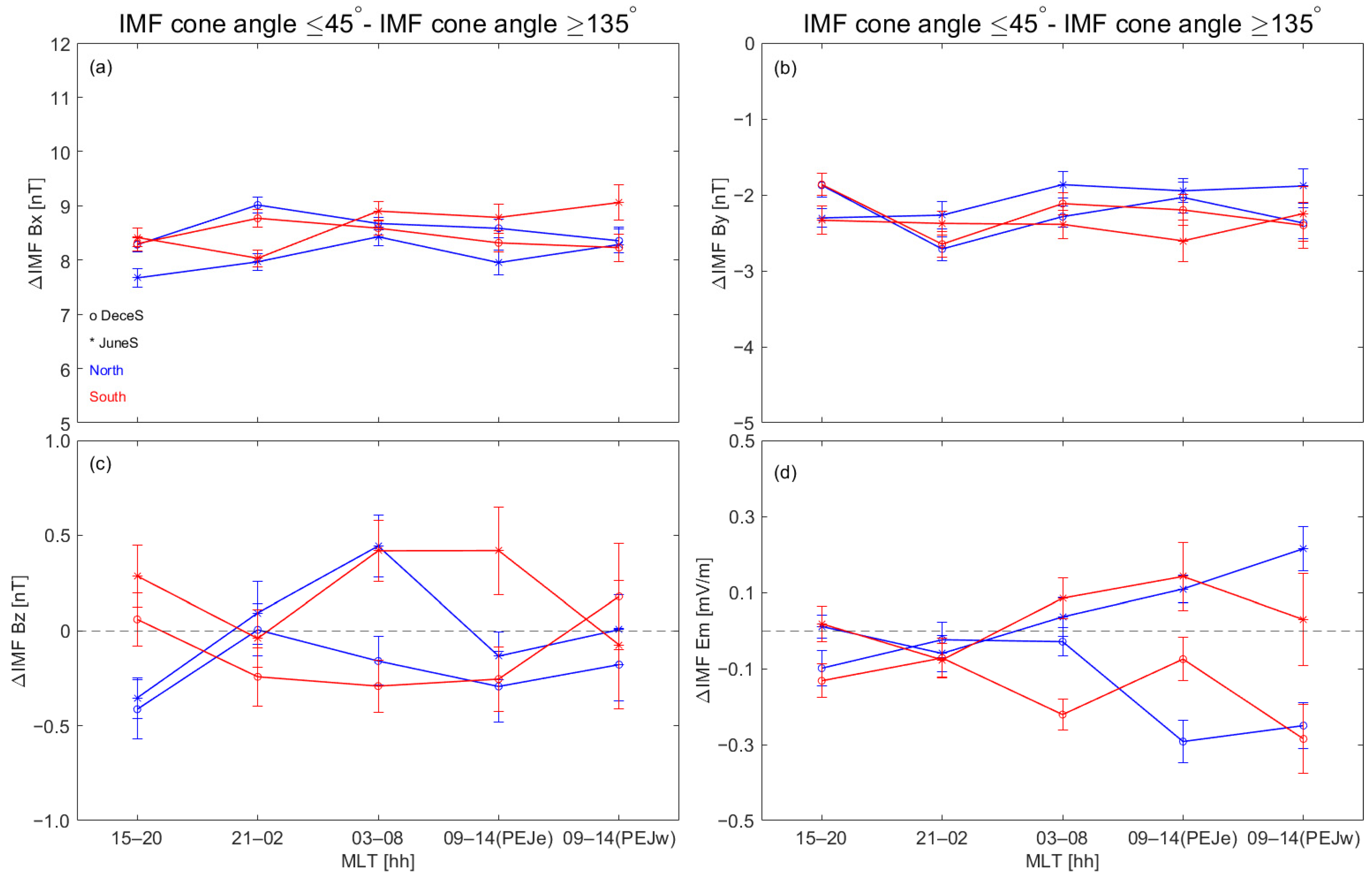
To further validate the effectiveness of this classification method in isolating the influence of IMF Bx, Figure 5 shows the differences in IMF Bx, By, Bz, and Em between the two selected IMF cone angle ranges (≤45° and ≥135°). The results reveal that IMF Bx ranges from 7.5 to 9.5 nT, IMF By ranges from −1.7 to −2.7 nT, IMF Bz remains within a ±0.5 nT range, and Em fluctuates within a ±0.3 mV/m range. The minimal differences in Bz and Em suggest that their effects are negligible and can be disregarded. Holappa et al. (2023) [24] reduced IMF |By| to less than 2 nT to minimize the influence of By, and while the present IMF By slightly exceeds 2.5 nT, it remains less than one-third of the magnitude of IMF Bx. Therefore, the observed variations in current density and latitude are predominantly driven by the influence of IMF Bx.

The influence of IMF Bx on downward FACp in the polar regions is primarily concentrated in the dawn, midnight, and noon sectors, where westward PEJ predominates (as shown in Figure 4). In contrast, its effect on the upward FACp in sectors dominated by eastward PEJ is comparatively weaker. The strong influence of IMF Bx on downward FACp in the dawn and midnight sectors is more apparent and may be attributed to the alignment of IMF Bx in the noon–meridional direction. Our previous study (Wang et al., 2024 [14]) indicated that the polarity of IMF Bx has varying effects on PEJ, with a stronger impact on westward PEJ than on eastward PEJ. For instance, the variations in eastward PEJ in the dawn sector are more pronounced than those in the westward PEJ, and the variations in westward PEJ are greater in the morning sector than in the dusk sector. This pattern is consistent with the observed behavior of FACp. Additionally, our earlier case study (Wang et al., 2014 [2]) showed that when IMF Bx < 0, there is an enhancement of downward FACp in the high-latitude Northern Hemisphere at noon. These results align with those of the present study, further confirming that IMF Bx exerts a significant influence on downward FACp at noon.

The impact of the IMF Bx component on FACp shows a hemispherical difference: in the NH, FAC intensity is greater when IMF Bx < 0, whereas in the SH, FAC intensity is greater when IMF Bx > 0. This hemispheric variation is attributed to magnetic field antiparallel reconnection, where the polarity of IMF Bx significantly influences the reconnection process between the solar wind IMF and the geomagnetic field in the two hemispheres. Previous studies by Cowley (1981) [25] and Reistad et al. (2014) [17] suggest that a negative IMF Bx favors magnetic tail reconnection in the NH, which generates greater magnetic tension on open field lines and enhances magnetospheric boundary currents. In contrast, positive IMF Bx favors reconnection in the SH, thereby enhancing boundary currents in that hemisphere. The resulting increase in magnetospheric electric fields, particularly near noon, can enhance FACp intensity. These findings are consistent with the theoretical background of our research. Laundal et al. (2018) [15] also observed that, under negative Bx conditions, R1 FACs in the NH are stronger, while under positive Bx conditions, R1 FACs in the SH are stronger. These observations align with our results. However, unlike in our study, Laundal et al. did not categorize FACs based on PEJ polarity, nor did they differentiate between FACp and FACe. Moreover, they did not analyze the data across four distinct local time sectors.

The influence of IMF Bx on equatorial FACe is generally weaker compared to its impact on FACp (except in the noon sector, as shown in Figure 4). This difference arises from the distinct sources of FACp and FACe in the magnetosphere. Region 1 currents, located on the polar side, originate at the magnetopause and are more sensitive to the solar wind and IMF, while Region 2 FACs on the equatorward side originate from the inner magnetosphere and are less directly influenced by the solar wind and IMF. During the noon sector, the effect of IMF Bx on FACe is more pronounced than in other local time sectors, but its polarity effect is opposite to that on FACp. In the noon sector, where westward PEJ dominates, FACe in the NH is stronger when IMF Bx < 0, while in the SH, the opposite trend is observed. Wang et al. (2024) [11] found that westward PEJ in the NH is stronger when IMF Bx < 0, while the SH exhibits the opposite IMF Bx polarity dependence. The response of FACe to IMF Bx resembles that of PEJ, which indicates a close relationship between equatorial FACe and PEJ during the noon sector.

The IMF Bx effect on the noontime and midnight PEJs is more obvious in summer, when the ionospheric conductivity is larger due to increased solar illumination. This can be explained by the following scenario: during periods when IMF Bx < 0 (Bx > 0), the reconnection site tends to occur around the northern (southern) magnetotail lobe, facilitating antiparallel reconnection between the earthward (sunward) IMF Bx and the northward geomagnetic field. In summer, the magnetotail shifts closer to the Sun, creating a geomagnetic configuration that favors lobe reconnection.

In comparison to the day–midnight sector, the influence of IMF Bx on FACp at dawn is more pronounced during the local winter than during the local summer. Specifically, throughout winter in the NH, a negative IMF Bx leads to a stronger westward PEJ than a positive IMF Bx. In contrast, throughout winter in the SH, a positive IMF Bx results in a stronger westward PEJ compared to a negative IMF Bx. This discovery corresponds with the research by Kubyshkina et al. (2023) [26], which showed that during NH winter, IMF Bx < 0 enhances the AL index, while IMF Bx > 0 suppresses it under similar driving conditions. Additionally, Tomita et al. (2011) [27] observed that stations within the 00:00–06:00 MLT range most pronouncedly influenced the AL index. Laundal et al. (2018) [15] further revealed that total currents attained their peak levels during the late-night hours between 03:00 and 04:00 MLT, particularly when the IMF pointed southward throughout all seasons. This supports the idea that the wintertime preference of FACp aligns with the AL index peak in the dawn sector.

Kubyshkina et al. (2023) [26] explained that the IMF Bx component can influence the configuration of the nightside magnetosphere, causing the auroral current system to shift northward or southward, depending on whether IMF Bx is negative or positive. Specifically, during periods of significant negative dipole tilt (i.e., NH winter), when the plasma sheet is located beneath its usual position, a negative IMF Bx can induce a shift in the current sheet toward the central plane, restoring symmetry and intensifying auroral activity. A similar effect occurs in the SH winter, characterized by a large positive dipole tilt and IMF Bx > 0. Another factor that explains why IMF Bx primarily affects the dawnside PEJ during winter is its influence on auroral precipitation. According to Shue et al. (2002) [16], auroral power in the NH is greater when IMF Bx is negative compared to when it is positive, while the SH exhibits the opposite trend. This dependence of auroral intensity on IMF Bx was further corroborated by Reistad et al. (2014) [17]. These findings could help to explain why IMF Bx has a stronger impact on PEJ during the local winter than during the local summer.

We also observed that the influence of IMF Bx on the location of FACs is primarily concentrated on the day–night side of the magnetosphere. Specifically, during the noontime and midnight sectors, when the westward auroral electrojet is dominant, FACs are located at higher latitudes in the NH for positive IMF Bx compared to those when it is negative. Conversely, the SH exhibits the opposite trend. For noontime FACs, where the eastward auroral electrojet dominates, this polarity dependence of IMF Bx is reversed. This observation aligns with the latitudinal variation in the auroral electrojet for IMF Bx polarity (Wang et al., 2024 [14]), suggesting that the observed changes in FAC location are linked to shifts in the position of the auroral oval, primarily driven by variations in the site of magnetic reconnection. Tang et al. (2013) [28] reported systematic north–south asymmetries arising from the interaction between specific IMF radial directions and the Earth’s magnetic field configuration. As a result, fluctuations in IMF Bx influence the latitudinal distribution of FACs in the ionosphere by altering the location of magnetic reconnection.

Additionally, we observed a relationship between FAC density and latitude in response to IMF Bx: for a given IMF Bx polarity, stronger FACp appears at lower latitudes. This suggests that when a specific IMF Bx polarity enhances magnetic reconnection, more energy is transferred into geospace, which strengthens FACs, expands the polar cap, and shifts the auroral oval equatorward.

The IMF Bz direction also influences the locations of magnetic reconnection between the Earth’s magnetosphere and IMF. For southward IMF Bz, the reconnection is more likely to occur on the dayside, whereas for IMF Bz > 0, reconnection typically takes place in the magnetotail lobe region. Although FAC strength and latitude vary with different IMF Bz orientations, our study found an increased occurrence of quiet-time FAC events during the observation period. Furthermore, the trend in ∆Em remained consistent (Figure 5d), with Em also reflecting the influence of IMF Bz. As a result, the direction of IMF Bz did not alter the fundamental conclusions of our study.

One can observe that the effect of IMF Bx differs from that of IMF By in terms of local time and seasonal variations. The effect of IMF Bx on FACs density and latitude is most pronounced in the noon–midnight sector and the dawnside, whereas IMF By has a significant influence at all local times. The impact of IMF Bx on FAC density is stronger on the day–night side during summer than in winter, while on the dawnside, it is stronger in winter than in summer. In contrast, the influence of IMF By on FAC density is generally stronger in summer than in winter. These differences primarily stem from distinct physical processes: the effect of IMF By can be attributed to interhemispheric FACs, whereas IMF Bx influences FACs through its regulation of antiparallel reconnection efficiency in the magnetotail lobes.

5. Conclusions

This study examines the impact of the IMF cone angle (i.e., Bx) on the maximum strengths and positions of FACs in both hemispheres, utilizing magnetic field observations of dual Swarm satellites, covering 2004 to 2020. Our results reveal substantial variations in the FAC response to IMF Bx, influenced by local time, season, and hemisphere. The main findings of our study are summarized as follows:

• In the NH, polar-side FACs (FACp) are larger for IMF Bx < 0 compared to those for IMF Bx > 0, whereas the opposite trend is observed in the SH. This IMF Bx effect is most pronounced in the MLT sectors of 03–08, 21–02, and 09–14, when the westward auroral electrojet dominates. During these times, FACp flows downward, while the auroral electrojet flows westward.
• The equatorward FAC (FACe) exhibits a weaker response to IMF Bx than FACp at dawn, dusk, and midnight (21–02 MLT). However, in the 09–14 MLT sector, the response of FACe to IMF Bx is opposite to that of FACp, which aligns with the behavior of the auroral electrojet.
• The influence of IMF Bx on FACs shows distinct seasonal variations. During local summer, the effect is more pronounced around noon and midnight due to higher ionospheric conductivity from solar illumination. In contrast, the Bx effect is stronger around dawn during local winter, influenced by the magnetic field geometry and particle precipitation, both of which are modulated by IMF Bx.
• The impact of IMF Bx on FAC latitude is most pronounced along the noon–midnight meridian. During local times dominated by westward (eastward) auroral electrojets, FACs in the Northern Hemisphere (NH) are positioned at higher latitudes when IMF Bx > 0 (<0) compared to when IMF Bx < 0 (>0). In contrast, the opposite pattern is observed for FACs in the Southern Hemisphere (SH). This behavior is consistent with changes in the latitude of the auroral electrojet.

To our knowledge, FACs have been studied primarily as a function of the IMF Bz and By components; however, the influence of the IMF Bx component has not been thoroughly explored. This study presents compelling satellite observations, demonstrating that the IMF Bx component plays a crucial role in modulating FACs concerning hemisphere, local time, and seasonal variations. It unveils a novel pathway for solar wind energy transfer into the magnetosphere, marking a significant advancement in our understanding of the energy coupling process in geospace.