Early Detection of Water Stress in Kauri Seedlings Using Multitemporal Hyperspectral Indices and Inverted Plant Traits
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Volumetric Water Content and Equivalent Water Thickness Measurement
2.3. Physiological Measurement
2.4. Leaf Hyperspectral Measurement
2.5. Inversion of Leaf-Level Functional Plant Traits (PTs) Derived from the PROSPECT-D Model
2.6. Treatment Differences in Measured and Calculated Variables
2.7. Classification of Control and Drought Treatments Using Random Forest
3. Results
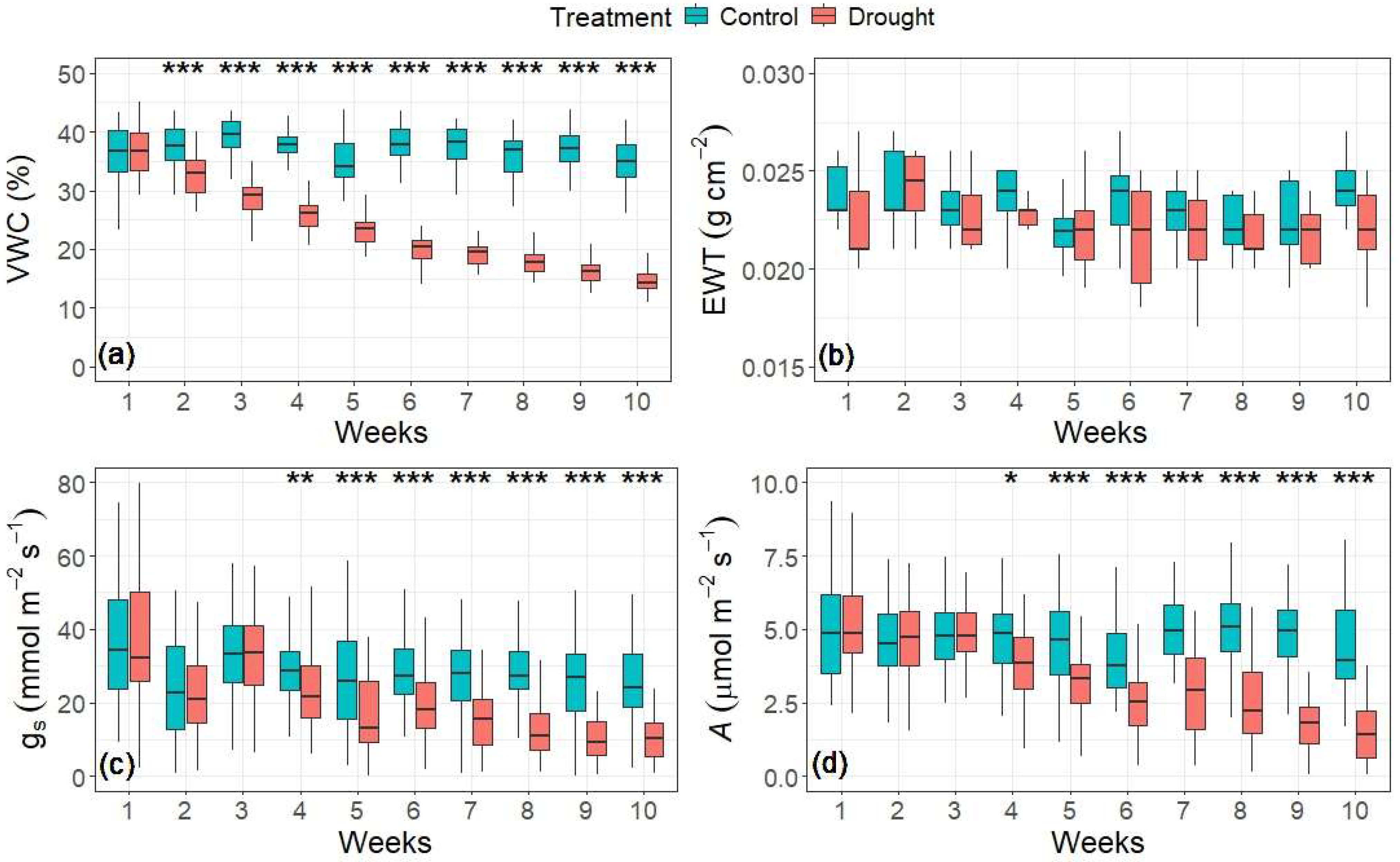
3.1. Changes in Water Content and Tree Physiology
3.2. Variation in Leaf-Level Reflectance
3.3. Differences in NBHIs and PTs Through Time
3.4. Classification of Control and Drought Treatment Using Single-Date and Multitemporal RF Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Index | Index Name | Equation |
|---|---|---|
| Chlorophyll and other photosynthetic pigment indices | ||
| CI | Chlorophyll Index | |
| GM1 | Gitelson and Merzlyak Index 1 | |
| GM2 | Gitelson and Merzlyak Index 2 | |
| MCARI | Mod. Chl. Absorp. Rfl. Index | |
| PSSRb | Pig. Spec. Simpl. Ratio Chl. b | |
| TCARI | Transf. Chl. Absorp. Rfl. Index | |
| VOG | Vogelmann Index | |
| Structural Indices | ||
| NDVI | Normalized Difference Vegetation Index | |
| OSAVI | Opt. Soil-Adjusted Veg. Index | |
| RDVI | Renormalized Diff. Veg. Index | |
| Physiological/Photochemical index | ||
| PRI | Photochemical Reflectance Index | |
| MPRI | Mod Photochemical Reflectance Index | |
| Water indices | ||
| Datt1 | Datt1 | |
| Datt2 | Datt2 | |
| DDI | Double Difference Index | |
| fWBI | Floating Position Water Band Index | |
| GVMI | Global Vegetation Moisture Index | |
| LWI | Leaf Water Index | |
| MSI | Moisture Stress Index | |
| MSI1 | Moisture Stress Index 1 | |
| MSI2 | Moisture Stress Index 2 | |
| NDII | Normalized Difference Infrared Index | |
| NDWI1 | Normalized Difference Water Index 1 | |
| NDWI2 | Normalized Difference Water Index 2 | |
| NDWI3 | Norm. Diff. Water Index 1640 nm | |
| NDWI4 | Norm. Diff. Water Index 2130 nm | |
| SIWSI | Shortwave Infrared Water Stress Index | |
| SRWI | Simple Ratio Water Index | |
| SRWI1 | Simple Ratio Water Index 1 | |
| SRWI2 | Simple Ratio Water Index 2 | |
| TM57 | Ratio of Thematic Mapper B5 to B7 | |
| WBI | Water Band Index | |
| WEEK | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| INDEX TYPE | Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Chlorophyll Indices | CI | 0.4801 | 0.1455 | 0.396 | 0.1465 | 0.2281 | 0.20939 | 0.05195 | 0.1214 | 0.04052 | 0.0272 |
| GM1 | 0.6098 | 0.4677 | 0.9466 | 0.7344 | 0.995 | 0.94677 | 0.57595 | 0.42301 | 0.30706 | 0.40718 | |
| GM2 | 0.5011 | 0.1146 | 0.351 | 0.1347 | 0.2176 | 0.19623 | 0.04358 | 0.07838 | 0.02335 | 0.014 | |
| MCARI | 0.2698 | 0.6146 | 0.3598 | 0.7649 | 0.491 | 0.76066 | 0.97133 | 0.17925 | 0.41289 | 0.80623 | |
| TCARI | 0.2698 | 0.6146 | 0.3598 | 0.7649 | 0.491 | 0.76066 | 0.97133 | 0.17925 | 0.41289 | 0.80623 | |
| PSSRb | 0.5161 | 0.105 | 0.2952 | 0.1208 | 0.2 | 0.14898 | 0.02055 | 0.01556 | 0.00251 | 0.00184 | |
| VOG | 0.4604 | 0.1661 | 0.412 | 0.1477 | 0.2306 | 0.21026 | 0.05493 | 0.14686 | 0.05324 | 0.03797 | |
| Structural Indices | NDVI | 0.526 | 0.0508 | 0.0392 | 0.0487 | 0.1172 | 0.06827 | 0.00691 | 0.00182 | 0.00051 | 0.00179 |
| OSAVI | 0.5267 | 0.0509 | 0.0394 | 0.0488 | 0.1174 | 0.06861 | 0.00694 | 0.00183 | 0.00052 | 0.00181 | |
| RDVI | 0.743 | 0.0937 | 0.1237 | 0.1134 | 0.212 | 0.21997 | 0.02804 | 0.01211 | 0.00428 | 0.02006 | |
| Photochemical Indices | PRI | 0.6404 | 0.5113 | 0.2709 | 0.2168 | 0.1607 | 0.0726 | 0.08885 | 0.15148 | 0.08869 | 0.03136 |
| MPRI | 0.6895 | 0.243 | 0.2181 | 0.1738 | 0.4197 | 0.21594 | 0.15159 | 0.12511 | 0.16824 | 0.11244 | |
| Water Indices | Datt1 | 0.0909 | 0.0694 | 0.1308 | 0.0126 | 0.014 | 0.01027 | 0.0002 | 0.00026 | 0.0005 | 0.00008 |
| Datt2 | 0.1039 | 0.096 | 0.2112 | 0.0203 | 0.0283 | 0.01896 | 0.00042 | 0.00031 | 0.00083 | 0.00011 | |
| DDI | 0.2813 | 0.142 | 0.3013 | 0.0431 | 0.0521 | 0.10009 | 0.00237 | 0.00264 | 0.00299 | 0.00101 | |
| fWBI | 0.4587 | 0.5875 | 0.1977 | 0.2459 | 0.1919 | 0.2919 | 0.01328 | 0.00144 | 0.06414 | 0.01223 | |
| GVMI | 0.0973 | 0.1092 | 0.1812 | 0.0105 | 0.0177 | 0.01332 | 0.0002 | 0.00006 | 0.00022 | 0.00004 | |
| LWI | 0.0422 | 0.1132 | 0.0385 | 0.0035 | 0.0147 | 0.0134 | 0.00047 | 0.00006 | 0.00038 | 0.00006 | |
| MSI | 0.102 | 0.1137 | 0.181 | 0.0107 | 0.0173 | 0.01331 | 0.00019 | 0.00006 | 0.00027 | 0.00006 | |
| MSI1 | 0.0746 | 0.0488 | 0.1979 | 0.0117 | 0.0343 | 0.01463 | 0.00024 | 0.00016 | 0.00014 | 0.00003 | |
| MSI2 | 0.1131 | 0.2585 | 0.1332 | 0.1218 | 0.1901 | 0.0842 | 0.01546 | 0.006 | 0.01597 | 0.00095 | |
| NDII | 0.0974 | 0.1093 | 0.1815 | 0.0105 | 0.0177 | 0.01335 | 0.0002 | 0.00006 | 0.00022 | 0.00004 | |
| NDWI1 | 0.3208 | 0.8172 | 0.851 | 0.2957 | 0.3289 | 0.09196 | 0.02215 | 0.00054 | 0.00885 | 0.00227 | |
| NDWI2 | 0.3431 | 0.8297 | 0.8532 | 0.3116 | 0.3259 | 0.09684 | 0.02669 | 0.00052 | 0.00866 | 0.00205 | |
| NDWI3 | 0.0987 | 0.1012 | 0.2399 | 0.0138 | 0.0311 | 0.01569 | 0.00028 | 0.00009 | 0.00023 | 0.00004 | |
| NDWI4 | 0.0474 | 0.0554 | 0.0708 | 0.0035 | 0.0087 | 0.0047 | 0.00007 | 0.00003 | 0.00011 | 0.00005 | |
| SIWSI | 0.0981 | 0.1011 | 0.2434 | 0.0141 | 0.0318 | 0.01584 | 0.0003 | 0.00009 | 0.00023 | 0.00004 | |
| SRWI | 0.3186 | 0.8098 | 0.8471 | 0.2958 | 0.326 | 0.0909 | 0.02254 | 0.00052 | 0.00871 | 0.00215 | |
| SRWI1 | 0.1785 | 0.4434 | 0.4194 | 0.0963 | 0.1502 | 0.05513 | 0.00381 | 0.00033 | 0.00382 | 0.00072 | |
| SRWI2 | 0.345 | 0.8009 | 0.8422 | 0.2923 | 0.3194 | 0.09167 | 0.02312 | 0.0005 | 0.00737 | 0.00169 | |
| TM57 | 0.0628 | 0.0653 | 0.0472 | 0.0057 | 0.011 | 0.00608 | 0.00011 | 0.00006 | 0.00019 | 0.00001 | |
| WBI | 0.5335 | 0.7006 | 0.2154 | 0.3613 | 0.3133 | 0.23663 | 0.02099 | 0.00273 | 0.10297 | 0.01816 | |
| INVERTED PLANT TRAITS | Cab | 0.415695 | 0.078412 | 0.12309 | 0.063679 | 0.147018 | 0.06717 | 0.011308 | 0.015496 | 0.003419 | 0.001288 |
| Car | 0.99467 | 0.499625 | 0.860499 | 0.635363 | 0.741383 | 0.790402 | 0.277473 | 0.097396 | 0.163481 | 0.095901 | |
| Ant | 0.664819 | 0.610147 | 0.972304 | 0.828026 | 0.9765 | 0.980957 | 0.750306 | 0.616734 | 0.462438 | 0.613397 | |
| EWTinv | 0.042279 | 0.148637 | 0.047829 | 0.007979 | 0.017504 | 0.002867 | 0.000538 | 0.000282 | 0.000746 | 3.41 × 10−6 | |
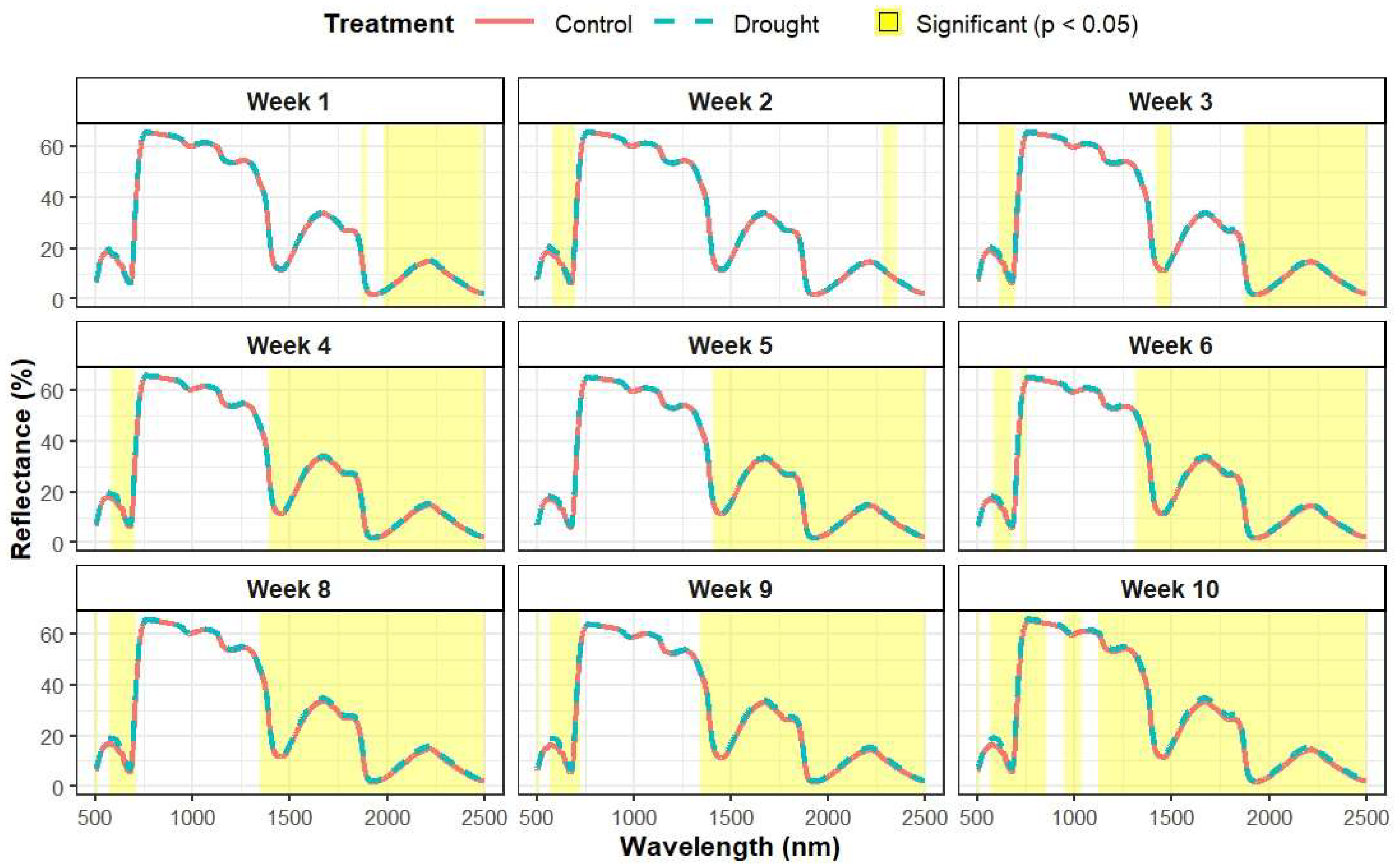
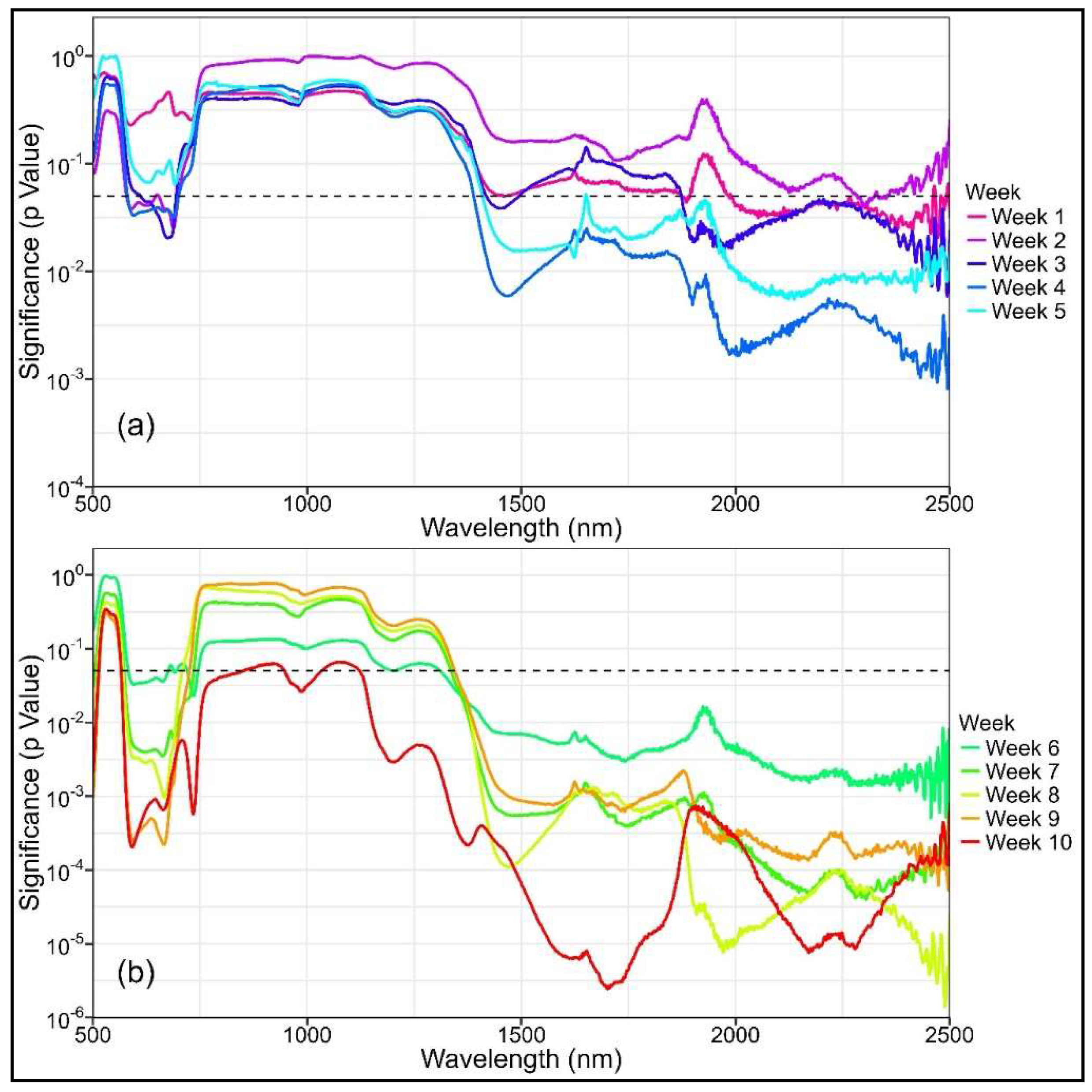

References
- Steward, G.A.; Beveridge, A.E. A review of New Zealand kauri (Agathis australis (D. Don) Lindl.): Its ecology, history, growth and potential for management for timber. N. Z. J. For. Sci. 2010, 40, 33–59. [Google Scholar]
- Wardle, D.A. Communities and Ecosystems: Linking the Aboveground and Belowground Components; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Craig, R.; Taonui, R.; Wild, S. The concept of taonga in Māori culture: Insights for accounting. Account. Audit. Account. J. 2012, 25, 1025–1047. [Google Scholar] [CrossRef]
- McDowell, N.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G.; et al. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? New Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Beever, R.E.; Waipara, N.W.; Ramsfield, T.D.; Dick, M.A.; Horner, I.J. Kauri (Agathis australis) under threat from Phytophthora? Phytophthoras For. Nat. Ecosyst. 2009, 74, 74–85. [Google Scholar]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.T.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Jactel, H.; Petit, J.; Desprez-Loustau, M.L.; Delzon, S.; Piou, D.; Battisti, A.; Koricheva, J. Drought effects on damage by forest insects and pathogens: A meta-analysis. Glob. Change Biol. 2012, 18, 267–276. [Google Scholar] [CrossRef]
- Seidl, R.; Schelhaas, M.J.; Lexer, M.J. Unraveling the drivers of intensifying forest disturbance regimes in Europe. Glob. Change Biol. 2011, 17, 2842–2852. [Google Scholar] [CrossRef]
- Carter, G.A.; Knapp, A.K. Leaf optical properties in higher plants: Linking spectral characteristics to stress and chlorophyll concentration. Am. J. Bot. 2005, 88, 677–684. [Google Scholar] [CrossRef]
- Meiforth, J.J.; Buddenbaum, H.; Hill, J.; Shepherd, J.D.; Dymond, J.R. Stress Detection in New Zealand Kauri Canopies with WorldView-2 Satellite and LiDAR Data. Remote Sens. 2020, 12, 1906. [Google Scholar] [CrossRef]
- Meiforth, J.J.; Buddenbaum, H.; Hill, J.; Shepherd, J. Monitoring of Canopy Stress Symptoms in New Zealand Kauri Trees Analysed with AISA Hyperspectral Data. Remote Sens. 2020, 12, 926. [Google Scholar] [CrossRef]
- Watt, M.S.; Buddenbaum, H.; Leonardo, E.M.C.; Estarija, H.J.; Bown, H.E.; Gomez-Gallego, M.; Hartley, R.J.L.; Pearse, G.D.; Massam, P.; Wright, L.; et al. Monitoring biochemical limitations to photosynthesis in N and P-limited radiata pine using plant functional traits quantified from hyperspectral imagery. Remote Sens. Environ. 2020, 248, 112003. [Google Scholar] [CrossRef]
- Watt, M.S.; Bartlett, M.; Soewarto, J.; de Silva, D.; Estarija, H.J.C.; Massam, P.; Cajes, D.; Yorston, W.; Graevskaya, E.; Dobbie, K. Previsual and early detection of myrtle rust on rose apple using indices derived from thermal imagery and visible-to-short-infrared spectroscopy. Phytopathology 2023, 113, 1405–1416. [Google Scholar] [CrossRef] [PubMed]
- Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Hyperspectral remote sensing of photosynthetic pigment concentrations and photosynthetic efficiency in stressed crops. Remote Sens. Environ. 2018, 113, 38–54. [Google Scholar]
- Hernández-Clemente, R.; Hornero, A.; Mottus, M.; Penuelas, J.; González-Dugo, V.; Jiménez, J.C.; Suárez, L.; Alonso, L.; Zarco-Tejada, P.J. Early Diagnosis of Vegetation Health From High-Resolution Hyperspectral and Thermal Imagery: Lessons Learned From Empirical Relationships and Radiative Transfer Modelling. Curr. For. Rep. 2019, 5, 169–183. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Okyere, F.G.; Cudjoe, D.K.; Virlet, N.; Castle, M.; Riche, A.B.; Greche, L.; Mohareb, F.; Simms, D.; Mhada, M.; Hawkesford, M.J. Hyperspectral Imaging for Phenotyping Plant Drought Stress and Nitrogen Interactions Using Multivariate Modeling and Machine Learning Techniques in Wheat. Remote Sens. 2024, 16, 3446. [Google Scholar] [CrossRef]
- Homolová, L.; Malenovský, Z.; Clevers, J.G.P.W.; García-Santos, G.; Schaepman, M.E. Review of optical-based remote sensing for plant trait mapping. Ecol. Complex. 2013, 15, 1–16. [Google Scholar] [CrossRef]
- Cranston, B.M.; Powers, B.F.; Macinnis-Ng, C. Inexpensive Throughfall Exclusion Experiment for Single Large Trees. Appl. Plant Sci. 2020, 8, e11325. [Google Scholar] [CrossRef]
- Rhodes, G.G. Physiological Responses of Three Native Plants to Drought and Heatwave. Master Thesis, The University of Auckland, Auckland, New Zealand, 2024. Available online: https://hdl.handle.net/2292/68823 (accessed on 5 November 2024).
- Jones, H.G. Stomatal control of photosynthesis and transpiration. J. Exp. Bot. 1998, 49, 387–398. [Google Scholar] [CrossRef]
- Flexas, J.; Medrano, H. Drought-inhibition of photosynthesis in C3 plants: Stomatal and non-stomatal limitations revisited. Ann. Bot. 2002, 89, 183–189. [Google Scholar] [CrossRef] [PubMed]
- Macinnis-Ng, C.; Webb, T.; Lin, Y.S.; Schwendenmann, L.; Medlyn, B. Leaf age-related and diurnal variation in gas exchange of kauri (Agathis australis). N. Z. J. Bot. 2016, 55, 80–99. [Google Scholar] [CrossRef]
- Féret, J.-B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Féret, J.B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing spectral indices and chemometric analysis of leaf chemical properties using radiative transfer modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef]
- Watt, M.S.; Estarija, H.J.C.; Bartlett, M.; Main, R.; Pasquini, D.; Yorston, W.; McLay, E.; Zhulanov, M.; Dobbie, K.; Wardhaugh, K.; et al. Early Detection of Myrtle Rust on Pōhutukawa Using Indices Derived from Hyperspectral and Thermal Imagery. Remote Sens. 2024, 16, 1050. [Google Scholar] [CrossRef]
- Wyse, S.V.; Macinnis-Ng, C.; Burns, B.R.; Clearwater, M.J.; Schwendenmann, L. Species assemblage patterns around a dominant emergent tree are associated with drought resistance. Tree Physiol. 2013, 33, 1269–1283. [Google Scholar] [CrossRef]
- Jones, H.G.; Higgs, K.H. Water Potential—Water Content Relationships In Apple Leaves. J. Exp. Bot. 1979, 30, 965–970. Available online: http://www.jstor.org/stable/23688948 (accessed on 5 November 2024). [CrossRef]
- Duursma, R.A.; Blackman, C.J.; Lopéz, R.; Martin-StPaul, N.K.; Cochard, H.; Medlyn, B.E. On the Minimum Leaf Conductance: Its Role in Models of Plant Water Use, and Ecological and Environmental Controls. New Phytol. 2019, 221, 693–705. [Google Scholar] [CrossRef]
- Emmerichs, T.; Lu, Y.-S.; Taraborrelli, D. The influence of plant water stress on vegetation–atmosphere exchanges: Implications for ozone modelling. Atmos. Chem. Phys. 2021, 21, 16419–16441. [Google Scholar] [CrossRef]
- Stephens, D.W.; Silvester, W.B.; Burns, B.R. Differences in water-use efficiency between Agathis australis and Dacrycarpus dacrydioides are genetically, not environmentally, determined. N. Z. J. Bot. 1999, 37, 361–367. [Google Scholar] [CrossRef]
- Ripullone, F.; Grassi, G.; Lauteri, M.; Borghetti, M. Photosynthesis–nitrogen relationships: Interpretation of different patterns between Pseudotsuga menziesii and Populus x euroamericana in a mini-stand experiment. Tree Physiol. 2003, 23, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Devi, A.S. Influence of trees and associated variables on soil organic carbon: A review. J. Ecol. Environ. 2021, 45, 5. [Google Scholar] [CrossRef]
- Vélez, S.; Martínez-Peña, R.; Castrillo, D. Beyond Vegetation: A Review Unveiling Additional Insights into Agriculture and Forestry through the Application of Vegetation Indices. J 2023, 6, 421–436. [Google Scholar] [CrossRef]
- Lo, A.; Chernoff, H.; Zheng, T.; Lo, S.H. Why significant variables aren't automatically good predictors. Proc. Natl. Acad. Sci. USA 2015, 112, 13892–13897. [Google Scholar] [CrossRef]
- Yu, S.; Fan, J.; Lu, X.; Wen, W.; Shao, S.; Liang, D.; Yang, X.; Guo, X.; Zhao, C. Deep learning models based on hyperspectral data and time-series phenotypes for predicting quality attributes in lettuces under water stress. Comput. Electron. Agric. 2023, 211, 108034. [Google Scholar] [CrossRef]
- Das Choudhury, S.; Saha, S.; Samal, A.; Mazis, A.; Awada, T. Drought stress prediction and propagation using time series modeling on multimodal plant image sequences. Front. Plant Sci. 2023, 14, 1003150. [Google Scholar] [CrossRef]
- Dao, P.D.; He, Y.; Proctor, C. Plant drought impact detection using ultra-high spatial resolution hyperspectral images and machine learning. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102364. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies: A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Peñuelas, J.; Garbulsky, M.F.; Filella, I. Photochemical reflectance index (PRI) and remote sensing of plant CO2 uptake. New Phytol. 2011, 191, 596–599. [Google Scholar] [CrossRef]
- Wong, C.Y.S.; Gamon, J.A. The photochemical reflectance index provides an optical indicator of spring photosynthetic activation in evergreen conifers. New Phytol. 2015, 206, 196–208. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.Y.S.; Gamon, J.A. Three causes of variation in the photochemical reflectance index (PRI) in evergreen conifers. New Phytol. 2015, 206, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Gamon, J.A.; Huemmrich, K.F.; Wong, C.Y.S.; Ensminger, I.; Garrity, S.; Hollinger, D.Y.; Noormets, A.; Peñuelas, J. A remotely sensed pigment index reveals photosynthetic phenology in evergreen conifers. Proc. Natl. Acad. Sci. USA 2016, 113, 13087–13092. [Google Scholar] [CrossRef] [PubMed]
- Anderegg, W.R.L.; Kane, J.M.; Anderegg, L.D.L. Consequences of widespread tree mortality triggered by drought and temperature stress. Nat. Clim. Change 2013, 3, 30–36. [Google Scholar] [CrossRef]
- Choat, B.; Brodribb, T.J.; Brodersen, C.R.; Duursma, R.A.; López, R.; Medlyn, B.E. Triggers of tree mortality under drought. Nature 2018, 558, 531–539. [Google Scholar] [CrossRef]

| Random Forest (RF) Model | Input Features | |
|---|---|---|
| Single-Date (SD) | SD-RF1 | all NBHIs |
| SD-RF2 | all NBHIs + PTs | |
| Multitemporal (M) | M-RF1 | all NBHIs |
| M-RF2 | all NBHIs + PTs | |
| M-RF3 | VNIR NBHIs only + PTs | |
| M-RF4 | SWIR NBHIs only + PTs | |
| F1 Score | ||||||
|---|---|---|---|---|---|---|
| Single-Date (SD) | Multitemporal (M) | |||||
| Week | SD-RF1 | SD-RF2 | M-RF1 | M-RF2 | M-RF3 | M-RF4 |
| 1 | 0.58 | 0.58 | 0.57 | 0.56 | 0.60 | 0.56 |
| 2 | 0.58 | 0.60 | 0.66 | 0.69 | 0.76 | 0.68 |
| 3 | 0.62 | 0.62 | 0.78 | 0.79 | 0.8 | 0.73 |
| 4 | 0.63 | 0.62 | 0.8 | 0.79 | 0.81 | 0.76 |
| 5 | 0.61 | 0.6 | 0.84 | 0.83 | 0.81 | 0.78 |
| 6 | 0.57 | 0.62 | 0.86 | 0.86 | 0.81 | 0.83 |
| 7 | 0.64 | 0.62 | 0.87 | 0.88 | 0.85 | 0.85 |
| 8 | 0.64 | 0.64 | 0.86 | 0.90 | 0.88 | 0.84 |
| 9 | 0.70 | 0.71 | 0.87 | 0.87 | 0.85 | 0.85 |
| 10 | 0.67 | 0.71 | 0.83 | 0.86 | 0.86 | 0.81 |
| LEGEND: | 0.7 < F1 score ≤ 0.8 | 0.8 < F1 score ≤ 0.9 | 0.9 < F1 score | |||
| (Good/Satisfactory) | (Excellent) | (Outstanding) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Felix, M.J.B.; Main, R.; Watt, M.S.; Arpanaei, M.-M.; Patuawa, T. Early Detection of Water Stress in Kauri Seedlings Using Multitemporal Hyperspectral Indices and Inverted Plant Traits. Remote Sens. 2025, 17, 463. https://doi.org/10.3390/rs17030463
Felix MJB, Main R, Watt MS, Arpanaei M-M, Patuawa T. Early Detection of Water Stress in Kauri Seedlings Using Multitemporal Hyperspectral Indices and Inverted Plant Traits. Remote Sensing. 2025; 17(3):463. https://doi.org/10.3390/rs17030463
Chicago/Turabian StyleFelix, Mark Jayson B., Russell Main, Michael S. Watt, Mohammad-Mahdi Arpanaei, and Taoho Patuawa. 2025. "Early Detection of Water Stress in Kauri Seedlings Using Multitemporal Hyperspectral Indices and Inverted Plant Traits" Remote Sensing 17, no. 3: 463. https://doi.org/10.3390/rs17030463
APA StyleFelix, M. J. B., Main, R., Watt, M. S., Arpanaei, M.-M., & Patuawa, T. (2025). Early Detection of Water Stress in Kauri Seedlings Using Multitemporal Hyperspectral Indices and Inverted Plant Traits. Remote Sensing, 17(3), 463. https://doi.org/10.3390/rs17030463






