Correction Method for Amplitude and Phase Errors Based on the h Function in 1-D Mirrored Aperture Synthesis Aimed at Geostationary Atmospheric Observation

Highlights

What are the main findings?

• This paper proposes a correction method for amplitude and phase errors based on the h function for 1-D mirrored aperture synthesis (1-D MAS).
• The proposed method does not require removing the reflector. Moreover, the proposed method is insensitive to the spatial offset of the h function.

What are the implications of the main findings?

• The proposed error information extraction framework based on the h function provides a basis for the future analysis and correction of the reflector position error, which is unique to MAS.
• The proposed correction method does not require reflector removal, thereby avoiding additional mechanical structures. Furthermore, it eliminates the strong dependence on precise position of the external source in the existing correction method, thereby enhancing the adaptability of correction method in practical observations.

Abstract

In passive microwave remote sensing, mirrored aperture synthesis (MAS) demonstrates significant potential for atmospheric observation from geostationary orbit. The amplitude and phase errors are among the key factors that degrade image reconstruction quality. The existing correction method requires additional mechanical structures to remove the reflector, thereby increasing system complexity. The method also requires that the external source used to extract error information be placed exactly at a specific location, which reduces the adaptability of the method and is difficult to achieve in practice. In this paper, an amplitude and phase error model based on the h function is established. Based on the error model, a new correction method for the amplitude and phase errors is proposed. The method uses the h function without errors as prior knowledge to extract error information. According to the extracted error information, the amplitude and phase errors are corrected. The proposed method does not require removing the reflector and is insensitive to the spatial offset of the h function. Simulation results show that the proposed method reduces the RMSE for an extended source from 162 K to 3.9 × 10⁻⁷ K . Experimental validation with a ceramic plate scene (extended source) further confirms its effectiveness, where the SSIM improves from –0.23 to 0.96 after correction, even under offset conditions. These results demonstrate the effectiveness and robustness of the proposed method.

1. Introduction

Atmospheric observations from geostationary orbit are of great significance for monitoring severe weather events such as deep convection and typhoons [1]. Currently, radiometers onboard geostationary satellites are primarily visible and infrared instruments, such as the Advanced Baseline Imager (ABI) [2], the Advanced Geostationary Radiation Imager (AGRI) [3], the Geostationary Interferometric Infrared Sounder (GIIRS) [4], and the Infrared Sounder (IRS) [5]. However, visible and infrared radiometers are highly susceptible to cloud and precipitation interference, which results in a lack of all-weather observation capability. Compared to visible and infrared sensing, microwaves can penetrate clouds, fog, and precipitation; thus, microwave radiometers have the characteristic of all-weather operation [6,7]. This capability makes microwave radiometers play an important role in environmental monitoring and data assimilation in numerical weather prediction models [8]. Nevertheless, microwave radiometers generally suffer from lower spatial resolution, making it difficult to meet spatial resolution requirement ($\le$50 km) for geostationary atmospheric observations. Consequently, no microwave radiometers are currently deployed in geostationary orbit.

To improve the spatial resolution of microwave radiometers and enable their deployment on geostationary satellites, various techniques have been proposed. Based on their operational principles, these techniques can be classified into two categories: real aperture and aperture synthesis. Projects that employ the real aperture technique are represented by the Geosynchronous Microwave sounder/imager (GEM) [9] and the Geostationary Observatory for Microwave Atmospheric Sounding (GOMAS) [10]. However, both projects rely on large antennas to achieve high spatial resolution. For example, the conceptual design of GEM employs a 2-m Cassegrain scanning antenna [9], while GOMAS is designed to use a 3-m antenna [10]. Such large apertures introduce significant engineering challenges, including manufacturing difficulties and the implementation of a reliable scanning mechanism, which limit the further development of these two projects. The aperture synthesis (AS) technique uses a sparse array to synthesize an equivalent large-aperture array, which improves the spatial resolution [11]. Projects that employ the AS technique are represented by the Geostationary Synthetic Thinned Aperture Radiometer (GeoSTAR) [12,13] and the Geostationary Atmospheric Sounder (GAS) [14]. GeoSTAR is designed to operate at 50–56 GHz and 183 GHz. A Y-shaped array is used in GeoSTAR. To achieve the spatial resolution better than 50 km at 50–56 GHz, more than 300 antenna elements are required in the Y-shaped array [15]. The excessive number of antennas results in high system complexity and implementation challenges. GAS is designed to operate at 53 GHz, 118 GHz, 183 GHz, and 380 GHz. To reduce the array size and system complexity, a spinning Y-shaped array is employed [16]. The array consists of approximately 100 antennas and achieves a spatial resolution of 30 km [15]. However, the rotation of the array reduces the temporal resolution.

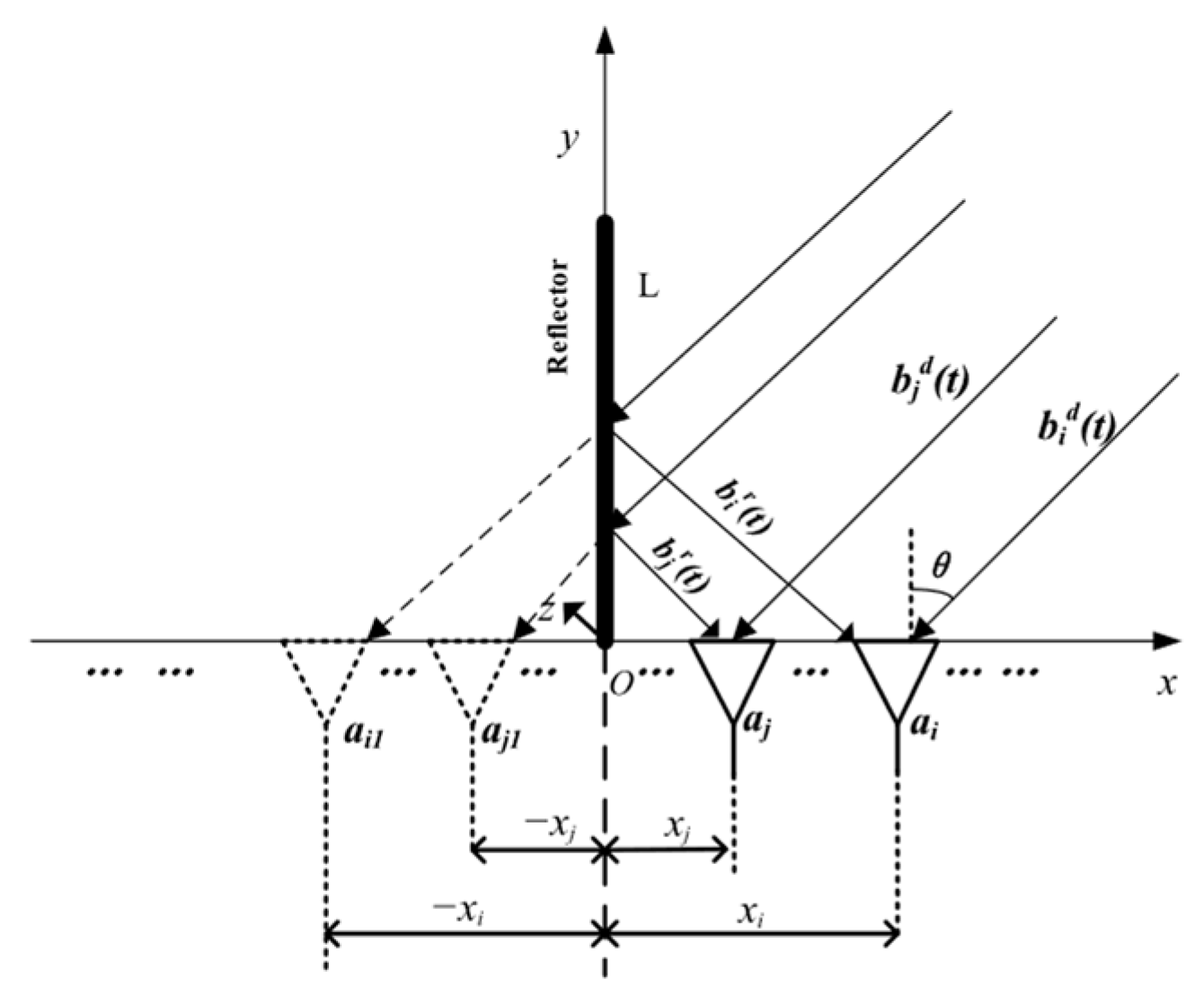
To improve the spatial resolution without extending the aperture of the array or reducing temporal resolution, mirrored aperture synthesis (MAS) has been proposed [17,18,19]. In MAS, one or more reflectors are placed around the array so that the reflected signals can be received by the array [20]. This process is equivalent to extending the aperture of the array, thereby improving the spatial resolution. In addition, I/Q demodulations are not required in MAS, which reduces system complexity [21]. With above advantages, MAS demonstrates significant potential for atmospheric observation from geostationary orbit [22].

In MAS, the transformation equations are used to establish the relationship between the cosine visibility and the cross-correlation. Solving these equations yields the cosine visibility. The cosine visibility and brightness temperature (BT) constitute a cosine transform pair, and the BT is reconstructed by the inverse cosine transform [17,18]. Errors in the cross-correlation directly affect the accuracy of the solved cosine visibility, thereby degrading the quality of BT reconstruction [23]. Therefore, the correction of the errors is essential for improving the quality of BT reconstruction.

In recent years, several studies have been conducted on the correction of errors. In [24], the impact of reflector angle errors on cross-correlation and BT reconstruction was analyzed. In [25,26], the influence of rank-deficient errors on BT reconstruction was investigated, and a full-rank array concept was proposed to eliminate such errors. For the amplitude and phase errors, ref. [23] established an error model and proposed a correction method based on an external source (hereafter referred to as the external-source method). In this method, the observed scene is measured by MAS to obtain the cross-correlation considering errors, while the external source is measured by AS instead of MAS to obtain the error information. Consequently, additional mechanical structures are required to remove the reflector and convert MAS into AS during the correction process. These mechanical structures increase the system complexity. Moreover, adjusting the reflector position onboard a satellite would change the system’s rotational inertia, which is undesirable from an engineering perspective. In addition, the external source must be placed at a specific location (i.e., $\xi$ = 0) exactly, and any deviation from the position introduces additional phase errors. In practice, it is difficult to position the external source precisely at $\xi$ = 0.

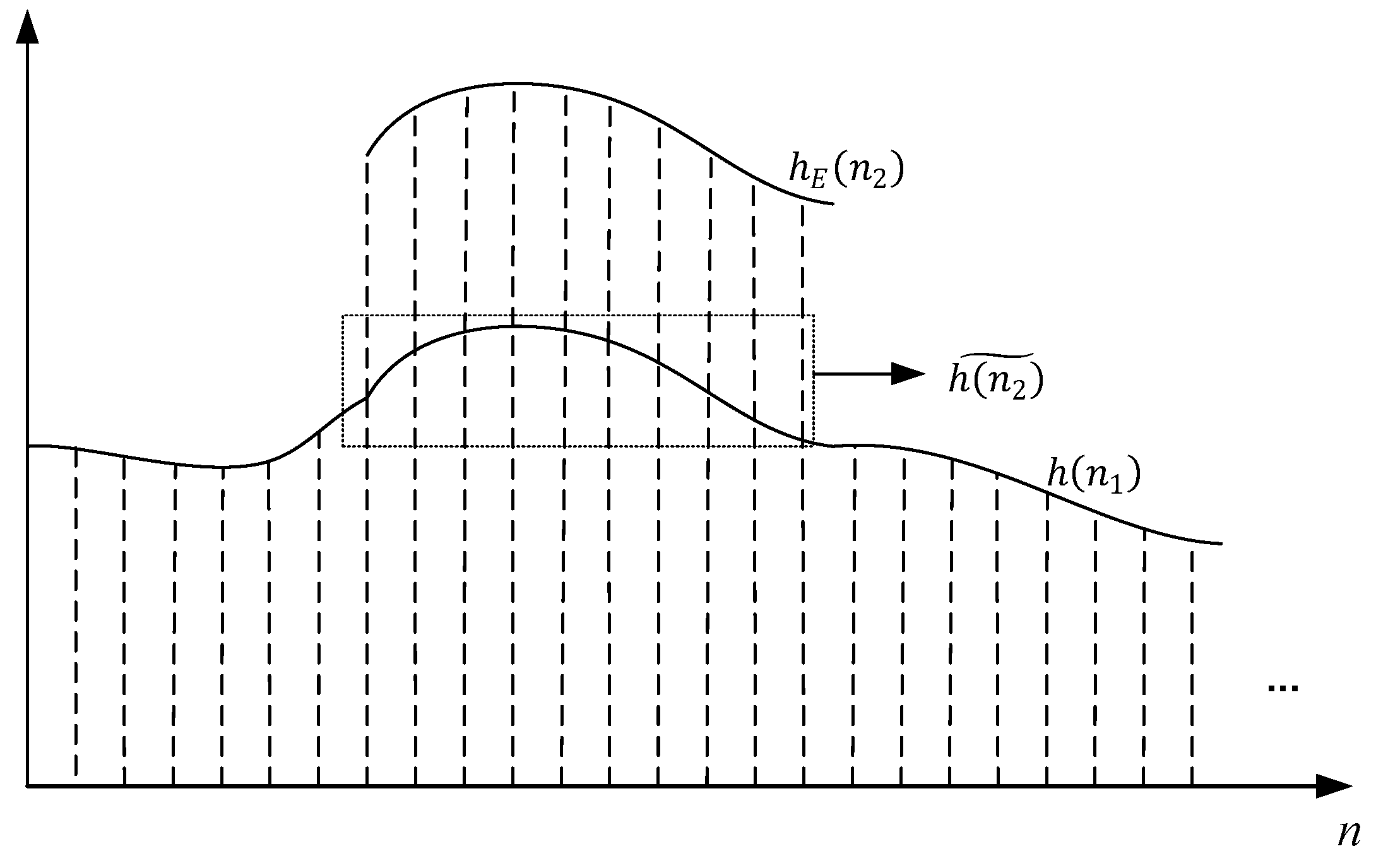
For 1-D mirrored aperture synthesis (1-D MAS), the cross-correlation can be expressed as the product of BT and the h function; therefore, the h function contains the error information [22]. In this paper, the amplitude and phase errors are modeled based on the h function. A correction method based on the model is proposed. In the proposed method, the h function without errors is used as prior knowledge to estimate the error information. The estimated error information is subsequently used to correct the errors. The proposed method does not require removing the reflector and imposes no constraints on the spatial offset of the h function. The simulation and experiment verify that the proposed method improves the quality of the BT reconstruction.

2. Theory and Methods

2.1. Principle of 1-D MAS

The principle diagram of 1-D MAS is shown in Figure 1. In the figure, a reflector of length L is placed along the y-axis, with one end intersecting the x-axis at the origin O. $a_i$ and $a_j$ are two antennas in the array with coordinates $(x_i,0)$ and $(x_j,0)$, where $x_j>x_i$. The signals received by antennas $a_i$ and $a_j$ are as follows [17]:

$$\begin{gathered} s_i\left(t\right)=b_i^d\left(t\right)+b_i^r\left(t\right) \\ {s}_j\left(t\right)=b_j^d\left(t\right)+b_j^r\left(t\right) \end{gathered}$$

(1)

where $b_i^d\left(t\right)$ and $b_j^d\left(t\right)$ denote the direct signals received by $a_i$ and $a_j$, respectively; $b_i^r\left(t\right)$ and $b_j^r\left(t\right)$ denote the reflected signals received by $a_i$ and $a_j$, respectively. Antennas $a_i$ and $a_j$ can form an antenna pair, and the cross-correlation of the antenna pair can be expressed as [17,25]:

$$R_{ij}=CV\left(u_1\right)+q·CV\left(u_2\right)$$

(2)

where $u_1=\left(x_i-x_j\right)/\lambda$, $u_2=\left(x_i+x_j\right)/\lambda$; $\lambda$ is the wavelength; $q$ is the polarization parameter [25]. CV(∙) is the cosine visibility [27]:

$$CV\left(u\right)=2{\int }_0^1{T}_b\left(\xi \right)\cos \left(2\pi u\xi \right)d\xi$$

(3)

where $T_b$ is the modified BT with $T_b\left(\xi \right)=T_{\mathsf{\Omega }}\left(\xi \right)/\sqrt{1-{\xi }^2}$; $T_{\mathsf{\Omega }}$ is the origin BT of the observed scene; $\xi =sin\theta$ is the direction cosine; $\theta$ is the incident angle of received signals.

The cross-correlation matrix is constructed by combining the cross-correlations of all antenna pairs in the array [28]:

$$\begin{array}{c}\mathit{R}={\left[R_{12},R_{13},\cdots ,R_{\beta \gamma },\cdots ,R_{(S-1)S}\right]}^T\end{array}$$

(4)

where $S$ is the number of antennas in the array. The relationship between the cross correlation matrix and cosine visibility can be established by the transformation equations [25]:

$$\begin{array}{c}{\displaystyle \genfrac{}{}{0pt}{}{\mathit{R}}{(K\times 1)}}={\displaystyle \genfrac{}{}{0pt}{}{\mathit{P}}{(K\times N)}}{\displaystyle \genfrac{}{}{0pt}{}{\mathit{C}\mathit{V}}{(N\times 1)}}\end{array}$$

(5)

where $K=S\times \left(S-1\right)$; $\mathit{C}\mathit{V}$ represents the matrix formed by cosine visibilities, and $N$ is the number of the cosine visibilities; $\mathit{P}$ is the transformation matrix, in which each row contains only two non-zero elements [25]. By solving the transformation equations, the cosine visibility can be obtained, and the BT can be reconstructed by inverse cosine transform [17]:

$$\begin{array}{c}T\left(\xi \right)=2{\int }_0^{\infty }CV\left(u\right)\cos \left(2\pi u\xi \right)du\end{array}$$

(6)

According to Equation (6), the quality of BT reconstruction depends on the accuracy of the solved cosine visibility, which is obtained by solving the transformation equations. Therefore, the amplitude and phase errors in the cross-correlation directly degrade the quality of BT reconstruction. It is essential to correct the amplitude and phase errors for enhancing the quality of BT reconstruction.

2.2. Error Model Based on the h Function

In [23], the amplitude and phase errors of the cross-correlation are modeled as follows:

$$\begin{array}{c}{R}_{ij}^E=c·R_{ij}\end{array}$$

(7)

where $R_{ij}^E$ is the cross-correlation considering the amplitude and phase errors; $c=m_i{m}_{j}exp\left[j\left({\phi }_j-{\phi }_i\right)\right]$ is the multiplicative error factor, which represents the amplitude and phase errors; $m_i{m}_j$ denotes the amplitude error of the antenna pair, and ${\phi }_j-{\phi }_i$ denotes the phase error of the antenna pair.

It is noted that the cross-correlation without errors, as given in Equation (2), can be written in a compact form [22]:

$$\begin{array}{c}{R}_{ij}={\int }_0^1{T}_b\left(\xi \right)h_s(\xi ,x_i,x_j,\rho ,L,F)d\xi \end{array}$$

(8)

where $\rho$ is the reflector reflectivity; L is the reflector length; F is the normalized antenna pattern; $h_s(\xi ,x_i,x_j,\rho ,L,F)$ is the h function without errors, which can be expressed as [22]:

$$\begin{array}{c}{h}_s\left(\xi ,x_i,x_j,\rho ,L,F\right)=\left\{\begin{array}{c}exp\left(j2\pi u_1\xi \right)F_i\left(\xi \right)F_j\left(\xi \right),\xi \in [0,\mathit{sin}\left(\mathit{arctan}\left({\displaystyle \frac{x_i}{L}}\right)\right))\\ h_2\left(\xi ,x_i,x_j,\rho ,L,F\right),\xi \in [\mathit{sin}\left(\mathit{arctan}\left({\displaystyle \frac{x_i}{L}}\right)\right),\mathit{sin}\left(\mathit{arctan}\left({\displaystyle \frac{x_j}{L}}\right)\right))\\ h_3\left(\xi ,x_i,x_j,\rho ,L,F\right),\xi \in [\mathit{sin}\left(\mathit{arctan}\left({\displaystyle \frac{x_j}{L}}\right)\right),1]\end{array}\right.\end{array}$$

(9)

where $F_{i,j}$ are the normalized antenna patterns of $a_i$ and $a_j$; $h_2\left(\xi ,x_i,x_j,\rho ,L,F\right)$ and $h_3\left(\xi ,x_i,x_j,\rho ,L,F\right)$ are as follows [22]:

$$h_2\left(\xi ,x_i,x_j,\rho ,L,F\right)=F_i\left(\xi \right)F_j\left(\xi \right)\left[\mathit{exp}\left(j2\pi u_1\xi \right)+q\rho \mathit{exp}\left(-j2\pi u_2\xi \right)\right]$$

(10)

$$\begin{array}{cc}{h}_3\left(\xi ,x_i,x_j,\rho ,L,F\right)=& F_i\left(\xi \right)F_j\left(\xi \right)[(\mathit{exp}\left(j2\pi u_1\xi \right)+2q\rho \mathit{cos}\left(2\pi u_2\xi \right)\\ & +{\rho }^2\mathit{exp}\left(-j2\pi u_1\xi \right)]\hfill \end{array}$$

(11)

Similarly, the cross-correlation considering amplitude and phase errors, as given in Equation (7), can also be written in a compact form:

$$\begin{array}{c}\begin{array}{cc}{R}_{ij}^E& =c·R_{ij}\hfill \\ & ={\int }_0^1{T}_b\left(\xi \right)c·h_s(\xi ,x_i,x_j,\rho ,L,F)d\xi \hfill \\ & ={\int }_0^1{T}_b\left(\xi \right)h_{Es}(\xi ,x_i,x_j,\rho ,L,F)d\xi \hfill \end{array}\end{array}$$

(12)

According to Equation (12), the influence of the amplitude and phase errors on the cross correlation is equivalent to their influence on the h function. Therefore, the amplitude and phase error model based on the h function can be expressed as:

$$\begin{array}{c}{h}_{Es}\left(\xi ,x_i,x_j,\rho ,L,F\right)=c·h_s(\xi ,x_i,x_j,\rho ,L,F)\end{array}$$

(13)

where $h_{Es}\left(\xi ,x_i,x_j,\rho ,L,F\right)$ is the h function considering the amplitude and phase errors.

2.3. Correction Method

Based on the error model established in Section 2.2, this section proposes a correction method for the amplitude and phase errors.

The h function can be discretized as a sequence, which can be expressed as:

$$\begin{array}{c}\begin{array}{c}h\left(n\right)=h_s\left(\left(n-1\right)\Delta \xi ,x_i,x_j,\rho ,L,F\right),n=1,2,\cdots ,N\\ h_E\left(n\right)=h_{Es}\left((n-1)\Delta \xi ,x_i,x_j,\rho ,L,F\right),n=1,2,\cdots ,N\end{array}\end{array}$$

(14)

where $\Delta \xi$ represents the sampling interval; N corresponds to the length of the discretized sequence; $h\left(n\right)$ is the sequence of the h function without the amplitude and phase errors; and $h_E\left(n\right)$ is the sequence of the h function considering the amplitude and phase errors. Based on the error model proposed in Section 2.2, the relationship of $h\left(n\right)$ and $h_E\left(n\right)$ can be expressed as:

$$\begin{array}{c}\begin{array}{c}h\left(n\right)=c^{-1}·h_E\left(n\right)\end{array}\end{array}$$

(15)

In general, the sequence $h_E\left(n\right)$ is obtained from practical observations. The sequence $h\left(n\right)$ can be obtained through simulations using system parameters identical to those in practical observations. The correction method of the amplitude and phase errors is regarded as estimating $c^{-1}$ accurately from $h\left(n\right)$ and $h_E\left(n\right)$.

2.3.1. Least-Squares Estimation of $c^{-1}$

To estimate the value of $c^{-1}$, an error correction coefficient $\alpha$ is introduced. The sequence of the h function corrected by $\alpha$ is given by:

$$\begin{array}{c}{h}_c\left(n\right)=\alpha ·h_E\left(n\right)\end{array}$$

(16)

where $h_c\left(n\right)$ is the corrected sequence. The estimation of $c^{-1}$ is equivalent to estimating α such that $h_c\left(n\right)$ is as closely as possible to $h\left(n\right)$. The sum of squared residuals between $h_c\left(n\right)$ and $h\left(n\right)$ can be expressed as [29]:

$$\begin{array}{cc}J\left(\alpha \right)& ={\displaystyle \sum _{n=1}^N}{\left|h\left(n\right)-h_c\left(n\right)\right|}^2\hfill \\ & ={‖\mathit{h}-\alpha ·{\mathit{h}}_{\mathit{E}}‖}_2^2\hfill \end{array}$$

(17)

where h and ${\mathit{h}}_{\mathit{E}}$ are the column vectors formed by the sequences $h\left(n\right)$ and $h_E\left(n\right)$, respectively. These vectors are expressed as follows:

$$\begin{array}{c}\mathit{h}={\left[h\left(1\right),h\left(2\right),\dots ,h\left(N\right)\right]}^T\\ {\mathit{h}}_{\mathit{E}}={\left[h_E\left(1\right),h_E\left(2\right),\dots ,h_E\left(N\right)\right]}^T\end{array}$$

(18)

The parameter estimation model based on the least-squares method can be expressed as [29]:

$$\begin{array}{c}\widehat{\alpha }\end{array}=arg \underset{\mathrm{\alpha }}{\min }J\left(\alpha \right)$$

(19)

where $\begin{array}{c}\widehat{\alpha }\end{array}$ is the least-squares estimate of $\alpha$, which also represents the least-squares estimate of $c^{-1}$; $\mathit{arg}\mathrm{m}\mathrm{i}\mathrm{n}(·)$ denotes the value of the variable at which the function attains its minimum. By expressing $\alpha$ as the sum of its real part $k_1$ and imaginary part $k_2$, the sum of squared residuals $J\left(\alpha \right)$ can be rewritten as:

$$\begin{array}{cc}J(k_1,k_2)& ={\mathit{h}}^H\mathit{h}-\alpha ·{\mathit{h}}^H{\mathit{h}}_{\mathit{E}}-{\alpha }^{\ast }·{\mathit{h}}_{\mathit{E}}^{H}h+{\left|\alpha \right|}^2{\mathit{h}}_{\mathit{E}}^H{\mathit{h}}_{\mathit{E}}\hfill \\ & =\left[k_1,k_2\right]\mathit{Q}{\left[k_1,k_2\right]}^T+{‖\mathit{h}‖}_2^2\hfill \\ & -2\left[Re\left({\mathit{h}}^H{\mathit{h}}_{\mathit{E}}\right),-Im\left({\mathit{h}}^H{\mathit{h}}_{\mathit{E}}\right)\right]{\left[k_1,k_2\right]}^T\hfill \end{array}$$

(20)

where * denotes the complex conjugate; $Re\left(·\right)$ and $Im\left(·\right)$ denote the real and imaginary parts of complex numbers, respectively; and $\mathit{Q}$ is the Hessian matrix of $J(k_1,k_2)$, which can be expressed as [30]:

$$\mathit{Q}=\left(\begin{array}{cc}{‖{\mathit{h}}_{\mathit{E}}‖}_2^2& 0\\ 0& {‖{\mathit{h}}_{\mathit{E}}‖}_2^2\end{array}\right)$$

(21)

It is evident that $\mathit{Q}$ is a positive-definite matrix; therefore $J(k_1,k_2)$ is a convex function [30]. Since $J\left(\alpha \right)=J\left(k_1+j{k}_2\right)$ is convex, the least-squares estimate of $\alpha$ is the global optimum, and no local optima exist [31]. The least-squares estimate of $\alpha$ corresponds to the point where the gradient of $J\left(\alpha \right)$ equals zero [29]:

$$\begin{array}{c}\widehat{\alpha }\end{array}={\displaystyle \frac{{\mathit{h}}_{\mathit{E}}^H\mathit{h}}{{\mathit{h}}_{\mathit{E}}^H{\mathit{h}}_{\mathit{E}}}}$$

(22)

Multiplying $\begin{array}{c}\widehat{\alpha }\end{array}$ by the cross-correlation $R_{ij}^E$, which considers the amplitude and phase errors, the corrected cross-correlation can be obtained:

$$\begin{array}{cc}{R}_{ij}^c& =\begin{array}{c}\widehat{\alpha }\end{array}·R_{ij}^E\hfill \\ & \approx c^{-1}·c·R_{ij}\hfill \\ & \approx R_{ij}\hfill \end{array}$$

(23)

where $R_{ij}^c$ is the cross-correlation after correction, and the influence of the amplitude and phase errors on the cross-correlation is eliminated.

However, the above estimation process must satisfy the following three conditions:

(a)

The two sequences have the same sampling interval;

(b)

The two sequences have the same length;

(c)

There should be no spatial offset between the two sequences.

In general, ensuring that the two sequences have the same sampling interval is relatively straightforward (i.e., condition a can be readily satisfied). Nevertheless, for conditions b and c, the movement range of the point source is limited in practical observations, therefore the sequence length of $h_E\left(n\right)$ is usually shorter than that of $h\left(n\right)$. Moreover, the two sequences generally exhibit a spatial offset. Considering these constraints, the two sequences can be expressed as:

$$\begin{array}{c}h\left(n_1\right)=h_s\left(\left(n_1-1\right)\Delta \xi ,x_i,x_j,\rho ,L,F\right),n_1=1,2,\cdots ,N_1\\ h_E\left(n_2\right)=h_{Es}\left(\left(n_2-1+\Delta n\right)\Delta \xi ,x_i,x_j,\rho ,L,F\right),n_2=1,2,\cdots ,N_2\end{array}$$

(24)

where N₁ and N₂ are the lengths of $h\left(n_1\right)$ and $h_E\left(n_2\right)$, respectively, with $N_1\ge N_2$; $\delta =\Delta n\Delta \xi$ represents the spatial offset. If the error correction coefficient is estimated by $h\left(n_1\right)$ and $h_E\left(n_2\right)$ directly, additional errors will be introduced. It is necessary to estimate the spatial offset and apply windowing to $h\left(n_1\right)$, so that the two sequences have the same length and are properly aligned.

2.3.2. Estimation of the Spatial Offset

Combining Equations (13) and (24), the sequence $h_E\left(n_2\right)$ considering the amplitude and phase errors can be expressed as:

$$h_E\left(n_2\right)=\mathrm{c}·h\left(n_2+\Delta n\right),n_2=1,2,\cdots ,N_2$$

(25)

where $\Delta n=0,1,2,\cdots ,N_1-N_2$. Based on the signal-estimation theory, $\Delta n$ can be estimated [32]. The cross-correlation function between $h\left(n_1\right)$ and $h_E\left(n_2\right)$ is given by [33]:

$$\begin{array}{c}\begin{array}{cc}{r}_h\left(k\right)& ={\displaystyle \sum _{n_3=1}^{N_2}}h\left(k+n_3\right)·h_E^{\ast }\left(n_3\right)\hfill \\ & =c^{\ast }·{\displaystyle \sum _{n_3=1}^{N_2}}h\left(k+n_3\right)·h^{\ast }\left(n_3+\Delta n\right)\hfill \end{array}\end{array}$$

(26)

According to the derivation in [32], when $k=\Delta n$, the modulus of the cross-correlation function reaches its maximum value. Therefore, the position of the maximum modulus of $r_h\left(k\right)$ corresponds to the estimation of $\Delta n$ [33]:

$$\begin{array}{c}\widehat{\Delta n}\end{array}=arg \underset{k}{\max }\left|r_h\left(k\right)\right|$$

(27)

where $\mathit{arg} \mathrm{m}\mathrm{a}\mathrm{x}(·)$ denotes the value of the variable at which the function attains its maximum. The spatial offset between the two sequences can be estimated by:

$$\begin{array}{c}\widehat{\delta }=\begin{array}{c}\widehat{\Delta n}\end{array}·\Delta \xi \end{array}$$

(28)

To make the two sequences have the same length and be properly aligned, the sequence without errors is windowed based on the estimated value of $\Delta n$:

$$\begin{array}{c}\widetilde{h\left(n_2\right)}=h\left(n_2+\begin{array}{c}\widehat{\Delta n}\end{array}\right),n_2=1,2,\cdots ,N_2\end{array}$$

(29)

The sequences $\widetilde{h\left(n_2\right)}$ and $h_E\left(n_2\right)$ are properly aligned, and these two sequences can be used to perform the least-squares estimation of the error correction coefficient. The relationship among the three sequences $h\left(n_1\right)$, $\widetilde{h\left(n_2\right)}$, and $h_E\left(n_2\right)$ is illustrated in Figure 2. In the figure, the portion of $h\left(n_1\right)$ enclosed by the dotted frame corresponds to the aligned sequence $\widetilde{h\left(n_2\right)}$.

In summary, the proposed correction method can be divided into the following seven steps, as illustrated in Figure 3:

(a)

The actual scene is observed by the MAS system to obtain the cross-correlation $R_{ij}^E$, which contains both the desired cosine visibility information as well as the amplitude and phase errors.

(b)

To extract the amplitude and phase error information contained in the cross-correlation, the h-function sequence that contains errors is required. This sequence is measured by observing a point source placed at multiple spatially equidistant positions with the MAS system.

(C)

The sequence $h\left(n\right)$ without errors is generated through simulation using the known physical parameters of the MAS system (e.g., reflector geometry, array arrangement, polarizations of the antennas, work frequency, and system bandwidth). In the simulation, the scene is set as a point source placed at multiple spatially equidistant positions.

(d)

The cross-correlation function $r_h\left(k\right)$ between $h\left(n\right)$ and $h_E\left(n\right)$ is calculated, and the spatial offset between the two sequences is estimated. This step is essential because the measured sequence $h_E\left(n\right)$ may not be spatially aligned with the simulated sequence $h\left(n\right)$.

(e)

The estimated spatial offset is then used to window and shift $h\left(n\right)$, and the sequence $\widetilde{h\left(n\right)}$ is obtained. The sequence $\widetilde{h\left(n\right)}$ and $h_E\left(n\right)$ have the same length and are properly aligned.

(f)

The sequences $\widetilde{h\left(n\right)}$ and $h_E\left(n\right)$ are used to perform the least-squares estimation of the error correction coefficient $\widehat{\alpha }$, which characterizes the amplitude and phase error information.

(g)

The cross-correlation $R_{ij}^E$ is multiplied by $\widehat{\alpha }$ to obtain the corrected cross-correlation $R_{ij}^c$, which is subsequently used for BT reconstruction through the inverse discrete cosine transform (IDCT).

The proposed method extracts error information using only two h-function sequences, which are measured by observing a noise source placed at multiple spatially equidistant positions with MAS. Therefore, the reflector need not be removed during the correction process, avoiding the extra mechanical. Moreover, the spatial offset between the two sequences can be estimated from their cross-correlation function; therefore, the proposed method imposes no specific requirements on the spatial offset of the h function. This improves the adaptability of the correction method.

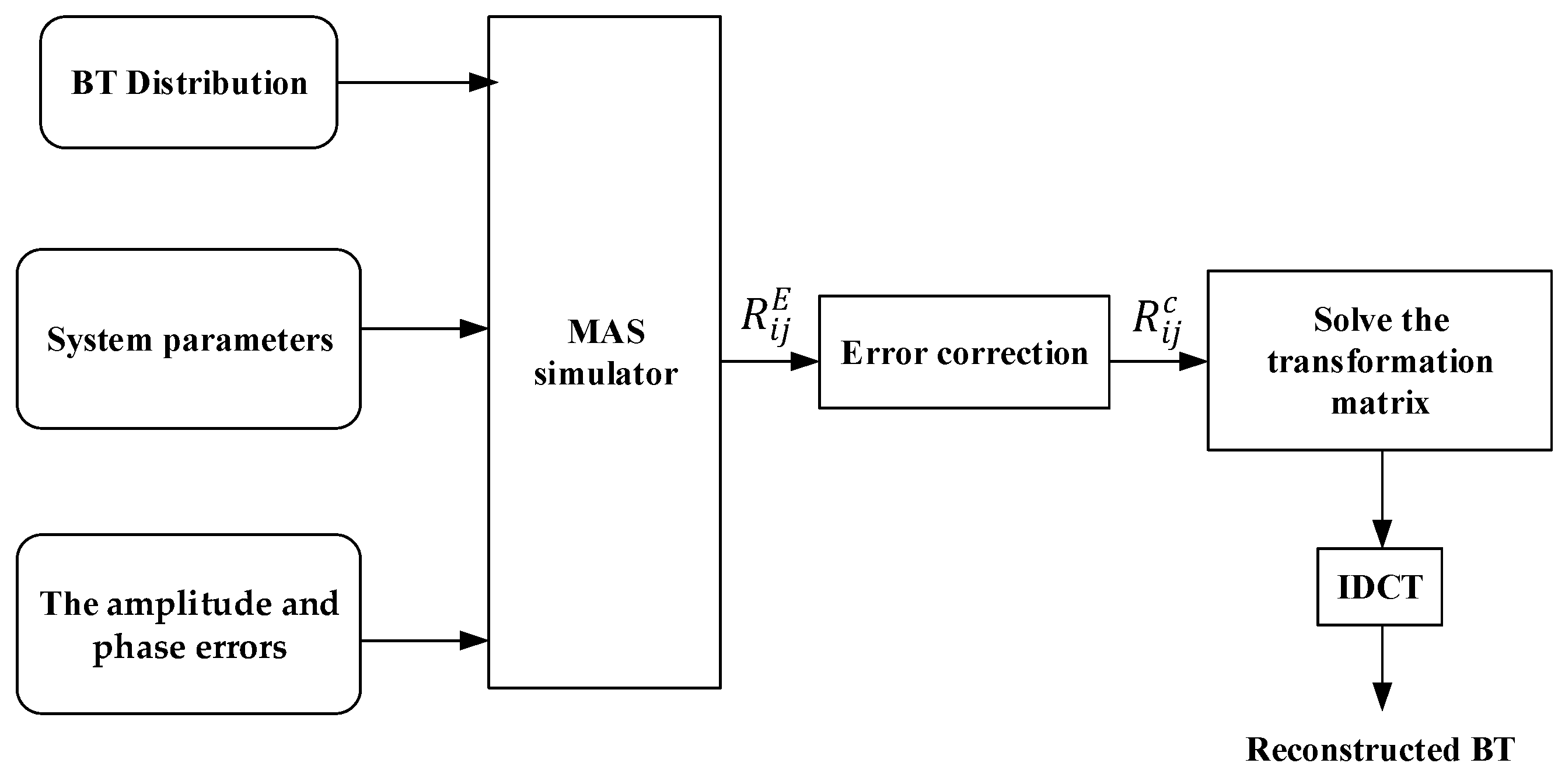
3. Simulation

In this section, the effectiveness of the proposed correction method is validated through the BT reconstruction simulation [17,27]. Additionally, the independence of the proposed method from the spatial offset of the h function is verified.

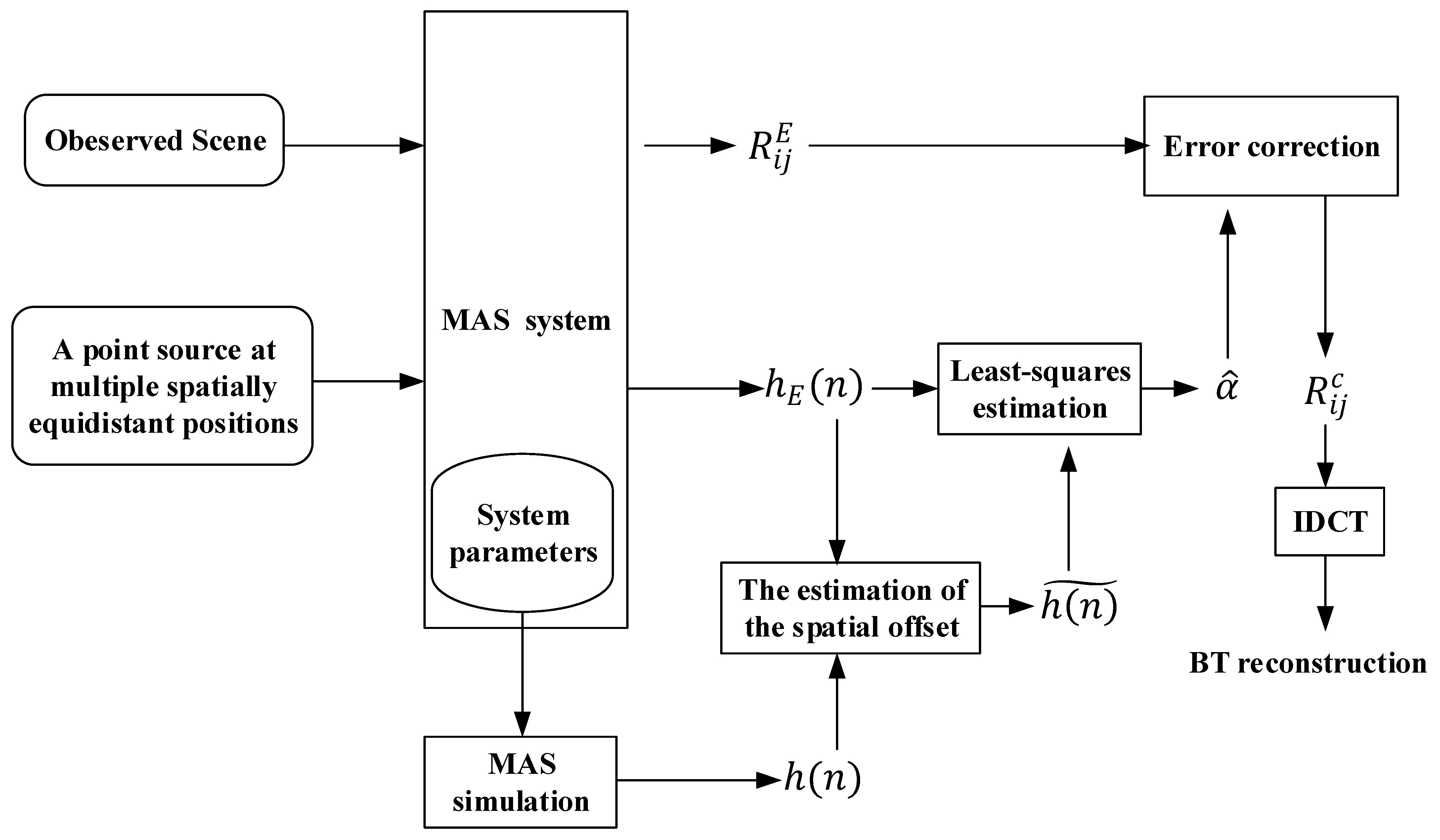
The simulation procedure for BT reconstruction is illustrated in Figure 4. First, the BT distribution $T_b\left(\xi \right)$ of the observed scene is specified. Next, the MAS system parameters are configured, including the reflector geometry, array arrangement, polarizations of the antennas, operating frequency, and system bandwidth. Then, the cross-correlation of antennas $a_i$ and $a_j$ is calculated by Equation (2). It is worth noting that the amplitude and phase errors can be introduced in this step by using Equation (7). After obtaining the cross-correlation with errors, different correction methods are applied to evaluate and compare their performance. Specifically, the measured cross-correlations are corrected by either the proposed method or the external-source method. Each method produces a corresponding corrected cross-correlation $R_{ij}^E$. For any two antennas $a_{\alpha }$ and $a_{\beta }$ in the array (where $\alpha$ and $\beta$ denotes their indices), the corrected cross-correlation $R_{\alpha \beta }^E$ of the corresponding antenna pair are obtained following the steps described above. By traversing all antenna pairs in the array, all corrected cross-correlations can be obtained. As shown in (2), each corrected cross-correlation corresponds to a linear equation for the cosine visibility. All linear equations are then assembled according to (4) to form the transformation equation. The corrected cross-correlations of all antenna pairs are combined to form the transformation equations. The cosine visibility is obtained by solving the transformation equations with the minimum-norm regularization. Finally, the BT image is reconstructed by IDCT.

The simulations are performed in MATLAB (R2017a). In simulations, the frequency is 51.6 GHz, corresponding to a wavelength of $\lambda =5.81$ mm; the bandwidth is set to 200 MHz, and the integration time is 6.4 ms. The array configuration is [1,2,9,13,17,21,23,26,28,29,30,31], where each value represents the normalized distance (relative to the wavelength) between each antenna and the reflector. The array is a 1-D rank-full array; therefore, the BT reconstruction is not be influenced by the rank-deficient errors [25]. The polarizations of the antennas are parallel polarization, with the polarization parameter $q=1$ [22,25]. To eliminate the influence of the normalized antenna pattern, reflector reflectivity, and reflector length on the BT reconstruction, these parameters are set to ideal values in simulations [22].

The simulations are performed under two conditions: with and without the amplitude and phase errors. The cross-correlation without amplitude and phase errors is calculated by Equation (2). The cross-correlation with amplitude and phase errors is calculated by Equation (7). The BT of scene is reconstructed by IDCT [17]. In simulations, the random amplitude errors follow a Gaussian distribution with a mean of 0 and a standard deviation of 50%. The random phase errors also follow a Gaussian distribution with a mean of 0 and a standard deviation of 60 degrees.

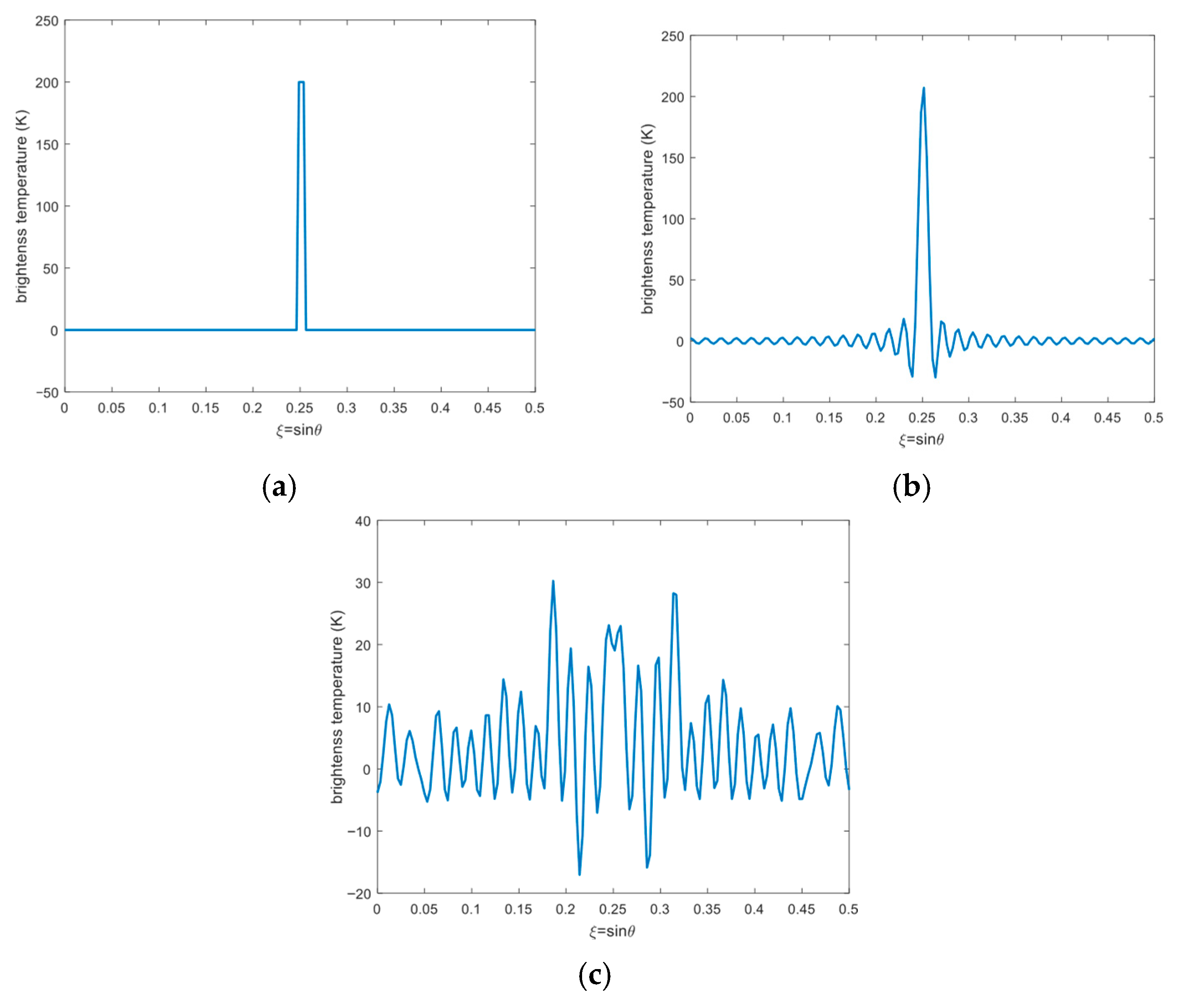
3.1. Point Source

A narrowband pulse at $\xi =0.25$ is used to represent the point source. The BT distribution of the scene is illustrated in Figure 5a. The BT reconstruction result without the amplitude and phase errors is shown in Figure 5b. The reconstructed image exhibits high quality, and the location of the point source is clearly identifiable. The BT reconstruction result with the amplitude and phase errors is shown in Figure 5c. Due to the influence of the errors, the BT reconstruction is severely distorted, and the point source cannot be recognized.

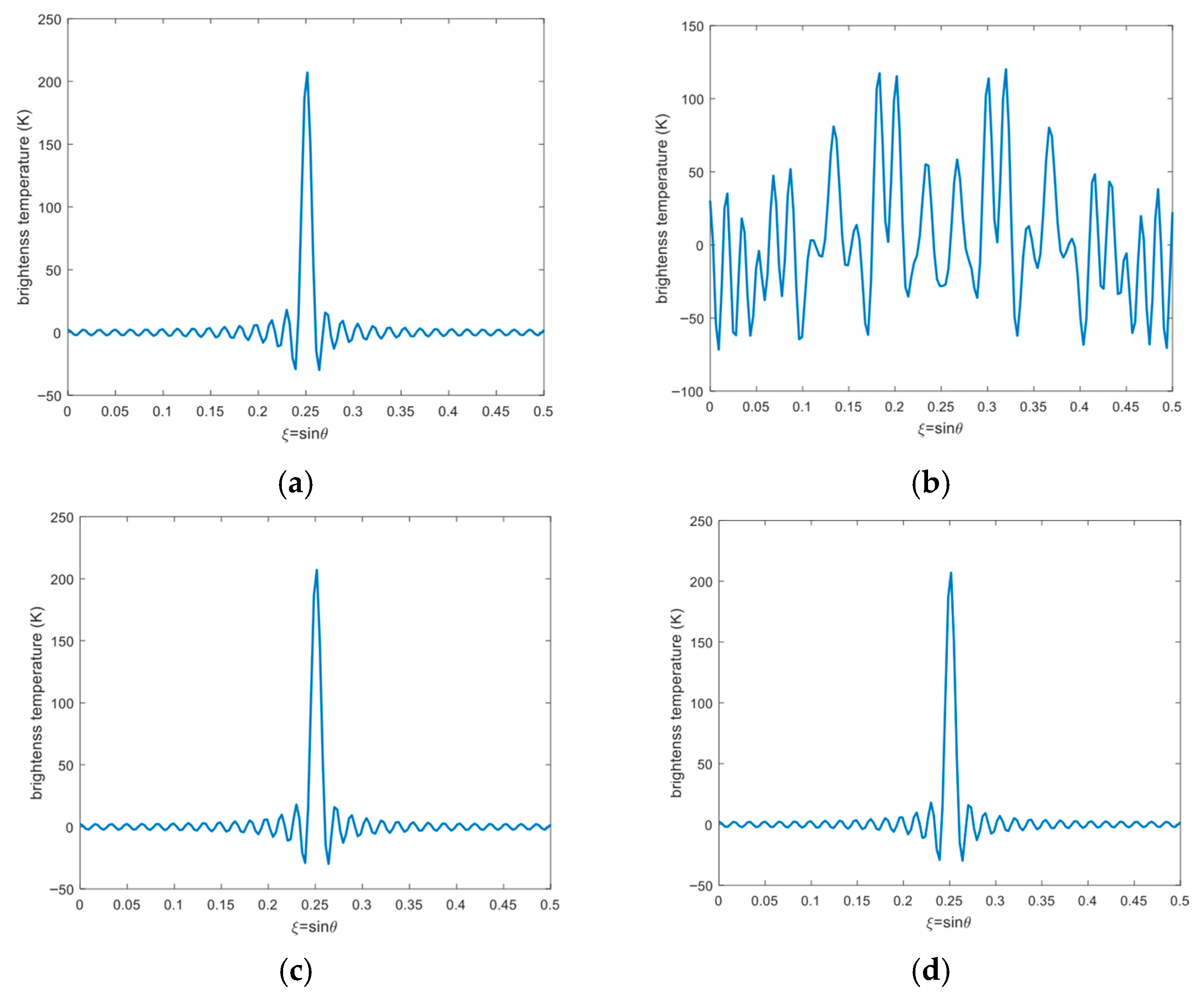
The simulation results after error correction are presented in Figure 6. The reconstruction results corrected by the external-source method are shown in Figure 6a,b. Figure 6a shows the result when the external source is located at $\xi =0$. The point source can be clearly identified. Therefore, the amplitude and phase errors are sufficiently corrected. Figure 6b is the result when the external source is located at $\xi =0.02$, additional errors are introduced in the image, resulting in noticeable image distortion. These results indicate that the effectiveness of the method external-source method strongly depends on the position of the external source [23].

The BT reconstruction results corrected by the proposed method are shown in Figure 6c,d. When the spatial offset between the two h-function sequences is $\delta =0$, the corresponding reconstruction result is shown in Figure 6c. The point source can be clearly identified, and the amplitude and phase errors are sufficiently corrected. When the spatial offset between the two h-function sequences is changed to $\delta =0.02$, the corresponding reconstruction result is shown in Figure 6d. The spatial offset is accurately estimated, and the image quality is improved. These results confirm that the proposed method can effectively correct the amplitude and phase errors in the cross-correlation. The performance of the proposed correction method is insensitive to the spatial offset between the h-function sequences.

3.2. Extended Source

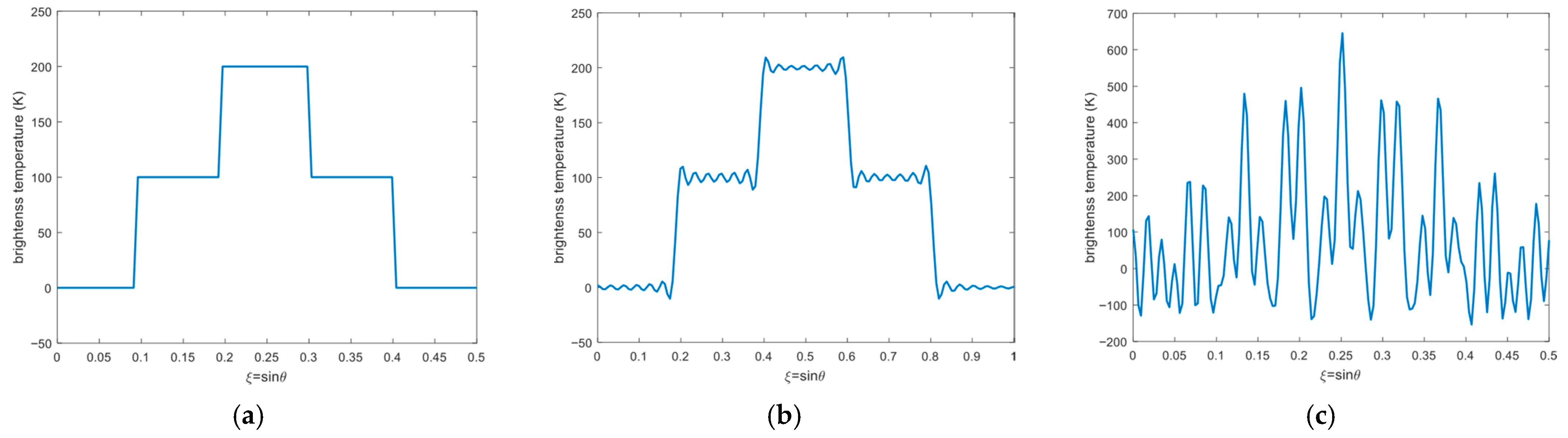
The BT distribution of the extended source is set as a stepwise distribution, as shown in Figure 7a. The root mean square error is used to quantify the effect of the correction method [19]:

$${RMSE}_T=\sqrt{{\displaystyle \frac{1}{N_T}}\sum _{p=1}^{N_T}{\left(T_r\left(p\right)-T_I\left(p\right)\right)}^2}$$

(30)

where $N_T$ is the number of pixels in the image; $T_r$ is the reconstructed BT; and $T_I$ is the reconstructed BT without the amplitude and phase errors.

The BT reconstruction results without and with the amplitude and phase errors are shown in Figure 7b and Figure 7c, respectively. The BT reconstruction is severely distorted when the amplitude and phase errors are introduced, with ${RMSE}_T=162$ K. The reconstruction results corrected by the external-source method are shown in Figure 8a,b. When the external source is located at $\xi =0$, the amplitude and phase errors are effectively corrected, with ${RMSE}_T=6.0\times {10}^{-7}$ K, and the quality of the BT reconstruction is improved. When the external source is located at $\xi =0.02$, the image exhibits distortion, with ${RMSE}_T=25$ K. The BT variations across the image become indistinguishable.

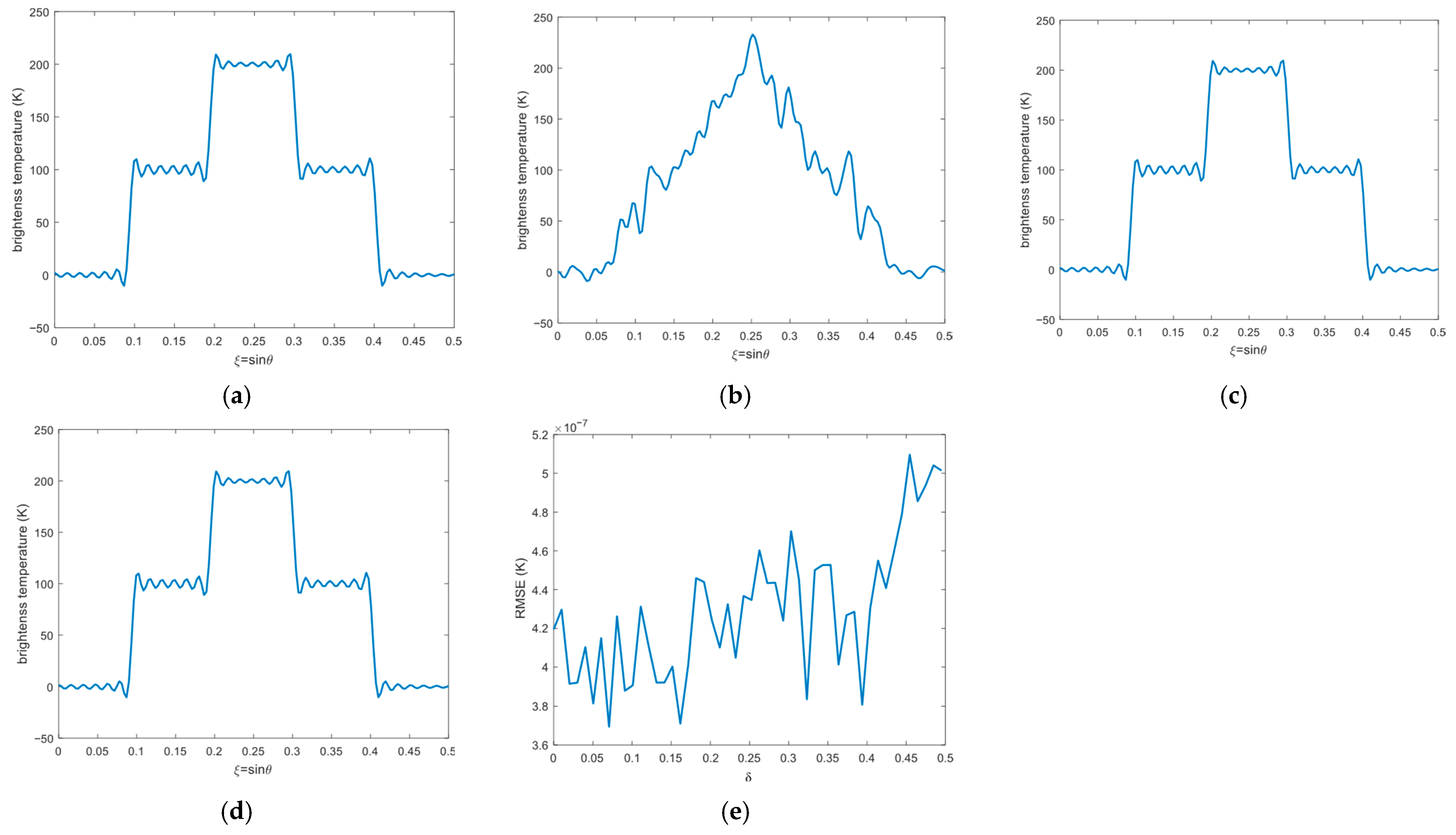
The BT reconstruction results corrected by the proposed method are shown in Figure 8c,d. When the spatial offsets between the two h-function sequences are $\delta =0$ and $\delta =0.02$, the ${RMSE}_T$ of the reconstructed images are $4.2\times {10}^{-7}$ K and $3.9\times {10}^{-7}$ K, respectively. In both cases, the quality of the BT is significantly improved. The variation of ${RMSE}_T$ with the spatial offset between the two h-function sequences is shown in Figure 8e, where all ${RMSE}_T$ values are less than $5.2\times {10}^{-7}$ K. These results verify that the performance of the proposed correction method is not affected by the spatial offset between the h-function sequences.

The above simulation results validate that, compared with the external-source method, the proposed method can also effectively correct the amplitude and phase errors in the cross-correlation and improve the quality of BT reconstruction. Moreover, the performance of the proposed method is insensitive to the spatial offset of the h function.

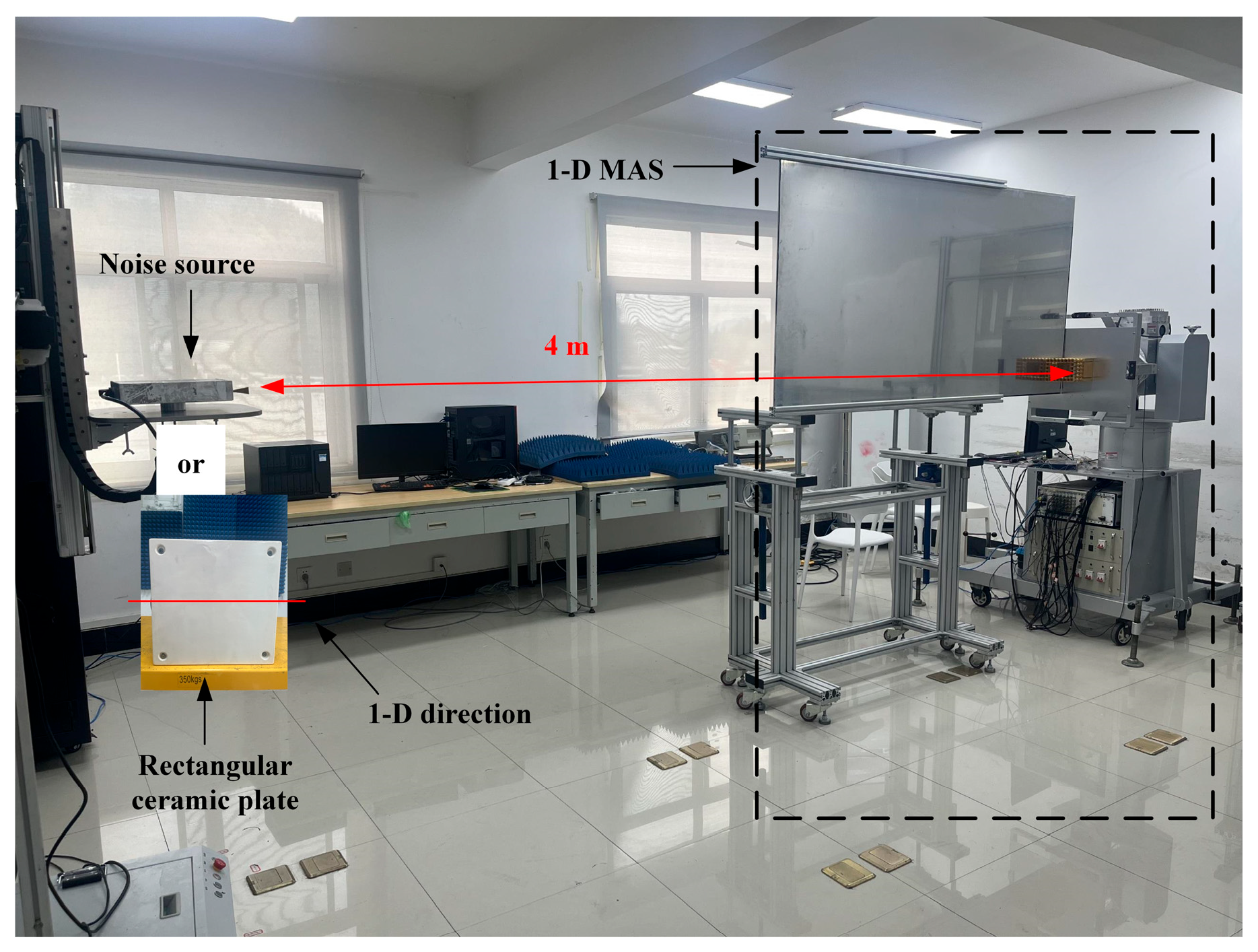
4. Experiment

To verify the effectiveness of the proposed correction method, an experiment is conducted with experimental system MAS-V [34]. The system operating at 51.6 GHz was developed by Huazhong University of Science and Technology (HUST) to validated the theory of MAS [35]. The MAS-V with a reflector (length of 2 m) are used for the 1-D MAS experiment, as shown in Figure 9. The arrangement of the array is [3.5, 7, 10.5, 14, 17.5, 21, 24.5, 28], where each value represents the normalized distance (relative to the wavelength) between each antenna and the reflector. The antennas in the array are rectangular horn antennas. The rectangular horn antenna is constructed by flaring a rectangular metal waveguide, and its polarization direction is parallel to the short side of the waveguide [36]. Therefore, the value of the polarization parameter $q$ in the experiment can be controlled by adjusting the orientation of the waveguide’s short side relative to the reflector. In the experiment, the short side of the waveguide is oriented perpendicular to the reflector, which corresponds to a polarization parameter of $q=1$ [25,37].

A noise source with high power is used in the experiment, which can generate a stable Gaussian white noise over 50–60 GHz [23]. The picture of the noise source is shown in Figure 10a. Because thermal emission of natural scenes exhibits broadband spectral characteristics, the radiation of the noise source in the 50–60 GHz band is comparable to that of natural scenes. In addition, the physical size of the emitting antenna is extremely small compared with its distance from the array, causing the noise source to behave as an angularly compact source. Therefore, the noise source can be regarded as a point source in natural scenes. In the experiment, the noise source serves as a point source for obtaining the h function.

The sequence of the h function containing errors is measured by observing a noise source placed at multiple spatially equidistant positions. The sampling interval of the h function is 1 cm, and the distance between the noise source and the array is 4 m. The least-squares method is applied to extract the error correction coefficient from the h-function sequence, which contains errors. Furthermore, the estimated error correction coefficient is used to correct the amplitude and phase errors in the cross-correlation.

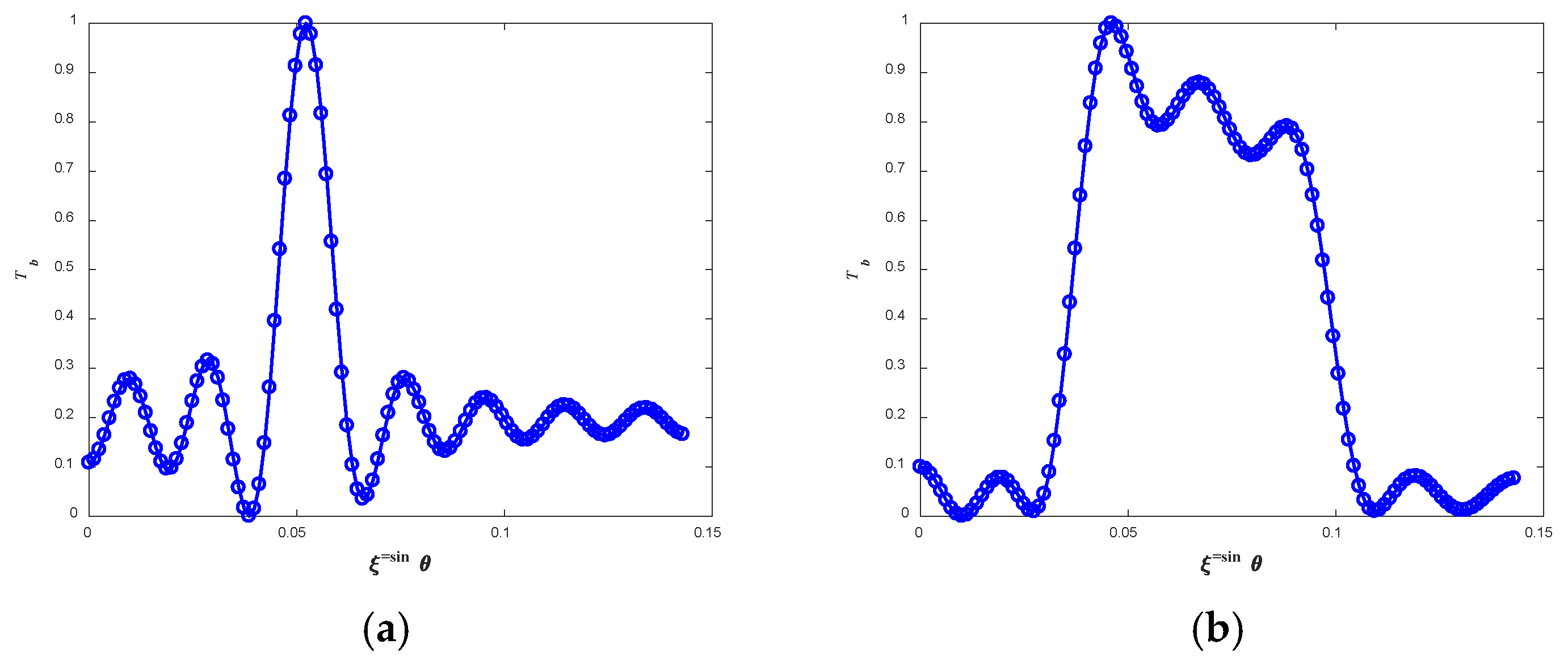
The observed scenes in the experiment are a noise source and a rectangular ceramic plate with high temperature, as shown in Figure 10. The experimental scenario is shown in Figure 11. In both cases, the distance between the scenes and the array is 4 m. The BT reconstruction results of the noise source and ceramic plate are shown in Figure 12 and Figure 13, respectively. To facilitate comparison, a simulation for the observed scenes is conducted. In the simulation, the reflector geometry, array configuration, antenna patterns, work frequency, polarization parameter, and system bandwidth are set to match those in the experiment. The simulation results for the noise source and ceramic plate are presented in Figure 14a and Figure 14b, respectively. As MAS-V is a prototype and still contains residual system errors (e.g., errors caused by the reflector), it is not suitable for calibration at this stage. Therefore, similar to [21], both the simulated and experimental results are normalized to the range [0, 1] for comparison. Because the MAS-V system is not absolutely calibrated [21], both the simulated and experimental results are normalized to the range of 0–1 based on their maximum and minimum values. The peak signal-to-noise ratio (PSNR) and the structural similarity (SSIM) are used to quantitatively evaluate the quality of BT reconstruction. The PSNR represents the ratio between the peak signal power and the average noise power; a higher PSNR indicates better reconstruction performance. The PSNR is defined as [19]:

$$\mathrm{P}\mathrm{S}\mathrm{N}\mathrm{R}=10 {\log }_{10}({\displaystyle \frac{D_T^2\times N_T}{\sum _{p=1}^{N_T}{\left(T_e\left(p\right)-T_s\left(p\right)\right)}^2}})$$

(31)

where $N_T$ denotes the number of pixels in the image; $T_e$ is the experimental reconstructed BT; $T_s$ is the simulated BT reconstruction; $D_T$ is the maximum peak-to-peak swing of $T_s$.

The SSIM is used to quantify the structural similarity between two images. A value of SSIM closer to 1 indicates stronger structural similarity and better quality of BT reconstruction. The SSIM is given by [38]:

$$SSIM({\mathit{T}}_{\mathit{e}},{\mathit{T}}_{\mathit{s}})={\displaystyle \frac{(2{\mu }_{{\mathit{T}}_{\mathit{e}}}{\mu }_{{\mathit{T}}_{\mathit{s}}}+c_1)(2{\sigma }_{{\mathit{T}}_{\mathit{e}}{\mathit{T}}_{\mathit{s}}}+c_2)}{\left({\mu }_{{\mathit{T}}_{\mathit{e}}}^2+{\mu }_{{\mathit{T}}_{\mathit{s}}}^2+c_1\right)\left({\sigma }_{{\mathit{T}}_{\mathit{e}}}^2+{\sigma }_{{\mathit{T}}_{\mathit{s}}}^2+c_2\right)}}$$

(32)

where ${\mu }_{{\mathit{T}}_{\mathit{e}}}$ and ${\mu }_{{\mathit{T}}_{\mathit{s}}}$ denote the mean values of ${\mathit{T}}_{\mathit{e}}$ and ${\mathit{T}}_{\mathit{s}}$, respectively; ${\sigma }_{{\mathit{T}}_{\mathit{e}}}$ and ${\sigma }_{{\mathit{T}}_{\mathit{s}}}$ are the corresponding standard deviations. The constants $c_1={\left(0.01D_T\right)}^2$ and $c_2={\left(0.03D_T\right)}^2$ are used to prevent numerical instability caused by division by zero. The PSNR and SSIM values of the experimental reconstructed BT are summarized in

Table 1. Evaluation indexes of the experiment.

Observed Scene	Method	PSNR (dB)	SSIM
Noise Source	Before Correction	8.27	−0.16
	External-source Method (external source at $\xi =0$)	24.04	0.95
	External-source Method (external source at $\xi =0.02$)	11.60	0.51
	Proposed Method (spatial offset is 0)	27.47	0.98
	Proposed Method (spatial offset is 0.02)	27.83	0.98
Ceramic Plate	Before Correction	5.70	−0.23
	External-source Method (external source at $\xi =0$)	18.34	0.94
	External-source Method (external source at $\xi =0.02$)	9.04	0.58
	Proposed Method (spatial offset is 0)	19.78	0.96
	Proposed Method (spatial offset is 0.02)	19.88	0.96

.

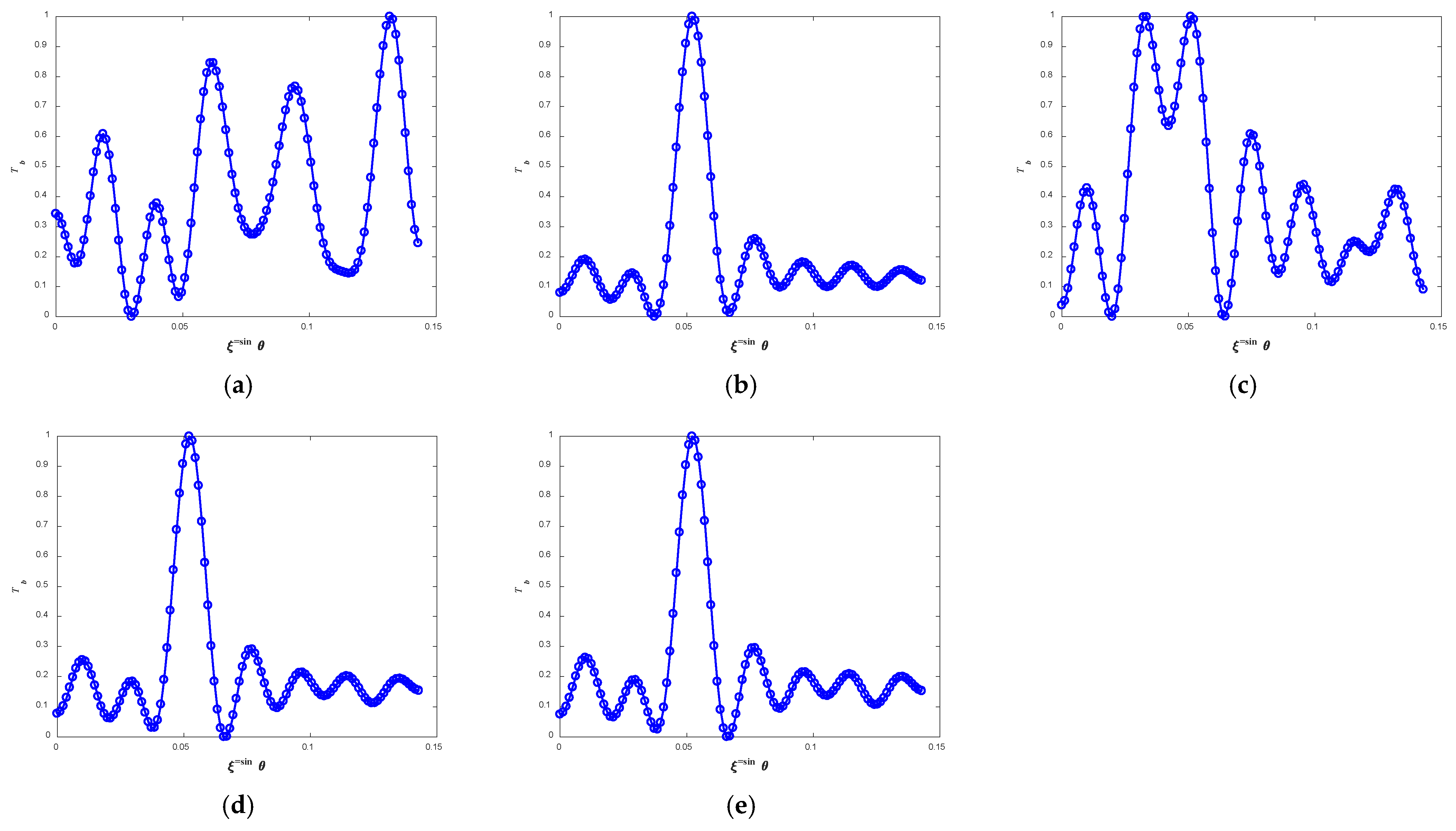
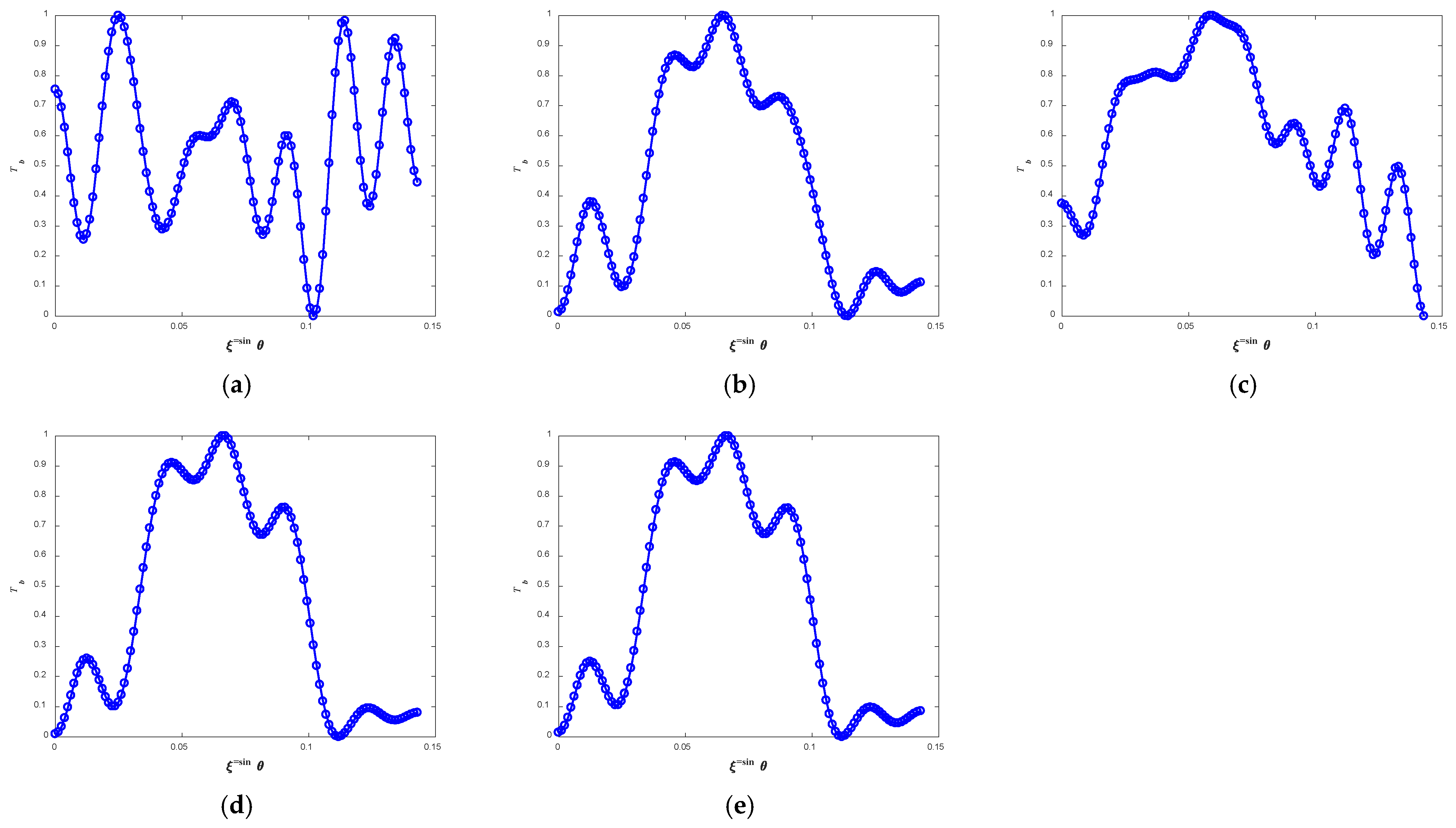
The results before correction are shown in Figure 12a for the noise source and Figure 13a for the ceramic plate. The PSNR values for the noise source and ceramic plate are 8.27 and 5.70 dB, respectively. The corresponding SSIM values are −0.16 and −0.23, respectively. Due to the influence of the errors, the images are severely distorted. The shapes of the noise source and the ceramic plate become unrecognizable.

After applying the external-source method [23], with the external source located at $\xi =0$, the reconstruction results of the noise source and ceramic plate are shown in Figure 12b and Figure 13b, respectively. The PSNR values for the noise source and ceramic plate increase to 24.04 and 18.34 dB, respectively. The corresponding SSIM values increase to 0.95 and 0.94, respectively. The noise source and the ceramic plate can be distinguished from the images, and the quality of BT reconstruction is significantly improved. As the external source is shifted to $\xi =0.02$, the reconstruction results of the noise source and the ceramic plate can be seen in Figure 12c and Figure 13c, respectively. Compared with the case when the external source is at $\xi =0$, the PSNR values for the noise source and ceramic plate decrease to 11.60 and 9.04 dB, respectively. The SSIM values similarly decrease to 0.51 and 0.58, respectively. The deviation of the external source from $\xi =0$ introduces additional errors. A spurious peak appears in the image of the noise source, and the corresponding high temperature region of the ceramic plate cannot be identified. The images are distorted. These results demonstrate that the effectiveness of the external-source method is highly sensitive to the position of the external source. In practice, it is challenging to position the external source at $\xi =0$ exactly.

The BT reconstruction results corrected by the proposed method with a spatial offset of $\delta =0$ are shown in Figure 12d for the noise source and Figure 13d for the noise source the ceramic plate. The PSNR values for the noise source and ceramic plate increase to 27.47 and 19.78 dB, respectively. The corresponding SSIM values increase to 0.98 and 0.96, respectively. In both figures, the shapes and positions of both the noise source and the ceramic plate are clearly distinguishable. The amplitude and phase errors are effectively corrected, and the image quality is significantly improved. When the spatial offset between the two h-function sequences is $\delta =0.02$, the results of the noise source and the ceramic plate are presented in Figure 12e and Figure 13e, respectively. The PSNR values for the noise source and ceramic plate increase to 27.83 and 19.88 dB, respectively. The corresponding SSIM values increase to 0.98 and 0.96, respectively. The PSNR and SSIM under this condition are close to those obtained when no spatial offset exists in two h-function sequences. This demonstrates that, by estimating the offset, the amplitude and phase errors can still be effectively corrected, leading to a significant improvement in BT image quality. It is noteworthy that neither obtaining the h-function sequences nor observing the scene requires removal of the reflector; therefore, the proposed method does not require reflector removal.

Compared with the external-source method, the proposed method achieves slightly higher PSNR and SSIM values, indicating that it provides a comparable or even superior correction performance. Additionally, the proposed method does not require removing the reflector during observations and imposes no special requirements on the spatial offset of the h function.

5. Discussion

The method proposed in the paper is a new method rather than a modification of the existing method. The existing method requires removing the reflector and using the AS system to measure the amplitude and phase errors. In contrast, the proposed method establishes a new correction framework: it estimates the error information from the simulated h function without errors and the measured h function that considers errors, both derived from MAS observations. Therefore, the proposed method does not require removing the reflector and represents a new correction strategy distinct from the existing method.

According to the quantitative error results in the extended source simulation, the $RMS{E}_T$ of the image is $6.0\times {10}^{-7}$ K after correcting by the external-source method (with the external source at $\xi =0$). When the spatial offsets of the h function are $\delta =0$ and $\delta =0.02$, the proposed method achieves $RMS{E}_T$ values of $4.2\times {10}^{-7}$ K and $3.9\times {10}^{-7}$ K, respectively. The quantitative evaluation results of the experiment are presented in Table 1. After applying the proposed method, the PSNR values for the noise source exceed 27 dB, and PSNR values reach 0.98; for the ceramic plate, the PSNR values exceed 19 dB, and the SSIM values reach 0.96. These results verify that the proposed method can effectively correct amplitude and phase errors and improve the quality of BT reconstruction. It is worth noting that all these evaluation metrics are slightly greater than those obtained by the external-source method. This is because the external-source method extracts the error information from a single AS measurement of the external source, whereas the proposed method extracts the error information from the h-function sequence obtained through multiple measurements of a point source placed at spatially equidistant positions. The system’s random errors are therefore attenuated through the multiple measurements.

In addition, removing or adjusting the reflector affects the motion characteristics of the platform and increases system complexity. Therefore, compared with the external-source method, the proposed method offers clear engineering advantages. Moreover, the spatial offset between the simulated and measured h-function sequences is inevitable in practical measurements. The offset can be automatically estimated through their cross-correlation function. As shown in Figure 8e, all ${RMSE}_T$ values are less than $5.2\times {10}^{-7}$ K in the simulation. In the experiment, when the offset is 0.02, the PSNR and SSIM show only small differences compared with the case when the offset is zero. These results confirm that the spatial offset is accurately estimated and that the performance of the proposed method is insensitive to the spatial offset of the h function.

However, the proposed method has two main disadvantages. (a) Compared with the external-source method, the proposed method requires multiple measurements of a point source at multiple spatially equidistant positions to obtain the h-function sequence, which increases the volume of acquired data and the overall processing time. In addition, estimating the spatial offset between two h-function sequences requires the computation of their cross-correlation function, which results in extra computational overhead. As a result, the proposed method has a higher time cost and computational complexity. (b) In the proposed error model, the error coefficient is assumed to be direction-independent. As a result, the proposed method can only correct the errors that are direction-independent (e.g., amplitude and phase errors). Direction-dependent errors (e.g., antenna pattern errors) require a more detailed error model and advanced parameter estimation techniques.

It is noteworthy that reflector position error is unique to MAS and does not exist in AS systems. The reflector position error is contained in the h function. The error information extraction strategy based on the h function in this paper may help future analysis and correction of the reflector position error.

6. Conclusions

In 1-D MAS, the existing correction method for amplitude and phase errors requires additional mechanical structures to remove the reflector and is highly sensitive to the position of the external source. To address these issues, this paper proposes a new correction method based on the h function.

The proposed method uses the h-function sequence without errors as prior knowledge to perform a least-squares estimation of the error correction coefficient. Furthermore, the estimated error correction coefficient is applied to correct the cross correlation. The proposed method does not require removing the reflector during measurements, thereby avoiding additional mechanical structures. In addition, the proposed method also imposes no special requirements on the spatial offset of the h function; therefore, the adaptability of correction method in practical observations is enhanced.

The simulation results indicate that the proposed method can improve the quality of BT reconstruction. The RMSE value before correction is $162\mathrm{K}$. When the spatial offsets are $\delta =$ 0 and $\delta =$ 0.02, the RMSE values of images corrected by the proposed method are $4.2\times {10}^{-7}$ K and $3.9\times {10}^{-7}$ K, respectively. The metric values show the proposed method effectively corrects the amplitude and phase errors. The RMSE values of the proposed method with different spatial offsets are all less than $5.2\times {10}^{-7}$ K, which verifies that the method is insensitive to the spatial offset of the h function.

In the experiment, the noise source and the ceramic plate are observed by the MAS-V. The PSNR values before correction are 8.27 dB for the noise source and 5.70 dB for the ceramic plate. The corresponding SSIM values are −0.16 and −0.23, respectively. For the ceramic plate, the PSNR values obtained by the proposed method with $\delta =0$ and $\delta =0.02$ increase to 19.78 and 19.88 dB, respectively. The PSNR value obtained by the external-source method is 18.34 dB. The SSIM values obtained by the proposed method increase to 0.96 for both $\delta =0$ and $\delta =0.02$. The SSIM value obtained by the external-source method is 0.94. A similar improvement exists in the quantitative results for the noise source. These quantitative results indicate that the proposed method provides slightly better performance than the external-source method and offers improved adaptability.

The simulation and experiment results demonstrate that, compared with the external-source method, the proposed method has two key advantages: it achieves comparable correction performance without requiring additional mechanical structures for reflector removal, and it provides enhanced adaptability.