A Dynamic Gaussian Modified Spectral Band Adjustment Factors Method for Radiometric Cross-Calibration of HJ-2A/HSI with ZY1-02D/AHSI

Highlights

What are the main findings?

• A DG-SBAF method was developed to model spectral channels with Gaussian response functions, dynamically matching multiple reference-sensor channels and optimizing SBAF weights.
• Applied to HJ-2A/HSI–ZY-1-02D/AHSI cross-calibration, the method achieved 12.11% and 8.64% relative improvements in VNIR and SWIR, respectively.

What are the implications of the main findings?

• DG-SBAF mitigates spectral mismatches and enhances radiometric stability.
• Enables more accurate on-orbit calibration and long-term radiometric consistency among sensors.

Abstract

The Huanjing Jianzai-2A (HJ-2A), launched in 2020 as China’s civilian operational environmental satellite, exhibits intrinsic non-uniformity from spectral channel distribution and inconsistency from the spectral resolution in its hyperspectral imager (HSI). These spectral characteristics compromise the spectral channel matching process, posing challenges to the traditional cross-calibration method. To overcome these spectral matching constraints, this study proposed a Dynamic Gaussian Spectral Band Adjustment Factors (DG-SBAF) method for cross-calibration that constructs a Gaussian distribution model for each spectral channel of the target sensor, dynamically matches the spectral channels of the reference sensor and optimizes SBAF compensation weights through Gaussian function values. The cross-calibration of HJ-2A/HSI was conducted using ZiYuan1-02D Advanced Hyperspectral Imager (ZY1-02D/AHSI) through three distinct test sites: Dunhuang, Baotou, and Taklamakan Desert. The cross-calibration results analysis across three sites revealed mean relative deviations of 6.46% (VNIR) and 8.67% (SWIR), demonstrating superior performance over the traditional SBAF method (7.35% to VNIR, 9.49% to SWIR). Analyses of SBAF fluctuation showed that the DG-SBAF method achieved SBAF distributions approaching 1 with mean RMSE values of 0.0312 (VNIR) and 0.1086 (SWIR). Validation through spectral consistency assessment showed spectral angles less than 5° and 7° in VNIR bands when compared with Gaofen-5B/AHSI and Land-sat-9/OLI-2, respectively, and less than 6° with GF-5B/AHSI in SWIR bands. The pro-posed method effectively corrects spectral channel discrepancies in the matching process, enhances radiometric stability, and provides effective supplementary on-orbit calibration capability.

1. Introduction

Huanjing Jianzai satellite-2A/B satellites (HJ-2A/B) were twin satellites launched in September 2020 with a five-year design lifespan [1]. They built upon the applications of disaster observation developed for their predecessors, the HJ-1A/B satellites, which have been in orbit for 12 years. The two satellites have been designed to rapidly acquire ground surface through co-orbital networking, with revisit periods of two days for visible and infrared multispectral data and 15 days for hyperspectral data [2]. Relying on the Disaster Reduction Application System of Satellite, the HJ series data have been successfully used within the realm of disaster observations, including disaster monitoring and risk assessment. The payload complement comprises four advanced sensors: a 16 m resolution multispectral camera, hyperspectral imager (HSI), infrared camera, and atmospheric corrector [3]. The HSI implements Large Aperture Static Imaging Spectrometer technology [4], featuring multi-component architecture that includes: a front optical system, lateral shear interferometer, Fourier transform len, detector, and data collection system. This innovative configuration enables spectral map generation through interferometric data acquisition at varying optical path differences, followed by Fourier transform processing [5]. The optical system and physical structure of the HSI are illustrated in Figure 1. Unlike traditional dispersive hyperspectral imagers, the interferometric design of the HSI enables more efficient energy utilization. However, its indirect data acquisition mechanism—requiring spectral reconstruction from interferometric signals—makes the resulting hyperspectral data more sensitive to calibration uncertainties, thereby demanding more rigorous and precise radiometric calibration.

Figure 1. HJ-2A/HSI optical system and optical structure: (a) Optical system of HJ-2A/HSI; (b) Physical structure of HJ-2A/HSI.

The radiometric response of the HSI sensor exhibits gradual degradation as a result of combined influences such as space radiation exposure, component aging, and mechanical vibration. Although the onboard calibration system provides basic spectral calibration capability, it is unable to capture short-term or rapid variations in radiometric response, and the low temporal frequency of site calibration campaigns further limits the ability to monitor real-time changes in sensor performance. A statistical analysis of the site calibration coefficients obtained [6] for HJ-2A/HSI from 2022 to 2024 confirms these limitations, as different degrees of radiometric degradation were observed across spectral bands, indicating clear temporal variations in the sensor’s on-orbit behavior. The temporal trends for the VNIR and SWIR bands are shown in Figure 2.

Figure 2. HJ-2A/HSI temporal trend of site radiometric calibration coefficients: (a) VNIR-temporal trend of calibration coefficients; (b) SWIR-temporal trend of calibration coefficients.

On-orbit radiometric calibration generally relies on a combination of onboard calibration, site calibration, and cross-calibration. Each contributes distinct and complementary information, and together they form a comprehensive framework for evaluating long-term radiometric stability. In the case of HJ-2A/HSI, however, the absence of an onboard absolute radiometric calibration unit and the fact that site calibration activities are typically performed only once per year impose significant constraints on maintaining timely and continuous characterization of its radiometric response. As a result, cross-calibration becomes an indispensable component of the overall calibration strategy. It provides higher temporal coverage, reduces operational cost, and enables traceable recalibration, thereby offering an effective means of compensating for the inherent limitations of onboard and site-based methods. The practical value of cross-calibration has been demonstrated in several operational Earth observation missions. For example, EO-1/Hyperion has used Landsat 7/ETM+ and Terra/MODIS as references to derive SBAF-corrected spectral differences and achieve better than 5% radiometric accuracy at four desert sites [7]; FY-4A/AGRI, referencing MODIS’s high-precision on-orbit calibration, realized 5.2% cross-calibration accuracy through rigorous geometric, spectral, and spatio-temporal matching [8]; and GF-1/PMS, employing matched-image adjustment factors with dual references (MODIS and Landsat 8/OLI), secured high-precision calibration over Dunhuang and Golmud while quantifying performance differences between its reference sensors [9]. Collectively, these applications highlight the continued evolution of cross-calibration methodologies.

Within the methodological evolution of cross-calibration, the Spectral Band Adjustment Factors (SBAFs) have emerged as a key technique for addressing sensor-specific variations in spectral response, owing to its superior spectral-matching performance compared with direct interpolation or downsampling. Initially proposed by [10], Vogelmann et al. attempted to resolve radiometric calibration discrepancies between the Landsat 5 Thematic Mapper (TM) and Landsat 7 Enhanced Thematic Mapper Plus (ETM+). The SBAF method was subsequently validated by [11] through a 20-year time series analysis. Markham et al. confirmed its stability and universality in cross-sensor radiometric consistency correction. Ref. [12] advanced the technique by integrating the MODTRAN atmospheric radiative transfer model, effectively addressing spectral response differences between the Moderate Resolution Imaging Spectroradiometer (MODIS) and Landsat8 Operational Land Imager (OLI). Further innovations by [13], Villaescusa-Nadal et al. introduced a dynamic SBAF framework adaptable to diverse surface types and atmospheric conditions, significantly reducing atmospheric path radiation interference. Most recently, [14] demonstrated SBAF’s applicability in ocean remote sensing by correcting spectral response discrepancies between the HY-1C Chinese Ocean Color and Temperature Scanner (COCTS) and Sentinel-3 Ocean and Land Colour Instrument (OLCI). While the SBAF has proven effective for multi-sensor cross-calibration [10,11,12,13,14,15], its application to hyperspectral systems—particularly interferometric hyperspectral imagers—faces two fundamental constraints: non-uniform spectral channel distributions across overlapping spectral ranges, and inconsistent spectral resolutions between sensor platforms. For interferometric hyperspectral imagers, the spectral channels are typically non-equidistant and exhibit wavelength-dependent variations in spectral resolution, making the conventional channel-matching strategy in the SBAF framework insufficient to fully correct for spectral discrepancies. The non-uniform channel distribution in overlapping spectral regions induces wavelength-dependent spectral registration errors during cross-calibration processes. Furthermore, spectral resolution discrepancies between multi-sensors lead to radiometric deviations through the convolution of spectral response functions (SRFs), particularly in wide-to-narrow band conversion scenarios.

To address the aforementioned limitations of the SBAF method, we propose a dynamic Gaussian distribution modified SBAF method for radiometric cross-calibration. The method constructs a Gaussian distribution model for each spectral channel of the target sensor, dynamically matches the spectral channels of the reference sensor, and optimizes SBAF compensation weights through Gaussian function values. Based on the proposed method, we conducted cross-calibration experiments using HJ-2A/HSI (China Aerospace Science and Technology Corporation (CASC), Beijing, China) as the target sensor and ZiYuan1-02D Advanced Hyperspectral Imager (ZY1-02D/AHSI) (China Aerospace Science and Technology Corporation (CASC), Beijing, China) as the reference sensor at three calibration sites: Dunhuang, Baotou, and Taklamakan Desert (Tak). The calibration results were validated using independent datasets from Gaofen-5B Advanced Hyperspectral Imager (GF-5B/AHSI) (China Aerospace Science and Technology Corporation (CASC), Beijing, China) and Landsat-9 Operational Land Imager-2 (Landsat-9/OLI-2) (NASA Goddard Space Flight Center (GSFC) Greenbelt, MD, USA). Moreover, we also discussed the limitations of our method and the factors that may affect the cross-calibration accuracy.

2. Calibration Sites and Data Preparation

2.1. Calibration Sites

The selection of calibration sites critically influences cross-calibration accuracy. Ideal sites should satisfy three criteria: (1) high spatial homogeneity of surface types; (2) flat terrain with sufficient spatial extent; and (3) smooth spectral reflectance curves without significant fluctuations [16,17]. Considering these criteria alongside imaging quality constraints, temporal synchronization between sensors, and viewing geometry limitations, three sites were selected: Dunhuang, Baotou, and Tak. The spatial distribution of chosen test sites is illustrated in Figure 3. Simultaneously, to further validate the cross-calibration results, two contrasting and representative land-cover types were selected as validation sites: a highly homogeneous desert site (Dunhuang) and a vegetated site (located in Baotou City). The uniform surface characteristics at the Dunhuang site enable precise evaluation of the proposed calibration method’s performance, while the spatial variability at the vegetation site provides a rigorous test of its robustness and stability under complex surface conditions.

Figure 3. Cross-calibration test sites. (A) Tak site, (B) Dunhuang site, (C) Baotou site.

The Dunhuang radiometric calibration site, located in a vegetation-free Gobi desert (40.04–40.28°N, 94.17–94.5°E, 1229 m altitude), features a homogeneous 25 km × 25 km flat terrain [18]. The coordinates of the selected trial area are 40.08°N, 94.18°E. This CEOS/WGCV-recognized site has been successfully employed for cross-calibration of multiple satellite missions, including the China-Brazil Earth Resources Satellite (CBERS) series [19], GF series [20], and FY series [21]. The Baotou calibration site (40.85°N, 109.62°E, 1236 m altitude) in Inner Mongolia’s Bayannur City was listed in 2020 as the fifth globally recognized site in the Radiometric Calibration Network (RadCalNet) [22]. It features a 1.5 km × 0.35 km natural sandy area maintained through on-site technical interventions to ensure high surface flatness and spectral uniformity [23,24]. In addition, a vegetated site located in the south-central part of Baotou City was selected as a representative vegetation validation site [25]. The area exhibits dense vegetation coverage during the summer growing season (August acquisition), providing suitable conditions for evaluating the cross-calibration performance over heterogeneous surface types. The coordinates of the selected area are 40.95°N, 109.94°E. The Tak Calibration Site (37–41°N, 78–88°E, 1200 m altitude), situated in the central Tarim Basin, features expansive and homogeneous desert terrain with exceptional spatial uniformity and minimal seasonal reflectance variation. The coordinates of the selected trial area are 38.54°N, 83.82°E. Recognized by CEOS/WGCV, this hyper-arid site (annual precipitation < 50 mm) provides optimal conditions for satellite calibration due to its stable atmospheric properties and vegetation-free surface [26].

2.2. Data Preparation

HJ-2A and ZY1-02D are both sun-synchronous orbits, and the specific parameters of the two satellites’ sensors are shown in Table 1 [27]. HJ-2A/HSI and ZY1-02D/AHSI are screened by data in Dunhuang, Baotou, and Tak to obtain cross-calibrated image pairs of the three sites. To mitigate radiometric discrepancies between the datasets, image pairs acquired by both sensors with closely matched acquisition times were collected. Imaging times were all in the interval of August to October to obtain stable atmospheric and surface conditions [17], as illustrated in Table 2.

Table 1. Parameters of HJ-2A/HSI, ZY1-02D/AHSI, GF-5B/AHSI and Landsat-9/OLI-2.

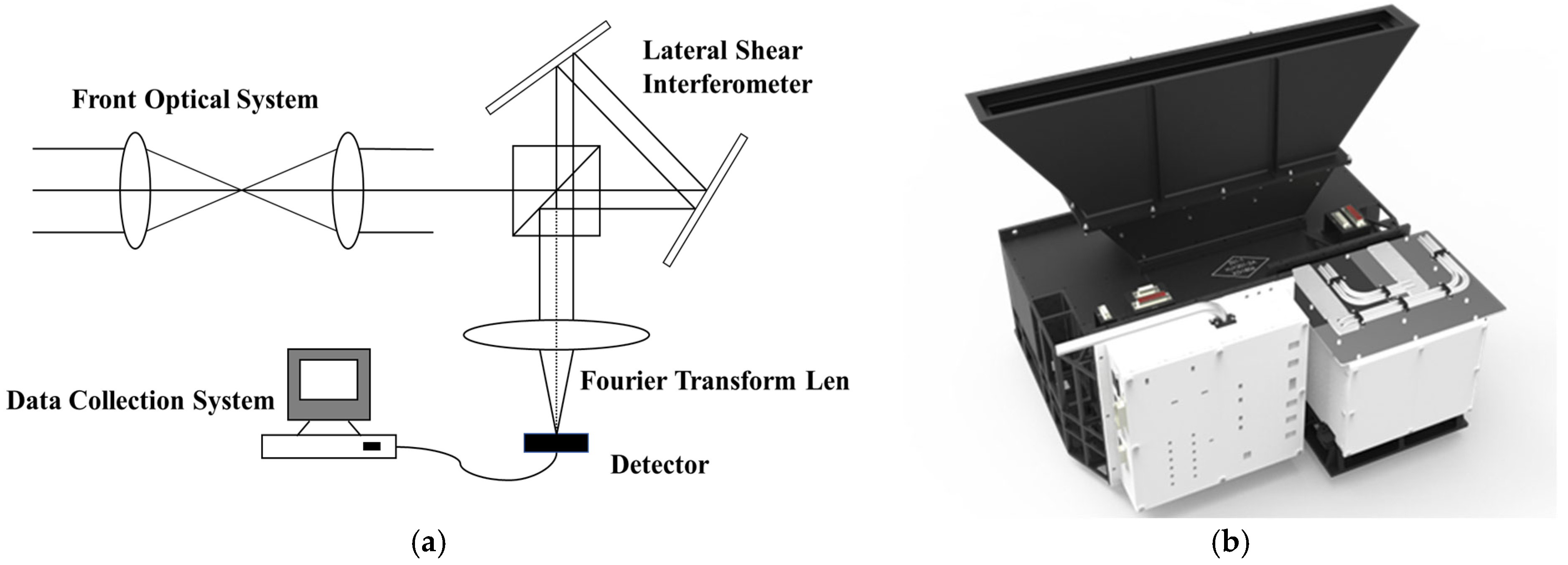
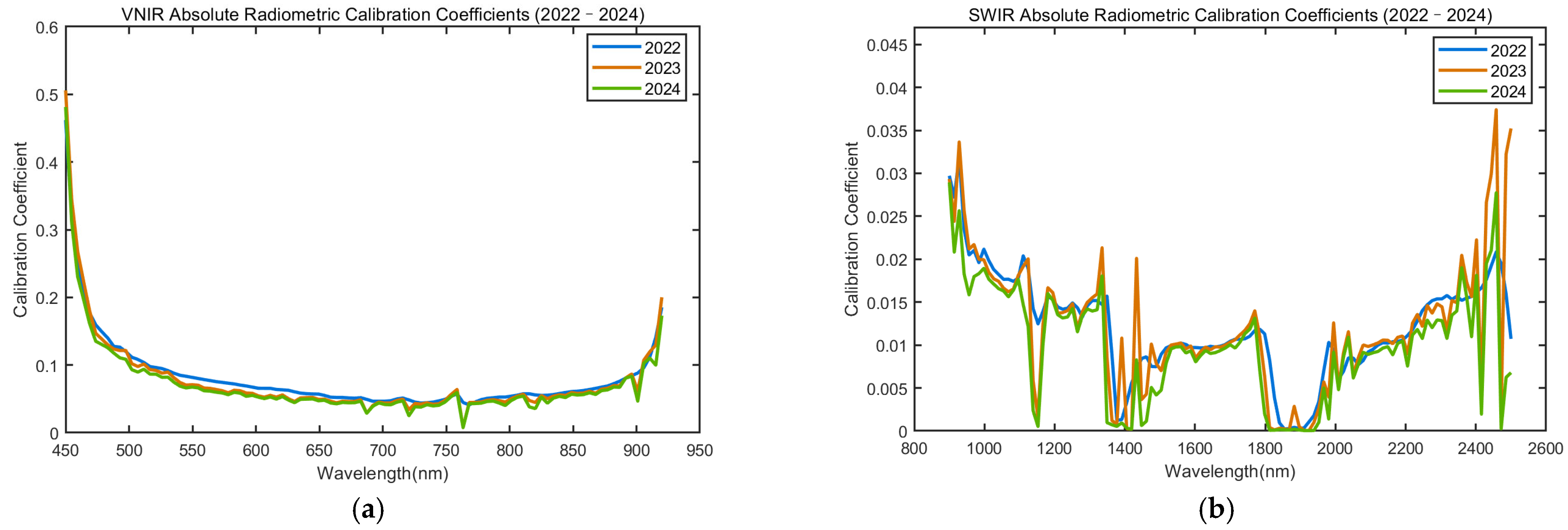
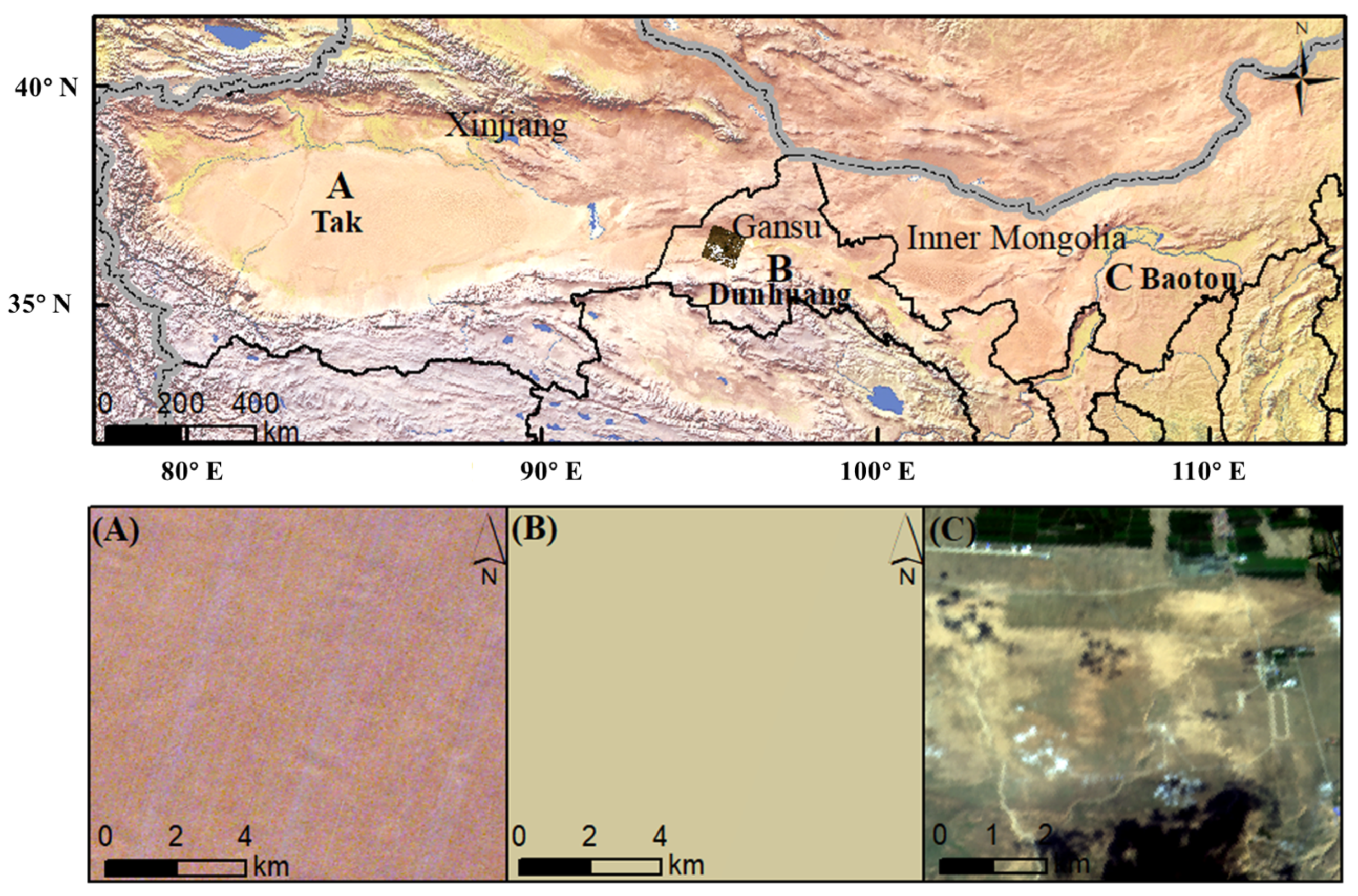
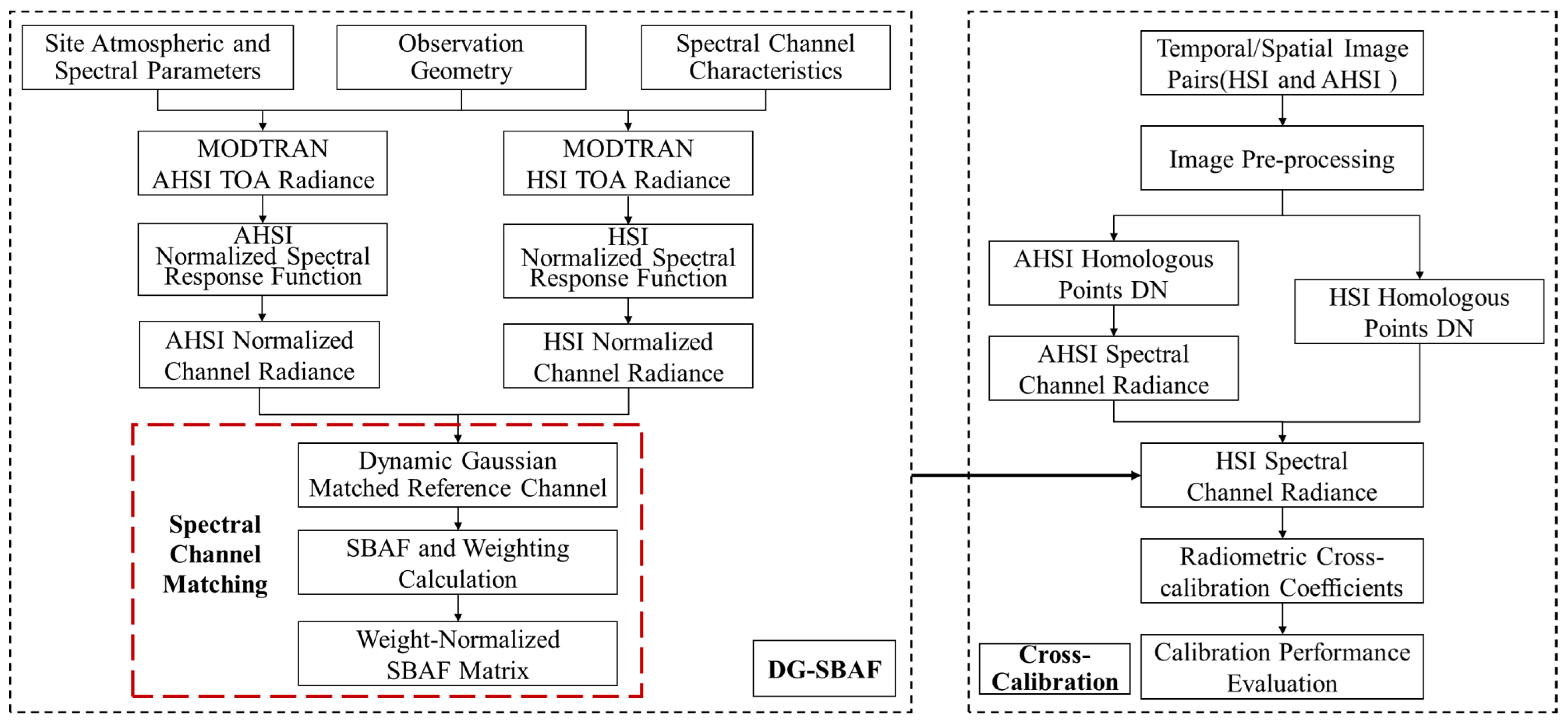
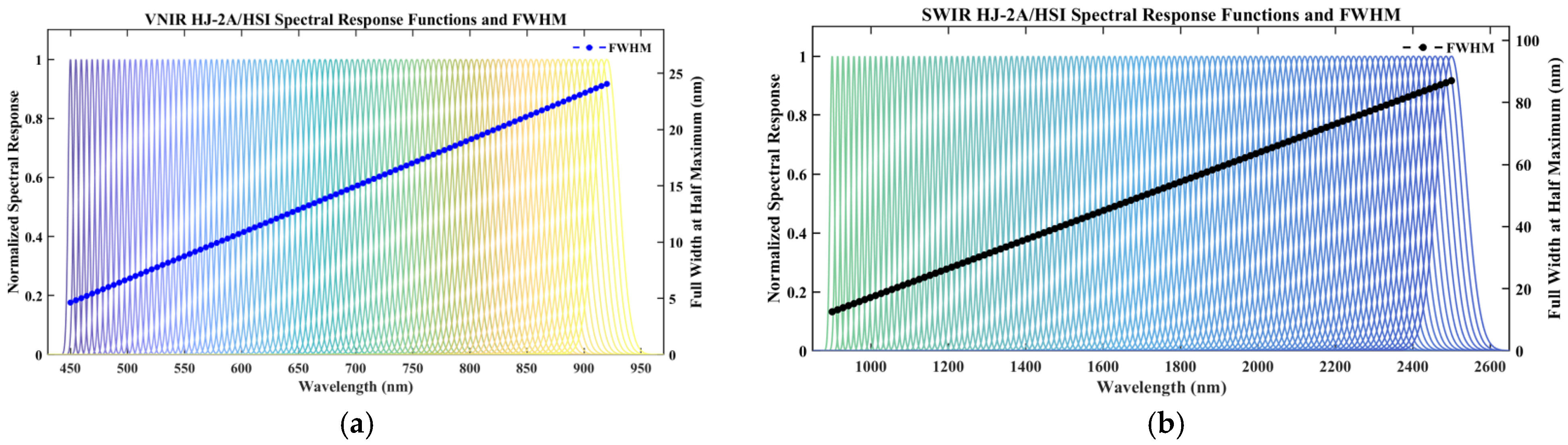
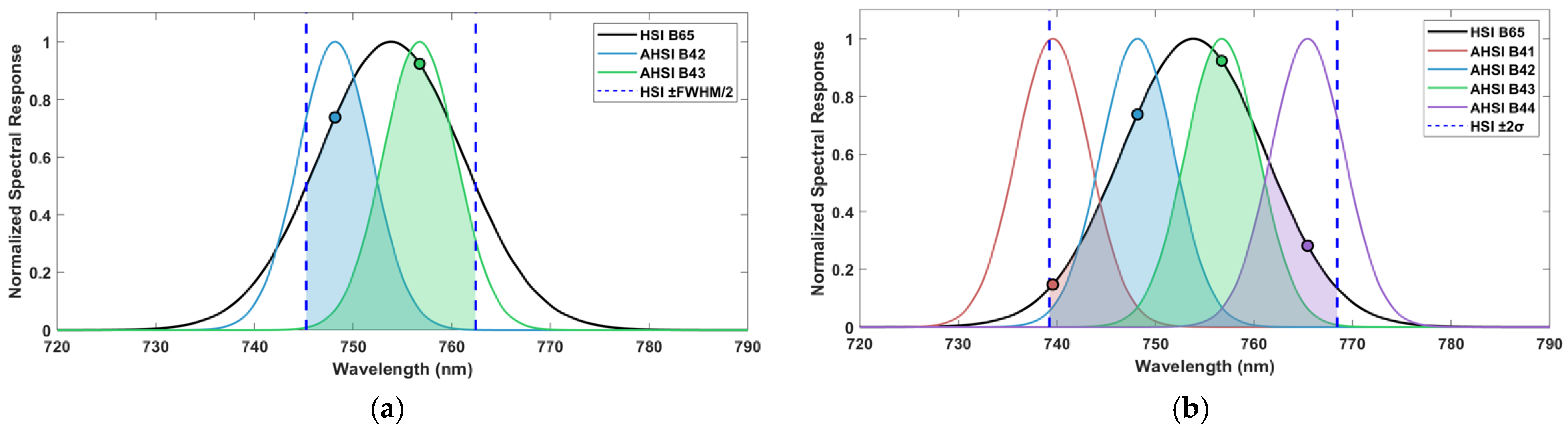
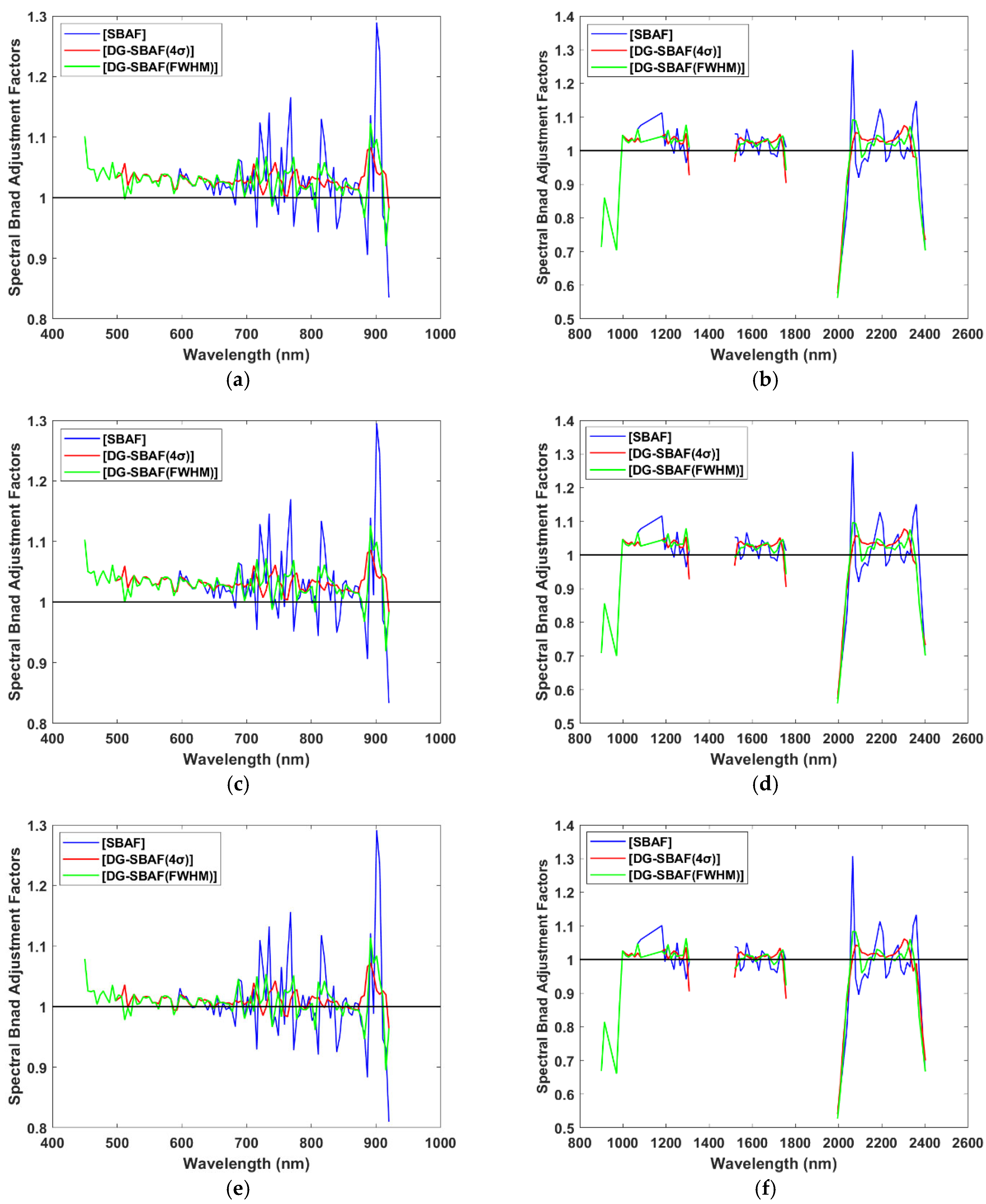
PARAMETER	HJ-2A/HSI	ZY1-02D/AHSI	GF-5B/AHSI	Landsat-9/OLI-2
Orbit altitude (km)	645	778	705	705
Revisit period (days)	41	55	51	16
Ground sample distance (m)	VNIR: 48 SWIR: 96	30	30	30 (1–7,9)
Swath width (km)	96	60	60	185
Spectral range (nm)	450–2500	400–2500	380–2500	430–2300
Spectral resolution (nm)	VNIR: 4~24 SWIR: 12~87	VNIR: 10 SWIR: 20	VNIR: 5 SWIR: 10	20–200
Spectral bands	215	166	330	9
Accuracy of the absolute radiometric calibration	--	<7%	<5%	<5%
Accuracy of the relative radiometric calibration	<3%	<3%	<3%	<1%

Table 2. Image pairs of HJ-2A/HSI and ZY1-02D/AHSI.

Sites	Sensors	Dates	Times	Solar Zenith	Solar Azimuth	Satellite Zenith	Satellite Azimuth
Dunhuang	HJ-2A/HSI	2 August 2024	T05:08:01	24.14°	156.76°	1.00°	164.57°
	ZY1-02D/AHSI	3 August 2024	T04:37:11	27.26°	140.07°	9.57°	280.35°
Baotou	HJ-2A/HSI	26 September 2024	T04:10:43	42.75°	171.18°	5.34°	110.50°
	ZY1-02D/AHSI	26 September 2024	T03:29:06	44.84°	157.11°	0.36°	174.43°
Tak	HJ-2A/HSI	26 September 2024	T05:48:55	40.65°	170.01°	0.97°	167.53°
	ZY1-02D/AHSI	26 September 2024	T05:10:14	42.65°	155.10°	0.36°	173.50°

The GF-5B/AHSI and Landsat-9/OLI-2 sensors are utilized as the validation sensors to verify the cross-calibration coefficients obtained by HJ-2A at the three sites. The absolute radiometric calibration accuracies of GF-5B and Landsat-9 are all 5% [28,29], respectively, which are indicative of their status as high-precision remote sensors on a global scale. The specific parameter information of the two is shown in Table 1 [29]. The Dunhuang site and Vegetation site were selected for validation, and the image pairs from July 2024 and August 2024, respectively, obtained through screening, are shown in Figure 4, with their specifications detailed in Table 3.

Figure 4. Validation image pairs: (a) Dunhuang site, (A) HJ-2A/HSI image, (B) GF-5B/AHSI image, (C) Landsat-9/OLI-2 image; (b) Vegetation site, (A) HJ-2A/HSI image, (B) GF-5B/AHSI image, (C) Landsat-9/OLI-2 image.

Table 3. Image pairs of GF-5B/AHSI AND Landsat-9/OLI-2 (Dunhuang and Vegetation).

Sites	Sensors	Dates	Times	Solar Zenith	Solar Azimuth	Satellite Zenith	Satellite Azimuth
Dunhuang	HJ-2A/HSI	29 July 2024	T05:11:10	23.21°	155.85°	5.38°	110.39°
	GF-5B/AHSI	30 July 2024	T04:45:00	25.95°	142.37°	0.09°	194.05°
	Landsat-9/OLI-2	30 July 2024	T04:25:41	28.78°	133.31°	0.21°	183.47°
Vegetation	HJ-2A/HSI	20 August 2024	T04:08:39	29.73°	162.28°	5.38°	110.49°
	GF-5B/AHSI	23 August 2024	T03:40:14	32.35°	150.99°	0.09°	194.38°
	Landsat-9/OLI-2	18 August 2024	T03:17:53	32.98°	140.16°	0.21°	183.47°

2.3. Data Preprocessing

After selecting the experimental sites, all image pairs were subjected to a uniform preprocessing workflow. First, cloud-cover and cloud-shadow pixels within the overlapping area of each image pair were identified and removed. From the remaining valid region, we selected 100 × 100–pixel subregions as candidate cross-calibration areas. Each candidate area was then processed with a 100 × 100 sliding window applied window-by-window. For every window and for each spectral band, the mean (μ) and standard deviation (σ) of the DN values were calculated, and then the coefficient of variation (CV) was calculated according to the following Equation (1):

$$CV={\displaystyle \frac{\sigma }{\mu }}$$

(1)

where σ is the DN standard deviation and μ is the DN mean under the window. A window was retained as a “homogeneous target region” for cross-calibration only if it satisfied both of the following criteria: (1) it contained a sufficient number of valid pixels (pixels that were neither missing nor equal to zero), and (2) its CV in the current band was below 0.03 (CV < 0.03) [30]. This procedure ensures a consistent selection of study regions across all image pairs.

Subsequently, the spatial resolution of the sensors was harmonized. Datasets from ZY1-02D/AHSI, GF-5B/AHSI, and Landsat-9/OLI-2 were resampled to 48 m using the nearest neighbor interpolation method, matching the native resolution of the HJ-2A/HSI sensor. The nearest-neighbor interpolation method most faithfully retains the original digital number (DN) values, thereby minimizing the effects of downsampling on subsequent analyses [31]. Following resampling, geometric registration was performed using feature-based matching. Specifically, the SURF (Speeded-Up Robust Features) algorithm was employed to extract and match control points. The final co-registration accuracy achieved was better than 5 m. Furthermore, the differences in solar zenith angles and sensor viewing angles between the image pairs in this study were small [32], and all acquisitions occurred near local solar noon (adjusted for time zone). Moreover, the calibration sites exhibit Lambertian reflection characteristics. Therefore, the influence of the Bidirectional Reflectance Distribution Function (BRDF) effects was not considered in this study.

3. Methodology

3.1. Overall Workflow for Cross-Calibration

Our cross-calibration method incorporates the spectral channel characteristics of the HSI to optimize the spectral channel matching process. The flowchart was illustrated in Figure 5.

Figure 5. Flowchart of HJ-2A/HSI and ZY1-02D/AHSI cross-calibration.

3.2. Dynamic Gaussian Modified SBAF Method

First, the top-of-atmosphere (TOA) radiances for the two sensor viewing geometries were simulated using the MODTRAN radiative-transfer model. Because both sensors acquired imagery over the same area at nearly the same time, MODTRAN’s built-in standard atmospheric profile, aerosol model, and water-vapor parameters corresponding to each image-pair acquisition date were used. Geometric inputs comprised the actual solar/satellite zenith and azimuth angles, the acquisition date and time, and the sensors’ viewing-geometry parameters (satellite zenith/azimuth and field of view), ensuring consistency between the two simulations. The TOA radiance values were then integrated with the SRF of each sensor channel to yield the radiometric response of each channel [33], as in Equation (2).

$$L^{\prime }({\lambda }_i)={\displaystyle \frac{{\int }_{{\lambda }_1}^{{\lambda }_2}{S}_i\left(\lambda \right)·L_{TOA}^{\prime }\left(\lambda \right)d\lambda }{{\int }_{{\lambda }_1}^{{\lambda }_2}{S}_i\left(\lambda \right)d\lambda }}$$

(2)

where, $S_i\left(\lambda \right)$ represents the spectral response function (SRF) of the sensor channel i, $L_{TOA}^{\prime }\left(\lambda \right)$ represents the MODTRAN-simulated top-of-atmosphere (TOA) radiance of the sensor, and $L^{\prime }\left({\lambda }_i\right)$ represents the channel radiance of $L_{TOA}^{\prime }\left(\lambda \right)$ after convolution with the SRF of the sensor channel i ${\lambda }_1$ and ${\lambda }_2$ are the lower and upper wavelength limits of channel i, respectively. Based on Equation (2), the radiance for all channels of HSI and AHSI can be simulated.

$L_{TOA}^{\prime }\left(\lambda \right)$ is simulated under the solar zenith angle corresponding to the actual scene acquisition, and the simulation inherently accounts for the differences in observation geometry between the two sensors. The simulated TOA radiance spectrum $L_{TOA}^{\prime }\left(\lambda \right)$ is subsequently convolved with the SRFs of both sensors to derive the band radiances (channel-integrated). Based on Equation (2), the radiance for all channels of the HSI and AHSI sensors can thus be simulated, and these simulated channel radiances are then used to calculate the radiance-based SBAF [15].

For each sensor, the channel radiances can be expressed as:

$$L_{HSI}^{\prime }({\lambda }_i)={\displaystyle \frac{{\int }_{{\lambda }_1}^{{\lambda }_2}{S}_i\left(\lambda \right)·L_{HSI,TOA}^{\prime }\left(\lambda \right)d\lambda }{{\int }_{{\lambda }_1}^{{\lambda }_2}{S}_i\left(\lambda \right)d\lambda }}$$

(3)

$$L_{AHSI}^{\prime }({\lambda }_j)={\displaystyle \frac{{\int }_{{\lambda }_3}^{{\lambda }_4}{S}_j\left(\lambda \right)·L_{AHSI,TOA}^{\prime }\left(\lambda \right)d\lambda }{{\int }_{{\lambda }_3}^{{\lambda }_4}{S}_j\left(\lambda \right)d\lambda }}$$

(4)

Next, the SBAF between the corresponding channels of the two sensors is then calculated as Equation (5):

$$SBAF={\displaystyle \frac{L_{HSI}^{\prime }\left({\lambda }_i\right)}{L_{AHSI}^{\prime }\left({\lambda }_j\right)}}$$

(5)

where $L_{HSI}^{\prime }\left({\lambda }_i\right)$ and $L_{AHSI}^{\prime }\left({\lambda }_j\right)$ are the simulated channel radiance from sensor i-th HSI and the sensor j-th AHSI.

The HJ-2A/HSI is an interferometric hyperspectral imager whose raw data exhibit an equidistant wavenumber distribution. Spectral data are obtained only after retrieval of the raw interferometric data and the retrieved spectral data exhibit non-uniform spectral channel distribution and inconsistent spectral resolution. Specifically, in the visible and near-infrared (VNIR) region (450–920 nm), spectral resolution fluctuations of 4–25 nm; in the short-wave infrared (SWIR) region (900–2500 nm), spectral resolution fluctuations of 12–87 nm. As shown in Figure 6, the SRF of the HSI reflects these spectral characteristics, exhibiting progressively broader response bandwidths after peak normalization. In contrast, the dispersive hyperspectral imager ZY1-02D/AHSI maintains consistent response bandwidths and peak magnitudes across VNIR-SWIR bands under identical normalization, as illustrated in Figure 7.

Figure 6. Spectral response functions (SRFs) and full width at half maximum (FWHM) of HJ-2A/HSI: (a) VNIR SRF and FWHM of HJ-2A/HSI; (b) SWIR SRF and FWHM of HJ-2A/HSI.

Figure 7. Spectral response functions (SRFs) and full width at half maximum (FWHM) of ZY1-02D/AHSI: (a) VNIR SRF and FWHM of ZY1-02D/AHSI; (b) SWIR SRF and FWHM of ZY1-02D/AHSI.

Based on the aforementioned HSI spectral channel characteristics, Gaussian distribution models for each HSI spectral channel were constructed, as defined in Equation (6), to dynamically match the spectral channels of the reference AHSI sensor.

$${Gaussian}_{{\lambda }_{HSI,i}}\left(\lambda ,{\sigma }_i\right)=\exp \left[{\displaystyle \frac{{\left(\lambda -{\lambda }_{HSI,i}\right)}^2}{2{{\sigma }_i}^2}}\right]$$

(6)

In Equation (6), ${\lambda }_{HSI,i}$ represents the central wavelength of the i-th spectral channel of HSI, the ${\sigma }_i$ was dynamically adjusted based on the channel-specific full width at half maximum (FWHM). $\lambda$ denotes an arbitrary wavelength within the spectral response range.

The Gaussian spectral response model defines two characteristic integration ranges for cross-sensor channel matching: [FWHM] and [4σ]. Firstly, based on the shape characteristics of the Gaussian function, the [FWHM] centric interval $\lambda \in \left[{\lambda }_{HSI,i}-{\displaystyle \frac{FWHM}{2}},{\lambda }_{HSI,i}+{\displaystyle \frac{FWHM}{2}}\right]$ covers 76.00% of the spectral energy, corresponding to the Gaussian main lobe, reflecting the region of highest energy density and ensuring that the peak energy dominates the matching. The [4σ] interval $\lambda \in \left[{\lambda }_{HSI,i}-2\sigma ,{\lambda }_{HSI,i}+2\sigma \right]$ covers 95.45% of the energy, including both central and wing contributions, providing a more complete characterization of the channel bandwidth. Secondly, based on the distribution characteristics of hyperspectral channels, the [FWHM] interval emphasizes central-band energy, reducing sensitivity to minor wavelength offsets, while [4σ] better accounts for inter-sensor differences in bandwidth and spectral shape, minimizing systematic biases. Therefore, both [FWHM] and [4σ] intervals were adopted in this study for robust spectral channel matching.

Taking the VNIR-65 and SWIR-51 bands of HSI as examples, the ZY1-02D/AHSI reference channels were identified within the [FWHM] range and the [4σ] range, respectively. In the figures, black lines represent the HSI channels, while colored lines indicate the matched reference channels. The blue dashed lines denote the width boundaries of the respective intervals, and the circle markers indicate the positions of the reference channel center wavelengths within the HSI channels’ Gaussian response. The matching results are illustrated in Figure 8 and Figure 9, respectively.

Figure 8. Spectral HJ-2A/HSI with ZY1-02D/AHSI spectral channel matching at two characteristic integration ranges using the VNIR-65 Band: (a) Spectral channel matching [FWHM]; (b) Spectral channel matching [4σ].

Figure 9. Spectral HJ-2A/HSI with ZY1-02D/AHSI spectral channel matching at two characteristic integration ranges using the SWIR-51 Band: (a) Spectral channel matching [FWHM]; (b) Spectral channel matching [4σ].

After the aforementioned dual-range matching strategy, the j-th spectral channels (j = 1, 2, …, G) of AHSI can be dynamically correlated. Using simulated at-sensor radiance data $L_{HSI}^{\prime }{(\lambda }_i)$ and $L_{AHSI}^{\prime }{(\lambda }_j)$, the SBAF for the i-th channel of HSI is calculated as:

$${SBAF}_{i,j}=\left[{\displaystyle \frac{L_{HSI}^{\prime }\left({\lambda }_i\right)}{L_{AHSI}^{\prime }\left({\lambda }_1\right)}} ,{\displaystyle \frac{L_{HSI}^{\prime }\left({\lambda }_i\right)}{L_{AHSI}^{\prime }\left({\lambda }_2\right)}} ,\dots ,{\displaystyle \frac{L_{HSI}^{\prime }\left({\lambda }_i\right)}{L_{AHSI}^{\prime }\left({\lambda }_G\right)}}\right]$$

(7)

In Equation (7), ${SBAF}_{i,j}$ represents the SBAF between the i-th channel of HSI and the j-th matched spectral channel of AHSI. Here, $L_{HSI}^{\prime }\left({\lambda }_i\right)$ and $L_{AHSI}^{\prime }\left({\lambda }_j\right)$ represent simulated radiance for the i-th (HSI) and j-th (AHSI) spectral channels.

The SBAF weighting values for matching the i-th HSI channel are derived by integrating the central wavelengths of the j-th AHSI channels into the Gaussian model, as shown in Equation (8):

$$w_{i,j}={Gaussian}_{{\lambda }_{HSI,i}}\left({\lambda }_{AHSI,j},\sigma \right)=\exp \left[{\displaystyle \frac{{\left({\lambda }_{AHSI,j}-{\lambda }_{HSI,i}\right)}^2}{2{\sigma }^2}}\right]$$

(8)

In Equation (9), ${w^{\prime }}_{i,j}$ represents the normalized weight coefficient for the SBAF of each AHSI channel.

$${w^{\prime }}_{i,j}={\displaystyle \frac{w_{i,j}}{\sum \left(w_{i,1}+w_{i,2}+\dots +w_{i,G}\right)}}$$

(9)

By applying these weights, the final SBAF group for the i-th channel of HSI is obtained as follows:

$${SBAF}_{i,j}^{\prime }={[w}_{i,1}^{\prime }\times {\displaystyle \frac{L_{HSI}^{\prime }\left({\lambda }_i\right)}{L_{AHSI}^{\prime }\left({\lambda }_1\right)}} {,w}_{i,2}^{\prime }\times {\displaystyle \frac{L_{HSI}^{\prime }\left({\lambda }_i\right)}{L_{AHSI}^{\prime }\left({\lambda }_2\right)}} ,{\dots ,w}_{i,G}^{\prime }\times {\displaystyle \frac{L_{HSI}^{\prime }\left({\lambda }_i\right)}{L_{AHSI}^{\prime }\left({\lambda }_G\right)}}]$$

(10)

In Equation (10), ${SBAF}_{i,j}^{\prime }$ is the set of SBAF corresponding to the i-th channel of the HSI.

Following the acquisition of SBAF for HSI spectral channels using the aforementioned method, the DN of multiple homologous regions in HSI-AHSI image pairs were extracted and averaged on a per-pixel basis. Leveraging AHSI’s calibration coefficients, the mean radiance of AHSI was calculated. The mean radiance of the i-th HSI channel was then derived via Equation (11), enabling the determination of HSI calibration coefficients through linear regression between the mean radiance and mean DN.

$$L_{HSI,i}={SBAF}_{i,j}^{\prime }·L_{AHSI,j}$$

(11)

$$L_{HSI,i}={gain}_i\times {DN}_i+{offset}_i$$

(12)

In Equation (12), ${gain}_i$ and ${offset}_i$ represent the calibration coefficients for the i-th channel of HSI: gain and offset, respectively. In this study, the HSI images used for cross-calibration have undergone pre-processing and dark current correction, ensuring the removal of band offsets. As a result, the offset for each band is 0, and the gain can be directly obtained using Equation (13).

$${gain}_{HSI,i}={\displaystyle \frac{L_{HSI,i}}{{DN}_i}}$$

(13)

3.3. Validation Metrics

Using the calibration coefficients obtained from cross-calibration, the sensor radiance was calculated and compared with the radiance calculated using the on-site calibration coefficients released by the Satellite Application Center for Ecology and Environment in 2024 [34]. These official site-based coefficients were produced through a rigorous national site calibration campaign conducted in September 2024 at the Dunhuang and Songshan national calibration sites [35], where synchronized satellite–ground observations and artificial reflectance targets were employed to comprehensively characterize the sensor’s radiometric response and derive absolute calibration coefficients. The standardized measurement procedures and complete calibration workflow ensured the reliability of these results, providing a robust benchmark for evaluating the performance of the cross-calibration. It should be noted that official site calibration is performed only once per year (within a ±6-month temporal window centered on the acquisition date). The imagery used in the cross-calibration experiments was acquired in August and September 2024, which was very close to the 2024 site calibration coefficients (less than 2 months). This temporal proximity ensures the time consistency and reliability of the validation results.

Using Equation (14), both sets of calibration coefficients were applied within a linear model to convert ${DN}_{\lambda }$ into radiance, where $L_{\lambda }$ represents the spectral radiance at wavelength λ, ${gain}_{\lambda }$ and ${offset}_{\lambda }$ denote the corresponding calibration parameters. The resulting radiance products can be further used in quantitative applications such as flux estimation, surface reflectance retrieval, and drought and wildfire monitoring.

$$L_{\lambda }={gain}_{\lambda }\times {DN}_{\lambda }+{offset}_{\lambda }$$

(14)

Based on the two sets of radiance calculations, the relative deviation was subsequently calculated using Equation (15). The relative deviation quantifies the consistency between the cross-calibration results and the official on-site calibration results, which can be defined as:

$$Relative Dev ={\displaystyle \frac{\left|{Rad}_{cross}-{Rad}_{site}\right|}{{Rad}_{site}}}\times 100\%$$

(15)

In Equation (15), ${Rad}_{cross}$ denotes the channel radiance acquired by the hyperspectral imager (HSI) through cross-calibration, ${Rad}_{site}$ represents the channel radiance calculated using site calibration coefficients, and $Relative Dev$ indicates the relative deviation between ${Rad}_{cross}$ and ${Rad}_{site}$.

In the cross-calibration experiment, the SBAF were calculated using both the traditional SABF method, the DG-SBAF(FWHM) and the DG-SBAF(4σ) method. The fluctuation of the SBAF under different methods was statistically analyzed. Root mean square error (RMSE) was calculated to assess systematic discrepancies between the derived SBAF and 1 across each method.

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left({SBAF}_i-1\right)}^2}$$

(16)

where ${SBAF}_i$ denotes the spectral matching factor for the i-th channel of the HSI, and N represents the total number of HSI spectral channels.

In the validation experiment, the cross-calibration coefficients derived from HSI were utilized to calculate the radiance values of homologous regions in the image pairs of GF-5B/AHSI and Landsat-9/OLI-2. These radiance values were then compared with those obtained from GF-5B and Landsat-9. The Spectral Angle Mapper (SAM) [36] was utilized to assess the consistency of spectral characteristics between HJ-2A/HSI and GF-5B/AHSI, as well as Landsat-9/OLI-2, within the VNIR and SWIR ranges. The formula for calculating the spectral angle is shown in Equation (17).

$$SAM=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}{\displaystyle \frac{L_{HSI}·L_{sensor}}{‖L_{HSI}‖·‖L_{sensor}‖}}$$

(17)

where $L_{HSI}$ and $L_{sensor}$ denote the per-channel radiance of HSI and the validation sensor at homologous regions, respectively.

4. Results

4.1. Cross-Calibration Results

Our method was tested at three locations: Dunhuang, Baotou, and Tak. Three methods were compared (including traditional SBAF cross-calibration and the proposed method DG-SBAF) and their respective channel radiance outputs at three calibration sites, as illustrated in Figure 10. Additionally, cross-calibration experiments were performed using historical 2021 data, with the results presented in the Supplementary File. Spectral channel matching was systematically applied across all VNIR bands. However, for the SWIR range, channels with atmospheric transmittance below 30% were excluded prior to matching the remaining channels [37]. Because such low-transmittance channels undergo severe signal attenuation, which results in critically low SNR and substantially increased radiometric uncertainty, they are not suitable for high-accuracy quantitative analysis and were therefore omitted from the cross-calibration workflow. A comparison result was shown in Table 4; the mean relative deviation (RD) across all channels at three calibration sites was calculated.

Figure 10. Comparison of HJ-2A/HSI channel radiance by different methods across three test sites: (a) Dunhuang VNIR channel radiance; (b) Dunhuang SWIR channel radiance; (c) Baotou VNIR channel radiance; (d) Baotou SWIR channel radiance; (e) Tak VNIR channel radiance; (f) Tak SWIR channel radiance.

Table 4. Mean relative deviation of radiance.

Band Range	Methods	Dunhuang	Baotou	Tak	Mean
VNIR	DG-SBAF(4σ)	4.68%	7.70%	6.99%	6.46%
	DG-SBAF(FWHM)	4.89%	8.12%	7.57%	6.86%
	Traditional SBAF	5.33%	8.74%	7.99%	7.35%
SWIR	DG-SBAF(4σ)	7.75%	9.79%	8.48%	8.67%
	DG-SBAF(FWHM)	8.08%	10.14%	9.02%	9.08%
	Traditional SBAF	8.40%	10.46%	9.62%	9.49%

Across the three calibration sites in both VNIR and SWIR spectral ranges, the DG-SBAF(4σ) method demonstrated superior radiometric consistency. In the VNIR range, mean relative deviations were 4.68%, 7.70%, and 6.99% at Dunhuang, Baotou, and Tak, respectively, outperforming DG-SBAF(FWHM) (4.89%, 8.12%, 7.57%) and the traditional SBAF method (5.33%, 8.74%, 7.99%). Similarly, in the SWIR range, DG-SBAF(4σ) achieved deviations of 7.75%, 9.79%, and 8.48%, compared to 8.08%, 10.14%, 9.02% for DG-SBAF(FWHM) and 8.40%, 10.46%, 9.62% for traditional SBAF. The overall mean RD across all sites was lowest for DG-SBAF(4σ): 6.46% (VNIR) and 8.67% (SWIR) versus 6.86%/9.08% (DG-SBAF(FWHM)) and 7.35%/9.49% (traditional SBAF).

To quantitatively illustrate the improvement of DG-SBAF over the traditional SBAF method, relative improvement ratios were calculated at each site and spectral range. In the VNIR range, DG-SBAF(4σ) reduced the mean RD from 5.33% to 4.68% at Dunhuang (12.2% improvement), from 8.74% to 7.70% at Baotou (11.8% improvement), and from 7.99% to 6.99% at Tak (12.5% improvement). In the SWIR range, deviations decreased from 8.40% to 7.75% at Dunhuang (7.7% improvement), from 10.46% to 9.79% at Baotou (6.4% improvement), and from 9.62% to 8.48% at Tak (11.8% improvement). Across all sites, the average improvement was 12.11% in VNIR and 8.64% in SWIR. These results quantitatively confirm that the dynamic Gaussian distribution mechanism in DG-SBAF(4σ) effectively mitigates spectral discontinuities caused by channel non-uniformity and resolution inconsistencies, demonstrating consistent and reliable gains over the traditional SBAF method.

In the spectral channel matching process, SBAF integrates contributions from two sensors with differing viewing geometries, spectral responses, atmospheric conditions, and surface characteristics. Due to inherent variations in spectral channel properties, the calculated SBAF values exhibit significant inconsistencies across channels. Figure 11 illustrates the SBAF distributions for spectral channels within the VNIR and SWIR ranges across three calibration sites. We quantified the SBAF fluctuation for each site under three methods using Root Mean Square Error (RMSE) analysis, with perfectly matched spectral channels (ideal SBAF = 1) serving as the evaluation benchmark. The comparative results are detailed in Table 5.

Figure 11. Comparison of HJ-2A/HSI SBAF by different methods across three test sites: (a) Dunhuang VNIR SBAF; (b) Dunhuang SWIR SBAF; (c) Baotou VNIR SBAF; (d) Baotou SWIR SBAF; (e) Tak VNIR SBAF; (f) Tak SWIR SBAF.

Table 5. Root mean square error (RMSE) of SBAF.

Band Range	Methods	Dunhuang	Baotou	Tak	Mean
VNIR	DG-SBAF(4σ)	0.0355	0.0374	0.0206	0.0312
	DG-SBAF(FWHM)	0.0391	0.0408	0.0287	0.0362
	Traditional SBAF	0.0636	0.0653	0.0602	0.0630
SWIR	DG-SBAF(4σ)	0.1053	0.1067	0.1137	0.1086
	DG-SBAF(FWHM)	0.1089	0.1102	0.1197	0.1129
	Traditional SBAF	0.1186	0.1202	0.1297	0.1228

From Table 5, in the VNIR band range, RMSE values of DG-SBAF(4σ) at the three test sites measure 0.0355, 0.0374, and 0.0206, outperforming both DG-SBAF(FWHM) (0.0391, 0.0408, 0.0287) and the traditional SBAF method (0.0636, 0.0653, 0.0602). Similarly, in the SWIR range, DG-SBAF(4σ) yields RMSE values of 0.1053, 0.1067, and 0.1137, demonstrating consistent advantages over DG-SBAF(FWHM) (0.1089, 0.1102, 0.1197) and the traditional method (0.1186, 0.1202, 0.1297). The DG-SBAF(4σ) method exhibits the smallest RMSE values across both spectral ranges (VNIR and SWIR) at all three test sites, demonstrating its superior efficacy in compensating for spectral discrepancies between target and reference channels. This optimal performance indicates enhanced radiometric consistency between the sensor under calibration and the reference sensor channels. Figure 11 illustrates that SWIR SBAF values exhibit greater fluctuation than those in the VNIR, regardless of method. In contrast, VNIR SBAF display tighter clustering and higher stability, confirming that VNIR channels benefit from more accurate spectral-response correction. Together, these results systematically validate that the DG-SBAF(4σ) method effectively improves cross-calibration accuracy by mitigating inter-channel spectral mismatches.

4.2. Validation Results

Implementing radiometric cross-calibration with high-precision reference sensors was essential for evaluating inter-sensor consistency. This process involves comparison of spectral signatures at homologous regions using validation imagery to quantify inter-sensor consistency. Following the interpolation approach described in the reference [21], the HJ-2A/HSI spectral radiances were resampled to the central wavelengths of GF-5B/AHSI and Landsat-9/OLI-2 bands. Per-band differences between the reference sensors and the interpolated HSI values were then calculated, and spectral fidelity was assessed using SAM comparisons over homologous regions. In the Dunhuang validation experiment, with GF-5B/AHSI as the reference sensor, the DG-SBAF (4σ) method achieved SAM values of 3.64°, 3.09°, and 2.92° in the VNIR band, marking an average 10.65% improvement over traditional methods (4.07°, 3.12°, 3.67°). For the SWIR band, SAM values were 4.00°, 3.46°, and 3.90°, showing a 6.72% average improvement compared to traditional results (4.34°, 3.60°, 4.26°). The detailed results are presented in Table 6. When Landsat-9/OLI-2 served as the reference sensor, DG-SBAF (4σ) produced VNIR-band SAM accuracies of 4.08°, 4.82°, and 4.04°, representing an average improvement of 4.22% compared to the traditional approach (4.24°, 4.85°, and 4.41°). The results are shown in Table 7.

Table 6. Sam Assessment of HJ-2A/HSI and GF-5B/AHSI (Dunhuang Site).

Band Range	Methods	Dunhuang	Baotou	Tak	Mean
VNIR	DG-SBAF(4σ)	3.64°	3.09°	2.92°	3.22°
	DG-SBAF(FWHM)	3.82°	3.11°	3.14°	3.36°
	Traditional SBAF	4.07°	3.12°	3.67°	3.62°
SWIR	DG-SBAF(4σ)	4.00°	3.46°	3.90°	3.79°
	DG-SBAF(FWHM)	4.04°	3.48°	3.90°	3.81°
	Traditional SBAF	4.34°	3.60°	4.26°	4.07°

Table 7. Sam Assessment of HJ-2A/HSI and Landsat-9/OLI-2 (Dunhuang and Vegetation Site).

Band Range	Methods	Dunhuang	Baotou	Tak	Mean
VNIR Dunhuang	DG-SBAF(4σ)	4.08°	4.82°	4.04°	4.31°
	DG-SBAF(FWHM)	4.14°	4.84°	4.21°	4.40°
	Traditional SBAF	4.24°	4.85°	4.41°	4.50°
VNIR Vegetation	DG-SBAF(4σ)	6.82°	5.90°	5.78°	6.12°
	DG-SBAF(FWHM)	6.84°	5.92°	5.82°	6.19°
	Traditional SBAF	6.97°	5.93°	5.87°	6.26°

In the Vegetation site validation experiment, using GF-5B/AHSI as reference, DG-SBAF (4σ) yielded VNIR SAM values of 3.79°, 4.23° and 4.48°, an average improvement of 4.14% over the traditional SBAF results (4.03°, 4.33° and 4.69°). In the SWIR band, SAM values were 4.95°, 4.08° and 4.84°, representing an average improvement of 9.77% relative to the traditional values (5.59°, 4.26° and 5.50°), the results are presented in Table 8. With Landsat-9/OLI-2 as the reference sensor, DG-SBAF (4σ) achieved VNIR-band SAM accuracies of 6.82°, 5.90° and 5.78°, corresponding to an average improvement of 2.24% over the traditional method (6.97°, 5.93° and 5.87°). The validation results from the two sites demonstrate that the performance gains afforded by the DG-SBAF (4σ) method differ between locations, with the Dunhuang site exhibiting greater improvements than the Vegetation site; likewise, the VNIR band shows more pronounced enhancement than the SWIR band. Nonetheless, irrespective of validation site or reference sensor (GF-5B/AHSI or Landsat-9/OLI-2), DG-SBAF (4σ) consistently outperforms the traditional SBAF approach, producing lower absolute SAM values across all configurations. These systematic comparisons demonstrate that although the degree of enhancement varies with site conditions, the DG-SBAF (4σ) method universally preserves spectral fidelity and strengthens radiometric consistency during cross-calibration, validating its efficacy in enhancing radiometric consistency across sensor systems.

Table 8. Sam Assessment of HJ-2A/HSI and GF-5B/AHSI (Vegetation Site).

Band Range	Methods	Dunhuang	Baotou	Tak	Mean
VNIR	DG-SBAF(4σ)	3.79°	4.23°	4.48°	4.17°
	DG-SBAF(FWHM)	3.80°	4.27°	4.51°	4.19°
	Traditional SBAF	4.03°	4.33°	4.69°	4.35°
SWIR	DG-SBAF(4σ)	4.95°	4.08°	4.84°	4.62°
	DG-SBAF(FWHM)	5.10°	4.16°	5.04°	4.77°
	Traditional SBAF	5.59°	4.26°	5.50°	5.12°

5. Discussion

5.1. DG-SBAF Method Generalizability and Limitations

The DG-SBAF method is based on the characteristics of Gaussian spectral response functions and the dense channel distribution typical of hyperspectral sensors. Most currently operational hyperspectral sensors possess these features; therefore, as long as the reference sensors and target sensors provide accurately characterized spectral response functions, DG-SBAF can be applied for cross-calibration across different hyperspectral platforms. By fully leveraging the high-precision spectral channels of the reference sensors, the method can further improve cross-calibration accuracy and ensure the long-term consistency and robustness of multi-source hyperspectral data.

The DG-SBAF cross-calibration method (DG-SBAF) shows significant advantages in the collaborative application of multi-source hyperspectral sensors, but also has certain limitations. The DG-SBAF (4σ) method operates within a 4σ spectral interval, providing approximately 95% effective energy coverage, while radiometric errors are substantially mitigated through weighted fusion of multi-reference spectral channels. However, the expanded energy coverage and multi-reference channels entail inherent performance compromises that necessitate careful consideration. First, the 4σ spectral interval introduces multiple reference spectral channels, where radiometric uncertainties of the reference sensor channels propagate through the SBAF matrix, and the interdependent weighting across fused channels amplifies systematic biases. Second, the weighted fusion process assigns greater weights to reference channels with higher energy contributions (spectral channels with higher signal-to-noise ratios, SNR), which inadvertently suppresses critical spectral features in low-SNR regions.

5.2. SBAF Fluctuation

The SBAF exhibited significant fluctuation across VNIR and SWIR band ranges at three test sites (Figure 11), with values fluctuating around 1. The three SBAF calculation methods exhibit distinctly different distributions. The DG-SBAF (4σ) curve displays the smallest variability—with the lowest peak height and most compact distribution—yielding SBAF values that cluster most closely around the ideal value of 1. This indicates a more robust and accurate correction of inter-sensor spectral response differences. In contrast, both the traditional SBAF method and DG-SBAF (FWHM) produce more scattered distributions with greater variability; although DG-SBAF (FWHM) shows some improvement over the traditional approach, its stability remains inferior to that of DG-SBAF (4σ). As a correction parameter for sensor spectral response discrepancies, the numerical characteristics of SBAF are fundamentally determined by the degree of spectral channel matching. Theoretically, the SBAF should precisely converge to 1 when ideal spectral channel matching is achieved between sensors. Consistent with this principle, our proposed DG-SBAF (4σ) method effectively reduced spectral channel mismatches through the SBAF matrix construction, thereby driving SBAF values closer to 1. This improvement was corroborated by the RMSE in Table 5, which showed that the DG-SBAF (4σ) method minimized both the RMSE value and fluctuation magnitude. Experimental results demonstrated that the DG-SBAF (4σ) based cross-calibration achieved superior performance, exhibiting the smallest radiance RD and optimal spectral consistency compared to the traditional SBAF method. These results underscore the critical importance of SBAF stability for radiometric calibration accuracy: values approaching 1 with minimal fluctuations indicate a more robust spectral response correction. Stable SBAF values ensure reliable multi-sensor data comparability, effectively mitigating systematic errors induced by spectral response discrepancies.

5.3. Calibration Sites Stability

The comparative analysis of three calibration sites reveals that the Dunhuang site exhibits smaller relative deviations compared to the site calibration results. This observation can be primarily attributed to the fact that the site calibration coefficients were predominantly derived from extensive calibration campaigns conducted at the Dunhuang site. Consequently, the measurements obtained from this site demonstrated closer alignment with the established calibration coefficients. In contrast, cross-calibration coefficients from the other sites display marginally larger deviations, potentially resulting from spatiotemporal variations in environmental conditions and seasonal atmospheric effects that may differ fundamentally from those characterizing the Dunhuang site. This discrepancy highlights the critical influence of site-specific characteristics on calibration coefficient applicability. Notably, while the Baotou site—a managed desert calibration target—shows potential alterations to natural spectral characteristics through artificial maintenance, its exceptional temporal stability and spatial uniformity maintain its status as a preferred calibration reference. Moreover, the superior performance observed at the Dunhuang test site compared to the Vegetation site further underscores the influence of site-specific characteristics on radiometric calibration. This paradox between controlled site management and natural state preservation warrants further investigation to optimize calibration site selection criteria. Our findings suggest that the generalization of calibration parameters to additional sites may require subsequent site-specific adjustments to account for unique environmental signatures.

5.4. Cross-Calibration Accuracy Limitation

The proposed DG-SBAF (4σ) method achieved a reduction in the mean RD by 12.11% (6.46% vs. 7.35%) in the VNIR bands and by 8.64% (8.67% vs. 9.49%) in the SWIR bands compared with the traditional SBAF method, thereby significantly improving cross-calibration accuracy. Nevertheless, there remains substantial room for further improvement. The current accuracy is primarily limited by the absolute radiometric accuracy and long-term stability of the reference sensor, which fundamentally determine the reliability of the calibration baseline. Additional uncertainty sources include the BRDF effect, observational geometry differences, spectral response mismatches, geometric co-registration errors, and spatiotemporal heterogeneity/instability of calibration sites. Among these, the reference sensor’s absolute accuracy and stability constitute the fundamental benchmark, while site-specific BRDF characteristics, site uniformity, and stability are significant contributors to noise. BRDF effects are particularly relevant, as differing observational geometries (e.g., solar zenith angle differences) between reference and target sensors introduce significant radiation deviations, especially amplified for non-Lambertian surfaces exhibiting directional reflectance or hotspot effects. Correctly characterizing and compensating for inter-sensor SRF discrepancies remains a key technical challenge in achieving high-accuracy cross-calibration. The proposed DG-SBAF method presented in this study specifically addresses this challenge and improves the robustness and accuracy of multi-sensor cross-calibration. Future work will refine this approach by incorporating an enhanced BRDF model and correction, ensuring consistent observation geometry, modelling uncertainties in radiometric references, and implementing improved site-selection strategies that prioritise locations with BRDF isotropy and long-term stability, thereby maximising overall performance and applicability.

6. Conclusions

To ensure data consistency and synergistic application among multi-source sensors, this study investigated radiometric cross-calibration between HJ-2A/HSI and ZY1-02D/AHSI sensors in the VNIR and SWIR spectral ranges using near-synchronous image pairs from three test sites: Dunhuang, Baotou, and Tak. In this work, we proposed a DG-SBAF method that integrated the Gaussian distribution into SBAF to adjust the number of reference spectral channels and the weight of spectral channel matching from two different sensors. Our method was designed to correct matched spectral channel discrepancies and improve the cross-calibration accuracy. The cross-calibration results were compared with site calibration and validated using independent datasets from GF-5B/AHSI and Landsat-9/OLI-2. Experimental results demonstrated that the DG-SBAF (4σ) method achieved a mean RD of 6.46% (VNIR) and 8.67% (SWIR) across three sites, outperforming the traditional SBAF method (7.35% and 9.49%, respectively). Validation further revealed that the DG-SBAF (4σ) method yielded a mean SAM of 3.67° (GF-5B/AHSI) and 5.22° (Landsat-9/OLI-2) in the VNIR range, and 4.21° (GF-5B/AHSI) in the SWIR range. These results confirm the superior reliability of the DG-SBAF (4σ) method over the traditional SBAF method and highlight the enhanced radiometric accuracy of cross-calibrated HJ-2A/HSI. In the future, we will consider fitting cross-calibration coefficients and fluctuation of SBAF across diverse test sites to improve methodological robustness and generalizability.