High-Precision Geolocation of SAR Images via Multi-View Fusion Without Ground Control Points

Highlights

What are the main findings?

• Proposes a novel GCP (Ground Control Points)-free high-precision geolocation method based on multi-view SAR (Synthetic Aperture Radar) image fusion, incorporating outlier detection, weighted fusion, and refined estimation technical strategies.
• For actualmeasured airborne SAR data, the proposedmethod achieves an average 84.78% improvement in positioning accuracy relative to dual-view fusion methods, attaining meter-level positioning precision. Ablation experiments confirm that outlier removal and refined estimation contribute 82.42% and 22.75% respectively to this accuracy gain.

What is the implication of the main finding?

• The proposed method is compatible with three or more multi-view images, while excluding outlier images with systematic geolocation errors inconsistent across views.
• The method integrates a weighted fusion strategy and the minimum norm least-squares criterion, enablingGCP-free high-precision estimation of planar systematic geolocation errors of individual images throughmaximizing utilization ofmulti-view redundant information.

Abstract

Synthetic Aperture Radar (SAR) images generated via range-Doppler (RD) model-based geometric correction often suffer from non-negligible systematic geolocation errors due to cumulative impacts of platform positioning inaccuracies, payload time synchronization offsets, and atmospheric propagation delays. These errors limit the applicability of SAR data in high-precision geometric applications, especially in scenarios where ground control points (GCPs)—traditionally used for calibration—are inaccessible or costly to acquire. To address this challenge, this study proposes a novel GCP-free high-precision geolocation method based on multi-view SAR image fusion, integrating outlier detection, weighted fusion, and refined estimation strategies. The method first establishes a positioning error correlation model for homologous point pairs in multi-view SAR images. Under the assumption of approximately equal positioning errors, initial systematic error estimates are obtained for all arbitrary dual-view combinations. It then identifies and removes outlier images with inconsistent systematic errors via coefficient of variation analysis, retaining a subset of multi-view images with stable calibration parameters. A weighted fusion strategy, tailored to the geometric error propagation model, is applied to the optimized subset to balance the influence of angular relationships on error estimation. Finally, the minimum norm least-squares method refines the fusion results to enhance consistency and accuracy. Validation experiments on both simulated and actual airborne SAR images demonstrate the method’s effectiveness. For actual measured data, the proposed method achieves an average positioning accuracy improvement of 84.78% compared with dual-view fusion methods, with meter-level precision. Ablation studies confirm that outlier removal and refined estimation contribute 82.42% and 22.75% to accuracy gains, respectively. These results indicate that the method fully leverages multi-view information to robustly estimate and compensate for 2D systematic errors (range and azimuth), enabling high-precision planar geolocation of airborne SAR images without GCPs.

1. Introduction

Synthetic Aperture Radar (SAR) systematic geocorrected products are typically geocoded to a map projection without ground control points (GCPs), relying on the range-Doppler (RD) signal model [1,2,3,4]. However, due to cumulative errors from aircraft positioning/attitude determination, payload time calibration, radio wave propagation delays, and local average elevation inaccuracies, even rigorous geolocation models may result in SAR images with non-negligible systematic geolocation errors, failing to meet the demands of high-precision applications [4,5]. Meter-level precise geolocation, a critical geometric correction step, traditionally requires a rigorous geometric model calibrated with user-collected GCPs [6]. Yet, GCP acquisition is often arduous in remote regions, featureless terrains (e.g., glaciers, deserts), or restricted areas [5,7], where reliable GCPs may be inaccessible or cost-prohibitive. Moreover, SAR-specific radiometric and geometric effects—such as speckle noise, foreshortening, layover, and shadow—render GCP identification and collection far more challenging than in optical imagery. Thus, developing GCP-free precise geolocation methods for SAR images remains an urgent need [5,7,8].

Recent efforts have explored stereo localization via multi-view SAR image fusion [9]. Chen and Dowman [10] proposed a spaceborne SAR 3D intersection algorithm based on weighted least-squares. Luo et al. [11] achieved robust multi-view spaceborne SAR 3D positioning using the range-Doppler model. Yin et al. [12] developed a two-stage stereo positioning method for multi-view spaceborne SAR, involving initial and secondary positioning on a normalized RD model to enhance accuracy and stability. However, these methods cannot eliminate positioning offsets induced by SAR system calibration parameter errors.

To address such errors, researchers have investigated high-precision GCP-free geolocation by fusing multi-pass, multi-view SAR data of the same area [13,14]. In the absence of GCPs, calibration parameters can be corrected using geometric relationships between overlapping SAR images under specific observation configurations [8,15]. For instance, a self-calibration model with symmetric geometric constraints [16] enables systematic error estimation but requires two images from different orbits with identical incident angles. Zhang et al. [17] proposed a self-calibration method using at least three overlapping images, leveraging spatial intersection residuals of conjugate points to detect timing offsets. For dual-view airborne SAR, Zhang et al. [18] estimated self-calibration parameters via a simple affine transformation model on ground-range images, improving GCP-free geolocation accuracy.

Key geometric calibration parameters for SAR include range-direction fast time and azimuth-direction slow time, which originate from systematic errors (e.g., instrument internal delays, GNSS-radar time synchronization errors). These parameters are generally assumed stable when the same radar acquires images from different perspectives [16,17,18], forming the basis for geometric self-calibration via multi-view data fusion.

However, for three or more multi-view SAR images, even from the same system, estimates of 2D calibration parameters (azimuth and range) derived from different dual-view combinations often exhibit large fluctuations. In some cases, individual images may show significant positioning offsets (see experimental results), qualifying as outliers. This arises because non-ideal factors causing systematic positioning errors are complex and diverse: minor error terms—such as platform positioning errors, antenna phase center offsets, atmospheric delays, and ground elevation projection errors—exhibit randomness across different viewing angles [19]. Consequently, effective outlier detection and removal are critical to avoid compromising self-calibration.

Notably, the stability of self-calibration and the handling of ill-conditioned problems in multi-view scenarios have attracted research attention. For spaceborne SAR, Yin et al. [20] proposed a sensitive geometric self-calibration method based on the RD model, utilizing the determinant and an accuracy stabilization factor to filter images, thereby mitigating singular solutions and enhancing robustness. That study identified satellite position error as the primary error source and recommended acquiring ipsilateral images with incidence angles greater than 8° to improve geometric configuration. For UAV-borne SAR with spatially variant slant range errors, Luo et al. [21] proposed a geometric auto-calibration method that incorporated a tie-point quality-based weighting strategy and an iterative eigenvalue-correction least-squares solution, achieving significant accuracy improvements. These methods underscore the importance of image selection, error source analysis, and robust solving in multi-view self-calibration. Nevertheless, the effective detection of outlier images and the optimal fusion of multi-view data for consistent and high-precision geolocation remain challenging.

This study presents a novel GCP-free high-precision geolocation approach based on multi-view synthetic aperture radar (SAR) image fusion. Focusing on multi-view airborne SAR ground-range images, the proposed method is implemented through the following steps:

(1)

A positioning error correlation model for homologous point pairs in multi-view SAR images is established, where model parameters are derived from an affine transformation-based geometric positioning model constructed using the four corner points of the ground-range image.

(2)

Under the assumption of approximately equal positioning errors, initial error estimates are obtained for all arbitrary dual-view combinations. And then potential outlier images are detected and eliminated to prevent interference with the self-calibration process.

(3)

The remaining multi-view data are fused in two successive steps using the weighted least squares method and the minimum norm least squares method, respectively, to suppress inconsistent errors across different views.

This approach significantly enhances both the GCP-free geolocation accuracy and algorithm robustness for multi-view SAR images. The main contributions of this work are summarized as follows:

(1)

By leveraging the stability of SAR geometric calibration parameters, an outlier detection and removal method is proposed to retain the subset of multi-view SAR images with the most consistent calibration parameters.

(2)

A weighted least squares fusion strategy based on a multi-view error propagation model is designed to accurately estimate self-calibration parameters. This strategy balances the influence of angular geometric relationships on positioning error estimation, with a particular focus on suppressing large error propagation caused by small angle differences.

(3)

The initial weighted fusion estimation results are further refined using the minimum norm least-squares principle. By minimizing residuals and balancing the respective equations, more accurate and robust results are obtained.

The remainder of this paper is organized as follows: Section 2 introduces the multi-view positioning error correlation model. Section 3 elaborates on the principles and steps of the proposed outlier removal and multi-view SAR fusion positioning method. Section 4 validates the method using both simulated and measured data, with performance analysis conducted via ablation and comparative experiments. Some factors affecting algorithm accuracy are discussed in Section 5. Finally, conclusions are drawn in Section 6.

2. Multi-View Positioning Error Correlation Model

In practical airborne SAR image processing, a simple first-order affine transformation model is typically established using the latitude and longitude coordinates of the four corner points attached to ground-range SAR images. This model describes the transformation from pixel coordinates $(i,j)$ to the systematic geolocation coordinates $(B,L)$ of scatterers:

$$\begin{array}{c}\hfill \left[\begin{array}{cc}B\hfill & L\hfill \end{array}\right]=\left[\begin{array}{cc}i\hfill & j\hfill \end{array}\right]\mathbf{C}+\mathbf{D},\end{array}$$

(1)

where B and L denote the geographic latitude and longitude of the scatterer’s systematic geolocation, respectively. C and D represent the coefficient matrices for the linear term and constant term of the affine transformation model, respectively, which can be derived inversely from the latitude and longitude coordinates of the image’s four corner points [18].

Considering residual errors in the SAR system’s geometric calibration parameters, the actual geographic coordinates of ground scatterers strictly satisfy:

$$\left[\begin{array}{cc}{B}_{real}& L_{real}\end{array}\right]=\left(\left[\begin{array}{cc}i& j\end{array}\right]+\left[\begin{array}{cc}{\displaystyle \frac{r}{{\rho }_r}}& {\displaystyle \frac{a}{{\rho }_a}}\end{array}\right]\right)\mathbf{C}+\mathbf{D},$$

(2)

where $B_{\mathrm{real}}$ and $L_{\mathrm{real}}$ are the true latitude and longitude of the scatterer $(i,j)$ in the SAR image; ${\rho }_r$ and ${\rho }_a$ are the ground sampling distances (GSD) in the range and azimuth directions, respectively; r and a denote the positioning offsets in the range and azimuth directions. These offsets are closely related to the SAR system’s range electronic delay and azimuth timing offset, exhibiting good numerical stability during multi-view image acquisition with slight random fluctuations across different views. Our objective is precisely to achieve geometric self-calibration by fusing multi-view SAR images, thereby estimating the 2D positioning offsets—i.e., range $\left(r\right)$ and azimuth $\left(a\right)$—of each image as accurately as possible.

After system-level positioning, rotational and scale differences between multi-view images are eliminated. Therefore, a high-precision area-based matching method [22] is employed to align multi-view SAR images, yielding multiple sets of homogenous points (sharing identical true geographic coordinates). Compared to feature-based methods, this approach yields more reliable homogenous point pairs. Based on these points, the positioning error correlation model for dual-view SAR homologous point pairs is established as follows:

$$\begin{array}{c}\hfill \left(\left[\begin{array}{cc}{i}_m\hfill & j_m\hfill \end{array}\right]+\left[\begin{array}{cc}{\displaystyle \frac{r_m}{{\rho }_{r_m}}}\hfill & {\displaystyle \frac{a_m}{{\rho }_{a_m}}}\hfill \end{array}\right]\right){\mathbf{C}}_m+{\mathbf{D}}_m\\ \hfill =\left(\left[\begin{array}{cc}{i}_n\hfill & j_n\hfill \end{array}\right]+\left[\begin{array}{cc}{\displaystyle \frac{r_n}{{\rho }_{r_n}}}\hfill & {\displaystyle \frac{a_n}{{\rho }_{a_n}}}\hfill \end{array}\right]\right){\mathbf{C}}_n+{\mathbf{D}}_n,\end{array}$$

(3)

where m and n correspond to SAR images from different views. Formula (3) can be rewritten as:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}{\displaystyle \frac{r_m}{{\rho }_{r_m}}}\hfill & {\displaystyle \frac{a_m}{{\rho }_{a_m}}}\hfill \end{array}\right]{\mathbf{C}}_m-\left[\begin{array}{cc}{\displaystyle \frac{r_n}{{\rho }_{r_n}}}\hfill & {\displaystyle \frac{a_n}{{\rho }_{a_n}}}\hfill \end{array}\right]{\mathbf{C}}_n\hfill \\ \hfill & =\left[\begin{array}{cc}{i}_n\hfill & j_n\hfill \end{array}\right]{\mathbf{C}}_n+{\mathbf{D}}_n-\left[\begin{array}{cc}{i}_m\hfill & j_m\hfill \end{array}\right]{\mathbf{C}}_m-{\mathbf{D}}_m\hfill \\ \hfill & =\left[\begin{array}{cc}{B}_n\hfill & L_n\hfill \end{array}\right]-\left[\begin{array}{cc}{B}_m\hfill & L_m\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\Delta B_{nm}\hfill & \Delta L_{nm}\hfill \end{array}\right],\hfill \end{array}$$

(4)

where $\left[B_m{L}_m\right]$ and $\left[B_n{L}_n\right]$ are the systematic geolocation coordinates of homologous points (Hps) in images m and n, respectively, calculated using (1); $[\Delta B_{nm}\Delta L_{nm}]$ represents the systematic geolocation difference of Hps between the dual-view images. Further transformation of (4) yields:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{r_m}{{\rho }_{r_m}}}{c}_{11}^m+{\displaystyle \frac{a_m}{{\rho }_{a_m}}}{c}_{21}^m-{\displaystyle \frac{r_n}{{\rho }_{r_n}}}{c}_{11}^n-{\displaystyle \frac{a_n}{{\rho }_{a_n}}}{c}_{21}^n=\Delta B_{nm}\hfill \\ \hfill & {\displaystyle \frac{r_m}{{\rho }_r}}{c}_{12}^m+{\displaystyle \frac{a_m}{{\rho }_a}}{c}_{22}^m-{\displaystyle \frac{r_n}{{\rho }_r}}{c}_{12}^n-{\displaystyle \frac{a_n}{{\rho }_a}}{c}_{22}^n=\Delta L_{nm}\hfill \end{array}$$

(5)

Formula (5) can be rewritten as:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}{\displaystyle \frac{c_{11}^m}{{\rho }_{r_m}}}& {\displaystyle \frac{c_{21}^m}{{\rho }_{a_m}}}& -{\displaystyle \frac{c_{11}^n}{{\rho }_{r_n}}}& -{\displaystyle \frac{c_{21}^n}{{\rho }_{a_n}}}\\ {\displaystyle \frac{c_{12}^n}{{\rho }_{r_m}}}& {\displaystyle \frac{c_{22}^n}{{\rho }_{a_m}}}& -{\displaystyle \frac{c_{12}^n}{{\rho }_{r_n}}}& -{\displaystyle \frac{c_{22}^n}{{\rho }_{a_n}}}\end{array}\right]\left[\begin{array}{c}{r}_m\\ a_m\\ r_n\\ a_n\end{array}\right]=\left[\begin{array}{c}\Delta B_{nm}\hfill \\ \Delta L_{nm}\hfill \end{array}\right]\end{array},$$

(6)

where $C_{ij}^m$ denotes the element in the i-th row and j-th column of $C_m$, and $C_{ij}^n$ denotes the element in the i-th row and j-th column of $C_n$. Since $r_m$, $a_m$, $r_n$, and $a_n$ are unknowns, this system of equations is rank-deficient and cannot be solved directly. Equation (6) establishes the relationship between range-azimuth positioning errors in dual-view images and latitude-longitude differences. Matrix elements reflect the influence of affine model coefficients and ground sampling distance on error propagation. To address this, dual-view fusion positioning typically assumes equal positioning errors for the two images to avoid rank deficiency. However, this assumption often leads to significant positioning accuracy loss in multi-view observation scenarios.

Generalizing to the case of N multi-view SAR images, the positioning error correlation model for multi-view SAR images is established as:

$$\begin{array}{c}\underset{N(N-1)\times 1}{\mathbf{Y}}=\underset{N(N-1)\times 2N}{\mathbf{A}}\underset{2N\times 1}{\mathbf{X}}\\ \mathbf{A}=\left[\begin{array}{cccccc}{\mathbf{T}}_1& -{\mathbf{T}}_2& \mathbf{0}& \cdots & \cdots & \mathbf{0}\\ {\mathbf{T}}_1& \mathbf{0}& -{\mathbf{T}}_3& \mathbf{0}& \cdots & \mathbf{0}\\ ⋮& ⋮& \mathbf{0}& \ddots & \mathbf{0}& ⋮\\ {\mathbf{T}}_1& \mathbf{0}& \cdots & \mathbf{0}& -{\mathbf{T}}_{N-1}& \mathbf{0}\\ {\mathbf{T}}_1& \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}& -{\mathbf{T}}_N\\ \mathbf{0}& {\mathbf{T}}_2& -{\mathbf{T}}_3& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{0}& {\mathbf{T}}_2& \mathbf{0}& -{\mathbf{T}}_4& \mathbf{0}& ⋮\\ ⋮& ⋮& ⋮& \mathbf{0}& \ddots & \mathbf{0}\\ \mathbf{0}& {\mathbf{T}}_2& \mathbf{0}& \cdots & \mathbf{0}& -{\mathbf{T}}_N\\ \begin{array}{c}\mathbf{0}\hfill \\ \mathbf{0}\hfill \\ \mathbf{0}\hfill \end{array}& \begin{array}{c}\mathbf{0}\hfill \\ \mathbf{0}\hfill \\ \mathbf{0}\hfill \end{array}& \begin{array}{c}\ddots \\ {\mathbf{T}}_m\\ \ddots \end{array}& \begin{array}{c}\ddots \\ \mathbf{0}\\ \ddots \end{array}& \begin{array}{c}⋮\\ -{\mathbf{T}}_n\\ \ddots \end{array}& \begin{array}{c}⋮\\ \mathbf{0}\\ ⋮\end{array}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{T}}_{N-1}& -{\mathbf{T}}_N\end{array}\right],\end{array}$$

(7)

where

$$\mathbf{X}={\left[\begin{array}{ccccccc}{r}_1& a_1& r_2& a_2& \dots & r_N& a_N\end{array}\right]}^T,$$

$$\mathbf{Y}={\left[\begin{array}{ccccccc}\Delta B_{21}& \Delta L_{21}& \Delta B_{31}& \Delta L_{31}& \dots & \Delta L_{NN-1}& \Delta L_{NN-1}\end{array}\right]}^T,$$

$${\mathbf{T}}_m=\left[\begin{array}{cc}{\displaystyle \frac{C_{11}^m}{{\rho }_{r_m}}}& {\displaystyle \frac{C_{21}^m}{{\rho }_{a_m}}}\\ {\displaystyle \frac{C_{12}^n}{{\rho }_{r_m}}}& {\displaystyle \frac{C_{22}^n}{{\rho }_{a_m}}}\end{array}\right].$$

$\mathbf{0}$ is a 2D zero matrix. Although this system remains rank-deficient, the increased observation dimension enables optimal estimation in the sense of minimum norm least squares.

3. Methodology

Figure 1 illustrates the main workflow of the proposed method. First, multi-view images are paired to perform dual-view fusion positioning, yielding rough estimates of 2D positioning offsets for each pair. While systematic 2D positioning offsets of multi-view SAR images are generally consistent, anomalous offsets may arise under complex influences (e.g., aircraft trajectory deviations caused by intense airflow disturbances). To address this, a coefficient of variation-based method is proposed to identify consistency in multi-view positioning errors and eliminate anomalous images, enabling outlier removal prior to multi-view fusion. Next, considering that error estimation accuracy of dual-view pairs is closely tied to their geometric relationships (e.g., angular differences), weighting coefficients are computed using the sensitivity of the error propagation model to fuse positioning error offsets across multi-view SAR images. Finally, fusion estimates are refined under the minimum norm least-squares criterion to achieve high-precision planar positioning for each SAR image. This method effectively suppresses the impact of inconsistent multi-view positioning errors. Additionally, the weighted fusion strategy accounts for error sensitivity differences arising from angular geometric characteristics, leveraging complementary and redundant information in multi-view images to maximize algorithm accuracy and robustness.

3.1. Consistency Identification of Multi-View Image Positioning Errors and Outlier Removal

Assuming equal systematic positioning errors for images m and n, Equation (3) can be simplified for any homologous point as:

$$\begin{array}{c}\left[\begin{array}{cc}{r}_{mn}& a_{mn}\end{array}\right]\left(\left[\begin{array}{cc}{\displaystyle \frac{1}{{\rho }_{r_m}}}& 0\\ 0& {\displaystyle \frac{1}{{\rho }_{a_m}}}\end{array}\right]{\mathbf{C}}_m-\left[\begin{array}{cc}{\displaystyle \frac{1}{{\rho }_{r_n}}}& 0\\ 0& {\displaystyle \frac{1}{{\rho }_{a_n}}}\end{array}\right]{\mathbf{C}}_n\right)=\left[\begin{array}{cc}\Delta B_{nm}& \Delta L_{nm}\end{array}\right],\hfill \end{array}$$

(8)

where $r_{mn}$ and $a_{mn}$ denote the range and azimuth positioning errors, respectively. Let

$$\begin{array}{c}{\mathbf{K}}^{(\mathrm{n},\mathrm{m})}=\left[\begin{array}{c}\begin{array}{cc}{k}_{11}^{(\mathrm{n},\mathrm{m})}& k_{12}^{(\mathrm{n},\mathrm{m})}\end{array}\\ \begin{array}{cc}{k}_{21}^{(\mathrm{n},\mathrm{m})}& k_{22}^{(\mathrm{n},\mathrm{m})}\end{array}\end{array}\right]={\left[\left[\begin{array}{cc}{\displaystyle \frac{1}{{\rho }_{r_m}}}& 0\\ 0& {\displaystyle \frac{1}{{\rho }_{a_m}}}\end{array}\right]{\mathbf{C}}_m-\left[\begin{array}{cc}{\displaystyle \frac{1}{{\rho }_{r_n}}}& 0\\ 0& {\displaystyle \frac{1}{{\rho }_{a_n}}}\end{array}\right]{\mathbf{C}}_n\right]}^{-1},\end{array}$$

(9)

where $k{(n,m)}_{ij}$ represents the element in the i-th row and j-th column of $K(n,m)$. Substituting (9) into (8) yields the range and azimuth positioning error estimates from dual-view fusion:

$$\left[\begin{array}{cc}{r}_{mn}& a_{mn}\end{array}\right]=\left[\begin{array}{cc}\Delta B_{nm}& \Delta L_{nm}\end{array}\right]{\mathbf{K}}^{(\mathrm{n},\mathrm{m})}.$$

(10)

The accuracy of dual-view estimates depends on both the consistency of positioning errors between views and the inherent angular difference in dual-view observation geometry. With additional multi-view SAR images, the subset with the most consistent positioning errors can be selected based on the dispersion of error estimates across all dual-view pairs.

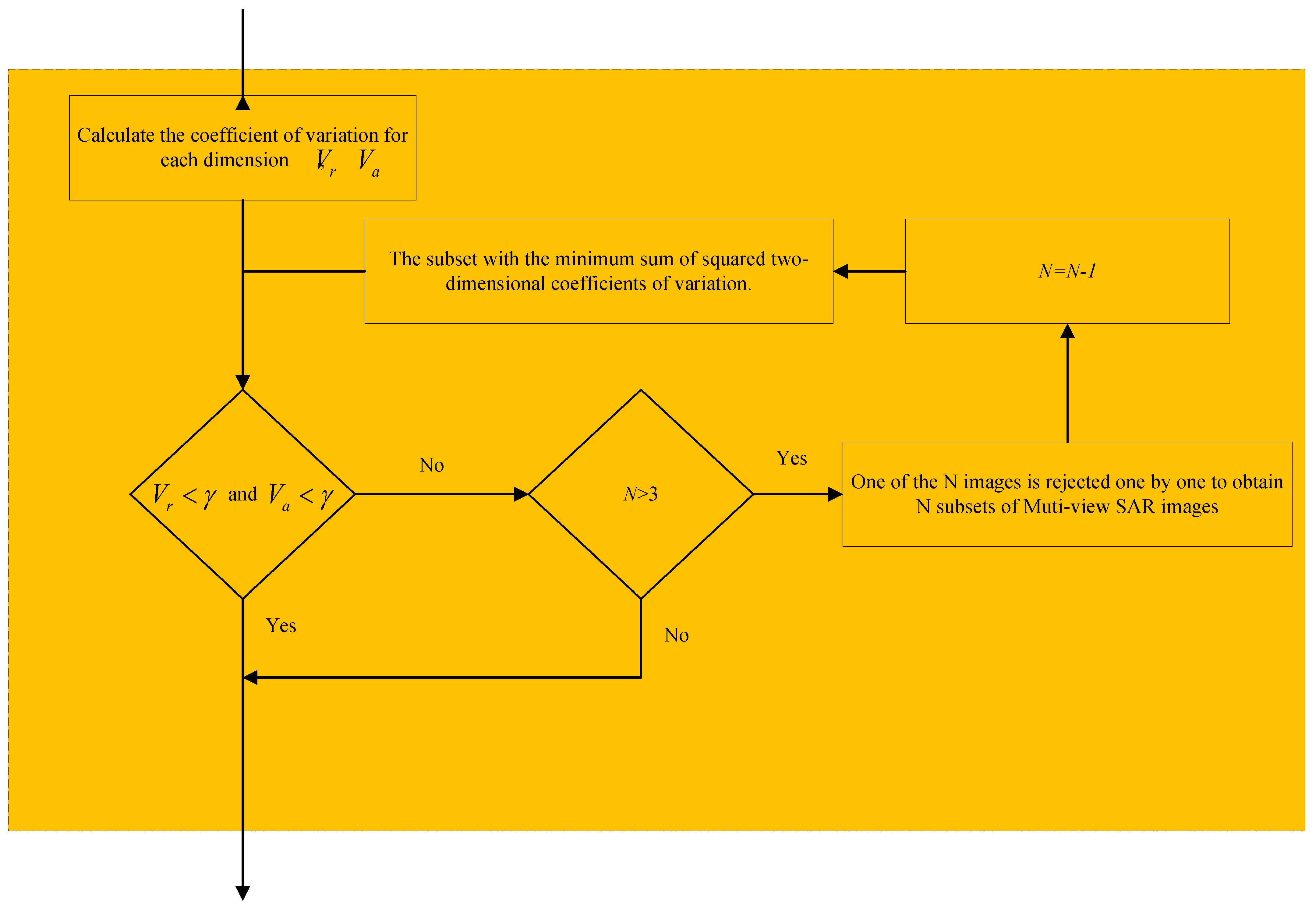
The workflow for identifying multi-view positioning error consistency and outlier removal is shown in Figure 2. For N multi-view SAR images, pairwise correlation yields $N(N-1)/2$ estimates via dual-view fusion. The dispersion of these estimates reflects the consistency of true positioning errors across multi-view images. Thus, the coefficient of variation [23] is employed to quantify this consistency, calculated separately for range and azimuth errors:

$$\begin{array}{c}{V}_r={\displaystyle \frac{s_r}{u_r}},V_a={\displaystyle \frac{s_a}{u_a}}.\hfill \end{array}$$

(11)

where $V_r$ and $V_a$ are the coefficients of variation for range and azimuth errors, respectively; $s_r$ and $s_a$ denote their standard deviations; $u_r$ and $u_a$ represent their means.

Consistency is evaluated by comparing $V_r$ and $V_a$ against a threshold $\gamma$. While a 20% threshold is typical in practice, error propagation effects inflate estimation dispersion, so $\gamma$ is adjusted to 1 in this algorithm.

Specifically, if either 2D coefficient of variation exceeds 1, actual positioning error discrepancies between images are unacceptably large, precluding accurate estimation. In such cases, images are sequentially excluded one at a time from the N images, generating N subsets each containing $N-1$ images. For each subset, estimates and 2D coefficients of variation are computed. The subset with the smallest coefficients is selected, and if both values are <1, it is adopted as the optimally consistent dataset. If not, exclusion continues until a subset with relatively consistent systematic positioning errors is identified.

If coefficients of variation in either dimension remain >1 even after reducing the subset to three images, the three images with the most consistent errors are selected for fusion positioning.

3.2. Multi-View Positioning Error Fusion Estimation Based on a Geometric Error Propagation Model

Consistency identification and outlier removal yield a subset of multi-view SAR images with relatively consistent systematic positioning errors. Concurrently, a geometric error propagation model for dual-view SAR positioning estimates is established, enabling a weighted fusion strategy to compute multi-view positioning error estimates. To quantify positioning errors between any two images, an equivalent equation is derived using true geographic coordinates of Hps:

$$\left[{\displaystyle \frac{r_m}{{\rho }_{r_m}}}{\displaystyle \frac{a_m}{{\rho }_{a_m}}}\right]{\mathbf{C}}_m-\left[{\displaystyle \frac{r_n}{{\rho }_{r_n}}}{\displaystyle \frac{a_n}{{\rho }_{a_n}}}\right]{\mathbf{C}}_n=\left[\begin{array}{cc}\Delta B_{nm}& \Delta L_{nm}\end{array}\right].$$

(12)

Let

$$\left[\begin{array}{cc}\Delta r_{mn}& \Delta a_{mn}\end{array}\right]=\left[\begin{array}{cc}{r}_m& a_m\end{array}\right]-\left[\begin{array}{cc}{r}_n& a_n\end{array}\right],$$

(13)

where $r_m,a_m$ and $r_n,a_n$ are the true range and azimuth positioning errors of images m and n, respectively; $r_{mn}$ and $a_{mn}$ denote their range and azimuth error differences. Substituting (13) into (12) yields

$$\begin{array}{c}\begin{array}{c}\hfill \left[\begin{array}{cc}{\displaystyle \frac{r_m}{{\rho }_{r_m}}}& {\displaystyle \frac{a_m}{{\rho }_{a_m}}}\end{array}\right]{\mathbf{C}}_m-\left[\begin{array}{cc}{\displaystyle \frac{r_m-\Delta r_{mn}}{{\rho }_{r_n}}}& {\displaystyle \frac{a_m-\Delta a_{mn}}{{\rho }_{a_n}}}\end{array}\right]{\mathbf{C}}_n=\left[\begin{array}{cc}\Delta B_{nm}& \Delta L_{nm}\end{array}\right].\end{array}\end{array}$$

(14)

Rearranging (14) gives

$$\begin{array}{c}\begin{array}{cc}\hfill \left[\begin{array}{cc}{r}_m\hfill & a_m\hfill \end{array}\right]=& \left[\begin{array}{cc}\Delta B_{nm}\hfill & \Delta L_{nm}\hfill \end{array}\right]{\mathbf{K}}^{(n,m)}-\left[\begin{array}{cc}\Delta r_{mn}\hfill & \Delta a_{mn}\hfill \end{array}\right]\left[\begin{array}{cc}{\displaystyle \frac{1}{{\rho }_{r_n}}}& 0\\ 0& {\displaystyle \frac{1}{{\rho }_{a_n}}}\end{array}\right]{\mathbf{C}}_n{\mathbf{K}}^{(n,m)}.\hfill \end{array}\end{array}$$

(15)

Thus, the estimation error introduced by image n into image m during dual-view positioning is

$$\begin{array}{c}\left[\begin{array}{cc}{\widehat{r}}_{mn}& {\widehat{a}}_{mn}\end{array}\right]-\left[\begin{array}{cc}{r}_m& a_m\end{array}\right]=\left[\begin{array}{cc}\Delta r_{mn}& \Delta a_{mn}\end{array}\right]\left[\begin{array}{cc}{\displaystyle \frac{1}{{\rho }_{r_n}}}& 0\\ 0& {\displaystyle \frac{1}{{\rho }_{a_n}}}\end{array}\right]{\mathbf{C}}_n{\mathbf{K}}^{(n,m)}.\hfill \end{array}$$

(16)

where ${\widehat{r}}_{mn}$ and ${\widehat{a}}_{mn}$ are the range direction positioning error estimate and azimuth direction positioning error estimate when the positioning errors of images m and n are assumed to be equal. (16) indicates that due to discrepancies in true systematic positioning errors, the error propagation matrix governing error transfer from image n to m satisfies

$${\mathbf{H}}^{(n,m)}=\left[\begin{array}{cc}{H}_{11}^{(n,m)}& H_{12}^{(n,m)}\\ H_{21}^{(n,m)}& H_{22}^{(n,m)}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{1}{{\rho }_{r_n}}}& 0\\ 0& {\displaystyle \frac{1}{{\rho }_{a_n}}}\end{array}\right]{\mathbf{C}}_n{\mathbf{K}}^{(n,m)},$$

(17)

where $\mathbf{H}(n,m)$ is the error propagation matrix from n to m. The larger the absolute value of an element, the stronger the interference of n’s error on m’s estimation result, providing a basis for weight design in subsequent weighted fusion. Substituting (17) into (16) yields:

$$\begin{gathered} \begin{array}{c}{\widehat{r}}_{nm}-r_n=\Delta r_{nm}·H_{11}^{(n,m)}+\Delta a_{mn}·H_{21}^{(n,m)},\hfill \end{array} \\ {\widehat{a}}_{nm}-a_n=\Delta r_{nm}·H_{12}^{(n,m)}+\Delta a_{mn}·H_{22}^{(n,m)}. \end{gathered}$$

(18)

Larger magnitudes of $|H_{11}(n,m)|$, $|H_{12}(n,m)|$, $|H_{21}(n,m)|$, and $|H_{22}(n,m)|$ indicate greater estimation errors induced by actual positioning error differences. This implies that errors introduced by SAR images at different angles to a reference image depend on their mutual geometric relationship. Let ${\alpha }_{n,m}^r$ and ${\alpha }_{n,m}^a$ denote the range and azimuth influence factors, defined as

$$\begin{gathered} \begin{array}{c}{\alpha }_{n,m}^r=\left|H_{11}^{(n,m)}\right|+\left|H_{21}^{(n,m)}\right|,\hfill \end{array} \\ {\alpha }_{n,m}^a=\left|H_{12}^{(n,m)}\right|+\left|H_{22}^{(n,m)}\right|. \end{gathered}$$

(19)

Systematic positioning error estimates from all pairwise combinations of multi-view images are then fused via a weighted strategy to enhance per-view error estimation accuracy. The fused positioning error for image m is

$$\begin{gathered} \begin{array}{c}{r_m}^{\left(0\right)}={\displaystyle \sum _{n=1,n\ne m}^N}{w}_{n,m}^r·{\widehat{r}}_{mn},\hfill \end{array} \\ {a_m}^{\left(0\right)}=\sum _{n=1,n\ne m}^N{w}_{n,m}^a·{\widehat{a}}_{mn}, \end{gathered}$$

(20)

where $r_m^{\left(0\right)}$ and $a_m^{\left(0\right)}$ are the fused range and azimuth error estimates for image m. The weights $w_{n,m}^r$ and $w_{n,m}^a$ satisfy

$$\begin{array}{c}{w}_{n,m}^r={\displaystyle \frac{{\displaystyle \frac{1}{{\alpha }_{n,m}^r}}}{{\displaystyle \sum _{n=1,n\ne m}^N}{\displaystyle \frac{1}{{\alpha }_{n,m}^r}}}},w_{n,m}^a={\displaystyle \frac{{\displaystyle \frac{1}{{\alpha }_{n,m}^a}}}{{\displaystyle \sum _{n=1,n\ne m}^N}{\displaystyle \frac{1}{{\alpha }_{n,m}^a}}}}.\hfill \end{array}$$

(21)

and

$$\begin{array}{c}{\displaystyle \sum _{n=1,n\ne m}^N}{w}_{n,m}^r=1,{\displaystyle \sum _{n=1,n\ne m}^N}{w}_{n,m}^a=1.\hfill \end{array}$$

(22)

This yields multi-view positioning error estimates consistent with the relative consistency of true errors. Subsequently, positioning errors of excluded views can be estimated using equivalent equations derived from Hps’ true geographic coordinates.

Substituting (18) into (20) shows that

$$\begin{array}{c}\begin{array}{cc}\hfill & {r_m}^{\left(0\right)}\hfill \\ \hfill & =\sum _{n=1,n\ne m}^N{w}_{n,m}^r·{\widehat{r}}_{mn}\hfill \\ \hfill & =r_m+\sum _{n=1,n\ne m}^N\left[w_{n,m}^r·\left(\Delta r_{mn}·H_{11}^{(n,m)}+\Delta a_{mn}·H_{21}^{(n,m)}\right)\right],\hfill \\ \hfill & a_m^{\left(0\right)}\hfill \\ \hfill & =\sum _{n=1,n\ne m}^N{w}_{n,m}^a·{\widehat{a}}_{mn}\hfill \\ \hfill & =a_m+\sum _{n=1,n\ne m}^N\left[w_{n,m}^a·\left(\Delta r_{mn}·H_{12}^{(n,m)}+\Delta a_{mn}·H_{22}^{(n,m)}\right)\right].\hfill \end{array}\end{array}$$

(23)

Estimation accuracy is ensured when errors are relatively consistent (i.e., $\Delta r_{nm}\ll r_m$). Equation (23) decomposes the fused range error and azimuth error estimate into two parts: the weighted sum of the true error and the dual view estimation error. The weight coefficients are determined by the geometric error propagation matrix, which means that images with smaller angular differences (i.e., larger propagation errors) will receive lower weights. When the error of multi view images is highly consistent, the weighted sum tends to zero, and the fusion result will approach the true error.

3.3. Refinement of Fusion Estimation Based on Minimum Norm Least Squares

Following multi-view positioning error fusion, results are refined using the minimum norm least-squares criterion [24,25], which relies on the Moore–Penrose generalized inverse [26] for solution, to achieve accurate error estimation, enabling high-precision planar positioning of SAR images. Equivalent equations between different views are used to derive the minimum norm least-squares solution for weighted fusion estimates.

Taking three images as an example:

$$\begin{gathered} \begin{array}{c}\mathbf{Y}=\mathbf{A}\mathbf{X},\end{array} \\ \mathbf{A}=\left[\begin{array}{cccccc}{\displaystyle \frac{C_{11}^1}{{\rho }_{r_1}}}& {\displaystyle \frac{C_{21}^1}{{\rho }_{a_1}}}& -{\displaystyle \frac{C_{11}}{{\rho }_{r_2}}}& -{\displaystyle \frac{C_{21}^2}{{\rho }_{a_2}}}& 0& 0\\ \\ {\displaystyle \frac{C_{12}^1}{{\rho }_{r_1}}}& {\displaystyle \frac{C_{22}^1}{{\rho }_{a_1}}}& -{\displaystyle \frac{C_{12}}{{\rho }_{r_2}}}& -{\displaystyle \frac{C_{22}}{{\rho }_{a_2}}}& 0& 0\\ \\ {\displaystyle \frac{C_{11}^1}{{\rho }_{r_1}}}& {\displaystyle \frac{C_{21}^1}{{\rho }_{a_1}}}& 0& 0& -{\displaystyle \frac{C_{11}^3}{{\rho }_{r_3}}}& -{\displaystyle \frac{C_{21}^3}{{\rho }_{a_3}}}\\ \\ {\displaystyle \frac{C_{12}^1}{{\rho }_{r_1}}}& {\displaystyle \frac{C_{22}^1}{{\rho }_{a_1}}}& 0& 0& -{\displaystyle \frac{C_{12}}{{\rho }_{r_3}}}& -{\displaystyle \frac{C_{22}^3}{{\rho }_{a_3}}}\\ \\ 0& 0& {\displaystyle \frac{C_{11}^2}{{\rho }_{r_2}}}& {\displaystyle \frac{C_{21}^2}{{\rho }_{a_2}}}& -{\displaystyle \frac{C_{11}^3}{{\rho }_{r_3}^3}}& -{\displaystyle \frac{C_{21}^3}{{\rho }_{a_3}}}\\ \\ 0& 0& {\displaystyle \frac{C_{12}^2}{{\rho }_{r_2}}}& {\displaystyle \frac{C_{22}^2}{{\rho }_{a_2}}}& -{\displaystyle \frac{C_{12}^3}{{\rho }_{r_3}}}& -{\displaystyle \frac{C_{22}^3}{{\rho }_{a_3}}}\end{array}\right], \\ \begin{array}{c}\mathrm{X}=\end{array}\left[\begin{array}{c}{r}_1\hfill \\ a_1\hfill \\ r_2\hfill \\ a_2\hfill \\ r_3\hfill \\ a_3\hfill \end{array}\right],\begin{array}{c}\mathrm{Y}=\end{array}\left[\begin{array}{c}\Delta B_{21}\hfill \\ \Delta L_{21}\hfill \\ \Delta B_{31}\hfill \\ \Delta L_{31}\hfill \\ \Delta B_{32}\hfill \\ \Delta L_{32}\hfill \end{array}\right]. \end{gathered}$$

(24)

Let ${\mathbf{X}}^{\left(0\right)}={\left[\begin{array}{cccccc}{r_1}^{\left(0\right)}& {a_1}^{\left(0\right)}& {r_2}^{\left(0\right)}& {a_2}^{\left(0\right)}& {r_3}^{\left(0\right)}& {a_3}^{\left(0\right)}\end{array}\right]}^T$ denote the fusion estimates. The residuals of the equation system satisfy

$${\mathbf{Y}}^{*}=\mathbf{Y}-\mathbf{A}{\mathbf{X}}^{\left(0\right)}=\mathbf{AX}-\mathbf{A}{\mathbf{X}}^{\left(0\right)}=\mathbf{A}\left(\mathbf{X}-{\mathbf{X}}^{\left(0\right)}\right)\triangleq \mathbf{A}\mathbf{Z}.$$

(25)

Due to rank deficiency, the Moore–Penrose generalized inverse of the coefficient matrix is used to solve for the minimum norm least-squares solution $\mathbf{Z}$ of (25):

$$\mathbf{Z}={\mathbf{A}}^{+}{\mathbf{Y}}^{*},$$

(26)

where ${\mathbf{A}}^{+}$ is the Moore–Penrose generalized inverse matrix of $\mathbf{A}$. The final positioning error estimate is

$${\mathbf{X}}^{*}={\mathbf{X}}^{\left(0\right)}+\mathbf{Z}.$$

(27)

Compared to initial fusion estimates, refined results exhibit smaller equation residuals and higher accuracy. This method balances residuals across equations, preventing dominance by extreme errors and enhancing robustness. Incorporating refined error estimates into latitude/longitude calculations and repositioning SAR images accordingly yields high-precision multi-view SAR positioning results.

4. Experiments and Analysis

To validate the effectiveness of the proposed method, performance evaluations were conducted using both simulated and actual measured airborne SAR images. Additionally, the impact of different algorithmic components on performance was analyzed, and the efficacy of each component was confirmed via ablation studies. Comparative experiments with the dual-view positioning method demonstrated that the proposed algorithm achieves higher estimation accuracy and more robust positioning results for both simulated and measured data.

4.1. Experiments and Analysis of Airborne SAR Simulated Data

In actual flight scenarios, the positioning error of the carrier is unpredictable, whereas in simulated flights, such errors can be explicitly designed. Thus, simulated data are utilized in this subsection to verify the effectiveness of the proposed algorithm.

For the convenience of simulation validation, this experiment neglected the influence of terrain relief, approximating the target area as a planar surface. In this context, adjusting the rotation angle of the airborne SAR image is equivalent to modifying the heading angle of the airborne SAR system. To simplify the experimental setup, we resampled the ground sampling distance for both the distance and azimuth directions to 1 m. For simulation experiments, we utilized image tiles covering a 1500 m × 1500 m area. The mapping relationship between pixel coordinates and geographic coordinates of the simulated images can be derived from that of actual ground-range airborne SAR images. Specifically, a real ground-range airborne SAR image was selected, as illustrated in Figure 3. It was then rotated to various angles and supplemented with distinct systematic positioning errors to construct the simulated multi-view SAR image dataset.

4.1.1. Parameter Settings

To verify the effectiveness of the proposed method, multiple experimental scenarios were designed, categorized into three types: (1) multi-view SAR images with relatively consistent systematic positioning errors under large angular differences; (2) multi-view SAR images with relatively consistent systematic positioning errors under small angular differences; and (3) multi-view SAR images with relatively inconsistent systematic positioning errors under large angular differences. The performance of the proposed algorithm was validated by comparing its results with those of the dual-view fusion positioning algorithm across these scenarios. Additionally, by analyzing the positioning errors of the proposed algorithm under different scenarios, the influence of angular geometric relationships on the algorithm’s estimation accuracy was investigated. Furthermore, the effectiveness of each algorithm module was verified by comparing positioning errors before and after the implementation of different steps within the same scenario.

(1) Scenario I: Multi-view SAR images with relatively consistent systematic positioning errors under large angular differences. Simulated images A, B, C, and D were generated by rotating the initial image by 0°, 90°, 160° and 260°, respectively, with distinct positioning errors introduced into each.

(2) Scenario II: Multi-view SAR images with relatively consistent systematic positioning errors under small angular differences. The simulated images in this scenario were created by rotating the initial image by 0°, 20°, 40° and 60°, followed by the introduction of positioning errors and cropping of the region of interest.

(3) Scenario III: Multi-view SAR images with relatively inconsistent systematic positioning errors under large angular differences. The simulated images in this scenario share the same rotation angles as those in Scenario I, but the positioning error introduced into image A was modified.

The specific parameters for the three scenarios are provided in

Table 1. Parameter Settings for Different Scenarios.

		Image A	Image B	Image C	Image D
Scenario I	Heading angle (°)	143.97	233.97	303.97	43.97
	2D positioning error (m)	(45, −35)	(35, −50)	(38, −45)	(42, −40)
	Planar positioning error (m)	57.01	61.03	58.9	58
Scenario II	Heading angle (°)	143.97	163.97	183.97	203.97
	2D positioning error (m)	(45, −35)	(35, −50)	(38, −45)	(42, −40)
	Planar positioning error (m)	57.01	61.03	58.9	58
Scenario III	Heading angle (°)	143.97	233.97	303.97	43.97
	2D positioning error (m)	(−45, 35)	(35, −50)	(38, −45)	(42, −40)
	Planar positioning error (m)	57.01	61.03	58.9	58

. The term “2D positioning errors” refers to errors in the range and azimuth directions.

4.1.2. Positioning Accuracy of the Proposed Algorithm Under Different Simulated Scenarios

After selecting Hps and estimating multi-view SAR image positioning errors using the proposed algorithm, a high-precision estimation of the 2D systematic positioning error for the initial ground-range SAR image was obtained. Using these estimates as the systematic positioning errors, a new mapping between pixel and geographic coordinates can be established, enabling repositioning of SAR images to achieve high-precision results. Furthermore, since the introduced positioning errors are consistent across the entire image, the positioning error at any single point is representative of the overall positioning accuracy. In this context, any pixel from the multi-view SAR images can be selected as a check point. The positioning error at this point—calculated by comparing its repositioning result with that of the actual ground-range SAR image—serves as the positioning accuracy metric for the simulated image.

(1) Scenario I: Multi-view SAR images with relatively consistent systematic positioning errors under large angular differences. To validate the effectiveness of the proposed method,

Table 2. Method Comparison and Ablation Experiments (Scenario I). “——” indicates that the positioning accuracy of this image cannot be estimated.

		Image A	Image B	Image C	Image D	Overall Mean
Simulated image planar positioning error (m)		57.01	61.03	58.90	58.00	58.74
Dual-view fusion positioning accuracy (m) [18]	A + B	12.75	12.75	——	——	——
	A + C	6.20	——	6.20	——	——
	A + D	3.81	——	——	3.81	——
	B + C	——	5.08	5.08	——	——
	B + D	——	6.13	——	6.13	——
	C + D	——	——	4.18	4.18	——
	Mean	7.58	7.99	5.15	4.71	6.36
The coefficient of variation before outlier removal, Vr = 0.11, Va = 0.11. No dataset optimization required
Multi-view fusion positioning accuracy (m)	Weighted fusion estimation	6.31	6.33	3.46	3.25	4.84
	Refined estimation	4.37	4.37	4.37	4.37	4.37
Improved positioning accuracy compared to [18]		42.35%	45.31%	15.15%	7.22%	31.26%

presents the positioning accuracy after multi-view fusion positioning, with comparisons to the dual-view fusion positioning method proposed by Zhang et al. [18].

Table 2 demonstrates that fusing four SAR images from different viewpoints significantly improves the positioning accuracy of airborne SAR images. The proposed method achieves an average positioning accuracy improvement of 31.26% (reduced from 6.36 m to 4.37 m) compared to the dual-view fusion method. A comparison between dual-view fusion estimates and weighted fusion estimates indicates that multi-view positioning error fusion estimation based on the geometric error propagation model effectively enhances positioning accuracy, with the weighted fusion estimates outperforming dual-view fusion by an average of 23.91% (reduced from 6.36 m to 4.84 m). Additionally, comparing weighted fusion estimates with refined results shows that correcting fusion estimates via the minimum norm least-squares method yields consistent positioning accuracy across multi-view SAR images, with an average improvement of 9.66% (reduced from 4.84 m to 4.37 m).

(2) Scenario II: Multi-view SAR images with relatively consistent systematic positioning errors under small angular differences

Table 3. Method comparison and ablation experiments (scenario II).

		Image A	Image B	Image C	Image D	Overall Mean
Simulated image planar positioning error (m)		57.01	61.03	58.90	58.00	58.74
Dual-view fusion positioning accuracy (m) [18]	A + B	51.91	51.91	——	——	——
	A + C	17.84	——	17.84	——	——
	A + D	5.83	——	——	5.83	——
	B + C	——	16.79	16.79	——	——
	B + D	——	17.84	——	17.84	——
	C + D	——	——	18.44	18.44	——
	Mean	25.19	28.85	17.69	14.04	21.44
The coefficient of variation before outlier removal, Vr = 0.59, Va = 0.42. No dataset optimization required
Multi-view fusion positioning accuracy (m)	Weighted fusion estimation	18.57	6.18	3.25	6.91	8.73
	Refined estimation	4.69	4.69	4.69	4.69	4.69
Improved positioning accuracy compared to [18]		81.38%	83.74%	73.49%	66.60%	78.13%

presents the positioning accuracy after multi-view fusion positioning. Table 3 shows that the proposed method achieves an average positioning accuracy improvement of 78.13% (reduced from 21.44 m to 4.69 m) over dual-view fusion positioning. A comparison of planar positioning accuracies between Scenarios I and II reveals slightly lower accuracy under smaller angular differences than under larger ones. However, the proposed algorithm still demonstrates significant improvements in accurate error estimation under small angular differences, highlighting its superior angular adaptability.

(3) Scenario III: Multi-view SAR images with inconsistent systematic positioning errors under large angular differences.

Table 4. Method comparison and ablation experiments (scenario III).

			Image A	Image B	Image C	Image D	Overall Mean
Simulated image planar positioning error (m)			57.01	61.03	58.90	58.00	58.74
Dual-view fusion positioning accuracy (m) [18]		A + B	82.54	82.54	——	——	——
		A + C	58.53	——	58.53	——	——
		A + D	74.97	——	——	74.97	——
		B + C	——	5.08	5.08	——	——
		B + D	——	6.13	——	6.13	——
		C + D	——	——	4.18	4.18	——
		Mean	72.01	31.25	22.60	28.43	38.57
Multi-view fusion positioning accuracy (m)	Before	The coefficient of variation	Vr = 2.36, Va = 1.21.
	outlier	Weighted fusion estimation	56.53	19.66	25.69	17.12	29.75
	removal	Refined estimation	26.17	26.17	26.17	26.17	26.17
	After	The coefficient of variation	Vr = 0.04, Va = 0.06. Reject image A
	outlier	Weighted fusion estimation	4.69	5.44	3.60	5.24	4.74
	removal	Refined estimation	4.69	4.69	4.69	4.69	4.69
Improved positioning accuracy compared to [18]			93.49%	84.99%	79.25%	83.50%	87.84%

presents the corresponding positioning accuracy. In principle, once an image is identified as an outlier, it is excluded from subsequent fusion calculations. However, to fully demonstrate the method’s effectiveness, we still calculate the positioning error of the outlier image (Image A) using the fusion positioning method (based on Image B, C, D)—this verifies that the method can even improve the accuracy of outliers (Image A’s accuracy improved from 72.01 m to 4.69 m), rather than retaining the outlier in the fusion process. As shown, the proposed method achieves an average positioning accuracy improvement of 87.84% (reduced from 38.57 m to 4.69 m) over dual-view fusion positioning under this scenario. A comparison of positioning accuracies before and after outlier removal indicates that, in the presence of images with significantly divergent systematic positioning errors, unoptimized fusion and refinement fail to effectively estimate systematic positioning errors, resulting in poor performance. In contrast, the integration of multi-view positioning error consistency identification and outlier removal in this study significantly enhances estimation accuracy, with an average improvement of 82.08% (reduced from 26.17 m to 4.69 m) in refined estimation accuracy after dataset optimization.

In summary, comparative analyses of the proposed method and the dual-view fusion method across different scenarios confirm the effectiveness of the proposed approach. A cross-scenario comparison (Scenarios I vs. II) reveals that angular geometric relationships between images influence estimation accuracy, with superior performance observed under larger angular differences. Ablation experiments within each scenario further validate the efficacy of three key steps: multi-view positioning error consistency identification and outlier removal, weighted fusion estimation of multi-view systematic positioning errors based on the geometric error propagation model, and refined estimation of multi-view systematic positioning errors via the minimum norm least-squares method. Overall, the proposed method achieves higher accuracy and robustness in positioning compared to the dual-view fusion method.

4.2. Monte Carlo Simulation Experiments and Analysis

To quantitatively validate the effectiveness and robustness of the proposed multi-view SAR image fusion positioning method, a series of Monte Carlo simulation experiments were conducted. These experiments were designed to compare the performance of the proposed method against the direct averaging method under various viewing angle configurations and positioning error conditions.

4.2.1. Experimental Setup

In the simulations, multi-view observations were emulated by applying rotational transformations to a real ground-range SAR image. To simplify the experimental scenario, we set the GSD for both the range and azimuth directions to 1 m. Systematic geolocation errors, commonly present in practical SAR systems, were simulated by adding random positioning errors to the image plane. Specifically, independent errors with a mean of 50 pixels and a standard deviation of 10 pixels were introduced in both the X and Y directions. To ensure statistical significance, the results for each scenario were obtained over 1000 independent Monte Carlo runs. The experiments were categorized into three distinct scenarios:

• Experiment 1 (Three Views): Images were configured with viewing angles of 0°, 90°, and 260°.
• Experiment 2 (Four Views, Consistent Errors): Images were configured with viewing angles of 0°, 90°, 260°, and 170°, with consistent systematic errors applied to all images.
• Experiment 3 (Four Views, Inconsistent Error): The viewing angles were identical to Experiment 2, but image 4 was introduced with a significantly divergent systematic positioning error (with a mean of −50 pixels and a standard deviation of 10 pixels) to simulate an outlier.

4.2.2. Results and Comparative Analysis

The positioning errors for all images in each experiment were recorded for a quantitative performance evaluation.

Table 5. Comparative Positioning Errors from Monte Carlo Simulations.

Experiment Scenario	Method	Image 1 Error (m)	Image 2 Error (m)	Image 3 Error (m)	Image 4 Error (m)
Experiment 1	Dual-view fusion positioning averaging accuracy [18]	11.87	9.99	10.57	–
	Proposed Method	7.41	7.41	7.41	–
Experiment 2	Dual-view fusion positioning averaging accuracy [18]	11.02	11.06	11.87	11.93
	Proposed Method	6.45	6.45	6.45	6.45
Experiment 3	Dual-view fusion positioning averaging accuracy [18]	31.83	40.26	44.23	94.02
	Proposed Method	7.66	7.66	7.66	7.66

summarizes the comparative results.

Under conditions of relatively consistent systematic errors across views (Experiments 1 and 2), the proposed method demonstrates a significant enhancement in both positioning accuracy and stability compared to the direct averaging approach. In the three-view configuration (Experiment 1), the mean positioning error was reduced from approximately 10.81 m to a consistent 7.41 m for all images, constituting a 31.5% accuracy improvement. This advantage became even more pronounced in the four-view scenario (Experiment 2), where the mean error was reduced from 11.46 m to 6.45 m, corresponding to a 43.7% improvement. Crucially, unlike the direct averaging method which produced fluctuating errors across images, the proposed method yielded a uniform error estimate for all images within each scenario. This consistent performance underscores its superior capability to effectively leverage the geometric constraints inherent in multiple views, a fundamental aspect entirely overlooked by the simplistic averaging approach.

Meanwhile, the proposed method exhibits exceptional robustness against outlier views, as unequivocally demonstrated in Experiment 3. When one image contained a severe, inconsistent positioning error, the direct averaging method suffered catastrophic failure, with errors soaring as high as 94.02 m due to contamination from the outlier. In stark contrast, the proposed method successfully maintained the positioning error at a stable 7.66 m for all images—a performance level comparable to the consistent four-view case in Experiment 2. This result provides strong empirical evidence for the high effectiveness of the integrated outlier detection and removal module. It confirms that the module reliably identifies and excludes images with anomalous systematic errors, thereby preserving the high accuracy of the fusion process even in challenging, non-ideal observational conditions.

4.3. Experiments and Analysis of Airborne SAR Measured Data

A positioning experiment was performed utilizing multi-view ground-range airborne SAR images of the same target area, which were acquired by an operational airborne SAR system. Figure 4 presents a high-definition optical image of the airborne radar observation area, where regions enclosed by rectangular boxes of different colors correspond to the areas imaged by the four SAR images. In this optical image, $Hpi(i=1,\dots ,10)$ denotes the locations of ten Hps selected from the SAR images, while $Tpi(i=1,\dots ,10)$ represents the locations of ten test points (Tps) evenly distributed across the SAR images. The true latitude and longitude of these Hps and Tps were pre-measured using a high-precision Global Positioning System (GPS). Notably, these true geographic coordinates were solely used for evaluating the positioning accuracy of the proposed method and were not involved in the positioning computation process.

4.3.1. Experimental Parameters of Measured Data

In this experiment, the airborne SAR system imaged the same target area in strip mode along different flight paths. The multi-view images acquired during four separate imaging campaigns are displayed in Figure 5.

4.3.2. Positioning Accuracy Evaluation of the Proposed Method

After multi-view image registration processing, 10 groups of Hps were extracted. The positions of these Hps are marked as Hp1 to Hp10 on the optical reference image in Figure 4. As can be seen from Figure 5, although each Hps on the four multi-view images exhibits a certain degree of anisotropic scattering characteristics, high-precision matching processing can still control the positional error of Hps at the pixel level (usually meter-level). Considering the randomness of the error, the impact of this error on the algorithm accuracy can basically be neglected through the sample adjustment effect of multiple groups of Hps can basically be neglected. Furthermore, we selected 10 Tps on the images, marked as Tp1–Tp10, and the geographic coordinates of each test point on the high-precision optical reference image were used as the true values for positioning error evaluation.

Table 6. True Values of 2D Positioning Errors for Multi-view SAR Images.

Point Position (m)	Figure 5a	Figure 5b	Figure 5c	Figure 5d
Tp1	[14.75, 5.25]	[14.93, 5.49]	[14.84, 5.05]	[10.46, 9.56]
Tp2	[14.93, 6.22]	[14.47, 6.50]	[14.56, 6.18]	[10.66, 8.68]
Tp3	[13.06, 4.05]	[13.57, 4.38]	[13.98, 4.57]	[9.36, 8.55]
Tp4	[14.82, 5.70]	[14.76, 5.88]	[14.54, 5.68]	[10.24, 10.34]
Tp5	[14.56, 6.60]	[14.38, 6.35]	[14.05, 6.19]	[10.67, 9.86]
Tp6	[14.76, 5.47]	[14.67, 5.73]	[14.53, 5.40]	[10.95, 8.42]
Tp7	[15.12, 5.37]	[15.00, 5.56]	[15.09, 5.73]	[10.88, 8.79]
Tp8	[14.07, 5.95]	[14.35, 5.77]	[13.69, 5.47]	[9.53, 10.78]
Tp9	[13.55, 5.40]	[13.89, 5.67]	[13.72, 5.23]	[9.98, 10.56]
Tp10	[14.47, 6.26]	[14.57, 5.78]	[14.32, 5.49]	[10.54, 9.78]
mean	[14.41, 5.63]	[14.46, 5.71]	[14.33, 5.50]	[10.33, 9.53]

lists the true 2D positioning errors (range and azimuth directions) of the multi-view SAR images. As indicated in Table 6, the real positioning errors of the images in Figure 5a–c are relatively consistent, whereas those of Figure 5d differ significantly from the others. Using the Hps selected based on Figure 4, the multi-view fusion positioning method proposed in this study was applied to estimate the positioning error of each SAR image, with the results presented in

Table 7. Estimated 2D Positioning Errors for Multi-view SAR Images.

Point Position (m)	Figure 5a	Figure 5b	Figure 5c	Figure 5d
Tp1	[15.19, 5.29]	[15.35, 5.61]	[15.22, 5.27]	[10.79, 9.86]
Tp2	[14.75, 7.00]	[14.45, 7.29]	[14.72, 6.96]	[11.00, 9.40]
Tp3	[14.71, 2.15]	[14.81, 2.19]	[14.71, 2.16]	[9.50, 6.04]
Tp4	[14.62, 6.27]	[14.68, 6.48]	[14.60, 6.28]	[10.43, 10.91]
Tp5	[15.17, 5.30]	[15.08, 4.88]	[15.09, 5.47]	[11.58, 10.87]
Tp6	[14.49, 5.88]	[14.49, 6.19]	[14.45, 5.88]	[10.99, 8.90]
Tp7	[14.30, 5.47]	[14.18, 5.49]	[14.30, 5.48]	[10.17, 8.37]
Tp8	[12.53, 6.30]	[13.54, 7.11]	[12.79, 4.43]	[9.56, 12.11]
Tp9	[13.94, 5.40]	[14.22, 6.00]	[13.97, 5.62]	[10.13, 11.00]
Tp10	[15.31, 5.66]	[15.48, 5.37]	[15.27, 5.42]	[11.49, 9.87]
mean	[14.50, 5.53]	[14.63, 5.66]	[14.51, 5.30]	[10.56, 9.73]

. Table 7 demonstrates that the proposed method exhibits good positioning stability across the ten Tps, with relatively consistent target positioning errors in both longitude and latitude. Specifically, the positioning errors of the ten Tps range from 0 to 3 m, and the root mean square error (RMSE) of the proposed method is 1.55 m.

A comparison between Table 6 and Table 7 reveals that the proposed method can effectively estimate the systematic positioning errors of multi-view SAR images, achieving meter-level positioning accuracy. The average of the estimation results was adopted as the systematic positioning error, which was then used to compensate for the latitude and longitude of the coarsely positioned quadrangle points. Repositioning the SAR image with this compensation yielded high-precision multi-view SAR positioning results. Taking the repositioned image in Figure 5a as an example, the planar positioning errors of the ten Tps were calculated, with the results shown in

Table 8. Positioning Errors of Figure 5a Obtained by the Proposed Method.

	$\mathbf{\Delta } \mathit{B}$ (m)	$\mathbf{\Delta } \mathit{L}$ (m)	Planar (m)
Tp1	−0.17	−1.12	1.13
Tp2	0.61	−0.77	0.99
Tp3	0.70	0.57	0.91
Tp4	−1.71	1.40	2.20
Tp5	−1.52	0.69	1.67
Tp6	−0.62	−0.90	1.10
Tp7	0.47	1.55	1.62
Tp8	1.12	0.11	1.13
Tp9	1.11	−0.59	1.25
Tp10	1.29	1.51	1.99
RMSE	1.04	1.15	1.55

.

4.3.3. Method Comparison and Ablation Experiments

Multi-view SAR images were repositioned using both the dual-view fusion positioning method and the proposed method, and the positioning accuracies of these approaches were evaluated using the Tps. The results are presented in

Table 9. Method Comparison and Ablation Experiments Results on Airborne SAR Measured Data.

			Figure 5a	Figure 5b	Figure 5c	Figure 5d	Overall Mean
Positioning accuracy of system-level geometric corrections			15.50	15.56	15.41	13.96	15.11
Dual-view fusion positioning accuracy (m) [18]		A + B	2.78	2.63	——	——	——
		A + C	1.38	——	1.26	——	——
		A + D	9.09	——	——	7.55	——
		B + C	——	5.08	5.11	——	——
		B + D	——	23.56	——	19.21	——
		C + D	——	——	27.38	23.51	——
		Mean	4.42	10.42	11.25	16.76	10.71
Multi-view fusion positioning accuracy (m)	Before	The coefficient of variation	Vr = 2.50, Va = 1.00.
	outlier	Weighted fusion estimation	5.27	12.28	8.61	14.05	10.05
	removal	Refined estimation	8.91	10.15	9.36	8.64	9.27
	After	The coefficient of variation	Vr = 0.24, Va = 0.04. Reject Figure 5d.
	outlier	Weighted fusion estimation	2.34	1.38	2.20	2.53	2.11
	removal	Refined estimation	1.55	1.48	1.60	1.89	1.63
Improved positioning accuracy compared to [18]			64.93%	85.80%	85.78%	88.72%	84.78%

, which integrates method comparisons and ablation experiments to facilitate analysis of algorithm component effects.

Table 9 indicates that the dual-view positioning method [18] exhibits unstable positioning accuracy, with performance degradation likely occurring under conditions of small heading angle differences and inconsistent systematic positioning errors. In contrast, the proposed algorithm significantly enhances positioning accuracy while ensuring estimation robustness. For the measured data, the proposed method achieves an average positioning accuracy improvement of 84.78% (reduced from 10.71 m to 1.63 m) compared to the dual-view fusion method.

Furthermore, a comparison of positioning accuracies before and after outlier removal reveals that weighted fusion estimation and refined estimation alone fail to effectively estimate systematic positioning errors when images exhibit large discrepancies in systematic positioning errors are present. However, the integration of multi-view positioning error consistency identification and outlier removal leads to significant enhancements in estimation accuracy, with the refined positioning accuracy achieving an 82.42% (reduced from 9.27 m to 1.63 m) improvement after optimization.

Additionally, a comparison between weighted fusion estimates and refined results demonstrates that without the minimum norm least-squares method, positioning accuracy is inconsistent and exhibits significant variability. After correcting fusion estimates using this method, the positioning accuracy across multi-view SAR images becomes more consistent, with an average improvement of 22.75% (reduced from 2.11 m to 1.63 m).

Without loss of generality, the SAR image from the first viewing angle as shown in Figure 5a is selected. As shown in the Figure 6, we selected three areas on the optical base map to demonstrate the results before and after applying the positioning method. Figure 7 illustrates the fitting effect between the positioning results before and after correction and the high-precision optical base map. It can be observed that, prior to multi-view fusion positioning, the initial SAR image exhibits significant positional offsets relative to the reference high-accuracy optical image in both latitudinal and longitudinal directions. After multi-view fusion positioning, by contrast, the calibrated SAR images show improved consistency with the optical image in terms of road networks and texture features.

These results confirm that the proposed algorithm can estimate and compensate for the 2D systematic positioning errors (in both range and azimuth directions) of each SAR image. Following the completion of four-corner positioning and slant-to-ground conversion using the RD model, this method enables high-precision planar positioning of SAR images without the need for GCPs.

5. Discussion

(1)

The Impact of Radar Target Anisotropy

The method in this paper needs to extract multiple sets of homologous point pairs from multi-view SAR images through high-precision registration. Although strictly speaking, the anisotropy of artificial targets will inevitably reduce the registration accuracy of multi-view images, especially in urban high-rise building areas. Considering that actual multi-view airborne SAR images used in the experiments of this paper have a large coverage area, the limited quantity with significant anisotropy ensures pixel-level registration accuracy and maintains homotopic point reliability. The positional error introduced by this non-ideal registration is far smaller than the systematic geolocation error (at least tens of pixels) of each SAR image. Therefore, the impact of radar target anisotropy on the method in this paper is negligible.

(2)

The Impact of Complex Terrain Scenarios

The method proposed in this paper focuses on correcting the overall geolocation offset of images, and it possesses both high efficiency and high precision, thus holding significant engineering application value. The space-variant systematic geolocation errors introduced by the errors of geolocation model parameters account for a relatively small proportion. The main source of the spatial variability of errors usually stems from terrain relief factors. Addressing this issue will significantly increase the complexity of the algorithm, which is not the research focus of this paper.

This study uses multi-view airborne SAR images of flat terrain as the experimental data to verify the effectiveness of the core innovations. For multi-view SAR images of mountainous and urban high-rise building scenarios, terrain undulations and tall buildings may locally cause layover, shadows, and additional relative positioning errors. On one hand, this tends to reduce the image registration accuracy in local areas; on the other hand, it will weaken the consistency of the systematic positioning errors of multi-view images in local areas, thereby posing technical challenges to the application of the method proposed in this paper.

In future work, we plan to avoid selecting Hps in urban high-rise building areas through regional masking, correct terrain-induced errors by integrating a Digital Elevation Model (DEM) to address the issue of spatial variability of errors in mountainous scenarios, and acquire more multi-view SAR image data under different scenarios to experimentally verify the adaptability of this method in complex terrains.

(3)

The number of multi-view images and the proportion of outlier images

When only 2 images from different viewing angles are input, the method in Reference [18] can be directly adopted. When conditions allow for the acquisition of more multi-view SAR images, the method proposed in this paper should be used. The new method not only makes full use of multi-view geometric structure information to improve fusion accuracy but also can automatically eliminate a small number of SAR images with inconsistent systematic errors, thereby significantly enhancing the accuracy and robustness of the algorithm.

Theoretically, the more multi-view images there are, the higher the fusion processing accuracy will be. Considering the limited sources of current multi-view SAR image data, this paper only compares the processing performance when 2, 3, or 4 images are input. Experimental results show that the fusion of 4 multi-view images yields results under different combinations that are significantly better than those obtained by fusing 2 or 3 images, with the highest positioning accuracy reaching 1.63 m, which is already close to the level of methods corrected using control points.

However, in practical applications, considering multiple factors such as geometric distortion of terrain and ground objects, differences in multi-view target scattering, and a certain degree of inconsistency in multi-view positioning errors, inputting too many images will not only fail to continuously improve algorithm performance but also significantly increase algorithm complexity. Therefore, considering both algorithm complexity and accuracy convergence, we suggest that the number of multi-view images in practical applications should be 3–7, among which the proportion of outlier images should not exceed 30% (i.e., 1–2 images are appropriate).

6. Conclusions

This study presents a novel approach for high-precision planar geolocation based on multi-view SAR image fusion, which eliminates the need for GCPs. The method accounts for discrepancies in positioning errors among multi-view airborne SAR images and employs the coefficient of variation to optimize the multi-view SAR image dataset. Additionally, a weighting strategy and a correction approach are developed to achieve high-precision fusion estimation of positioning errors for each view image. Simulation experiments analyze the influence of angular geometric relationships between images on estimation accuracy across different scenarios. Furthermore, cross-scenario result comparisons validate the effectiveness of the consistency identification and outlier removal modules. Within each scenario, ablation experiments are conducted to investigate the complex interactions between the proposed algorithm’s components and their respective impacts on overall performance. To further validate the method, experiments using actual airborne SAR measured data are performed. Results show that the proposed method achieves an average positioning accuracy improvement of 84.78% compared with alternative methods. These findings demonstrate that the method fully leverages information from multiple distinct SAR views, thereby enhancing both the positioning accuracy and robustness of multi-view SAR images.