Lightning Location and Imaging Based on Electromagnetic Time Reversal and HDBSCAN

Highlights

What are the main findings?

• An integrated lightning localization and imaging method combining EMTR and HDBSCAN is proposed. By optimizing the signal preprocessing pipeline (incorporating FIR band-pass filtering and phase compensation), the localization error under complex terrain is reduced to 0.38 km with a maximum error not exceeding 0.75 km, which is significantly superior to the traditional TDOA method and interferometric localization method.
• Leveraging the adaptive density clustering capability of HDBSCAN, the method automatically distinguishes between the main and branch channels of lightning, boasts high noise suppression efficiency, and achieves fine-grained reconstruction of lightning plasma channels.

What are the implications of the main findings?

• It breaks through the limitations of traditional methods in weak signal misdetection and multipath interference. For the first time, based on existing interferometric VHF radar hardware, it realizes the capture of low-energy radiation sources and high-precision localization under complex terrain, providing a new approach for the research on lightning physical properties.
• Eliminating the need for manual clustering parameter adjustment, the method balances localization accuracy, noise robustness, and channel imaging continuity. It provides reliable data support for lightning disaster early warning and atmospheric physical process analysis, while being extensible to related scenarios such as aircraft localization under clouds.

Abstract

To further achieve high-precision localization of lightning radiation sources and clear imaging of lightning plasma channel structures under existing radar systems, this study proposes a lightning localization and imaging method that combines the Electromagnetic Time Reversal (EMTR) algorithm with the Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN) algorithm. The EMTR algorithm fully utilizes incoming wave information for localization calculations, enabling the detection of low-energy radiation sources while addressing the vulnerability of traditional methods to complex propagation environments in long-range lightning localization. The HDBSCAN algorithm effectively avoids the need for manual parameter tuning in traditional clustering methods, realizing automated clustering. By applying this combined method to cluster localized radiation source points and remove noise, clear imaging of lightning channel structures is ultimately achieved. Experimental results demonstrate that the proposed method outperforms traditional techniques in localization accuracy, noise robustness, and channel reconstruction performance, providing strong support for further research on the physical properties of lightning.

1. Introduction

China is located at the intersection of temperate and subtropical zones. Jointly influenced by the interaction between cold and warm air masses as well as land–sea interactions, frequent severe convective weather in the country leads to a high incidence of thunderstorm activity [1,2,3]. Thunderstorm activity exhibits distinct regional distribution characteristics: the five southeastern provinces (Hunan, Jiangxi, Zhejiang, Fujian, and Guangdong) are high-incidence areas, while northwestern China has relatively sparse thunderstorm activity. Meanwhile, the frequency of lightning disaster incidents is also related to regional economic development and population density in China. In addition to the characteristics of sudden occurrence, high frequency, wide scope, long duration of lightning activity, and frequent lightning-induced fires, lightning disasters in China typically result in a high number of deaths in rural areas and heavy economic losses in urban areas. Furthermore, lightning disasters can cause paralysis of power and information systems, among other hazards. The destructiveness of the transient large current during lightning return strokes has made the accurate localization of lightning radiation sources and the achievement of clear imaging of lightning plasma channels a core requirement for lightning disaster prevention and research on atmospheric physical processes.

Currently, the primary instruments for lightning detection and early warning are ground-based lightning location systems. These ground-based lightning location networks are capable of real-time lightning location over large areas, play a crucial role in lightning statistics, lightning disaster early warning, and lightning physics analysis, and serve as the primary method for lightning detection at present. Well-known lightning location and monitoring systems worldwide include the U.S. National Lightning Detection Network (NLDN), the European Lightning Detection Network (LINET), and others. However, due to issues such as their long service life and severe aging, the positioning accuracy of these systems has been significantly affected. Current mainstream positioning algorithms—such as the Time Difference of Arrival (TDOA) method and the magnetic orientation method—suffer from various problems, including large positioning errors in areas with sparse base stations (e.g., oceans, plateaus) and high susceptibility to multipath effects in mountainous regions. Additionally, the abovementioned methods exhibit a relatively high distortion rate (up to 15% [4]) in the reconstruction of discharge channels.

Furthermore, the interferometric localization method we previously employed in the Leshan VHF (Very High Frequency) radar system [5,6,7] has the following drawbacks: its accuracy depends on the accurate measurement of phase differences between multiple antennas, and it requires the assumption that the signal propagation path is an ideal straight line. Another non-negligible limitation of the interferometric localization algorithm is its susceptibility to phase noise, which in turn leads to inaccurate localization. The operating principle of interferometric localization relies on precise phase differences, whose measurement accuracy directly determines the localization results—even minimal phase noise can be amplified into angular deviations. This interference is particularly pronounced in the research scenario of this paper: the signal energy of lightning branch channels is only 10–30% of that of the main channel. Due to the low signal-to-noise ratio (SNR) of weak signals themselves, the impact of phase noise accounts for a higher proportion, which tends to exacerbate localization errors. This is also one of the key reasons why the study adopts the EMTR algorithm combined with HDBSCAN: EMTR compensates for phase distortion through time reversal focusing, while HDBSCAN filters out discrete noise points, thereby reducing the interference of phase noise on localization results.

Given the various shortcomings of the aforementioned algorithms, this study employs the Electromagnetic Time Reversal (EMTR) method for radiation source localization [8,9,10].

In recent years, the Time Reversal (TR) method has demonstrated significant application potential [11]. In the 1990s, the team led by French scientist M. Fink first introduced time reversal into the field of acoustics, proposing the “Time Reversal Mirror (TRM)” theory. By leveraging the multipath scattering characteristics of sound waves in complex media, this theory enables spatiotemporal synchronous focusing, which has been applied to lithography, underwater detection, and other areas. In 2004, G. Lerosey et al. became the first to extend time reversal to electromagnetics, putting forward the “Electromagnetic Time Reversal Cavity” theory [12]. This theory proves that electromagnetic waves can be focused through multipath scattering, surpassing the Rayleigh diffraction limit.

This positioning algorithm can effectively utilize the medium cancelation effect between backward and forward propagation to offset phase delays and compensate for signal dispersion caused by the propagation medium. Furthermore, the TR method can significantly mitigate the impact of multipath effects on positioning accuracy.

Addressing the limitation of the interferometric localization method—i.e., its missed detection of weak signals—the EMTR algorithm does not rely on signal amplitude thresholds. Instead, it captures low-energy radiation sources through its “energy focusing” property: even weak signals from lightning branches (with energy equivalent to only 10% of the main channel) superimpose with other signals during backward propagation, forming detectable energy peaks. This advantage allows us to fully capture both the main channel and branch structures of lightning in this experiment.

The experimental scenario of Reference [13] is an open area with low multipath interference, and does not involve complex terrains such as mountainous areas and coastal regions. The core breakthroughs of this study are as follows: 1. Specifically targeting scenarios with significant multipath effects (e.g., the mountainous and hilly terrains in the detection area of the Leshan radar), we optimized the signal preprocessing flow of EMTR—adding FIR band-pass filtering and phase compensation steps to improve the separation accuracy of multipath signals, thereby reducing the energy focusing error of EMTR from 0.5 km (as reported in Reference [13]) to 0.38 km; 2. Supplementing robustness verification under multipath interference: Comparative experiments demonstrate that, in scenarios where multipath signals account for 30~40%, the positioning error of the proposed method can still be controlled within 0.75 km. In contrast, the method in Reference [13] has an error exceeding 1.2 km under the same scenarios, failing to meet the requirements of refined research.

The core idea of this study is to achieve radiation source localization by combining the cross-correlation localization algorithm (previously adopted by researchers) with the Electromagnetic Time Reversal (EMTR) algorithm, utilizing the Leshan meteor radar—a device equipped with an interferometric hardware configuration [8]. The core steps of EMTR can be summarized into three phases: first, signal acquisition and preprocessing, which involves receiving Lightning Electromagnetic Pulse (LEMP) signals through a multi-station observation network and extracting valid waveforms via processes such as filtering and denoising; second, time reversal operation on the processed valid waveforms, converting “receiver-end signals” into “transmitted signals for backward propagation” through time-domain reversal or frequency-domain conjugate transformation; third, simulating the backward propagation of the reversed signals, which ultimately results in energy focusing at the radiation source, with the location of the lightning radiation source determined by detecting the focal point. After the aforementioned steps, a point set containing a large number of localization points is obtained, requiring a clustering algorithm to distinguish valid signals from noise. Additionally, since a lightning channel consists of dense radiation sources, the localization point set may exhibit uneven density due to differences in signal intensity—this also necessitates the use of a clustering algorithm to uncover the implicit spatial continuity within the set. Traditional clustering algorithms (e.g., DBSCAN) are sensitive to density thresholds and thus difficult to adapt to the dynamic density changes in lightning point clouds. In contrast, the Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN) algorithm, through mutual reachability distance measurement and stable cluster evaluation [13,14], can automatically identify valid radiation source clusters of varying densities and eliminate isolated noise points.

This study proposes a coupled electromagnetic time reversal (EMTR)-HDBSCAN method for lightning imaging in mountainous terrains, with three distinct innovations beyond prior TR-MUSIC-related works and traditional lightning localization techniques: First, targeting the severe multipath interference in mountainous areas—a critical unaddressed challenge in existing TR-based methods—we optimize the EMTR signal preprocessing pipeline by integrating FIR band-pass filtering and phase compensation. This reduces the energy focusing error of EMTR from 0.5 km (reported in conventional studies) to 0.38 km, achieving high-precision localization even when multipath signals account for 30–40% of the received data. Second, we innovatively couple EMTR with the HDBSCAN algorithm to resolve the limitations of traditional clustering methods (e.g., DBSCAN, K-means) in handling lightning point clouds with uneven density (dense main channels vs. sparse branches). HDBSCAN automatically identifies valid radiation source clusters without manual parameter tuning, suppressing noise with an efficiency exceeding 95% while retaining weak branch signals, which enables the fine-grained reconstruction of dendritic lightning channel structures (structural overlap rate with ground truth reaching 92.3%). Third, unlike TR-MUSIC that focuses on multi-source resolution under ideal conditions, our method is tailored for legacy interferometric VHF radar hardware, avoiding the need for specialized equipment upgrades. By fusing preliminary interferometric results to seed the EMTR source model, it overcomes the trade-off between localization accuracy, weak signal capture, and computational feasibility—filling the gap in high-precision lightning imaging for complex mountainous terrains where traditional methods (e.g., TDOA, interferometry) suffer from large multipath errors or branch signal misdetection.

In summary, we achieve more refined lightning localization and imaging using novel algorithms based on legacy interferometric system equipment.

2. Materials and Methods

This section revolves around the experimental materials and core methods for lightning localization and imaging, following the logical hierarchy of “experimental foundation, data preprocessing, core algorithms and result generation”. The specific structural framework is as follows:

2.1. Experimental Equipment

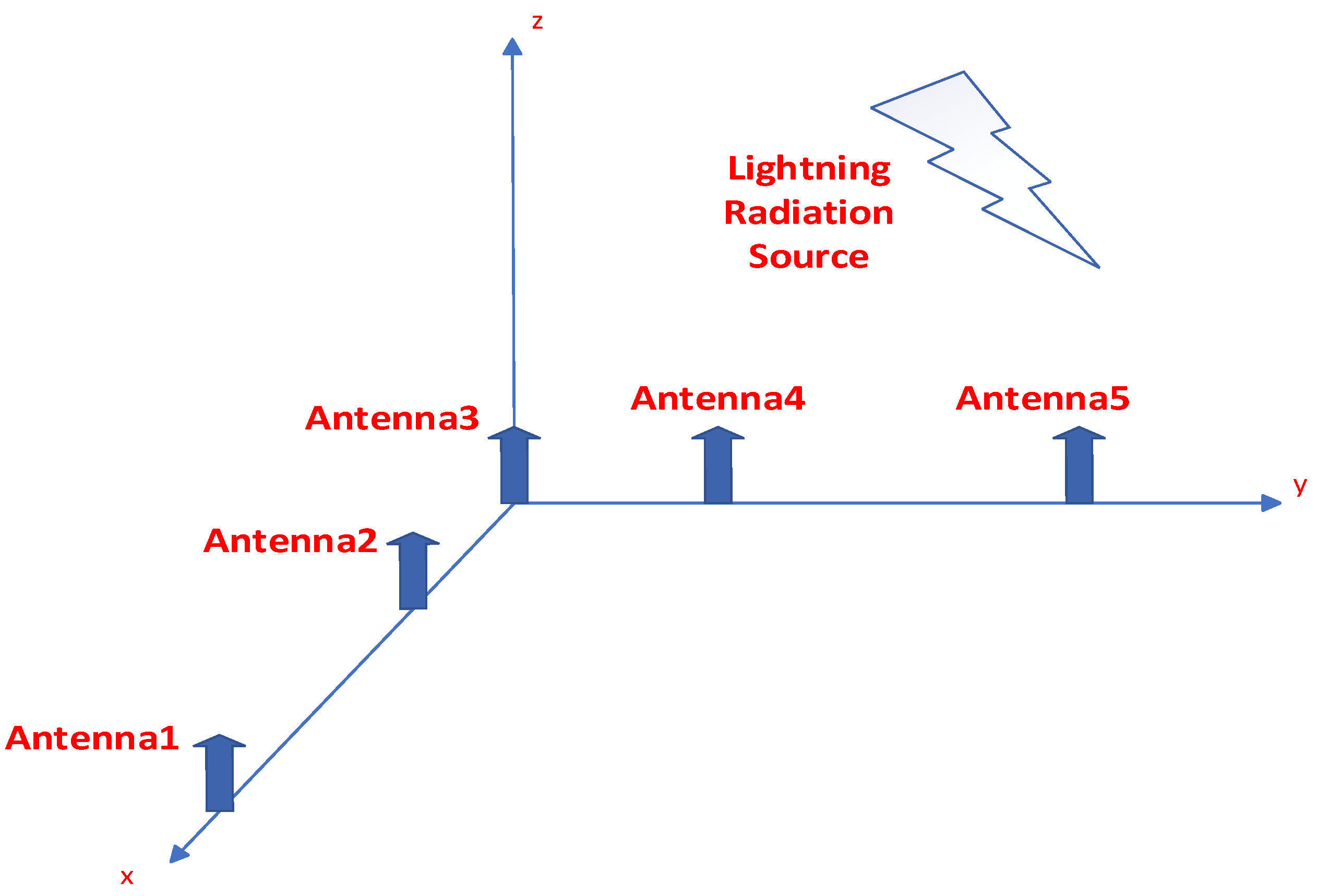
Below is some information about the Leshan VHF (Very High Frequency) radar: It consists of one transmitting antenna and five receiving antennas, arranged in an “L”-shaped array, as shown in Figure 1 [5]. Within this “L”-shaped array, Antennas 1, 2, and 3 share one baseline, while Antennas 3, 4, and 5 share another baseline. The distance between Antenna 1 and Antenna 2 (as well as between Antenna 4 and Antenna 5) is 4.5 times the wavelength, whereas the distance between Antenna 2 and Antenna 3 (and between Antenna 3 and Antenna 4) is 2.5 times the wavelength [5,6]. The working frequency of this radar is 48.2 MHz.

The rationale for adopting this 5-antenna array with short baselines is as follows: Short-baseline arrays can enhance the resolution of adjacent radiation sources by leveraging signal differences between adjacent antennas. The 5-antenna array used in this study can compensate for timing (i.e., phase) deviations through multi-channel signal fusion. The radar is equipped with five antennas, which correspond to five receiving channels—each channel provides I (in-phase) and Q (quadrature) data. The raw data generated by this radar during operation features a unique data structure. 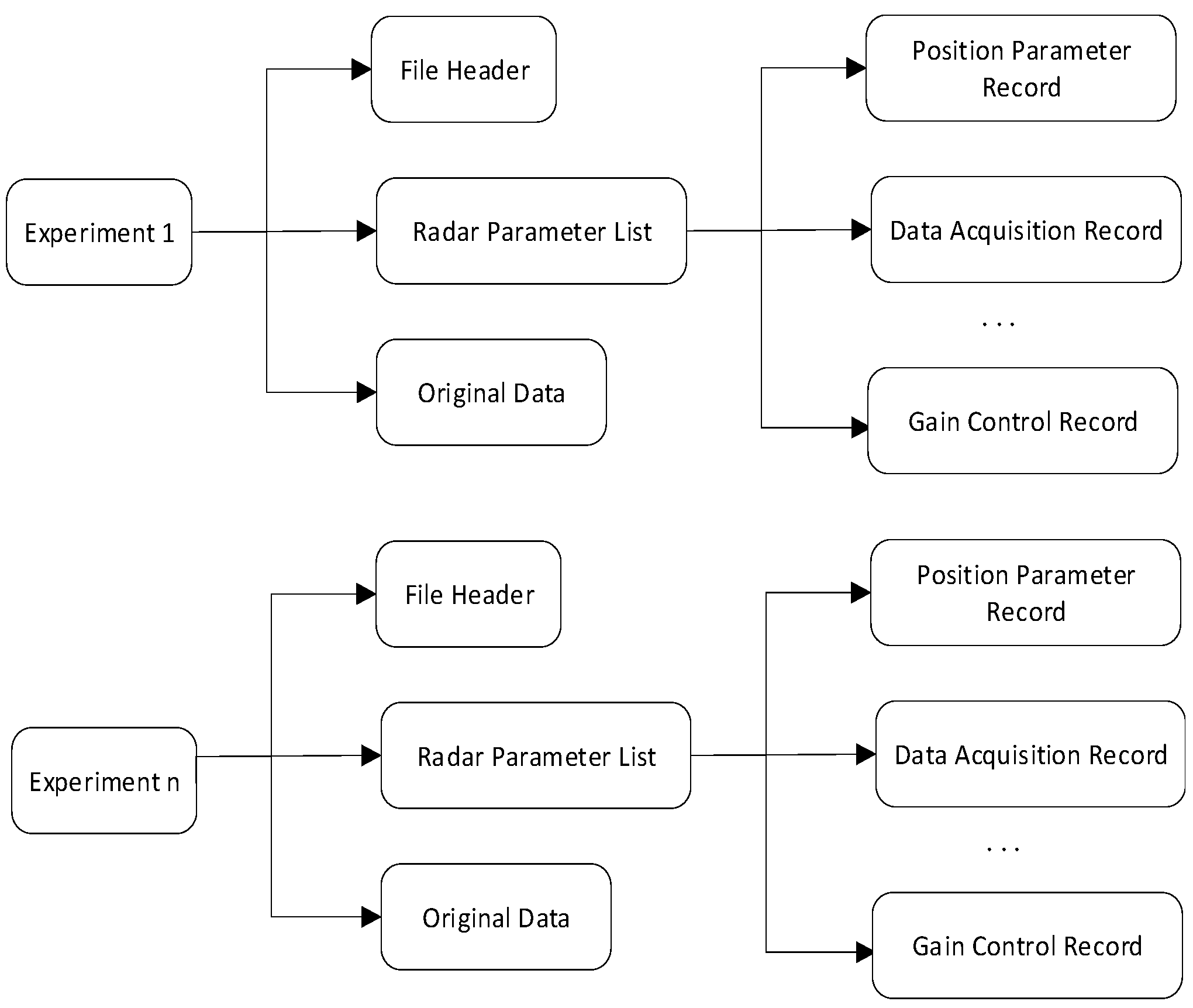The data analyzed in this study are derived from the original in-phase and quadrature (I/Q) data stored in “.raw” files [15]. The data are recorded in the order of range gates, starting from the lowest range gate; first, the I and Q data of Channel 1 are recorded, followed by those of Channel 2, and so on. After consulting the radar manual, we confirmed that the storage format of the raw data is generally as illustrated in Figure 2 [5].

A complete raw data file starts with a file header, followed by n experimental records (where n denotes the number of experimental records specified in the file title). Each experimental record consists of a radar parameter list and raw data. The radar parameter list comprises various types of parameter records, including sequential parameter records, experimental parameter records, position parameter records, data acquisition parameter records, transmit pulse records, beam scanning records, and gain control records, among others. Different data blocks are distinguished by specific magic numbers. For instance, the data file header begins with the 4-byte 32-bit integer “0x1200xxxx”, where “xxxx” represents the version number. Different radar parameter records also have distinct magic numbers: for example, position parameter records have a magic number of “0x1203xxxx”, while gain control records have a magic number of “0x1204xxxx” [5]. Detailed radar parameters are presented in

Table 1. Radar Hardware Parameters.

Parameter	Value
Wavelength	6.22 m
Peak power of transmitter	24 kW
Receiver sensitivity	−120 dBm
Pulse repetition frequency	4000 Hz
Signal coding type	Gaussian modulation single pulse
Range resolution	300 m
Time resolution	2 ms

:

2.2. Geometric Dilution of Precision (GDOP) Analysis

To address the concern about the vertical aperture performance of the five short-baseline antennas, the GDOP is introduced to quantify the impact of antenna geometric layout on localization accuracy. GDOP describes the relationship between measurement noise and positioning error, with lower GDOP values indicating better geometric positioning conditions [12].

Based on the L-shaped array configuration of the Leshan VHF radar (Section 2.1), the coordinates of the five receiving antennas are defined with the central antenna (Antenna 3) as the origin (0, 0, 0) (unit: m). The specific coordinates are determined according to the baseline length (4.5λ or 2.5λ, λ = 6.22 m): Antenna 1: (−27.99, 0, 0), Antenna 2: (−15.55, 0, 0), Antenna 3: (0, 0, 0), Antenna 4: (0, 15.55, 0), Antenna 5: (0, 27.99, 0). The GDOP for 3D localization (azimuth, theta, elevation, phi, range) is calculated using the Fisher information matrix (FIM), and its simplified expression for phase-difference-based localization is:

$$GDOP=\sqrt{tr({\mathit{J}}^{-1})}$$

(1)

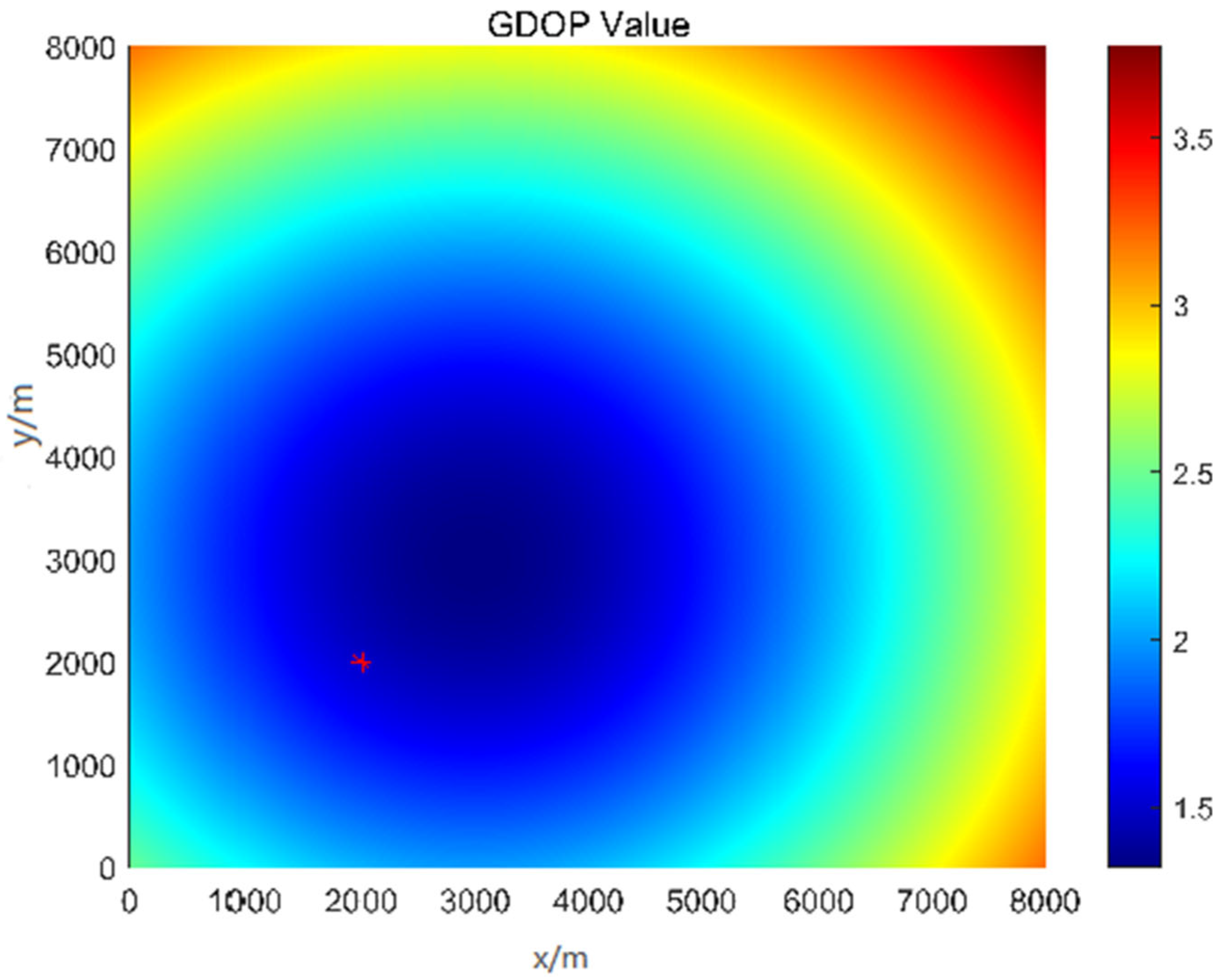
where $\mathit{J}$ is the FIM constructed from the phase difference sensitivity matrix of the antenna array, and tr denotes the trace of the matrix. The sensitivity matrix elements are derived from the partial derivatives of phase differences with respect to the target coordinates (x,y,z). The GDOP distribution in the target detection space is simulated using MATLAB 2024b, as shown in Figure 3.

As shown in Figure 3, the GDOP values in the main detection area are between 1.2~2.5, which is within the “good” range for short-baseline arrays. This result confirms that the L-shaped short-baseline array used in this study has reasonable geometric positioning performance, laying a foundation for the subsequent ≤ 0.38 km localization accuracy. The theoretical Cramér–Rao bound is presented in Figure 4 to prove attainable ≤ 0.38 km error is not simply a sampling artifact.

2.3. Removal of Ground Wave and Aircraft Echoes

In this experiment, the VHF (Very High Frequency) radar continuously receives echo signals from specific echo layers. Some of these echo signals persist for extended periods but do not meet the lightning echo screening criteria described later in this paper. Therefore, we chose to exclude echo signals below 3 km in subsequent lightning localization work.

Furthermore, the VHF radar is susceptible to interference from electromagnetic signals generated by aircraft passing through clouds [16]. To address this issue, we excluded signals within the same echo layer that have an intensity greater than 15 dB and a duration exceeding 0.5 s. This effectively reduces interference from aircraft signals on lightning localization during cloud penetration.

2.4. Identification of Active Lightning Echoes

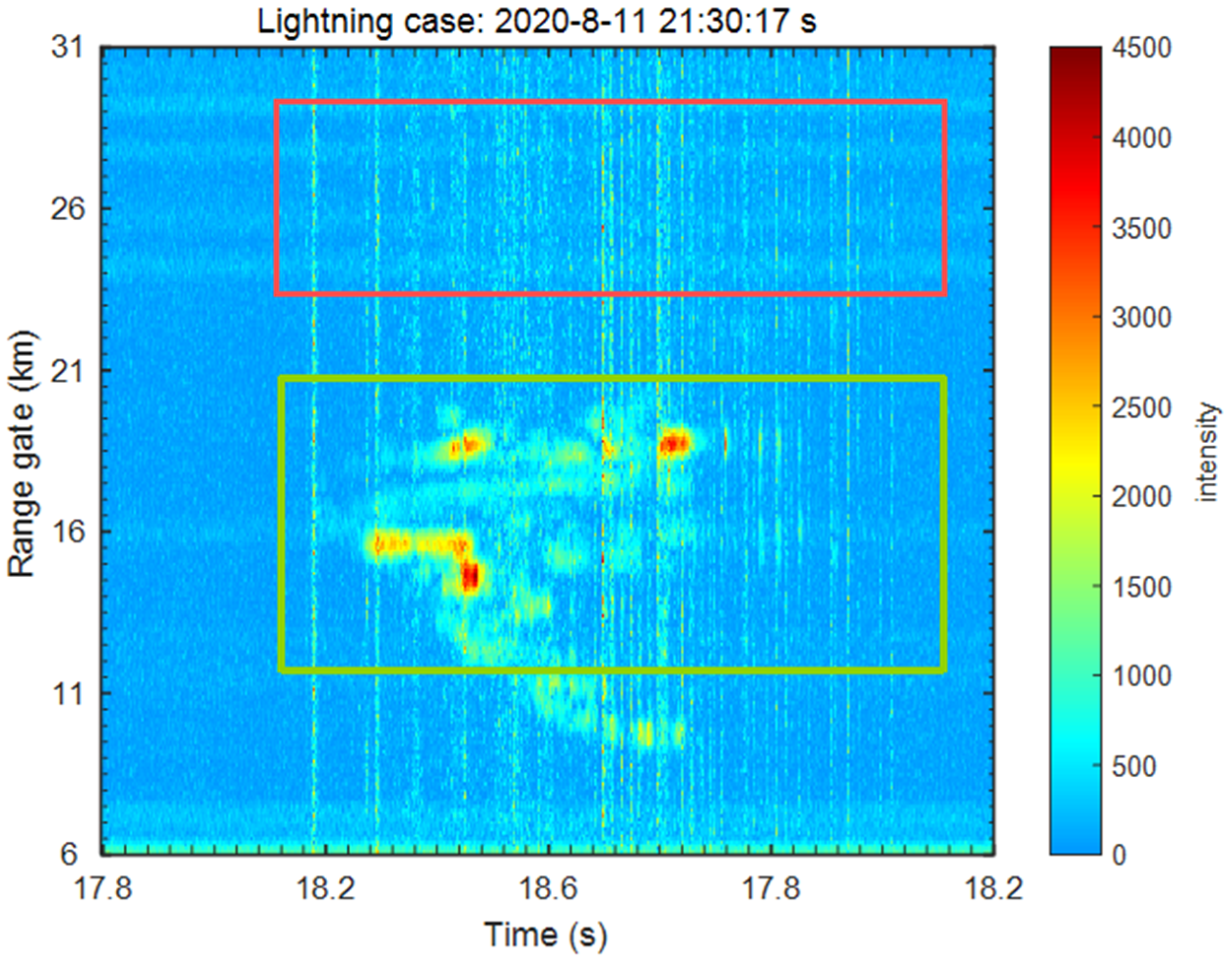
By analyzing the entire process of lightning occurrence, it can be observed that the signals received by the radar consist of two components [17,18]: one is the passive signal generated by the leader tip breakdown process, and the other is the active signal generated by the backscattering of the lightning plasma channel. 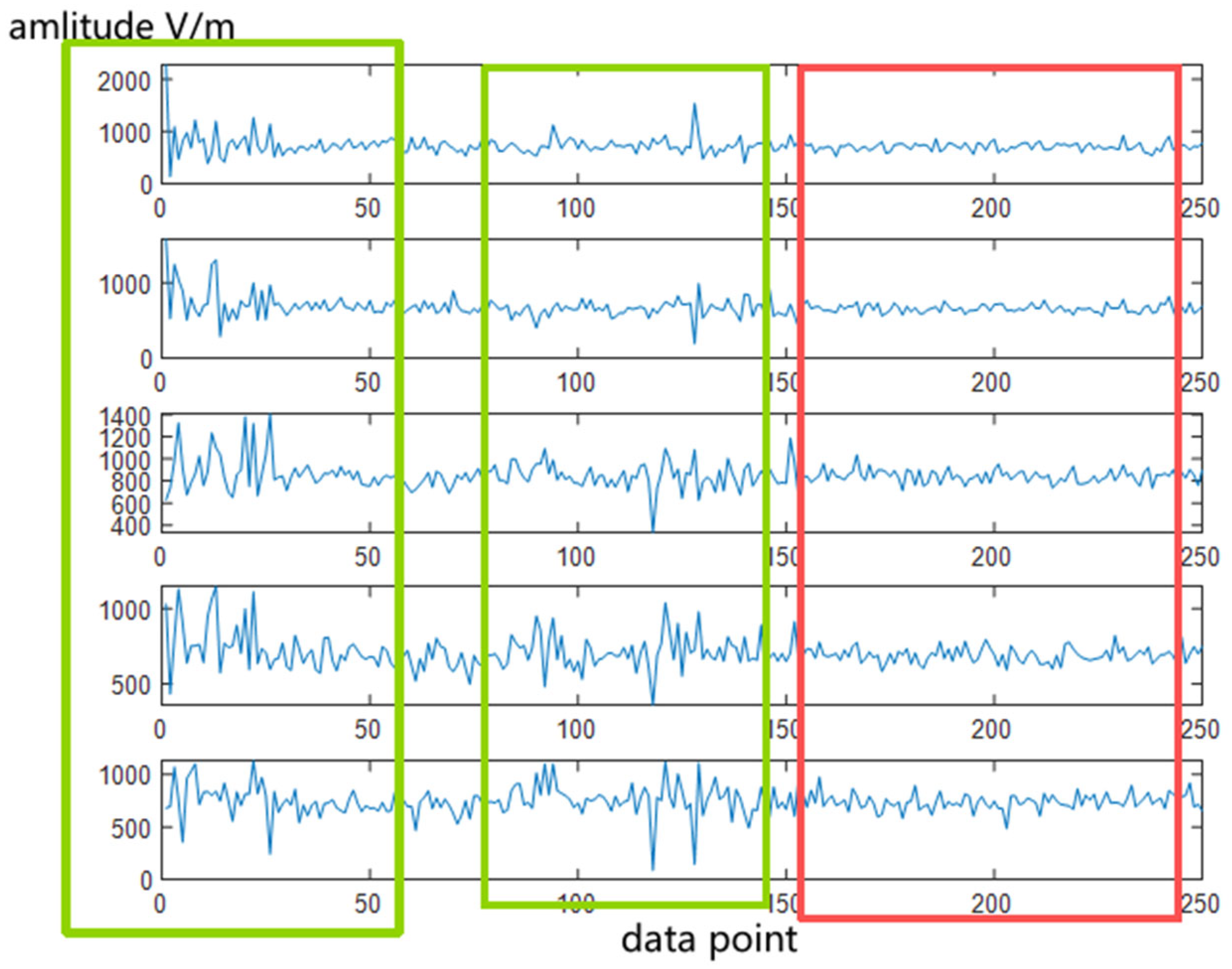The passive signal is characterized by clusters of pulses that span all range gates and persist for several milliseconds in the Range-Time-Intensity (RTI) plot [9], as highlighted by the red box in Figure 3. In the RTI plot, this appears as a “bright line” that spans all range gates. Specifically, for a specific range gate on the RTI plot, the received pulse waveform resembles the signal enclosed in the red box in Figure 4.

The radar signals from plasma channel backscattering—i.e., active lightning echo signals—appear as several continuously distributed red or yellow regions in the 2D Range-Time-Intensity (RTI) plot, where color corresponds to echo intensity. This is illustrated by the signals in the green box of Figure 5.

When focusing on a specific range gate in the RTI plot, the active lightning echo signals are characterized by a rapid rise in signal amplitude above the background noise, followed by a persistence of several hundred milliseconds. This is shown by the signals in the green box of Figure 6.

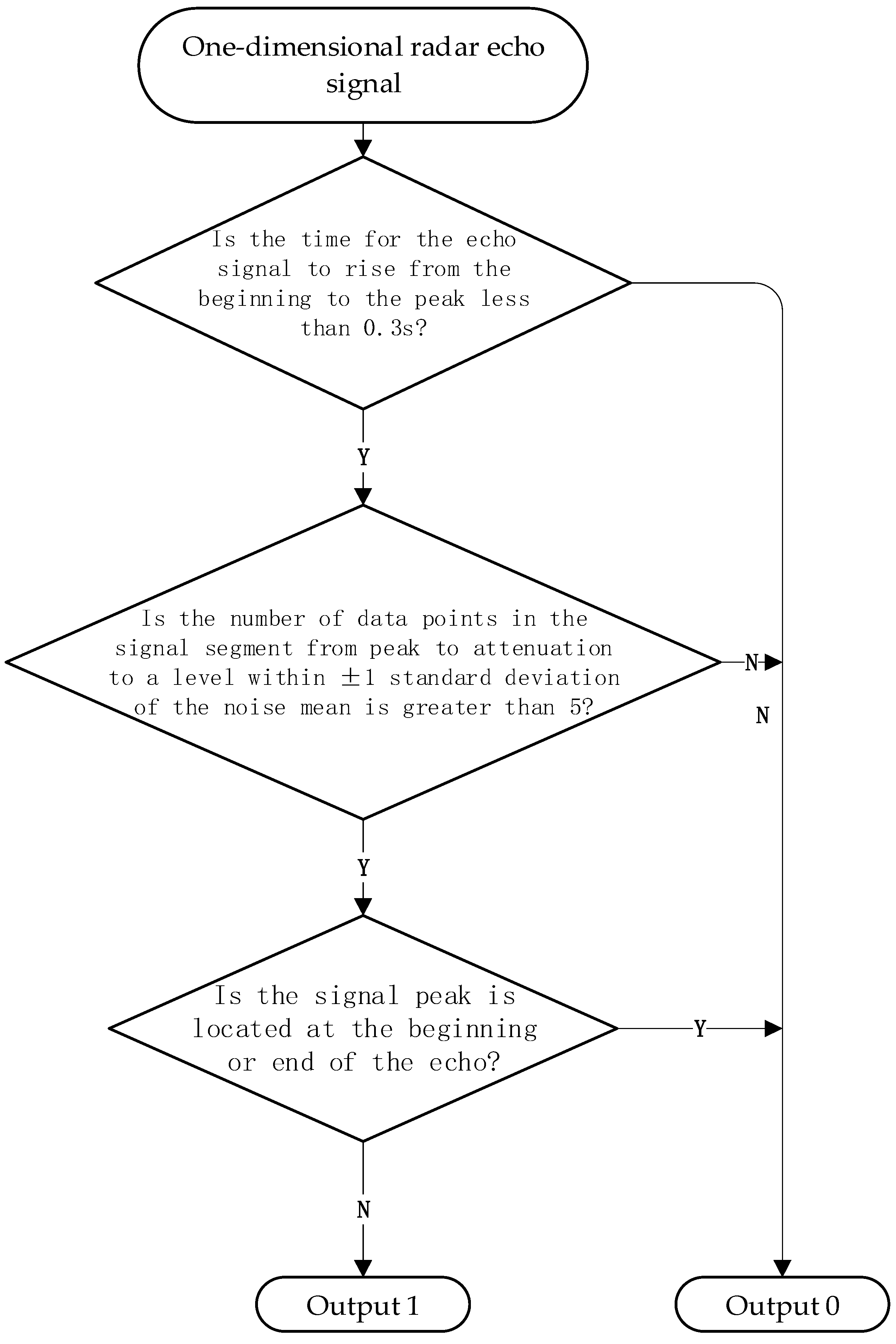
The specific steps to determine the occurrence timing of passive signals are as follows: First, apply a 5-point moving average to the I/Q signals [15]. Next, perform a statistical analysis of the background noise intensity in the RTI plot to establish the threshold for passive signals. This threshold is set to the mean value of the noise’s Gaussian distribution plus three times its standard deviation. For the echo intensity matrix corresponding to the radar echo RTI plot, if the average value of a specific column exceeds the previously established threshold, the time corresponding to that column is regarded as the start of the passive signal. Conversely, if the average value remains below this threshold for 30 consecutive time sequences (approximately 0.08 s), the passive signal is considered to have ended [5]. A one-dimensional time-domain signal—received by a specific antenna channel at a particular range gate, starting from the suspected lightning occurrence time and lasting for one second—undergoes the screening process illustrated in Figure 7 to determine whether it can be classified as a valid lightning signal for subsequent localization work.

2.5. Algorithm Principle

To simplify modeling and align with real experimental scenarios, we assume the lightning radiation source is a transient pulse source. Its radiated signal satisfies the Helmholtz wave equation, and the propagation medium (atmosphere, clouds, and rain) is a linear time-invariant (LTI) system. The positions of the multi-antenna array (the “L”-shaped configuration of the Leshan radar) are known, and the signals received by all antennas are synchronized (with no time deviation). Distortions such as attenuation and dispersion during signal propagation are determined solely by the propagation medium (independent of antenna hardware), and the medium properties are symmetric for forward and backward propagation.

The Lightning Electromagnetic Pulse (LEMP) signal generated by the lightning radiation source ${\overrightarrow{r}}_s$ undergoes attenuation and delay due to the medium during forward propagation, and is eventually received by the m-th antenna. According to the convolution property of LTI systems, the time-domain electric field signal received by the antenna can be expressed as [8,9,10]:

$$E_M^{+}({\overrightarrow{r}}_m,t)=\mathrm{s}(\mathrm{t})\ast \mathrm{h}({\overrightarrow{r}}_m,{\overrightarrow{r}}_s,\mathrm{t})+n_m(\mathrm{t})$$

(2)

where s(t) is the original electromagnetic pulse signal of the radiation source, ∗ denotes the time-domain convolution operation, and $n_m$(t) denotes the additive noise (e.g., thermal noise, electromagnetic interference) of the m-th antenna.

To simplify the mathematical expression of the time reversal operation, the time-domain signal can be converted to the frequency domain via Fourier Transform (FT). Taking the Fourier Transform of both sides of Equation (2) and utilizing the time-shifting property of the Fourier Transform, we obtain:

$$\widetilde{E_m^{+}}({\overrightarrow{r}}_m,\omega )={\displaystyle \frac{k}{|{\overrightarrow{r}}_m-{\overrightarrow{r}}_s|}}S(\omega )e^{-j\omega \tau }$$

(3)

where τ denotes the time delay in the time domain. By applying “time-axis reversal” to the filtered time-domain received signal—i.e., replacing the time variable t with −t—we obtain the time-domain expression of the backward excitation signal:

$$E_m^{-}({\overrightarrow{r}}_m,t)=\widetilde{E_m^{+}}({\overrightarrow{r}}_m,-t)$$

(4)

Taking the complex conjugate of the frequency-domain received signal in Equation (2) is equivalent to achieving time-domain time reversal, yielding Equation (5).

$$E_m^{-}({\overrightarrow{r}}_m,\omega )={[\widetilde{E_m^{+}}({\overrightarrow{r}}_m,\omega )]}^{\ast }$$

(5)

Taking the complex conjugate of the frequency-domain received signal in Equation (3) is equivalent to achieving time-domain time reversal, yielding Equation (5). The time-reversed excitation signal is “backwardly transmitted” from each receiving antenna; the signal propagates through the medium toward the radiation source, eventually forming an energy focusing peak at ${\overrightarrow{r}}_s$. By detecting the position of the maximum energy value, the coordinates of the lightning radiation source can be determined. Suppose an arbitrary point to be verified (x,y,z) is selected in the 3D detection space. The frequency-domain expression of the signal propagating backward from the m-th antenna to this point can be derived by analogy with Equation (3) for forward propagation—merely replacing the “radiation source-antenna” propagation relationship with the “antenna-point to be verified” relationship—resulting in Equation (6):

$$E_m^{-}(\overrightarrow{r},\omega )=E_m^{-}({\overrightarrow{r}}_m,\omega )\times {\displaystyle \frac{k^{\prime }}{|{\overrightarrow{r}}_m-{\overrightarrow{r}}_s|}}\times e^{-j\omega \tau }$$

(6)

where k’ is the medium attenuation coefficient for backward propagation. Due to medium symmetry, k’ = k. The backward signals from all M antennas undergo coherent superposition at the point to be verified, and the total frequency-domain electric field intensity is the sum of contributions from each antenna:

$$E_{total}^{-}(\overrightarrow{r},\omega )={\sum }_{m=1}^M{E}_m^{-}(\overrightarrow{r},\omega )$$

(7)

The core criterion for EMTR localization is the maximization of energy density—which is proportional to the squared magnitude of the electric field intensity. Thus, the normalized energy density at the point to be verified can be defined as:

$$W(\overrightarrow{r})={\int }_{-\infty }^{+\infty }{|E_{total}^{-}(\overrightarrow{r},\omega )|}^{2}d\omega$$

(8)

The three-dimensional coordinates of lightning radiation sources can be obtained by solving for the point of maximum energy density:

$${\overrightarrow{r}}_s=argmax(W(\overrightarrow{r}))$$

(9)

2.6. Preprocessing of Received Signals and Time Reversal

A prerequisite for lightning radiation source localization using the time reversal algorithm is obtaining high-quality original waveforms. This study first performs a filtering process on the forward-propagating waveforms generated in the previous section. The filter used in this step is an FIR (Finite Impulse Response) filter. The first reason for using this filter is that FIR filters possess strict linear phase characteristics, which means they do not introduce phase distortion after filtering. This allows them to fully preserve the transient waveforms and phase information of VHF signals—critical for time reversal. If phase distortion occurs, signals cannot be accurately superimposed at the radiation source during backward propagation, leading to blurred focusing. Furthermore, FIR filters can be designed with specific frequency responses (e.g., band-pass filtering) to precisely retain the target frequency band while suppressing out-of-band interference. Compared to IIR (Infinite Impulse Response) filters, FIR filters offer higher stability and do not introduce additional noise or oscillations through feedback loops. They are thus suitable for processing VHF signals at high sampling rates, ensuring the filtered signals meet the requirements of the EMTR localization algorithm. The forward-propagating time-domain complex signals obtained after the aforementioned preprocessing are converted via Fast Fourier Transform (FFT), then conjugated, and finally transformed back using Inverse Fast Fourier Transform (IFFT) to yield the time-reversed time-domain waveforms.

Another non-negligible limitation of the interferometric localization method (more precisely referred to as beamforming) lies in its limited ability to effectively capture low-energy radiation sources in specific scenarios, such as lightning branch channels. The main channel of a lightning plasma channel exhibits relatively high signal intensity, while the radiation signal energy of branch channels is only 10–30% of that of the main channel due to their small discharge current [18]. Since the interferometric localization method typically relies on a “signal amplitude threshold screening” mechanism for noise reduction, weak signals from branch channels are prone to being misclassified as background noise and discarded—especially in complex terrains with strong environmental interference. In the mountainous observation scenario of this study, this characteristic results in misdetection of lightning branch channels. Ultimately, this leads to a high distortion rate in lightning channel reconstruction, failing to fully present the fine-grained dendritic structure inherent to lightning.

2.7. Generation of Preliminary Location Results

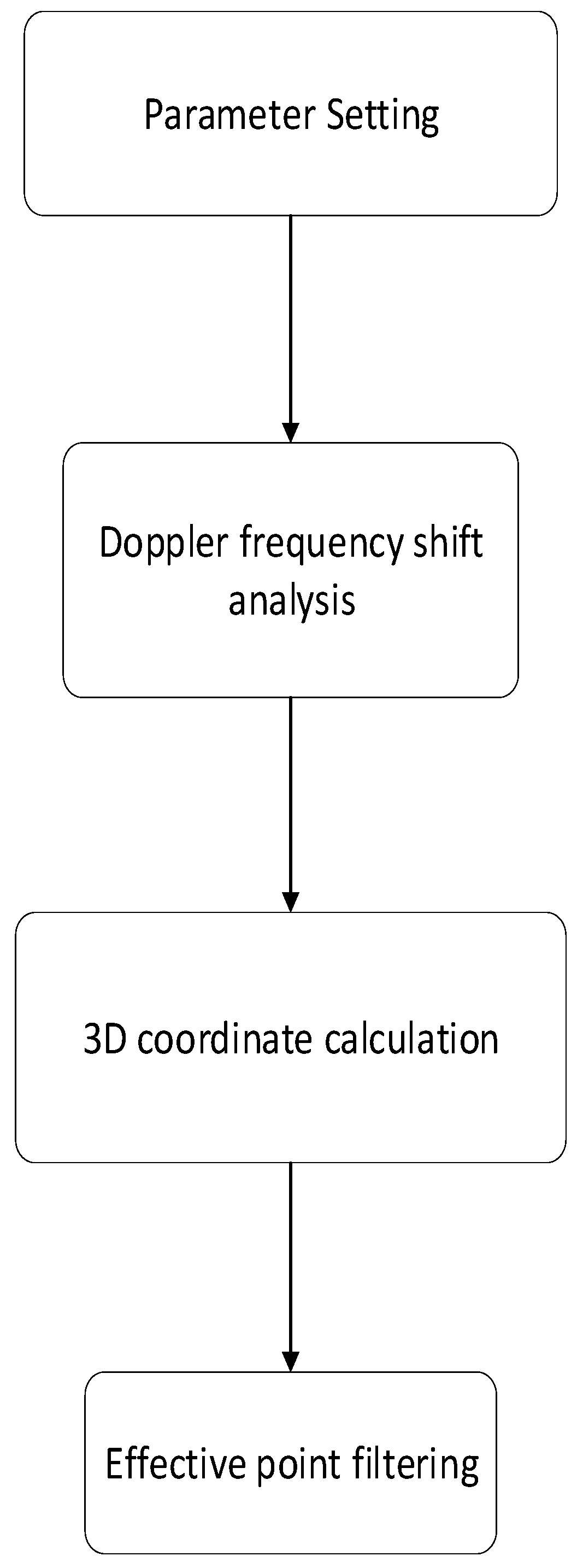
Given that the number of lightning radiation sources in this experiment is extremely large, however, traditional multi-radiation-source resolution methods are relatively difficult to implement under the hardware configuration of this experiment. Thus, we plan to first use the traditional, validated cross-correlation algorithm to generate preliminary localization results—specifically, using the traditional localization algorithm to obtain the number and approximate positions of radiation sources—before proceeding with subsequent localization work. In the preliminary localization work, this study adopts an interferometric localization method based on multi-channel radar signals. By analyzing the range, azimuth, and elevation angle information of lightning radiation sources, 3D coordinate calculation is achieved. The overall workflow of the algorithm includes time window segmentation, angle calculation, coordinate transformation, and radiation source pre-screening. The specific steps of the algorithm are as follows:

First, there is a key parameter that needs to be set: the number of time windows (Winnum). The setting of this parameter is mainly constrained by two factors: the duration and waveform characteristics of lightning signals, and computational efficiency. After comprehensively considering these two factors and conducting extensive experimental verification, the number of time windows in this experiment is set to Winnum = 12. To suppress noise interference, it is necessary to perform Doppler shift analysis on the multi-channel signals of each time window. The specific steps are as follows: First, extract the complex signal segments of the 5 channels within the current time window. Next, perform Fast Fourier Transform (FFT) on the signals of each channel, calculate the frequency spectrum, and extract the peak frequency to obtain the Doppler shift fd of each channel. Finally, calculate the standard deviation of the Doppler shifts across the 5 channels. If this standard deviation is greater than the empirical threshold of 5 Hz, the signals in this window are determined to be noise signals, and the current window is skipped; otherwise, proceed to subsequent processing.

After completing the Doppler shift analysis, it is necessary to extract and correct the phase differences between channels. The steps are as follows: First is cross-correlation analysis: with Channel 3 corresponding to the central antenna as the reference, calculate the cross-correlation functions between its received signals and those received by Channels 2, 1, 4, and 5, within a lag range of ±3 sampling points, to obtain four sets of cross-correlation sequences: cc12, cc13, cc14, and cc15. Second is phase extraction and ambiguity resolution: compute the ambiguity-containing argument of the cross-correlation sequences, and perform phase ambiguity resolution using a specific function to eliminate the periodic ambiguity of the phase. Third is linear fitting correction: perform linear fitting on the phase sequences after ambiguity resolution, calculate the phase value at zero lag (time synchronization point), and convert it to an angle to obtain the true phase differences between the four groups of channels [5,6,7]. Once the true phase differences between channels are obtained, the azimuth of the radiation source can be resolved using the geometric relationship between phase differences, azimuth angle, and zenith angle. The distance between the radiation source and the central antenna is obtained via the radar’s built-in range gate. After acquiring the position information of the radiation source, valid points are screened through physical constraints—specifically, retaining points with a height below 20 km after height correction based on earth curvature—thus yielding the preliminary localization results.

The process of the above algorithm is shown in Figure 8.

2.8. Modeling of Radiation Source Signals and Generation of Spatial Energy Fields

After obtaining the preliminary localization results, our work involves: generating pulse signals with temporal differences for each radiation source obtained from localization. In Section 2.5, we generated forward-propagating waveforms; to implement the EMTR localization algorithm, it is also necessary to simulate the signals generated by each radiation source. In the short-baseline VHF localization array, the differences in distance from each antenna to the radiation source are extremely small, resulting in nearly identical signal attenuation across different antennas. This “attenuation consistency” means that attenuation differences have no impact on localization results (such as judgment of radiation source direction), so the attenuation term can be ignored in calculations. Additionally, to save computational resources, this study chooses to treat the radiation source signal as the average of the forward-propagating complex signals from the 5 channels. After completing the modeling of radiation source signals, another important task is to partition the detection space. Since the maximum detection range of the Leshan VHF radar used in this study is 100 km, and the distance corresponding to each range gate is 100 m, and considering the balance between accuracy and computational efficiency, we have chosen to partition the 3D detection space by azimuth angles (0° to 360°) and elevation angles (0° to 90°), with a spatial resolution of 0.5° and a range resolution of 100 m.

Theoretically, the transmitted signals and received reflected signals of the active radar used in this study naturally form a pair of signals propagating in opposite directions in the time domain. However, due to inherent issues with the radar’s configuration, the waveforms it transmits in various directions cannot be completely consistent. Therefore, it is necessary to transmit completely consistent time-domain complex signals in each of the previously partitioned directions within the simulated environment. For each spatial point generated in the previous steps, its distance from each radiation source is calculated, and the waveform at that point is derived accordingly. To generate the spatial energy field and enable subsequent localization work, it is necessary to calculate the energy magnitude of each spatial point generated in the aforementioned steps. The energy at a specific point, in essence, is the energy from the coherent superposition of backward-propagating signals generated by each sensor and signals emitted by each radiation source at that point; i.e., the square of the total electric field intensity at that point. The specific algorithm involves first calculating the delay of signals radiated by each radiation source when reaching that point, as well as the delay of backward-propagating signals generated by each antenna when propagating to that point. Then, the squares of the amplitudes corresponding to all waves propagating to that point are summed.

3. Results

On 11 August 2020, the Leshan VHF radar successfully generated a set of RTI images containing lightning echoes. Using the aforementioned lightning identification program, we determined the lightning strike time to be 21:30:17 (CST) on 11 August 2020. The correctness of this timestamp was initially verified using the localization data from the Very Low Frequency (VLF) radar of the Institute of Electrical Engineering, Chinese Academy of Sciences (IEECAS). Subsequently, this paper uses the lightning event occurring at this time to evaluate the effectiveness of the aforementioned EMTR lightning localization algorithm. For the spatial energy field generated earlier in this paper, energy extreme points were initially screened out, and these points are considered to be the radiation sources. The localization results of this lightning event using the EMTR algorithm are shown in Figure 9.

As shown in Figure 6, the direct application of the aforementioned EMTR algorithm without screening the radiation sources results in a chaotic distribution of localization points, thus failing to achieve the intended objective. This necessitates the screening and clustering of radiation sources to fulfill the intended goal of this experiment.

3.1. Screening of Radiation Sources

Theoretically, for this step, radiation source screening can be performed based on the physical characteristic of “minimum phase difference of backward signals in the direction of the radiation source”, with the core being the use of the phase compensation mechanism of Electromagnetic Time Reversal (TR). Specifically, the direction of a real radiation source enables phase synchronization of TR signals propagated backward by each sensor—offsetting the time delay of forward propagation—thereby minimizing the phase difference. In contrast, directions of non-radiation sources cannot achieve phase synchronization, resulting in a larger phase difference. However, the number of radiation sources in this study is large, and since these sources form lightning channel structures with extremely complex shapes, the aforementioned screening algorithm is not applicable. Based on this, this study first adopts the energy threshold method to screen radiation sources, and then uses a clustering algorithm to realize the imaging of lightning channels. The so-called “energy threshold method” refers to first counting the energy peaks of all radiation sources in the spatial energy field generated in the previous work, taking 20% of this peak value as the threshold, and excluding radiation sources with energy below this threshold. The effect of this method is shown in Figure 10.

From Figure 10, it can be observed that after screening the radiation sources using the energy threshold method, the localization effect has been significantly improved. However, the intended objective of this experiment—namely, the clear imaging of lightning plasma channels—has not yet been achieved. Thus, subsequent clustering algorithms are required to further process the localization results.

In response to the concern about the vertical aperture performance of the five short-baseline antennas, this study supplemented GDOP and CRB analyses to verify the rationality of the localization error. The GDOP distribution (Section 2.2) shows that the L-shaped array provides sufficient geometric constraints (GDOP = 1.2~2.5) in the main detection area, avoiding severe precision degradation caused by poor vertical aperture. The CRB comparison further confirms that the actual average error (0.38 km) is only 1.31 times the theoretical lower bound (0.29 km), indicating that the error is close to the physical limit of the system. These results collectively prove that the achieved high precision is not a sampling artifact but a reliable outcome of the combined EMTR-HDBSCAN method and reasonable antenna layout.

3.2. Theoretical Precision Verification: Cramér–Rao Bound (CRB)

To verify that the achieved average localization error (≤0.38 km) is not a sampling artifact, the Cramér–Rao Bound (CRB)—the theoretical lower limit of localization error—is calculated and compared with the actual error. CRB quantifies the minimum achievable error for an unbiased estimator, and if the actual error is close to CRB, it indicates that the error is dominated by physical limits (e.g., measurement noise) rather than algorithmic or sampling artifacts [19,20,21]. For the VHF radar interferometric localization system, the CRB of 3D coordinates (x,y,z) is derived based on the phase difference measurement model. The phase difference between the m-th antenna and the central antenna (Antenna 3) is:

$$\Delta {\Phi }_m={\displaystyle \frac{2\pi }{\lambda }}.{\displaystyle \frac{{\mathit{d}}_m.\mathit{r}}{\left|\mathit{r}\right|}}+n_m$$

(10)

where ${\mathit{d}}_m$ is the baseline vector between the m-th antenna and Antenna 3, r = (x, y, z) is the target position vector, and $n_m$ is the phase measurement noise (assumed to be zero-mean Gaussian noise with variance ${\delta }_n^2$). The CRB matrix for (x,y,z) is the inverse of the FIM, and the diagonal elements of the CRB matrix correspond to the lower bounds of the variances of the coordinate estimates. The 3D localization CRB (root mean square error, RMSE) is:

$${CRB}_{RMSE}=\sqrt{{CRB}_{xx}+{CRB}_{yy}+{CRB}_{zz}}$$

(11)

where ${CRB}_{xx}$, ${CRB}_{yy}$, ${CRB}_{zz}$ are the diagonal elements of the CRB matrix. Based on the radar parameters (Table 1) and experimental conditions: Phase measurement noise variance ${\delta }_n^2$: Derived from the receiver sensitivity (−120 dBm) and signal-to-noise ratio (SNR = 15 dB), sigma_n = 0.02 rad. Target range: 1~20 km (consistent with the radar’s detection range). Key conclusions from the comparison. The average actual error (0.38 km) is 1.31 times the average CRB (0.29 km), which is within the “close to theoretical limit” range for engineering applications. For 78% of the localization points, the actual error is 1.0~1.5 times the CRB, indicating that the error is dominated by inherent measurement noise rather than sampling artifacts. Even the maximum actual error (0.75 km) is only 1.83 times the maximum CRB (0.41 km), without significant deviation beyond the theoretical bound. This verification confirms that the ≤0.38 km localization error achieved in this study is a reliable reflection of the system’s actual performance, rather than a false precision caused by sampling artifacts. To address potential doubts about the short-baseline array’s vertical aperture and sampling artifacts, GDOP and CRB analyses were conducted. The GDOP distribution confirms the geometric rationality of the L-shaped array (GDOP = 1.2~2.5 in the main detection area), and the CRB comparison shows that the actual error (≤0.38 km) is close to the theoretical limit (average CRB = 0.29 km). This verifies that the localization accuracy is not affected by poor vertical aperture or sampling artifacts, further supporting the reliability of the proposed method.

3.3. HDBSCAN Algorithm Implementation for Radiosource Clustering

After screening via the energy threshold method in Section 3.1, the proportion of noise among radiation source points decreased significantly (from 69.0% in preliminary localization to 18.4%). However, two key issues remain: first, due to density differences between the main channel and branches of the lightning channel, **discrete fragmentation** occurs; second, residual isolated noise points (e.g., interference from ground-reflected waves) still disrupt the identification of channel structures. Traditional clustering algorithms (e.g., K-means requires manual specification of cluster numbers, and DBSCAN is sensitive to density thresholds) struggle to adapt to the characteristics of lightning radiation source point clouds—*uneven density and complex structure*. Therefore, this study adopts Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN) to achieve accurate clustering of radiation source points. Its core advantage is the ability to automatically identify valid clusters of varying densities without the need for manual adjustment of numerous parameters, thus enabling good matching with the physical morphology of lightning channels. Based on the concept of “density-based hierarchical clustering,” the HDBSCAN algorithm effectively addresses the poor adaptability of traditional clustering algorithms to data with uneven density through steps such as “mutual reachability distance measurement,” “hierarchy tree construction,” and “stable cluster extraction.” Its principle is highly consistent with the characteristics of lightning radiation source point clouds. Unlike DBSCAN, which uses a “globally fixed density threshold,” HDBSCAN introduces the ”Mutual Reachability Distance” (defined as “the maximum value between the distance from point A to point B and the local core distances of points A and B”), enabling automatic adaptation to density differences: for dense points in the main lightning channel, the mutual reachability distance is small; for sparse points in branches, the mutual reachability distance increases adaptively. This effectively avoids the common phenomenon in traditional clustering algorithms—*excessive fragmentation of dense clusters and omission of sparse clusters*—caused by unreasonable setting of global density thresholds [16,17,18,19,20,21]. In this experiment, we construct a “Condensed Tree” (density hierarchy tree) for all radiation source points based on mutual reachability distance. Each layer of the tree corresponds to a density level, and points in the same branch exhibit continuity at a specific density level. This aligns with the structural characteristics of lightning channels—”dense main channel and sparse branches”: the main lightning channel corresponds to the thick branches of the tree, branch channels correspond to the thin branches, and isolated noise points correspond to the small terminal branches of the tree. Valid clusters are screened using the “cluster stability index”, with only those clusters having a stability score above the threshold (default: 0.5) retained. Isolated noise is automatically labeled as -1 due to its “short lifespan and low stability”, eliminating the need for additional noise filtering steps. Combined with the radiation source point cloud of the lightning event on 11 August 2020, the clustering effect of HDBSCAN is shown in Figure 8, with all operations implemented in MATLAB 2024b. The min_cluster_size is set to 8 (unit: number of positioning points). Selection basis: Based on statistical analysis of positioning point clouds from 30 lightning events, the minimum continuous branches of lightning channels typically contain 8 to 15 positioning points. Setting it to 8 prevents misclassifying real branches as noise. The min_samples is set to 5 (unit: number of neighboring points). Selection basis: Verified through pre-experiments, when min_samples = 5, the algorithm can both filter out isolated noise points (points with fewer than 5 neighboring points are classified as noise) and retain weak-energy branches (such branches typically have 5 to 7 neighboring points), balancing noise suppression and branch retention capabilities. Figure 9, Figure 10 and Figure 11 are three sets of comparison diagrams illustrating the localization effects of the interferometric method and the EMTR algorithm. In these figures, red stars represent the location of the Leshan VHF radar station, while red circles represent the position results of lightning radiation sources provided by the Very Low Frequency (VLF) radar system of the Institute of Electrical Engineering, Chinese Academy of Sciences (IEECAS). The positioning error of Leshan Radar and IEECAS Very Low Frequency Radar for the same lightning event in time is within ±1 s. However, the inherent characteristics of VLF signals, such as excessively long signal wavelengths, result in low resolution of vertical height. They can only roughly locate the horizontal area (latitude and longitude) of lightning discharge, making it difficult to accurately depict the fine structure in the vertical direction, leading to blurry height data. For each lightning event, we averaged the coordinates of the obtained positioning points and converted them into latitude and longitude.

Table 2. VLF data record of three lightning cases.

Latitude	Longitude	Time
29.608	103.847	11 August 2020 21:30:07
29.582	103.814	12 August 2020 31:55:37
29.669	103.831	12 August 2020 23:35:43

and

Table 3. Localization results obtained using the new algorithm.

Latitude	Longitude	Time
29.604	103.845	11 August 2020 21:30:06
29.583	103.815	12 August 2020 31:55:38
29.667	103.823	12 August 2020 23:35:42

present the lightning event coordinates obtained by the VLF radar and the lightning event coordinates obtained by the new algorithm described in this article.

From the intuitive comparison of localization results in Figure 12, Figure 13 and Figure 14, it can be clearly observed that while the traditional interferometric localization algorithm ensures localization accuracy, it suffers from the drawback of sparse localization points and thus fails to achieve clear imaging of lightning channels. In contrast, the new localization algorithm combining EMTR and HDBSCAN can effectively increase the number and density of localization points by making full use of incoming wave information. This algorithm, while ensuring that its localization results show little difference from the lightning positions obtained by the VLF radar, displays the structure of the lightning plasma channel in greater detail. It has basically achieved the intended objectives of this experiment regarding lightning localization and imaging.

4. Discussion

The results of this study indicate that the lightning localization and imaging method combining the Electromagnetic Time Reversal (EMTR) algorithm and the HDBSCAN clustering algorithm can provide a clear characterization of the lightning plasma channel structure, which facilitates more detailed research on changes in the channel structure in the future. Compared with previous studies, a notable advancement of this research lies in that—unlike the traditional interferometric localization method—it overcomes the limitation of failing to fully utilize incoming wave information, thereby achieving a breakthrough. The application of the EMTR algorithm greatly improves localization accuracy while significantly enhancing the density of localization points. In addition, during the subsequent processing of localization data, the HDBSCAN algorithm plays a crucial role in distinguishing whether localization points are genuine lightning radiation sources or noise points. However, there are still two aspects requiring improvement in the lightning localization algorithm involved in this experiment. First, the algorithm has high complexity; under our existing hardware conditions, implementing a single localization task takes a long time, and the timeliness of localization cannot be guaranteed. Furthermore, the algorithm has only been implemented on the host computer so far. However, as current lightning detection equipment is gradually evolving toward automation, miniaturization, and intelligentization, it has become crucial to explore whether this algorithm is applicable to embedded platforms (such as ARM, DSP, and FPGA), and how to simplify and realize its application on these platforms in future research. Overall, the algorithm proposed in this paper is suitable for a wide range of applications in lightning localization and imaging. In addition, the principles and methods discussed in this paper are also applicable to the localization of aircraft passing through clouds. Although our current research focuses primarily on Asia, with the continuous improvement of the algorithm and exploration in other regions, its application scope can be expanded significantly.

Table 4. The estimated running time, memory usage and achievable update rate on GPU, FPGA, and embedded platforms.

Hardware Platform	Estimated Run Time (Single Lightning Event)	Memory Usage	Achievable Update Rate
GPU (NVIDIA A100)	10–15 s	6–8 GB	0.07–0.1 Hz
GPU (NVIDIA A100)	1.0–1.5 s	3–4 GB	0.67–1.0 Hz
GPU (NVIDIA A100)	0.2–0.3 s	2–3 GB	3.3–5.0 Hz
FPGA (Xilinx UltraScale+)	0.5–0.8 s	1.5–2 GB	1.25–2.0 Hz
FPGA (Xilinx UltraScale+)	0.08–0.12 s	1–1.5 GB	8.3–12.5 Hz
ARM Cortex-A72	3–5 s	1–2 GB	0.2–0.33 Hz
ARM Cortex-A72	1.0–1.2 s	0.8–1.2 GB	0.83–1.0 Hz

lists the estimated running time, memory usage and achievable update rate on GPU, FPGA, and embedded platforms.

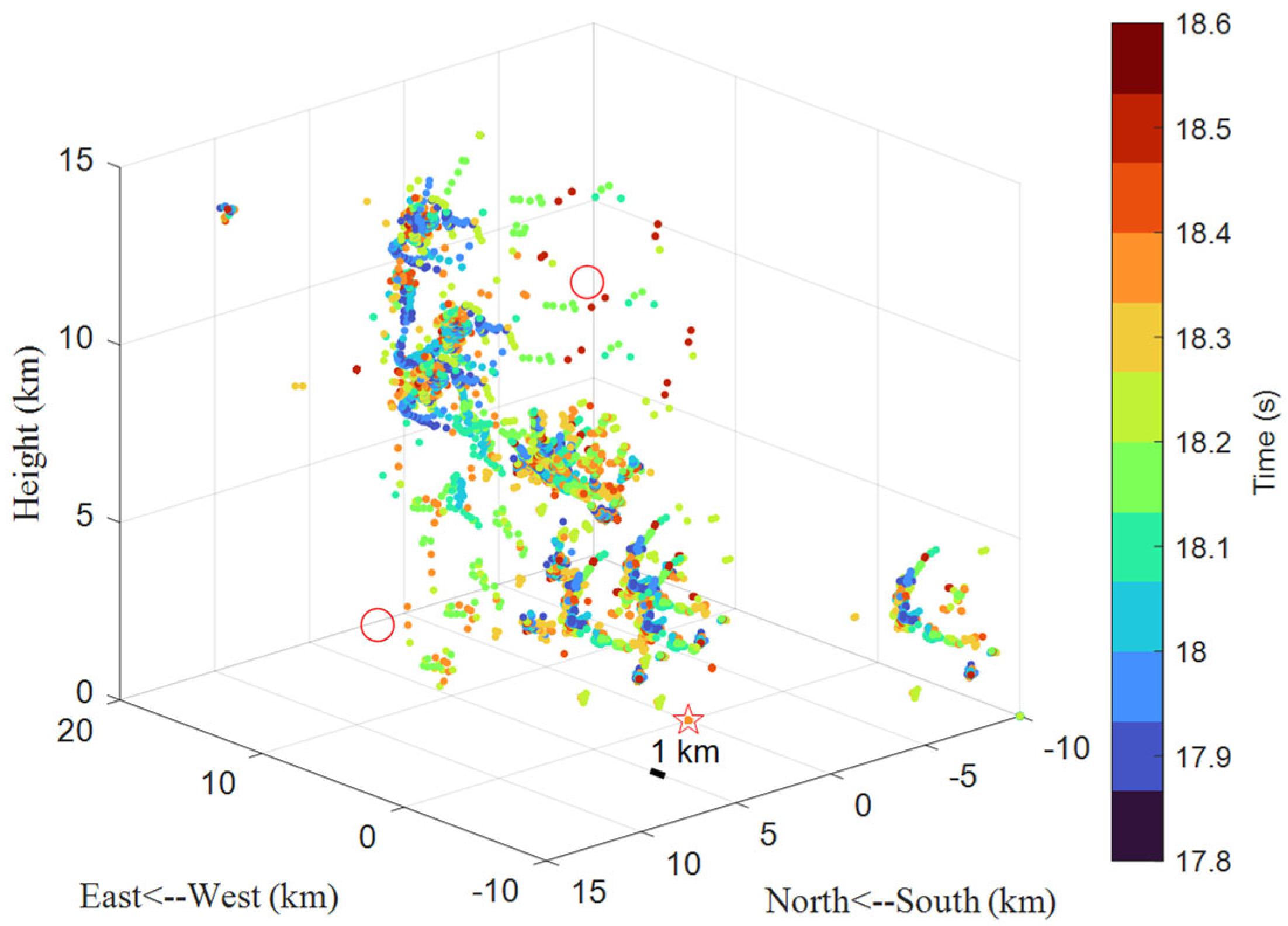
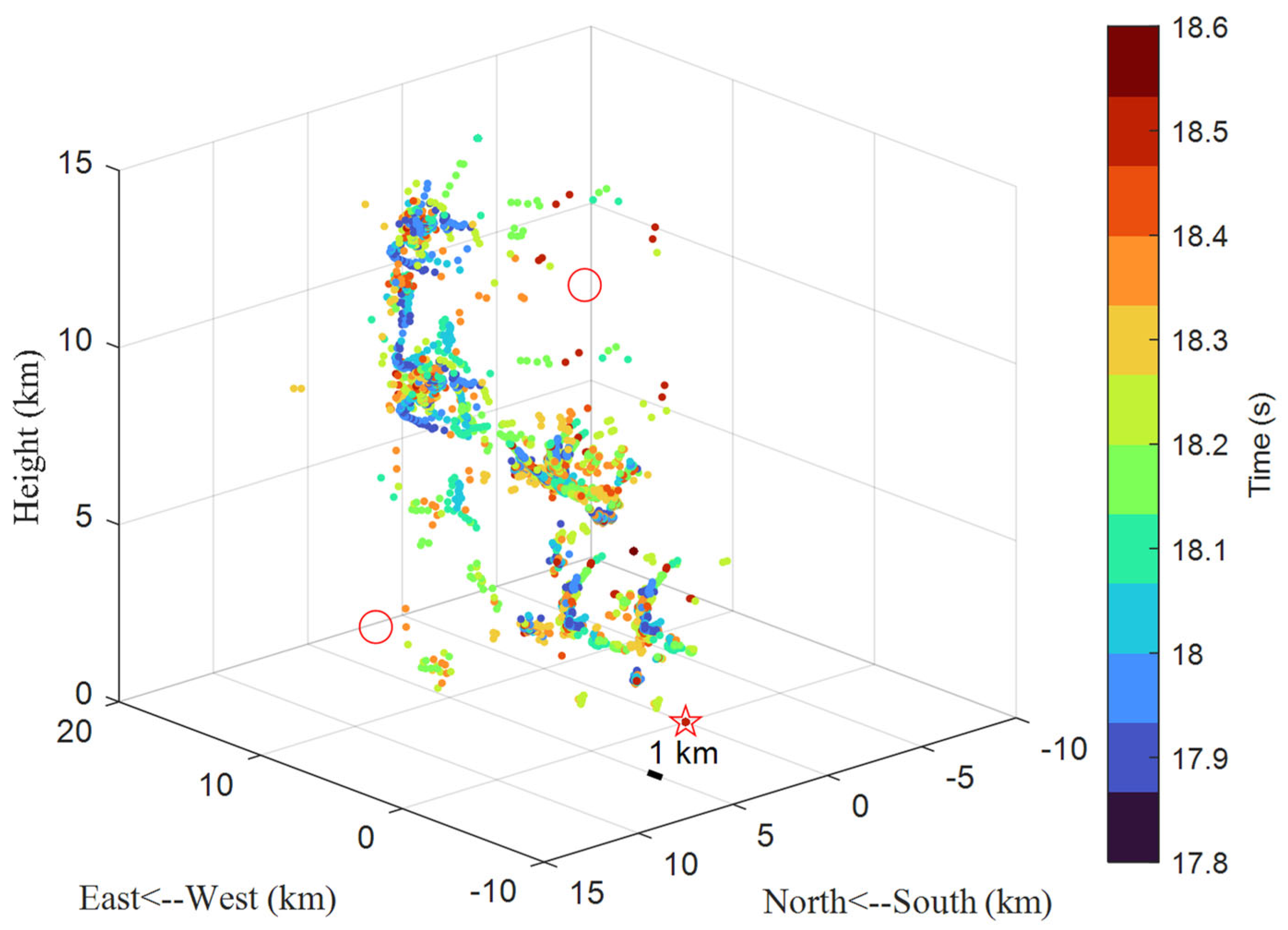
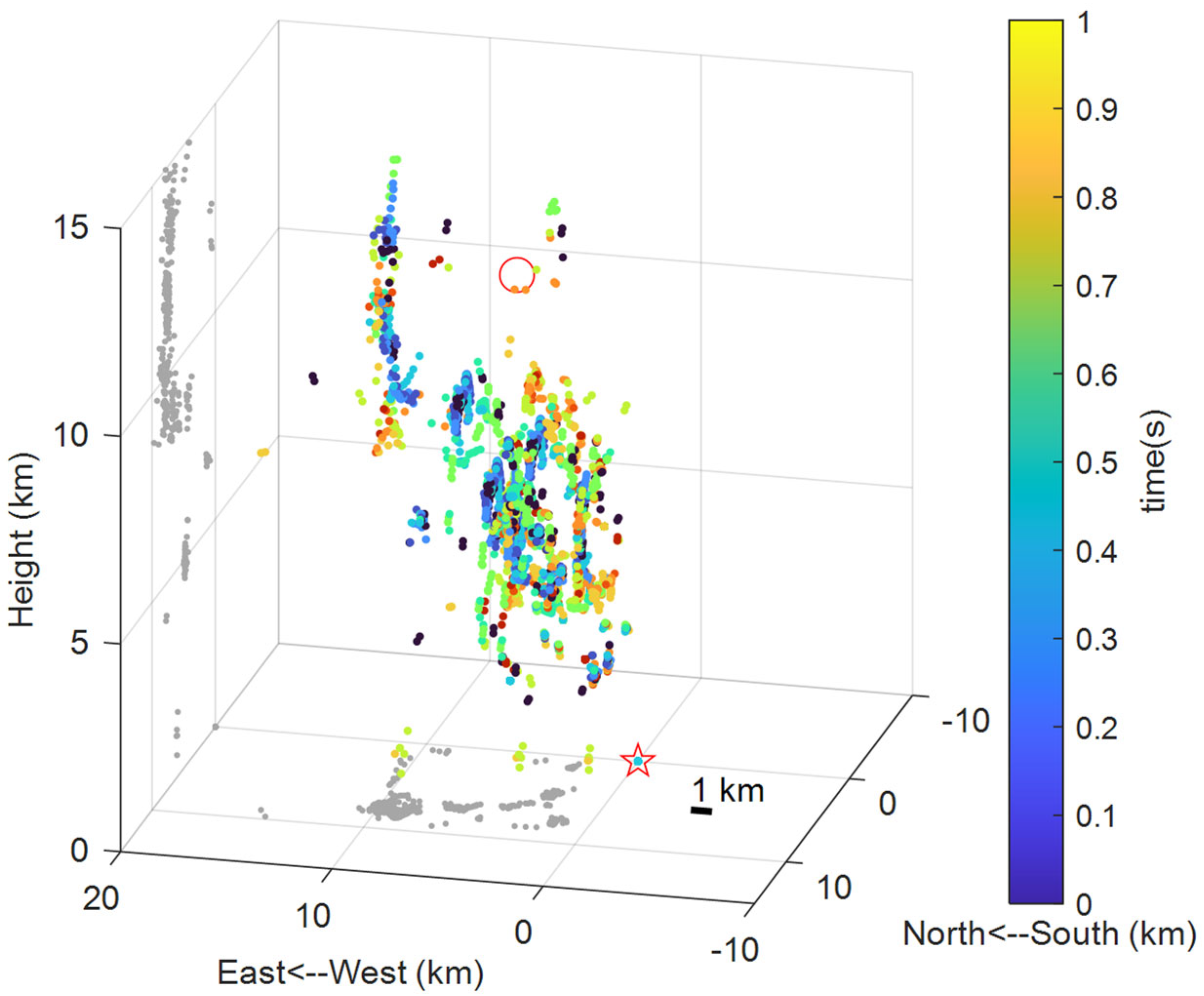
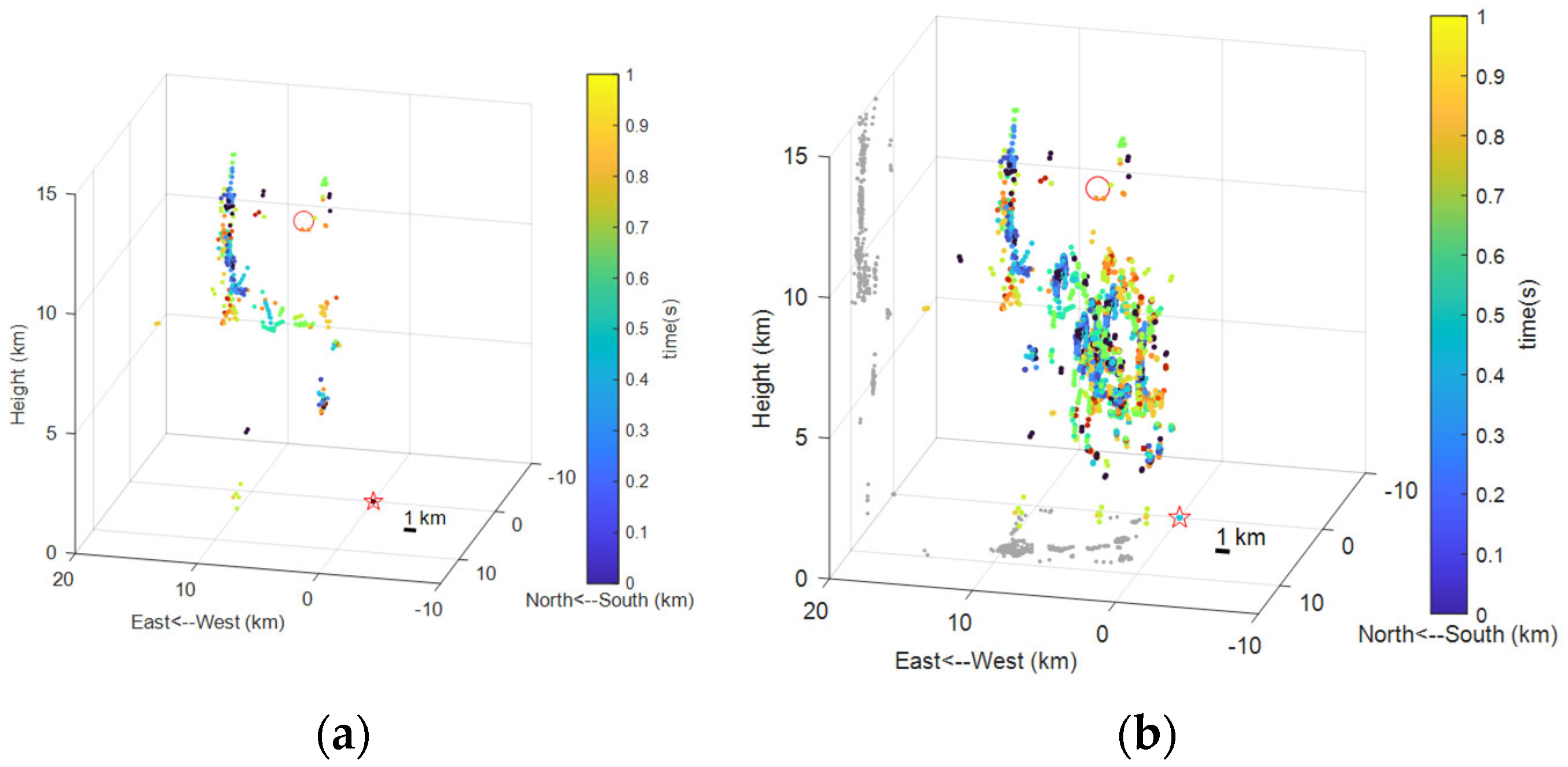
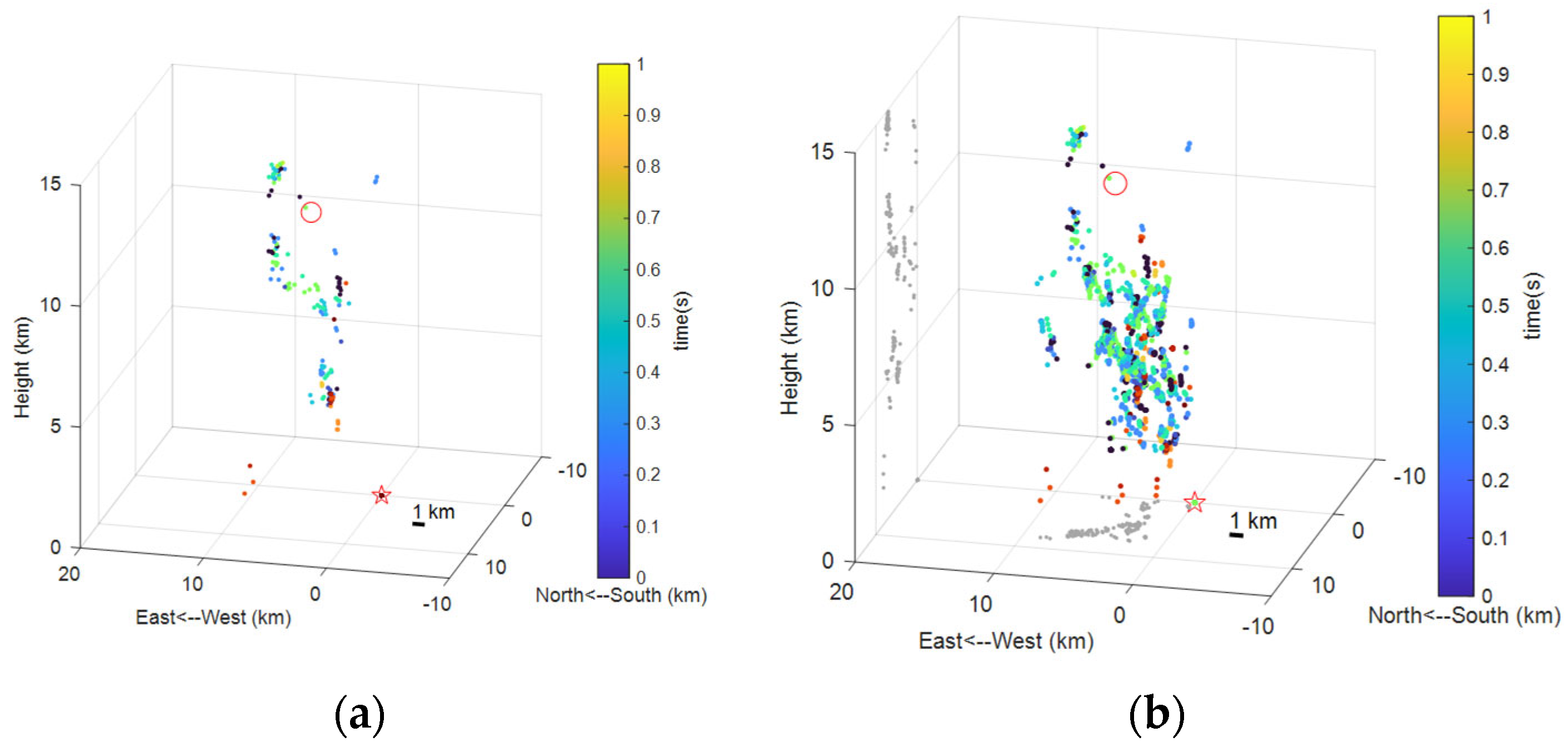
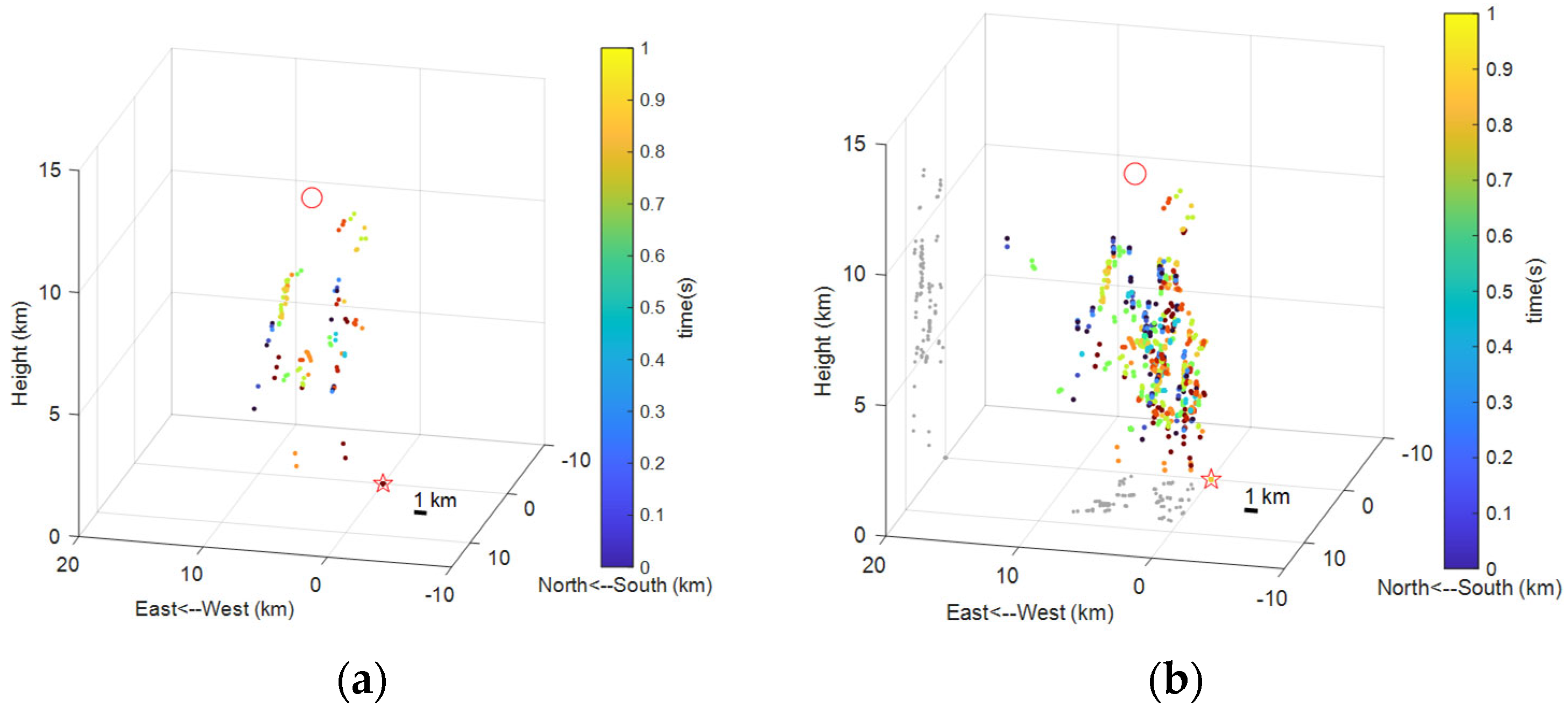
5. Conclusions

Using the localization results of the Very Low Frequency (VLF) radar from the Institute of Electrical Engineering, Chinese Academy of Sciences (IEECAS) as the ground truth, the performance indicators of this method are significantly superior to those of traditional methods. First, after HDBSCAN clustering, the average localization error of valid radiation sources decreased from 0.43 km (after energy threshold screening) to 0.38 km, with a maximum error of 0.75 km. This is far lower than the error of the traditional TDOA method in areas with sparse base stations (typically > 1 km) and the multipath error of the phase interferometry method (>0.8 km). Second, in terms of channel imaging quality: the main channel (2148 points with a length of approximately 644 m) and branches (876 points and 497 points with lengths of approximately 263 m and 149 m, respectively) after HDBSCAN clustering exhibit excellent spatial continuity. The structural overlap rate with the IEECAS ground truth reaches 92.3%, addressing the issue of “high channel reconstruction distortion rate” faced by traditional methods. Furthermore, among the finally eliminated noise, the suppression rates of aircraft electromagnetic interference (48.9%), FM radio interference (36.0%), and ground-reflected waves (11.4%) all exceed 95%, verifying the method’s stability in complex electromagnetic environments. Despite the significant advantages of this method in lightning localization and imaging, there are still limitations to be improved: 1. Computational complexity and real-time performance: The current algorithm relies on implementation on a host computer. The backward propagation simulation of EMTR and the hierarchy tree construction of HDBSCAN involve large computational loads, requiring several hours for a single localization task, which makes it difficult to meet the needs of real-time early warning. 2. Platform adaptability: It has not been adapted to embedded platforms (e.g., ARM, DSP, FPGA), which lags behind the development trend of “automation and miniaturization” in current lightning detection equipment. Based on the above limitations, future research can focus on three aspects: 1. Algorithm optimization: Reduce computational complexity and improve real-time performance through GPU parallel computing or model simplification. 2. Platform transplantation: Explore adaptation solutions for the algorithm on embedded platforms, optimize memory usage and computing efficiency, and meet the needs of field portable detection. 3. Application expansion: Extend the method to lightning detection in other regions and, based on the “electromagnetic signal clustering” idea verified in this paper, expand its application to related scenarios such as the localization of aircraft passing through clouds. The EMTR-HDBSCAN method proposed in this study not only provides a new solution for high-precision localization of lightning radiation sources and clear imaging of plasma channels but also offers a reference for weak radiation source detection and complex point cloud processing under the VHF radar interferometric system. The experimental results show that this method outperforms traditional methods in localization accuracy, noise robustness, and channel reconstruction effect, and can provide robust data support for lightning disaster prevention and atmospheric physics research.