Fourier Fusion Implicit Mamba Network for Remote Sensing Pansharpening
Highlights
- This study proposes a Fourier Fusion Implicit Mamba Network (FFIMamba). It integrates Mamba’s long-range dependency modeling ability with a Fourier-domain spatial–frequency fusion mechanism to overcome limitations of traditional Implicit Neural Representation (INR) models, such as insufficient global perception and low-frequency bias.
- Experimental results on multiple benchmark datasets (WorldView-3, QuickBird, and GaoFen-2) show that FFIMamba outperforms both traditional pansharpening algorithms and state-of-the-art deep learning methods in visual quality and quantitative metrics.
- This study shows that integrating the Mamba framework with Fourier-based implicit neural representations can address the shortcomings of conventional INR models in pansharpening. The proposed approach enhances global feature perception and restores high-frequency spatial details, enabling more precise reconstruction of high-resolution multispectral images (HR-MSIs).
- The proposed FFIMamba framework and its modular architecture (e.g., the spatial–frequency interactive fusion module) offer a constructive reference for future pansharpening models. This design enhances the quality and efficiency of remote sensing image fusion, and broadens the potential applications of Mamba and implicit neural representations (INRs) in computer vision, facilitating further exploration in multimodal remote sensing image analysis.
Abstract
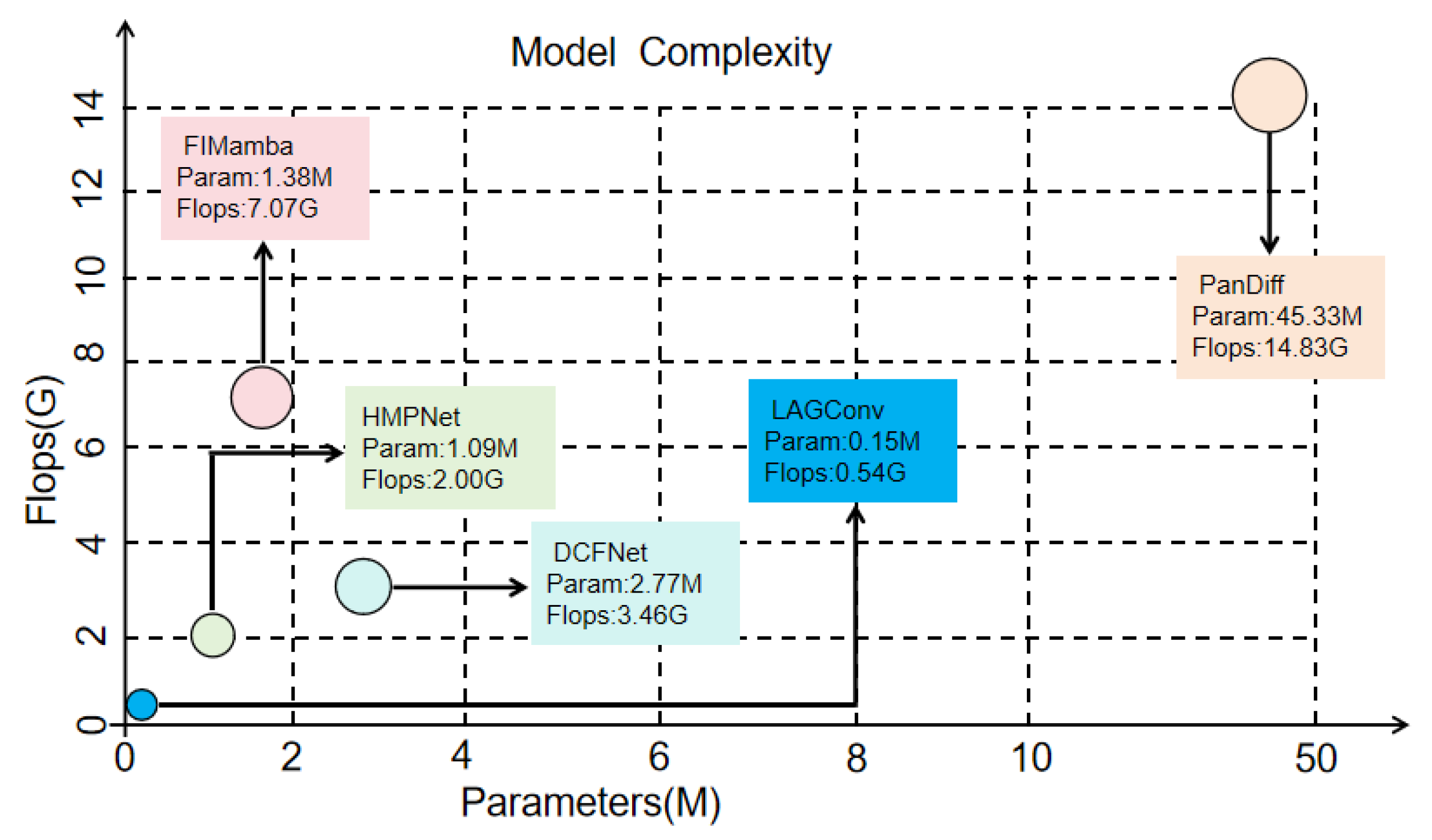
1. Introduction
- We propose an efficient panchromatic sharpening method, FIMamba, to achieve effective continuous feature perception and effective fusion of local and global information.
- Our method designs a structure that combines Mamba with implicit spatial–frequency fusion to alleviate the Mamba model’s insensitivity to local information and extract abundant high-frequency detail information.
- We propose an enhanced Spatial–Frequency Feature Interaction Module (SF-FIM) to enable efficient multi-modal feature interaction and fusion, and comprehensively evaluate its performance across multiple benchmark datasets.
2. Related Work
2.1. Implicit Neural Representation
2.2. Feature Enhancement Based on Fourier Transform
2.3. From SSM to Mamba
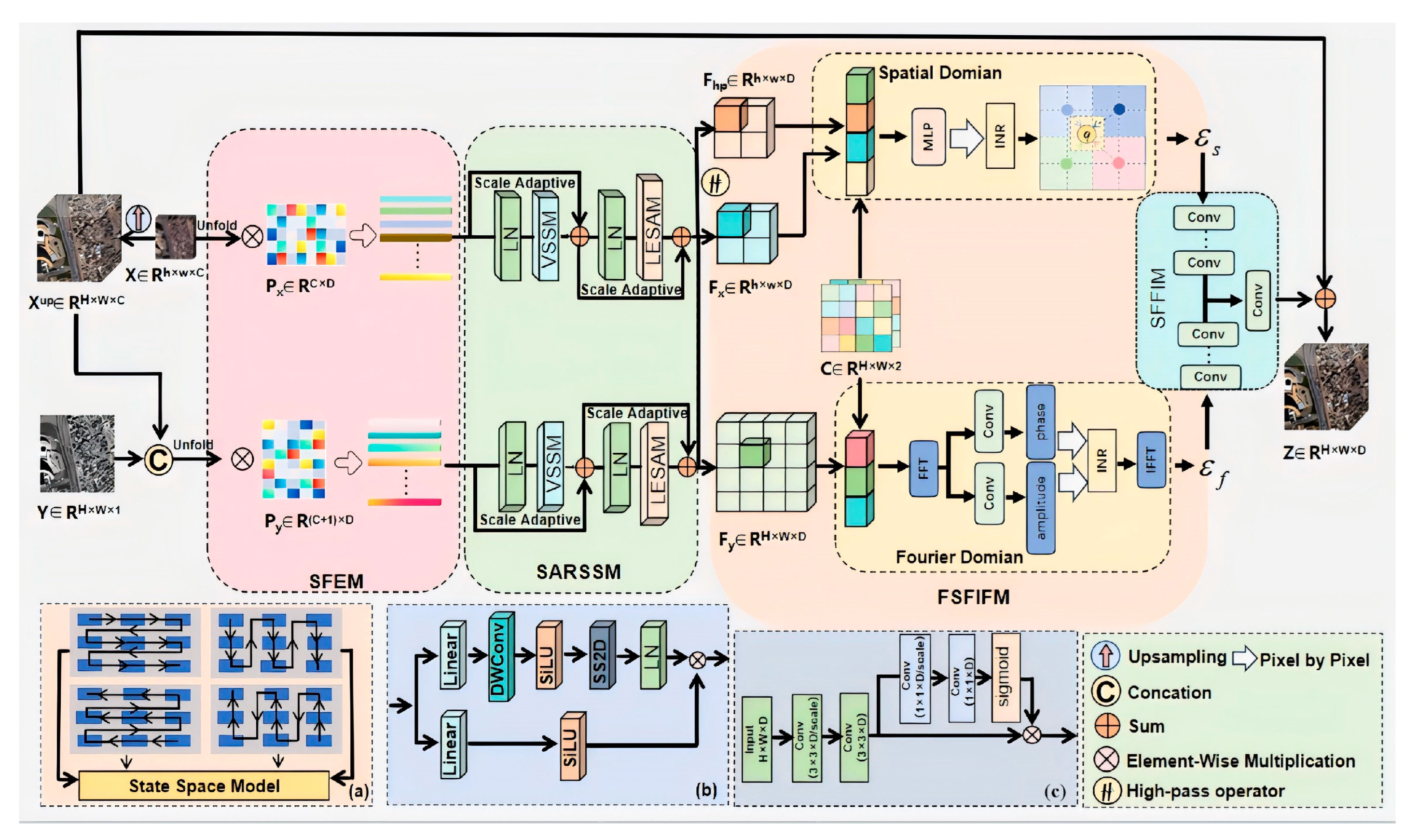
3. Proposed Methods
3.1. Preliminary A: Implicit Neural Representation
3.2. Preliminary B: State-Space Model
3.3. Overview of the FFIMamba Framework
3.3.1. Shallow Feature Extraction Networks
3.3.2. Scale Adaptive Residual State Space Networks
3.3.3. Spatial Implicit Fusion Function
3.3.4. Fourier Frequency Implicit Fusion Function
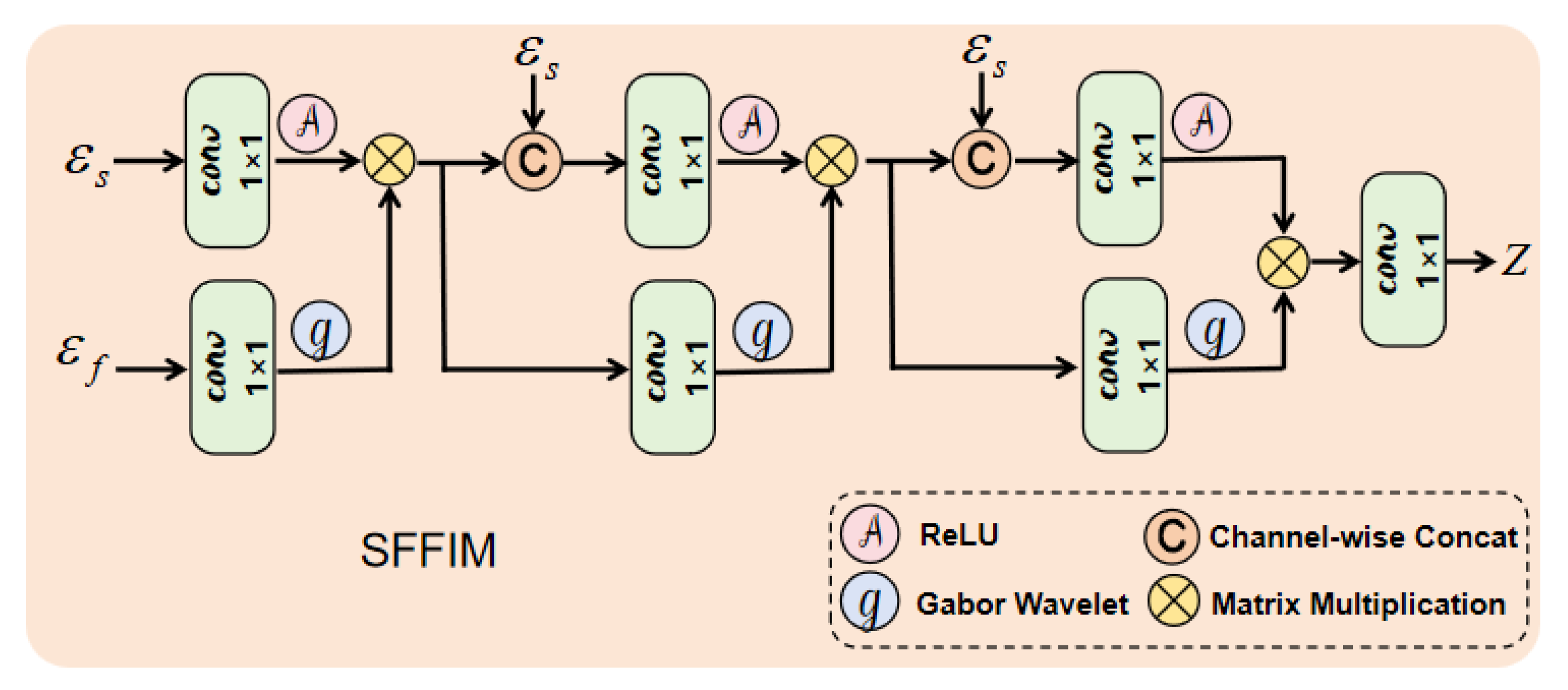
3.3.5. Spatial–Frequency Feature Interaction Module
4. Experiment
4.1. Datasets and Implementation Details
4.2. Results
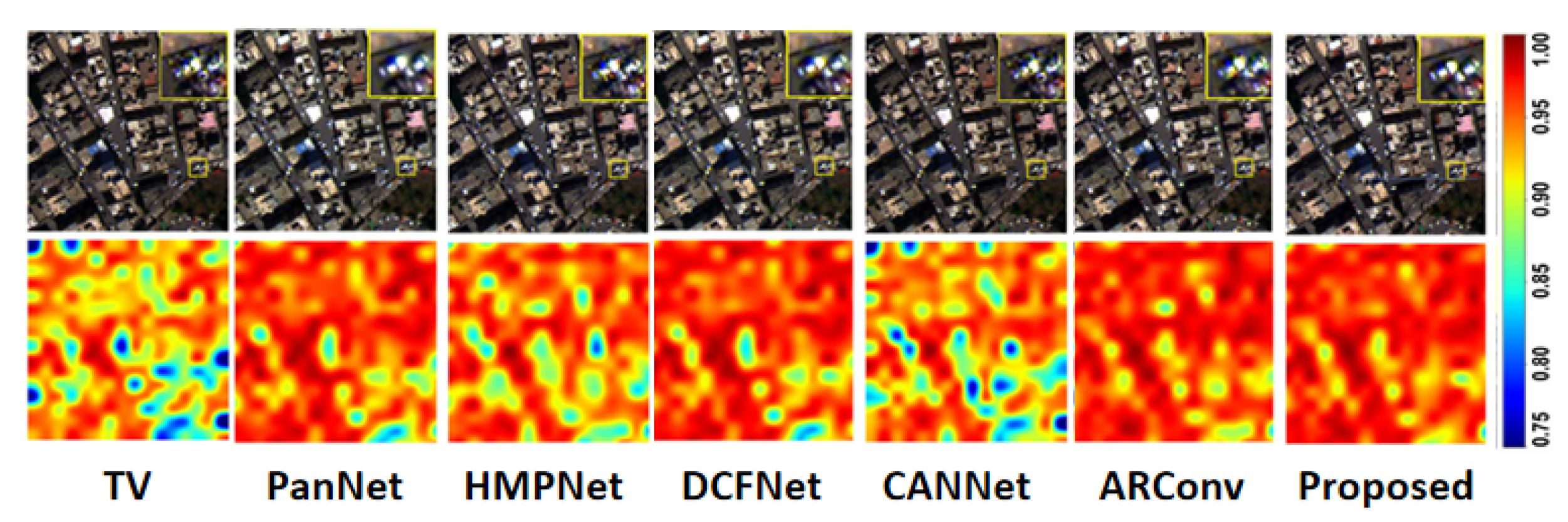
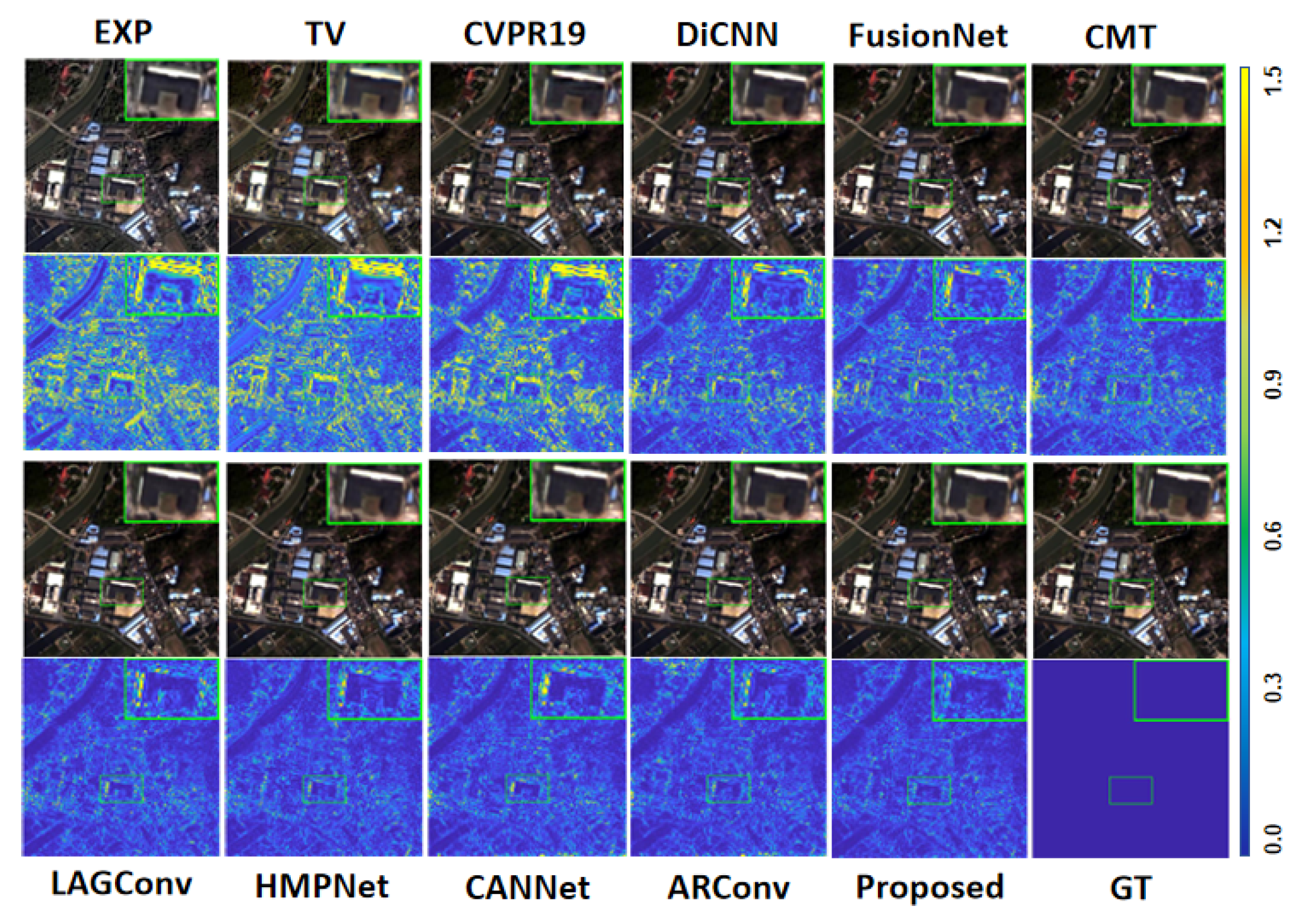
4.2.1. Results on the WorldView-3 Dataset
4.2.2. Results on QuickBird (QB)
4.2.3. Results on GaoFen-2 (GF2)
4.2.4. Results on the WorldView2 Dataset
4.3. Ablation Studies
4.3.1. Significance of VSSM
4.3.2. Core Value of the SARSSM
4.3.3. Importance of FSFIFM
4.3.4. Indispensability of SFFIM
4.3.5. Comparison of Upsampling Methods
4.3.6. Inference Time
5. Limitation
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of Remote Sensing in Precision Agriculture: A Review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Wang, J.; Miao, J.; Li, G.; Tan, Y.; Yu, S.; Liu, X.; Zeng, L.; Li, G. Pan-Sharpening Network of Multi-Spectral Remote Sensing Images Using Two-Stream Attention Feature Extractor and Multi-Detail Injection (TAMINet). Remote Sens. 2023, 16, 75. [Google Scholar] [CrossRef]
- Wang, Z.G.; Kang, Q.; Xun, Y.J.; Shen, Z.Q.; Cui, C.B. Military reconnaissance application of high-resolution optical satellite remote sensing. In Proceedings of the International Symposium on Optoelectronic Technology and Application 2014: Optical Remote Sensing Technology and Applications, Beijing, China, 13–15 May 2014; Volume 9299, pp. 301–305. [Google Scholar]
- Wei, X.; Yuan, M. Adversarial pan-sharpening attacks for object detection in remote sensing. Pattern Recognit. 2023, 139, 109466. [Google Scholar] [CrossRef]
- Rokni, K. Investigating the impact of Pan Sharpening on the accuracy of land cover mapping in Landsat OLI imagery. Geod. Cartogr. 2023, 49, 12–18. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Capobianco, L.; Garzelli, A.; Marchesi, S.; Nencini, F. Change detection from pansharpened images: A comparative analysis. IEEE Geosci. Remote Sens. Lett. 2010, 7, 53–57. [Google Scholar] [CrossRef]
- Feng, X.; Wang, J.; Zhang, Z.; Chang, X. Remote sensing image pan-sharpening via Pixel difference enhance. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104045. [Google Scholar] [CrossRef]
- Choi, J.; Yu, K.; Kim, Y. A New Adaptive Component-Substitution-Based Satellite Image Fusion by Using Partial Replacement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 295–309. [Google Scholar] [CrossRef]
- Vivone, G. Robust Band-Dependent Spatial-Detail Approaches for Panchromatic Sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full Scale Regression-Based Injection Coefficients for Panchromatic Sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and Error-Based Fusion Schemes for Multispectral Image Pansharpening. IEEE Geosci. Remote Sens. Lett. 2014, 11, 930–934. [Google Scholar] [CrossRef]
- Fu, X.; Lin, Z.; Huang, Y.; Ding, X. A Variational Pan-Sharpening with Local Gradient Constraints. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10257–10266. [Google Scholar] [CrossRef]
- Tian, X.; Chen, Y.; Yang, C.; Ma, J. Variational Pansharpening by Exploiting Cartoon-Texture Similarities. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Ma, L.; Bai, Z.; Chan, J.C.W. Going Deeper with Densely Connected Convolutional Neural Networks for Multispectral Pansharpening. Remote Sens. 2019, 11, 2608. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, S.; Xie, W.; Chen, M.; Prisacariu, V.A. NeRF–: Neural Radiance Fields Without Known Camera Parameters. arXiv 2022, arXiv:2102.07064. [Google Scholar] [CrossRef]
- Lv, J.; Guo, J.; Zhang, Y.; Zhao, X.; Lei, B. Neural Radiance Fields for High-Resolution Remote Sensing Novel View Synthesis. Remote Sens. 2023, 15, 3920. [Google Scholar] [CrossRef]
- Lee, J.; Jin, K.H. Local Texture Estimator for Implicit Representation Function. arXiv 2022, arXiv:2111.08918. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, S.; Wang, X. Learning Continuous Image Representation with Local Implicit Image Function. arXiv 2021, arXiv:2012.09161. [Google Scholar] [CrossRef]
- Chen, H.W.; Xu, Y.S.; Hong, M.F.; Tsai, Y.M.; Kuo, H.K.; Lee, C.Y. Cascaded Local Implicit Transformer for Arbitrary-Scale Super-Resolution. arXiv 2023, arXiv:2303.16513. [Google Scholar] [CrossRef]
- Sitzmann, V.; Martel, J.N.P.; Bergman, A.W.; Lindell, D.B.; Wetzstein, G. Implicit Neural Representations with Periodic Activation Functions. arXiv 2020, arXiv:2006.09661. [Google Scholar] [CrossRef]
- Rahaman, N.; Baratin, A.; Arpit, D.; Draxler, F.; Lin, M.; Hamprecht, F.A.; Bengio, Y.; Courville, A. On the Spectral Bias of Neural Networks. arXiv 2019, arXiv:1806.08734. [Google Scholar] [CrossRef]
- Gilles, J.; Tran, G.; Osher, S. 2D Empirical Transforms. Wavelets, Ridgelets, and Curvelets Revisited. SIAM J. Imaging Sci. 2014, 7, 157–186. [Google Scholar] [CrossRef]
- Loui, A.; Venetsanopoulos, A.; Smith, K. Morphological autocorrelation transform: A new representation and classification scheme for two-dimensional images. IEEE Trans. Image Process. 1992, 1, 337–354. [Google Scholar] [CrossRef]
- Grigoryan, A. Method of paired transforms for reconstruction of images from projections: Discrete model. IEEE Trans. Image Process. 2003, 12, 985–994. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Z.; Shi, H. UltraSR: Spatial Encoding is a Missing Key for Implicit Image Function-based Arbitrary-Scale Super-Resolution. arXiv 2022, arXiv:2103.12716. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Beksi, W.J. Single Image Super-Resolution via a Dual Interactive Implicit Neural Network. arXiv 2022, arXiv:2210.12593. [Google Scholar] [CrossRef]
- Tang, J.; Chen, X.; Zeng, G. Joint Implicit Image Function for Guided Depth Super-Resolution. In Proceedings of the 29th ACM International Conference on Multimedia, MM ’21, Virtual, 20–24 October 2021; pp. 4390–4399. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Fang, L. Learning a Low Tensor-Train Rank Representation for Hyperspectral Image Super-Resolution. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2672–2683. [Google Scholar] [CrossRef]
- Yang, Y.; Xing, Z.; Yu, L.; Huang, C.; Fu, H.; Zhu, L. Vivim: A Video Vision Mamba for Medical Video Segmentation. arXiv 2024, arXiv:2401.14168. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, L.; Huang, S.; Wan, W.; Tu, W.; Lu, H. Multiband Remote Sensing Image Pansharpening Based on Dual-Injection Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1888–1904. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, W.; Dong, C.; Hu, C. Wavelet-based Fourier Information Interaction with Frequency Diffusion Adjustment for Underwater Image Restoration. arXiv 2023, arXiv:2311.16845. [Google Scholar] [CrossRef]
- Chi, L.; Jiang, B.; Mu, Y. Fast fourier convolution. In Proceedings of the 34th International Conference on Neural Information Processing Systems, NIPS ’20, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Rao, Y.; Zhao, W.; Zhu, Z.; Lu, J.; Zhou, J. Global Filter Networks for Image Classification. arXiv 2021, arXiv:2107.00645. [Google Scholar] [CrossRef]
- Li, C.; Guo, C.L.; Zhou, M.; Liang, Z.; Zhou, S.; Feng, R.; Loy, C.C. Embedding Fourier for Ultra-High-Definition Low-Light Image Enhancement. arXiv 2023, arXiv:2302.11831. [Google Scholar] [CrossRef]
- Gu, A.; Goel, K.; Ré, C. Efficiently Modeling Long Sequences with Structured State Spaces. arXiv 2022, arXiv:2111.00396. [Google Scholar] [CrossRef]
- Xie, X.; Cui, Y.; Tan, T.; Zheng, X.; Yu, Z. FusionMamba: Dynamic Feature Enhancement for Multimodal Image Fusion with Mamba. arXiv 2025, arXiv:2404.09498. [Google Scholar] [CrossRef]
- Guo, H.; Li, J.; Dai, T.; Ouyang, Z.; Ren, X.; Xia, S.T. MambaIR: A Simple Baseline for Image Restoration with State-Space Model. arXiv 2024, arXiv:2402.15648. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X.; Quan, C.; Zhao, T.; Huo, W.; Huang, Y. Mamba-STFM: A Mamba-Based Spatiotemporal Fusion Method for Remote Sensing Images. Remote Sens. 2025, 17, 2135. [Google Scholar] [CrossRef]
- Zhu, Q.; Cai, Y.; Fang, Y.; Yang, Y.; Chen, C.; Fan, L.; Nguyen, A. Samba: Semantic Segmentation of Remotely Sensed Images with State Space Model. arXiv 2024, arXiv:2404.01705. [Google Scholar] [CrossRef]
- Yan, L.; Feng, Q.; Wang, J.; Cao, J.; Feng, X.; Tang, X. A Multilevel Multimodal Hybrid Mamba-Large Strip Convolution Network for Remote Sensing Semantic Segmentation. Remote Sens. 2025, 17, 2696. [Google Scholar] [CrossRef]
- Chen, K.; Chen, B.; Liu, C.; Li, W.; Zou, Z.; Shi, Z. RSMamba: Remote Sensing Image Classification with State Space Model. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Liao, J.; Wang, L. HyperspectralMamba: A Novel State Space Model Architecture for Hyperspectral Image Classification. Remote Sens. 2025, 17, 2577. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Deng, L.j.; Vivone, G.; Paoletti, M.E.; Scarpa, G.; He, J.; Zhang, Y.; Chanussot, J.; Plaza, A. Machine Learning in Pansharpening: A benchmark, from shallow to deep networks. IEEE Geosci. Remote Sens. Mag. 2022, 10, 279–315. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Boardman, J.W. Automating Spectral Unmixing of AVIRIS Data Using Convex Geometry Concepts. 1993. Available online: https://ntrs.nasa.gov/citations/19950017428 (accessed on 10 November 2025).
- Wald, L. Data Fusion. Definitions and Architectures—Fusion of Images of Different Spatial Resolutions; École des Mines Paris—PSL: Paris, France, 2002. [Google Scholar]
- Garzelli, A.; Nencini, F. Hypercomplex Quality Assessment of Multi/Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Arienzo, A.; Vivone, G.; Garzelli, A.; Alparone, L.; Chanussot, J. Full-Resolution Quality Assessment of Pansharpening: Theoretical and hands-on approaches. IEEE Geosci. Remote Sens. Mag. 2022, 10, 168–201. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A New Pansharpening Algorithm Based on Total Variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Wu, Z.C.; Huang, T.Z.; Deng, L.J.; Huang, J.; Chanussot, J.; Vivone, G. LRTCFPan: Low-Rank Tensor Completion Based Framework for Pansharpening. IEEE Trans. Image Process. 2023, 32, 1640–1655. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by Convolutional Neural Networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A Deep Network Architecture for Pan-Sharpening. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1753–1761. [Google Scholar] [CrossRef]
- He, L.; Rao, Y.; Li, J.; Chanussot, J.; Plaza, A.; Zhu, J.; Li, B. Pansharpening via Detail Injection Based Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1188–1204. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Jin, C.; Chanussot, J. Detail Injection-Based Deep Convolutional Neural Networks for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6995–7010. [Google Scholar] [CrossRef]
- Wu, X.; Huang, T.Z.; Deng, L.J.; Zhang, T.J. Dynamic Cross Feature Fusion for Remote Sensing Pansharpening. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 14667–14676. [Google Scholar] [CrossRef]
- Jin, Z.R.; Zhang, T.J.; Jiang, T.X.; Vivone, G.; Deng, L.J. LAGConv: Local-Context Adaptive Convolution Kernels with Global Harmonic Bias for Pansharpening. Proc. AAAI Conf. Artif. Intell. 2022, 36, 1113–1121. [Google Scholar] [CrossRef]
- Tian, X.; Li, K.; Zhang, W.; Wang, Z.; Ma, J. Interpretable Model-Driven Deep Network for Hyperspectral, Multispectral, and Panchromatic Image Fusion. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 14382–14395. [Google Scholar] [CrossRef]
- Shu, W.J.; Dou, H.X.; Wen, R.; Wu, X.; Deng, L.J. CMT: Cross Modulation Transformer with Hybrid Loss for Pansharpening. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Duan, Y.; Wu, X.; Deng, H.; Deng, L.J. Content-Adaptive Non-Local Convolution for Remote Sensing Pansharpening. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 27738–27747. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Z.; Shao, J.; Duan, Y.; Deng, L.J. Adaptive Rectangular Convolution for Remote Sensing Pansharpening. arXiv 2025, arXiv:2503.00467. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]

| Hyperparameter Category | Specific Parameter | Parameter Value | Description |
|---|---|---|---|
| Network Structure Parameters | Sliding Window Size (k) | Applied in the Shallow Feature Extraction Module (SFEM) for local feature aggregation. It scans the image to unfold regional information via a sliding window; the value is determined by empirical tuning. | |
| Feature Channel Number (D) | 64 | Used to define the dimension of the projection matrix in SFEM, which maps input features to a unified latent feature space; the value is determined by empirical tuning. | |
| Channel Compression Ratio (r) | Utilized for channel compression in the 3D convolution of the Local Enhanced Spectral Attention Module (LESAM). It reduces computational cost and enhances spectral representation; the value is determined by empirical tuning. | ||
| Frequency Encoding Hyperparameter (m) | 10 | Employed for frequency encoding of relative position coordinates in the spatial implicit fusion function, controlling the encoding dimension; the value is determined by empirical tuning. | |
| Gabor Wavelet Param. (a) for SFFIM | 30 (initial value) | Controls the center frequency of the Gabor wavelet in the frequency domain (a learnable parameter); the initial value is determined by empirical tuning. | |
| Gabor Wavelet Param. (b) for SFFIM | 10 (initial value) | Controls the standard deviation of the Gaussian function in the Gabor wavelet (a learnable parameter); the initial value is determined by empirical tuning. | |
| Training Parameters | Learning Rate | Set for the Adam optimizer to control the parameter update step size; the value is determined by empirical tuning. | |
| Batch Size | 4 | Number of samples input in each training iteration; the value is determined by empirical tuning. | |
| Training Epochs | 1000 | Total number of complete training cycles of the model on the training set; the value is determined by empirical tuning. | |
| Input Sample Size | Size of image samples input to the model during training; the value is determined by empirical tuning. | ||
| Loss Function | Loss | Used to calculate the error between the model’s predictions and the ground truth (GT), guiding parameter optimization; the selection is determined by empirical tuning. | |
| Optimizer | Adam | Optimization algorithm for model parameter updates; the selection is determined by empirical tuning. |
| Methods | Reduced-Resolution Metrics | Full-Resolution Metrics | ||||
|---|---|---|---|---|---|---|
| SAM ↓ | ERGAS ↓ | Q8 ↑ | ↓ | ↓ | HQNR ↑ | |
| EXP [51] | ||||||
| TV [52] | ||||||
| MTF-GLP-FS [10] | ||||||
| BSDS-PC [9] | ||||||
| CVPR2019 [12] | ||||||
| LRTCFPan [53] | ||||||
| PNN [54] | ||||||
| PanNet [55] | ||||||
| DiCNN [56] | ||||||
| FusionNet [57] | ||||||
| DCFNet [58] | ||||||
| LAGConv [59] | ||||||
| HMPNet [60] | ||||||
| CMT [61] | ||||||
| CANNet [62] | ||||||
| ARConv [63] | ||||||
| Proposed | ||||||
| Methods | SAM ↓ | ERGAS ↓ | Q4 ↑ |
|---|---|---|---|
| EXP [51] | |||
| TV [52] | |||
| MTF-GLP-FS [10] | |||
| BSD-PC [9] | |||
| CVPR2019 [12] | |||
| LRTCFPan [53] | |||
| PNN [54] | |||
| PanNet [55] | |||
| DiCNN [56] | |||
| FusionNet [57] | |||
| DCFNet [58] | |||
| LAGConv [59] | |||
| HMPNet [60] | |||
| CMT [61] | |||
| CANNet [62] | |||
| ARConv [63] | |||
| Proposed |
| Methods | SAM ↓ | ERGAS ↓ | Q4 ↑ |
|---|---|---|---|
| EXP [51] | |||
| TV [52] | |||
| MTF-GLP-FS [10] | |||
| BSD-PC [9] | |||
| CVPR2019 [12] | |||
| LRTCFPan [53] | |||
| PNN [54] | |||
| PanNet [55] | |||
| DiCNN [56] | |||
| FusionNet [57] | |||
| DCFNet [58] | |||
| LAGConv [59] | |||
| HMPNet [60] | |||
| CMT [61] | |||
| CANNet [62] | |||
| ARConv [63] | |||
| Proposed |
| Methods | SAM ↓ | ERGAS ↓ | SCC ↑ | Q2n ↑ |
|---|---|---|---|---|
| EXP [51] | ||||
| TV [52] | ||||
| MTF-GLP-FS [10] | ||||
| BDS-PC [9] | ||||
| PNN [54] | ||||
| PanNet [55] | ||||
| DiCNN [56] | ||||
| FusionNet [57] | ||||
| Proposed |
| Methods | SAM ↓ | ERGAS ↓ | Q8 ↑ |
|---|---|---|---|
| (a) w/o VSSM | |||
| (b) w/o SARSSM | |||
| (c) w/o FSFIFM | |||
| (d) w/o SFFIM | |||
| Proposed |
| Methods | SAM ↓ | ERGAS ↓ | Q8 ↑ |
|---|---|---|---|
| (a) w/o VSSM | |||
| (b) w/o SARSSM | |||
| (c) w/o FSFIFM | |||
| (d) w/o SFFIM | |||
| Proposed |
| Methods | SAM (↓) | ERGAS (↓) | Q8 (↑) |
|---|---|---|---|
| Bilinear | |||
| Bicubic | |||
| Pixel Shuffle | |||
| Proposed |
| Method | FIMmamba | ARConv | DCFNet | MMNet | LAGConv |
|---|---|---|---|---|---|
| Runtime (s) | 0.383 | 0.336 | 0.548 | 0.348 | 1.381 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.-Z.; Dou, H.-X.; Liang, Y.-J. Fourier Fusion Implicit Mamba Network for Remote Sensing Pansharpening. Remote Sens. 2025, 17, 3747. https://doi.org/10.3390/rs17223747
He Z-Z, Dou H-X, Liang Y-J. Fourier Fusion Implicit Mamba Network for Remote Sensing Pansharpening. Remote Sensing. 2025; 17(22):3747. https://doi.org/10.3390/rs17223747
Chicago/Turabian StyleHe, Ze-Zheng, Hong-Xia Dou, and Yu-Jie Liang. 2025. "Fourier Fusion Implicit Mamba Network for Remote Sensing Pansharpening" Remote Sensing 17, no. 22: 3747. https://doi.org/10.3390/rs17223747
APA StyleHe, Z.-Z., Dou, H.-X., & Liang, Y.-J. (2025). Fourier Fusion Implicit Mamba Network for Remote Sensing Pansharpening. Remote Sensing, 17(22), 3747. https://doi.org/10.3390/rs17223747







