Figure 1.
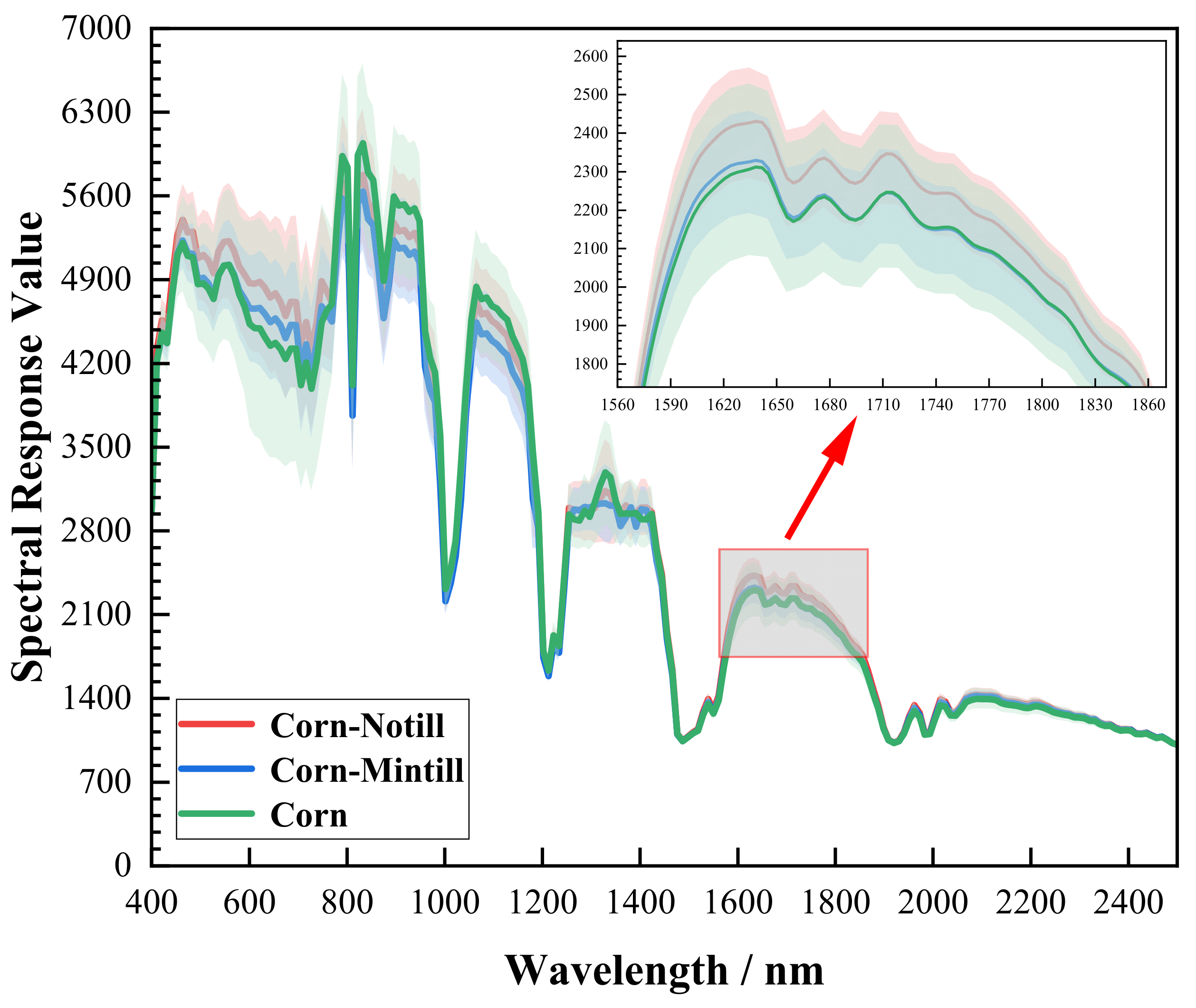
Spectral curves of three types of ground objects in the Indian dataset. Each colored curve represents the average spectral response values of all pixels in the corresponding class. The shaded region around each curve represents the standard deviation of spectral response for that class (Corn-Notill: 1428 pixels; Corn-Mintill: 830 pixels; Corn class: 237 pixels).
Figure 1.
Spectral curves of three types of ground objects in the Indian dataset. Each colored curve represents the average spectral response values of all pixels in the corresponding class. The shaded region around each curve represents the standard deviation of spectral response for that class (Corn-Notill: 1428 pixels; Corn-Mintill: 830 pixels; Corn class: 237 pixels).
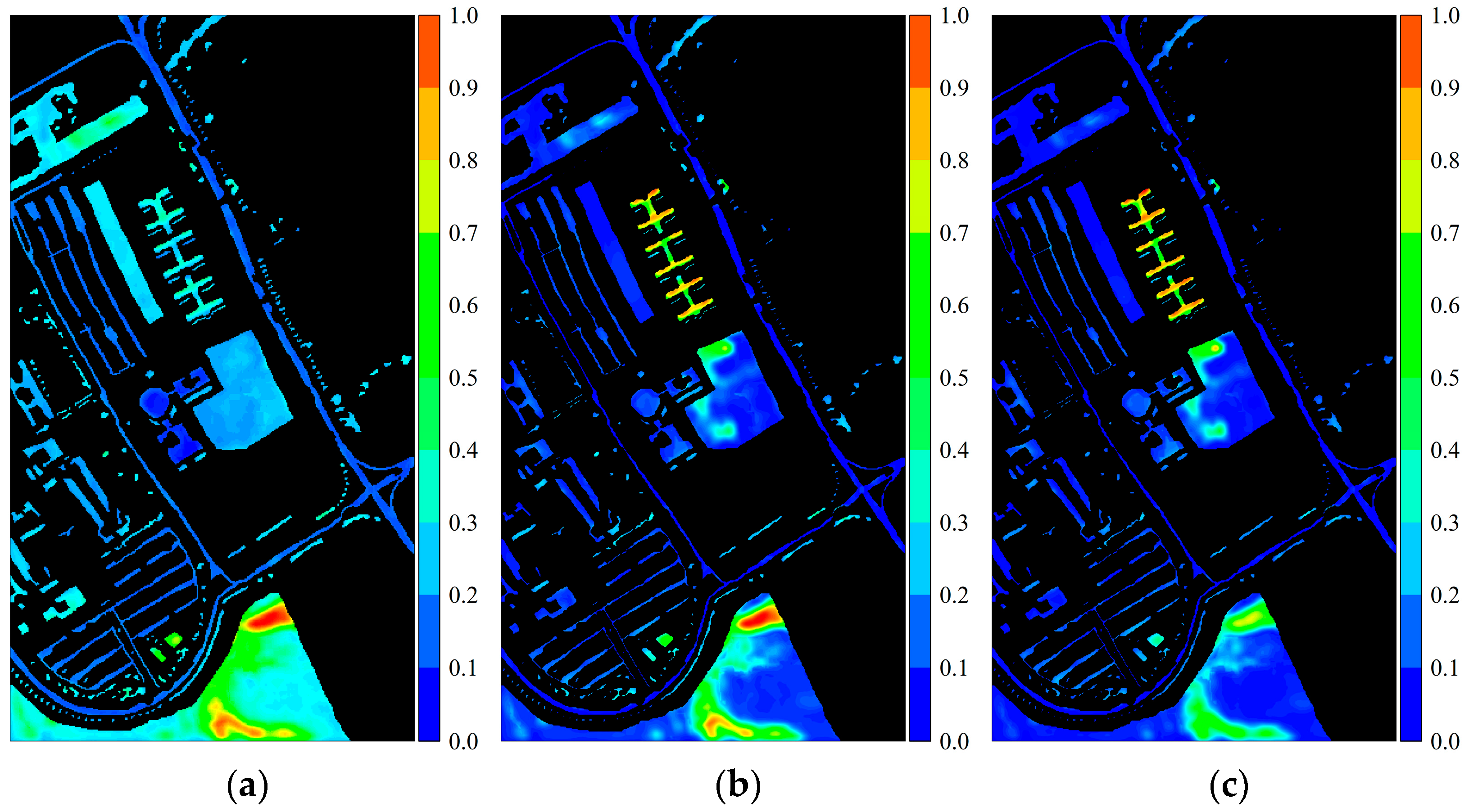
Figure 2.
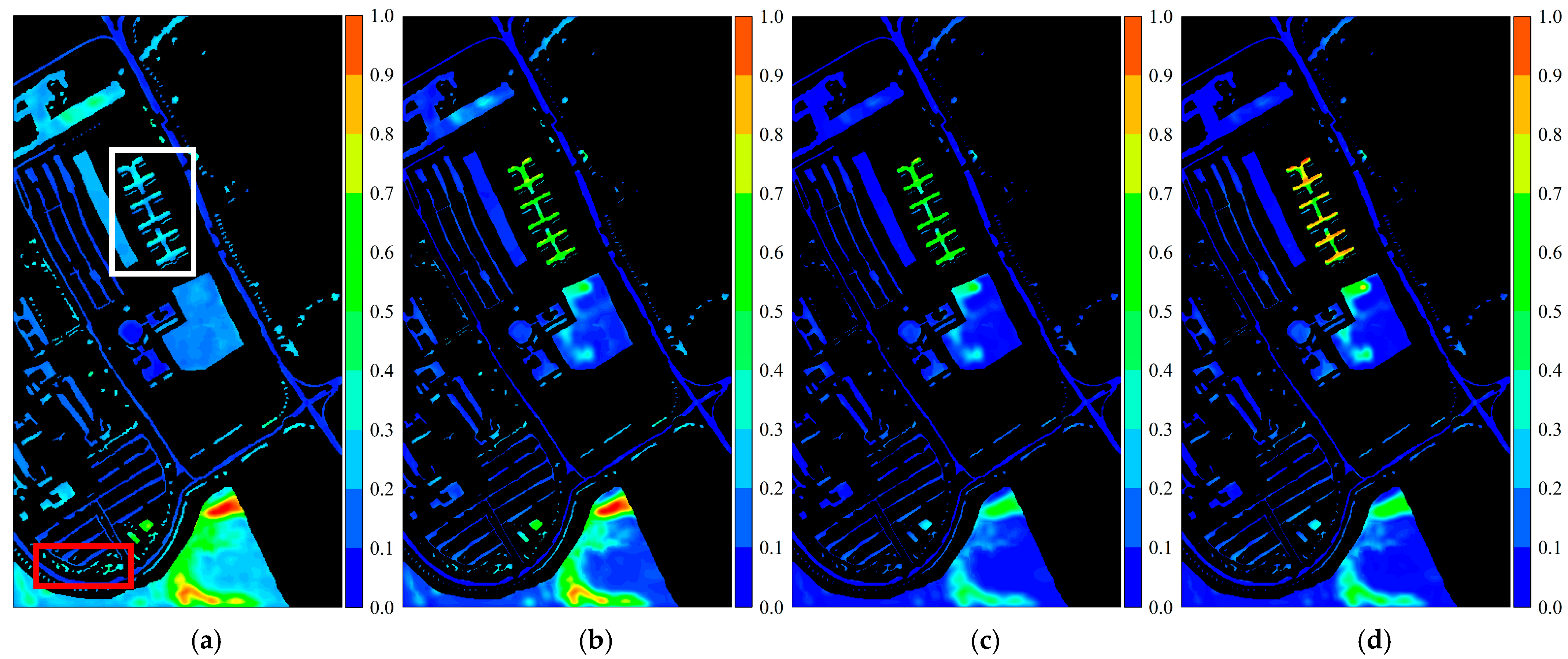
Activation response heatmaps obtained from the PaviaU dataset using different convolutional kernels: (a) 3 × 3 convolutional kernel; (b) 5 × 5 convolutional kernel; (c) 7 × 7 convolutional kernel; (d) 9 × 9 convolutional kernel. The red box represents the Trees class, and the white box represents the Painted Metal Sheets class.
Figure 2.
Activation response heatmaps obtained from the PaviaU dataset using different convolutional kernels: (a) 3 × 3 convolutional kernel; (b) 5 × 5 convolutional kernel; (c) 7 × 7 convolutional kernel; (d) 9 × 9 convolutional kernel. The red box represents the Trees class, and the white box represents the Painted Metal Sheets class.
Figure 3.
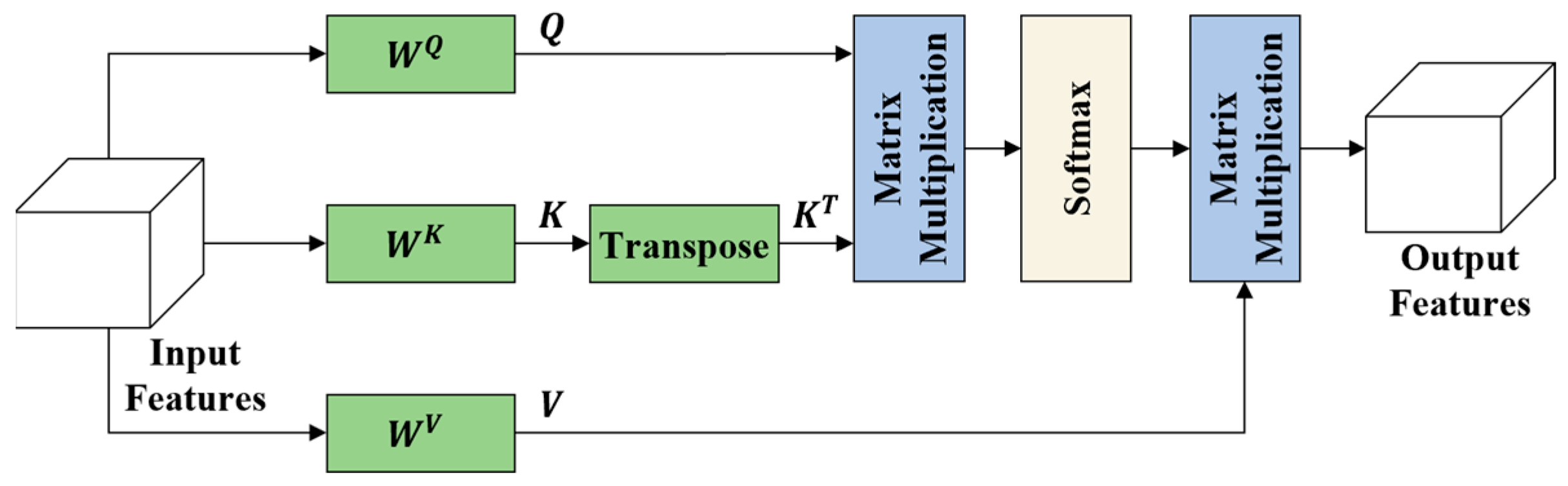
The self-attention mechanism.
Figure 3.
The self-attention mechanism.
Figure 4.
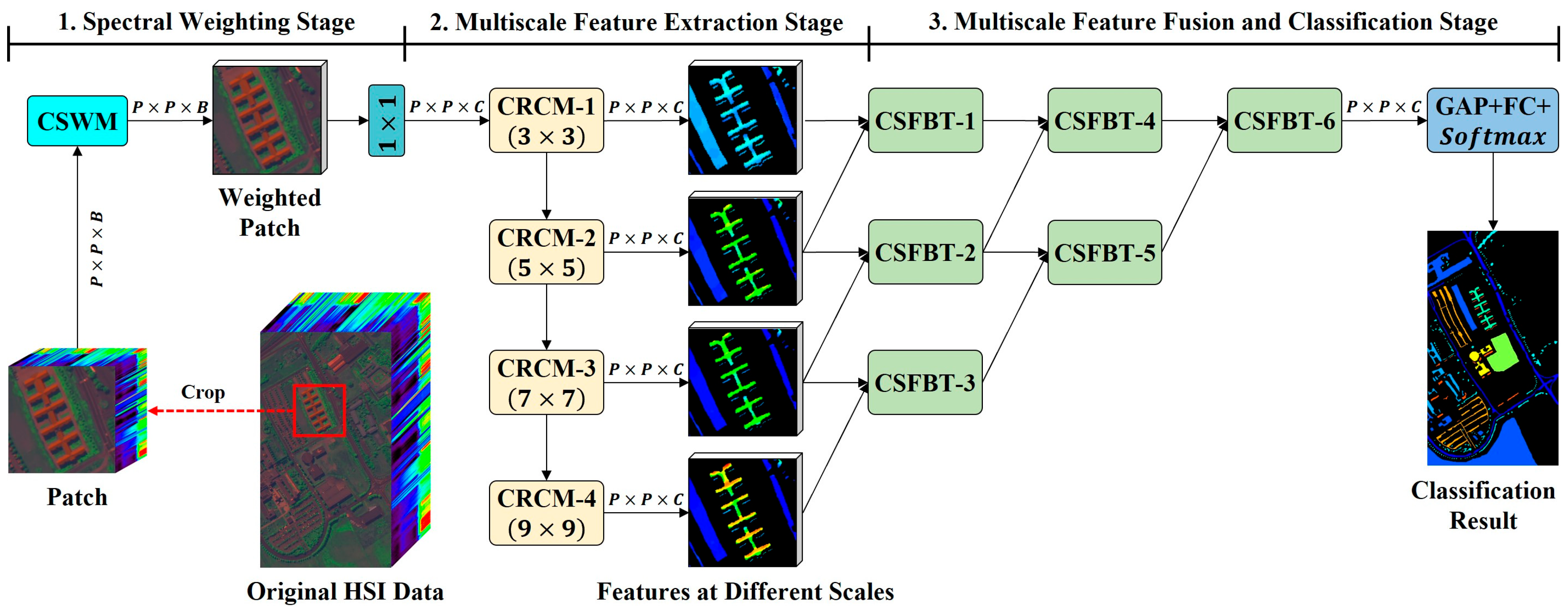
The overall framework of CPMFFormer. CPMFFormer is composed of one CSWM, four CRCMs, and six cross-scale fusion bottleneck transformers (CSFBT). CSWM, CRCM, and CSFBT are used to obtain class-specific spectral weights, features at different scales, and progressive fusion features, respectively. Following CSFBT-6, CPMFFormer uses a global average pooling (GAP) layer, a fully connected (FC) layer, and a function to predict the final classification result.
Figure 4.
The overall framework of CPMFFormer. CPMFFormer is composed of one CSWM, four CRCMs, and six cross-scale fusion bottleneck transformers (CSFBT). CSWM, CRCM, and CSFBT are used to obtain class-specific spectral weights, features at different scales, and progressive fusion features, respectively. Following CSFBT-6, CPMFFormer uses a global average pooling (GAP) layer, a fully connected (FC) layer, and a function to predict the final classification result.
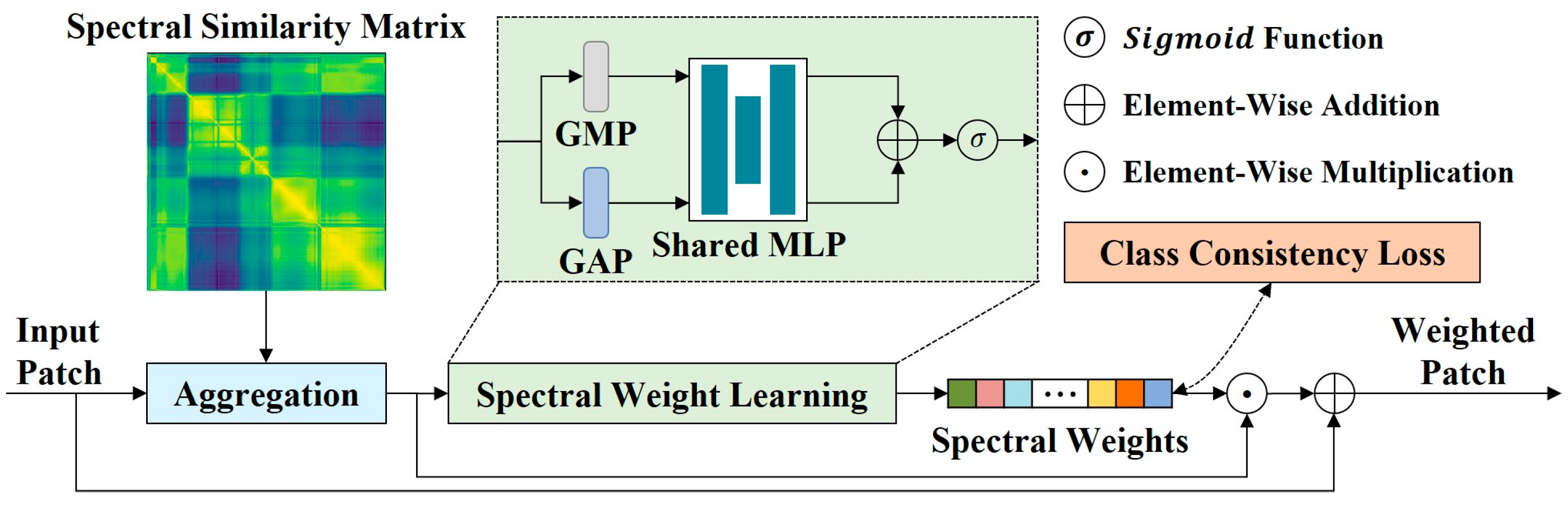
Figure 5.
The framework of CSWM. CSWM is composed of an aggregation operation, a spectral wight learning block, and a class consistency loss function. The aggregation operation smooths the spectral information differences between intra-class input patches. The spectral weight learning block performs adaptive spectral weighting. The class consistency loss function is used to learn the spectral weight centers of different ground objects and generate class-specific spectral weights.
Figure 5.
The framework of CSWM. CSWM is composed of an aggregation operation, a spectral wight learning block, and a class consistency loss function. The aggregation operation smooths the spectral information differences between intra-class input patches. The spectral weight learning block performs adaptive spectral weighting. The class consistency loss function is used to learn the spectral weight centers of different ground objects and generate class-specific spectral weights.
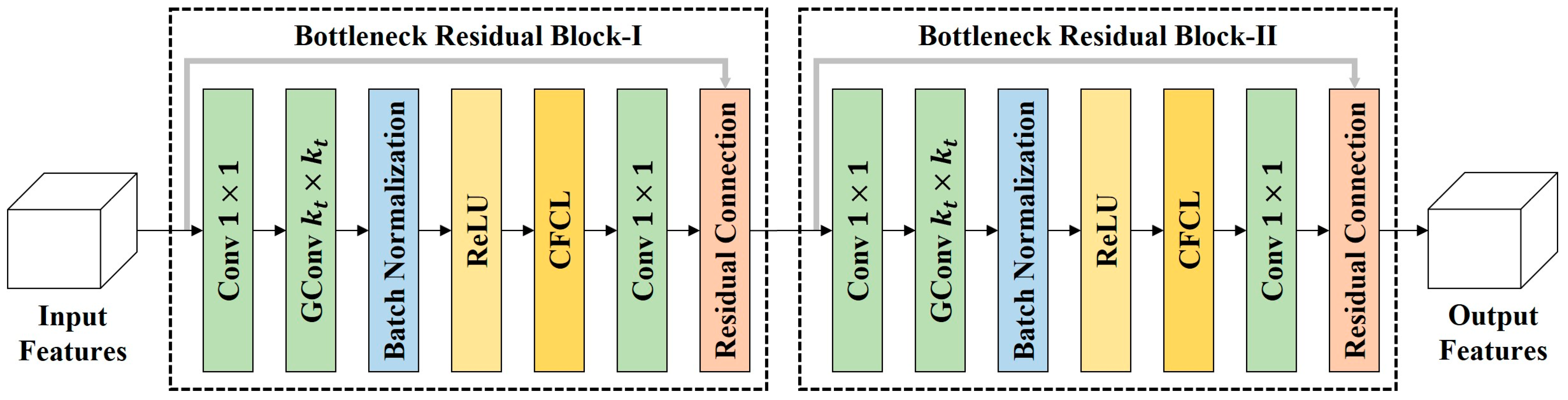
Figure 6.
The framework of CRCM. CRCM is composed of two bottleneck residual blocks. In each bottleneck residual block, two convolutional layers are used to form the bottleneck structure, and a group convolution layer is used to extract features at the tth scale. Moreover, the embedded center feature calibration layer (CFCL) is used to model the dependencies between the center pixel and its neighboring pixels. This helps CRCM to reduce the impact of interference information introduced by abnormal pixels on the classification decision of the center pixel.
Figure 6.
The framework of CRCM. CRCM is composed of two bottleneck residual blocks. In each bottleneck residual block, two convolutional layers are used to form the bottleneck structure, and a group convolution layer is used to extract features at the tth scale. Moreover, the embedded center feature calibration layer (CFCL) is used to model the dependencies between the center pixel and its neighboring pixels. This helps CRCM to reduce the impact of interference information introduced by abnormal pixels on the classification decision of the center pixel.
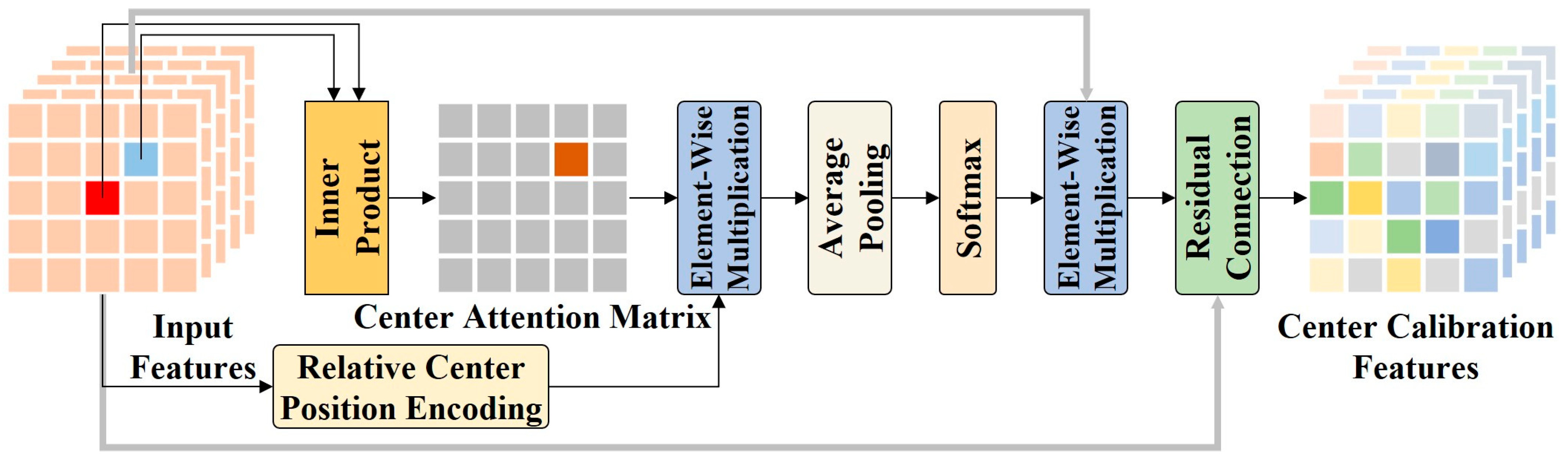
Figure 7.
The framework of CFCL. CFCL computes the correlations between the center pixel and its neighboring pixels through an inner product attention mechanism. Moreover, CFCL introduces a relative center position encoding to enhance spatial relationship modeling capabilities. This enables CFCL to highlight neighboring pixels that are relevant to the center pixel while suppressing irrelevant background information. This improves the representational capability of the center pixel.
Figure 7.
The framework of CFCL. CFCL computes the correlations between the center pixel and its neighboring pixels through an inner product attention mechanism. Moreover, CFCL introduces a relative center position encoding to enhance spatial relationship modeling capabilities. This enables CFCL to highlight neighboring pixels that are relevant to the center pixel while suppressing irrelevant background information. This improves the representational capability of the center pixel.
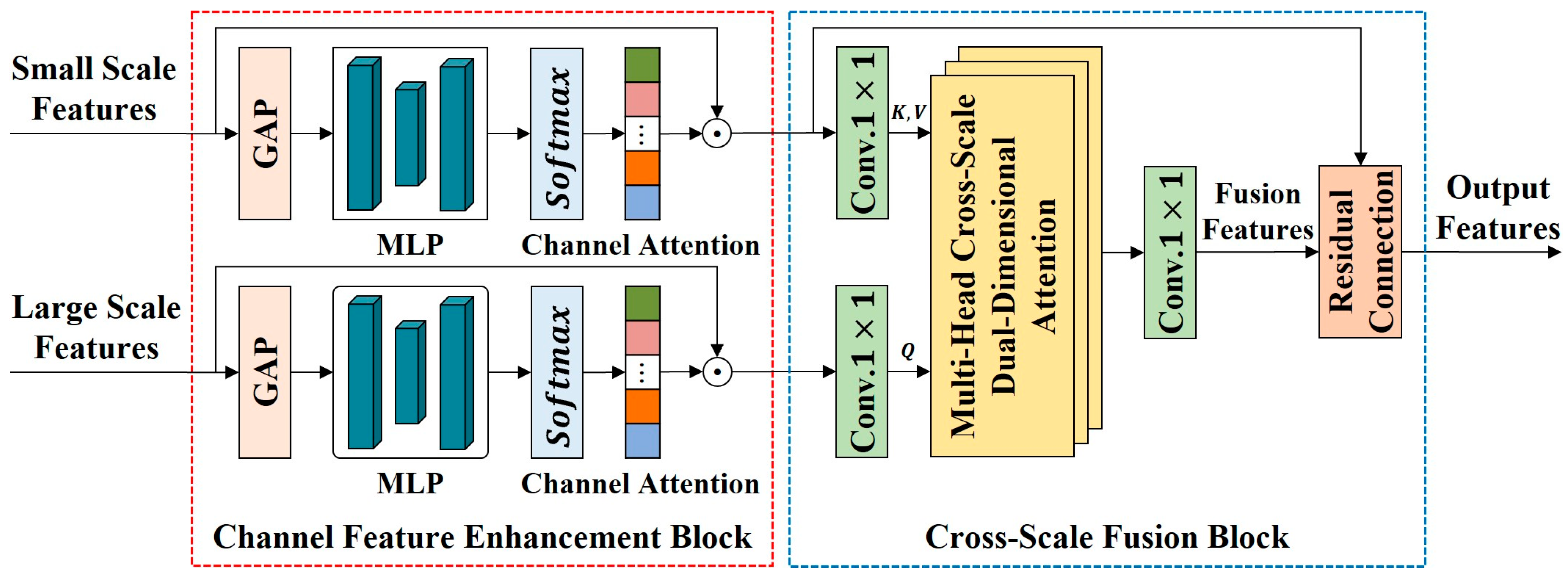
Figure 8.
The framework of CSFBT. CSFBT takes adjacent scale features as input. It consists of a channel feature enhancement block (CFEB) and a cross-scale fusion block (CSFB). CFEB models inter-channel dependencies and emphasizes valuable channel features. CSFB uses a multi-head cross-scale dual-dimensional attention (MHCSD2A) mechanism to integrate complementary information across adjacent scale features from both spatial and channel dimensions.
Figure 8.
The framework of CSFBT. CSFBT takes adjacent scale features as input. It consists of a channel feature enhancement block (CFEB) and a cross-scale fusion block (CSFB). CFEB models inter-channel dependencies and emphasizes valuable channel features. CSFB uses a multi-head cross-scale dual-dimensional attention (MHCSD2A) mechanism to integrate complementary information across adjacent scale features from both spatial and channel dimensions.
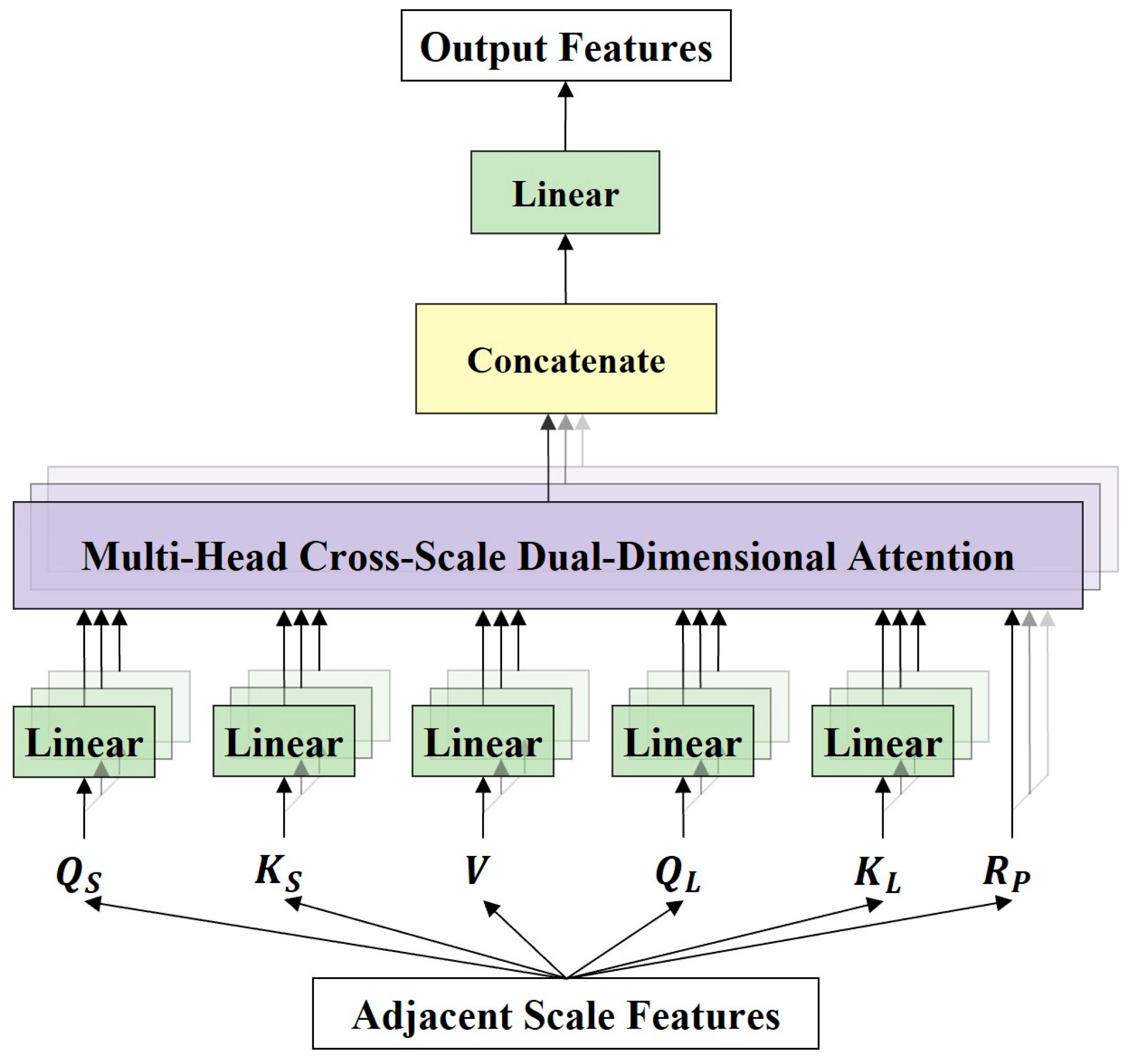
Figure 9.
The framework of MHCSD2A. MHCSD2A first maps the input features to different attention heads using five linear projection layers. Then, the cross-scale dual-dimensional attention (CSD2A) mechanism is computed in each head. Finally, the computation results of all heads are concatenated, and a linear projection layer is used to obtain the final output features.
Figure 9.
The framework of MHCSD2A. MHCSD2A first maps the input features to different attention heads using five linear projection layers. Then, the cross-scale dual-dimensional attention (CSD2A) mechanism is computed in each head. Finally, the computation results of all heads are concatenated, and a linear projection layer is used to obtain the final output features.
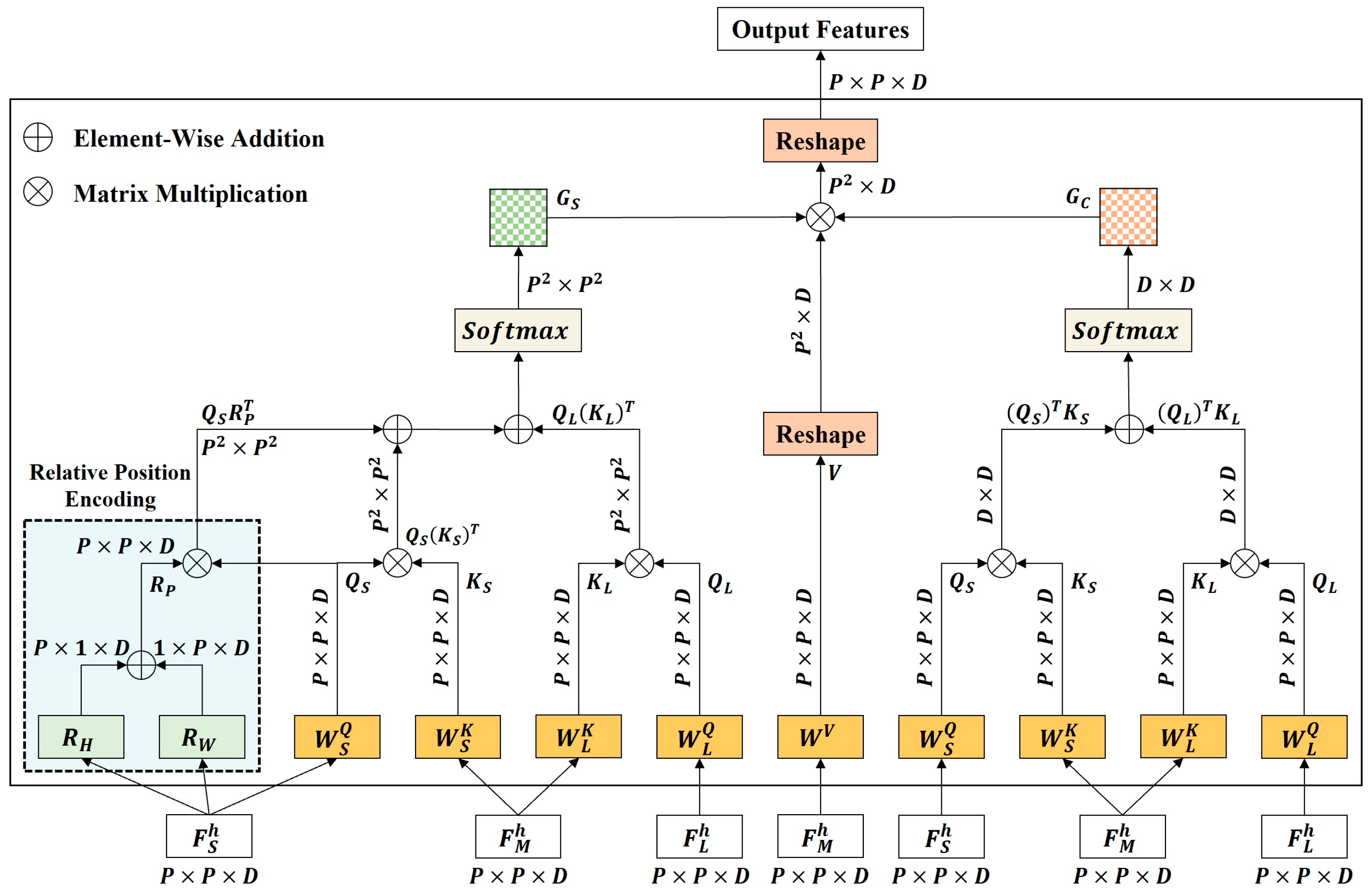
Figure 10.
The framework of CSD2A. CSD2A achieves complementary semantic fusion between small-scale features and large-scale features by computing attention from both spatial and channel dimensions. This mechanism introduces the relative position encoding to better model complex spatial relationships and preserves structural details during cross-scale fusion.
Figure 10.
The framework of CSD2A. CSD2A achieves complementary semantic fusion between small-scale features and large-scale features by computing attention from both spatial and channel dimensions. This mechanism introduces the relative position encoding to better model complex spatial relationships and preserves structural details during cross-scale fusion.
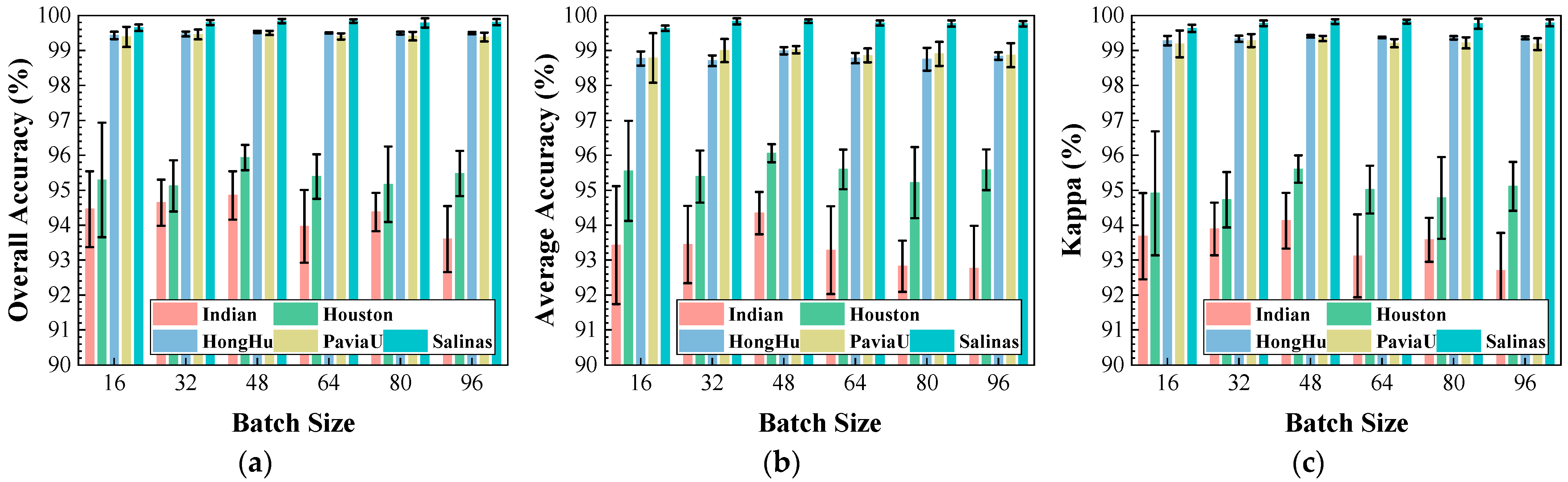
Figure 11.
Impact of batch size on classification performance: (a) OA; (b) AA; (c) .
Figure 11.
Impact of batch size on classification performance: (a) OA; (b) AA; (c) .
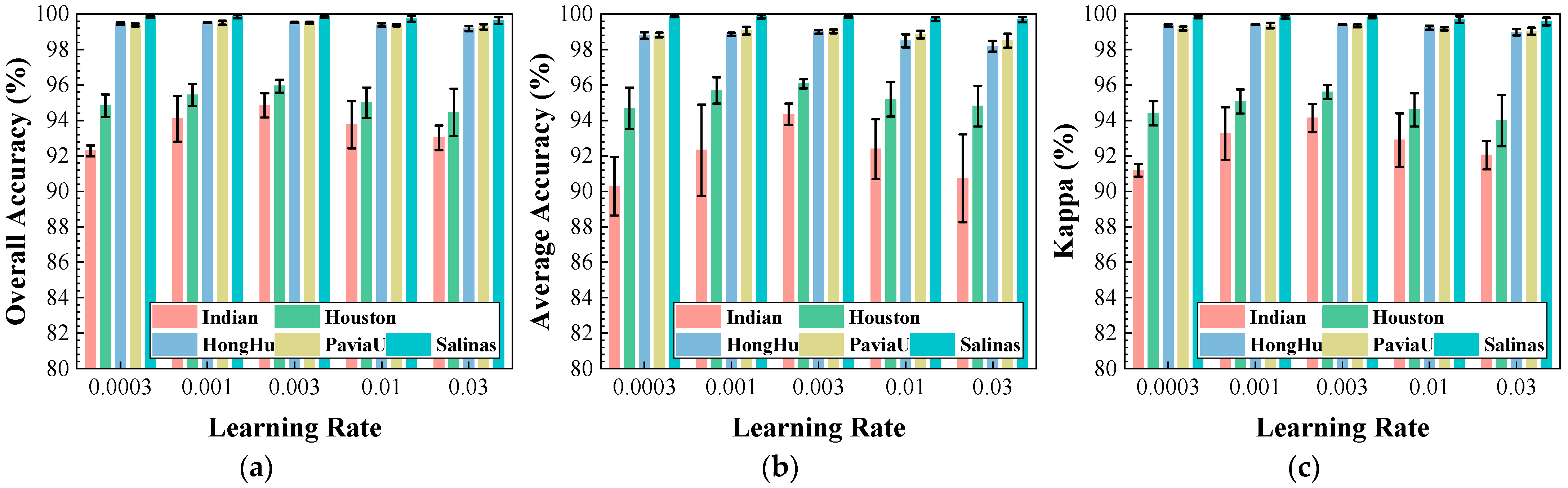
Figure 12.
Impact of learning rate on classification performance: (a) OA; (b) AA; (c) .
Figure 12.
Impact of learning rate on classification performance: (a) OA; (b) AA; (c) .
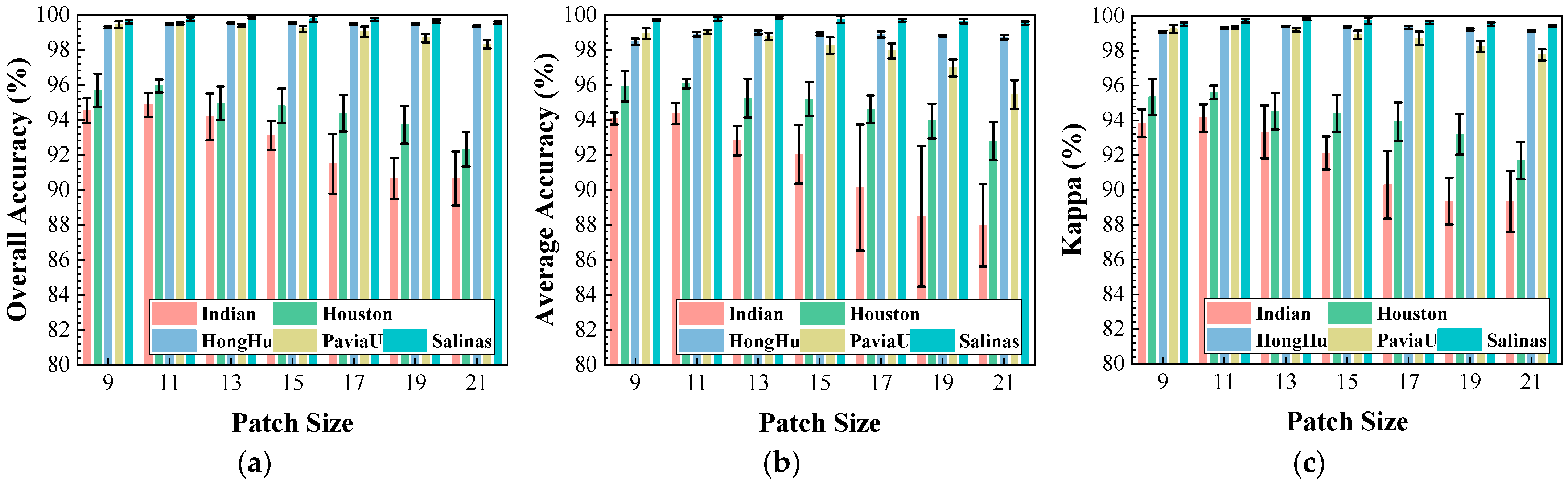
Figure 13.
Impact of patch size on classification performance: (a) OA; (b) AA; (c) .
Figure 13.
Impact of patch size on classification performance: (a) OA; (b) AA; (c) .
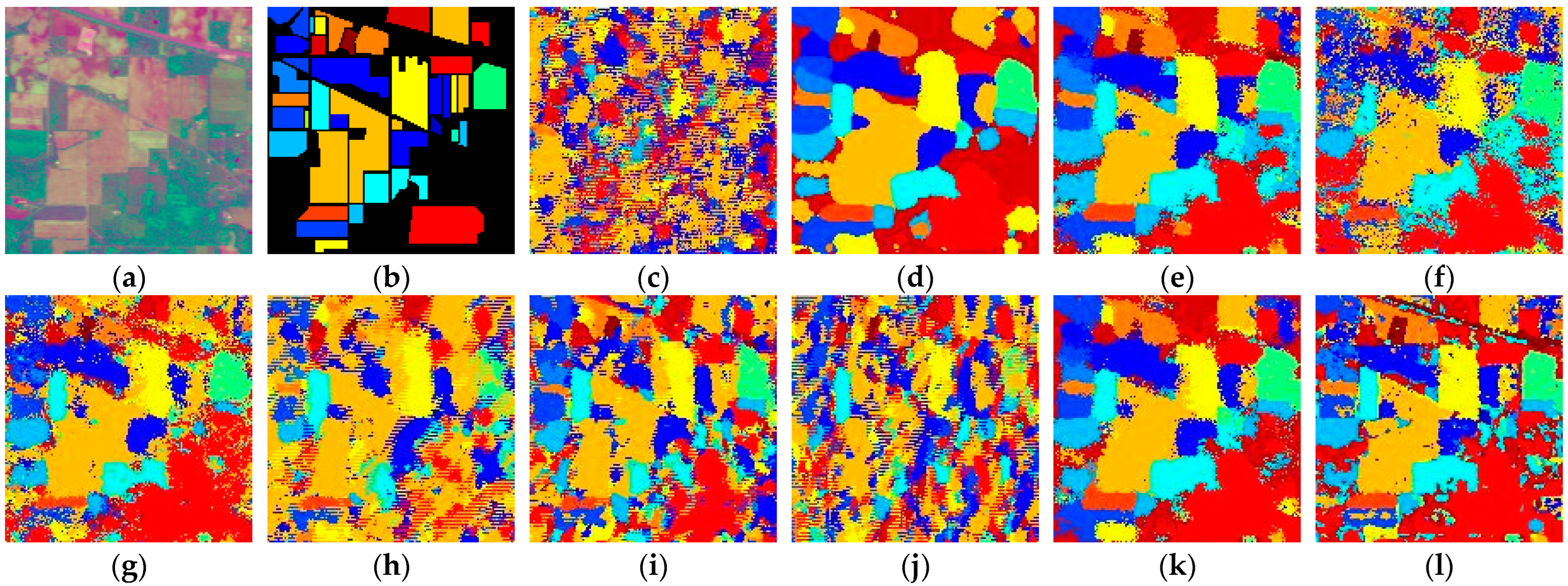
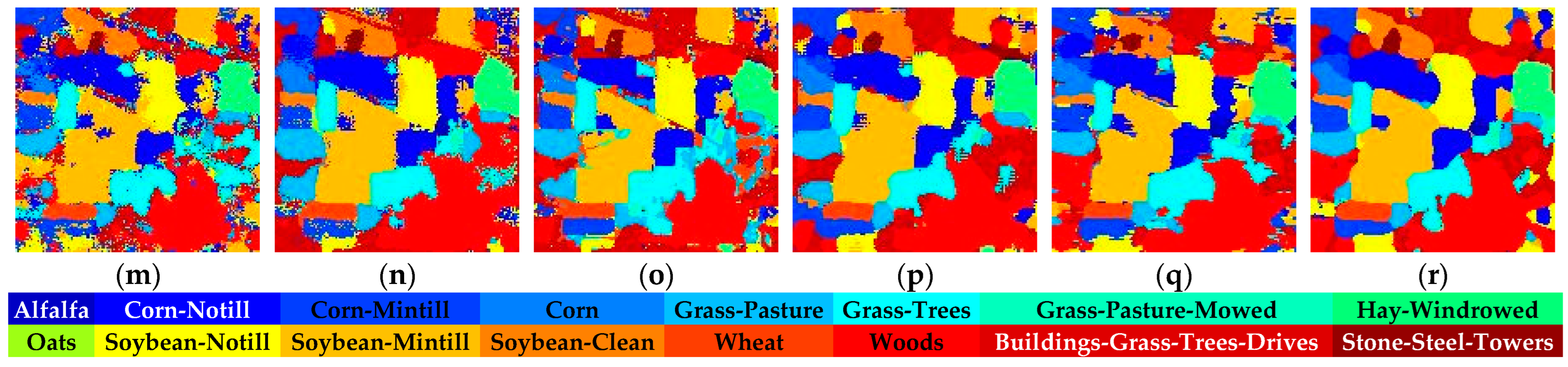
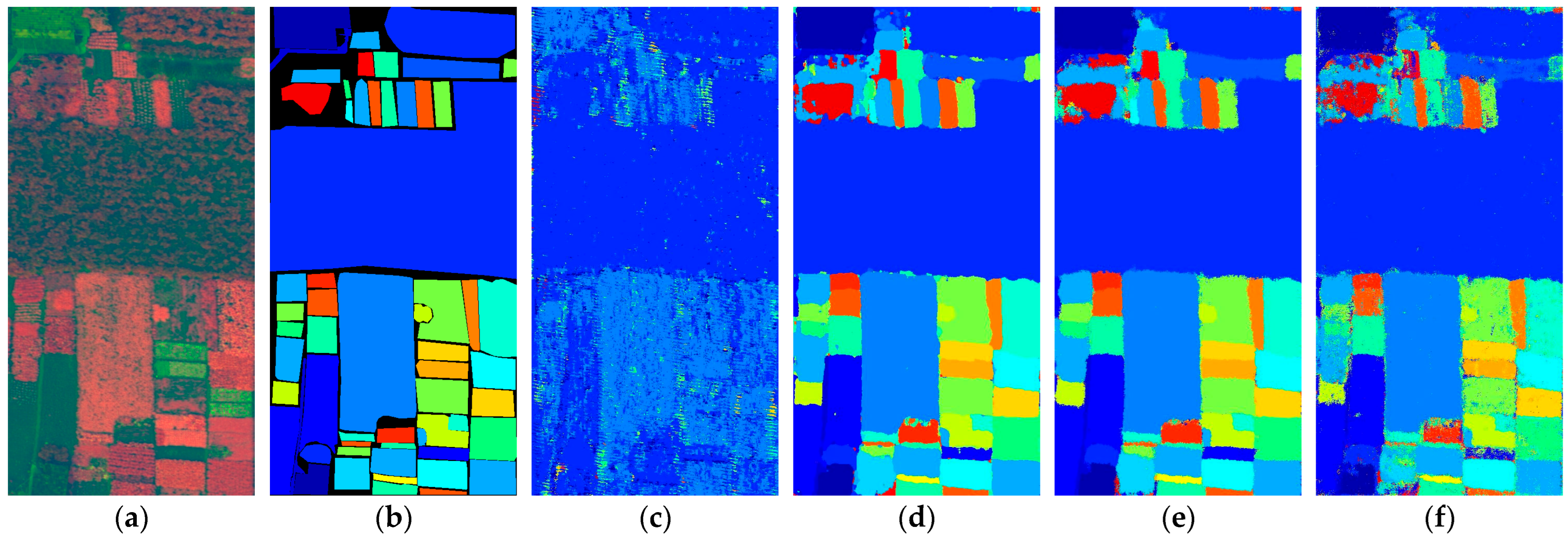
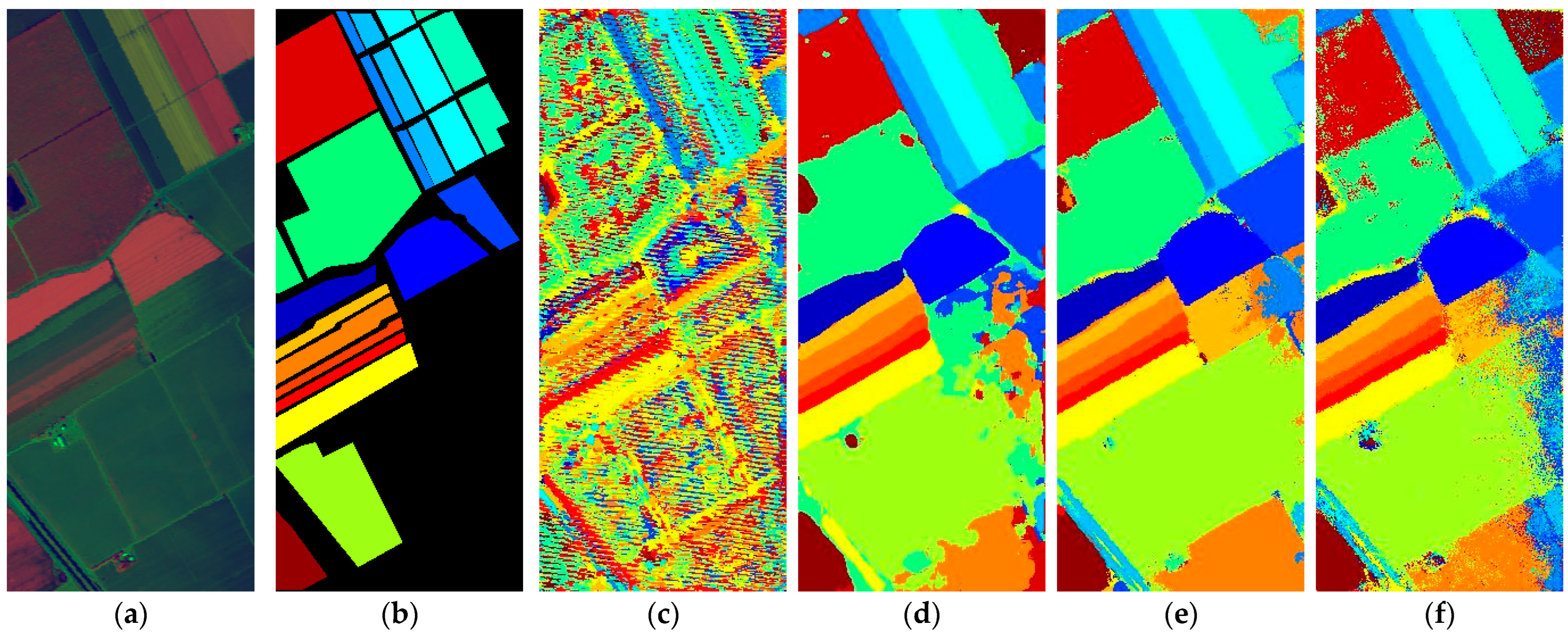
Figure 14.
Full-Scene classification results obtained by different networks from the Indian dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 14.
Full-Scene classification results obtained by different networks from the Indian dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 15.
Full-Scene classification results obtained by different networks using the Houston dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 15.
Full-Scene classification results obtained by different networks using the Houston dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 16.
Full-Scene classification results obtained by different networks from the HongHu dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 16.
Full-Scene classification results obtained by different networks from the HongHu dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 17.
Full-Scene classification results obtained by different networks from the PaviaU dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 17.
Full-Scene classification results obtained by different networks from the PaviaU dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 18.
Full-Scene classification results obtained by different networks from the Salinas dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
Figure 18.
Full-Scene classification results obtained by different networks from the Salinas dataset: (a) false-color image; (b) ground truth; (c) S3ARN; (d) PMCN; (e) S3GAN; (f) ViT; (g) SFormer; (h) HFormer; (i) MHCFormer; (j) D2S2BoT; (k) SQSFormer; (l) EATN; (m) CFormer; (n) SSACFormer; (o) CPFormer; (p) DSFormer; (q) LGDRNet; (r) CPMFFormer.
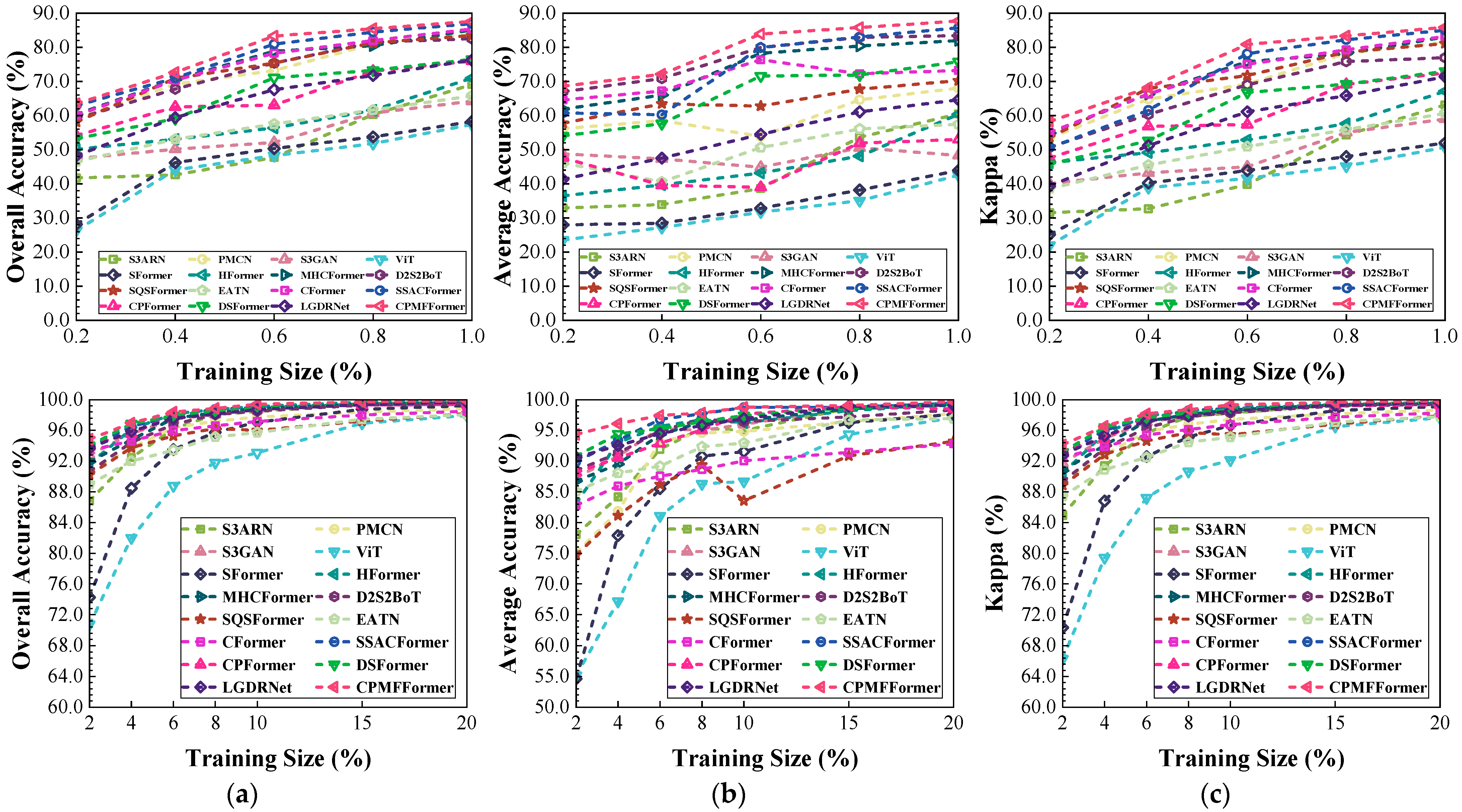
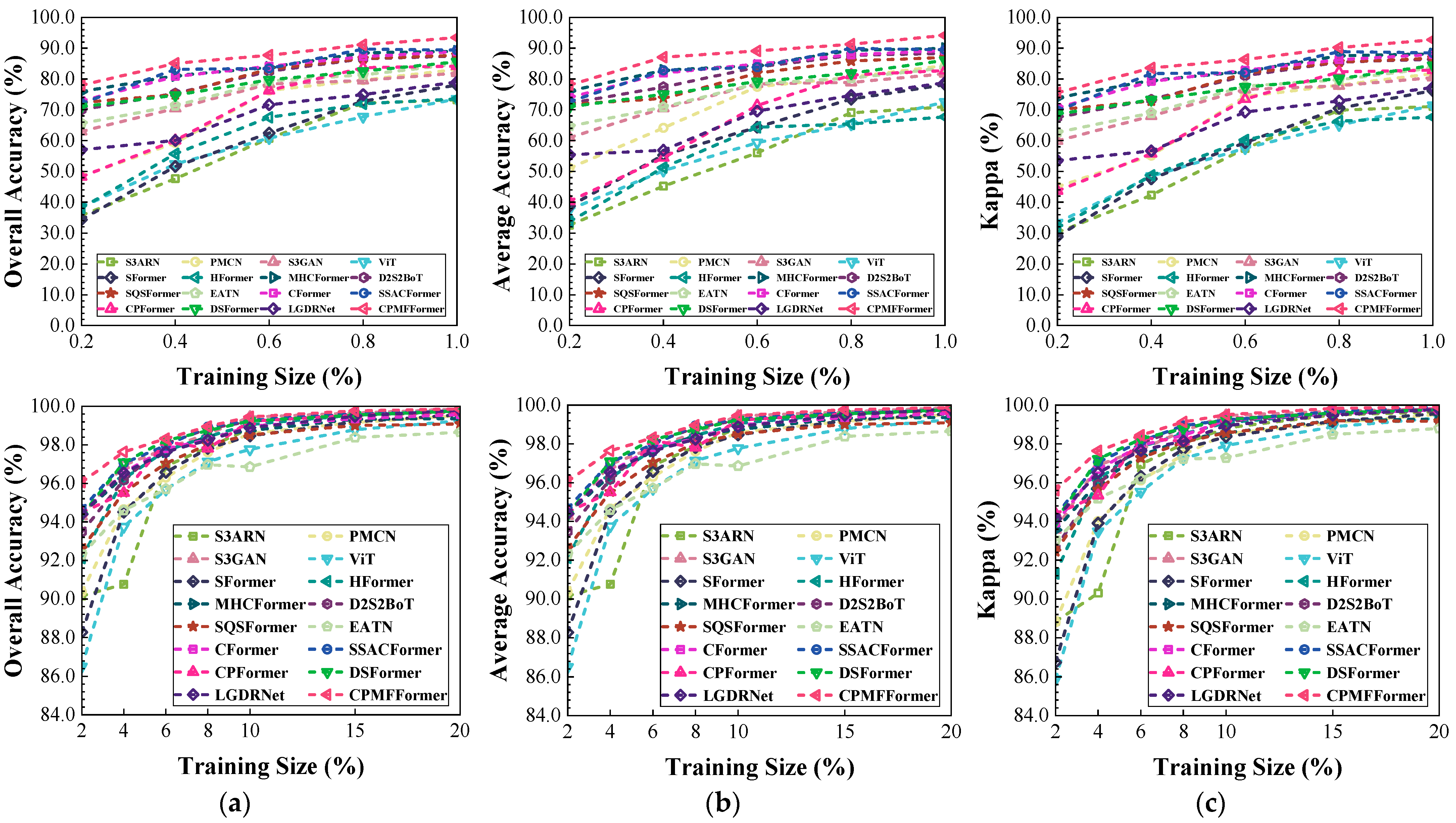
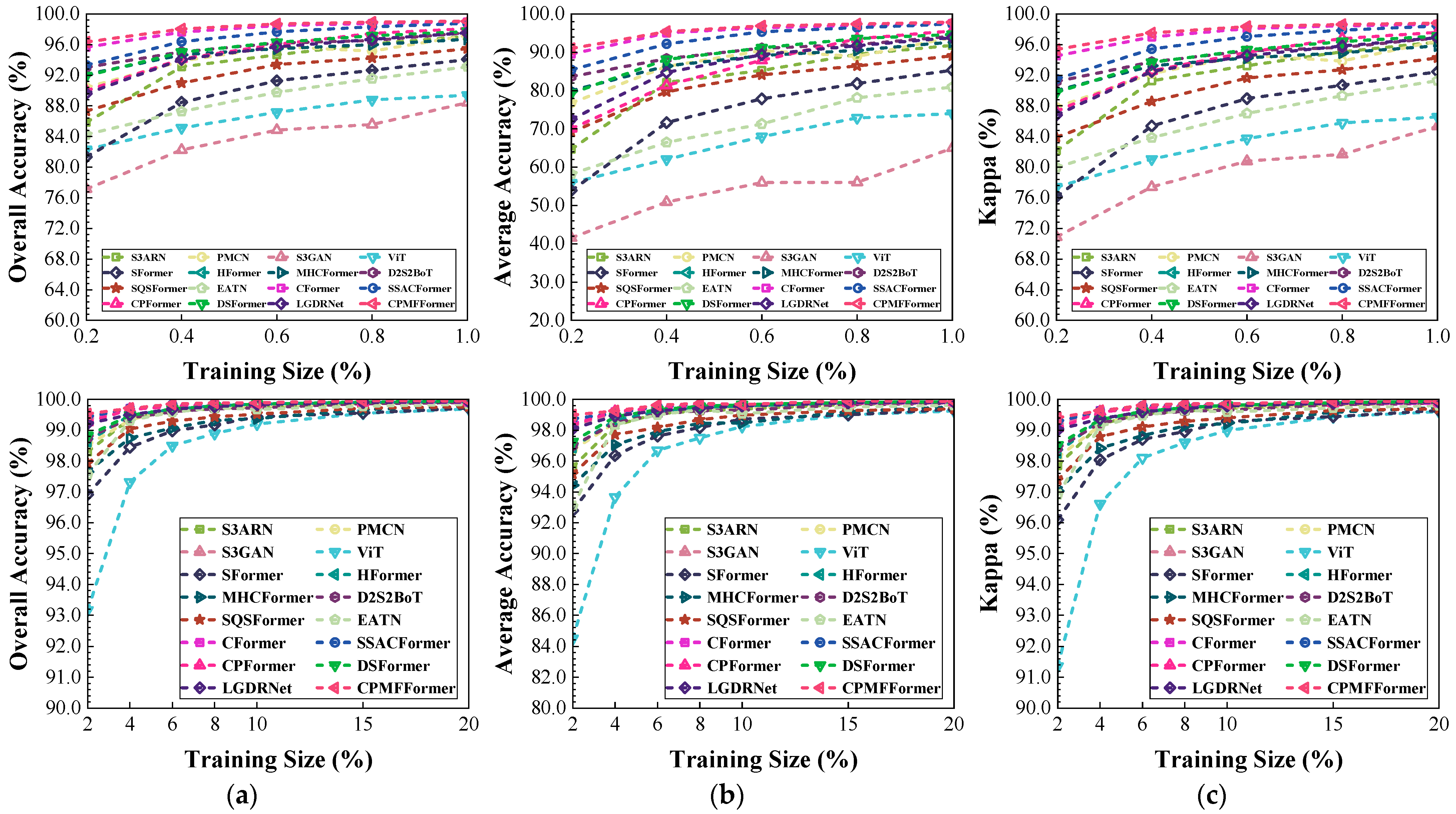
Figure 19.
Classification performance obtained by different networks with different training sample sizes from the Indian dataset: (a) OA; (b) AA; (c) .
Figure 19.
Classification performance obtained by different networks with different training sample sizes from the Indian dataset: (a) OA; (b) AA; (c) .
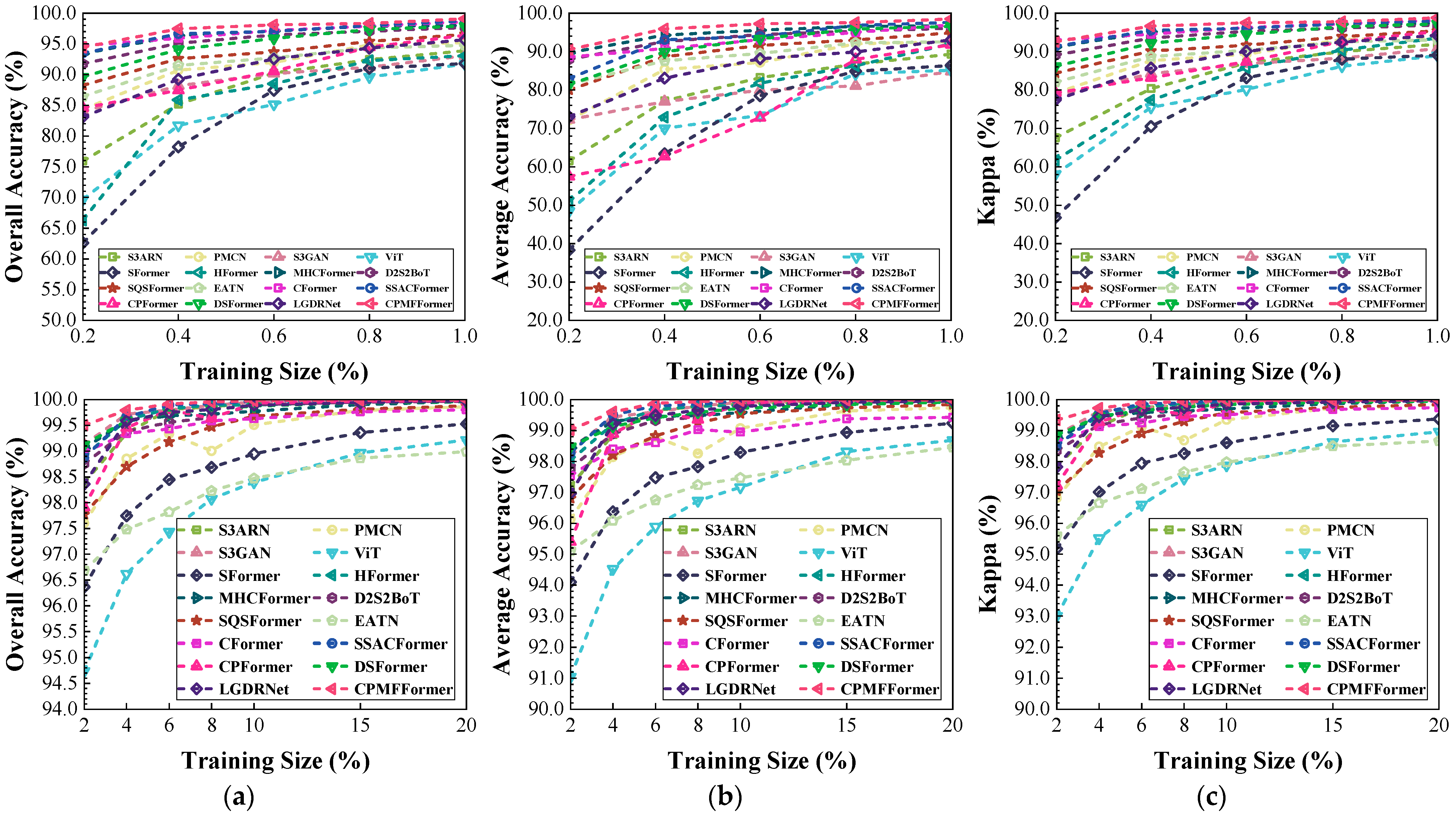
Figure 20.
Classification performance obtained by different networks with different training sample sizes from the Houston dataset: (a) OA; (b) AA; (c) .
Figure 20.
Classification performance obtained by different networks with different training sample sizes from the Houston dataset: (a) OA; (b) AA; (c) .
Figure 21.
Classification performance obtained by different networks with different training sample sizes from the HongHu dataset: (a) OA; (b) AA; (c) .
Figure 21.
Classification performance obtained by different networks with different training sample sizes from the HongHu dataset: (a) OA; (b) AA; (c) .
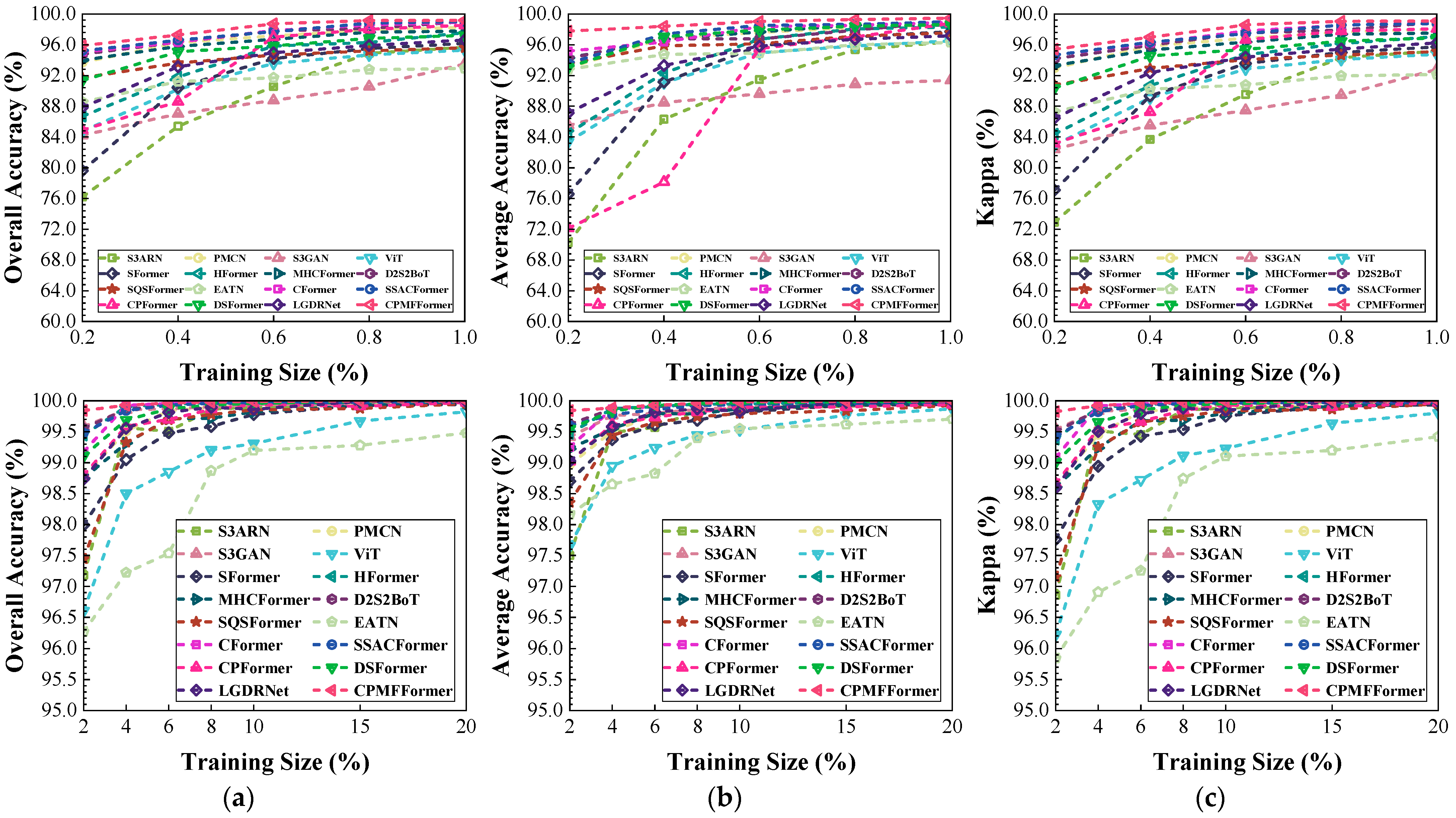
Figure 22.
Classification performance obtained by different networks with different training sample sizes from the PaviaU dataset: (a) OA; (b) AA; (c) .
Figure 22.
Classification performance obtained by different networks with different training sample sizes from the PaviaU dataset: (a) OA; (b) AA; (c) .
Figure 23.
Classification performance obtained by different networks with different training samples sizes from the Salinas datasets: (a) OA; (b) AA; (c) .
Figure 23.
Classification performance obtained by different networks with different training samples sizes from the Salinas datasets: (a) OA; (b) AA; (c) .
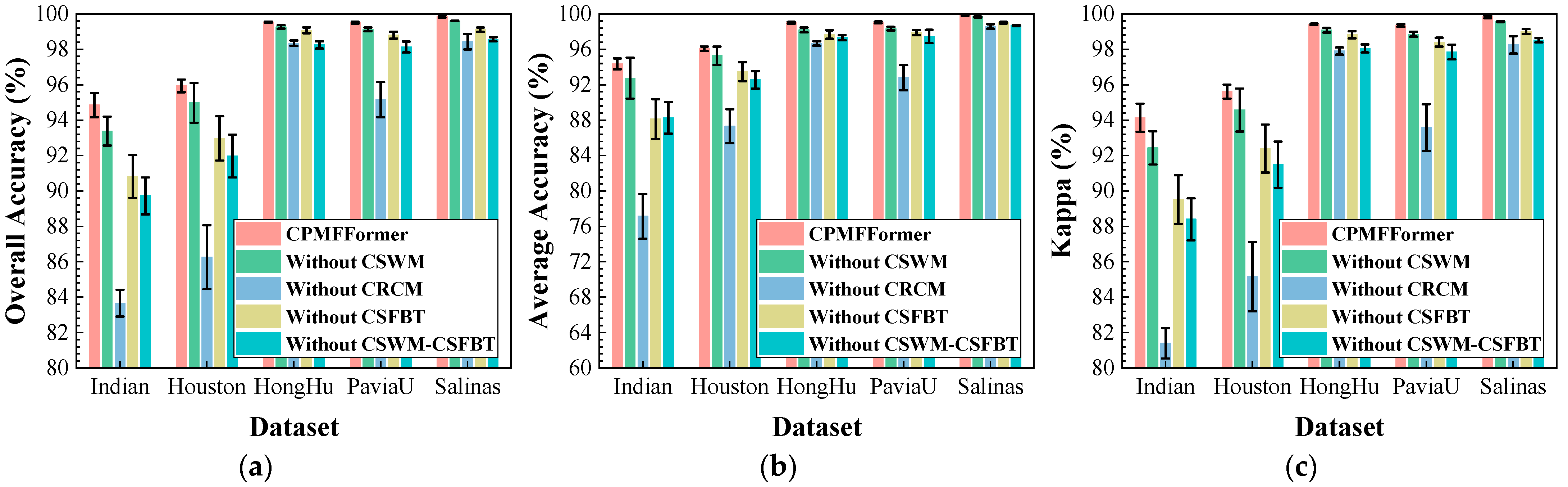
Figure 24.
Impact of different modules on classification performance: (a) OA; (b) AA; (c) .
Figure 24.
Impact of different modules on classification performance: (a) OA; (b) AA; (c) .
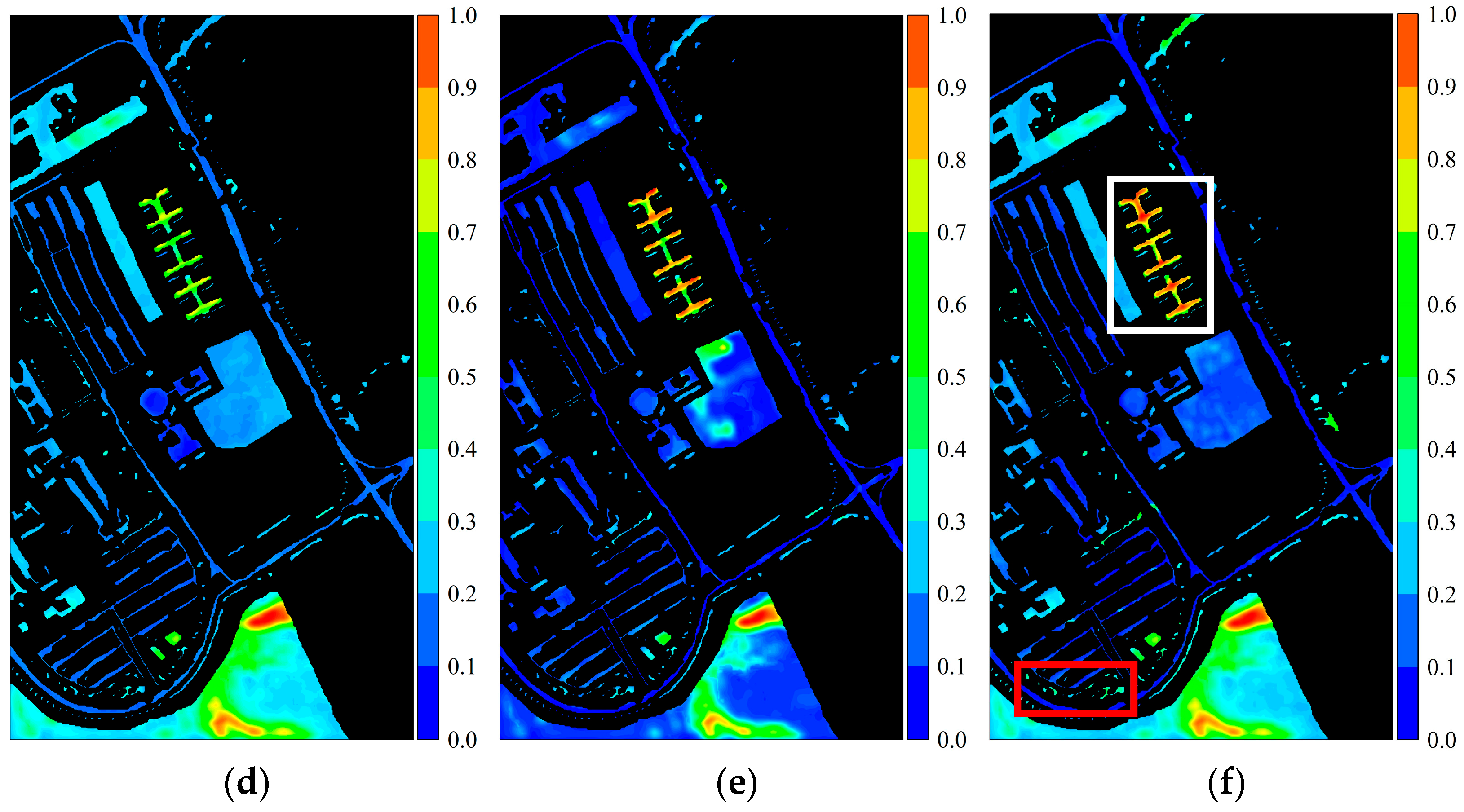
Figure 25.
Activation response heatmaps obtained by different CSFBTs from the PaviaU dataset: (a) CSFBT-1; (b) CSFBT-2; (c) CSFBT-3; (d) CSFBT-4; (e) CSFBT-5; (f) CSFBT-6. The red box represents the Trees class, and the white box represents the Painted Metal Sheets class.
Figure 25.
Activation response heatmaps obtained by different CSFBTs from the PaviaU dataset: (a) CSFBT-1; (b) CSFBT-2; (c) CSFBT-3; (d) CSFBT-4; (e) CSFBT-5; (f) CSFBT-6. The red box represents the Trees class, and the white box represents the Painted Metal Sheets class.
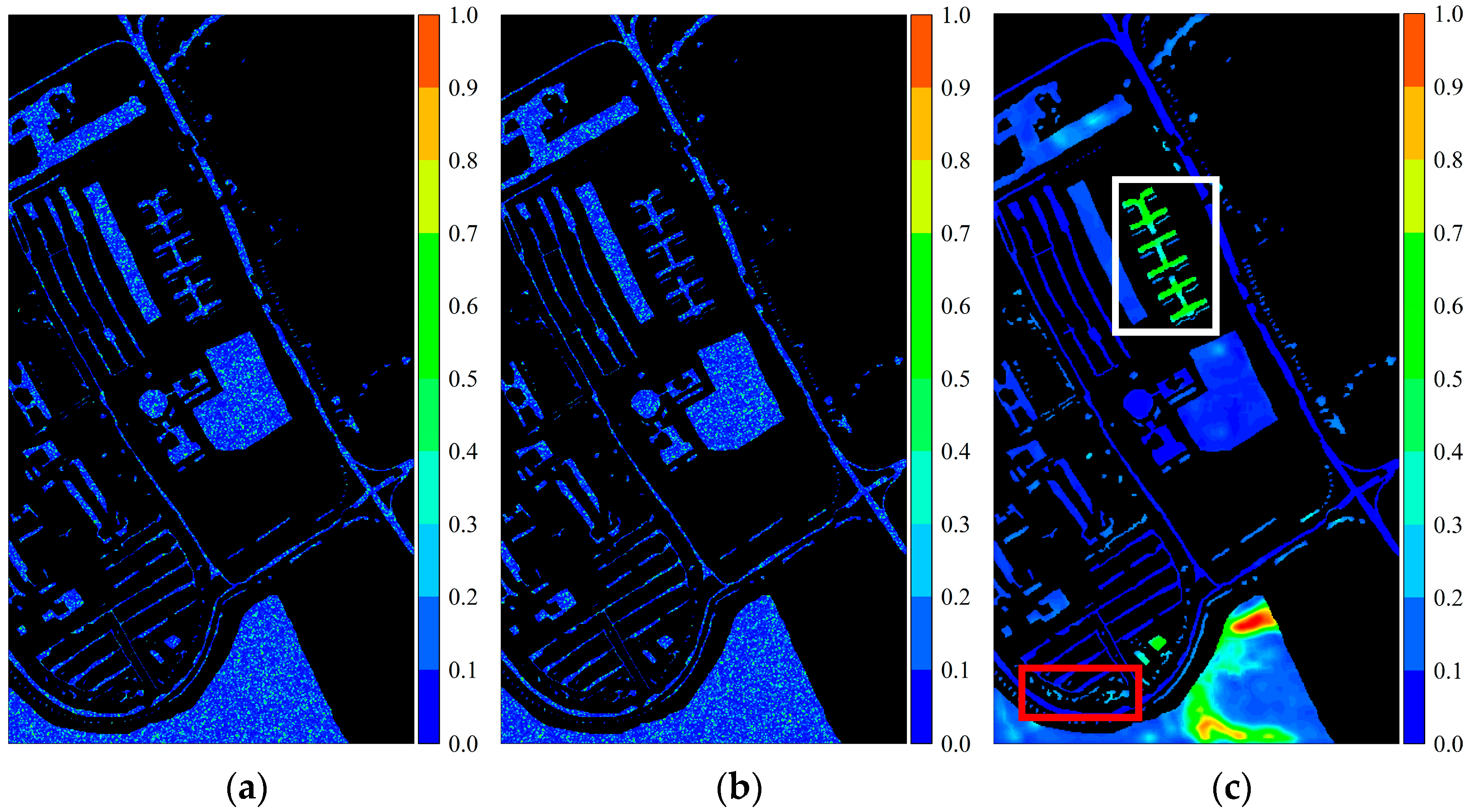
Figure 26.
Activation response heatmaps obtained by current multiscale fusion strategies from the PaviaU dataset: (
a) concatenation; (
b) element-wise addition; (
c) attention method in the literature [
35]. The red box represents the Trees class, and the white box represents the Painted Metal Sheets class.
Figure 26.
Activation response heatmaps obtained by current multiscale fusion strategies from the PaviaU dataset: (
a) concatenation; (
b) element-wise addition; (
c) attention method in the literature [
35]. The red box represents the Trees class, and the white box represents the Painted Metal Sheets class.
Figure 27.
Impact of different spectral weighting mechanism on classification performance: (a) OA; (b) AA; (c) .
Figure 27.
Impact of different spectral weighting mechanism on classification performance: (a) OA; (b) AA; (c) .
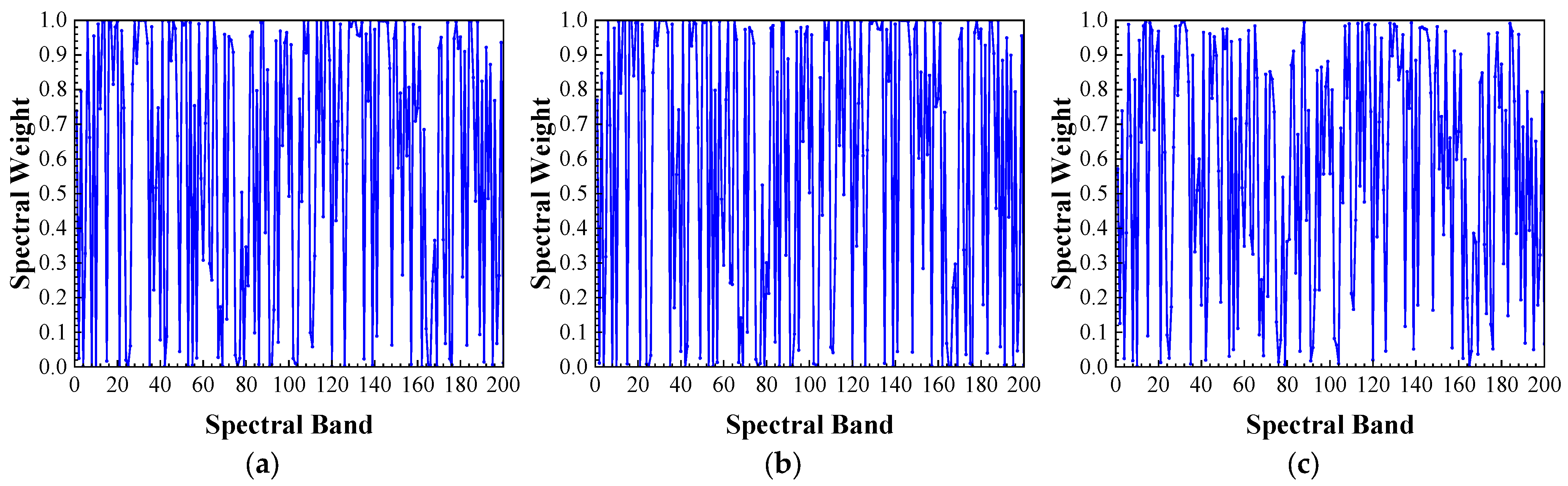
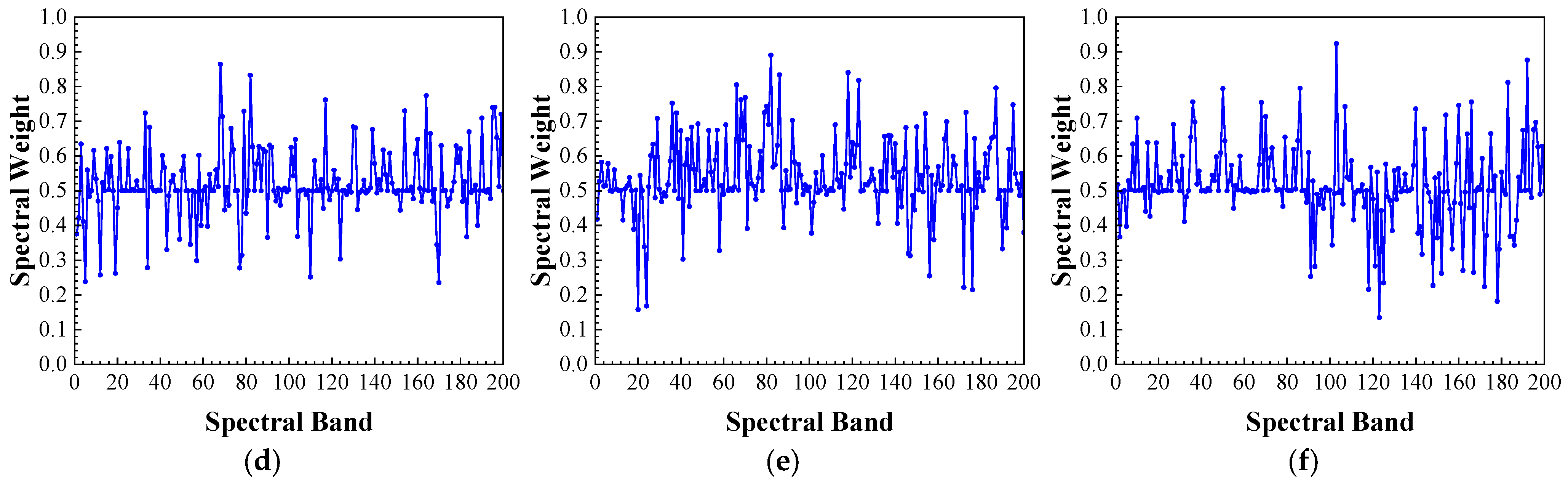
Figure 28.
Average spectral weights learned by CSWM and SWL: (a–c): average spectral weights learned by SWL for the Corn-Notill, Corn-Mintill, and Corn classes; (d–f): average spectral weights learned by CSWM for the Corn-Notill, Corn-Mintill, and Corn classes.
Figure 28.
Average spectral weights learned by CSWM and SWL: (a–c): average spectral weights learned by SWL for the Corn-Notill, Corn-Mintill, and Corn classes; (d–f): average spectral weights learned by CSWM for the Corn-Notill, Corn-Mintill, and Corn classes.
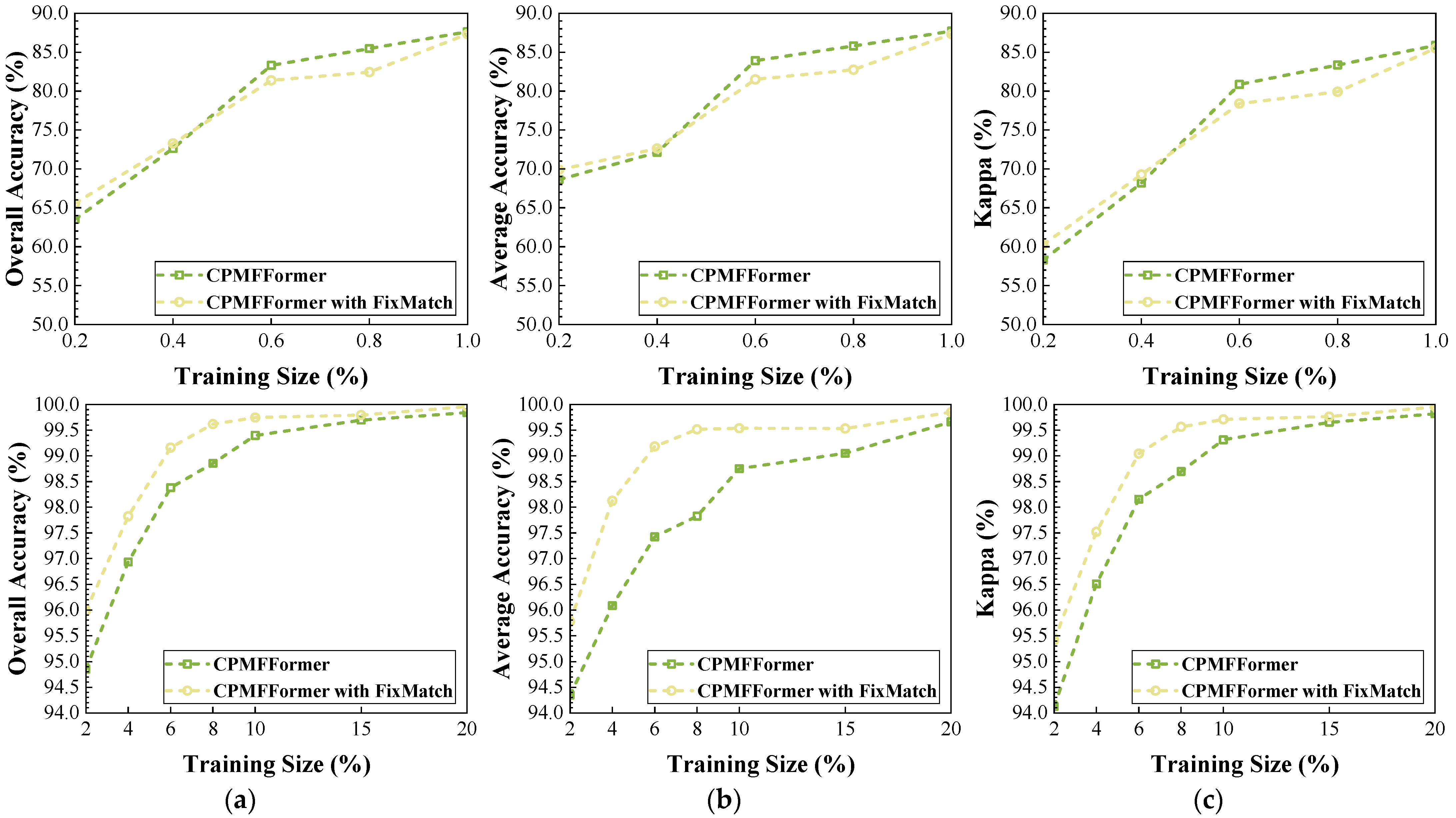
Figure 29.
The performance changes in CPMFFormer after introducing FixMatch: (a) OA; (b) AA; (c) .
Figure 29.
The performance changes in CPMFFormer after introducing FixMatch: (a) OA; (b) AA; (c) .
Table 1.
The number of homogeneous patches and heterogeneous patches in five public HSI datasets. The homogeneous patch indicates that all pixels in the patch belong to the same class. The heterogeneous patch means that the patch contains background noise or heterogeneous pixels.
Table 1.
The number of homogeneous patches and heterogeneous patches in five public HSI datasets. The homogeneous patch indicates that all pixels in the patch belong to the same class. The heterogeneous patch means that the patch contains background noise or heterogeneous pixels.
| Dataset | Indian | Houston | HongHu | PaviaU | Salinas |
|---|
| Homogeneous Patches | 1402 | 32 | 10,740 | 26,561 | 9179 |
| Heterogeneous Patches | 8847 | 14,997 | 375,953 | 27,568 | 33,597 |
Table 2.
The implementation process of CSWM.
Table 2.
The implementation process of CSWM.
| Layer Name | Kernel Size | Output Size |
|---|
| Aggregation | - | 11 × 11 × 200 |
| Spectral Weight Learning | - | 1 × 1 × 200 |
| Element-Wise Multiplication | - | 11 × 11 × 200 |
| Element-Wise Addition | - | 11 × 11× 200 |
Table 3.
The implementation process of CRCM (3 × 3).
Table 3.
The implementation process of CRCM (3 × 3).
| Layer Name | Kernel Size | Output Size |
|---|
| Conv | 1 × 1 | 11 × 11 × 64 |
| GConv-BN-ReLU | 3 × 3 | 11 × 11 × 64 |
| CFCL | - | 11 × 11 × 64 |
| Conv | 1 × 1 | 11 × 11 × 128 |
| Residual Connection | - | 11 × 11 × 128 |
| Conv | 1 × 1 | 11 × 11 × 64 |
| GConv-BN-ReLU | 3 × 3 | 11 × 11 × 64 |
| CFCL | - | 11 × 11 × 64 |
| Conv | 1 × 1 | 11 × 11 × 128 |
| Residual Connection | - | 11 × 11 × 128 |
Table 4.
The implementation process of CSFBT.
Table 4.
The implementation process of CSFBT.
| Layer Name | Kernel Size | Output Size |
|---|
| CFEB | - | 11 × 11 × 128
11 × 11 × 128 |
| Conv | 1 × 1 | 11 × 11 × 12
11 × 11 × 12 |
| MHCSD2A | - | 11 × 11 × 12 |
| Conv | 1 × 1 | 11 × 11 × 128 |
| Residual Connection | - | 11 × 11 × 128 |
Table 5.
The types of ground objects and samples distribution in the Indian datasets.
Table 5.
The types of ground objects and samples distribution in the Indian datasets.
| Class | Name | Training | Validation | Test | Total |
|---|
| 1 | Alfalfa | 1 | 1 | 44 | 46 |
| 2 | Corn-Notill | 29 | 29 | 1370 | 1428 |
| 3 | Corn-Mintill | 17 | 17 | 796 | 830 |
| 4 | Corn | 5 | 5 | 227 | 237 |
| 5 | Grass-Pasture | 10 | 10 | 463 | 483 |
| 6 | Grass-Trees | 15 | 15 | 700 | 730 |
| 7 | Grass-Pasture-Mowed | 1 | 1 | 26 | 28 |
| 8 | Hay-Windrowed | 10 | 10 | 458 | 478 |
| 9 | Oats | 1 | 1 | 18 | 20 |
| 10 | Soybean-Notill | 20 | 20 | 932 | 972 |
| 11 | Soybean-Mintill | 50 | 50 | 2355 | 2455 |
| 12 | Soybean-Clean | 12 | 12 | 569 | 593 |
| 13 | Wheat | 5 | 5 | 195 | 205 |
| 14 | Woods | 26 | 26 | 1213 | 1265 |
| 15 | Buildings-Grass-Trees-Drives | 8 | 8 | 370 | 386 |
| 16 | Stone-Steel-Towers | 2 | 2 | 89 | 93 |
| Total | | 212 | 212 | 9825 | 10,249 |
Table 6.
The types of ground objects and sample distribution in the Houston datasets.
Table 6.
The types of ground objects and sample distribution in the Houston datasets.
| Class | Name | Training | Validation | Test | Total |
|---|
| 1 | Healthy Grass | 26 | 26 | 1199 | 1251 |
| 2 | Stressed Grass | 26 | 26 | 1202 | 1254 |
| 3 | Synthetic Grass | 14 | 14 | 669 | 697 |
| 4 | Trees | 25 | 25 | 1194 | 1244 |
| 5 | Soil | 25 | 25 | 1192 | 1242 |
| 6 | Water | 7 | 7 | 311 | 325 |
| 7 | Residential | 26 | 26 | 1216 | 1268 |
| 8 | Commercial | 25 | 25 | 1194 | 1244 |
| 9 | Road | 26 | 26 | 1200 | 1252 |
| 10 | Highway | 25 | 25 | 1177 | 1227 |
| 11 | Railway | 25 | 25 | 1185 | 1235 |
| 12 | Parking Lot1 | 25 | 25 | 1183 | 1233 |
| 13 | Parking Lot2 | 10 | 10 | 449 | 469 |
| 14 | Tennis Court | 9 | 9 | 410 | 428 |
| 15 | Running Track | 14 | 14 | 632 | 660 |
| Total | | 308 | 308 | 14,413 | 15,029 |
Table 7.
The types of ground objects and sample distribution in the HongHu datasets.
Table 7.
The types of ground objects and sample distribution in the HongHu datasets.
| Class | Name | Training | Validation | Test | Total |
|---|
| 1 | Red Roof | 281 | 281 | 13,479 | 14,041 |
| 2 | Road | 71 | 71 | 3370 | 3512 |
| 3 | Bare Soil | 437 | 437 | 20,947 | 21,821 |
| 4 | Cotton | 3266 | 3266 | 156,753 | 163,285 |
| 5 | Cotton Firewood | 125 | 125 | 5968 | 6218 |
| 6 | Rape | 892 | 892 | 42,773 | 44,557 |
| 7 | Chinese Cabbage | 483 | 483 | 23,137 | 24,103 |
| 8 | Pakchoi | 82 | 82 | 3890 | 4054 |
| 9 | Cabbage | 217 | 217 | 10,385 | 10,819 |
| 10 | Tuber Mustard | 248 | 248 | 11,898 | 12,394 |
| 11 | Brassica Parachinensis | 221 | 221 | 10,573 | 11,015 |
| 12 | Brassica Chinensis | 180 | 180 | 8594 | 8954 |
| 13 | Small Brassica Chinensis | 451 | 451 | 21,605 | 22,507 |
| 14 | Lactuca Sativa | 148 | 148 | 7060 | 7356 |
| 15 | Celtuce | 21 | 21 | 960 | 1002 |
| 16 | Film-Covered Lettuce | 146 | 146 | 6970 | 7262 |
| 17 | Romaine Lettuce | 61 | 61 | 2888 | 3010 |
| 18 | Carrot | 65 | 65 | 3087 | 3217 |
| 19 | White Radish | 175 | 175 | 8362 | 8712 |
| 20 | Garlic Sprout | 70 | 70 | 3346 | 3486 |
| 21 | Broad Bean | 27 | 27 | 1274 | 1328 |
| 22 | Tree | 81 | 81 | 3878 | 4040 |
| Total | | 7748 | 7748 | 371,197 | 386,693 |
Table 8.
The types of ground objects and sample distribution in the PaviaU datasets.
Table 8.
The types of ground objects and sample distribution in the PaviaU datasets.
| Class | Name | Training | Validation | Test | Total |
|---|
| 1 | Asphalt | 133 | 133 | 6365 | 6631 |
| 2 | Meadows | 373 | 373 | 17,903 | 18,649 |
| 3 | Gravel | 42 | 42 | 2015 | 2099 |
| 4 | Trees | 62 | 62 | 2940 | 3064 |
| 5 | Painted Metal Sheets | 27 | 27 | 1291 | 1345 |
| 6 | Bare Soil | 101 | 101 | 4827 | 5029 |
| 7 | Bitumen | 27 | 27 | 1276 | 1330 |
| 8 | Self-Blocking Bricks | 74 | 74 | 3534 | 3682 |
| 9 | Shadows | 19 | 19 | 909 | 947 |
| Total | | 858 | 858 | 41,060 | 42,776 |
Table 9.
The types of ground objects and sample distribution in the Salinas datasets.
Table 9.
The types of ground objects and sample distribution in the Salinas datasets.
| Class | Name | Training | Validation | Test | Total |
|---|
| 1 | Broccoli Green Weeds 1 | 41 | 41 | 1927 | 2009 |
| 2 | Broccoli Green Weeds 2 | 75 | 75 | 3576 | 3726 |
| 3 | Fallow | 40 | 40 | 1896 | 1976 |
| 4 | Fallow Rough Plow | 28 | 28 | 1338 | 1394 |
| 5 | Fallow Smooth | 54 | 54 | 2570 | 2678 |
| 6 | Stubble | 80 | 80 | 3799 | 3959 |
| 7 | Celery | 72 | 72 | 3435 | 3579 |
| 8 | Grapes Untrained | 226 | 226 | 10,819 | 11,271 |
| 9 | Soil Vineyard Develop | 125 | 125 | 5953 | 6203 |
| 10 | Corn Senesced Green Weeds | 66 | 66 | 3146 | 3278 |
| 11 | Lettuce Romaine 4 wk. | 22 | 22 | 1024 | 1068 |
| 12 | Lettuce Romaine 5 wk. | 39 | 39 | 1849 | 1927 |
| 13 | Lettuce Romaine 6 wk. | 19 | 19 | 878 | 916 |
| 14 | Lettuce Romaine 7 wk. | 22 | 22 | 1026 | 1070 |
| 15 | Vineyard Untrained | 146 | 146 | 6976 | 7268 |
| 16 | Vineyard Vertical Trellis | 37 | 37 | 1733 | 1807 |
| Total | | 1092 | 1092 | 51,945 | 54,129 |
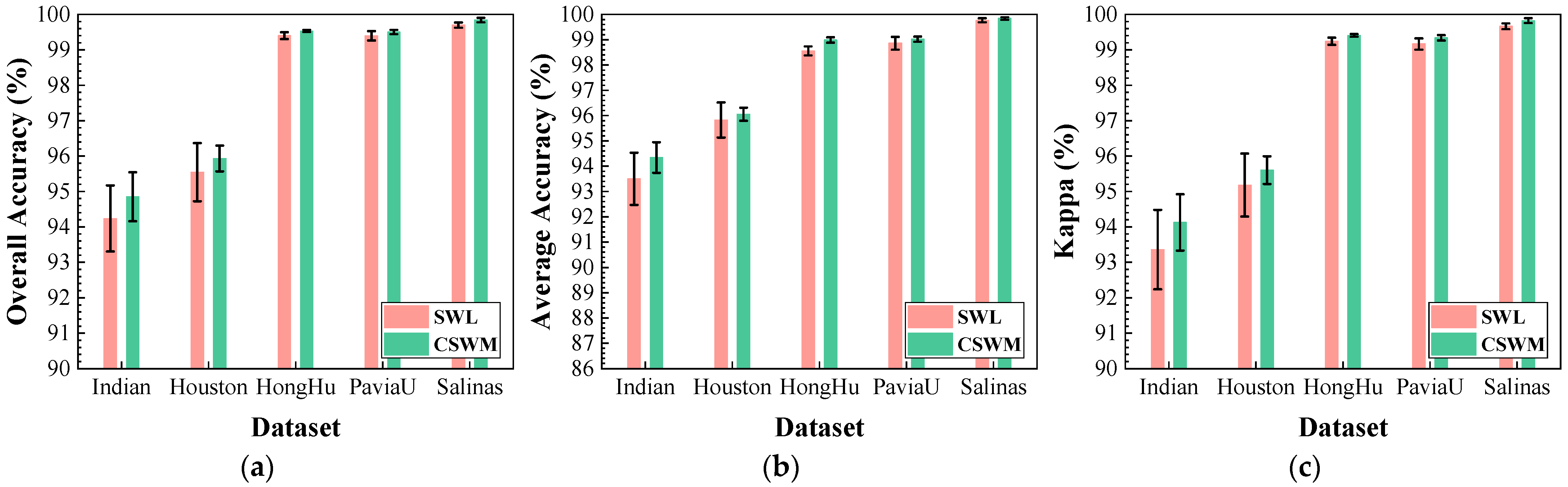
Table 10.
Impact of the number of CRCM on classification performance. The optimal results are in red.
Table 10.
Impact of the number of CRCM on classification performance. The optimal results are in red.
| Datasets | Metrics | CRCM = 2 | CRCM = 3 | CRCM = 4 | CRCM = 5 | CRCM = 6 |
|---|
| Indian | OA (%) | 93.70 ± 1.06 | 94.83 ± 0.92 | 94.85 ± 0.69 | 94.84 ± 0.83 | 93.94 ± 0.78 |
| AA (%) | 92.88 ± 0.97 | 93.48 ± 1.36 | 94.35 ± 0.61 | 94.33 ± 0.60 | 92.93 ± 1.21 |
| κ (%) | 92.82 ± 1.21 | 94.12 ± 1.04 | 94.13 ± 0.80 | 94.14 ± 0.95 | 93.09 ± 0.89 |
| Houston | OA (%) | 95.76 ± 0.62 | 95.88 ± 0.73 | 95.93 ± 0.36 | 95.91 ± 0.40 | 95.29 ± 0.52 |
| AA (%) | 95.93 ± 0.81 | 96.01 ± 0.73 | 96.06 ± 0.26 | 95.92 ± 0.53 | 95.51 ± 0.64 |
| κ (%) | 95.42 ± 0.67 | 95.55 ± 0.78 | 95.61 ± 0.39 | 95.60 ± 0.44 | 94.91 ± 0.56 |
| HongHu | OA (%) | 99.53 ± 0.04 | 99.50 ± 0.04 | 99.53 ± 0.03 | 99.50 ± 0.05 | 99.49 ± 0.05 |
| AA (%) | 98.92 ± 0.20 | 98.83 ± 0.16 | 98.99 ± 0.10 | 98.82 ± 0.20 | 98.68 ± 0.06 |
| κ (%) | 99.40 ± 0.05 | 99.37 ± 0.04 | 99.41 ± 0.04 | 99.36 ± 0.07 | 99.24 ± 0.06 |
| PaviaU | OA (%) | 99.45 ± 0.12 | 99.45 ± 0.22 | 99.50 ± 0.06 | 99.48 ± 0.13 | 99.35 ± 0.09 |
| AA (%) | 98.95 ± 0.27 | 98.88 ± 0.45 | 99.02 ± 0.10 | 99.01 ± 0.20 | 98.74 ± 0.14 |
| κ (%) | 99.27 ± 0.15 | 99.27 ± 0.29 | 99.34 ± 0.08 | 99.31 ± 0.18 | 99.13 ± 0.12 |
| Salinas | OA (%) | 99.81 ± 0.12 | 99.77 ± 0.13 | 99.84 ± 0.06 | 99.84 ± 0.06 | 99.75 ± 0.13 |
| AA (%) | 99.81 ± 0.13 | 99.79 ± 0.08 | 99.84 ± 0.05 | 99.86 ± 0.02 | 99.75 ± 0.09 |
| κ (%) | 99.79 ± 0.14 | 99.74 ± 0.14 | 99.82 ± 0.07 | 99.82 ± 0.07 | 99.72 ± 0.15 |
Table 11.
Impact of the number of bottleneck residual blocks within CRCM on classification performance. The optimal results are in red.
Table 11.
Impact of the number of bottleneck residual blocks within CRCM on classification performance. The optimal results are in red.
| Datasets | Metrics | BRB = 1 | BRB = 2 | BRB = 3 | BRB = 4 | BRB = 5 |
|---|
| Indian | OA (%) | 94.10 ± 0.56 | 94.85 ± 0.69 | 94.29 ± 0.42 | 94.57 ± 0.89 | 94.74 ± 0.72 |
| AA (%) | 93.05 ± 1.89 | 94.35 ± 0.61 | 93.73 ± 0.70 | 93.30 ± 2.47 | 93.66 ± 0.53 |
| κ (%) | 93.26 ± 0.65 | 94.13 ± 0.80 | 93.49 ± 0.49 | 93.80 ± 1.02 | 94.00 ± 0.82 |
| Houston | OA (%) | 96.02 ± 0.48 | 95.93 ± 0.36 | 95.09 ± 1.24 | 95.66 ± 0.53 | 95.65 ± 0.55 |
| AA (%) | 96.04 ± 0.63 | 96.06 ± 0.26 | 95.35 ± 1.12 | 95.82 ± 0.54 | 95.77 ± 0.73 |
| κ (%) | 95.70 ± 0.52 | 95.61 ± 0.39 | 94.69 ± 1.34 | 95.31 ± 0.57 | 95.30 ± 0.60 |
| HongHu | OA (%) | 99.47 ± 0.05 | 99.53 ± 0.03 | 99.47 ± 0.01 | 99.52 ± 0.03 | 99.49 ± 0.03 |
| AA (%) | 98.77 ± 0.15 | 98.99 ± 0.10 | 98.75 ± 0.05 | 98.78 ± 0.11 | 98.71 ± 0.18 |
| κ (%) | 99.33 ± 0.07 | 99.41 ± 0.04 | 99.34 ± 0.01 | 99.40 ± 0.03 | 99.36 ± 0.04 |
| PaviaU | OA (%) | 99.39 ± 0.10 | 99.50 ± 0.06 | 99.38 ± 0.15 | 99.34 ± 0.14 | 99.43 ± 0.14 |
| AA (%) | 98.77 ± 0.19 | 99.02 ± 0.10 | 98.80 ± 0.38 | 98.74 ± 0.33 | 98.82 ± 0.33 |
| κ (%) | 99.19 ± 0.13 | 99.34 ± 0.08 | 99.18 ± 0.19 | 99.12 ± 0.19 | 99.25 ± 0.19 |
| Salinas | OA (%) | 99.83 ± 0.09 | 99.84 ± 0.06 | 99.79 ± 0.06 | 99.82 ± 0.13 | 99.79 ± 0.08 |
| AA (%) | 99.83 ± 0.05 | 99.84 ± 0.05 | 99.79 ± 0.07 | 99.84 ± 0.09 | 99.81 ± 0.06 |
| κ (%) | 99.81 ± 0.10 | 99.82 ± 0.07 | 99.76 ± 0.07 | 99.80 ± 0.15 | 99.77 ± 0.09 |
Table 12.
Impact of feature channel dimension on classification performance. The optimal results are in red.
Table 12.
Impact of feature channel dimension on classification performance. The optimal results are in red.
| Datasets | Metrics | C = 32 | C = 64 | C = 96 | C = 128 | C = 160 | C = 192 |
|---|
| Indian | OA (%) | 93.67 ± 0.43 | 94.05 ± 1.39 | 94.52 ± 0.97 | 94.85 ± 0.69 | 94.30 ± 1.00 | 94.47 ± 0.72 |
| AA (%) | 92.79 ± 1.16 | 93.22 ± 2.34 | 94.07 ± 1.67 | 94.35 ± 0.61 | 93.93 ± 1.95 | 94.56 ± 0.68 |
| κ (%) | 92.78 ± 0.50 | 93.21 ± 1.59 | 93.75 ± 1.11 | 94.13 ± 0.80 | 93.50 ± 1.14 | 93.70 ± 0.81 |
| Houston | OA (%) | 95.28 ± 1.22 | 95.93 ± 0.36 | 95.76 ± 0.61 | 95.58 ± 0.80 | 95.40 ± 0.73 | 95.12 ± 0.94 |
| AA (%) | 95.41 ± 1.53 | 96.06 ± 0.26 | 95.82 ± 0.62 | 95.77 ± 0.72 | 95.71 ± 0.72 | 95.38 ± 0.96 |
| κ (%) | 94.89 ± 1.32 | 95.61 ± 0.39 | 95.41 ± 0.66 | 95.23 ± 0.87 | 95.02 ± 0.79 | 94.72 ± 1.02 |
| HongHu | OA (%) | 99.45 ± 0.08 | 99.53 ± 0.03 | 99.51 ± 0.05 | 99.47 ± 0.08 | 99.48 ± 0.08 | 99.50 ± 0.05 |
| AA (%) | 98.71 ± 0.23 | 98.99 ± 0.10 | 98.85 ± 0.21 | 98.85 ± 0.18 | 98.86 ± 0.19 | 98.85 ± 0.18 |
| κ (%) | 99.31 ± 0.11 | 99.41 ± 0.04 | 99.38 ± 0.07 | 99.33 ± 0.10 | 99.34 ± 0.10 | 99.37 ± 0.06 |
| PaviaU | OA (%) | 99.44 ± 0.12 | 99.43 ± 0.15 | 99.47 ± 0.10 | 99.50 ± 0.06 | 99.39 ± 0.12 | 99.39 ± 0.08 |
| AA (%) | 98.88 ± 0.31 | 98.89 ± 0.26 | 98.92 ± 0.22 | 99.02 ± 0.10 | 98.82 ± 0.31 | 98.87 ± 0.21 |
| κ (%) | 99.25 ± 0.16 | 99.24 ± 0.20 | 99.29 ± 0.13 | 99.34 ± 0.08 | 99.19 ± 0.16 | 99.19 ± 0.11 |
| Salinas | OA (%) | 99.76 ± 0.05 | 99.84 ± 0.06 | 99.82 ± 0.07 | 99.83 ± 0.08 | 99.82 ± 0.06 | 99.76 ± 0.13 |
| AA (%) | 99.75 ± 0.05 | 99.84 ± 0.05 | 99.82 ± 0.06 | 99.82 ± 0.05 | 99.79 ± 0.07 | 99.78 ± 0.14 |
| κ (%) | 99.75 ± 0.05 | 99.82 ± 0.07 | 99.80 ± 0.08 | 99.81 ± 0.09 | 99.79 ± 0.06 | 99.73 ± 0.14 |
Table 13.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the Indian dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 13.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the Indian dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | S3ARN | PMCN | S3GAN | ViT | SFormer | HFormer | MHCFormer | D2S2BoT |
|---|
| 1 | 52.89 ± 8.80 | 16.00 ± 15.5 | 62.22 ± 13.7 | 6.222 ± 8.52 | 3.554 ± 2.53 | 44.89 ± 11.9 | 42.67 ± 14.7 | 80.00 ± 12.7 |
| 2 | 88.84 ± 4.47 | 90.82 ± 1.85 | 93.00 ± 2.33 | 65.75 ± 10.9 | 76.80 ± 12.8 | 91.87 ± 2.38 | 91.39 ± 2.56 | 85.75 ± 4.03 |
| 3 | 90.95 ± 4.71 | 86.27 ± 4.76 | 90.96 ± 2.68 | 53.16 ± 10.8 | 55.33 ± 14.3 | 87.50 ± 8.96 | 87.99 ± 7.05 | 87.01 ± 9.05 |
| 4 | 53.53 ± 25.0 | 84.74 ± 10.1 | 84.27 ± 11.5 | 21.38 ± 10.4 | 22.76 ± 10.1 | 71.81 ± 12.7 | 76.38 ± 12.5 | 85.00 ± 13.2 |
| 5 | 89.18 ± 4.81 | 90.86 ± 3.11 | 90.23 ± 3.83 | 65.12 ± 8.46 | 75.10 ± 7.97 | 89.77 ± 4.66 | 91.37 ± 2.08 | 90.36 ± 1.46 |
| 6 | 93.12 ± 2.27 | 93.79 ± 1.43 | 94.58 ± 3.06 | 87.97 ± 3.10 | 86.41 ± 4.26 | 94.46 ± 2.88 | 96.39 ± 2.50 | 94.46 ± 1.99 |
| 7 | 73.33 ± 16.2 | 8.888 ± 19.9 | 87.04 ± 7.09 | 17.78 ± 14.7 | 2.222 ± 3.31 | 71.11 ± 18.8 | 82.22 ± 15.6 | 93.33 ± 7.59 |
| 8 | 94.49 ± 5.59 | 99.40 ± 0.46 | 99.79 ± 0.30 | 97.09 ± 2.21 | 93.59 ± 4.15 | 99.87 ± 0.29 | 99.96 ± 0.09 | 99.15 ± 0.88 |
| 9 | 70.53 ± 25.4 | 1.052 ± 2.35 | 56.58 ± 15.1 | 6.316 ± 11.4 | 2.106 ± 4.71 | 70.53 ± 20.9 | 82.11 ± 16.1 | 61.05 ± 38.1 |
| 10 | 78.02 ± 2.22 | 83.68 ± 3.83 | 82.14 ± 1.93 | 61.32 ± 8.43 | 70.69 ± 8.38 | 84.45 ± 2.85 | 83.95 ± 4.10 | 84.51 ± 2.86 |
| 11 | 90.54 ± 3.49 | 93.24 ± 3.30 | 96.30 ± 2.00 | 76.61 ± 3.15 | 83.21 ± 8.12 | 96.06 ± 2.97 | 94.80 ± 2.79 | 93.48 ± 3.11 |
| 12 | 66.16 ± 7.39 | 86.68 ± 6.18 | 89.67 ± 4.45 | 52.98 ± 5.25 | 52.53 ± 7.81 | 87.37 ± 4.86 | 90.91 ± 4.28 | 81.89 ± 7.99 |
| 13 | 96.10 ± 2.53 | 96.80 ± 2.39 | 97.38 ± 0.85 | 86.10 ± 5.75 | 75.10 ± 14.7 | 95.30 ± 3.65 | 98.40 ± 1.78 | 98.00 ± 1.87 |
| 14 | 96.01 ± 2.83 | 97.69 ± 1.38 | 98.15 ± 2.00 | 93.04 ± 2.28 | 88.86 ± 4.63 | 97.50 ± 1.21 | 97.19 ± 2.94 | 97.29 ± 2.00 |
| 15 | 79.52 ± 14.8 | 87.67 ± 6.60 | 88.89 ± 12.6 | 53.81 ± 16.9 | 53.97 ± 14.4 | 90.00 ± 6.72 | 84.50 ± 5.54 | 89.63 ± 6.60 |
| 16 | 35.16 ± 19.8 | 82.86 ± 12.0 | 86.27 ± 9.35 | 38.02 ± 20.7 | 32.09 ± 36.7 | 57.36 ± 23.7 | 87.91 ± 6.73 | 94.51 ± 3.39 |
| OA (%) | 86.80 ± 0.94 | 90.64 ± 1.15 | 92.78 ± 0.78 | 70.73 ± 3.91 | 74.27 ± 4.53 | 91.62 ± 0.98 | 91.91 ± 1.20 | 90.65 ± 1.93 |
| AA (%) | 78.02 ± 2.74 | 75.03 ± 2.77 | 87.34 ± 1.23 | 55.17 ± 5.16 | 54.64 ± 5.67 | 83.12 ± 1.11 | 86.76 ± 2.20 | 88.46 ± 3.29 |
| κ (%) | 84.91 ± 1.09 | 89.31 ± 1.29 | 91.75 ± 0.88 | 66.28 ± 4.58 | 70.34 ± 5.25 | 90.42 ± 1.11 | 90.75 ± 1.37 | 89.33 ± 2.20 |
Table 14.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the Indian dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 14.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the Indian dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | SQSFormer | EATN | CFormer | SSACFormer | CPFormer | DSFormer | LGDRNet | CPMFFormer |
|---|
| 1 | 6.956 ± 3.89 | 65.65 ± 29.9 | 80.98 ± 16.7 | 97.29 ± 2.74 | 69.57 ± 25.2 | 95.22 ± 2.38 | 82.61 ± 10.2 | 96.96 ± 3.64 |
| 2 | 89.10 ± 2.20 | 89.93 ± 2.85 | 94.28 ± 1.88 | 90.58 ± 4.11 | 95.73 ± 1.15 | 91.74 ± 2.11 | 91.88 ± 3.27 | 94.06 ± 2.06 |
| 3 | 86.46 ± 5.63 | 76.00 ± 4.82 | 91.87 ± 2.36 | 88.17 ± 2.01 | 93.95 ± 4.65 | 92.77 ± 3.53 | 92.98 ± 3.57 | 90.60 ± 5.31 |
| 4 | 77.64 ± 8.40 | 78.06 ± 12.9 | 93.99 ± 7.29 | 86.39 ± 14.1 | 85.23 ± 13.5 | 89.28 ± 6.31 | 94.31 ± 8.45 | 91.90 ± 9.81 |
| 5 | 94.16 ± 1.46 | 91.92 ± 2.09 | 91.77 ± 3.81 | 89.75 ± 2.80 | 90.17 ± 1.60 | 91.30 ± 2.45 | 89.86 ± 6.65 | 90.10 ± 2.84 |
| 6 | 98.79 ± 0.50 | 98.27 ± 1.83 | 93.15 ± 1.10 | 99.18 ± 0.25 | 98.70 ± 1.42 | 98.49 ± 1.00 | 94.63 ± 2.12 | 97.31 ± 1.50 |
| 7 | 20.00 ± 9.98 | 85.71 ± 7.58 | 48.22 ± 35.3 | 73.22 ± 48.9 | 98.22 ± 3.57 | 91.43 ± 5.42 | 85.72 ± 19.4 | 99.29 ± 1.60 |
| 8 | 99.92 ± 0.12 | 99.66 ± 0.35 | 99.27 ± 1.19 | 100.0 ± 0.00 | 99.69 ± 0.27 | 100.0 ± 0.00 | 98.95 ± 0.57 | 99.79 ± 0.30 |
| 9 | 7.000 ± 2.74 | 48.00 ± 23.1 | 15.00 ± 16.8 | 47.50 ± 49.9 | 26.25 ± 12.5 | 49.00 ± 14.8 | 65.00 ± 8.16 | 88.00 ± 4.47 |
| 10 | 81.23 ± 5.41 | 86.52 ± 6.71 | 85.55 ± 1.85 | 86.86 ± 4.52 | 90.54 ± 0.71 | 87.99 ± 2.61 | 90.05 ± 2.45 | 91.93 ± 4.97 |
| 11 | 91.22 ± 1.88 | 87.89 ± 2.75 | 97.02 ± 1.29 | 95.61 ± 1.69 | 94.16 ± 3.48 | 95.66 ± 1.12 | 94.69 ± 0.78 | 96.94 ± 1.21 |
| 12 | 88.47 ± 5.20 | 82.19 ± 6.44 | 88.95 ± 6.44 | 93.30 ± 3.18 | 88.20 ± 5.13 | 87.62 ± 0.91 | 87.69 ± 8.09 | 88.40 ± 6.84 |
| 13 | 99.51 ± 0.60 | 99.31 ± 0.27 | 95.24 ± 4.46 | 99.39 ± 0.73 | 98.66 ± 0.83 | 99.61 ± 0.41 | 98.41 ± 1.34 | 99.12 ± 1.70 |
| 14 | 97.86 ± 1.55 | 96.33 ± 1.57 | 99.37 ± 0.13 | 99.78 ± 0.17 | 99.05 ± 0.76 | 98.62 ± 0.56 | 98.83 ± 1.13 | 98.59 ± 0.59 |
| 15 | 90.98 ± 5.61 | 83.52 ± 3.82 | 87.50 ± 7.90 | 96.63 ± 2.41 | 87.83 ± 10.6 | 96.16 ± 1.34 | 95.53 ± 3.41 | 93.63 ± 6.31 |
| 16 | 66.24 ± 18.8 | 91.83 ± 8.31 | 62.63 ± 10.4 | 94.36 ± 4.42 | 94.35 ± 4.15 | 87.31 ± 4.39 | 88.44 ± 10.4 | 92.90 ± 7.15 |
| OA (%) | 90.22 ± 0.48 | 88.96 ± 1.07 | 93.39 ± 0.93 | 93.78 ± 0.94 | 94.08 ± 1.60 | 94.02 ± 0.59 | 93.69 ± 0.22 | 94.85 ± 0.69 |
| AA (%) | 74.72 ± 0.92 | 85.05 ± 4.14 | 82.80 ± 1.98 | 89.87 ± 6.02 | 88.14 ± 3.65 | 90.76 ± 1.26 | 90.60 ± 1.38 | 94.35 ± 0.61 |
| (%) | 88.84 ± 0.55 | 87.41 ± 1.25 | 92.46 ± 1.06 | 92.90 ± 1.07 | 93.26 ± 1.81 | 93.17 ± 0.67 | 92.82 ± 0.26 | 94.13 ± 0.80 |
Table 15.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, Hformer, MHCFormer, and D2S2BoT from the Houston dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 15.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, Hformer, MHCFormer, and D2S2BoT from the Houston dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | S3ARN | PMCN | S3GAN | ViT | SFormer | HFormer | MHCFormer | D2S2BoT |
|---|
| 1 | 96.78 ± 3.75 | 96.68 ± 1.46 | 98.50 ± 0.84 | 95.20 ± 1.81 | 97.66 ± 0.94 | 97.55 ± 1.67 | 97.89 ± 1.15 | 96.57 ± 2.14 |
| 2 | 88.16 ± 4.43 | 91.12 ± 2.42 | 92.86 ± 4.62 | 92.21 ± 3.88 | 91.30 ± 2.67 | 93.32 ± 4.18 | 95.34 ± 4.93 | 94.72 ± 3.29 |
| 3 | 98.83 ± 1.24 | 98.10 ± 1.16 | 99.75 ± 0.18 | 99.97 ± 0.07 | 98.80 ± 1.24 | 98.83 ± 0.87 | 98.77 ± 0.76 | 98.48 ± 1.56 |
| 4 | 92.66 ± 1.10 | 93.24 ± 3.89 | 97.71 ± 2.95 | 94.60 ± 4.65 | 96.10 ± 1.91 | 96.13 ± 3.59 | 97.82 ± 2.46 | 94.70 ± 3.10 |
| 5 | 97.25 ± 3.54 | 99.52 ± 0.38 | 100.0 ± 0.00 | 99.87 ± 0.17 | 99.79 ± 0.29 | 100.0 ± 0.00 | 99.95 ± 0.04 | 99.72 ± 0.22 |
| 6 | 90.41 ± 2.45 | 89.62 ± 3.52 | 89.54 ± 4.17 | 83.02 ± 7.22 | 95.85 ± 4.79 | 88.74 ± 2.16 | 90.25 ± 4.81 | 90.06 ± 4.12 |
| 7 | 83.25 ± 0.23 | 84.30 ± 4.09 | 93.99 ± 4.12 | 76.57 ± 3.73 | 85.53 ± 3.75 | 86.78 ± 4.37 | 93.73 ± 2.66 | 91.30 ± 2.82 |
| 8 | 70.92 ± 4.36 | 73.67 ± 6.20 | 83.80 ± 6.47 | 76.83 ± 5.73 | 74.40 ± 7.38 | 79.08 ± 3.98 | 79.92 ± 5.78 | 80.82 ± 4.51 |
| 9 | 78.71 ± 2.08 | 79.14 ± 3.19 | 85.86 ± 3.81 | 72.43 ± 7.40 | 67.91 ± 8.27 | 80.41 ± 4.19 | 83.56 ± 3.62 | 84.93 ± 5.08 |
| 10 | 93.34 ± 5.88 | 88.84 ± 5.46 | 98.33 ± 1.33 | 83.53 ± 6.04 | 87.14 ± 5.40 | 92.28 ± 4.12 | 95.72 ± 3.55 | 96.41 ± 2.25 |
| 11 | 90.74 ± 6.66 | 91.52 ± 2.49 | 93.91 ± 7.56 | 87.79 ± 7.97 | 89.59 ± 2.31 | 95.34 ± 2.80 | 97.50 ± 2.07 | 95.78 ± 2.98 |
| 12 | 96.28 ± 3.27 | 87.45 ± 4.34 | 89.76 ± 4.89 | 87.18 ± 6.19 | 79.12 ± 7.34 | 93.26 ± 4.38 | 92.53 ± 4.58 | 90.60 ± 6.49 |
| 13 | 82.46 ± 6.01 | 83.71 ± 2.96 | 91.21 ± 3.07 | 66.23 ± 7.16 | 61.22 ± 10.6 | 80.70 ± 2.88 | 93.51 ± 0.81 | 89.24 ± 2.05 |
| 14 | 93.32 ± 9.45 | 98.85 ± 0.59 | 99.06 ± 0.83 | 83.67 ± 11.7 | 99.67 ± 0.49 | 99.38 ± 0.90 | 99.71 ± 0.20 | 98.90 ± 1.94 |
| 15 | 99.23 ± 1.10 | 99.72 ± 0.17 | 100.0 ± 0.00 | 98.36 ± 1.82 | 100.0 ± 0.00 | 100.0 ± 0.00 | 99.88 ± 0.28 | 99.91 ± 0.08 |
| OA (%) | 89.67 ± 0.21 | 89.64 ± 1.00 | 94.05 ± 1.42 | 86.94 ± 1.84 | 87.74 ± 1.98 | 91.96 ± 0.87 | 94.04 ± 0.92 | 93.17 ± 1.24 |
| AA (%) | 90.15 ± 0.45 | 90.37 ± 0.85 | 94.29 ± 1.27 | 86.50 ± 1.86 | 88.27 ± 2.21 | 92.12 ± 0.70 | 94.41 ± 0.93 | 93.48 ± 1.18 |
| (%) | 88.83 ± 0.22 | 88.80 ± 1.08 | 93.57 ± 1.54 | 85.88 ± 1.99 | 86.74 ± 2.14 | 91.30 ± 0.94 | 93.56 ± 1.00 | 92.61 ± 1.34 |
Table 16.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the Houston dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 16.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the Houston dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | SQSFormer | EATN | CFormer | SSACFormer | CPFormer | DSFormer | LGDRNet | CPMFFormer |
|---|
| 1 | 97.18 ± 1.08 | 98.11 ± 1.13 | 95.29 ± 2.98 | 98.43 ± 0.90 | 96.40 ± 1.68 | 98.37 ± 0.58 | 96.29 ± 1.35 | 97.94 ± 0.56 |
| 2 | 95.81 ± 4.25 | 97.92 ± 1.58 | 90.91 ± 2.83 | 92.85 ± 5.72 | 93.38 ± 6.12 | 98.64 ± 0.45 | 97.16 ± 2.07 | 95.49 ± 3.32 |
| 3 | 99.97 ± 0.06 | 99.74 ± 0.12 | 98.17 ± 0.91 | 100.0 ± 0.00 | 100.0 ± 0.00 | 97.05 ± 0.83 | 99.51 ± 0.60 | 98.51 ± 1.30 |
| 4 | 96.61 ± 2.34 | 98.75 ± 1.53 | 93.11 ± 1.99 | 97.81 ± 2.12 | 97.35 ± 2.44 | 97.62 ± 2.62 | 95.79 ± 1.85 | 97.07 ± 3.35 |
| 5 | 100.0 ± 0.00 | 98.87 ± 0.60 | 99.98 ± 0.04 | 100.0 ± 0.00 | 99.62 ± 0.50 | 100.0 ± 0.00 | 98.42 ± 1.06 | 99.94 ± 0.07 |
| 6 | 92.98 ± 3.50 | 88.80 ± 5.65 | 90.16 ± 5.51 | 91.32 ± 4.30 | 86.00 ± 13.9 | 85.35 ± 5.08 | 86.34 ± 6.78 | 93.41 ± 5.82 |
| 7 | 93.11 ± 2.90 | 96.13 ± 2.34 | 96.12 ± 1.58 | 95.54 ± 3.87 | 96.41 ± 1.29 | 97.30 ± 2.44 | 94.10 ± 2.00 | 95.03 ± 2.70 |
| 8 | 80.61 ± 6.06 | 89.74 ± 3.41 | 83.02 ± 9.35 | 82.43 ± 7.00 | 83.42 ± 5.15 | 87.72 ± 8.33 | 88.17 ± 4.40 | 89.42 ± 1.26 |
| 9 | 82.28 ± 2.50 | 86.51 ± 5.35 | 89.54 ± 2.57 | 87.89 ± 5.22 | 92.19 ± 2.36 | 82.15 ± 6.67 | 87.91 ± 4.30 | 90.14 ± 3.80 |
| 10 | 96.53 ± 3.11 | 97.12 ± 2.90 | 99.88 ± 0.24 | 98.89 ± 1.39 | 99.78 ± 0.10 | 92.99 ± 3.04 | 98.08 ± 1.04 | 98.65 ± 0.92 |
| 11 | 96.53 ± 2.10 | 92.15 ± 3.14 | 98.12 ± 2.00 | 97.09 ± 1.20 | 95.04 ± 5.74 | 93.97 ± 4.24 | 93.36 ± 2.08 | 97.22 ± 1.54 |
| 12 | 91.91 ± 3.75 | 87.30 ± 8.34 | 94.36 ± 5.56 | 93.58 ± 4.40 | 93.39 ± 3.68 | 93.79 ± 1.60 | 94.34 ± 3.13 | 95.44 ± 1.26 |
| 13 | 68.06 ± 12.0 | 56.67 ± 8.85 | 88.01 ± 4.60 | 84.44 ± 4.86 | 85.87 ± 2.51 | 90.53 ± 2.43 | 89.98 ± 5.33 | 93.22 ± 1.66 |
| 14 | 98.04 ± 2.60 | 97.71 ± 2.35 | 100.0 ± 0.00 | 99.91 ± 0.13 | 98.42 ± 2.70 | 99.67 ± 0.39 | 97.71 ± 4.00 | 99.44 ± 0.79 |
| 15 | 99.55 ± 0.48 | 99.03 ± 0.68 | 99.96 ± 0.08 | 99.79 ± 0.40 | 99.89 ± 0.23 | 100.0 ± 0.00 | 98.91 ± 1.38 | 99.97 ± 0.07 |
| OA (%) | 93.01 ± 0.84 | 93.54 ± 0.80 | 94.37 ± 1.19 | 94.71 ± 1.43 | 94.81 ± 1.04 | 94.49 ± 1.10 | 94.58 ± 1.06 | 95.93 ± 0.36 |
| AA (%) | 92.61 ± 0.82 | 92.31 ± 0.79 | 94.44 ± 1.23 | 94.66 ± 1.19 | 94.48 ± 1.34 | 94.34 ± 1.11 | 94.40 ± 1.12 | 96.06 ± 0.26 |
| (%) | 92.45 ± 0.91 | 93.01 ± 0.87 | 93.91 ± 1.29 | 94.28 ± 1.54 | 94.39 ± 1.12 | 94.04 ± 1.19 | 94.14 ± 1.14 | 95.61 ± 0.39 |
Table 17.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the HongHu dataset. The optimal and suboptimal results are in red and blue, respectively.
Table 17.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the HongHu dataset. The optimal and suboptimal results are in red and blue, respectively.
| Class | S3ARN | PMCN | S3GAN | ViT | SFormer | HFormer | MHCFormer | D2S2BoT |
|---|
| 1 | 98.90 ± 0.53 | 98.85 ± 0.30 | 98.71 ± 0.87 | 96.25 ± 0.73 | 97.66 ± 0.44 | 98.59 ± 0.56 | 98.44 ± 0.55 | 98.86 ± 0.32 |
| 2 | 91.91 ± 2.33 | 90.32 ± 1.95 | 91.53 ± 0.76 | 78.43 ± 7.80 | 88.05 ± 2.57 | 90.32 ± 1.27 | 93.11 ± 3.32 | 94.24 ± 2.24 |
| 3 | 98.12 ± 0.50 | 97.81 ± 0.38 | 99.09 ± 0.18 | 94.08 ± 1.67 | 96.18 ± 0.44 | 98.34 ± 0.40 | 97.37 ± 0.47 | 98.17 ± 0.27 |
| 4 | 99.84 ± 0.03 | 99.83 ± 0.03 | 99.95 ± 0.02 | 99.39 ± 0.24 | 99.67 ± 0.10 | 99.87 ± 0.13 | 99.63 ± 0.13 | 99.84 ± 0.15 |
| 5 | 96.16 ± 1.59 | 96.49 ± 0.60 | 99.46 ± 0.43 | 83.17 ± 2.47 | 90.28 ± 1.99 | 96.83 ± 1.15 | 89.20 ± 3.84 | 96.18 ± 1.91 |
| 6 | 99.35 ± 0.22 | 99.60 ± 0.19 | 99.87 ± 0.05 | 96.96 ± 0.98 | 99.21 ± 0.18 | 99.74 ± 0.08 | 99.27 ± 0.16 | 99.53 ± 0.16 |
| 7 | 96.92 ± 0.52 | 97.41 ± 0.24 | 98.98 ± 0.36 | 89.30 ± 4.19 | 94.91 ± 1.60 | 97.22 ± 0.69 | 96.04 ± 0.83 | 98.05 ± 0.32 |
| 8 | 83.31 ± 3.88 | 96.04 ± 0.78 | 98.88 ± 0.49 | 54.05 ± 8.83 | 85.55 ± 5.71 | 94.06 ± 3.55 | 86.17 ± 4.68 | 92.16 ± 2.58 |
| 9 | 99.53 ± 0.28 | 99.34 ± 0.34 | 99.50 ± 0.15 | 96.06 ± 1.35 | 98.70 ± 0.68 | 99.17 ± 0.38 | 98.70 ± 0.48 | 99.39 ± 0.12 |
| 10 | 97.81 ± 0.76 | 96.95 ± 0.84 | 98.98 ± 0.35 | 85.59 ± 1.80 | 93.09 ± 0.84 | 97.63 ± 0.76 | 95.77 ± 0.88 | 97.80 ± 0.89 |
| 11 | 95.75 ± 1.78 | 96.48 ± 0.60 | 98.66 ± 0.48 | 81.27 ± 3.97 | 91.31 ± 4.02 | 96.21 ± 1.22 | 94.95 ± 1.65 | 97.59 ± 0.48 |
| 12 | 93.17 ± 2.39 | 95.82 ± 0.70 | 98.44 ± 0.53 | 71.46 ± 4.04 | 88.13 ± 1.46 | 95.49 ± 2.36 | 91.21 ± 1.06 | 95.42 ± 2.13 |
| 13 | 96.71 ± 0.52 | 96.63 ± 1.16 | 99.07 ± 0.33 | 81.96 ± 3.76 | 94.12 ± 1.23 | 97.57 ± 0.95 | 94.96 ± 1.64 | 97.76 ± 0.95 |
| 14 | 97.64 ± 0.56 | 96.45 ± 0.75 | 98.57 ± 0.28 | 86.64 ± 4.94 | 92.58 ± 1.44 | 95.62 ± 2.00 | 97.05 ± 0.78 | 98.11 ± 0.72 |
| 15 | 94.21 ± 4.33 | 94.15 ± 2.10 | 95.17 ± 3.62 | 83.71 ± 2.56 | 84.04 ± 10.9 | 96.13 ± 3.17 | 92.64 ± 4.28 | 94.19 ± 4.90 |
| 16 | 98.96 ± 0.59 | 98.05 ± 0.91 | 99.22 ± 0.50 | 92.88 ± 0.71 | 96.45 ± 1.48 | 98.51 ± 1.15 | 98.69 ± 0.83 | 98.11 ± 0.94 |
| 17 | 97.55 ± 0.58 | 97.82 ± 0.77 | 98.84 ± 0.92 | 82.99 ± 3.35 | 92.81 ± 2.14 | 98.82 ± 0.52 | 92.82 ± 2.47 | 98.34 ± 0.75 |
| 18 | 92.30 ± 3.29 | 95.77 ± 0.96 | 96.85 ± 1.09 | 88.43 ± 6.90 | 93.38 ± 2.86 | 96.45 ± 2.02 | 94.99 ± 2.21 | 95.91 ± 2.27 |
| 19 | 96.54 ± 1.41 | 96.65 ± 1.24 | 97.36 ± 0.86 | 90.11 ± 4.08 | 94.49 ± 0.89 | 97.69 ± 0.50 | 96.69 ± 1.61 | 97.75 ± 0.32 |
| 20 | 96.55 ± 1.24 | 94.83 ± 1.94 | 97.54 ± 1.25 | 84.91 ± 2.39 | 91.32 ± 2.73 | 95.66 ± 3.14 | 94.62 ± 2.42 | 95.56 ± 1.71 |
| 21 | 85.37 ± 5.96 | 95.65 ± 1.50 | 97.73 ± 1.35 | 56.11 ± 18.0 | 88.79 ± 2.35 | 96.19 ± 2.53 | 83.55 ± 3.48 | 92.99 ± 3.73 |
| 22 | 96.82 ± 0.43 | 96.81 ± 1.46 | 99.34 ± 0.40 | 84.94 ± 6.60 | 90.68 ± 2.65 | 95.60 ± 2.78 | 91.67 ± 4.76 | 97.78 ± 1.15 |
| OA (%) | 98.30 ± 0.11 | 98.52 ± 0.09 | 99.34 ± 0.09 | 93.17 ± 0.72 | 96.91 ± 0.36 | 98.63 ± 0.25 | 97.65 ± 0.22 | 98.75 ± 0.10 |
| AA (%) | 95.61 ± 0.48 | 96.72 ± 0.14 | 98.25 ± 0.07 | 84.49 ± 1.48 | 92.79 ± 0.98 | 96.90 ± 0.35 | 94.43 ± 0.72 | 96.99 ± 0.33 |
| (%) | 97.85 ± 0.14 | 98.12 ± 0.11 | 99.17 ± 0.17 | 91.36 ± 0.91 | 96.10 ± 0.46 | 98.27 ± 0.31 | 97.03 ± 0.29 | 98.42 ± 0.13 |
Table 18.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the HongHu dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 18.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the HongHu dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | SQSFormer | EATN | CFormer | SSACFormer | CPFormer | DSFormer | LGDRNet | CPMFFormer |
|---|
| 1 | 98.39 ± 0.35 | 98.13 ± 0.46 | 99.49 ± 0.19 | 99.42 ± 0.15 | 99.29 ± 0.50 | 99.21 ± 0.58 | 99.19 ± 0.36 | 99.45 ± 0.18 |
| 2 | 88.42 ± 1.76 | 87.28 ± 4.91 | 93.07 ± 2.02 | 96.24 ± 1.95 | 95.54 ± 0.67 | 95.64 ± 0.79 | 96.56 ± 1.69 | 94.89 ± 1.21 |
| 3 | 97.04 ± 0.73 | 96.70 ± 1.30 | 98.85 ± 0.39 | 99.10 ± 0.13 | 98.79 ± 0.36 | 98.79 ± 0.30 | 98.96 ± 0.16 | 99.04 ± 0.19 |
| 4 | 99.76 ± 0.14 | 99.83 ± 0.02 | 99.97 ± 0.02 | 99.99 ± 0.04 | 99.90 ± 0.07 | 99.91 ± 0.03 | 99.95 ± 0.02 | 99.98 ± 0.02 |
| 5 | 94.31 ± 2.76 | 88.68 ± 4.49 | 99.31 ± 0.58 | 98.95 ± 0.43 | 99.13 ± 0.88 | 97.30 ± 0.54 | 97.63 ± 0.93 | 99.57 ± 0.30 |
| 6 | 99.09 ± 0.30 | 99.48 ± 0.19 | 99.83 ± 0.07 | 99.88 ± 0.13 | 99.71 ± 0.13 | 99.38 ± 0.05 | 99.64 ± 0.13 | 99.87 ± 0.04 |
| 7 | 97.16 ± 1.07 | 95.82 ± 0.88 | 98.88 ± 0.20 | 99.52 ± 0.28 | 98.45 ± 0.48 | 98.12 ± 0.21 | 98.73 ± 0.50 | 99.20 ± 0.32 |
| 8 | 92.21 ± 5.13 | 78.58 ± 6.89 | 97.64 ± 1.97 | 99.21 ± 0.46 | 98.40 ± 1.39 | 91.46 ± 1.24 | 94.05 ± 2.41 | 99.45 ± 0.77 |
| 9 | 99.31 ± 0.21 | 98.38 ± 0.61 | 99.81 ± 0.26 | 99.70 ± 0.10 | 99.65 ± 0.12 | 99.64 ± 0.14 | 99.50 ± 0.14 | 99.79 ± 0.16 |
| 10 | 96.22 ± 1.28 | 96.54 ± 0.80 | 98.98 ± 0.41 | 98.49 ± 0.24 | 97.89 ± 0.93 | 98.10 ± 0.33 | 98.42 ± 0.34 | 98.76 ± 0.35 |
| 11 | 94.64 ± 1.19 | 95.26 ± 2.36 | 98.66 ± 0.62 | 98.57 ± 0.24 | 98.05 ± 0.46 | 97.49 ± 0.65 | 98.33 ± 0.39 | 98.58 ± 0.46 |
| 12 | 94.37 ± 1.64 | 93.08 ± 1.30 | 98.53 ± 0.72 | 99.12 ± 0.66 | 98.47 ± 1.13 | 95.50 ± 0.94 | 97.99 ± 0.42 | 99.18 ± 0.40 |
| 13 | 94.33 ± 1.72 | 95.04 ± 0.79 | 99.01 ± 0.40 | 98.63 ± 0.41 | 98.94 ± 0.34 | 97.12 ± 0.29 | 98.32 ± 0.45 | 99.13 ± 0.31 |
| 14 | 98.11 ± 0.54 | 96.14 ± 1.54 | 99.18 ± 0.45 | 98.46 ± 0.36 | 98.17 ± 0.25 | 97.85 ± 0.76 | 98.99 ± 0.13 | 98.73 ± 0.80 |
| 15 | 87.67 ± 1.95 | 91.50 ± 4.34 | 95.73 ± 2.59 | 97.80 ± 3.15 | 95.83 ± 1.71 | 96.51 ± 1.34 | 94.63 ± 3.98 | 99.38 ± 0.36 |
| 16 | 98.04 ± 1.04 | 97.81 ± 0.83 | 99.38 ± 0.42 | 99.06 ± 0.39 | 99.37 ± 0.17 | 98.88 ± 0.76 | 99.61 ± 0.40 | 99.50 ± 0.38 |
| 17 | 97.27 ± 1.39 | 94.65 ± 1.75 | 99.30 ± 0.49 | 99.30 ± 0.48 | 99.34 ± 0.40 | 97.86 ± 1.33 | 99.08 ± 0.49 | 99.48 ± 0.27 |
| 18 | 94.38 ± 1.90 | 97.53 ± 0.76 | 96.85 ± 1.64 | 99.19 ± 1.11 | 97.49 ± 0.94 | 97.45 ± 0.55 | 97.68 ± 0.48 | 97.96 ± 0.41 |
| 19 | 95.16 ± 0.59 | 95.48 ± 0.56 | 98.41 ± 0.44 | 96.38 ± 1.00 | 97.48 ± 1.25 | 97.34 ± 1.09 | 97.97 ± 0.49 | 99.17 ± 0.39 |
| 20 | 92.72 ± 1.85 | 93.88 ± .57 | 98.92 ± 0.54 | 97.65 ± 0.54 | 98.56 ± 0.82 | 96.15 ± 0.94 | 97.18 ± 1.02 | 98.00 ± 1.60 |
| 21 | 89.22 ± 9.14 | 62.63 ± 8.69 | 97.68 ± 1.47 | 99.85 ± 0.50 | 95.78 ± 6.76 | 93.15 ± 0.73 | 97.08 ± 0.83 | 99.80 ± 0.20 |
| 22 | 95.67 ± 2.16 | 94.82 ± 1.02 | 98.40 ± 1.29 | 97.70 ± 0.85 | 99.28 ± 0.59 | 96.74 ± 2.21 | 98.85 ± 0.36 | 98.96 ± 0.90 |
| OA (%) | 97.93 ± 0.39 | 97.55 ± 0.16 | 99.41 ± 0.06 | 99.43 ± 0.05 | 99.26 ± 0.10 | 98.83 ± 0.07 | 99.22 ± 0.04 | 99.53 ± 0.03 |
| AA (%) | 95.16 ± 1.03 | 93.06 ± 0.62 | 98.45 ± 0.21 | 98.74 ± 0.19 | 98.34 ± 0.41 | 97.25 ± 0.16 | 98.11 ± 0.19 | 98.99 ± 0.10 |
| (%) | 97.38 ± 0.49 | 96.91 ± 0.20 | 99.25 ± 0.06 | 99.28 ± 0.07 | 99.06 ± 0.13 | 98.52 ± 0.09 | 99.01 ± 0.05 | 99.41 ± 0.04 |
Table 19.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the PaviaU dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 19.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the PaviaU dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | S3ARN | PMCN | S3GAN | ViT | SFormer | HFormer | MHCFormer | D2S2BoT |
|---|
| 1 | 97.08 ± 1.20 | 97.55 ± 0.33 | 99.62 ± 0.26 | 95.36 ± 1.50 | 95.91 ± 1.20 | 98.98 ± 0.43 | 99.37 ± 0.19 | 99.46 ± 0.38 |
| 2 | 99.85 ± 0.15 | 99.67 ± 0.08 | 99.98 ± 0.02 | 99.04 ± 0.67 | 99.73 ± 0.11 | 99.99 ± 0.01 | 99.83 ± 0.07 | 99.96 ± 0.04 |
| 3 | 90.97 ± 5.18 | 91.52 ± 2.41 | 94.52 ± 1.89 | 78.37 ± 1.78 | 81.00 ± 5.20 | 94.58 ± 1.15 | 94.04 ± 2.87 | 96.84 ± 1.52 |
| 4 | 98.65 ± 0.66 | 95.27 ± 1.32 | 97.62 ± 1.76 | 94.66 ± 2.06 | 95.62 ± 1.98 | 97.39 ± 1.15 | 98.09 ± 1.66 | 96.68 ± 1.26 |
| 5 | 99.89 ± 0.15 | 98.59 ± 0.96 | 100.0 ± 0.00 | 99.59 ± 0.71 | 99.98 ± 0.04 | 99.71 ± 0.44 | 99.95 ± 0.07 | 99.77 ± 0.39 |
| 6 | 99.52 ± 0.46 | 98.17 ± 1.47 | 99.92 ± 0.14 | 95.43 ± 2.29 | 97.50 ± 0.48 | 100.0 ± 0.00 | 99.59 ± 0.23 | 99.65 ± 0.49 |
| 7 | 92.39 ± 1.75 | 98.40 ± 0.78 | 100.0 ± 0.00 | 82.95 ± 10.7 | 93.95 ± 1.39 | 99.23 ± 1.36 | 98.65 ± 1.42 | 99.25 ± 0.96 |
| 8 | 97.20 ± 1.08 | 92.21 ± 3.90 | 96.51 ± 1.88 | 83.92 ± 6.00 | 87.78 ± 1.54 | 95.49 ± 2.30 | 97.24 ± 1.45 | 96.80 ± 0.97 |
| 9 | 99.20 ± 0.67 | 93.81 ± 1.51 | 97.38 ± 2.54 | 90.09 ± 7.85 | 95.43 ± 2.63 | 96.96 ± 1.29 | 99.18 ± 0.48 | 96.72 ± 0.16 |
| OA (%) | 98.39 ± 0.51 | 97.60 ± 0.44 | 99.13 ± 0.05 | 94.73 ± 0.94 | 96.37 ± 0.30 | 98.90 ± 0.25 | 99.05 ± 0.23 | 99.09 ± 0.21 |
| AA (%) | 97.20 ± 0.85 | 96.13 ± 0.58 | 98.39 ± 0.16 | 91.05 ± 1.64 | 94.10 ± 0.77 | 98.04 ± 0.43 | 98.44 ± 0.42 | 98.35 ± 0.35 |
| (%) | 97.86 ± 0.68 | 96.82 ± 0.59 | 98.84 ± 0.07 | 93.00 ± 1.25 | 95.17 ± 0.40 | 98.54 ± 0.33 | 98.74 ± 0.30 | 98.79 ± 0.28 |
Table 20.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the PaviaU dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 20.
Classification performances obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the PaviaU dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | SQSFormer | EATN | CFormer | SSACFormer | CPFormer | DSFormer | LGDRNet | CPMFFormer |
|---|
| 1 | 98.00 ± 1.32 | 96.24 ± 1.37 | 99.83 ± 0.20 | 99.16 ± 0.37 | 98.19 ± 1.67 | 99.28 ± 0.49 | 98.13 ± 0.81 | 99.78 ± 0.16 |
| 2 | 99.25 ± 0.18 | 99.19 ± 0.33 | 99.92 ± 0.06 | 100.0 ± 0.00 | 99.90 ± 0.14 | 99.97 ± 0.03 | 99.89 ± 0.05 | 99.96 ± 0.06 |
| 3 | 86.40 ± 2.44 | 84.27 ± 4.84 | 98.90 ± 1.10 | 93.49 ± 4.58 | 90.90 ± 7.28 | 96.82 ± 1.57 | 95.28 ± 2.39 | 97.74 ± 1.31 |
| 4 | 96.91 ± 1.75 | 96.27 ± 1.54 | 92.24 ± 2.04 | 98.33 ± 0.33 | 98.69 ± 1.10 | 98.15 ± 0.53 | 95.89 ± 1.79 | 97.75 ± 0.68 |
| 5 | 99.97 ± 0.07 | 99.70 ± 0.55 | 99.76 ± 0.10 | 100.0 ± 0.00 | 99.96 ± 0.10 | 99.98 ± 0.04 | 98.93 ± 0.94 | 99.45 ± 0.56 |
| 6 | 98.75 ± 0.72 | 97.22 ± 0.89 | 100.0 ± 0.00 | 99.90 ± 0.20 | 99.85 ± 0.14 | 99.05 ± 1.50 | 99.44 ± 0.59 | 99.96 ± 0.06 |
| 7 | 98.17 ± 2.07 | 92.48 ± 1.34 | 99.91 ± 0.13 | 99.98 ± 0.04 | 79.40 ± 44.4 | 98.42 ± 0.60 | 93.46 ± 3.75 | 99.85 ± 0.16 |
| 8 | 94.33 ± 1.47 | 91.10 ± 1.22 | 99.07 ± 0.64 | 93.65 ± 2.99 | 94.01 ± 4.63 | 97.15 ± 1.49 | 95.50 ± 0.51 | 98.85 ± 0.60 |
| 9 | 99.45 ± 0.37 | 99.45 ± 0.67 | 88.22 ± 2.54 | 99.89 ± 0.11 | 97.70 ± 2.85 | 97.50 ± 0.12 | 96.18 ± 1.86 | 97.89 ± 0.29 |
| OA (%) | 97.77 ± 0.39 | 96.68 ± 0.42 | 98.98 ± 0.15 | 98.87 ± 0.39 | 97.91 ± 1.89 | 99.13 ± 0.14 | 98.36 ± 0.26 | 99.50 ± 0.06 |
| AA (%) | 96.80 ± 0.65 | 95.10 ± 0.59 | 97.54 ± 0.43 | 98.27 ± 0.68 | 95.40 ± 5.92 | 98.48 ± 0.15 | 96.97 ± 0.62 | 99.02 ± 0.10 |
| (%) | 97.05 ± 0.52 | 95.59 ± 0.56 | 98.64 ± 0.19 | 98.50 ± 0.52 | 97.22 ± 2.53 | 98.84 ± 0.19 | 97.82 ± 0.34 | 99.34 ± 0.08 |
Table 21.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the Salinas dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 21.
Classification performances obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from the Salinas dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | S3ARN | PMCN | S3GAN | ViT | SFormer | HFormer | MHCFormer | D2S2BoT |
|---|
| 1 | 98.84 ± 1.29 | 99.50 ± 0.91 | 98.75 ± 1.38 | 99.13 ± 0.35 | 99.82 ± 0.19 | 99.48 ± 0.58 | 99.83 ± 0.28 | 99.95 ± 0.06 |
| 2 | 99.12 ± 0.69 | 99.87 ± 0.12 | 99.93 ± 0.06 | 99.81 ± 0.15 | 99.93 ± 0.11 | 99.92 ± 0.14 | 99.53 ± 0.46 | 99.92 ± 0.14 |
| 3 | 96.70 ± 2.19 | 99.93 ± 0.09 | 99.66 ± 0.22 | 97.42 ± 3.94 | 99.88 ± 0.20 | 100.0 ± 0.00 | 99.88 ± 0.11 | 99.99 ± 0.02 |
| 4 | 97.83 ± 1.06 | 97.78 ± 1.99 | 99.51 ± 0.15 | 97.51 ± 2.69 | 98.26 ± 0.34 | 99.40 ± 0.40 | 98.84 ± 0.74 | 99.22 ± 0.22 |
| 5 | 96.78 ± 2.20 | 98.96 ± 0.72 | 99.01 ± 0.45 | 97.83 ± 1.70 | 97.54 ± 1.03 | 99.71 ± 0.26 | 99.76 ± 0.22 | 99.53 ± 0.39 |
| 6 | 99.73 ± 0.58 | 99.87 ± 0.05 | 99.96 ± 0.05 | 99.95 ± 0.04 | 99.96 ± 0.04 | 99.86 ± 0.22 | 99.97 ± 0.04 | 99.96 ± 0.04 |
| 7 | 98.46 ± 1.69 | 99.77 ± 0.13 | 99.84 ± 0.03 | 98.95 ± 1.06 | 99.99 ± 0.01 | 99.76 ± 0.19 | 99.94 ± 0.08 | 99.86 ± 0.13 |
| 8 | 96.39 ± 2.07 | 97.93 ± 1.30 | 99.58 ± 0.35 | 93.90 ± 1.94 | 95.92 ± 0.62 | 99.23 ± 0.55 | 97.80 ± 0.61 | 99.24 ± 0.37 |
| 9 | 99.68 ± 0.16 | 99.97 ± 0.03 | 99.91 ± 0.12 | 99.92 ± 0.09 | 99.95 ± 0.06 | 99.98 ± 0.03 | 99.99 ± 0.01 | 100.0 ± 0.00 |
| 10 | 98.49 ± 0.69 | 99.10 ± 0.41 | 99.46 ± 0.61 | 97.43 ± 0.67 | 98.72 ± 0.88 | 99.82 ± 0.26 | 98.76 ± 0.55 | 99.51 ± 0.46 |
| 11 | 96.14 ± 3.61 | 99.56 ± 0.62 | 99.08 ± 0.31 | 98.95 ± 0.89 | 99.41 ± 0.79 | 99.56 ± 0.27 | 99.50 ± 0.21 | 99.71 ± 0.29 |
| 12 | 99.32 ± 0.80 | 99.25 ± 0.59 | 99.88 ± 0.17 | 99.33 ± 0.44 | 99.67 ± 0.41 | 99.82 ± 0.24 | 100.0 ± 0.00 | 99.89 ± 0.10 |
| 13 | 96.01 ± 4.84 | 97.32 ± 0.78 | 99.37 ± 0.32 | 96.01 ± 3.44 | 98.33 ± 1.20 | 98.84 ± 0.43 | 99.60 ± 0.37 | 99.58 ± 0.27 |
| 14 | 97.83 ± 1.77 | 98.55 ± 0.75 | 98.22 ± 2.10 | 97.75 ± 1.37 | 98.53 ± 0.64 | 98.55 ± 1.30 | 99.20 ± 0.90 | 99.14 ± 0.78 |
| 15 | 92.17 ± 3.63 | 96.68 ± 1.76 | 99.76 ± 0.09 | 89.71 ± 0.85 | 94.20 ± 1.96 | 98.43 ± 1.31 | 95.79 ± 0.89 | 98.92 ± 0.28 |
| 16 | 96.53 ± 5.96 | 99.43 ± 0.54 | 98.76 ± 0.59 | 98.93 ± 1.36 | 99.07 ± 0.71 | 99.20 ± 1.39 | 99.17 ± 1.27 | 99.54 ± 0.55 |
| OA (%) | 97.18 ± 1.37 | 98.77 ± 0.27 | 99.59 ± 0.07 | 96.61 ± 0.46 | 97.99 ± 0.17 | 99.44 ± 0.28 | 98.75 ± 0.16 | 99.55 ± 0.07 |
| AA (%) | 97.50 ± 1.37 | 98.97 ± 0.21 | 99.42 ± 0.09 | 97.66 ± 0.23 | 98.70 ± 0.23 | 99.47 ± 0.23 | 99.22 ± 0.08 | 99.62 ± 0.09 |
| (%) | 96.86 ± 1.53 | 98.64 ± 0.30 | 99.54 ± 0.08 | 96.22 ± 0.51 | 97.76 ± 0.19 | 99.38 ± 0.32 | 98.61 ± 0.18 | 99.50 ± 0.08 |
Table 22.
Classification performances obtained by SQSFormer, ENTA, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the Salinas dataset. The optimal results and suboptimal results are in red and blue, respectively.
Table 22.
Classification performances obtained by SQSFormer, ENTA, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from the Salinas dataset. The optimal results and suboptimal results are in red and blue, respectively.
| Class | SQSFormer | ENTA | CFormer | SSACFormer | CPFormer | DSFormer | LGDRNet | CPMFFormer |
|---|
| 1 | 99.89 ± 0.11 | 99.97 ± 0.07 | 100.0 ± 0.00 | 100.0 ± 0.00 | 98.91 ± 1.17 | 99.43 ± 0.85 | 99.92 ± 0.18 | 99.96 ± 0.09 |
| 2 | 99.92 ± 0.08 | 99.90 ± 0.21 | 100.0 ± 0.00 | 100.0 ± 0.00 | 99.20 ± 1.40 | 100.0 ± 0.00 | 99.75 ± 0.34 | 100.0 ± 0.00 |
| 3 | 100.0 ± 0.00 | 99.55 ± 0.97 | 99.93 ± 0.11 | 100.0 ± 0.00 | 98.33 ± 3.45 | 100.0 ± 0.00 | 99.18 ± 1.67 | 100.0 ± 0.00 |
| 4 | 99.45 ± 0.41 | 99.86 ± 0.12 | 99.11 ± 1.11 | 99.83 ± 0.12 | 99.15 ± 0.98 | 99.70 ± 0.29 | 98.52 ± 0.97 | 99.47 ± 0.39 |
| 5 | 98.21 ± 1.10 | 97.40 ± 2.99 | 97.29 ± 3.25 | 99.27 ± 0.26 | 99.15 ± 0.57 | 99.83 ± 0.17 | 99.54 ± 0.30 | 99.69 ± 0.26 |
| 6 | 99.94 ± 0.06 | 99.98 ± 0.02 | 99.49 ± 0.98 | 99.99 ± 0.02 | 99.90 ± 0.05 | 100.0 ± 0.00 | 99.65 ± 0.67 | 100.0 ± 0.00 |
| 7 | 99.94 ± 0.07 | 99.92 ± 0.07 | 99.99 ± 0.03 | 100.0 ± 0.00 | 99.65 ± 0.41 | 99.99 ± 0.01 | 98.87 ± 0.97 | 99.97 ± 0.05 |
| 8 | 94.63 ± 1.66 | 91.98 ± 2.73 | 98.89 ± 1.41 | 99.05 ± 0.91 | 96.52 ± 4.79 | 97.99 ± 1.17 | 97.84 ± 1.02 | 99.62 ± 0.32 |
| 9 | 100.0 ± 0.00 | 99.95 ± 0.05 | 100.0 ± 0.00 | 100.0 ± 0.00 | 99.98 ± 0.04 | 100.0 ± 0.00 | 99.81 ± 0.11 | 100.0 ± 0.00 |
| 10 | 98.53 ± 0.99 | 98.55 ± 0.61 | 98.58 ± 1.68 | 99.74 ± 0.24 | 99.02 ± 0.75 | 99.02 ± 0.79 | 98.16 ± 0.52 | 99.89 ± 0.06 |
| 11 | 99.42 ± 0.28 | 98.90 ± 0.95 | 99.74 ± 0.48 | 99.85 ± 0.23 | 99.19 ± 0.76 | 99.93 ± 0.08 | 98.71 ± 0.74 | 99.89 ± 0.10 |
| 12 | 99.80 ± 0.11 | 99.99 ± 0.02 | 99.41 ± 0.38 | 100.0 ± 0.00 | 99.75 ± 0.33 | 99.98 ± 0.03 | 99.98 ± 0.04 | 99.74 ± 0.33 |
| 13 | 98.34 ± 1.87 | 99.54 ± 0.46 | 98.23 ± 1.70 | 98.75 ± 0.99 | 99.43 ± 0.56 | 100.0 ± 0.00 | 98.86 ± 0.99 | 99.78 ± 0.28 |
| 14 | 94.51 ± 4.43 | 98.99 ± 0.98 | 99.23 ± 0.95 | 98.73 ± 0.83 | 97.18 ± 2.96 | 99.68 ± 0.47 | 99.27 ± 0.97 | 99.83 ± 0.23 |
| 15 | 92.28 ± 1.89 | 87.19 ± 4.48 | 98.25 ± 1.11 | 98.38 ± 1.24 | 99.59 ± 0.29 | 97.29 ± 0.78 | 97.14 ± 1.17 | 99.92 ± 0.11 |
| 16 | 98.79 ± 0.92 | 98.88 ± 0.58 | 99.87 ± 0.24 | 99.98 ± 0.03 | 99.31 ± 0.57 | 99.93 ± 0.09 | 99.23 ± 1.13 | 99.68 ± 0.32 |
| OA (%) | 97.44 ± 0.27 | 96.27 ± 0.41 | 99.17 ± 0.24 | 99.48 ± 0.14 | 98.80 ± 1.03 | 99.11 ± 0.24 | 98.74 ± 0.24 | 99.84 ± 0.06 |
| AA (%) | 98.35 ± 0.22 | 98.16 ± 0.24 | 99.25 ± 0.32 | 99.60 ± 0.07 | 99.02 ± 0.34 | 99.55 ± 0.10 | 99.03 ± 0.19 | 99.84 ± 0.05 |
| (%) | 97.15 ± 0.30 | 95.84 ± 0.45 | 99.08 ± 0.26 | 99.42 ± 0.15 | 98.66 ± 1.14 | 99.01 ± 0.26 | 98.59 ± 0.27 | 99.82 ± 0.07 |
Table 23.
Full-scene classification performance obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from five public HSI datasets. The optimal results and suboptimal results are in red and blue, respectively.
Table 23.
Full-scene classification performance obtained by S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT from five public HSI datasets. The optimal results and suboptimal results are in red and blue, respectively.
| Datasets | Metrics | S3ARN | PMCN | S3GAN | ViT | SFormer | HFormer | MHCFormer | D2S2BoT |
|---|
| Indian | MI (%) | 36.87 ± 5.30 | 89.33 ± 1.18 | 79.99 ± 0.71 | 50.83 ± 6.78 | 62.02 ± 4.52 | 45.74 ± 3.47 | 67.55 ± 1.78 | 50.63 ± 4.53 |
| BF1 (%) | 63.39 ± 2.25 | 98.26 ± 0.48 | 97.90 ± 1.00 | 78.23 ± 3.73 | 83.05 ± 3.40 | 66.68 ± 1.34 | 85.37 ± 0.83 | 68.45 ± 0.62 |
| SSIM (%) | 53.93 ± 5.62 | 88.92 ± 0.63 | 88.97 ± 0.90 | 66.35 ± 2.47 | 72.35 ± 2.85 | 68.99 ± 1.51 | 73.47 ± 0.72 | 58.72 ± 0.77 |
| Houston | MI (%) | 44.51 ± 5.21 | 91.00 ± 0.49 | 81.41 ± 0.97 | 65.50 ± 5.05 | 73.69 ± 3.51 | 49.62 ± 4.41 | 66.18 ± 1.13 | 60.81 ± 1.55 |
| BF1 (%) | 95.86 ± 1.34 | 96.74 ± 0.23 | 96.98 ± 0.12 | 96.78 ± 0.31 | 97.04 ± 0.05 | 94.37 ± 1.49 | 96.81 ± 0.36 | 95.63 ± 0.23 |
| SSIM (%) | 94.40 ± 1.43 | 98.34 ± 0.05 | 98.56 ± 0.04 | 98.08 ± 0.14 | 98.20 ± 0.10 | 97.24 ± 0.12 | 98.05 ± 0.07 | 96.90 ± 0.14 |
| HongHu | MI (%) | 61.16 ± 8.24 | 96.97 ± 0.22 | 94.98 ± 0.49 | 83.96 ± 1.13 | 90.51 ± 0.74 | 52.68 ± 2.21 | 66.03 ± 3.14 | 45.44 ± 2.05 |
| BF1 (%) | 26.40 ± 5.74 | 97.32 ± 0.08 | 95.36 ± 1.39 | 53.36 ± 3.36 | 77.59 ± 2.58 | 20.60 ± 1.38 | 26.49 ± 0.70 | 16.32 ± 2.22 |
| SSIM (%) | 26.62 ± 10.1 | 91.42 ± 0.02 | 90.12 ± 0.75 | 66.89 ± 2.24 | 78.95 ± 1.31 | 24.25 ± 9.36 | 37.17 ± 3.70 | 13.52 ± 0.21 |
| PaviaU | MI (%) | 51.99 ± 2.18 | 90.02 ± 0.61 | 77.37 ± 1.79 | 63.28 ± 1.97 | 69.59 ± 2.10 | 53.99 ± 2.28 | 66.56 ± 0.73 | 52.35 ± 1.86 |
| BF1 (%) | 64.96 ± 3.38 | 84.61 ± 0.30 | 85.21 ± 0.16 | 85.57 ± 1.29 | 87.03 ± 0.78 | 72.66 ± 1.13 | 77.30 ± 0.75 | 66.68 ± 0.82 |
| SSIM (%) | 69.03 ± 0.86 | 84.73 ± 0.41 | 85.56 ± 0.08 | 81.64 ± 0.78 | 83.40 ± 0.20 | 71.59 ± 0.60 | 75.47 ± 0.89 | 69.54 ± 0.34 |
| Salinas | MI (%) | 51.64 ± 5.72 | 96.05 ± 0.28 | 94.54 ± 0.39 | 82.53 ± 1.54 | 89.10 ± 3.18 | 51.58 ± 1.16 | 71.83 ± 1.83 | 50.82 ± 3.08 |
| BF1 (%) | 29.40 ± 1.59 | 97.11 ± 0.14 | 96.48 ± 0.60 | 81.43 ± 1.99 | 89.38 ± 0.52 | 33.26 ± 1.14 | 49.25 ± 1.73 | 27.54 ± 0.63 |
| SSIM (%) | 55.38 ± 2.14 | 94.19 ± 0.22 | 93.44 ± 0.63 | 85.22 ± 1.63 | 88.79 ± 0.47 | 58.38 ± 0.54 | 65.33 ± 1.91 | 54.65 ± 0.61 |
Table 24.
Full-scene classification performance obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from five public HSI datasets. The optimal results and suboptimal results are in red and blue, respectively.
Table 24.
Full-scene classification performance obtained by SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer from five public HSI datasets. The optimal results and suboptimal results are in red and blue, respectively.
| Datasets | Metrics | SQSFormer | EATN | CFormer | SSACFormer | CPFormer | DSFormer | LGDRNet | CPMFFormer |
|---|
| Indian | MI (%) | 78.65 ± 1.22 | 76.89 ± 0.84 | 72.78 ± 2.79 | 83.54 ± 2.75 | 80.96 ± 2.69 | 88.53 ± 0.83 | 87.34 ± 1.13 | 91.78 ± 0.95 |
| BF1 (%) | 96.21 ± 0.76 | 91.00 ± 0.66 | 93.93 ± 1.62 | 97.19 ± 1.15 | 97.63 ± 0.64 | 97.96 ± 0.69 | 98.18 ± 0.36 | 99.17 ± 0.10 |
| SSIM (%) | 86.64 ± 0.73 | 81.74 ± 0.95 | 82.91 ± 1.54 | 88.54 ± 1.49 | 87.97 ± 0.96 | 89.31 ± 0.87 | 87.66 ± 0.78 | 92.73 ± 0.39 |
| Houston | MI (%) | 82.25 ± 0.84 | 73.20 ± 1.81 | 79.67 ± 0.75 | 83.48 ± 1.41 | 79.01 ± 2.47 | 85.40 ± 0.88 | 89.22 ± 1.30 | 91.31 ± 0.44 |
| BF1 (%) | 96.77 ± 0.23 | 97.02 ± 0.13 | 96.99 ± 0.06 | 96.85 ± 0.32 | 97.04 ± 0.41 | 96.90 ± 0.15 | 97.09 ± 0.20 | 97.12 ± 0.17 |
| SSIM (%) | 98.44 ± 0.06 | 98.47 ± 0.05 | 98.46 ± 0.04 | 98.43 ± 0.07 | 98.44 ± 0.08 | 98.48 ± 0.05 | 98.44 ± 0.11 | 98.62 ± 0.05 |
| HongHu | MI (%) | 92.67 ± 0.46 | 91.18 ± 0.37 | 92.82 ± 0.41 | 97.19 ± 0.26 | 96.57 ± 0.29 | 96.24 ± 0.08 | 96.29 ± 0.14 | 97.66 ± 0.11 |
| BF1 (%) | 87.03 ± 1.41 | 83.09 ± 1.42 | 88.93 ± 2.02 | 98.24 ± 0.18 | 97.06 ± 0.70 | 93.93 ± 0.23 | 95.92 ± 0.49 | 98.53 ± 0.05 |
| SSIM (%) | 86.49 ± 0.63 | 83.99 ± 0.63 | 84.85 ± 1.16 | 92.13 ± 0.16 | 91.22 ± 0.46 | 89.67 ± 0.12 | 90.58 ± 0.36 | 92.54 ± 0.08 |
| PaviaU | MI (%) | 74.94 ± 0.61 | 70.91 ± 0.63 | 72.42 ± 0.68 | 77.70 ± 2.27 | 82.00 ± 1.86 | 88.69 ± 0.39 | 87.88 ± 0.62 | 91.80 ± 0.25 |
| BF1 (%) | 85.33 ± 0.59 | 85.50 ± 0.53 | 86.46 ± 0.61 | 85.80 ± 0.32 | 85.15 ± 1.25 | 85.27 ± 0.25 | 85.45 ± 0.45 | 86.84 ± 0.16 |
| SSIM (%) | 85.02 ± 0.26 | 83.49 ± 0.19 | 84.29 ± 0.30 | 85.43 ± 0.25 | 85.29 ± 0.90 | 85.52 ± 0.08 | 84.86 ± 0.40 | 85.98 ± 0.13 |
| Salinas | MI (%) | 93.37 ± 0.64 | 90.52 ± 0.87 | 89.31 ± 1.85 | 96.41 ± 0.22 | 94.83 ± 0.56 | 95.84 ± 0.23 | 95.29 ± 0.59 | 96.67 ± 0.11 |
| BF1 (%) | 87.15 ± 1.74 | 80.37 ± 2.04 | 94.15 ± 0.53 | 96.73 ± 0.92 | 96.47 ± 1.17 | 94.75 ± 0.96 | 94.48 ± 1.04 | 97.99 ± 0.20 |
| SSIM (%) | 88.99 ± 0.36 | 84.15 ± 0.79 | 91.28 ± 0.43 | 93.95 ± 0.6 | 93.63 ± 1.06 | 92.57 ± 0. | 92.26 ± 0.40 | 95.19 ± 0.17 |
Table 25.
Computational complexity of S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT.
Table 25.
Computational complexity of S3ARN, PMCN, S3GAN, ViT, SFormer, HFormer, MHCFormer, and D2S2BoT.
| Dataset | Metrics | S3ARN | PMCN | S3GAN | ViT | SFormer | HFormer | MHCFormer | D2S2BoT |
|---|
| Indian | Params (M) | 8.1104 | 0.2288 | 0.0866 | 0.0954 | 0.3426 | 3.3918 | 0.4090 | 0.4560 |
| FLOPs (G) | 1.0752 | 0.9697 | 2.6063 | 0.0381 | 0.0708 | 0.6258 | 0.0569 | 0.3742 |
| Training Time(s) | 67.03 | 130.72 | 366.14 | 23.87 | 26.40 | 59.59 | 40.95 | 37.07 |
| Testing Time (s) | 3.31 | 7.06 | 12.94 | 1.22 | 1.61 | 3.68 | 2.10 | 2.09 |
| Houston | Params (M) | 5.2644 | 0.1936 | 0.0599 | 0.0954 | 0.2262 | 2.8042 | 0.4089 | 0.4559 |
| FLOPs (G) | 0.5612 | 0.7040 | 2.4428 | 0.0275 | 0.0448 | 0.3628 | 0.0569 | 0.3742 |
| Training Time(s) | 82.79 | 137.26 | 461.06 | 26.50 | 34.21 | 76.08 | 57.44 | 51.93 |
| Testing Time (s) | 4.41 | 7.28 | 17.70 | 1.75 | 2.25 | 4.62 | 3.36 | 3.04 |
| HongHu | Params (M) | 12.3283 | 0.2730 | 0.1259 | 0.0958 | 0.5415 | 4.4071 | 0.4094 | 0.4567 |
| FLOPs (G) | 1.9505 | 1.3020 | 5.7876 | 0.0514 | 0.1100 | 1.0737 | 0.0569 | 0.3742 |
| Training Time(s) | 2675.17 | 7416.70 | 31,776.6 | 900.77 | 1006.45 | 1919.27 | 1338.53 | 1281.81 |
| Testing Time (s) | 132.11 | 360.21 | 1032.46 | 50.36 | 72.69 | 125.23 | 80.79 | 76.82 |
| PaviaU | Params (M) | 3.4804 | 0.1675 | 0.0465 | 0.0950 | 0.1644 | 2.4754 | 0.4085 | 0.4552 |
| FLOPs (G) | 0.2912 | 0.5094 | 2.3408 | 0.0197 | 0.0289 | 0.2239 | 0.0569 | 0.3742 |
| Training Time(s) | 204.73 | 297.33 | 1464.42 | 70.12 | 93.51 | 193.33 | 147.42 | 140.20 |
| Testing Time (s) | 12.30 | 16.27 | 49.14 | 4.72 | 6.02 | 12.06 | 8.87 | 8.61 |
| Salinas | Params (M) | 8.3308 | 0.2313 | 0.0878 | 0.0954 | 0.3524 | 3.4407 | 0.4090 | 0.4560 |
| FLOPs (G) | 1.1182 | 0.9887 | 2.6163 | 0.0389 | 0.0729 | 0.6478 | 0.0569 | 0.3742 |
| Training Time(s) | 332.57 | 735.30 | 2063.5 | 93.17 | 147.86 | 270.07 | 198.95 | 179.84 |
| Testing Time (s) | 16.51 | 35.26 | 68.83 | 6.52 | 9.23 | 18.49 | 10.76 | 16.51 |
Table 26.
Computational complexity of SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer.
Table 26.
Computational complexity of SQSFormer, EATN, CFormer, SSACFormer, CPFormer, DSFormer, LGDRNet, and CPMFFormer.
| Dataset | Metrics | SQSFormer | EATN | CFormer | SSACFormer | CPFormer | DSFormer | LGDRNet | CPMFFormer |
|---|
| Indian | Params (M) | 0.2585 | 0.3914 | 0.6156 | 0.7060 | 0.6142 | 0.5939 | 0.3550 | 0.6688 |
| FLOPs (G) | 0.0839 | 0.0949 | 0.1235 | 0.2319 | 0.2592 | 0.0421 | 2.8689 | 0.1495 |
| Training Time(s) | 9.53 | 129.32 | 67.61 | 182.40 | 116.98 | 47.19 | 38.88 | 33.04 |
| Testing Time (s) | 0.76 | 3.01 | 6.54 | 5.57 | 10.05 | 2.66 | 1.58 | 2.53 |
| Houston | Params (M) | 0.1490 | 0.3168 | 0.6118 | 0.3799 | 0.3202 | 0.5938 | 0.3549 | 0.2065 |
| FLOPs (G) | 0.0469 | 0.0769 | 0.1219 | 0.2525 | 0.1353 | 0.0421 | 3.1857 | 0.0467 |
| Training Time(s) | 9.50 | 201.38 | 98.34 | 262.50 | 131.67 | 55.93 | 41.70 | 42.89 |
| Testing Time (s) | 0.55 | 4.05 | 7.53 | 9.65 | 11.62 | 3.94 | 2.40 | 3.33 |
| HongHu | Params (M) | 0.1614 | 0.5025 | 0.6217 | 1.2527 | 1.1136 | 0.5947 | 0.3553 | 0.2855 |
| FLOPs (G) | 0.0508 | 0.1701 | 0.1255 | 0.7171 | 0.4692 | 0.0421 | 2.9004 | 0.0898 |
| Training Time(s) | 214.56 | 1358.34 | 1041.4 | 9239.8 | 2074.2 | 1464.4 | 1578.6 | 1557.54 |
| Testing Time (s) | 15.61 | 155.57 | 359.00 | 254.58 | 450.38 | 96.87 | 73.89 | 103.06 |
| PaviaU | Params (M) | 0.1597 | 0.2699 | 0.6076 | 0.2035 | 0.1597 | 0.5930 | 0.3546 | 0.5526 |
| FLOPs (G) | 0.0508 | 0.0656 | 0.1207 | 0.1125 | 0.0508 | 0.0421 | 2.2926 | 0.1224 |
| Training Time(s) | 23.75 | 192.68 | 114.54 | 332.19 | 247.22 | 147.11 | 133.71 | 149.93 |
| Testing Time (s) | 1.72 | 7.53 | 14.87 | 17.59 | 24.36 | 9.72 | 6.62 | 9.69 |
| Salinas | Params (M) | 0.1606 | 0.3972 | 0.6159 | 0.7331 | 0.6389 | 0.5939 | 0.3550 | 0.2434 |
| FLOPs (G) | 0.1324 | 0.0963 | 0.1236 | 0.3347 | 0.2025 | 0.0421 | 2.3463 | 0.0769 |
| Training Time(s) | 93.21 | 225.69 | 167.73 | 539.63 | 339.52 | 201.26 | 177.06 | 202.99 |
| Testing Time (s) | 35.26 | 13.63 | 31.36 | 29.27 | 39.40 | 13.36 | 8.55 | 10.76 |
Table 27.
Impact of different attention mechanisms on classification performance. The best results are in red.
Table 27.
Impact of different attention mechanisms on classification performance. The best results are in red.
| Dataset | Metrics | Without CFCL | Without CFEB | Without CSSA | Without CSCA | Without MHCSD2A | CPMFFormer |
|---|
| Indian | OA (%) | 93.84 ± 0.91 | 93.96 ± 1.03 | 93.54 ± 1.49 | 93.05 ± 1.00 | 92.61 ± 2.17 | 94.85 ± 0.69 |
| AA (%) | 93.14 ± 1.34 | 93.69 ± 2.50 | 93.66 ± 4.35 | 93.03 ± 2.09 | 91.17 ± 3.14 | 94.35 ± 0.61 |
| (%) | 92.97 ± 0.99 | 93.11 ± 1.16 | 92.63 ± 1.69 | 92.07 ± 1.13 | 91.59 ± 2.45 | 94.13 ± 0.80 |
| Houston | OA (%) | 92.95 ± 3.12 | 94.63 ± 1.01 | 94.99 ± 0.54 | 94.49 ± 1.18 | 93.73 ± 4.11 | 95.93 ± 0.36 |
| AA (%) | 93.44 ± 2.82 | 95.07 ± 0.88 | 95.26 ± 0.74 | 94.75 ± 1.14 | 93.99 ± 3.84 | 96.06 ± 0.26 |
| (%) | 92.38 ± 3.38 | 94.20 ± 1.10 | 94.59 ± 0.59 | 94.05 ± 1.28 | 93.22 ± 4.45 | 95.61 ± 0.39 |
| HongHu | OA (%) | 99.35 ± 0.11 | 99.36 ± 0.08 | 99.34 ± 0.04 | 99.45 ± 0.04 | 99.18 ± 0.04 | 99.53 ± 0.03 |
| AA (%) | 98.47 ± 0.65 | 98.37 ± 0.15 | 98.46 ± 0.13 | 98.62 ± 0.13 | 98.37 ± 0.18 | 98.99 ± 0.10 |
| (%) | 99.18 ± 0.14 | 99.20 ± 0.10 | 99.17 ± 0.05 | 99.31 ± 0.05 | 99.02 ± 0.05 | 99.41 ± 0.04 |
| PaviaU | OA (%) | 99.26 ± 0.13 | 99.31 ± 0.21 | 99.36 ± 0.21 | 99.27 ± 0.17 | 99.13 ± 0.25 | 99.50 ± 0.06 |
| AA (%) | 98.64 ± 0.25 | 98.72 ± 0.41 | 98.78 ± 0.36 | 98.68 ± 0.29 | 98.20 ± 0.56 | 99.02 ± 0.10 |
| (%) | 99.01 ± 0.17 | 99.08 ± 0.28 | 99.15 ± 0.28 | 99.04 ± 0.22 | 98.84 ± 0.33 | 99.34 ± 0.08 |
| Salinas | OA (%) | 99.75 ± 0.07 | 99.69 ± 0.08 | 99.68 ± 0.10 | 99.65 ± 0.08 | 99.37 ± 0.20 | 99.84 ± 0.06 |
| AA (%) | 99.69 ± 0.08 | 99.65 ± 0.09 | 99.61 ± 0.11 | 99.57 ± 0.09 | 99.52 ± 0.09 | 99.84 ± 0.05 |
| (%) | 99.72 ± 0.09 | 99.66 ± 0.08 | 99.65 ± 0.11 | 99.62 ± 0.09 | 99.19 ± 0.22 | 99.82 ± 0.07 |