PLISA: An Optical–SAR Remote Sensing Image Registration Method Based on Pseudo-Label Learning and Interactive Spatial Attention

Highlights

What are the main findings?

• PLISA is a self-supervised method for optical–SAR registration. It tackles key challenges by introducing a CIA module for feature alignment and a pseudo-label learning strategy, which generates supervision signals.
• Extensive experiments on multiple datasets demonstrate that PLISA surpasses state-of-the-art methods in accuracy and robustness under challenging conditions like rotation, scale changes, and noise. It also exhibits strong generalization across varying resolutions and cloud cover.

What are the implications of the main finding?

• This study shows that self-supervised pseudo-labeling can address the scarcity of annotated keypoints in optical–SAR registration.
• PLISA maintains high accuracy with high computational efficiency, serving as a reliable tool for real-world remote sensing image registration.

Abstract

Multimodal remote sensing image registration faces severe challenges due to geometric and radiometric differences, particularly between optical and synthetic aperture radar (SAR) images. These inherent disparities make extracting highly repeatable cross-modal feature points difficult. Current methods typically rely on image intensity extreme responses or network regression without keypoint supervision for feature point detection. Moreover, they not only lack explicit keypoint annotations as supervision signals but also fail to establish a clear and consistent definition of what constitutes a reliable feature point in cross-modal scenarios. To overcome this limitation, we propose PLISA—a novel heterogeneous image registration method. PLISA integrates two core components: an automated pseudo-labeling module (APLM) and a pseudo-twin interaction network (PTIF). The APLM introduces an innovative labeling strategy that explicitly defines keypoints as corner points, thereby generating consistent pseudo-labels for dual-modality images and effectively mitigating the instability caused by the absence of supervised keypoint annotations. These pseudo-labels subsequently train the PTIF, which adopts a pseudo-twin architecture incorporating a cross-modal interactive attention (CIA) module to effectively reconcile cross-modal commonalities and distinctive characteristics. Evaluations on the SEN1-2 dataset and OSdataset demonstrate PLISA’s state-of-the-art cross-modal feature point repeatability while maintaining robust registration accuracy across a range of challenging conditions, including rotations, scale variations, and SAR-specific speckle noise.

1. Introduction

The complex demands of terrestrial monitoring applications frequently exceed the capabilities of single-sensor systems, driving the need for multisensor integration to achieve comprehensive Earth observation [1]. Multimodal remote sensing image registration, a prerequisite for effectively utilizing complementary information from these diverse sources [2], aligns images of the same geographic area acquired by different sensors. Registering optical and SAR images, however, is particularly challenging. Their fundamentally different imaging mechanisms lead to significant nonlinear radiometric differences (NRD) and complex geometric distortions, resulting in difficulties for feature extraction and representation during cross-modal image registration.

Traditional image registration methods can be categorized into two types: area-based methods and feature-based methods [3]. The core of area-based methods lies in optimizing a similarity metric to estimate geometric transformation parameters, effectively driving the alignment process through a template matching strategy [4]. Feature-based matching methods typically comprise three key steps: feature detection, feature description, and feature matching. Here, feature detection is crucial in robustly extracting distinctive and repeatable keypoints. A core limitation of these feature-based methods lies in their feature point detection stage, where they heavily rely on image intensity or gradient information. Due to the significant nonlinear radiometric distortions between optical images and SAR images, the intensity distribution patterns and gradient structures of identical objects exhibit drastic changes, or even inversions, between these two modalities. This radiometric discrepancy can be abstracted as an unknown, complex nonlinear function $\mathcal{F}$ mapping the intensity values between modalities:

$$I_s(u,v)=\mathcal{F}\left(I_o(x,y)\right)+\eta (u,v)$$

(1)

where $I_o$ and $I_s$ are the optical and SAR image intensities, $(x,y)$ and $(u,v)$ are corresponding points related by a geometric transformation ${\mathcal{T}}_{\mathit{\theta }}$, and $\eta$ represents SAR speckle noise. This discrepancy severely undermines the repeatability and localization accuracy of feature points extracted by traditional methods, leading to missed and false detections.

In recent years, deep learning-based remote sensing image registration methods have demonstrated considerable potential in multimodal remote sensing image matching. These methods employ neural networks to extract image feature points, generate feature descriptors, or compute image transformation matrices. Due to the large-scale dimensions inherent in remote sensing imagery, keypoint-based registration methodologies demonstrate marked advantages over dense registration approaches in terms of computational efficiency. However, current deep learning-based feature point detection methods face significant challenges. Crucially, the lack of large-scale, high-quality annotated datasets containing corresponding optical–SAR keypoints hinders supervised learning approaches. Furthermore, existing methods usually depend on image intensity extreme responses [5] or network regression without keypoint supervision [6,7] for feature point extraction. Methods relying on image intensity extreme responses are prone to feature instability due to imaging differences. On the other hand, methods based on network regression without keypoint supervision lack intermediate supervision, which can lead to spatially inconsistent predictions and increased susceptibility to occlusion and ambiguous patterns. Both limitations adversely impact the performance of subsequent feature descriptor construction and matching.

To learn how to extract stable and repeatable keypoints across optical and SAR images, we build upon the concept of self-supervised keypoint generation [8] and propose a novel pseudo-label generation method. This concept was successfully applied to single-modal optical image registration, leveraging synthetic data to explicitly generate stable keypoints without manual annotation. This strategy shares high-level capabilities with other self-supervised methods that create training data through synthetic transformations, such as geometric matching networks [9] and deep image homography estimation [10] for estimating global transformations. However, a limitation of these methods is that they lack interest points and point correspondences, which are crucial for registration. Furthermore, in the realm of unsupervised image registration, another common approach is to directly predict a dense deformation field to warp the moving image towards the fixed image, optimizing similarity metrics without manual annotations. The pivotal distinction of our work lies in its objective: instead of estimating global transformations or dense deformation fields, our method is specifically designed to self-supervise the generation of keypoint location labels. However, directly applying this concept to optical–SAR cross-modal scenarios presents obstacles [11], as it is challenging to generate high-quality virtual synthetic image pairs that accurately reflect genuine cross-modal keypoint characteristics. In the absence of such highly representative virtual training data, it is difficult to train a keypoint detection network capable of co-annotating corresponding feature points across both modalities under reliable cross-modal supervision. To address this, this article proposes a pseudo-label generation method that can simultaneously generate reliable feature point labels for both optical and SAR image pairs.

In deep learning-based remote sensing image registration, early research primarily utilized Siamese networks to simultaneously detect and describe features from cross-modal image pairs [12,13,14]. However, extensive experiments reveal that Siamese networks underperform in heterogeneous image pairs like optical–SAR due to the inadequate modeling of intermodal distinctions [5]. This limitation motivated a shift toward pseudo-Siamese network architectures [5,12,15,16], whose core advantage lies in independently learning modality-specific features. Nevertheless, effectively fusing this modality-specific information with modality-shared information for robust registration remains a critical challenge. The registration objective can be formulated as finding the optimal transformation parameters ${\mathit{\theta }}^{\ast }$ that align the two images:

$${\mathit{\theta }}^{\ast }=\underset{\mathit{\theta }}{argmin}\mathbf{\sum }_i\mathcal{L}\left({\Phi }_s\left(I_s\left({\mathbf{p}}_s^i\right)\right),{\Phi }_o\left(I_o\left({\mathcal{T}}_{\mathit{\theta }}\left({\mathbf{p}}_s^i\right)\right)\right)\right)$$

(2)

where ${\Phi }_o$ and ${\Phi }_s$ are feature extractors for optical and SAR images, ${\mathcal{T}}_{\mathit{\theta }}$ is the geometric transformation, and $\mathcal{L}$ is a feature similarity loss. To address this, we propose the pseudo-twin interaction network (PTIF) as a unified feature detection and description backbone.

Based on the analysis above, the main contributions of this paper are summarized as follows:

(1)

It proposes an automated pseudo-labeling module (APLM) to address the challenge of lacking annotated corresponding keypoints. The APLM generates stable keypoint pseudo-labels simultaneously for optical–SAR pairs without manual annotation, enabling effective SAR keypoint extraction through transfer learning from visible synthetic data while avoiding the difficulty of generating high-quality optical–SAR synthetic pairs.

(2)

We design and implement the PTIF using a pseudo-twin architecture integrated with a cross-modal interactive attention (CIA) module. This module captures spatial correspondences and learns cross-modal shared features, thereby effectively fusing modality-specific and modality-shared information.

(3)

We introduce PLISA, an end-to-end registration method built upon the APLM and PTIF. Evaluations on the SEN1-2 dataset and OSdataset demonstrate PLISA’s superior accuracy and robustness against challenges including large perspective rotations, scale variations, and inherent SAR speckle noise.

The remainder of this article is structured as follows. A brief overview of methods in the field of image registration is introduced in Section 2. The proposed method is explained in detail in Section 3. Section 4 discusses the experimental results under various conditions. Finally, Section 5 concludes this article.

2. Background

2.1. Traditional Remote Sensing Image Registration

Region-based registration methods [17,18,19,20,21] determine image transformations by evaluating the similarity within template windows using metrics like MI [22], NCC [23], and SSD [24]. However, SSD and NCC are sensitive to nonlinear grayscale distortions, leading to suboptimal performance in multimodal registration. While MI is resistant to nonlinear distortions, it is computationally intensive and sensitive to local grayscale differences [17]. Critically, all region-based methods face inherent limitations, because they are generally limited to small pixel shifts [4], highly sensitive to rotation and scale changes, and sensitive to illumination and modality variations. Consequently, robust feature-based methods have largely replaced region-based approaches for multimodal remote sensing image registration [25].

Feature-based methods like Moravec [26], Harris [27], DoG [28], FAST [29], SIFT [28], and SURF [30] are widely used. SIFT [28] identifies scale-space extrema in a DoG pyramid, assigns the dominant orientation via gradient histograms, and forms a 128-D descriptor by pooling gradients in spatial bins. SURF [30] accelerates feature detection and description using integral images and Haar wavelets. However, when confronted with multimodal remote sensing image pairs such as optical and SAR imagery, severe NRD and geometric distortions significantly degrade the registration performance of these methods [4]. This results in the low repeatability of cross-modal feature points, lower localization accuracy, and elevated rates of false and missed detections. The cause lies in the significant discrepancies in the intensity and gradient patterns exhibited by identical ground objects under different imaging mechanisms.

To address these challenges, the remote sensing community has developed three primary categories of enhancement strategies. Gradient optimization methods such as SAR-SIFT [31] and OS-SIFT [32] enhance the robustness against modality-specific noise and NRD by redesigning gradient computation. For instance, SAR-SIFT utilizes the ROEWA operator in SAR imagery to suppress speckle noise. However, these methods typically rely on modality-specific gradient definitions, which limits their generalization capabilities. Local self-similarity methods like DOBSS [33] and HOSS [34] construct descriptors using log-polar spatial structures, correlating regional patterns or encoding self-similarity histograms to improve the NRD resistance. Nevertheless, such descriptors’ limited discriminative capacity can compromise the matching robustness under complex nonlinear radiometric distortions. Phase congruency methods including RIFT [35] exploit the illumination and contrast-invariant properties of phase consistency for keypoint detection and description. These methods maintain robustness under severe NRD, making them particularly suitable for tasks such as optical and SAR image registration. However, these approaches carry large computational burdens that limit their practical deployment on large-scale remote sensing imagery.

In summary, existing traditional approaches, encompassing both region-based methods and feature-based methods, are constrained by their dependence on handcrafted features and similarity measures. This limitation inherently compromises their robustness against severe NRD, significant geometric distortions, modality-specific noise, and diverse imaging conditions, which often leads to insufficient keypoint repeatability, poor descriptor discriminativity, and limited model generalization. These persistent limitations motivate a paradigm shift, moving beyond manual feature engineering. To address this gap, we proposes PLISA, an end-to-end deep learning method that learns robust, modality-invariant representations directly from image data, effectively bypassing the inherent limitations of traditional design paradigms.

2.2. Learning-Based Registration Methods

To effectively address the significant NRD between optical and SAR images and the inherent speckle noise in SAR images, researchers have proposed a variety of learning-based registration methods. These approaches aim to extract more discriminative and robust feature representations. In this section, we review these methods by categorizing them into four primary strands: Siamese and pseudo-Siamese network frameworks, cross-modality translation via style transfer, CNN-based feature representation and matching methods, and advanced architectures for image registration. This categorization allows us to systematically explore the strengths and limitations of existing methods and clearly motivates our proposed approach.

2.2.1. Siamese and Pseudo-Siamese Network Frameworks

Siamese and pseudo-Siamese networks have emerged as pivotal frameworks for feature extraction in image registration. Conventional Siamese networks employ weight-shared branches to process homogeneous inputs. For instance, Merkle et al. [36] and Zhang et al. [14] employed Siamese fully convolutional networks for deep feature extraction. Merkle et al. [36] and Zhang et al. [14] both employed Siamese fully convolutional networks to extract deep common features. The former adopted dilated convolutions to expand the receptive fields, while the latter established feature correspondences through convolutional linking operations. Building on this foundation, Cao et al. [37] trained phase congruency networks using Siamese architectures, and Xiang et al. [38] developed the Siamese Cross-Stage Partial Network (Sim-CSPNet) specifically for SAR image registration. However, these weight sharing mechanisms prove inadequate in capturing intermodal discrepancies inherent in heterogeneous modality pairs, such as optical and SAR images [5].

This limitation led to the development of pseudo-Siamese variants. Hughes et al. [39] pioneered the use of independent convolutional streams for optical and SAR inputs, without weight sharing. Similarly, CMM-Net [5] established a dual-branch framework where shallow non-shared layers extract modality-specific features, while deep shared layers learn modality-invariant representations. To achieve deeper fusion, recent refinements have been proposed. For example, Zhou et al. [40] proposed Multiscale Convolutional Gradient Features (MCGF) based on a pseudo-Siamese network to preserve spatial precision through a fully convolutional design. Zhang et al. [12] introduced OSMNet, which is also built upon a pseudo-Siamese architecture. This framework incorporates multilevel feature fusion, multifrequency channel attention, and an adaptive weighted loss to enhance the matching accuracy between optical and SAR images.

While pseudo-Siamese networks allow different processing for each modality, their feature fusion methods still have limitations. Existing fusion mechanisms still lack the modeling of spatial correspondence. It is these limitations that directly motivate our proposed PTIF, which introduces a CIA module to model spatial correspondences and dynamically learn modality-shared features, aiming to address the insufficient fusion in current methods.

2.2.2. Cross-Modality Translation via Style Transfer

An alternative strategy focuses on pixel-level image translation to unify modality representations. This approach converts cross-modal images into a unified modality, enabling the direct application of well-established homogeneous image registration methods. This approach is primarily implemented using GANs [41]. A K-means clustering GAN [42] uses the K-means segmentation of SAR images as input to the GAN to control spatial information. It can stabilize training and generate a natural high-frequency structure to enhance texture details. Merkle et al. [43] utilized a conditional GAN to generate pseudo-SAR images from optical images, thereby improving the matching accuracy of traditional methods. Hughes et al. [39] proposed using a GAN and a variational autoencoder to generate new SAR image patches. Han et al. [44] proposed an image transformation module based on HOG-GAN to generate pseudo-optical images and enhance the discriminability of local features. Subsequently, high-precision matching was achieved through EDs based on scale-angle estimation (SAE) and descriptor co-learning. James et al. [45] proposed a conditional GAN-based image registration method, which is a method for image registration based on a conditional GAN and fast Fourier transform. The main idea of this method is to use the conditional GAN to convert heterogeneous remote sensing images into uniform images and then perform image registration. In addition to using GANs to achieve modality unification, Song et al. [46] implemented a style transfer algorithm based on the VGG network, obtaining a composite image that provides content information from the floating image and style information from the reference image. The composite image is then registered with the reference image to achieve better results.

Despite these efforts, current pixel-level image translation methods still have limitations. Crucially, the converted images have poor quality, especially in optical-to-SAR cases. This directly reduces the registration accuracy [4]. While deep learning can handle some nonlinear differences, the differences between how optical and SAR sensors capture images, combined with the unique speckle noise in SAR, make it extremely difficult to produce high-quality converted images.

2.2.3. CNN-Based Feature Representation and Matching Methods

CNNs represent some of the most widely adopted architectures in image registration. In the field of keypoint detection, early methods such as D2-Net [13] employed CNNs to extract descriptors but depended on unstable local extrema for detection. CMM-Net [5] enhanced the keypoint quality by selecting channel-wise maxima. R2D2 [7] introduced separate learnable maps for repeatability and reliability, enhancing the registration performance by jointly optimizing keypoint repeatability and reliability. ReDFeat [6] decoupled detection and description through mutual weighting and stabilized training via gradient decoupling. To enhance the reliability of feature extraction, Li et al. [47] proposed PMNet, which integrates an MKD for more robust keypoint localization. Similarly, Xiang et al. [48] introduced a feature intersection-based keypoint detector that combines phase consistency, gradient direction, and local variation coefficient measures to extract highly repeatable keypoints, significantly improving the adaptability under highly complex imaging conditions. SuperPoint [8] introduces a self-supervised method called homographic adaptation to generate high-quality pseudo-ground-truth keypoint labels without human annotation. It first pre-trains a base detector, MagicPoint, on a synthetic dataset of simple geometric shapes where corners are well-defined. Then, for each real image, it applies multiple random homographies, detects points on warped versions, aggregates the results back into the original image space, and uses these consistent points as pseudo-labels to train the full SuperPoint model.

In terms of feature description, Liao et al. [49] proposed MatchosNet, which incorporates a local deep CNN descriptor trained with the L2 loss. Xiang et al. [50] also introduced FDNet, consisting of RDNet and a PSFCN, designed to separately learn noise-robust features and semantic features, further enhancing the robustness in noisy environments.

Regarding matching strategies, several methods have also shown notable progress. Hoffmann et al. [51] proposed a fully convolutional network-based registration approach that outperformed traditional mutual information-based metrics in matching accuracy. In outlier rejection, Chen et al. [52] enhanced StateNet with adaptive dual-aggregation convolution and point rendering layers, improving the matching robustness under complex transformations.

Despite these advances, significant challenges remain in optical–SAR image registration. Many methods rely on extremum detection or direct network predictions to locate keypoints, and they lack a clear and consistent definition of what constitutes a reliable feature point in cross-modal scenarios. Furthermore, annotation strategies like those used in SuperPoint [8] struggle to generalize to SAR-specific artifacts due to domain shift.

2.2.4. Advanced Architectures for Image Registration

In recent years, emerging architectures such as Transformers and GNNs have been widely adopted in the field of image registration. Detector-free methods eschew explicit feature detection, instead establishing dense correspondences directly between images. Representative approaches like LoFTR [53] leverage Transformer architectures to achieve robust matching, even in textureless regions. Efforts like Efficient LoFTR [54] improve the efficiency through novel attention mechanisms, while frameworks such as RCM [55] attempt to balance sparse and dense matching. RSOMNet [56] further advances this paradigm with a coarse-to-fine matching cascade refined by non-shared content filtering. Alternative strategies bypass the traditional pipeline entirely; for instance, Li et al. [3] directly predict displacement parameters. However, slight prediction errors can accumulate, potentially resulting in significant deviations in the final transformation matrix. Meanwhile, ADRNet [57] integrates affine and deformable transformations with dilated attention. RoMa [58] is a robust dense feature matching method that leverages frozen pre-trained DINOv2 features combined with specialized fine-level features, an improved Transformer match decoder, and a robust loss formulation. It should be noted that the substantial computational demands inherent in these detector-free dense matching methods render them prohibitively expensive for large-scale, high-resolution image pairs.

In contrast, detector-based methods often incorporate learned feature detectors within an framework. For instance, Chen et al. [59] designed Shape-Former, which integrates CNN and Transformer blocks with permutation-invariant operations to enhance shape-aware feature extraction. Lin et al. [60] introduced a hybrid CNN–Transformer descriptor that achieves a balance between performance and computational efficiency through dense connectivity and transition layers. Similarly, CSR-Net, developed by Chen et al. [61], incorporates structural representation learning and attention mechanisms to enhance fine-grained pattern recognition. MBGA [62] enhances cross-modal matching with a multibranch global attention module.

Matching strategies have also advanced significantly. SuperGlue [63] formulates feature matching as an optimal transport problem, solved using attention-based GNNs. Its efficient variant, LightGlue [64], reduces the computational overhead through adaptive depth and early exiting mechanisms. These methods are often integrated with learnable detectors to form end-to-end differentiable pipelines.

While some of the aforementioned methods work well for natural image registration, they often fail to generalize to optical–SAR scenarios. Even the remaining algorithms specifically designed for optical–SAR matching still face considerable challenges, primarily due to differences in imaging mechanisms between SAR and optical sensors. These include severe radiometric distortions, geometric variations such as layover and shadowing in SAR, speckle noise, and divergent textural characteristics between the two modalities. Such inherent discrepancies often lead to ambiguous feature correspondences, unreliable keypoint detection, and difficulties in achieving consistent alignment in heterogeneous regions, limiting the robustness and generalization of current learning-based methods.

Beyond the image–image registration scope, significant progress has also been made in the alignment of image and point cloud data, which represents another critical multimodal registration scenario. For instance, NRLI-UAV [65] enhances low-cost UAV LiDAR quality by non-rigidly registering sequential raw laser scans and images through trajectory correction and depth optimization. Meanwhile, CoFiI2P [66] tackles cross-modal registration with a coarse-to-fine framework and an I2P transformer for robust correspondence. Complementarily, SE-Calib [67] enables online sensor calibration by aligning semantic edges between LiDAR and cameras using a soft consistency metric. These works demonstrate the potential of advanced architectures in addressing complex multimodal alignment challenges beyond traditional image pairs.

3. Method

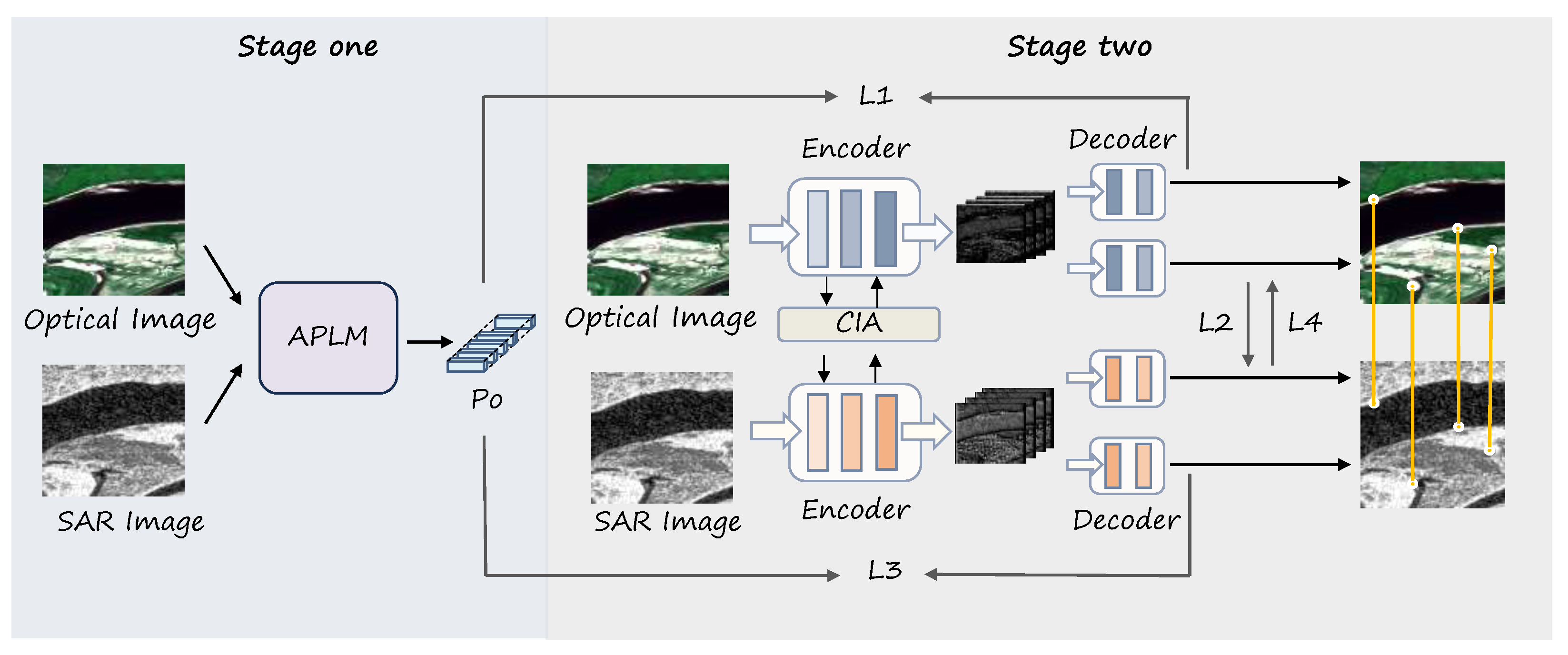
This article proposes a novel framework termed PLISA for optical and SAR image registration, as shown in Figure 1. PLISA comprises two sequential stages. In the first stage, the APLM generates pseudo-labels Po representing corresponding points in the optical and SAR image pair. In the second stage, these pseudo-labels Po are leveraged as supervision to train the PTIF registration network. The PTIF is optimized via a composite loss function including feature point localization losses for both the optical (L1) and SAR (L3) images and bidirectional cross-modal descriptor matching losses (L2: optical to transformed SAR; L4: SAR to transformed optical). This design enables the framework to optimize feature localization and robust cross-modal descriptor matching, thereby enhancing the registration accuracy.

3.1. Automated Pseudo-Labeling Module

The APLM is designed to provide stable and repeatable feature points for both optical and SAR images. We adopt the core concept of feature point annotation from SuperPoint [8].

Nevertheless, Superpoint [8] is primarily designed for the optical spectrum and cannot be directly applied to annotate feature points in SAR images. To overcome this limitation, we propose the APLM, which directly extends its underlying principles to cross-modal scenarios. Given the challenges in generating synthetic SAR datasets, we adhered to SuperPoint’s paradigm by training MagicPoint exclusively on synthetic optical data, subsequently deploying it for feature point detection in real-world optical and SAR imagery. Experimental results indicate that, while MagicPoint accurately labels feature points in optical images, it produces sparser detections in SAR images. This suggests that a method is required to increase the consistency of feature point detection across cross-modal image pairs. The implementation details for the application of MagicPoint to real optical and SAR images are shown in Figure 2.

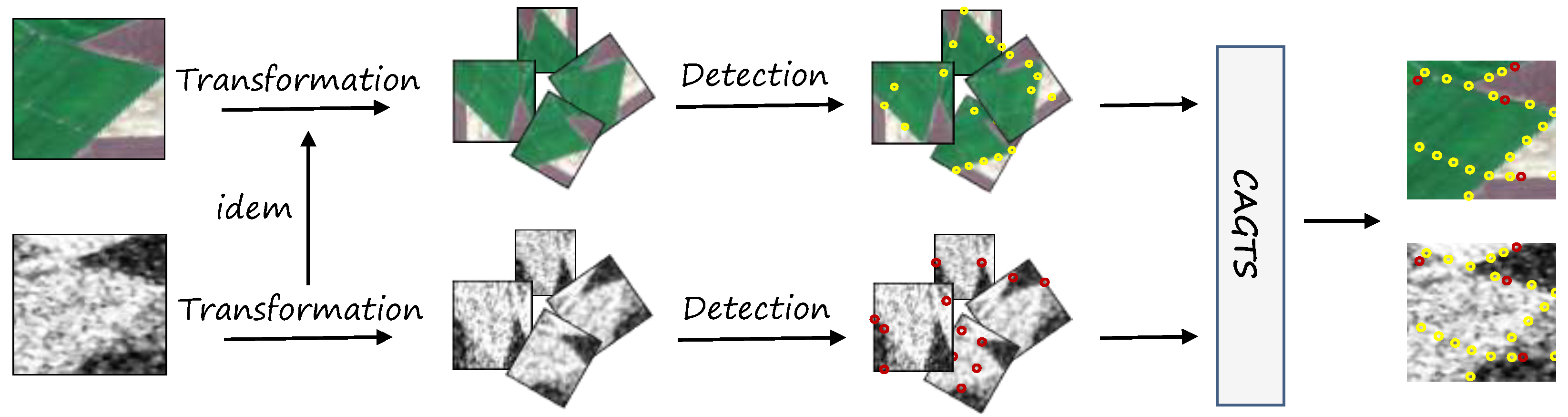
In response, we propose the Consistency-Aware Pseudo-Ground-Truth Selector (CAGTS) for the pseudo-ground-truth labeling of both optical and SAR images, using only optical synthetic data. This method is inspired by the homographic adaptation strategy [8]. The CAGTS presents the idea of soft labels. This scheme maintains the precise localization of feature points in optical images while effectively preserving feature points characterized by SAR-specific imaging properties.

We initially annotated feature points in optical and SAR images with MagicPoint. This process generates initial sets of candidate feature point locations, denoted as {$P_{\mathrm{VIS}}$} for the optical image and {$P_{\mathrm{SAR}}$} for the corresponding SAR image. The final pseudo-ground-truth points are selected from the complete initial set {$P_{\mathrm{VIS}}$} of optical images and the filtered points from the initial SAR image set {$P_{\mathrm{SAR}}$}.

The filtering begins with a distance-based hard constraint. For each candidate SAR point $P_{\mathrm{SAR}}$ in the initial set {$P_{\mathrm{SAR}}$}, its nearest neighbor optical point $P_{\mathrm{VIS}}$ within the set {$P_{\mathrm{VIS}}$} is identified. The Euclidean distance $d(P_{\mathrm{SAR}},P_{\mathrm{VIS}})$ is calculated. A predefined distance threshold T is applied: if $d(P_{\mathrm{SAR}},P_{\mathrm{VIS}})\ge T$, $P_{\mathrm{SAR}}$ is discarded due to being too isolated from any optical point to be considered consistent; if $d(P_{\mathrm{SAR}},P_{\mathrm{VIS}})<T$, $P_{\mathrm{SAR}}$ is retained as a provisionally consistent candidate, forming a subset $P_{\mathrm{SAR}\_\mathrm{prov}}$. Next, a soft confidence score $C\left(P_{\mathrm{SAR}}\right)$ is calculated for each provisionally consistent SAR point $P_{\mathrm{SAR}}$ in $P_{\mathrm{SAR}\_\mathrm{prov}}$. A search radius T is defined, centered at $P_{\mathrm{SAR}}$. All optical points $P_{\mathrm{VIS}}^i$ falling within this radius T are identified, and N denotes the number of such points. The confidence score is computed as the average of the inverse distances to all these neighboring optical points within T:

$$B_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}d(P_{\mathrm{SAR}},P_{\mathrm{VIS}}^i)<T\hfill \\ 0,\hfill & \mathrm{if}d(P_{\mathrm{SAR}},P_{\mathrm{VIS}}^i)>T\hfill \end{array}\right.$$

(3)

$$C\left(P_{\mathrm{SAR}}\right)={\displaystyle \frac{1}{N}}\mathbf{\sum }_{i=1}^N{\displaystyle \frac{1}{B_i\times d(P_{\mathrm{SAR}},P_{\mathrm{VIS}}^i)}}$$

(4)

$$C\left(P_{\mathrm{SAR}}\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}C\left(P_{\mathrm{SAR}}\right)>1\hfill \\ 0,\hfill & \mathrm{if}C\left(P_{\mathrm{SAR}}\right)\le \alpha \hfill \end{array}\right.$$

(5)

where, $P_{\mathrm{VIS}}^i$ denotes the i-th keypoint in the optical image, and $d(P_{\mathrm{SAR}},P_{\mathrm{VIS}}^i)$ represents the Euclidean distance between $P_{\mathrm{SAR}}$ and $P_{\mathrm{VIS}}^i$. N refers to the total number of keypoints in the optical image. It is crucial to emphasize that this strategy must be applied to a pair of already co-registered optical and SAR images for annotation. A confidence threshold $\alpha$ is then applied to $C\left(P_{\mathrm{SAR}}\right)$ for final selection. This threshold critically controls the strictness of SAR point selection, directly influencing the quantity and quality of the pseudo-ground truth. If $C\left(P_{\mathrm{SAR}}\right)$ > $\alpha$, $P_{\mathrm{SAR}}$ is accepted as a final pseudo-ground-truth point for the SAR image; if $C\left(P_{\mathrm{SAR}}\right)\le \alpha$, $P_{\mathrm{SAR}}$ is rejected due to lacking sufficient consistent local evidence despite passing the initial distance filter. The optimal value of $\alpha$ was determined through extensive empirical analysis (see Section 4.9 for details), balancing the inclusion of sufficient correspondence points against the exclusion of noisy outliers. Our experiments indicate that $\alpha$ = 0.15 yields the best overall performance. Consequently, the final pseudo-ground-truth points sets are defined as follows: the optical image pseudo-ground-truth points remain the initial set {$P_{\mathrm{VIS}}$} generated by the homographic adaptation strategy [8]; the SAR image pseudo-ground-truth points comprise the subset of the initial {$P_{\mathrm{SAR}}$} points that survived both the hard distance filter and the soft confidence threshold.

The pseudo-ground-truth point set obtained through the above process not only reflects the correspondence between the two image types but also enhances the repeatability of the feature points. The CAGTS helps to filter out inaccurate or isolated feature points that result from structural differences between images from different sources, thereby providing high-quality feature point labels for subsequent image registration.

3.2. Pseudo-Twin Interaction Network

Siamese networks, sharing parameters, perform exceptionally well in feature extraction for homogeneous modalities. However, when applied to cross-modal feature extraction involving optical and SAR remote sensing images, the dual branches can interfere with each other. This not only compromises the quality of feature extraction but also yields suboptimal results. Therefore, in multisource image registration tasks, researchers tend to adopt pseudo-Siamese network architectures to extract features from images of different modalities.

Accordingly, we design a PTIF for the extraction of feature points and descriptors. The architecture of the PTIF mainly consists of two parallel branches, with each branch dedicated to processing input images from different modalities.

3.2.1. Encoder

In the encoder section, the network utilizes a VGG-like backbone, which is configured with six 3 × 3 convolutional layers. After every two convolutional layers, a 2 × 2 max pooling layer is applied for spatial downsampling. Notably, between the first four convolutional layers—specifically after every two convolution operations—a CIA module is introduced between two distinct branches.

3.2.2. Decoder

Within the decoder, there are three 3 × 3 convolutional layers followed by a 1 × 1 convolutional layer, outputting a 65-channel feature point tensor and a 256-channel descriptor tensor.

Regarding the feature point tensor, it represents the probability of each position being a feature point, where the 65 channels include 64 positions from an 8 × 8 pixel grid and one “garbage bin” category [8]. The “garbage bin” category is used to indicate the absence of significant feature points within this 8 × 8 pixel region. During training, the ground truth label $y_{hw}$ for each $8\times 8$ region is determined based on the presence of annotated feature points. When the region contains at least one feature point, $y_{hw}$ is set to the grid position index corresponding to the feature point closest to the region center; when the region contains no feature points, $y_{hw}$ is set to 65.

As for the descriptor tensor, it has 256 channels, where both the width and height are ${\displaystyle \frac{1}{8}}$ of the original image size. To reduce the memory and processing time consumption, this tensor is bilinearly interpolated based on the locations of feature points to obtain 256-dimensional descriptors corresponding to the original size.

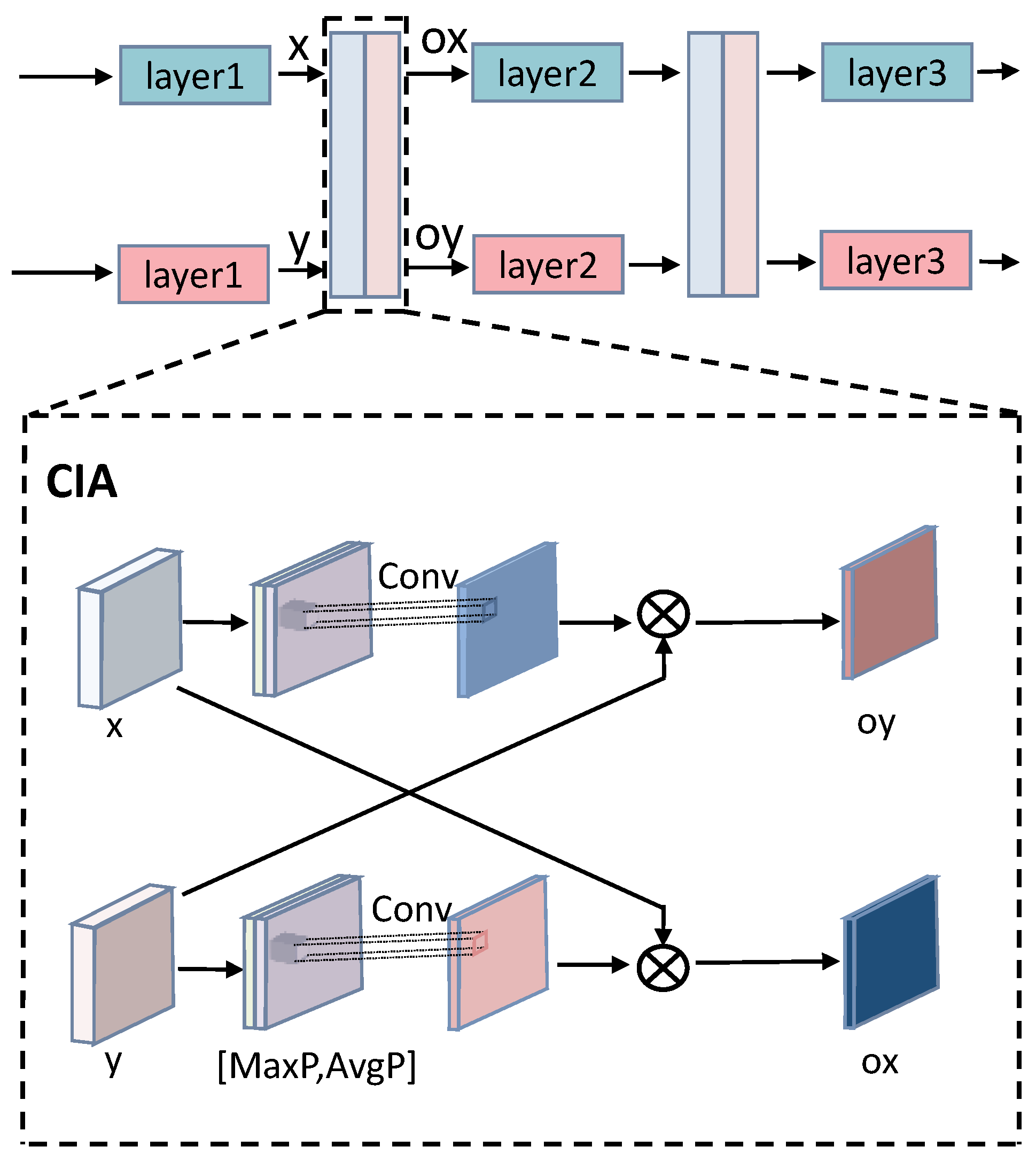
3.2.3. Cross-Modal Interactive Attention

Relying solely on the pseudo-Siamese network structure can only ensure the independence of feature extraction across different modalities, without achieving effective interaction and knowledge sharing between the two modalities. Thus, we introduce the CIA module in the network to enhance the learning capabilities across different modalities. The CIA module is designed to highlight salient structural regions in images. Through cross-modal learning, it adjusts the weight and attention distributions across locations in one modality based on information from the other. This not only helps the model to better capture the spatial structure in the input data but also improves the quality of feature representation.

As shown in Figure 3, the CIA module performs max pooling and average pooling operations on the feature map of one modality to capture the global contextual information of this modality. Then, the results of these two pooling operations are concatenated and processed through a 1 × 1 convolutional layer to generate a set of spatial attention weights. These spatial attention weights are subsequently multiplied with the feature map of the other modality, emphasizing the salient parts that both modalities focus on while suppressing irrelevant or interfering regions. The fused feature map integrates the key information from both modalities, enhancing the consistency and complementarity of the cross-modal features.

3.3. Loss Function

The final loss of our network comprises four parts: L1 for optical image feature point localization, L2 for descriptor matching between optical and transformed SAR images, L3 for SAR image feature point localization, and L4 for descriptor matching between SAR and transformed optical images. The formula is as follows:

$$L=L_1+\lambda L_2+L_3+\lambda L_4$$

(6)

where, $\lambda$ is a pivotal hyperparameter that balances the contributions between the task of keypoint detection and the task of descriptor learning. A higher $\lambda$ value encourages the network to focus on learning discriminative descriptors for matching, while a lower $\lambda$ prioritizes the accurate localization of feature points. The optimal value of $\lambda$ is determined through ablation studies, as detailed in Section 4.9. The feature point loss is defined as

$$L_{1,3}={\displaystyle \frac{1}{H_C{W}_C}}\mathbf{\sum }_{h=1,w=1}^{H_C{W}_C}-log\left({\displaystyle \frac{e^{X_{hw}\left[y_{hw}\right]}}{{\mathbf{\sum }}_{k=1}^{65}{e}^{X_{hw}\left[k\right]}}}\right)$$

(7)

The shape of the feature map of the feature points output by the network is $(H_C,W_C,65)$, where $y_{hw}$ represents the ground truth label, $X_{hw}\left[y_{hw}\right]$ is the predicted value for the class $y_{hw}$, and $X_{hw}\left[k\right]$ ($k=1,2,\dots ,65$) denotes the predicted values for other classes. This cross-entropy loss function treats all categories equally. When $y_{hw}=65$, the network is forced to learn high-probability predictions for the garbage bin category; when $y_{hw}$ is a position index, the network is forced to learn probability predictions for the corresponding feature point location. The descriptor loss is defined as

$$s=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\parallel H·P_{hw}-P_{h^{\prime }{w}^{\prime }}\parallel \le 8\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

$$L_{2,4}={\displaystyle \frac{1}{{\left(H_C{W}_C\right)}^2}}\mathbf{\sum }_{h=1,w=1}^{H_C,W_C}\mathbf{\sum }_{h^{\prime }=1,w^{\prime }=1}^{H_C,W_C}l(d,d^{\prime },s)$$

(9)

In computing the descriptor loss, a function $l(d,d^{\prime },s)$ is defined as $l(d,d^{\prime },s)={\lambda }_d\times s\times max(0,m_p-d^T{d}^{\prime })+(1-s)\times max(0,d^T{d}^{\prime }-m_n)$. Here, $P_{hw}$ and $P_{h^{\prime }{w}^{\prime }}$ represent the keypoints at the center positions of the $(h,w)$ cells in the two images, while d and $d^{\prime }$ denote the descriptor vectors corresponding to each cell in the two images. The hyperparameters within the descriptor loss function—the weighting term ${\lambda }_d$ and the margins $m_p$, $m_n$—are adopted directly from the SuperPoint design [8], as they effectively govern the internal balance of positive and negative pairs and have been proven to work well in practice. The weighting term ${\lambda }_d$ addresses the fact that negative correspondences vastly outnumber positive correspondences.

4. Results

In this section, we first present an overview of the primary metrics, relevant datasets, and the detailed experimental setup. Then, we compare the performance of the proposed innovative method with that of multiple existing baseline methods to verify its superiority. We then assess the impact of varying levels of image noise on registration accuracy and analyze the performance of two feature point and descriptor decoupling strategies. Furthermore, we systematically evaluate the effects of two distinct optimizers on the training stability and final performance of PLISA. Finally, comprehensive ablation studies and parameter analysis are conducted.

4.1. Evaluation Metrics

We evaluate the image registration performance using four metrics: the root mean square error (RMSE), matching success rate (SR), number of correctly matched points (NCM), and repeatability [3]. Among them, the repeatability metric is specifically designed to validate the quality of the extracted feature points. All metric values reported in the following represent averages computed over the complete test dataset.

4.1.1. RMSE

The RMSE is used to quantify the registration accuracy between the reference image and the target image after the predicted transformation, with smaller values indicating higher registration accuracy [68]. The RMSE is calculated as follows:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{m}}\mathbf{\sum }_{i=1}^m\left[{(x_i^{o^{\prime }}-x_i^s)}^2+{(y_i^{o^{\prime }}-y_i^s)}^2\right]}$$

(10)

where $(x_i^o,y_i^o)$ and $(x_i^s,y_i^s)$ are the coordinates of the i-th correctly matched feature point pair in the reference image and the target image, respectively, after removing mismatched points using the FSC algorithm. The variable m represents the number of correct matching point pairs remaining after the FSC-based mismatch removal process.

The point $(x_i^o,y_i^o)$ from the reference image is then transformed to obtain its predicted coordinates $(x_i^{o^{\prime }},y_i^{o^{\prime }})$ in the target image. The RMSE is computed based on the differences between these predicted coordinates and the actual corresponding point coordinates $(x_i^s,y_i^s)$ in the target image, providing an objective measure of the registration transformation accuracy.

4.1.2. NCM

NCM denotes the number of correct matches. This metric provides a direct measure of the number of feature points that are accurately matched between the reference and target images. The definition of a correct match is as follows [8]:

$$\mathrm{correct}\mathrm{match}=|X(x,y)-T_{\mathrm{truth}}\ast Y(x,y)|<3$$

(11)

In this case, $X(x,y)$ represents the feature point location of the target image after the predicted transformation, $Y(x,y)$ denotes the corresponding feature point location on the target image after the actual transformation, and $T_{\mathrm{truth}}$ refers to the actual transformation matrix.

4.1.3. SR

A match is considered successful when the RMSE for an image pair is below 3 pixels. The SR is calculated as the proportion of successfully matched pairs relative to the total number of pairs [44].

4.1.4. Repeatability (REP)

Repeatability simply measures the probability that a point is detected in the second image. We compute the repeatability by measuring the distances between the extracted 2D point centers [8]. More specifically, let us assume that we have $N_1$ points in the first image and $N_2$ points in the second image. Correctness in repeatability experiments is defined as follows: a point is considered correctly repeated if the distance from its corresponding point in the other image is below a threshold d. Empirically, d is set to 3 pixels [31,69,70]; hence, this metric is commonly referred to as the 3-pixel repeatability. In this work, we also adopt d = 3 as the threshold.

$$\begin{array}{c}\hfill \mathrm{Corr}\left(x_i\right)=\left(\underset{j\in \{1,\dots ,N_2\}}{min}\parallel x_i-{\widehat{x}}_j\parallel \right)\le d\end{array}$$

(12)

$$\begin{array}{c}\hfill \mathrm{Rep}={\displaystyle \frac{1}{N_1+N_2}}\left(\mathbf{\sum }_i\mathrm{Corr}\left({\mathbf{x}}_i\right)+\mathbf{\sum }_j\mathrm{Corr}\left({\mathbf{x}}_j\right)\right)\end{array}$$

(13)

4.2. Dataset

The experiment uses two public multimodal remote sensing image matching and registration datasets, SEN1-2 [71] and OSdataset [72]. The model’s performance is evaluated on the test splits of both the SEN1-2 dataset and OSdataset, with the latter used exclusively to further assess the generalizability to unseen data. Figure 4 shows three groups of multimodal image samples from OSdataset and the SEN1-2 dataset, where significant nonlinear radiometric differences between the SAR images [3] and the corresponding visible images can be clearly observed, posing an additional challenge for cross-modal image processing. The specifics of each dataset are as follows.

The SEN1-2 dataset [71] consists of SAR and optical image patches, with SAR images provided by the Sentinel-1 satellite and the corresponding optical images provided by Sentinel-2. All image patches are standardized to a size of 256 × 256 pixels, with a spatial resolution of 10 m. The training set consists of 9036 pairs and the test set consists of 1260 pairs.

OSdataset [72] contains co-registered SAR and optical image pairs in both 256 × 256 and 512 × 512 pixel sizes. In this study, we utilize the 256 × 256 version, which provides 10,692 image pairs with a 1-meter spatial resolution. From this collection, 1696 pairs of images were randomly chosen as the test set.

M4-SAR [73] is a multiresolution, multipolarization, multiscenario, and multisource dataset designed for object detection based on the fusion of optical and SAR images. It was jointly developed by the PCA Lab of Nanjing University of Science and Technology, the Key Laboratory of Intelligent Computing and Signal Processing of the Ministry of Education at Anhui University, and the College of Computer Science at Nankai University. The dataset contains 112,184 precisely aligned image pairs and nearly one million annotated instances. For the evaluation of the model’s generalization capabilities, we randomly selected 406 optical and SAR image pairs with a spatial resolution of 60 m as the test set.

The SEN12MS-CR [74] dataset comprises 122,218 patch triplets, each containing a Sentinel-1 SAR image, a Sentinel-2 optical image, and a cloud-covered Sentinel-2 optical image. From this collection, we randomly selected 383 cloud-covered optical and SAR image pairs to constitute the test set.

To address the challenge of partial overlap registration, we created the OSD-PO dataset, which is derived from the original OSdataset and consists of 1000 image pairs. These were constructed by first extracting 512 × 512 image patches from OSdataset, which were then cropped with controlled overlap ratios ranging from 50% to 80%. To simulate realistic imaging perturbations, we applied a series of geometric transformations: 70% of the pairs underwent slight translation, 20% were subjected to scale transformation, and the remaining 10% received combined rotation and scale transformations.

4.3. Experimental Details

All experiments were conducted using an NVIDIA RTX 3090 GPU. In the training process, we adopted Adam as an optimizer. Hyperparameters were set to $\lambda =1$ and $\alpha =0.15$. The positive margin $m_p$ for the descriptor hinge loss was set to 1, and the negative margin $m_n$ was set to 0.2. Prior to the commencement of the experiments, necessary data preprocessing steps were applied to the SAR images to enhance the image quality and improve the subsequent processing results, including histogram equalization and Lee filtering.

4.4. Comparative Experiments

We evaluated seven state-of-the-art methods alongside our proposed approach across three different scenarios: slight translation, scale transformation, and rotation and scale transformation. Here, slight translation refers to minimal global image displacement, typically constrained to a range of ±5 pixels, without involving scale, rotation, or perspective alterations. Scaling transformation is achieved by sampling random scale factors from a truncated normal distribution centered at 1.0 with a ±10% amplitude. The rotation and scale transformations simultaneously applied random rotation across a continuous range of −90° to +90° and scaling within the range of 0.9–1.1. Additionally, all methods were tested on the partially overlapping OSD-PO dataset. The seven methods are RIFT (2019) [35], Superpoint (2017) [8], CMM-Net (2021) [5], ReDFeat (2022) [6], ADRNet (2024) [57], MINIMA-LG (2024) [75], and MINIMA-RoMa (2024) [75], as shown in

Table 1. Comparative summary of key characteristics of representative image registration methods.

Method	Core Idea	Advantages	Limitations	Key Differentiation from PLISA
RIFT [35]	Uses phase congruency to detect and describe features simultaneously.	Maintains robustness under severe nonlinear radiometric differences.	Computationally intensive, unsuitable for large-scale processing.	PLISA achieves better efficiency with lower computational cost while maintaining comparable robustness.
SuperPoint [8]	Self-supervised framework using pseudo-labels for interest point detection.	Excellent performance on optical images with strong generalization.	Fails to handle domain shift in cross-modal scenarios.	PLISA specifically addresses optical–SAR matching through adapted self-supervision.
CMM-Net [5]	Pseudo-Siamese network with separate and shared layers for different features.	Effectively combines modality-specific and invariant characteristics.	Simple feature fusion without spatial modeling.	PLISA introduces CIA module for dynamic spatial relationship modeling.
ReDFeat [6]	Decoupled learning of detector and descriptor via mutual weighting.	Enhances training stability and feature reliability.	Cannot ensure consistent keypoints across modalities.	PLISA employs APLM for consistent keypoint extraction across modalities.
ADRNet [57]	Detector-free approach with deformable transformations and attention.	Handles complex deformations and captures long-range dependencies.	Prohibitively high computational requirements.	PLISA uses efficient detector-based approach suitable for large-scale applications.
MINIMA—LG [75]	Integrates LightGlue matching with generative data engine for cross-modal matching.	Strong generalization via large-scale synthetic data, efficient matching.	Limited effectiveness for optical–SAR modality registration.	PLISA focuses on architectural innovations rather than data scaling.
MINIMA—RoMa [75]	Combines RoMa’s robust matching with generative data scaling.	Exceptional robustness to viewpoint/illumination changes, handles multimodal distributions.	Detector-free approach suffers from slow inference and high GPU memory consumption.	PLISA employs sparse matching for real-time performance.

.

4.4.1. Slight Translation Scenario

Evaluations of RIFT, Superpoint, CMM-Net, ReDFeat, ADRNet, MINIMA-LG, MINIMA-RoMa, and the proposed method on the SEN1-2 dataset and OSdataset under slight translation transformations reveal varying performance levels. The corresponding quantitative evaluation results are provided in

Table 2. Slight translation scenario. Results of different methods on the SEN1-2 dataset and OSdataset. The bolded data indicates the optimal values.

Method	Year	Ref.	SEN1-2				OSdataset
			SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
RIFT	2019	[35]	72.619	54.973	2.826	16.232	72.465	60.747	4.224	19.354
Superpoint	2017	[8]	0.000	0.070	62.564	9.250	0.000	1.854	53.421	8.400
CMM-Net	2021	[5]	4.360	8.930	6.891	6.600	9.300	11.407	6.077	7.670
ReDFeat	2022	[6]	100.000	200.470	0.408	18.900	65.500	37.180	12.010	19.000
ADRNet	2024	[57]	100.000	-	0.242	-	77.830	-	2.092	-
MINIMA-LG	2024	[75]	12.600	36.791	43.381	12.200	36.900	73.235	28.292	22.100
MINIMA-RoMa	2024	[75]	99.400	1341.507	0.657	-	99.500	5115.110	0.421	-
Ours	-	-	100.000	258.500	0.120	88.360	99.700	101.468	0.398	81.100

.

On the SEN1-2 dataset, the proposed method achieves an SR of 100%, matching ReDFeat and ADRNet while significantly outperforming RIFT (72.619%), Superpoint (0%), and CMM-Net (4.360%). In terms of overall performance, MINIMA-RoMa also demonstrates impressive results across multiple metrics, particularly achieving an exceptionally high NCM, which is attributed to its detector-free matching paradigm that involves dense pixel-level correspondence. Our method attains a competitively high NCM while maintaining computational efficiency. Most notably, our approach achieves the lowest RMSE and the highest repeatability, demonstrating superior matching accuracy and robustness. Our method maintains competitive efficiency while delivering substantially improved matching precision.

Similar trends are observed on OSdataset, where our method again achieves a near-perfect SR (99.7%), exceeding ReDFeat (65.5%), ADRNet (77.83%), and RIFT (72.465%). Its NCM is also significantly lower than that of MINIMA-RoMa, but our method achieves the lowest RMSE and the highest repeatability. Superpoint and CMM-Net exhibit notably poor performance across all metrics. These results underscore our method’s effectiveness under slight translational deformations.

The qualitative results in Figure 5 and Figure 6 visually corroborate the quantitative findings. Among all competitors, MINIMA-RoMa also produces commendable registration results, followed by ReDFeat, which shows relatively good performance. Nevertheless, the proposed method consistently yields the most reliable matches.

In summary, the proposed method demonstrates consistently superior performance across both datasets, proving highly robust and accurate under translation transformations.

4.4.2. Scale Transformation Scenario

Scale transformations presented significant challenges for most evaluated methods, as clearly evidenced by the quantitative results in

Table 3. Scale transformation scenario. The bolded data indicates the optimal values.

Method	Year	Ref.	SEN1-2				OSdataset
			SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
RIFT	2019	[35]	37.063	25.826	4.804	22.125	45.991	30.164	6.002	25.550
Superpoint	2017	[8]	0.000	0.037	62.384	10.889	0.000	1.118	56.377	9.330
CMM-Net	2021	[5]	0.550	6.850	8.271	6.500	0.940	7.930	8.202	6.140
ReDFeat	2022	[6]	20.700	6.900	37.625	23.700	13.700	5.646	48.324	23.660
ADRNet	2024	[57]	1.667	-	19.1711	-	1.590	-	20.513	-
MINIMA-LG	2024	[75]	15.100	47.588	41.898	15.300	55.100	140.962	20.365	37.700
MINIMA-RoMa	2024	[75]	99.800	1566.301	0.564	-	99.800	5220.652	0.419	-
Ours	-	-	100.000	138.540	0.147	82.740	98.990	58.000	0.728	73.500

. While the majority of the approaches suffered from substantial performance degradations, MINIMA-RoMa maintained relatively strong performance across key metrics, demonstrating notable resilience to scale variations. The proposed method also achieved consistently superior results despite the challenging conditions.

On the SEN1-2 dataset, our method achieves a perfect SR of 100%, demonstrating clear superiority over other approaches. While MINIMA-RoMa also maintains strong performance, with a 99.8% SR and exceptionally high NCM value, our method achieves the lowest RMSE and highest repeatability. The performance gap becomes particularly evident when comparing it with other methods: RIFT achieves only a 37.063% SR, while ADRNet fails functionally under scale changes, with only a 1.667% SR.

On OSdataset, our method maintains outstanding performance, with a 98.99% SR, closely matching MINIMA-RoMa (99.8% SR) while achieving superior repeatability. MINIMA-LG shows inconsistent performance across datasets, achieving moderate results on SEN1-2 (15.1% SR) but better performance on OSdataset (55.1% SR), albeit still substantially below the leading methods.

The qualitative results in Figure 7 and Figure 8 corroborate these findings. MINIMA-RoMa produces commendable matching results across all test pairs. MINIMA-LG shows acceptable performance on the three image pairs from the SEN1-2 dataset but exhibits noticeable degradation on the OSdataset examples. The proposed method sustains reliable matches across all test pairs, maintaining robustness where other methods experience significant performance deterioration.

In summary, while MINIMA-RoMa maintains competitive performance in scale transformation scenarios, our method also demonstrates exceptional scale invariance, achieving a perfect or near-perfect SR while maintaining superior matching precision and repeatability across diverse datasets.

4.4.3. Rotation and Scale Transformation Scenario

Large-angle rotation and scale transformations combined represent the most challenging scenario. The quantitative results in

Table 4. Rotation and scale transformation scenario. The bolded data indicates the optimal values.

Method	Year	Ref.	SEN1-2				OSdataset
			SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
RIFT	2019	[35]	2.777	3.496	23.026	22.089	4.658	3.587	50.840	23.748
Superpoint	2017	[8]	0.000	0.048	65.329	10.700	0.000	0.667	62.600	9.590
CMM-Net	2021	[5]	0.150	1.980	21.377	5.010	0.170	2.090	25.889	3.570
ReDFeat	2022	[6]	7.380	2.160	77.630	23.990	1.650	0.741	92.715	24.300
ADRNet	2024	[57]	0.158	-	122.124	-	0.117	-	122.174	-
MINIMA-LG	2024	[75]	2.500	7.255	48.531	2.500	14.300	29.588	42.554	10.400
MINIMA-RoMa	2024	[75]	83.400	401.520	1.860	-	87.300	1657.154	1.481	-
Ours	-	-	100.000	136.496	0.171	82.120	98.500	48.100	0.896	71.500

reveal a stark performance gap: the proposed method delivers near-flawless accuracy, while most competing methods exhibit functional breakdown.

On the SEN1-2 dataset, our approach achieves a perfect 100% SR, demonstrating remarkable robustness to rotation and scale transformations. MINIMA-RoMa emerges as the second-best performer with an 83.4% SR, although its performance shows noticeable degradation compared to scale transformation scenarios. The gap becomes particularly evident when considering other methods: ReDFeat achieves only a 7.38% SR, while RIFT and ADRNet fall below a 3% SR. Our method also dominates in matching quality, achieving the lowest RMSE and highest repeatability.

The qualitative results in Figure 9 and Figure 10 visually demonstrate the performance hierarchy under these conditions. The proposed method clearly produces the most reliable correspondences, maintaining robust matching quality despite the combined large-angle rotation and scale transformations. MINIMA-RoMa emerges as the second-best performer, generating substantially better matches than other approaches. Other competing methods, including RIFT and CMM-Net, exhibit near-complete failure and lack practical utility for registration tasks.

In particular, under rotation and scale transformation conditions, we focus on demonstrating the advantages of the proposed method compared to other state-of-the-art methods. The checkerboard visualization results of six pairs of high-difficulty images are shown in Figure 11, clearly illustrating the superior performance of our method in multimodal image registration tasks.

4.4.4. Evaluation on Partially Overlapping Dataset

The partially overlapping scenario represents an extremely challenging condition for image registration, as clearly evidenced by the quantitative results in

Table 5. Partially overlapping dataset. The bolded data indicates the optimal values.

Method	Year	Ref.	OSD-PO
			SR (%)	NCM	RMSE	REP (%)
RIFT	2019	[35]	0.000	0.710	30.408	14.400
Superpoint	2017	[8]	0.000	0.080	80.481	2.640
CMM-Net	2021	[5]	0.000	2.054	29.550	3.000
ReDFeat	2022	[6]	5.300	2.915	43.529	24.96
ADRNet	2024	[57]	0.000	-	121.365	-
MINIMA-LG	2024	[75]	7.000	9.604	46.982	5.300
MINIMA-RoMa	2024	[75]	20.100	258.249	23.117	-
Ours	-	-	5.560	3.080	31.859	27.760

. The overall performance across all evaluated methods remains limited, highlighting the difficulty of this task. Among the compared approaches, MINIMA-RoMa achieves the highest SR at 20.1%, along with significantly superior NCM values, although its matching accuracy, as reflected in the RMSE, still requires substantial improvement. Our method attains a 5.56% SR, comparable to ReDFeat and MINIMA-LG, while achieving the best repeatability among all methods. Notably, RIFT, SuperPoint, CMM-Net, and ADRNet completely fail to produce any successful registrations under these demanding conditions.

We acknowledge the current limitations of our approach in handling severe partial overlap scenarios, particularly in achieving a higher SR. The generally constrained performance across all methods is evident, including the relatively high-performing MINIMA-RoMa. We attribute the generally poor performance across all methods to the absence of non-overlapping image pairs in the training data. This limitation highlights an important direction for future research, where incorporating explicitly non-overlapping training samples could potentially enhance the method’s capabilities in handling extreme partial overlap scenarios.

4.4.5. Computational Efficiency Discussion

We evaluate the inference speed and GPU memory consumption of our method alongside other approaches, with all experiments conducted under the same environment on an NVIDIA RTX 3090 GPU. As shown in

Table 6. Computational efficiency comparison.

Method	INFERENCE TIME (s)	GPU MEMORY (Mib)
Superpoint	0.757	1654
CMM-Net	0.200	1744
ReDFeat	0.060	504
ADRNet	0.039	1930
MINIMA-LG	0.129	1452
MINIMA-RoMa	2.437	13,100
Ours	0.126	1680

, our method achieves an inference time of 0.126 s per image pair and memory usage of 1680 MiB. While ReDFeat and ADRNet exhibit faster inference speeds, and ReDFeat also consumes significantly less memory, our approach still maintains competitive efficiency. Notably, MINIMA-RoMa, which delivers superior performance compared to ReDFeat and ADRNet and is among the best performers aside from our method, incurs significantly higher computational costs due to its detector-free design. Although our method is not the absolute best in terms of computational efficiency, it strikes a favorable balance between performance and resource demands, making it a practically viable and efficient solution for real-world applications.

4.4.6. Discussion of Generalization Capabilities

This study intentionally employs the SEN1-2 dataset, OSdataset, and the M4-SAR dataset, with significantly different spatial resolutions, to rigorously evaluate the generalization capabilities of the proposed method. As shown in

Table 7. Cross-dataset generalization performance evaluation.

Dataset	SR (%)	NCM	RMSE	REP (%)
OSdataset	98.500	48.100	0.896	71.500
SEN1-2	100.000	136.496	0.171	82.120
M4-SAR	96.059	26.881	1.471	43.843
SEN12MS-CR	100.000	94.214	0.243	71.000

, the consistently high performance across both datasets demonstrates notable robustness to significant variations in the ground sampling distance. Although a performance decrease is observed on the M4-SAR dataset, the overall results remain satisfactory.

Additionally, the SEN12MS-CR dataset is included to assess the method’s performance under cloud cover conditions. The empirical results confirm that our approach maintains reliable feature matching capabilities despite atmospheric disturbances.

We attribute this robustness to the characteristics of the feature points that our method leverages. The detected feature points are predominantly high-quality corners. Such features maintain their distinctive characteristics across resolution variations because their salience originates from the local geometric structure rather than intensity variations, which tend to be highly sensitive to resolution changes. As a result, identical physical structures, such as building corners or road intersections, produce consistent feature representations in 60 m and 1 m imagery.

The empirical evidence indicates that the method successfully bridges substantial resolution gaps and maintains functionality under challenging conditions like cloud cover, making it highly suitable for practical applications involving multisource remote sensing data.

4.5. Discussion of the Effectiveness of the APLM

The proposed APLM serves as the cornerstone for generating supervisory signals in our self-supervised framework. To comprehensively validate its efficacy, this section provides a detailed analysis from two critical perspectives: the quality of the generated pseudo-labels and the robustness of the model to potential inaccuracies within them.

First, to validate the quality of the generated pseudo-labels, we conducted manual verification. A prerequisite for the success of our method is the availability of high-quality pseudo-labels for training the feature matcher. To quantitatively assess this, we performed manual verification on a randomly selected set of 600 image pairs from the training corpus. The statistical results confirm the exceptional reliability of our APLM, yielding average pseudo-label accuracy of 93.9%. This high precision ensures that the supervisory signal provided to the matcher is overwhelmingly correct, thereby effectively guiding the learning process.

Second, we designed an experiment to investigate the model’s robustness to noise. Specifically, we systematically introduced errors into the training data. For each image pair, 10% of the pseudo-label point correspondences were corrupted by shifting the coordinates of the SAR image points by 3 pixels in a random direction, while the corresponding optical image points remained unaltered.

The model was subsequently trained and evaluated on this perturbed dataset. The impact on the matching performance across key datasets is summarized in

Table 8. Performance comparison under clean and noisy pseudo-labels.

	SEN1-2				OSdataset
	SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
Clean	100.000	136.496	0.171	82.120	98.500	48.100	0.896	71.500
Noise	100.000	106.047	0.200	81.010	97.500	39.941	1.3087	70.470

. On the SEN1-2 dataset, the performance remained highly stable, with the SR and repeatability showing negligible changes, while the RMSE saw a minor increase of 0.03, and the NCM decreased by 30. A contained effect was observed on OSdataset, where the repeatability decreased by 1%, the SR decreased by 1%, the RMSE increased by 0.3, and the NCM was reduced by 10. Crucially, the training process remained stable and converged normally under both conditions.

These results robustly demonstrate that our framework is not critically sensitive to a small proportion of erroneous pseudo-labels, confirming that the APLM provides a sufficiently clean and robust supervisory signal for effective model convergence.

4.6. Impact of Noise on Cross-Modal Registration Accuracy

This section analyzes the effect of synthetic noise on the performance of PLISA. To simulate realistic noise while maintaining experimental control, we introduced two types of synthetic noise into pre-denoised SAR images. The first type was based on the original SAR sensor noise that had been initially removed from the SEN1-2 dataset using a Lee filter. We scaled this noise with coefficients of 0.6, 1.2, 1.8, 2.4, 3.0 and injected it back into the pre-denoised images. A coefficient of 1.0 corresponds exactly to the inherent noise level of the original SAR images, providing a realistic baseline for comparison. The second type was Gaussian noise, which was added at three intensity levels, with sigma values of 30, 50, and 70, into the pre-denoised SAR images.

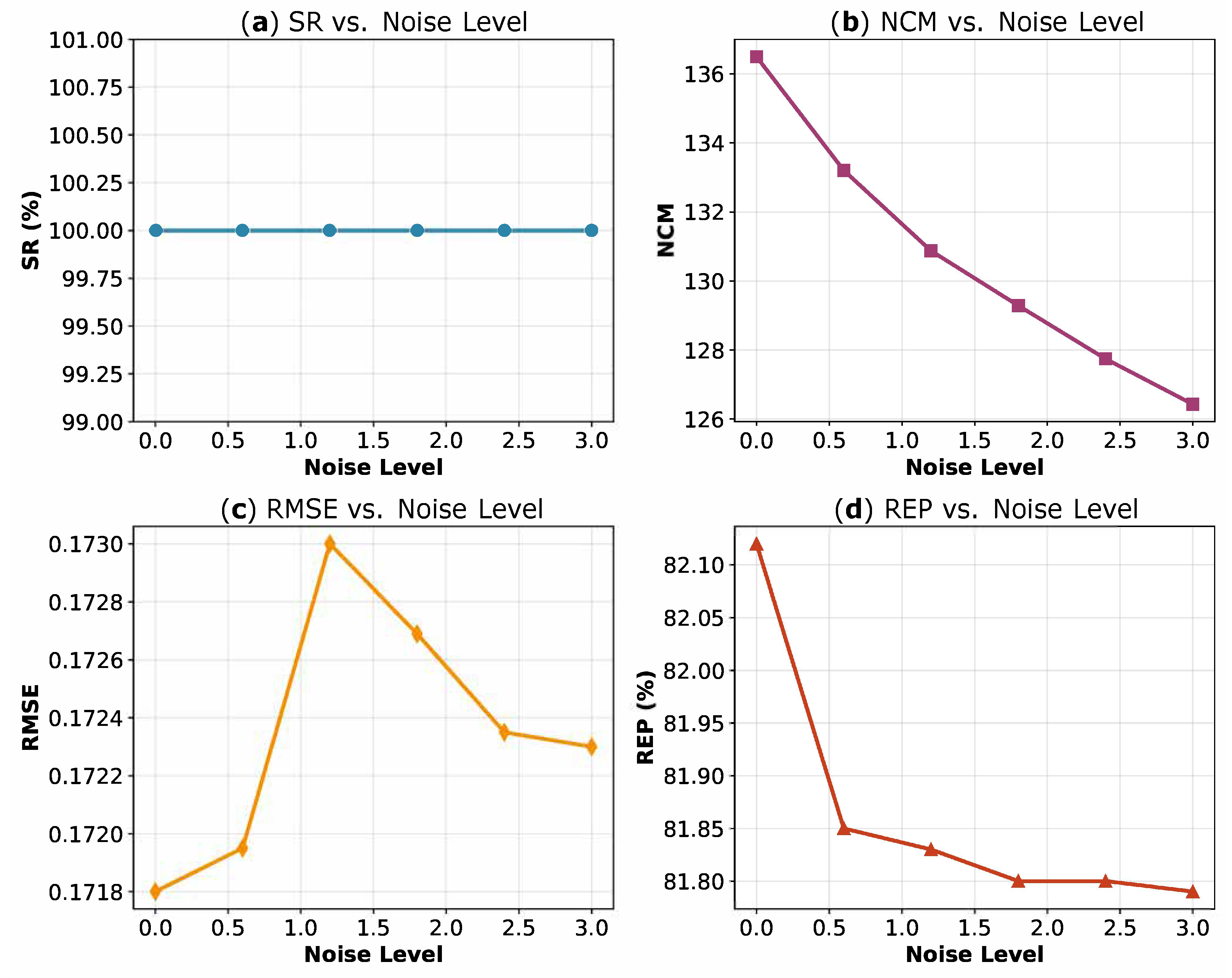
As illustrated in Figure 12 for the first type of noise and

Table 9. Performance comparison different levels of Gaussian noise.

Noise Level	SEN1-2
	SR (%)	NCM	RMSE	REP (%)
$\sigma =0$	100.000	136.496	0.171	82.120
$\sigma =30$	100.000	136.200	0.171	82.100
$\sigma =50$	100.000	129.560	0.174	82.020
$\sigma =70$	100.000	122.550	0.179	81.900

for the second type, all metrics exhibit consistent trends with increasing noise: the SR and NCM show a steady decline, while the RMSE rises slightly and the repeatability decreases modestly. Despite these variations, PLISA maintains robust performance across all noise levels, demonstrating its practical utility in real-world scenarios, where the image quality is often compromised.

4.7. Influence of Feature Point and Descriptor Decoupling Strategy

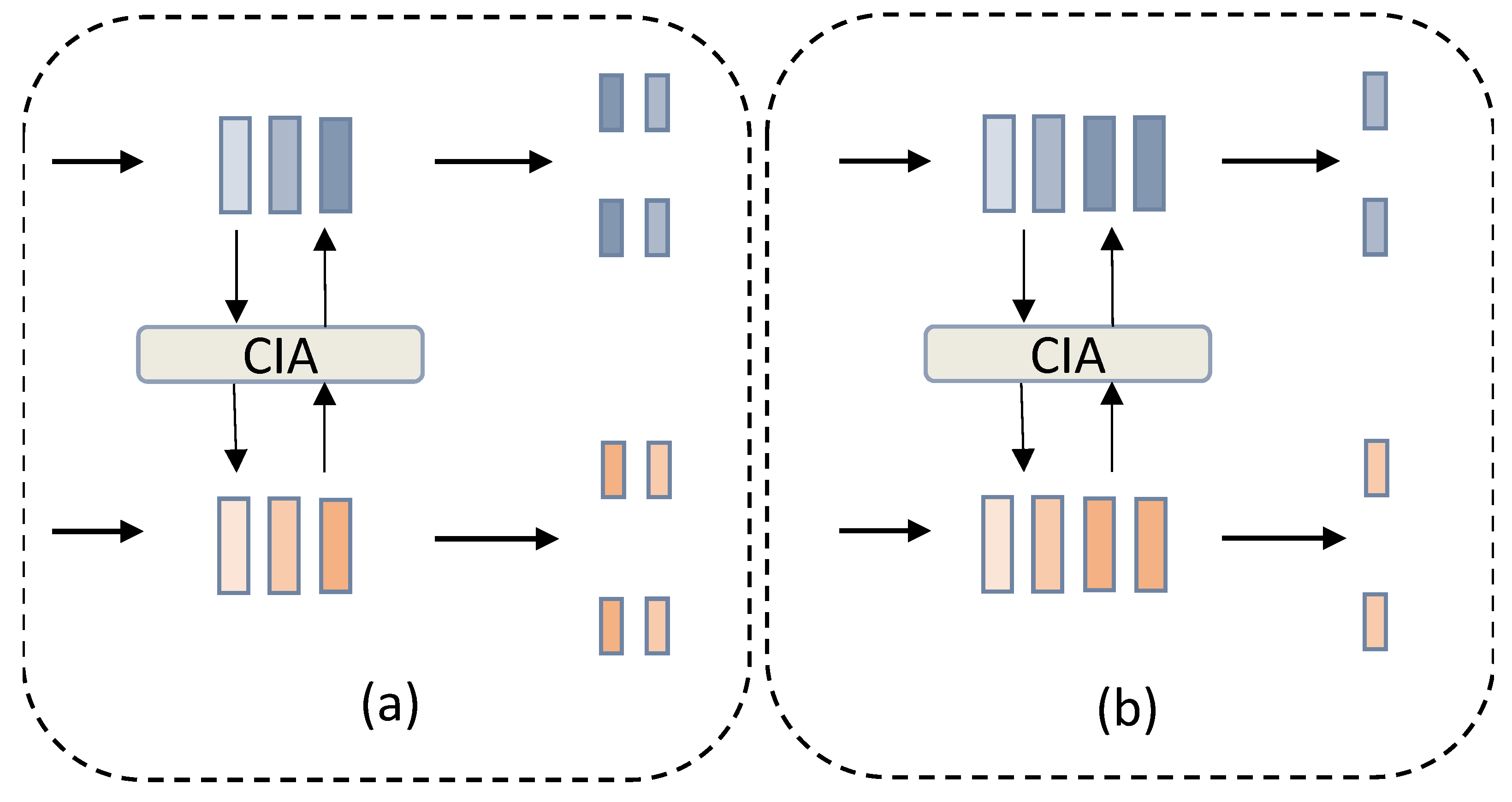
To evaluate the impact of the feature point and descriptor decoupling strategy on the experimental results, we conduct a comparative analysis of two different decoupling schemes and perform an in-depth study of their effects. Figure 13 illustrates the network architectures under these two decoupling strategies, with the key difference lying in the depth of the network at which the decoupling occurs: the first strategy, termed the early-stage decoupling strategy (EDS), separates the feature point detection and descriptor generation tasks at an earlier stage, while the second strategy, referred to as the deep-layer decoupling strategy (DDS), performs this separation at a deeper layer of the network.

Experimental results reflecting the changes in the metrics when applying the two decoupling strategies are shown in

Table 10. Performance comparison of different decoupling strategies.

Strategy	SEN1-2			OSdataset
	SR (%)	NCM	RMSE	SR (%)	NCM	RMSE
EDS	100.000	136.496	0.171	98.500	48.1	0.896
DDS	100.000	129.160	0.177	98.100	43.950	0.978

. On the SEN1-2 dataset, EDS achieved a lower RMSE of 0.171, compared to 0.177 under DDS, along with a higher NCM value of 136.496 versus 129.160. The improvement is even more pronounced on the more challenging OSdataset, where EDS attained an RMSE of 0.896—a reduction of 0.082 compared to DDS—and improved both the NCM and SR substantially.

The observed performance disparities are predominantly attributable to the distinct decoupling positions within the network architecture. Specifically, when decoupling is implemented at deeper layers of the network, the interplay between the feature point detection network and the descriptor generation network is intensified. This heightened interaction, while beneficial in certain contexts, may introduce complexities that impede the independent optimization of their respective tasks.

Conversely, adopting an early decoupling strategy enables each subnetwork to focus more singularly on its designated task. By minimizing the mutual interference between the two networks, early decoupling facilitates a more focused optimization process. This, in turn, enhances the overall performance of the system by allowing each subnetwork to operate more efficiently within its specialized domain.

4.8. Experiments with Adam and AdaBoB Optimizers

To evaluate the robustness and consistency of the proposed PLISA framework under different optimizers, we conducted comparative experiments using both the Adam and AdaBoB [76] optimizers. Adam is a classic and widely adopted optimization algorithm, well validated across numerous tasks. In contrast, AdaBoB [76] is a more recent method that integrates the gradient confidence mechanism from AdaBelief and the dynamic learning rate bounds from AdaBound. This combination ensures stable convergence, theoretical guarantees, and low computational complexity. The experiments were designed to compare the performance of PLISA under both optimizers. Default parameters were used for AdaBoB [76] throughout the experiments.

The quantitative results are summarized in

Table 11. Performance comparison under different optimizers (Adam vs. AdaBoB).

Method	SEN1-2				OSdataset
	SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
Adam	100.000	136.496	0.171	82.120	98.500	48.100	0.896	71.500
AdaBoB	100.000	119.939	0.165	82.490	98.300	47.653	0.896	72.900

. PLISA exhibits minimal performance variation between Adam and AdaBoB [76], with all metrics remaining highly consistent. This indicates that the method is robust to the choice of optimizer.

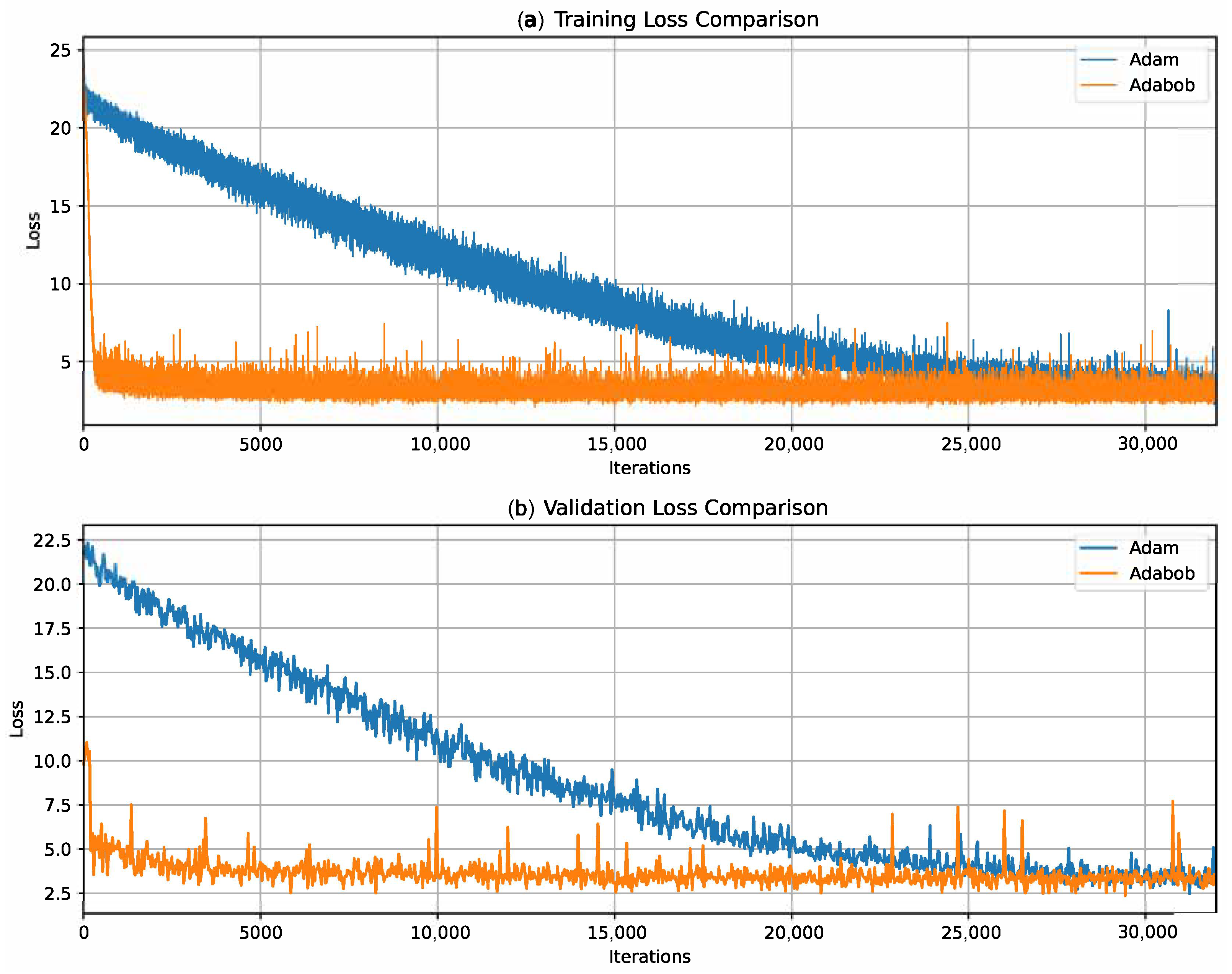
The training and validation loss curves are shown in Figure 14. Both optimizers effectively reduce the loss, with the training loss dropping rapidly from an initial value of 20–25 and eventually converging close to zero. AdaBoB, however, demonstrates smoother loss curves in the mid-to-late training phase, with almost no visible fluctuations. This aligns with its design goal of suppressing gradient noise and enforcing stable convergence through dynamic learning rate constraints.

In summary, PLISA maintains strong and consistent performance across both optimizers. These results confirm the optimization stability and reliability of the proposed framework.

4.9. Ablation Study

To validate the effectiveness of the components in our framework, we conducted an ablation study using the SEN1-2 dataset and OSdataset, with a particular focus on evaluating the contributions of the proposed CIA module and APLM.

The results, presented in

Table 12. Ablation study on the CIA module and the APLM.

Method	SEN1-2				OSdataset
	SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
Ours	100.000	136.496	0.171	82.120	98.500	48.100	0.896	71.500
w/o APLM	0.000	0.000	50.000	0.000	0.000	0.000	49.95	0.01
w/o CIA	0.390	0.065	100.968	17.637	0.230	0.060	116.607	17.214

, clearly show that removing either the CIA module or the APLM causes a substantial drop in performance across all evaluation metrics on both datasets. Specifically, the absence of the APLM leads to a complete failure in feature matching, underscoring its essential role in generating reliable pseudo-labels for supervisory signals. Conversely, removing the CIA module severely weakens cross-modal feature interaction, resulting in a sharp decline in matching accuracy. These findings strongly affirm that both components are critical for learning robust feature representations and achieving the accurate registration of optical–SAR image pairs.

Building upon the foundational ablation study, we further validate the efficacy of the proposed CIA module and justify its specific design choice by comparing its performance against two other representative interactive attention mechanisms: interactive channel attention (ICA) and interactive convolutional block attention (ICBAM). The quantitative results are presented in

Table 13. Performance comparison of different network architectures for the CIA module.

Method	SEN1-2				OSdataset
	SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
CIA	100.000	136.496	0.171	82.120	98.500	48.100	0.896	71.500
ICA	25.500	13.834	71.460	34.000	0.200	0.138	113.000	17.500
ICBAM	0	-	-	-	0	-	-	-

. It is essential to first elucidate the conceptual differences between these three interaction paradigms to provide context for their performance disparities.

The ICA mechanism is rooted in the channel attention paradigm. Its core operation focuses on modeling interdependencies between channels across modalities, generating channel-wise weights to recalibrate the feature importance. However, this interaction occurs on spatially compressed descriptors, which risks diluting the critical spatial information that is paramount for geometric registration tasks. In contrast, the ICBA module employs a cascaded structure, typically processing channel attention first and then spatial attention in sequence. A critical drawback of this design is the inherent risk of error propagation, where suboptimal interactions in the initial channel stage are passed into and amplified by the subsequent spatial stage.

Our CIA module is designed with a fundamentally different philosophy, prioritizing direct spatial interaction. It bypasses intricate channel recalibration and instead generates spatial attention maps from one modality to directly guide the feature selection of the other. This design is intrinsically aligned with the core objective of image registration—establishing precise spatial correspondences. It explicitly forces both modalities to focus on spatially co-occurring salient regions, thereby preserving the structural integrity and enhancing the geometric consistency.

As unequivocally evidenced in Table 13, the performance of both ICA and ICBA is significantly inferior to that of our proposed CIA module. This performance disparity is a direct consequence of the misalignment between their core operational principles and the intrinsic requirements of cross-modal registration. The limitation of ICA originates from its channel-centric optimization. In cross-modal scenarios, where feature channels can embody vastly different physical interpretations, forcibly performing interchannel interaction often disrupts modality-specific information and fails to establish meaningful correlations for geometric matching. ICBA’s failure, conversely, exposes the structural vulnerability of its cascaded pipeline. The sequential process propagates distortions from the first interaction stage directly into the second, causing the spatial attention weights to be computed from already corrupted representations, which in turn amplifies errors and leads to poor overall performance.

The superior efficacy of our CIA module is therefore attributed to its dedicated spatial interaction strategy. By enabling a mutual focus on spatially co-occurring regions, it directly augments the geometric consistency between modalities. This approach effectively preserves the unique characteristics of each modality while selectively suppressing irrelevant interference, making it uniquely powerful for building robust spatial correspondences between optical and SAR images.

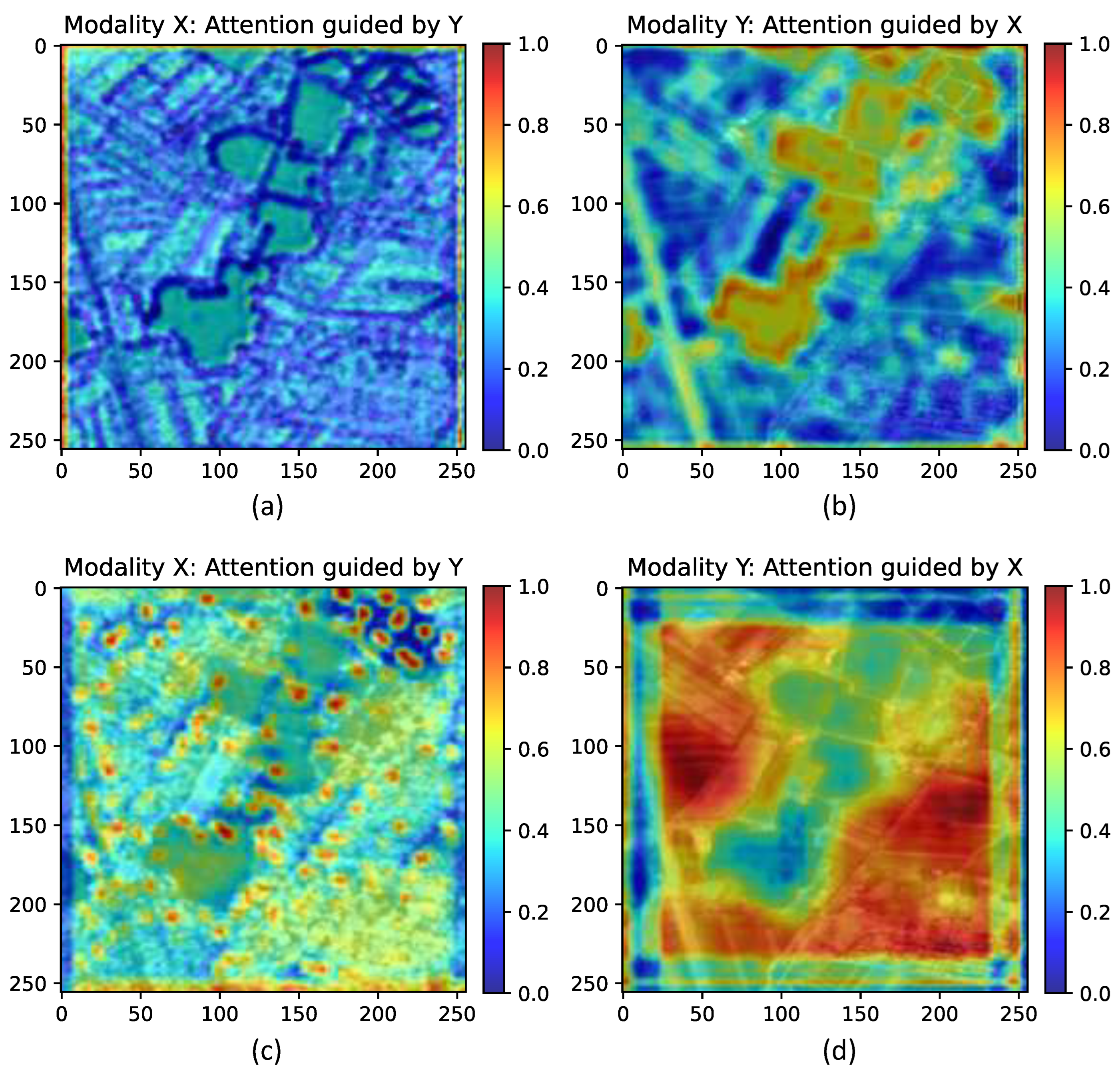
To validate the effectiveness of the CIA module, we conducted a visual analysis of the network outputs. Figure 15 illustrates the changes in the attention maps of optical and SAR images before and after one CIA module operation.

The results demonstrate that, without CIA, the attention maps of both modalities primarily focus on salient regions within their respective images, yet these regions exhibit significant discrepancies. For instance, salient regions in optical images focus on texture-rich areas, whereas SAR images emphasize regions with strong reflectivity. After CIA processing, however, the attention map of the optical image begins to converge towards salient regions of the SAR image and vice versa. This indicates that the CIA module enables mutual guidance between modalities, allowing it to learn complementary salient information and extract more consistent representations. 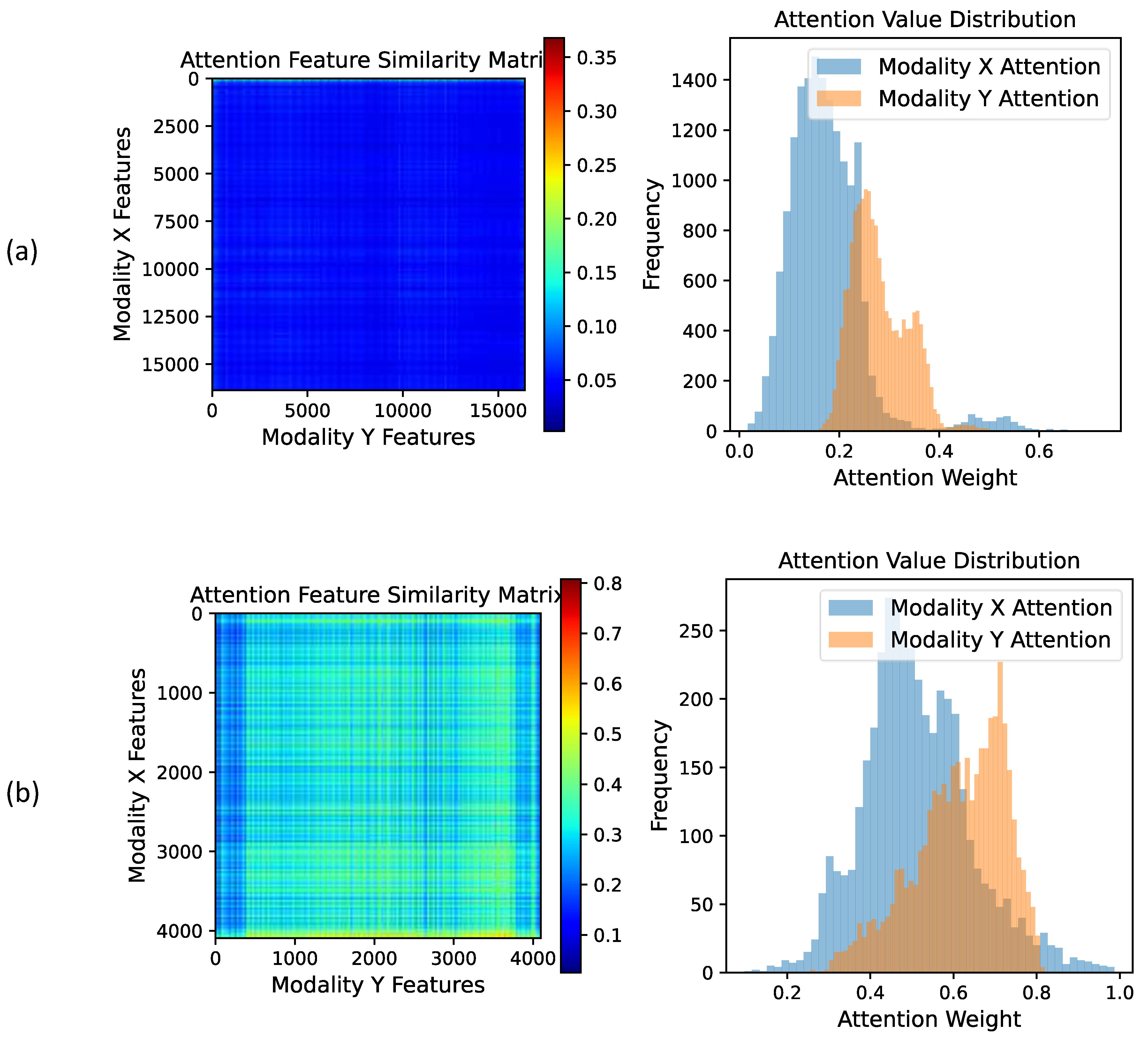Furthermore, Figure 16 presents the post-CIA attention value distribution and feature similarity matrix. The distribution of the attention weights reveals that, following the application of the CIA module, the alignment between modalities is significantly enhanced, as the distribution of the attention weights across different modalities becomes increasingly similar. By directing each modality to focus on the same salient regions as the other modality, the CIA module facilitates the extraction of more repeatable feature points and the generation of more similar feature vectors for the same point, which is crucial for multimodal image registration. The similarity matrix indicates a significant increase in cross-modal feature similarity after CIA processing, thereby demonstrating the module’s ability to extract more consistent features and, consequently, improving the accuracy of multimodal image registration.

Based on these experimental analyses, we conclude that the CIA module demonstrates significant effectiveness in optical–SAR image registration. By enabling mutual guidance between modalities, it facilitates the extraction of highly consistent cross-modal features, substantially enhancing the registration accuracy.

4.10. Parameter Analysis

As introduced in Section 3.2 and Section 3.3, the proposed method relies on several key hyperparameters, which can be categorized into two groups: the architectural parameter and functional parameters. The architectural parameter is the descriptor dimensionality and the functional parameters are $\lambda$ and $\alpha$.

For the architectural parameter, we observed that the model performance remains robust across a certain range. The analysis of the descriptor dimensionality, as detailed in

Table 14. Performance comparison with different descriptor dimensions.

Method	SEN1-2				OSdataset
	SR (%)	NCM	RMSE	REP (%)	SR (%)	NCM	RMSE	REP (%)
128	99.469	115.317	0.363	77.820	98.500	47.940	0.897	71.612
256	100.000	136.496	0.171	82.120	98.500	48.100	0.896	71.500
512	100.000	127.057	0.178	81.113	98.290	44.724	1.014	71.650

, indicates a consistent trend. While the 128-dimensional configuration serves as a computationally efficient baseline, increasing the dimensionality to 256 brings consistent performance gains on both datasets. Specifically, on the SEN1-2 dataset, the 256-dimensional descriptor achieves the highest NCM and repeatability, showing a noticeable improvement over the 128-dimensional version. This trend is further supported on OSdataset, where the 256-dimensional setup also attains the highest NCM and the lowest RMSE. In contrast, the 512-dimensional descriptor introduces higher computational costs without outperforming the 256-dimensional configuration and even leads to a performance degradation regarding certain metrics. Thus, we conclude that the 256-dimensional descriptor offers the best balance, enhancing the representational capacity and matching accuracy while avoiding the unnecessary overhead of higher dimensions.

Regarding the functional parameters, $\lambda$ controls the weight ratio of the descriptor loss in the loss function; a higher $\lambda$ value increases the proportion of the descriptor loss in the total loss, potentially enhancing the network’s focus on the descriptor generation task. The $\alpha$ parameter determines the number of feature points selected from the SAR image; a larger $\alpha$ value means that fewer SAR image feature points are used, reducing the amount of SAR information introduced, while a smaller $\alpha$ value may result in the inclusion of excessive noise points, thereby interfering with the network’s learning process.

Through systematic ablation studies on the SEN1-2 dataset, we investigated the influences of hyperparameters $\lambda$ and $\alpha$ on model performance. The experimental results demonstrate that both parameters impact the matching accuracy, yet they exhibit distinct effects across different metrics.

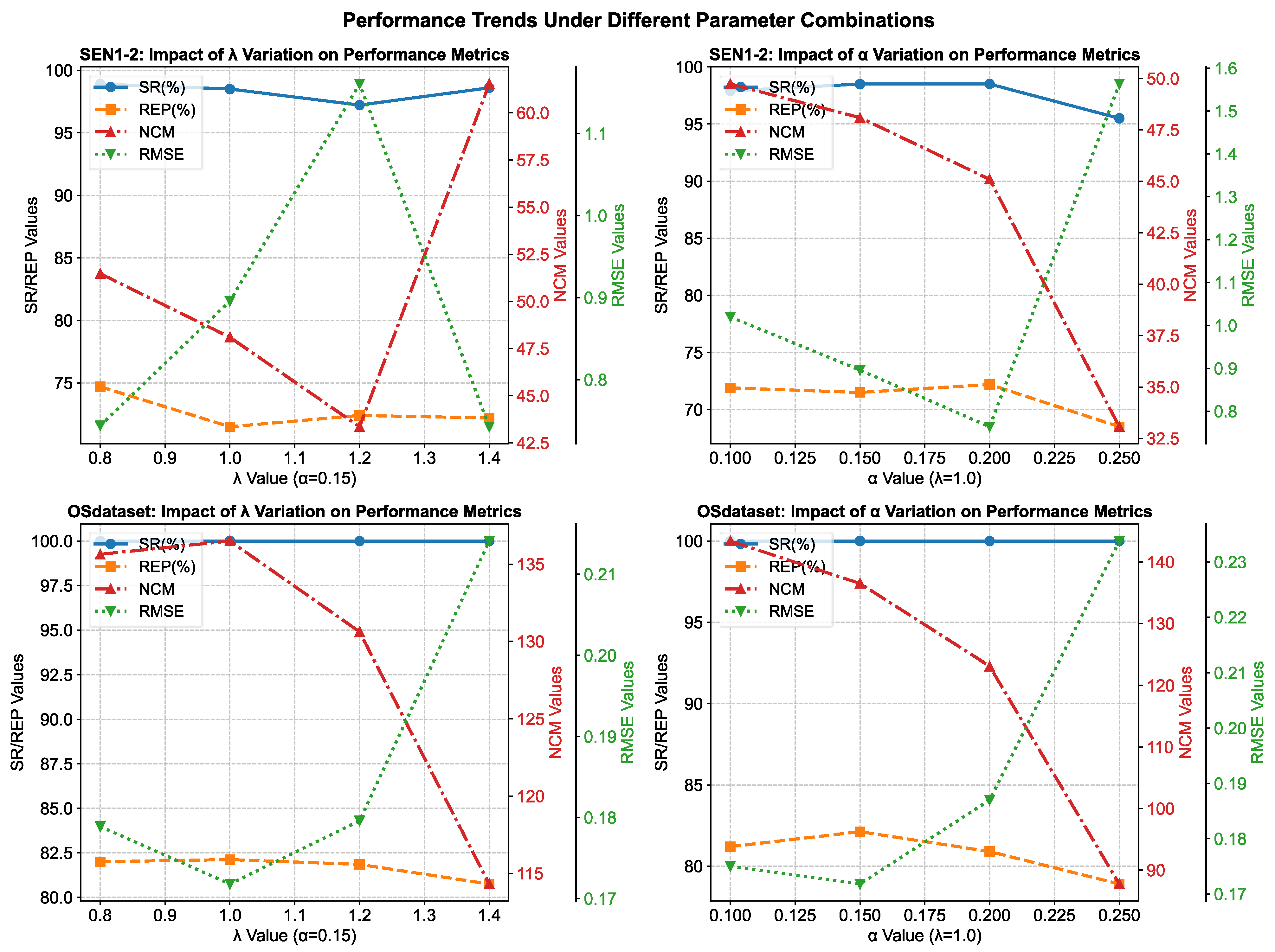
Our systematic ablation studies on the SEN1-2 dataset reveal influence patterns (Figure 17). For $\lambda$, we observe a performance peak at $\lambda =1.0$. When $\lambda$ is too low, the model underfits the descriptor learning task, leading to a noticeable drop in matching accuracy. Conversely, an excessively high value causes the network to overprioritize descriptor optimization at the expense of feature detection. This indicates that $\lambda$ is crucial for balancing the two core subtasks. Similarly, $\alpha$ exhibits a pronounced optimal range. The best overall performance is achieved at $\alpha =0.15$. A smaller $\alpha$ introduces excessive feature points, including many low-quality and noisy candidates, which disrupts the matching process. A larger $\alpha$ overfilters the features, resulting in insufficient information for robust matching. This demonstrates that $\alpha$ effectively acts as a noise filter and information regulator.

Notably, on OSdataset—used exclusively to test generalization—the model maintained excellent performance across all parameter configurations. While the lowest RMSE was observed at $\lambda =1.0$, the highest NCM occurred at $\alpha =0.10$, indicating dataset-specific characteristics. However, based on the comprehensive validation on SEN1-2, we fixed the parameters at $\lambda =1.0$ and $\alpha =0.15$ for final evaluation. The model achieved remarkably strong performance on OSdataset even with these fixed parameters, demonstrating robust generalization capabilities.

These findings confirm that, while the optimal parameters may vary across datasets, the selected configuration provides an excellent balance between feature detection and descriptor learning, enabling robust performance across diverse scenarios.

5. Conclusions

This article proposes a novel heterogeneous remote sensing image registration method that aims to address the registration challenges between optical images and SAR images. By introducing the PLM and PTIF, the method significantly improves the performance of multimodal remote sensing image registration in multiple aspects. The PLM enhances the feature point detection repeatability by providing stable and repeatable feature pair annotations for optical–SAR image pairs. The PTIF concurrently extracts discriminative and complementary cross-modal features to optimize the cross-modal matching performance.

The experimental results reveal that the proposed PLISA exhibits outstanding performance in handling speckle noise inherent in SAR images, as well as rotational transformations and scale variations. Specifically, the proposed method demonstrates superiority in key metrics, while maintaining stability and reliability under geometric transformations and multimodal differences. In the future, we would like to prioritize research on network lightweighting by exploring model compression pathways—including knowledge distillation and model pruning—to significantly enhance the computational efficiency of PLISA. Concurrently, we aim to incorporate more advanced architectures—such as Transformers—and leverage pre-trained models to address key challenges in optical and SAR remote sensing image registration, thereby substantially improving the robustness. Furthermore, we plan to extend our method to tackle the registration of partially overlapping image pairs—a persistent and critical challenge in real-world scenarios.