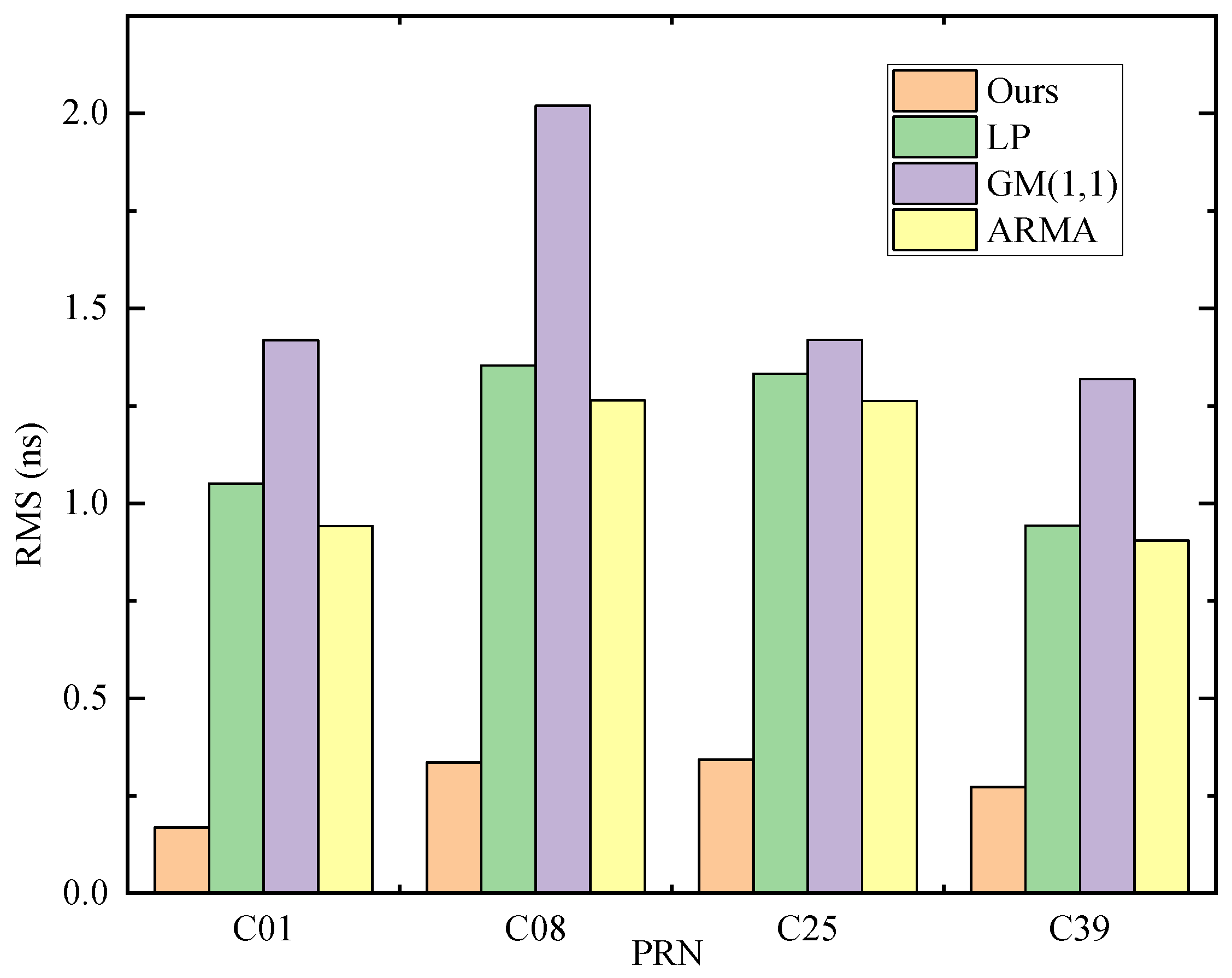1. Introduction
Precise point positioning (PPP) is a primary method to achieve high-precision positioning in global navigation satellite systems (GNSS), delivering centimeter-to-decimeter-level accuracy [
1,
2,
3,
4]. The international GNSS service (IGS) initiated its real-time service (RTS) in 2013. Leveraging the IGS global infrastructure, RTS provides precise satellite orbit and clock corrections, enabling real-time PPP (RT-PPP) and associated applications [
5,
6,
7,
8]. Despite RTS products offering high-accuracy satellite ephemeris and clock data, significant operational challenges persist: frequent data gaps, outliers, clock jumps, and interruptions and latency induced by server anomalies or network delays [
9,
10]. Furthermore, satellite clock offsets for all GNSS constellations, including BDS, Galileo, and GPS, exhibit complex nonlinear behaviors—including periodic oscillations and stochastic variations—driven by external environmental factors [
11,
12,
13]. These universal limitations hinder applications requiring stringent timeliness and precision. Addressing these issues necessitates robust, constellation-specific strategies to sustain PPP performance during SSR data outages. This study focuses on developing and validating such a strategy for the BDS.
To ensure reliable real-time PPP, continuous and stable reception of SSR corrections streams is essential. Existing research has addressed interruptions in real-time SSR data, specifically orbit and clock corrections. For mitigating SSR outages, Hadas et al., 2015 [
14] proposed orbit corrections prediction via polynomial fitting. This method confines orbit corrections errors below 2 cm for up to 8 min (GPS) and 4 min (GLONASS). El-Mowafy et al., 2017 [
15] proposed using higher-order polynomials to compensate for short-term (minute-level) orbit outages for GPS, while switching to IGS ultra-rapid products (IGU) predicted orbits for longer outages. The GPS clock offsets were predicted by modeling them with a second-order polynomial plus a sinusoidal term. Experiments demonstrated that this approach can maintain GPS positioning accuracy better than 10 cm within 2 h. Yan et al., 2020 [
16] proposed a linear regression-based clock offsets prediction approach for GNSS, achieving 1 ns precision within 900 s through optimization of the historical data window (300 s). Janicka et al., 2020 [
17] proposed the direct prediction of SSR orbit corrections variations for GPS satellites using linear, quadratic, and constant models. Their experimental results demonstrated negligible differences among these approaches, indicating that utilizing the latest available corrections suffices for practical implementation. Qafisheh et al., 2022 [
18] proposed utilizing ARMA and SVR models to predict SSR corrections for GPS and GLONASS to address latency issues. Experiments demonstrated reductions in positioning error by 13% and 9%. Li et al., 2022 [
19] proposed combining a quadratic polynomial with an eighth-order harmonic function to resolve data outages for GPS satellites. The extrapolation achieved an accuracy of 0.81 ns within 6 h, significantly outperforming IGS ultra-rapid products. Mu et al., 2024 [
20] proposed a real-time multi-system PPP method resilient to SSR latency. During communication anomalies, positioning stability was maintained by extrapolating using the time-differenced carrier phase (TDCP) method. Under a 10 min latency, horizontal accuracy reached 0.7 cm and vertical accuracy reached 5.0 cm. Since satellite clocks are susceptible to external environmental influences, clock corrections inevitably contain noise, resulting in periodic and stochastic variations in the satellite clock corrections [
21,
22].
Current research primarily focuses on using traditional methods to predict orbit and clock corrections over short time periods. Compared with traditional models, which have limitations in representing the nonlinear characteristics of clock offsets and face accuracy improvement bottlenecks, neural networks, due to their sensitivity to nonlinear problems, can overcome these traditional limitations and achieve higher-precision predictions. Lv et al., 2022 [
23] proposed a BP neural network model for GPS clock corrections prediction based on heterogeneous ensemble learning and dynamic multi-swarm particle swarm optimization (DMS-PSO). Experimental results showed that the average prediction accuracy reached 0.15 ns within 60 min, meeting centimeter-level positioning requirements. While traditional recurrent neural networks and their improved versions (such as LSTM and GRU) have mitigated the vanishing gradient problem through gating unit designs, they still face challenges when processing very long time-series data, such as limited memory capacity and dilution of temporal features [
24,
25]. Moreover, existing research has primarily focused on clock offsets sequence prediction, without fully considering the correlation between real-time orbit and clock offsets. It should be noted that reference [
26] proposed the iTransformer model for time-series forecasting, which innovatively reverses the dimensional features of the Transformer. By treating the full time series of each variable as independent tokens, the model constructs a multivariate correlation capture framework based on the attention mechanism and integrates a feedforward network to extract non-linear features. This approach addresses the computational bottlenecks and dependency modeling limitations of traditional Transformers in long-sequence tasks, while enhancing the model’s ability to capture multivariate relationships, thus opening new paths for time-series forecasting.
It is noteworthy that research on long-term prediction of real-time orbit and clock offsets for the BeiDou-2/3 integrated system remains limited. Satellite-based augmentation services urgently require robust prediction frameworks to mitigate positioning degradation during SSR outages. To address this challenge, this paper proposes a novel deep learning framework based on a residual-enhanced iTransformer architecture for predicting SSR offsets. The study aims to resolve several key challenges identified in BeiDou SSR corrections, including significant non-stationarity with substantial fluctuations, complex periodic patterns particularly in orbital components, and occasional anomalous behaviors in clock offsets. We design a residual convolutional-attention fusion mechanism that enhances local feature extraction while maintaining global temporal dependencies. The framework specifically focuses on modeling cross-variable interactions among orbital components and clock offsets to overcome limitations of traditional approaches that treat these parameters separately. Validation using stations from the multi-GNSS experiment (MGEX) network and low-cost receivers will evaluate the method’s capability to maintain precise positioning performance during extended SSR interruptions.
2. Materials and Methods
2.1. iTransformer Fundamentals
Previous Transformer-based models for time-series forecasting typically treat each time step as a token by concatenating the multivariate observations at that step, thereby computing attention along the temporal dimension [
27,
28]. However, this paradigm suffers from a fundamental limitation: it directs the model’s focus towards interdependencies between temporal points, while failing to explicitly capture the intrinsic dependencies among variables. These complex inter-variable interactions are often the key driver behind the evolution of multivariate series, yet they are obscured within the temporal attention maps, hindering the model’s ability to learn meaningful multivariate representations.
To overcome this limitation, we introduce the iTransformer model, which reframes the representation learning paradigm for multivariate series. The core of our approach is to represent each individual variable’s entire lookback sequence as a distinct “variable token.” This token encapsulates the unique characteristics and temporal dynamics of that variable. The self-attention mechanism is then applied across these variable tokens, enabling the model to directly and adaptively learn the associations between variables. Finally, each representation, now enriched by inter-variable attention, is processed independently by feedforward networks to decode future sequence values. By shifting the modeling priority from temporal dependencies to variable dependencies, our method establishes a more powerful representational foundation for multivariate forecasting. Within the iTransformer framework, the process of predicting the future sequence
of each specific variable based on historical sequences
is formally formulated as
where
contains
N embedding tokens with dimension
D, and the superscripts denote layer indices. The embedding function Embedding:
and the projection function Projection:
are both implemented by multi-layer perceptrons (MLPs). The obtained variable tokens interact via self-attention and are independently processed by a shared feedforward network in each TrmBlock.
2.2. SSR Data Characteristics
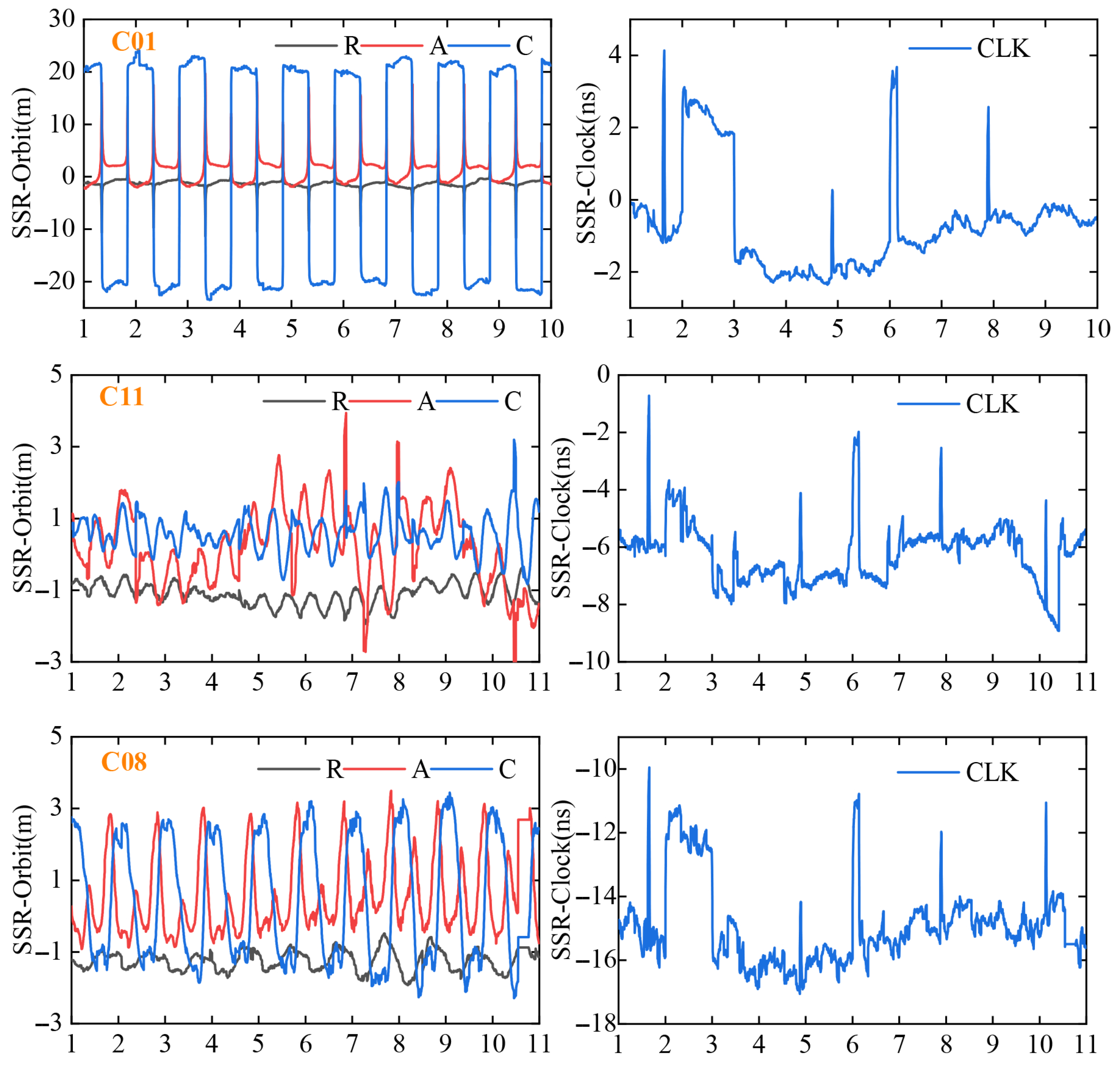
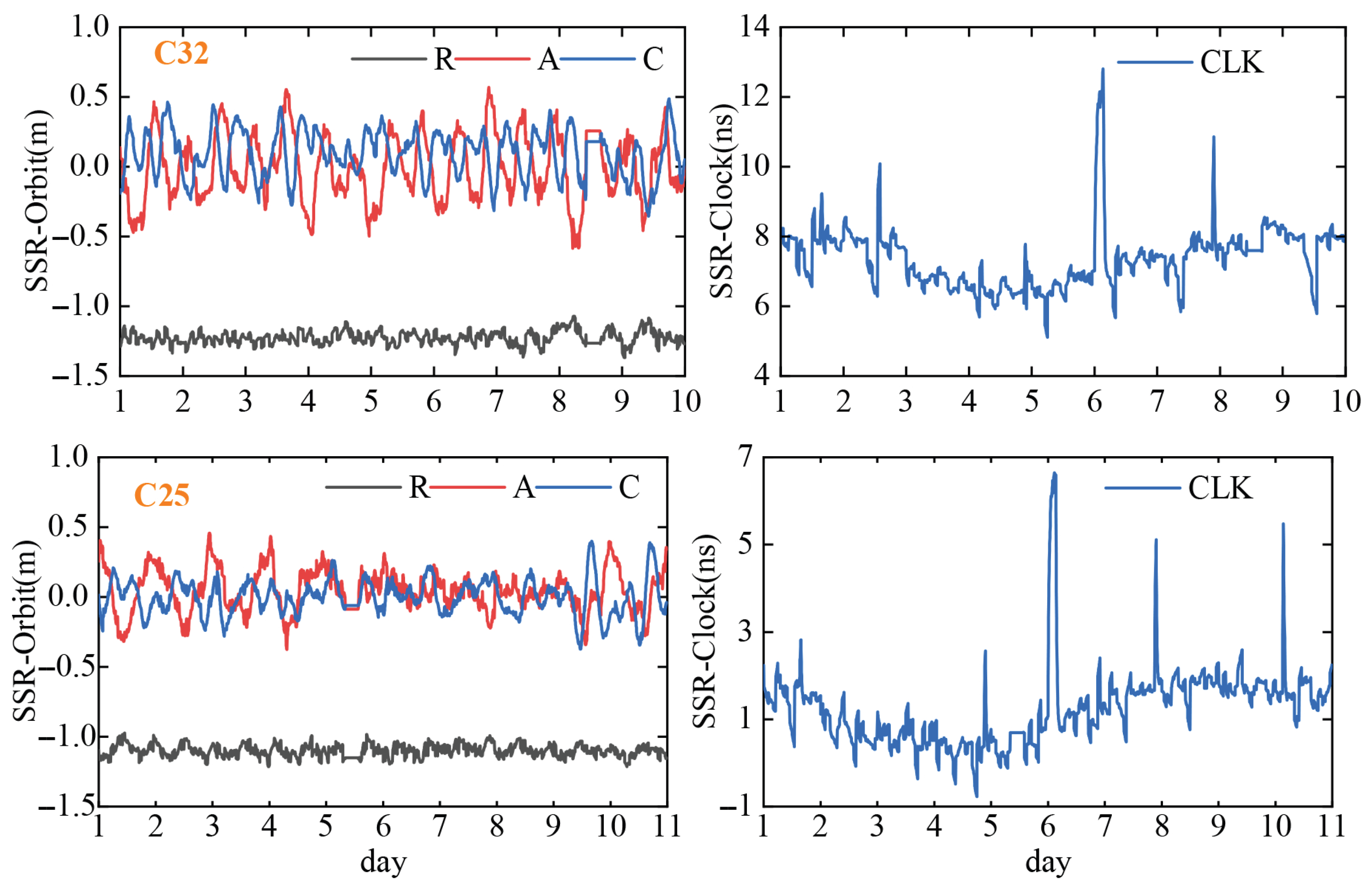
To investigate the long-term time-varying characteristics of the BDS orbit and clock correction parameters, this study performed a systematic analysis. The data used in this study comprise a 20-day continuous series of real-time correction sequences for orbits and clocks, sourced from the Wuhan University IGS data center, commencing on the day of year (DOY) 341, 2024. The corresponding data visualizations are presented in
Figure 1.
Regarding orbit correction parameters, distinct characteristics are observed across different satellites. The along-track (A) and cross-track (C) variations of Satellite C01 exhibit a high degree of correlation and periodic oscillations, while the radial variation remains relatively stable. For Satellite C08, the radial (R) component demonstrates smaller correction amplitudes, while its A and C components exhibit pronounced periodic fluctuations. All three-dimensional correction amplitudes remain within ±3 m. In contrast, Satellite C11 displays aperiodic characteristics in 3D orbit corrections, with the A component showing the most significant fluctuations (maximum amplitude > 5 m), whereas the R component maintains a relatively confined variation range. In contrast, Satellite C25 presents unique orbital dynamics: its R component remains stable, while the A and C components exhibit submeter-level fluctuations during days 5–8 of observation, with all variations constrained below 1 m. All components of Satellite C32 are highly similar to those of C25.
Regarding clock correction parameters, none of the three satellites exhibit periodic characteristics in their time-series variations. Analysis of the 10-day continuous correction sequences reveals significant temporal continuity, characterized by stable variation gradients between consecutive days. In particular, distinct clock jumps exceeding 2 ns in magnitude were observed at specific epochs (days 1, 4, 6, and 8). During non-jump intervals, the clock corrections for C08 and C25 maintain stability with fluctuations constrained within a 2 ns threshold; by comparison, C11 demonstrates relatively pronounced fluctuation behavior.
2.3. The Proposed Residual-Enhanced iTransformer Model
As evidenced by the preceding time-series analysis, orbit correction demonstrates relatively smooth variations, whereas clock correction exhibits intricate patterns with heightened noise levels. This necessitates dedicated processing modules for clock corrections when employing the same prediction network for both orbit and clock parameters.
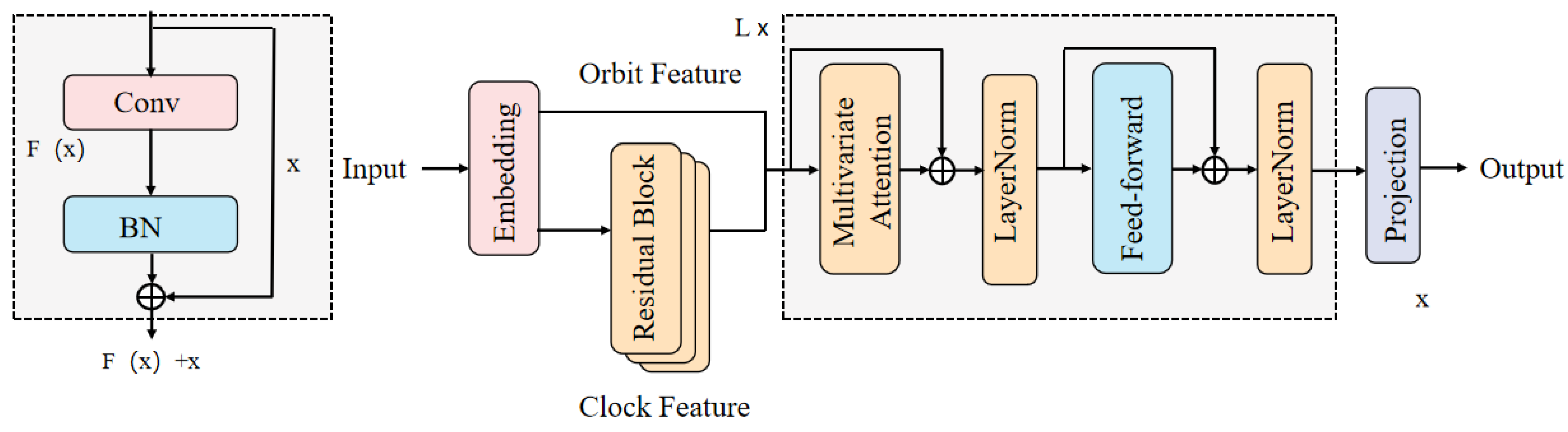
Residual neural networks (ResNets) [
29] mitigate gradient degradation in deep network training by incorporating residual learning modules into traditional convolutional neural network (CNN) architectures. This is achieved through identity mapping shortcuts that enable multi-path gradient propagation via skip connections, thereby enhancing model convergence and feature representation capabilities. For clock offset prediction, this residual learning mechanism enables the model to focus on capturing the differential features between normal variations and anomalous jumps. By explicitly modeling these residuals, the network develops enhanced sensitivity to abrupt changes and demonstrates improved robustness in handling gross errors, allowing for quicker recovery of prediction stability following clock jump events. The modified residual block structure and our proposed network architecture are illustrated in
Figure 2, with the ResNet output formulated as
The real-time BDS orbit and clock correction sequences undergo processing via a sliding window sampling strategy, which segments continuous time-series data into contiguous overlapping subsequences. Each timestamp is mapped to a feature vector, transforming raw data into a feature matrix. These subsequences are then fed into an inverse dimension embedding module that independently embeds each univariate time series as a token. Subsequently, the embedded clock corrections and associated temporal features are processed by a residual module employing 1D causal convolutions. This architecture enables each time step to incorporate localized temporal context, capturing short-term dependencies. Following layer normalization and residual connections, three such blocks are stacked to model long-range dependencies. Finally, the processed orbital and clock features are channel-wise concatenated for downstream network processing.
2.4. Experimental Setup for SSR Prediction
This subsection describes the dataset, training configuration, and evaluation metrics specifically for the SSR corrections prediction task.
2.4.1. Dataset and Preprocessing
The experimental dataset comprises 20 consecutive days (DOY 341-360, 2024) of SSR-derived satellite clock and orbit correction parameters. Given the original 5 s broadcast frequency exhibiting negligible variations within 1–2 h intervals, rendering it suboptimal for direct model input, we downsampled the data to 5 min resolution. Predictions were subsequently linearly interpolated to restore 5 s temporal resolution. To preserve the inherent chronological order of this time-series dataset, samples maintain strict temporal sequencing without shuffling. The dataset was partitioned sequentially into training, validation, and test sets at a 7:1:2 ratio.
2.4.2. Evaluation Metrics
The evaluation employs mean absolute error (MAE) and root mean square error (RMSE) as primary prediction performance metrics. These indicators facilitate quantification of the deviation between predicted and actual values while providing complementary assessment perspectives, thereby contributing to model accuracy and reliability verification.
2.4.3. Loss Function
Based on the characteristics of high-frequency noise interference in clock corrections within this experimental scenario, the Huber loss function with robust characteristics was adopted for optimization training. This function introduces a dynamic threshold mechanism: it preserves mean squared error properties within the threshold range, while transitioning to a linear loss function beyond the threshold. This piecewise characteristic simultaneously maintains gradient stability and significantly reduces sensitivity to anomalous samples, thereby mitigating overfitting while preserving model convergence efficiency. The mathematical expression of the Huber loss function is defined as follows:
2.5. Experimental Setup for PPP Positioning Performance Validation
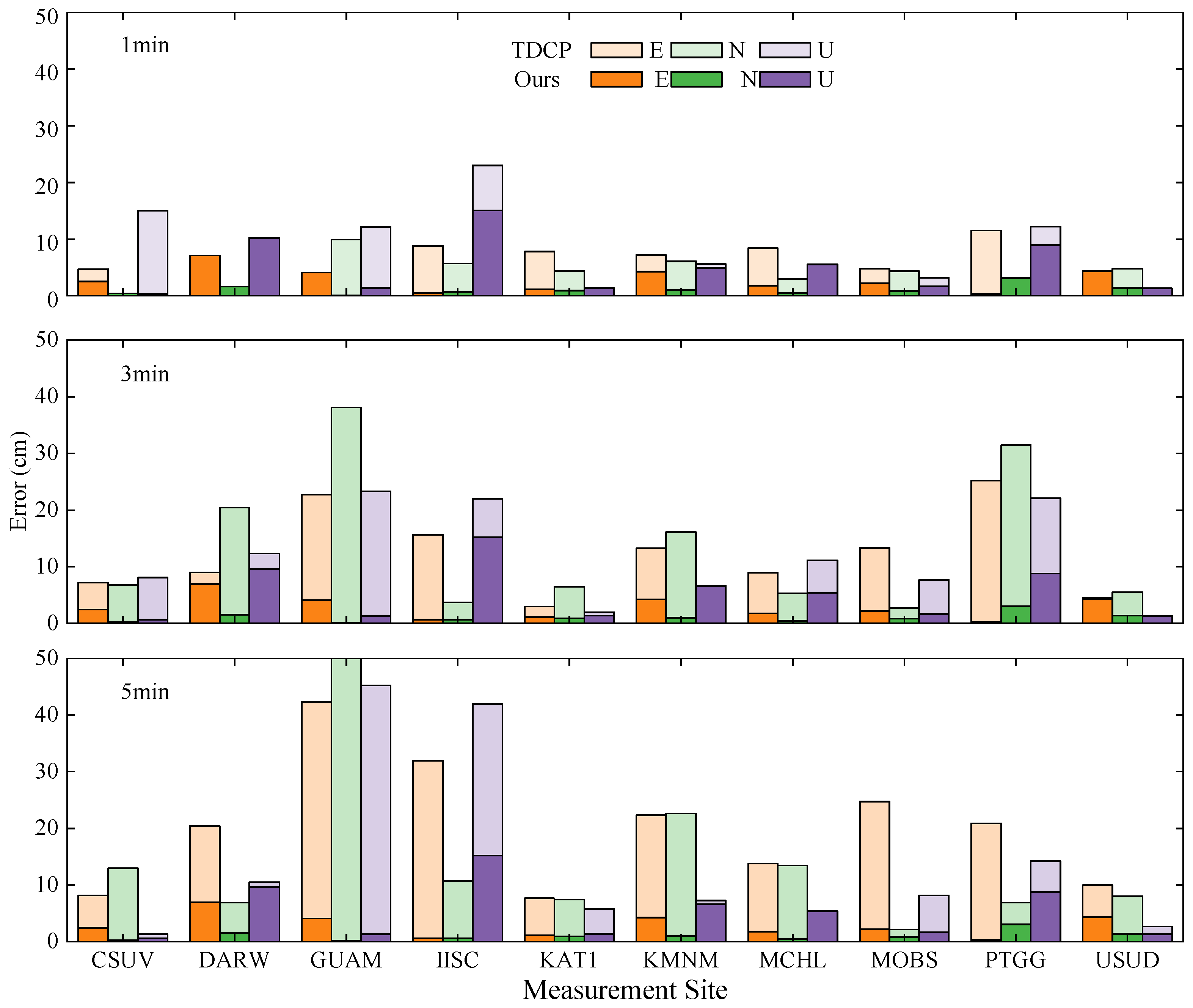
To systematically evaluate the impact of SSR data predicted by the residual network-based iTransformer model on real-time PPP performance, this study employed simulated SSR data interruption scenarios. The model was used to predict future SSR information to maintain positioning continuity. To validate the model’s generalization capability across different device environments, the experimental design utilized two platforms: MGEX stations and a self-developed low-cost receiver (UM980 module). This design facilitates a comparative analysis of the positioning error distribution, convergence time, and robustness differences when using predicted SSR data in geodetic-grade reference stations (millimeter-level accuracy) versus low-cost terminals (centimeter-level accuracy).
2.5.1. BDS PPP Positioning Experiment
We utilized the post-processing module of the RTKLIB software package (version 2.4.3) [
30] to simulate and achieve real-time BDS PPP positioning. This choice was based on its robust implementation of standard PPP algorithms, including built-in procedures for cycle-slip detection and ambiguity resolution. All specific parameter settings governing the positioning filter and error modeling are provided in
Table 1. The CUSV station is sourced from the IGS MGEX network. The precise reference coordinates for the station CUSV in the ITRF2014 reference frame were obtained from the IGS data center at scripps orbit and permanent array center (SOPAC). The coordinates used were X = −1,248,307.769 m, Y = −4,818,425.225 m, Z = 3,976,507.439 m.
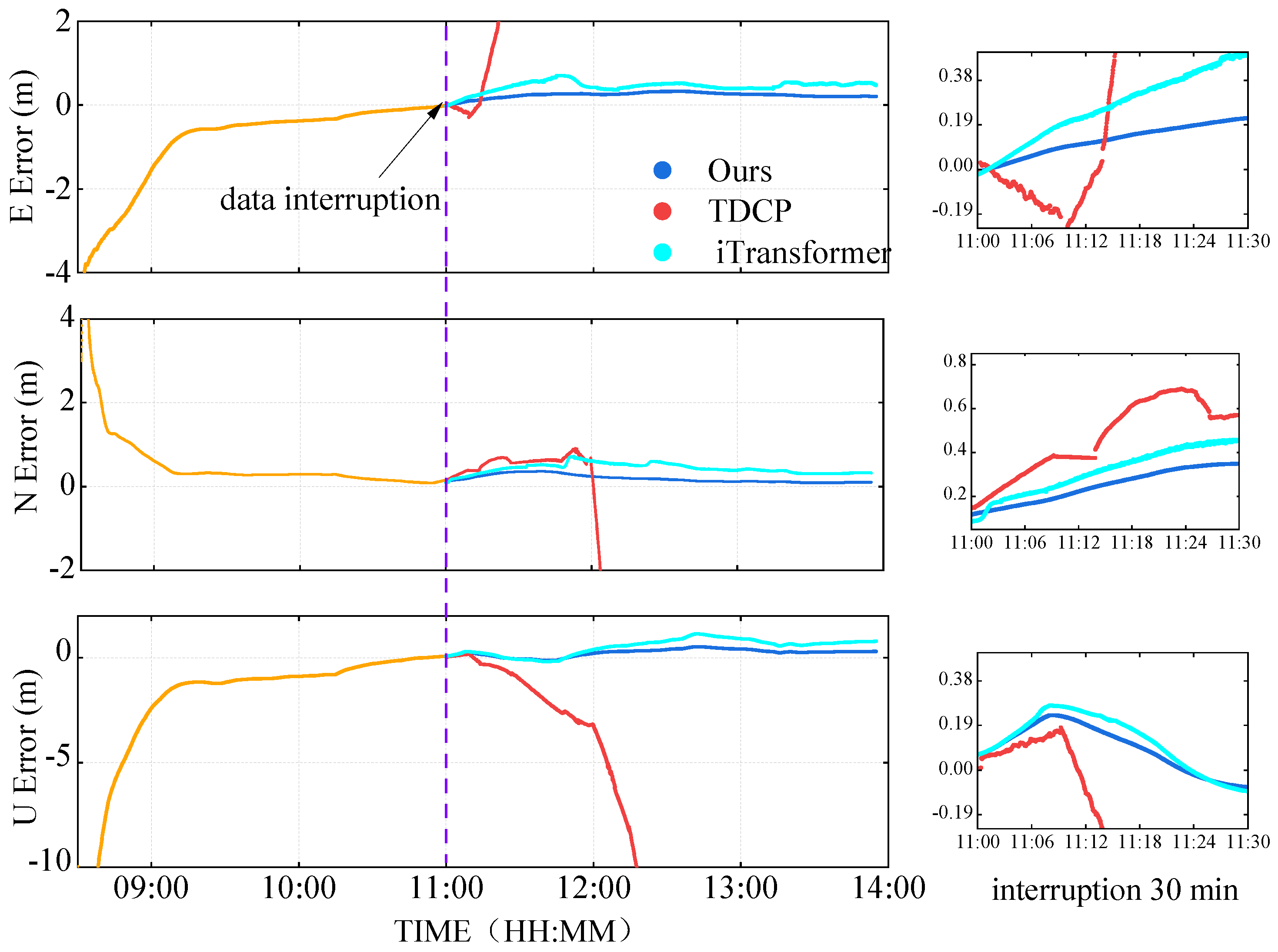
To evaluate the effectiveness of the predicted data in real-time PPP, the proposed method is compared against both the TDCP model—which accounts for SSR delays, as introduced by Mu et al., 2024 [
20]—and the original iTransformer model. The TDCP approach utilizes high-rate observation data and calculates differences in phase observations between consecutive epochs. This process mitigates the impact of various errors over short time spans, enabling the estimation of receiver position increments between epochs.
To evaluate the positioning accuracy, the derived geocentric coordinates (ITRF2014) were directly compared against the known reference coordinates of the station CUSV. This comparison and the transformation of the coordinate differences into East-North-Up (ENU) components were performed automatically by the RTKLIB rnx2rtkp module during the solution output.
2.5.2. Low-Cost Receiver Positioning Experiment
To validate the positioning performance (accuracy and reliability) of the proposed method in real-world scenarios, this study conducted a static BDS positioning experiment based on the UM980 low-cost receiver module. The experiment was carried out on 30 December 2024, from 08:30 to 14:00, lasting for 5.5 h. The observation environment was an open rooftop area (free of signal obstructions) to ensure data collection quality. After data collection, post-processing analysis was performed using the RTKLIB software (version 2.4.3). The parameter settings for the RTK post-processing solution are consistent with those of the PPP experiment (see
Table 1), with the following key exceptions: The RTK method adopts a relative positioning mode, with reference station coordinates sourced from the China Mobile continuously operating reference station (CORS) network at a baseline length of approximately 35 km; it utilizes between-station differencing techniques to eliminate ionospheric and tropospheric errors, and ultimately achieves fixed integer ambiguity resolution.
To obtain high-precision reference coordinates for positioning error assessment, this study utilized the entire collected static observation data. The PPP technique was employed, combined with the final precise orbit and clock products released by the IGS, to compute the station’s coordinates in the earth-centered, earth-fixed (ECEF) frame as the reference truth: (−1,695,038.185 m, 5,015,952.426 m, 3,545,214.553 m).
For the positioning algorithm verification, to simulate and improve real-time SSR services, this study used SSR data saved from the two days preceding the experiment. Orbit and clock corrections at 5 min intervals were extracted as the input sequence. A pre-trained model was used to perform time-series prediction of the real-time orbit and clock corrections during the observation period, aiming to compensate for potential gaps and delays in the real-time data stream. The prediction results were then linearly interpolated to a 5 s interval to match the requirements of high-frequency positioning solutions.
4. Discussion
This study establishes a novel residual-enhanced iTransformer framework for predicting BDS SSR corrections and validates its efficacy in maintaining real-time PPP accuracy during data outages. The experimental results presented in the previous section prompt a detailed discussion on several key points.
4.1. High-Accuracy SSR Prediction
4.1.1. Performance in Orbit and Clock Prediction
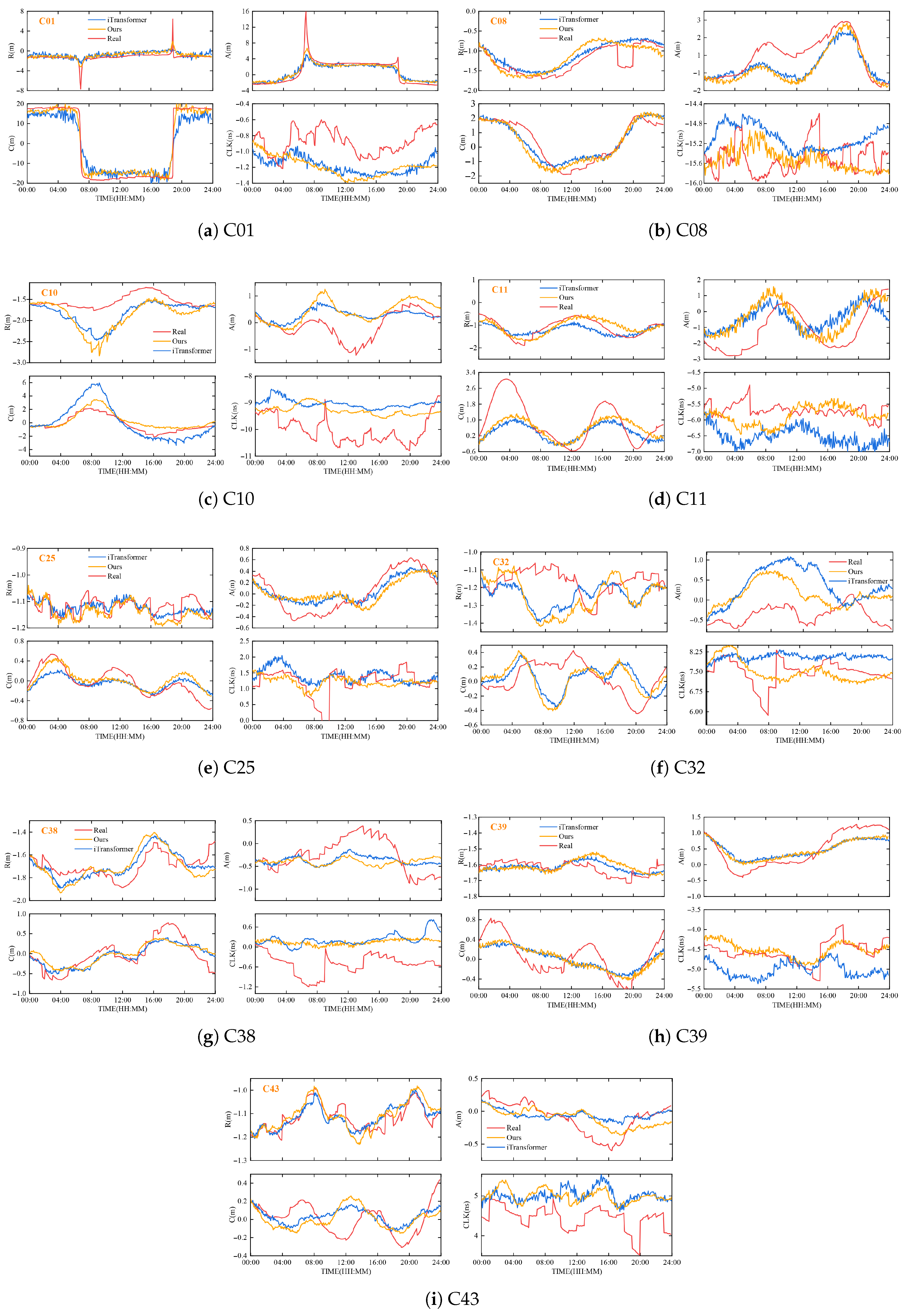
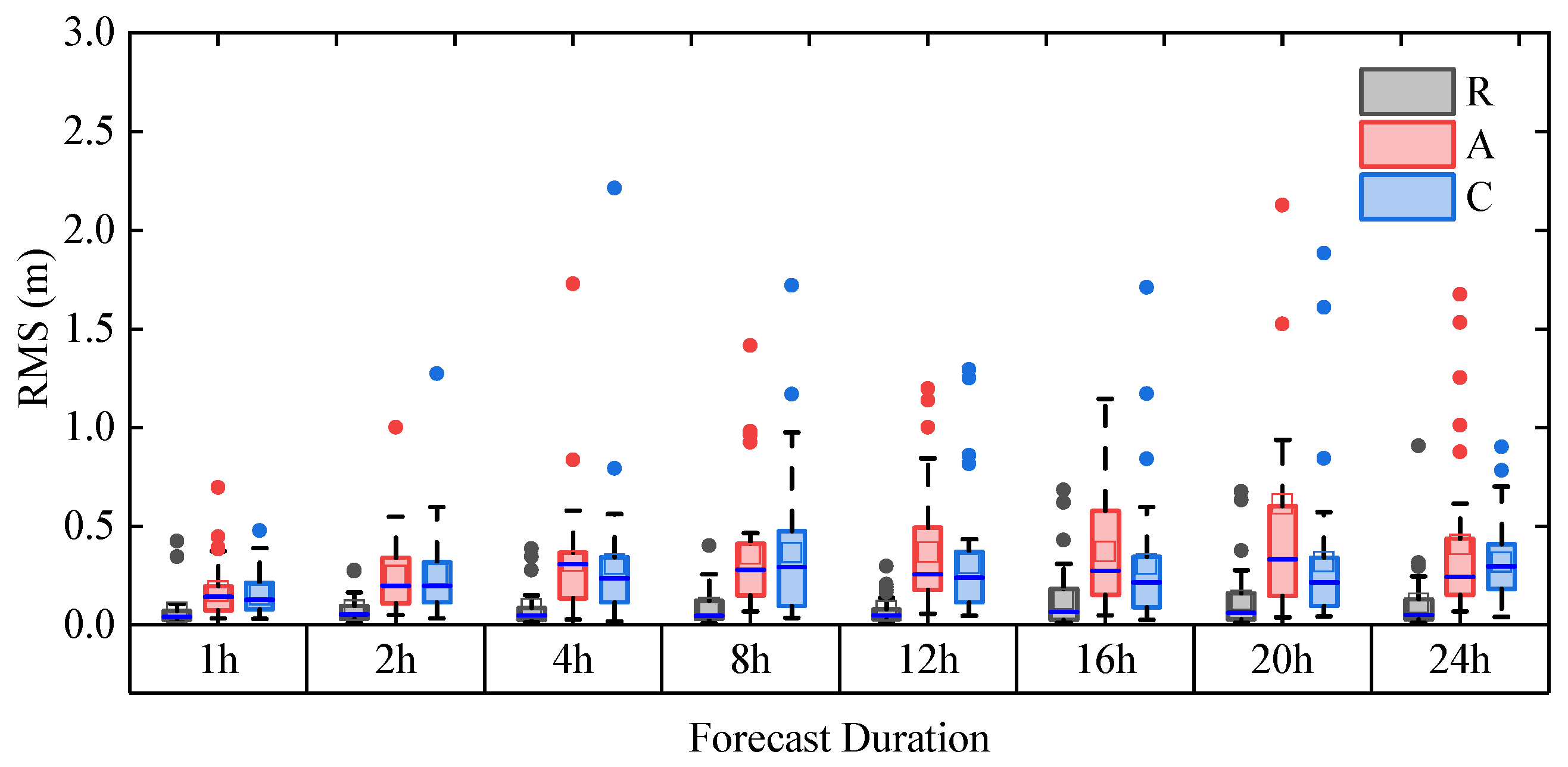
The proposed residual-enhanced iTransformer model demonstrates remarkable advancements in SSR prediction accuracy across both orbit and clock corrections. For orbit predictions, the model maintains precision levels of 0.10 m (R), 0.20 m (A), and 0.20 m (C) within 2 h prediction windows, representing a significant improvement over traditional approaches. The R component consistently shows the highest accuracy, corresponding to its inherently smaller variation range in actual orbital dynamics.
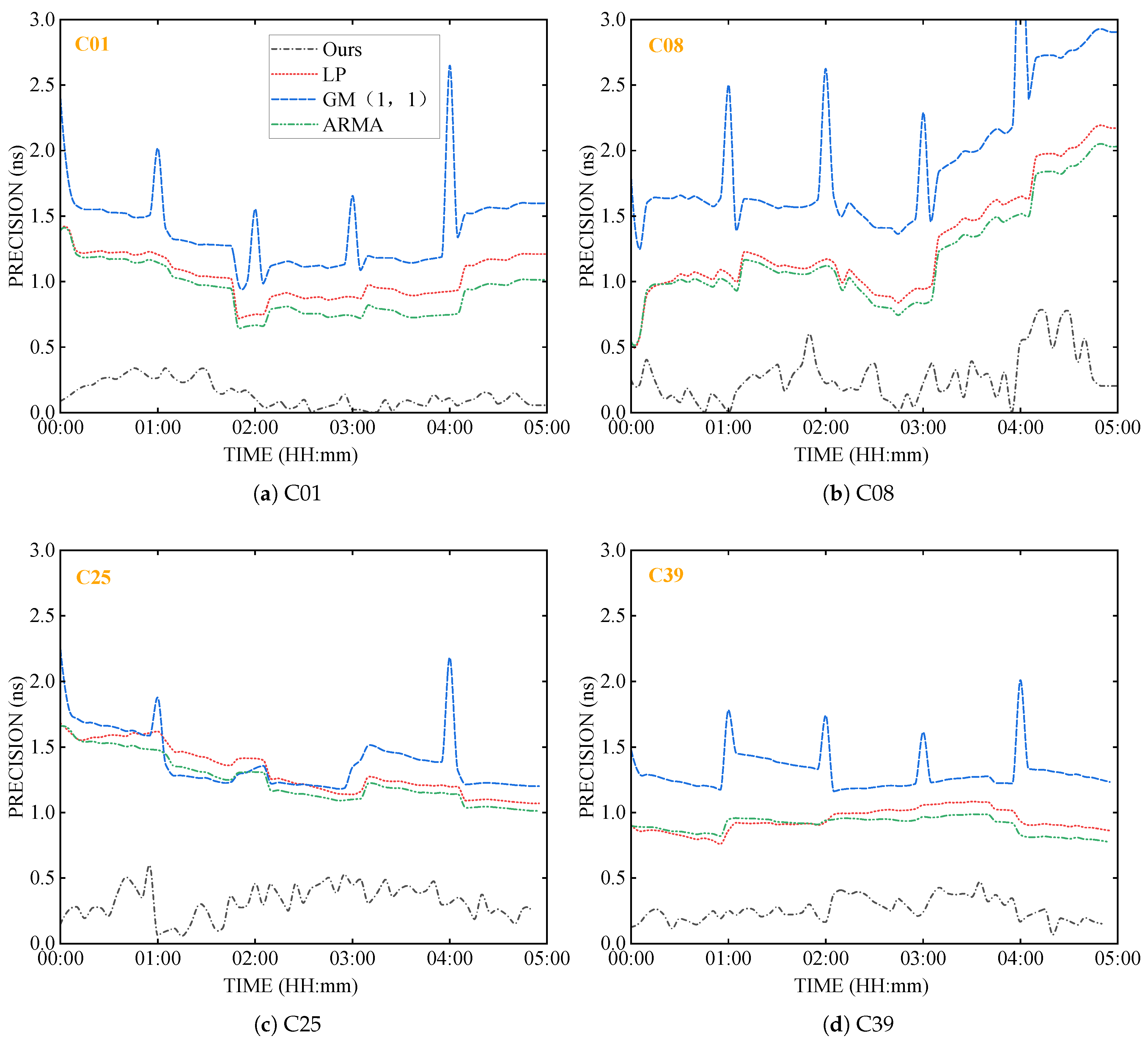
The improved iTransformer demonstrates remarkable advantages over traditional methods including linear polynomial (LP), grey model (GM (1,1)), and ARMA models. While conventional approaches rely on manually designed features and fixed mathematical formulations that struggle to capture complex nonlinear dynamics, our model achieves a substantial 72–85% reduction in prediction errors for 30 min forecasts and maintains sub-0.4 ns accuracy even in 3 h scenarios. This performance breakthrough stems from the model’s ability to autonomously extract deep spatiotemporal features and effectively model long-range dependencies through its end-to-end learning mechanism. The results clearly demonstrate the superiority of the proposed architecture in handling the complex characteristics of satellite clock offsets, providing more accurate and stable predictions across various time horizons.
4.1.2. Cross-Satellite Compatibility and Generalization
The model exhibits distinct performance characteristics across different BDS satellite generations and orbital types. For BDS-3 satellites, the model shows optimal compatibility, achieving a 31.3% reduction in clock error for IGSO satellites while maintaining stable orbit corrections. This superior performance with newer-generation satellites suggests the model’s enhanced adaptability to modern satellite technologies with more stable behavioral patterns.
However, the limited effectiveness on BDS-2 GEO satellites reveals important insights into model limitations. The slight increase in clock error (from 0.6000 ns to 0.6292 ns) for these satellites indicates that the model’s performance is influenced by the unique orbital characteristics and potentially higher inherent uncertainties of GEO satellites. This observation underscores the importance of considering satellite-specific attributes in prediction model design.
4.1.3. Temporal Performance Characteristics
The temporal evolution of prediction accuracy reveals crucial patterns for practical applications. Short-term predictions (≤2 h) demonstrate exceptional stability with minimal error dispersion, making them particularly suitable for real-time PPP applications. The model’s ability to maintain <0.5 ns clock accuracy and <0.2 m orbit accuracy during this period directly supports continuous high-precision positioning during typical SSR interruption scenarios.
For medium- to long-term predictions (≥8 h), while error accumulation becomes evident, the model shows adaptive characteristics through the contracting error distribution in cross-track components during 12–24 h intervals. This phenomenon suggests the model’s capability to leverage orbital periodicities, particularly noticeable in the C direction where orbital repeat patterns are most pronounced.
4.1.4. Architectural Advantages and Limitations
The residual-enhanced iTransformer architecture addresses several critical challenges in SSR prediction. The integration of residual networks significantly improves the handling of clock noise and jumps, allowing the model to focus on differential features during anomalous periods. Meanwhile, the inverted transformer architecture enables effective modeling of cross-variable dependencies between orbital components and clock offsets, providing physically consistent predictions that are crucial for maintaining PPP solution stability.
However, the model shows limitations in predicting full magnitudes of sudden clock jumps, with maximum absolute errors reaching 2.5 ns during jump events. This limitation, combined with the observed performance variations across satellite types, suggests directions for future improvements, including the potential development of specialized processing branches for different satellite categories and enhanced anomaly detection mechanisms.
4.2. Positioning Experiment
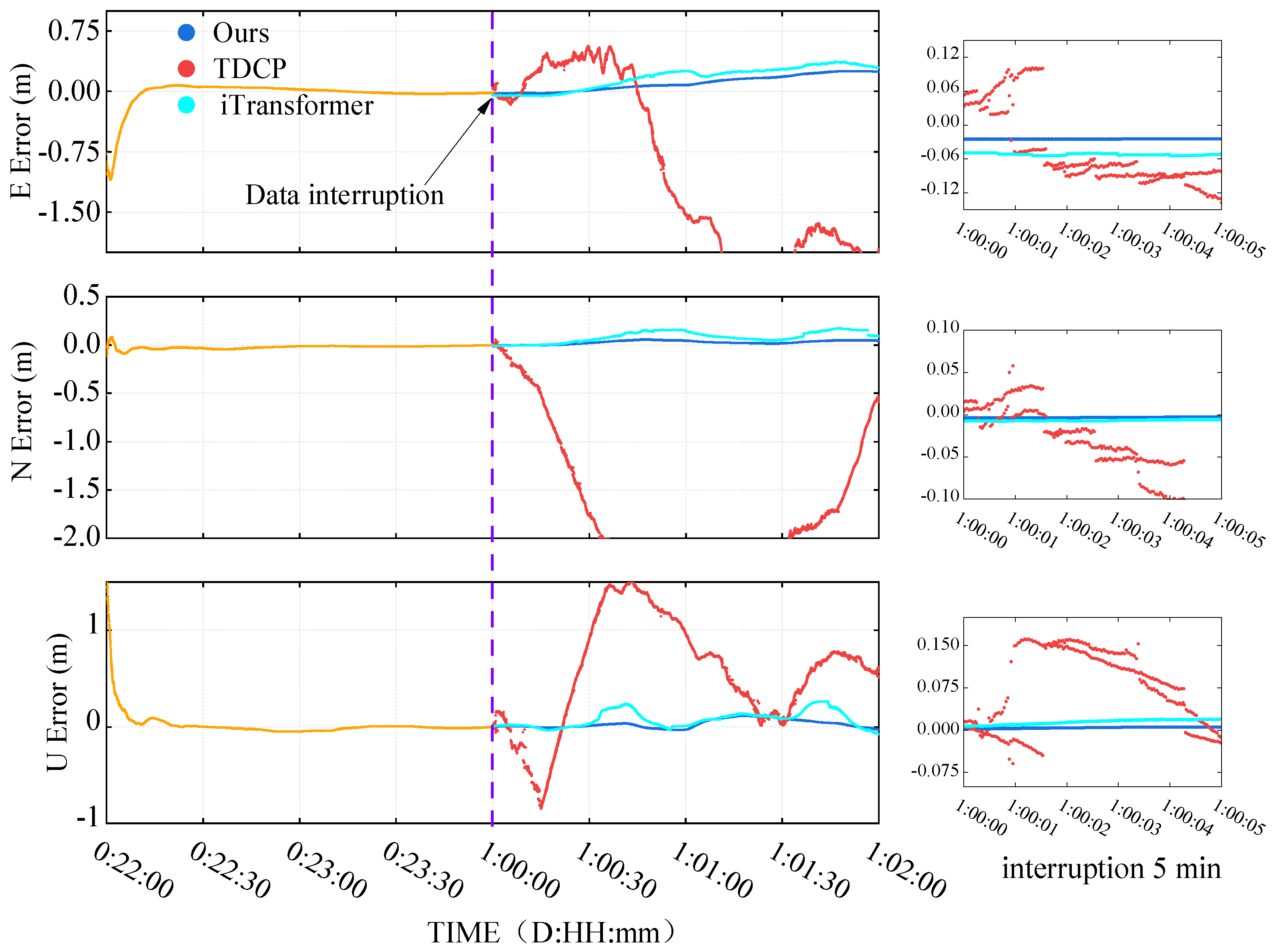
The positioning experimental results validate the effectiveness of the SSR prediction model at the application level. In simulated SSR interruption experiments, the improved model maintained decimeter-level positioning accuracy at both MGEX stations and low-cost receivers, directly confirming the reliability of the SSR prediction accuracy discussed earlier.
Compared with the traditional TDCP method, our approach exhibits fundamentally different error characteristics. While the TDCP method can maintain positioning accuracy during short interruptions (1–5 min), its errors show exponential growth as the interruption duration extends, particularly exceeding 1.5 m in the horizontal direction during 2 h interruptions. This divergence stems from TDCP’s inherent relative positioning nature—while it eliminates errors through epoch differencing, it simultaneously loses the absolute position reference, leading to continuous error accumulation.
In contrast, the improved iTransformer model adopts a completely different technical approach. By providing continuous SSR correction predictions, it maintains the integrity of the PPP absolute positioning framework. This enables the method to keep horizontal errors within 10 cm and vertical errors below 17 cm during 30 min interruptions. This stable error growth pattern indicates that the method can provide reliable performance boundaries for real-time PPP applications.
Notably, the model demonstrates strong adaptability across different receiver types. At MGEX stations equipped with professional geodetic receivers, the improved model achieved approximately 50% enhancement in vertical accuracy compared with the original iTransformer over a 2 h period. When deployed with the low-cost UM980 receiver, although the absolute accuracy experienced some degradation, it still maintained decimeter-level positioning capability—a characteristic of significant importance for mass-market applications.
Vertical accuracy remains the most challenging aspect across all methods. Although the improved model achieved over 85% accuracy improvement in the vertical direction compared with TDCP, its errors remain 2–3 times those in the horizontal direction. This phenomenon aligns with the fundamental geometric characteristics of satellite navigation positioning, while also suggesting the need for special attention to vertical error suppression in future work.
Comprehensive positioning experimental results demonstrate that the deep learning-based SSR prediction method not only effectively handles short-term SSR interruptions but also shows significant advantages in long-term interruption scenarios, providing a viable technical solution for continuous high-precision positioning in critical application fields.
5. Conclusions
To address the degradation of PPP accuracy caused by interruptions in real-time BDS SSR data streams, this paper proposes a deep learning prediction method based on an improved iTransformer model.
First, continuous 20-day real-time BDS SSR data streams broadcast from the WHU mount point were collected, with the accuracy of a 10-day subset being analyzed to support subsequent data processing. Then, an enhanced iTransformer model incorporating residual networks was constructed according to SSR data characteristics. This model was employed to predict real-time orbit and clock corrections sequences for all BDS satellites. Analysis of prediction results across different orbital satellite types demonstrates that the model achieves stable orbit correction accuracies within R/A/C directions of 0.1 m/0.2 m/0.2 m for up to 2 h, with a clock offset correction accuracy below 0.5 ns.
Furthermore, the model exhibits remarkable generalization across different platforms, delivering reliable performance on both geodetic-grade MGEX stations and low-cost receivers, which underscores its potential for broad applicability in both professional and mass-market navigation services.
In summary, this study establishes a critical and effective linkage between deep learning-based time-series forecasting and the continuity of high-precision PPP services. The proposed framework provides a scalable and resilient solution for mitigating the impacts of SSR data stream discontinuities. Future work will focus on extending the model to multi-GNSS interoperability and exploring a lightweight dual-branch architecture to better decouple and handle the challenging issue of clock bias jumps.