Highlights
What are the main findings?
- A complete annual/seasonal cycle was observed, based on the correlations between ice mass variations, three climatic indices (i.e., NAO, GBI, AMO), and meteorological parameters (i.e., Temperature, Precipitation, Albedo).
- Interannual oscillations are also observed with periodicities ranging from 4 to 7 years. They could be related to mixed effects from the solid Earth’s rotation and atmospheric oscillations. A second interannual frequency is observed at 11 years, corresponding to the solar cycle.
What is the implication of the main finding?
- With a complex climatic system regulating ice mass variations in Greenland, a single external forcing on one of these indices and parameters could have a cascading effect in space and time at an annual and interannual scale.
Abstract
The ongoing global warming threatens the Greenland Ice Sheet (GIS), which has exhibited an overall mass loss since 1990. This loss varies annually and interannually, reflecting the intricate interactions between the ice sheet and atmospheric and oceanic circulations. We investigate GIS mass balance variations (2002–2024) using data from the Gravity Recovery and Climate Experiment (GRACE) and its Follow-On (GRACE-FO) missions. Monthly mass anomalies from the International Combination Service for Time-variable Gravity Fields (COST-G) solution are compared with cumulative climate indices (North Atlantic Oscillation—NAO, Greenland Blocking Index—GBI, Atlantic Multidecadal Oscillation—AMO) and meteorological parameters (temperature, precipitation, surface albedo). Empirical Orthogonal Function analysis reveals five principal modes of variations, the first capturing annual and interannual frequencies (4–7 and 11 years), while subsequent modes only describe interannual frequencies. Wavelet analysis shows significant annual correlations between GIS mass changes and temperature (r = −0.88), NAO (r = 0.74), and GBI (r = −0.85). An annual cycle connects GIS mass changes, climatic indices, and meteorological parameters, while interannual variations highlight the role of the AMO and the NAO. The presence of an 11-year periodicity with the mass variations for NAO, GBI, and temperature strongly correlates with solar activity.
1. Introduction
The Greenland Ice Sheet (GIS) is the largest contributor to contemporary sea level rise after the thermal expansion of oceans [1]. Its ongoing mass loss can largely be explained using a simple linear trend, as presented to the general public on the NASA website [2], showing a loss rate of −269 Gt/yr between 2002 and 2023.
To quantify ice mass changes, several satellite-based techniques and methodologies have been developed. Satellite altimetry measures variations in surface elevation, from which mass changes are inferred by converting height variations into equivalent mass using modeled snow and firn densities [3]. Some altimetry results estimate mass loss over Greenland to be about −200 Gt/yr [4,5] to −251 Gt/yr [6], with ref. [6] observing two years of high mass loss: (1) in 2012 with −453 Gt and (2) in 2019 with −498 Gt. The input–output method estimates the mass balance as the difference between surface mass input (i.e., precipitation) and outputs from surface processes (e.g., melting, evaporation) and ice discharge at marine termini (e.g., calving). Results from this method estimate Greenland’s ice loss to be between −239 Gt/yr [7] and −272 Gt/yr [8], with a loss rate increasing over time [7] and reaching −428 Gt in 2012 [9]. Multi-method compilations combine several independent datasets, such as altimetry, input–output, and gravimetry estimates, to reduce uncertainties and provide more robust mass balance assessments [10,11]. Studies [10,11] of the Ice Sheet Mass Balance Inter-comparison Exercise (IMBIE) are showing, using this method, that mass loss in Greenland has steadily increased, from around −30 Gt/yr in 1992 to −180 Gt/yr in 2003 and to −257 Gt/yr in 2020. Finally, thanks to the gravimetric satellites mission Gravity Recovery and Climate Experiment (GRACE) and its Follow-On (GRACE-FO) missions, Earth’s monthly temporal variations in gravity can be monitored over more than two decades [12,13]. The changes in gravity are predominantly caused by water mass storage variations [14,15] as well as ice mass changes in glaciers, ice caps, and ice sheets in polar regions [16,17]. Gravimetric estimates of ice mass loss over the GIS tend to show values ranging from −195 Gt/yr [18,19] to around −265 Gt/yr [20,21,22], with the year 2012 reaching up to −437 Gt [23].
Underlying the GIS acceleration in mass loss [11], both annual and interannual variability have been observed. Annually, the GIS mass amplitude varies between 114 Gt and 172 Gt [24], while several studies [19,23,25] have observed a period of high losses (e.g., 2010–2013) followed by a subsequent deceleration. These fluctuations are related to variability in processes such as ice discharge, surface melting, and precipitation [26]. These variations reflect the complex responses of the GIS to both internal and external climatological forcing [27], such as the surface temperature, the type and amount of precipitation, and the oceanic temperature [28,29]. All these climatic changes are ultimately driven by insolation, the fundamental energy source influencing directly or indirectly the climatic system across multiple time scales [30,31,32,33,34,35,36,37].
Several climatic modes of variability can strongly influence the GIS. Climate indices such as the Greenland Blocking Index (GBI), which measures the persistence and intensity of anticyclonic events [38], the North Atlantic Oscillation (NAO) that measures the difference in atmospheric pressure between systems of pressure above the Azores and Iceland [39], and the Atlantic Multidecadal Oscillation (AMO), corresponding to the sea surface temperature (SST) of the North Atlantic [40], have been shown to influence the ice sheet at different spatiotemporal scales. For example, it is suggested that both NAO and GBI are correlated with mass loss through their impact on the number of melt days [41]. Moreover, all three indices have been associated with runoff and temperature, with the GBI showing the strongest correlation [42].
Specific events illustrate the sensitivity of the GIS to climatic forcing. For example, the massive ice loss event of 2012 (~464 ± 62 Gt/yr from GRACE [23]) was attributed to various drivers like persistent anticyclonic conditions, an extremely negative NAO index, and surface albedo and temperatures [8,23,43]. More recently, in 2018, an event of destabilization of the K.J.V. Steenstrups Nordre Bræ glacier (North-East Greenland) was shown to be caused by an increase in oceanic temperature [44].
The complexity of Greenland’s climatic system is such that, despite extensive research, a complete review of all interacting factors across different time scales is still lacking. As such, our objective is to help, in that regard, by proposing a better understanding of the dynamics linking several indices (NAO, GBI, and AMO), parameters of temperature, precipitation, and albedo, and mass variation in the GIS, at an annual and interannual time scale, as well as confirming the presence or absence of links between them.
To do this, we focus on the period between April 2002 and the end of 2023, with mass loss recovered from the monthly gravimetric satellite dataset of GRACE and GRACE-FO. We implement a method where indices are cumulated over time and compared to the modes of the Empirical Orthogonal Function (EOF) of the time series of ice loss [45]. This allows us to directly compare the cumulative effect of each climatic event over the mass variations. After presenting the different data, their treatment, and the EOF and cross-wavelet analysis method, we present the principal modes of variations and observe the most significant correlations between the mass changes, the climatic indices, and the meteorological parameters. In the discussion, we explore in more detail the common cycles and investigate the behavior of those intertwined elements with each other, to propose a scenario for a complete annual cycle.
2. Materials
In this section, we detail the sources of the different datasets, as well as the processing used to obtain our dataset. The first part explains how the gravimetric data from GRACE(-FO) are recomposed, reduced, and temporally interpolated into a complete monthly time series of mass variations over Greenland. Then, the cumulation treatment used on both indices and meteorological parameters is introduced. It is followed by the explanation of what each index is, the current understanding of them, and their relevance. Finally, the parameters of temperature, precipitation, and albedo are described.
2.1. GRACE/GRACE-FO
We chose the GRACE and GRACE-FO solutions, release one and two, respectively, from the International Combination Service for Time-variable Gravity Fields (COST-G), which combine those of other centers with different weights depending on the month. The data extend from April 2002 to December 2023 and are in the form of monthly Stokes coefficients, i.e., dimensionless spherical harmonics (SH) coefficients of the Earth’s potential with a maximum degree of 90. They are available at the International Centre for Global Earth Models (ICGEM) [46,47,48].
We processed those SH to obtain a 1° grid over Greenland using Equation (1), which enables us to reconstruct mass change in terms of equivalent water height at each time , colatitude , and longitude .
where is the load Love number k for the corresponding harmonic degree l. and are the monthly Stokes coefficients for the degree l and order m, whereas and are the averaged coefficients at l and m. The normalized associated Legendre function is noted . Earth’s radius is equal to 6,378,140 m, while Earth’s average density and the water density are, respectively, 5517 kg/m3 and 1000 kg/m3.
Finally, the equivalent water height obtained is converted to gigatons of mass by knowing the corresponding surface area of each grid point.
The C20 coefficient (Earth’s oblateness) is replaced by Satellite Laser Ranging (SLR) derived values, and the geocenter coefficients (C10, C11, and S11) are inserted following the corresponding Technical Notes [49,50]. Geocenter coefficients transcribe both north–south and equatorial translations of Earth’s mass center compared with the geometric center.
When recomposing the SH, a Decorrelation and Denoising Kernel filter of level 5 (DDK-5) was applied to remove the stripping effects otherwise present [51]. This filter offers a good compromise between smoothing and denoising; its effective diameter in Greenland’s latitude is close to the spatial resolution of GRACE/GRACE-FO, i.e., ~360 km.
We also correct the effect of the Glacial Isostatic Adjustment (GIA). We chose the most recent model from the ICE-xG series, named ICE-7G_NA (VM7), an upgrade from the previous ICE-6G [52,53].
We use forward modeling to reduce the methodological leakage errors resulting from the recomposition of SH, e.g., land–ocean leakage along the coast. This method requires estimating a global map of mass change. Then, as we want to reduce the leakage from the land to the ocean, ocean values are set to zero, and the initial iteration map is recombined into SH. The same filter is reapplied, and the mass variations are reconstructed. The difference between the estimated global map and the newly constructed map is calculated and added to the map of the current iteration. If the difference is less than 1% of mass change over Greenland between two iterations, we stop the cycle. This method is an effective solution to leakage over Greenland or even basin-wide areas [25,54,55].
Temporal mass variations recovered from the GRACE COST-G solutions are sampled at a constant monthly timestep. However, there are temporal gaps in the time series; for the small ones, up to 2 months, the gaps are simply linearly interpolated. Otherwise, for the large gap between GRACE and GRACE-FO in 2018, we use a frequency interpolation method commonly used for quasi-periodic signals. We fill this gap with the inverse Fast Fourier Transform (FFT) of the FFT coefficients estimated for this period. Those coefficients are obtained from the linear interpolation of the FFT coefficients of the preceding and following years of GRACE and GRACE-FO, respectively. The completed Greenland mass change profile is presented in Figure 1.
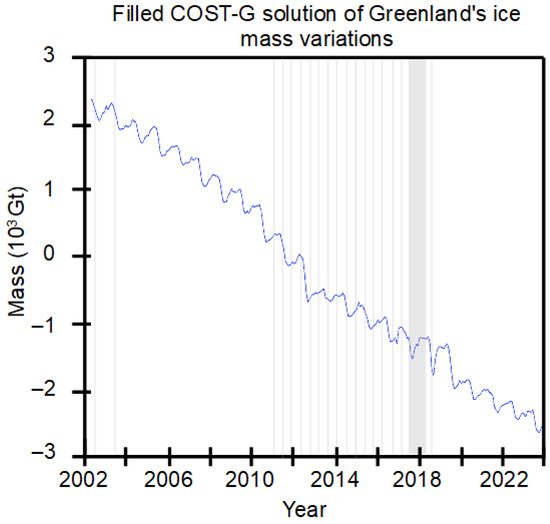
Figure 1.
Gap-filled ice mass variations over Greenland, from the COST-G solutions, expressed in Gt, from 2002 to 2023, the gray bands represent the gaps during and in between GRACE and GRACE-FO missions.
2.2. Climate Indices
We consider using climate indices to uncover climatic and meteorological links between them and the GIS mass variations. Over Greenland, the three indices, the GBI, NAO, and AMO, were shown to directly or indirectly cause mass variations [56,57,58,59,60]. That is the reason why they were chosen over other indices. Those three climatic indices capture large portions of all atmospheric and oceanic forcing most relevant to the GIS variability. In fact, the NAO reflects large-scale atmospheric pressure anomalies that regulate cloud cover, temperature, and precipitation over Greenland [56,61,62,63], thus strongly influencing surface mass balance. The GBI quantifies how persistent the high-pressure blocking is over Greenland. It is directly associated with extreme melt events [59] and surface albedo feedbacks [64,65,66]. On the other hand, the AMO characterizes multidecadal variability in the sea surface temperatures (SST), which primarily modulates Greenland’s marine-terminating glaciers’ stability [67]. Together, these indices represent dominant modes of climate variability that drive annual to multidecadal changes in Greenland Ice Sheet mass balance.
The indices NAO, GBI, and AMO are treated following the method used by ref. [45] for interannual ice mass variations in Antarctica. The method consists of a time integration of an index. This index is normalized and then summed. We truncated the data to correspond to the considered GRACE and GRACE-FO period, between April 2002 and December 2023. We remove a linear trend to isolate the annual and interannual variations. This method reveals the cumulative effect of individual events in the raw index, where each event reflects the instantaneous rate of mass variations when interconnected [45]. Consequently, the time-integrated indices correspond to the observed mass changes from gravimetric satellites rather than mass flux, as with the raw indices. This relationship has been demonstrated in prior studies linking: (a) Antarctic ice dynamics through indices, GRACE, and altimetry data [45,68,69]; (b) NAO and SST [70]; (c) Ice shelf elevation changes with El Niño-Southern Oscillation [71].
2.2.1. NAO
The NAO index is a climate index that measures the difference in atmospheric pressure between the Subtropical High, over the Azores, and the Subpolar Low, over Iceland. It is the leading mode of atmospheric variability in the North Atlantic and strongly influences weather and climate over Greenland. The strength of this teleconnection pattern provides information about the atmospheric circulation influencing the climate of the Atlantic basin [39]. A positive phase of NAO corresponds to an increase in the dipole pressure difference, which means pressure on the Subpolar Low has decreased and/or the pressure on the Subtropical High has increased.
The NAO is provided by the Climate Prediction Center from the National Center for Environmental Prediction of the National Oceanic and Atmospheric Administration (NOAA) and the National Weather Service. The dataset is the monthly mean value of NAO from January 1950 to the present. This index is calculated from the projection of the NAO loading pattern, which is the first mode of a rotated EOF over 0° to 90° of latitude for the monthly mean anomaly data between 1950 and 2000, over the daily anomaly for the 500 mbar height field [72,73,74].
It exhibits marked annual variability [75] and several interannual periodicities, in particular 7 and 13 years [76]. The NAO is correlated with climatic indices such as the AMO [77], as well as ice sheet mass variations [56]. It influences Greenland’s ice loss through its control on: (1) cloud cover and temperature [63]; (2) precipitation and runoff [56]; and (3) the albedo feedback during melt events [64].
2.2.2. GBI
The GBI quantifies the occurrence and intensity of atmospheric blocking events, which are stationary or slow-moving high-pressure systems. Those persistent anticyclonic systems are, in Greenland, associated with extreme summer temperature and ice sheet melting [78]. This metric serves as an indicator of high-pressure blocking events over this area [38], positive GBI values indicating more blocking with the presence of a persistent anticyclonic regime.
The GBI is available through NOAA’s Physical Sciences Laboratory (PSL). The format is a daily coverage from 1948 onward, derived from the NCEP/NCAR Reanalysis [79], which we aggregated into monthly values. This GBI covers the region (20°–80°W, 60°–80°N) and represents the mean 500 hPa geopotential height over Greenland.
The GBI exhibits seasonal variations [80], and a 7–8-year oscillation [38]. It is anti-correlated with the NAO [80], and potentially positively to the AMO [81]. This index increases Greenland’s ice loss [59] by: (1) reducing cloud cover, enhancing shortwave radiation and increasing temperature [65]; and (2) reducing surface albedo [82].
2.2.3. AMO
The AMO is a climate index describing the long-term variations in the North Atlantic sea surface temperature (SST). It reflects the multidecadal variability in ocean heat content and circulation, which affects the climate of the Northern Hemisphere by modifying atmospheric circulation, precipitation, and temperature [83]. In its positive phase, the SST of the Atlantic Ocean is stronger than in a negative phase.
The AMO index is obtained from the PSL of NOAA. The dataset consists of monthly, unsmoothed values spanning January 1856 through January 2023. It represents a weighted average estimated over the North Atlantic SST using the Kaplan SST dataset (5° × 5° resolution). The AMO computation encompasses the zonal area between 0 and 70° N [40,84].
The AMO exhibits annual variability driven by insolation changes [85], and decadal oscillations with a 10–30-year periodicity [86]. It is related to atmospheric processes such as blocking events over Greenland (GBI), which is positively correlated with it [87]. This index partially enhances Greenland’s coastal ice loss [57] by melting glaciers’ front and destabilizing them [44]. It is also correlated to temperature [56].
2.3. Meteorological Parameters
To enhance our understanding of the dynamics between the GIS and the climatic indices, we analyze key meteorological parameters such as the NST, the volume of precipitation, and the surface albedo over the area of Greenland. Those three parameters are from the Copernicus Arctic Regional ReAnalysis (CARRA) on the Climate Data Store of Copernicus Climate Change Service [88].
All data from CARRA have a 2.5 km horizontal resolution. Daily data points were extracted from 1 January 2002 to 31 December 2023. The three parameters we focus on are the 2 m temperature, the albedo, and the total precipitation. Those datasets were downscaled to monthly 1° grids.
Temperatures are used to assess the thermal impact on the GIS. We compute a time-integrated temperature index (Equation (2)), which accounts for both duration and intensity above the melting threshold. While 0 °C is classically used as the threshold, this represents an overestimation of the temperature needed for melt initiation, as in Antarctica, where melting can start at subzero temperatures due to surface energy balance processes [89].
where the time-integrated temperature TDT, in °C, represents the available thermal energy to influence ice melting for the month (i) and only for positive temperatures (+°C). TD is estimated as the percentage of days per month (i) where positive temperatures (+°C) are reached. This is multiplied by the average positive Temperatures (T+°C) during the month (i).
The surface Albedo (Al) represents the spatially averaged fraction of incoming solar radiation reflected by a surface. It exhibits temporal variability due to changes in snow and ice properties, including grain size, evolution, and presence of light-absorbing impurities like dust, black carbon, or algae, and the surface type characteristics [65,82,90,91]. In the ablation zone, surface albedo has a critical control on the melt variability, with an albedo-melt feedback mechanism potentially responsible for up to 50% of increased melting [64].
Finally, precipitations (P) are a critical mass balance component as they are the GIS’s only source of ice mass gain. This parameter comprises all solid, liquid, and in-between types of precipitation (e.g., rain, sleet, snow) [88]. Precipitation patterns are regulated by atmospheric dynamics, including pressure systems, moisture content, and circulation patterns, as well as by the local topography [92]. However, climate projections indicate that increased precipitation under warmer conditions will be insufficient to offset mass losses from enhanced meltwater runoff [93].
3. Methods
In this section, we explain the Empirical Orthogonal Function (EOF) approach used to separate into different modes of variability the mass variations, and the cross wavelet transform approach used to compare and find the corresponding frequencies and phase shift common to both modes of ice mass variability and climatic indices or meteorological parameters.
3.1. Empirical Orthogonal Function
We use the EOF method, which provides an orthogonal decomposition of a spatiotemporal dataset into N number of modes that maximize the explained variance [94,95]. This is utilized to separate the distinct temporal modes of ice mass variability that could correspond to the effect of different forcing on the GIS. The covariance matrix C of the initial mass change dataset Z(x,y,t), defined in space (x,y) and time t, is first computed, for n months, as follows (Equation (3)):
The eigenvalue problem: , in which CSk is the projection of the eigenvector Sk, which is the spatial structure of the mode k, in the space defined by the covariance matrix C, and λk represents the associated eigenvalues, which indicate the variance fraction explained by each mode. The corresponding time-varying amplitude of each mode is called a principal component (PCk(t)) and is obtained with Equation (4):
The original field can thus be reconstructed with Equation (5):
This method provides a robust framework for identifying the dominant modes of interannual ice mass redistribution variability, effectively characterizing spatiotemporal redistribution patterns through its orthogonal decomposition approach [45,96,97]. We removed a linear trend at each grid point (x,y) of the mass change obtained through SH, to focus on interannual variability. Then, the dataset is decomposed into temporal and spatial orthogonal oscillations, and the total variance explained by each EOF mode is estimated. To determine the optimal number of significant modes, we employed two complementary criteria. Firstly, we use the North’s test [98] to find which mode is distinct from one another, and secondly, we confirm that their frequency components are higher than red noise [99].
3.2. Cross Wavelet Transform
We use a time-frequency representation to analyze and cross-correlate the temporal mass variations and the climatic/meteorological variables defined in 2.2 and 2.3. We perform the cross wavelet transform (XWT) analysis from the “Cross Wavelet and Wavelet Coherence toolbox” [100]. Its utility is to unveil common frequencies, the type of correlation, and the lead-lag (phase shift) between two temporal signals. The time difference can be estimated by multiplying the frequency (e.g., 1 year) by the angle shown by arrows divided by 360°; for example, an arrow pointing down (90°) at the 1-year frequency (12 months) indicates that the first signal is leading the second by months. Statistically significant common periodicities (p < 0.05) appear as black contours in the wavelet spectrum. They are determined through Monte Carlo simulations against an autoregressive (AR1) red noise background. The 2σ threshold (95% confidence level) indicates there is only a 5% probability that these coherent regions occur randomly, while all non-contoured regions represent noise.
The Wavelet Transform (WT) employs a mother wavelet function (ψ) that undergoes scaling to generate daughter wavelets of varying wavelengths. This operation effectively functions as a band-pass filter bank applied to the time series. When a daughter wavelet exhibits strong temporal correspondence with the signal, high localized spectral power emerges at the associated frequency. To account for boundary effects, we define a cone of influence (COI) where edge artifacts become significant, typically shaded in wavelet power spectra.
We chose ψ as a Morlet wavelet (Equation (6)) for its balance between time and frequency localization, which is suitable for studying non-stationary physical signals, such as mass variations [100,101,102,103,104].
where η is the dimensionless time parameter defined as η = t/s, t being the time and s the wavelet’s scale; β the dimensionless frequency, is set at 6 for a good balance between time and frequency localization [105].
The XWT compares two WT of two time series (X and Y), and is defined as follows, Equation (7):
where is the cross wavelet power at time t and for a wavelet scale of s. The complex argument is the local phase of the signal X and the is the complex conjugate of the local phase of signal Y.
Assuming that our processed signals are cyclic over time. We can increase the precision of the frequencies by duplicating the signals on both ends.
4. Results
Comparison of detrended GRACE mass balance data with climatic indices and meteorological parameters reveals clear annual-scale linkages. Thus, decomposing the signal into dominant modes of variability through EOF analysis is required to identify and characterize the interannual drivers of ice mass variations. Our results demonstrate statistically significant relationships between GRACE-derived annual and interannual mass changes, key climatic indices, and meteorological parameters. These relationships emerge from combined EOF decomposition and XWT analysis, which, together, reveal the temporal phasing of these interactions.
4.1. GRACE EOF Modes
Figure 2a–e show the first five dominant modes (M1, M2, M3, M4, and M5) of GRACE-derived mass variability in Gt over Greenland. These modes correctly explain 67.5% of the total variance, with individual contributions of 31.9% (M1), 17% (M2), 8.5% (M3), 5.7% (M4), and 4.4% (M5). North’s test of significance [98] confirms that the first four modes are statistically distinct from one another. Although Mode 5 (M5) lies next to the statistical significance threshold, our analysis reveals statistically significant features (p < 0.05), suggesting M5 captures physically meaningful signals. All five modes have an explained variance exceeding that of random noise (p < 0.05) and have spectral power significantly above red noise background [99]. Higher-order modes (each explaining <4% variance) are excluded from further analysis (Figure 2f).
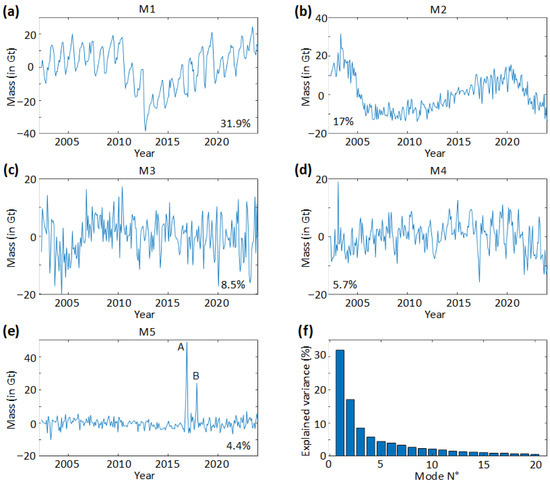
Figure 2.
Principal components of the EOF analysis of Greenland ice mass changes, derived from GRACE(-FO), between 2002 and 2024. (a–e) are the first five modes, in order of explained variance, and peaks named ‘A’ and ‘B’ are noted next to their corresponding peak in M5 in (e), and (f) the bar representation of the explained variance of the first twenty modes.
The M1 mode, Figure 2a, is characterized by annual oscillations, superimposed on a longer period variation. The annual oscillation has an amplitude of ~20 Gt, while the interannual variability reaches amplitudes of up to ~50 Gt. The separation of the yearly component may not be perfect, and could also be found in the other modes. However, higher frequencies dominate in these cases, and there is no clear annual signal.
The pattern of M2 exhibits a distinct long-period variation up to ~30 Gt, which contrasts with M1, suggesting a potential forcing by different climate modes. Modes 3 and 4 (M3-M4) display primarily high-frequency seasonal signals with no discernible lower-frequency components. The last mode, M5, differs fundamentally from the other modes, resembling residual noise except for two prominent anomalies: Peak A (November 2016, +50 Gt), and Peak B (November 2017, +20 Gt) (Figure 2e). These anomalies substantially exceed the background variability (~10 Gt of amplitude) and will be examined separately in the Discussion. Subsequent analysis focuses on M1–M4.
4.2. Correlations Between Ice Mass Changes and Climate Indices
We conducted a comprehensive comparison between each climate index and all possible combinations of the first five EOF modes (M1–M5) using cross-wavelet transform (XWT) analysis. This approach identifies the statistically significant common periodicities (95% confidence level; 2σ threshold) and their phase relationships. For each significant shared frequency, we computed the maximum correlation coefficient while accounting for optimal time lags.
Figure 3 presents the strongest overall correlation between the decomposed GRACE-derived timeseries of mass variations and one of the indices: M1 compared to the NAO (Figure 3a), the combined signal of M1 and M2 compared to the GBI (Figure 3b), and to the AMO (Figure 3c). Alongside those compared signals, the corresponding XWT analysis allows the identification of the common frequencies. It shows the procedure used to derive the values reported in Table 1, which summarizes all significant correlation coefficients in accordance with the shared frequency.
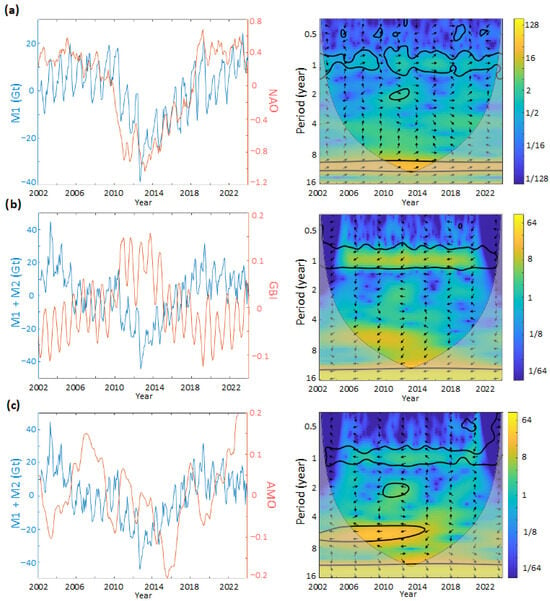
Figure 3.
Comparison of the cumulated indices (in red) with the modes or summation of modes of ice mass changes in Gt (in blue) between 2002 and 2024, and, at the right, the corresponding XWT analysis. In (a), the NAO is compared with the M1, (b) is the GBI with M1 + M2, and (c) is the AMO with the sum of M1 and M2 as well. On the XWT, the color scale represents the amplitude in units of normalized variance, the arrows are the phase shift (positive correlation pointing right (0°), anti-correlation pointing left (180°), and the progressive time shift in between is estimated as ), the bold line delimits the zones with a significance level of 5%, and the shaded area is the cone of influence where edge effect is important.

Table 1.
Coefficients of correlated common frequencies (more than 2σ of confidence) between the GIS modes or sum of modes (M1, M2, M3, M4, and M5) and the climatic indices (North Atlantic Oscillation (NAO), Greenland Blocking Index (GBI), and Atlantic Multidecadal Oscillation (AMO)) or the meteorological parameters (Temperature (TDT), Precipitation (P), and Albedo (Al)). “to” means the sum of the encompassed modes. The highly positively correlated coefficient, superior to 0.7, and the highly negatively correlated ones, inferior to −0.7, are in bold. Values between −0.5 and 0.5, or with p > 0.05, are not represented.
The comparison between M1 and NAO, in Figure 3a, reveals two significant common frequencies. The first is an annual correlation (r = 0.74, p = 10−70, Table 1), while the second is a decadal-scale variability (~11 years), with a 1-year lead from the NAO when considering M1 alone. Both correlations have a positive phase alignment, indicating that positive NAO phases coincide with increases in ice mass.
The GBI demonstrates two significant anti-correlated relationships with the combined modes M1 and M2. The first is a negative correlation at an annual scale, with the GBI leading the ice mass signal by one to two months. On longer timescales (>15 years), the combined modes M1+M2 display a strong anti-correlation (r = −0.91, p = 10−274, Table 1). This suggests that atmospheric blocking tends to precede and intensify mass losses on Greenland. Also, although the long-term trend appears within the cone of influence (COI) due to the limited observation span, its coherence across the entire 22-year period indicates a persistent large-scale relationship between the two signals, as we can see in Figure 3b.
The AMO is associated with three significant correlation bands, one at the annual frequency, another at ~7 years, and the last one beyond 15 years. The first two shared frequencies are showing negative correlation (arrows at 180° Figure 3c; negative values Table 1), implying that a rise in surface oceanic temperature, reflected by the AMO, would coincide with ice mass loss across Greenland over different timescales. When comparing only the sum of M1 and M2 to the AMO, the interannual frequency found around 7 years stops after 2014. The last shared frequency is a multi-decadal variability with positive correlation (r = 0.73, p = 10−66, Table 1) and a notable 3.5-year lag of the AMO relative to ice mass. This long-period coherence suggests a potential delayed response from the Atlantic SST to the GIS mass variations, although longer records are required for full confirmation, as it lies within the COI; see Figure 3c.
Beyond the illustrative cases shown in Figure 3, all significant coefficients across EOF modes of mass variation, climatic indices, and meteorological parameters are summarized in Table 1.
This table shows that the annual frequency observed on all indices and parameters is better represented by the first mode (M1) of the decomposed GIS mass variations, with absolute values ranging from 0.54 (P) to 0.90 (Al). The interannual common frequencies are grouped into three timescales: (1) a medium interannual periodicity with low time localization, oscillating between 4 and 7 years, with an absolute correlation coefficient ~0.80 (AMO, Al only), (2) a decadal periodicity of ~11 years, with an absolute coefficient ~0.75 (NAO, TDT, P), and (3) a long-term coherence between the signals across the entire 22 years of data, with absolute correlation coefficient values ranging from 0.73 (AMO) to 0.91 (GBI). Those frequencies are best represented by the combination of multiple modes, going all the way from M1 + M2 (GBI, AMO) up to the sum of M1 to M5 (P). In Table 1, it is shown that Temperature (TDT) is the only variable that does not require the second mode (M2) to observe a common interannual frequency with mass, whereas the AMO stands out as the sole index exhibiting two distinct interannual correlations.
For the climatic index, in terms of correlation sign, the NAO is the only one being positively correlated, indicating that its phases correspond with the mass variations. In contrast, the GBI and AMO are predominantly anti-correlated at the annual and interannual timescale, reflecting their role in amplifying Greenland mass loss. The only exception is the multi-decadal coherence of AMO, where the relationship shifts to a delayed positive correlation, suggesting a long-term influence of ice mass variations on the oceanic surface.
It is important to note a few points regarding the phase relationships and temporal persistence of the correlation bands for the different common frequencies. For the ~11-year periodicity, the NAO observes a perfect phase alignment when considering the combined modes M1 to M4, whereas it was not the case with M1 alone (1-year lead), see Figure 3a. The GBI annual correlation with M1 demonstrates a consistent anti-phase relationship, with the index leading by one or two months the mass variations. In the case of the AMO, the annual band with M1 shows no delay, while the interannual band (~7 years) has a complete coherence band across the entire record when comparing it to the combined mode M1 up to M4, contrary to the band shown in Figure 3c, which stopped in 2014.
4.3. Links Between Ice Mass Changes and Meteorological Parameters
Figure 4 illustrates representative examples of the strongest overall correlation between the decomposed GRACE-derived mass variations and the meteorological parameters: TDT (temperatures), precipitation, and surface albedo. In the same way as for Figure 3, each panel combines time series comparisons with the corresponding XWT analysis, providing both temporal and spectral perspectives of the relationships.
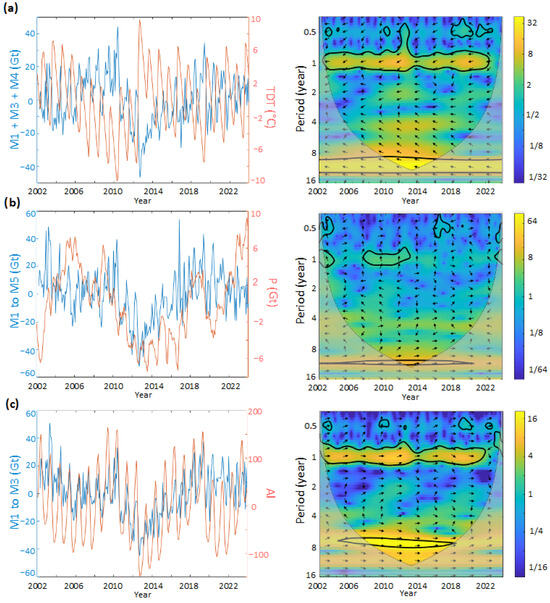
Figure 4.
Comparison of each cumulated meteorological parameter (in red) with the summation of modes of ice mass changes in Gt (in blue) between 2002 and 2024, and the corresponding XWT analysis. In (a), the TDT (temperature index) is compared with M1 + M3 and M4 modes, (b) is the Precipitation (P) with M1 to M5, and in (c), the Albedo (Al) is compared with the sum of M1 to M3. On the XWT, the color scale represents the amplitude in units of normalized variance, the arrows represent the phase shift (positive correlation pointing right (0°), anti-correlated pointing left (180°), and the progressive time shift in between is estimated as ), the bold line delimits the zones with a significance level of 5%, and the shaded area is the cone of influence where edge effect is important.
The optimal correlation is found with the combined M1 + M3 + M4 for the temperature (TDT) (Figure 4a); it is best represented by the full mode combination (M1 to M5) for precipitation (P) (Figure 4b); and Albedo (Al) is dominantly explained by M1 to M3 (Figure 4c).
The TDT signal exhibits a pronounced annual and decadal-scale anti-correlation with ice mass variability. On Figure 4a, a significant oscillation at ~11-years emerges between this parameter and the combined M1 + M3 + M4 modes (r = −0.71, p = 10−59). However, the annual anti-correlation is more strongly coupled with the use of only M1; see Table 1. This annual periodicity has the particularity to show that temperature anomalies lead the ice mass changes by up to two months. These negative coefficients reflect the dynamic of increasing ice mass loss, in case of an augmentation in the thermal energy available, observed through the TDT parameter.
When considering all five leading modes (M1 to M5), Figure 4b, precipitation only displays a strong positive correlation with mass variability at the ~11-year periodicity (r = 0.75, p = 10−74). This narrow coherence band is extremely localized in the frequency domain. A weaker, but consistent, annual positive correlation exists when considering only M1 (r = 0.54, p = 10−25, Table 1), with precipitation leading the ice mass signal by ~3 months.
For the albedo (Al), the comparison with the combined signal from M1 to M3 shows two significant positive correlation bands: a dominant annual cycle, and an interannual (~7-year) coherence persisting between 2004 and 2018 (r = 0.80, p = 10−102). The annual shared frequency is more strongly displayed when comparing only M1 to the albedo, whereas the interannual periodicity appears more dominant with the combined M1 to M3 modes. These strong correlations highlight albedo’s role in Greenland’s surface mass balance, operating through both seasonal and interannual feedback mechanisms (Figure 4c).
The correlation analysis demonstrates that Greenland ice mass variability is contemporaneous with atmospheric, oceanic, and local meteorological drivers across multiple time scales. These results provide a framework to identify the dominant climatic processes influencing the ice sheet. In the following sections, we use this framework to interpret the origins of the observed annual, interannual, and multi-decadal mass variability.
5. Discussion and Interpretation
This section first assesses the validity of the GRACE(-FO)-derived mass variations against alternative datasets. We then explore the dynamics between the climatic indices and meteorological parameters through their correlations. The different common periodicities are subsequently interpreted, beginning with the dominant seasonal/annual signal. Based on the cross-wavelet transform (XWT) results, we synthesize a complete annual cycle observed through two sets of correlations: (1) in Table 1 between the GIS and indices and parameters, and (2) among the indices themselves relative to temperature, precipitation, and albedo. We then link the decadal oscillation (~11 years) to the solar cycle, before exploring the other interannual periodicities ranging from 4 to 7 years. Finally, we examine a potential long-term pattern in the AMO index and the non-periodic peak identified in the fifth mode of the decomposed mass variations.
5.1. Mass Changes Validation
GRACE-derived mass changes, presented in Figure 1, are compared to (1) the 2023 compilation results from the Ice Sheet Mass Balance Inter-comparison Exercise (IMBIE) team utilizing multiple datasets derived from altimetry, the input–output method, and gravimetry, which includes nine different GRACE(-FO) datasets [11], (2) a recent altimetry dataset using multiple sources [106] (Figure 5).
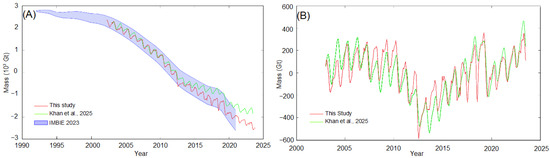
Figure 5.
The complete mass variation signals from our study, that of the IMBIE team [11], and the one from ref. [106], are shown in (A), and in (B) are the linearly detrended signal of our study against that of the altimetry one from ref. [106].
GRACE-derived mass variations are well encompassed in the IMBIE variation extent, which is not the case for the end of the altimetry dataset. Our result follows the altimetry curve for the first half, before showing more mass loss, ~700 Gt at the end (Figure 5A). However, after removing a linear trend from both gravimetric and altimetry data, both signals vary in the same way, annually and interannually (Figure 5B).
The discrepancy between the gravimetric results of this study and contemporary altimetry-based estimates [106] shows a statistically significant shift in dynamics around 2011. From 2003 to 2011, the mass difference decreased at an average rate of −10 Gt/yr (95% Confidence Interval (CI95%): −18 to −1 Gt/yr), indicating a gradual convergence between the two datasets. After 2011, this trend reversed sharply, with the difference increasing at +42 Gt/yr (CI95%: +38 to +46 Gt/yr), marking a period of sustained divergence.
A Chow test for a structural break confirmed that this regime shift, around 2011, was highly statistically significant (F = 65, p < 0.001). To further quantify the discrepancy, we performed a non-parametric bootstrap test (10,000 resamples) on the mean difference for each period. During the convergent period (2003–2011), the mean difference was 44 Gt (CI95%: 24 to 63 Gt), indicating a small but statistically significant systematic offset. For the divergent period (2011–2023), the mean difference increased to 352 Gt (CI95%: 324 to 381 Gt). The fact that neither confidence interval includes zero confirms that the discrepancy between the two observational techniques is significant in both periods, evolving from a minor offset to a major divergence.
Thus, the two signals only observe a small mean offset (~44 Gt) that tends toward convergence during the first period (2003–2011). From 2011 onward, a clear break occurs, the mean difference reaches ~352 Gt, and a considerable increase in the gap is observed (+42 Gt/yr).
The apparent convergence between the gravimetric and altimetric estimates from 2003 to 2011 (−10 Gt/yr on average) could largely be attributed to differences in the applied GIA corrections. In our study, the ICE-7G GIA model introduces a mass gain of ~6 Gt/yr over Greenland, whereas the altimetric study of [106], which applies the GNET-GIA empirical model, adds mass loss of around −3 Gt/yr. This results in a net difference of roughly ~9 Gt/yr attributed to the GIA correction, which is consistent with the observed convergence rate (10 Gt/yr) during this period. However, this offset alone cannot account for the divergence observed after 2011. As this large divergence coincides with the start of CryoSat-2 data acquisition, we hypothesize that the use of this dataset could be the origin of the divergent trend. This difference could be caused by factors such as (1) the incomplete spatial sampling of the altimetry database and the interpolation method, (2) the firn model and the radar signal penetration, or (3) the signal from peripheral glaciers not taken into account by the altimetry data [107,108].
5.2. Correlation Between Indices and Parameters
Our results show correlations between ice mass variations and changes in climate indices or meteorological parameters. The potential causes of these correlations are more or less evident depending on the frequency of the phenomenon and the multiple indices and parameters correlated.
Among the three indices, the GBI shows the strongest correlation (r = −0.85 and r = −0.91, Table 1) with mass variations. This is an expected result given that this index is specifically designed for Greenland. This contrasts with the NAO, which focuses on atmospheric pressures like the GBI, but is calculated for the entire dipole covering the North Atlantic rather than just Greenland. Similarly, the AMO only accounts for waters south of 70°N, and stops in the Labrador Sea, not taking into account Greenland’s western coast with its particularly active glaciers like the Jakobshavn Isbrae, or the north and northeastern region, with, e.g., the Zachariæ Isstrøm. This result follows what was already observed in different studies [42,109]. Both the NAO and AMO encompass a mix of climatic systems; their signal is not only representative of Greenland’s climatic system. In fact, for the NAO, it is known that the Azores High does not correlate with precipitation, contrary to the Icelandic Low [109].
To understand the complex mechanisms that affect the GIS, we start by examining which meteorological parameters are correlated with the NAO, GBI, and AMO indices using XWT.
Table 2 summarizes the statistically significant (p < 0.05) correlation coefficients and their corresponding common frequencies between the climate indices and the meteorological parameters. Three frequency bands emerge from this comparison: (1) an annual cycle, (2) a 4 to 7-year periodicity, and (3) a decadal-scale oscillation (~11 years). These frequencies are consistent with those identified earlier between these variables and the EOF modes of the GIS mass variations.

Table 2.
Coefficients of correlated common frequencies (more than two sigma of confidence) between the climatic indices (North Atlantic Oscillation (NAO), Greenland Blocking Index (GBI), and Atlantic Multidecadal Oscillation (AMO)) and the meteorological parameters (Temperature (TDT), Precipitation (P), and Albedo (Al)). The highly positively correlated coefficient, superior to 0.7, and the highly negatively correlated ones, inferior to −0.7, are in bold. Values between −0.5 and 0.5, or with p > 0.05, are not represented.
Overall, temperatures and precipitation are correlated with all three indices, while albedo shows strong coherence only with the GBI. The strongest correlations occur between the GBI and both temperature (r = 0.89, p = 10−217, Table 2) and albedo (r = −0.95, p = 10−525, Table 2), at the annual frequency. The other indices display their strongest connections with precipitation, particularly the AMO, which presents significant coherence bands across multiple frequencies.
In terms of phase relationships, the comparison with TDT (temperature) indicates that both NAO and GBI variations are synchronized with it at the annual periodicity, whereas the AMO is delayed by one to two months. At the decadal scale, the NAO is lagging by two years, while the AMO seems to be delayed by four to five years.
For precipitation (P), the GBI lags the annual oscillation by two months, while the AMO leads by three months this parameter. At the interannual (4–7-year) frequency, the AMO shows a variable phase relationship: between 2002 and 2012, it lagged behind precipitation by three months to one year, whereas since 2012, this relation has inverted, with the AMO now leading. For the decadal frequency, the AMO lags by about two years.
The blocking index leads the albedo by one or two months in the annual frequency. The anti-correlation between the two is indirectly related to the atmospheric pressure above Greenland, reflected by the GBI. It was shown that atmospheric pressure controls the amount of precipitation and temperature [64,109,110,111], which, in turn, influences the reflective quality of the GIS surface (more precipitation increases the albedo when the atmospheric blocking decreases), and causes the surface to darken in summer by maximizing the albedo feedback [64,65,66].
While the NAO shows a positive correlation interannually, we could have expected to find a correlation for the annual frequency, which is a known correlation over Greenland [62]. However, this frequency did not appear; we hypothesize that it was caused by the dampening of the coefficient by the opposed west–east correlation dipole it exhibits with the precipitation [56,61]. On the GBI side, the negative coefficient is consistent with what was expected, the conditions favorable to precipitation being when the GBI decreases and vice versa [64,109]. The relationship between AMO and precipitation is more complex. The positive coefficient indicates that both sea surface temperature, presented through the AMO, and the amount of precipitation over Greenland, co-vary with a lead-lag relationship fluctuating between frequencies.
The stronger coefficient found between GBI and temperature, compared to the NAO and AMO, had already been observed [42]. This index implies that more frequent and elevated high-pressure events over Greenland would cause anticyclonic conditions, resulting in clear skies, which increases the insolation and, thus, the temperature [112]. The NAO, with a negative correlation, implies the same phenomenon. Its low anti-correlation values could be caused by the difference in behavior between the northeastern and southern Greenland, the first being correlated to global temperature rise, compared to the other correlated to the NAO index [113]. On the other hand, the positive coefficient found between the AMO and TDT was expected due to a heat transfer from one to the other [42,56].
To better interpret these correlations, the discussion will now focus on the dominant shared frequencies between ice mass, climate indices, and meteorological parameters. We will start by discussing in more detail the two periodicities for which there are strong correlations: the 1-year period and the decadal one (~11 years). Then, we will discuss the other frequency detected in the signals, and we will finish by analyzing the source of the punctual events detected in the high-order mode (M5) of the EOF decomposition.
5.3. Annual Cycle
The annual variability is found between almost all of these factors. It is possible to link the different parameters to propose a synthetic scenario, grouping them all, which shows their respective participation. By exploring in more detail all the interactions that emerge from our study, we managed to represent a complete cycle over one year. This annual cycle shows when each of the climatic or meteorological factors intervenes in the variations in ice mass over a year. It is represented in Figure 6.
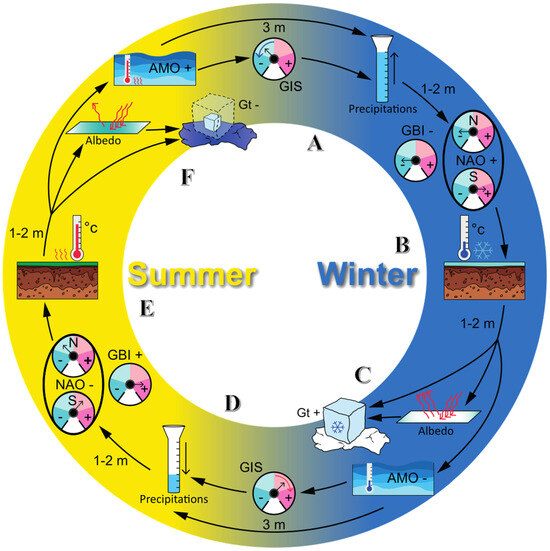
Figure 6.
Clockwise summary of the interactions between the GIS, the indices, and the meteorological parameters. This is the annual cycle implied by their respective relationship to each other. The arrows are not direct causal links; they imply that specific events show a positive or negative correlation to one another. A time lag of 1, 2, or 3 months is added to some arrows. This annual cycle is depicted with the summer part of the year on the left and the winter one on the right. The letters A to F help to follow the description in the text.
To describe how this cycle functions, we start at the top (A), at the transition between Summer and Winter. During this period, the atmospheric pressure difference, observed through NAO, increases while the blocking over Greenland decreases. The reason behind this variation is thought to be caused by the SST, which, while still warm at the mid-latitude, becomes colder in the high-latitude, and induces changes in atmospheric pressure thanks to the energy transfer between the ocean and the atmosphere [56,114]. The strengthened pressure gradient has been previously associated with increases in advection from south to north, allowing humid air from the still-warm surface of the North Atlantic Ocean to move northward [115,116,117]. Those conditions lead to a high amount of precipitation.
After one to two months (B), the NAO attains its maximum, which is corroborated by the low levels of blocking over Greenland reached at the same time. The available energy for melting (TDT) is also at its minimum, and the mean temperature is at its lowest. The observed correlation between NST and atmospheric conditions (NAO, GBI) is related to the positive feedback between them, which was uncovered by ref. [31].
Between 1 and 2 months later (C), the albedo reaches its maximum. This is caused by the freshly deposited snow cover induced by the last cyclones of the cyclonic season or by the polar low depression season [118]. In parallel to the albedo, and for the same reasons, the peak of mass is reached for the GIS. At this point in time, the SST, as depicted by the AMO, is also at its lowest. This is driven by less insolation, as well as thermal exchange with the coupled atmospheric system [85,119].
Then, the cycle reverses itself, blocking systems over Greenland are on the rise, and the NAO weakens. This known behavior [80] is encouraged by the low temperature of the ocean, which limits evaporation and makes the air less buoyant [81,115].
Three months after the negative AMO’s peak (D), precipitation over Greenland reaches its minimum. This drought condition results from a strengthened atmospheric blocking system, which dries the air mass over the ice sheet [92]. The subsequent intensification of this blocking is clearly observed 1–2 months later (E), as the Greenland Blocking Index (GBI) reaches its annual maximum and the North Atlantic Oscillation (NAO) dipole weakens. Concurrently, the TDT index peaks, indicating a large influx of energy available to drive melt. These elevated temperatures are primarily a direct result of increased solar radiation under the clear skies due to the persistent anticyclonic blocking [42,59].
Thus, the albedo and GIS mass decrease, reaching a minimum approximately 1–2 months before the AMO temperature peaks (F). This albedo reduction is driven by an anticyclonic system over Greenland, which induces high thermal availability and initiates a positive ice-albedo feedback loop [64,66].
With fewer storms, the snow cover is not renewed, and the grain sizes of the aging snow cover increase [82], which causes ice darkening, and lowers the percentage of radiation reflected, increasing the absorption of shortwaves [120]. This induces a rise in temperature and more melting, uncovering more surface of lesser albedo than that of snow [65]. With those conditions, the GIS mass also attains its lowest value of the year. The mass loss processes are varied; they encompass melting, evaporation, sublimation, runoff, and calving [62]. The 1- to 2-month difference between the mass variations and the temperature peak could be due to the time required for meltwater to flow and drain from the ice sheet to the ocean [121]. As the AMO index reaches its maximum, the warm Atlantic waters also exacerbate the calving by reaching glaciers’ outlet, melting their bottoms, and destabilizing their grounding line [44,56,57,67].
The observed 1- or 2-month lag between the AMO and the temperature can be explained by two phenomena. The heating imbalance from solar radiation is caused by the difference in latitude and the thermal inertia of the ocean [85,119,122], as well as the heat transfer between the atmosphere and the ocean, which requires 15 days for a water column of 10 meters of depth [123].
The annual cycle is governed by a series of coupled processes:
- Sea surface temperature, as shown with the AMO, drives pressure variations over the North Atlantic and modulates precipitation over Greenland.
- The NAO or GBI, and near-surface temperatures are intrinsically linked and mutually reinforcing.
- Precipitation and temperature influence albedo and ice mass, while albedo amplifies the effect of solar radiation on mass variations.
- Heat exchange between the land (NST) and the ocean (AMO) occurs with a one- to two-month lag due to oceanic thermal inertia.
- Finally, the AMO directly forces glacier retreat by promoting ice discharge at marine-terminating glaciers through enhanced calving and frontal melting, driven by oceanic thermal forcing.
5.4. Decadal Oscillation
The periodicities of 8 and 12 years appear regularly between the GIS, the indices, and the parameters. We investigate a possible link with the well-known solar cycle. Even though the average period of solar activity is 11.2 years, it varies between 8 and 15 years [124]. As such, there could be a relation between increases and decreases in solar emissions and the ice mass variations in the ice sheet. We recovered the radio emission from the Sun at a wavelength of 10.7 cm on the Space Weather website of the Government of Canada [125]. This dataset is available daily from 2004 to the present.
As shown in Figure 7, with the example of NAO, a common cycle between 8 and 12 years is visible in the XWT.
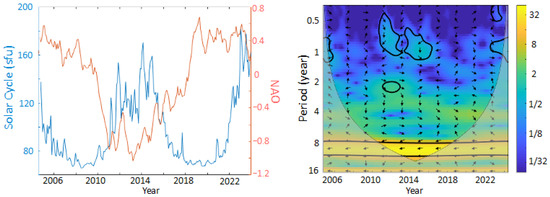
Figure 7.
Comparison of the NAO (in red) and the Solar cycle F10.7cm radio flux (sfu, in blue) between 2002 and 2024. On the XWT, the color scale represents the amplitude in units of normalized variance, the arrows represent the phase shift (positive correlation pointing right, anti-correlated pointing left, and the progressive time shift in between), the bold line delimits the zones with a significance level of 5%, and the shaded area is the cone of influence where edge effect is important.
Such oscillations around 11 years are visible for almost all parameters and indices we looked for. The sun can be the driving force of this cycle since it affects almost all climate actors [35,36,37,126]. An explanation of the principles behind the dynamical response of the atmosphere with variations in solar irradiance was given by Lean in 2017. It was shown that an addition of 0.1% of irradiance increases Earth’s surface temperature by 0.10 °C. This global effect is less than the warming of the atmosphere at 20 km (0.30 °C). The added energy alters the equator-to-pole relationship and induces warmer or cooler areas at mid to high latitudes. The climatic systems are also impacted by the modified vertical thermal gradient [127].
From the different correlations observed at this period, it appears that a high positive NAO, with an exacerbated atmospheric pressure dipole, is correlated to more precipitation in Greenland, and the same happens with the AMO. An increase in precipitation also means more mass gain on the GIS. The NAO is anti-correlated (r = −0.58, Table 2) to the TDT parameter, whereas the AMO is correlated but with a delay of 4 to 5 years (r = 0.79, Table 2). This delay is similar to what was previously found with the solar/geomagnetic activity influencing the AMO with a 4-year lead [37].
Nonetheless, as this period is half of our observation window, it will be interesting to confirm this result when a longer series becomes available.
5.5. Periodicities at 4 and 7 Years
Interannual cycles, varying from 4 to 7 years, are discernible in the relations between GIS, precipitation, AMO, and albedo. Such periodicities can also be found in the Antarctic [45].
There is ice loss when the GIS has a low albedo or when the AMO index is high. In the first case, the surface is darkening and it absorbs more radiation, so the ice melts and evaporates, or melts and flows away [64,66]. In parallel, the high AMO sea surface temperature directly melts ice at glaciers’ outlets and increases the calving [44,57,67].
There is also a complex link between precipitation and the AMO index at those frequencies. Like in the case of the yearly cycle and from what is already known, we expect the AMO index to be one of the causes of Greenland’s precipitation [92,115,116,117,128]. This is the case since 2012, when the AMO has had a head start of 3 months to a year over the precipitation (r = 0.76, p = 10−79, Table 2). However, the relation between them is inverted during the preceding period, 2002–2012, with the AMO lagging behind precipitation (r = 0.59, p = 10−32, Table 2).
We hypothesize this difference could come from the effect of fresh water from precipitation on the ocean dynamics and the mixing of the surface layer. The freshwater induced by meltwater discharge and meteoric water input is predominant in regions such as the Baffin Bay [129]. This fresh water influences the vertical mixing and stratification of the ocean. Other factors also influence the stratification; wind and lateral processes can increase or decrease the layering. In fact, between 2006 and 2012, it was reported that in the Canadian basin, a strong stratification occurred [130]. When less vertical mixing and a strong stratification of the ocean are present, like in the case of the China Sea in 2016, it has for effect to enhance the surface warming by trapping the thermal energy from the atmosphere and solar radiation in the surface layer [131,132].
The cause of these cycles could be related to atmospheric oscillations already observed for those frequencies [133]. Some part may come from a deeper origin. It has been shown that a relation between the angular momentum of the atmosphere with the solid Earth’s rotation over a 6-year period exists. It implies the possible link between the dynamical processes of the core, the solid Earth, and the different superficial fluid envelopes [134]. Further research on those periodicities must be performed to understand their origin and impact.
5.6. AMO’s Overall Correlation
While a potential long-term pattern is observed within the 22 years of GRACE and GRACE-FO measurement windows, there is insufficient data to establish any kind of cyclic behavior between the AMO, the GBI, and the GIS. However, the AMO relationship with the Greenland mass changes during those 22 years shows a potential positive correlation (r = 0.73) with a striking lag of 3.5 years across the entire time series. This would mean that an ice mass loss over Greenland will influence the AMO signal 3.5 years later. This lag could be related to the time needed to displace the oceanic water from Greenland coasts or from the Arctic Ocean to the North Atlantic area where the AMO index is calculated. In fact, it was determined that in the event of an increased blocking activity over Greenland, the sea ice and fresh water would accumulate in the Arctic Ocean, until it flushes out several years after ref. [87]. Such a blocking event leading to the accumulation of sea ice was observed in 1964 and affected the Atlantic Ocean 4 years after ref. [135]. In the same way, for Greenland’s western coast, it was shown that drifters anchored at a depth of 15 meters take ~6 months to cross the Labrador Sea, going from the Davis Strait to the Flemish Pass [136]. A similar lag between NAO and the sea surface temperature, on the Northeast Continental Shelf, induced by the displacement of water from the Labrador Sea to the rest of the North Atlantic Ocean, has already been described [137]. Nonetheless, we need more time, or the use of other methods or more complete SST data, to verify if the AMO delayed link to the GIS mass changes is a lasting behavior.
5.7. Non-Periodic Events
Our EOF analysis, Figure 2e, identified two apparent mass gain events in the M5 mode. The first one corresponds to the peak A in November 2016 (valid observation), and the second one to peak B in November 2017 (GRACE/GRACE-FO missions gap period).
The November 2017 event (peak B) coincides with the 11-month gap between the two GRACE(-FO) missions (July 2017 to May 2018). Therefore, it is likely an interpolation artifact rather than a real signal. This conclusion is confirmed by performing the interpolation method using the FFT coefficients of adjacent years. In the study, we use the 2016–2017 year, which is marked by the presence of a mass gain feature in November 2016. However, the November 2017 anomaly disappears when we use an alternative year instead, e.g., 2015–2016. In contrast, peak A (November 2016) represents a valid observation. We investigated its potential connection to extreme precipitation events through XWT analysis of M5 and the non-cumulated P in Figure 8.
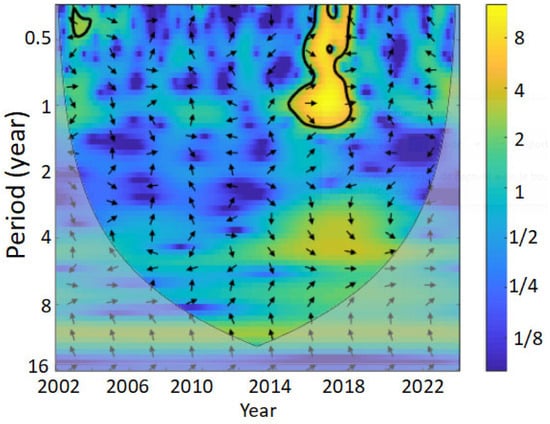
Figure 8.
XWT analysis of the fifth mode and the non-cumulated precipitation signal over Greenland between 2002 and 2024. The color scale represents the amplitude in units of normalized variance, the arrows represent the phase shift (positive correlation pointing right, anti-correlation pointing left, and the progressive time shift in between), the bold line delimits the zones with a significance level of 5%, and the shaded area is the cone of influence where the edge effect is important.
Figure 8 reveals a statistically significant positive correlation (p < 0.05) between precipitation anomalies and the GIS mass variations from early 2016 to mid-2017. This correlation strongly suggests that peak A (November 2016) in M5 reflects the impact of an extreme precipitation event. This anomalous mass gain coincides with exceptional winter accumulation (2016–2017), particularly associated with (1) a record precipitation in October 2016, and (2) the remnants of Hurricane Nicole, which reached southeastern Greenland in late October 2016 [62,138].
The interpolation method used to bridge the data gap effectively reconstructs the dominant periodic signal, such as the annual oscillation. However, this approach is susceptible to high-frequency artifacts. These artifacts arise when non-periodic, transient events—masked within the underlying oscillation used for the interpolation—are inadvertently incorporated into the gap-filled record.
Alternative approaches, such as incorporating data from Greenland’s Global Navigation Satellite System (GNSS) network (GNET), show significant promise for improving gap reconstruction in mass balance records. For instance, ref. [139] established GNET’s capability to model Greenland mass changes directly. Critically, GNSS-derived loading measurements are particularly adept at capturing high-frequency signals, which could substantially reduce interpolation artifacts during unsampled periods.
6. Conclusions
Our study investigates the mass balance of the Greenland Ice Sheet (GIS) from April 2002 to December 2023, revealing complex annual-to-interannual variability driven by coupled atmospheric, oceanic, and cryosphere dynamics. Through Empirical Orthogonal Function (EOF) analysis, we decomposed the mass signal into five significant modes (M1–M5), which together explain 67.5% of the total variance. Wavelet Cross-Correlation analysis further revealed the teleconnections between GIS mass balance and time series corresponding to key climate indices (NAO, GBI, AMO) and meteorological parameters (temperature, precipitation, albedo).
These results identify three dominant periodicities in GIS mass variability: 1 year, 4–7 years, and 11 years. The strongest is the annual cycle, which reveals a coherent loop of interactions between all the selected key climate indices (NAO, GBI, AMO) and meteorological parameters (temperature, precipitation, albedo) within the Greenland region. We propose a conceptual cyclic model in which the Atlantic Multidecadal Oscillation (AMO) exerts the primary forcing, leading to variations in the North Atlantic Oscillation (NAO) and Greenland Blocking Index (GBI). These atmospheric patterns, in turn, regulate regional temperature and precipitation. Subsequently, temperature and precipitation anomalies drive changes in surface albedo and ice mass, with albedo feedbacks amplifying the impact of solar radiation on melt. The ocean’s thermal inertia, reflected in the AMO, introduces a 1–2-month lag in sea surface temperature responses. Additionally, the AMO directly influences ice discharge at marine-terminating glaciers through oceanic thermal forcing, calving, and frontal melting.
Beyond the annual cycle, we identify significant interannual signals. The 11-year periodicity is consistent with the solar cycle, while the origin of the 4–7-year signal remains uncertain, potentially involving interactions between Earth’s rotation and atmospheric oscillations. A persistent multi-year correlation exists between the AMO and GIS mass, with the AMO lagging by approximately 3.5 years, suggesting a longer-term oceanic control that requires further investigation with extended data records. The AMO and GBI also exhibit a possible correlation over the full 22-year period. Confirming this signal as a persistent oscillation and elucidating its underlying mechanism will require analysis of a more extended GRACE-FO record.
Finally, our study also examined non-periodic signals, such as the prominent peak in the M5 EOF mode, which highlights the system’s sensitivity to transient forcing events, including extreme weather events. This underscores the GIS’s vulnerability to episodic, high-magnitude perturbations.
In this highly coupled system, external forcing on any single component can cascade across multiple spatiotemporal scales. While this study confirmed the influence of regional climate modes, future work should assess remote drivers such as the Pacific Decadal Oscillation or the Southern Oscillation Index. Furthermore, moving beyond temporal correlations to investigate the spatial heterogeneity of the GIS response is critical. Identifying regions of heightened vulnerability, zones of resilient accumulation, and local-scale ice-dynamical mechanisms will be essential for refining projections of Greenland’s contribution to sea-level rise.
Author Contributions
This study has been conceptualized by F.C. and M.L.; J.D. introduced the EOF and Wavelet method, whereas F.C. did the overall methodology. The data curation, the formal analysis, the use of software, and the investigation were performed by F.C. Figures were created by F.C. and completed with the ideas of M.L. The funding acquisition was performed by J.D., M.L. and F.C.; F.C. was supervised by M.L., J.D., L.S. and G.R. All authors have participated in the validation process, as well as the writing of the original draft and the revisions. All authors have read and agreed to the published version of the manuscript.
Funding
This article’s processing charges were covered by the TOSCA Gravietudes project (2025) supported by the CNES.
Data Availability Statement
Codes and data used in the article are subsequently listed, and their links are provided. All used codes were in MATLAB language, version R2018b. The code to perform wavelet analysis is the “Cross Wavelet and Wavelet Coherence toolbox”, available at https://github.com/grinsted/wavelet-coherence?tab=License-1-ov-file (accessed on 25 October 2025) or in another format via http://www.glaciology.net/wavelet-coherence (accessed on 25 October 2025). The GRACE(-FO) COST-G solution is available at the International Centre for Global Earth Models (ICGEM) website: https://icgem.gfz-potsdam.de/sl/temporal (accessed on 25 October 2025). All three indices, NAO, GBI, and AMO, come from the National Center for Environmental Prediction of the National Oceanic and Atmospheric Administration (NOAA). For NAO, data and information are found on the Climate Prediction Center and the National Weather Service: https://www.cpc.ncep.noaa.gov/data/teledoc/nao.shtml (accessed on 25 October 2025). The GBI and the AMO indices are available on the Physical Sciences Laboratory (PSL) website, with their respective URL being: https://psl.noaa.gov/data/timeseries/month/DS/GBI_UL (accessed on 25 October 2025) and https://psl.noaa.gov/data/timeseries/AMO/ (accessed on 25 October 2025). The meteorological parameters, temperature, precipitation, and albedo, are data from the C3S Arctic Regional Reanalysis (CARRA) and are stored in the Climate Data Store of Copernicus Climate Change Service. https://cds.climate.copernicus.eu/datasets/reanalysis-carra-single-levels?tab=overview (accessed on 25 October 2025). The solar cycle data is available on the Space Weather website of the Government of Canada [125]: https://spaceweather.gc.ca/forecast-prevision/solar-solaire/solarflux/sx-5-en.php (accessed on 25 October 2025).
Acknowledgments
The authors gratefully thank the Centre National d’Etudes Spatiales (CNES), TOSCA Gravietudes project (2025), and the Bureau Gravimétrique International (BGI) for their support. We also thank Etienne Berthier and Anthony Mémin for their fruitful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Al | Albedo |
| AMO | Atlantic Multidecadal Oscillation |
| AMOC | Atlantic Meridional Overturning Circulation |
| CARRA | Copernicus Arctic Regional ReAnalysis |
| COI | Cone of Influence |
| CI95% | 95% confidence interval |
| EOF | Empirical Orthogonal Function |
| FFT | Fast Fourier Transform |
| GBI | Greenland Blocking Index |
| GIS | Greenland Ice Sheet |
| GNET | Greenland’s GNSS network |
| GNSS | Global Navigation Satellite System |
| GRACE | Gravity Recovery and Climate Experiment |
| GRACE-FO | Gravity Recovery and Climate Experiment Follow-On |
| ICGEM | International Centre for Global Earth Models |
| IMBIE | Ice Sheet Mass Balance Inter-comparison Exercise |
| NAO | North Atlantic Oscillation |
| NOAA | National Oceanic and Atmospheric Administration |
| NST | Near-Surface Temperature |
| P | Precipitation |
| PSL | Physical Sciences Laboratory |
| SH | Spherical Harmonics |
| SLR | Satellite Laser Ranging |
| SST | Sea Surface Temperature |
| WT | Wavelet Transform |
| XWT | Cross Wavelet Transform |
References
- Cazenave, A.; Palanisamy, H.; Ablain, M. Contemporary Sea Level Changes from Satellite Altimetry: What Have We Learned? What Are the New Challenges? Adv. Space Res. 2018, 62, 1639–1653. [Google Scholar] [CrossRef]
- NASA; JPL/Caltech Greenland Ice Mass Loss 2002–2023. Available online: https://svs.gsfc.nasa.gov/31156/ (accessed on 23 October 2025).
- Hansen, N.; Sørensen, L.S.; Spada, G.; Melini, D.; Forsberg, R.; Mottram, R.; Simonsen, S.B. Revisiting Ice Sheet Mass Balance: Insights into Changing Dynamics in Greenland and Antarctica from ICESat-2 2023. Cryosphere Discuss 2023. [Google Scholar] [CrossRef]
- Ravinder, N.; Shepherd, A.; Otosaka, I.; Slater, T.; Muir, A.; Gilbert, L. Greenland Ice Sheet Elevation Change From CryoSat-2 and ICESat-2. Geophys. Res. Lett. 2024, 51, e2024GL110822. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Barletta, V.R.; Colgan, W.T.; Sørensen, L.S. Greenland Ice Sheet Mass Balance (1992–2020) From Calibrated Radar Altimetry. Geophys. Res. Lett. 2021, 48, e2020GL091216. [Google Scholar] [CrossRef]
- Khan, S.A.; Bamber, J.L.; Rignot, E.; Helm, V.; Aschwanden, A.; Holland, D.M.; Broeke, M.; King, M.; Noël, B.; Truffer, M.; et al. Greenland Mass Trends From Airborne and Satellite Altimetry During 2011–2020. JGR Earth Surf. 2022, 127, e2021JF006505. [Google Scholar] [CrossRef] [PubMed]
- Mouginot, J.; Rignot, E.; Bjørk, A.A.; van den Broeke, M.; Millan, R.; Morlighem, M.; Noël, B.; Scheuchl, B.; Wood, M. Forty-Six Years of Greenland Ice Sheet Mass Balance from 1972 to 2018. Proc. Natl. Acad. Sci. USA 2019, 116, 9239–9244. [Google Scholar] [CrossRef]
- Box, J.E.; Hubbard, A.; Bahr, D.B.; Colgan, W.T.; Fettweis, X.; Mankoff, K.D.; Wehrlé, A.; Noël, B.; Van Den Broeke, M.R.; Wouters, B.; et al. Greenland Ice Sheet Climate Disequilibrium and Committed Sea-Level Rise. Nat. Clim. Change 2022, 12, 808–813. [Google Scholar] [CrossRef]
- Mankoff, K.D.; Fettweis, X.; Langen, P.L.; Stendel, M.; Kjeldsen, K.K.; Karlsson, N.B.; Noël, B.; van den Broeke, M.R.; Solgaard, A.; Colgan, W.; et al. Greenland Ice Sheet Mass Balance from 1840 through next Week. Earth Syst. Sci. Data 2021, 13, 5001–5025. [Google Scholar] [CrossRef]
- The IMBIE Team Mass Balance of the Greenland Ice Sheet from 1992 to 2018. Nature 2020, 579, 233–239. [CrossRef] [PubMed]
- Otosaka, I.N.; Shepherd, A.; Ivins, E.R.; Schlegel, N.-J.; Amory, C.; van den Broeke, M.; Horwath, M.; Joughin, I.; King, M.; Krinner, G.; et al. Mass Balance of the Greenland and Antarctic Ice Sheets from 1992 to 2020. Earth Syst. Sci. Data 2023, 15, 1597–1616. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Yao, Y.; Zhang, W. GRACE and Mass Budget Method Reveal Decelerated Ice Loss in East Greenland in the Past Decade. Remote Sens. Environ. 2023, 286, 113450. [Google Scholar] [CrossRef]
- Wang, W.; Shen, Y.; Chen, Q.; Wang, F. High-Resolution Mascon Solutions Reveal Glacier-Scale Mass Changes over the Greenland Ice Sheet from 2002 to 2022. Geophys. J. Int. 2023, 236, 494–515. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time Variability of the Earth’s Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Ramillien, G.; Seoane, L.; Darrozes, J. An Innovative Slepian Approach to Invert GRACE KBRR for Localized Hydrological Information at the Sub-Basin Scale. Remote Sens. 2021, 13, 1824. [Google Scholar] [CrossRef]
- Bevis, M.; Harig, C.; Khan, S.A.; Brown, A.; Simons, F.J.; Willis, M.; Fettweis, X.; van den Broeke, M.R.; Madsen, F.B.; Kendrick, E.; et al. Accelerating Changes in Ice Mass within Greenland, and the Ice Sheet’s Sensitivity to Atmospheric Forcing. Proc. Natl. Acad. Sci. USA 2019, 116, 1934–1939. [Google Scholar] [CrossRef]
- Graf, M.; Pail, R. Combination of Geometric and Gravimetric Data Sets for the Estimation of High-Resolution Mass Balances of the Greenland Ice Sheet. Geophys. J. Int. 2023, 235, 2149–2167. [Google Scholar] [CrossRef]
- Bian, Y.; Yue, J.; Gao, W.; Li, Z.; Lu, D.; Xiang, Y.; Chen, J. Analysis of the Spatiotemporal Changes of Ice Sheet Mass and Driving Factors in Greenland. Remote Sens. 2019, 11, 862. [Google Scholar] [CrossRef]
- Gałdyn, F.; Sośnica, K.; Zajdel, R.; Meyer, U.; Jäggi, A. Long-Term Ice Mass Changes in Greenland and Antarctica Derived from Satellite Laser Ranging. Remote Sens. Environ. 2024, 302, 113994. [Google Scholar] [CrossRef]
- Forsberg, R.; Sørensen, L.; Simonsen, S. Greenland and Antarctica Ice Sheet Mass Changes and Effects on Global Sea Level. Surv. Geophys. 2017, 38, 89–104. [Google Scholar] [CrossRef]
- Velicogna, I.; Mohajerani, Y.; A, G.; Landerer, F.; Mouginot, J.; Noel, B.; Rignot, E.; Sutterley, T.; van den Broeke, M.; van Wessem, M.; et al. Continuity of Ice Sheet Mass Loss in Greenland and Antarctica From the GRACE and GRACE Follow-On Missions. Geophys. Res. Lett. 2020, 47, e2020GL087291. [Google Scholar] [CrossRef]
- Mu, Y.; Wei, Y.; Wu, J.; Ding, Y.; Shangguan, D.; Zeng, D. Variations of Mass Balance of the Greenland Ice Sheet from 2002 to 2019. Remote Sens. 2020, 12, 2609. [Google Scholar] [CrossRef]
- Sasgen, I.; Wouters, B.; Gardner, A.S.; King, M.D.; Tedesco, M.; Landerer, F.W.; Dahle, C.; Save, H.; Fettweis, X. Return to Rapid Ice Loss in Greenland and Record Loss in 2019 Detected by the GRACE-FO Satellites. Commun. Earth Env. 2020, 1, 8. [Google Scholar] [CrossRef]
- Groh, A.; Horwath, M.; Horvath, A.; Meister, R.; Sørensen, L.; Barletta, V.; Forsberg, R.; Wouters, B.; Ditmar, P.; Ran, J.; et al. Evaluating GRACE Mass Change Time Series for the Antarctic and Greenland Ice Sheet—Methods and Results. Geosciences 2019, 9, 415. [Google Scholar] [CrossRef]
- Zou, F.; Tenzer, R.; Fok, H.; Nichol, J. Mass Balance of the Greenland Ice Sheet from GRACE and Surface Mass Balance Modelling. Water 2020, 12, 1847. [Google Scholar] [CrossRef]
- Sasgen, I.; Van Den Broeke, M.; Bamber, J.L.; Rignot, E.; Sørensen, L.S.; Wouters, B.; Martinec, Z.; Velicogna, I.; Simonsen, S.B. Timing and Origin of Recent Regional Ice-Mass Loss in Greenland. Earth Planet. Sci. Lett. 2012, 333–334, 293–303. [Google Scholar] [CrossRef]
- Wunderling, N.; Von Der Heydt, A.S.; Aksenov, Y.; Barker, S.; Bastiaansen, R.; Brovkin, V.; Brunetti, M.; Couplet, V.; Kleinen, T.; Lear, C.H.; et al. Climate Tipping Point Interactions and Cascades: A Review. Earth Syst. Dynam. 2024, 15, 41–74. [Google Scholar] [CrossRef]
- Ryan, J.C.; Medley, B.; Stevens, C.M.; Sutterley, T.C.; Siegfried, M.R. Role of Snowfall Versus Air Temperatures for Greenland Ice Sheet Melt-Albedo Feedbacks. Earth Space Sci. 2023, 10, e2023EA003158. [Google Scholar] [CrossRef]
- Schmid, T.; Radić, V.; Tedstone, A.; Lea, J.M.; Brough, S.; Hermann, M. Atmospheric Drivers of Melt-Related Ice Speed-up Events on the Russell Glacier in Southwest Greenland. Cryosphere 2023, 17, 3933–3954. [Google Scholar] [CrossRef]
- Boyd, C.E. Solar Radiation and Water Temperature. In Water Quality; Springer International Publishing: Cham, Switzerland, 2020; pp. 21–39. ISBN 978-3-030-23334-1. [Google Scholar]
- Blau, M.T.; Ha, K.-J.; Chung, E.-S. Extreme Summer Temperature Anomalies over Greenland Largely Result from Clear-Sky Radiation and Circulation Anomalies. Commun. Earth Environ. 2024, 5, 405. [Google Scholar] [CrossRef]
- Teng, C.-K.-M.; Gu, S.-Y.; Qin, Y.; Dou, X. Impact of Solar Activity on Global Atmospheric Circulation Based on SD-WACCM-X Simulations from 2002 to 2019. Atmosphere 2021, 12, 1526. [Google Scholar] [CrossRef]
- Bei, N.; Xiao, B.; Wang, R.; Yang, Y.; Liu, L.; Han, Y.; Li, G. Impacts of Aerosol-Radiation and Aerosol-Cloud Interactions on a Short-Term Heavy Rainfall Event—A Case Study in the Guanzhong Basin, China. Atmos. Chem. Phys. 2025, 25, 10931–10948. [Google Scholar] [CrossRef]
- Wang, W.; Zender, C.S.; Van As, D.; Fausto, R.S.; Laffin, M.K. Greenland Surface Melt Dominated by Solar and Sensible Heating. Geophys. Res. Lett. 2021, 48, e2020GL090653. [Google Scholar] [CrossRef]
- Drews, A.; Huo, W.; Matthes, K.; Kodera, K.; Kruschke, T. The Sun’s Role in Decadal Climate Predictability in the North Atlantic. Atmos. Chem. Phys. 2022, 22, 7893–7904. [Google Scholar] [CrossRef]
- Kuroda, Y.; Kodera, K.; Yoshida, K.; Yukimoto, S.; Gray, L. Influence of the Solar Cycle on the North Atlantic Oscillation. JGR Atmos. 2022, 127, e2021JD035519. [Google Scholar] [CrossRef]
- Mares, C.; Dobrica, V.; Mares, I.; Demetrescu, C. Solar Signature in Climate Indices. Atmosphere 2022, 13, 1898. [Google Scholar] [CrossRef]
- Hanna, E.; Cropper, T.E.; Hall, R.J.; Cappelen, J. Greenland Blocking Index 1851–2015: A Regional Climate Change Signal. Int. J. Climatol. 2016, 36, 4847–4861. [Google Scholar] [CrossRef]
- Hurrell, J.W. North Atlantic Oscillation (NAO). In Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2001; pp. 65–72. ISBN 978-0-12-374473-9. [Google Scholar]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic Multidecadal Oscillation and Its Relation to Rainfall and River Flows in the Continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Välisuo, I.; Vihma, T.; Pirazzini, R.; Schäfer, M. Interannual Variability of Atmospheric Conditions and Surface Melt in Greenland in 2000–2014. JGR Atmos. 2018, 123, 10443–10463. [Google Scholar] [CrossRef]
- Hanna, E.; Jones, J.M.; Cappelen, J.; Mernild, S.H.; Wood, L.; Steffen, K.; Huybrechts, P. The Influence of North Atlantic Atmospheric and Oceanic Forcing Effects on 1900–2010 Greenland Summer Climate and Ice Melt/Runoff. Int. J. Climatol. 2013, 33, 862–880. [Google Scholar] [CrossRef]
- Tedesco, M.; Fettweis, X.; Mote, T.; Wahr, J.; Alexander, P.; Box, J.E.; Wouters, B. Evidence and Analysis of 2012 Greenland Records from Spaceborne Observations, a Regional Climate Model and Reanalysis Data. Cryosphere 2013, 7, 615–630. [Google Scholar] [CrossRef]
- Chudley, T.R.; Howat, I.M.; King, M.D.; Negrete, A. Atlantic Water Intrusion Triggers Rapid Retreat and Regime Change at Previously Stable Greenland Glacier. Nat. Commun. 2023, 14, 2151. [Google Scholar] [CrossRef]
- King, M.A.; Lyu, K.; Zhang, X. Climate Variability a Key Driver of Recent Antarctic Ice-Mass Change. Nat. Geosci. 2023, 16, 1128–1135. [Google Scholar] [CrossRef]
- Meyer, U.; Jean, Y.; Kvas, A.; Dahle, C.; Lemoine, J.M.; Jäggi, A. Combination of GRACE Monthly Gravity Fields on the Normal Equation Level. J. Geod. 2019, 93, 1645–1658. [Google Scholar] [CrossRef]
- Meyer, U.; Jaeggi, A.; Dahle, C.; Flechtner, F.; Kvas, A.; Behzadpour, S.; Mayer-Gürr, T.; Lemoine, J.-M.; Bourgogne, S. International Combination Service for Time-Variable Gravity Fields (COST-G); Monthly GRACE Series 2020; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Meyer, U.; Lasser, M.; Dahle, C.; Förste, C.; Behzadpour, S.; Koch, I.; Jäggi, A. Combined Monthly GRACE-FO Gravity Fields for a Global Gravity-Based Groundwater Product. Geophys. J. Int. 2023, 236, 456–469. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing Estimates of Annual Variations and Trends in Geocenter Motion and J2 from a Combination of GRACE Data and Geophysical Models. JGR Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output. J. Geophys. Res. 2008, 113, 2007JB005338. [Google Scholar] [CrossRef]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE Time-Variable Gravity Solutions by GFZ, and Their Validation Using a Hydrological Model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
- Roy, K.; Peltier, W.R. Relative Sea Level in the Western Mediterranean Basin: A Regional Test of the ICE-7G_NA (VM7) Model and a Constraint on Late Holocene Antarctic Deglaciation. Quat. Sci. Rev. 2018, 183, 76–87. [Google Scholar] [CrossRef]
- Peltier, W.R. The ICE-7G_NA (VM7) Ice Thickness and Paleotopography 0–26 Ka, Borealis, V1. 2020. Available online: https://borealisdata.ca/dataset.xhtml?persistentId=doi:10.5683/SP2/ZCDLY1 (accessed on 23 October 2025). [CrossRef]
- Chen, J.L.; Wilson, C.R.; Li, J.; Zhang, Z. Reducing Leakage Error in GRACE-Observed Long-Term Ice Mass Change: A Case Study in West Antarctica. J. Geod. 2015, 89, 925–940. [Google Scholar] [CrossRef]
- Jin, S.; Zou, F. Re-Estimation of Glacier Mass Loss in Greenland from GRACE with Correction of Land–Ocean Leakage Effects. Glob. Planet. Change 2015, 135, 170–178. [Google Scholar] [CrossRef]
- Li, Z.; Chao, B.F.; Zhang, Z.; Jiang, L.; Wang, H. Greenland Interannual Ice Mass Variations Detected by GRACE Time-Variable Gravity. Geophys. Res. Lett. 2022, 49, e2022GL100551. [Google Scholar] [CrossRef]
- Wood, M.; Rignot, E.; Fenty, I.; An, L.; Bjørk, A.; Van Den Broeke, M.; Cai, C.; Kane, E.; Menemenlis, D.; Millan, R.; et al. Ocean Forcing Drives Glacier Retreat in Greenland. Sci. Adv. 2021, 7, eaba7282. [Google Scholar] [CrossRef] [PubMed]
- Fettweis, X.; Mabille, G.; Erpicum, M. Circulations Atmosphériques et Anomalies de Fonte à La Surface de La Calotte Glaciaire Du Groenland. Bull. Société Géographique Liège 2008, 51, 91–104. [Google Scholar]
- Preece, J.R.; Wachowicz, L.J.; Mote, T.L.; Tedesco, M.; Fettweis, X. Summer Greenland Blocking Diversity and Its Impact on the Surface Mass Balance of the Greenland Ice Sheet. JGR Atmos. 2022, 127, e2021JD035489. [Google Scholar] [CrossRef]
- Maure, D.; Kittel, C.; Lambin, C.; Delhasse, A.; Fettweis, X. Spatially Heterogeneous Effect of Climate Warming on the Arctic Land Ice. Cryosphere 2023, 17, 4645–4659. [Google Scholar] [CrossRef]
- Bjørk, A.A.; Aagaard, S.; Lütt, A.; Khan, S.A.; Box, J.E.; Kjeldsen, K.K.; Larsen, N.K.; Korsgaard, N.J.; Cappelen, J.; Colgan, W.T.; et al. Changes in Greenland’s Peripheral Glaciers Linked to the North Atlantic Oscillation. Nat. Clim. Change 2018, 8, 48–52. [Google Scholar] [CrossRef]
- Shang, P.; Su, X.; Luo, Z. Characteristics of the Greenland Ice Sheet Mass Variations Revealed by GRACE/GRACE Follow-On Gravimetry. Remote Sens. 2022, 14, 4442. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, C.; Xia, Y.; Yang, Y. North Atlantic Oscillation–Associated Variation in Cloud Phase and Cloud Radiative Forcing over the Greenland Ice Sheet. J. Clim. 2023, 36, 3203–3215. [Google Scholar] [CrossRef]
- Box, J.E.; Fettweis, X.; Stroeve, J.C.; Tedesco, M.; Hall, D.K.; Steffen, K. Greenland Ice Sheet Albedo Feedback: Thermodynamics and Atmospheric Drivers. Cryosphere 2012, 6, 821–839. [Google Scholar] [CrossRef]
- Lewis, G.; Osterberg, E.; Hawley, R.; Marshall, H.P.; Meehan, T.; Graeter, K.; McCarthy, F.; Overly, T.; Thundercloud, Z.; Ferris, D.; et al. Atmospheric Blocking Drives Recent Albedo Change Across the Western Greenland Ice Sheet Percolation Zone. Geophys. Res. Lett. 2021, 48, e2021GL092814. [Google Scholar] [CrossRef]
- Tedesco, M.; Fettweis, X.; Van Den Broeke, M.R.; Van De Wal, R.S.W.; Smeets, C.J.P.P.; Van De Berg, W.J.; Serreze, M.C.; Box, J.E. The Role of Albedo and Accumulation in the 2010 Melting Record in Greenland. Environ. Res. Lett. 2011, 6, 014005. [Google Scholar] [CrossRef]
- Noël, B.; Fettweis, X.; Van De Berg, W.J.; Van Den Broeke, M.R.; Erpicum, M. Sensitivity of Greenland Ice Sheet Surface Mass Balance to Perturbations in Sea Surface Temperature and Sea Ice Cover: A Study with the Regional Climate Model MAR. Cryosphere 2014, 8, 1871–1883. [Google Scholar] [CrossRef]
- Kim, B.-H.; Seo, K.-W.; Eom, J.; Chen, J.; Wilson, C.R. Antarctic Ice Mass Variations from 1979 to 2017 Driven by Anomalous Precipitation Accumulation. Sci Rep 2020, 10, 20366. [Google Scholar] [CrossRef]
- King, M.A.; Christoffersen, P. Major Modes of Climate Variability Dominate Nonlinear Antarctic Ice-Sheet Elevation Changes 2002–2020. Geophys. Res. Lett. 2024, 51, e2024GL108844. [Google Scholar] [CrossRef]
- Mazzarella, A. Time-Integrated North Atlantic Oscillation as a Proxy for Climatic Change. Nat. Sci. 2013, 05, 149–155. [Google Scholar] [CrossRef]
- Paolo, F.S.; Padman, L.; Fricker, H.A.; Adusumilli, S.; Howard, S.; Siegfried, M.R. Response of Pacific-Sector Antarctic Ice Shelves to the El Niño/Southern Oscillation. Nat. Geosci. 2018, 11, 121–126. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Chen, W.Y.; Dool, H.V. den Sensitivity of Teleconnection Patterns to the Sign of Their Primary Action Center. Mon. Weather Rev. 2003, 131, 2885–2899. [Google Scholar] [CrossRef]
- van den Dool, H.M.; Saha, S.; Johansson, Å. Empirical Orthogonal Teleconnections. J. Clim. 2000, 13, 1421–1435. [Google Scholar] [CrossRef]
- Brils, M.; Kuipers Munneke, P.; Van Den Broeke, M.R. Spatial Response of Greenland’s Firn Layer to NAO Variability. JGR Earth Surf. 2023, 128, e2023JF007082. [Google Scholar] [CrossRef]
- Seip, K.L.; Grøn, Ø.; Wang, H. The North Atlantic Oscillations: Cycle Times for the NAO, the AMO and the AMOC. Climate 2019, 7, 43. [Google Scholar] [CrossRef]
- Sun, C.; Li, J.; Kucharski, F.; Xue, J.; Li, X. Contrasting Spatial Structures of Atlantic Multidecadal Oscillation between Observations and Slab Ocean Model Simulations. Clim. Dyn. 2019, 52, 1395–1411. [Google Scholar] [CrossRef]
- Luu, L.N.; Hanna, E.; De Alwis Pitts, D.; Maddison, J.; Screen, J.A.; Catto, J.L.; Fettweis, X. Greenland Summer Blocking Characteristics: An Evaluation of a High-Resolution Multi-Model Ensemble. Clim. Dyn. 2024, 62, 10503–10523. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Hanna, E.; Cropper, T.E.; Jones, P.D.; Scaife, A.A.; Allan, R. Recent Seasonal Asymmetric Changes in the NAO (a Marked Summer Decline and Increased Winter Variability) and Associated Changes in the AO and Greenland Blocking Index. Int. J. Climatol. 2015, 35, 2540–2554. [Google Scholar] [CrossRef]
- Hanna, E.; Fettweis, X.; Hall, R.J. Brief Communication: Recent Changes in Summer Greenland Blocking Captured by None of the CMIP5 Models. Cryosphere 2018, 12, 3287–3292. [Google Scholar] [CrossRef]
- Dozier, J.; Schneider, S.R.; McGinnis, D.F. Effect of Grain Size and Snowpack Water Equivalence on Visible and Near-infrared Satellite Observations of Snow. Water Resour. Res. 1981, 17, 1213–1221. [Google Scholar] [CrossRef]
- Zheng, F.; Liu, X.; Chen, J.; Huang, W.; Sun, C.; Wang, H. Physical Mechanism of Winter Temperature Multidecadal Variations in Arid Central Asia: The Role of the Atlantic Multidecadal Oscillation (AMO). J. Clim. 2023, 36, 7363–7377. [Google Scholar] [CrossRef]
- Kaplan, A.; Cane, M.A.; Kushnir, Y.; Clement, A.C.; Blumenthal, M.B.; Rajagopalan, B. Analyses of Global Sea Surface Temperature 1856–1991. J. Geophys. Res. 1998, 103, 18567–18589. [Google Scholar] [CrossRef]
- Donohoe, A.; Dawson, E.; McMurdie, L.; Battisti, D.S.; Rhines, A. Seasonal Asymmetries in the Lag between Insolation and Surface Temperature. J. Clim. 2020, 33, 3921–3945. [Google Scholar] [CrossRef]
- Kim, H.; An, S.; Kim, D. Timescale-dependent AMOC–AMO Relationship in an Earth System Model of Intermediate Complexity. Int. J. Climatol. 2021, 41, E3298–E3306. [Google Scholar] [CrossRef]
- Hao, X.; Sein, D.V.; Spiegl, T.; Niu, L.; Chen, X.; Lohmann, G. Modeling the Atlantic Multidecadal Oscillation: The High-Resolution Ocean Brings the Timescale; the Atmosphere, the Amplitude. Ocean-Land-Atmos. Res. 2025, 4, 0085. [Google Scholar] [CrossRef]
- Schyberg, H.; Yang, X.; Køltzow, M.A.Ø.; Amstrup, B.; Bakketun, Å.; Bazile, E.; Bojarova, J.; Box, J.E.; Dahlgren, P.; Hagelin, S.; et al. Arctic Regional Reanalysis on Single Levels from 1991 to Present. 2020. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-carra-single-levels?tab=overview (accessed on 23 October 2025).
- Zheng, Y.; Golledge, N.R.; Gossart, A.; Picard, G.; Leduc-Leballeur, M. Statistically Parameterizing and Evaluating a Positive Degree-Day Model to Estimate Surface Melt in Antarctica from 1979 to 2022. Cryosphere 2023, 17, 3667–3694. [Google Scholar] [CrossRef]
- Dumont, M.; Brun, E.; Picard, G.; Michou, M.; Libois, Q.; Petit, J.-R.; Geyer, M.; Morin, S.; Josse, B. Contribution of Light-Absorbing Impurities in Snow to Greenland’s Darkening since 2009. Nat. Geosci 2014, 7, 509–512. [Google Scholar] [CrossRef]
- Wang, S.; Tedesco, M.; Alexander, P.; Xu, M.; Fettweis, X. Quantifying Spatiotemporal Variability of Glacier Algal Blooms and the Impact on Surface Albedo in Southwestern Greenland. Cryosphere 2020, 14, 2687–2713. [Google Scholar] [CrossRef]
- Huai, B.; Ding, M.; Van Den Broeke, M.R.; Reijmer, C.H.; Noël, B.; Sun, W.; Wang, Y. Future Large-Scale Atmospheric Circulation Changes and Greenland Precipitation. npj Clim. Atmos. Sci. 2025, 8, 10. [Google Scholar] [CrossRef]
- Fettweis, X.; Franco, B.; Tedesco, M.; Van Angelen, J.H.; Lenaerts, J.T.M.; Van Den Broeke, M.R.; Gallée, H. Estimating the Greenland Ice Sheet Surface Mass Balance Contribution to Future Sea Level Rise Using the Regional Atmospheric Climate Model MAR. Cryosphere 2013, 7, 469–489. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. ADVANCED SPECTRAL METHODS FOR CLIMATIC TIME SERIES. Rev. Geophys. 2002, 40, 3-1–3-41. [Google Scholar] [CrossRef]
- Preisendorfer, R.W.; Mobley, C.D. Principal Component Analysis in Meteorology and Oceanography; Developments in atmospheric science; Elsevier: Amsterdam, The Netherlands, 1988; ISBN 978-0-444-43014-4. [Google Scholar]
- Li, Z.; Chao, B.F.; Wang, H.S.; Zhang, Z.Z. Antarctica Ice-Mass Variations on Interannual Timescale: Coastal Dipole and Propagating Transports. Earth Planet. Sci. Lett. 2022, 595, 117789. [Google Scholar] [CrossRef]
- Mémin, A.; Flament, T.; Alizier, B.; Watson, C.; Rémy, F. Interannual Variation of the Antarctic Ice Sheet from a Combined Analysis of Satellite Gravimetry and Altimetry Data. Earth Planet. Sci. Lett. 2015, 422, 150–156. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Wea. Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Maity, S.; Nayak, S.; Nayak, H.P.; Bhatla, R. Comprehensive Assessment of RegCM4 towards Interannual Variability of Indian Summer Monsoon Using Multi-Year Simulations. Theor. Appl. Climatol. 2022, 148, 491–516. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlin. Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Goupillaud, P.; Grossmann, A.; Morlet, J. Cycle-Octave and Related Transforms in Seismic Signal Analysis. Geoexploration 1984, 23, 85–102. [Google Scholar] [CrossRef]
- Lopez, T.; Ramillien, G.; Antoine, R.; Darrozes, J.; Cui, Y.-J.; Kerr, Y. Investigation of Short-Term Evolution of Soil Characteristics over the Lake Chad Basin Using GRACE Data. Remote Sens. 2018, 10, 924. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave Propagation and Sampling Theory—Part I: Complex Signal and Scattering in Multilayered Media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Xu, Y.; Burton, P.W. Himalayan Tectonic Belt: Morlet Wavelet Variation and Seismic Harmony. Pure Appl. Geophys. 2021, 178, 3471–3488. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. BAMS 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Khan, S.A.; Seroussi, H.; Morlighem, M.; Colgan, W.; Helm, V.; Cheng, G.; Berg, D.; Barletta, V.R.; Larsen, N.K.; Kochtitzky, W.; et al. Smoothed Monthly Greenland Ice Sheet Elevation Changes during 2003–2023. Earth Syst. Sci. Data 2025, 17, 3047–3071. [Google Scholar] [CrossRef]
- McMillan, M.; Leeson, A.; Shepherd, A.; Briggs, K.; Armitage, T.W.K.; Hogg, A.; Kuipers Munneke, P.; Van Den Broeke, M.; Noël, B.; Van De Berg, W.J.; et al. A High-resolution Record of Greenland Mass Balance. Geophys. Res. Lett. 2016, 43, 7002–7010. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Sørensen, L.S. Implications of Changing Scattering Properties on Greenland Ice Sheet Volume Change from Cryosat-2 Altimetry. Remote Sens. Environ. 2017, 190, 207–216. [Google Scholar] [CrossRef]
- Auger, J.D.; Birkel, S.D.; Maasch, K.A.; Mayewski, P.A.; Schuenemann, K.C. Examination of Precipitation Variability in Southern Greenland. JGR Atmos. 2017, 122, 6202–6216. [Google Scholar] [CrossRef]
- Hermann, M.; Papritz, L.; Wernli, H. A Lagrangian Analysis of the Dynamical and Thermodynamic Drivers of Large-Scale Greenland Melt Events during 1979–2017. Weather Clim. Dynam. 2020, 1, 497–518. [Google Scholar] [CrossRef]
- Rowley, N.A.; Carleton, A.M.; Fegyveresi, J. Relationships of West Greenland Supraglacial Melt-lakes with Local Climate and Regional Atmospheric Circulation. Int. J. Climatol. 2020, 40, 1164–1177. [Google Scholar] [CrossRef]
- Zhang, Q.; Huai, B.; Van Den Broeke, M.R.; Cappelen, J.; Ding, M.; Wang, Y.; Sun, W. Temporal and Spatial Variability in Contemporary Greenland Warming (1958–2020). J. Clim. 2022, 35, 2755–2767. [Google Scholar] [CrossRef]
- Chylek, P.; Lohmann, U. Ratio of the Greenland to Global Temperature Change: Comparison of Observations and Climate Modeling Results. Geophys. Res. Lett. 2005, 32, 2005GL023552. [Google Scholar] [CrossRef]
- Desbiolles, F.; Meroni, A.N.; Renault, L.; Pasquero, C. Environmental Control of Wind Response to Sea Surface Temperature Patterns in Reanalysis Dataset. J. Clim. 2023, 36, 3881–3893. [Google Scholar] [CrossRef]
- Chen, S.; Wu, R.; Chen, W. The Changing Relationship between Interannual Variations of the North Atlantic Oscillation and Northern Tropical Atlantic SST. J. Clim. 2015, 28, 485–504. [Google Scholar] [CrossRef]
- Ramos Buarque, S.; Salas, Y.; Melia, D. Link between the North Atlantic Oscillation and the Surface Mass Balance Components of the Greenland Ice Sheet under Preindustrial and Last Interglacial Climates: A Study with a Coupled Global Circulation Model. Clim. Past 2018, 14, 1707–1725. [Google Scholar] [CrossRef]
- Robson, J.; Sutton, R.T.; Archibald, A.; Cooper, F.; Christensen, M.; Gray, L.J.; Holliday, N.P.; Macintosh, C.; McMillan, M.; Moat, B.; et al. Recent Multivariate Changes in the North Atlantic Climate System, with a Focus on 2005–2016. Int. J. Climatol. 2018, 38, 5050–5076. [Google Scholar] [CrossRef]
- Zahn, M.; Von Storch, H. A Long-term Climatology of North Atlantic Polar Lows. Geophys. Res. Lett. 2008, 35, 2008GL035769. [Google Scholar] [CrossRef]
- Saes, M.J.M.; Gjelstrup, C.V.B.; Visser, A.W.; Stedmon, C.A. Separating Annual, Interannual and Regional Change in Sea Surface Temperature in the Northeastern Atlantic and Nordic Seas. JGR Ocean. 2022, 127, e2022JC018630. [Google Scholar] [CrossRef]
- Silva, T.; Abermann, J.; Noël, B.; Shahi, S.; Van De Berg, W.J.; Schöner, W. The Impact of Climate Oscillations on the Surface Energy Budget over the Greenland Ice Sheet in a Changing Climate. Cryosphere 2022, 16, 3375–3391. [Google Scholar] [CrossRef]
- Ran, J.; Ditmar, P.; Van Den Broeke, M.R.; Liu, L.; Klees, R.; Khan, S.A.; Moon, T.; Li, J.; Bevis, M.; Zhong, M.; et al. Vertical Bedrock Shifts Reveal Summer Water Storage in Greenland Ice Sheet. Nature 2024, 635, 108–113. [Google Scholar] [CrossRef]
- Lee, C.; Song, H.; Choi, Y.; Cho, A.; Marshall, J. Observed Multi-Decadal Increase in the Surface Ocean’s Thermal Inertia. Nat. Clim. Change 2025, 15, 308–314. [Google Scholar] [CrossRef]
- Zavialov, P.O. Physical Oceanography of the Dying Aral Sea; Springer Praxis Books; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-06171-4. [Google Scholar]
- Ambastha, A. The Active and Explosive Sun. In Lectures on Solar Physics; Antia, H.M., Bhatnagar, A., Ulmschneider, P., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2003; Volume 619, pp. 127–172. ISBN 978-3-540-01528-4. [Google Scholar]
- Penticton, B.C. Canada Solar 10.7 cm Radio Flux Values (Sfu) 2024. Available online: https://spaceweather.gc.ca/forecast-prevision/solar-solaire/solarflux/sx-5-en.php (accessed on 23 October 2025).
- Georgieva, K.; Kirov, B.; Tonev, P.; Guineva, V.; Atanasov, D. Long-Term Variations in the Correlation between NAO and Solar Activity: The Importance of North–South Solar Activity Asymmetry for Atmospheric Circulation. Adv. Space Res. 2007, 40, 1152–1166. [Google Scholar] [CrossRef][Green Version]
- Lean, J.L. Sun-Climate Connections. In Oxford Research Encyclopedia of Climate Science; Oxford University Press: Oxford, UK, 2017; ISBN 978-0-19-022862-0. [Google Scholar][Green Version]
- Berdahl, M.; Rennermalm, A.; Hammann, A.; Mioduszweski, J.; Hameed, S.; Tedesco, M.; Stroeve, J.; Mote, T.; Koyama, T.; McConnell, J.R. Southeast Greenland Winter Precipitation Strongly Linked to the Icelandic Low Position. J. Clim. 2018, 31, 4483–4500. [Google Scholar] [CrossRef]
- Kopec, B.G.; Klein, E.S.; Feldman, G.C.; Pedron, S.A.; Bailey, H.; Causey, D.; Hubbard, A.; Marttila, H.; Welker, J.M. Arctic Freshwater Sources and Ocean Mixing Relationships Revealed With Seawater Isotopic Tracing. JGR Ocean. 2024, 129, e2023JC020583. [Google Scholar] [CrossRef]
- Rosenblum, E.; Stroeve, J.; Gille, S.T.; Lique, C.; Fajber, R.; Tremblay, L.B.; Galley, R.; Loureiro, T.; Barber, D.G.; Lukovich, J.V. Freshwater Input and Vertical Mixing in the Canada Basin’s Seasonal Halocline: 1975 versus 2006–12. J. Phys. Oceanogr. 2022, 52, 1383–1396. [Google Scholar] [CrossRef]
- Kang, S.-Y.; Moon, J.-H.; Kim, T.; Jeon, C.; Song, Y.T. Impact of River-Discharged Freshwater on Surface Ocean Environments Revealed by Synergistic Use of Satellite Measurements in the East China Sea. Estuar. Coast. Shelf Sci. 2024, 307, 108909. [Google Scholar] [CrossRef]
- Moon, J.-H.; Kim, T.; Son, Y.B.; Hong, J.-S.; Lee, J.-H.; Chang, P.-H.; Kim, S.-K. Contribution of Low-Salinity Water to Sea Surface Warming of the East China Sea in the Summer of 2016. Prog. Oceanogr. 2019, 175, 68–80. [Google Scholar] [CrossRef]
- Offermann, D.; Kalicinsky, C.; Koppmann, R.; Wintel, J. Very Long-Period Oscillations in the Atmosphere (0–110 Km). Atmos. Chem. Phys. 2021, 21, 1593–1611. [Google Scholar] [CrossRef]
- Pfeffer, J.; Cazenave, A.; Rosat, S.; Moreira, L.; Mandea, M.; Dehant, V.; Coupry, B. A 6-Year Cycle in the Earth System. Glob. Planet. Change 2023, 229, 104245. [Google Scholar] [CrossRef]
- Ionita, M.; Scholz, P.; Lohmann, G.; Dima, M.; Prange, M. Linkages between Atmospheric Blocking, Sea Ice Export through Fram Strait and the Atlantic Meridional Overturning Circulation. Sci. Rep. 2016, 6, 32881. [Google Scholar] [CrossRef] [PubMed]
- Duyck, E.; Foukal, N.P.; Frajka-Williams, E. Circulation of Baffin Bay and Hudson Bay Waters on the Labrador Shelf and into the Subpolar North Atlantic. Ocean Sci. 2025, 21, 241–260. [Google Scholar] [CrossRef]
- Xu, H.; Kim, H.-M.; Nye, J.A.; Hameed, S. Impacts of the North Atlantic Oscillation on Sea Surface Temperature on the Northeast US Continental Shelf. Cont. Shelf Res. 2015, 105, 60–66. [Google Scholar] [CrossRef]
- Stendel, M. Polar Portal Season Report 2017; DMI, GEUS, DTU-Space and DTU-Byg. 2018. Available online: https://web.archive.org/web/20250322091307/https://polarportal.dk/fileadmin/polarportal/Polar-portal-saeson-rapport-2017-UK.pdf (accessed on 23 October 2025).
- Barletta, V.R.; Bordoni, A.; Khan, S.A. GNET Derived Mass Balance and Glacial Isostatic Adjustment Constraints for Greenland. Geophys. Res. Lett. 2024, 51, e2023GL106891. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).