Highlights
What are the main findings?
- The proposed DA-GSGTNet, which integrates gated graph-guided Transformer blocks (GSGT-Block) with a density-adaptive downsampling module (DATD) and distance-biased relative position encoding, achieves state-of-the-art multispectral LiDAR segmentation (mIoU 86.43%) and substantially improves IoU on slender/under-represented classes (e.g., power line, car).
- Cross-domain pretraining on large open point cloud datasets (DALES, Sensat) followed by lightweight fine-tuning (≈30% target data, 30 epochs) attains >90% of full-training accuracy and significantly speeds up convergence.
What is the implication of the main finding?
- DA-GSGTNet enables robust and efficient deployment of multispectral LiDAR segmentation in annotation-scarce urban applications, reducing labeling costs while improving detection of critical infrastructure and fine structures.
- The combined design (GSGT + DATD) provides a practical architectural pattern for future 3D spectral–spatial models and can be adapted for smart-city, environmental monitoring, and autonomous perception tasks.
Abstract
Multispectral LiDAR point clouds, which integrate both geometric and spectral information, offer rich semantic content for scene understanding. However, due to data scarcity and distributional discrepancies, existing methods often struggle to balance accuracy and efficiency in complex urban environments. To address these challenges, we propose DA-GSGTNet, a novel segmentation framework that integrates Gated Stratified Graph Transformer Blocks (GSGT-Block) with Dynamic Aggregation Transition Down (DATD). The GSGT-Block employs graph convolutions to enhance the local continuity of windowed attention in sparse neighborhoods and adaptively fuses these features via a gating mechanism. The DATD module dynamically adjusts k-NN strides based on point density, while jointly aggregating coordinates and feature vectors to preserve structural integrity during downsampling. Additionally, we introduce a relative position encoding scheme using quantized lookup tables with a Euclidean distance bias to improve recognition of elongated and underrepresented classes. Experimental results on a benchmark multispectral point cloud dataset demonstrate that DA-GSGTNet achieves 86.43% mIoU, 93.74% mAcc, and 90.78% OA, outperforming current state-of-the-art methods. Moreover, by fine-tuning from source-domain pretrained weights and using only ~30% of the training samples (4 regions) and 30% of the training epochs (30 epochs), we achieve over 90% of the full-training segmentation accuracy (100 epochs). These results validate the effectiveness of transfer learning for rapid convergence and efficient adaptation in data-scarce scenarios, offering practical guidance for future multispectral LiDAR applications with limited annotation.
1. Introduction
Land cover classification is a core task in remote sensing and plays a vital role in a wide range of domains, including environmental monitoring [1,2] urban planning [3,4] agricultural management [5,6] and climate change research [7,8]. By identifying and classifying different surface features (e.g., buildings, roads, vegetation), it accurately reflects spatial distributions on the Earth’s surface and provides a reliable data foundation for land resource management, ecological conservation, and post-disaster reconstruction. With global population growth, accelerating urbanization, and increasingly severe environmental pollution, precise land cover classification has become essential for addressing these challenges.
Early studies in this field primarily relied on satellite and aerial optical imagery to obtain large-scale, high-resolution feature information. Traditional pixel-based classification techniques such as support vector machines (SVMs), decision trees, k-nearest neighbors (k-NN), and early deep learning methods were employed for feature recognition [9,10,11,12,13]. More recently, to overcome the limitations of convolutional neural networks in capturing long-range dependencies and handling large receptive fields, Liu et al. proposed a multi-branch attention framework that fuses graph convolutional networks and CNNs for hyperspectral image classification [14], and subsequently developed MSLKCNN, a simple yet powerful multi-scale large-kernel CNN with kernels as large as 15 × 15 for enhanced spectral–spatial feature extraction [15]. While these methods have contributed meaningfully to land management and environmental monitoring, they remain limited in practical applications. Optical image classification is highly dependent on pixel spectral features, making it susceptible to interference from atmospheric conditions such as clouds, haze, and shadows. Additionally, conventional 2D imagery lacks the capacity to capture the three-dimensional object structures, impeding accurate assessment of height and morphology and constraining further improvements in classification accuracy. As urbanization progresses and surface environments become increasingly complex, traditional optical image–based land cover classification techniques are increasingly inadequate for extracting high-precision, multidimensional information.
With the rapid advancement of Light Detection and Ranging (LiDAR) technology, point cloud data has emerged as a primary data source for describing ground objects and environments. LiDAR directly acquires high-precision 3D spatial coordinates and echo intensity, supporting applications in topographic mapping, urban modeling, emergency response, and object detection [16,17,18,19,20]. Most existing studies have focused on three-dimensional spatial data of point clouds combined with single-band intensity information. While single-band point clouds capture useful geometric cues, the absence of rich spectral data limits their ability to distinguish between complex surface materials, leading to suboptimal classification performance in heterogeneous scenes [21,22]. To address this issue, some researchers have attempted to fuse LiDAR point cloud data with hyperspectral imagery. Although such multimodal approaches can enrich the feature space, they introduce practical challenges such as cross-model registration errors and sensitivity to atmospheric conditions like cloud cover and illumination variations in 2D imagery [23,24].
Recent advances in LiDAR hardware have led to the development of multispectral laser scanning systems, which simultaneously capture 3D spatial structure and spectral reflectance without requiring post hoc data fusion or registration. These systems enable high-resolution, co-registered spatial–spectral Earth observation, significantly enhancing classification potential [25]. Wichmann et al. [26] first explored the feasibility of land cover classification using the Optech Titan multispectral LiDAR system in 2015. Subsequently, Bakuła et al. [27] demonstrated that multispectral LiDAR data outperforms traditional fusion methods, achieving overall classification accuracies exceeding 90%.
To further exploit the rich spectral and 3D spatial information in multispectral point clouds for higher precision and generalization, researchers have begun applying deep learning to the task of multispectral point cloud segmentation. For example, Jing et al. [28] introduced SE-PointNet++, augmenting the PointNet++ architecture with Squeeze-and-Excitation blocks, and achieved promising semantic segmentation. More recently, researchers have introduced Graph Convolutional Networks (GCNs) and Transformer-based architectures [29,30], which have shown superior generalization and accuracy compared to conventional multilayer perceptron (MLP) models in multispectral point cloud segmentation tasks.
Although these efforts have significantly advanced deep learning-based multi-spectral point cloud segmentation, several limitations remain. For example, Transformer models demonstrate outstanding capabilities in capturing global semantic context, but they often struggle to characterize local geometric structures in point clouds. Moreover, conventional relative position encoding strategies, although useful for basic spatial reference, lack explicit incorporation of Euclidean distance information, which is essential for representing richer spatial relationships. Additionally, most current approaches rely on static k-NN sampling, which fails to adapt to varying in point cloud density, thus limiting structural detail preservation during downsampling.
To address these challenges, we propose a novel multispectral point cloud segmentation framework that integrates Transformers with Graph Convolutional Networks (GCNs). Specifically, our approach introduces a gated GCN module to compensate for the Transformer’s local geometric deficiency, enriches the quantized relative-position encoding with Euclidean distance bias, and employs a density-adaptive k-NN downsampling mechanism that dynamically adjusts sampling intervals based on local point density. These components collectively enable more effective mining of 3D spatial and spectral information in multispectral point clouds data.
Furthermore, the high acquisition cost and scarcity of publicly annotated multi-spectral LiDAR datasets make large-scale supervised training expensive and impractical. To mitigate this, we adopt a cross-domain transfer learning strategy. Our approach explores pretraining on publicly available datasets—including the image-synthetic Sensat point cloud dataset and the single-band LiDAR DALES dataset—to learn generalized point cloud representations, which are then fine-tuned on the target multi-spectral dataset. This enables more efficient convergence and improved performance under data-scarce conditions. The main contributions of this work are as follows:
(1) GSGT-Block: We introduce a learnable gated GraphConv–windowed attention module [31]. This module fuses Graph Convolution and window-based multi-head self-attention through a gating mechanism. As a result, the model captures both global sparse context and local geometric continuity.
(2) DATD Module: We propose a novel Dynamic Aggregation Transition Down mechanism that dynamically adjusts the k-NN stride based on local density. It jointly aggregates spatial coordinates and spectral features to preserve macro-context while maintaining micro-structures integrity during downsampling.
(3) Cross-domain Transfer Learning Strategy: To the best of our knowledge, we present the first application of transfer learning from conventional point cloud datasets (DALES and Sensat) to multispectral LiDAR. By fine-tuning with only 30% of target domain data over 30 training epochs, our model achieves an mIoU of 80.28%, demonstrating the efficiency and feasibility of pretraining for low-annotation scenarios.
2. Related Work
2.1. Point Cloud Semantic Segmentation
Because point cloud data are inherently unordered and irregular, traditional deep learning-based approaches typically convert raw point clouds into regularized representations to facilitate network input and processing. Early methods include voxelization and projection [32,33,34]. Voxelization converts the point cloud into a regular 3D grid, enabling standardized network input but incurring exponentially increasing memory and computational costs as resolution rises. Projection-based methods map the 3D cloud data onto 2D planes, which simplifies processing but inevitably leads to the loss of spatial information, thereby degrading classification and segmentation accuracy.
In recent years, driven by the widespread adoption of point cloud data and rapid advances in deep learning, numerous deep learning-based point cloud processing methods have emerged, achieving significant progress in geometric feature learning and structural modeling. Qi et al. [35] introduced PointNet in 2007, the first end-to-end network operating directly on raw point clouds. It encodes each point via multi-layer perceptrons (MLPs) and uses symmetric functions (e.g., max-pooling) to aggregate global features, ensuring permutation invariance. While effective for object classification, PointNet lacks the ability to capture fine-grained local structures, limiting its segmentation performance in complex scenes. To address this, Qi et al. [36] proposed PointNet++ in 2017, introducing a hierarchical feature-learning mechanism that recursively samples point clouds by distance or density and captures local geometries at multiple scales, thereby significantly enhancing detail representation and improving segmentation performance.
Subsequent research expanded upon this foundation. In 2018, Li et al. and Chen et al. [37] employed self-organizing maps (SOMs) to model spatial distributions and perform hierarchical feature fusion. In the same year, Li et al. [38] introduced PointCNN with the X-Transformation, which converts unordered point cloud features into locally ordered representations, enabling convolution-like operations that improved performance in complex environments. SpiderCNN [39] proposed parameterized convolutional filters based on Taylor expansions and step functions to capture local geometries pattern directly.
Dynamic Graph CNN (DGCNN) [40] further advanced local feature modeling by constructing dynamic graphs over point neighborhoods and employing EdgeConv modules for robust relational learning. KPConv [41] introduced kernel-point convolution directly in Euclidean space with deformable kernels, achieving state-of-the-art segmentation accuracy. RandLA-Net [42], proposed in 2020, combined random sampling with lightweight local aggregation to enable efficient and scalable segmentation on large-scale point cloud datasets.
With the success of Transformers in computer vision, Zhao et al. [43] introduced Point Transformer in 2021, applying self-attention to point clouds to model long-range dependencies between points, thereby improving segmentation accuracy and narrowing the gap with 2D image segmentation. Point Cloud Transformer [44] and Stratified Transformer [45] further explored hierarchical attention, with the latter employing a hybrid sampling strategy to balance local density and global sparsity, thereby expanding the receptive field efficiently. In 2022, Qian et al. [46] introduced PointNeXt, a systematic enhancement of PointNet++ incorporating improved training strategies, data augmentation, and architectural optimization such as inverted residual bottlenecks and separable MLPs, achieving strong performance on benchmarks datasets such as ScanObjectNN and S3DIS.
Overall, these methods—from simple fully connected networks to hierarchical, graph convolutional, and self-attention architectures—have progressively improved the ability to characterize both local structures and global semantics in point cloud segmentation. They provide a strong technical foundation for 3D scene interpretation and highlight promising directions such as multi-scale feature fusion and computationally efficient network design.
2.2. Transfer Learning with Point Cloud Data
With the growing maturity of transfer learning, researchers have increasingly applied it to point cloud segmentation using three principal strategies: leveraging image segmentation knowledge, utilizing simulated 3D point clouds, and exploiting real-world point cloud datasets.
2.2.1. Transfer Learning via Image Segmentation Knowledge
One approach to transfer learning in point cloud analysis involves transferring knowledge from well-established 2D image segmentation models. In 2019, Zhao et al. [47] proposed a CNN-based point cloud classification method that integrates multi-scale features with transfer learning to enhance classification performance. Lei et al. [48] subsequently optimized this architecture in 2020 to further enhance efficiency in point cloud classification.
In 2021, Imad et al. [49] applied 2D transfer learning to 3D object detection by converting point clouds into bird’s-eye-view (BEV) representations and leveraging pretrained classification models, achieving high mean average precision and fast inference. Subsequently, Murtiyoso et al. [50] and Wang et al. [51] introduced 3D point cloud semantic segmentation techniques based on 2D image transfer learning, effectively boosting segmentation accuracy.
In 2022, Ding et al. [52] proposed an innovative saliency knowledge transfer method, migrating saliency prediction expertise from images to point clouds to further enhance 3D semantic segmentation performance. In 2023, Laazoufi et al. [53] proposed a point cloud quality assessment framework based on a 1D VGG16 network coupled with support vector regression (SVR) for quality score prediction, demonstrating effective transfer learning performance.
Most recently, in 2024, Yao et al. [54] introduced a transfer learning-based road extraction approach using a pretrained DeepLabV3+ model [55], achieving high segmentation accuracy on 3D LiDAR data. Similarly, Schäfer et al. [56] proposed a 3D-CNN-based method for above-ground forest biomass estimation and compared it with a random forest model, confirming that deep learning models—particularly 3D CNNs—outperformed traditional methods under limited training data.
2.2.2. Transfer Learning with Simulated 3D Point Clouds
Simulated datasets have emerged as valuable resources for transfer learning in point cloud applications, especially in scenarios with limited real-world annotations. In 2022, Xiao et al. [57] built the large-scale synthetic LiDAR dataset SynLiDAR and designed the point cloud translator PCT to reduce domain gaps between synthetic and real data. This significantly improved semantic segmentation performance and underscored the practical applications of simulated training data. Huang et al. [58] proposed a multi-fidelity point cloud neural network for melt-pool modeling. By transfer learning integration of low-fidelity models with high-fidelity simulations, they achieved efficient melt-pool prediction, demonstrating transfer learning’s potential in multi-fidelity contexts.
In 2023, Wu et al. [59] extended transfer learning in point cloud segmentation by proposing a sim-to-real approach for robotic disassembly. Training on simulated data and deploying on real data, this method overcomes annotation challenges and provides a practical pathway for applying simulated point clouds in real-world scenarios. That same year, Biehler et al. [60] introduced PLURAL, a contrastive learning-based transfer method that learns domain-invariant features to bridge domain gaps, achieving significant performance gains on both synthetic and real datasets.
2.2.3. Transfer Learning from Real-World Point Cloud Datasets
Recent work has also explored transfer learning using large-scale real-world point cloud datasets. In 2023, Zhou et al. [61] proposed TSANet, a semantic segmentation network combining sampling and attention mechanisms; by leveraging transfer learning, it reduced data dependency and demonstrated high accuracy and efficiency on the Cambridge and Birmingham urban point cloud datasets. Similarly, Enes et al. [62] integrated RandLA-Net with transfer learning, achieving competitive segmentation accuracy across point cloud datasets from three Chinese cities.
In 2024, Yuanyuan et al. [63] introduced KCGATNet, a segmentation network integrating kernel convolution and graph attention mechanisms. Transfer learning enabled the model to generalize effectively across various livestock point clouds, with particularly excellent performance in pig and cattle segmentation tasks. Zhang et al. [64] also utilized pretrained weights on the S3DIS dataset to achieve high-precision indoor scene segmentation.
These studies affirm the growing success of transfer learning in point cloud processing, especially in semantic segmentation. However, most existing work has pre-dominantly focused on simulated point clouds, single-band LiDAR data, and 3D reconstructed point clouds, with limited attention to multispectral point clouds. Moreover, while Transformer-based models are proficient in capturing global context, they often struggle to encode fine-grained topological relationships and lack the ability to adapt their receptive fields to variations in point cloud density.
To overcome these limitations, we introduce DA-GSGTNet, a unified framework that integrates graph-guided, gated windowed attention with a density-adaptive downsampling mechanism. This architecture enables precise modeling of local geometric structures and robust aggregation of features across diverse spatial resolutions. Combined with enhanced relative position encoding and cross-domain pretraining strategies, DA-GSGTNet effectively fuses geometric and spectral cues for accurate and efficient multispectral point cloud segmentation.
3. Multispectral Data Acquisition
3.1. Study Area and Dataset
This study utilizes point cloud data acquired using the Optech Titan MW (14SEN/CON340) multispectral LiDAR system, which provides intensity measurements across three spectral channels: 1550 MIR (C1), 1064 NIR (C2), and 532 nm Green (C3) [65]. The key system specifications are provided in Table 1. The dataset was collected by the National Center for Airborne Laser Mapping (NCALM) over the University of Houston main campus and its adjacent urban regions in the United States. We selected this publicly available dataset because it offers high-quality multispectral returns and a rich diversity of land cover types, along with detailed metadata, enabling reproducible and accurate evaluation of our segmentation framework.

Table 1.
Performance and data acquisition parameters of the Optech Titan multispectral LiDAR system.
The dataset covers the University of Houston main campus and its adjacent urban regions in the United States. The entire point cloud is divided into 14 tiles, from which 20 subregions were selected for manual annotation. To ensure a representative sampling of scene variability, we selected regions that are spatially distributed across the study area and that collectively contain all six classes: impervious ground, grassland, tree, building, car, and power line. The annotated points within these regions (areas) were then labeled according to the six defined classes. Areas 1–14 were designated for training, and Areas 15–20 were reserved for testing. The spatial distribution of these annotated regions is shown in Figure 1.
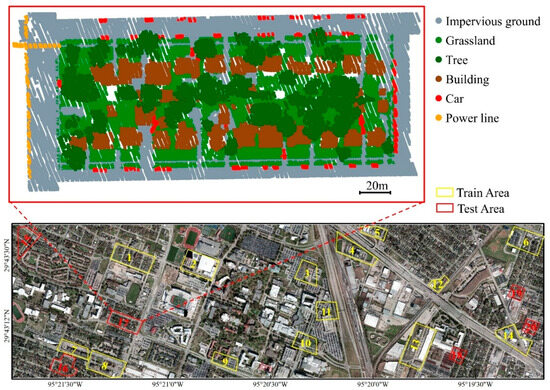
Figure 1.
Spatial distribution and annotation of dataset regions.
3.2. Data Fusion and Annotation
Due to hardware limitations, the Optech Titan multispectral LiDAR system employs three independent laser transmitters—each operating at a distinct wavelength (C1: 1550 nm, C2: 1064 nm, C3: 532 nm)—rather than a single emitter capable of capturing all spectral channels simultaneously. During acquisition, the system concurrently collects three separate point clouds from these channels. To generate a unified multispectral point cloud, spatial registration and attribute fusion are required across the three bands.
In this study, the multispectral feature fusion stage employs a nearest neighbor search-based spatial registration strategy. First, the band with the fewest points (C1 in this dataset) is used as the reference, and KD-trees are constructed for the other two bands. A fixed spatial matching threshold of 0.5 m is applied during fusion. This threshold was determined based on three factors: (1) among the three bands, C1 exhibits the lowest density, approximately 19.8 pts/m2, corresponding to an average point spacing of about 0.22 m, making 0.5 m an appropriate search radius to ensure neighborhood coverage; (2) the smallest ground object class (“car”) has an average width of over 1.8 m, so a 0.5 m threshold is sufficiently small to preserve fine structural details; and (3) typical ground cover types (e.g., paved surfaces and grass patches) span several meters in width, so the threshold still accommodates minor spatial offsets between bands while maintaining precision.
Then, within this 0.5 m radius, each point in the C1 band retrieves its nearest neighbors from the other bands. Their corresponding intensity values are then interpolated and fused into the C1 reference point to produce a multispectral attribute vector. Points in C1 that do not find neighbors in both bands are discarded to avoid incomplete spectral information. The result is a geometrically aligned and spectrally enriched point cloud in which each retained point contains 3D coordinates along with tri-band intensity attributes, as illustrated in Figure 2.
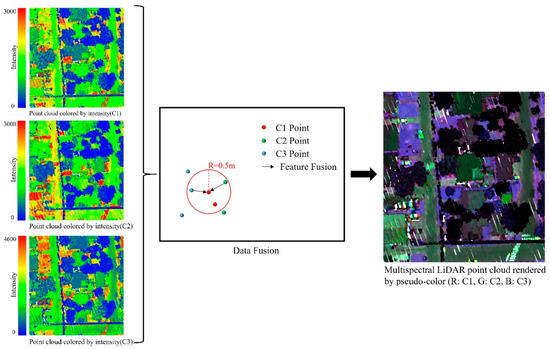
Figure 2.
Data fusion process.
Following fusion, manual annotation is carried out for the 20 selected regions on point and attribute fusion across bands, yielding multispectral point clouds (Figure 3).
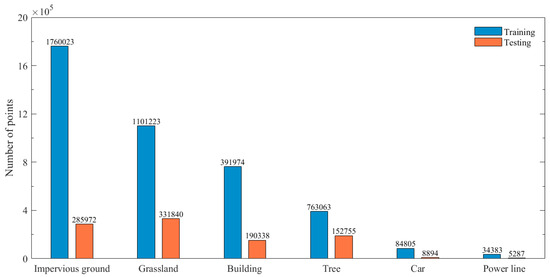
Figure 3.
Point count distribution per category.
4. Method
4.1. Overview of DA-GSGTNet
As shown in Figure 4, DA-GSGTNet adopts an encoder–decoder architecture, ingesting point cloud xyz coordinates alongside three-band intensity features (1550 nm, 1064 nm, 532 nm). The processing begins with a Kernel Point Convolution (KPConv) layer that captures local geometric features through learnable spatial kernels.
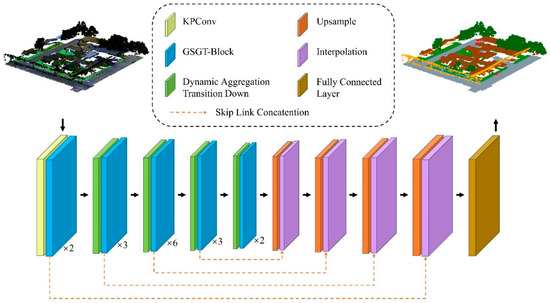
Figure 4.
DA-GSGTNet segmentation network.
Unlike conventional segmentation pipelines, subsequent encoder stages of DA-GSGTNet integrate two key modules in an interleave manner: Gated Stratified Graph Transformer Blocks (GSGT-Blocks) for feature extraction and Dynamic Aggregation Transition Down (DATD) layers for downsampling. DATD layers reduce point counts in stages [N/4, N/16, N/64, N/256] while the GSGT-Blocks operate at the given resolution to enrich feature representations; feature dimensions expand progressively to [32, 64, 128, 256, 512].
The GSGT-Block fuses graph convolution with windowed multi-head self-attention via a learnable gate, capturing sparse global context while preserving local topological continuity.
The DATD module adaptively adjusts its k-NN sampling stride based on local density and parallel aggregate neighborhood coordinates and features, thereby preserving macro-scale semantic context and micro-scale structural fidelity across downsampling stages.
We further enrich this multi-scale hierarchy with a relative position encoding that combines quantized lookup tables and a Euclidean distance bias to sharpen sensitivity to slender or underrepresented classes.
In the decoder, trilinear interpolation is employed to progressively restore point density. A final fully connected layer assigns semantic labels to each point.
4.2. GSGT-Block
Stratified Transformer significantly reduces memory complexity by partitioning 3D space into fixed-size, non-overlapping cubic windows. Each query attends only to points within its window, while a shifted-window mechanism enables cross-window communication. It further employs a hierarchical sampling strategy: “dense” keys (Kdense) are drawn from within the same local window, and “sparse” keys (Ksparse) are sampled via FPS over a larger region. These key sets are then merged and input into the attention mechanism, substantially enlarging the receptive field and improving long-range context modeling at a minimal cost. The workflow comprises the following:
(1) Partition input into non-overlapping windows, and project into query (Q), key (K) and value (V) spaces using three learnable linear mappings:
where are the projection matrices, , represents the dimensionality of the point features, is the number of heads, and is the dimension of each head. The downstream multi-head self-attention mechanism operates directly on the same Q, K, and V projections to produce the output features.
(2) Key set construction:
Dense keys:
Sparse keys:
Merge both for attention:
(3) Perform multi-head self-attention:
However, a Transformer alone cannot explicitly aggregate fine-grained topological relations in point clouds. To address this, we introduce the GSGT-Block, which augments Stratified Transformer with a graph convolution branch.
In parallel to the Transformer branch, we construct a k-NN graph over each point and apply graph convolution:
where is the updated feature, (i) is the neighbor set, W is the weight matrix, and σ is (ReLU) the activation.
Finally, a gating module dynamically fuses the Transformer and GCN branches:
where denotes the gate weights, and ⊙ denotes element-wise multiplication. Through this gated fusion, the GSGT-Block effectively combines the global semantic reasoning of Transformers with the local structural sensitivity of GCNs. This hybrid design leads to improved segmentation accuracy, particularly in scenes with sparse or irregular object distributions. A detailed diagram of the GSGT-Block architecture is provided in Figure 5.
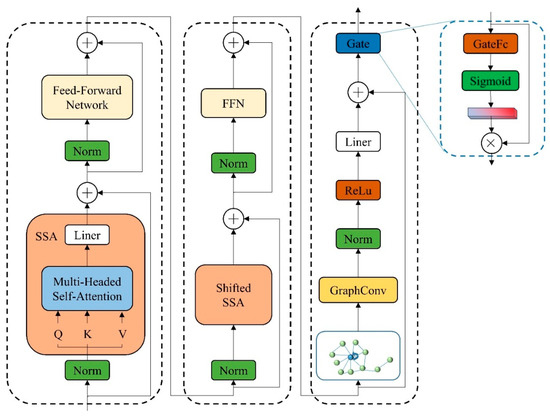
Figure 5.
GSGT-Block structure.
4.3. Dynamic Aggregation Transition Down
The Dynamic Aggregation Transition Down (DATD) module is designed to perform downsampling while aggregating local point cloud coordinates and feature vectors using FPS and a dynamic k-NN algorithm. Unlike conventional fixed-stride downsampling methods, DATD dynamically adjusts its sampling stride based on local point cloud density variations, which is particularly important for multispectral datasets with spatially heterogeneous distributions. The main steps are as follows:
(1) Distance Sequence Computation: Let be the centroid at the s-th downsampling layer. We apply the standard k-NN algorithm to retrieve its nearest neighbors ( = 46) and compute their sorted distance sequence:
(2) Density variation metric: Compute the mean and standard deviation of the distance sequence, and then define the coefficient of variation:
where ε prevents division by zero. A high ratio indicates large local density variation (requiring finer sampling), whereas a low ratio permits a larger stride to increase the receptive field.
(3) Dynamic stride computation: Map to a sampling stride using a base stride and sensitivity α:
where, in this work, = 3, α = 2, = 1, and = 3.
(4) Uniform-Strided Neighbor Sampling and Feature Aggregation: Based on the computed dynamic stride , the first 16 neighbors are sampled at uniform intervals:
Final neighborhood definition:
After determining the neighborhood for each downsampled point , the corresponding coordinates and features are aggregated together. The coordinates and features are concatenated, then transformed through a linear layer and normalization operation. Finally, a max pooling layer is applied to produce the aggregated features Fi and the corresponding new coordinates .
By leveraging this dynamic k-NN strategy, the module adaptively selects the sampling stride based on local point cloud density variations: smaller strides in regions with high density fluctuation (e.g., building edges) ensure fine-grained structural capture; larger strides in uniform areas (e.g., grassland) expand the receptive field without extra memory overhead, aggregating richer contextual information.
4.4. Enhanced Position Encoding
Due to the spatial complexity of 3D point clouds, position encoding plays a critical role in feature extraction. Zhao et al. [42] proposed Contextual Relative Position Encoding (cRPE), which employs three learnable lookup tables corresponding to the x, y, and z axes. The continuous relative coordinates are uniformly quantized into discrete bins and mapped to table indices , where denotes the quantization function. The lookup tables then retrieve the corresponding embeddings , which are summed to produce the positional encoding . To further exploit coordinate information, we augment cRPE with a linear mapping of the Euclidean distance. Specifically, we first compute the Euclidean distance between two points:
where and denote the layer’s weight and bias.
We then sum the distance embedding, DE, with the cRPE, PE, to form the final positional encoding:
This hybrid approach, combining cRPE with linear distance mapping, more comprehensively captures the spatial structure of point clouds. In our experiments, this method demonstrated superior performance in multispectral point cloud segmentation.
4.5. Upsampling and Interpolation
In the decoder phase of DA-GSGTNet, we adopt a U-Net [66] architecture for progressive feature restoration through upsampling and interpolation. Starting from the input, the downsampling branch’s feature and coordinate are first processed by Layer Normalization and a linear projection. Next, we perform interpolation to map from to , yielding upsampled features aligned with the target coordinate set . Simultaneously, the encoder’s skip-connection feature and coordinate undergo the same LayerNorm and linear transformation to produce a second set of projected features. These two projections are spatially aligned and are combined via element-wise summation to produce the fused decoding feature y at coordinate . The final output (y, ) is then passed to the subsequent upsampling stage or the segmentation head, as shown in Figure 6.
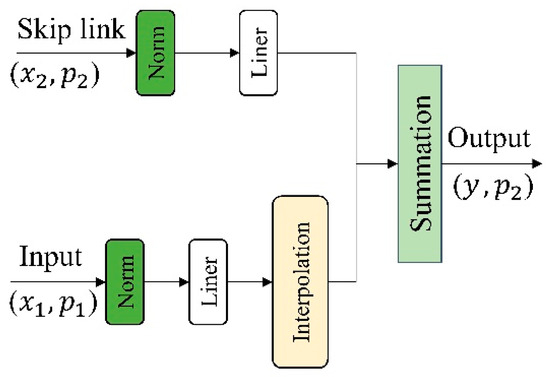
Figure 6.
Upsampling and interpolation module.
4.6. Transfer Learning Based on DA-GSGTNet
In practical applications, obtaining fully annotated multispectral LiDAR point cloud datasets is costly and labor-intensive, often resulting in limited labeled data. Directly training deep models such small datasets can lead to overfitting, slow convergence, and suboptimal accuracy. To address this, we explore a transfer learning strategy that leverages pretraining on large-scale single-band point cloud datasets, followed by fine-tuning on the target multispectral dataset to improve segmentation accuracy and accelerate convergence.
We adopt a two-stage fine-tuning strategy. In the first stage, the DA-GSGTNet model is pretrained on large-scale open-source datasets, specifically DALES and Sensat, which serve as the source dataset . The pretraining objective is to minimize the segmentation loss:
where represents the pretrained network parameters.
In the second stage, the pretrained model weights Θs are used as initialization parameters for further training on a small-scale multispectral point cloud dataset , where :
We observe domain gaps in point density, spatial distribution, and class definitions—DALES comprises 8 classes, Sensat 13, and Titan only 6. To address density and spatial discrepancies, we downsample the source datasets to approximate Titan’s characteristics; to reconcile class-count mismatches, we preserve the pretrained feature extractor weights while reinitializing the classification head for each dataset. And layer-wise freezing was not employed; instead, global fine-tuning was performed across all layers to enable full adaptation to the Titan domain. To mitigate source–target feature distribution shifts, min–max normalization was applied to input point coordinates and multispectral intensity values.
Through this fine-tuning strategy, DA-GSGTNet can achieve faster convergence and significant performance improvements in data-scarce multispectral scenarios, as illustrated in Figure 7.
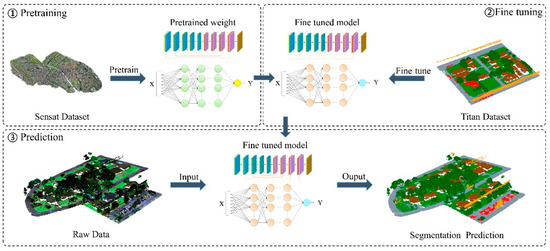
Figure 7.
Transfer learning workflow.
5. Result
To evaluate the performance of DA-GSGTNet for semantic segmentation of multispectral point cloud, we conducted comprehensive experiments on a multispectral point cloud dataset comprising X, Y, Z coordinates and three spectral bands: 1550 nm MIR (C1), 1064 nm NIR, and 532 nm Green.
5.1. Experimental Settings
To ensure consistency in the experimental environment, all model training was conducted on the same Linux server (Linux version 5.4.0) equipped with two NVIDIA GeForce RTX 3090 GPUs, each with 24 GB of memory. The model was trained using the AdamW optimizer, with an initial learning rate of 0.006. To ensure stable convergence, the learning rate was exponentially decayed by a factor of 100 every 30 epochs. The total number of training epochs was set to 100.
5.2. Evaluation Metrics
To comprehensively assess the performance of DA-GSGTNet and compare it with baseline models, we employed the following standard evaluation metrics widely used in point cloud semantic segmentation:
Intersection over Union (IoU):
Mean Intersection over Union (mIoU):
Overall Accuracy (OA):
Mean Accuracy (mAcc):
Here, denotes the number of points correctly predicted as class , denotes the number of points incorrectly predicted as class iii, and denotes the number of points of class iii incorrectly predicted as other classes. represents the total number of classes.
5.3. Overall Performance
To validate the effectiveness of the proposed DA-GSGTNet model for multispectral LiDAR point cloud semantic segmentation, we conducted comparative experiments against five representative baseline methods: PointNet++ [36], PointNeXt-b [46], PointNeXt-l [46], RandLA-Net [42], and Stratified Transformer [45]. These models span classical MLP-based architectures to more recent Transformer-based frameworks, providing a balanced comparison.
PointNet++ serves as a foundational benchmark for point cloud learning. PointNeXt-b and PointNeXt-l are modern MLP-based variants emphasizing scalability and efficient design. RandLA-Net is known for lightweight and real-time segmentation of large-scale outdoor scenes. Stratified Transformer integrates the Vision Transformer paradigm into point cloud segmentation.
Table 2 summarizes the quantitative results, reporting per-class IoU along with mIoU, mAcc, and OA. As shown, DA-GSGTNet achieves the best performance across all three metrics, with an mIoU of 86.43%, mAcc of 93.74%, and OA of 90.78%.

Table 2.
Accuracy metrics of different segmentation methods on test scenes (best values in bold).
In terms of individual classes performance, DA-GSGTNet achieves the highest IoUs of 75.03% for impervious ground, 78.28% for grassland, and 90.30% for car, significantly outperforming other models. In particular, for visually similar classes such as impervious ground and grassland, which require fine-grained feature distinction. DA-GSGTNet is the only model to surpass 75% IoU on both.
Among baseline models, PointNet++ performs the worst, with an mIoU of 68.52%, particularly struggling on sparse classes such as car (65.80%) and power line (23.82%). The PointNeXt variants improve slightly but still underperform in large-scale scenes due to the lack of sufficient long-range dependency modeling; particularly, the power line category remains under 50%. RandLA-Net and Stratified Transformer demonstrate competitive results in certain classes (e.g., tree, building) but fail to match DA-GSGTNet’s overall balance and accuracy across all classes. Importantly, DA-GSGTNet delivers consistently strong results without clear weaknesses, with tree and building IoUs of 96.36% and 94.60%, respectively, and power line segmentation accuracy exceeding 80%.
Figure 8 visualizes segmentation results across six test areas. DA-GSGTNet produces clearer boundaries and more accurate class distinctions, particularly in regions where impervious ground and grassland boundaries are ambiguous. It also excels in detail-rich areas such as buildings, vehicles, and power lines. For instance, in Test Areas 16 and 20, DA-GSGTNet accurately identifies sparsely distributed power lines, whereas PointNet++ and PointNeXt exhibit higher misclassification rates; in Area 19, DA-GSGTNet effectively differentiates the two ground classes, demonstrating superior spatial context modeling.

Figure 8.
Visualization of segmentation results by different methods in the test scenes.
Collectively, both quantitative metrics and visual analysis validate that DA-GSGTNet achieves state-of-the-art performance in multispectral LiDAR point cloud scenes, offering robust and precise classification across a diverse range of object classes.
5.4. Specific Scene Segmentation Results
To intuitively compare model differences, we selected four sub-scenes prone to misclassification (Scenes A–D) from six test areas for detailed visual comparative analysis, as shown in Figure 9.
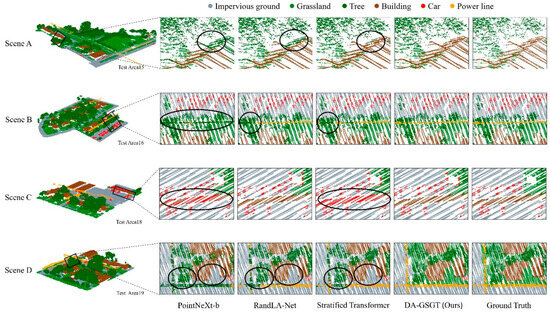
Figure 9.
Segmentation results in specific challenging scenes.
Scene A, from part of Test Area 15, features a minimal gap between houses and trees, causing segmentation confusion. The first row of Figure 9 shows that our method precisely separates the house from the trees; Stratified Transformer segments most points but incurs minor errors around the eaves; RandLA-Net and PointNeXt-b suffer significant roof segmentation errors. This improvement stems from the complementary Transformer–GCN architecture, which maintains long-range dependencies while capturing stronger spatial features, resulting in more precise boundary delineation.
Scene B, from part of Test Area 16, is challenged by a power line crossing closely above trees, leading to frequent misclassification. The second row of Figure 9 shows that only DA-GSGTNet segments the entire power line; the other models exhibit line breaks, with PointNeXt-b misclassifying nearly the whole line as trees.
Scene C, from part of Test Area 18, depicts a low-height, non-typical canopy in a parking lot that is often misclassified as a vehicle due to its narrow, roof-like form. The third row of Figure 9 indicates that our method and RandLA-Net correctly identify the canopy, while Stratified Transformer and PointNeXt-b misclassify it as a car.
Scene D, from part of Test Area 19, is complex with power lines near trees and small irregular grass patches among buildings. The fourth row of Figure 9 demonstrates that DA-GSGTNet delivers satisfactory segmentation for both the power lines and the grass, whereas the other models underperform on these classes. This success is primarily attributed to the DATD module: by dynamically increasing the k-NN sampling interval for grass and impervious surfaces based on local density, it expands the receptive field to accommodate varying shapes and enhances feature extraction.
These scene-specific results confirm DA-GSGTNet’s ability to capture both global semantic context and fine-grained geometric cues, thereby achieving high segmentation precision in complex and ambiguous environments.
5.5. Ablation Study
To assess each individual module’s contribution to overall performance, we created three ablated variants of DA-GSGTNet and compared their IoU and mIoU scores against the full model on the same test set. The detailed results are presented in Table 3.

Table 3.
Ablation study results (best values in bold).
- (1)
- Variant A (−GCN/−Gate): The graph-convolution branch and gating fusion module are removed from the encoder, retaining only the Transformer, DATD, and skip connections.
- (2)
- Variant B (−DATD): The Dynamic Aggregation Transition Down module is omitted; feature aggregation reverts to standard k-NN, with a fixed stride of 1, and does not include neighbor coordinate aggregation.
- (3)
- Variant C (−Dist): The Euclidean distance bias is removed, using only the quantized coordinate difference lookup tables for relative position encoding.
From Table 3, Variant A yields an mIoU of 85.50%, a 0.93% decline compared to the full model, indicating that the GCN branch and gating contribute a modest yet consistent improvement. The largest drop is observed for the power line class (−5.82%), underscoring the role of the GCN and gating mechanism in enhancing neighborhood information and feature fusion for slender and underrepresented classes. Other classes such as tree, building, and car also experience small reductions in IoU, suggesting that the GCN–Transformer fusion improves overall semantic representation.
Variant B shows the most significant performance degradation, with an mIoU of 79.82%, a 6.61-point drop from the full model. All class IoUs suffer substantial declines, particularly power line (−17.89%) and grassland (−5.23%). This highlights the DATD module’s pivotal function in adaptive receptive field adjustment and the integration of local structure via coordinate–feature aggregation. Without DATD, the model struggles to handle structural variability and fails to generalize across densities.
Variant C records a mIoU of 85.56%, a 0.87% reduction versus the full model. The car and power line classes decline by 1.96% and 2.49%, respectively, indicating that incorporating Euclidean distance into pairwise attention enhances sensitivity to physical spacing and improves discrimination of small or slender objects. Conversely, impervious ground and grassland see slight IoU gains (+0.92% and +0.28%) without distance bias, suggesting limited benefit for large, homogeneous surfaces.
The ablation results clearly demonstrate that all three modules contribute to the high performance of DA-GSGTNet. Among them, the DATD module’s pivotal role in preserving high-quality downsampled features is particularly underscored, ensuring robust feature representation across varying point densities. Additionally, the gated GCN fusion and enhanced position encoding significantly improve fine-grained segmentation, especially for small and sparse classes. Together, these components form a cohesive framework optimized for semantic segmentation in complex multispectral point cloud environments.
5.6. Multispectral Point Cloud Transfer Learning
We pretrained DA-GSGTNet on two well-annotated open-source point cloud datasets: the single-band LiDAR DALES dataset and the photogrammetry-based Sensat dataset. To emulate data-scarce conditions, we reduced the number of training regions from 14 to 4 (Areas 1, 2, 8, and 13) while keeping the test set (15–20) unchanged. All other experimental settings remained as in Section 5.3. The results are shown in Table 4; “Resampling” denotes spatial preprocessing with a 0.3 m threshold to lower point cloud density to match the multispectral dataset.

Table 4.
Transfer learning performance results (best values in bold).
Pretraining on large-scale open-source datasets substantially improves segmentation accuracy. The baseline model without any pretraining achieves only 63.29% mIoU overall; impervious ground and grassland attain 65.37% and 65.23%, respectively, and power line drops to 48.53%. Only tree shows strong performance (92.31%), likely due to its distinctive geometry and prevalence in the training set. These findings highlight the performance bottleneck of deep models under limited annotations.
After pretraining on DALES, the overall mIoU increases to 78.35%. Notably, building and car IoUs climb from 57.75% and 50.57% to 92.91% and 77.27% (gains of 35.0 and 26.7 points), demonstrating that DALES’s rich urban geometry annotations greatly enhance semantic understanding. The power line IoU also rises from 48.53% to 61.30%. When DALES is resampled at 0.3 m, the overall mIoU drops to 75.22%, but that of power line further improves to 66.22%, indicating that resampling helps preserve sparse details. Pretraining on Sensat yields an overall mIoU of 79.12%. Similarly to DALES, all class accuracies improve, with impervious ground reaching 71.79%—the highest among all pretraining settings. After 0.3 m resampling of Sensat, the mIoU further increases to 80.28%, the top result; grassland, tree, building, car, and power line improve to 76.34%, 95.72%, 95.41%, 82.53%, and 62.52%, respectively.
As shown in Table 5, pretraining on DALES and Sensat recovers most of the full-training mIoU while reducing the epochs required for convergence. Figure 10 illustrates that pretraining also accelerates convergence. While the non-pretrained model requires approximately 15–20 epochs to reduce the validation loss below 0.3 and raise OA above 90%, models pretrained on DALES or Sensat achieve this within 5–10 epochs and maintain stable convergence thereafter. Resampling has little effect on convergence speed, indicating that this preprocessing step has limited impact on training dynamics.

Table 5.
Data efficiency and convergence comparison across training regimes (best values in bold).
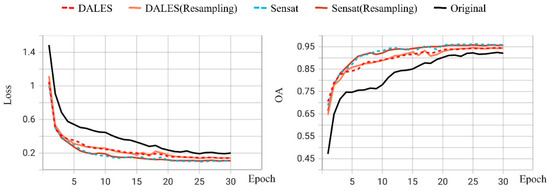
Figure 10.
Training loss and accuracy curves.
Overall, transfer learning delivers dual benefits in multispectral LiDAR segmentation: on one hand, pretraining on large-scale, diverse datasets like DALES and Sensat significantly boosts recognition accuracy for both macrostructures and fine details; on the other hand, pretrained weights enable rapid convergence to target performance (over 90% accuracy) using only 30 epochs and four training regions, matching what full-scale (100-epoch) training on the complete dataset achieves. This “learn generic geometry first, then fine-tune multispectral details” strategy offers a practical solution for efficient network deployment under data-scarce conditions.
6. Discussion
The proposed DA-GSGTNet addresses multispectral point clouds from both geometric and spectral perspectives by integrating GSGT-Blocks (graph convolution with gated fusion) and the Dynamic Aggregation Transition Down (DATD) module. This complementary design achieves a balanced aggregation of fine-grained local features and sparse long-range context. Quantitative evaluations demonstrate that DA-GSGTNet outperforms PointNet++, PointNeXt variants, RandLA-Net, and Stratified Transformer, achieving state-of-the-art results in mIoU, mAcc, and OA. Notably, it attains an average IoU of 87.15% on underrepresented, slender classes such as power lines and cars, confirming the effectiveness of augmenting relative position encoding with Euclidean distance bias and dynamic graph sampling for capturing complex structures. Visualizations further highlight the model’s excellence in challenging scenarios—such as building–ground boundaries, power line–tree edges, and roof–ground distinctions under dense canopies.
Compared to existing MLP-based hierarchical networks and pure Transformer approaches, DA-GSGTNet’s primary advantage lies in fusing graph structural information with windowed attention. The graph convolution branch compensates for the Transformer’s limited perception of local continuity in sparse neighborhoods, while the DATD module’s density-aware dynamic k-NN sampling and coordinate aggregation prevent redundancy and information loss inherent to fixed-stride k-NN. This design enables rapid capture of broad contextual cues alongside precise recovery of fine-scale geometric details, leading to significant performance gains in classes and regions where other methods struggle.
Furthermore, DA-GSGTNet demonstrates outstanding transfer learning capability for multispectral LiDAR data. By pretraining on large-scale open-source datasets (DALES, Sensat) and fine-tuning with a small set of multispectral annotations, the model’s mIoU rises from 63.3% (without pretraining) to 80.28%—achieving over 90% accuracy using only four training areas, comparable to full training on 14 areas for 100 epochs—while also substantially accelerating convergence with just 30 fine-tuning epochs. Among the source datasets, Sensat consistently outperforms DALES—likely due to its RGB bands and smaller domain gap relative to the target Titan multispectral data.
Our experimental results further validate the effectiveness of pretraining DA-GSGTNet on large-scale single-band and photogrammetric point cloud datasets (DALES and Sensat), which leads to a marked improvement in segmentation accuracy on multispectral LiDAR data. These gains are most pronounced in categories requiring complex spatial context or fine geometric structure—such as buildings, vehicles, and power lines—indicating that the model successfully learns generalizable geometric and attribute features that provide strong priors for downstream tasks.
Among the source datasets, Sensat consistently outperforms DALES, likely because Sensat includes three spectral channels (RGB) and exhibits smaller domain shift relative to the target Titan data, whereas DALES provides only one band. After spatial resampling, the Sensat-pretrained model shows a slight performance increase, whereas the DALES-pretrained model declines. We attribute this divergence to the differing feature dependencies: with only one band, the DALES-pretrained model relies heavily on geometric cues, which are degraded by downsampling; in contrast, the RGB features in Sensat remain robust under resampling, and the relative weight of color information even increases, enhancing overall segmentation performance.
Looking ahead, DA-GSGTNet could be applied to precision agriculture, for example, crop-type mapping and plant health monitoring, and to forestry tasks such as species classification and storm damage assessment. It may also support infrastructure inspection by segmenting power lines and bridge components from complex 3D scenes. Thanks to its strong transfer learning ability, where pretraining on large public point cloud datasets allows fine-tuning with only a few labeled areas, DA-GSGTNet can be readily adapted to novel sensors (e.g., UAV-mounted hyperspectral LiDAR) or new environments with minimal annotation effort.
Despite these advances, DA-GSGTNet faces challenges in computational efficiency and data diversity. Graph convolutions and multi-head attention introduce additional overhead, necessitating further model compression for embedded or real-time applications. Moreover, the hyperparameters of DATD and relative position encoding exhibit sensitivity, which future work should address via automated search or adaptive optimization strategies. Finally, we plan to investigate more efficient transfer learning paradigms tailored to multispectral point clouds, such as adapter modules and partial fine-tuning, aiming to mitigate overfitting and reduce the resource footprint associated with full-parameter tuning.
7. Conclusions
This study presents DA-GSGTNet, a novel architecture for semantic segmentation of multispectral LiDAR point clouds, which effectively integrates geometric structure and spectral information. The model’s key contributions are as follows:
(1) GSGT-Block: A gated fusion of graph convolution and windowed multi-head self-attention that combines the global contextual modeling capability of Transformers with the local structural sensitivity of graph-based methods, ensuring robust feature extraction in sparse 3D neighborhoods.
(2) Dynamic Aggregation Transition Down (DATD): A density-aware downsampling mechanism that adaptively adjusts the k-NN sampling stride based on local point cloud density and aggregates both spatial coordinates and spectral features. This design preserves critical structural detail across multiple resolution scales.
(3) Enhanced Relative Position Encoding: An augmentation of contextual relative encoding with an additional Euclidean distance bias, improving the model’s sensitivity to slender and underrepresented objects such as power lines and vehicles in complex urban environments.
Extensive quantitative comparisons against five baseline methods—PointNet++, PointNeXt-b, PointNeXt-l, RandLA-Net, and Stratified Transformer—demonstrate that DA-GSGTNet attains superior segmentation accuracy, achieving an mIoU of 86.43%, mAcc of 93.74%, and OA of 90.78%. Ablation studies confirm the individual and complementary benefits of each module: DATD is crucial for preserving global structure during downsampling, while GSGT-Blocks and distance-biased position encoding significantly enhance the discrimination of fine and sparse objects.
Furthermore, the proposed transfer learning strategy, which involves pretraining on large-scale, open-source point cloud datasets (DALES and Sensat) and fine-tuning on a limited multispectral dataset, significantly improves training efficiency. With only 30 epochs on four training regions (~ 30% of the full data), the model achieves over 90% of the performance obtained by full-scale training (14 regions, 100 epochs).
These findings establish DA-GSGTNet as a robust and adaptable framework for multispectral LiDAR segmentation, particularly well-suited for data-scarce, detail-sensitive applications in remote sensing and 3D scene understanding.
Author Contributions
Q.D.; Conceptualization, Writing—reviewreview and editing, Project administration. R.Z.; Conceptualization, Methodology, Software, Validation, Visualization, Writing—original draft, Writing—reviewreview and editing. A.H.-M.N.; Conceptualization, Methodology, Writing—original draft, Writing—reviewreview and editing. L.T.; Funding acquisition, Conceptualization. B.L.; Conceptualization, Methodology. D.W.; Investigation, Writing—review. Y.H.; Investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 42274017; in part by the Program for Guangdong Introducing Innovative and Entrepreneurial Teams under Grant 2019ZT08L213; in part by Guangdong Basic and Applied Basic Research Foundation under Grant 2023A1515030184; and in part by Guangzhou Science and Technology Plan Project under Grant 2025A04J5190.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Doost, Z.H.; Yaseen, Z.M. The impact of land use and land cover on groundwater fluctuations using remote sensing and geographical information system: Representative case study in Afghanistan. Environ. Dev. Sustain. 2023, 27, 9515–9538. [Google Scholar] [CrossRef]
- Scaioni, M.; Höfle, B.; Baungarten Kersting, A.P.; Barazzetti, L.; Previtali, M.; Wujanz, D. Methods from information extraction from lidar intensity data and multispectral lidar technology. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 1503–1510. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, X.; Liang, S.; Zhou, T.; Du, X.; Xu, P.; Wu, D. Assessing the thermal contributions of urban land cover types. Landsc. Urban Plan. 2020, 204, 103927. [Google Scholar] [CrossRef]
- Arif, M.; Sengupta, S.; Mohinuddin, S.; Gupta, K. Dynamics of land use and land cover change in peri urban area of Burdwan city, India: A remote sensing and GIS based approach. GeoJournal 2023, 88, 4189–4213. [Google Scholar] [CrossRef]
- Chase, A.S.; Weishampel, J. Using LiDAR and GIS to investigate water and soil management in the agricultural terracing at Caracol, Belize. Adv. Archaeol. Pract. 2016, 4, 357–370. [Google Scholar] [CrossRef]
- Pande, C.B.; Moharir, K.N. Application of hyperspectral remote sensing role in precision farming and sustainable agriculture under climate change: A review. In Climate Change Impacts on Natural Resources, Ecosystems and Agricultural Systems; Springer: Berlin/Heidelberg, Germany, 2023; pp. 503–520. [Google Scholar]
- Macarringue, L.S.; Bolfe, É.; Pereira, P.R.M. Developments in land use and land cover classification techniques in remote sensing: A review. J. Geogr. Inf. Syst. 2022, 14, 1–28. [Google Scholar] [CrossRef]
- Hasan, M.A.; Mia, M.B.; Khan, M.R.; Alam, M.J.; Chowdury, T.; Al Amin, M.; Ahmed, K.M.U. Temporal changes in land cover, land surface temperature, soil moisture, and evapotranspiration using remote sensing techniques—A case study of Kutupalong Rohingya Refugee Camp in Bangladesh. J. Geovisualization Spat. Anal. 2023, 7, 11. [Google Scholar] [CrossRef]
- Zheng, Z.; Liu, H.; Wang, Z.; Lu, P.; Shen, X.; Tang, P. Improved 3D-CNN-based method for surface feature classification using hyperspectral images. Remote Sens. Nat. Resour. 2023, 35, 105. [Google Scholar]
- Jinxi, Y.; Chengzhi, X.; Zhi, Z.; Lang, W.; Kun, Z. Vegetation feature type extraction in arid regions based on GEE multi-source remote sensing data. Arid Zone Res. 2024, 41, 157–168. [Google Scholar]
- Lv, Z.; Zhang, P.; Sun, W.; Benediktsson, J.A.; Lei, T. Novel land-cover classification approach with nonparametric sample augmentation for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4407613. [Google Scholar] [CrossRef]
- Phuong, V.T.; Thien, B.B. A multi-temporal Landsat data analysis for land-use/land-cover change in the Northwest mountains region of Vietnam using remote sensing techniques. In Forum Geografic; University of Craiova, Department of Geography: Craiova, Romania, 2023. [Google Scholar]
- Mishra, A.; Arya, D.S. Assessment of land-use land-cover dynamics and urban heat island effect of Dehradun city, North India: A remote sensing approach. Environ. Dev. Sustain. 2024, 26, 22421–22447. [Google Scholar] [CrossRef]
- Liu, X.; Ng, A.H.-M.; Ge, L.; Lei, F.; Liao, X. Multi-branch Fusion: A Multi-branch Attention Framework by Combining Graph Convolutional Network and CNN for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5528817. [Google Scholar]
- Liu, X.; Ng, A.H.-M.; Lei, F.; Ren, J.; Guo, L.; Du, Z. MSLKCNN: A Simple and Powerful Multi-scale Large Kernel CNN for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5513314. [Google Scholar] [CrossRef]
- Eitel, J.U.; Höfle, B.; Vierling, L.A.; Abellán, A.; Asner, G.P.; Deems, J.S.; Glennie, C.L.; Joerg, P.C.; LeWinter, A.L.; Magney, T.S. Beyond 3-D: The new spectrum of lidar applications for earth and ecological sciences. Remote Sens. Environ. 2016, 186, 372–392. [Google Scholar] [CrossRef]
- Kukkonen, M.; Maltamo, M.; Korhonen, L.; Packalen, P. Multispectral airborne LiDAR data in the prediction of boreal tree species composition. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3462–3471. [Google Scholar] [CrossRef]
- Podgorski, J.; Pętlicki, M.; Kinnard, C. Revealing recent calving activity of a tidewater glacier with terrestrial LiDAR reflection intensity. Cold Reg. Sci. Technol. 2018, 151, 288–301. [Google Scholar] [CrossRef]
- Haotian, Y.; Yanqiu, X.; Tao, P.; Jianhua, D. Effects of different LiDAR intensity normalization methods on Scotch pine forest leaf area index estimation. Acta Geod. Et Cartogr. Sin. 2018, 47, 170. [Google Scholar]
- Zhang, R.; Ding, Q.; Ng, A.H.-M.; Wang, D.; Deng, J.; Xu, M.; Hou, Y. TripletA-Net: A Deep Learning Model for Automatic Railway Track Extraction from Airborne LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 9195–9210. [Google Scholar] [CrossRef]
- Shi, S.; Bi, S.; Gong, W.; Chen, B.; Chen, B.; Tang, X.; Qu, F.; Song, S. Land Cover Classification with Multispectral LiDAR Based on Multi-Scale Spatial and Spectral Feature Selection. Remote Sens. 2021, 13, 4118. [Google Scholar] [CrossRef]
- Nima, E.; Craig, G.; Carlos, F.D.J. Classification of Airborne Multispectral Lidar Point Clouds for Land Cover Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2068–2078. [Google Scholar]
- Huang, M.-J.; Shyue, S.-W.; Lee, L.-H.; Kao, C.-C. A knowledge-based approach to urban feature classification using aerial imagery with lidar data. Photogramm. Eng. Remote Sens. 2008, 74, 1473–1485. [Google Scholar] [CrossRef]
- Zhou, K.; Ming, D.; Lv, X.; Fang, J.; Wang, M. CNN-Based Land Cover Classification Combining Stratified Segmentation and Fusion of Point Cloud and Very High-Spatial Resolution Remote Sensing Image Data. Remote Sens. 2019, 11, 2065. [Google Scholar] [CrossRef]
- Gong, W.; Shi, S.; Chen, B.; Song, S.; Wu, D.; Liu, D.; Liu, Z.; Liao, M. Development and application of airborne hyperspectral LiDAR imaging technology. Acta Opt. Sin. 2022, 42, 1200002. [Google Scholar]
- Wichmann, V.; Bremer, M.; Lindenberger, J.; Rutzinger, M.; Georges, C.; Petrini-Monteferri, F. Evaluating the potential of multispectral airborne lidar for topographic mapping and land cover classification. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 113–119. [Google Scholar] [CrossRef]
- Bakuła, K.; Kupidura, P.; Jełowicki, Ł. Testing of land cover classification from multispectral airborne laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 161–169. [Google Scholar] [CrossRef]
- Jing, Z.; Guan, H.; Zhao, P.; Li, D.; Yu, Y.; Zang, Y.; Wang, H.; Li, J. Multispectral LiDAR point cloud classification using SE-PointNet++. Remote Sens. 2021, 13, 2516. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Z.; Huang, J.; Shen, T.; Gu, Y. Multikernel Graph Structure Learning for Multispectral Point Cloud Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 5637–5650. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, T.; Tang, X.; Lei, X.; Peng, Y. Introducing improved transformer to land cover classification using multispectral LiDAR point clouds. Remote Sens. 2022, 14, 3808. [Google Scholar] [CrossRef]
- Morris, C.; Ritzert, M.; Fey, M.; Hamilton, W.L.; Lenssen, J.E.; Rattan, G.; Grohe, M. Weisfeiler and leman go neural: Higher-order graph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 4602–4609. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Wang, L.; Huang, Y.; Hou, Y.; Zhang, S.; Shan, J. Graph attention convolution for point cloud semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10296–10305. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Li, J.; Chen, B.M.; Lee, G.H. So-net: Self-organizing network for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9397–9406. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 87–102. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.-E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Guo, M.-H.; Cai, J.-X.; Liu, Z.-N.; Mu, T.-J.; Martin, R.R.; Hu, S.-M. Pct: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Lai, X.; Liu, J.; Jiang, L.; Wang, L.; Zhao, H.; Liu, S.; Qi, X.; Jia, J. Stratified transformer for 3D point cloud segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8500–8509. [Google Scholar]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. Pointnext: Revisiting pointnet++ with improved training and scaling strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Zhao, C.; Yu, D.; Xu, J.; Zhang, B.; Li, D. Airborne LiDAR point cloud classification based on transfer learning. In Proceedings of the Eleventh International Conference on Digital Image Processing (ICDIP 2019), Guangzhou, China, 10–13 May 2019; pp. 550–556. [Google Scholar]
- Lei, X.; Wang, H.; Wang, C.; Zhao, Z.; Miao, J.; Tian, P. ALS point cloud classification by integrating an improved fully convolutional network into transfer learning with multi-scale and multi-view deep features. Sensors 2020, 20, 6969. [Google Scholar] [CrossRef] [PubMed]
- Imad, M.; Doukhi, O.; Lee, D.-J. Transfer learning based semantic segmentation for 3D object detection from point cloud. Sensors 2021, 21, 3964. [Google Scholar] [CrossRef]
- Murtiyoso, A.; Lhenry, C.; Landes, T.; Grussenmeyer, P.; Alby, E. Semantic segmentation for building façade 3D point cloud from 2D orthophoto images using transfer learning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 201–206. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, Z.; Chen, T.; Fan, H.; Wang, Z. Can we solve 3D vision tasks starting from a 2D vision transformer? arXiv 2022, arXiv:2209.07026. [Google Scholar] [CrossRef]
- Ding, G.; Imamoglu, N.; Caglayan, A.; Murakawa, M.; Nakamura, R. SalLiDAR: Saliency Knowledge Transfer Learning for 3D Point Cloud Understanding. In Proceedings of the BMVC, London, UK, 21–24 November 2022; p. 584. [Google Scholar]
- Laazoufi, A.; El Hassouni, M.; Cherifi, H. Point Cloud Quality Assessment using 1D VGG16 based Transfer Learning Model. In Proceedings of the 2023 17th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Bangkok, Thailand, 8–10 November 2023; pp. 381–387. [Google Scholar]
- Yao, Y.; Gao, W.; Mao, S.; Zhang, S. Road Extraction from Point Cloud Data with Transfer Learning. IEEE Geosci. Remote Sens. Lett. 2024, 21, 6502005. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Schäfer, J.; Winiwarter, L.; Weiser, H.; Höfle, B.; Schmidtlein, S.; Novotný, J.; Krok, G.; Stereńczak, K.; Hollaus, M.; Fassnacht, F.E. CNN-based transfer learning for forest aboveground biomass prediction from ALS point cloud tomography. Eur. J. Remote Sens. 2024, 57, 2396932. [Google Scholar] [CrossRef]
- Xiao, A.; Huang, J.; Guan, D.; Zhan, F.; Lu, S. Transfer learning from synthetic to real lidar point cloud for semantic segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; pp. 2795–2803. [Google Scholar]
- Huang, X.; Xie, T.; Wang, Z.; Chen, L.; Zhou, Q.; Hu, Z. A transfer learning-based multi-fidelity point-cloud neural network approach for melt pool modeling in additive manufacturing. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2022, 8, 011104. [Google Scholar] [CrossRef]
- Wu, C.; Bi, X.; Pfrommer, J.; Cebulla, A.; Mangold, S.; Beyerer, J. Sim2real transfer learning for point cloud segmentation: An industrial application case on autonomous disassembly. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 4531–4540. [Google Scholar]
- Biehler, M.; Sun, Y.; Kode, S.; Li, J.; Shi, J. PLURAL: 3D point cloud transfer learning via contrastive learning with augmentations. IEEE Trans. Autom. Sci. Eng. 2023, 21, 7550–7561. [Google Scholar] [CrossRef]
- Zhou, Y.; Ji, A.; Zhang, L.; Xue, X. Sampling-attention deep learning network with transfer learning for large-scale urban point cloud semantic segmentation. Eng. Appl. Artif. Intell. 2023, 117, 105554. [Google Scholar] [CrossRef]
- Enes Bayar, A.; Uyan, U.; Toprak, E.; Yuheng, C.; Juncheng, T.; Alp Kindiroglu, A. Point Cloud Segmentation Using Transfer Learning with RandLA-Net: A Case Study on Urban Areas. arXiv 2023, arXiv:2312.11880. [Google Scholar]
- Shi, Y.; Wang, Y.; Yin, L.; Wu, Z.; Lin, J.; Tian, X.; Huang, Q.; Zhang, S.; Li, Z. A transfer learning-based network model integrating kernel convolution with graph attention mechanism for point cloud segmentation of livestock. Comput. Electron. Agric. 2024, 225, 109325. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, Z.; Xiao, Z.; Ji, A.; Wu, B. Dual hierarchical attention-enhanced transfer learning for semantic segmentation of point clouds in building scene understanding. Autom. Constr. 2024, 168, 105799. [Google Scholar] [CrossRef]
- Fernandez-Diaz, J.C.; Carter, W.E.; Glennie, C.; Shrestha, R.L.; Pan, Z.; Ekhtari, N.; Singhania, A.; Hauser, D.; Sartori, M. Capability assessment and performance metrics for the Titan multispectral mapping lidar. Remote Sens. 2016, 8, 936. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. pp. 234–241. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).