Method for Obtaining Water-Leaving Reflectance from Unmanned Aerial Vehicle Hyperspectral Remote Sensing Based on Air–Ground Collaborative Calibration for Water Quality Monitoring
Abstract
Highlights
- This study proposed an air–ground collaboration + neural network method, which achieved superior water-leaving reflectance inversion (450–900 nm band), with inversion curves closely matching ground measurements obtained using an analytical spectral device (ASD). In addition, the proposed method reduced the average spectral angle matching (SAM) from 0.5433 using existing methods to 0.1070, improving quantitative accuracy of approximately 80%.
- High-precision water quality inversion models (R2 > 0.85 for turbidity, color, TN, and TP) were established and validated in both the demonstration areas (Three Gorges and Poyang Lake), showing strong applicability across diverse water bodies.
- It addresses key limitations of traditional water-leaving reflectance methods, such as satellite dependence, limited ground applicability, and low-accuracy UAV approaches. It introduces a reliable UAV hyperspectral processing solution that enables accurate three-dimensional water monitoring.
- The constructed water quality parameter inversion models demonstrated high accuracy and verified the feasibility of air–ground integrated UAV monitoring, thereby addressing the research gap in non-linear conversion from hyperspectral to water-leaving reflectance and providing practical support for water quality assessment.
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Area and Data Collection
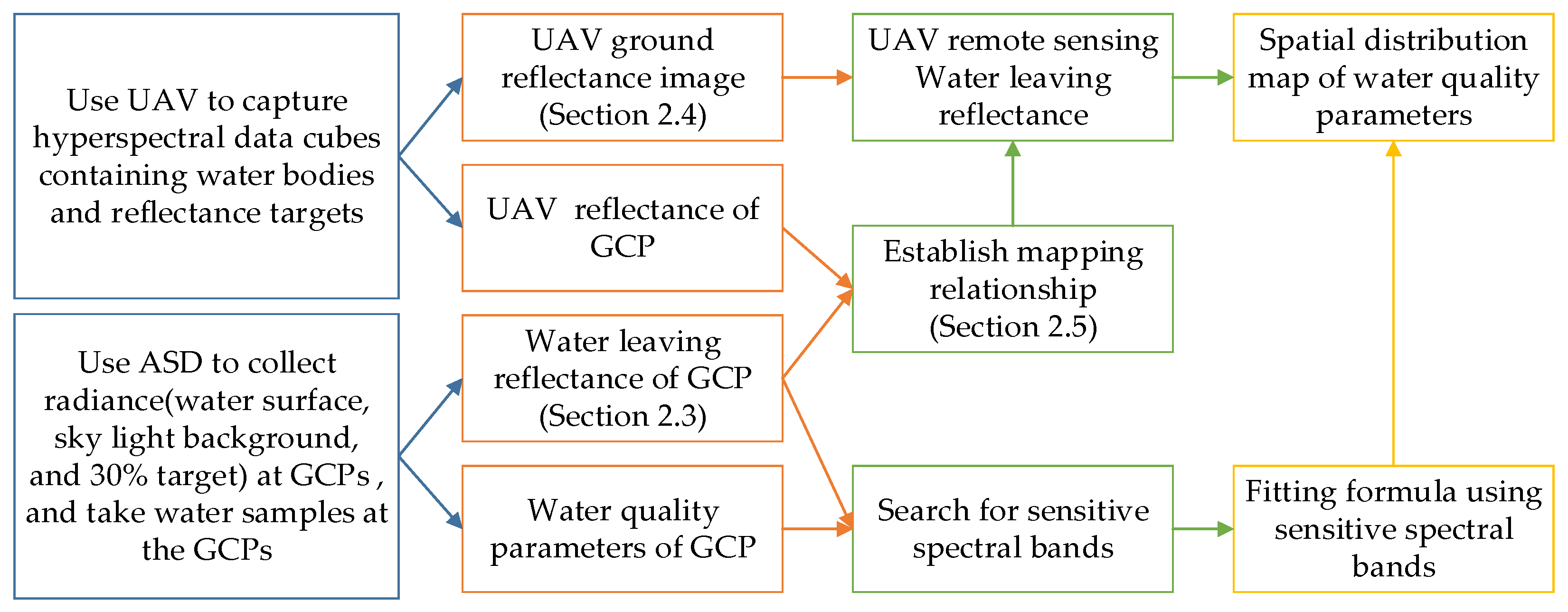
2.2. Air–Ground Collaborative UAV Hyperspectral Water Quality Monitoring Method
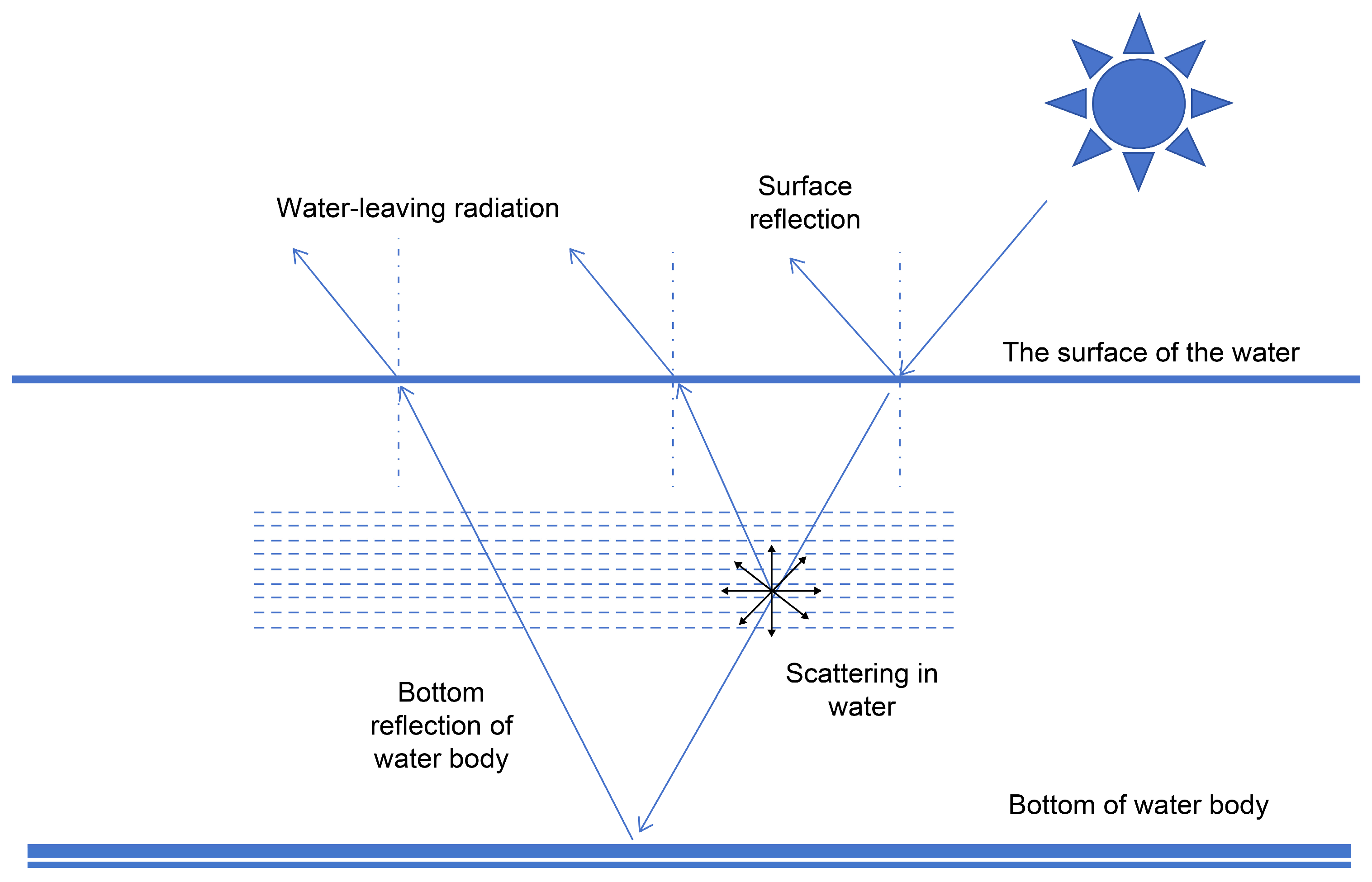
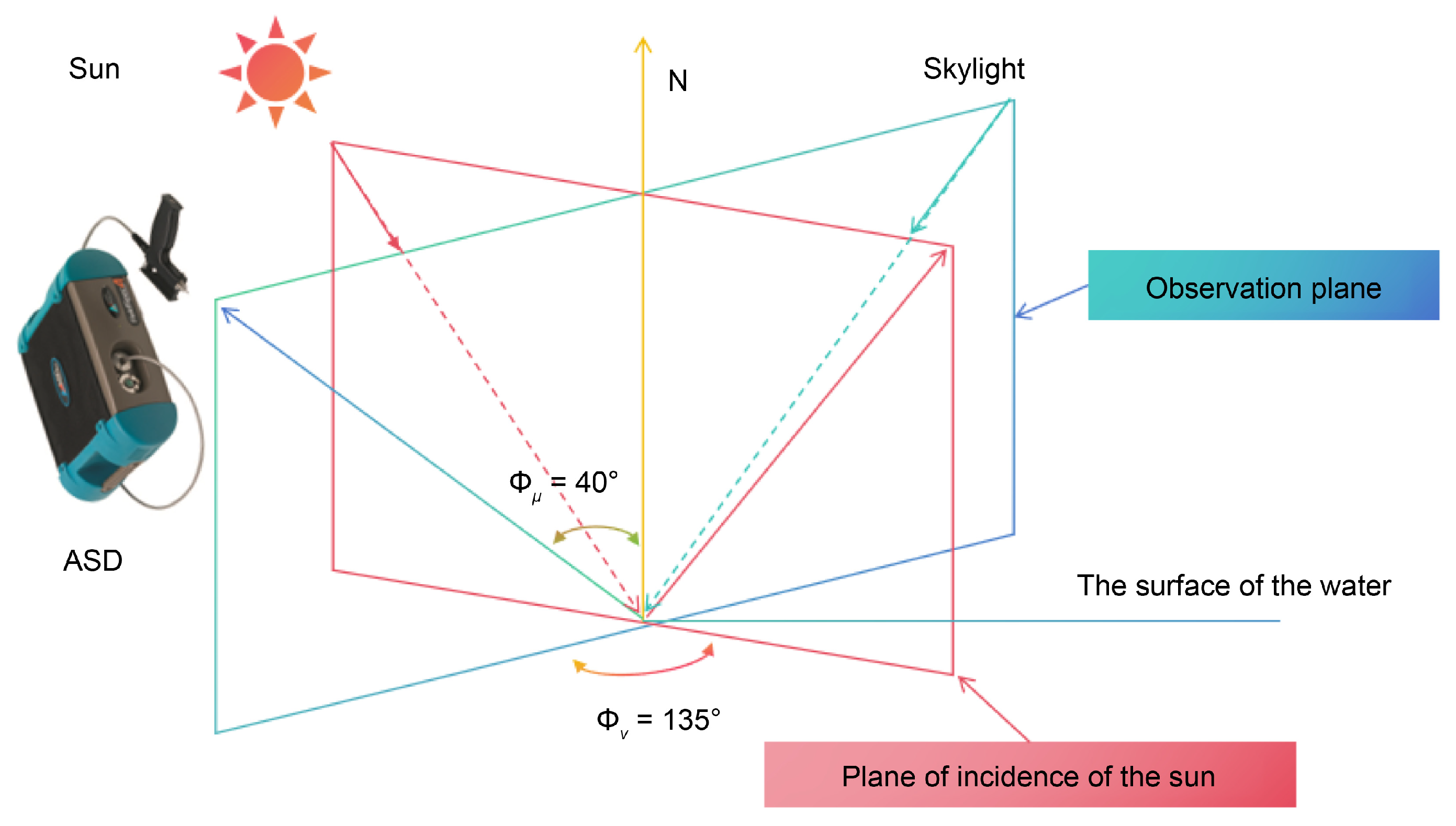
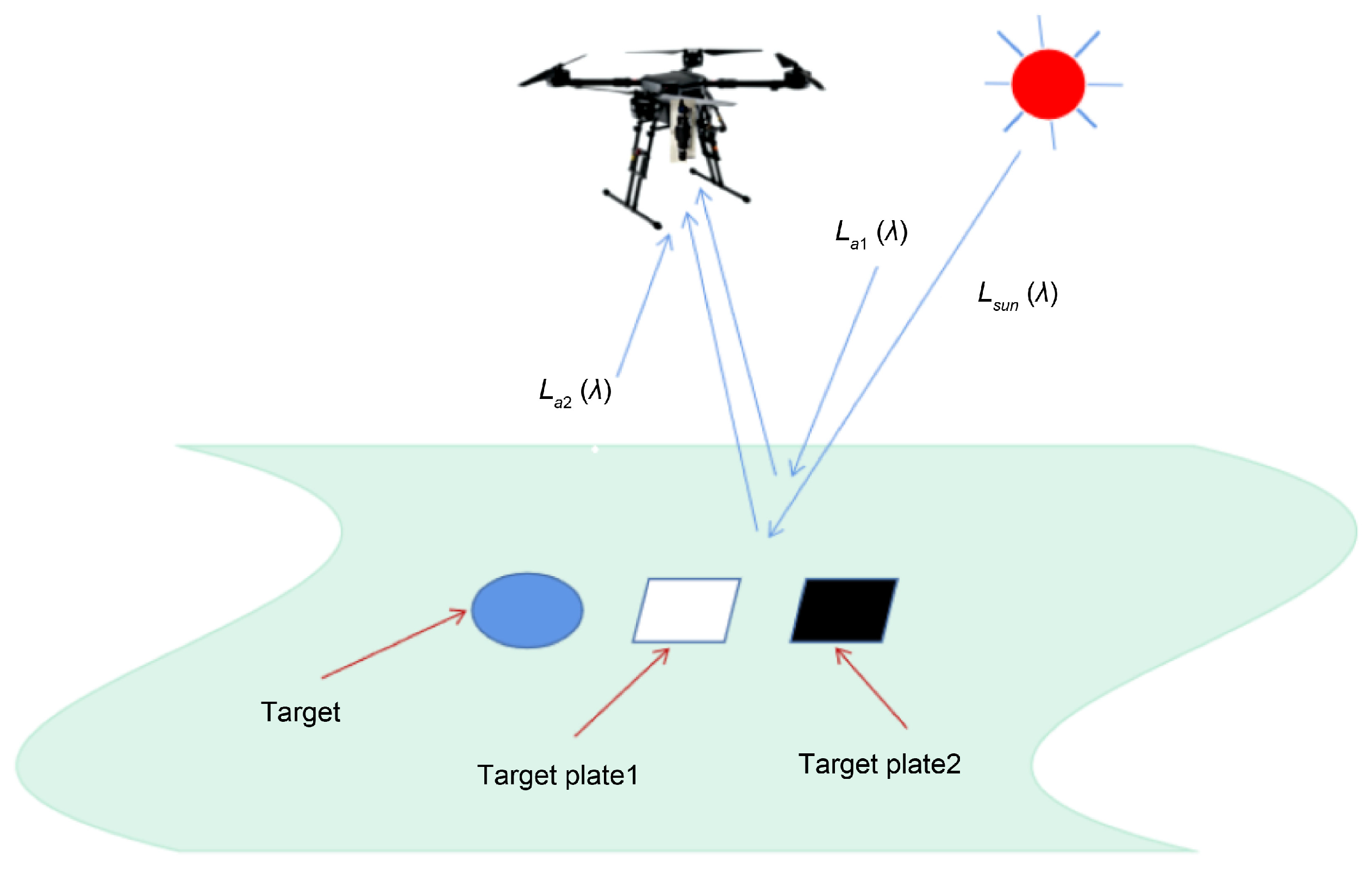
2.3. Method for Obtaining the Water-Leaving Reflectance of the Ground near the Water End
2.4. Method for Obtaining the Reflectance of Remote Sensing Objects via UAVs
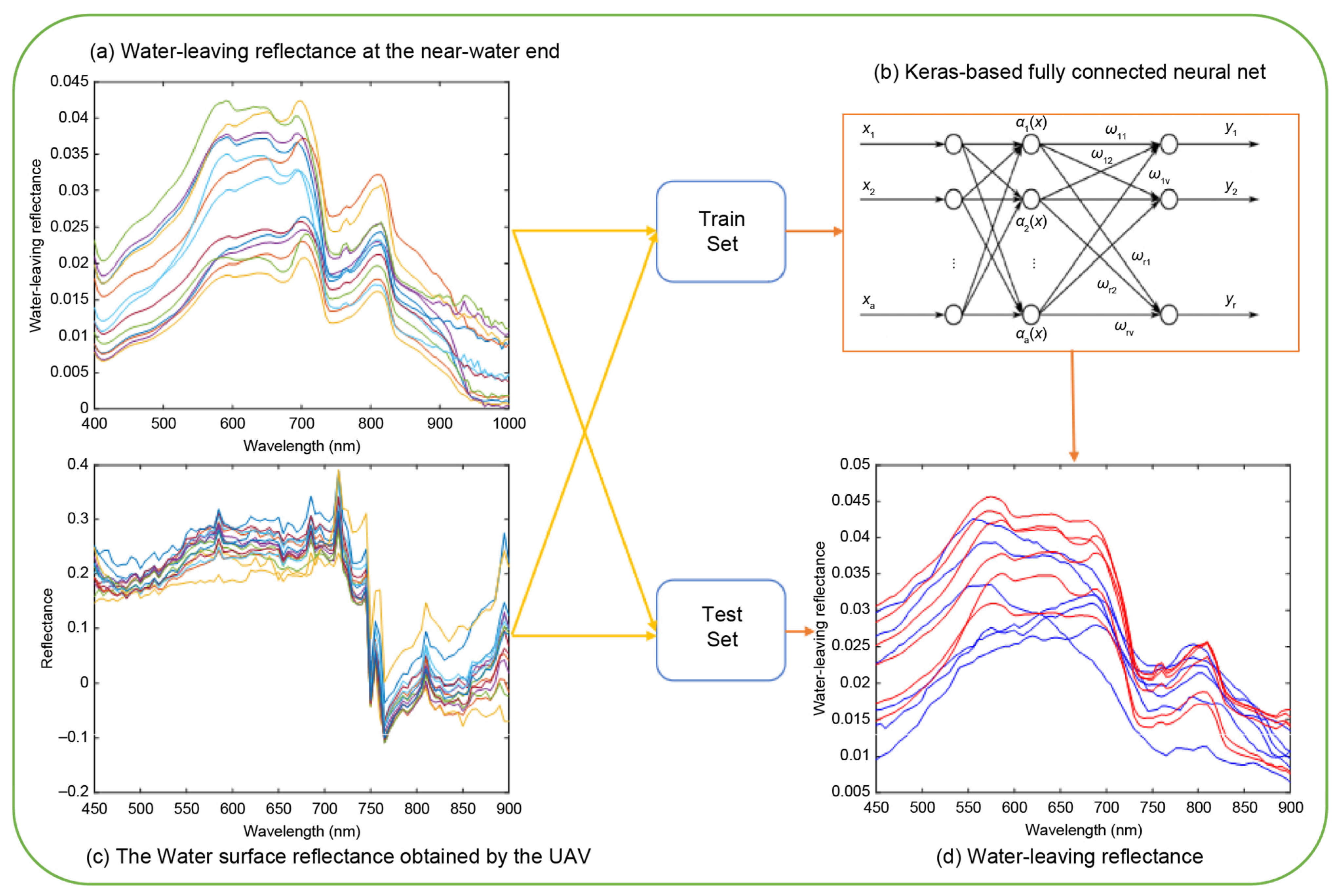
2.5. Conversion Method for UAV Hyperspectral Water-Leaving Reflectance Based on a Fully Connected Neural Network Model
2.6. Evaluation Indicators
- (1)
- Spectral angle mapping (SAM) [46]
- (2)
- Root mean squared error (RMSE) [47]
- (3)
- Residual prediction deviation (RPD) [48]
3. Results
3.1. Results of Obtaining Hyperspectral Water Reflectance from UAVs
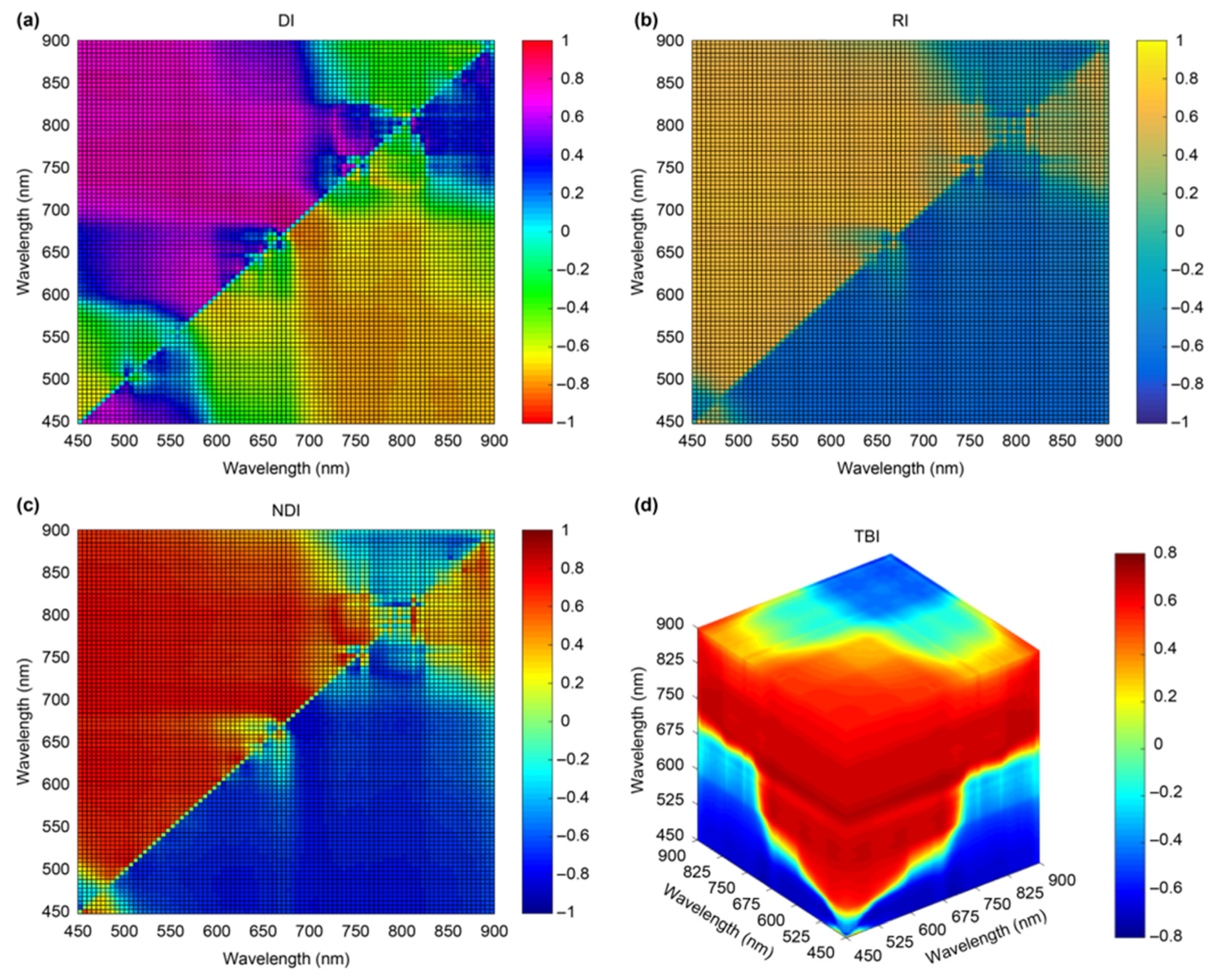
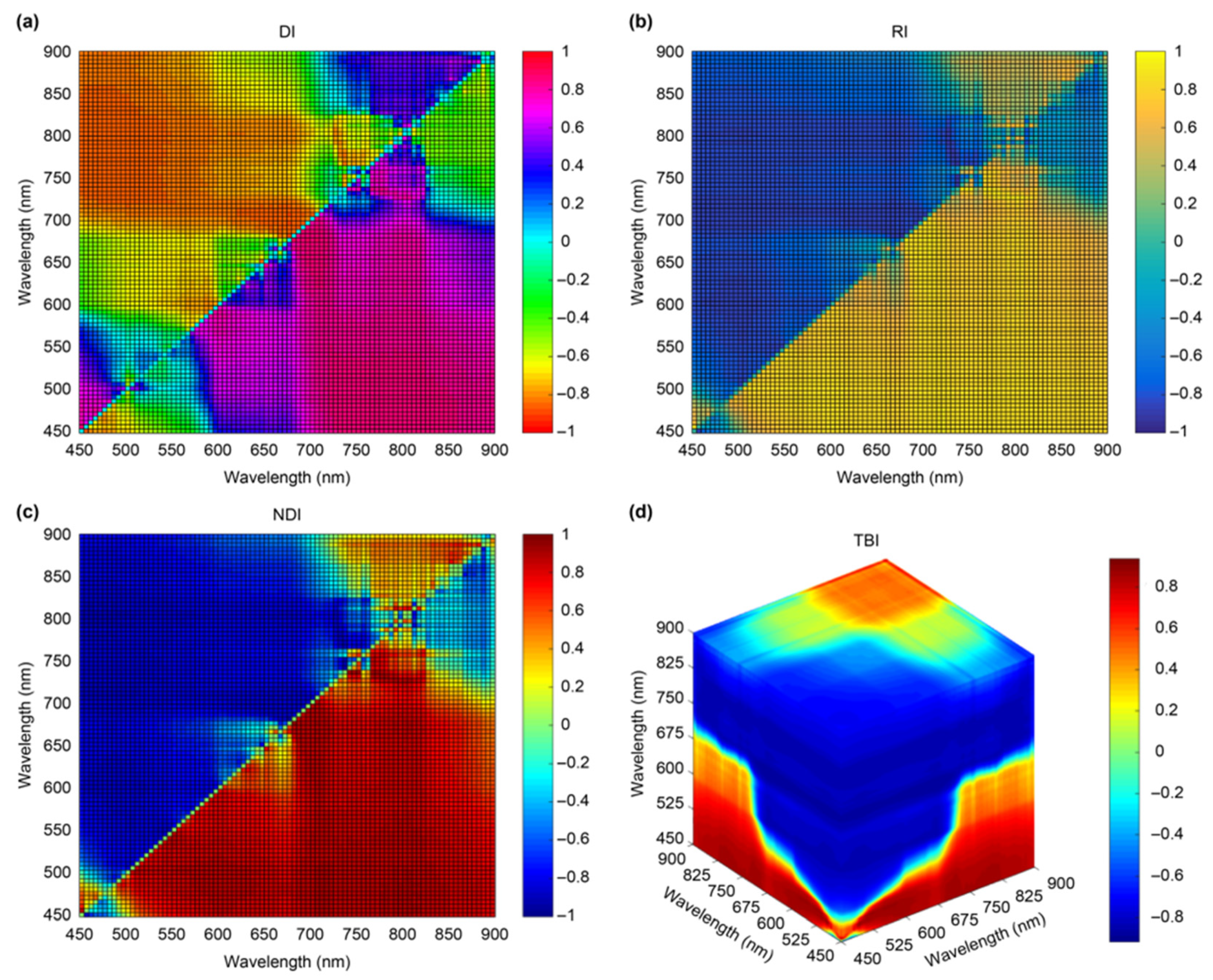
3.2. Acquisition of Results from Sensitive Spectral Bands for Water Quality Monitoring
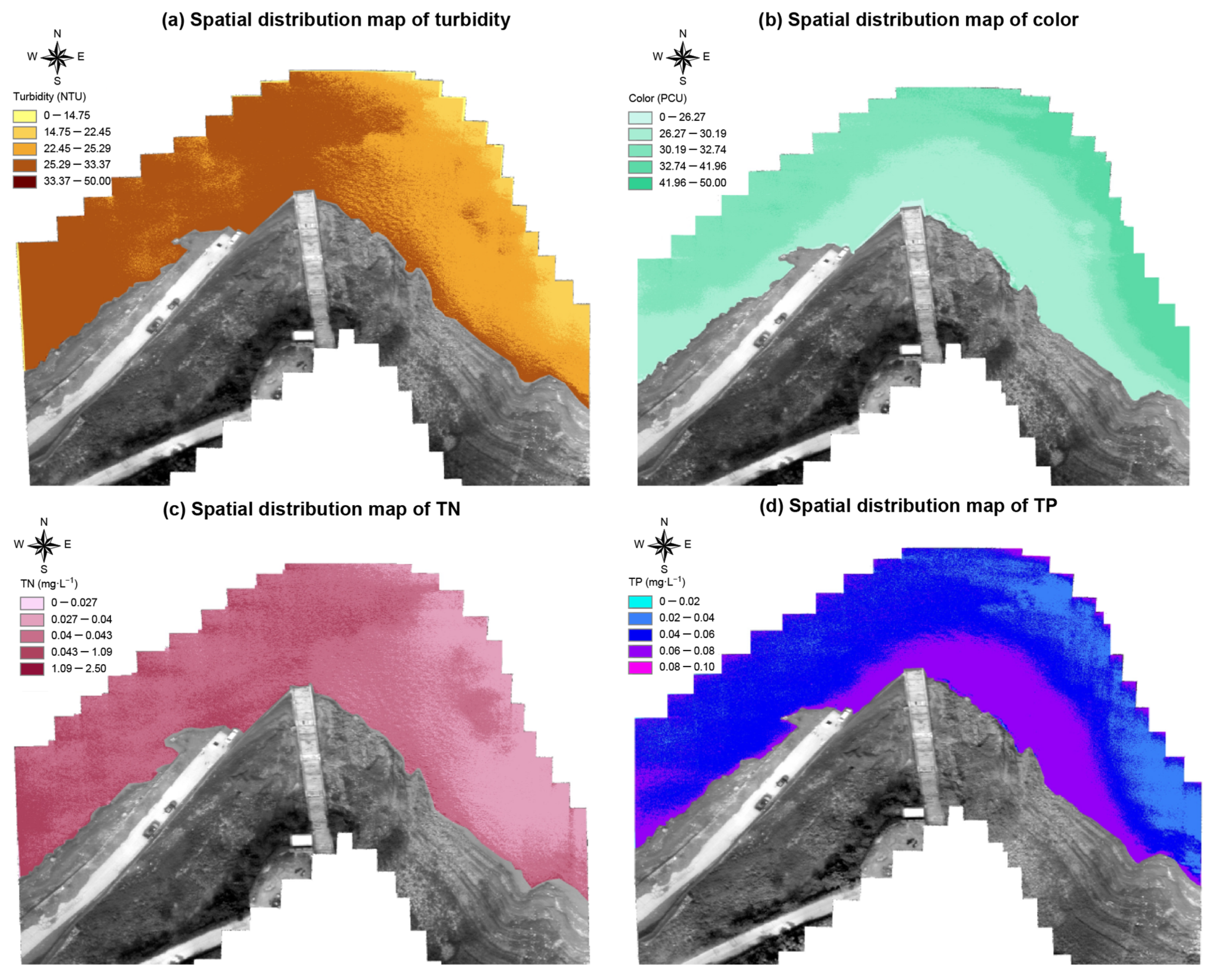
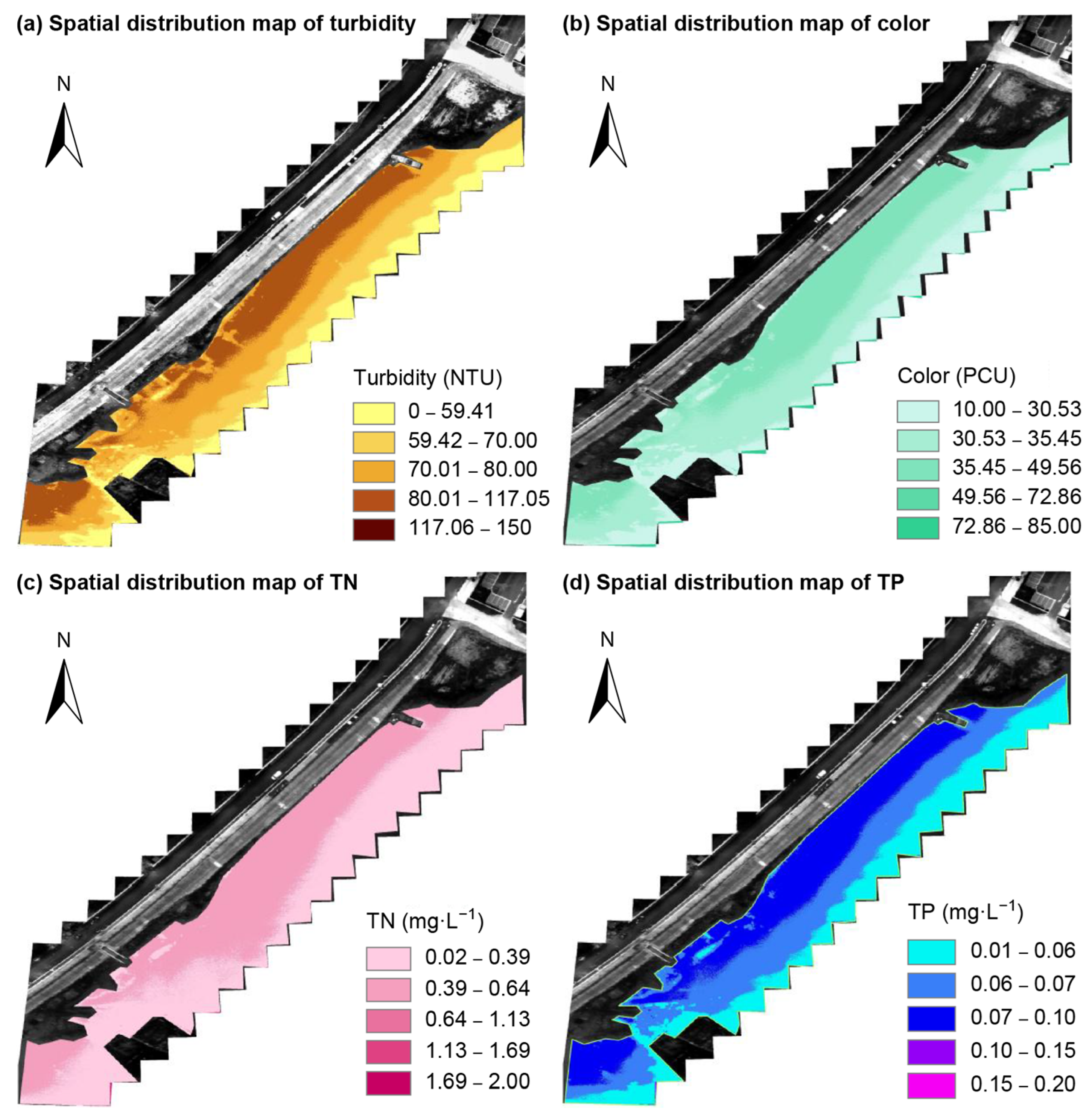
3.3. Water Quality Parameter Inversion Results
4. Discussion
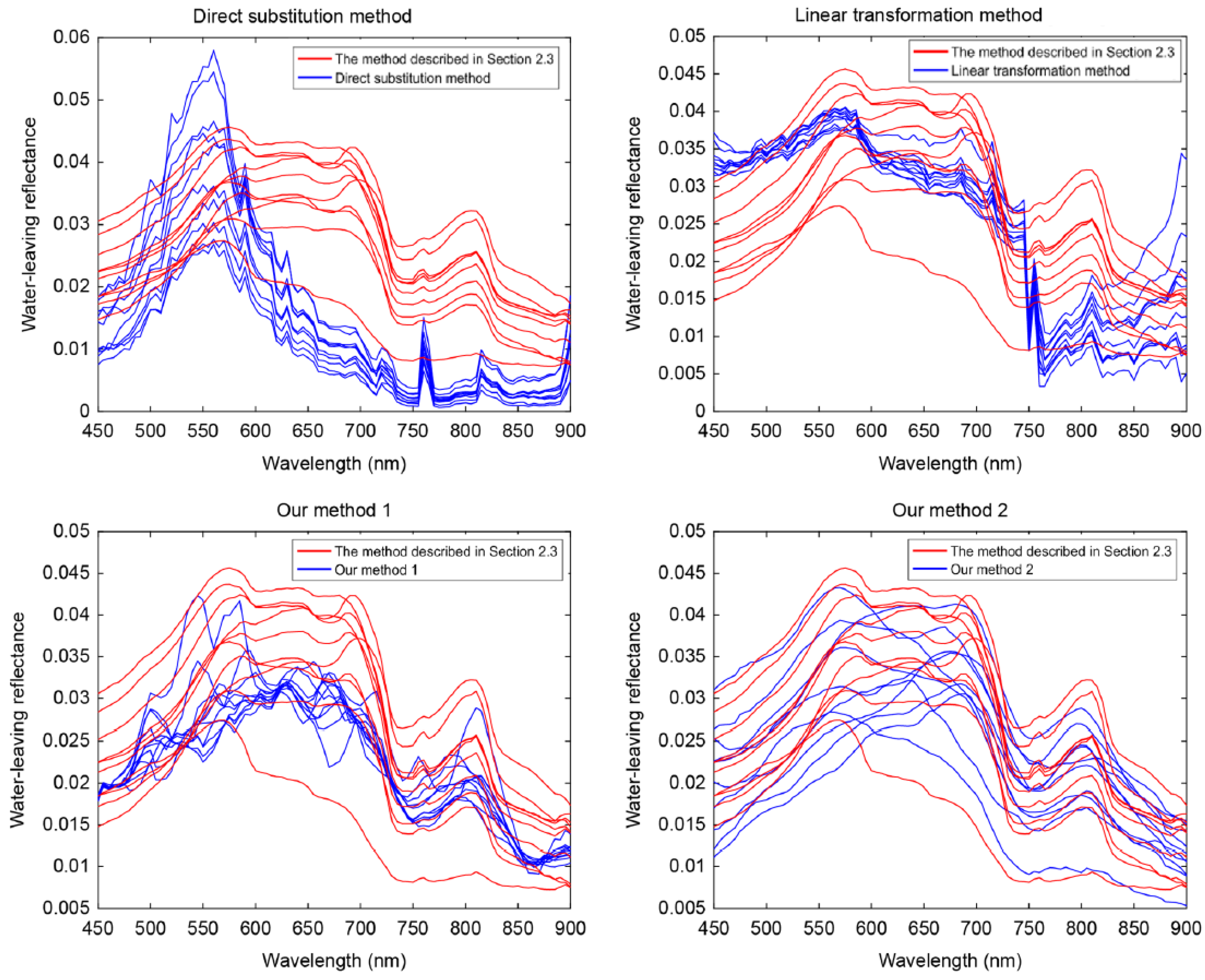
4.1. Methods for Obtaining the Water-Leaving Reflectance Curve
4.2. Concentration Inversion from Water Quality Parameters
4.3. Limitations of the Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AOTF | Acousto-Optic Tunable Filter |
| ASD | Analytical Spectral Device |
| C.V. | Coefficient of Variation |
| DI | Difference Index |
| DN | Digital Number |
| FCNN | Fully Connected Neural Network |
| GCP | Ground Control Point |
| NDI | Normalized Difference Index |
| NTU | Nephelometric Turbidity Units |
| PCU | Platinum-Cobalt Units (Color) |
| R2 | Coefficient of Determination |
| RI | Ratio Index |
| RMSE | Root Mean Squared Error |
| RPD | Residual Prediction Deviation |
| SAM | Spectral Angle Mapping |
| STD | Standard Deviation |
| SWIR | Shortwave Infrared |
| TN | Total Nitrogen |
| TP | Total Phosphorus |
| TBI | Triple-Band Index |
| UAV | Unmanned Aerial Vehicle |
References
- Wu, J.; Cao, Y.; Wu, S.; Parajuli, S.; Zhao, K.; Lee, J. Current capabilities and challenges of remote sensing in monitoring freshwater cyanobacterial blooms: A scoping review. Remote Sens. 2025, 17, 918. [Google Scholar] [CrossRef]
- Wasehun, E.T.; Beni, L.H.; Di Vittorio, C.A. UAV and satellite remote sensing for inland water quality assessments: A literature review. Environ. Monit. Assess. 2024, 196, 277. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Wang, J.; Chen, R.; Kang, Y.; Ding, Y.; Lv, Z.; Ding, D.; Feng, H. Research progress of inland river water quality monitoring technology based on unmanned aerial vehicle hyperspectral imaging technology. Environ. Res. 2024, 257, 119254. [Google Scholar] [CrossRef]
- Liang, Y.-H.; Deng, R.-R.; Liang, Y.-J.; Liu, Y.-M.; Wu, Y.; Yuan, Y.-H.; Ai, I.X.-J. Spectral characteristics of sediment reflectance under the background of heavy metal polluted water and analysis of its contribution to water-leaving reflectance. Spectrosc. Spect. Anal. 2024, 44, 111–117. [Google Scholar]
- Guo, X.; Liu, H.; Zhong, P.; Hu, Z.; Cao, Z.; Shen, M.; Tan, Z.; Liu, W.; Liu, C.; Li, D.; et al. Remote retrieval of dissolved organic carbon in rivers using a hyperspectral drone system. Int. J. Digit. Earth 2024, 17, 2358863. [Google Scholar] [CrossRef]
- Jung, S.H.; Kwon, S.; Seo, I.W.; Kim, J.S. Comparison between hyperspectral and multispectral retrievals of suspended sediment concentration in rivers. Water 2024, 16, 1275. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, A.; Lyu, R.; Xue, X.; Zhang, Y.; Pang, J. Assessing river water quality using different remote sensing technologies. J. Irrig. Drain. 2023, 42, 121–130. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Measurement of total dissolved solids and total suspended solids in water systems: A review of the issues, conventional, and remote sensing techniques. Remote Sens. 2023, 15, 3534. [Google Scholar] [CrossRef]
- Kieu, H.T.; Pak, H.Y.; Trinh, H.L.; Pang, D.S.C.; Khoo, E.; Law, A.W.-K. UAV-based remote sensing of turbidity in coastal environment for regulatory monitoring and assessment. Mar. Pollut. Bul. 2023, 196, 115482. [Google Scholar] [CrossRef]
- Ma, Q.; Li, S.; Qi, H.; Yang, X.; Liu, M. Rapid prediction and inversion of pond aquaculture water quality based on hyperspectral imaging by unmanned aerial vehicles. Water 2025, 17, 40517. [Google Scholar] [CrossRef]
- Trinh, H.L.; Kieu, H.T.; Pak, H.Y.; Pang, D.S.C.; Tham, W.W.; Khoo, E.; Law, A.W.-K. A comparative study of multi-rotor unmanned aerial vehicles (UAVs) with spectral sensors for real-time turbidity monitoring in the coastal environment. Sensors 2024, 8, 52. [Google Scholar] [CrossRef]
- Zeng, H.; He, X.; Bai, Y.; Gong, F.; Wang, D.; Zhang, X. Design and construction of UAV-based measurement system for water hyperspectral remote-sensing reflectance. Sensors 2025, 25, 2879. [Google Scholar] [CrossRef]
- Wei, J.; Wang, M.; Lee, Z.; Ondrusek, M.; Zhang, S.; Ladner, S. Experimental analysis of the measurement precision of spectral water-leaving radiance in different water types. Opt. Express 2021, 29, 2780–2797. [Google Scholar] [CrossRef]
- Wang, S.; Shen, F.; Li, R.; Li, P. Research on water surface glint removal and information reconstruction methods for unmanned aerial vehicle hyperspectral images. J. East. China Norm. Univ. Nat. Sci. 2024, 2024, 36–49. [Google Scholar]
- Yang, X.; Huang, H.; Liu, Y.; Yan, L. Direction characteristic of radiation energy and transmission characteristic of waters at water-air surface. Geomat. Inf. Sci. Wuhan. Univ. 2013, 38, 1003–1008. [Google Scholar]
- Su, X.; Cui, J.; Zhang, J.; Guo, J.; Xu, M.; Gao, W. “Ground-Aerial-Satellite” atmospheric correction method based on UAV hyperspectral data for coastal waters. Remote Sens. 2025, 17, 2768. [Google Scholar] [CrossRef]
- Zhong, P.; Guo, X.; Jiang, X.; Zhai, Y.; Duan, H. Study on the effect of sky scattered light on the reflectance of UAV hyperspectral about remote sensing of water color. Remote Sens. Technol. Appl. 2024, 39, 1128–1140. [Google Scholar]
- He, X.; Pan, T.; Bai, Y.; Shanmugam, P.; Wang, D.; Li, T.; Gong, F. Intelligent atmospheric correction algorithm for polarization ocean color satellite measurements over the open ocean. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4201322. [Google Scholar] [CrossRef]
- Kim, M.; Danielson, J.; Storlazzi, C.; Park, S. Physics-based satellite-derived bathymetry (SDB) using Landsat OLI images. Remote Sens. 2024, 16, 843. [Google Scholar] [CrossRef]
- Rodrigues, G.; Potes, M.; Costa, M.J. Assessment of water surface reflectance and optical water types over two decades in Europe’s largest artificial lake: An intercomparison of ESA and NASA satellite data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 2942–2958. [Google Scholar] [CrossRef]
- Gao, B.-C.; Li, R.-R. A multi-band atmospheric correction algorithm for deriving water leaving reflectances over turbid waters from VIIRS data. Remote Sens. 2023, 15, 425. [Google Scholar] [CrossRef]
- Liu, X.; Warren, M.; Selmes, N.; Simis, S.G.H. Quantifying decadal stability of lake reflectance and chlorophyll-a from medium-resolution ocean color sensors. Remote Sens. Environ. 2024, 306, 114120. [Google Scholar] [CrossRef]
- Luo, Y.; Zhong, X.; Fu, D.; Yan, L.; Zhang, Y.; Liu, Y.; Huang, H.; Zhang, Z.; Qi, Y.; Wang, Q. Evaluation of applicability of Sentinel-2-MSI and Sentinel-3- OLCI water-leaving reflectance products in Yellow River Estuary. J. Atmos. Environ. Opt. 2023, 18, 585–601. [Google Scholar] [CrossRef]
- Bernstein, L.S.; Adler-Golden, S.M.; Sundberg, R.L.; Levine, R.Y.; Perkins, T.C.; Berk, A.; Ratkowski, A.J.; Felde, G.; Hoke, M.L. A new method for atmospheric correction and aerosol optical property retrieval for VIS-SWIR multi- and hyperspectral imaging sensors: QUAC (QUick Atmospheric Correction). In Proceedings of the 25th IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2005), Seoul, Republic of Korea, 25–29 July 2005; pp. 3549–3552. [Google Scholar]
- Feng, C.; Fang, C.; Yuan, G.; Wu, J.; Wang, Q.; Dong, C. Water pollution monitoring based on unmanned aerial vehicle (UAV) hyperspectral and BP neural network. Chin. J. Environ. Eng. 2023, 17, 3996–4006. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, J.; He, X.; Cao, H.; Zhao, K. Comparison and accuracy evaluation of UAV hyperspectral atmospheric and radiometric correction methods. Geomat. Spat. Inf. Technol. 2022, 45, 98–104. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J.; Jing, Y.; Zhang, S.; Sun, D.; Li, Q. ESA-MDN: An ensemble self-attention enhanced mixture density framework for UAV multispectral water quality parameter retrieval. Remote Sens. 2025, 17, 3202. [Google Scholar] [CrossRef]
- Bai, R.; He, X.; Ye, X.; Li, H.; Bai, Y.; Ma, C.; Song, Q.; Jin, X.; Zhang, X.; Gong, F. Development of the operational atmospheric correction algorithm for the COCTS2 onboard the Chinese new-generation ocean color satellite. Opt. Express 2025, 33, 38029–38053. [Google Scholar] [CrossRef]
- Zang, C.S.F.; Yang, Z. Aquatic environmental monitoring of inland waters based on UAV hyperspectral remote sensing. Nat. Resour. Remote Sens. 2021, 33, 45–53. [Google Scholar] [CrossRef]
- De Keukelaere, L.; Moelans, R.; Knaeps, E.; Sterckx, S.; Reusen, I.; De Munck, D.; Simis, S.G.H.; Constantinescu, A.M.; Scrieciu, A.; Katsouras, G.; et al. Airborne drones for water quality mapping in inland, transitional and coastal Waters—MapEO water data processing and validation. Remote Sens. 2023, 15, 1345. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Zhong, Y.; Wang, Z.; Hu, X.; Lin, L. Inland waters suspended solids concentration retrieval based on PSO-LSSVM for UAV-borne hyperspectral remote sensing imagery. Remote Sens. 2019, 11, 1455. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Wang, Z.; Wang, Z.; Zhou, X.; Cao, L. Monitoring of urban black-odor water based on Nemerow index and gradient boosting decision tree regression using UAV-borne hyperspectral imagery. Remote Sens. 2019, 11, 2402. [Google Scholar] [CrossRef]
- Shanmugam, V.; Shanmugam, P. Retrieval of water-leaving radiance from UAS-based hyperspectral remote sensing data in coastal waters. Int. J. Remote Sens. 2025, 46, 4883–4915. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, P.; Guan, H.; Zhao, Y. A mobile triaxial stabilized ship-borne radiometric system for in situ measurements: Case study of Sentinel-3 OLCI validation in highly turbid waters. Remote Sens. 2025, 17, 1223. [Google Scholar] [CrossRef]
- Coqué, A.; Morin, G.; Peroux, T.; Martinez, J.-M.; Tormos, T. Lake SkyWater—A portable buoy for measuring water-leaving radiance in lakes under optimal geometric conditions. Sensors 2025, 25, 1525. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, Y.; Wang, K.; Zhang, Y.; Wang, Z.; Liu, X.; Yan, S.; Ye, X. Design and Characterization of a portable multiprobe high-resolution system (PMHRS) for enhanced inversion of water remote sensing reflectance with surface glint removal. Sensors 2024, 11, 837. [Google Scholar] [CrossRef]
- Hong, L.; Tao, Y.; Bingliang, H.; Xingsong, H.; Zhoufeng, Z.; Xiao, L.; Jiacheng, L.; Xueji, W.; Jingjing, Z.; Zhengxuan, T.; et al. UAV-borne hyperspectral imaging remote sensing system based on acousto-optic tunable filter for water quality monitoring. Remote Sens. 2021, 13, 204069. [Google Scholar] [CrossRef]
- Calpe-Maravilla, J.; Vila-Frances, J.; Ribes-Gomez, E.; Duran-Bosch, V.; Munoz-Mari, J.; Amoros-Lopez, J.; Gomez-Chova, L.; Tajahuerce-Romera, E. 400-to 1000-nm imaging spectrometer based on acousto-optic tunable filters. J. Electron. Imaging 2006, 15, 023001. [Google Scholar] [CrossRef]
- Liu, H.; Hou, X.; Hu, B.; Yu, T.; Zhang, Z.; Liu, X.; Liu, J.; Wang, X.; Zhong, J.; Tan, Z. Image blurring and spectral drift in imaging spectrometer system with an acousto-optic tunable filter and its application in UAV remote sensing. Int. J. Remote Sens. 2022, 43, 6957–6978. [Google Scholar] [CrossRef]
- Dji. Available online: https://www.dji.com/cn (accessed on 6 February 2025).
- Ronin-MX. Available online: https://store.dji.com/cn/product/ronin-mx (accessed on 6 February 2024).
- Zhang, H.; Zhang, B.; Wei, Z.; Wang, C.; Huang, Q. Lightweight integrated solution for a UAV-borne hyperspectral imaging system. Remote Sens. 2020, 12, 657. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Y.; Jiang, Y.; Cao, Y.; Zhou, J.; Dong, H.; Liu, X.; Wang, Z.; Ye, X. Kohler-polarization sensor for glint removal in water-leaving radiance measurement. Water 2025, 17, 1977. [Google Scholar] [CrossRef]
- Tang, J.; Tian, G.; Wang, X.; Wang, X.; Song, Q. The methods of water spectra measurement and analysis I: Above-water method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Mo, Y.; Kang, X.; Duan, P.; Li, S. A robust UAV hyperspectral image stitching method based on deep feature matching. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5517514. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Feng, S.; Zhao, Z.; Wang, M.; Sun, C.; Song, N.; Yang, J. Study on parameter inversion model construction and evaluation method of UAV hyperspectral urban inland water pollution dynamic monitoring. Remote Sens. 2023, 15, 4131. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Liu, S.-B.; Zhu, J.-W.; Ma, T.-T. Inversion of chemical oxygen demand in surface water based on hyperspectral data. Spectrosc. Spectr. Anal. 2024, 44, 997–1004. [Google Scholar] [CrossRef]
- Xu, X.; Chen, Y.; Wang, M.; Wang, S.; Li, K.; Li, Y. Improving estimates of soil salt content by using two-date image spectral changes in Yinbei, China. Remote Sen. 2021, 13, 4165. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Z.; Liu, Y.; Yang, Y.; Zhou, W.; Yang, Z.; Li, C. A general multilayer analytical radiative transfer-based model for reflectance over shallow water. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4205320. [Google Scholar] [CrossRef]
- Syariz, M.A.; Lin, B.-Y.; Denaro, L.G.; Jaelani, L.M.; Math Van, N.; Lin, C.-H. Spectral-consistent relative radiometric normalization for multitemporal Landsat 8 imagery. ISPRS J. Photogramm. Remote Sens. 2019, 147, 56–64. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Deng, L.; Ouyang, B. Retrieval of water quality parameters from hyperspectral images using a hybrid feedback deep factorization machine model. Water Res. 2021, 204, 117618. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, L.; Huang, J.; Chi, D.; Devlin, A.T.; Wu, H. Seasonal dynamics of chromophoric dissolved organic matter in Poyang Lake, the largest freshwater lake in China. J. Hydrol. 2022, 605, 127298. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, F.; Ge, X.; Zhang, X.; Chan, N.W.; Qi, Y. Measurement of Total Nitrogen Concentration in Surface Water Using Hyperspectral Band Observation Method. Water 2020, 12, 1842. [Google Scholar] [CrossRef]
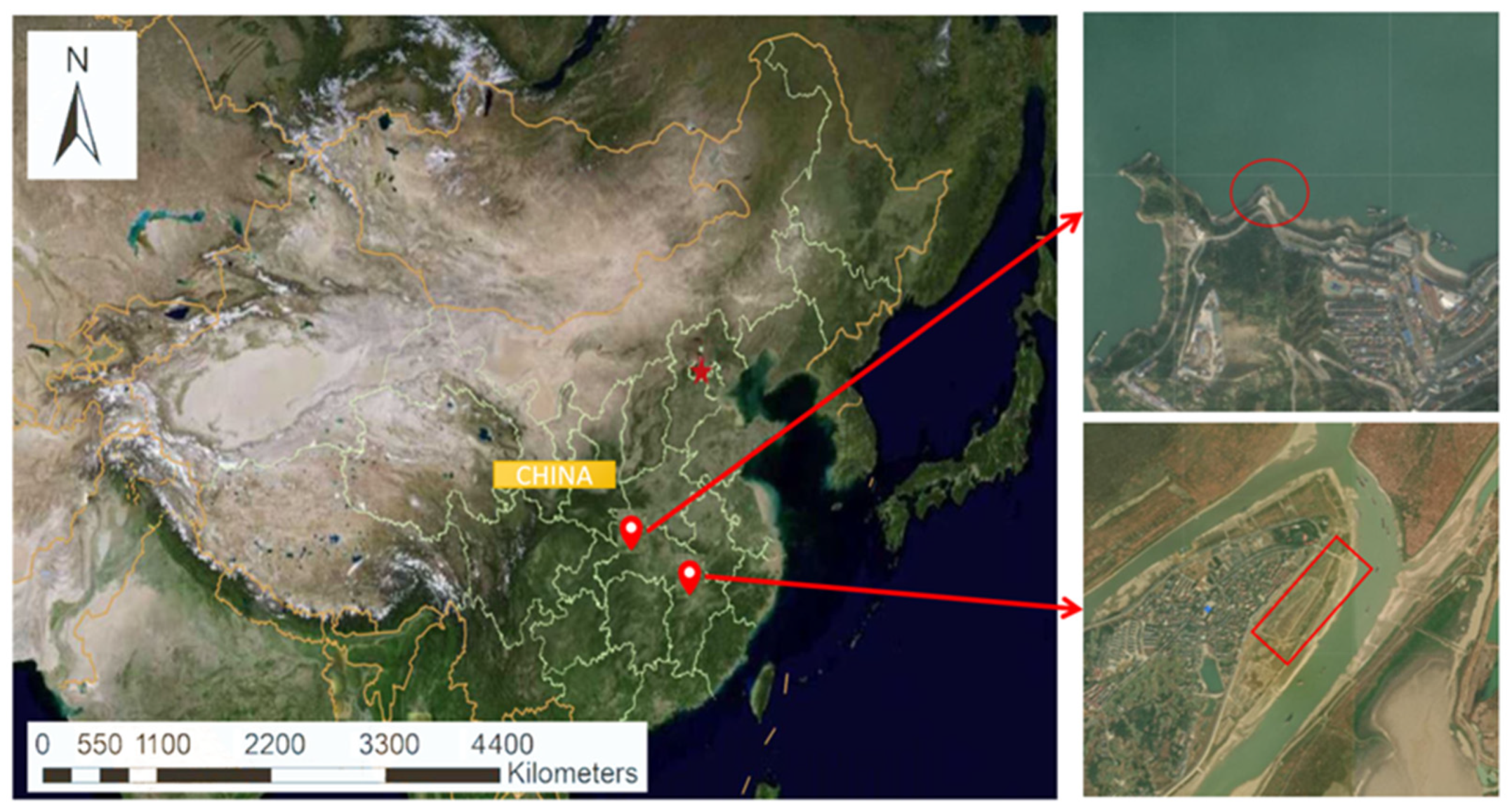



| Technical Parameters | Details | Technical Parameters | Details |
|---|---|---|---|
| Spectral range | 400–1000 nm | Flight time | ≤30 min |
| Spectral resolution | 8 nm @ 625 nm | Flight speed | ≤50 km/h |
| Focal length | 12 mm | Flight altitude | ≤500 m |
| Aperture | F2.8–F16.0 | Data capacity | 200 GB |
| Pixel size | 4.8 × 4.8 µm | Mounting weight | ≤7.5 kg |
| Resolution | 600 × 2048 | Transmission distance | ≤3.5 km |
| Direct Substitution Method [29,30] | Linear Transformation Method [31,32] | Our Method 1 | Our Method 2 | |
|---|---|---|---|---|
| 1 | 0.5006 | 0.1976 | 0.0741 | 0.0444 |
| 2 | 0.3308 | 0.1567 | 0.2213 | 0.0915 |
| 3 | 0.5134 | 0.2581 | 0.1066 | 0.1175 |
| 4 | 0.5177 | 0.2526 | 0.0953 | 0.0841 |
| 5 | 0.5268 | 0.1529 | 0.1330 | 0.0716 |
| 6 | 0.7336 | 0.4582 | 0.1597 | 0.0644 |
| 7 | 0.6072 | 0.2847 | 0.1060 | 0.0361 |
| 8 | 0.5532 | 0.2899 | 0.1085 | 0.1379 |
| 9 | 0.5740 | 0.2452 | 0.0955 | 0.1768 |
| 10 | 0.5753 | 0.3029 | 0.1816 | 0.2453 |
| Mean | 0.5433 | 0.2599 | 0.1282 | 0.1070 |
| Water Quality Parameters | Modeling Method | Independent Variables | Mathematical Model | Train Set | Test Set | RMSE | RPD |
|---|---|---|---|---|---|---|---|
| R2 | R2 | ||||||
| Turbidity | DI | b787 − b774 | y = −4237.43x − 67.00 | 0.38 | 0.44 | 18.89 | 1.47 |
| RI | b768/b774 | y = −120.30x + 161.96 | 0.97 | 0.92 | 6.84 | 4.07 | |
| NDI | (b768 − b774)/(b768 + b774) | y = −239.74x + 37.26 | 0.97 | 0.94 | 6.52 | 4.26 | |
| TBI | (b768/b774) − (b768/b758) | y = 106.23x − 213.71 | 0.95 | 0.92 | 6.76 | 4.11 |
| Water Quality Parameters | Modeling Method | Independent Variables | Mathematical Model | Train Set | Test Set | RMSE | RPD |
|---|---|---|---|---|---|---|---|
| R2 | R2 | ||||||
| Color | DI | b613 − b623 | y = 11254.15x + 51.31 | 0.93 | 0.93 | 32.21 | 4.30 |
| RI | b683/b718 | y = 655.70x − 589.21 | 0.97 | 0.86 | 47.05 | 2.94 | |
| NDI | (b683 − b713)/(b683 + b713) | y = 1565.60x + 69.06 | 0.97 | 0.87 | 44.41 | 3.12 | |
| TBI | (b819/b774) − (b819/b840) | y =−549.65x + 1316.47 | 0.69 | 0.53 | 86.43 | 1.60 |
| Water Quality Parameters | Modeling Method | Independent Variables | Mathematical Model | Train Set | Test Set | RMSE | RPD |
|---|---|---|---|---|---|---|---|
| R2 | R2 | ||||||
| Total nitrogen | DI | b844 − b855 | y = −76.66x + 2.15 | 0.69 | 0.49 | 0.433 | 1.22 |
| RI | b517/b548 | y = 2.62x − 0.07 | 0.87 | 0.77 | 0.27 | 1.91 | |
| NDI | (b517 − b548)/(b517 + b548) | y = 4.31x + 2.53 | 0.85 | 0.81 | 0.28 | 1.86 | |
| TBI | (b661/b639) − (b661/b548) | y = 1.46x − 0.20 | 0.86 | 0.88 | 0.26 | 2.06 |
| Water Quality Parameters | Modeling Method | Independent Variables | Mathematical Model | Train Set | Test Set | RMSE | RPD |
|---|---|---|---|---|---|---|---|
| R2 | R2 | ||||||
| Total phosphorus | DI | b819 − b824 | y = 4.03x + 0.12 | 0.75 | 0.82 | 0.02 | 2.61 |
| RI | b542/b527 | y = 0.32x − 0.27 | 0.78 | 0.85 | 0.02 | 2.71 | |
| NDI | (b542 − b527)/(b542 + b527) | y = 0.71x + 0.05 | 0.78 | 0.81 | 0.02 | 2.50 | |
| TBI | (b558/b588) − (b558/b527) | y = 0.16x − 0.23 | 0.69 | 0.53 | 0.03 | 1.60 |
| Water Quality Parameters | Turbidity/ (NTU) | Color/ (PCU) | TN/ (mg·L−1) | TP/ (mg·L−1) |
|---|---|---|---|---|
| Minimum | 1.41 | 8.85 | 0.49 | 0.01 |
| Maximum | 41.40 | 48.66 | 2.17 | 0.07 |
| Mean | 7.28 | 23.61 | 1.81 | 0.05 |
| STD | 6.68 | 10.64 | 0.32 | 0.01 |
| C.V. | 0.92 | 0.45 | 0.18 | 0.29 |
| Water Quality Parameters | Turbidity/ (NTU) | Color/ (PCU) | TN/ (mg·L−1) | TP/ (mg·L−1) |
|---|---|---|---|---|
| Minimum | 5.69 | 30.96 | 0.70 | 0.05 |
| Maximum | 144.00 | 79.63 | 1.81 | 0.15 |
| Mean | 44.15 | 53.31 | 1.31 | 0.07 |
| STD | 27.28 | 11.70 | 0.24 | 0.02 |
| C.V. | 0.62 | 0.22 | 0.19 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Hou, X.; Hu, B.; Yu, T.; Zhang, Z.; Liu, X.; Wang, X.; Tan, Z. Method for Obtaining Water-Leaving Reflectance from Unmanned Aerial Vehicle Hyperspectral Remote Sensing Based on Air–Ground Collaborative Calibration for Water Quality Monitoring. Remote Sens. 2025, 17, 3413. https://doi.org/10.3390/rs17203413
Liu H, Hou X, Hu B, Yu T, Zhang Z, Liu X, Wang X, Tan Z. Method for Obtaining Water-Leaving Reflectance from Unmanned Aerial Vehicle Hyperspectral Remote Sensing Based on Air–Ground Collaborative Calibration for Water Quality Monitoring. Remote Sensing. 2025; 17(20):3413. https://doi.org/10.3390/rs17203413
Chicago/Turabian StyleLiu, Hong, Xingsong Hou, Bingliang Hu, Tao Yu, Zhoufeng Zhang, Xiao Liu, Xueji Wang, and Zhengxuan Tan. 2025. "Method for Obtaining Water-Leaving Reflectance from Unmanned Aerial Vehicle Hyperspectral Remote Sensing Based on Air–Ground Collaborative Calibration for Water Quality Monitoring" Remote Sensing 17, no. 20: 3413. https://doi.org/10.3390/rs17203413
APA StyleLiu, H., Hou, X., Hu, B., Yu, T., Zhang, Z., Liu, X., Wang, X., & Tan, Z. (2025). Method for Obtaining Water-Leaving Reflectance from Unmanned Aerial Vehicle Hyperspectral Remote Sensing Based on Air–Ground Collaborative Calibration for Water Quality Monitoring. Remote Sensing, 17(20), 3413. https://doi.org/10.3390/rs17203413






