2.2. Relative Gravity Measurements
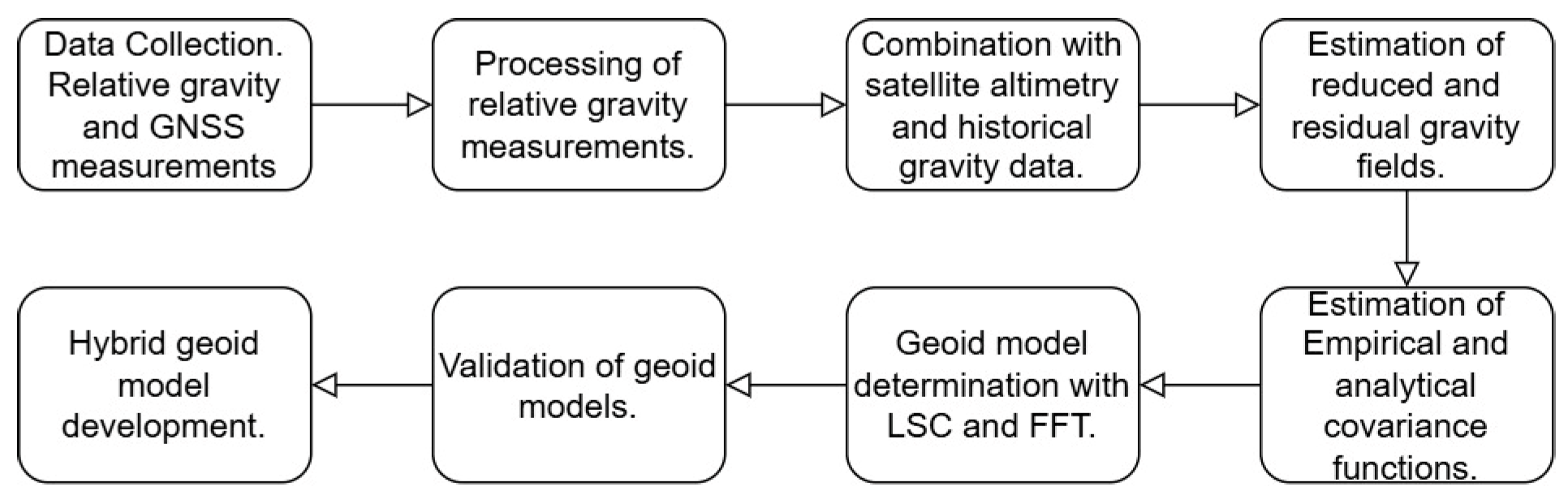
The development of the regional gravimetric geoid model for Central Macedonia involved the integration of extensive databases, including gravity measurements and GNSS observations, aiming to gather new data close to CORS and fill in places where the current land free-air gravity anomaly database of the Laboratory of Gravity Field Research and Applications (GravLab) has gaps, voids, and data of lower quality [
8,
10,
11,
12]. This database mainly consists of historical gravity data for Greece and surrounding countries, shipborne gravity data, and terrestrial gravity data collected by GravLab in the frame of various research projects [
16,
17,
18,
19]. The necessary pre-processing steps regarding the gravity data evaluation and validation in terms of their consistency with the used geodetic reference system, tide system, and gravity reference system have been performed so as to form a consistent and homogeneous dataset [
10,
12]. All the available land and marine gravity data were validated and cleaned by removing blunders and erroneous observations employing a least squares collocation (LSC) [
20] approach within a remove–compute–restore (RCR) procedure [
21]. This pre-processing analysis resulted in a unified and consistent gravity database with 34,683 point gravity values in GRS80 [
22], IGSN71 [
23], and the tide free system [
24,
25] (see black dots in
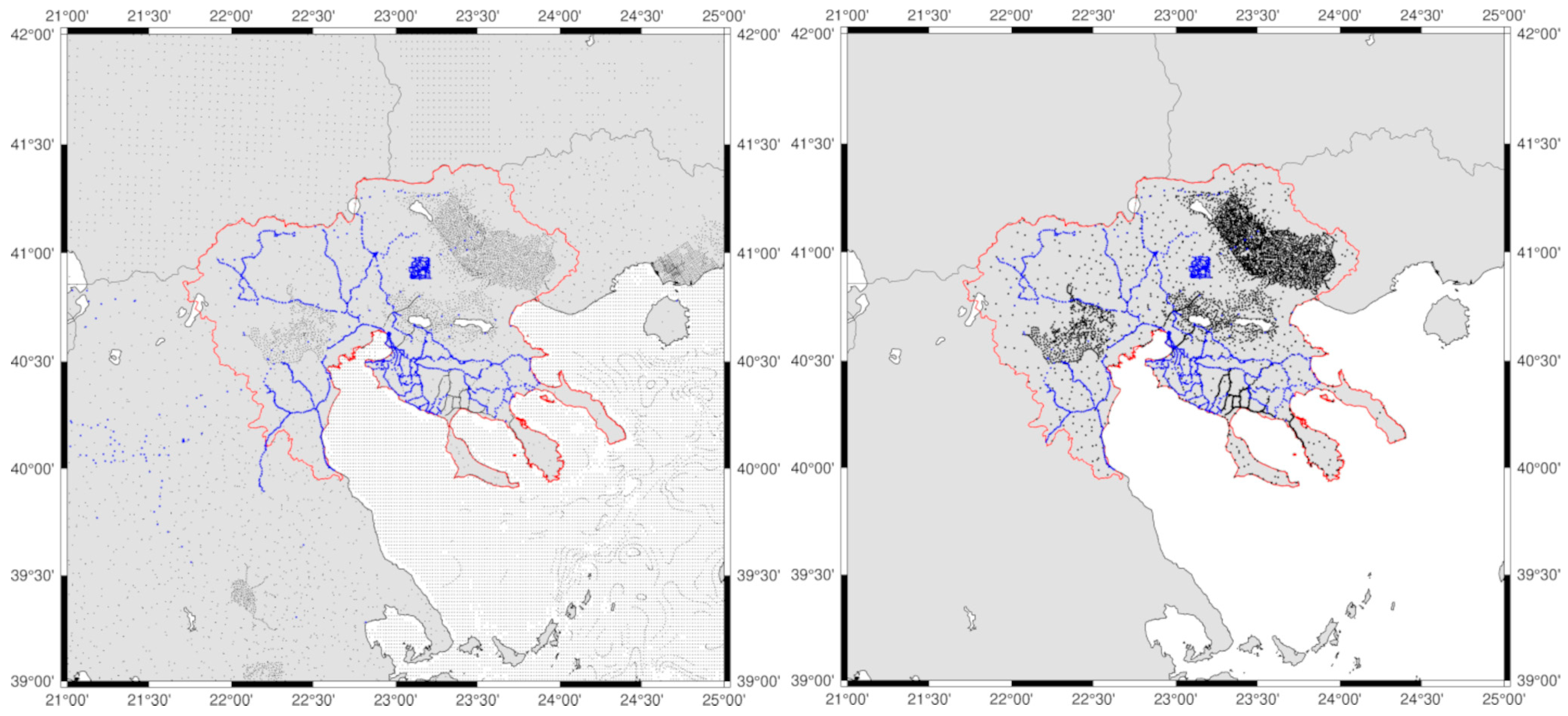
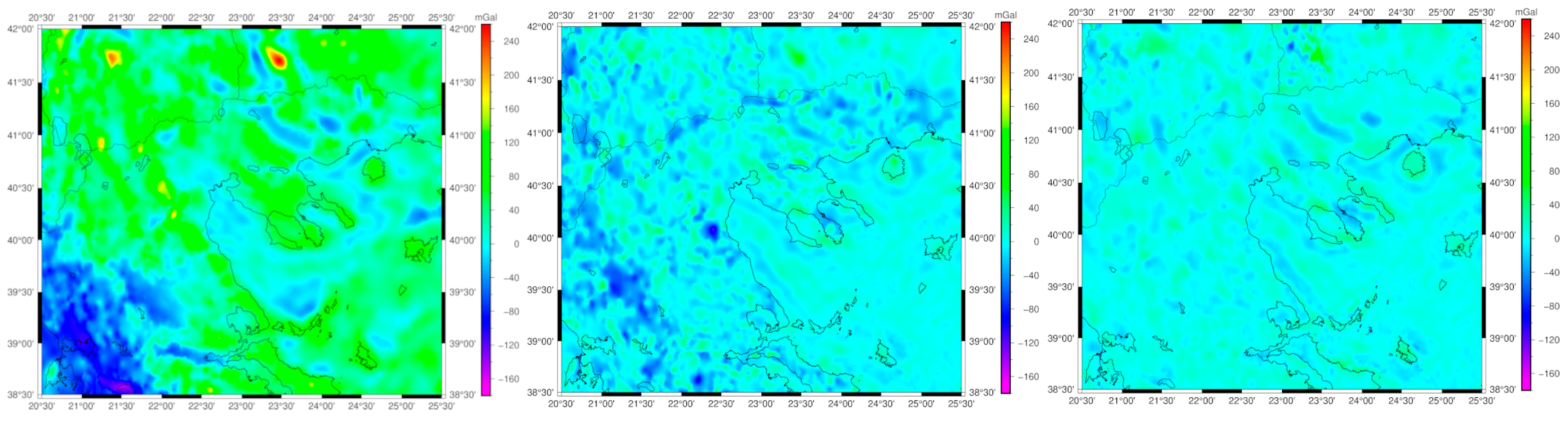
Figure 3).
As it can be seen from
Figure 3, the available land gravity database has an overall good distribution in the eastern and central-west part of the area, but significant voids in the Chalkidiki peninsula, the north-west part, and close to Olympus Mountain. Given this, relative gravity surveys have been planned to cover, as homogeneously as possible, the entire study region, with a particular focus on areas with significant topographic gradients and around the established CORS stations. For the data collection, GravLab’s Scrintex CG-5 relative gravity meter (S/N 070540268) has been used, which is one of the most well-established instruments for gravity surveys with a reading resolution of less than 1 μGal, an accuracy of less than 5 μGal, and a residual drift of less than 20 μGal per day [
26,
27]. As in all relative gravity campaigns intended to determine absolute gravity values at newly established densification points, a reference point with a known absolute gravity value is essential. This ensures that the calculated gravity differences, relative to a known location, can be used to obtain absolute gravity values. In all gravity campaigns, GravLab’s AUT1 absolute gravity station has been used as reference [
5,
6]. The AUT1 station is situated on the Aristotle University campus premises and was established by GravLab using the Microg-Lacoste A10 (#027) absolute gravity meter, with a recorded gravity value of 980,276,178.42 ± 10.05 μGal. If we assume that the absolute gravity value at AUT1 is determined and denoted with
, then, given relative gravity observations
between points AUT1 and B, we can estimate the gravity value at the new point B as follows:
Our approach to campaign planning followed a round-trip method, always starting from the AUT1 reference station, occupying a number of densification points, and then completing the campaign at the AUT1 station. This strategy enables the adjustment of residual drift during the day and its distribution across the measured points of that day. Prior to the campaign, the instrument was calibrated for linear drift,
X-axis and
Y-axis offsets, temperature coefficient, and linear drift. To calculate the daily residual drift, given that
m points were measured during the survey, the residual drift was estimated using observations at the initial point AUT1, after corrections for tides, air pressure, height reduction, and temperature, as follows [
5]:
where
is the residual drift, and
and
are the gravity observations in mGal at AUT1 at the end of the survey (time
) and the beginning of the survey
. We should mention here that the drift after Equation (2) is estimated in
, so that after its estimation, the observed gravity difference between station
and the initial point
is
where
and
are the observed gravity values at point AUT1, which is the reference station, and
Pi, which is the newly established point. They can be corrected for the residual drift as follows:
As a result, the final gravity value after the correction for point
i can be estimated as
where
is the estimated gravity at point
and
is the known gravity at the base AUT1. The error at each new point can be calculated through error propagation using the following equation:
where
is the accuracy of gravity at point
,
is the determined accuracy of
, and
is the propagated error of every gravity observation with the CG-5 (both at the starting point and new points). Considering uncorrelated errors, Equation (6) can be rewritten as
where
and
are the standard deviations estimated during the relative gravity measurements at the new gravity points.
The relative gravity campaigns have started at the end of August 2022 and finished by the end of May 2023, resulting in a total of 85 days of measurements. The instrument linear drift was estimated every month, 9 times in total, at the premises of the Thessaloniki Seismological Station [
28] (TSS). TSS was specifically selected as it offers increased stability and negligible seismic noise due to the bedrock that the station is built on and the existence of a concrete slab that hosts the TSS instruments. The estimation of the drift was obtained by performing cyclic 60 sec measurements, with a relaxation interval between measurements at 5 s, while each measurement session for drift determination lasted 24 h. After this, the estimated stationary drift value was used to adjust the drift correction factor, previously determined on the instrument according to the CG-5 user manual [
29]. For each campaign, the next criteria were followed:
- o
The CG-5 was leveled with an accuracy of >10 arcseconds.
- o
The CG-5 height was measured with an accuracy of 1 mm on all three sides.
- o
Each new point was marked.
- o
At each occupation, the CG-5 was left undisturbed for 10 min to allow the measuring system to settle and reach the ambient temperature.
- o
At each point, 6 measurement cycles were performed to have at least 5 valid measurement cycles at the time of the measurements.
- o
During measurement at each point, the following criteria were satisfied:
The ambient temperature, air pressure, and height of the gravimeter have been measured.
The leveling of the gravimeter was continuously monitored to not exceed 10 s.
At points where the difference in readings due to disturbances was greater than 15 μGal, the measurements were repeated.
The CG-5 was protected with an umbrella from sun and wind during the measurement process.
In total, 2490 new gravity data were established and measured with their 3D location being determined with network real-time kinematic (NRTK) GNSS measurements. At every point, 10 epochs of 1 s GNSS observations have been collected using the virtual reference station (VRS) employing the Hellenic Positioning System service (HEPOS) [
30]. Error propagation has been carried out with Equation (9) for all 2490 newly acquired gravity benchmarks, where, given the accuracy of the absolute gravity value at AUT1 (
), a mean accuracy at the 26.21 μGal level and a standard deviation at the 4.36 μGal have been achieved.
After determining the gravity value at each location, gravity anomalies
and free-air gravity anomalies
have been calculated. The gravity anomaly at each point was determined as follows:
where
stands for the normal gravity in the GRS80 ellipsoid evaluated with Somigliana’s formula [
31], while free-air gravity anomalies were estimated through the mean normal gradient of
:
In Equation (9),
is the orthometric height of the point location referring to the TG station at Piraeus harbor where the zero level for Hellenic vertical datum is located [
32,
33,
34].
After finishing the data processing, the final gravity values and their accuracy at the new points were estimated. The final gravity database (see
Figure 3) utilized consisted of 38,973 point free-air gravity anomalies, comprising 36,483 historical (black dots) measurements and 2490 newly (blue dots) collected observations with their statistics reported in
Table 1. Within the specific study area of the RCM (see
Figure 3, right panel), 6993 land gravity observations were employed, which included 5100 historical (black dots) measurements and 1893 newly (blue dots) collected data.
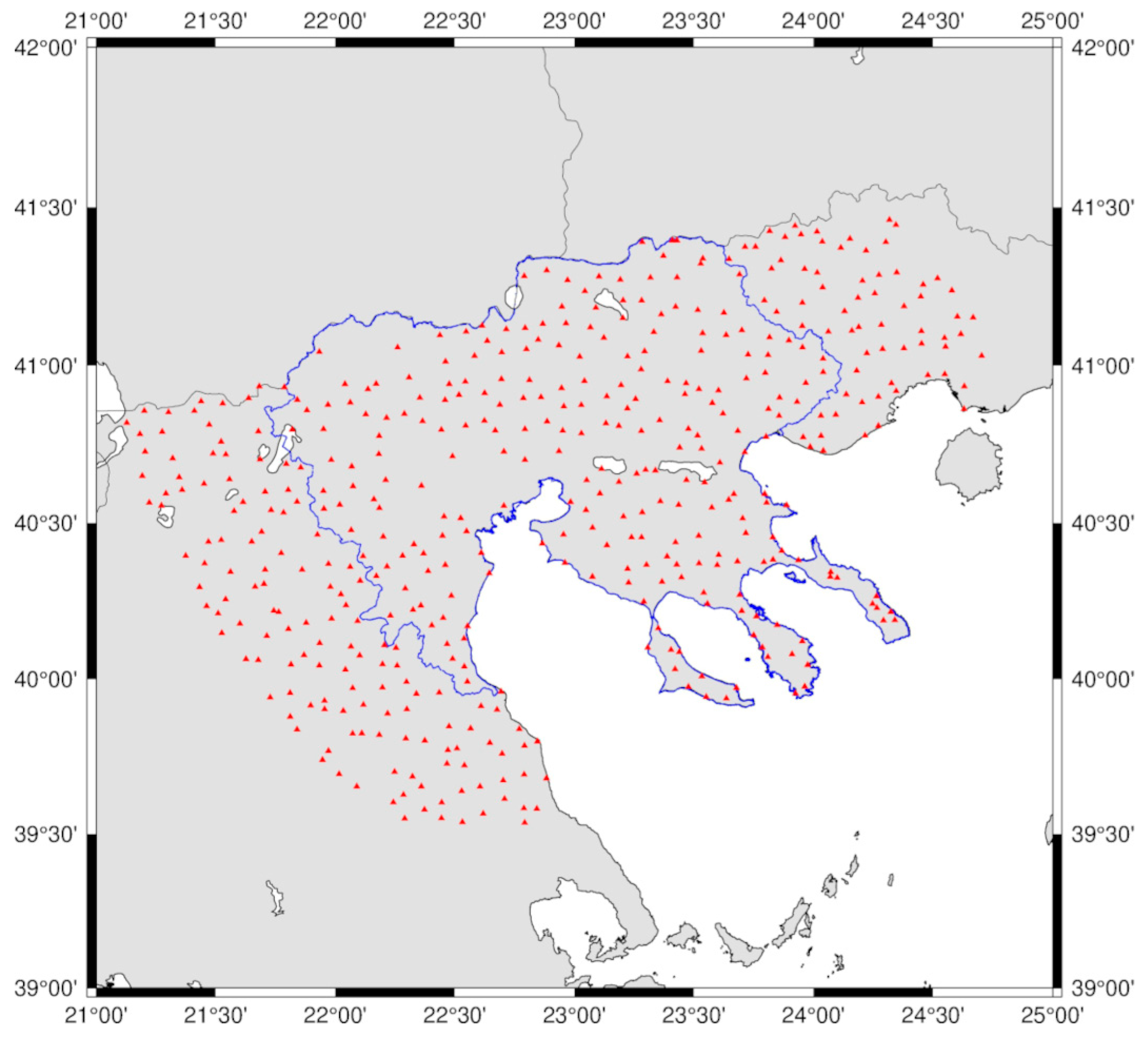
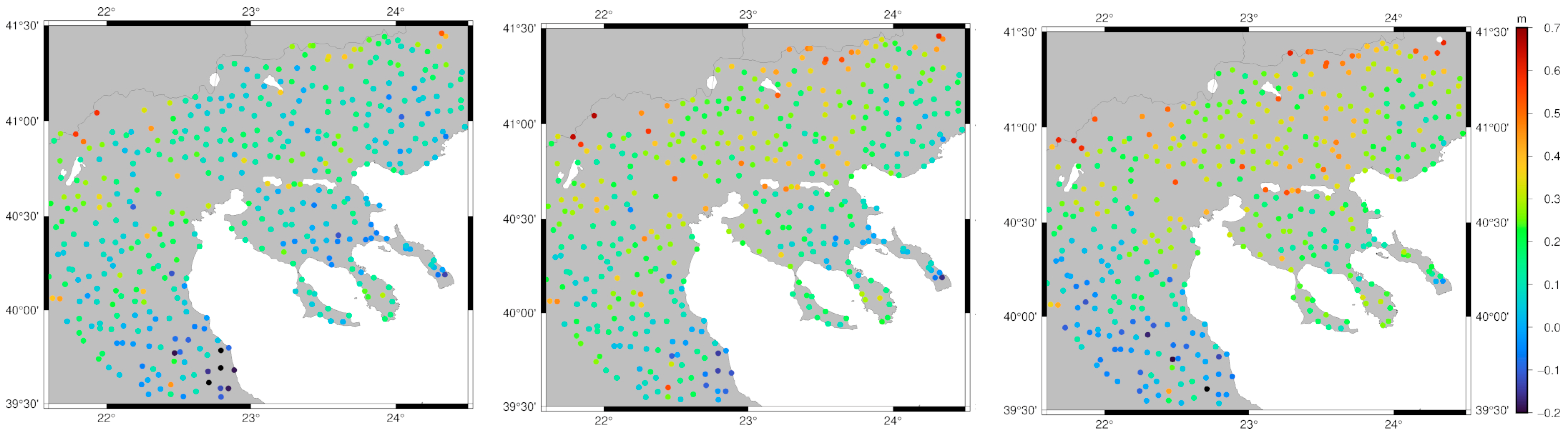
For the validation of the final geoid model developed, 462 GNSS/leveling BMs located within or up to 50 km outside the main focus area of the RCM were used (see
Figure 4). The ellipsoidal heights of these BMs have been determined as part of the Hellenic Cadastre project by Ktimatologio S.A., which conducted a nationwide GNSS survey to gather static GNSS data on geodetic BMs, achieving a mean accuracy of 2–5 cm [
33]. The orthometric heights, at the BMs provided by the HMGS, are formally reported to have an accuracy of 1–2 cm; however, their actual accuracy remains largely uncertain [
33,
34].
Table 2 tabulates the statistics of the 462 GNSS/leveling BMs, while it should be mentioned that the geoid heights mentioned in this table are formed as
; hence, these represent a geometric computation of geoid heights and not gravimetric ones.