Automatic Rooftop Solar Panel Recognition from UAV LiDAR Data Using Deep Learning and Geometric Feature Analysis
Abstract
Highlights
- Developed a Machine Learning approach using drone-based LiDAR point clouds to classify rooftop solar panels from building surfaces.
- Achieved very high classification accuracy, with F1 scores of 99% for commercial-scale panels and 95–96% for residential-scale panels.
- LiDAR geometry and reflectance features enable reliable rooftop solar detection, overcoming limitations of imagery-based methods that are often obstructed by trees, shadows, and roof orientation.
- Provides a scalable approach for applying ML-based classification to unlabelled urban datasets, supporting solar energy mapping and planning.
Abstract
1. Introduction
- Evaluate the effectiveness of geometric and spectral features for differentiating rooftop solar panels from rooftop surfaces using LiDAR data.
- Compare the performance of two MLP-based deep learning models, developed using PyTorch and Scikit-learn, for supervised classification of roof and solar panels.
- Assess classification performance across two urban datasets (UniSQ and Newcastle), with UniSQ having commercial structures and Newcastle being primarily residential, using evaluation measures such as F1-score and overall accuracy.
2. Materials and Methods
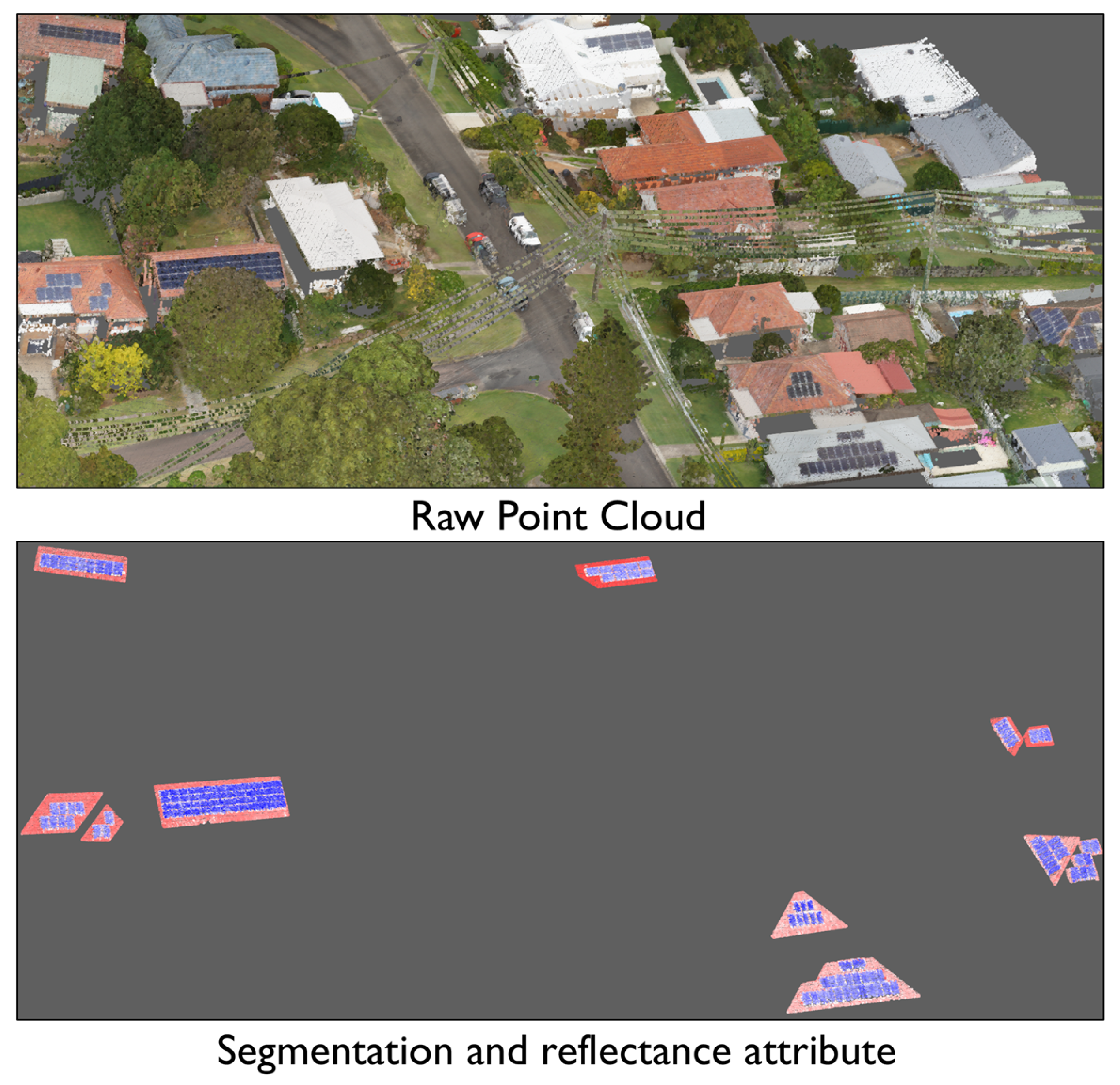
2.1. Datasets
2.1.1. UniSQ Dataset
2.1.2. Newcastle Dataset
2.2. Geometric Feature Selection
Histogram Overlap and KL Divergence
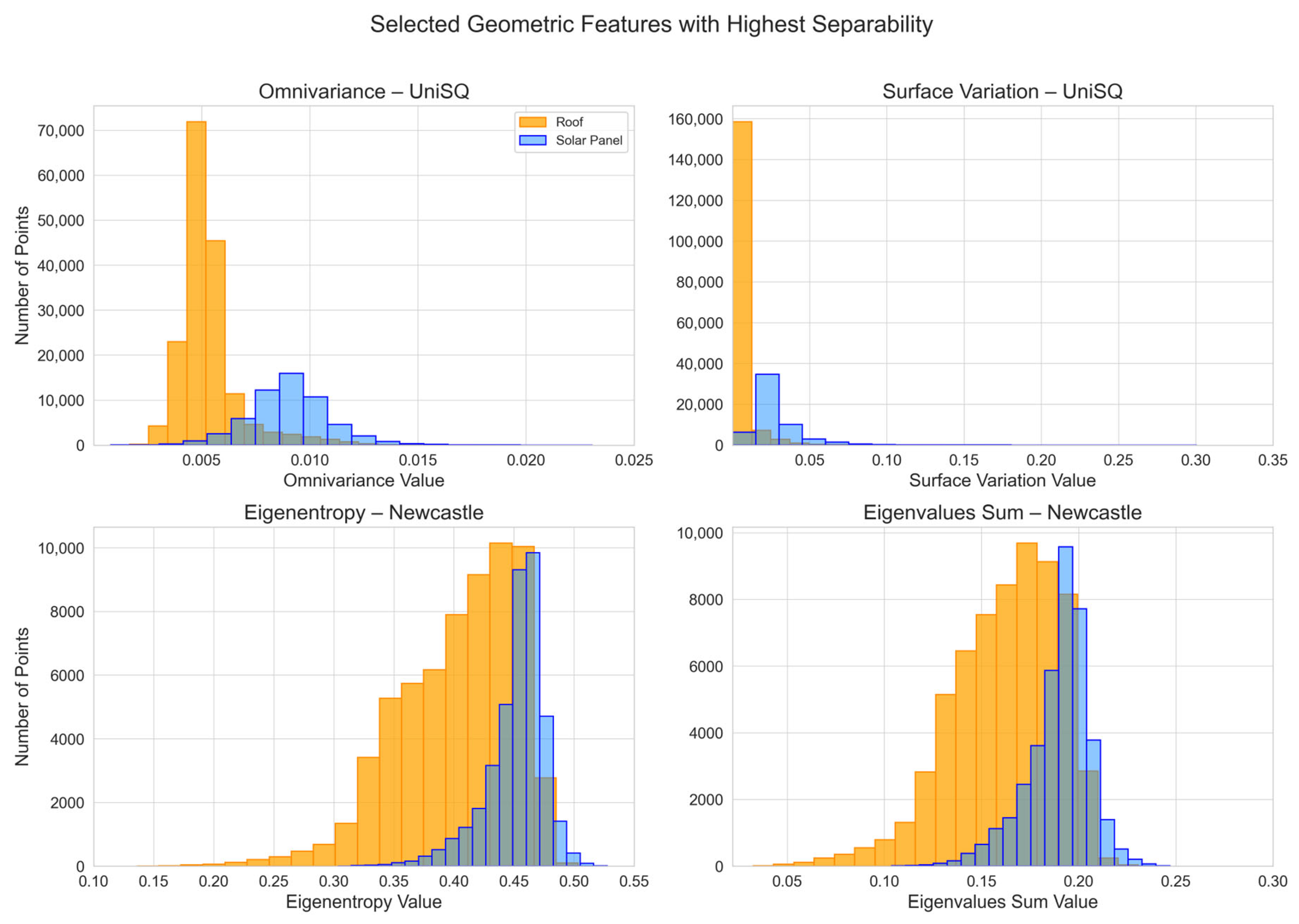
2.3. Selected Geometric Features
2.3.1. UniSQ Feature Selection
2.3.2. Newcastle Feature Selection
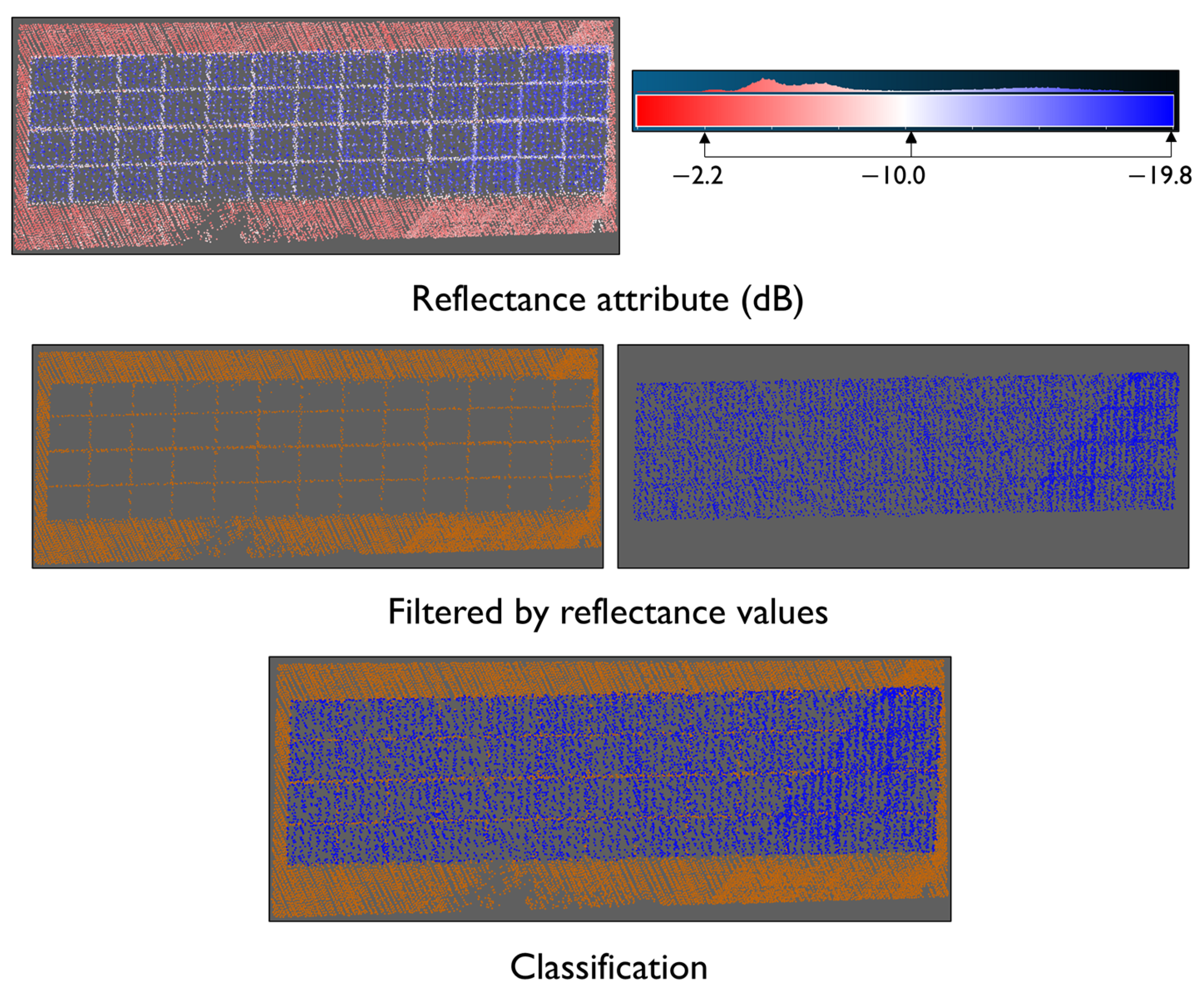
2.3.3. RGB Analysis
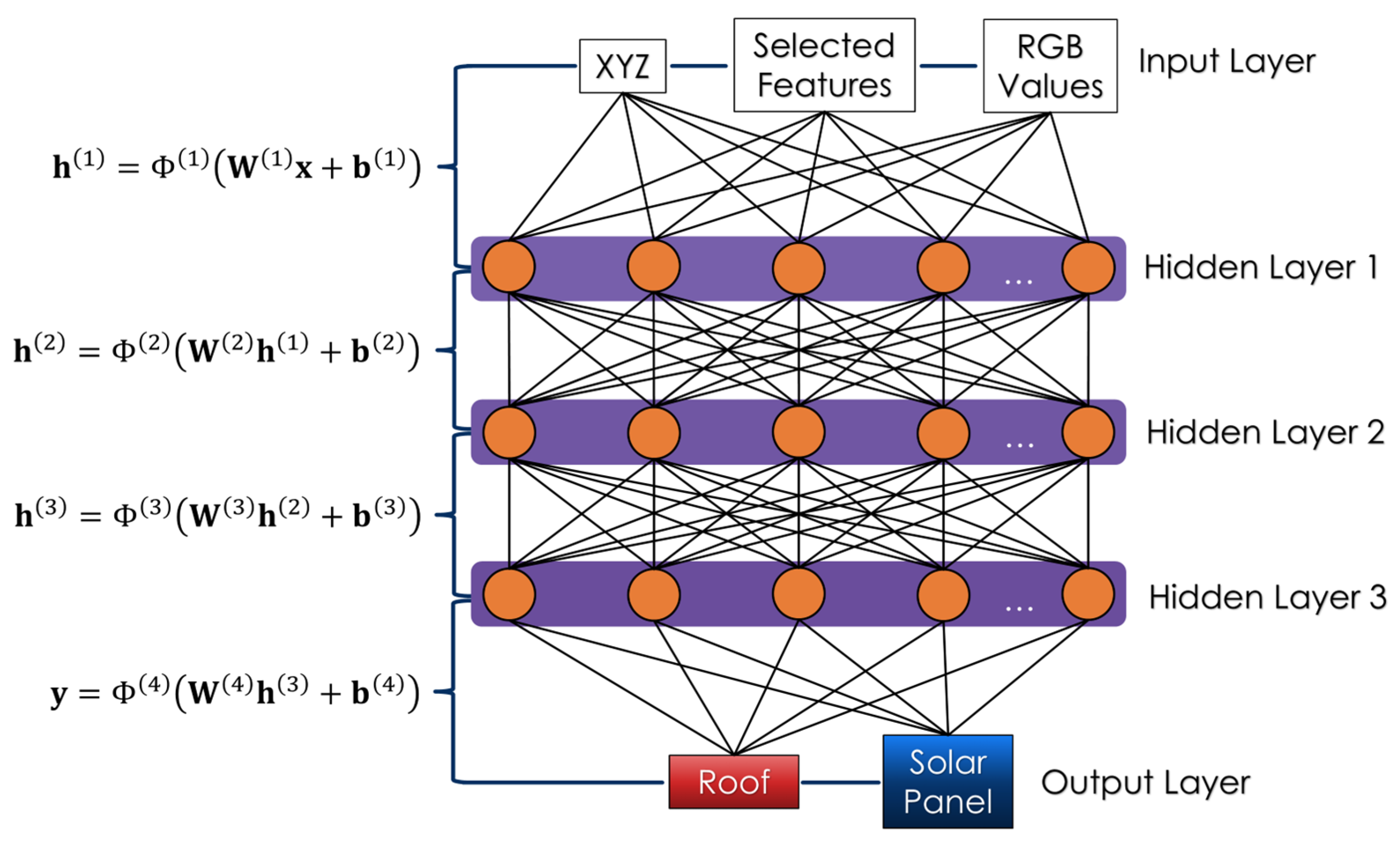
2.4. MLP Workflow
2.4.1. MLP Configuration
2.4.2. Validation Strategy
- True Positive (TP): Solar panel points correctly classified as class 1.
- True Negative (TN): Roof points correctly classified as class 0.
- False Positive (FP): Roof points incorrectly classified as panels.
- False Negative (FN): Panel points incorrectly classified as roof.
3. Results
3.1. Feature Performance and Histogram Analysis
3.1.1. Geometric Features Histogram Analysis
3.1.2. RGB Channel Analysis
3.2. Classification Performance
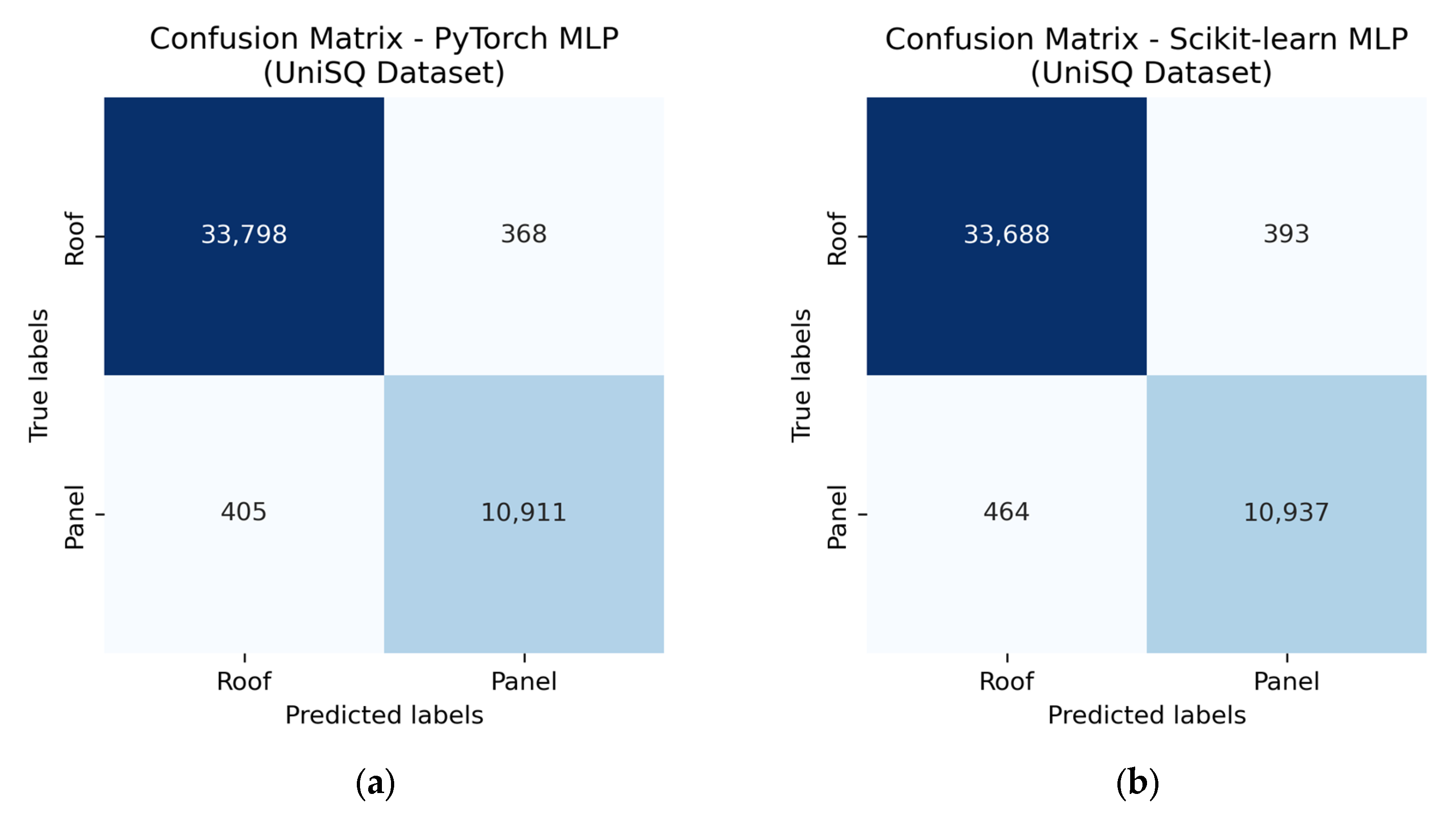
3.2.1. Results—PyTorch and Scikit-Learn Models—UniSQ Dataset
3.2.2. Results—PyTorch and Scikit-Learn Models—Newcastle Dataset
4. Discussion
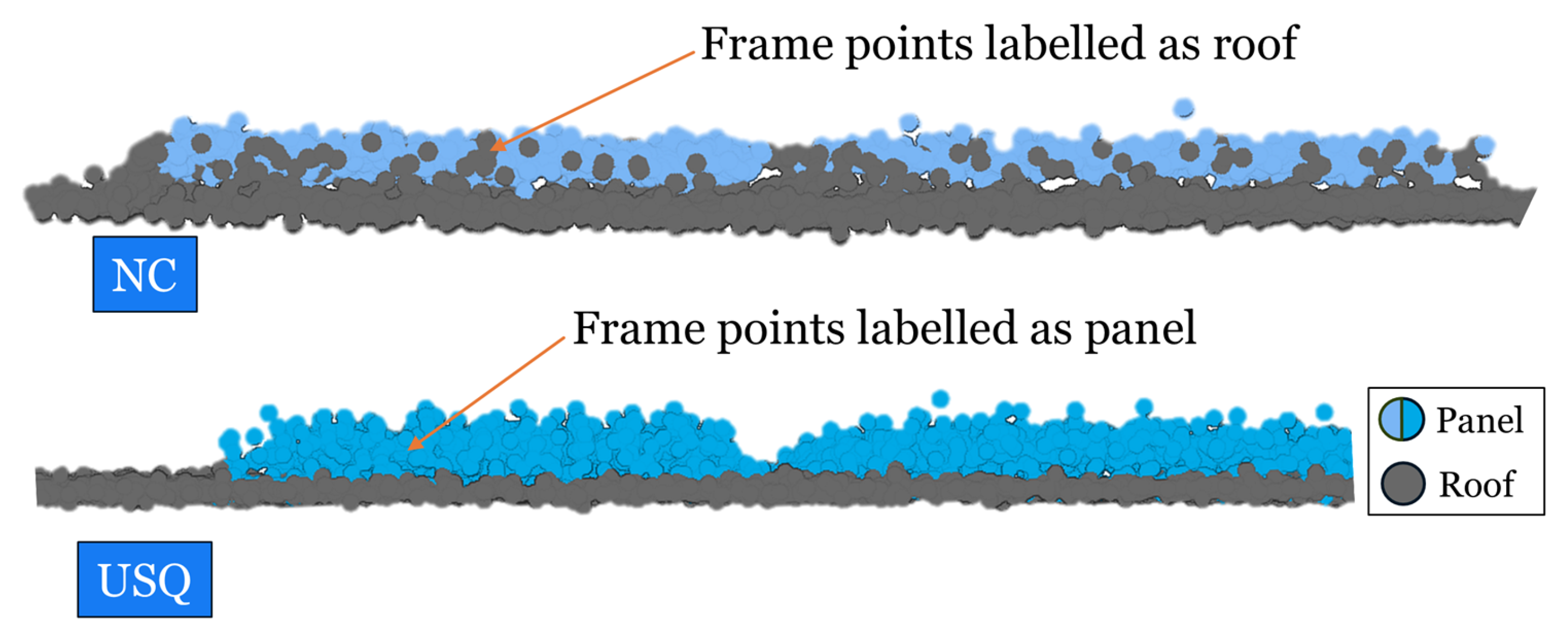
4.1. Dataset Quality
4.2. Model Performance and Feature Relevance
5. Conclusions
Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McTegg, S.J.; Tarsha Kurdi, F.; Simmons, S.; Gharineiat, Z. Comparative approach of unmanned aerial vehicle restrictions in controlled airspaces. Remote Sens. 2022, 14, 822. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Amakhchan, W.; Gharineiat, Z.; Boulaassal, H.; El Kharki, O. Contribution of geometric feature analysis for deep learning classification algorithms of urban LiDAR data. Sensors 2023, 23, 7360. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Garg, R.D. Building footprint extraction from aerial photogrammetric point cloud data using its geometric features. J. Build. Eng. 2023, 76, 107387. [Google Scholar] [CrossRef]
- Pellerin Le Bas, X.; Froideval, L.; Mouko, A.; Conessa, C.; Benoit, L.; Perez, L. A New Open-Source Software to Help Design Models for Automatic 3D Point Cloud Classification in Coastal Studies. Remote Sens. 2024, 16, 2891. [Google Scholar] [CrossRef]
- Hosseini, M.; Bagheri, H. Improving the resolution of solar energy potential maps derived from global DSMs for rooftop solar panel placement using deep learning. Heliyon 2025, 11, e41193. [Google Scholar] [CrossRef]
- Yadav, Y.; Harshit; Kushwaha, S.K.P.; Zlatanova, S.; Boccardo, P.; Jain, K. Assessing Photo-Voltaic Potential in Urban Environments: A Comparative Study between Aerial Photogrammetry and LiDAR Technologies. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 48, 533–539. [Google Scholar] [CrossRef]
- Jiang, H.; Yao, L.; Lu, N.; Qin, J.; Liu, T.; Liu, Y.; Zhou, C. Multi-resolution dataset for photovoltaic panel segmentation from satellite and aerial imagery. Earth Syst. Sci. Data Discuss. 2021, 13, 5389–5401. [Google Scholar] [CrossRef]
- Clark, C.N.; Pacifici, F. A solar panel dataset of very high resolution satellite imagery to support the Sustainable Development Goals. Sci. Data 2023, 10, 636. [Google Scholar] [CrossRef]
- Duran, Z.; Ozcan, K.; Atik, M.E. Classification of photogrammetric and airborne lidar point clouds using machine learning algorithms. Drones 2021, 5, 104. [Google Scholar] [CrossRef]
- Amakhchan, W.; Kurdi, F.T.; Gharineiat, Z.; Boulaassal, H.; El Kharki, O. Classification of Forest LiDAR Data Using Deep Learning Pipeline Algorithm and Geometric Feature Analysis. Int. J. Environ. Sci. Nat. Resour. 2023, 32, 556340. [Google Scholar] [CrossRef]
- Kushwaha, S.; Harshit; Jain, K. Solar Roof Panel Extraction from UAV Photogrammetric Point Cloud. In Proceedings of the International Conference on Unmanned Aerial System in Geomatics, Roorkee, India, 2–4 April 2021; pp. 173–185. [Google Scholar]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Extended RANSAC algorithm for automatic detection of building roof planes from LiDAR data. Photogramm. J. Finl. 2008, 21, 97–109. [Google Scholar]
- RIEGL. LAS Extrabytes Implementation in RIEGL Software; RIEGL Laser Measurement Systems GmbH: Horn, Austria, 2019; p. 12. [Google Scholar]
- Weinmann, M.; Jutzi, B.; Mallet, C. Feature relevance assessment for the semantic interpretation of 3D point cloud data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 313–318. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Contour detection in unstructured 3D point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1610–1618. [Google Scholar]
- Thomas, H.; Goulette, F.; Deschaud, J.-E.; Marcotegui, B.; LeGall, Y. Semantic classification of 3D point clouds with multiscale spherical neighborhoods. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 390–398. [Google Scholar]
- Demantké, J.; Vallet, B.; Paparoditis, N. Streamed vertical rectangle detection in terrestrial laser scans for facade database production. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 99–104. [Google Scholar] [CrossRef]
- CloudCompare. Roughness. Available online: https://www.cloudcompare.org/doc/wiki/index.php/Roughness (accessed on 27 March 2025).
- Swain, M.J.; Ballard, D.H. Color indexing. Int. J. Comput. Vis. 1991, 7, 11–32. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Dehbi, Y.; Koppers, S.; Plümer, L. Probability Density Based Classification and Reconstruction of Roof Structures from 3D Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 177–184. [Google Scholar] [CrossRef]
- Cardoso, A.; Jurado-Rodríguez, D.; López, A.; Ramos, M.I.; Jurado, J.M. Automated detection and tracking of photovoltaic modules from 3D remote sensing data. Appl. Energy 2024, 367, 123242. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Scikit-Learn. Neural Networks—Supervised. Available online: https://scikit-learn.org/stable/modules/neural_networks_supervised.html (accessed on 6 May 2025).
- Paszke, A. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Amakhchan, W.; Tarsha Kurdi, F.; Gharineiat, Z.; Boulaassal, H.; El Kharki, O. Automatic filtering of LiDAR building point cloud using multilayer perceptron Neuron Network. In Proceedings of the 3rd International Conference on Big Data and Machine Learning (BML22’), Istanbul, Turkey, 23–24 May 2022. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.M.I.T. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Grosse, R. Multilayer Perceptrons (Lecture 5). Available online: https://www.cs.toronto.edu/~rgrosse/courses/csc321_2018/readings/L05%20Multilayer%20Perceptrons.pdf (accessed on 20 June 2025).
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- PyTorch-Developers. CrossEntropyLoss-Pytorch Documentation. Available online: https://docs.pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html (accessed on 20 June 2025).
- Scikit-Learn-Developers. MLPClassifier—Multi-Layer Perceptron Classifier. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html (accessed on 20 June 2025).
- Wu, H.; Shen, G.; Lin, X.; Li, M.; Zhang, B.; Li, C.Z. Screening patents of ICT in construction using deep learning and NLP techniques. Eng. Constr. Archit. Manag. 2020, 27, 1891–1912. [Google Scholar] [CrossRef]
- Li Persson, L. Automatic Processing of LiDAR Point Cloud Data Captured by Drones; Digitala Vetenskapliga Arkivet (DiVA): Uppsala, Sweden, 2023. [Google Scholar]
- Zhou, K.; Lindenbergh, R.; Gorte, B.; Zlatanova, S. LiDAR-guided dense matching for detecting changes and updating of buildings in Airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 200–213. [Google Scholar] [CrossRef]
- Pena Pereira, S.; Rafiee, A.; Lhermitte, S. Automated rooftop solar panel detection through Convolutional Neural Networks. Can. J. Remote Sens. 2024, 50, 2363236. [Google Scholar] [CrossRef]
- Tiwari, A.; Meir, I.A.; Karnieli, A. Object-based image procedures for assessing the solar energy photovoltaic potential of heterogeneous rooftops using airborne LiDAR and orthophoto. Remote Sens. 2020, 12, 223. [Google Scholar] [CrossRef]






| Feature (UniSQ) | Histogram Overlap | KL Divergence (Roof||Panel) | KL Divergence (Panel||Roof) | Acceptance |
|---|---|---|---|---|
| Eigenvalues Sum | 0.8 | 0.1 | 0.2 | No |
| Omnivariance | 0.2 | 2.4 | 2.1 | Yes |
| Eigenentropy | 0.8 | 0.1 | 0.2 | No |
| Anisotropy | 0.2 | 1.5 | 2.0 | Yes |
| Planarity | 0.6 | 0.6 | 0.4 | Yes |
| Linearity | 0.7 | 0.3 | 0.2 | No |
| PCA1 | 0.8 | 0.1 | 0.1 | No |
| PCA2 | 0.7 | 0.5 | 0.3 | No |
| Surface Variation | 0.1 | 3.5 | 2.4 | Yes |
| Sphericity | 0.2 | 1.5 | 2.0 | Yes |
| Verticality | 0.3 | 1.3 | 2.7 | Yes |
| Roughness | 0.6 | 0.5 | 0.8 | Yes |
| Feature (Newcastle) | Histogram Overlap | KL Divergence (Roof||Panel) | KL Divergence (Panel||Roof) | Acceptance |
|---|---|---|---|---|
| Eigenvalues Sum | 0.5 | 1.4 | 0.7 | Yes |
| Omnivariance | 0.6 | 3.3 | 0.5 | No |
| Eigenentropy | 0.5 | 1.5 | 0.8 | Yes |
| Anisotropy | 0.7 | 0.4 | 0.2 | No |
| Planarity | 0.6 | 0.7 | 0.5 | Yes |
| Linearity | 0.6 | 0.8 | 0.5 | Yes |
| PCA1 | 0.6 | 0.8 | 0.5 | Yes |
| PCA2 | 0.6 | 0.8 | 0.5 | Yes |
| Surface Variation | 0.8 | 0.3 | 0.2 | No |
| Sphericity | 0.7 | 0.4 | 0.2 | No |
| Verticality | 0.8 | 0.4 | 0.1 | No |
| Roughness | 0.6 | 0.4 | 0.5 | Yes |
| Parameters | PyTorch Model | Scikit-Learn Model |
|---|---|---|
| Execution Mode | GPU | CPU |
| Architecture | MLP (3 hidden layers) | MLP (3 hidden layers) |
| Neuron Structure | 100→100→50 | 100→100→50 |
| Activation Function | ReLU | ReLU |
| Batch Normalisation | BatchNorm1d | Not available |
| Learning Rate Schedule | StepLR (Halved every 10 epochs) | Constant learning rate |
| Optimiser | Adam | Adam |
| Training Epochs | 50 | 50 |
| Data Split | 70% Training 10% Validation 20% Testing | |
| Number of Features | 13 (UniSQ)/12 (Newcastle) | 13 (UniSQ)/12 (Newcastle) |
| Batch Size | 256 | 256 |
| Average Training Time | ~109 s (UniSQ)/~50 s (Newcastle) | ~110 s (UniSQ)/~47 s (Newcastle) |
| Evaluation | Accuracy, Precision, Recall, F1 Score | |
| Dataset | Feature | Histogram Overlap | KL Divergence (Roof||Panel) | KL Divergence (Panel||Roof) | Acceptance |
|---|---|---|---|---|---|
| Red | 0.4 | 0.8 | 1.2 | Yes | |
| UniSQ | Green | 0.4 | 0.9 | 1.1 | Yes |
| Blue | 0.3 | 1.1 | 1.2 | Yes | |
| Red | 0.3 | 3.3 | 1.7 | Yes | |
| Newcastle | Green | 0.5 | 1.6 | 0.8 | Yes |
| Blue | 0.7 | 1.1 | 0.3 | No |
| Class | Measure | PyTorch | Scikit-Learn |
|---|---|---|---|
| Precision | 0.99 | 0.99 | |
| Roof (0) | Recall | 0.99 | 0.99 |
| F1-Score | 0.99 | 0.99 | |
| Precision | 0.97 | 0.97 | |
| Solar Panel (1) | Recall | 0.96 | 0.96 |
| F1-Score | 0.97 | 0.96 |
| Class | Measure | PyTorch | Scikit-Learn |
|---|---|---|---|
| Precision | 0.97 | 0.97 | |
| Roof (0) | Recall | 0.95 | 0.93 |
| F1-Score | 0.96 | 0.95 | |
| Precision | 0.91 | 0.90 | |
| Solar Panel (1) | Recall | 0.95 | 0.95 |
| F1-Score | 0.93 | 0.92 |
| Measure (UniSQ) | PyTorch | PyTorch (No RGB) | Difference | Scikit-Learn | Scikit-Learn (No RGB) | Difference |
|---|---|---|---|---|---|---|
| True Positives (TP) | 10,911 | 10,937 | 26 | 10,831 | 10,833 | 2 |
| False Negatives (FN) | 405 | 464 | 59 | 485 | 568 | 83 |
| True Negatives (TN) | 33,798 | 33,688 | 110 | 33,792 | 33,665 | 127 |
| False Positives (FP) | 368 | 393 | 25 | 374 | 416 | 42 |
| Accuracy (%) | 98.30 | 98.12 | −0.18 | 98.11 | 97.84 | −0.27 |
| Measure (Newcastle) | PyTorch | PyTorch (No Red/Green) | Difference | Scikit-Learn | Scikit-Learn (No Red/Green) | Difference |
|---|---|---|---|---|---|---|
| True Positives (TP) | 7412 | 7388 | 24 | 7481 | 7037 | 444 |
| False Negatives (FN) | 415 | 439 | 24 | 422 | 866 | 444 |
| True Negatives (TN) | 12,095 | 11,498 | 597 | 11,864 | 11,470 | 394 |
| False Positives (FP) | 696 | 1293 | 597 | 851 | 1245 | 394 |
| Accuracy (%) | 94.61 | 91.60 | −3.01 | 93.83 | 89.76 | −4.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coglan, J.; Gharineiat, Z.; Tarsha Kurdi, F. Automatic Rooftop Solar Panel Recognition from UAV LiDAR Data Using Deep Learning and Geometric Feature Analysis. Remote Sens. 2025, 17, 3389. https://doi.org/10.3390/rs17193389
Coglan J, Gharineiat Z, Tarsha Kurdi F. Automatic Rooftop Solar Panel Recognition from UAV LiDAR Data Using Deep Learning and Geometric Feature Analysis. Remote Sensing. 2025; 17(19):3389. https://doi.org/10.3390/rs17193389
Chicago/Turabian StyleCoglan, Joel, Zahra Gharineiat, and Fayez Tarsha Kurdi. 2025. "Automatic Rooftop Solar Panel Recognition from UAV LiDAR Data Using Deep Learning and Geometric Feature Analysis" Remote Sensing 17, no. 19: 3389. https://doi.org/10.3390/rs17193389
APA StyleCoglan, J., Gharineiat, Z., & Tarsha Kurdi, F. (2025). Automatic Rooftop Solar Panel Recognition from UAV LiDAR Data Using Deep Learning and Geometric Feature Analysis. Remote Sensing, 17(19), 3389. https://doi.org/10.3390/rs17193389







